- 1School of Advanced Sciences, Vellore Institute of Technology, Chennai, India
- 2Department of Mathematics, Loyola College, Chennai, India
Topological descriptors are widely utilized as graph theoretical measures for evaluating the physicochemical properties of organic frameworks by examining their molecular structures. Our current research validates the usage of topological descriptors in studying frameworks such as metal-butylated hydroxytoluene, NH-substituted coronene transition metal, transition metal-phthalocyanine, and conductive metal-octa amino phthalocyanine. These metal organic frameworks are crucial in nanoscale research for their porosity, adaptability, and conductivity, making them essential for advanced materials and modern technology. In this study, we provide the topological and entropy characterizations of these frameworks by employing robust reverse degree based descriptors, which offer insightful information on structural complexities. This structural information is applied to predict the graph energy of the considered metal organic frameworks using statistical regression models.
1 Introduction
Two-dimensional metal organic frameworks (MOFs) are revolutionizing nanoscale research with their unique blend of inorganic and organic components, offering exceptional advantages like porosity and tunability. These porous crystals feature cage-like architectures formed by aromatic organic moieties and square-planar metal ions, finding diverse applications in gas catalysis, drug delivery, sensors, optoelectronics, storage, and adsorption (Kinoshita et al., 1959; Lee et al., 2009; Horcajada et al., 2008; Murray et al., 2009). Metal-organic surfaces based on metal-butylated hydroxytoluene (MBHT) exhibit promising electronic and magnetic properties, particularly for transition metals like M = {Co, Fe, Mn, Cr} (Clough et al., 2015; Chakravarty et al., 2016a). Among MBHT-derived materials, CoBHT, FeBHT, and MnBHT display planar ferromagnetic half-metallism, while CrBHT possesses a spin-frustrated kagome lattice leading to antiferromagnetic semimetallic behavior. These frameworks exhibit high sensitivity towards gas molecules like carbon monoxide, altering their electronic and magnetic properties significantly upon adsorption. A coronene molecule substituted with an
Transition metal-phthalocyanine (TM-Pc) based MOFs exhibit captivating two-dimensional structures with distinctive electronic and magnetic features. TM-Pc is derived from the transition metal-tetracyanobenzene (TM-TCNB) framework through benzene ring rotation and on-surface polymerization, involving transition metals TM = {Ti, V, Cr, Co, Ni, Cu, Zn} (Mabrouk and Hayn, 2015). TM-Pc demonstrates superior stability over TM-TCNB by approximately
In mathematical chemistry, graph theoretical techniques are employed to study molecular structures, properties, and reactions. Topological descriptors play a crucial role in this field, serving as essential tools for analyzing complex molecular systems. These descriptors are numerical values derived from molecular structure connectivity, representing the positions of atoms and bonds within the molecule. The widespread use of distance-based indices like the Wiener index and degree-based indices such as the Zagreb indices has significantly advanced the field of topological indices (Wiener, 1947; Gutman and Trinajstić, 1972; Raza et al., 2023a; Arockiaraj et al., 2023a). Applications of degree and distance-based topological indices are creating new possibilities in drug discovery and neural network research (Zhang et al., 2022; Zhang et al., 2024; Arockiaraj et al., 2024a). In particular, the robust refinement of reverse degree indices significantly improved the correlation with the physicochemical properties of molecules and was applied to drug compounds related to coronavirus, blood cancer and cardiovascular drug compounds (Arockiaraj et al., 2023b; Arockiaraj et al., 2023c; Arockiaraj et al., 2024b). This approach develops various graph degree sequences with variable parameters, enhancing statistical models for the considered datasets. In this work, we implement the modified reverse degree method to the recently introduced hybrid topological indices (Arockiaraj et al., 2023a).
Structural entropy, introduced by Shannon, deals with unpredictability or uncertainty in datasets (Shannon, 1948; Arockiaraj et al., 2023d). It indicates micro-state diversity, reflecting various positions in a system with atoms and molecules. Higher entropy within a system implies greater disorder, signifying more potential micro-states. This principle extends to chemical structures, providing a valuable tool for analyzing their stability and structural data (Dehmer, 2008). Graph entropies link probability distributions to graph elements, such as vertices and edges, aiding in comprehensive graph analysis. These explorations aid in predicting the graph energies of MOFs using graph theoretical and statistical techniques.
Recent studies on degree-based descriptors have been instrumental in analyzing various metal organic and covalent organic frameworks, such as phthalocyanine frameworks, trans-Pd–(NH2)S lattice, metal butylated hydroxytoluene frameworks, and FeTPyP-CO MOFs (Nadeem et al., 2021; Azeem et al., 2021; Zaman et al., 2023; Yu et al., 2023; Al-Dayel et al., 2024). Additionally, entropy-based investigations have focused on metal phthalocyanine COFs, isoreticular metal-organic frameworks, and coronene-based MOFs (Arockiaraj et al., 2023e; Abraham et al., 2022; Manzoor et al., 2021; Raza et al., 2023b; Imran et al., 2023; Waheed et al., 2023; Ghani et al., 2022; Abul Kalaam and Berin Greeni, 2024; Yang et al., 2023). This paper presents the implementation of modified reverse degree-based descriptors for four types of MOFs, the computation of entropy measures through bond-wise comparative analysis, and the development of predictive models for graph energy.
2 Methodology
In this study, MOFs are displayed through two-dimensional graph structures. We denote such a two-dimensional structure by
Therefore, the general form of topological descriptors
Here,
Suppose the edge set of
Therefore, the overall modified reverse degree descriptors for graph
The modified reverse degree based topological descriptor functions considered in this study are stated below.
• Modified reverse first Zagreb descriptor:
• Modified reverse second Zagreb descriptor:
• Modified reverse forgotten descriptor:
• Modified reverse hyper-Zagreb descriptor:
• Modified reverse third redefined Zagreb descriptor:
• Modified reverse bi-Zagreb descriptor:
• Modified reverse tri-Zagreb descriptor:
• Modified reverse bi-Zagreb harmonic descriptor:
• Modified reverse tri-Zagreb harmonic descriptor:
3 Computation of modified reverse degree metrics
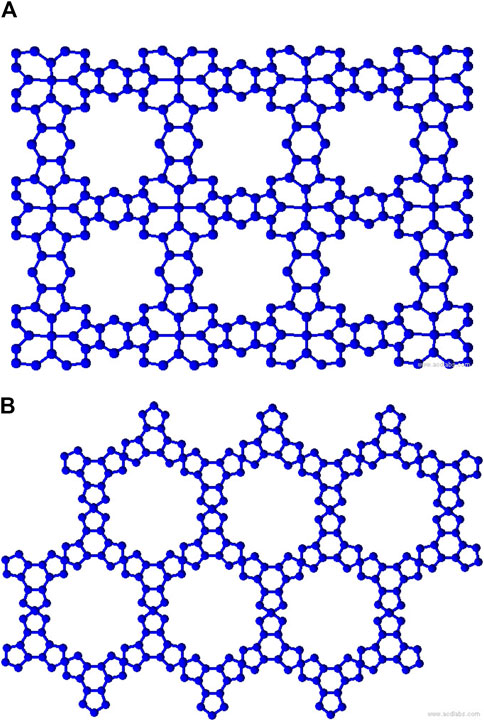
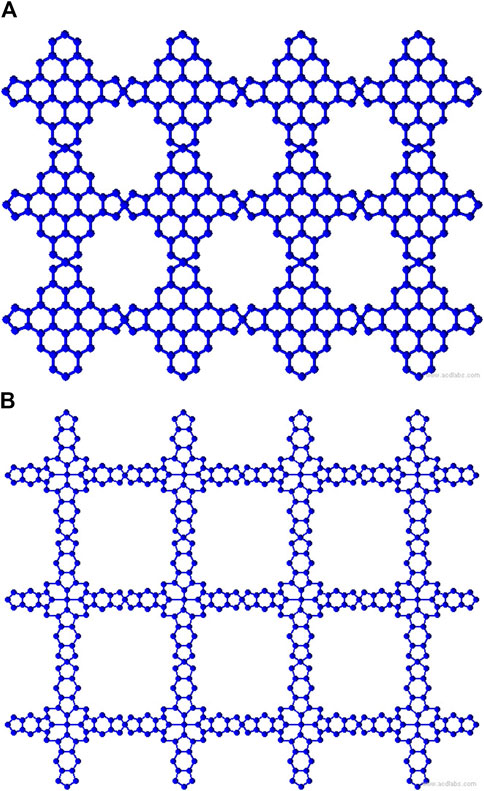
Metal organic frameworks based on transition metal-phthalocyanine, conductive metal-octa amino phthalocyanine, metal-butylated hydroxytoluene, and NH-substituted coronene transition metal are respectively denoted as TM-Pc
To compute the bond-additive modified reverse degree-based topological descriptors, we need the edge partitions of MOFs based on the normal degrees, which are presented in Table 1. Given the complexity of computing each descriptor and variable parameter, we illustrate the first Zagreb descriptor in Equation 1 with the modified reverse variable
For
Similarly for
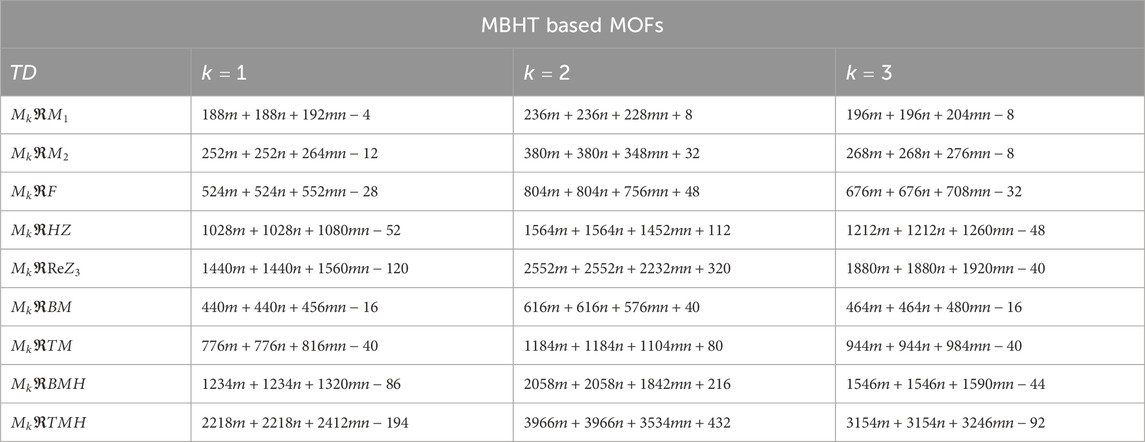
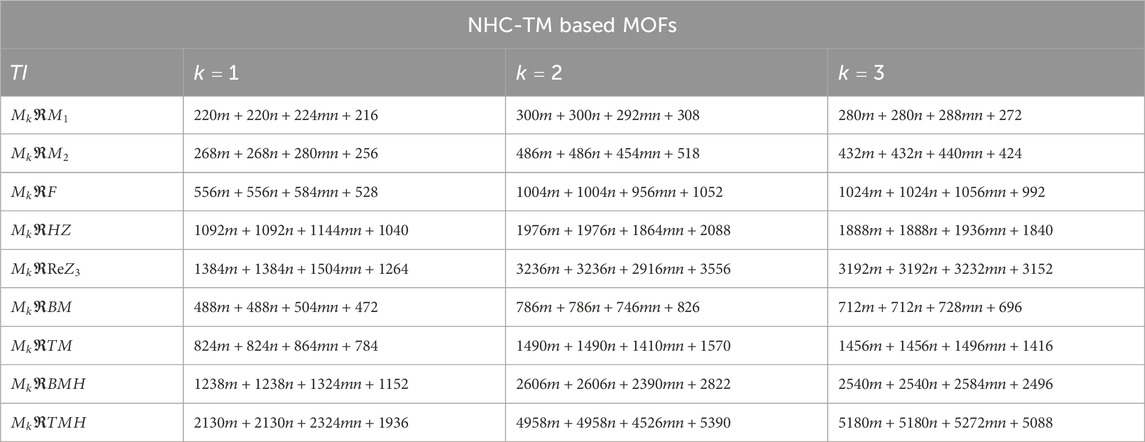
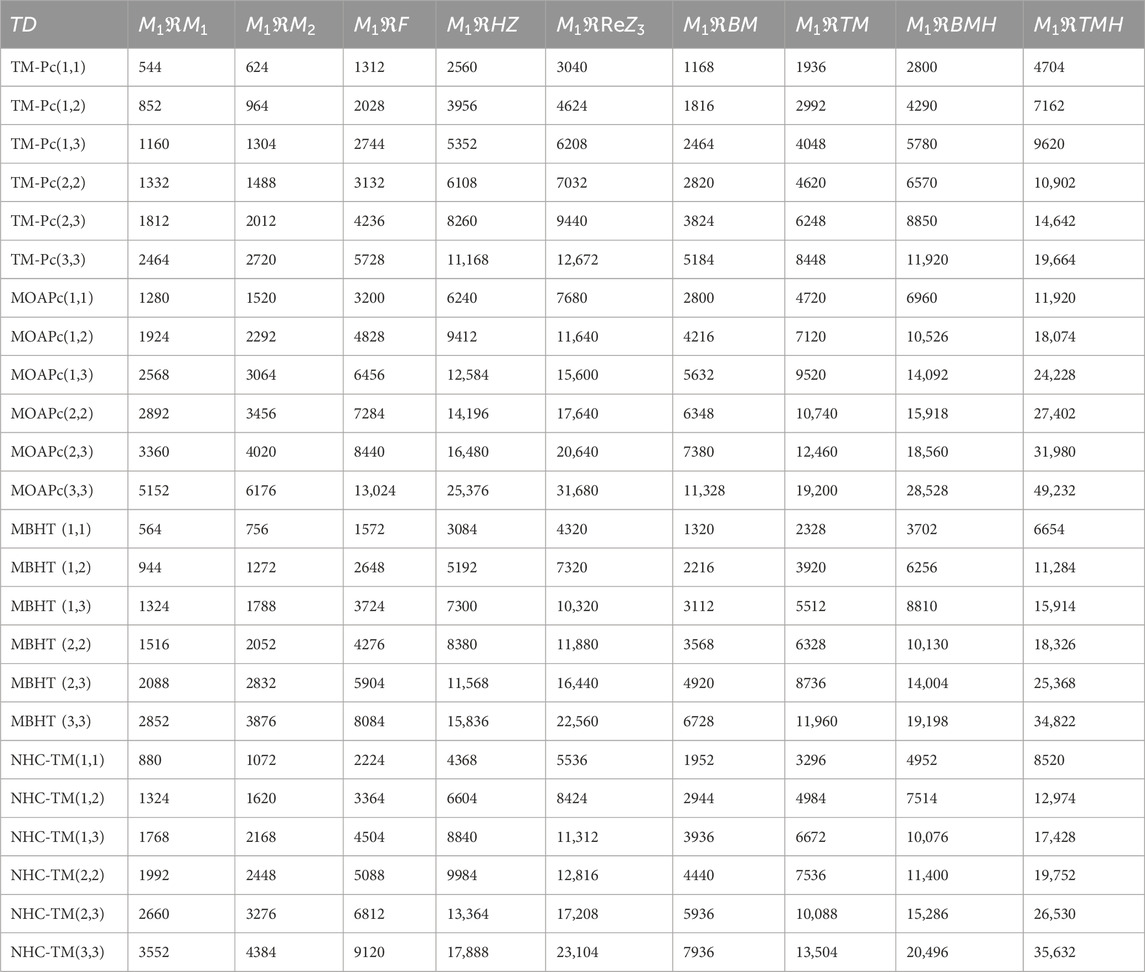
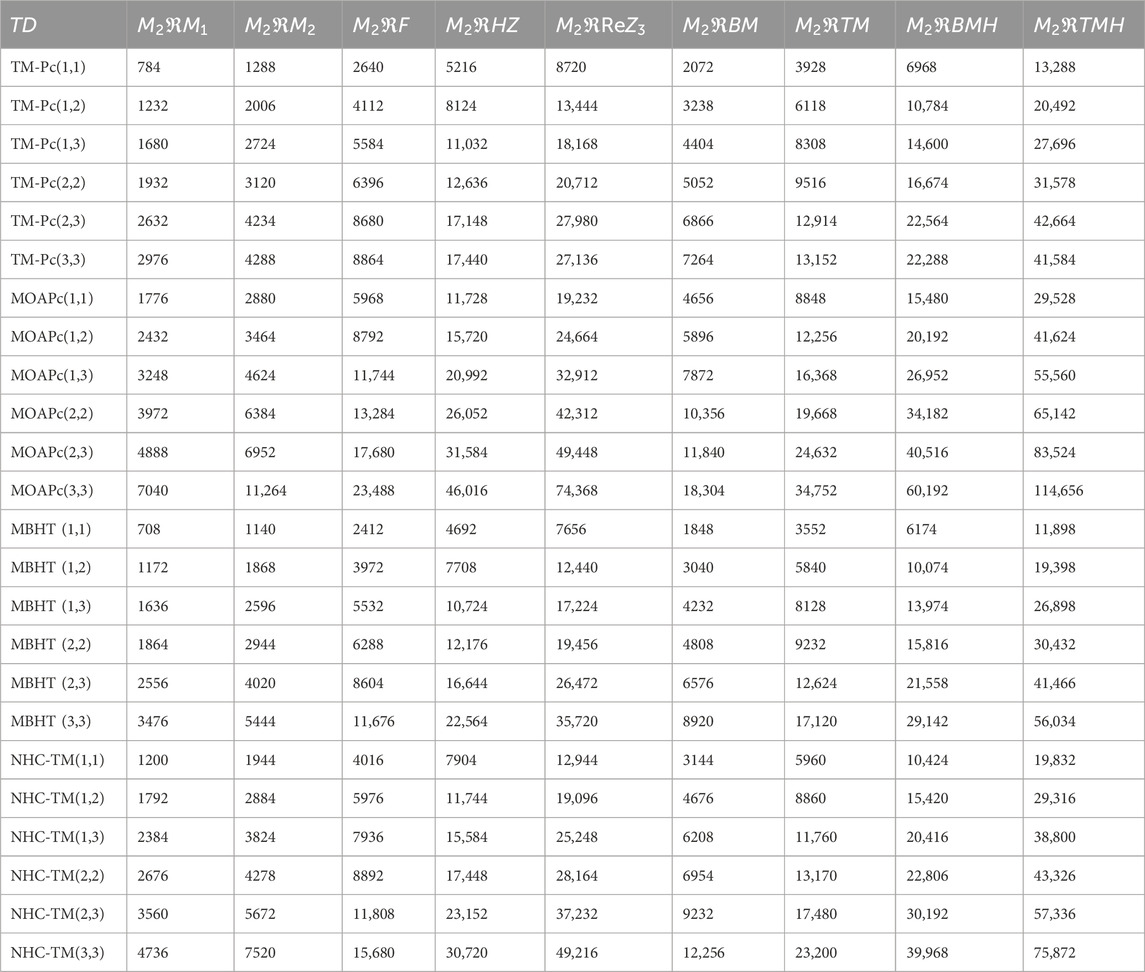
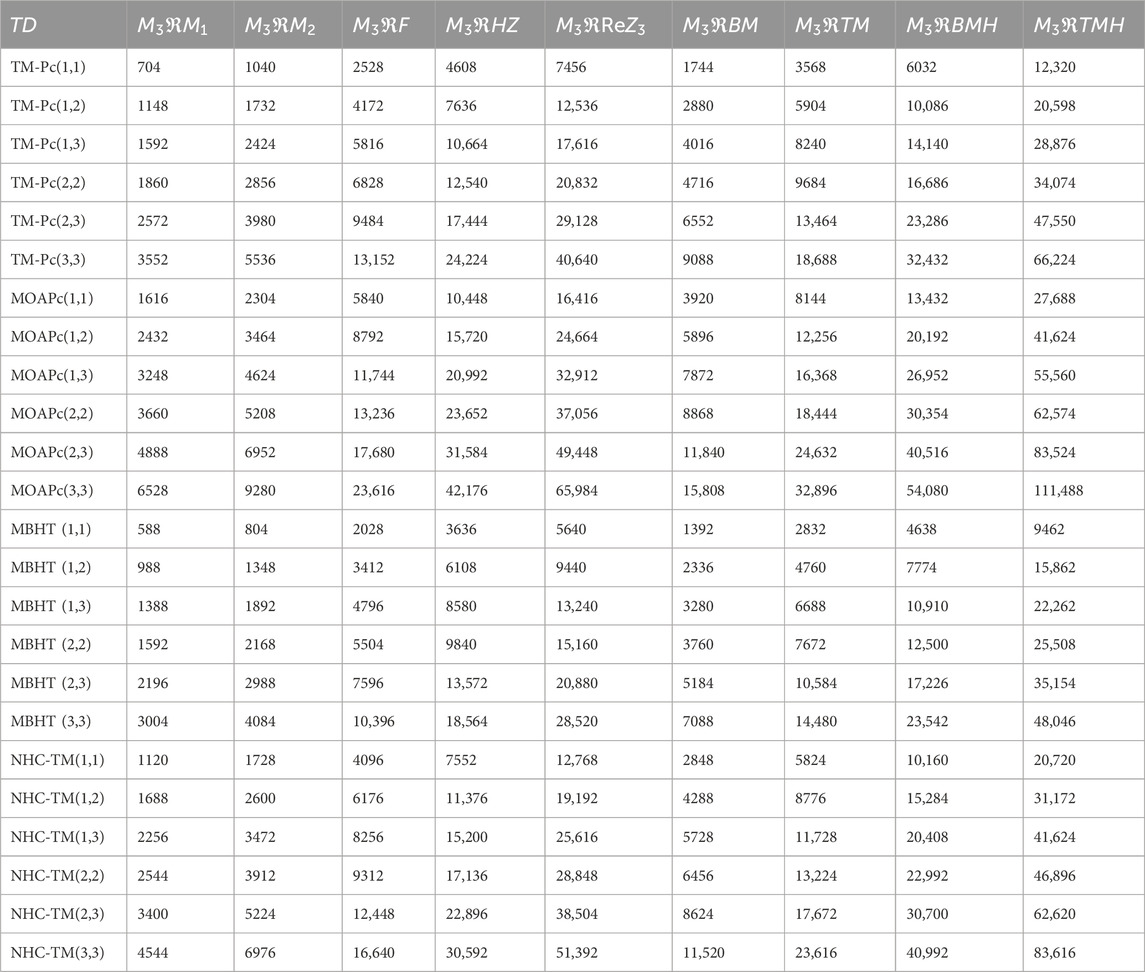
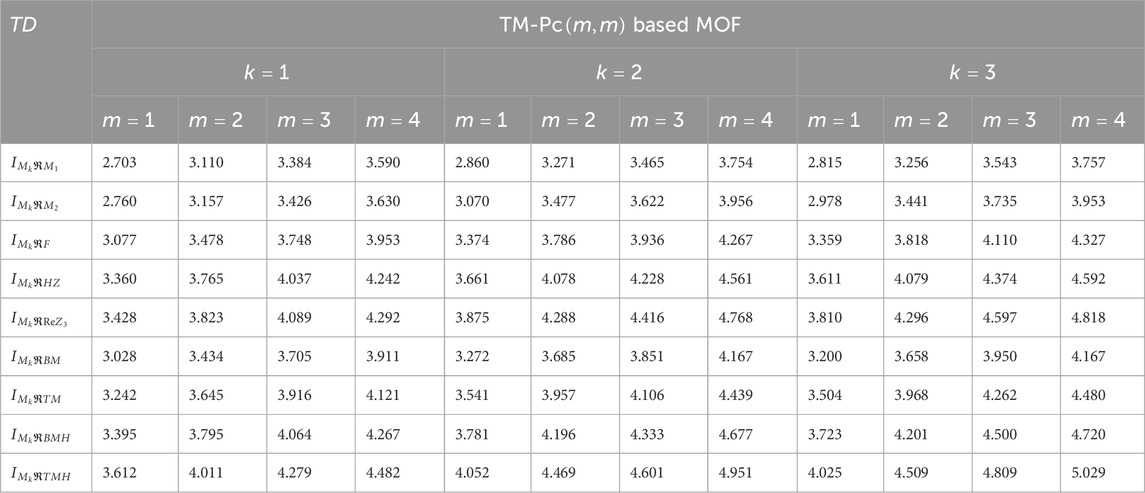
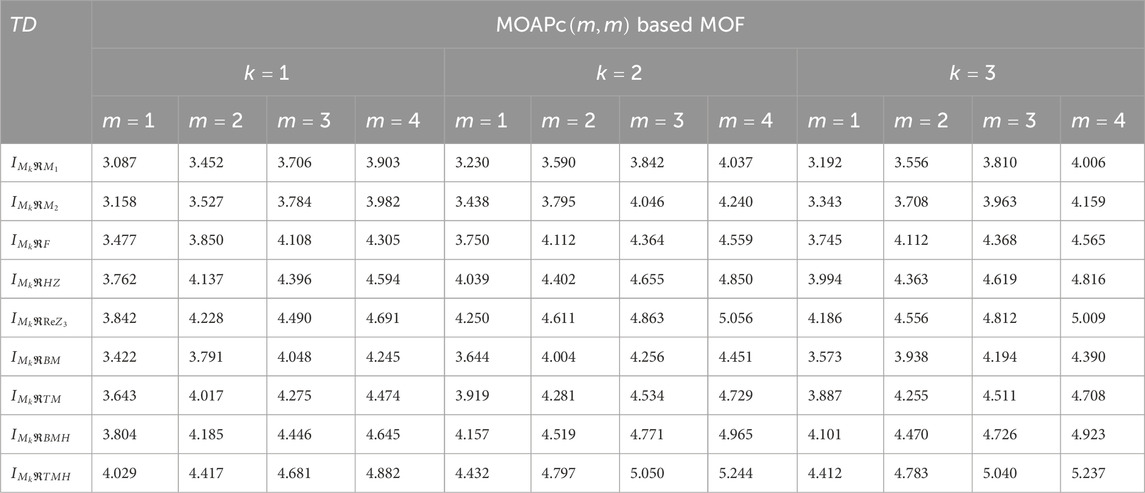
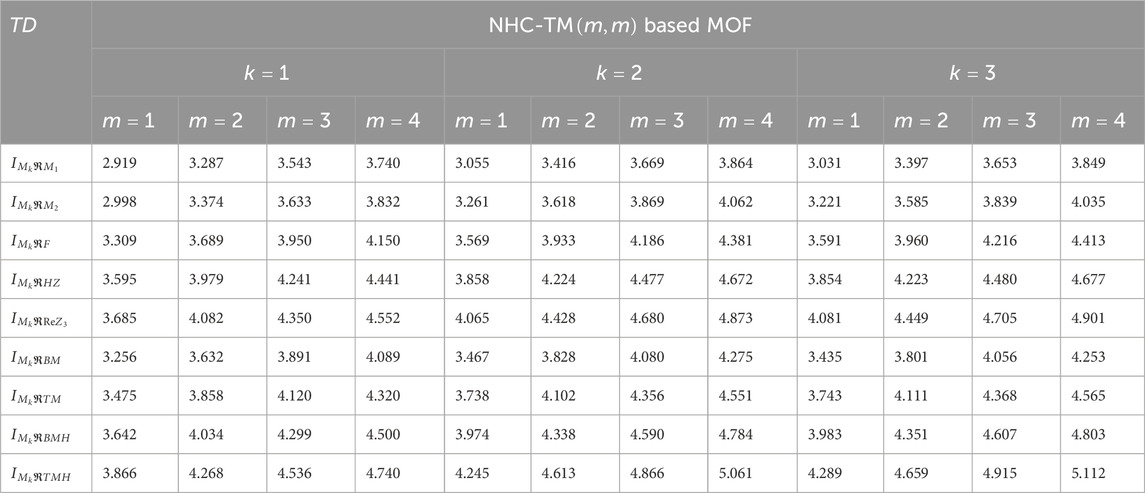
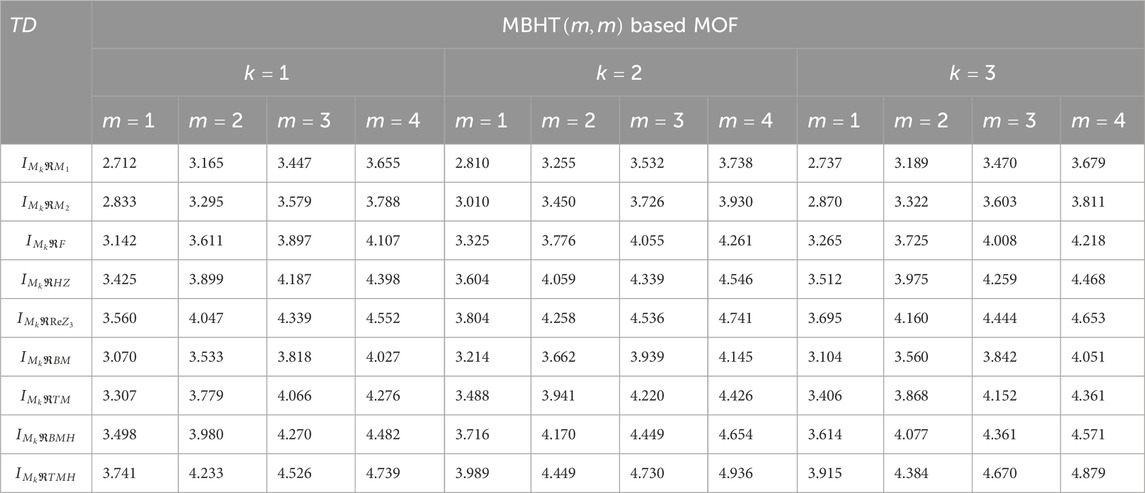
Using the modified reverse topological descriptors detailed in Equations 1–9 and the edge partitions in Table 1, we computed the topological indices for MOFs, which are systematically presented in Tables 2–5 for reversing parameters
We computed the numerical values for the derived topological descriptors of MOFs, which are presented in Tables 6–8 and illustrated in Figure 3. It is clear that the majority of descriptors have largest numerical values for the MOAPc framework, indicating a high level of structural coherence in these MOFs. For all frameworks, the modified reverse degree descriptors
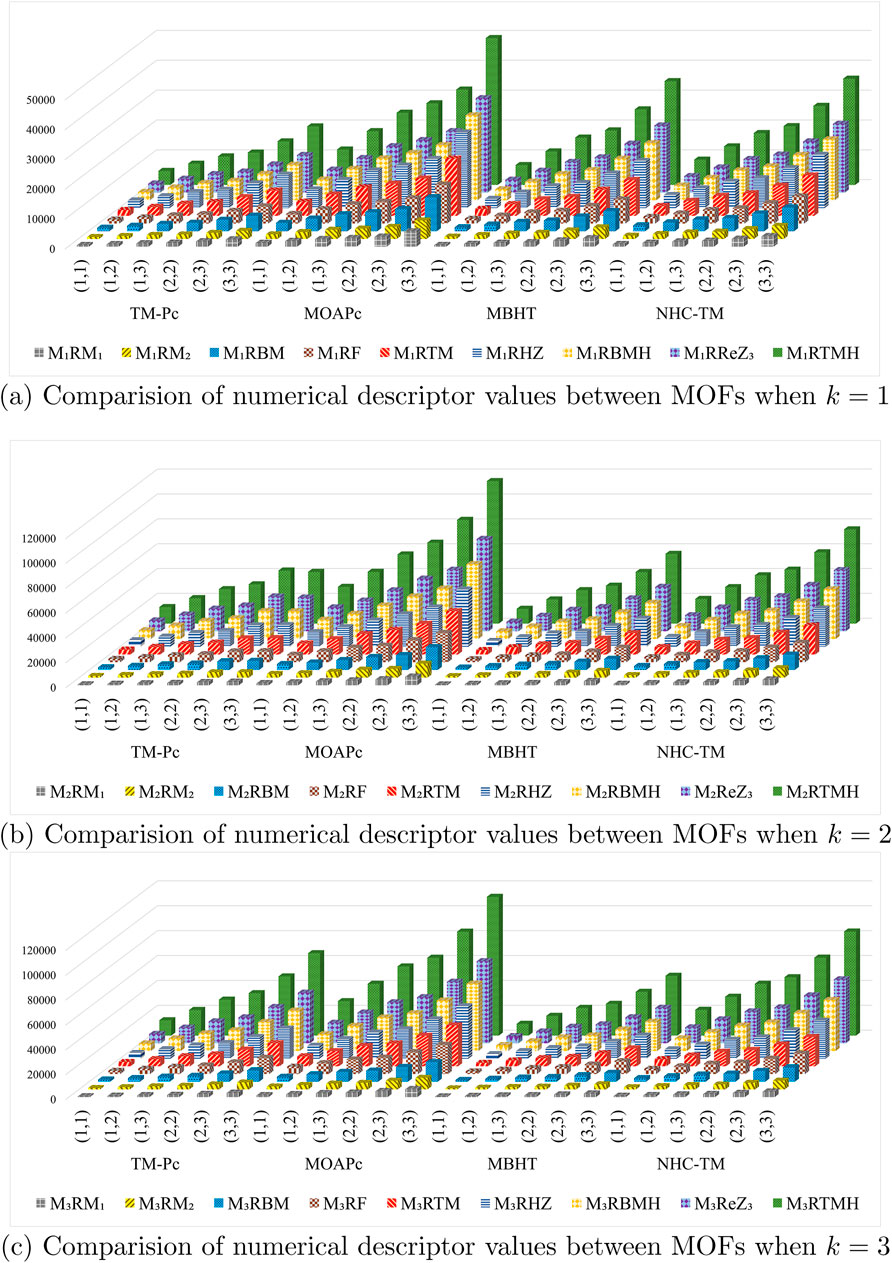
Figure 3. Graphical comparison of numerical descriptors for all MOFs across a range of
4 Comparative study of entropy levels
Consider a subset
A recent study (Paul et al., 2023) scrutinized the aforementioned expression, involving the replacement of the term
We now illustrate the calculation of the first Zagreb entropy value for the TM-Pc structure. Let
By substituting the edge partition classes specified in Table 1, we can express entropy for TM-Pc
Assuming
The above-outlined approach is implemented to calculate the entropy levels for MOFs based on the reverse degree indices. We would like to point out that recent literature includes a comprehensive comparative analysis across diverse chemical structures such as graphene, graphyne, graphdiyne,
In evaluating the entropy levels from Tables 9–12, we explore dynamic variations across MOFs at
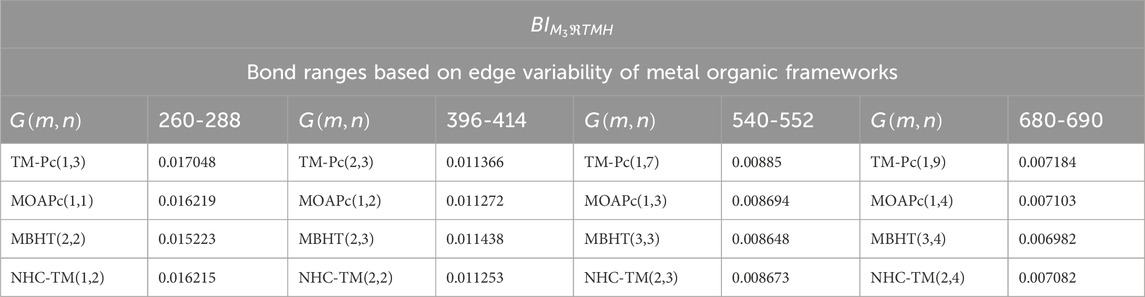
Now, we consider the bond ranges with reasonably acceptable classes and compute the bond-wise entropy for the tri-Zagreb harmonic index, which are represented in Table 11.
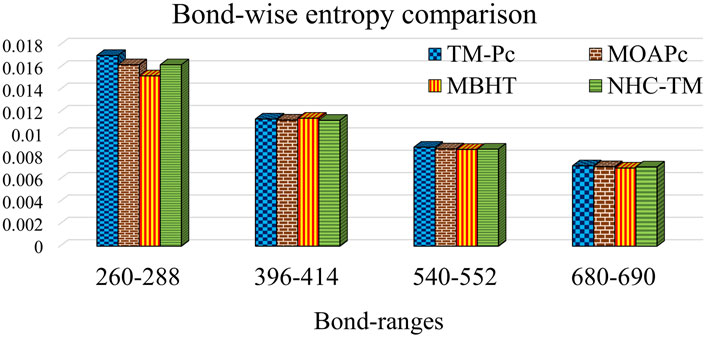
Table 13 and Figure 4 provide a comparison of bond-wise entropies across different structures, maintaining consistent
5 Estimating graph energy with regression models
Graph energy significantly influences electronic properties, impacting chemical reactions, materials science, energy conservation, and optoelectronics. Moreover, graph energy directly relates to total
In the literature, studies focused on distance, degree, degree-sum based topological descriptors, and energies for structures such as zeolite frameworks, benzenoid hydrocarbons, polyhex nanotubes, hypercubes, and porous graphene (Taherpour and Mohammadinasab, 2010; Hayat et al., 2020; Hayat et al., 2021a; Balasubramanian, 2023; Govardhan and Roy, 2023; Hayat et al., 2021b). However, in this study, we investigate the relationship between graph energy
Calculating graph energy for higher-order dimensions
5.1 Regression models for prediction of spectral properties
In this section, we conduct a comprehensive correlation analysis of the topological descriptors and spectral characteristics of various metal organic frameworks.
The predictive regression models are proposed using the following equations.
where
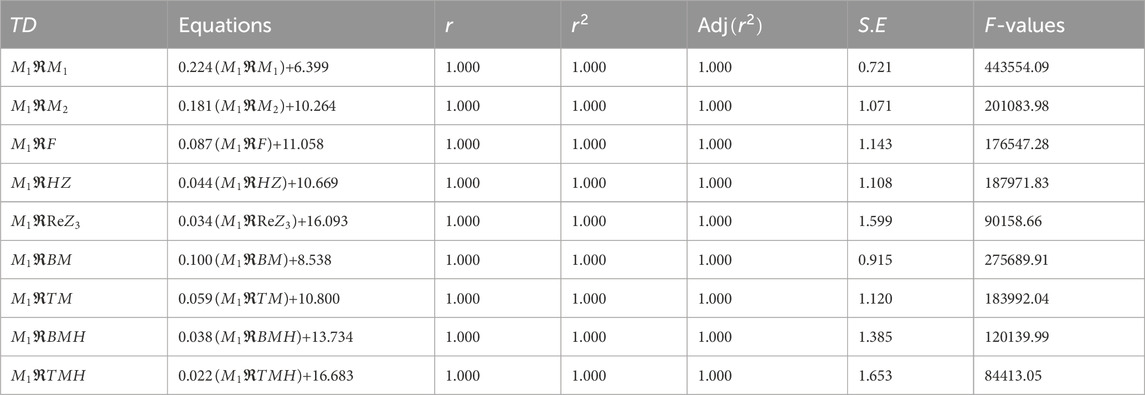
We perform a regression analysis to identify the best predicting topological descriptor for the considered metal organic frameworks. This analysis explores the relationship between the graph energy values provided in Table 14 and the molecular descriptors listed in Tables 6–8, emphasizing descriptors that display strong positive correlations. To improve predictive accuracy, we analyze individual MOFs separately. As an example, we illustrate the regression analysis for the NHC-TM
Table 15, shows that the values of
Table 16 demonstrates that the regression equation for
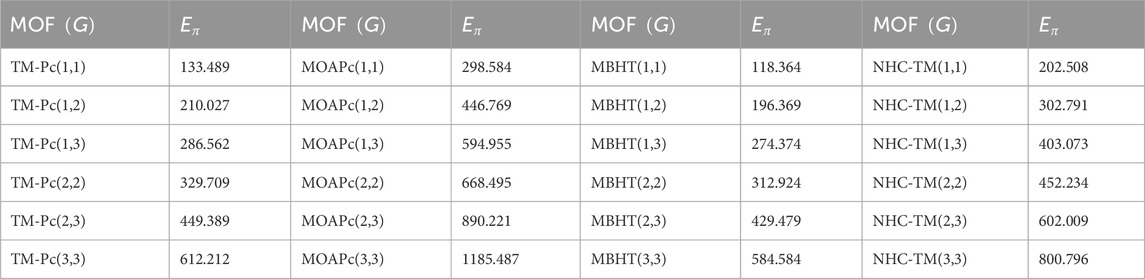
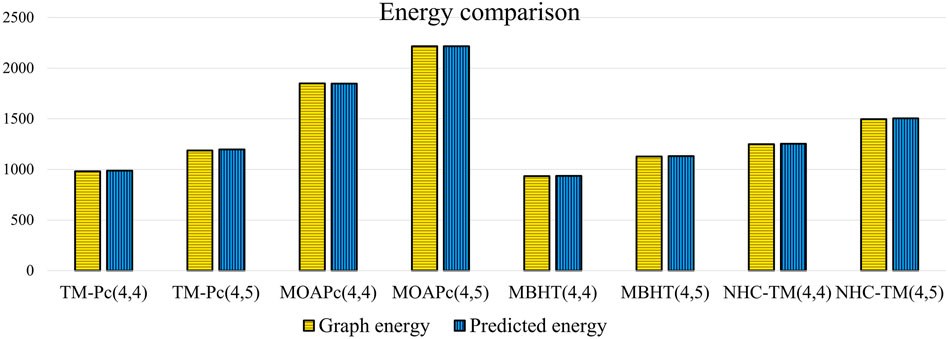
Utilizing the regression models from Table 17, we predict the graph energies of higher-dimensional metal organic frameworks and present a comparison between the actual graph energies and the predicted energies using the optimal model and present in the Table 18.
Table 18 and Figure 5 illustrate that the predictive model provides energy values closely matching the actual graph energies computed by the newGRAPH software. This capability enables accurate prediction of graph energy values for higher-dimensional distinct MOFs.
6 Conclusion
We have conducted a comprehensive analysis by calculating modified reverse degree topological descriptors for four types of MOFs. Simultaneously, we have performed a detailed assessment of entropy levels for each MOF and compared these levels with the bond-wise scaled entropy approach across all frameworks. Moreover, we have presented an optimal linear regression model for predicting the graph energy of distinct structural frameworks, aiming to reduce the computational complexity of software and produce results in polynomial time. The graph theoretical and statistical methods explored in this study can enhance machine learning applications in computational chemistry and QSAR/QSPR studies for material advancements.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
AK: Methodology, Writing–original draft, Conceptualization. AG: Formal Analysis, Investigation, Methodology, Supervision, Writing–review and editing. MA: Methodology, Supervision, Validation, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abraham, J., Arockiaraj, M., Jency, J., Kavitha, S. R., and Balasubramanian, K. (2022). Graph entropies, enumeration of circuits, walks and topological properties of three classes of isoreticular metal organic frameworks. J. Math. Chem. 60 (4), 695–732. doi:10.1007/s10910-021-01321-8
Abul Kalaam, A. R., and Berin Greeni, A. (2024). Comparative analysis of modified reverse degree topological indices for certain carbon nanosheets using entropy measures and multi criteria decision-making analysis. Int. J. Quantum Chem. 124 (1), 27326. doi:10.1002/qua.27326
Al-Dayel, I., Nadeem, M. F., and Khan, M. A. (2024). Topological analysis of tetracyanobenzene metal–organic framework. Sci. Rep. 14 (1), 1789. doi:10.1038/s41598-024-52194-1
Arockiaraj, M., Campena, F. J., Greeni, A. B., Ghani, M. U., Gajavalli, S., Tchier, F., et al. (2024a). QSPR analysis of distance-based structural indices for drug compounds in tuberculosis treatment. Heliyon 10 (2), e23981. doi:10.1016/j.heliyon.2024.e23981
Arockiaraj, M., Greeni, A. B., and Kalaam, A. A. (2023b). Linear versus cubic regression models for analyzing generalized reverse degree based topological indices of certain latest corona treatment drug molecules. Int. J. Quantum Chem. 123 (16), e27136. doi:10.1002/qua.27136
Arockiaraj, M., Greeni, A. B., and Kalaam, A. A. (2023c). Comparative analysis of reverse degree and entropy topological indices for drug molecules in blood Cancer treatment through QSPR regression models. Polycycl. Aromat. Compd., 1–18. doi:10.1080/10406638.2023.2271648
Arockiaraj, M., Greeni, A. B., Kalaam, A. A., Aziz, T., and Alharbi, M. (2024b). Mathematical modeling for prediction of physicochemical characteristics of cardiovascular drugs via modified reverse degree topological indices. Eur. Phys. J. E 47 (8), 53. doi:10.1140/epje/s10189-024-00446-3
Arockiaraj, M., Jency, J., Mushtaq, S., Shalini, A. J., and Balasubramanian, K. (2023e). Covalent organic frameworks: topological characterizations, spectral patterns and graph entropies. J. Math. Chem. 61, 1633–1664. doi:10.1007/s10910-023-01477-5
Arockiaraj, M., Paul, D., Clement, J., Tigga, S., Jacob, K., and Balasubramanian, K. (2023a). Novel molecular hybrid geometric-harmonic-Zagreb degree based descriptors and their efficacy in QSPR studies of polycyclic aromatic hydrocarbons. Environ. Res. 34, 569–589. doi:10.1080/1062936x.2023.2239149
Arockiaraj, M., Paul, D., Ghani, M. U., Tigga, S., and Chu, Y. M. (2023d). Entropy structural characterization of zeolites BCT and DFT with bond-wise scaled comparison. Sci. Rep. 13 (1), 10874. doi:10.1038/s41598-023-37931-2
Azeem, M., Aslam, A., Iqbal, Z., Binyamin, M. A., and Gao, W. (2021). Topological aspects of 2D structures of trans-Pd (NH2) S lattice and a metal-organic superlattice. Arabian J. Chem. 14 (3), 102963. doi:10.1016/j.arabjc.2020.102963
Balasubramanian, K. (2023). Topological indices, graph spectra, entropies, Laplacians, and matching polynomials of n-dimensional hypercubes. Symmetry 15 (2), 557. doi:10.3390/sym15020557
Chakravarty, C., Mandal, B., and Sark, P. (2016a). Bis (dithioline)-based metal–organic frameworks with superior electronic and magnetic properties: spin frustration to spintronics and gas sensing. J. Phys. Chem. C 120 (49), 28307–28319. doi:10.1021/acs.jpcc.6b09416
Chakravarty, C., Mandal, B., and Sark, P. (2016b). Coronene-based metal–organic framework: a theoretical exploration. Phys. Chem. Chem. Phys. 18 (36), 25277–25283. doi:10.1039/c6cp05495a
Clough, A. J., Yoo, J. W., Mecklenburg, M. H., and Marinescu, S. C. (2015). Two-dimensional metal–organic surfaces for efficient hydrogen evolution from water. J. Am. Chem. Soc. 137 (1), 118–121. doi:10.1021/ja5116937
Dehmer, M. (2008). Information processing in complex networks: graph entropy and information functionals. Appl. Math. Comput. 201, 82–94. doi:10.1016/j.amc.2007.12.010
Dong, R., Zhang, Z., Tranca, D. C., Zhou, S., Wang, M., Adler, P., et al. (2018). A coronene-based semiconducting two-dimensional metal-organic framework with ferromagnetic behavior. Nat. Commun. 9 (1), 2637. doi:10.1038/s41467-018-05141-4
Ediz, S. (2015). Maximum chemical trees of the second reverse Zagreb index. Pac. J. Appl. Math. 7 (4), 287.
Ghani, M. U., Sultan, F., Tag El Din, E. S., Khan, A. R., Liu, J. B., and Cancan, M. (2022). A paradigmatic approach to find the valency-based K-banhatti and redefined Zagreb entropy for niobium oxide and a metal–organic framework. Molecules 27 (20), 6975. doi:10.3390/molecules27206975
Govardhan, S., and Roy, S. (2023). Topological analysis of hexagonal and rectangular porous graphene with applications to predicting π electron energy. Eur. Phys. J. Plus 138 (7), 670. doi:10.1140/epjp/s13360-023-04307-4
Govardhan, S., Roy, S., Prabhu, S., and Arulperumjothi, M. (2024). Topological characterization of cove-edged graphene nanoribbons with applications to NMR spectroscopies. J. Mol. Struct. 1303, 137492. doi:10.1016/j.molstruc.2024.137492
Gutman, I., Radenković, S., Dordević, S., Milovanović, I. Z., and Milovanović, E. I. (2017). Extending the McClelland formula for total π -electron energy. J. Math. Chem. 55 (10), 1934–1940. doi:10.1007/s10910-017-0772-6
Gutman, I., and Trinajstić, N. (1972). Graph theory and molecular orbitals. Total φ-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 17 (4), 535–538. doi:10.1016/0009-2614(72)85099-1
Hayat, S., Khan, S., and Imran, M. (2021b). Quality testing of spectrum-based distance descriptors for polycyclic aromatic hydrocarbons with applications to carbon nanotubes and nanocones. Arabian J. Chem. 14 (3), 102994. doi:10.1016/j.arabjc.2021.102994
Hayat, S., Khan, S., Khan, A., and Imran, M. (2020). Distance-based topological descriptors for measuring the π-electronic energy of benzenoid hydrocarbons with applications to carbon nanotubes. Math. Methods Appl. Sci. doi:10.1002/mma.6668
Hayat, S., Khan, S., Khan, A., and Imran, M. (2021a). A computer-based method to determine predictive potential of distance-spectral descriptors for measuring the π-electronic energy of benzenoid hydrocarbons with applications. IEEE Access 9, 19238–19253. doi:10.1109/access.2021.3053270
Horcajada, P., Serre, C., Maurin, G., Ramsahye, N. A., Balas, F., Vallet-Regí, M., et al. (2008). Flexible porous metal-organic frameworks for a controlled drug delivery. J. Am. Chem. Soc. 130 (21), 6774–6780. doi:10.1021/ja710973k
Imran, M., Khan, A. R., Husin, M. N., Tchier, F., Ghani, M. U., and Hussain, S. (2023). Computation of entropy measures for metal-organic frameworks. Molecules 28 (12), 4726. doi:10.3390/molecules28124726
Kavitha, S. R. J., Abraham, J., Arockiaraj, M., Jency, J., and Balasubramanian, K. (2021). Topological characterization and graph entropies of tessellations of kekulene structures: existence of isentropic structures and applications to thermochemistry, nuclear Magnetic Resonance, and electron Spin Resonance. J. Phys. Chem. A 125 (36), 8140–8158. doi:10.1021/acs.jpca.1c06264
Kinoshita, Y., Matsubara, I., Higuchi, T., and Saito, Y. (1959). The crystal structure of bis (adiponitrile) copper (I) nitrate. Bull. Chem. Soc. Jpn. 32 (11), 1221–1226. doi:10.1246/bcsj.32.1221
Lee, J., Farha, O. K., Roberts, J., Scheidt, K. A., Nguyen, S. T., and Hupp, J. T. (2009). Metal–organic framework materials as catalysts. Chem. Soc. Rev. 38 (5), 1450–1459. doi:10.1039/b807080f
Li, W., Sun, L., Qi, J., Jarillo-Herrero, P., Dincă, M., and Li, J. (2017). High temperature ferromagnetism in π-conjugated two-dimensional metal–organic frameworks. Chem. Sci. 8 (4), 2859–2867. doi:10.1039/c6sc05080h
Mabrouk, M., and Hayn, R. (2015). Magnetic moment formation in metal-organic monolayers. Phys. Rev. B 92 (18), 184424. doi:10.1103/physrevb.92.184424
Mabrouk, M., Hayn, R., Denawi, H., and Chaabane, R. B. (2018). Possibility of a ferromagnetic and conducting metal-organic network. J. Magnetism Magnetic Mater. 453, 48–52. doi:10.1016/j.jmmm.2018.01.005
Manzoor, S., Siddiqui, M. K., and Ahmad, S. (2021). On physical analysis of degree-based entropy measures for metal–organic superlattices. Eur. Phys. J. Plus 136 (3), 287. doi:10.1140/epjp/s13360-021-01275-5
Murray, L. J., Dincă, M., and Long, J. R. (2009). Hydrogen storage in metal–organic frameworks. Chem. Soc. Rev. 38 (5), 1294–1314. doi:10.1039/b802256a
Nadeem, M. F., Imran, M., Siddiqui, H. M., Azeem, M., Khalil, A., and Ali, Y. (2021). Topological aspects of metal-organic structure with the help of underlying networks. Arabian J. Chem. 14 (6), 103157. doi:10.1016/j.arabjc.2021.103157
Park, C., Baek, J. W., Shin, E., and Kim, I. D. (2023). Two-dimensional electrically conductive metal–organic frameworks as chemiresistive sensors. ACS Nanosci. Au 3 (5), 353–374. doi:10.1021/acsnanoscienceau.3c00024
Paul, D., Arockiaraj, M., Jacob, K., and Clement, J. (2023). Multiplicative versus scalar multiplicative degree based descriptors in QSAR/QSPR studies and their comparative analysis in entropy measures. Eur. Phys. J. Plus 138 (4), 323. doi:10.1140/epjp/s13360-023-03920-7
Peter, P., and Clement, J. (2024). Predictive models on potential energies of zeolite ZK-5 using bond weighted information entropy measures. J. Mol. Struct. 1307, 137945. doi:10.1016/j.molstruc.2024.137945
Rahul, M. P., Clement, J., Junias, J. S., Arockiaraj, M., and Balasubramanian, K. (2022). Degree-based entropies of graphene, graphyne and graphdiyne Using Shannon’s Approach. J. Mol. Struct. 1260, 132797. doi:10.1016/j.molstruc.2022.132797
Raja, N. J., and Anuradha, A. (2024). Topological entropies of single walled carbon nanotubes. J. Math. Chem. 62 (4), 809–818. doi:10.1007/s10910-023-01532-1
Raza, Z., Akhter, S., and Shang, Y. (2023a). Expected value of first Zagreb connection index in random cyclooctatetraene chain, random polyphenyls chain, and random chain network. Front. Chem. 10, 1067874. doi:10.3389/fchem.2022.1067874
Raza, Z., Arockiaraj, M., Maaran, A., Kavitha, S. R., and Balasubramanian, K. (2023b). Topological entropy characterization, NMR and ESR spectral patterns of coronene-based transition metal organic frameworks. ACS omega 8 (14), 13371–13383. doi:10.1021/acsomega.3c00825
Shannon, C. E. (1948). A mathematical theory of communication. Bell Syst. Tech. J. 27 (3), 379–423. doi:10.1002/j.1538-7305.1948.tb01338.x
Stevanović, L., Brankov, V., Cvetković, D., and Simić, S. (2021). newGRAPH: a fully integrated environment used for research process in graph theory. Available at: http://www.mi.sanu.ac.rs/newgraph/index.html.
Taherpour, A., and Mohammadinasab, E. (2010). Topological relationship between Wiener, Padmaker-Ivan, and Szeged Indices and energy and electric moments in armchair polyhex nanotubes with the same circumference and varying lengths. Fullerenes, Nanotub. Carbon Nanostructures 18 (1), 72–86. doi:10.1080/15363830903291580
Waheed, M., Saleem, U., Javed, A., and Jamil, M. K. (2023). Computational aspects of entropy measures for metal organic frameworks. Mol. Phys. 122, 2254418. doi:10.1080/00268976.2023.2254418
Wiener, H. (1947). Structural determination of paraffin boiling points. J. Am. Chem. Soc. 69, 17–20. doi:10.1021/ja01193a005
Yang, J., Siddiqui, M. K., Bashir, A., Manzoor, S., Eldin, S. M., and Cancan, M. (2023). On physical analysis of topological co-indices for beryllium oxide via curve fitting models. J. Mol. Struct. 1278, 134933. doi:10.1016/j.molstruc.2023.134933
Yu, Y., Khalid, A., Aamir, M., Siddiqui, M. K., Muhammad, M. H., and Bashir, Y. (2023). On some topological indices of metal-organic frameworks. Polycycl. Aromat. Compd. 43 (6), 5607–5628. doi:10.1080/10406638.2022.2105909
Zaman, S., Jalani, M., Ullah, A., Ahmad, W., and Saeedi, G. (2023). Mathematical analysis and molecular descriptors of two novel metal–organic models with chemical applications. Sci. Rep. 13 (1), 5314. doi:10.1038/s41598-023-32347-4
Zhang, X., Bajwa, Z. S., Zaman, S., Munawar, S., and Li, D. (2024). The study of curve fitting models to analyze some degree-based topological indices of certain anti-cancer treatment. Chem. Pap. 78 (2), 1055–1068. doi:10.1007/s11696-023-03143-1
Keywords: metal organic frameworks, reverse degree based descriptors, bond-wise entropy analysis, graph energies, structure property regression models
Citation: Kalaam ARA, Greeni AB and Arockiaraj M (2024) Modified reverse degree descriptors for combined topological and entropy characterizations of 2D metal organic frameworks: applications in graph energy prediction. Front. Chem. 12:1470231. doi: 10.3389/fchem.2024.1470231
Received: 25 July 2024; Accepted: 29 August 2024;
Published: 25 September 2024.
Edited by:
Sudip Pan, Jilin University, ChinaReviewed by:
Shahid Zaman, University of Sialkot, PakistanXiujun Zhang, Chengdu Neusoft University, China
Muhammad Kamran Siddiqui, COMSATS University Islamabad, Pakistan
Copyright © 2024 Kalaam, Greeni and Arockiaraj. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: A. Berin Greeni, YmVyaW5ncmVlbmlAZ21haWwuY29t
 A. R. Abul Kalaam
A. R. Abul Kalaam A. Berin Greeni
A. Berin Greeni Micheal Arockiaraj
Micheal Arockiaraj