- 1College of Engineering, Shandong Xiehe University, Jinan, China
- 2Key Laboratory for Liquid-Solid Structural Evolution and Processing of Materials, Ministry of Education, Shandong University, Jinan, China
Novel perovskites pertain to newly discovered or less studied variants of the conventional perovskite structure, characterized by distinctive properties and potential for diverse applications such as ferroelectric, optoelectronic, and thermoelectric uses. In recent years, advancements in computational methods have markedly expedited the discovery and design of innovative perovskite materials, leading to numerous pertinent reports. However, there are few reviews that thoroughly elaborate the role of computational methods in studying novel perovskites, particularly for state-of-the-art perovskite categories. This review delves into the computational discovery of novel perovskite materials, with a particular focus on antiperovskites and chalcogenide perovskites. We begin with a discussion on the computational methods applied to evaluate the stability and electronic structure of materials. Next, we highlight how these methods expedite the discovery process, demonstrating how rational simulations contribute to researching novel perovskites with improved performance. Finally, we thoroughly discuss the remaining challenges and future outlooks in this research domain to encourage further investigation. We believe that this review will be highly beneficial both for newcomers to the field and for experienced researchers in computational science who are shifting their focus to novel perovskites.
1 Introduction
Perovskite and perovskite-related compounds represent an extensive class of materials with a multitude of applications across various domains of contemporary technology, including ceramics, thin films, solar cells, electronics, ferroelectrics, magnetic materials, superconductors, solid oxide fuel cells, ion conductors, catalysts, quantum materials, and biomedical applications (Dey et al., 2021; Jena et al., 2019; Kim et al., 2016; Zhang et al., 2016; Fu et al., 2019; Kovalenko et al., 2017; Wang K. et al., 2019). The unique structural characteristics of perovskites, primarily the ABX3 crystal structure, where A and B are cations of different sizes, and X is an anion, contribute to their diverse functionalities and tunable properties.
Novel perovskites refer to new or less explored variations of the traditional perovskite structure that exhibit unique properties and potential for various applications. These materials extend beyond the conventional ABX3 structure, incorporating modifications that provide enhanced or entirely new functionalities. Therefore, they display unique properties that broaden the functionalities of traditional perovskites, presenting promising opportunities for applications in energy, electronics, and other advanced technological industries.
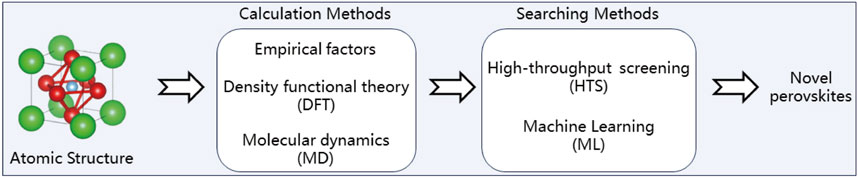
The development of novel perovskite materials is a challenging process that demands significant time for theoretical design and experimental validation. Therefore, finding an effective toolbox to expedite the development process has become increasingly urgent. In recent years, advancements in computational methods have significantly accelerated the discovery and design of novel perovskite materials. Empirical factors such as the Goldschmidt tolerance (τ) factor and the octahedral index (μ) are essential for predicting the stability of perovskites based on ionic radii (Travis et al., 2016; Li et al., 2016). In addition, density functional theory (DFT) calculations offer a comprehensive understanding of the electronic, structural, thermodynamic, and mechanical properties of these materials, particularly when combined with high-throughput screening (HTS) techniques (Allam et al., 2018). In this case, HTS facilitates the rapid evaluation of numerous compositions to identify those with optimal properties for specific applications, including solar cells, light-emitting diodes (LEDs), and catalysis. Meanwhile, machine learning (ML) techniques improve the efficiency of exploring extensive chemical spaces by predicting material properties from large datasets, thereby reducing the computational costs associated with DFT calculations (Chen C. et al., 2020). Therefore, these approaches expedite the identification of novel perovskites with optimal properties, such as appropriate band gaps for solar cells or enhanced stability for prolonged applications.
Among these novel perovskites, antiperovskites and chalcogenide perovskites are especially noteworthy. Antiperovskites exhibit distinctive structural and electronic properties compared to their traditional perovskite counterparts. For example, molecular ferroelectrics with antiperovskite structure exhibit excellent ferroelectric properties (Shi et al., 2020a; Wei Z. et al., 2018; Ye et al., 2018; Liao et al., 2019; Zhang et al., 2018; Li et al., 2019), including higher Curie temperatures (TC), stronger ferroelectric polarization, larger piezoelectric coefficients, and lower coercive fields, which are superior to their counterparts with conventional perovskite structure (Wei W. et al., 2018; Tang et al., 2021; Chen XG. et al., 2020). The exploration of chalcogenide perovskites, another novel class of perovskites, has highlighted their potential in optoelectronic and thermoelectric applications due to their unique electronic structures and phase stability under various environmental conditions (Perera et al., 2016). Specifically, computational calculations reveal that predicted chalcogenide perovskites are ionic semiconductors with moderate band gaps. More importantly, most chalcogenide perovskites exhibit direct band gaps, which benefits to their optoelectronic properties. In addition, their diverse phase transitions and composition modifications with different chalcogenide elements (S or Se) result in the effective tuning of their band gaps. Therefore, chalcogenide perovskites behave potential for excellent optoelectronic properties. In addition to optoelectronic properties, Sb-based chalcogenide perovskites behave significantly enhanced thermal conductivity because of their p-type semiconducting feature. As a result, chalcogenide perovskites, with their ionic characteristics, exhibit exceptional thermoelectric potential.
This review explores the computational discovery of novel perovskite materials, with focus on antiperovskites and chalcogenide perovskites, as shown in Scheme 1. It examines the computational methods used to assess the stability and electronic structures of these materials. Additionally, it highlights how these methods accelerate the discovery process, illustrating how rational simulations contribute to the research of novel perovskite materials with improved performance or unexpected phenomena. The integration of theoretical predictions with experimental validation emphasizes the potential of these advanced computational techniques in advancing the development of next-generation perovskite materials for various applications such as solid-state lighting, display, thermoelectric field, and so on.
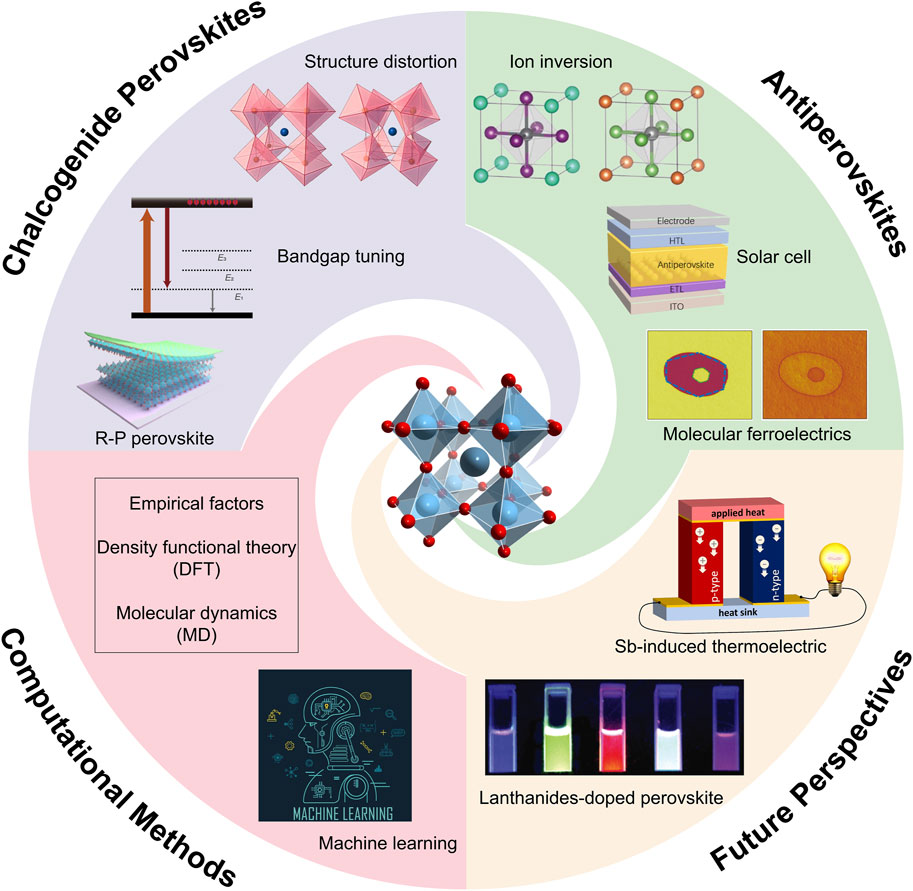
Scheme 1. Computational applications on discovering novel antiperovskites and chalcogenide perovskites.
2 Computational methods and applications
2.1 Computational methods
Following Scheme 2, the computational-enhanced discovery of novel perovskites begins with the consideration of empirical factors and computational methods, such as Density Functional Theory (DFT) and Molecular Dynamics (MD), to model and understand material properties at an atomic level. These computational approaches feed into high-throughput screening (HTS) processes, which allow for the rapid assessment of numerous material candidates. Finally, Machine Learning (ML) techniques are applied to analyze the data generated from HTS, enabling the identification of promising materials with desired properties more efficiently.
2.1.1 Empirical factors
For perovskite materials, certain reliable empirical factors are used to assess structural stability. These factors enable a rapid evaluation of perovskite material stability through straightforward calculations, significantly reducing the required time compared to DFT simulations. Among these factors, ionic radii play a crucial role in shaping our understanding of bonding and stability in perovskites. For instance, Goldschmidt’s tolerance factor has been widely employed to assess the stability of perovskite structures (Travis et al., 2016; Li et al., 2016):
Here, ri (where i denotes A, B, or X) represents the radius of a specific ion in perovskites. The calculated tolerance factors for typical perovskite materials range between 0.81 and 1.11. Therefore, predicting the stability of perovskites using the tolerance factor requires only their chemical compositions. Furthermore, when the octahedral index:
falls within the range of 0.41–0.90, it indicates significant distortion of the octahedral geometry and a high likelihood of multiphase coexistence (Travis et al., 2016). The ionic radii, tolerance factor, and octahedral factor are considered the most critical criteria for classification, highlighting that steric and geometric packing effects are essential to the stability of halide perovskites.
2.1.2 Density functional theory
DFT calculation is a powerful computational tool for characterizing the electronic, structural, thermodynamic, and mechanical properties of perovskites, particularly when combined with high-throughput screening techniques (Allam et al., 2018). This approach facilitates a deeper understanding of perovskites and accelerates the discovery of novel materials with optimal properties. However, DFT derived from Kohn–Sham orbitals describing the conduction band minimum and maximum, approximate the real optical excitation problem but neglect excitonic effects. In practice, the selection of a proper DFT functional should be very careful (Vona et al., 2022).
2.1.3 High-throughput screening
HTS involves the rapid and automated testing of large numbers of materials to identify those with desirable properties. It employs computational simulations and experimental techniques to evaluate electronic, optical, and structural properties across a wide range of compositions. This systematic approach accelerates the discovery and optimization of novel perovskite materials for various applications, including solar cells, LEDs, and catalysis.
2.1.4 Global optimization technique
The actual structure of a material typically corresponds to the global minimum (GM) on the potential energy surface (PES), representing the lowest energy point. Identifying this GM is a crucial global optimization (GO) problem (23). Recently, advanced GO software such as CALYPSO, USPEX, and AIRSS have been emerged as powerful tools in the crystal prediction and discovery of novel structures, particularly for antiperovskites and chalcogenide perovskites. For example, Lee et al. successfully filtered 18,133 hypothetical X3BA down to seven exceptional candidates with outstanding room-temperature ionic conductivity, using GO techniques. Techniques such as genetic algorithms, basin hopping, minimum hopping, topological methods, particle swarm optimization, and tabu search have contributed to enhancing the efficiency and effectiveness of these optimization processes (Zhao et al., 2015).
2.1.5 Machine learning technique
While accurate methods like DFT calculations have revolutionized material prediction and design, their high computational costs and limited scalability constrain their effectiveness in exploring the vast chemical spaces of novel perovskites (Chen C. et al., 2020). ML techniques facilitate the rapid and direct prediction of material properties from extensive datasets, significantly reducing the computational costs associated with DFT calculations and allowing for more efficient exploration of larger chemical spaces (Allam et al., 2018). Popular ML methods include graph neural networks, support vector machines (SVMs), and Gaussian processes (Pilania et al., 2016). Additionally, active learning combined with Bayesian optimization can efficiently identify novel perovskites from large materials databases. Table 1 presents a list of popular datasets used for screening novel perovskites. While some datasets include experimental data, the largest datasets typically rely on computational methods to generate labels. These datasets often focus on specific targets, such as the electronic bandgap, relevant for energy applications.
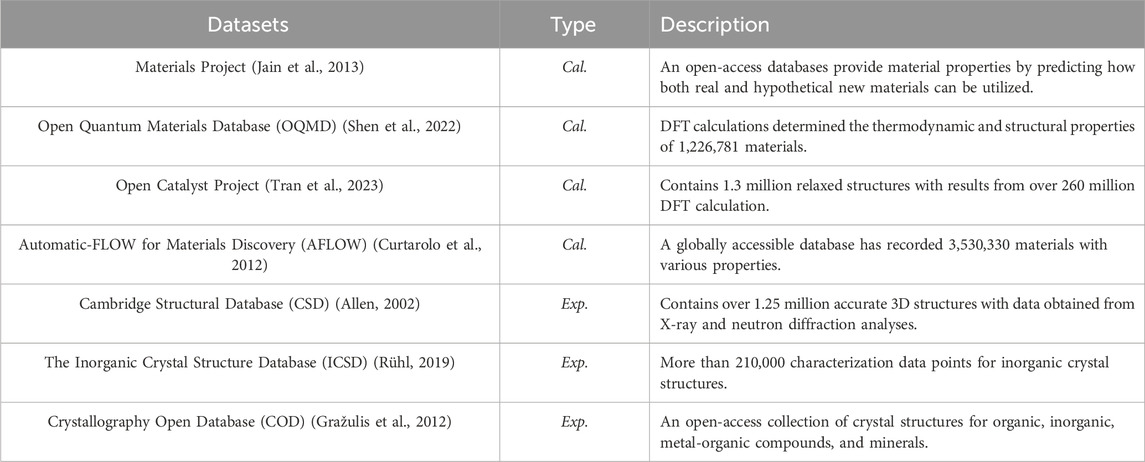
Table 1. Common datasets used for high-throughput screening and machine learning applications in the discovery of novel perovskites, with data sourced from experiments (Exp.) or calculations (Cal.). The amount of data is recorded as of August 2024, and can be still updated.
Note that the accuracy of DFT calculation is crucial. High-precision DFT ensures that the ML model learns from accurate representations of atomic structures and DFT-calculated result, which is essential for making correct predictions in new, unseen scenarios (Bogojeski et al., 2020).
2.1.6 Molecular dynamics
To evaluate time- and temperature-dependent stability, molecular dynamics (MD) simulations can assess whether a perovskite maintains structural integrity under varying environmental conditions (Lu et al., 2018). Unlike static methods such as DFT calculations, MD focuses on the dynamic and statistical properties of a system (Shi et al., 2021). Additionally, solvent effects can be considered, as they can sometimes destabilize perovskites (Tan et al., 2020). Classical MD uses empirical force fields to model these interactions, which is computationally less intensive but may be less accurate for complex systems. In contrast, ab initio molecular dynamics (AIMD) employs quantum mechanical calculations to simulate atomic interactions, providing highly accurate results.
2.2 Applications of computational methods on evaluation of stability
Predicting the structural stability of perovskites remains a significant challenge in the discovery of novel perovskites. For new perovskite materials, the use of empirical factors to assess lattice stability may vary, necessitating adjustments for specific cases. For example, the effective tolerance factor (teff) and octahedral index (μeff) for quaternary antiperovskites X6B2AA′ and X6BB′A2 are defined as follows (Han et al., 2021):
where ri (i = A, A′, B, B′, X) stands for the radii of ions in antiperovskites.
Obtained from DFT calculations, the formation energy is crucial for assessing the stability and synthesizability of perovskites. A negative formation energy indicates that the material is energetically favorable to form and is likely to be stable under standard conditions relative to its constituent elements or compounds. Thermodynamic stability is typically estimated using either the DFT formation energy (Ef, relative to its constituent elements) or the energy above the convex hull (Ehull, relative to competing phases in the phase diagram) (Wang H. et al., 2020). Here, competing phases typically refer to the most stable phases among a range of conditions of temperature, pressure, or chemical composition. The formation energy can be used to identify the most energetically favorable structure, e.g., atomic orderings and types of novel perovskites (Jain et al., 2013; Togo and Tanaka, 2015). This energy is particularly significant when applied in HTS, such as in identifying stable M3XZ antiperovskites from the Materials Project database (Singh et al., 2018). However, since different compounds would form during the decomposition process under varying conditions (e.g., pressure and temperature), the convex hull will vary. Therefore, compared to Ehull, Ef would be more practical in ML applications (Ong et al., 2008). Moreover, the incompleteness in the phase diagram or artificially stabilized phases from DFT errors can cause significant inaccuracies in Ehull (Chen C. et al., 2020). In contrast, Ef is a more reliable regression target.
In the study of novel perovskites such as antiperovskites and chalcogenide perovskites, structural distortion is of greater significance compared to traditional perovskites. These materials often display unconventional arrangements of A-site and B-site ions, resulting in pronounced structural distortions. For example, chalcogenide perovskites predominantly manifest three phases under ambient conditions compared to ideal cubic perovskite structure, namely, orthorhombic distorted phase, hexagonal phase, and needle-like phase (Tranchitella et al., 1997; Takeda et al., 1976; Lee et al., 2005; Lelieveld and IJdo, 1980). In some cases, the distorted phase exhibits better performances (Sun et al., 2015). Controlling and understanding these distortions is essential for tailoring functionalities. Furthermore, MD simulations conducted under various conditions, such as elevated temperatures, corroborate the robust stability of these hybrid chalcogenide perovskites (Baek et al., 2018; Li N. et al., 2020).
2.3 Applications of computational methods on electronic structure
The electronic structure is crucial in the research of novel perovskites such as antiperovskites and chalcogenide perovskites, as their unique electronic properties largely determine their performance. In antiperovskites, understanding the electronic structure helps elucidate their ferroelectric, topological, and transport properties, which are critical for applications in sensors, actuators, and quantum devices. Similarly, optimizing the electronic structure of chalcogenide perovskites can enhance their photovoltaic and thermoelectric performance.
The density of states (DOS) is pivotal in studying novel perovskites. The DOS at the Fermi energy significantly affects their magnetic, transport, thermoelectric, superconducting, and optoelectronic properties. The calculated electronic structure can be illustrated through a computed absorption spectrum, which corresponds to transitions between states with high DOS, providing detailed insights into how novel perovskites absorb light at different wavelengths (Kangsabanik et al., 2018; Ma et al., 2021). Dielectric properties, such as the dielectric constant and loss, impact the perovskites’ ability to store and release electric energy under an applied electric field. For novel perovskites, the dielectric response influences their suitability for various electronic applications, ranging from photovoltaics to electronic devices.
Among the various properties, the bandgap is a crucial parameter that significantly impacts performances. Tuning the bandgap is essential for optimizing the optoelectronic and thermoelectric properties of novel perovskites such as antiperovskites and chalcogenide perovskites. In photovoltaic applications, an optimal bandgap allows for efficient absorption of sunlight and conversion to electricity, maximizing the efficiency of solar cells. The Shockley-Queisser limit dictates that single-junction solar cells with an ideal bandgap of 1.34 eV can achieve a maximum solar conversion efficiency (SCE) of 33% (Rühle, 2016). Consequently, predicting or screening the bandgap is typically the initial step in computationally designing materials for solar cells (Chen C. et al., 2020). For thermoelectric applications, the bandgap influences the Seebeck coefficient and electrical conductivity, which are critical for effective thermal to electrical energy conversion. Additionally, the Seebeck coefficient and electrical conductivity are often calculated within the framework of Boltzmann transport theory using tools such as the BoltzTrap code (Schleder et al., 2019).
The Berry phase plays a significant role in the study of novel perovskites. For instance, it is used to calculate electric polarization in ferroelectric antiperovskites, aiding in determining the magnitude and direction of polarization in various states. Analyzing the change in polarization among different states, such as during a phase transition, can reveal the dynamics of polarization switching (Wang ZX. et al., 2019). Additionally, the Berry phase influences the transport properties of materials, such as the Hall effect and magnetoresistance, providing theoretical support for understanding conductivity and thermoelectric performance. By analyzing the Berry curvature, researchers can also identify and characterize topological phases in antiperovskites, such as topological insulators or Weyl semimetals (Kawakami et al., 2018).
The DFT electronic structure, derived from Kohn–Sham orbitals describing the conduction band minimum and maximum, approximate the real optical excitation problem but neglect excitonic effects; however, the accurate depiction of electronic structure is further complicated by the interplay between strong electron-electron interactions and spin-orbit coupling (SOC), which becomes important for heavy elements significantly reduce the band gap (Das et al., 2022). To address this, researchers often employ ad hoc DFT hybrid functionals tailored to match the band gap of each specific perovskite (IOPscience, 2011). While this approach introduces a degree of empiricism and limits the ability to reliably predict the properties and band gaps of unknown perovskites, it is also common practice to include SOC effects in calculations to improve accuracy (Umari et al., 2014). Through testing, G0W0 method performs best compared with experimental result but is computationally remarkably expensive. At the DFT level, HSE method gives overall the better estimation for novel perovskites (Vona et al., 2022; Fuchs et al., 2007). It is because that HSE incorporates a portion of exact exchange from Hartree-Fock theory, which helps improve the accuracy of the electronic structure calculations, particularly for systems with strong correlation effects (Janesko et al., 2009). Thus, HSE have currently widely utilized as a proper practice in the electronic structure calculation (Sun et al., 2015; Liu et al., 2021).
Some workflows were also developed to predict an accurate electronic structure. For example, Gebhardt et al. take the SOC, many-particle theory, and the dynamical behavior of the perovskites into account. The developed workflow could predict the band gaps within 0.2 eV as compared to experimental data. In some cases, the dynamical effects should be considered using the MD simulations, such for the higher symmetry of the α-phase (high-temperature) phase (Vona et al., 2022). Some workflows take the SOC, many-particle theory, and the dynamical behavior of the perovskites into account were also developed to predict an accurate electronic structure. For example, Gebhardt et al. (Gebhardt et al., 2021). developed such a workflow that comprises computations on an equal footing by efficient DFT methods and predict the band gaps within 0.2 eV as compared to experimental data.
It is worth noting that for novel perovskites, complex structural issues such as structural distortion, defects, impurities, and phase transitions under varying conditions can arise. These structural variations not only impact the perovskites’ physical properties but also induce changes in their electronic structure. For example, the electronic structure among different states of rotated BX6 octahedra reveals that it is significantly impacted by the distortion, due to the intricate hybridization from orbital interactions (Niu et al., 2018a).
3 Accelerated discovery of novel antiperovskites
As the most extensive family of perovskite materials, ABX3 -type compounds—where A and B are cations and X is typically oxygen, halide, or chalcogenide—have garnered significant global research interest due to their versatile multifunctionality and the intriguing scientific principles they embody (Protesescu et al., 2015; Nedelcu et al., 2015). A conventional perovskite structure consists of a framework of corner-sharing AX6 octahedra, with A cations occupying the interstitial sites (Varadwaj et al., 2022). In contrast to conventional perovskites, antiperovskites or so-called inverse perovskites are derivatives of the ideal perovskite structure in which the positions of cations and anions are reversed, resulting in an electronically inverted structure (Wang Y. et al., 2020; Lin et al., 2017; Zhong et al., 2023; Zhong et al., 2021; Han et al., 2022; Feng et al., 2023). Consequently, their fundamental structural unit is not a cation-centered octahedron BX6 but an anion-centered octahedron XA6. From a structural perspective, antiperovskites are expected to offer similar advantages to those of perovskite-type structures, as they can accommodate a wide range of elements, forming a diverse family of functional materials (Krivovichev, 2024). As anticipated, antiperovskites have exhibited a variety of intriguing properties, including ionic conductivity, superconductivity, negative thermal expansion, and the ability to serve as host materials for photoluminescence, among other functionalities. These properties are likely to drive a new phase of development for functional antiperovskites (Deng et al., 2022; Ohashi et al., 2020). Consequently, it is valuable to explore how computational methods can be used to strategically design antiperovskites to enhance their performance or uncover previously unforeseen phenomena.
In this section, we explore the prediction of three novel categories of antiperovskites using various simulation methods, offering a detailed explanation of each simulation process. Additionally, we compare the simulation results with corresponding experimental reports, demonstrating the good alignment of experimental results with theoretical calculations.
3.1 Quaternary antiperovskite materials
In a recent study, two novel classes of pnictogen-based quaternary antiperovskites, with the formulas X6B2AA′ and X6BB′A2, were devised through ion type inversion and anion ordering on perovskite lattice sites (Han et al., 2021). Their phase stability and tunable band gaps were comprehensively predicted using DFT calculations. Further screening of these materials for photovoltaic applications identified several stable compounds with suitable direct band gaps, small carrier effective masses, low exciton binding energies, and strong optical absorption due to dipoles, making them promising candidates for photovoltaic absorber materials. Notably, the theoretical maximum solar cell efficiencies for these stable antiperovskites exceed 31%, which is comparable to or even surpasses the efficiencies of MAPbI3 -based (MA = methylamine) solar cells (Han et al., 2021). This simulation study highlights the significant potential of quaternary antiperovskites in the optoelectronic field and provides a novel approach to designing lead-free and air-stable perovskite-based photovoltaic absorber materials.
To predict the quaternary compositions and their corresponding lattice structures, DFT calculations were performed (Perdew et al., 1996; Kresse and Furthmüller, 1996). Unlike the typical perovskite configuration ABX3, antiperovskites X3BA feature an electronically inverted structure with one cationic X-site and two anionic A- and B-site, as illustrated in Figure 1. Building on previous reports that all-inorganic antiperovskites X3NA, where X represents divalent metals and A represents pnictogens, exhibit favorable optoelectronic properties for photovoltaic applications, the structure X3BAX was transformed into two novel quaternary antiperovskites: X6B2AA and X6BB′A2 through anion ordering. This process involves splitting the anionic A- or B-site, leading to a total of 48 potential component combinations, as shown in Figure 1.
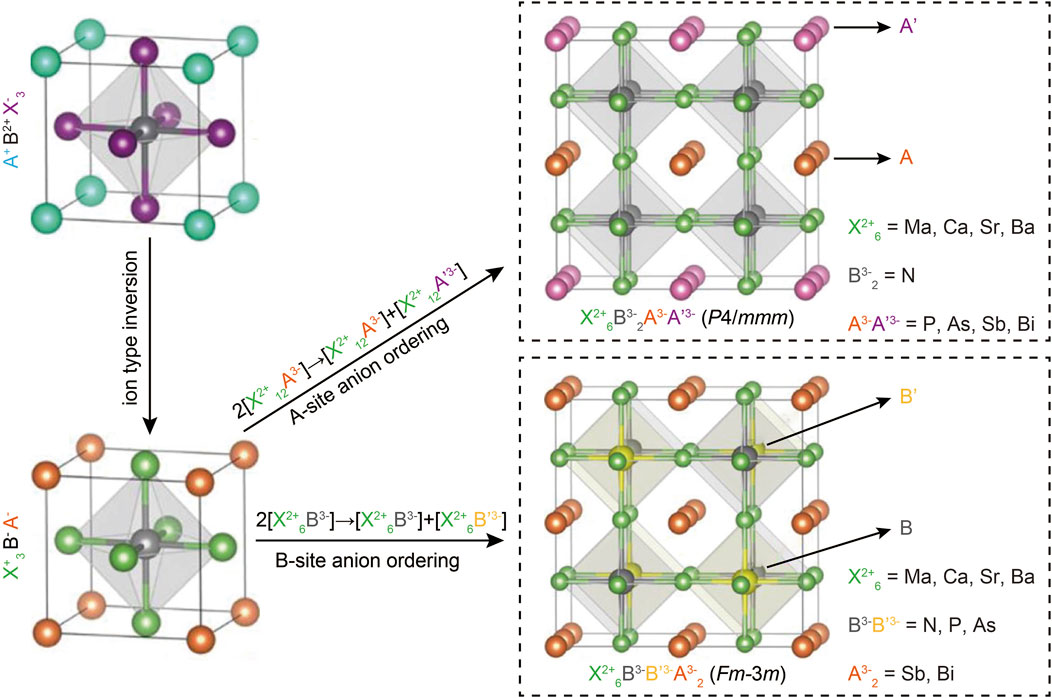
Figure 1. The schematic of two novel quaternary antiperovskites derived from typical cubic halide perovskites, along with the potential compositions. Reprinted with permission from Ref. (Han et al., 2021). Copyright 2021, American Chemical Society.
The prediction of potential antiperovskites began by identifying the most energetically favorable anionic ordering types in two structures (Jain et al., 2013; Togo and Tanaka, 2015). A supercell was constructed by doubling the standard cubic distortion-free unit cell of the antiperovskite X3BA. Various arrangements of AA′ and BB′ anionic pairs, denoted as A to F, were then considered within this supercell, as illustrated in Figure 2A. The calculated total energies of two A-site ordered quaternary antiperovskites (Mg6 N2SbBi and Sr6 N2 AsBi) and two B-site ordered quaternary antiperovskites (Mg6NPSb2 and Ca6 NAsBi2) were presented as examples. Simulation results show that the favored configurations of A- and B-site anion ordering in quaternary antiperovskites align with the cation ordering observed in conventional double perovskite oxides. Specifically, A-site cations tend to exhibit tetragonal layered ordering, while B-site cations prefer cubic rock-salt type ordering (King and Woodward, 2010). It is noteworthy that the simulated energy differences between various configurations of A-site cation-ordered regular double perovskites are typically minor, a finding consistent with previous reports (Gou et al., 2017).
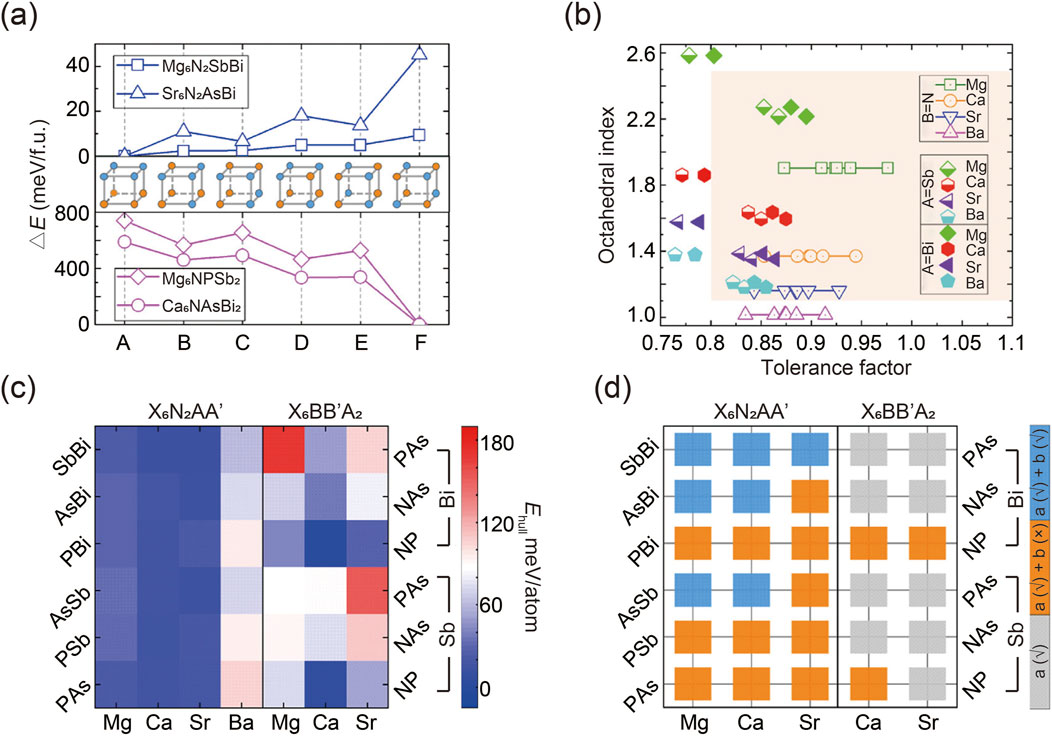
Figure 2. (A) Calculated total energies of two quaternary antiperovskites. (B) Statistical graph of potential quaternary antiperovskites involving tolerance factor and octahedral index. (C) Decomposition energy Ehull of two antiperovskites. (D) Evaluation of dynamic stability of thermodynamically stable antiperovskites. Gray squares represent compounds that are thermodynamically unstable, orange squares denote compounds that are thermodynamically stable but dynamically unstable, and blue squares indicate compounds that are stable both thermodynamically and dynamically. Reprinted with permission from Ref. (Han et al., 2021). Copyright 2021, American Chemical Society.
To evaluate the lattice stability of the quaternary antiperovskites of interest, empirical metrics such as the tolerance factor and octahedral index were calculated (Travis et al., 2016; Goldschmidt, 1926; Kieslich et al., 2015; Kieslich et al., 2014). The results, shown in Figure 2B, indicate that most predicted compositions fall within the empirically stable region of traditional perovskites, while several unstable components were excluded.
Equally important as crystalline stability is thermodynamic robustness, which estimates the ease of decomposition for predicted compounds. Generally, a negative decomposition energy or Ehull indicates thermodynamic stability against degradation. Researchers integrated DFT calculations for specific quaternary compounds with data on all relevant elemental substances and binary and ternary phases from the Materials Project database. This approach expedited the assessment of thermodynamic stability, as illustrated in Figure 2C (Jong et al., 2016). By establishing a suitable threshold for Ehull (e.g., 25 meV/atom in this report, corresponding to kBT at room temperature), potential antiperovskites can be categorized as either thermodynamically stable or unstable, considering the potential for entropic stabilization (Dawson et al., 2018; Lu et al., 2020). Based on this criterion, several specific antiperovskites were identified as thermodynamically stable. Notably, compositions with large Ehull consistently exhibited crystallographic instability, suggesting a correlation between structural stability and thermal stability.
Furthermore, in addition to thermodynamic stability, dynamic stability—reflecting the gradual distortion of the structure over time—was assessed through phonon spectrum computations using the frozen phonon simulation technique (Togo and Tanaka, 2015). As shown in Figure 2D, seven quaternary antiperovskites are dynamically stable because they exhibit no imaginary modes (Han et al., 2021). Interestingly, simulation results reveal that antiperovskites with a higher degree of asymmetry demonstrate greater stability compared to typical cubic perovskites ABX3 and double perovskites A2 BB′X6. This finding is contrary to conventional expectations (Flerov et al., 1998; Glazer, 1972; Howard et al., 2003). As a result, distorted quaternary antiperovskites show promise for photovoltaic applications due to their enhanced dynamic stability and increased structural distortion, which can amplify the photoelectric effect through the boundary-breaking bulk photovoltaic effect.
3.2 Antiperovskite molecular ferroelectrics
Ferroelectrics are multifunctional electroactive materials with a wide range of applications (Liu et al., 2018a; Liu et al., 2018b). Their temperature-dependent spontaneous polarization can be modulated by electric fields or mechanical forces, making them highly suitable for temperature sensing, data storage, mechanical actuation, and energy harvesting (Liu et al., 2018c; Hussain et al., 2022; Liu et al., 2017). The phenomenon of ferroelectricity was first discovered in 1921 with Rochelle salt, followed by the identification of ferroelectric properties in other molecular systems. Significant progress in ferroelectric research was achieved with the discovery of ferroelectricity in perovskite materials like barium titanate (BTO) and lead zirconate titanate (PZT) (Lupascu and Rödel, 2005; Heywang, 1971; Luo et al., 2003; Vijatovic et al., 2008).
Unlike all-inorganic ferroelectrics, organic-inorganic hybrid ferroelectrics—often termed molecular ferroelectrics—offer several advantages, including lightweight construction, mechanical flexibility, and environmentally sustainable processing methods (Peng et al., 2020; Siwach et al., 2022; Liu et al., 2020). Recent studies have highlighted significant advancements in molecular ferroelectrics, characterized by high Curie temperatures, superior piezoelectric coefficients compared to all-inorganic ferroelectrics, sensitivity to polarized light due to chirality, photochromic properties, enhanced electrocaloric effects, and lanthanide-mediated fluorescence emission (Xu et al., 2020; Shi et al., 2020b; Xu et al., 2021; Xu et al., 2011; Fu et al., 2011; Tang et al., 2019; Zhang Y. et al., 2020; Shi et al., 2017).
Since ferroelectric properties arise from the polarization asymmetry within the crystal lattice, DFT calculations can provide theoretical insights into the dynamics of polarization switching during the ferroelectric-paraelectric phase transition (Wang ZX. et al., 2019). The following example illustrates meticulously engineered antiperovskite molecular ferroelectric materials. Specifically, substituting one of the methyl groups in [(CH3)3NH]-CdCl3 with an ethyl group disrupted the existing mirror plane, potentially resulting in a polar crystal capable of displaying ferroelectric behavior. To further diminish the crystal symmetry, a fluorination strategy was employed to replace the ethyl group, thereby converting the perovskite structure into antiperovskites, as shown in Figure 3A (Zhang et al., 2020b; Shi et al., 2019). This compound demonstrates a ferroelectric phase below its TC, while a paraelectric phase emerges above the phase transition point (Wang ZX. et al., 2019).
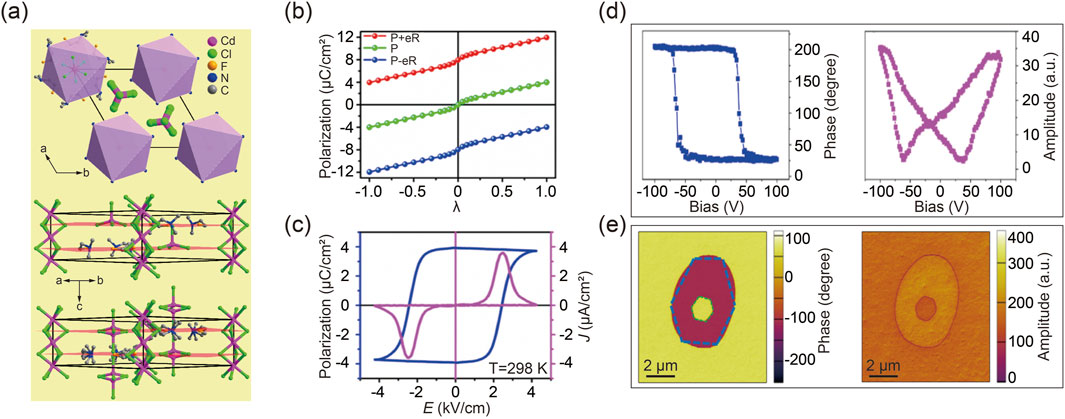
Figure 3. (A) The arrangement of designed antiperovskite molecular ferroelectrics [(CH3)2(F-CH2CH2) NH]6-CdCl3 (upper), along with its corresponding packing views in the ferroelectric (middle) and paraelectric (bottom) phases. (B) DFT calculated polarization strength as a function of structure distortion from nonpolar paraelectric phase to ferroelectric phases. (C) Spontaneous polarization strength as temperature varies, determined through the integration of pyroelectric current. (D) Typical phase and amplitude characteristics as a function of tip bias in molecular ferroelectrics. Reprinted with permission from Ref (Wei Z. et al., 2018). Copyright 2018, American Chemical Society. (E) Box-box switching of vertical phase (left) and amplitude (right) images. Reprinted with permission from Ref (Wang ZX. et al., 2019). Copyright 2019, American Chemical Society.
The observed structural distortion in the ferroelectric phase accounts for both the organic cations and inorganic anions, considering the symmetry transition of the crystal structure. As illustrated in Figure 3B, DFT calculations define the paraelectric configuration as λ = 0 and the ferroelectric phase as λ = 1. Simulation results reveal that the polarization variation along the dynamic path shows that the positive extremum of ferroelectric polarization, initially along the c-axis from the starting state of λ = 1, gradually diminishes to zero at λ = 0 and then reverses to reach the end state of λ = −1 with negative extremum polarization [48]. This progression indicates a ferroelectric-paraelectric-ferroelectric phase transition, in alignment with previous studies on ferroelectric perovskites (Shi et al., 2020a; Wang S. et al., 2020; Pan et al., 2017). Subsequent experimental data have validated the DFT calculations’ accuracy, as depicted in Figure 3C. It is important to note that, according to recent polarization theory, quantum polarization might exaggerate the polarization strength, which should be excluded from calculations.
A fundamental characteristic of ferroelectrics is their electrically switchable spontaneous polarization. Therefore, a local Piezo-response Force Microscopy (PFM)-based hysteresis loop measurement was performed for antiperovskite molecular ferroelectrics, as shown in Figure 3D. The distinct 180° reversal of the PFM phase signal and the characteristic butterfly loop in the amplitude signal are indicative of polarization switching within ferroelectric domains (Fu et al., 2013; Zhang et al., 2013; You et al., 2017; Rabe et al., 2007; Resta, 1994; Spaldin, 2012). Furthermore, to further investigate dynamic ferroelectric switching in antiperovskite molecular ferroelectrics, an equal but opposite bias was applied to the materials. A box-in-box contrast image was then captured during both phase and amplitude transitions, as demonstrated in Figure 3E (Li L. et al., 2020; Zhang et al., 2020c; Wei et al., 2020).
In addition to demonstrating powerful capabilities in predicting compositions and functionalities for quaternary antiperovskites and antiperovskite molecular ferroelectrics, computational methods have also played a significant role in accelerating the development of compositions with advanced X-ray detection capabilities. In a very recent study, a novel antiperovskite (2-Habch)3Cl(PtI6) was developed that features indirect transition and low orbital symmetry (Liu et al., 2024). These characteristics enable such material to exhibit a carrier lifetime exceeding 3 ms, resulting in remarkable carrier mobility (μτ = 6.25 × 10−3 cm2 V−1) and high resistivity (1012 Ω cm). The electrical performance of this antiperovskite surpasses that of most existing X-ray detector materials. In-depth DFT calculations reveal that the low-dimensional characteristics of this material are the reason for the localized behavior of its band structure in various directions. Additionally, the low symmetry of the Pt 5d orbitals significantly reduces the dipole matrix elements. The indirect band gap nature of the material further decreases the dipole matrix elements.
In another groundbreaking study, researchers developed an atomic-position splitting method to design novel antiperovskites, effectively resolving the issue of suboptimal photovoltaic performance in previously reported antiperovskites (Tang et al., 2024). This research introduced a class of antiperovskite-derived materials with the formula X3BA3’, achieved by splitting the A anion, originally positioned at the corner site of the cubic antiperovskite structure, into three edge-centered sites, thereby preserving the three-dimensional octahedral framework. First-principles calculations confirmed that these potential compositions exhibit robust thermodynamic and dynamical stability. Notably, nine promising derivatives demonstrated maximum solar conversion efficiencies exceeding 24.5%, comparable to MAPbI3. Moreover, interpretable machine learning techniques were developed to identify critical regulatory factors that influence their thermodynamic stability and band gap. Therefore, computational methods play a crucial role in the design and development of novel semiconductor materials, guiding the optimization of their outstanding optoelectronic properties.
4 Accelerated discovery of chalcogenide perovskites
Over the past decade, there has been an unprecedented surge of interest in inorganic-organic hybrid perovskites, driven by their diverse chemical and physical properties (Egger et al., 2016). This intensified focus has led to significant breakthroughs, particularly highlighted by the dramatic increase in solar energy conversion efficiency from 3.8% to 25.5% within just 10 years (Kojima et al., 2009). Despite these advances, persistent challenges such as toxicity, degradability, and instability remain substantial barriers to their widespread industrial adoption. As a result, researchers are turning their attention to a new class of perovskites known as chalcogenide perovskites. Characterized by their lead-free composition, natural abundance in the Earth’s crust, and exceptional stability under ambient conditions, these perovskites offer a promising solution to the limitations of their predecessors (Swarnkar et al., 2019). Numerous experimental studies have successfully synthesized chalcogenide perovskites, revealing their potential and advantageous properties (Nie et al., 2018; Liang et al., 2023; Niu et al., 2018b; Niu et al., 2018c; Cao et al., 2014).
4.1 Typical chalcogenide perovskites ABX3
Inspired by halide perovskites, chalcogenide perovskites are expected to display distinctive properties due to their ABX3 configuration, where A represents bivalent metals, B denotes tetravalent cations, and X stands for either sulfur (S) or selenium (Se) (Perera et al., 2016). As illustrated in Figure 4A, unlike the conventional perovskite structure, which is typically free of distortion, chalcogenide perovskites primarily exhibit three phases under ambient conditions, including orthorhombic distorted phase (No. 62, Pnma), hexagonal phase (No. 194, P63/mmc), and needle-like phase (No. 62, Pnma) (Tranchitella et al.; Takeda et al., 1976; Lee et al., 2005; Lelieveld and IJdo, 1980). Throughout these phase transitions, alterations in coordination numbers frequently occur. For instance, in the hexagonal phase, the cation coordination is analogous to that in the cubic perovskite structure, with A/B-site cations adopting a 12/6-coordination arrangement. Conversely, in the needle-like phase, the coordination number of the A cation is reduced to 9, signifying a collapse of the perovskite structure.
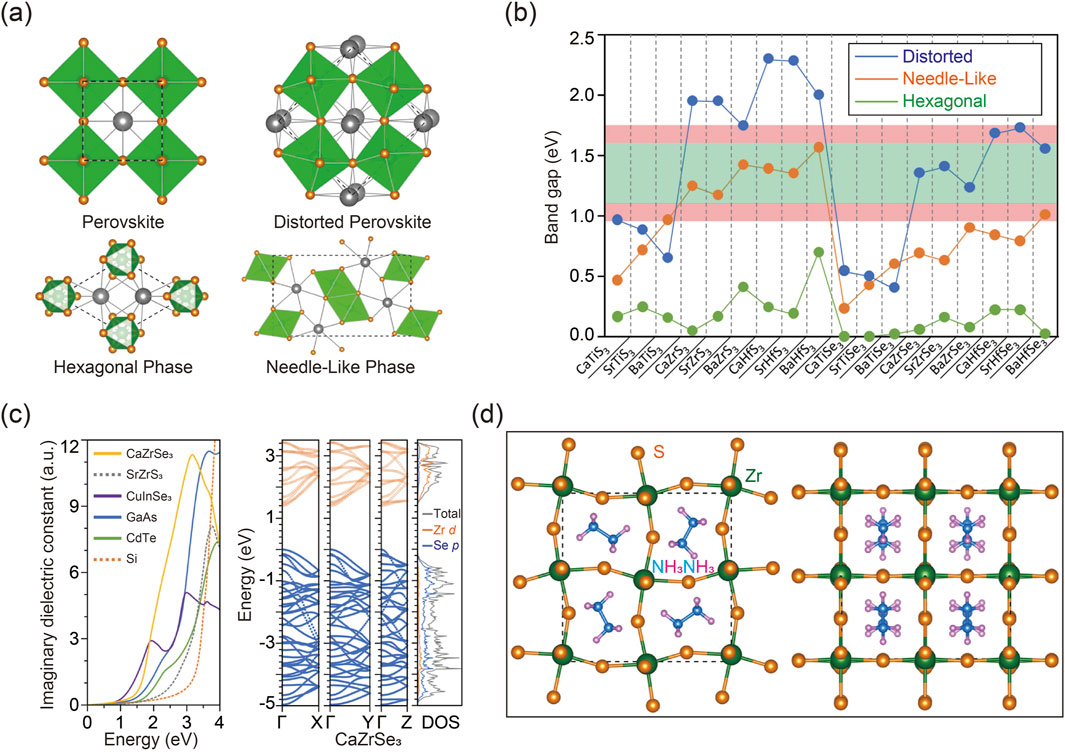
Figure 4. (A) Various phases for the ABX3 chalcogenide perovskites of cubic perovskite phase without distortion (upper left), distorted perovskite phase (upper right), hexagonal phase (bottom left), and needle-like phase (bottom right). (B) Calculated bandgaps of ABX3 chalcogenide perovskites obtained using DFT calculation. (C) Imaginary dielectric constant computed for CaZrSe3 with distorted perovskite phase and SrZrS3 with the needle-like phase according to DFT calculation (left). Band structure as well as the DOS of CaZrSe3 in the distorted perovskite phase (middle). Site-projected DOS alongside total DOS (right). (D) Atomic configuration of CH3NH3ZrS3 viewed along the c-axis (left) and perpendicular to the c-axis (right). Reprinted with permission from Ref (Sun et al., 2015). Copyright 2015, American Chemical Society.
The band gaps of predicted chalcogenide perovskites were simulated using various calculation methods with carefully optimized parameters to ensure precision (Perera et al., 2016; Sun et al., 2015; Basera and Bhattacharya, 2022; Guo and Wang, 2019; Sun et al., 2019; Ju et al., 2017). As depicted in Figure 4B, simulation results reveal that, among the same chalcogenide perovskites, the distorted perovskite phase generally exhibits the largest band gap, while the hexagonal phase often shows the smallest band gap. Additionally, sulfide perovskites typically demonstrate larger band gaps compared to their selenide counterparts in both distorted and needle-like phases. This is attributed to the lower energy level of sulfur’s 3p orbitals compared to selenium’s 4p orbitals. Moreover, Hf-based chalcogenide perovskites usually exhibit larger band gaps compared to Zr-based counterparts, owing to the higher energy level of Hf 5d orbitals relative to Zr 4d orbitals. Importantly, the band gap calculations of potential chalcogenide perovskites have identified several promising candidates with suitable optical absorption ranges for solar cell applications. For example, some Zr- and Hf-based chalcogenide perovskites with needle-like or distorted phases and appropriate band gaps are suitable for solar cell fabrication, whereas their hexagonal counterparts, with relatively smaller band gaps, are less effective within the visible spectrum. Furthermore, the simulations confirm that several compositions with direct band gaps exhibit high power conversion efficiencies approaching the theoretical Shockley-Queisser limit, as indicated within the light red range in Figure 4B, highlighting their promising potential for photovoltaic applications (Shockley and Queisser, 1961).
The imaginary component of the dielectric function is a critical parameter for evaluating the optical absorption of semiconductor materials, with a higher dielectric constant generally indicating more intense absorption. Researchers have thus employed calculations to assess the absorption characteristics of chalcogenide perovskites, aiming to further evaluate their effectiveness for solar energy harvesting applications. Figure 4C displays the computational results of the dielectric function, compared to those of well-established solar cell materials (Burst et al., 2016; Adachi, 1985; Rockett and Birkmire, 1991; Ruch and Kino, 1968; Wasim, 1986). Among these compounds, CaZrSe3 in the distorted perovskite structure shows a dielectric function comparable to that of the commercial CuInSe2, suggesting its promising potential as a photovoltaic material. In contrast, although Zr- and Hf-based sulfide perovskites in the needle-like phase possess suitable band gaps, their optical absorption edges significantly surpass their fundamental band gaps. Consequently, chalcogenide perovskites in the needle-like phase exhibit indirect band gaps, making them unsuitable for solar cell applications. A deeper understanding of these distinctions can be obtained by analyzing their band structures using computational methods, as illustrated in Figure 4C. The lowest conduction bands display greater dispersion along the direction of the octahedral chains compared to the perpendicular directions, resulting in higher anisotropy of electron mobility in the hexagonal and needle-like phases compared to the distorted perovskite phase.
To identify additional potential chalcogenide perovskites, computational methods combined with stability assessments can be utilized through A- and B-site substitutions. It is noteworthy that substituting A-site constituents generally has a minimal impact on the overall properties of perovskite materials (Baek et al., 2018; Li N. et al., 2020). For example, inorganic A-site metals can be replaced with organic molecular cations, as demonstrated by the case of BaZrS3 depicted in Figure 4D. Computational results indicate that the band structure and properties of the optimized compounds closely mirror those of the original material. Additionally, AIMD simulations performed at elevated temperatures confirm the exceptional stability of these hybrid chalcogenide perovskites. These findings highlight the crucial role of computational methods not only in predicting material properties but also in expanding the range of possible material types.
4.2 Ruddlesden−Popper chalcogenide perovskites A3B2X7
Ruddlesden−Popper (R-P) phases, a specific structural type within perovskite materials, are characterized by the general formula A2' [An-1BnX3n+1] and form two-dimensional (2D) geometrical configurations (Chen et al., 2018; Yu et al., 2017). These atomically thin layered structures exhibit notable octahedral rotations and distortions, which can lead to non-centrosymmetric configurations essential for polar characteristics and ferroelectric properties (Wang et al., 2016). Like conventional perovskite materials, chalcogenide perovskites can be engineered into two-dimensional R-P layered structures through compositional modifications, as indicated by simulation results. This approach enables the development of a wider variety of chalcogenide perovskite compounds.
The packing structure of R-P A3B2X7 chalcogenide perovskites is illustrated in Figure 5A, where two neighboring corner-sharing BX6 octahedra are separated by an intercalated AX layer (Niu et al., 2018a). To gain a deeper understanding of the bonding characteristics and stability of the 2D layered structure, an electron localization function (ELF) simulation was conducted using Ca3Sn2S7 as an example, as shown in Figure 5B (Du and Shi, 2019). An ELF value approaching zero indicates a metal-chalcogenide ionic bond with minimal electron density between the ions. Conversely, an ELF value approaching one signifies a strong covalent bond. Notably, the simulation reveals a partial covalent bond with an ELF value approximately 0.25 between Sn4+ and S2-, which contrasts with the ionic bonds typically found in halide perovskites (Cai et al., 2018). This Sn-S covalent bonding enhances the structural stability and charge transfer efficiency in 2D R-P chalcogenide perovskites. Additionally, compared to halide perovskites, the structural integrity of R-P chalcogenide perovskites is further reinforced by stronger Coulomb interactions among ions with higher valence states.
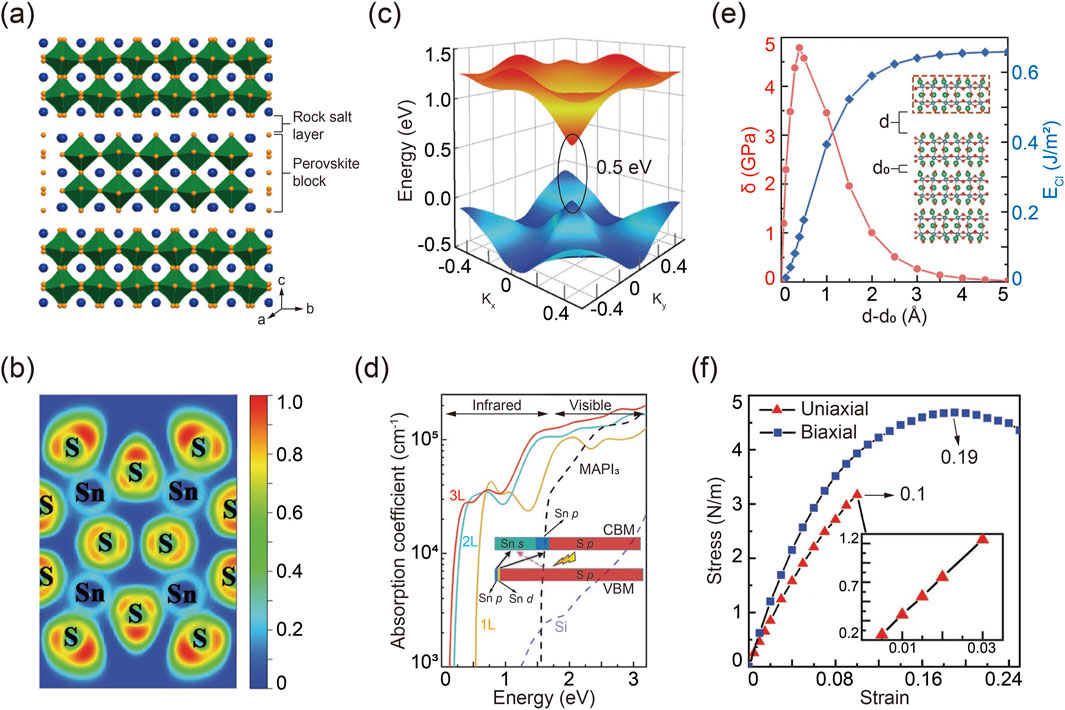
Figure 5. (A) Schematic packing configuration of R-P chalcogenide perovskites. Reprinted with permission from Ref (Niu et al., 2018a). Copyright 2018, American Chemical Society. (B) Simulated Sn-S bonding feature in R-P Ca3Sn2S7. (C) Three-dimensional band structure and corresponding bandgap of Ca3Sn2S7. (D) Calculated absorption behavior of R-P Ca3Sn2S7. (E) Calculated cleavage energy ECl and corresponding cleavage strength σ, varied by the distance of d-d0. (F) Stress evolution as a function of strain in R-P Ca3Sn2S7 under uniaxial and biaxial modes. Reprinted with permission from Ref (Du and Shi, 2019). Copyright 2019, Wiley.
Simulation methods were employed to investigate the band structure of R-P chalcogenide perovskites. It is important to note that standard DFT calculations tend to underestimate band gaps. Therefore, the modified GGA-1/2 method proved more accurate for determining the true band gap. The three-dimensional band structure, illustrated in Figure 5C, highlights the band edge dispersion features of R-P chalcogenide perovskites. Remarkably, these materials exhibit semiconductor properties like graphene, characterized by linear electronic band edge dispersion and a relatively small direct quasi-particle band gap. Further band structure calculations under various configurations of rotated octahedra show that the electronic structure is notably influenced by the distortion of the BX6 octahedra, due to the complex hybridization from the interaction between the delocalized p orbitals of S and the s orbitals of Sn atoms (Niu et al., 2018a). According to the optimized band structure, R-P chalcogenide perovskites demonstrate intriguing optical absorption characteristics, as depicted in Figure 5D (Ravindran et al., 1997). They exhibit a broad absorption spectrum extending from the infrared to the ultraviolet regions, with absorption intensity increasing by two orders of magnitude in the infrared range, attributed to their direct band gap. Notably, the absorption edge shifts to higher energies with a decrease in layer number, due to the quantum confinement effect. Furthermore, the optical absorption capacity and spectral width of R-P chalcogenide perovskites surpass those of other advanced photovoltaic materials, such as MAPbI3 and silicon, highlighting their promising potential for solar cell applications (Wu et al., 2017; Alsalloum et al., 2020).
Mechanical exfoliation techniques are commonly used to obtain 2D monolayer materials from their 3D counterparts, which requires that the layered materials exhibit weak interlayer interactions (Liao et al., 2018; Huang et al., 2020; Yi and Shen, 2015). R-P chalcogenide perovskites, being a type of layered material, are amenable to easy exfoliation. The calculated cleavage energy ECl, defined as the minimum energy required to overcome interlayer coupling during the exfoliation process, is depicted in Figure 5E (Medvedeva et al., 1996; Zhao et al., 2014). As the separation distance increases, ECl reaches its maximum value but remains significantly lower compared to other layered materials such as Ca2N (Druffel et al., 2016). Similarly, the cleavage strength σ shows a comparable trend.
Beyond exfoliation characteristics, mechanical strength and elastic strain limits are crucial, determined by analyzing the stress-strain relationships of layered chalcogenide perovskites. The Young’s modulus, obtained from the stress-strain curve using linear regression, is shown in Figure 5F. Notably, the stress-strain curves along the x-direction and y-direction are identical, indicating that 2D layered chalcogenide perovskites are isotropic elastic materials. As tensile strain increases, these perovskites approach their breaking limit, with an elastic strain limit of approximately 20%, comparable to layered MoS2 and graphene (Andrew et al., 2012; Mortazavi and Cuniberti, 2014).
In addition to optical and mechanical properties, DFT calculations predict the potential for ferroelectricity in R-P layered chalcogenide perovskites. Simulation results demonstrate that ferroelectric chalcogenide perovskites A3B2X7 can transform from their paraelectric ABX3 counterparts (Wang et al., 2016). Theoretical analysis highlights the tolerance factor as a key determinant of ferroelectric behavior (Zhang et al., 2017). For example, both Ba3Zr2S7 and Ba3Hf2S7, which have large tolerance factors, remain paraelectric due to the suppression of in-phase rotation—an essential feature for hybrid improper ferroelectricity. In contrast, Ca3Zr2S7, Ca3Hf2S7, and Ca3Zr2Se7, with smaller tolerance factors, exhibit in-phase rotation and can stabilize into the ferroelectric phase with significant polarization.
4.3 Other potential chalcogenide perovskites
In addition to ABX3- and A3B2X7-type chalcogenide perovskites, computational methods have predicted the potential of other chalcogenide perovskite variants, including NaBiX2, A′La2BX10 (where A′ = Ba, Sr, Ca; B = Hf, Zr), CsLnMX3 (where Ln = rare earth elements; M = Zn, Cd, Hg), and A2MM′X6 (where M = Bi or Sb; M′ = V, Nb, Ta), which are in their early research stage. Each of these materials offers unique advantages. For example, NaBiS2 exhibits higher absorption coefficients compared to established direct-bandgap thin-film absorbers and has potential as a photocatalyst for degrading organic matter (Huang et al., 2022; Rosales et al., 2018; Kumar et al., 2022). Additionally, A’La2BX10 shows higher carrier mobility, stronger optical absorption intensity, and an optimal Shockley-Queisser limit, making it a promising candidate for solar cell materials (lang et al., 2020). Lanthanides in CsLnMX3 can display characteristic emission through intrinsic 4f-4f transitions (Park et al., 2022; Yao et al., 2004; Mitchell et al., 2003; Jin et al., 2007). Furthermore, Sb-doped SrHfSe3 chalcogenide perovskites are predicted to possess thermoelectric properties due to their p-type semiconducting nature (Moroz et al., 2018).
5 Outstanding challenges and future perspectives
The exploration of novel perovskites, including antiperovskites and chalcogenide perovskites, represents a significant advancement in materials science. These materials offer unique properties that extend the functionalities of traditional perovskites, presenting promising opportunities for applications in energy, electronics, and other high-tech industries. In this review, we highlight the crucial role of advanced computational methods in the discovery and optimization of these novel perovskites, particularly focusing on antiperovskites and chalcogenide perovskites. We elaborate the computational techniques used to assess the stability and electronic structure of these materials, which accelerate the discovery process of new perovskites. Overall, the integration of advanced computational methods with experimental approaches is driving the development of the next-generation of high-performance perovskite materials.
Although the application of computational methods in discovering novel perovskites has advanced significantly in recent years, there are still many key challenges and opportunities within this emerging field, especially for ML techniques.
5.1 Interpretability of machine learning techniques
ML techniques have significantly accelerated the identification of promising materials by efficiently exploring vast chemical spaces. However, a key challenge is developing ML techniques that are not only accurate but also interpretable. Scientific disciplines often prefer simpler, more interpretable models over complex “black box” approaches. To enhance model interpretability, several strategies can be employed:
(1) Graph-Based Models. These models encode bonding relationships between atoms in crystals, creating frameworks that naturally incorporate physical and chemical constraints. This approach helps make the models more interpretable by aligning with known chemical principles.
(2) Symbolic Regression. This technique generates mathematical formulas or visual representations that illustrate how input features influence model predictions. By revealing the underlying relationships between features and predictions, symbolic regression helps demystify the “black box” nature of deep learning models.
5.2 Data challenges and solutions
Another major challenge in applying ML to materials science is the limited availability of high-quality data, particularly for specific and difficult-to-measure properties. While datasets for general properties like formation energies and band gaps are relatively abundant, niche properties such as alkali ionic conductivities or surface binding energies often suffer from data scarcity. To address these challenges, several strategies can be employed.
(1) Transfer Learning. This approach leverages knowledge from well-established models in domains with ample data (e.g., formation energies) to enhance model performance in areas with limited data (e.g., elastic moduli). By transferring insights from one domain to another, transfer learning can help mitigate data scarcity issues and improve predictive accuracy.
(2) Data Fusion: Combining data from various sources or types, such as integrating computational data with experimental results, can enhance the quality of overall dataset and provide a more comprehensive basis for model training.
By employing strategies, researchers can address the data limitations in the discovery of novel perovskites and improve the effectiveness of ML models.
Although aforementioned challenges related to small data, transfer learning, and data fusion have been well-established in materials science field, they are particularly pertinent in this emerging field where the exploration of novel perovskites often outpaces the availability of high-quality data. Our discussion goes beyond simply acknowledging these challenges by highlighting recent advancements and specific strategies tailored to overcome data limitations in the context of novel perovskites. For instance, we explore how graph-based models and symbolic regression can enhance the interpretability of ML techniques in these materials, making the “black box” nature of models more transparent. Such techniques are particularly usefully in crystals system like perovskites.
6 Conclusion
The exploration of novel perovskites, such as antiperovskites and chalcogenide perovskites, represents a significant advancement in materials science. These materials exhibit unique properties that extend the functionalities of traditional perovskites, offering promising opportunities for applications in energy, electronics, and other high-tech industries. In this review, the pivotal role of advanced computational methods in the discovery and optimization of novel perovskite have been highlighted, particularly antiperovskites and chalcogenide perovskites. It discusses the computational methods employed to evaluate the stability and electronic properties of these materials, thus, to accelerated discovery process of novel perovskites. Overall, the combination of advanced computational methods with experimental work is paving the way for the development of the next-generation of high-performance novel perovskite.
Author contributions
MS: Conceptualization, Data curation, Methodology, Resources, Software, Validation, Visualization, Writing–original draft. SW: Conceptualization, Funding acquisition, Project administration, Visualization, Writing–original draft. HZ: Formal Analysis, Validation, Writing–review and editing. ZL: Investigation, Supervision, Writing–review and editing. GZ: Funding acquisition, Project administration, Validation, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by Natural Science Foundation of Shandong Province (ZR2024QE319, ZR2024QF165, ZR2024QE167).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adachi, S. (1985). GaAs, AlAs, and Al x Ga1− x As: material parameters for use in research and device applications. J. Appl. Phys. 58 (3), R1–R29. doi:10.1063/1.336070
Allam, O., Holmes, C., Greenberg, Z., Kim, K. C., and Jang, S. S. (2018). Density functional theory – machine learning approach to analyze the bandgap of elemental halide perovskites and ruddlesden-popper phases. ChemPhysChem. 19 (19), 2559–2565. doi:10.1002/cphc.201800382
Allen, F. H. (2002). The Cambridge Structural Database: a quarter of a million crystal structures and rising. Acta Crystallogr. Sect. B 58 (3–1), 380–388. doi:10.1107/s0108768102003890
Alsalloum, A. Y., Turedi, B., Zheng, X., Mitra, S., Zhumekenov, A. A., Lee, K. J., et al. (2020). Low-temperature crystallization enables 21.9% efficient single-crystal MAPbI 3 inverted perovskite solar cells. ACS Energy Lett. 5 (2), 657–662. doi:10.1021/acsenergylett.9b02787
Andrew, R. C., Mapasha, R. E., Ukpong, A. M., and Chetty, N. (2012). Mechanical properties of graphene and boronitrene. Phys. Rev. B 85 (12), 125428. doi:10.1103/physrevb.85.125428
Baek, S., Kim, S., Noh, J. Y., Heo, J. H., Im, S. H., Hong, K., et al. (2018). Development of mixed-cation Cs x Rb 1– x PbX 3 perovskite quantum dots and their full-color film with high stability and wide color gamut. Adv. Opt. Mater. 6 (15), 1800295. doi:10.1002/adom.201800295
Basera, P., and Bhattacharya, S. (2022). Chalcogenide perovskites (abs 3; A = Ba, Ca, Sr; B = Hf, Sn): an emerging class of semiconductors for optoelectronics. J. Phys. Chem. Lett. 13 (28), 6439–6446. doi:10.1021/acs.jpclett.2c01337
Bogojeski, M., Vogt-Maranto, L., Tuckerman, M. E., Müller, K.-R., and Burke, K. (2020). Quantum chemical accuracy from density functional approximations via machine learning. Nat. Commun. 11, 5223. doi:10.1038/s41467-020-19093-
Burst, J. M., Duenow, J. N., Albin, D. S., Colegrove, E., Reese, M. O., Aguiar, J. A., et al. (2016). CdTe solar cells with open-circuit voltage breaking the 1 V barrier. Nat. Energy 1 (3), 16015. doi:10.1038/nenergy.2016.15
Cai, B., Chen, X., Xie, M., Zhang, S., Liu, X., Yang, J., et al. (2018). A class of Pb-free double perovskite halide semiconductors with intrinsic ferromagnetism, large spin splitting and high Curie temperature. Mater Horiz. 5 (5), 961–968. doi:10.1039/c8mh00590g
Cao, S., Liu, T., Hussain, S., Zeng, W., Peng, X., and Pan, F. (2014). Hydrothermal synthesis of variety low dimensional WS2 nanostructures. Mater. Lett. 129, 205–208. doi:10.1016/j.matlet.2014.05.013
Chen, C., Zuo, Y., Ye, W., Li, X., Deng, Z., and Ong, S. P. (2020a). A critical review of machine learning of energy materials. Adv. Energy Mater. 10 (8), 1903242. doi:10.1002/aenm.201903242
Chen, X. G., Song, X. J., Zhang, Z. X., Li, P. F., Ge, J. Z., Tang, Y. Y., et al. (2020b). Two-dimensional layered perovskite ferroelectric with giant piezoelectric voltage coefficient. J. Am. Chem. Soc. 142 (2), 1077–1082. doi:10.1021/jacs.9b12368
Chen, Y., Sun, Y., Peng, J., Tang, J., Zheng, K., and Liang, Z. (2018). 2D ruddlesden–popper perovskites for optoelectronics. Adv. Mater. 30 (2), 1703487. doi:10.1002/adma.201703487
Curtarolo, S., Setyawan, W., Wang, S., Xue, J., Yang, K., Taylor, R. H., et al. (2012). AFLOWLIB.ORG: a distributed materials properties repository from high-throughput ab initio calculations. Comput. Mater. Sci. 58, 227–235. doi:10.1016/j.commatsci.2012.02.002
Das, T., Di Liberto, G., and Pacchioni, G. (2022). Density functional theory estimate of halide perovskite band gap: when spin orbit coupling helps. J. Phys. Chem. C 126 (4), 2184–2198. doi:10.1021/acs.jpcc.1c09594
Dawson, J. A., Attari, T. S., Chen, H., Emge, S. P., Johnston, K. E., and Islam, M. S. (2018). Elucidating lithium-ion and proton dynamics in anti-perovskite solid electrolytes. Energy Environ. Sci. 11 (10), 2993–3002. doi:10.1039/c8ee00779a
Deng, Z., Ni, D., Chen, D., Bian, Y., Li, S., Wang, Z., et al. (2022). Anti-perovskite materials for energy storage batteries. InfoMat 4 (2), e12252. doi:10.1002/inf2.12252
Dey, A., Ye, J., De, A., Debroye, E., Ha, S. K., Bladt, E., et al. (2021). State of the art and prospects for halide perovskite nanocrystals. ACS Nano 15 (7), 10775–10981. doi:10.1021/acsnano.0c08903
Druffel, D. L., Kuntz, K. L., Woomer, A. H., Alcorn, F. M., Hu, J., Donley, C. L., et al. (2016). Experimental demonstration of an electride as a 2D material. J. Am. Chem. Soc. 138 (49), 16089–16094. doi:10.1021/jacs.6b10114
Du, J., and Shi, J. (2019). 2D Ca 3 Sn 2 S 7 chalcogenide perovskite: a graphene-like semiconductor with direct bandgap 0.5 eV and ultrahigh carrier mobility 6.7 × 10 4 cm 2 V −1 s −1. Adv. Mater. 31 (51), 1905643. doi:10.1002/adma.201905643
Egger, D. A., Rappe, A. M., and Kronik, L. (2016). Hybrid organic–inorganic perovskites on the move. Acc. Chem. Res. 49 (3), 573–581. doi:10.1021/acs.accounts.5b00540
Feng, C., Wu, C., Luo, X., Hu, T., Chen, F., Li, S., et al. (2023). Pressure-dependent electronic, optical, and mechanical properties of antiperovskite X 3 NP (X = Ca, Mg): a first-principles study. J. Semicond. 44 (10), 102101. doi:10.1088/1674-4926/44/10/102101
Flerov, I. N., Gorev, M. V., Aleksandrov, K. S., Tressaud, A., Grannec, J., and Couzi, M. (1998). Phase transitions in elpasolites (ordered perovskites). Mater. Sci. Eng. R Rep. 24 (3), 81–151. doi:10.1016/s0927-796x(98)00015-1
Fu, D., Zhang, W., Cai, H., Ge, J., Zhang, Y., and Xiong, R. (2011). Diisopropylammonium chloride: a ferroelectric organic salt with a high phase transition temperature and practical utilization level of spontaneous polarization. Adv. Mater. 23 (47), 5658–5662. doi:10.1002/adma.201102938
Fu, D. W., Cai, H. L., Liu, Y., Ye, Q., Zhang, W., Zhang, Y., et al. (2013). Diisopropylammonium bromide is a high-temperature molecular ferroelectric crystal. Science 339 (6118), 425–428. doi:10.1126/science.1229675
Fu, Y., Zhu, H., Chen, J., Hautzinger, M. P., Zhu, X. Y., and Jin, S. (2019). Metal halide perovskite nanostructures for optoelectronic applications and the study of physical properties. Nat. Rev. Mater 4 (3), 169–188. doi:10.1038/s41578-019-0080-9
Fuchs, F., Furthmüller, J., Bechstedt, F., Shishkin, M., and Kresse, G. (2007). Quasiparticle band structure based on a generalized Kohn-Sham scheme. Phys. Rev. B 76, 115109. doi:10.1103/PhysRevB.76.115109
Gebhardt, J., Wei, W., and Elsässer, C. (2021). Efficient modeling workflow for accurate electronic structures of hybrid perovskites. J. Phys. Chem. C 125 (34), 18597–18603. doi:10.1021/acs.jpcc.1c04817
Glazer, A. M. (1972). The classification of tilted octahedra in perovskites. Acta Crystallogr. B Struct. Crystallogr. Cryst. Chem. 28 (11), 3384–3392. doi:10.1107/s0567740872007976
Goldschmidt, V. M. (1926). Die Gesetze der Krystallochemie. Naturwissenschaften 14 (21), 477–485. doi:10.1007/bf01507527
Gou, G., Young, J., Liu, X., and Rondinelli, J. M. (2017). Interplay of cation ordering and ferroelectricity in perovskite tin iodides: designing a polar halide perovskite for photovoltaic applications. Inorg. Chem. 56 (1), 26–32. doi:10.1021/acs.inorgchem.6b01701
Gražulis, S., Daškevič, A., Merkys, A., Chateigner, D., Lutterotti, L., Quirós, M., et al. (2012). Crystallography Open Database (COD): an open-access collection of crystal structures and platform for world-wide collaboration. Nucleic Acids Res. 40 (D1), D420–D427. doi:10.1093/nar/gkr900
Guo, R., and Wang, S. (2019). Anion-dependent hot carrier dynamics in chalcogenide perovskites SrSnX 3 (X = S, Se). J. Phys. Chem. C 123 (1), 29–35. doi:10.1021/acs.jpcc.8b08041
Han, D., Du, M. H., Huang, M., Wang, S., Tang, G., Bein, T., et al. (2022). Ground-state structures, electronic structure, transport properties and optical properties of Ca-based anti-Ruddlesden-Popper phase oxide perovskites. Phys. Rev. Mater. 6 (11), 114601. doi:10.1103/physrevmaterials.6.114601
Han, D., Feng, C., Du, M. H., Zhang, T., Wang, S., Tang, G., et al. (2021). Design of high-performance lead-free quaternary antiperovskites for photovoltaics via ion type inversion and anion ordering. J. Am. Chem. Soc. 143 (31), 12369–12379. doi:10.1021/jacs.1c06403
Heywang, W. (1971). Semiconducting barium titanate. J. Mater Sci. 6 (9), 1214–1224. doi:10.1007/bf00550094
Howard, C. J., Kennedy, B. J., and Woodward, P. M. (2003). Ordered double perovskites – a group-theoretical analysis. Acta Crystallogr. B Struct. Sci. 59 (4), 463–471. doi:10.1107/s0108768103010073
Huang, Y., Pan, Y. H., Yang, R., Bao, L. H., Meng, L., Luo, H. L., et al. (2020). Universal mechanical exfoliation of large-area 2D crystals. Nat. Commun. 11 (1), 2453. doi:10.1038/s41467-020-16266-w
Huang, Y. T., Kavanagh, S. R., Righetto, M., Rusu, M., Levine, I., Unold, T., et al. (2022). Strong absorption and ultrafast localisation in NaBiS2 nanocrystals with slow charge-carrier recombination. Nat. Commun. 13 (1), 4960. doi:10.1038/s41467-022-32669-3
Hussain, A., Jabeen, N., Hassan, N. U., Rahman, A. U., Khan, M. U., Naz, A., et al. (2022). Influence of Mn ions’ insertion in pseudo-tetragonal phased CaBi4Ti4O15-based ceramics for highly efficient energy storage devices and high-temperature piezoelectric applications. IJMS 23 (21), 12723. doi:10.3390/ijms232112723
IOPscience (2011). Hybrid functionals applied to perovskites. Available at: https://iopscience.iop.org/article/10.1088/0953-8984/26/25/253202/pdf (Accessed August 18, 2024).
Jain, A., Ong, S. P., Hautier, G., Chen, W., Richards, W. D., Dacek, S., et al. (2013). Commentary: the Materials Project: a materials genome approach to accelerating materials innovation. Apl. Mater. 1 (1), 011002. doi:10.1063/1.4812323
Janesko, B. G., Henderson, T. M., and Scuseria, G. E. (2009). Screened hybrid density functionals for solid-state chemistry and physics. Phys. Chem. Chem. Phys. 11 (3), 443–454. doi:10.1039/b812838c
Jena, A. K., Kulkarni, A., and Miyasaka, T. (2019). Halide perovskite photovoltaics: background, status, and future prospects. Chem. Rev. 119 (5), 3036–3103. doi:10.1021/acs.chemrev.8b00539
Jin, G. B., Choi, E. S., Guertin, R. P., Brooks, J. S., Bray, T. H., Booth, C. H., et al. (2007). Syntheses, structure, magnetism, and optical properties of the ordered mixed-lanthanide sulfides γ-LnLn‘S 3 (Ln = La, Ce; Ln‘ = Er, Tm, Yb). Chem. Mater. 19 (3), 567–574. doi:10.1021/cm062349c
Jong, U. G., Yu, C. J., Ri, J. S., Kim, N. H., and Ri, G. C. (2016). Influence of halide composition on the structural, electronic, and optical properties of mixed CH 3 NH 3 Pb (I 1 − x Br x) 3 perovskites calculated using the virtual crystal approximation method. Phys. Rev. B 94 (12), 125139. doi:10.1103/physrevb.94.125139
Ju, M., Dai, J., Ma, L., and Zeng, X. C. (2017). Perovskite chalcogenides with optimal bandgap and desired optical absorption for photovoltaic devices. Adv. Energy Mater. 7 (18), 1700216. doi:10.1002/aenm.201700216
Kangsabanik, J., Sugathan, V., Yadav, A., Yella, A., and Alam, A. (2018). Double perovskites overtaking the single perovskites: a set of new solar harvesting materials with much higher stability and efficiency. Phys. Rev. Mater. 2 (5), 055401. doi:10.1103/physrevmaterials.2.055401
Kawakami, T., Okamura, T., Kobayashi, S., and Sato, M. (2018). Topological crystalline materials of $J=3/2$ electrons: antiperovskites, Dirac points, and high winding topological superconductivity. Phys. Rev. X 8 (4), 041026. doi:10.1103/physrevx.8.041026
Kieslich, G., Sun, S., and Cheetham, A. K. (2014). Solid-state principles applied to organic–inorganic perovskites: new tricks for an old dog. Chem. Sci. 5 (12), 4712–4715. doi:10.1039/c4sc02211d
Kieslich, G., Sun, S., and Cheetham, A. K. (2015). An extended Tolerance Factor approach for organic–inorganic perovskites. Chem. Sci. 6 (6), 3430–3433. doi:10.1039/c5sc00961h
Kim, Y. H., Cho, H., and Lee, T. W. (2016). Metal halide perovskite light emitters. Proc. Natl. Acad. Sci. U. S. A. 113 (42), 11694–11702. doi:10.1073/pnas.1607471113
King, G., and Woodward, P. M. (2010). Cation ordering in perovskites. J. Mater Chem. 20 (28), 5785. doi:10.1039/b926757c
Kojima, A., Teshima, K., Shirai, Y., and Miyasaka, T. (2009). Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 131 (17), 6050–6051. doi:10.1021/ja809598r
Kovalenko, M. V., Protesescu, L., and Bodnarchuk, M. I. (2017). Properties and potential optoelectronic applications of lead halide perovskite nanocrystals. Science 358 (6364), 745–750. doi:10.1126/science.aam7093
Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54 (16), 11169–11186. doi:10.1103/physrevb.54.11169
Krivovichev, S. V. (2024). Structural diversity and complexity of antiperovskites. Coord. Chem. Rev. 498, 215484. doi:10.1016/j.ccr.2023.215484
Kumar, V. G. D., Balaji, K. R., Viswanatha, R., Ambika, G., Roopa, R., Basavaraja, B. M., et al. (2022). Visible light photodegradation of 2,4-dichlorophenol using nanostructured NaBiS2: kinetics, cytotoxicity, antimicrobial and electrochemical studies of the photocatalyst. Chemosphere 287, 132174. doi:10.1016/j.chemosphere.2021.132174
lang, C. Y., jie, S. J., Zhang, M., Wu, M., Du, J., Guo, W. hui, et al. (2020). Design of lead-free and stable two-dimensional dion–jacobson-type chalcogenide perovskite A′la 2 B 3 S 10 (A′ = Ba/Sr/Ca; B = Hf/Zr) with optimal band gap, strong optical absorption, and high efficiency for photovoltaics. Chem. Mater 32 (6), 2450–2460. doi:10.1021/acs.chemmater.9b04985
Lee, C. S., Kleinke, K. M., and Kleinke, H. (2005). Synthesis, structure, and electronic and physical properties of the two SrZrS3 modifications. Solid State Sci. 7 (9), 1049–1054. doi:10.1016/j.solidstatesciences.2005.02.010
Lelieveld, R., and Ijdo, D. J. W. (1980). Sulphides with the GdFeO 3 structure. Acta Crystallogr. B Struct. Sci. 36 (10), 2223–2226. doi:10.1107/s056774088000845x
Li, G., Lu, S., Chen, X., Liao, W., Tang, Y., and Xiong, R. (2019). A three-dimensional M 3 AB-type hybrid organic–inorganic antiperovskite ferroelectric: [C 3 H 7 FN] 3 [SnCl 6 ]Cl. Chem. A Eur. J. 25 (72), 16625–16629. doi:10.1002/chem.201903678
Li, L., Liu, X., He, C., Wang, S., Ji, C., Zhang, X., et al. (2020b). A potential Sn-based hybrid perovskite ferroelectric semiconductor. J. Am. Chem. Soc. 142 (3), 1159–1163. doi:10.1021/jacs.9b11341
Li, N., Song, L., Jia, Y., Dong, Y., Xie, F., Wang, L., et al. (2020a). Stabilizing perovskite light-emitting diodes by incorporation of binary alkali cations. Adv. Mater. 32 (17), 1907786. doi:10.1002/adma.201907786
Li, Z., Yang, M., Park, J. S., Wei, S. H., Berry, J. J., and Zhu, K. (2016). Stabilizing perovskite structures by tuning tolerance factor: formation of formamidinium and cesium lead iodide solid-state alloys. Chem. Mater 28 (1), 284–292. doi:10.1021/acs.chemmater.5b04107
Liang, Y., Zhang, Y., Xu, J., Ma, J., Jiang, H., Li, X., et al. (2023). Parametric study on controllable growth of SrZrS3 thin films with good conductivity for photodetectors. Nano Res. 16 (5), 7867–7873. doi:10.1007/s12274-023-5412-9
Liao, C., Li, Y., and Tjong, S. (2018). Graphene nanomaterials: synthesis, biocompatibility, and cytotoxicity. IJMS 19 (11), 3564. doi:10.3390/ijms19113564
Liao, W. Q., Zhao, D., Tang, Y. Y., Zhang, Y., Li, P. F., Shi, P. P., et al. (2019). A molecular perovskite solid solution with piezoelectricity stronger than lead zirconate titanate. Science 363 (6432), 1206–1210. doi:10.1126/science.aav3057
Lin, W., Stoumpos, C. C., Liu, Z., Das, S., Kontsevoi, O. Y., He, Y., et al. (2017). TlSn 2 I 5, a robust halide antiperovskite semiconductor for γ-ray detection at room temperature. ACS Photonics 4 (7), 1805–1813. doi:10.1021/acsphotonics.7b00388
Liu, L., Liu, S. Y., Shi, Y., Fang, C. L., Zhao, S., Shen, H. Y., et al. (2024). Anti-perovskites with long carrier lifetime for ultralow dose and stable X-ray detection. Nat. Phot. 18, 990–997. doi:10.1038/s41566-024-01482-3
Liu, Y. L., Ge, J. Z., Wang, Z. X., and Xiong, R. G. (2020). Metal–organic ferroelectric complexes: enantiomer directional induction achieved above-room-temperature homochiral molecular ferroelectrics. Inorg. Chem. Front. 7 (1), 128–133. doi:10.1039/c9qi01197h
Liu, Z., Mi, R., Ji, G., Liu, Y., Fu, P., Hu, S., et al. (2021). Bandgap engineering and thermodynamic stability of oxyhalide and chalcohalide antiperovskites. Ceram. Int. 47 (23), 32634–32640. doi:10.1016/j.ceramint.2021.08.159
Liu, Z., Wu, B., and Wu, J. (2018b). Reduced dielectric loss and high piezoelectric constant in Ce and Mn co-doped BiScO3-PbCe Ti1-O3-Bi(Zn0.5Ti0.5)O3 ceramics. Ceram. Int. 44 (14), 16483–16488. doi:10.1016/j.ceramint.2018.06.065
Liu, Z., Zhao, C., Li, J. F., Wang, K., and Wu, J. (2018c). Large strain and temperature-insensitive piezoelectric effect in high-temperature piezoelectric ceramics. J. Mater Chem. C 6 (3), 456–463. doi:10.1039/c7tc04975g
Liu, Z., Zhao, C., Xie, R., and Wu, J. (2018a). Tailored electrical properties in ternary BiScO3-PbTiO3 ceramics by composition modification. Ceram. Int. 44 (7), 8057–8063. doi:10.1016/j.ceramint.2018.01.247
Liu, Z., Zheng, T., Zhao, C., and Wu, J. (2017). Composition design and electrical properties in BiFeO3–BaTiO3–Bi(Zn0.5Ti0.5)O3 lead-free ceramics. J. Mater Sci. Mater Electron. 28 (17), 13076–13083. doi:10.1007/s10854-017-7140-y
Lu, S., Zhou, Q., Ouyang, Y., Guo, Y., Li, Q., and Wang, J. (2018). Accelerated discovery of stable lead-free hybrid organic-inorganic perovskites via machine learning. Nat. Commun. 9 (1), 3405. doi:10.1038/s41467-018-05761-w
Lu, Z., Liu, J., and Ciucci, F. (2020). Superionic conduction in low-dimensional-networked anti-perovskites. Energy Storage Mater. 28, 146–152. doi:10.1016/j.ensm.2020.03.005
Luo, Y., Szafraniak, I., Zakharov, N. D., Nagarajan, V., Steinhart, M., Wehrspohn, R. B., et al. (2003). Nanoshell tubes of ferroelectric lead zirconate titanate and barium titanate. Appl. Phys. Lett. 83 (3), 440–442. doi:10.1063/1.1592013
Lupascu, D., and Rödel, J. (2005). Fatigue in bulk lead zirconate titanate actuator materials. Adv. Eng. Mater 7 (10), 882–898. doi:10.1002/adem.200500117
Ma, J., Wang, H., and Li, D. (2021). Recent progress of chiral perovskites: materials, synthesis, and properties. Adv. Mater. 33 (26), 2008785. doi:10.1002/adma.202008785
Medvedeva, N. I., Mryasov, O. N., Gornostyrev, Y. N., Novikov, D. L., and Freeman, A. J. (1996). First-principles total-energy calculations for planar shear and cleavage decohesion processes in B 2-ordered NiAl and FeAl. Phys. Rev. B 54 (19), 13506–13514. doi:10.1103/physrevb.54.13506
Mitchell, K., Huang, F. Q., McFarland, A. D., Haynes, C. L., Somers, R. C., Van Duyne, R. P., et al. (2003). The CsLnMSe 3 semiconductors (Ln = rare-earth element, Y; M = Zn, Cd, Hg). Inorg. Chem. 42 (13), 4109–4116. doi:10.1021/ic020733f
Moroz, N. A., Bauer, C., Williams, L., Olvera, A., Casamento, J., Page, A. A., et al. (2018). Insights on the synthesis, crystal and electronic structures, and optical and thermoelectric properties of Sr 1– x Sb x HfSe 3 orthorhombic perovskite. Inorg. Chem. 57 (12), 7402–7411. doi:10.1021/acs.inorgchem.8b01038
Mortazavi, B., and Cuniberti, G. (2014). Atomistic modeling of mechanical properties of polycrystalline graphene. Nanotechnology 25 (21), 215704. doi:10.1088/0957-4484/25/21/215704
Nedelcu, G., Protesescu, L., Yakunin, S., Bodnarchuk, M. I., Grotevent, M. J., and Kovalenko, M. V. (2015). Fast anion-exchange in highly luminescent nanocrystals of cesium lead halide perovskites (CsPbX 3, X = Cl, Br, I). Nano Lett. 15 (8), 5635–5640. doi:10.1021/acs.nanolett.5b02404
Nie, R., Mehta, A., Park, B. wook, Kwon, H. W., Im, J., and Seok, S. I. (2018). Mixed sulfur and iodide-based lead-free perovskite solar cells. J. Am. Chem. Soc. 140 (3), 872–875. doi:10.1021/jacs.7b11332
Niu, S., Milam-Guerrero, J., Zhou, Y., Ye, K., Zhao, B., Melot, B. C., et al. (2018c). Thermal stability study of transition metal perovskite sulfides. J. Mater Res. 33 (24), 4135–4143. doi:10.1557/jmr.2018.419
Niu, S., Sarkar, D., Williams, K., Zhou, Y., Li, Y., Bianco, E., et al. (2018a). Optimal bandgap in a 2D ruddlesden–popper perovskite chalcogenide for single-junction solar cells. Chem. Mater 30 (15), 4882–4886. doi:10.1021/acs.chemmater.8b01707
Niu, S., Zhao, H., Zhou, Y., Huyan, H., Zhao, B., Wu, J., et al. (2018b). Mid-wave and long-wave infrared linear dichroism in a hexagonal perovskite chalcogenide. Chem. Mater 30 (15), 4897–4901. doi:10.1021/acs.chemmater.8b02279
Ohashi, N., Mora-Fonz, D., Otani, S., Ohgaki, T., Miyakawa, M., and Shluger, A. (2020). Inverse perovskite oxysilicides and oxygermanides as candidates for nontoxic infrared semiconductor and their chemical bonding nature. Inorg. Chem. 59 (24), 18305–18313. doi:10.1021/acs.inorgchem.0c02897
Ong, S. P., Wang, L., Kang, B., and Ceder, G. (2008). Li−Fe−P−O 2 phase diagram from first principles calculations. Chem. Mater 20 (5), 1798–1807. doi:10.1021/cm702327g
Pan, Q., Liu, Z. B., Tang, Y. Y., Li, P. F., Ma, R. W., Wei, R. Y., et al. (2017). A three-dimensional molecular perovskite ferroelectric: (3-ammoniopyrrolidinium)RbBr 3. J. Am. Chem. Soc. 139 (11), 3954–3957. doi:10.1021/jacs.7b00492
Park, SCh, Kuratieva, N. V., Pomelova, T. A., and Naumov, N. G. (2022). SYNTHESIS AND CRYSTAL STRUCTURE OF CsLnZnS3 (Ln = Gd, Dy). J. Struct. Chem. 63 (6), 868–873. doi:10.1134/s0022476622060038
Peng, Y., Liu, X., Sun, Z., Ji, C., Li, L., Wu, Z., et al. (2020). Exploiting the bulk photovoltaic effect in a 2D trilayered hybrid ferroelectric for highly sensitive polarized light detection. Angew. Chem. Int. Ed. 59 (10), 3933–3937. doi:10.1002/anie.201915094
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/physrevlett.77.3865
Perera, S., Hui, H., Zhao, C., Xue, H., Sun, F., Deng, C., et al. (2016). Chalcogenide perovskites – an emerging class of ionic semiconductors. Nano Energy 22, 129–135. doi:10.1016/j.nanoen.2016.02.020
Pilania, G., Balachandran, P. V., Kim, C., and Lookman, T. (2016). Finding new perovskite halides via machine learning. Front. Mater 3. doi:10.3389/fmats.2016.00019
Protesescu, L., Yakunin, S., Bodnarchuk, M. I., Krieg, F., Caputo, R., Hendon, C. H., et al. (2015). Nanocrystals of cesium lead halide perovskites (CsPbX 3, X = Cl, Br, and I): novel optoelectronic materials showing bright emission with wide color gamut. Nano Lett. 15 (6), 3692–3696. doi:10.1021/nl5048779
K. M. Rabe, C. H. Ahn, and J. M. Triscone (2007). Physics of ferroelectrics: a modern perspective (Berlin ; New York: Springer), 388. (Topics in applied physics).
Ravindran, P., Delin, A., Ahuja, R., Johansson, B., Auluck, S., Wills, J. M., et al. (1997). Optical properties of monoclinic SnI 2 from relativistic first-principles theory. Phys. Rev. B 56 (11), 6851–6861. doi:10.1103/physrevb.56.6851
Resta, R. (1994). Modern theory of polarization in ferroelectrics. Ferroelectrics 151 (1), 49–58. doi:10.1080/00150199408244722
Rockett, A., and Birkmire, R. W. (1991). CuInSe2 for photovoltaic applications. J. Appl. Phys. 70 (7), R81–R97. doi:10.1063/1.349175
Rosales, B. A., White, M. A., and Vela, J. (2018). Solution-grown sodium bismuth dichalcogenides: toward earth-abundant, biocompatible semiconductors. J. Am. Chem. Soc. 140 (10), 3736–3742. doi:10.1021/jacs.7b12873
Ruch, J. G., and Kino, G. S (1968). Transport properties of GaAs. Physical Review, 174 (3), 921. doi:10.1103/PhysRev.174.921
Rühl, S. (2019). The inorganic crystal structure database (icsd): a tool for materials sciences. Mater. Inf., 41–54. doi:10.1002/9783527802265.ch2
Rühle, S. (2016). Tabulated values of the Shockley–Queisser limit for single junction solar cells. Sol. Energy 130, 139–147. doi:10.1016/j.solener.2016.02.015
Schleder, G. R., Padilha, A. C. M., Acosta, C. M., Costa, M., and Fazzio, A. (2019). From DFT to machine learning: recent approaches to materials science–a review. J. Phys. Mater 2 (3), 032001. doi:10.1088/2515-7639/ab084b
Shen, J., Griesemer, S. D., Gopakumar, A., Baldassarri, B., Saal, J. E., Aykol, M., et al. (2022). Reflections on one million compounds in the open quantum materials database (OQMD). J. Phys. Mater 5 (3), 031001. doi:10.1088/2515-7639/ac7ba9
Shi, C., Ma, J. J., Jiang, J. Y., Hua, M. M., Xu, Q., Yu, H., et al. (2020a). Large piezoelectric response in hybrid rare-earth double perovskite relaxor ferroelectrics. J. Am. Chem. Soc. 142, 9634–9641. doi:10.1021/jacs.0c00480
Shi, C., Ye, L., Gong, Z. X., Ma, J. J., Wang, Q. W., Jiang, J. Y., et al. (2020b). Two-dimensional organic–inorganic hybrid rare-earth double perovskite ferroelectrics. J. Am. Chem. Soc. 142 (1), 545–551. doi:10.1021/jacs.9b11697
Shi, P. P., Lu, S. Q., Song, X. J., Chen, X. G., Liao, W. Q., Li, P. F., et al. (2019). Two-dimensional organic–inorganic perovskite ferroelectric semiconductors with fluorinated aromatic spacers. J. Am. Chem. Soc. 141 (45), 18334–18340. doi:10.1021/jacs.9b10048
Shi, P. P., Tang, Y. Y., Li, P. F., Ye, H. Y., and Xiong, R. G. (2017). De novo discovery of [hdabco]BF 4 molecular ferroelectric thin film for nonvolatile low-voltage memories. J. Am. Chem. Soc. 139 (3), 1319–1324. doi:10.1021/jacs.6b12377
Shi, X., Lin, X., Luo, R., Wu, S., Li, L., Zhao, Z. J., et al. (2021). Dynamics of heterogeneous catalytic processes at operando conditions. JACS Au 1 (12), 2100–2120. doi:10.1021/jacsau.1c00355
Shockley, W., and Queisser, H. J (1961). Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 32, 510–519. doi:10.1063/1.1736034
Singh, H. K., Zhang, Z., Opahle, I., Ohmer, D., Yao, Y., and Zhang, H. (2018). High-throughput screening of magnetic antiperovskites. Chem. Mater. 30 (20), 6983–6991. doi:10.1021/acs.chemmater.8b01618
Siwach, P., Sikarwar, P., Halpati, J. S., and Chandiran, A. K. (2022). Design of above-room-temperature ferroelectric two-dimensional layered halide perovskites. J. Mater Chem. A 10 (16), 8719–8738. doi:10.1039/d1ta09537d
Spaldin, N. A. (2012). A beginner’s guide to the modern theory of polarization. J. Solid State Chem. 195, 2–10. doi:10.1016/j.jssc.2012.05.010
Sun, Q., Chen, H., and Yin, W. J. (2019). Do chalcogenide double perovskites work as solar cell absorbers: a first-principles study. Chem. Mater 31 (1), 244–250. doi:10.1021/acs.chemmater.8b04320
Sun, Y. Y., Agiorgousis, M. L., Zhang, P., and Zhang, S. (2015). Chalcogenide perovskites for photovoltaics. Nano Lett. 15 (1), 581–585. doi:10.1021/nl504046x
Swarnkar, A., Mir, W. J., Chakraborty, R., Jagadeeswararao, M., Sheikh, T., and Nag, A. (2019). Are chalcogenide perovskites an emerging class of semiconductors for optoelectronic properties and solar cell? Chem. Mater 31 (3), 565–575. doi:10.1021/acs.chemmater.8b04178
Takeda, Y., Kanamura, F., Shimada, M., and Koizumi, M. (1976). The crystal structure of BaNiO3. Acta Crystallogr. B Struct. Crystallogr. Cryst. Chem. 32 (8), 2464–2466. doi:10.1107/s056774087600798x
Tan, Z., Chu, Y., Chen, J., Li, J., Ji, G., Niu, G., et al. (2020). Lead-free perovskite variant solid solutions Cs 2 Sn 1– x Te x Cl 6: bright luminescence and high anti-water stability. Adv. Mater 32 (32), 2002443. doi:10.1002/adma.202002443
Tang, G., Liu, X., Wang, S., Hu, T., Feng, C., Zhu, C., et al. (2024). Designing antiperovskite derivatives via atomic-position splitting for photovoltaic applications. Mater Horiz. doi:10.1039/d4mh00526k
Tang, Y., Ai, Y., Liao, W., Li, P., Wang, Z., and Xiong, R. (2019). H/F-Substitution-Induced homochirality for designing high- T c molecular perovskite ferroelectrics. Adv. Mater. 31 (29), 1902163. doi:10.1002/adma.201902163
Tang, Y. Y., Liu, J. C., Zeng, Y. L., Peng, H., Huang, X. Q., Yang, M. J., et al. (2021). Optical control of polarization switching in a single-component organic ferroelectric crystal. J. Am. Chem. Soc. 143 (34), 13816–13823. doi:10.1021/jacs.1c06108
Togo, A., and Tanaka, I. (2015). First principles phonon calculations in materials science. Scr. Mater. 108, 1–5. doi:10.1016/j.scriptamat.2015.07.021
Tran, R., Lan, J., Shuaibi, M., Wood, B. M., Goyal, S., Das, A., et al. (2023). The open catalyst 2022 (OC22) dataset and challenges for oxide electrocatalysts. ACS Catal. 13 (5), 3066–3084. doi:10.1021/acscatal.2c05426
Tranchitella, L. J., Chen, B. -H., Fettinger, J. C., and Eichhorn, B. W. (1997). Structural evolutions in the Sr1– xBaxZrSe3 series. J. Solid State Chem. 130 (1), 20–27. doi:10.1006/jssc.1996.7253
Travis, W., Glover, E. N. K., Bronstein, H., Scanlon, D. O., and Palgrave, R. G. (2016). On the application of the tolerance factor to inorganic and hybrid halide perovskites: a revised system. Chem. Sci. 7 (7), 4548–4556. doi:10.1039/c5sc04845a
Umari, P., Mosconi, E., and De Angelis, F. (2014). Relativistic GW calculations on CH3NH3PbI3 and CH3NH3SnI3 perovskites for solar cell applications. Sci. Rep. 4 (1), 4467. doi:10.1038/srep04467
Varadwaj, A., Varadwaj, P. R., Marques, H. M., and Yamashita, K. (2022). The pnictogen bond, together with other non-covalent interactions, in the rational design of one-two- and three-dimensional organic-inorganic hybrid metal halide perovskite semiconducting materials, and beyond. IJMS 23 (15), 8816. doi:10.3390/ijms23158816
Vijatovic, M. M., Bobic, J. D., and Stojanovic, B. D. (2008). History and challenges of barium titanate: Part II. Sci. Sinter. 40 (3), 235–244. doi:10.2298/sos0803235v
Vona, C., Nabok, D., and Draxl, C. (2022). Electronic structure of (Organic-)Inorganic metal halide perovskites: the dilemma of choosing the right functional. Adv. Theory Simulations 5 (1), 2100496. doi:10.1002/adts.202100496
Wang, H., Gou, G., and Li, J. (2016). Ruddlesden–Popper perovskite sulfides A3B2S7: a new family of ferroelectric photovoltaic materials for the visible spectrum. Nano Energy. 22, 507–513. doi:10.1016/j.nanoen.2016.02.036
Wang, H., Ji, Y., and Li, Y. (2020a). Simulation and design of energy materials accelerated by machine learning. WIREs Comput. Mol. Sci. 10 (1), e1421. doi:10.1002/wcms.1421
Wang, K., Yang, D., Wu, C., Sanghadasa, M., and Priya, S. (2019a). Recent progress in fundamental understanding of halide perovskite semiconductors. Prog. Mater. Sci. 106, 100580. doi:10.1016/j.pmatsci.2019.100580
Wang, S., Li, L., Weng, W., Ji, C., Liu, X., Sun, Z., et al. (2020c). Trilayered lead chloride perovskite ferroelectric affording self-powered visible-blind ultraviolet photodetection with large zero-bias photocurrent. J. Am. Chem. Soc. 142 (1), 55–59. doi:10.1021/jacs.9b10919
Wang, Y., Zhang, H., Zhu, J., Lü, X., Li, S., Zou, R., et al. (2020b). Antiperovskites with exceptional functionalities. Adv. Mater. 32 (7), 1905007. doi:10.1002/adma.201905007
Wang, Z. X., Zhang, Y., Tang, Y. Y., Li, P. F., and Xiong, R. G. (2019b). Fluoridation achieved antiperovskite molecular ferroelectric in [(CH 3) 2 (F-CH 2 CH 2)NH] 3 (CdCl 3)(CdCl 4). J. Am. Chem. Soc. 141 (10), 4372–4378. doi:10.1021/jacs.8b13109
Wasim, S. M. (1986). Transport properties of CuInSe2. Sol. Cells 16, 289–316. doi:10.1016/0379-6787(86)90091-8
Wei, W., Li, W., Butler, K. T., Feng, G., Howard, C. J., Carpenter, M. A., et al. (2018b). An unusual phase transition driven by vibrational entropy changes in a hybrid organic–inorganic perovskite. Angew. Chem. 130 (29), 9070–9074. doi:10.1002/ange.201803176
Wei, Z., Liao, W. Q., Tang, Y. Y., Li, P. F., Shi, P. P., Cai, H., et al. (2018a). Discovery of an antiperovskite ferroelectric in [(CH 3) 3 NH] 3 (MnBr 3)(MnBr 4). J. Am. Chem. Soc. 140 (26), 8110–8113. doi:10.1021/jacs.8b05037
Wei, Z. H., Jiang, Z. T., Zhang, X. X., Li, M. L., Tang, Y. Y., Chen, X. G., et al. (2020). Rational design of ceramic-like molecular ferroelectric by quasi-spherical theory. J. Am. Chem. Soc. 142 (4), 1995–2000. doi:10.1021/jacs.9b11665
Wu, Y., Xie, F., Chen, H., Yang, X., Su, H., Cai, M., et al. (2017). Thermally stable MAPbI 3 perovskite solar cells with efficiency of 19.19% and area over 1 cm 2 achieved by additive engineering. Adv. Mater. 29 (28), 1701073. doi:10.1002/adma.201701073
Xu, G. C., Zhang, W., Ma, X. M., Chen, Y. H., Zhang, L., Cai, H. L., et al. (2011). Coexistence of magnetic and electric orderings in the metal–formate frameworks of [NH 4 ] [M(HCOO) 3 ]. J. Am. Chem. Soc. 133 (38), 14948–14951. doi:10.1021/ja206891q
Xu, H., Guo, W., Wang, J., Ma, Y., Han, S., Liu, Y., et al. (2021). A metal-free molecular antiferroelectric material showing high phase transition temperatures and large electrocaloric effects. J. Am. Chem. Soc. 143 (35), 14379–14385. doi:10.1021/jacs.1c07521
Xu, Z., Weng, W., Li, Y., Liu, X., Yang, T., Li, M., et al. (2020). 3D-to-2D dimensional reduction for exploiting a multilayered perovskite ferroelectric toward polarized-light detection in the solar-blind ultraviolet region. Angew. Chem. 132 (48), 21877–21881. doi:10.1002/ange.202009329
Yao, J., Deng, B., Sherry, L. J., McFarland, A. D., Ellis, D. E., Van Duyne, R. P., et al. (2004). Syntheses, structure, some band gaps, and electronic structures of CsLnZnTe 3 (Ln = La, Pr, Nd, Sm, Gd, Tb, Dy, Ho, Er, Tm, Y). Inorg. Chem. 43 (24), 7735–7740. doi:10.1021/ic040071p
Ye, H. Y., Tang, Y. Y., Li, P. F., Liao, W. Q., Gao, J. X., Hua, X. N., et al. (2018). Metal-free three-dimensional perovskite ferroelectrics. Science 361 (6398), 151–155. doi:10.1126/science.aas9330
Yi, M., and Shen, Z. (2015). A review on mechanical exfoliation for the scalable production of graphene. J. Mater Chem. A 3 (22), 11700–11715. doi:10.1039/c5ta00252d
You, Y. M., Liao, W. Q., Zhao, D., Ye, H. Y., Zhang, Y., Zhou, Q., et al. (2017). An organic-inorganic perovskite ferroelectric with large piezoelectric response. Science 357 (6348), 306–309. doi:10.1126/science.aai8535
Yu, Y., Zhang, D., and Yang, P. (2017). Ruddlesden–popper phase in two-dimensional inorganic halide perovskites: a plausible model and the supporting observations. Nano Lett. 17 (9), 5489–5494. doi:10.1021/acs.nanolett.7b02146
Zhang, H., Wei, Z., Li, P., Tang, Y., Liao, W., Ye, H., et al. (2018). The narrowest band gap ever observed in molecular ferroelectrics: hexane-1,6-diammonium pentaiodobismuth(III). Angew. Chem. 130 (2), 535–539. doi:10.1002/ange.201709588
Zhang, H. Y., Song, X. J., Chen, X. G., Zhang, Z. X., You, Y. M., Tang, Y. Y., et al. (2020c). Observation of vortex domains in a two-dimensional lead iodide perovskite ferroelectric. J. Am. Chem. Soc. 142 (10), 4925–4931. doi:10.1021/jacs.0c00371
Zhang, H. Y., Zhang, Z. X., Song, X. J., Chen, X. G., and Xiong, R. G. (2020b). Two-dimensional hybrid perovskite ferroelectric induced by perfluorinated substitution. J. Am. Chem. Soc. 142 (47), 20208–20215. doi:10.1021/jacs.0c10686
Zhang, W., Eperon, G. E., and Snaith, H. J. (2016). Metal halide perovskites for energy applications. Nat. Energy 1 (6), 16048. doi:10.1038/nenergy.2016.48
Zhang, W., Ye, H. Y., Graf, R., Spiess, H. W., Yao, Y. F., Zhu, R. Q., et al. (2013). Tunable and switchable dielectric constant in an amphidynamic crystal. J. Am. Chem. Soc. 135 (14), 5230–5233. doi:10.1021/ja3110335
Zhang, Y., Shimada, T., Kitamura, T., and Wang, J. (2017). Ferroelectricity in ruddlesden–popper chalcogenide perovskites for photovoltaic application: the role of tolerance factor. J. Phys. Chem. Lett. 8 (23), 5834–5839. doi:10.1021/acs.jpclett.7b02591
Zhang, Y., Song, X. J., Zhang, Z. X., Fu, D. W., and Xiong, R. G. (2020a). Piezoelectric energy harvesting based on multiaxial ferroelectrics by precise molecular design. Matter 2 (3), 697–710. doi:10.1016/j.matt.2019.12.008
Zhao, J., Huang, X., Shi, R., Tang, L., Su, Y., and Sai, L. (2015). Ab initio global optimization of clusters. Available at: https://books.rsc.org/books/edited-volume/1505/chapter/958374/Ab-initio-global-optimization-of-clusters (Accessed September 24, 2024).
Zhao, S., Li, Z., and Yang, J. (2014). Obtaining two-dimensional electron gas in free space without resorting to electron doping: an electride based design. J. Am. Chem. Soc. 136 (38), 13313–13318. doi:10.1021/ja5065125
Zhong, H., Feng, C., Wang, H., Han, D., Yu, G., Xiong, W., et al. (2021). Structure–composition–property relationships in antiperovskite nitrides: guiding a rational alloy design. ACS Appl. Mater Interfaces 13 (41), 48516–48524. doi:10.1021/acsami.1c10137
Keywords: perovskites, computational methods, antiperovskites, chalcogenide perovskites, stability, electronic structure
Citation: Sheng M, Wang S, Zhu H, Liu Z and Zhou G (2024) Computational applications for the discovery of novel antiperovskites and chalcogenide perovskites: a review. Front. Chem. 12:1468434. doi: 10.3389/fchem.2024.1468434
Received: 22 July 2024; Accepted: 30 September 2024;
Published: 11 October 2024.
Edited by:
Hong Fang, Rutgers University Camden, United StatesReviewed by:
Gang Tang, Beijing Institute of Technology, ChinaChuanzhao Zhang, Yangtze University, China
Copyright © 2024 Sheng, Wang, Zhu, Liu and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhuang Liu, bGl1LnpodWFuZ0BzZHUuZWR1LmNu; Guangtao Zhou, Y2hhcmxpZUBzZHhpZWhlLmVkdS5jbg==
†These authors have contributed equally to this work and share first authorship
 Ming Sheng1†
Ming Sheng1† Zhuang Liu
Zhuang Liu