- 1Beijing National Laboratory for Molecular Sciences, Institute of Chemistry, Chinese Academy of Sciences, Beijing, China
- 2School of Chemical Sciences, University of Chinese Academy of Sciences, Beijing, China
By means of highly accurate ab initio and dynamical calculations, we identify a suitable laser cooling candidate that contains a transition metal element, namely zinc monohydride (ZnH). The internally contracted multireference configuration interaction method is employed to compute the five lowest-lying Λ-S states of ZnH with the spin-orbit coupling effects included, and very good agreement is obtained between our calculated and experimental spectroscopic data. Our findings show that the position of crossing point of the A2Π and B2Σ+ states of ZnH is above the v′ = 2 vibrational level of the A2Π state indicating that the crossings with higher electronic states will have no effect on laser cooling. Hence, we construct a feasible laser-cooling scheme for ZnH using five lasers based on the A2Π1/2 → X2Σ+ 1/2 transition, which features a large vibrational branching ratio R00 (0.8458), a large number of scattered photons (9.8 × 103) and an extremely short radiative lifetime (64 ns). The present work demonstrates the importance of electronic state crossings and spin-orbit couplings in the study of molecular laser cooling.
1 Introduction
In recent years, it has attracted great research interests to establish more promising laser cooling candidates owing to their importance for a lot of potential applications such as precision measurements, quantum information storage and quantum computers (Hudson et al., 2011; Yan et al., 2013; Baron et al., 2014). Around a decade ago, the SrF molecules were successfully cooled to the micro-kelvin level using the direct laser cooling method (Shuman et al., 2010), and after that much research in molecular laser cooling has been initiated. However, so far only a few kinds of diatomic molecules have been experimentally cooled to the ultracold regime. Therefore, it is of considerable interests in searching for more promising candidates for laser cooling, and theoretical calculations could play an important role (Wells and Lane, 2011; Fu et al., 2017; Cao et al., 2019; Moussa et al., 2021; Xia et al., 2021). There are three criteria for laser cooling candidates that are generally recognized (Di Rosa, 2004): a highly diagonal Franck-Condon factor (FCF) matrix, a very short radiative lifetime, and no interference from intermediate states. In addition, Bian (Li et al., 2020) recently proposed the fourth criterion for molecular laser cooling, that is, no electronic-state crossing, or the crossing point between the two electronic states is high enough in energy relative to the ground vibrational level. Therefore, when searching for molecular candidates, all electronic states that are close to those selected for the cooling scheme should be computed and checked in advance.
Research on the spectroscopic investigation of ZnH has been ongoing since 1923, when Hulthen observed and analysed the A2Π → X2Σ+ transition of ZnH for the first time (Hulthen, 1923). Forty years later, there has been extensive progress in the determination of electronic states of ZnH such as C2Σ+ → X2Σ+ transition was observed and analysed by M.A. Khan (Khan, 1962) in 1962. Balfour and co-workers (Balfour et al., 1986) investigated B2Σ+ → X2Σ+ transition using high resolution photographic spectroscopy and reported the approximate FCFs for this transition in 1986. Moreover, ZnH remained a subject of FTIR and rotational spectroscopy. Hence, Shayesteh et al. (Shayesteh et al., 2006) measured the high resolution infrared emission spectra of ZnH in 2006 and Bucchino et al. (Bucchino and Ziurys, 2013) recorded pure rotational spectra, including the N = 0 → 1 and N = 1 → 2 (here N represents the rotational energy levels) transitions, for the ground state of ZnH in 2013. Bucchino and co-workers also determined the fine structure and hyperfine constants, including the Fermi contact, dipolar, and electric quadrupole parameters of Zn nuclei. Subsequently, Abbasi et al. (Abbasi and Shayesteh, 2017) detected the high-resolution emission spectra of the A2Π → X2Σ+ and B2Σ+ → X2Σ+ transitions for ZnH using a Fourier transform spectrometer in 2017. They obtained the Dunham coefficients, empirical band constants, and determined the purely electronic matrix elements.
Apart from experiments, ZnH has been of great interest to theoretical and computational scientists. Such as, in 1967, the spin-orbit coupling (SOC) constant of the A2Π state was computed for ZnH by means of the self-consistent field molecular orbital (SCF MO) theory (Ishiguro and Kobori, 1967). In 1994, Jamorski applied an averaged relativistic effective Hamiltonian method to get the spectroscopic constants of four Λ-S states and corresponding Ω states of ZnH (Jamorski et al., 1994). On the other hand, in 2009, Hayashi and co-workers (Hayashi et al., 2009) did ab initio study for the low-lying electronic states of ZnH and ZnH+. They used highly accurate multireference configuration interaction (MRCI) method with the Davidson correction (+Q) and calculated the spectroscopic constants for the bound states. Likewise, in 2017 Zhao et al. (2017) applied internally contracted MRCI+Q (icMRCI + Q) method and obtained the PECs of the seven lowest-lying Λ-S states and corresponding Ω states of ZnH. Moreover, they estimated radiative lifetimes, calculated FCFs for many transitions as well as reported the spectroscopic constants of five bound Λ-S and corresponding Ω states.
So far, as far as we know, there have not been any theoretical investigations reported on laser cooling of ZnH. In this work, by means of highly accurate ab initio and dynamical calculations including the SOC effects, we identify a suitable molecular candidate for laser cooling, which can fulfil the known criteria of molecular laser cooling including the fourth one proposed in our recent work. The paper is organized as follows. Section 2 briefly describes the theoretical methods and computational details. In Section 3, we discuss our calculated results, underscoring the importance of electronic state crossings and SOCs on laser cooling, and construct a feasible laser cooling scheme for ZnH. The conclusions are presented in Section 4.
2 Methods and computational details
In this paper, all the ab initio calculations of ZnH are carried out in the C2v point group with the MOLPRO 2015.1 program package (Werner et al., 2015). The potential energies of the five Λ-S states of ZnH are computed with the complete active space self-consistent field (CASSCF) (Werner and Knowles, 1985) method. The seven-state averaged CASSCF calculations are performed for the orbital optimization, using the HF orbitals as the starting guess. Then, these CASSCF energies are taken as the reference to compute the energies of each electronic state by the icMRCI + Q method. (Langhoff and Davidson, 1974). The electrons in the 3s and 3p orbitals of the Zn atom are not included in the active space, so the core correlation on Zn is not considered in this work. It is well-known that the selection of a reasonable active space plays a crucial role in the CASSCF and MRCI + Q calculations (Liu et al., 2009; Yu and Bian, 2011; Yu and Bian, 2012). The active space of ZnH is denoted as CAS (3e, 6o) including the Zn 4s4p5s and H 1s orbitals. The outer virtual orbitals are added to give a better description on the dissociation behavior, particularly for excited electronic states (Shen et al., 2017). As for basis sets, we use the aug-cc-pwCV5Z-DK basis sets for Zn and H (Dunning and Peterson, 2000; van Mourik et al., 2000). Moreover, the SOC effects are considered by means of the state interaction approach with the Breit-Pauli Hamiltonian (HBP) in the SOC calculations (Berning et al., 2000), indicating that the SO eigenstates are acquired by diagonalizing Ĥel + ĤSO in the basis of eigenfunctions of Ĥel. Additionally, the ĤSO and Ĥel are derived from the icMRCI + Q computations.
The Einstein spontaneous emission coefficient (Aν′ν) from the higher-energy state (v′, J′) to the lower-energy state (v, J) can be determined with the expression (Herzberg, 1950):
Whereas Aν′ν is expressed in units of s-1,
The Rν′ν can be determined by the following expression:
For a given vibrational level ν′ of an excited state, the radiative lifetime (
The Doppler temperature (
where h and kB are Planck′s and Boltzmann′s constants, respectively, and τ is the radiative lifetime of the excited state.
The recoil temperature (
where m is the relative molecular mass and λ is the laser wavelength λ00.
For the bound Λ-S and Ω states of ZnH, We use the LEVEL 8.0 program (Le Roy, 2017) to determine the Aν′ν, FCFs, and the spectroscopic constants including the equilibrium bond length (Re), adiabatic relative electronic energy referred to the ground state (Te), the harmonic and anharmonic vibrational frequencies (ωe and ωeχe), dissociation energy (De) and the rotational constant (Be).
3 Results and discussion
3.1 PECs and molecular spectroscopic constants
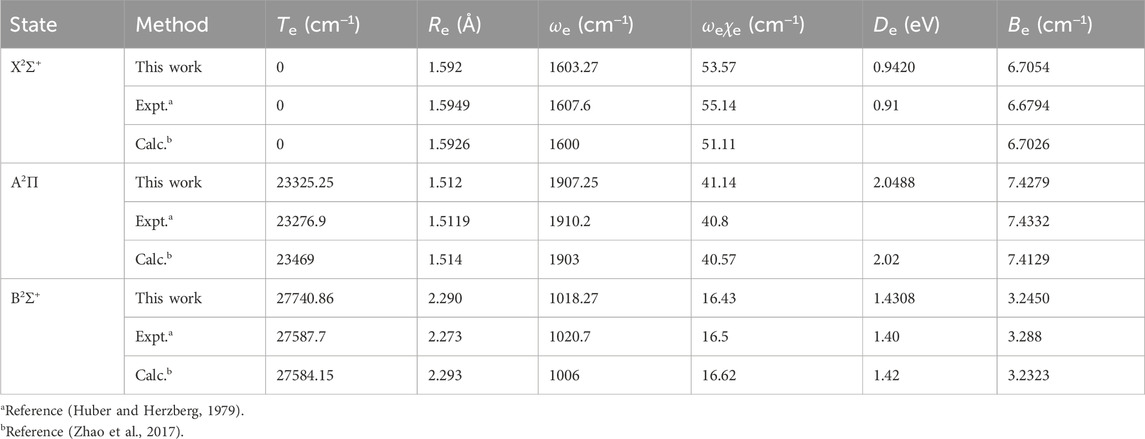
The icMRCI + Q calculations are carried out to check the convergence of the computed results with distinct basis sets (the aug-cc-pwCVTZ-DK, aug-cc-pwCVQZ-DK and aug-cc-pwCV5Z-DK basis sets are denoted as AVTZ, AVQZ and AV5Z, respectively), and the calculated Te results of the A2Π state are shown in Figure 1. Here the complete basis set (CBS) energy is evaluated by a three-point extrapolation scheme. (Peterson et al., 1994; Koput and Peterson, 2002; Peterson and Dunning, 2002). The plotted curve in Figure 1 indicates that the result obtained by the AV5Z (aug-cc-pwCV5Z-DK) basis sets is very close to the CBS result, and in very good agreement with the experimental value. (Huber and Herzberg, 1979). We conclude that the aug-cc-pwCV5Z-DK basis set is large enough and thus is used for further calculations in this work. Figure 2 depicts the PECs of the five lowest-lying Λ-S electronic states of ZnH, derived from the icMRCI + Q calculations. As can be seen, the ground state X2Σ+ converges towards the lowest neutral atomic Zn (1Sg) + H (2Sg) limit, while the A2Π, B2Σ+ and a4Π states correlate with the Zn (3Pu) + H (2Sg) limit. Additionally, the C2Σ+ state corresponds to the Zn+(2Sg) + H−(1Sg) limit. In this work the A2Π state is used to establish laser cooling cycles for ZnH, and thus we did not consider much higher excited states (e.g., the 14Σ+ state), which will not influence our discussion. As the values of spectroscopic constants for the low-lying bound states of ZnH are already determined experimentally and reported in literature, we compared our computed results with these data that could verify the accuracy and reliability of our calculations. Table 1 provides a comparison of our computed and already available spectroscopic constants values of the three bound Λ-S states of ZnH. For the first excited state A2Π, the experimentally determined value (Huber and Herzberg, 1979) is 23276.9 cm-1 whereas our computed value is 23325.25 cm−1, using larger basis set. In contrast, the previously computed value (Zhao et al., 2017) at smaller basis sets (aug-cc-pwCVTZ-DK) is 23469 cm-1, deviated from experimental value by approximately 190 cm-1. Furthermore, our computed spectroscopic constants, i.e., Re, ωe, ωeχe and Be values of the A2Π state and Re, ωe, ωeχe, De and Be values of the ground state X2Σ+ are very close to the experimental values (Huber and Herzberg, 1979). Moreover, our computed Re, ωe, ωeχe and Be values of the B2Σ+ state are highly consistent to the measurements (Huber and Herzberg, 1979). Over all, it can be seen that our results align very well with the experimental data (Huber and Herzberg, 1979), though the deviation in the Te value for the B2Σ+ between our calculated data and the experimental result is slightly larger than that from the previous calculations (Zhao et al., 2017). It is worth noting that accurate determination of the Te value for the A2Π state plays a pivotal role in obtaining the laser wavelengths for laser-driven cycling. In this regard, our calculated Te values match well with corresponding experimental results, raising the confidence to further investigate laser cooling of ZnH.
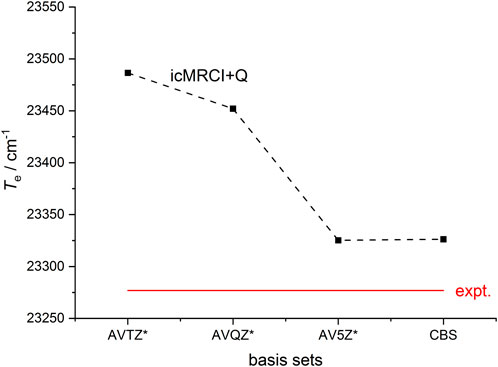
Figure 1. The convergence pattern of the adiabatic relative electronic energy relative to the ground state (Te) of the A2Π state for ZnH toward the estimated complete basis set (CBS) limit using the icMRCI(3e, 6o) + Q method with the AVnZ* (n = T, Q, 5) basis sets. AVnZ* represents aug-cc-pwCVTZ-DK, aug-cc-pwCVQZ-DK and aug-cc-pwCV5Z-DK respectively. The corresponding experimental value (Huber and Herzberg, 1979) is also shown.

Figure 2. Potential energy curves of ZnH as a function of the interatomic distance (R) for the five lowest-lying Λ-S states at the icMRCI + Q level.
Inclusion of the SOC effects has resulted in the splitting of five Λ-S states (X2Σ+, A2Π, B2Σ+, C2Σ+ and a4Π) of ZnH into 9 Ω states, of which 6 states have Ω = 1/2 (X2Σ+ 1/2, A2Π1/2, B2Σ+ 1/2, C2Σ+ 1/2, a4Π1/2 and (2) a4Π1/2), two states have Ω = 3/2 (A2Π3/2 and a4Π3/2), and one state has Ω = 5/2 (a4Π5/2). The PECs of the 9 Ω states of ZnH are depicted in Figure 3. The spectroscopic constants of the 4 Ω states of ZnH, namely, X2Σ+ 1/2, A2Π1/2, A2Π3/2 and B2Σ+ 1/2, are presented in Table 2. As can be seen, the spectroscopic constants of the 2 Ω states X2Σ+ 1/2 and B2Σ+ 1/2 are very close to those of Λ-S states of ZnH. In addition, our calculated SO splitting value of the A2Π state (331.84 cm−1) is in very good agreement with the experimental value (Huber and Herzberg, 1979) (342.66 cm−1) and outperforms the previous theoretical result (Zhao et al., 2017) (241.96 cm−1). It is evident that SO splitting value of the A2Π state is relatively large and indicates that the SOC effects should be considered while studying the excited states of ZnH. Hence, SOC effects are important for laser cooling of ZnH.
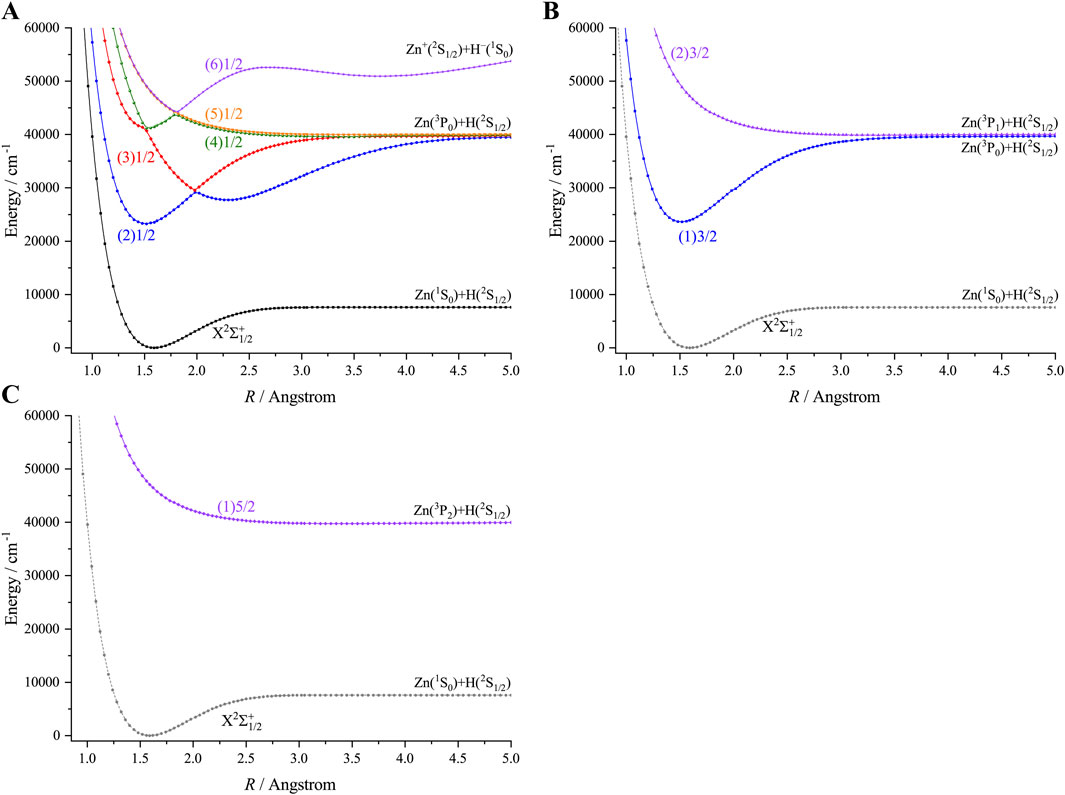
Figure 3. Potential energy curves of ZnH as a function of the interatomic distance (R) for (A) Ω = 1/2, (B) Ω = 3/2 and (C) Ω = 5/2 at the icMRCI + Q level.
3.2 The effects of the electronic state crossings and spin-orbit couplings
From Figure 2, we can see that the A2Π and B2Σ+ states of ZnH have a crossing point, which can lead to nonradiative transition (Wu et al., 2019), and result in predissociation. It is evident that, for polyatomic molecules, this type of electronic state crossings will become potential energy surface intersections (Liu et al., 2003; Zhao et al., 2006). We can see that the location of crossing point between the A2Π and B2Σ+ states of ZnH is above the ν′ = 2 vibrational level of the A2Π state (1540 cm-1) indicating that the crossings with higher electronic states will not affect laser cooling. With the inclusion of the SOC effects, the A2Π state will split into two states (A2Π1/2 and A2Π3/2), and the potential energy of the A2Π1/2 state is a little lower than that of A2Π3/2. Thus we will use the A2Π1/2 → X2Σ+ 1/2 transition to construct a laser cooling scheme for ZnH. Consequently, hereafter, a feasible laser cooling scheme for ZnH is constructed on the basis of the A2Π1/2 → X2Σ+ 1/2 transition, which meets the known criteria including the fourth one proposed in our recent work (Li et al., 2020).
3.3 Laser cooling scheme proposed for ZnH using specific spin-orbit states
Given the significance of the SOC effects as demonstrated above, we construct a laser cooling scheme for ZnH based on the A2Π1/2 → X2Σ+ 1/2 transition, which is free from interference by any intermediate state. In this scheme, ZnH molecules are initially excited from the X2Σ+ 1/2 (ν = 0) state to the A2Π1/2 (ν′ = 0) state, then they decay back to the X2Σ+ 1/2 state. This will generate ultracold ZnH molecules when the cooling cycles are consistently repeated.
Figure 4 presents the permanent dipole moments (PDMs) and transition dipole moments (TDMs) for the A2Π1/2 → X2Σ+ 1/2 transition of ZnH at the icMRCI + Q level. As can be seen, the TDMs of ZnH gradually decrease with the increasing bond length, reaching 1.88 debye at Re. In addition, our computed FCF (fν′ν) value of the A2Π1/2 (ν′ = 0) → X2Σ+ 1/2 (ν = 0) transition (or the f00 value) for ZnH is 0.8367. This relatively large f00 value indicates that the spontaneous decays to ν = 1–4 vibrational levels of the X2Σ+ 1/2 state are highly suppressed. Based on the A2Π1/2 → X2Σ+ 1/2 transition, we use the ν′ = 0, 1 levels of the A2Π1/2 state of ZnH with five lasers to establish laser cooling scheme. Furthermore, we have computed and tabulated the Einstein A coefficients (Aν′ν, Equation 1) and vibrational branching ratios (Rν′ν, Equation 2) values of the A2Π1/2 → X2Σ+ 1/2 transition (see Table 3), since the relative strengths of photon loss channels are directly linked to the Rν′ν rather than the fν′ν in laser cooling process. A very large A00 value of 1.32×107 s-1 and very minimal scattering probabilities into off-diagonal bands provide favourable conditions for rapid and efficient laser cooling cycles.
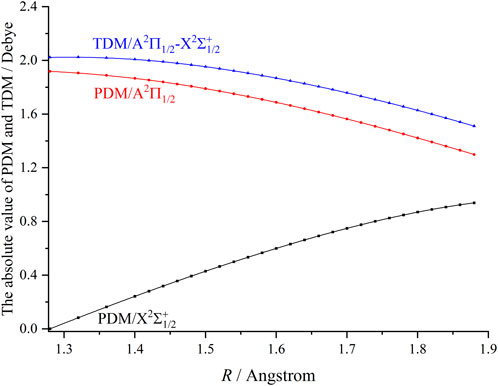
Figure 4. The computed permanent dipole moments (PDMs) and transition dipole moments (TDMs) for the X2Σ+ 1/2 and A2Π1/2 states of ZnH at the icMRCI + Q level.
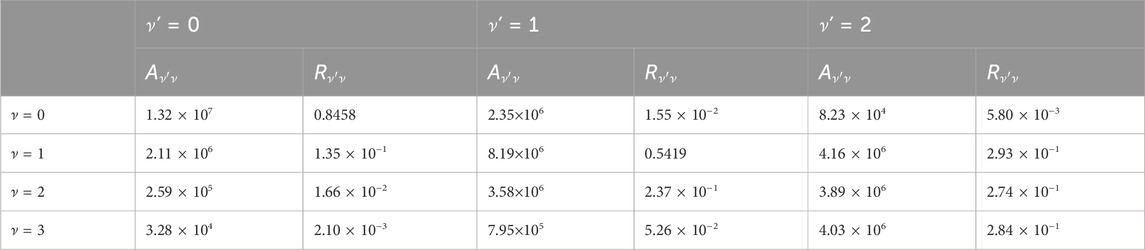
Table 3. Calculated Einstein A coefficients Aν′ν and vibrational branching ratio Rν′ν of the A2Π1/2 (ν′) → X2Σ+ 1/2 (ν) transition for ZnH.
In addition, the evaluated Doppler and recoil temperatures (TDoppler and Trecoil can be evaluated with the Equations 3 and 4, respectively) for the A2Π1/2 (ν′ = 0) → X2Σ+ 1/2 (ν = 0) transition of ZnH are 59.73 µK and 1.59 µK, respectively. The computed radiative lifetime (
Our constructed five-laser cooling scheme for the production of ultracold ZnH is depicted in Figure 5. As illustrated, the laser wavelength for the main cycling will drive the X2Σ+ 1/2 (ν = 0, J = 1) → A2Π1/2 (ν′ = 0, J′ = 0) transition of ZnH at the wavelength λ00 of 426.7 nm (here J means the rotational quantum number). According to the angular momentum and parity selection rules, the A2Π1/2 (ν′ = 0, J′ = 0) state can only decay back to the initial X2Σ+ 1/2 (ν = 0, J = 1) state, thereby eliminating rotational branching. Additionally, to minimize vibrational branching losses, another 4 repump lasers are employed to recover the molecules that have decayed to the X2Σ+ 1/2 (ν = 1, 2, 3, 4) states of ZnH. Consequently, quasi-closed cooling cycles could be achieved using the constructed cooling scheme as presented in Figure 5. Furthermore, the calculated R00 value of ZnH is 0.8458, indicating that the A2Π1/2 (ν′ = 0) → X2Σ+ 1/2 (ν = 0) transition of ZnH has the largest possibility, whereas the vibrational branching loss should be solved in laser cooling cycle process. Thus the off-diagonal Rν'ν of ZnH are also computed. In addition, we use

Figure 5. Constructed five-laser cooling scheme for ZnH using the A2Π1/2 (ν′) → X2Σ+ 1/2 (ν) transitions. Solid arrows indicate laser-driven transitions at certain wavelengths λν′ν. Dashed arrows indicate spontaneous decays from the A2Π1/2 (ν′ = 0, 1) states with the calculated vibrational branching ratios.
4 Conclusions
In this work, the five lowest-lying Λ-S states of ZnH are investigated by means of highly accurate ab initio and dynamical calculations including the SOC effects. Our computational results agree very well with experimental spectroscopic data. In addition, we study direct laser cooling of ZnH, and reveal the effects of electronic state crossings and SOC. Our calculations indicate that ZnH is a suitable candidate for laser cooling, which can fulfil the known criteria including the fourth one proposed in our recent work. The position of crossing point between the A2Π and B2Σ+ states of ZnH is higher than the ν′ = 2 vibrational level of the A2Π state indicating that the crossings with higher electronic states will not affect the laser cooling. Hence, we construct a practical laser-cooling scheme for ZnH based on the A2Π1/2 → X2Σ+ 1/2 transition. Our calculated excitation energy to the A2Π state of ZnH is 23325.25 cm-1, which closely matches with the experimental value of 23276.9 cm-1 38. This enables us to determine laser wavelengths in laser-cooling cycles accurately. The Doppler and recoil temperatures for the main transition of ZnH are 59.73 µK and 1.59 µK, respectively. The vibrational branching ratios (Rν′ν) for the A2Π1/2 (ν′ = 0) → X2Σ+ 1/2 transition of ZnH are shown to be diagonally distributed with R00 being 0.8458. The radiative lifetime for the A2Π1/2 (ν′ = 0) → X2Σ+ 1/2 (ν = 0) transition of ZnH is extremely short (64 ns). The present constructed scheme is able to scatter 9.8 × 103 photons for ZnH, which are sufficient for cooling ZnH to ultracold temperatures. It is expected that this theoretical study will encourage for the experimental laser cooling of ZnH to ultracold temperatures.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
DL: Conceptualization, Data curation, Formal analysis, Investigation, Writing–original draft, Writing–review and editing. FF: Writing–original draft, Validation, Writing–review and editing. WB: Conceptualization, Formal analysis, Funding acquisition, Investigation, Resources, Supervision, Validation, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (Nos. 22320102004, 21773251) and the Junior Fellow Program of Beijing National Laboratory for Molecular Science (No. 2022BMS20096).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbasi, M., and Shayesteh, A. (2017). Fourier transform emission spectra and deperturbation analysis of the A2Π → X2Σ+ and B2Σ+ → X2Σ+ electronic transitions of ZnH. J. Mol. Spectrosc. 340, 21–28. doi:10.1016/j.jms.2017.07.012
Balfour, W. J., Chandrasekhar, K. S., and Lindgren, B. (1986). The B2Σ+ state of zinc deuteride. J. Mol. Spectrosc. 119, 126–136. doi:10.1016/0022-2852(86)90207-9
Baron, J., Campbell, W. C., DeMille, D., Doyle, J. M., Gabrielse, G., Gurevich, Y. V., et al. (2014). Order of magnitude smaller limit on the electric dipole moment of the electron. Science 343, 269–272. doi:10.1126/science.1248213
Berning, A., Schweizer, M., Werner, H.-J., Knowles, P. J., and Palmieri, P. (2000). Spin-orbit matrix elements for internally contracted multireference configuration interaction wavefunctions. Mol. Phys. 98, 1823–1833. doi:10.1080/00268970009483386
Bucchino, M. P., and Ziurys, L. M. (2013). Terahertz spectroscopy of 25MgH (X2Σ+) and 67ZnH (X2Σ+): bonding in simple metal hydrides. J. Phys. Chem. A 117, 9732–9737. doi:10.1021/jp3123743
Cao, J., Li, F., Xia, W., and Bian, W. (2019). van der Waals interactions in bimolecular reactions. Chin. J. Chem. Phys. 32, 157–166. doi:10.1063/1674-0068/cjcp1901007
Di Rosa, M. D. (2004). Laser-cooling molecules: concept, candidates, and supporting hyperfine-resolved measurements of rotational lines in the A-X (0,0) band of CaH. Eur. Phys. J. D 31, 395–402. doi:10.1140/epjd/e2004-00167-2
Dunning, T. H., and Peterson, K. A. (2000). Approximating the basis set dependence of coupled cluster calculations: evaluation of perturbation theory approximations for stable molecules. J. Chem. Phys. 113, 7799–7808. doi:10.1063/1.1316041
Fu, M., Ma, H., Cao, J., and Bian, W. (2017). Laser cooling of CaBr molecules and production of ultracold Br atoms: a theoretical study including spin-orbit coupling. J. Chem. Phys. 146, 134309. doi:10.1063/1.4979566
Hayashi, S., Leonard, C., and Chambaud, G. (2009). Ab initio study of HZnF. J. Phys. Chem. A 113, 14615–14624. doi:10.1021/jp9043607
Huber, K. P., and Herzberg, G. (1979). Molecular spectra and molecular structure IV: constants of diatomic molecules. New York: NY: Van Nostrand Reinhold.
Hudson, J. J., Kara, D. M., Smallman, I. J., Sauer, B. E., Tarbutt, M. R., and Hinds, E. A. (2011). Improved measurement of the shape of the electron. Nature 473, 493–496. doi:10.1038/nature10104
Ishiguro, E., and Kobori, M. (1967). Spin orbit coupling constants in simple diatomic molecules. J. Phys. Soc. Jpn. 22, 263–270. doi:10.1143/jpsj.22.263
Jamorski, C., Dargelos, A., Teichteil, C., and Daudey, J. P. (1994). Theoretical determination of spectral lines for the Zn atom and the ZnH molecule. J. Chem. Phys. 100, 917–925. doi:10.1063/1.466574
Khan, M. A. (1962). New band systems of ZnH and ZnD in the far ultra-violet region. Proc. Phys. Soc. Lond. 80, 599–607. doi:10.1088/0370-1328/80/3/303
Koput, J., and Peterson, K. A. (2002). Ab initio potential energy surface and vibrational-rotational energy levels of X2Σ+ CaOH. J. Phys. Chem. A 106, 9595–9599. doi:10.1021/jp026283u
Langhoff, S. R., and Davidson, E. R. (1974). Configuration interaction calculations on the nitrogen molecule. Int. J. Quantum Chem. 8, 61–72. doi:10.1002/qua.560080106
Le Roy, R. J. (2017). LEVEL: a computer program for solving the radial Schrödinger equation for bound and quasibound levels. J. Qual. Spectrosc. Radiat. Transfer 186, 167–178.
Li, D., Fu, M., Ma, H., Bian, W., Du, Z., and Chen, C. (2020). A theoretical study on laser cooling feasibility of group IVA hydrides XH (X = Si, Ge, Sn, and Pb): the role of electronic state crossing. Front. Chem. 8, 20. doi:10.3389/fchem.2020.00020
Li, R., Yuan, X., Liang, G., Wu, Y., Wang, J., and Yan, B. (2019). Laser cooling of the SiO+ molecular ion: a theoretical contribution. Chem. Phys. 525, 110412. doi:10.1016/j.chemphys.2019.110412
Liu, C., Zhang, D., and Bian, W. (2003). Theoretical investigation of the reaction of Co+ with OCS. J. Phys. Chem. A 107, 8618–8622. doi:10.1021/jp034693s
Liu, K., Yu, L., and Bian, W. (2009). Extensive theoretical study on various low-lying electronic states of silicon monochloride cation including spin-orbit coupling. J. Phys. Chem. A 113, 1678–1685. doi:10.1021/jp809618y
Moussa, A., El-Kork, N., and Korek, M. (2021). Laser cooling and electronic structure studies of CaK and its ions CaK±. New J. Phys. 23, 013017. doi:10.1088/1367-2630/abd50d
Peterson, K. A., and Dunning, T. H. (2002). Accurate correlation consistent basis sets for molecular core-valence correlation effects: the second row atoms Al-Ar, and the first row atoms B-Ne revisited. J. Chem. Phys. 117, 10548–10560. doi:10.1063/1.1520138
Peterson, K. A., Woon, D. E., and Dunning, T. H. (1994). Benchmark calculations with correlated molecular wave functions. IV. The classical barrier height of the H + H2 → H2 + H reaction. J. Chem. Phys. 100, 7410–7415. doi:10.1063/1.466884
Shayesteh, A., Le Roy, R. J., Varberg, T. D., and Bernath, P. F. (2006). Multi-isotopologue analyses of new vibration-rotation and pure rotation spectra of ZnH and CdH. J. Mol. Spectrosc. 237, 87–96. doi:10.1016/j.jms.2006.03.004
Shen, Z., Ma, H., Zhang, C., Fu, M., Wu, Y., Bian, W., et al. (2017). Dynamical importance of van der Waals saddle and excited potential surface in C(1D) + D2 complex-forming reaction. Nat. Commun. 8, 14094. doi:10.1038/ncomms14094
Shuman, E. S., Barry, J. F., and DeMille, D. (2010). Laser cooling of a diatomic molecule. Nature 467, 820–823. doi:10.1038/nature09443
van Mourik, T., Dunning, T. H., and Peterson, K. A. (2000). Ab initio characterization of the HCOx (x = -1, 0, +1) species: structures, vibrational frequencies, CH bond dissociation energies, and HCO ionization potential and electron affinity. J. Phys. Chem. A 104, 2287–2293. doi:10.1021/jp9925583
Wells, N., and Lane, I. C. (2011). Electronic states and spin-forbidden cooling transitions of AlH and AlF. Phys. Chem. Chem. Phys. 13, 19018–19025. doi:10.1039/c1cp21313j
Werner, H.-J., and Knowles, P. J. (1985). A second order multiconfiguration SCF procedure with optimum convergence. J. Chem. Phys. 82, 5053–5063. doi:10.1063/1.448627
Werner, H.-J., Knowles, P. J., Lindh, R., Manby, F. R., Schütz, M., Celani, P., et al. (2015). Molpro, Version 2015.1, A package of ab initio programs. Available at: http://www.molpro.net.
Wu, Y., Cao, J., Ma, H., Zhang, C., Bian, W., Nunez-Reyes, D., et al. (2019). Conical intersection-regulated intermediates in bimolecular reactions: insights from C(1D) + HD dynamics. Sci. Adv. 5, eaaw0446. doi:10.1126/sciadv.aaw0446
Xia, W., Ma, H., and Bian, W. (2021). Production of ultracold CaCCH and SrCCH molecules by direct laser cooling: a theoretical study based on accurate ab initio calculations. J. Chem. Phys. 155, 204304. doi:10.1063/5.0072013
Yan, B., Moses, S. A., Gadway, B., Covey, J. P., Hazzard, K. R. A., Rey, A. M., et al. (2013). Observation of dipolar spin-exchange interactions with lattice-confined polar molecules. Nature 501, 521–525. doi:10.1038/nature12483
Yu, L., and Bian, W. (2011). Extensive theoretical study on electronically excited states and predissociation mechanisms of sulfur monoxide including spin-orbit coupling. J. Comput. Chem. 32, 1577–1588. doi:10.1002/jcc.21737
Yu, L., and Bian, W. (2012). Electronically excited-state properties and predissociation mechanisms of phosphorus monofluoride: a theoretical study including spin-orbit coupling. J. Chem. Phys. 137, 014313. doi:10.1063/1.4731635
Zhao, H., Bian, W., and Liu, K. (2006). A theoretical study of the reaction of O(3P) with isobutene. J. Phys. Chem. A 110, 7858–7866. doi:10.1021/jp060583k
Keywords: electronic state crossing, vibrational branching ratio, ultracold molecule, ab initio, spin-orbit coupling
Citation: Li D, Fayyaz F and Bian W (2024) A theoretical study on excited-state dynamical properties and laser cooling of zinc monohydride including spin-orbit couplings. Front. Chem. 12:1460224. doi: 10.3389/fchem.2024.1460224
Received: 05 July 2024; Accepted: 05 August 2024;
Published: 20 August 2024.
Edited by:
Guangjiu Zhao, Tianjin University, ChinaReviewed by:
Jun Chen, Chinese Academy of Sciences (CAS), ChinaSomnath Bhowmick, The Cyprus Institute, Cyprus
Copyright © 2024 Li, Fayyaz and Bian. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wensheng Bian, YmlhbkBpY2Nhcy5hYy5jbg==
 Donghui Li
Donghui Li Faiza Fayyaz
Faiza Fayyaz Wensheng Bian
Wensheng Bian