- Department of Mathematics, School of Advanced Sciences, Vellore Institute of Technology, Chennai, India
Domination is an important factor in determining the robustness of a graph structure. A thorough examination of the graph’s topological structure is necessary for analyzing and examining it for various aspects. Understanding the stability of a chemical compound is a significant criterion in chemistry, which necessitates conducting numerous experimental tests. The domination number and power domination number are pivotal in defining a wide range of physical properties, which include physiochemical properties, thermodynamic properties, chemical activities, and biological activities. The one-pentagonal carbon nanocone (1-PCNC) is a member of the carbon nanocone family and has a structure similar to that of honeycomb networks, which are renowned for their robustness. In this paper, we find the domination number and power domination number of 1-PCNC by considering it as an (m-1)-layered infinite graph.
1 Introduction
In the field of nanotechnology, the study of carbon-based nanomaterials like fullerenes, carbon nanotubes, carbon nanohorns, carbon nanowires, and carbon nanocones using a graph theoretical approach is becoming very intense and popular because of its application in the real world. Carbon nanocones (CNCs) are gaining priority in the field of research because of their applications in multidisciplinary areas. The study and practical application of domination and its variants have attracted significant attention, particularly in the realm of neural networks (Prabhu et al., 2022) and in the family of chemical graphs (Vukičević and Klobučar, 2007; Quadras et al., 2015; Gao et al., 2018; Hutchinson et al., 2018; Chithra and Menon, 2020; Iqbal et al., 2020; Prabhu et al., 2021). Researchers have discovered that chemical graphs offer significant insights into molecular structure, reactivity, and other characteristics, which allow for the prediction of molecular behavior and facilitate the creation of new compounds with specific properties. The application of the domination number in the analysis of secondary RNA structure (Haynes et al., 2006) and the encryption of bit strings into a DNA sequence (Yamuna and Karthika, 2014) has given rise to numerous research avenues within the domain of chemical graph theory. The chemical graph theory involves analyzing chemical structures by representing them as graphs, in which vertices correspond to the atoms of the chemical compound, while the edges represent the bonds between the atoms. QSAR and QSPR investigations have consistently revealed the significant association between graph theoretical invariants, commonly referred to as topological indices or molecular descriptors, and a wide range of physical and chemical properties exhibited by molecules. To examine the physiochemical characteristics of a molecule, it is crucial to conduct a comprehensive analysis of its topological indices or molecular descriptors (Zaman et al., 2023; Ullah et al., 2024; Zaman et al., 2024). The Wiener index, classified as a topological index, for 1-PCNC was determined by employing JAVA programming (Alipour and Ashrafi, 2009). Recently, the topological properties of carbon nanocones, employing the cut technique on strength-weighted graphs to identify various topological indices, were investigated and studied. Using this methodology, analytical formulations for numerous distance-based topological indices of CNCs were derived (Arockiaraj et al., 2018). To find the desired sizes and chemical reactivity for 1-PCNC, topological modeling methods have been used (Bultheel and Ori, 2018). In contrast to the Weiner index, the edge-Wiener index plays a crucial role in molecular analysis. The edge-Wiener and vertex-edge-Wiener indices were specifically investigated in coronoid systems, carbon nanocones, and SiO2 nanostructures. This examination included breaking down the original graph into smaller strength-weighted quotient graphs using the Djoković–Winkler relation (Arockiaraj et al., 2019b). A computational method was employed to calculate the Mostar, edge-Mostar, and total-Mostar indices by considering the strength-weighted parameters. These techniques were then applied to determine the three indices for various coronoid and carbon nanocone structures (Arockiaraj et al., 2019a). Expanding the study further on 1-PCNC, the edge metric dimension and the bounds on the partition dimension of the 1-PCNC structure were calculated (Sharma et al., 2021; Koam et al., 2022). Carbon-based nanomaterials are characterized by their remarkable flexibility and strength, making them well-suited for manipulating various nanoscale structures. This unique property suggests that carbon nanomaterials will be instrumental in advancing the field of nanotechnology engineering. The development of 3D all-carbon architectures has the potential to revolutionize power storage, field emission transistors, photovoltaic systems, supercapacitors, biomedical implants, and high-performance catalysts (Sharma et al., 2021). We delve further into this research endeavor because of its immense practicality and widespread implementation in various areas. We explore the domination and power domination of 1-PCNC by examining its brick diagram, akin to that of n-layered honeycomb networks (HC(n)) (Stojmenovic, 1997). This paper provides an overview of the intricate layout of the brick diagram of 1-PCNC, along with the precise calculations of the domination number, independent domination number, power domination number, and k-power domination number.
2 Preliminaries
A graph G is represented as an ordered pair [V(G), E(G)], where V(G) denotes a non-empty set of vertices and E(G) represents a set of unordered pairs of distinct elements from V(G), which are known as edges. A subgraph S of a graph G is essentially a graph where the set of vertices V(S) is a subset of V(G) and the set of edges E(S) is a subset of E(G). The order of the graph G is characterized by the total count of vertices within G. Simultaneously, the size of the graph G is determined by the total count of edges present in G. The count of edges connected to a vertex x is termed the degree of the vertex, represented by deg(x). The maximum degree within the graph is symbolized as Δ. The distance between two vertices within a graph refers to the count of edges present in the shortest path connecting them. The collection of vertices adjacent to x is known as the neighborhood of x, symbolized as N(x), and N[x] = N(x) ∪{x} is called the closed neighborhood of vertex x. A cut vertex is a vertex x ∈ V such that G \{x} disconnects the graph G. Assigning a dominating vertex to each vertex in a graph such that every vertex is dominated exactly once is called saturation. A vertex with degree 1 is commonly referred to as a pendant vertex, and if one of the vertices of an edge is a pendant vertex, then the edge is called a pendant edge. A cut C denoted as (T, H) is a partition of the vertex set V in a graph G into two subsets, T and H. The cut-set of a cut C = (T, H) is represented by the set {(x, y) ∈ E|x ∈ T, y ∈ H}, which includes edges having one endpoint in the set T and the other endpoint in the set H. A hexagonal system is a finitely connected planar network with no cut vertices, where every inner area is a regular hexagon that is mutually congruent. A hexagonal chain (HC) is described as a hexagonal arrangement in which each hexagon is adjacent to a maximum of two other hexagons, and if every shared edge between two adjacent hexagons is parallel to the other, the HC is said to be linear. A hexagon in an HC is a linear hexagon h if it has two inner vertices in different lines. A unique vertex y that is situated at a distance of 3 from the specified vertex x in a hexagon is called the diagonally opposite vertex of x.
A dominating set for a graph G is a subset D of vertices where each vertex not in D is adjacent to at least one vertex in D. The domination number γ(G) signifies the count of vertices in the smallest dominating set for G. A dominating set is said to be an independent dominating set when no two vertices within the set are adjacent, and the independent domination number, γi(G), expresses the minimum cardinality of such a set. A dominating set D is said to be a power dominating set if every vertex in G is dominated by D concerning the following domination rule: (a) every vertex incident on a dominated edge is dominated. (b) Every edge joining two dominated vertices is dominated. (c) If a vertex is connected to i > 1 edges and i − 1 of these edges are dominated, then all i of these edges must be dominated, and the power domination number, denoted by γp(G), indicates the smallest cardinality of such a set. A dominating set D is said to be a k-power dominating set if every vertex in G is dominated by D concerning the following domination rule: (a) every vertex incident to a dominated edge is dominated. (b) Every edge joining two dominated vertices is dominated. (c) If a vertex is connected to i > k edges and i − k of these edges are dominated, then all i of these edges must be dominated, and the k-power domination number, γp,k(G), indicates the smallest cardinality of such a set.
Theorem 1. (Berge, 1973) In a graph G with order m, m ≥ 1 and maximum degree Δ, it is established that the domination number γ(G) satisfies
Proposition 1. (Bermudo et al., 2020) If H is a hexagonal chain and D is a minimum dominating set in H, then every linear hexagon in H contains at least two vertices of D.
Theorem 2. (Bermudo et al., 2020) Suppose H is a hexagonal chain comprising h hexagons where h
Proposition 2. (Bermudo et al., 2020) Suppose H is a hexagonal chain comprising h hexagons where h
Theorem 3. (Alanko et al., 2011) For a grid graph G = (V, E), with order m × n, suppose S1 ⊆ V and S2 ⊆ V with |S1| = |S2| and D(S1) ⊆ D(S2). To determine a minimum dominating set of G, it is sufficient to exclude S1 and focus solely on dominating sets that extend S2.
Lemma 1. (Chang et al., 2012) Consider a connected graph G with a maximum degree, Δ(G) ≤ k + 1, for k ≥ 1 then γp,k = 1.
3 Address of blocks in the brick diagram
CNCs consist of an interconnected arrangement of carbon atoms in a hexagonal lattice structure. CNCs were first synthesized in 1994 (Ge and Sattler, 1994), in which the distinct hollow carbon structures, identified as carbon cones, were observed on a flat graphite surface alongside tubules. The chemical graph of CNCs denoted by CNCt[m] with m ≥ 2 exhibits a tapered structure with edges and vertices arranged in a specific pattern, and at its core, there is a cycle of size with the same order t. Surrounding this central cycle, there are (m-1) hexagon layers forming the tapered surface. CNCs are carbon frameworks that can be depicted as infinite cubic plane graphs featuring 1 ≤ P
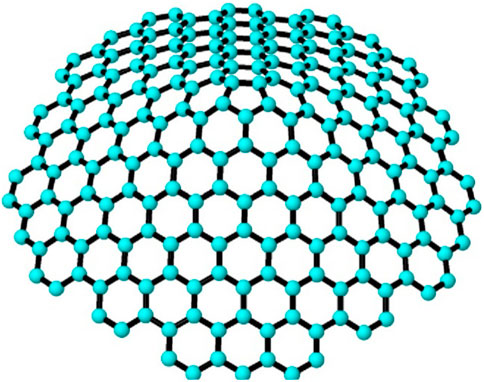
Figure 1. Pentagonal nanocone structure (Sharma et al., 2021).
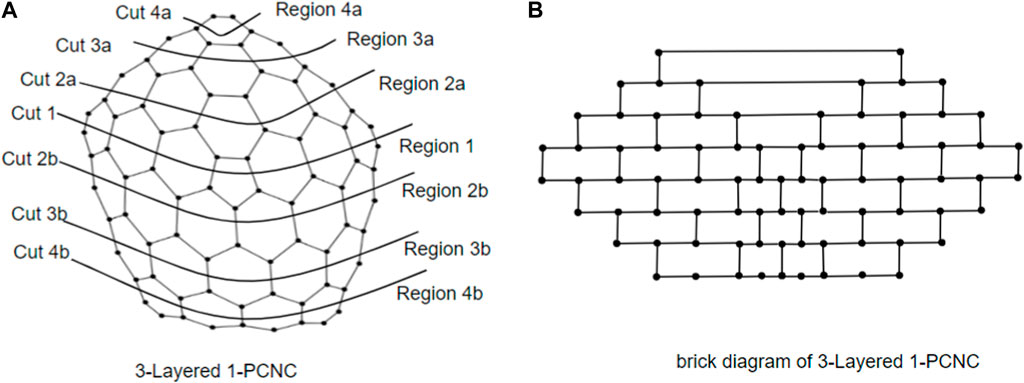
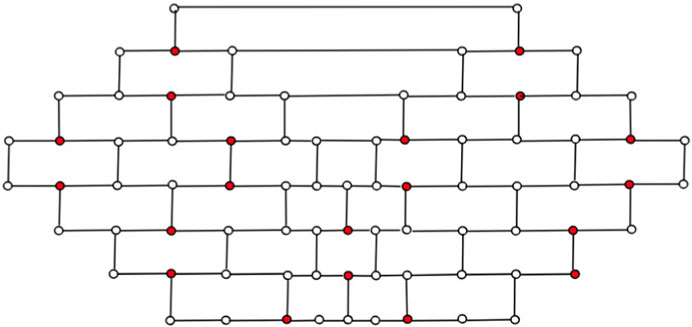
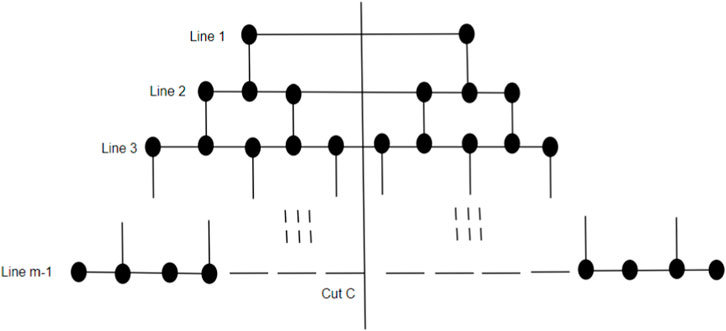
Now, we model a brick diagram of CNC5[m], m ≥ 2, which facilitates our understanding of the 1-PCNC structure. Initially, our approach involves depicting a series of cuts on the graph, starting from Region 1 and extending downward until all regions are encompassed. These cuts are systematically labeled to denote their origin and direction. For instance, in Figure 2A, we identify the cut surrounding the core of CNC5 [4] within Region 1 as “cut 1.” Moving onward, as we ascend into Region 2a, we establish a new cut labeled “cut 2a.” This pattern continues as we progress through the regions, with each successive cut being denoted by appending the region identifier to the numeric label (e.g., “cut 4a” in Region 4a). As we descend from Region 1, we continue the process of defining cuts, assigning labels such as “cut 2b,” “cut 3b,” and “cut 4b” in a manner consistent with our established pattern. Each cut serves to delineate a boundary within the graph, segregating regions and defining the interconnected structure. In the brick diagram representation, the effect of these cuts becomes visually apparent. A straight horizontal line emerges when extending the zigzag lines above and below each cut. The edges intersecting with these cut lines correspond to the vertical lines depicted in the brick diagram, while the regions depicted by the cuts form distinct blocks within the diagram (as illustrated in Figure 2B).
To simplify the visualization of a CNC5[2], we may identify it using its brick diagram, as shown in Figure 3C. A higher-level 1-PCNC network is generated by expanding a lower-level network using a level numbering approach similar to the method that was used to build honeycomb networks (Sharieh et al., 2008). In the context of CNC5[m], where m ≥ 2, the quantity 5m2 denotes the number of vertices, and
4 Main result
In this section, we compute the domination number, independent domination number, power domination number, and k-power domination number for 1-PCNC. To streamline the explanation of the lemmas, we introduce certain notations that prove to be beneficial for the subsequent discussion.
• For any x ∈ D, A(x) denotes the collection of vertices adjacent to x.
• For a set S ⊆ V, the collection of vertices adjacent to S is denoted by A(S).
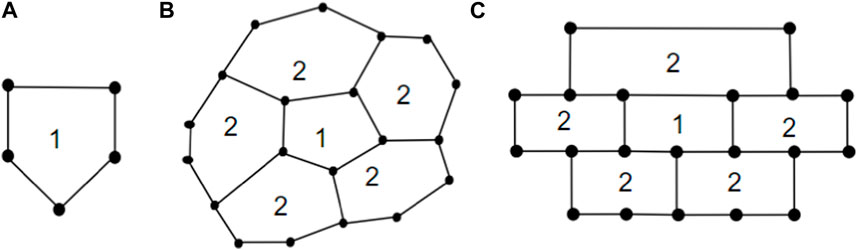
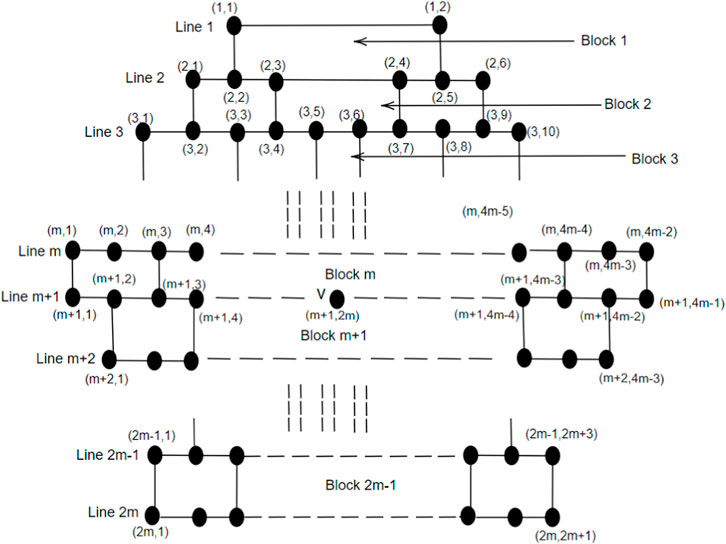
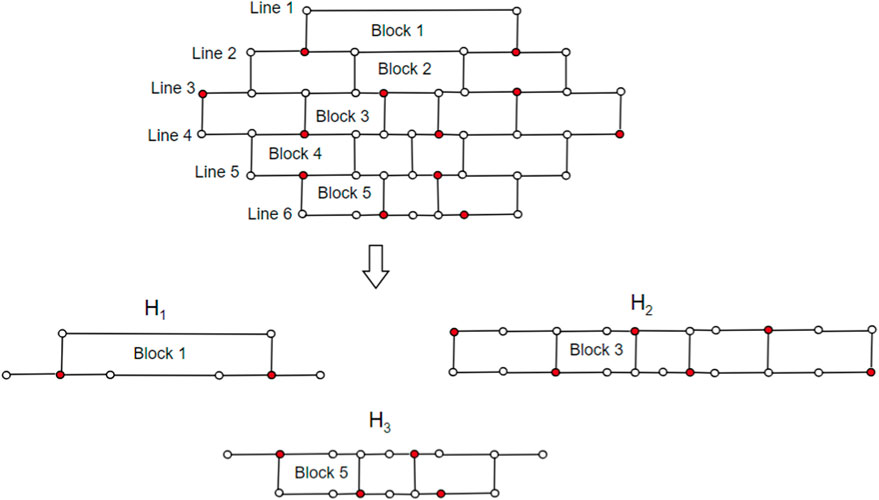
• In a brick diagram of CNC5[m], the Block m is called a 1-pentagonal hexagonal chain and denoted by 1-PH.
• In a linear hexagonal chain, if there are exactly two pendant edges attached to the first and last hexagon, we define it as a 2-pendant linear hexagonal chain, denoted by 2P-HC.
Observation. Let G = CNC5[m] be a connected undirected graph, m ≥ 2. Then, we have the following observations.
1. In the CNC5[m] graph, there are 5m vertices with degree 2, while the remaining vertices have a degree 3.
2. The last Block, B2m−1, consists of exactly m number of hexagons.
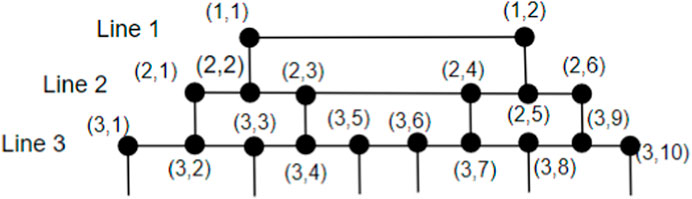
3. From line L1 to line Lm, the number of vertices is increased by 4; from line Lm to line Lm+1, the number of vertices is increased by 1; and from line Lm+1 to line L2m, the number of vertices is decreased by 2.
4. The diameter of CNC5[m] is 4m-2.
Proof: The first, second, and third observations can be easily deduced from the structure of 1-PCNC. However, to establish the validity of the fourth observation, we employ mathematical induction. Within the core of 1-PCNC, there exists a pentagon where the distance between any two nodes within the pentagon is less than or equal to 2. Now, let us assume that the distance between any two nodes in CNC5[m − 1] is less than or equal to 4(m − 1) − 2. Each node situated on the boundary of CNC5[m] is at a distance of either 1 or 2 from a node belonging to CNC5[m − 1]. Consider two nodes, u and v, in CNC5[m], and let |uv| represent the distance between nodes u and v. We can find two nodes, u′ and v′, from CNC5[m − 1] such that |uu′| ≤ 2 and |vv′| ≤ 2. Consequently, we have |uv| ≤ |uu′| + |u′v′| + |v′v| ≤ 4m − 2.
Lemma 2. In G = CNC5[m], every vertex v ∈ V(G) is dominated exactly once when m is even.
Proof. By constructing an m-layered CNC5[m] graph recursively, one may build hexagonal layers in a circular pattern around a one pentagon. The number of vertices of degree 2 is 5m, and the count of vertices with a degree of 3 is 5m(m − 1). When m is even, one can symmetrically select exactly
Lemma 3. Let G=2P-HC. Then,
Proof. When h is odd: from proposition 2, we know that the domination number for a linear HC is h+1. Now, in 2P-HC, we begin by choosing the second vertex of line 1 and proceed by selecting the diagonally opposite vertices such that all the vertices of the hexagons are dominated (with exactly two vertices) except the pendant vertex of the pendant edge attached to the last hexagon. We must choose the second-last vertex from line 1 to dominate the remaining pendent vertex. Hence, the number of vertices selected to dominate the 2P-HC is h+2, which is depicted in Figure 7.
When h is even: we begin by choosing the second vertex of line 1 in 2P-HC and proceed by selecting the diagonally opposite vertices from it, such that all the vertices of the hexagons are dominated. Hence, the number of vertices selected to dominate the 2P-HC is h+1, as represented in Figure 8.
Lemma 4. Consider H as a subgraph of G = CNC5[m], which consists of lines up to (m − 1), where m is odd. Then,
Proof. We subdivide the subgraph H as shown in Figure 9 into two partitions by making a cut C = (S, T), where S contains 2i − 1 vertices from each line i, 1 ≤ i ≤ (m − 1). Two vertices vi and vj in S are connected if and only if the edge vivj ∈ E(H). It is enough to dominate S, as T is the mirror image of S and follows an equal number of vertices to constitute the same dominating set as that of S. To dominate S, we select vertices line-wise, dominating one vertex of line 1 by choosing exactly one vertex with address (2, 2). Proceeding by selecting the diagonally opposite vertices up to line (m − 1) such that all the vertices are dominated exactly once, in general, we get the following:
Lemma 5. Consider G = CNC5[m] as a connected undirected graph m ≥ 2. Then, we have γ(1-PH) = 2m.
Proof. In 1-PH, the number of hexagons is 2m − 2, arranged with the pentagon at the center, flanked by (m − 1) hexagons on each side. By proposition 2 to dominate the hexagons on the left side, we require m vertices. Similarly, to dominate the hexagons on the right side, another set of m vertices is needed. Therefore, a total of 2m vertices are required to dominate the entire 1-PH.
Theorem 4. Consider G = CNC5[m] as a connected undirected graph m ≥ 2. Then, we have
Proof. Case (i) When m is even. By Lemma 2 and Theorem 1, it is straightforward that
Case (ii) When m is odd. The m-layered CNC5[m] graph has 2m lines and 2m − 1 blocks. We consider three subgraphs: H1, H2, and H3. The subgraph H1 contains Block 1, Block 2, … Block (m − 2). The subgraph H2 contains Block m; the subgraph H3 contains Block (m + 2), Block (m + 3),…Block (2m − 1). Let D ⊆ V be a dominating set, and we select vertices from H1, H2, and H3 in a set D as follows:H1 consists of (m-1) lines and (m-2) blocks. Using Lemma 4,
The subgraph H2 consists of 1-PH, i.e., Block m, using Lemma 5, γ(1-PH) = 2m. Now, we consider the subgraph H3, and to find the dominating vertices of H3, we employ the depth-first search (DFS) algorithm, known for its exhaustive search approach, where |H3| is the input parameter, and it consists of lines m + 2 to 2m. To select vertices from |H3| in D, we first fix the root vertex as (m + 2, 2), and we maintain two sets D1 and A (D1), where D1 is the dominating set of H3. The algorithm gets terminated once |A (D1)| = |H3 − D1|. We begin by dominating the vertices of H3 in a sequential order of the index i, i.e., we proceed by covering all the vertices (m + i, 1) where 1 ≤ i ≤ m and continuing up to all the vertices (m + i, j), where 1 ≤ j ≤ 4m − (2i − 1) are dominated. We use Theorem 2, Theorem 3, Proposition 1, and Lemma 3 to select vertices in set D1 such that |A (D1)| = |H3 − D1|.
Hence, the total number of vertices in D is
On the other hand, to prove
Theorem 4 establishes that the dominating set created by choosing vertices coincides with an independent set, which leads to the assertion of Theorem 5.
Theorem 5. Let G = CNC5 [m] as a connected undirected graph m ≥ 2. Then, we have
Theorem 6. Let G = CNC5[m], m ≥ 2. Then,
Proof. Consider D to be a minimum power dominating set and D1 to be a power dominating set. When m = 2, it is easy to verify from the brick diagram that D = {(2, 2), (3, 3)} is a minimum power dominating set. Now, we prove for m ≥ 3. To prove
Case (i) when m = 3i for all i ≥ 1, consider D1 = (3n − 1, 4n − 2) ∪ (3n, 4n + 1), 1 ≤ n ≤ i; this implies that
Case (ii) when m = 3i + 1 for all i ≥ 1, consider D1 = (3n − 1, 4n − 2) ∪ (3n, 4n + 1) ∪ (3i + 2, 4i + 1), 1 ≤ n ≤ i; this implies that
Case (iii) when m = 3i + 2 for all i ≥ 1, consider D1 = (3n − 1, 4n − 2) ∪ (3n, 4n + 1) ∪ (3i + 2, 4i + 2) ∪ (3i + 3, 4i + 4), 1 ≤ n ≤ i; this implies that
To prove
Theorem 7. Let G = CNC5 [m], m ≥ 2. Then, γp,k(G) = 1.
Proof. Since Δ(G) = 3 by Lemma 1, its straightforward.
5 Conclusion
In this research, we have conducted a thorough investigation of the 1-PCNC graph by analyzing different domination parameters. Modeling the brick diagram associated with 1-PCNC allowed us to identify several crucial parameters, including the domination number, independent domination number, power domination number, and k-power domination number. We believe that these findings will assist researchers in gaining insights into and predicting the physiochemical properties associated with these chemical structures. Moving forward, we aim to expand our work by understanding in depth the physiochemical properties of chemical structures using different variants of domination.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author contributions
SP: conceptualization, methodology, and writing–original draft. MN: formal analysis, supervision, validation, and writing–review and editing.
Funding
The authors declare that no financial support was received for the research, authorship, and/or publication of this article.
Acknowledgments
We want to express our utmost gratitude to the referees for their diligent scrutiny of this manuscript, as well as their enlightening comments and constructive feedback. Their discerning perspectives have resulted in a number of significant improvements to this paper.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alanko, S., Crevals, S., Isopoussu, A., Östergård, P., and Pettersson, V. (2011). Computing the domination number of grid graphs. Electron. J. Comb. Electron. 18, P141. doi:10.37236/628
Alipour, M., and Ashrafi, A. (2009). Computer calculation of the wiener index of one-pentagonal carbon nanocone. Dig. J. Nanomater. Biostructures (DJNB) 4, 1–6.
Arockiaraj, M., Clement, J., and Balasubramanian, K. (2018). Topological properties of carbon nanocones. Polycycl. Aromat. Compd. 40, 1332–1346. doi:10.1080/10406638.2018.1544156
Arockiaraj, M., Clement, J., and Tratnik, N. (2019a). Mostar indices of carbon nanostructures and circumscribed donut benzenoid systems. Int. J. Quantum Chem. 119, e26043. doi:10.1002/qua.26043
Arockiaraj, M., Klavžar, S., Clement, J., Mushtaq, S., and Balasubramanian, K. (2019b). Edge distance-based topological indices of strength-weighted graphs and their application to coronoid systems, carbon nanocones and sio2 nanostructures. Mol. Inf. 38, 1900039. doi:10.1002/minf.201900039
Bermudo, S., Higuita, R. A., and Rada, J. (2020). Domination in hexagonal chains. Appl. Math. Comput. 369, 124817. doi:10.1016/j.amc.2019.124817
Brinkmann, G., and Van Cleemput, N. (2011). Classification and generation of nanocones. Discrete Appl. Math. 159, 1528–1539. doi:10.1016/j.dam.2011.06.014
Bultheel, A., and Ori, O. (2018). Topological modeling of 1-pentagon carbon nanocones–topological efficiency and magic sizes. Fullerenes, Nanotub. Carbon Nanostructures 26, 291–302. doi:10.1080/1536383x.2018.1437543
Chang, G. J., Dorbec, P., Montassier, M., and Raspaud, A. (2012). Generalized power domination of graphs. Discrete Appl. Math. 160, 1691–1698. doi:10.1016/j.dam.2012.03.007
Chithra, M., and Menon, M. K. (2020). Secure domination of honeycomb networks. J. Comb. Optim. 40, 98–109. doi:10.1007/s10878-020-00570-8
Gao, Y., Zhu, E., Shao, Z., Gutman, I., and Klobučar, A. (2018). Total domination and open packing in some chemical graphs. J. Math. Chem. 56, 1481–1492. doi:10.1007/s10910-018-0877-6
Ge, M., and Sattler, K. (1994). Observation of fullerene cones. Chem. Phys. Lett. 220, 192–196. doi:10.1016/0009-2614(94)00167-7
Haynes, T., Knisley, D., Seier, E., and Zou, Y. (2006). A quantitative analysis of secondary rna structure using domination based parameters on trees. BMC Bioinforma. 7, 108–111. doi:10.1186/1471-2105-7-108
Hutchinson, L., Kamat, V., Larson, C. E., Mehta, S., Muncy, D., and Van Cleemput, N. (2018). Automated conjecturing vi: domination number of benzenoids. Match-Communications Math. Comput. Chem. 80, 821–834.
Iqbal, T., Imran, M., and Bokhary, S. A. U. H. (2020). Domination and power domination in certain families of nanostars dendrimers. IEEE Access 8, 130947–130951. doi:10.1109/access.2020.3007891
Koam, A. N., Ahmad, A., Azeem, M., and Nadeem, M. F. (2022). Bounds on the partition dimension of one pentagonal carbon nanocone structure. Arabian J. Chem. 15, 103923. doi:10.1016/j.arabjc.2022.103923
Prabhu, S., Deepa, S., Arulperumjothi, M., Susilowati, L., and Liu, J.-B. (2022). Resolving-power domination number of probabilistic neural networks. J. Intelligent Fuzzy Syst. 43, 6253–6263. doi:10.3233/jifs-220218
Prabhu, S., Deepa, S., Murugan, G., and Arulperumjothi, M. (2021). “On total domination number of hypercube and enhanced hypercube networks,” in Sustainable communication networks and application: proceedings of ICSCN 2020 (Springer), 363–371.
Quadras, J., Sajiya Merlin Mahizl, A., Rajasingh, I., and Sundara Rajan, R. (2015). Domination in certain chemical graphs. J. Math. Chem. 53, 207–219. doi:10.1007/s10910-014-0422-1
Sharieh, A., Qatawneh, M., Almobaideen, W., and Sleit, A. (2008). Hex-cell: modeling, topological properties and routing algorithm. Eur. J. Sci. Res. 22, 457–468.
Sharma, S. K., Raza, H., and Bhat, V. K. (2021). Computing edge metric dimension of one-pentagonal carbon nanocone. Front. Phys. 9, 749166. doi:10.3389/fphy.2021.749166
Stojmenovic, I. (1997). Honeycomb networks: topological properties and communication algorithms. IEEE Trans. parallel distributed Syst. 8, 1036–1042. doi:10.1109/71.629486
Ullah, A., Jamal, M., Zaman, S., and Udin, S. (2024). Connection based novel al topological descriptors and structural property of the zinc oxide metal organic frameworks. Phys. Scr. 99, 055202. doi:10.1088/1402-4896/ad350c
Vukičević, D., and Klobučar, A. (2007). K-dominating sets on linear benzenoids and on the infinite hexagonal grid. Croat. Chem. acta 80, 187–191.
Yamuna, M., and Karthika, K. (2014). Medicine names as a dna sequence using graph domination. Pharm. Lett. 6, 175–183.
Zaman, S., Ullah, A., Naseer, R., and Rasool, K. B. (2024). Mathematical concepts and empirical study of neighborhood irregular topological indices of nanostructures tuc 4 c 8 and gtuc. J. Math. 2024, 7521699. doi:10.1155/2024/7521699
Keywords: chemical graph, one-pentagonal carbon nanocone, domination, power domination, brick diagram
Citation: Pandian S and N. M (2024) Domination and power domination in a one-pentagonal carbon nanocone structure. Front. Chem. 12:1423055. doi: 10.3389/fchem.2024.1423055
Received: 25 April 2024; Accepted: 23 May 2024;
Published: 20 June 2024.
Edited by:
Micheal Arockiaraj, Loyola College, Chennai, IndiaReviewed by:
Arulperumjothi M., St. Joseph’s College of Engineering, IndiaAsad Ullah, Karakoram International University, Pakistan
Copyright © 2024 Pandian and N. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mohana N., bW9oYW5hLm5Adml0LmFjLmlu
 Shoba Pandian
Shoba Pandian Mohana N.
Mohana N.