- 1Department of Chemistry, University of Sialkot, Sialkot, Pakistan
- 2Department of Mathematics, University of Sialkot, Sialkot, Pakistan
Topological indices (TIs) have rich applications in various biological contexts, particularly in therapeutic strategies for cancer. Predicting the performance of compounds in the treatment of cancer is one such application, wherein TIs offer insights into the molecular structures and related properties of compounds. By examining, various compounds exhibit different degree-based TIs, analysts can pinpoint the treatments that are most efficient for specific types of cancer. This paper specifically delves into the topological indices (TIs) implementations in forecasting the biological and physical attributes of innovative compounds utilized in addressing cancer through therapeutic interventions. The analysis being conducted to derivatives of sulfonamides, namely, 4-[(2,4-dichlorophenylsulfonamido)methyl]cyclohexanecarboxylic acid (1), ethyl 4-[(naphthalene-2-sulfonamido)methyl]cyclohexanecarboxylate (2), ethyl 4-[(2,5-dichlorophenylsulfonamido)methyl]cyclohexanecarboxylate (3), 4-[(naphthalene-2-sulfonamido)methyl]cyclohexane-1-carboxylic acid (4) and (2S)-3-methyl-2-(naphthalene-1-sulfonamido)-butanoic acid (5), is performed by utilizing edge partitioning for the computation of degree-based graph descriptors. Subsequently, a linear regression-based model is established to forecast characteristics, like, melting point and formula weight in a quantitative structure-property relationship. The outcomes emphasize the effectiveness or capability of topological indices as a valuable asset for inventing and creating of compounds within the realm of cancer therapy.
1 Introduction
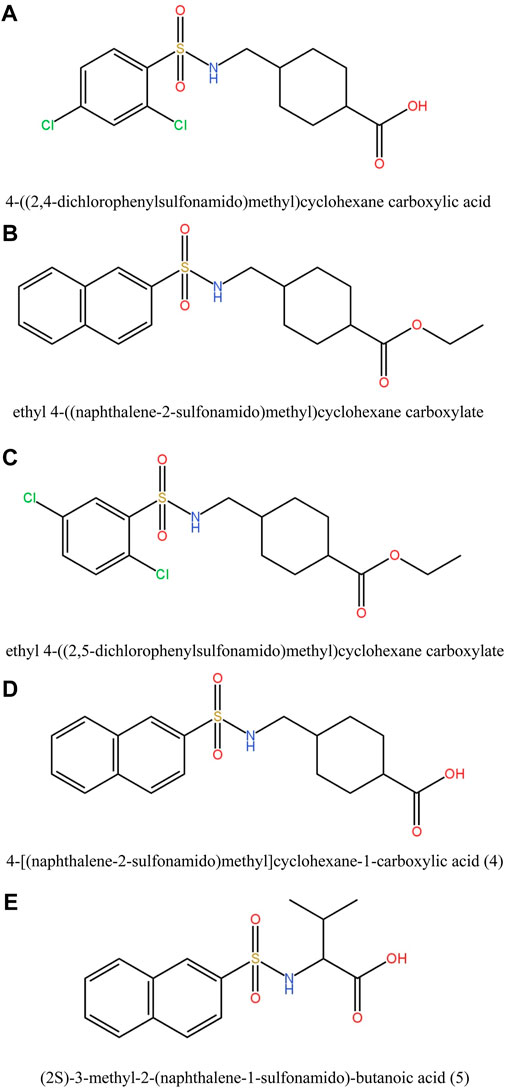
Sulfa drugs, commonly known as sulfonamides, encompass a significant functional group exhibiting distinctive biological activities (Boufas et al., 2014). Apart from medicinal applications as antibacterial agent, they are also widely applied in agriculture. Various derivatives of sulfonamides are applied as enzyme inhibitors (Zhong et al., 2004) such as carbonic anhydrase (Winum et al., 2006), metalloproteinase (Cheng et al., 2008), and serine protease (Groutas et al., 2001; Supuran and Scozzafava, 2002). Celecoxib (Penning et al., 1997) and valdecoxib (Talley et al., 2000) are two sulfonamide moieties that act as cyclooxygenase inhibitors. In addition, some sulfonamide compounds show different therapeutic applications in diuretics (Burger and Abraham, 2003), hypoglycemia, HIV protease (Markgren et al., 2002) as phosphodiesterase-5 inhibitor (Rotella, 2002) and in cancer chemotherapy (Crespo et al., 2010). Recently, esters derived from sulfonamides have received considerable attention due to their potential use as cell proliferation inhibitors (Das et al., 2004). Due to the versatile applications of sulfonamides and their derivatives (Danish et al., 2019) in medicinal field, we report on five compounds, 4-[(2, 4-dichloro- phenylsulfonamido)methyl]cyclohexanecarboxylic acid (1), ethyl 4-((naphthalene-2-sulfonamido)-methyl)cyclohexanecarboxylate (2), ethyl 4-[(2, 5-dichlorophenylsulfonamido)methyl]cyclo-hexanecarboxylate (3) (Danish et al., 2021), 4-[(naphthalene-2-sulfonamido)methyl]cyclohexane-1-carboxylic acid (4) (Danish et al., 2015a), and (2S)-3-methyl-2-(naphthalene-1-sulfonamido)-butanoic acid (5) (Danish et al., 2015b).
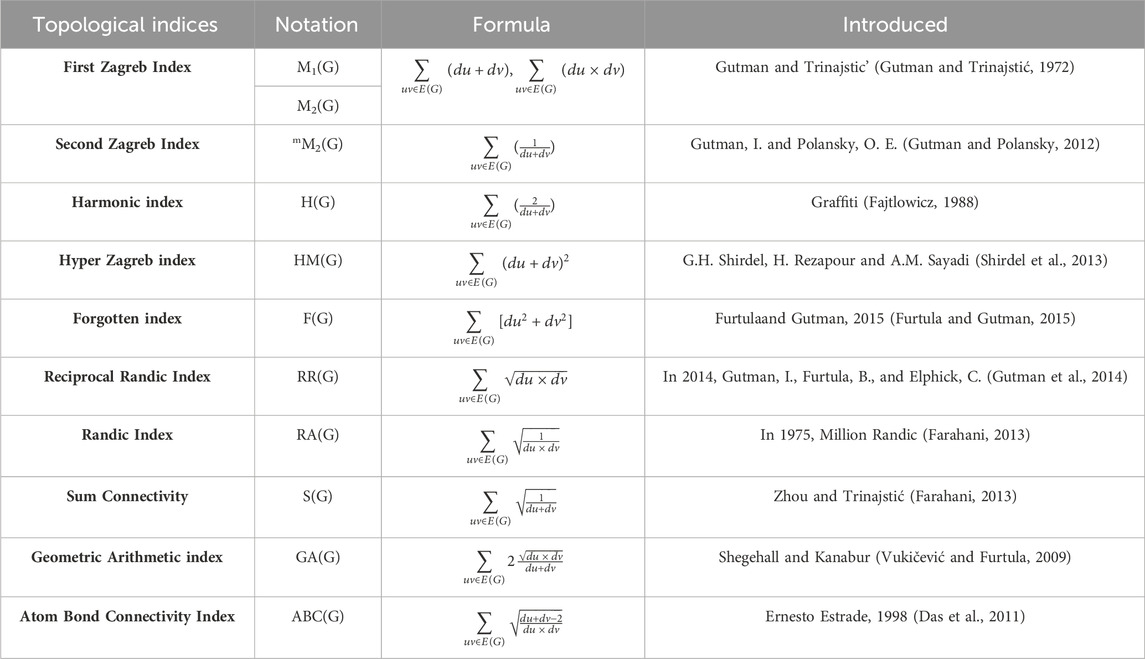
The calculation of topological indices (TIs) for the mentioned compounds includes using their chemical configurations as well as depicting their molecular compositions. The notion of topological indices (TIs), pioneered by H. Wiener in 1947 (Wiener, 1947), proves to be a valuable tool for characterizing the constructions of molecular graphs (Ramírez Alfaro, 2022). These indices provide quantitative measures that help describe the connectivity patterns within the compounds, offering insights into the structural features of the molecules. This information is crucial for understanding the relationships between molecular structures and properties, particularly in the context of anti-cancer compounds. Some of the topological indices we have discussed include first and second Zagreb (M1, M2 and mM2), harmonic (H), hyper Zagreb (HM), forgotten (F), reciporcal Randic (RR), Randic (RA), sum connectivity (S), geometric arithmetic (GA) and atom bond connectivity (ABC) index.
Numerical values, obtained from the molecular formulas of the compounds (Mohammed et al., 2016), are provided by these topological indices. These indices utilize mathematical algorithms based on the structural information encoded in the molecular graphs, offering quantitative insights into the compounds’ topological features and connectivity patterns. Some interesting results on topological indices are characterized in (Natarajan et al., 2022; Zaman and He, 2022; Ullah et al., 2023a; Ullah et al., 2023b; Yan et al., 2023; Zaman et al., 2023; Arockiaraj et al., 2024a; Hayat et al., 2024a; Arockiaraj et al., 2024b; Hayat et al., 2024b; Arockiaraj et al., 2024c; Chidambaram et al., 2024). This numerical representation facilitates the characterization and comparison of different molecular structures, contributing to the understanding of their properties and potential activities, including anti-cancer effects.
Molecular descriptors find applications in diverse fields, including biology and mathematics (Aslam et al., 2017; Gutman et al., 2018). In this study, linear regression (Hosamani et al., 2017) employed to calculate various properties of these compounds, such as melting point (MP) and formula weight (FW), aiming to establish correlations between topological indices (TIs) and physicochemical characterizations. Linear regression analysis may be extended to higher-order regression models by using higher-order predictor variables. In basic linear regression, a linear equation represents the connection between predictors and response variables. To represent nonlinear connections, higher-order regression models include words like squared, cubed, and interaction. Leveraging the derived correlations, QSPR modeling (Duchowicz et al., 2008) will be conducted to accurately estimate the physical and chemical characteristics of the compounds (Hansen and Jurs, 1988). The significance of employing degree-based indices for QSPR analysis stems from their simplicity, resilience, interpretability, computational efficiency, adaptability, and compatibility with graph-based approaches. These indices give useful insights into the structural aspects of molecules and can help to construct predictive models for a variety of chemical attributes.
Numerous uses exist for topological indices (TIs) in the development of compounds. By examining the molecular structures graphs utilize these indices, analysts can point-out the most efficacious compounds (Shanmukha et al., 2022) for particular types of cancer and anticipate the toxicity and potential side effects of the compounds and contribute to the invention and creation of novel compounds. In summary, the using of topological indices (TIs) in compound exploitation has the capability to significantly advance the treatment of cancer and deepen our comprehension of molecular structures.
Compounds’ molecular structures are depicted as graphs, with atoms as vertices and the connecting bonds as edges. The graph
2 Results and discussions
Molecular descriptors find extensive applications in medicine, particularly in the domains of inventing and creating compounds. In the context of cancer treatment, the application of topological indices (TIs) becomes crucial for identifying potential compound candidates possessing the targeted physicochemical properties. Applying topology-related degree indices to compounds for the treatment of cancer allows for a deeper understanding of their structural characteristics and facilitates the correlation of these features with their biological activity. This approach provides valuable insights for the targeted design and discovery of compounds tailored for effective blood cancer treatment.
The quantitative structure-property relationship (QSPR) modeling approach proves beneficial for analyzing the relationship among molecular attributes and the physico-chemical characteristics of compounds for addressing cancer. These aspects are instrumental in estimating the physical and chemical characteristics of newly discovered compounds, candidates according to their structural attributes, thus enhancing the efficiency of compound discovered. By leveraging QSPR modeling, researchers can gain valuable insights into how specific structural elements influence the properties of compounds, facilitating a more informed and targeted approach to identifying promising candidates for cancer treatment.
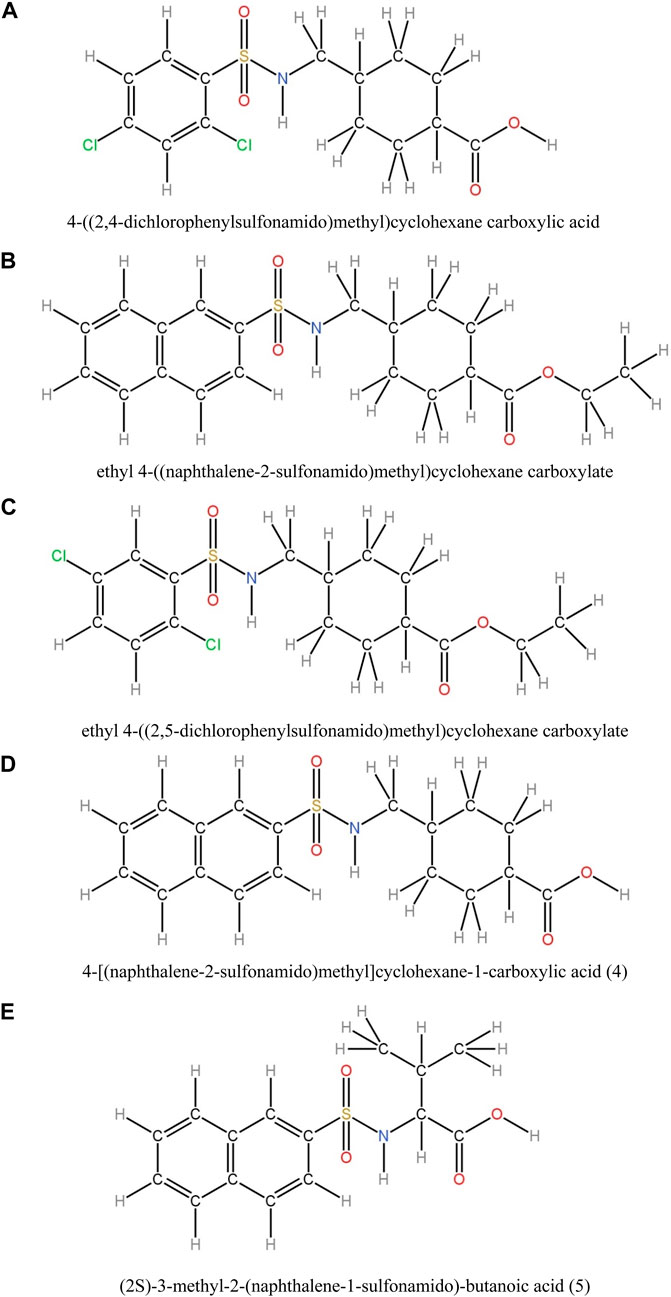
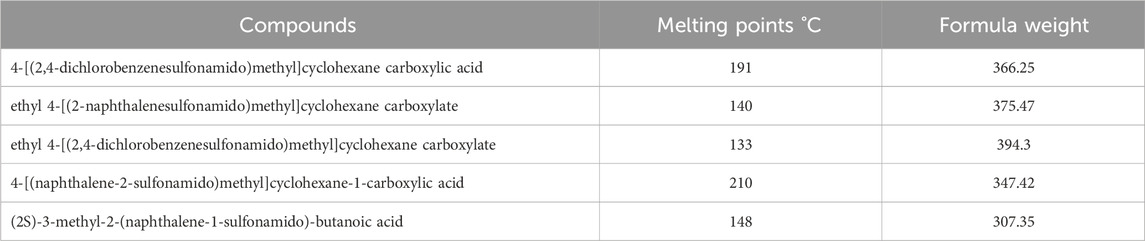
In this study, various compounds employed in cancer treatment underwent analysis utilizing topological indices and QSPR modeling. The compounds examined encompassed 4-[(2,4-dichlorophenylsulfonamido)methyl]cyclohexanecarboxylic acid, ethyl 4-((naphthalene-2-sulfona-mido)methyl)cyclohexanecarboxylate, ethyl 4-[(2,5-dichlorophenylsulfonamido)methyl]cyclo-hexanecarboxylate, 4-[(naphthalene-2-sulfonamido)methyl]cyclohexane-1-carboxylic acid and (2S)-3-methyl-2-(naphthalene-1-sulfonamido)-butanoic acid, as illustrated by their molecular structure in Figure 1 and chemical structure in Figure 2. Employing degree-based topological indices on these compounds enabled the calculation of numerical values, facilitating the correlation of these indices with their respective physicochemical properties.
The findings from the current analysis hold significant implications for advancing the creation of novel compounds in the treatment of cancer. Identifying the structural attributes and physicochemical properties of effective compounds provides valuable insights for designing new compounds with comparable attributes and potentially enhanced efficacy.
Moreover, this approach supports the enhancement of existing compounds through strategic modifications to their structural features, aimed at improving physical and chemical properties and augmenting its efficacy in the treatment of cancer. Analytical regression played a crucial role in the calculations conducted in this study.
2.1 Model of regression
The model of regression serves as a valuable tool in establishing relation between molecular attributes and the physico-chemical properties of compounds employed for addressing cancer. The results indicate a robust relationship between topological indices (TIs), the physical and chemical properties of these compounds.
The utilization of topological indices (TIs) in the context of cancer research is multifaceted. These descriptors prove instrumental in analyzing the structures of various compounds used in cancer treatment, spanning chemotherapeutic agents, targeted therapies, hormonal therapies, and immunotherapies. Analyzing topological indices in compound design aids in identifying new compounds and optimizing those already in existence. For instance, molecular descriptors enable the prediction of the efficacy of novel compounds in the treatment of cancer by scrutinizing their inherent structure.
Furthermore, Topological indices play a crucial role in determining the mechanism of action of compounds for addressing cancer, offering insightful understandings into the biological processes, underlying these compounds. In summary, the integration of topological indices (TIs) in cancer studies holds the potential to unearth new compounds and enhance the effectiveness of those already in use. The acquired outcomes undergo rigorous testing through mathematical expression 1.
Here, the sign P signifies a parameter associated with the physical and chemical properties of a compound. TI stands for some topological indices, whereas A, B represent the coefficients of regression utilized in this observation. With the aid of a linear QSPR model, the eleven TIs of potential cancer treatments are examined, as well as their physical characteristics. Using (1), we create a linear regression model for TIs of the potential compounds listed below.
Theorem 1. Let G1 denotes the 4-[(2, 4-dichlorophenylsulfonamido)methyl]cyclohexane carboxylic acid, then the following axioms holds;
i. M1 (G1) = 136
ii. M2 (G1) = 162
iii. mM2 (G1) = 5.58
iv. H (G1) = 11.18
v. HM(G1) = 714
vi. F (G1) = 390
vii. RR (G1) = 64.17
viii. RA (G1) = 12.01
ix. S (G1) = 12.22
x. GA (G1) = 25.38
xi. ABC(G1) = 19.82
Proof. Let G1 belongs to 4-[(2,4-dichlorophenylsulfonamido)methyl]cyclohexane carboxylic acid, with the edge set represented as E and E1 (u, v) denoting the set of edges in G1 that adds degrees vertices “u” and “v,” the frequencies are provided as follows:
|E11,3 | = 4, |E12,2 | = 3, |E12,3 | = 9, |E13,4 | = 4, |E11,2 | = 1, |E13,3 | = 2, |E11,4 | = 4. Then.
i) By applying the first Zagreb index (M1) and the provided edge partitions E1 (u, v), we obtain:
ii) By applying new version first Zagreb index (M2) and the provided edge partitions E1 (u, v), we obtain:
iii) By applying second Zagreb index (mM2) and the provided edge partitions E1 (u, v), we obtain:
iv) By applying harmonic index (H) and the provided edge partitions E1 (u, v), we obtain:
v) By applying hyper Zagreb index (HM) and the provided edge partitions E1 (u, v), we obtain:
vi) By applying forgotten index (F) and the provided edge partitions E1 (u, v), we obtain:
vii) By applying reciprocal randic index (RR) and the provided edge partitions E1 (u, v), we obtain:
viii) By applying randic index (RA) and the provided edge partitions E1 (u, v), we obtain:
ix) By applying sum connectivity index (S) and the provided edge partitions E1 (u, v), we obtain:
x) By applying geometric arithmetic index (GA) and the provided edge partitions E1 (u, v), we obtain:
xi) By applying atom bond connectivity index (ABC) and the provided edge partitions E1 (u, v), we obtain:
Theorem 2. Let G2 denotes the ethyl 4-[(naphthalene-2-sulfonamido)methyl]cyclohexane carboxylate, then the following axioms satisfied for G2.
i. M1 (G2) = 186
ii. M2 (G2) = 222
iii. mM2 (G2) = 7.19
iv. H (G2) = 14.39
v. HM(G2) = 996
vi. F (G2) = 552
vii. RR (G2) = 87.09
viii. RA (G2) = 15.56
ix. S (G2) = 16.03
x. GA (G2) = 33.61
xi. ABC(G2) = 26.67
Proof. Let G2 belongs to ethyl 4-[(naphthalene-2-sulfonamido)methyl]cyclohexane carboxylate with the edge set represented as E2 and E2 (u, v) denoting the set of edges in G2 that adds degrees vertices “u” and “v,” the frequencies are provided as follows:
|E2(2,2)| = 6, |E2(2,3)| = 11, |E2(3,4)| = 4, |E2(1,4)| = 9, |E2(1,3)| = 2, |E2(3,3)| = 2, |E2(2,4) | = 1, |E2(4,4)| = 1. Then.
i) Applying first Zagreb index (M1) and the provided edge partition E2 (u, v), we obtain:
ii) By applying new version first Zagreb index (M2) and the provided edge partition E2 (u, v), we obtain:
iii) By applying second Zagreb index (mM2) and the provided edge partition E2 (u, v), we obtain:
iv) By applying harmonic index (H) and the provided edge partition E2 (u, v), we obtain:
v) By applying hyper Zagreb index (HM) and the provided edge partition E2 (u, v), we obtain:
vi) By applying forgotten index (F) and the provided edge partition E2 (u, v), we obtain:
vii) By applying reciprocal randic index (RR) and the provided edge partition E2 (u, v), we obtain:
viii) By applying randic index (RA) and the provided edge partition E2 (u, v), we obtain:
ix) By applying sum connectivity index (S) and the provided edge partition E2 (u, v), we obtain:
x) By applying geometric arithmetic index (GA) and the provided edge partition E2 (u, v), we obtain:
xi) By applying atom bond connectivity index (ABC) and the provided edge partition E2 (u, v), we obtain:
Theorem 3. Let G3 denotes the ethyl 4-[(2, 5-dichlorophenylsulfonamido)methyl]cyclohexane carboxylate, then the following axioms satisfied for G3.
i. M1 (G3) = 172
ii. M2 (G3) = 204
iii. mM2 (G3) = 6.54
iv. H (G3) = 13.09
v. HM(G3) = 930
vi. F (G3) = 522
vii. RR (G3) = 79.67
viii. RA (G3) = 14.4
ix. S (G3) = 14.63
x. GA (G3) = 30.38
xi. ABC(G3) = 24.76
Proof. Let G3 belongs to ethyl 4-[(2,5-dichlorophenylsulfonamido)methyl]cyclohexane carboxylate with the edge set represented as E3 and E3 (u,v) denoting the set of edges in G3 that adds degrees vertices “u” and “v,” the frequencies are provided as follows:
|E3(1,3)| = 4, |E3(2,3)| = 9, |E3(2,2)| = 3, |E3(1,4)| = 9, |E3(3,4)| = 4, |E3(4,4)| = 1, |E3(3,3) | = 2, |E3(2,4)| = 1. Then.
i) By applying first Zagreb index (M1) and the provided edge partitions E3 (u, v), we obtain:
ii) By applying new version first Zagreb index (M2) and the provided edge partitions E3 (u, v), we obtain:
iii) By applying second Zagreb index (mM2) and the provided edge partitions E3 (u, v), we obtain:
iv) By applying harmonic index (H) and the provided edge partitions E3 (u, v), we obtain:
v) By applying hyper Zagreb index (HM) and the provided edge partitions E3 (u, v), we obtain:
vi) By applying forgotten index (F) and the provided edge partitions E3 (u, v), we obtain:
vii) By applying reciprocal randic index (RR) and the provided edge partitions E3 (u, v), we obtain:
viii) By applying randic index (RA) and the provided edge partitions E3 (u, v), we obtain:
ix) By applying sum connectivity index (S) and the provided edge partitions E3 (u, v), we obtain:
x) By applying geometric arithmetic index (GA) and the provided edge partitions E3 (u, v), we obtain:
xi) By applying atom bond connectivity index (ABC) and the provided edge partitions E3 (u, v), we obtain:
Theorem 4. Let G4 denotes the 4-[(naphthalene-2-sulfonamido)methyl]cyclohexane-1-carboxylic acid, then the following axioms satisfied for G4.
i. M1 (G4) = 150
ii. M2 (G4) = 180
iii. mM2 (G4) = 6.33
iv. H (G4) = 12.49
v. HM(G4) = 780
vi. F (G4) = 420
vii. RR (G4) = 72.66
viii. RA (G4) = 13.2
ix. S (G4) = 13.67
x. GA (G4) = 28.62
xi. ABC(G4) = 21.82
Proof. Let G4 belongs to 4-[(naphthalene-2-sulfonamido)methyl]cyclohexane-1-carboxylic acid with the edge set represented as E4 and E4 (u,v) denoting the set of edges in G4 that adds degrees vertices “u” and “v,” the frequencies are provided as follows:
|E41,2 | = 1, |E41,3| = 2, |E41,4 | = 4, |E42,2 | = 6, |E42,3 | = 11, |E43,3 | = 2, |E43,4 | = 4. Then.
i) By applying first Zagreb index (M1) and the provided edge partitions E4 (u, v), we obtain:
ii) By applying new version first Zagreb index (M2) and the provided edge partitions E4 (u, v), we obtain:
iii) By applying second Zagreb index (mM2) and the provided edge partitions E4 (u, v), we obtain:
iv) By applying harmonic index (H) and the provided edge partitions E4 (u, v), we obtain:
v) By applying hyper Zagreb index (HM) and the provided edge partitions E4 (u, v), we obtain:
vi) By applying forgotten index (F) and the provided edge partitions E4 (u, v), we obtain:
vii) By applying reciprocal randic index (RR) and the provided edge partitions E4 (u, v), we obtain:
viii) By applying randic index (RA) and the provided edge partitions E4 (u, v), we obtain:
ix) By applying sum connectivity index (S) and the provided edge partitions E4 (u, v), we obtain:
x) By applying geometric arithmetic index (GA) and the provided edge partitions E4 (u, v), we obtain:
xi) By applying atom bond connectivity index (ABC) and the provided edge partitions E4 (u, v), we obtain:
Theorem 5. Let G5 denotes the (2S)-3-methyl-2-(naphthalene-1-sulfonamido)-butanoic acid, then the following axioms satisfied for G5.
i. M1 (𝐺5) = 170
ii. M2 (𝐺5) = 211
iii. mM2 (𝐺5) = 6.35
iv. H (G5) = 12.71
v. HM(G5) = 954
vi. F (G5) = 532
vii. RR (G5) = 78.86
viii. RA (G5) = 13.98
ix. S (G5) = 14.21
x. GA (G5) = 29.5
xi. ABC(G5) = 23.94
Proof. Let G5 belongs to (2S)-3-methyl-2-(naphthalene-1-sulfonamido)-butanoic acid with the edge set represented as E5 and E5 (u, v) denoting the set of edges in G5 that adds degrees vertices “u” and “v,” the frequencies are provided as follows:
|E51,2 | = 1, |E51,3| = 2, |E51,4 | = 10, |E52,2 | = 4, |E52,3 | = 7, |E53,3 | = 1, |E53,4 | = 4, |E54,4 | = 3. Then.
i) By applying first Zagreb index (M1) and the provided edge partitions E5 (u, v), we obtain:
ii) By applying new version first Zagreb index (M2) and the provided edge partitions E5 (u, v), we obtain:
iii) By applying second Zagreb index (mM2) and the provided edge partitions E5 (u, v), we obtain:
iv) By applying harmonic index (H) and the provided edge partitions E5 (u, v), we obtain:
v) By applying hyper Zagreb index (HM) and the provided edge partitions E5 (u, v), we obtain:
vi) By applying forgotten index (F) and the provided edge partitions E5 (u, v), we obtain:
vii) By applying reciprocal randic index (RR) and the provided edge partitions E5 (u, v), we obtain:
viii) By applying randic index (RA) and the provided edge partitions E5 (u, v), we obtain:
ix) By applying sum connectivity index (S) and the provided edge partitions E5 (u, v), we obtain:
x) By applying geometric arithmetic index (GA) and the provided edge partitions E5 (u, v), we obtain:
xi) By applying atom bond connectivity index (ABC) and the provided edge partitions E5 (u, v), we obtain:
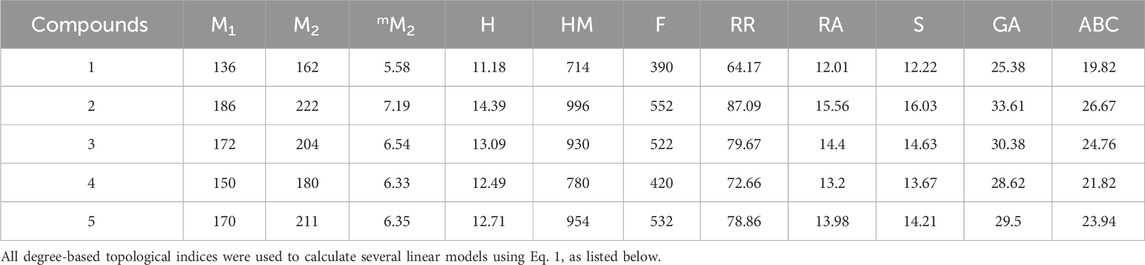
The topological indices for five sulfonamide derivatives can be derived using a technique similar to that employed in Theorem 1, 2, 3,4, and Theorem 5, albeit with distinct topological indices. In Table 2, we have computed values for these indices, along with a comprehensive list of values for all medicines.
2.1.1 Models of regression for first zagreb index M1(G)
Melting Point = 401.739979445015–1.45786228160329 [M1(G)]
Formula Weight = 327.945883864337 + 0.185578108941419 [M1(G)]
2.1.2 Models of regression for first zagreb index M2(G)
Melting Point = 392.229215752272–1.16358128576237 [M2(G)]
Formula Weight = 368.553655334904–0.053093234601144 [M2(G)]
2.1.3 Models of regression for second zagreb index mM2(G)
Melting Point = 395.746667875601–36.1592166107535 [mM2(G)]
Formula Weight = 283.74487245746 + 11.6306857678243 [mM2(G)]
2.1.4 Models of regression for harmonic index H(G)
Melting Point = 412.460456296563–19.4222092308615 [H(G)]
Formula Weight = 279.663069658677 + 6.14586050276565 [H(G)]
2.1.5 Models of regression for hyper zagreb index HM(G)
Melting Point = 381.262784438463–0.247899845037109 [HM(G)]
Formula Weight = 361.338523366773–0.00363571486828149 [HM(G)]
2.1.6 Models of regression for forgotten index F(G)
Melting Point = 369.886126342673–0.425261023060167 [F(G)]
Formula Weight = 357.286639375047 + 0.00180331255164138 [F(G)]
2.1.7 Models of regression for reciporcal randic index RR(G)
Melting Point = 398.050582636146–3.05465528351609 [RR(G)]
Formula Weight = 327.13593281809 + 0.405570233781015 [RR(G)]
2.1.8 Models of regression for randic index RA(G)
Melting Point = 438.484955174762–19.8181457103949 [RA(G)]
Formula Weight = 289.559269575579 + 4.96013958238766 [RA(G)]
2.1.9 Models of regression for sum connectivity S(G)
Melting Point = 412.040944213121–17.4986534915999 [S(G)]
Formula Weight = 291.494041389597 + 4.71056801938973 [S(G)]
2.1.10 Models of regression for geometric arithmetic index GA(G)
Melting Point = 395.647832235126–7.83944105482153 [GA(G)]
Formula Weight = 292.301160109422 + 2.2325866123323 [GA(G)]
2.1.11 Models of regression for ABC index ABC(G)
Melting Point = 412.683250150638–10.6094885116929 [ABC(G)]
Formula Weight = 303.014847528394 + 2.35634358053184 [ABC(G)]
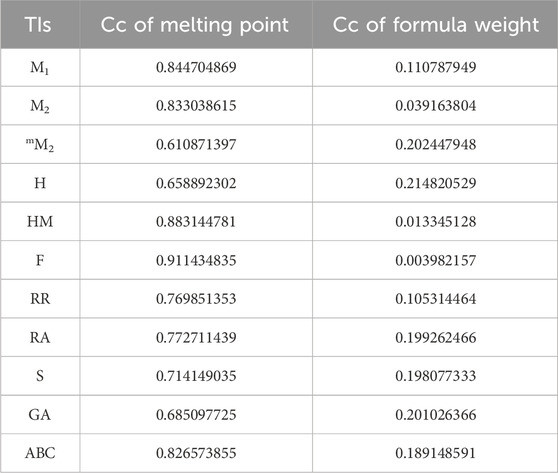
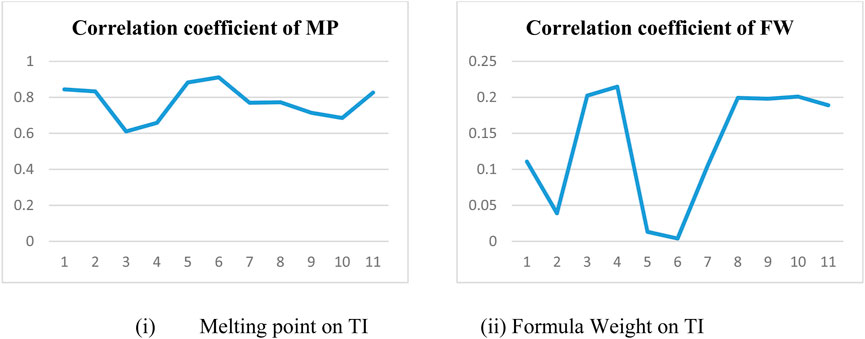
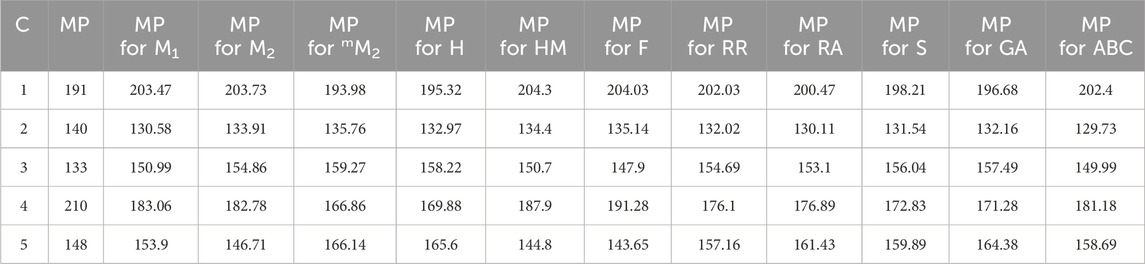
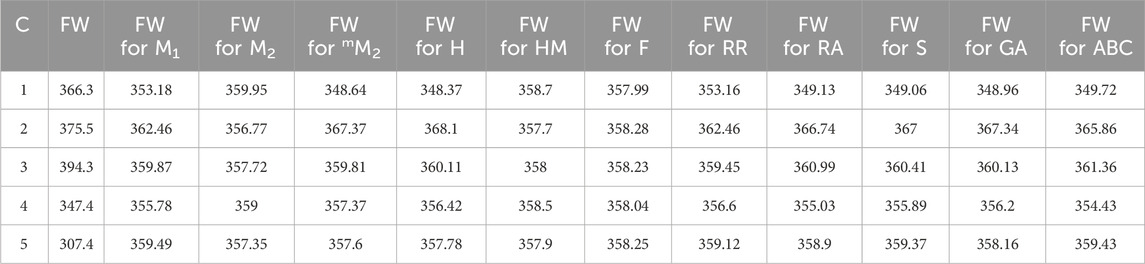
In a quantitative structure analysis, the comparison of topological indices and correlation coefficients of physicochemical parameters is essential. Table 3 provides the physicochemical characteristics of cancer medications, while Table 1 displays the calculated TI values derived from their molecular structures. The association correlation coefficients between TIs and two physicochemical characteristics are enumerated in Table 4. Figure 3 depicts the correlation among the topological index (TIs) and the physical and chemical characteristics of compounds, including their corresponding correlation coefficients.
2.2 Calculation of statistical metrics/parameters
In our study, quantitative structure-property relationship (QSPR) modeling is conducted to establish a correlation between the physical and chemical properties of cancer compounds as well as their determined topological indices (TIs) of degree-based, the model of regression incorporates topological features as the independent variable. In this model, “B” stands for the constant of model, “r” indicates the correlation coefficient, and “N” signifies the number of sample compounds.
The theoretical and experimental computations highlighted in the tables emphasize a significant correlation coefficient. This testing methodology proves useful for comparisons between various models and evaluating their comparative enhancements. It is noteworthy that, in the majority of cases, the p-value exceeds 0.05, and the value of r surpasses 0.6. Hence, these findings suggest the significance of all attributes.
Tables 5–15 present the statistical parameters, with the abbreviations PP used for physiochemical properties, MP for melting point, and FW for formula weight.
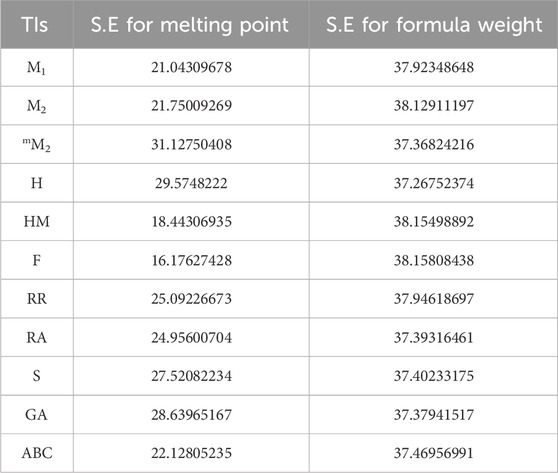
2.3 Standard error of approximation (SE) and resemblance
Standard error (S.E), as presented in below table (Table 16), serves as an indicator of the extent to which an analysis deviates from the approximated regression line. It also offers insights into the accuracy of predictions derived from the regression line. For additional comparisons, both practically and in theory determined predictions of the models, focusing on their physical and chemical characteristics, are included in Tables 17,18.
3 Conclusion
The utilization of topological indices (TIs) and statistical parameters in direct quantitative structure-property relationship (QSPR) models has revealed robust correlation coefficients across various physicochemical characteristics of medications employed for addressing cancer. The outcomes of this analysis provide beneficial perspectives for the therapeutic industry, offering guidance within creating novel treatments and establishing safety precautions for cancer therapies. The noteworthy influence of correlation coefficients between diverse topological indices (TIs) for these medications underscores the capable to predict the physical and chemical characteristics of recently identified anticancer sulfonamides compounds, especially for addressing specific cancer conditions. These results hold promise for analysts engaged in pharmaceutical research, providing a potent tool for compound discovery and development.
In particular, our analysis revealed the greatest correlation value of r = .911 for forgotten [F(G)] index with melting point, signifying its relevance. Additionally, the harmonic [H(G)] index demonstrated a substantial correlation of r = .21 with formula weight, further contributing to the understanding of these medications’ characteristics. This work not only contributes to our understanding of medications for cancer treatment but also offers practical implications for advancing pharmaceutical research and development in this critical area. In the near future, we aim to calculate the resistance distance based topological indices for the certain drugs.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
MD: Conceptualization, Data curation, Investigation, Methodology, Project administration, Resources, Software, Visualization, Writing–original draft, Writing–review and editing. TL: Conceptualization, Data curation, Investigation, Methodology, Project administration, Resources, Visualization, Writing–original draft, Writing–review and editing. FA: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Writing–original draft, Writing–review and editing. SZ: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Arockiaraj, M., Celin Fiona, J., Abraham, J., Klavžar, S., and Balasubramanian, K. (2024c). Guanidinium and hydrogen carbonate rosette layers: distance and degree topological indices, Szeged-type indices, entropies, and NMR spectral patterns. Heliyon 10 (3), e24814. doi:10.1016/j.heliyon.2024.e24814
Arockiaraj, M., Fiona, J. C., and Shalini, A. J. (2024b). Comparative study of entropies in silicate and oxide frameworks. Silicon, 1–12. doi:10.1007/s12633-024-02892-2
Arockiaraj, M., Raza, Z., Maaran, A., Abraham, J., and Balasubramanian, K. (2024a). Comparative analysis of scaled entropies and topological properties of triphenylene-based metal and covalent organic frameworks. Chem. Pap., 1–24. doi:10.1007/s11696-023-03295-0
Aslam, A., Bashir, Y., Ahmad, S., and Gao, W. (2017). On topological indices of certain dendrimer structures. Z. für Naturforsch. A 72 (6), 559–566. doi:10.1515/zna-2017-0081
Boufas, W., Dupont, N., Berredjem, M., Berrezag, K., Becheker, I., Berredjem, H., et al. (2014). Synthesis and antibacterial activity of sulfonamides. SAR and DFT studies. J. Mol. Struct. 1074, 180–185. doi:10.1016/j.molstruc.2014.05.066
Cheng, X.-C., Wang, Q., Fang, H., and Xu, W. F. (2008). Role of sulfonamide group in matrix metalloproteinase inhibitors. Curr. Med. Chem. 15 (4), 368–373. doi:10.2174/092986708783497300
Chidambaram, N., Kamran, M., Balasubramanian, D., Hameed, S., Mehmood, S., Raza, W., et al. (2024). Novel distance-based molecular descriptors for styrene butadiene rubber structures. JTAM J. Teori Dan. Apl. Mat. 8 (2), 411–424. doi:10.31764/jtam.v8i2.20037
Crespo, R., de Bravo, M. G., Colinas, P. A., and Bravo, R. D. (2010). In vitro antitumor activity of N-glycosyl sulfonamides. Bioorg. Med. Chem. Lett. 20 (22), 6469–6471. doi:10.1016/j.bmcl.2010.09.052
Danish, M., Akhtar, A., Ashfaq, M., Arshad, M. N., and Asiri, A. M. (2021). Synthesis crystal structure and spectral properties of new sulfonamides. J. Chem. Crystallogr. 51, 543–552. doi:10.1007/s10870-021-00878-1
Danish, M., Bibi, A., Gilani, K., Raza, M. A., Ashfaq, M., Arshad, M. N., et al. (2019). Antiradical, antimicrobial and enzyme inhibition evaluation of sulfonamide derived esters; synthesis, X-Ray analysis and DFT studies. J. Mol. Struct. 1175, 379–388. doi:10.1016/j.molstruc.2018.07.116
Danish, M., Tahir, M. N., Hussain, A., Ashfaq, M., and Sadiq, M. N. (2015a). Crystal structure of 4-{[(naphthalen-2-yl) sulfonylamino] methyl} cyclohexanecarboxylic acid. Acta Crystallogr. Sect. E Crystallogr. Commun. 71 (3), o145. doi:10.1107/s2056989015002054
Danish, M., Tahir, M. N., Jabeen, N., and Raza, M. A. (2015b). Crystal structure of (2S)-3-methyl-2-[(naphthalen-1-ylsulfonyl) amino] butanoic acid. Acta Crystallogr. Sect. E Crystallogr. Commun. 71 (5), o308. doi:10.1107/s2056989015007057
Das, B., Reddy, V. S., and Reddy, M. R. (2004). An efficient and selective tosylation of alcohols with p-toluenesulfonic acid. Tetrahedron Lett. 45 (36), 6717–6719. doi:10.1016/j.tetlet.2004.07.076
Das, K. C., Gutman, I., and Furtula, B. (2011). On atom-bond connectivity index. Chem. Phys. Lett. 511 (4-6), 452–454. doi:10.1016/j.cplett.2011.06.049
Duchowicz, P. R., Talevi, A., Bruno-Blanch, L. E., and Castro, E. A. (2008). New QSPR study for the prediction of aqueous solubility of drug-like compounds. Bioorg. Med. Chem. 16 (17), 7944–7955. doi:10.1016/j.bmc.2008.07.067
Fajtlowicz, S. (1988). “On conjectures of Graffiti,” in Annals of discrete mathematics (Elsevier), 113–118.
Farahani, M. R. (2013). On the Randic and sum-connectivity index of nanotubes. Ann. West Univ. Timisoara-Mathematics Comput. Sci. 51 (2), 39–46. doi:10.2478/awutm-2013-0014
Furtula, B., and Gutman, I. (2015). A forgotten topological index. J. Math. Chem. 53 (4), 1184–1190. doi:10.1007/s10910-015-0480-z
Groutas, W. C., He, S., Kuang, R., Ruan, S., Tu, J., and Chan, H. K. (2001). Inhibition of serine proteases by functionalized sulfonamides coupled to the 1, 2, 5-thiadiazolidin-3-one 1, 1 dioxide scaffold. Bioorg. Med. Chem. 9 (6), 1543–1548. doi:10.1016/s0968-0896(01)00037-2
Gutman, I., Furtula, B., and Elphick, C. (2014) “Three new/old vertex-degree-based topological indices,” in MATCH communications in mathematical and in computer chemistry.
Gutman, I., Furtula, B., and Katanić, V. (2018). Randić index and information. AKCE Int. J. Graphs Comb. 15 (3), 307–312. doi:10.1016/j.akcej.2017.09.006
Gutman, I., and Polansky, O. E. (2012) Mathematical concepts in organic chemistry. Springer Science and Business Media.
Gutman, I., and Trinajstić, N. (1972). Graph theory and molecular orbitals. Total φ-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 17 (4), 535–538. doi:10.1016/0009-2614(72)85099-1
Hansen, P. J., and Jurs, P. C. (1988). Chemical applications of graph theory. Part I. Fundamentals and topological indices. J. Chem. Educ. 65 (7), 574. doi:10.1021/ed065p574
Hayat, S., Arshad, M., and Khan, A. (2024b). Graphs with given connectivity and their minimum Sombor index having applications to QSPR studies of monocarboxylic acids. Heliyon 10 (1), e23392. doi:10.1016/j.heliyon.2023.e23392
Hayat, S., Khan, A., Ali, K., and Liu, J. B. (2024a). Structure-property modeling for thermodynamic properties of benzenoid hydrocarbons by temperature-based topological indices. Ain Shams Eng. J. 15 (3), 102586. doi:10.1016/j.asej.2023.102586
Hosamani, S., Perigidad, D., Jamagoud, S., Maled, Y., and Gavade, S. (2017). QSPR analysis of certain degree based topological indices. J. Statistics Appl. Probab. 6 (2), 361–371. doi:10.18576/jsap/060211
Markgren, P.-O., Schaal, W., Hämäläinen, M., Karlén, A., Hallberg, A., Samuelsson, B., et al. (2002). Relationships between structure and interaction kinetics for HIV-1 protease inhibitors. J. Med. Chem. 45 (25), 5430–5439. doi:10.1021/jm0208370
Mohammed, M. A., Atan, K. A., Khalaf, A. M., Said, M. R., and Hasni, R. (2016). “On atom bond connectivity index of some molecular graphs,” in AIP conference proceedings (AIP Publishing), 1739, No. 1.
Natarajan, C., Selvamuthukumaran, S., and Farahani, M. R. (2022) On leap Zagreb indices of some cycle related graphs.
Penning, T. D., Talley, J. J., Bertenshaw, S. R., Carter, J. S., Collins, P. W., Docter, S., et al. (1997). Synthesis and biological evaluation of the 1, 5-diarylpyrazole class of cyclooxygenase-2 inhibitors: identification of 4-[5-(4-methylphenyl)-3-(trifluoromethyl)-1 H-pyrazol-1-yl] benzenesulfonamide (SC-58635, celecoxib). J. Med. Chem. 40 (9), 1347–1365. doi:10.1021/jm960803q
Ramírez Alfaro, J. J. (2022) Estudio de La concentración de metales en el proceso de una empresa productora de premezclas alimenticias granuladas.
Rotella, D. P. (2002). Phosphodiesterase 5 inhibitors: current status and potential applications. Nat. Rev. Drug Discov. 1 (9), 674–682. doi:10.1038/nrd893
Shanmukha, M., Usha, A., Praveen, B. M., and Douhadji, A. (2022). Degree-based molecular descriptors and QSPR analysis of breast cancer drugs. J. Math. 2022, 1–13. doi:10.1155/2022/5880011
Supuran, C. T., and Scozzafava, A. (2002). Applications of carbonic anhydrase inhibitors and activators in therapy. Expert Opin. Ther. Pat. 12 (2), 217–242. doi:10.1517/13543776.12.2.217
Talley, J. J., Brown, D. L., Carter, J. S., Graneto, M. J., Koboldt, C. M., Masferrer, J. L., et al. (2000). 4-[5-Methyl-3-phenylisoxazol-4-yl]-benzenesulfonamide, valdecoxib: a potent and selective inhibitor of COX-2. J. Med. Chem. 43 (5), 775–777. doi:10.1021/jm990577v
Ullah, A., Zaman, S., Hamraz, A., and Muzammal, M. (2023a). On the construction of some bioconjugate networks and their structural modeling via irregularity topological indices. Eur. Phys. J. E 46 (8), 72. doi:10.1140/epje/s10189-023-00333-3
Ullah, A., Zaman, S., Hussain, A., Jabeen, A., and Belay, M. B. (2023b). Derivation of mathematical closed form expressions for certain irregular topological indices of 2D nanotubes. Sci. Rep. 13 (1), 11187. doi:10.1038/s41598-023-38386-1
Vukičević, D., and Furtula, B. (2009). Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges. J. Math. Chem. 46, 1369–1376. doi:10.1007/s10910-009-9520-x
Wiener, H. (1947). Structural determination of paraffin boiling points. J. Am. Chem. Soc. 69 (1), 17–20. doi:10.1021/ja01193a005
Winum, J. Y., Scozzafava, A., Montero, J. L., and Supuran, C. T. (2006). Therapeutic potential of sulfamides as enzyme inhibitors. Med. Res. Rev. 26 (6), 767–792. doi:10.1002/med.20068
Yan, T., Kosar, Z., Aslam, A., Zaman, S., and Ullah, A. (2023). Spectral techniques and mathematical aspects of K 4 chain graph. Phys. Scr. 98 (4), 045222. doi:10.1088/1402-4896/acc4f0
Zaman, S., and He, X. (2022). Relation between the inertia indices of a complex unit gain graph and those of its underlying graph. Linear Multilinear Algebra 70 (5), 843–877. doi:10.1080/03081087.2020.1749224
Zaman, S., Jalani, M., Ullah, A., Ahmad, W., and Saeedi, G. (2023). Mathematical analysis and molecular descriptors of two novel metal–organic models with chemical applications. Sci. Rep. 13 (1), 5314. doi:10.1038/s41598-023-32347-4
Keywords: compounds with anti-cancer/anti-tumor sulfonamides, topological indices(TIs), quantitative structure-property relationship QSPR analysis, and regression models, graph theory
Citation: Danish M, Liaquat T, Ashraf F and Zaman S (2024) Predictive modeling and regression analysis of diverse sulfonamide compounds employed in cancer therapy. Front. Chem. 12:1413850. doi: 10.3389/fchem.2024.1413850
Received: 08 April 2024; Accepted: 08 May 2024;
Published: 27 May 2024.
Edited by:
Micheal Arockiaraj, Loyola College, Chennai, IndiaReviewed by:
Muhammad Fawad, Zhejiang University, ChinaNatarajan Chidambaram, SASTRA University, India
Copyright © 2024 Danish, Liaquat, Ashraf and Zaman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shahid Zaman, emFtYW4ucmF2aWFuQGdtYWlsLmNvbQ==
 Muhammad Danish1
Muhammad Danish1 Shahid Zaman
Shahid Zaman