
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Chem. , 13 June 2023
Sec. Solid State Chemistry
Volume 11 - 2023 | https://doi.org/10.3389/fchem.2023.1210081
This article is part of the Research Topic Syntheses Under Extreme Conditions View all 9 articles
 Fariia Iasmin Akbar1,2*
Fariia Iasmin Akbar1,2* Alena Aslandukova1
Alena Aslandukova1 Andrey Aslandukov1,2
Andrey Aslandukov1,2 Yuqing Yin1,3
Yuqing Yin1,3 Florian Trybel4
Florian Trybel4 Saiana Khandarkhaeva1
Saiana Khandarkhaeva1 Timofey Fedotenko5
Timofey Fedotenko5 Dominique Laniel6
Dominique Laniel6 Maxim Bykov7
Maxim Bykov7 Elena Bykova2
Elena Bykova2 Natalia Dubrovinskaia1,4
Natalia Dubrovinskaia1,4 Leonid Dubrovinsky2
Leonid Dubrovinsky2Chemical reactions between dysprosium and carbon were studied in laser-heated diamond anvil cells at pressures of 19, 55, and 58 GPa and temperatures of ∼2500 K. In situ single-crystal synchrotron X-ray diffraction analysis of the reaction products revealed the formation of novel dysprosium carbides, Dy4C3 and Dy3C2, and dysprosium sesquicarbide Dy2C3 previously known only at ambient conditions. The structure of Dy4C3 was found to be closely related to that of dysprosium sesquicarbide Dy2C3 with the Pu2C3-type structure. Ab initio calculations reproduce well crystal structures of all synthesized phases and predict their compressional behavior in agreement with our experimental data. Our work gives evidence that high-pressure synthesis conditions enrich the chemistry of rare earth metal carbides.
Carbides are important compounds in science and technology due to their useful chemical, mechanical, electrical, magnetic, and optical properties (Sakai et al., 1981a; Davaasuren et al., 2010; Lengauer, 2012). The structure, bonding, and phase transitions of lanthanide carbides are of interest due to their potential applications in mechanical and electrical devices. Structural variations at high-pressure conditions can lead to a sharp change in the properties and unusual crystal chemistry of carbides.
Metal carbides containing [C2]2− ion are known for many elements at ambient conditions (for instance, Ca, Sr, Ba, Y, La-Nd, Sm, Gd-Dy, Er-Lu) (Yupko et al., 1974; Sakai et al., 1981b). Carbon dimers are particularly interesting due to the relationship between their lengths and the superconducting transition temperatures Tc (Kobayashi et al., 2019) of the compounds which feature these dimers. Since the C-C bond is quite short, the phonon frequency for the C-C stretching phonon modes is expected to be very high. Thus, for example, relatively high Tc values in La2C3 and Y2C3 [up to 13.4 K (Kim et al., 2007) and 18 K (Amano et al., 2004; Nakane et al., 2004), respectively] are ascribed to electron-phonon coupling between high-frequency phonons and C-C antibonding states at the Fermi level.
The lanthanide carbides family shows a large variety of possible phases with different stoichiometry at ambient pressure: RC6 (R = Eu), RC2 (R = Y, La-Lu), R4C7 (R = Y, Dy-Tm, Lu), R2C3 (La-Nd, Sm-Ho), R3C4 (Sc, Y, Tb-Lu), R4C5 (Y, Gd-Ho), R4C3 (R = Sc), RCx (x ∼ 0.33-0.54, R = Sc, Y, Sm-Lu) (Babizhetskyy et al., 2017). Still, the number of known binary carbon compounds is significantly smaller than the number of known binary oxygen compounds (1,290 vs. 4,331) according to the ICSD database [Version 4.9.0 (build 20221006-1701)–Data Release 2022.2]. Considering that vast amount of the data corresponds to ambient conditions, the chemistry of carbides under high pressure has been poorly studied in principle. A recent discovery (Aslandukova et al., 2021) of the new γ-Y4C5 phase with non-linear [C3] groups synthesized above 40 GPa illustrates the importance of investigations of carbides at high pressures and motivates further studies of lanthanides carbides at non-ambient conditions. In this work, we report the high-pressure synthesis in laser-heated diamond anvil cells (DACs) of two novel carbides Dy4C3 and Dy3C2, and the formation of dysprosium sesquicarbide Dy2C3, already known at ambient conditions.
The summary of all experiments is presented in Supplementary Table S1 (see Supplementary Information). In our experiments we used BX90-type diamond anvil cells with a large X-ray aperture (Kantor et al., 2012). As anvils we employed Boehler-Almax-type diamonds with culets diameter of 250 μm. Rhenium gaskets with an initial thickness of 200 μm were indented to ∼28 μm and a hole of ∼100 μm in diameter was drilled in the center of the indentation. Dysprosium flakes (99.9% purity, Merc Inc.) were loaded between one of the diamond anvils and a layer of dry sodium chloride (99.999% purity, ChemPUR) which played the role of a thermal insulator and a pressure transmitting medium; diamond anvils were used as a carbon source. Samples were compressed to the desired pressures and laser heated up to 2500 K. Laser heating of the samples was carried out using our in house double-sided YAG laser (1,064 nm wavelength) heating setup (Fedotenko et al., 2019). Thermal emission spectra from the heated area were collected using an IsoPlane SCT 320 spectrometer with a 1,024 × 2,560 PI-MAX 4 camera. Pressure was determined using the equation of states (EoS) of NaCl (Dorogokupets and Dewaele, 2007; Sakai et al., 2011).
The reaction products were analyzed by single-crystal X-ray diffraction (SCXRD) at several synchrotron beamlines: P02.2 of DESY, Hamburg, Germany (λ = 0.2894 Å, beam size ∼ 2 × 2 μm2) (Liermann et al., 2015); ID11 (λ = 0.2844 Å, beam size ∼ 0.75 × 0.75 μm2) and ID15B (λ = 0.4100 Å, beam size ∼ 1.5 × 2 μm2) of ESRF, Grenoble, France. During single-crystal data collection, the cell was rotated from −38° to +38° around the vertical ω axis with narrow 0.5° steps. XRD maps were created using the XDI software (Hrubiak et al., 2019) and helped to visualize the special distribution of various phases within the pressure chamber as well as to locate the areas where the step-scans should be performed. Powder XRD (PXRD) images were collected upon continuous rotation of the sample in a range of ±20° around the vertical ω axis at DESY, and ±1° around the vertical ω axis at ESRF. The CrysAlisPro software package (CrysAlisPRO) was used for the analysis of the single-crystal XRD data (peak hunting, indexing, data integration, frame scaling, and absorption correction). The DAFi program (Aslandukov et al., 2022) was used for the search of reflections’ groups belonging to individual single-crystal domains. Using the OLEX2 software package (Dolomanov et al., 2009), the structures were solved with the ShelXT structure solution program (Sheldrick, 2015b) using intrinsic phasing and refined with the ShelXL (Sheldrick, 2015a) refinement package using least-squares minimization. Crystal structure visualization was made with the VESTA software (Momma and Izumi, 2011).
The properties of the Dy4C3, Dy2C3, and Dy3C2 were determined through the first-principles calculations using the framework of density functional theory (DFT) as implemented in the VASP (Vienna ab initio simulation package) code (Kresse and Furthmüller, 1996). To expand the electronic wave function in plane waves we used the Projector-Augmented-Wave (PAW) method (Blöchl, 1994). The Generalized Gradient Approximation (GGA) functional was used for calculating the exchange-correlation energies, as proposed by Perdew–Burke–Ernzerhof (PBE) (Perdew et al., 1996). The PAW potentials with the following valence configurations of 5s5p6s5d for Dy and 2s2p for C were used to describe the interaction between the core and the valence electrons in frozen f-electrons approximation for Dy (Kresse and Furthmüller, 1996). Convergence tests with a threshold of 2 meV per atom in energy led to an energy cutoff for the plane wave expansion of 600 eV for all phases and a Monkhorst-Pack (Monkhorst and Pack, 1976) k-point grid of 4 × 4 × 4 for Dy4C3 and Dy2C3, and k-point grid of 5 × 5 × 9 for Dy3C2. Computations were performed for eight volumes that cover the pressure range of 0–100 GPa. Harmonic lattice dynamics calculations were performed with the PHONOPY software (Togo and Tanaka, 2015) using the finite displacement method for 2 × 2 × 2 (Dy4C3 and Dy2C3) and 2 × 2 × 3 (Dy3C2) supercells with respectively adjusted k-points. The tetrahedron method was used for Brillouin zone integrations, employing a mesh of 8 × 8 × 8 k-points for Dy4C3 and Dy2C3, and 10 × 10 × 18 k-points for Dy3C2 (Rath and Freeman, 1975; Friedrich, 2019). The integrated values of the crystal orbital bond index (ICOBI) (Müller et al., 2021) and Mulliken charges were calculated using LOBSTER v4.1.0 software (Maintz et al., 2016). The charge distribution in the ionic approximation based on a generalization of Pauling’s concept of bond strength (Pauling, 1929) was made using CHARDI 2015 (Nespolo and Guillot, 2016). In our calculations, temperature, configurational entropy, and the entropy contribution due to lattice vibrations were neglected.
The dysprosium carbide Dy4C3 was synthesized at 19, 55, and 58 GPa (Supplementary Table S1). This compound was hitherto unknown. It has the anti-Th3P4-type structure (space group I-43d) shown in Figures 1A–C, which has been described for scandium carbide, Sc4C3, but not observed in lanthanide carbides or Y carbides (Adachi et al., 1991; Babizhetskyy et al., 2017). At 19 GPa its unit cell parameter is equal to a = 7.4774 (8) Å.
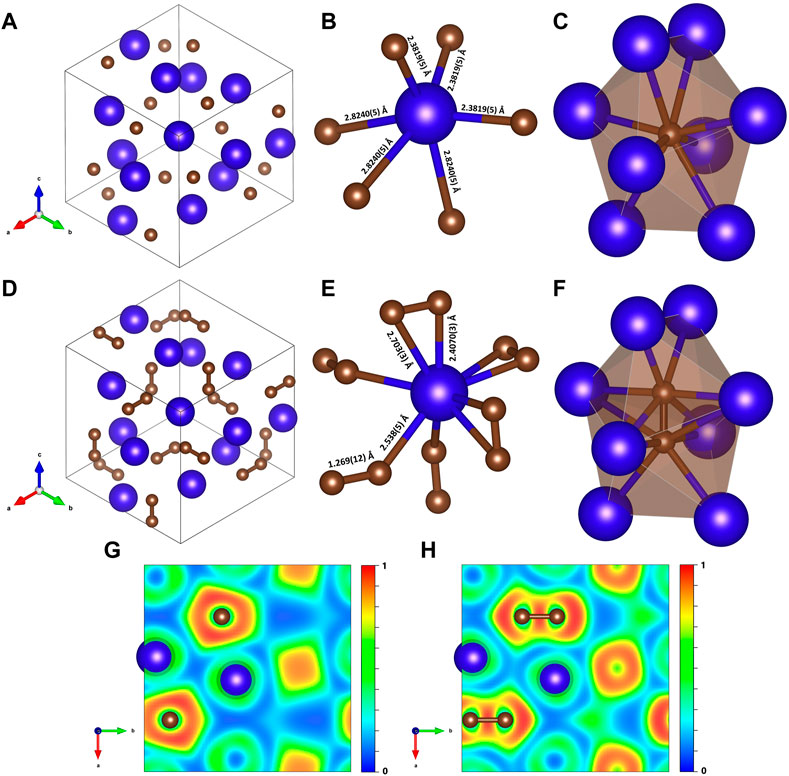
FIGURE 1. Crystal structures and corresponding 2D electron localization function (ELF) maps of Dy4C3 and Dy2C3 at 19 GPa. The blue and brown spheres represent dysprosium and carbon, respectively. Dy4C3: (A) Unit cell in projection along the [111] direction; (B) coordination polyhedron of Dy; (C) coordination environment of a carbon atom. Dy2C3: (D) Unit cell in projection along the [111] direction; (E) coordination polyhedron of Dy; (F) carbon dumbbell in a cage of eight Dy atoms. (G) and (H) are cross sections of the computed ELF shown in the (001) plane in Dy4C3 and Dy2C3, respectively.
In the structure of Dy4C3 (Figures 1A–C; Table 1), dysprosium and carbon atoms occupy the 16c and 12a Wyckoff sites, respectively (Supplementary Tables S2–S4). The coordination polyhedron of Dy cations is an irregular octahedron formed by the six nearest carbon atoms at distances of either 2.3819 (5) Å or 2.8240 (5) Å at 19 GPa (Figure 1B). Carbon atoms are surrounded by eight Dy atoms forming strongly distorted cubes (octaverticons) (Figure 1C).
The cubic Dy2C3 sesquicarbide was synthesized in this work at 19 GPa (Supplementary Table S1). It has the Pu2C3-type structure (space group I-43d) with the unit cell parameter a = 7.9208 (5) Å at 19 GPa (Figures 1D–F; Table 1). The Dy2C3 sesquicarbide was earlier reported at ambient conditions with the lattice parameter equal to a = 8.198 (2) Å at 1 bar (Spedding et al., 1958). The dysprosium and carbon atoms occupy the 16c and 24d Wyckoff sites, respectively (Supplementary Table S5). The structure of Dy2C3 contains [C2] dumbbells with a length of ∼1.27 Å at 19 GPa.
The structures of Dy2C3 and Dy4C3 (described above) are closely related (see Figure 1): they have the same space group (I-43d), and the former can be easily derived from the latter, as the positions of the centers of [C2] dumbbells in Dy2C3 coincide with the positions of single carbon atoms in Dy4C3, whereas the coordinates of Dy atoms are the same in both structures. Thus, the coordination number of Dy atoms in Dy2C3 increases to nine (Figure 1E), whereas the coordination environment of [C2] dumbbells (Figure 1F) is similar to that of a single carbon atom in Dy4C3 (Figure 1C).
One more dysprosium carbide, Dy3C2, with a tetragonal unit cell (space group P4/mbm), was discovered at 55 GPa (Supplementary Table S1). At this pressure it has the following unit cell parameters: a = 5.9896 (13) Å, c = 3.3880 (12) Å (Figure 2; Table 1). Rare-earth metal carbides of such a stoichiometry have not been previously observed (Babizhetskyy et al., 2017), but the structure of the new Dy3C2 was found to be of the U3Si2-type, which is common for silicides (Zachariasen, 1948), borides (Riabov et al., 1999), and intermetallides (Chai and Corbett, 2011). Such structure was also theoretically predicted for a high-pressure calcium carbide Ca3C2 (Li et al., 2015).
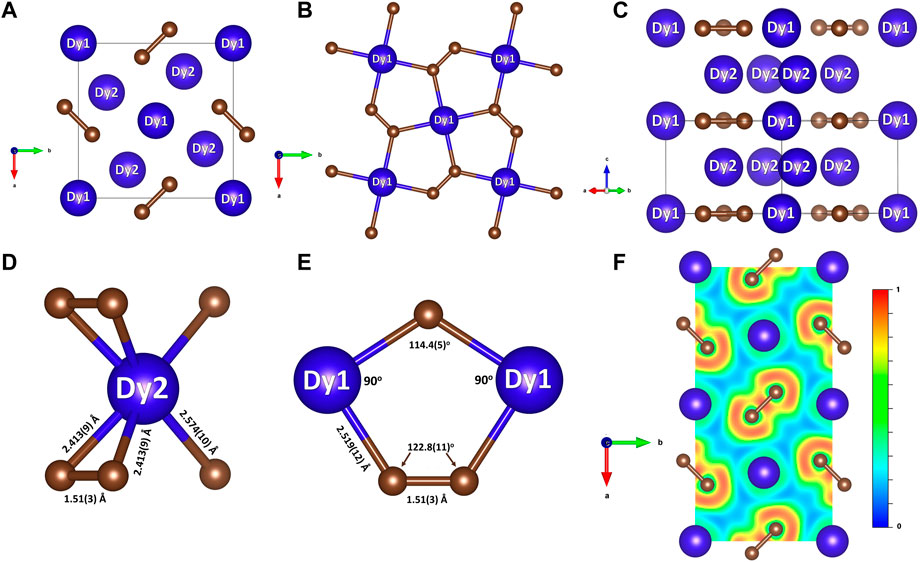
FIGURE 2. Crystal structure of Dy3C2 at 55 GPa and a cross section of the computed ELF. Blue and brown spheres represent dysprosium and carbon, respectively. (A) The structure viewed along the c direction; (B) the Dy1-C plane with the highlighted Cairo pentagonal tiling formed by Dy1 and C atoms; (C) the projection of the structure along the (110) direction highlighting the Dy1-C and Dy2 layers stacking in the c direction; (D) coordination of Dy2 atoms by carbon atoms; (E) interatomic distances in the Dy1-C plane; (F) the 2D ELF shown in the Dy1-C plane.
In the structure of Dy3C2 (Figure 2; Table 1) carbon atoms occupying a single 4 g Wyckoff position and form [C2] dumbbells. Two dysprosium atoms are crystallographically distinct, occupying the Wyckoff positions 2a (Dy1) and 4h (Dy2). Figure 2A shows the structure of Dy3C2, as viewed along the c direction. Dy1 atoms lie in the same ab plane as the [C2] dumbbells, forming together the Cairo pentagonal tiling comprised of (Dy1)2C3 pentagons (Figure 2B). Such a structural motif is known in nickel diazenide NiN2, whose structure possesses atomic-thick layers comprised of Ni2N3 pentagons (Bykov et al., 2021), and in other compounds (Shao et al., 2018; Deng et al., 2020; Duan et al., 2022). Dy2 atoms are located in a parallel plane, separated from the described one by ½ c (Figure 2C). The Dy2-C inter-layer distances are of 2.413 (9) Å or 2.574 (10) Å (Figure 2D). As seen in Figure 2B, the Dy1 atoms are four-fold coordinated by C atoms with the Dy1-C distance equal to 2.519 (12) Å at 55 GPa. The length of the [C2] dumbbell is equal to 1.51 (3) Å (Figure 2E).
Dysprosium carbide Dy4C3 was synthesized at three different pressures (19, 55, and 58 GPa) that enabled us to analyse its structural response to compression. As expected, the shorter Dy-C contacts are less flexible than the longer ones: those being 2.3819 (5) Å and 2.8240 (5) Å at 19 GPa (Figure 1B) contract by ∼3.6% and ∼9.7%, respectively, upon compression to 58 GPa. The results of our DFT calculations agree well with the experimental data, suggesting ∼3.3% and ∼8.5%, correspondingly (Supplementary Tables S2–S4). Due to the anisotropy of compression, DyC6 polyhedra become less distorted with the distortion indices (D) equal to 0.085 and 0.053 at 19 and 58 GPa, respectively. A distortion index characterizes the average deviation of interatomic distances and angles from their mean values (Baur, 1974). Ab initio calculations reproduced well the experimental data with D = 0.084 at 19 GPa vs. D = 0.057 at 58 GPa.
In order to obtain the pressure dependence of the volume for the three dysprosium carbides and to determine the parameters of their equations of states (EOSes), we would need to measure volumes on decompression. However, as we performed our experiments in a solid pressure transmitting medium (NaCl), such data could not be reliable because of stresses. Due to that, we instead performed ab initio density functional theory (DFT) calculations in the pressure range up to 100 GPa. Their results are shown in Figure 3, and the parameters of the 3rd order Birch-Murnaghan (BM3) EOS, based on DFT calculations for Dy2C3, Dy3C2, and Dy4C3, are summarised in Table 2.
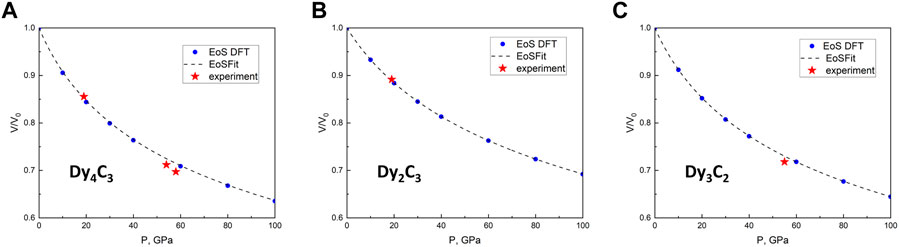
FIGURE 3. Pressure dependence of the relative volume for three Dy carbides. (A) Dy4C3, (B) Dy2C3 and (C) Dy3C2. The density functional theory (DFT)-calculated volumes for given pressures are shown by blue dots and dashed lines. Red stars indicate experimental data points.
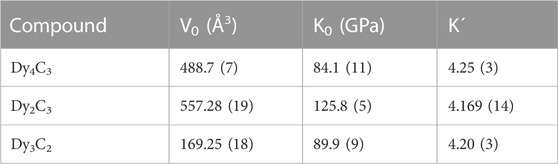
TABLE 2. Parameters of Birch-Murnaghan equation of state of studied dysprosium carbides obtained from ab initio calculations.
Dysprosium sesquicarbide Dy2C3 contains [C2] dumbbells with a length of ∼1.27 Å at 19 GPa, which is slightly shorter than the length of the double bond in ethylene and sesquicarbides Y2C3 and La2C3 at ambient pressure (Gready, 1984; Craig et al., 2006; Kim et al., 2007; Kobayashi et al., 2019). This suggests a formal charge of 4- for the [C2] dumbbell, so that the formula of Dy2C3 can be written as Dy3+4 [C2]4–3, and the compound can be called dysprosium (III) ethenide. The [C2] units in Dy3C2 have a length of ∼1.51 Å at 55 GPa, which is just a bit shorter than the C-C bond length in ethane (Gready, 1984). The compound may be described as Dy2+3 [C2]6− and called dysprosium (II) ethanide. The Dy4C3 consists of single carbon atoms. With the formula Dy3+4C4−3 it is dysprosium (III) methanide.
In order to get a deeper insight into the crystal chemistry of the novel compounds, we performed a detailed charge and bond order analysis. Mulliken charge analysis (Müller et al., 2021) for the dysprosium atoms in carbides synthesized in this work yields the values of 1.62 in Dy4C3, 1.72 in Dy2C3, and 1.01 for Dy1 and 1.12 for Dy2 in Dy3C2 (Supplementary Table S7). The values for Dy4C3 and Dy2C3 are in agreement with Mulliken charges known for other dysprosium-containing compounds (Gupta et al., 2016; Ahuja et al., 2017). Our calculations of Mulliken charges for trivalent Dy carbides known at ambient conditions (DyC2 and Dy4C5 (Spedding et al., 1958; Adachi et al., 1976; Czekalla et al., 1997); are in a good agreement with those obtained for Dy4C3 and Dy2C3 (Supplementary Table S8). For Dy3C2, Mulliken charges of dysprosium are obviously lower, thus supporting our assessment of the cation in this compound as Dy2+ (see above). Notable is that at the same pressure of 55 GPa, the Dy-C distance in Dy3C2 is larger than in Dy4C3 (Supplementary Tables S3, S6), which also speaks in favor of a lower charge of dysprosium in the novel ethanide.
Assuming all Dy atoms to have integer charges, one can analyse carbon charges and the C-C chemical bonds in carbon dimers in different dysprosium carbides. The integrated crystal orbital bond indexes (ICOBI) obtained for DyC2 (Adachi et al., 1976), Dy4C5 (Czekalla et al., 1997), and Dy2C3 are close to 2 (Supplementary Table S8). The small deviations can be explained by shared-electron interactions due to the metallicity of the studied solids. This suggests a C=C double bond in these compounds, which is in a good agreement with its C-C distance (Supplementary Table S9). For Dy3C2 the ICOBI index for the C-C bond in the [C2] dimer differs significantly from those in other carbides (1.116) and suggests the bond order of 1, which is also consistent with the C-C bond length. Additionally, the assigned bond orders are well reflected in individual charges of C atoms and their anions, as obtained in both Mulliken and CHARDI approximations (Supplementary Table S8) (Nespolo and Guillot, 2016; Müller et al., 2021).
The character of the chemical bonding can be judged from calculated electron localization functions (ELF) (Savin et al., 1991). Relevant cross sections of ELFs at 19 GPa for Dy4C3 and Dy3C2 are shown in Figures 1G, H. They reveal ionic bonding between Dy and C in both compounds and strong covalent bonding in the [C2] dimers of Dy2C3. The 2D ELF for Dy3C2 at 55 GPa is shown in Figure 2F. It gives evidence of strong covalent bonding between carbon atoms in dimers and ionic bonds between Dy and C atoms.
For 19 simple binary metal-nitrogen compounds containing [N2]x–species, a linear correlation was found between the length of the N–N dimers and their formal charges (Laniel et al., 2022). We used the literature data on 12 metal carbides studied at ambient conditions (Atoji et al., 1958; Spedding et al., 1958; Atoji, 1967b; 1967a; Krupka et al., 1969; Adachi et al., 1976; Czekalla et al., 1997; Vohn et al., 2000; 1999; Yosida, 2002; Babizhetskyy et al., 2014; Aslandukova et al., 2021) and our own results to analyse the relationship between the length of carbon dimers and their formal charges. For the novel Dy3C2, the C-C length at ambient pressure was obtained by DFT calculations, as well as for γ-Y4C5 in (Aslandukova et al., 2021); for Dy2C3 we included both the experimental value (Spedding et al., 1958) and the one DFT-calculated in this work, as they are a bit different. It appeared that the linear correlation holds also for carbides featuring [C2]x− dimers at ambient conditions (Figure 4).
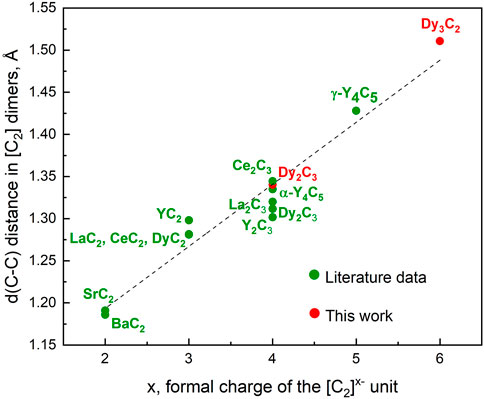
FIGURE 4. A correlation between the lengths of [C2] dimers, d (C-C), and their formal charges x in a number of binary metal-carbon compounds containing [C2]x− species. All data corresponds to ambient pressure. Literature data are from experiments [(Atoji et al., 1958; Spedding et al., 1958; Atoji, 1967b; 1967a; Krupka et al., 1969; Adachi et al., 1976; Czekalla et al., 1997; Vohn et al., 2000; 1999; Yosida, 2002; Babizhetskyy et al., 2014; Aslandukova et al., 2021)], except for γ-Y4C5 (Aslandukova et al., 2021) and for Dy2C3 and Dy3C2 (this work, DFT-computed structures fully relaxed at 1 bar).
According to ab initio simulations of the phonon densities of state (pDOS) (Togo and Tanaka, 2015) in the harmonic approximation at 0 K, Dy4C3 and Dy2C3 compounds are dynamically stable at their synthesis pressure of 19 GPa (Figures 5A, B), whereas Dy3C2 is unstable both at its synthesis pressure of 55 GPa and at 1 bar (Figures 5C, F).
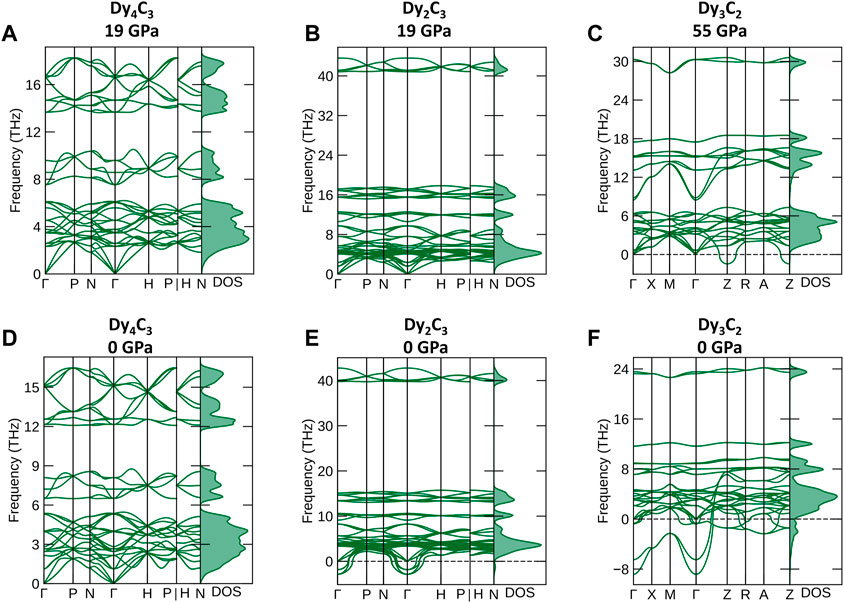
FIGURE 5. Phonon dispersion curves along high-symmetry directions in the Brillouin zone and phonon density of states. (A) Dy4C3, (B) Dy2C3 calculated at 19 GPa and (C) Dy3C2 at 55 GPa, (D) Dy4C3, (E) Dy2C3 and (F) Dy3C2 calculated at ambient pressure.
According to our calculations at 1 bar, Dy2C3 is not dynamically stable (Figure 5E), although it is known to exist at ambient conditions (Spedding et al., 1958). These inconsistency indicates some limitations of the theoretical analysis method we apply. Therefore, the predicted dynamical stability of Dy4C3 (Figure 5D) at ambient pressure should be considered with caution.
To explore the thermodynamic stability of Dy4C3, Dy2C3, and Dy3C2 in comparison to other Dy carbides, convex hull diagrams were constructed considering known carbides [Dy2C (Atoji, 1981), Dy4C5 (Czekalla et al., 1997; Babizhetskyy et al., 2019; The Materials Project, 2020b), Dy3C4 (Hüfken and Jeitschko, 1998; The Materials Project, 2020a), DyC2 (Adachi et al., 1976)] at various pressures. Structure models for Dy4C5 (α-Y4C5 type) (The Materials Project, 2020b) and Dy3C4 (Sc3C4 type) (The Materials Project, 2020a) were acquired from Materials Project database, while those for Dy2C (Atoji, 1981) and DyC2 (Adachi et al., 1976)–from CIFs deposited in the ICSD database. The formation enthalpies were computed relative to the DFT total energies of the end-member elements Dy and C according to the equation: ΔHf = (HDyCx—HDy—x‧HC)/(1 + x). The results are shown in Figure 6. As seen, pressure has a very significant effect on the chemistry of the Dy-C system. Some phases (e.g., Dy2C and Dy4C5), which are stable at ambient pressure, become unstable already at 20 GPa. According to the convex hull diagram computed at 60 GPa, only those phases, which we observed in this work (Dy4C3, Dy2C3, and Dy3C2), are expected to be thermodynamically stable at such a high pressure.
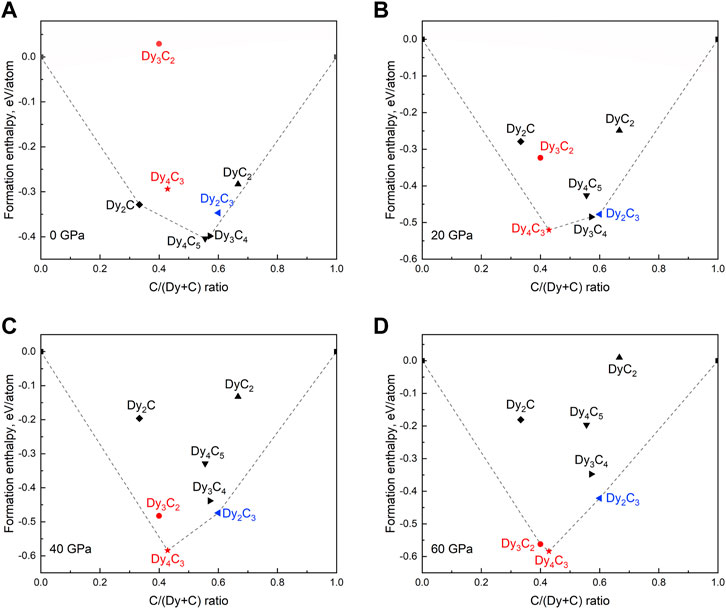
FIGURE 6. Calculated convex hull diagrams constructed for the Dy-C binary system for known dysprosium carbides. (A) 0 GPa, (B) 20 GPa, (C) 40 GPa, and (D) 60 GPa. Dashed lines indicate the convex hulls; carbides previously reported are marked by black symbols; carbides synthesized in this work are given in red and blue, indicating previously unknown and known, respectively.
The chemical reactions of dysprosium and carbon in diamond anvil cells at pressures of 19, 55, and 58 GPa and temperatures of ∼2500 K led to the synthesis of two novel dysprosium carbides, Dy4C3 at 19 GPa and Dy3C2 at 55 GPa, and one compound previously known at ambient condition, Dy2C3 at 19 GPa. The carbon atoms in the Dy3C2 and Dy2C3 form [C2] dumbbells, while there are single carbon atoms in Dy4C3. The crystal structure of Dy4C3 is of an anti-Th3P4 type. The structure of Dy2C3 can be derived from that of Dy4C3 if individual carbon atoms are replaced by dumbbells [C2]. Based on our new data, as well as literature data, we found a linear correlation between the formal charges of [C2]x− groups and C–C interatomic distances. Theoretical calculations support our observations and also suggest that pressure drastically changes the chemistry of the Dy-C system.
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://www.ccdc.cam.ac.uk/structures/-, 2248722, 2248721, 2248720, 2248679, and 2248647.
LD and ND conceptualised the research; FA, AnA, YY, SK, TF, DL, MB, and EB performed synchrotron experiments; FA and LD processed the data; FA, AlA, and FT performed theoretical calculations; FA, LD, and ND analysed the results and wrote the paper; All authors contributed to the article and approved the submitted version.
The work was financially supported by the following agencies: the Federal Ministry of Education and Research, Germany (BMBF, Grant No. 05K19WC1), the Deutsche Forschungsgemeinschaft (DFG projects DU 954–11/1, DU 393–9/2, and DU 393–13/1), the Swedish Government Strategic Research Area in Materials Science on Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU No. 2009 00971). DL thanks the UKRI Future Leaders Fellowship (MR/V025724/1) for financial support.
The authors acknowledge the Deutsches Elektronen- Synchrotron (DESY, PETRA III) for provision of beam-time at the P02.2, the European Synchrotron Radiation Facility (ESRF) for the provision of beamtimes at the ID15b and ID11 beamlines. For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission. FT acknowledges support from the Knut and Alice Wallenberg Foundation (Wallenberg Scholar grant no. KAW-2018.0194). Computations were enabled by resources provided by the University of Bayreuth and the Swedish National Infrastructure for Computing (SNIC) using LUMI at the IT Center for Science (CSC), Finland (SNIC 2022/21-10). MB acknowledges the support of Deutsche Forschungsgemeinschaft (DFG Emmy-Noether project BY112/2-1).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2023.1210081/full#supplementary-material
Adachi, G.-Y., Imanaka, N., and Fuzhong, Z. (1991). Rare Earth carbides. Handb. Phys. Chem. Rare Earths 189, 61. doi:10.1016/S0168-1273(05)80005-4
Adachi, G. Y., Shibata, Y., Ueno, K., and Shiokawa, J. (1976). Heats of the tetragonal-cubic transformation in rare Earth dicarbides and mixed rare Earth dicarbide solid solutions. J. Inorg. Nucl. Chem. 38, 1023–1026. doi:10.1016/0022-1902(76)80021-8
Ahuja, G., Science, F., and Raj, U. (2017). Study of electronic properties of Dy2O3 using first principles calculations. Int. J. Pure Appl. Phys. 13, 123–126.
Amano, G., Akutagawa, S., Muranaka, T., Zenitani, Y., and Akimitsu, J. (2004). Superconductivity at 18 K in yttrium sesquicarbide system, Y2C3. J. Phys. Soc. Jpn. 73, 530–532. doi:10.1143/JPSJ.73.530
Aslandukov, A., Aslandukov, M., Dubrovinskaia, N., and Dubrovinsky, L. (2022). Domain auto finder (DAFi) program: The analysis of single-crystal X-ray diffraction data from polycrystalline samples. J. Appl. Crystallogr. 55, 1383–1391. doi:10.1107/s1600576722008081
Aslandukova, A., Aslandukov, A., Yuan, L., Laniel, D., Khandarkhaeva, S., Fedotenko, T., et al. (2021). Novel high-pressure yttrium carbide containing [C2] and nonlinear [C3] units with unusually large formal charges. Phys. Rev. Lett. 127, 135501. doi:10.1103/PhysRevLett.127.135501
Atoji, M., Gschneidner, K., Daane, A. H., Rundle, R. E., and Spedding, F. H. (1958). The structures of lanthanum dicarbide and sesquicarbide by X-ray and neutron diffraction. J. Am. Chem. Soc. 80, 1804–1808. doi:10.1021/ja01541a008
Atoji, M. (1967a). Magnetic and crystal structures of CeC2, PrC2, NdC2, TbC2, and HoC2 at low temperatures. J. Chem. Phys. 46, 1891–1901. doi:10.1063/1.1840950
Atoji, M. (1967b). Neutron diffraction study of Ce2C3 at low temperatures. J. Chem. Phys. 46, 4148–4149. doi:10.1063/1.1840499
Atoji, M. (1981). Neutron-diffraction studies of Tb2C and Dy2C in the temperature range 4-296 K. J. Chem. Phys. 75, 1434–1441. doi:10.1063/1.442150
Babizhetskyy, V., Jepsen, O., Kremer, R. K., Simon, A., Ouladdiaf, B., and Stolovits, A. (2014). Structure and bonding of superconducting LaC2. J. Phys. Condens. Matter 26, 025701. doi:10.1088/0953-8984/26/2/025701
Babizhetskyy, V., Kotur, B., Levytskyy, V., and Michor, H. (2017). Alloy systems and compounds containing rare earth metals and carbon. Handb. Phys. Chem. Rare Earths 52, 1–263. doi:10.1016/bs.hpcre.2017.09.001
Babizhetskyy, V., Kotur, B., and Levytskyy, V. (2019). Phase equilibria and crystal structure of the ternary compounds in Dy–B–C system at 1270 K. Proc. Shevchenko Sci. Soc. Chem. Sci. LVI, 45–55. doi:10.37827/ntsh.chem.2019.56.045
Baur, W. H. (1974). The geometry of polyhedral distortions. Predictive relationships for the phosphate group. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 30, 1195–1215. doi:10.1107/s0567740874004560
Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953–17979. doi:10.1103/PhysRevB.50.17953
Bykov, M., Bykova, E., Ponomareva, A. V., Tasnádi, F., Chariton, S., Prakapenka, V. B., et al. (2021). Realization of an ideal Cairo tessellation in nickel diazenide NiN2: High-pressure route to pentagonal 2D materials. ACS Nano 15, 13539–13546. doi:10.1021/acsnano.1c04325
Chai, P., and Corbett, J. D. (2011). Two new compounds, β-ScTe and Y3Au2, and a reassessment of Y2Au. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 67, 53–55. doi:10.1107/S010827011103589X
Craig, N. C., Groner, P., and McKean, D. C. (2006). Equilibrium structures for butadiene and Ethylene: compelling evidence for Π-electron delocalization in butadiene. J. Phys. Chem. A 110, 7461–7469. doi:10.1021/jp060695b
Czekalla, R., Hüfken, T., Jeitschko, W., Hoffmann, R. D., and Pöttgen, R. (1997). The rare earth carbides R4C5 with R=Y, Gd, Tb, Dy, and Ho. J. Solid State Chem. 132, 294–299. doi:10.1006/jssc.1997.7461
Davaasuren, B., Kniep, R., and Ruck, M. (2010). Intermediate phases in the ternary systems RE-T-C (RE = Y, La, Gd-Er. Fe, Ru: T = Cr, 211.
Deng, Y., Huang, L., Dong, X., Wang, L., Ok, K. M., Zeng, H., et al. (2020). K2Sb(P2O7)F: Cairo pentagonal layer with bifunctional genes reveal optical performance. Angew. Chem. - Int. Ed. 59, 21151–21156. doi:10.1002/anie.202009441
Dolomanov, O. V., Bourhis, L. J., Gildea, R. J., Howard, J. A. K., and Puschmann, H. (2009). OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 42, 339–341. doi:10.1107/S0021889808042726
Dorogokupets, P. I., and Dewaele, A. (2007). Equations of state of MgO, Au, Pt, NaCl-B1, and NaCl-B2: Internally consistent high-temperature pressure scales. High. Press. Res. 27, 431–446. doi:10.1080/08957950701659700
Duan, R., He, Y., Zhu, C., Wang, X., Zhu, C., Zhao, X., et al. (2022). 2D Cairo pentagonal PdPS: Air-stable anisotropic ternary semiconductor with high optoelectronic performance. Adv. Funct. Mat. 32, 2113255. doi:10.1002/adfm.202113255
Fedotenko, T., Dubrovinsky, L., Aprilis, G., Koemets, E., Snigirev, A., Snigireva, I., et al. (2019). Laser heating setup for diamond anvil cells for in situ synchrotron and in house high and ultra-high pressure studies. Rev. Sci. Instrum. 90, 104501. doi:10.1063/1.5117786
Friedrich, C. (2019). Tetrahedron integration method for strongly varying functions: Application to the GT self-energy. Phys. Rev. B 100 (15), 075142. doi:10.1103/PhysRevB.100.075142
Gready, J. E. (1984). The value of the π-bond order–bond length relationship in geometry prediction and chemical bonding interpretation. J. Comput. Chem. 5, 411–426. doi:10.1002/jcc.540050502
Gupta, T., Velmurugan, G., Rajeshkumar, T., and Rajaraman, G. (2016). Role of lanthanide-ligand bonding in the magnetization relaxation of mononuclear single-ion magnets: A case study on pyrazole and carbene ligated LnIII(ln=Tb, Dy, Ho, Er) complexes. J. Chem. Sci. 128, 1615–1630. doi:10.1007/s12039-016-1147-4
Hrubiak, R., Smith, J. S., and Shen, G. (2019). Multimode scanning X-ray diffraction microscopy for diamond anvil cell experiments. Rev. Sci. Instrum. 90, 025109. doi:10.1063/1.5057518
Hüfken, T., and Jeitschko, W. (1998). The high-temperature (β) modification of Y4C7 with Lu4C7 type and Dy3C4 with Sc3C4 type structure. J. Alloys Compd. 278, 161–164. doi:10.1016/S0925-8388(98)00541-6
Kantor, I., Prakapenka, V., Kantor, A., Dera, P., Kurnosov, A., Sinogeikin, S., et al. (2012). BX90: A new diamond anvil cell design for X-ray diffraction and optical measurements. Rev. Sci. Instrum. 83, 125102. doi:10.1063/1.4768541
Kim, J. S., Xie, W., Kremer, R. K., Babizhetskyy, V., Jepsen, O., Simon, A., et al. (2007). Strong electron-phonon coupling in the rare-Earth carbide superconductor La2C3. Phys. Rev. B - Condens. Matter Mat. Phys. 76, 014516–14612. doi:10.1103/PhysRevB.76.014516
Kobayashi, K., Horigane, K., Horie, R., and Akimitsu, J. (2019). Superconductivity of carbides. Supercond. Carbides. Phys. Chem. Carbon-Based Mat. Basics Appl., 149–209. doi:10.1007/978-981-13-3417-7_6
Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B - Condens. Matter Mat. Phys. 54, 11169–11186. doi:10.1103/PhysRevB.54.11169
Krupka, M. C., Giorgi, A. L., Krikorian, N. H., and Szklaizz, E. G. (1969). High-pressure synthesis of yttrium-thorium sesquicarbide: A new high-temperature superconductor. J. Less-Common Mater. 19, 113–119. doi:10.1016/0022-5088(69)90026-5
Laniel, D., Winkler, B., Fedotenko, T., Aslandukova, A., Aslandukov, A., Vogel, S., et al. (2022). High-pressure Na3(N2)4, Ca3(N2)4, Sr3(N2)4, and Ba(N2)3 featuring nitrogen dimers with noninteger charges and anion-driven metallicity. Phys. Rev. Mat. 6, 023402–023408. doi:10.1103/PhysRevMaterials.6.023402
Lengauer, W. (2012). Carbides: Transition-Metal solid-state ChemistryUpdate based on the original article by walter lengauer,Encyclopedia of inorganic ChemistrySecond edition © 2005, john wiley & sons, ltd. Encycl. Inorg. Bioinorg. Chem. doi:10.1002/9781119951438.eibc0032.pub2
Li, Y. L., Wang, S. N., Oganov, A. R., Gou, H., Smith, J. S., and Strobel, T. A. (2015). Investigation of exotic stable calcium carbides using theory and experiment. Nat. Commun. 6, 6974–6979. doi:10.1038/ncomms7974
Liermann, H. P., Konôpková, Z., Morgenroth, W., Glazyrin, K., Bednarčik, J., McBride, E. E., et al. (2015). The Extreme conditions beamline P02.2 and the Extreme conditions science infrastructure at PETRA III. J. Synchrotron Radiat. 22, 908–924. doi:10.1107/S1600577515005937
Maintz, S., Deringer, V. L., Tchougréeff, A. L., and Dronskowski, R. (2016). Lobster: A tool to extract chemical bonding from plane-wave based DFT. J. Comput. Chem. 37, 1030–1035. doi:10.1002/jcc.24300
Momma, K., and Izumi, F. (2011). VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276. doi:10.1107/S0021889811038970
Monkhorst, H. J., and Pack, J. D. (1976). Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192. doi:10.1103/PhysRevB.13.5188
Müller, P. C., Ertural, C., Hempelmann, J., and Dronskowski, R. (2021). Crystal orbital bond index: Covalent bond orders in solids. J. Phys. Chem. C 125, 7959–7970. doi:10.1021/acs.jpcc.1c00718
Nakane, T., Mochiku, T., Kito, H., Itoh, J., Nagao, M., Kumakura, H., et al. (2004). Superconducting properties of the 18 K phase in yttrium sesquicarbide system. Appl. Phys. Lett. 84, 2859–2861. doi:10.1063/1.1702132
Nespolo, M., and Guillot, B. (2016). CHARDI2015: Charge distribution analysis of non-molecular structures. J. Appl. Crystallogr. 49, 317–321. doi:10.1107/S1600576715024814
Pauling, L. (1929). The principles determining the structure of complex ionic crystals. J. Am. Chem. Soc. 51, 1010–1026. doi:10.1021/ja01379a006
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865
Rath, J., and Freeman, A. J. (1975). Generalized magnetic susceptibilities in metals: Application of the analytic tetrahedron linear energy method to Sc. linear energy method S. C. 11, 2109–2117. doi:10.1103/PhysRevB.11.2109
Riabov, A. B., Yartys, V. A., Hauback, B. C., Guegan, P. W., Wiesinger, G., and Harris, I. R. (1999). Hydrogenation behaviour, neutron diffraction studies and microstructural characterisation of boron oxide-doped Zr–V alloys. J. Alloys Compd. 293, 93–100. doi:10.1016/S0925-8388(99)00306-0
Sakai, T., Adachi, G., Yoshida, T., and Al, E. (1981b). Magnetic and electrical properties of LaC2, CeC2, PrC2, NdC2, and SmC2. J. Chem. Phys. 75, 3027–3032. doi:10.1063/1.442396
Sakai, T., Adachi, G. Y., Yoshida, T., and Shiokawa, J. (1981a). Magnetic and electrical properties of rare Earth dicarbides and their solid solutions. J. Less-Common Mater. 81, 91–102. doi:10.1016/0022-5088(81)90272-1
Sakai, T., Ohtani, E., Hirao, N., and Ohishi, Y. (2011). Equation of state of the NaCl-B2 phase up to 304 GPa. J. Appl. Phys. 109, 084912. doi:10.1063/1.3573393
Savin, A., Becke, A. D., Flad, J., Nesper, R., Preuss, H., and von Schnering, H. G. (1991). A new look at electron localization. Angew. Chem. Int. Ed. Engl. 30, 409–412. doi:10.1002/anie.199104091
Shao, X., Liu, X., Zhao, X., Wang, J., Zhang, X., and Zhao, M. (2018). Electronic properties of a π-conjugated Cairo pentagonal lattice: Direct band gap, ultrahigh carrier mobility, and slanted Dirac cones. Phys. Rev. B 98, 085437–85510. doi:10.1103/PhysRevB.98.085437
Sheldrick, G. M. (2015a). Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 71, 3–8. doi:10.1107/S2053229614024218
Sheldrick, G. M. (2015b). Shelxt - integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A Found. Crystallogr. 71, 3–8. doi:10.1107/S2053273314026370
Spedding, F. H., Gschneidner, K., and Daane, A. H. (1958). The crystal structures of some of the rare earth carbides. J. Am. Chem. Soc. 80, 4499–4503. doi:10.1021/ja01550a017
The Materials Project (2020a). Materials data on Dy3C4 by materials project. United States. https://doi.org/10.17188/1665344
The Materials Project (2020b). Materials data on Dy4C5 by materials project. United States. https://doi.org/10.17188/1664795
Togo, A., and Tanaka, I. (2015). First principles phonon calculations in materials science. Scr. Mat. 108, 1–5. doi:10.1016/j.scriptamat.2015.07.021
Vohn, V., Knapp, M., and Ruschewitz, U. (2000). Synthesis and crystal structure of SrC2. J. Solid State Chem. 151, 111–116. doi:10.1006/jssc.2000.8630
Vohn, V., Kockelmann, W., and Ruschewitz, U. (1999). On the synthesis and crystal structure of BaC2. J. Alloys Compd. 284, 132–137. doi:10.1016/S0925-8388(98)00957-8
Yosida, Y. (2002). Surface superconductivity and structural analysis of YC2 single crystals encapsulated in carbon nanocages. J. Appl. Phys. 92, 5494–5497. doi:10.1063/1.1510946
Yupko, V. L., Makarenko, G. N., and Paderno, Y. B. (1974). Physical properties of carbides of rare-earth metals. Refract. Carbides, 251–259. doi:10.1007/978-1-4684-8598-1_28
Keywords: high-pressure, diamond anvil cell, rare-earth carbides, carbides, rare-earth elements, lanthanides carbides, dysprosium carbide
Citation: Akbar FI, Aslandukova A, Aslandukov A, Yin Y, Trybel F, Khandarkhaeva S, Fedotenko T, Laniel D, Bykov M, Bykova E, Dubrovinskaia N and Dubrovinsky L (2023) High-pressure synthesis of dysprosium carbides. Front. Chem. 11:1210081. doi: 10.3389/fchem.2023.1210081
Received: 21 April 2023; Accepted: 30 May 2023;
Published: 13 June 2023.
Edited by:
Vladimir Dmitriev, European Synchrotron Radiation Facility, FranceReviewed by:
Bogdan M. Benin, Northeast Ohio Medical University, United StatesCopyright © 2023 Akbar, Aslandukova, Aslandukov, Yin, Trybel, Khandarkhaeva, Fedotenko, Laniel, Bykov, Bykova, Dubrovinskaia and Dubrovinsky. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fariia Iasmin Akbar, RmFyaWlhLkFrYmFyQHVuaS1iYXlyZXV0aC5kZQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.