Qianchen Liu
Alberto Perez- Department of Chemistry and Quantum Theory Project, University of Florida, Gainesville, FL, United States
Integrins in the cell surface interact with functional motifs found in the extracellular matrix (ECM) that queue the cell for biological actions such as migration, adhesion, or growth. Multiple fibrous proteins such as collagen or fibronectin compose the ECM. The field of biomechanical engineering often deals with the design of biomaterials compatible with the ECM that will trigger cellular response (e.g., in tissue regeneration). However, there are a relative few number of known integrin binding motifs compared to all the possible peptide epitope sequences available. Computational tools could help identify novel motifs, but have been limited by the challenges in modeling the binding to integrin domains. We revisit a series of traditional and novel computational tools to assess their performance in identifying novel binding motifs for the I-domain of the α2β1 integrin.
1 Introduction
The integrin superfamily (Hynes, 1987) encompasses 24 different integrins in humans responsible for communication and singaling between cells and with the extracellular matrix (ECM). Structurally, they are αβ heterodimers with two non-covalent subunits (arising from 18 α and 8 β subunits) located on the cell’s membrane (Hynes, 2002; Takada et al., 2007). Their normal behavior controls cellullar processes such as cell adhesion, migration and differentiation [(Critchley et al., 1999); (Mizuno et al., 2000); (Mercurio et al., 2001)]. Usually, these integrins recognize specific peptide epitope motifs present in large fibrous proteins that form the extracellular matrix such as collagen or fibronectins (see Figure 1). Hence, designing molecules that disrupt or enhance these interactions has long been a potential therapeutic target. A recent study (Slack et al., 2022) shows over 60 integrin-target therapies have been recorded (https://www.clinical-trials.gov and https://www.clinical-trialsregister.eu/ctrsearch/search using the search term “integrin”) targeting diseases like Multiple Sclerosis (Kawamoto et al., 2012) or Crohn’s disease (Hutchinson, 2007). Most binding occurs through an “I-like domain” in the β subunit which contains a “metal ion-dependent adhesion site” (MIDAS). Some peptide epitope binding motifs like RGD (Arginine-Glycine-Aspartic) are present in many ECM fibers and bind many integrins (Hatley et al., 2018). However, there is selectivity and specificity among their ligands—and even for the RGD motif there is an interplay between the conformation it adopts and the specificity to a particular integrin (Aumailley et al., 1991; Kapp et al., 2017). In the field of biomaterial engineering, there is growing interest to develop computational pipelines that can identify functional motifs to incorporate into engineered ECMs that trigger cellular response (Perez et al., 2021).
FIGURE 1. Sytem of study. Artistic representation of the α2β1 binding collagen. The inset corresponds to the PDB structure 1dzi, focusing on the specific motif area “GFOGER” on the collagen fiber (orange).
Our existing understanding of integrin-ligand recognition has mainly been driven from experimental observations including affinity chromatography Otey et al. (1993), antibodies against cell epitopes Ley et al. (2016), and the use of NMR experiments Siebert et al. (2010). Computational tools on the other hand have been challenged by the complexity of modeling integrin-ECM interactions as well as the diversity of function/structure relationships arising from the multidomain architecture that merit attention such as the origin of selectivity, mechanism for signal transduction (Kalli et al., 2011), effect of the lipid environment (Kalli et al., 2017), or interaction between the different domains and their role in active/inactive conformations to name a few (Chen et al., 2011). Although the number of computational studies for integrin systems is limited, there is a wide range of approaches that have been used including physics based approaches such as docking (Guzzetti et al., 2017), atomistic and coarse grained molecular dynamics (MD) (Craig et al., 2004; Murcia et al., 2008; Choi et al., 2010; Zhu et al., 2010; Wang et al., 2015; Farina et al., 2016; Fratev and Sirimulla, 2019), QM/MM approaches (Freindorf et al., 2012), and machine learning (Mehdi et al., 2013; Prytuliak et al., 2017; Asgari et al., 2019). Typically, ligand docking calculations are applied to filter ligands with high affinity, MD approaches are used to either predict free energy differences with thermodynamic integration (TI) or conformational changes via enhanced sampling, while ML approaches have been traditionally used to discover new binding motifs in protein-peptide complexes such as the well-known RGD, GPR (the recognition site for αxβ2), or DLLEL (the binding site for αvβ6) for integrins.
We focus on the I-domain of the α2β1 integrin, which contains a binding motif and has been shown to retain the binding activity of the whole integrin in recombinant studies expressing only the I motif (PDB code 1dzi) (Emsley et al., 2000). The binding domain undergoes a conformational change between the unbound and bound forms in which three loops participate in coordinating a central metal ion, with a glutamic acid from the collagen completing the coordination of the metal (Emsley et al., 2000). The collagen used here introduces a six aminoacid peptide motif (GFOGER, where O stands for hydroxyproline), that forms triple helices analogous to canonical collagen. Even though the three strands are homologous for triple-helix formation, during binding each strand becomes distinct, with one containing a critical Glutamic acid residue (E) for binding (“leading strand”). By comparison, the other two strands have been previously named “middle” and “trailing” strands) (Emsley et al., 2000). Given the 206 possible peptide sequences covering the length of the GFOGER motif, we expect there are many other sequences that might bind this integrin. Indeed, amongst integrins that bind collagen, there are differences amongst canonical motifs (GxOGER, where x = F, L, M, A) and non-canonical motifs (Hamaia et al., 2012). Hence we ask the question of whether computational pipelines can suggest new motifs and if they are capable of assessing which of those suggested motifs are actually better binders.
We seek to assess the advantages/disadvantages of using traditional and novel pipelines combining multiple computational techniques readily available. We divide the pipelines in three stages: 1) predicting new motifs, 2) predicting their ability to bind, and 3) predicting their stability. Overall, finding new interacting motifs against integrins remains challenging regardless of the pipeline used.
2 Computational methods
2.1 Identification of novel motifs
We started from the X-ray crystal structure of the α2 I domain from α2β1 in complex with collagen [PDBid: 1dzi (Emsley et al., 2000)] and performed a scan of all possible mutations (for the 20 common amino acids) at each position along the “GFOGER” motif, collecting the expected free energy changes (ΔΔG) these programs predict. Integrin complexes were first optimized in the FoldX suite. Next, a position scan was conducted with the command “Position Scan” on the GFOGER motif and the output results showed the difference of binding energy for each mutation per amino acid on collagen. ΔΔGbind was also calculated using RosettaDDG predictions, with the backrub trajectory stride set to 35,000 and making three trials for each ΔΔG calculation.
The ProteinMPNN (message passing neural network) (Dauparas et al., 2022) has recently been developed as a way to identify the ideal sequence that will adopt a certain 3D structure. In this model, we provided the PDB structure of the complex and asked the model to design new motifs to replace the native GFOGER motif.
2.2 Stability MD simulations
We used standard minimization and equilibration protocols (Braun et al., 2018) followed by production runs using Langevin dynamics for 500 ns in the NPT ensemble using a Monte Carlo barostat (Åqvist et al., 2004). Simulations used AMBER’s (Case et al., 2020) pmemd module (Salomon-Ferrer et al., 2013). We simulated the top 20 FoldX and Rosetta predictions using ff14SB (Maier et al., 2015) solvated in a truncated octahedron box [OPC water model (Izadi et al., 2014)], and 150 mM concentration of Na+ and Cl− ions (Joung and Cheatham, 2008). As a control, we simulated the I-domain in the presence and absence of the wild type (WT) collagen (PDBid: 1dzi). All simulations were carried out with a Co2+ ion in the MIDAS binding site. We simulated 10,000 steps of energy minimization, switching from steepest descent to conjugate gradient after 5,000 cycles. The resulting minimized system was heated from 0 to 100 K in NVT condition for 50 ps with Langevin dynamics, and 100–300 K in NPT for 500 ps using Langevin dynamics, followed by a short (5 ns) equilibration process at constant pressure (1 atm) and temperature (300 K). Finally, unbiased and unrestrained system went through production in a periodic boundary condition for 500 ns in NPT by Langevin thermostat and Monte Carlo barostat conditions. Bonds involving hydrogen were constrained by the SHAKE algorithm. Cpptraj (Roe and Cheatham, 2013) was used to analyze the root mean square deviation (RMSD) and Dynamical Cross Correlation (Kamberaj and Vaart, 2009) within the ensembles comparing them to the wild type complex.
2.3 Structure predictions with AlphaFold
We used Alphafold Multimer (Evans et al., 2021b) to predict the structure of the complex using either sequence data or templates (containing the collagen and integrin domain far from each other). Results were analyzed in terms of the predicted local distance difference test (pLDDT) score as is standard in the field (Jumper et al., 2021). In short, the pLDDT score gives a per residue and global value to show how confident the Alpha Fold prediction results are. Results above 80 typically reflect high confidence in the prediction.
2.4 Thermodynamic integration (TI) calculations
TI was used to calculate the relative binding affinity (
2.5 Sampling collagen binding modes with MELD
The Modeling Employing Limited Data (MELD) approach uses H,T-REMD (Sugita and Okamoto, 1999) to sample rare events. The method changes the Hamiltonian by enforcing information that guides to different conformations that might be compatible with the end state. The caveat is that the data is framed as ambiguous and noisy—thus MELD relies on Bayesian inference to identify the best interpretation of the data compatible with the forcefield. In this process, analyzing the resulting ensemble (e.g., through clustering) identifies the states (conformations) most compatible with the information and force field.
To guide the binding process we first placed harmonic distance restraints amongst native contacts in the integrin (so it would not unfold), and also between the three collagen strands, so it would not dissociate. We then selected residues in the active site of the integrin and in those of the collagen binding motif. Based on those two lists of residues, we generated a list of twenty five possible contacts (some of which were present in the native state and some of which were not). We found that when enforcing 15 or more restraints, replica exchanges were inefficient, leading to poor sampling. At the other extreme, satisfying less than four restraints sampling was not restrictive enough to sample native-like bound conformations. We thus required that only eight restraints out of the 25 possible ones be satisfied. Satisfying different subsets of eight restraints give rise to different binding modes.
MELD simulations used the ff14SB force field (Maier et al., 2015) for side chains and ff99SB (Hornak et al., 2006) for backbone, together with the GBneck2 (Nguyen et al., 2013) implicit solvent model. The collagen fiber was placed over 30 Å away from the integrin. The temperature range was set between 300 and 500 K, with 30 replicas. Ensembles were analyzed using hierarchical clustering as implemented in CPPTRAJ (Roe and Cheatham, 2013) with an ϵ = 2 value, including heavy atoms at the interface of the complex in the native state.
3 Results
3.1 Local search for new interaction motifs
Traditional design strategies start with a known binding motif and search for single amino acid mutants that increase binding affinity (ΔΔGbind). Such strategies lead to local sequence optimization, with designs similar to the original motif. Here we used FoldX (Schymkowitz et al., 2005) and Rosetta (Barlow et al., 2018) (see methods), two traditional approaches with varying computational cost and success rate. We observed that FoldX single point mutations have a wider ΔΔGbind distribution, and are generally shifted towards higher energies (see Figure 2A). While there is good agreement on the failed mutations, the more computationally demanding Rosetta is better at discriminating mutations that FoldX finds favorable.
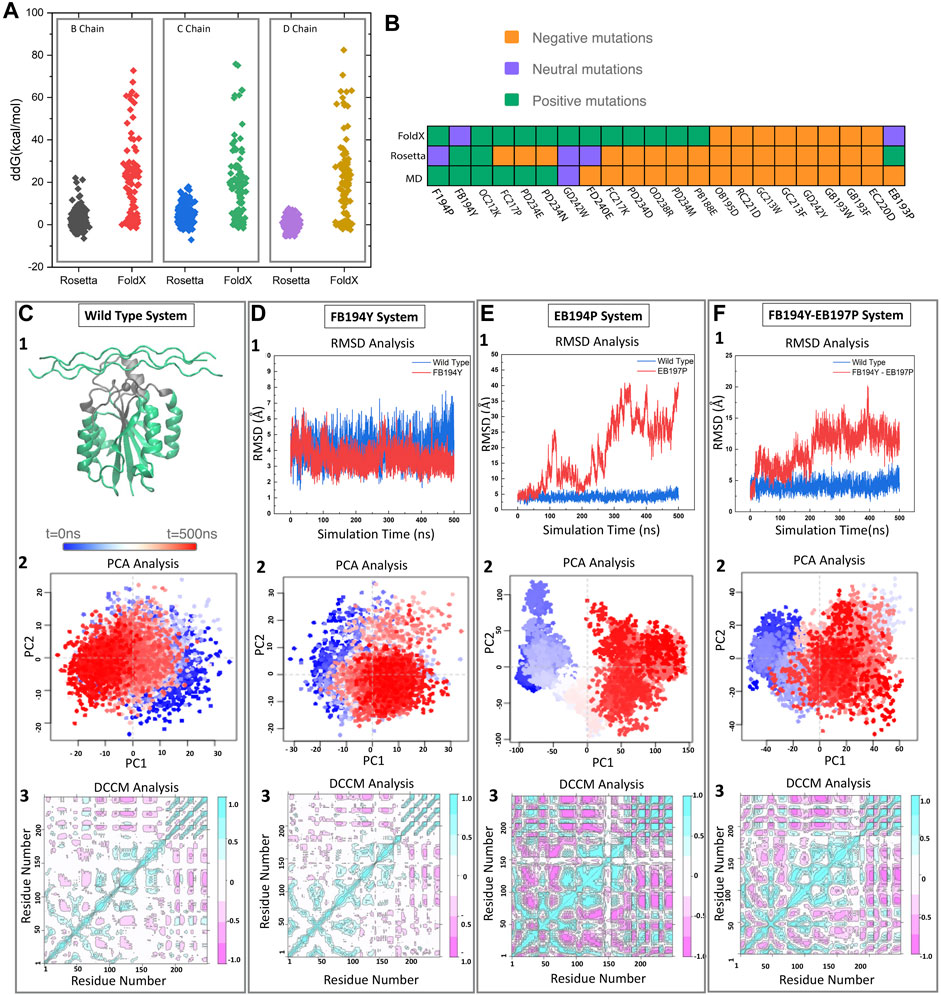
FIGURE 2. Pipeline for selecting new motifs. (A) FoldX and Rosetta are used to estimate relative free energy changes upon mutating each residue in the binding motif to all possible amino acids. (B) Predicted effect of mutations by three different methods (FoldX, Rosetta, and MD) for a set of 22 mutations. (C) The wild type samples a single state throughout the trajectory as identified by projecting onto the two first principal components. Reference Dynamic cross correlation matrix (DCCM) for the wild type state. (D–F) Examples of a stable (D) and unstable (E,F) mutations as identified from RMSD, PCA, and DCCM.
To further assess the predicted motifs with an independent methodology, we performed MD simulations of a selected group of 15 mutants. We expect that monitoring standard structural and dynamical properties like RMSD and dynamical cross correlation functions would be enough to distinguish those mutations that remain stable in the 500 ns timescale vs. those that are unlikely to bind (see Figures 2C–F). We monitored the RMSD of the interface region, defined as heavy atom contacts to collagen in the native structure (using a 10 Å cutoff). In this timescale, the integrin oscillates around 1 Å from the initial structures, with few deviations to higher RMSD values (2.5 Å). In the presence of collagen we observe a similar behavior, where there are no deviations to larger RMSD states in the 500 ns timescale. The RMSD of the whole complex oscillates at around 4 Å. Figure 2 showcases the behavior of the wild type, neutral and negative mutation on sampling [RMSD and projection on the top two principal components using the Bio3d package (Grant et al., 2006)]. Figure 2 exemplifies a negative control mutation (which rapidly dissociates) and a neutral mutation that remains close to the starting conformation.
We find that the more computationally efficient FoldX is capable of filtering out mutations that are likely detrimental to the binding affinity. While the ones predicted to be beneficial do not always agree with MD and Rosetta results (see Figure 2B). We notice several disagreements with Rosetta and MD—this is not surprising as Rosetta has been designed to predict free energy differences while short conventional MD trajectories do not contain enough sampling to assess the free energy. We thus decided to perform thermodynamic integration calculations to further identify the agreement between Rosetta and MD-based approaches.
Thermodynamic integration increases the complexity in system setup and analysis with respect a conventional MD trajectory—but the computational costs (considering replicates needed, see methods) remains relatively small compared to other MD approaches. We selected 15 mutations and compared results using Rosetta and TI (see Supplementary Figure S1). For most residue mutations, both programs agree in sign if not in magnitude. Previous work points to systems including multiple binding modes or systems that are sensitive to local conformational changes (such as the MIDAS binding site) (Armacost et al., 2020) as problematic for TI. For example, Guest and coworkers performed free energy perturbation studies on a series of small molecule inhibitors to the β6 integrin with an average error of 1.5 kcal/mol with respect to the experimental results (Guest et al., 2020).
We searched for alternative binding modes by using the MELD approach, which can simulate multiple binding/unbinding events. MELD combines ambiguous/noisy information with molecular simulations through Bayesian inference and has been routinely used for predict the binding of macromolecules [protein-protein (Brini et al., 2019), protein-peptide (Morrone et al., 2017; Mondal et al., 2022), protein-DNA (Bauzá and Pérez, 2021), and protein-small molecule (Liu et al., 2020)]. We derived ambiguous information based on native contacts present in the crystal structure in such a way that different interpretations of the data is compatible with different binding modes. We expected, that the force field would be able to recognize the most native-like amongst the binding modes for those sequences that have a high affinity (clusters with high population) (Lang and Perez, 2021). Unfortunately, due to the small interface region between collagen and the integrin, the different binding modes found give rise to large deviations in binding angles between the collagen in MELD simulations with respect to the native structure (see Supplementary Figure S2). On the other hand, satisfying more information overrides the force field preferences and yields native-like binding modes regardless of the sequence. Similarly, competitive binding simulations (Morrone et al., 2017) with MELD also failed to distinguish which collagen mutations were more likely to lead to more stable complexes. Presumably, these limitations arise from the use of an implicit solvent (Nguyen et al., 2013) needed for the MELD binding simulations.
Similarly, the recent successes of the AlphaFold (AF) (Evans et al., 2021a) machine learning approach did not translate to this system. We used a local installation of AlphaFold and performed predictions in the presence/absence of structural templates. In our hands, Alphafold multimer predictions were confident about the α2 I-domain structure (high pLDDT scores), but failed to predict the structure of the collagen triple helix structure—and hence of the complex (see Supplementary Figure S2).
3.2 Recent machine learning approaches can suggest novel sequences based on the structure
Whereas we used FoldX and Rosetta to predict local changes in the sequence (single mutants), the recent protein MPNN (Dauparas et al., 2022) machine learning approach can in principle find an optimal sequence given the structure of the complex. Contrary to the other two methods, this approach does not provide a relative binding affinity. We first generated two predictions in which we allowed any residue in the motif along the tree collagen strands to change (see “Prediction 1″ and “Prediction 2” in Supplementary Figure S3). This gave rise to four different binding motifs. We next generated four more sequences by creating homo-trimer collagen strands with each of the four predicted motifs (see the latter four motifs in Supplementary Figure S3A). We assessed the viability of these motifs by running conventional MD. All sequences in which the leading strand had an E to P mutation were unstable. Whereas if this mutation occurred in other strands, the system remained stable. This is expected as the Glutamic acid coordinates with a divalent site when interacting with the integrin.
4 Discussion
In this work we focused on identifying collagen-like motifs that bind the I-domain of the α2β1 integrin. Despite their biological relevance and some successes (Craig et al., 2004; Murcia et al., 2008; Choi et al., 2010; Zhu et al., 2010; Wang et al., 2015; Farina et al., 2016; Fratev and Sirimulla, 2019), integrins remain challenging systems to study through molecular modeling. The collagen fiber with the GFOGER motif that we study was initially suggested based on docking calculations (Emsley et al., 2000), which led to the crystallization of the complex (pdb code 1dzi). Our use of local (single mutant) and global (proteinMPNN) approaches shows that current methodologies are better at discerning unfavorable mutations than at providing reliable predictions. However, consensus between different methods increases the likelihood of success. Our use of MD stability analysis showed that it can be a helpful tool to distinguish unfavorable mutations, but stable simulations are not a guarantee of favorable mutations as timescales remain limited. This becomes an issue even when using thermodynamic integration, as multiple binding modes are possible. While this is an actively developed field for small molecule binders Gill et al. (2018), it remains more challenging for flexible molecules such as collagen. For such flexible systems, we have previously found the MELD Bayesian inference approach can typically identify differences amongst different binder sequences. Due to the small interface area, our standard protocol results in binding modes where the collagen binds in the right region, but with orientations that can deviate up to 90° from their experimental binding mode. The caveat of increasing the number of restraints in MELD to solve this issue leads to the inability to distinguish motif sequence preferences.
Molecular modeling pipelines are undergoing rapid and drastic changes thanks to the eruption of machine learning approaches. The CASP event served as the perfect scenario for the first iteration of AlphaFold to show the potential of machine learning in protein structure prediction (Senior et al., 2020). Their initial approach relied on following the leading strategies in the field: determine pair-wise distance distributions between residues to impose as restraints to predict structures. Two years later, AlphaFold presented a novel strategy based on attention networks with an impressive performance in CASP (Jumper et al., 2021). Making the network available to the community and the appearance of collaborative notebooks (Mirdita et al., 2022) rapidly allowed groups to apply it to a myriad of problems: for molecular recognition (protein-protein and protein-peptide) (Humphreys et al., 2021; Tsaban et al., 2022), for predicting multiple biological states (Wayment-Steele et al., 2022), relative binding affinities (Chang and Perez, 2022), or even for designing new proteins via deep network hallucination (Anishchenko et al., 2021). As these networks learn from data deposited in the protein data Bank, they also implicitly learn about the position of ions or ligands in active sites. However, AF multimer was not able to predict the structures of the 1dzi complex. Recent work showed that partial retraining pf AF weights for specific targets could lead to an improved ability to correctly identify bound or unbound peptides binding to the Major Histocompatibility Complex (MHC) (Motmaen et al., 2022). This was possible thanks to a large database of peptides known to be either binders/non-binders to MHC. Such type of initiatives could soon provide accurate results for predicting complexes involving integrins, which combined with competitive binding strategies (Chang and Perez, 2022) could lead to rapid identification of functional motifs.
During the writing of this paper, several new machine learning approaches appeared in the literature which make us optimistic about the future: we highlight three that are relevant to the discussion above. The first one is RosettaFoldNA (Baek et al., 2022), which predicts the folding of RNA as well as nucleic acid-protein complexes. The approach draws on the AF principles but incorporates an additional physics-inspired term (Lennard Jones potentials taken from Rosetta) to better reproduce geometries (e.g., reduce the overlap between protein and nucleic acids). In this process, the algorithm has learned to assemble double-stranded DNA, much like we hope the collagen triple helix can be predicted. The second development is the OpenFold (Ahdritz et al., 2022) initiative—a pyTorch-based implementation trainable to reproduce AlphaFold levels of accuracy at a lower computational cost. The authors also report the OpenProteinSet used to train the model. In the last few months, the field used AF beyond what it was originally designed to do. OpenFold will now give users the possibility to retrain a tool equivalent to AF for new purposes. Finally, a recent study (Akdel et al., 2022) highlights the potentially transformative role of AF in structural biology, its accuracy matching experiments for many applications, as well as the role of potential biases, and its ability to identify features that are not typically present in databases.
5 Conclusion
In this work we assessed the role of different computational tools to identify novel collagen-integrin binding motifs. FoldX serves as a fast mutant screen, to filter out mutations that do not improve binding affinity. A combination of Rosetta and MD (TI) serves to further identify those mutations most likely to lead to improved binding affinities. Although we were very enthusiastic about the possibility of using AlphaFold to differentiate amongst binding motifs, we found no evidence that it could predict the native state. However, in light of recent work it seems like partial retraining of the weights against known binders/non-binders might lead to a feasible pipeline. Finally, proteinMPNN was able to correctly identify that mutations to the glutamic acid involved in binding would be deleterious only in the leading strand. Although further assessment is needed, proteinMPNN paves the way to identifying functional motifs far from the starting sequence motif.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors upon request.
Author contributions
QL performed computational simulations and analysis. QL and AP discussed the results and wrote the paper.
Funding
Research was sponsored by the Army Research Office under Grant Number W911NF-22-1-0142. The views and conclusion contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the ARO or the U.S. Government. The authors acknowledge University of Florida Research Computing for providing computational resources and support that have contributed to the research results reported in this publication.
Acknowledgments
We are thankful for startup resources to run simulations on UF research computing resources.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2023.1107400/full#supplementary-material
References
Ahdritz, G., Bouatta, N., Kadyan, S., Xia, Q., Gerecke, W., O’Donnell, T. J., et al. (2022). OpenFold: Retraining AlphaFold2 yields new insights into its learning mechanisms and capacity for generalization. doi:10.1101/2022.11.20.517210
Akdel, M., Pires, D. E. V., Pardo, E. P., Jänes, J., Zalevsky, A. O., Mészáros, B., et al. (2022). A structural biology community assessment of AlphaFold2 applications. Nat. Struct. Mol. Biol. 29, 1056–1067. doi:10.1038/s41594-022-00849-w
Anishchenko, I., Pellock, S. J., Chidyausiku, T. M., Ramelot, T. A., Ovchinnikov, S., Hao, J., et al. (2021). De novo protein design by deep network hallucination. Nature 1, 547–552. doi:10.1038/s41586-021-04184-w
Åqvist, J., Wennerström, P., Nervall, M., Bjelic, S., and Brandsdal, B. O. (2004). Molecular dynamics simulations of water and biomolecules with a Monte Carlo constant pressure algorithm. Chem. Phys. Lett. 384, 288–294. doi:10.1016/j.cplett.2003.12.039
Armacost, K. A., Riniker, S., and Cournia, Z. (2020). Exploring novel directions in free energy calculations. J. Chem. Inf. Model. 60, 5283–5286. doi:10.1021/acs.jcim.0c01266
Asgari, E., McHardy, A. C., and Mofrad, M. R. K. (2019). Probabilistic variable-length segmentation of protein sequences for discriminative motif discovery (DiMotif) and sequence embedding (ProtVecX). Sci. Rep. 9, 3577. doi:10.1038/s41598-019-38746-w
Aumailley, M., Gurrath, M., Müller, G., Calvete, J., Timpl, R., and Kessler, H. (1991). Arg-gly-asp constrained within cyclic pentapoptides strong and selective inhibitors of cell adhesion to vitronectin and laminin fragment p1. FEBS Lett. 291, 50–54. doi:10.1016/0014-5793(91)81101-d
Baek, M., McHugh, R., Anishchenko, I., Baker, D., and DiMaio, F. (2022). Accurate prediction of nucleic acid and protein-nucleic acid complexes using RoseTTAFoldNA. doi:10.1101/2022.09.09.507333
Barlow, K. A., Ó Conchúir, S., Thompson, S., Suresh, P., Lucas, J. E., Heinonen, M., et al. (2018). Flex ddg: Rosetta Ensemble-Based estimation of changes in Protein-Protein binding affinity upon mutation. J. Phys. Chem. B 122, 5389–5399. doi:10.1021/acs.jpcb.7b11367
Bauzá, A., and Pérez, A. (2021). MELD-DNA: A new tool for capturing protein-DNA binding. bioRxiv. 2021.06.24.449809. doi:10.1101/2021.06.24.449809
Braun, E., Gilmer, J., Mayes, H. B., Mobley, D. L., and Monroe, J. I. (2018). Best practices for foundations in molecular simulations. Article v1. 0.
Brini, E., Kozakov, D., and Dill, K. (2019). Predicting protein dimer structures using MELD × MD. J. Chem. theory Comput. 15, 3381–3389. doi:10.1021/acs.jctc.8b01208
Case, D., Belfon, K., Ben-Shalom, I., Brozell, S., Cerutti, D., Cheatham, T., et al. (2020). Amber 2020.
Chang, L., and Perez, A. (2022). Ranking peptide binders by affinity with AlphaFold. Angew. Chem. Int. Ed., e202213362. doi:10.1002/anie.202213362
Chen, W., Lou, J., Hsin, J., Schulten, K., Harvey, S. C., and Zhu, C. (2011). Molecular dynamics simulations of forced unbending of integrin V3. PLoS Comput. Biol. 7, e1001086. doi:10.1371/journal.pcbi.1001086
Choi, Y., Kim, E., Lee, Y., Han, M. H., and Kang, I.-C. (2010). Site-specific inhibition of integrin αvβ3-vitronectin association by a ser-asp-val sequence through an Arg-Gly-Asp-binding site of the integrin. Proteomics 10, 72–80. doi:10.1002/pmic.200900146
Craig, D., Gao, M., Schulten, K., and Vogel, V. (2004). Structural insights into how the MIDAS ion stabilizes integrin binding to an RGD peptide under force. Structure 12, 2049–2058. doi:10.1016/j.str.2004.09.009
Critchley, D. R., Holt, M. R., Barry, S. T., Priddle, H., Hemmings, L., and Norman, J. (1999). Integrin-mediated cell adhesion: The cytoskeletal connection. Biochem. Soc. Symp. 65, 79–99.
Dauparas, J., Anishchenko, I., Bennett, N., Bai, H., Ragotte, R. J., Milles, L. F., et al. (2022). Robust deep learning–based protein sequence design using ProteinMPNN. Science 378, 49–56. doi:10.1126/science.add2187
Emsley, J., Knight, C., Farndale, R. W., Barnes, M. J., and Liddington, R. C. (2000). Structural basis of collagen recognition by integrin 21. Cell 101, 47–56. doi:10.1016/s0092-8674(00)80622-4
Evans, R., O’Neill, M., Pritzel, A., Antropova, N., Senior, A., Green, T., et al. (2021a). Protein complex prediction with alphafold-multimer. bioRxiv. doi:10.1101/2021.10.04.463034
Evans, R., O’Neill, M., Pritzel, A., Antropova, N., Senior, A., Green, T., et al. (2021b). Protein complex prediction with AlphaFold-Multimer. bioRxiv. 2021.10.04.463034. doi:10.1101/2021.10.04.463034
Farina, B., de Paola, I., Russo, L., Capasso, D., Liguoro, A., Gatto, A. D., et al. (2016). A combined NMR and computational approach to determine the RGDechi-hCit-αv β3 integrin recognition mode in isolated cell membranes. Chemistry 22, 681–693. doi:10.1002/chem.201503126
Fratev, F., and Sirimulla, S. (2019). An improved free energy perturbation FEP+ sampling protocol for flexible ligand-binding domains. Sci. Rep. 9, 16829. doi:10.1038/s41598-019-53133-1
Freindorf, M., Furlani, T. R., Kong, J., Cody, V., Davis, F. B., and Davis, P. J. (2012). Combined QM/MM study of thyroid and steroid hormone analogue interactions with integrin. J. Biomed. Biotechnol. 2012, 1–12. doi:10.1155/2012/959057
Gill, S. C., Lim, N. M., Grinaway, P. B., Rustenburg, A. S., Fass, J., Ross, G. A., et al. (2018). Binding modes of ligands using enhanced sampling (BLUES): Rapid decorrelation of ligand binding modes via nonequilibrium candidate Monte Carlo. J. Phys. Chem. B 122, 5579–5598. doi:10.1021/acs.jpcb.7b11820
Grant, B. J., Rodrigues, A. P., ElSawy, K. M., McCammon, J. A., and Caves, L. S. (2006). Bio3d: An r package for the comparative analysis of protein structures. Bioinformatics 22, 2695–2696. doi:10.1093/bioinformatics/btl461
Guest, E. E., Oatley, S. A., Macdonald, S. J. F., and Hirst, J. D. (2020). Molecular simulation of v6 integrin inhibitors. J. Chem. Inf. Model. 60, 5487–5498. doi:10.1021/acs.jcim.0c00254
Guzzetti, I., Civera, M., Vasile, F., Arosio, D., Tringali, C., Piarulli, U., et al. (2017). Insights into the binding of cyclic RGD peptidomimetics to α5β1 integrin by using Live-Cell NMR and computational studies. ChemistryOpen 6, 128–136. doi:10.1002/open.201600112
Hamaia, S. W., Pugh, N., Raynal, N., Némoz, B., Stone, R., Gullberg, D., et al. (2012). Mapping of potent and specific binding motifs, GLOGEN and GVOGEA, for integrin 11 using collagen toolkits II and III. J. Biol. Chem. 287, 26019–26028. doi:10.1074/jbc.m112.353144
Hatley, R. J. D., Macdonald, S. J. F., Slack, R. J., Le, J., Ludbrook, S. B., and Lukey, P. T. (2018). Anv-RGD integrin inhibitor toolbox: Drug discovery insight, challenges and opportunities. Angew. Chem. Int. Ed. 57, 3298–3321. doi:10.1002/anie.201707948
He, X., Liu, S., Lee, T.-S., Ji, B., Man, V. H., York, D. M., et al. (2020). Fast, accurate, and reliable protocols for routine calculations of protein–ligand binding affinities in drug design projects using AMBER GPU-TI with ff14SB/GAFF. ACS Omega 5, 4611–4619. doi:10.1021/acsomega.9b04233
Hornak, V., Abel, R., Okur, A., Strockbine, B., Roitberg, A., and Simmerling, C. (2006). Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins 65, 712–725. doi:10.1002/prot.21123
Humphreys, I. R., Pei, J., Baek, M., Krishnakumar, A., Anishchenko, I., Ovchinnikov, S., et al. (2021). Computed structures of core eukaryotic protein complexes. Science 374, eabm4805. doi:10.1126/science.abm4805
Hutchinson, M. (2007). Natalizumab: A new treatment for relapsing remitting multiple sclerosis. Ther. Clin. Risk Manag. 3, 259–268. doi:10.2147/tcrm.2007.3.2.259
Hynes, R. O. (1987). Integrins: A family of cell surface receptors. Cell 48, 549–554. doi:10.1016/0092-8674(87)90233-9
Hynes, R. O. (2002). Integrins: Bidirectional, allosteric signaling machines. Cell 110, 673–687. doi:10.1016/s0092-8674(02)00971-6
Izadi, S., Anandakrishnan, R., and Onufriev, A. V. (2014). Building water models: A different approach. J. Phys. Chem. Lett. 5, 3863–3871. doi:10.1021/jz501780a
Joung, I. S., and Cheatham, T. E. (2008). Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J. Phys. Chem. B 112, 9020–9041. doi:10.1021/jp8001614
Jumper, J., Evans, R., Pritzel, A., Green, T., Figurnov, M., Ronneberger, O., et al. (2021). Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589. doi:10.1038/s41586-021-03819-2
Kalli, A. C., Campbell, I. D., and Sansom, M. S. P. (2011). Multiscale simulations suggest a mechanism for integrin inside-out activation. Proc. Natl. Acad. Sci. 108, 11890–11895. doi:10.1073/pnas.1104505108
Kalli, A. C., Rog, T., Vattulainen, I., Campbell, I. D., and Sansom, M. S. P. (2017). The integrin receptor in biologically relevant bilayers: Insights from molecular dynamics simulations. J. Membr. Biol. 250, 337–351. doi:10.1007/s00232-016-9908-z
Kamberaj, H., and Vaart, A. v. d. (2009). Correlated motions and interactions at the onset of the DNA-induced partial unfolding of ets-1. Biophysical J. 96, 1307–1317. doi:10.1016/j.bpj.2008.11.019
Kapp, T. G., Rechenmacher, F., Neubauer, S., Maltsev, O. V., Cavalcanti-Adam, E. A., Zarka, R., et al. (2017). A comprehensive evaluation of the activity and selectivity profile of ligands for RGD-binding integrins. Sci. Rep. 7, 39805. doi:10.1038/srep39805
Kawamoto, E., Nakahashi, S., Okamoto, T., Imai, H., and Shimaoka, M. (2012). Anti-integrin therapy for multiple sclerosis. Autoimmune Dis. 2012, 1–6. doi:10.1155/2012/357101
Lang, L., and Perez, A. (2021). Binding ensembles of p53-MDM2 peptide inhibitors by combining bayesian inference and atomistic simulations. Molecules 26, 198. doi:10.3390/molecules26010198
Ley, K., Rivera-Nieves, J., Sandborn, W. J., and Shattil, S. (2016). Integrin-based therapeutics: Biological basis, clinical use and new drugs. Nat. Rev. Drug Discov. 15, 173–183. doi:10.1038/nrd.2015.10
Liu, C., Brini, E., Perez, A., and Dill, K. A. (2020). Computing ligands bound to proteins using MELD-accelerated MD. J. Chem. Theory Comput. 16, 6377–6382. doi:10.1021/acs.jctc.0c00543
Maier, J. A., Martinez, C., Kasavajhala, K., Wickstrom, L., Hauser, K. E., and Simmerling, C. (2015). ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. theory Comput. 11, 3696–3713. doi:10.1021/acs.jctc.5b00255
Mehdi, A. M., Sehgal, M. S. B., Kobe, B., Bailey, T. L., and Bodén, M. (2013). Dlocalmotif: A discriminative approach for discovering local motifs in protein sequences. Bioinformatics 29, 39–46. doi:10.1093/bioinformatics/bts654
Mercurio, A. M., Rabinovitz, I., and Shaw, L. M. (2001). The α6β4 integrin and epithelial cell migration. Curr. Opin. cell Biol. 13, 541–545. doi:10.1016/s0955-0674(00)00249-0
Mirdita, M., Schütze, K., Moriwaki, Y., Heo, L., Ovchinnikov, S., and Steinegger, M. (2022). ColabFold: Making protein folding accessible to all. Nat. Methods 19, 679–682. doi:10.1038/s41592-022-01488-1
Mizuno, M., Fujisawa, R., and Kuboki, Y. (2000). Type i collagen-induced osteoblastic differentiation of bone-marrow cells mediated by collagen-α2β1 integrin interaction. J. Cell. physiology 184, 207–213. doi:10.1002/1097-4652(200008)184:2<207::aid-jcp8>3.0.co;2-u
Mondal, A., Swapna, G., Hao, J., Ma, L., Roth, M. J., Montelione, G. T., et al. (2022). Structure determination of protein-peptide complexes from NMR chemical shift data using MELD. bioRxiv. 2021.12.31.474671. doi:10.1101/2021.12.31.474671
Morrone, J. A., Perez, A., MacCallum, J., and Dill, K. A. (2017). Computed binding of peptides to proteins with MELD-accelerated molecular dynamics. J. Chem. Theory Comput. 13, 870–876. doi:10.1021/acs.jctc.6b00977
Motmaen, A., Dauparas, J., Baek, M., Abedi, M. H., Baker, D., and Bradley, P. (2022). Peptide binding specificity prediction using fine-tuned protein structure prediction networks. bioRxiv. 2022.07.12.499365. doi:10.1101/2022.07.12.499365
Murcia, M., Jirouskova, M., Li, J., Coller, B. S., and Filizola, M. (2008). Functional and computational studies of the ligand-associated metal binding site of 3 integrins. Proteins Struct. Funct. Bioinforma. 71, 1779–1791. doi:10.1002/prot.21859
Nguyen, H., Roe, D. R., and Simmerling, C. (2013). Improved generalized born solvent model parameters for protein simulations. J. Chem. theory Comput. 9, 2020–2034. doi:10.1021/ct3010485
Otey, C. A., Vasquez, G. B., Burridge, K., and Erickson, B. W. (1993). Mapping of the alpha-actinin binding site within the beta 1 integrin cytoplasmic domain. J. Biol. Chem. 268, 21193–21197. doi:10.1016/s0021-9258(19)36909-1
Perez, J. J., Perez, R. A., and Perez, A. (2021). Computational modeling as a tool to investigate PPI: From drug design to tissue engineering. Front. Mol. Biosci. 8, 681617–681637. doi:10.3389/fmolb.2021.681617
Prytuliak, R., Volkmer, M., Meier, M., and Habermann, B. H. (2017). HH-MOTiF: De novo detection of short linear motifs in proteins by hidden markov model comparisons. Nucleic Acids Res. 45, 10921–W477. doi:10.1093/nar/gkx810
Roe, D. R., and Cheatham, T. E. (2013). PTRAJ and CPPTRAJ: Software for processing and analysis of molecular dynamics trajectory data. J. Chem. theory Comput. 9, 3084–3095. doi:10.1021/ct400341p
Salomon-Ferrer, R., Götz, A. W., Poole, D., Grand, S. L., and Walker, R. C. (2013). Routine microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent particle mesh ewald. J. Chem. theory Comput. 9, 3878–3888. doi:10.1021/ct400314y
Schymkowitz, J., Borg, J., Stricher, F., Nys, R., Rousseau, F., and Serrano, L. (2005). The FoldX web server: An online force field. Nucleic Acids Res. 33, W382–W388. doi:10.1093/nar/gki387
Senior, A. W., Evans, R., Jumper, J., Kirkpatrick, J., Sifre, L., Green, T., et al. (2020). Improved protein structure prediction using potentials from deep learning. Nature 577, 706–710. doi:10.1038/s41586-019-1923-7
Shirts, M. R., Pitera, J. W., Swope, W. C., and Pande, V. S. (2003). Extremely precise free energy calculations of amino acid side chain analogs: Comparison of common molecular mechanics force fields for proteins. J. Chem. Phys. 119, 5740–5761. doi:10.1063/1.1587119
Siebert, H.-C., Burg-Roderfeld, M., Eckert, T., Stötzel, S., Kirch, U., Diercks, T., et al. (2010). Interaction of the α2A domain of integrin with small collagen fragments. Protein Cell 1, 393–405. doi:10.1007/s13238-010-0038-6
Slack, R. J., Macdonald, S. J. F., Roper, J. A., Jenkins, R. G., and Hatley, R. J. D. (2022). Emerging therapeutic opportunities for integrin inhibitors. Nat. Rev. Drug Discov. 21, 60–78. doi:10.1038/s41573-021-00284-4
Steinbrecher, T., Joung, I., and Case, D. A. (2011). Soft-core potentials in thermodynamic integration: Comparing one-and two-step transformations. J. Comput. Chem. 32, 3253–3263. doi:10.1002/jcc.21909
Sugita, Y., and Okamoto, Y. (1999). Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 314, 141–151. doi:10.1016/s0009-2614(99)01123-9
Takada, Y., Ye, X., and Simon, S. (2007). The integrins. Genome Biol. 8, 215. doi:10.1186/gb-2007-8-5-215
Tsaban, T., Varga, J. K., Avraham, O., Ben-Aharon, Z., Khramushin, A., and Schueler-Furman, O. (2022). Harnessing protein folding neural networks for peptide–protein docking. Nat. Commun. 13, 176. doi:10.1038/s41467-021-27838-9
Wang, L., Wu, Y., Deng, Y., Kim, B., Pierce, L., Krilov, G., et al. (2015). Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. J. Am. Chem. Soc. 137, 2695–2703. doi:10.1021/ja512751q
Wayment-Steele, H. K., Ovchinnikov, S., Colwell, L., and Kern, D. (2022). Prediction of multiple conformational states by combining sequence clustering with AlphaFold2. bioRxiv. 2022.10.17.512570. doi:10.1101/2022.10.17.512570
Keywords: molecular recognition, integrin, AlphaFold, moecular modeling, binding
Citation: Liu Q and Perez A (2023) Assessing a computational pipeline to identify binding motifs to the α2β1 integrin. Front. Chem. 11:1107400. doi: 10.3389/fchem.2023.1107400
Received: 24 November 2022; Accepted: 27 January 2023;
Published: 13 February 2023.
Edited by:
Sergio Pantano, Pasteur Institute of Montevideo, UruguayReviewed by:
Simón Poblete, Universidad Austral de Chile, ChileCopyright © 2023 Liu and Perez. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alberto Perez, perez@chem.ufl.edu