- School of Mathematics and Physics, Hechi University, Yizhou, China
The zero-divisor graph of a commutative ring R, denoted by Γ(R), is a graph whose two distinct vertices x and y are joined by an edge if and only if xy = 0 or yx = 0. The main problem of the study of graphs defined on algebraic structure is to recognize finite rings through the properties of various graphs defined on it. The main objective of this article is to study the Wiener index of zero-divisor graph and compressed zero-divisor graph of the ring of integer modulo psqt for all distinct primes p, q and
Introduction
The study of graphs defined on algebraic structures has been an active topic of research in the last few decades. The main question in the area is to recognize finite rings through the properties of various graphs defined on it. The notion of the zero-divisor graph of a commutative ring was introduced by I. Beck in (Beck, 1988), where he considered the set of zero divisors including zero and introduced the concepts such as diameter, grith and clique number of a zero divisor graph. Then later on in (Anderson and Livingston, 1999), Anderson and Livingston changed the vertex set of the zero-divisor graph, they considered only the vertices of the non-zero zero-divisors. For more details, one may see the survey (Singh and Bhat, 2020) and the references therein for the vast literature on the study of zero-divisor graphs.
The Wiener index is one of the important graph indices, and has a variety of applications in pharmaceutical science and in the structure of nanotubes. For results and applications of Wiener index, see (Devillers and Balaban, 1999; Dobrynin et al., 2001; Dehmer and Emmert-Streib, 2014; Dobrynin and Iranmanesh, 2020). There are some works of the Wiener index were done for the ring of integers modulo n. Let us review some of the work done on the topological indices of the zero-divisor graphs. Let p, q be distinct prime numbers. Ahmadi et al. (Ahmadi and Nezhad, 2011) in 2011 has provided an algorithm to determining the Wiener index of
In this paper, we are interested in the parameter Wiener index of graphs for the rings of integers modulo psqt. Although the formulas in the general case for the rings of
Preliminaries
Throughout this paper we assume that R denotes a commutative ring with identity, Z(R) be its set of zero-divisors, the (nonempty) set of nonzero zero-divisors and unit elements denoted by Z(R)* and U(R). We use
Definition 1. Let G be a graph and let u and v be two vertices of G. The distance between u and v, denoted by dG(u, v), is defined to be the length of the shortest path between u and v. The Wiener index of the graph G, denoted by W(G), is defined to be the sum of all distanced between any two vertices of G.Let dG(v) denote the sum of distances of the vertex v from all the vertices of G, then the Wiener index can be redefined as
Let R be an arbitrary finite commutative ring with unity. We define an equivalence relation ∼ on Z(R)* as follows. For x, y ∈ Z(R)*, define x ∼ y if and only if ann(x) = ann(y) where ann(x) = {r ∈ R|rx = 0}. We call these classes the equiv-annihilator classes of the zero-divisor graph Γ(R).We write d (x, y) to denote the distance between x and y in Z(R)*, and write x ∼ y to denote x and y are adjacent, otherwise x ≁ y. Let U, V be subsets of the vertex of Γ(R), the U ↔ V shall denote that each vertex of U is adjacent to every vertex of V, and U ↮ V denotes that no vertex of U is adjacent to every vertex of V.The so-called compressed zero-divisor graph of a ring was first defined by the Spiroff et al. in (Spiroff and Wickham, 2011).
Definition 2. For a commutative ring R with 1 ≠ 0, a compressed zero-divisor graph of a ring R is the undirected graph ΓE(R) with vertex set Z(RE) − [0] = RE − {[0], [1]} defined by RE = {[x]|x ∈ R}, where [x] = {y ∈ R|ann(x) = ann(y)} and two distinct vertices [x] and [y] are adjacent if and only if [x][y] = [0] = [xy], that is, if and only if xy = 0.In what follows, we use the graph-theoretic notions from (Douglas, 2001).
Main results
In this section, we first give a structure of
Let p, q be distinct prime numbers and
We noted that Vst =∅ and
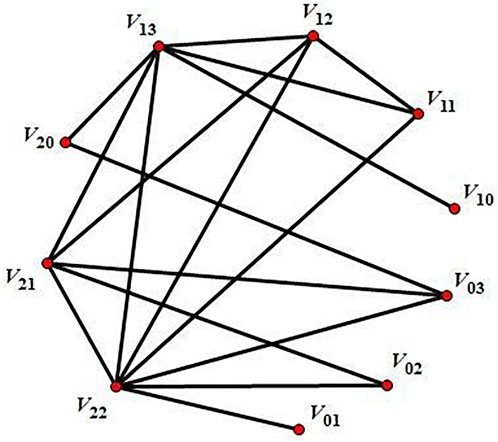
Example 1. Consider the ring
It is not difficult to see that Vij be the equiv-annihilator classes of
Lemma 1. For distinct prime numbers p, q, let n = psqt for some
(1)
(2) Vij ↔ Vi′j′ if and only if i + i′ ≥ s and j + j′ ≥ t.
Proof. (1) we consider the following cases.Case 1: i ≠ s and j ≠ t.Let Sij be the set of all the elements that can be divisible by piqj in
Note that |Sij| = |{kpiqj|0 ≤ k < ps−iqt−j}| = ps−iqt−j. Since
And
Then
Case 2: i = s.Since
Then
Case 3: j = t.Since
Then
(2) Let x = kijpiqj ∈ Vij, y = ki′j′pi′qj′ ∈ Vi′j′. If i + i′ ≥ s and j + j′ ≥ t, then
So x is adjacent to y.Conversely, suppose Vij ↔ Vi′j′. If i + i′ < s or j + j′ < t. We have xy = kijki′j′pi+i′qj+j′ can’t be a multiple of n, a contradiction. The following result characterized the distance between the equiv-annihilator classes.
Proposition 1. For distinct prime numbers p, q, let
Proof. Let. V01, V10, ⋯ , Vs,t−1, Vs−1,t be the equiv-annihilator classes of
And
Thus
Then
And
Thus
Theorem 1. For distinct prime numbers p, q, and some
where
Proof. Let. n = psqt, we have V01, V10, …, Vs−1,t, Vs,t−1 is the partition of
Case 2:
Let x and y be the elements in the two different equiv-annihilator classes, Vij and Vi′j′, respectively. Consider the following cases.Case 3: i + i′ ≥ s and j + j′ ≥ t.By Lemma 1, d (x, y) = 1. Then
Case 4: 0 < i + i′ < s or 0 < j + j′ < t.Subcase 4.1: i = 0 and j′ = 0.In this case, we have d (x, y) = 3. Hence
Subcase 4.2: i′ = 0 and j = 0.In this case, d (x, y) = 3. Hence
Subcase 4.3: If i, j′ are not both equal to 0, and i′, j are not both equal to 0.In this case, d (x, y) = 2. Hence
In conclusion, the Weiner index is
Therefore the result holds, by Lemma 1. The following Table gives the exact value of
Example 2. Consider the ring
Lemma 2. For distinct prime numbers p, q, let n = psqt for some
(1) V(G) = {Vij|0 ≤ i ≤ s, 0 ≤ j ≤ t} .
(2)
Proof. (1) Note that
where
(2) Let
There are the following cases.Case 1: i = 0 and 0 < j < t.By Lemma 1 there are Vij ↔ Vi′j′ if and only if i + i′ ≥ s and j + j′ ≥ t. So in this case
Hence, dG (Vij) = 2 (s + 1) (t + 1) + s − j − 6.Case 2: i = 0 and j = t.As case 1,
Hence, dG (Vij) = 2 (s + 1) (t + 1) + s − t − 7.Case 3: 0 < i < s and j = 0.A similar argument as in Case 1 shows that, dG (Vij) = 2 (s + 1) (t + 1) + t − i − 6.Case 4: i = s and j = 0.A similar argument as in Case 2 shows that, dG (Vij) = 2 (s + 1) (t + 1) + t − s − 7.Case 5:
Hence, dG (Vij) = 2 (s + 1) (t + 1) − (i + 1) (j + 1) − 5.Case 6:
Hence, dG (Vij) = 2 (s + 1) (t + 1) − (i + 1) (j + 1) − 4.This completes the proof of the lemma.
Remark 1. From the above lemma, it can be easily seen that the cardinalities of the vertex set of G, that is, |V(G)| = (s + 1) (t + 1) − 2. So
Theorem 2. For distinct prime numbers p, q, and some
Proof. Let . n = psqt, and
Example 3. Consider the ring
By Theorem 2.
Conclusion
In this paper, we have described the structure of the graph
In addition, we run the formula obtained through MATLAB software and get the data in Table 1. Then, we studied the structure of the compressed zero-factor graph of
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
RL conceived of the presented idea, and WY developed the theory and performed the computations, verified the analytical methods. RL investigated and supervised the findings of this work. All authors discussed the results and contributed to the final manuscript.
Funding
The authors are very grateful to the referee for careful reading of the manuscript and helpful suggestions. This work was supported by the National Science Foundation of China (11961021 and 11561019), Guangxi Natural Science Foundation (2020GXNSFAA159084), Hechi University Research Fund for Advanced Talents (2019GCC005) and Hechi University Research Fund (2018XJQN007).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahmadi, M. R., and Nezhad, R. J. (2011). Energy and Wiener index of zero-divisor graphs. Iran. J. Math. Chem. 2 (1), 45–51. doi:10.22052/ijmc.2011.5166
Anderson, D. F., and Livingston, P. S. (1999). The zero-divisor graph of a commutative ring. J. Algebra 217 (2), 434–447. doi:10.1006/jabr.1998.7840
Asir, T., and Rabikka, V. (2021). The Wiener index of the zero-divisor graph of Zn. Discrete. Appl. Math. 319, 461–471. doi:10.1016/j.dam.2021.02.035,
Beck, I. (1988). Coloring of commutative rings. J. Algebra. 116, 116 208–226. doi:10.1016/0021-8693(88)90202-5
Dehmer M, and Emmert-Streib F (Editors) (2014). Quantitative graph theory: Mathematical foundations and applications (Florida, United States: CRC Press).
J. Devillers, and A. T. Balaban (Editors) (1999). Topological indices and related descriptors in QSAR and QSPR (Amsterdam: Gordon and Breach Science Publishers).
Dobrynin, A., Entringer, R., and Gutman, I. (2001). Wiener index of trees: Theory and applications. Acta Appl. Math. 66 (3), 211–249. doi:10.1023/a:1010767517079
Dobrynin, A., and Iranmanesh, A. (2020). Wiener index of edge thorny graphs of catacondensed benzenoids. Mathematics 8 (4), 467. doi:10.3390/math8040467
Mohammad, H. Q., and Authman, M. N. (2018). Hosoya polynomial and wiener index of zero-divisor graph of Z_n. AL-Rafidain J. Comput. Sci. Math. 12 (1), 47–59. doi:10.33899/csmj.2018.163570
Pirzada, S., Aijaz, M., and Imran Bhat, M. (2020). On the divisor graphs of the Rings Zn. Afr. Mat. 31, 31 727–737. doi:10.1007/s13370-019-00755-3
Selvakumar, K., Gangaeswari, P., and Arunkumar, G. (2022). The Wiener index of the zero-divisor graph of a finite commutative ring with unity. Discrete. Appl. Math., 311, 72–84. doi:10.1016/j.dam.2022.01.012
Singh, Pradeep, and Bhat, Vijay Kumar (2020). Zero-divisor graphs of finite commutative rings: A survey. Surv. Math. Appl., 15 371–397.
Keywords: wiener index, zero-divisor graphs, compressed zero-divisor graph, residue class rings, equivalence classification
Citation: Wei Y and Luo R (2022) The wiener index of the zero-divisor graph for a new class of residue class rings. Front. Chem. 10:985001. doi: 10.3389/fchem.2022.985001
Received: 03 July 2022; Accepted: 04 August 2022;
Published: 13 September 2022.
Edited by:
Xiyun Zhang, Jinan University, ChinaReviewed by:
Hongjie Bi, Okinawa Institute of Science and Technology Graduate University, JapanWei Wang, Chongqing Medical University, China
Copyright © 2022 Wei and Luo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ricai Luo, aGN4eWxvckAxMjYuY29t
 Yinhu Wei
Yinhu Wei Ricai Luo
Ricai Luo