Evaluating the performance of ReaxFF potentials for sp2 carbon systems (graphene, carbon nanotubes, fullerenes) and a new ReaxFF potential

We study the performance of eleven reactive force fields (ReaxFF), which can be used to study sp² carbon systems. Among them a new hybrid ReaxFF is proposed combining two others and introducing two different types of C atoms. The advantages of that potential are discussed. We analyze the behavior of ReaxFFs with respect to 1) the structural and mechanical properties of graphene, its response to strain and phonon dispersion relation; 2) the energetics of (n, 0) and (n, n) carbon nanotubes (CNTs), their mechanical properties and response to strain up to fracture; 3) the energetics of the icosahedral C₆₀ fullerene and the 40 C₄₀ fullerene isomers. Seven of them provide not very realistic predictions for graphene, which made us focusing on the remaining, which provide reasonable results for 1) the structure, energy and phonon band structure of graphene, 2) the energetics of CNTs versus their diameter and 3) the energy of C₆₀ and the trend of the energy of the C₄₀ fullerene isomers versus their pentagon adjacencies, in accordance with density functional theory (DFT) calculations and/or experimental data. Moreover, the predicted fracture strain, ultimate tensile strength and strain values of CNTs are inside the range of experimental values, although overestimated with respect to DFT. However, they underestimate the Young’s modulus, overestimate the Poisson’s ratio of both graphene and CNTs and they display anomalous behavior of the stress - strain and Poisson’s ratio - strain curves, whose origin needs further investigation.

1 Introduction

The isolation of graphene, 2 decades ago (Novoselov et al. (2004)) provided a new material with extremely interesting and unique properties, both from the scientific and the technological point of view. Graphene is not only the first two-dimensional (2D) material, but it also has unique properties including (among others) the linear bands at the Fermi level (Castro Neto et al. (2009)), the large Young’s modulus (Fthenakis and Lathiotakis (2015)) and thermal conductivity (Berber et al. (2000); Fthenakis and Tománek (2012); Fthenakis et al. (2014)). Moreover, some of those properties are shared with several three-fold coordinated carbon structures, which can be considered as graphene derivatives, e.g. carbon nanotubes (Iijima (1991)), fullerenes (Kroto et al. (1985)), haeckelites (pentaheptites (Terrones et al. (2000); Fthenakis and Lathiotakis (2015); Crespi et al. (1996)), tetraoctites (Liu et al. (2012); Sheng et al. (2012); Fthenakis and Lathiotakis (2015)), or even three-dimensional structures (Côté et al. (1998); Liu and Cohen (1992); Fthenakis (2016)), foams (Zhu et al. (2014); Inagaki et al. (2015); Liu et al. (2020); Bellucci and Tozzini (2020)), honeycombs (Fthenakis (2017); Krainyukova and Zubarev (2016)), which also attracted a lot of interest.

Several theoretical and computational studies have been devoted to those systems (Bellucci and Tozzini (2020); Berber et al. (2000); Castro Neto et al. (2009); Côté et al. (1998); Crespi et al. (1996); Fthenakis (2016, 2017); Fthenakis and Lathiotakis (2015); Fthenakis and Tománek (2012); Fthenakis et al. (2014); Liu and Cohen (1992); Liu et al. (2012); Terrones et al. (2000); Zhu et al. (2014)). Depending on the size, more or less accurate methods are appropriate. For relatively small systems (up to hundreds of atoms¹), the more accurate, but more computationally demanding ab initio methods, can be used. For larger systems, however, these become practically unfeasible to be performed and therefore less time consuming methods should be used. Semi-empirical methods using parameterized approximations for the superposition integrals (Elstner et al. (1998); Lathiotakis et al. (1996); Fthenakis et al. (2003); Hoffmann (1963)) can apply up to thousands of atoms. For even larger systems, one must abandon the explicit quantum description of electronic structure and adopt classical potentials, also called “Force Fields” (FF), implicitly including the effect of electrons. These potentials are usually analytic expressions of the energy of the system as a function of the internal coordinates, with parameters fitted onto ab initio calculations or based on experimental data of different origin (Schuler et al. (2001); Weiner et al. (1984, 1986)). Since the parameterization is typically optimized based on a given set of configurations and/or in given chemical-physical conditions, its interpolation or extrapolation in different situations implies possible inaccuracies raising the well-known problem of the FF transferability.

Historically, the first attempt to develop a classical potential for carbon lead to the Tersoff potential (Tersoff (1988)). Its analytical form (Abell (1985)) describes the dependence of the interaction on the bond order (BO), allowing the treatment of different carbon allotropes (Berber et al. (2000); Fthenakis and Tománek (2012); Fthenakis et al. (2014); Zhao et al. (2019); Ng et al. (2013)). Similar potentials were subsequently proposed, by Chelikowsky (Chelikowsky (1992)), Khor–Das Sharma (Khor and Das Sarma (1988)) and Takai et al (Takai et al. (1990)). Moreover, different parameterizations of the original Tersoff potential were developed attempting to provide a more accurate description of phonon dispersion relation (Lindsay and Broido (2010)) and mechanical properties (Rajasekaran et al. (2016)) in graphene and diamond (Shi et al. (2021)). Subsequently, an new version of the Tersoff potential was suggested by Brenner (Brenner (1990)) to extend the FF to hydrocarbons, improve the description of conjugation and sp² and sp³ bonds.

The potentials described so far, may be considered as the first generation of BO potentials (BOPs). The second generation includes the so called “Reactive Empirical Bond Order” (REBO) potentials REBO-I (Brenner et al. (2002)) and REBO-II (Pastewka et al. (2008)). In these, the BO is described in terms of σ − π and π contributions, allowing the description of covalent intramolecular bonding, breaking and formation, and including dihedral angle torsional interactions. Several such potentials have been developed to represent elements beside carbon, e.g. S and H (Beardmore and Smith (1996); Dyson and Smith (1996)), or O and H (Ni et al. (2004); Fonseca et al. (2011)) or F and H (Jang and Sinnott (2004)). One issue of these potentials is the poor representation of the van der Waals (vdW) forces, preventing the description of inter-molecular interactions. The so called “Long range Carbon Bond Order Potentials” (LCBOPs) were therefore developed, available in two subsequently improved versions LCBOP-I (Los and Fasolino (2003)) and LCBOP-II (Los et al. (2005)). With the same aim, the so called “Adaptive Intermolecular Reactive Empirical Bond Order (AIREBO)” potentials (Stuart et al. (2000)) and AIREBO(-M) (O’Connor et al. (2015)) were developed.

A different approach is adopted in the class of molecular mechanics FFs (MM-FFs), characterized by a distinction between bonded and non bonded terms of the interactions, implying that the chemical connectivity, or topology, must be given as an input in the model. As a consequence, the energy can be written as a sum of energy contributions from bond stretching, bond angle bending, proper and improper dihedral angle torsion terms, i.e., the chemical or bonding terms assigned based on the given topology, plus terms describing van der Waals interactions and electrostatics. With respect to BOPs and reactive FFs, these are much simpler concerning the analytical forms and implementation, more numerically robust and, up to two orders of magnitude computationally cheaper. On the other hand, they are a step lower in the scale of transferability, requiring different sets of parameters optimized for different cases. For this reason, many different such FF have been developed. A non exhaustive list includes: MM2 (Allinger (1977)), MM3 (Allinger et al. (1989)) and MM4 (Allinger et al. (1996)) for hydrocarbons, the universal FFs UFF (Rappe et al. (1992)) and COMPASS (Sun (1998)), and those specialized for bio-molecules, such as Amber (Weiner et al. (1984; 1986)), CHARMM (Brooks et al. (1983); Nilsson and Karplus (1986)), DREIDING (Mayo et al. (1990)), GROMOS (Schuler et al. (2001)). A potential of that category has been also developed by Fthenakis et al. (Fthenakis et al. (2017); Chatzidakis et al. (2018); Kalosakas et al. (2013, 2021)) for the description of three-fold coordinated carbon systems. The main drawback of these FFs is their inability to describe chemical reactions.

Aiming to fix this problem, the group of Van Duin provided new ideas resulting in the ReaxFF potentials (van Duin et al. (2001)), which can be considered as an evolution of the BOPs and are now the state-of-the-art potentials to reproduce reactivity. Indeed, their (large number of) parameters are fitted to a large training set of atomic arrangements in the configuration space provided by ab initio simulations, which include also reactive chemical conditions. To the best of our knowledge, the FFs belonging to the ReaxFF class developed for C and other elements are:

1) RDX (Strachan et al. (2003)), originally developed to study the chemistry of nitramine explosions

2) CHO-2008 (Chenoweth et al. (2008)), for the combustion of hydrocarbons

3) Budzien potential (Budzien et al. (2009)), including interactions between C, N, O and H

4) Mattsson potential (Mattsson et al. (2010)), including interactions between C, O and H

5) CHON-2010 (Kamat et al. (2010)), developed to study the formation of soot particles and their interactions with several substances including noble gases

6) The low gradient (lg) potential (Liu et al. (2011)), an extension of the RDX potential including London dispersion terms

7) The charge-implicit ci-CH (Kański et al. (2018)) potential for hydrocarbons improved in terms of computational cost

8) C-2013 (Srinivasan et al. (2015)) for carbon condensed phases

9) CHO-2016 (Ashraf and van Duin (2017))–CHON-2019 (Kowalik et al. (2019)), subsequent improvements of CHO-2008 including C parameters from C-2013 and parameters for N, for simulations of (bio) polymers

Although (on general grounds) ReaxFFs are more accurate than BOPs and more general than MM-FFs, the earlier ReaxFF potentials still suffered from transferability problems, being trained on specific systems and under specific conditions. The subsequent evolution brings improvements in this respect: C-2013 was developed to replace CHO-2008 for the study of carbon condensed phases (Jensen et al. (2015); Srinivasan et al. (2015)), while CHO-2016 was aimed at improving the performances on small hydrocarbons (Ashraf and van Duin (2017)).

Here, we test the performance of the above mentioned ReaxFFs, i.e. potentials (1)-(9) and GR-RDX-2021, on graphene and other sp² carbon systems (nanotubes and fullerenes) as a first step for the evaluation of their adequacy to be used in the study of interactions between these systems and other molecules, which is the focus of a forthcoming paper. In detail, we study: 1) the structural, energetic and mechanical properties of graphene, its response to strain and phonon dispersion, 2) the structural, energetic and mechanical properties of (n, 0) and (n, n) carbon nanotubes (CNTs), and their response to strain up to the fracture limit and 3) the structural and energetic properties of the 40 C₄₀ fullerene isomers and the icosahedral C₆₀, examining the predictions of the considered potentials with respect to the pentagon adjacency penalty rule. Seven of those potentials predict a Poisson’s ratio value near to unit. Such an unphysical value affect significantly the mechanical or thermal deformations of graphene. We therefore focus on the remaining potentials, namely, C-2013, CHO-2016/CHON-2109 and we propose a new one, called GR-RDX-2021, which is a combination of the C-2013 and RDX potentials with improved accuracy obtained by a limited reintroduction of the concept of atom type.

2 Methods

2.1 Model systems and general setup

Simulations and calculations were performed with the software LAMMPS (Thompson et al. (2022)). Periodic boundary conditions were applied using the natural periodicity in xy direction for graphene, and z for nanotubes. In the other directions and for fullerenes, we left gaps of free space of at least 100 Å, to avoid interactions between periodic images. Specifically:

• graphene: we used rectangular supercell built by the 12 × 21 repetition of the rectangular 4-atom unit cell along the xy-plane (see Figure 1A, the supercell includes 1,008 atoms).

• CNTs: we considered single wall CNTs with (n, 0) and (n, n) chiralities (n = 1–100 for (n, 0) CNTs and n = 1–20 for (n, n)), at different values of the strain along the axis. The supercells were built by repeating 10 4n-atom unit cells.

• Fullerenes: we focused on the icosahedral C₆₀ and the 40 C₄₀ isomers, corresponding to all possible arrangements of pentagonal and hexagonal rings (Fowler and Manolopoulos (1995)).

FIGURE 1

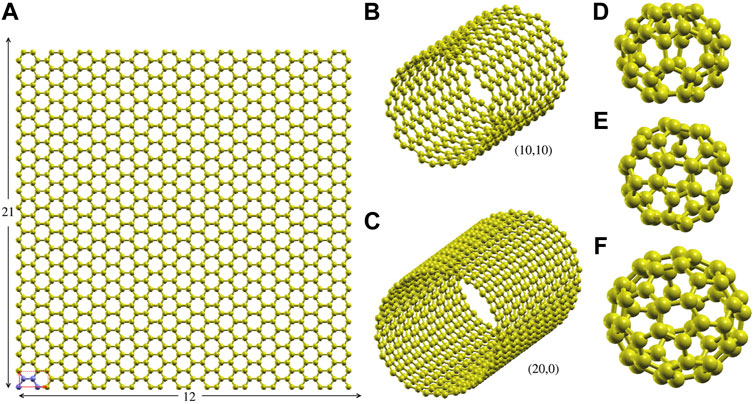
FIGURE 1. Supercells and representative structures. (A) The 1,008 atom 12 × 21 graphene rectangular supercell (size $\approx 51.12$ Å × 51.65 Å). The 4-atom rectangular unit cell is shown in the left down corner of the structure (red rectangle). (B) and (C) The supercell of the (10.10) and (20.0) carbon nanotubes, as representatives of the (n, n) and (n, 0) nanotubes. (D), (E) The no. 38 and 39 C₄₀ fullerene isomers, as representatives of the 40 C₄₀ fullerene isomers. (F) The icosahedral C₆₀ fullerene.

To calculate the response to strain, structure relaxations are performed at fixed strain using a grid of equidistant strain values along x and y directions for graphene (arm chair and zig-zag) and along z for CNTs. The convergence criteria were set at 10^–6 kcal/(mole Å) ($\approx 4\times 10^{-8}$ eV/Å) for the forces on atoms and 10^–4 kcal/mol (or 4 × 10^–9 eV/atom) for the global energy variation. The Young’s modulus E and the Poisson’s ratio ν are calculated using the dependence of energy on strain and correlation between strain components. Phonon dispersion relations in graphene are calculated evaluating the forces for given structural distortions (“frozen phonon” method), as described in the corresponding sections, where additional details of the calculations are reported.

2.2 A new hybrid ReaxFF

As it will be shown in the next sections, most of the ReaxFF potentials predict an unrealistic value of ν. The solution to this problem might follow the strategy of the generalization of ReaxFFs by training on extended systems, as for the recently developed CHON-2019 potential (Kowalik et al. (2019)), which requires, however, a dedicated effort. In this work, we obtain similar performances in terms of both mechanical properties and reactivity towards organic molecules with a simpler approach based on the combination of previous ReaxFF potentials without reparameterizing them. Specifically we combined C-2013 (Srinivasan et al. (2015)), for the interactions between three-fold coordinated carbons in graphene, with RDX (Strachan et al. (2003)), for all other interactions, within a hybrid new potential that we call GR-RDX-2021. This will incorporate the good mechanical properties of C-2013, developed for extended sp² systems, and of RDX developed to describe interactions between C, H, N and O.

To follow this idea, 2 C atoms types are defined: those belonging to graphene (or other three-fold coordinated carbon systems) and all others. Denoting the former as “C_g” and the latter as “C”, one has three kinds of carbon-carbon interactions, namely C_g-C_g, C_g-C and C-C, and three kinds of interaction with other elements (E), namely C_g-E, C-E and E-E. In GR-RDX-2021, C_g-C_g are described by C-2013, and C-C, C-E, E-E by RDX. C_g-C and C-C interactions are equivalent, as well as, C_g-E and C-E.

ReaxFF potentials have two groups of parameters. The first includes some general ones, e.g. those related to the description of the switch function, same for all interactions. The second group contains those describing the element dependent 2-, 3- and 4-body interactions. As C-2013 and RDX have different parameters of the first group, we chose those from the RDX for the hybrid potential. This means that for interactions of C, H, O, N, and of them with C_g, it behaves as in RDX, while for the C_g-C_g behaves as a modified C-2013. The general performance of the new potential specifically regarding C_g-C and C_g-E interactions must also be tested, which is the matter of a forthcoming paper. It is worth noting that GR-RDX-2021 is intrinsically capable of representing the sp²-sp³ and sp³ interactions, inherited by C-2013 and can therefore be used to represent carbon foams, nanoporous carbon or diamond-like systems.

The definition of multiple atom types for carbon brings a disadvantage: if C_g and C atoms interchange their position, the description might be less accurate. However, because C_g-C and C-C interactions are the same, the description is still correct when a C_g atom takes the place of a C atom. Of course the GR-RDX-2021 potential, carries inaccuracies inherent to both RDX and C-2013, as well as possible ones due to the modifications in C-2013 general parameters. The file with the parameters of GR-RDX-2021 in LAMMPS format is included as the Supplementary Information to this work.

3 Results

3.1 Graphene

3.1.1 Structural properties and energetics

Here we present our results for the cohesive energy U_coh and the structural properties of relaxed graphene structures, obtained with the potentials (1)-(9) and GR-RDX-2021. We started optimizations both by exactly flat and rippled structures, to avoid introducing biases and optimizing both the structure and the supercell size. We found flat exact hexagonal symmetries for the stable state in all cases, though with different bond lengths, a₀, reported in Table 1 in descending order, together with the cohesive energies U_coh. In the same table, we also report experimental and ab initio values for comparison. The potentials can be classified in two groups: the first includes the Mattsson, ci-CH, RDX, lg, Budzien, CHO-2008 and CHON-2010 potentials, and has a₀ in the range [1.48.1.44] Å and U_coh in the range [-8.9,-8.4] eV; the second includes the GR-RDX-2021, C-2013, CHO-2016 and CHON-2019 potentials, and a₀ in the range [1.420.1.422] Å and U_coh in the range [-7.43,-7.40] eV. The values of a₀ for CHO-2008 and C-2013 potentials are in agreement with those found by Lebedeva et al (Lebedeva et al. (2019)). The results of U_coh versus a₀ are also presented in Figure 2B, where the distinction between the two groups is evident. While the second group reasonably reproduces the experimental values, the first one overestimates a₀ by 1.4–4.2% and U_coh (in absolute value) by 13.5–20.3%. The bond length overestimation in first group is not that large, but if the supercell size is forced to a value corresponding to the experimental length of 1.42 Å, the structure turns to a rippled one, as shown in Figure 2A obtained with CHON-2010. These results, for contracted graphene are in accordance with other DFT results, where similar ripples appear in laterally compressed graphene sheets (Tozzini and Pellegrini (2011); Rossi et al. (2015)).

TABLE 1

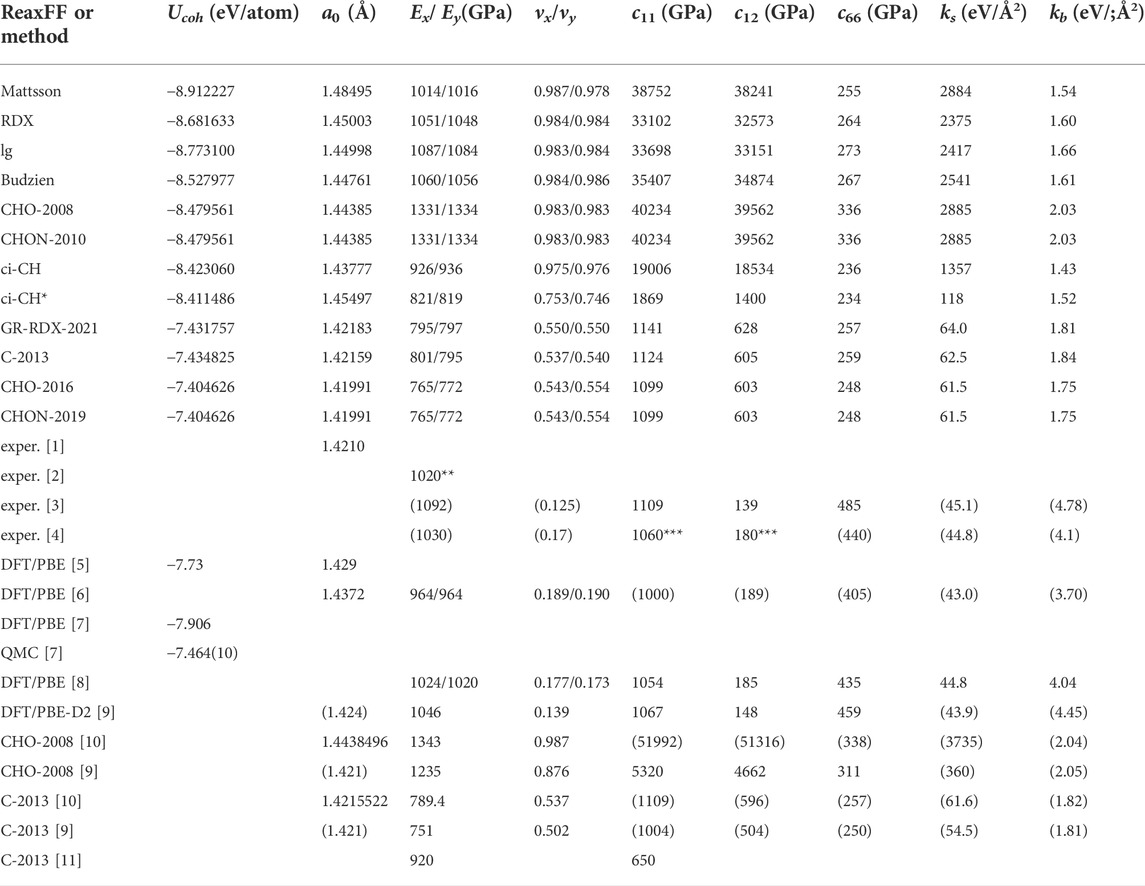
TABLE 1. Predictions of the ReaxFF potentials considered in the present study for the structural, energetic and mechanical properties of graphene. 1) Cohesive energy U_coh and 2) bond length a₀ of the optimum energetically graphene structure, 3) Young’s modulus E_x = σ_xx/ɛ_xx and 4) Poisson’s ratio ν_x = −ɛ_yy/ɛ_xx for uniaxial strain ɛ_xx along x-direction, 5) Young’s modulus E_yy = σ_yy/ɛ_yy and 6) Poisson’s ratio ν_y = −ɛ_xx/ɛ_yy for uniaxial strain ɛ_yy along y-direction, 6) spring constant k_s for bond stretching and 7) k_b for bond angle bending 8) - 10) the elastic constants c₁₁ = c₂₂, c₁₂ = λ* and c₆₆ = G = μ (G is the shear modulus, and λ and μ the first and second Lamé’s coefficients, respectively). Directions x and y correspond to the arm chair and zig-zag directions, respectively. Ab initio and experimental values are included for comparison. The k_s, k_b, c₁₁, c₁₂ and c₆₆ values in parenthesis, have been calculated by us, based on the average of the provided E and ν values. [1]: (Lynch and Drickamer (1966)), [2]: (Lee et al. (2008)), [3]: graphite (Bosak et al. (2007)), [4]: graphite (Blakslee et al. (1970)), [5]: AIMPRO (Ivanovskaya et al. (2010)), [6]: Siesta (Fthenakis and Menon (2019)), [7]: Quantum Espresso and QM-CPACK (Shin et al. (2014)), [8]: Quantum Espresso (Fthenakis and Lathiotakis (2015; 2017)), [9]: (Jensen et al. (2015)) [10]: (Lebedeva et al. (2019)) [11]: (Qian et al. (2021)), * 2nd minimum, ** ±150, *** ±20.

FIGURE 2

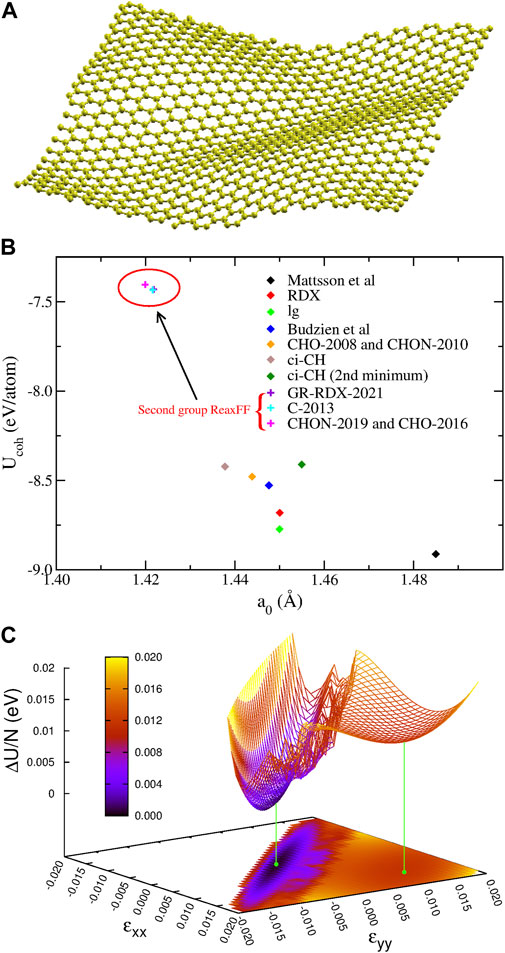
FIGURE 2. Optimizations for graphene: (A) The optimized 1,008 atom 12 × 21 rectangular graphene supercell for a₀ = 1.42 Å using the CHON-2010 potential. (B) Cohesive energy U_coh as a function of bond length a₀ for graphene for the different ReaxFF. (C) The potential energy surface U(ɛ_xx, ɛ_yy) of graphene derived from ci-CH potential. The two minima are shown with the green points and lines.

Additionally, ci-CH potential was found to have two minima differing by 0.0116 eV/atom, whose structure differs only by the bond length (of 1.2%), the shorter one being more stable. In order to better understand the origin of this splitting, we calculated the potential energy surface (PES) as a function of the strains ɛ_xx, ɛ_yy along the x and y directions, respectively, shown in Figure 2C. The saddle point connecting the two minima appears at ɛ_xx = ɛ_yy = 0.006, and lies 0.0134 eV/atom above the absolute minimum and 0.0018 eV/atom above the secondary one, which is very shallow. Moreover, the transition region between the minima appears rather noisy, possibly due to reasons described below, in Section 3.1.3).

3.1.2 Mechanical properties

We calculate the Young’s modulus E, and the Poisson’s ratio ν for uniaxial strain along x and y directions and, based on them, the elastic constants c₁₁, c₁₂ and c₆₆. Figure 3A shows the strain energy per atom ΔU/N of the fully optimized uniaxially strained graphene for low strain values (−0.005 ≤ ɛ ≤ 0.01). Here ΔU = U(ɛ) − U₀, with U₀ the energy at zero strain. Figure 3B shows the corresponding transverse relaxed strain ɛ_⊥ vs. the longitudinal imposed one. For small strain values, the energy and the transverse strain has a quadratic and a linear dependence on strain, respectively, as shown in Figures 3A,B. We may then write

$U\left({\epsilon }_{xx}\right)={\kappa }_x{\epsilon }_{xx}^2+U_0(1)$

${\epsilon }_{\perp }={\epsilon }_{yy}=-{\nu }_x{\epsilon }_{xx}(2)$

where ν_x is the Poisson’s ratio for strain along x direction. It is easy to show that

$E_x={\sigma }_{xx}/{\epsilon }_{xx}=2{\kappa }_x/V,V=L_x{L}_y{d}_0,(3)$

with E_x being the Young’s modulus for strain along x and V the volume evaluated using the xy supercell size and the sheet thickness d₀ = 3.34 Å, corresponding to the graphite interlayer separation distance (Fthenakis and Lathiotakis (2015)). The corresponding equations along y direction are obtained by interchanging x with y, i.e., $U({\epsilon }_{yy})={\kappa }_y{\epsilon }_{yy}^2+U_0$, ɛ_⊥ = ɛ_xx = −ν_yɛ_yy, and E_y = σ_yy/ɛ_yy = 2κ_y/V. The values of κ_x and κ_y (and of E_x and E_y) can be found with a quadratic fit of the (ɛ, ΔU/N) points of Figure 3A, while ν_x and ν_y with a linear fit to (ɛ, ɛ_⊥) of Figure 3B. The E_x, E_y, ν_x and ν_y values found here for the ReaxFF potentials are reported in Table 1, and compared with the DFT theoretical predictions and experimental values, as well as, with the results found by Qian et al (Qian et al. (2021)) for C-2013 potential, and by Jensen et al (Jensen et al. (2015)) and Lebedeva et al (Lebedeva et al. (2019)) for both C-2013 and CHO-2008 potentials.

FIGURE 3

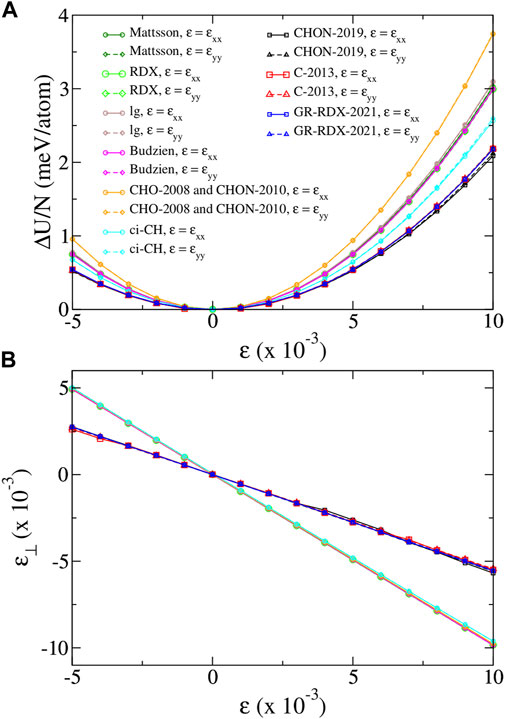
FIGURE 3. (A) Strain energy per atom ΔU/N and (B) transverse strain ɛ_⊥, versus strain ɛ, for uniaxial strain along x and y directions, for the ReaxFF potentials of the present study. For strain along x (arm chair) direction, ɛ = ɛ_xx, ɛ_⊥ = ɛ_yy and σ_yy = 0. For strain along y (zig-zag) direction, ɛ = ɛ_yy, ɛ_⊥ = ɛ_xx and σ_xx = 0. Legends of panel (A) apply in both panels.

We first observe that Figure 3 shows basically no anisotropy: all curves depending on ɛ_xx superimpose to the corresponding for ɛ_yy, leading to (almost) identical values of the corresponding elastic moduli. Figure 3B also clearly shows that all data collapse on two lines only, corresponding to potentials of the two groups previously defined according to the cohesive energy predictions. The first group returns an unrealistically high ν ∼ 0.983–0.987, while the second returns values 0.537–0.554 nearer to the DFT one, although still substantially overestimated. In turn, the curves of panel 1) for the potentials of the first group are very similar, yielding E ∼926–1,087 GPa, while for the potentials of the second group they collapse to the same curve yielding E ∼ 765–801 GPa. The results we find for the CHO-2008 potential, are very similar with those found by Lebedeva et at (Lebedeva et al. (2019)), although not very similar with those found by Jensen et al (Jensen et al. (2015)). Moreover, the results we find for the C-2013 potential are very similar with those found by both Lebedeva et al (Lebedeva et al. (2019)) and Jensen et al (Jensen et al. (2015)), though slightly different from those of Qian et al (Qian et al. (2021)). Therefore, on average, E values from first group matches better experimental and DFT data than that by the second, which yields a value lower by at least 25%. This could have been considered as a success of the first-group potentials, if their ν values were not so large, meaning that deformations would be practically achieved only through bond angle bending, with negligible bond stretching.

Table 1 also reports the elastic constants, related to ν and E (see Ref. Chou and Pagano (1992))

$c_{11}=c_{22}=\frac{E}{1-{\nu }^2},(4)$

$c_{12}={\lambda }^{\ast }=\frac{E\nu }{1-{\nu }^2},(5)$

$c_{66}=G=\mu =\frac{E}{2\left(1+\nu \right)},(6)$

with these equations being valid for isotropic 2D materials. G is the shear modulus, coinciding with the second Lamé’s coefficient μ, and λ* is the first Lamé’s coefficients for 2D isotropic materials (differing by its three-dimensional version which is λ = νE/[(1 + ν) (1 − 2ν)]). The elastic constants c₁₁ and c₁₂ predicted by the potentials of the first group are extremely high due to the 1 − ν² in the denominator of Eqs. 4, 5. For the second group the c₁₁ values are very close to those derived from DFT, but the c₁₂ are approximately 3–4 times larger. As for the shear modulus G (or the c₆₆ elastic constant), the first and second group predict more or less the same value, approximately half the value derived by DFT.

To understand the origin of the discrepancies between the ReaxFF potentials and the experimental and DFT results, we evaluate the bond stretching and bending spring constants k_s and k_b of an equivalent stick and spiral model in terms of E and ν. Within this model (Fthenakis and Lathiotakis (2017)) the deformation energy ΔU of graphene is

$\mathrm{\Delta }U=\frac{1}{2}\sum _i\left(k_s\delta l_i^2+\frac{1}{2}\sum _j{k}_b{a}_0^2\delta {\varphi }_{ij}^2\right),(7)$

where δl_i = l_i − a₀ is ith bond elongation, δϕ_ij = ϕ_ij − ϕ₀ is the deformation of the angle between bonds i and j with respect to the sp² angle ϕ₀ = 120^o. Using Eq. 7, one gets

$E=\frac{8\sqrt{3}}{d_0}\frac{k_s{k}_b}{k_s+18k_b}\mathrm{a}\mathrm{n}\mathrm{d}\nu =\frac{k_s-6k_b}{k_s+18k_b}(8)$

or equivalently

$k_s=\sqrt{3}{d}_0\frac{E}{1-\nu }\mathrm{a}\mathrm{n}\mathrm{d}{k}_b=\frac{d_0}{2\sqrt{3}}\frac{E}{3\nu +1}.(9)$

Fitting DFT data (Fthenakis and Lathiotakis (2017)) to this model leads to the values k_s ≈ 45 eV/Ų and k_b ≈ 4 eV/Ų, in consistency with E = 1,012 GPa and ν = 0.1744 also obtained by DFT (Fthenakis and Lathiotakis (2015)). Using the E and ν values for each potential we derived k_s and k_b, shown in the last columns of Table 1. As previously, the spring constants are different for the two potential groups. For the first group, k_s is 1,357–2885 eV/Ų and k_b 1.43–2.03 eV/Ų, i.e. the bond stretching is 30–64 times stronger than that provided by DFT, while the bond-angle bending is weaker by a factor $\approx 1/3-1/2$. The extremely high k_s values are due to near unit value of ν in the potentials of the first group. For the second group, k_s ≈ 61.5–64 eV/Ų and k_b ≈ 1.75–1.84 eV/Ų, i.e., only $\approx 4/3$ stronger and $\approx 2/5$ weaker than the corresponding DFT values, respectively. As a consequence, the energy penalty e.g. for ɛ = 0.01 stretching in the first group, is ΔU = 260 meV, while the same amount of energy is sufficient to generate an angular distortion as large as δϕ = 23^o, or a stretching of up to 7% with the potentials of the second group or DFT. Conversely, for the second group, the amount of energy needed for a stretching of 1% is only 4.5–6.3 meV. As a summary of the above discussion, and to highlight the importance of the correct reproduction of the Poisson ratio, we observe that from Eq. 9 one gets

$\frac{k_s}{k_b}=6\frac{3\nu +1}{1-\nu },(10)$

which clearly shows the divergence of the k_s/k_b ratio as ν → 1. In conclusion, the potentials of the first group might provide unreliable results for graphene. Therefore, in the following we will focus only on those of the second group.

3.1.3 Response to strain

Figure 4 shows the energy per atom (U/N), stress (σ) and Poisson’s ratio (ν) vs. ɛ of the potentials of the second group, for uniaxial strain along zig-zag and arm chair directions in the range [0, 0.22]. The results by C-2013 and GR-RDX-2021 are similar, and not very different from those by CHON-2019. The behavior is isotropic at low strain values, while anisotropy appears at ɛ⪆0.10. The break of isotropy and harmonicity occurs even earlier, at ɛ = 0.07 in panel (a), while DFT calculations (Fthenakis and Menon (2019); Fthenakis and Lathiotakis (2015)) show a similar behavior at ɛ⪆0.15. ReaxFF agrees with DFT in predicting a smaller stiffness at large stress along the zig-zag with respect to the armchair direction.

FIGURE 4

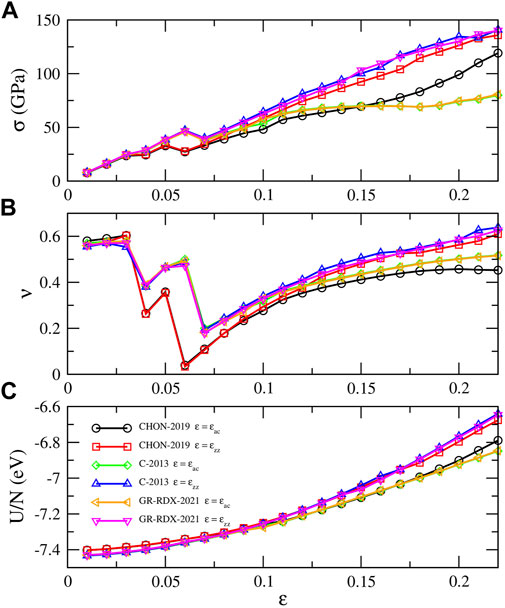
FIGURE 4. Response of graphene to uniaxial strain along arm chair and zig-zag directions. (A) Stress σ, (B) Poisson’s ratio ν and (C) energy per atom U/N along the strain direction. The legends of panel (C) applies in all panels.

Additionally, the stress in Figure 4A shows a net drop occurring at ɛ ≈ 0.05–0.06 for the different potentials, also observed in the studies by Jensen et al (Jensen et al. (2015)) and by Qian et al (Qian et al. (2021)). These “drops” are accompanied by strain “jumps” in the lateral direction, which results in corresponding “jumps” in the Poisson’s ratio (panel B). Similar results for the Poison’s ratio were obtained by Lebedeva et al (Lebedeva et al. (2019)) using the C-2013 ReaxFF. While up to ɛ ≈ 0.03 the sheet normally “shrinks” in the lateral strain direction at ɛ ≈ 0.04 it displays an expansion and a subsequent shrinking, but with different coefficients dependent on the potentials. These drops repeat a couple of time before ν assumes a monotonically increasing though non linear behavior. These alternating jumps in ν are not observed in DFT studies (Fthenakis and Menon (2019); Fthenakis and Lathiotakis (2015)), where a smoothly decreasing behavior is observed.

To get further insight in this anomalous behavior of ν, we performed a finer sampling of the energy and stress values in the ɛ_xx- ɛ_yy plane, using CHON-2019, reported as a function of ɛ_yy at given values of ɛ_xx in Figure 5, left side panels. The right side panels reports a zoom into the anomalous region. The thick red solid line crossing the curves in each panel connects the equilibrium points at given constant ɛ_xx. The anomalous behavior is visible in (panels B) and (C) of Figure 5 as a narrow shaded strip where the curves change slope. In (panels C) the strip connects approximately the points (ɛ_yy, σ_xx) ≈ (-0.10, 50 GPa)–(0, 25 GPa), in (panels C) the points (ɛ_yy, σ_yy) ≈ (-0.10, -40 GPa)–(0, 5 GPa). Below the strip, the system behaves elastically, with almost linear dependence of σ on ɛ. Above the strip, the behavior appears again almost linear, but with a different slope suddenly changing in the strip area. For instance, the stress curve for ɛ_xx = 0.09 change its slope at ɛ_yy ≈ − 0.03 and ɛ_yy ≈ − 0.08. The corresponding transition area in the energy plots (panels A) has clearly a curve shape less easily identifiable, which can be estimated from the σ − ɛ plots. In panel (AI) it is shown as the shaded area between the thick blue lines.

FIGURE 5

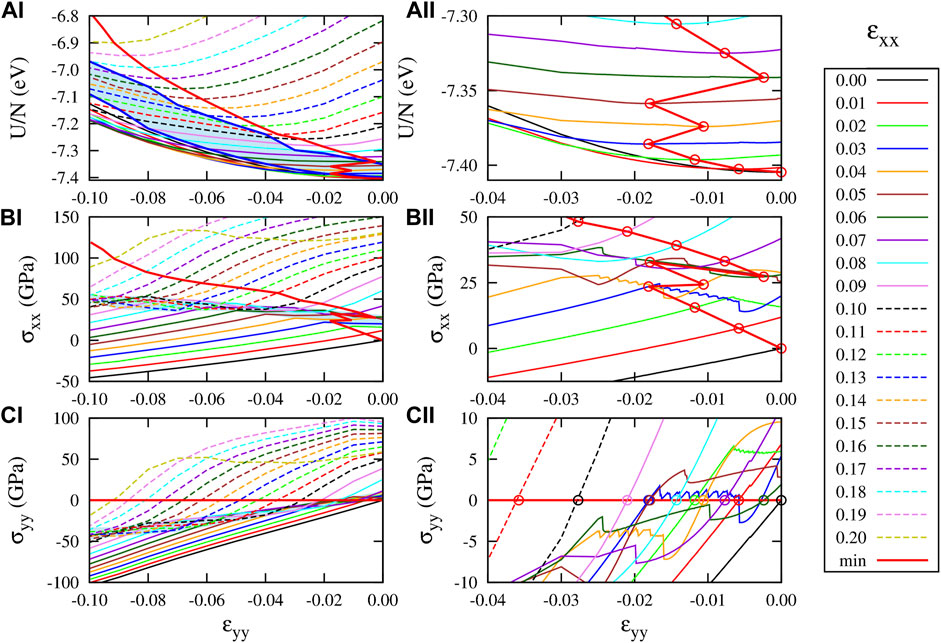
FIGURE 5. Response of graphene to strain ɛ_xx and ɛ_yy according to the CHON-2019 potential. (AI) And (AII) U(ɛ_xx, ɛ_yy)/N (BI) and (BII) σ_xx(ɛ_xx, ɛ_yy), and (CI) and (CII) σ_yy(ɛ_xx, ɛ_yy). The right panels ((AII) (BII) and (CII)), present the same results with those presented in the left panels ((AI) (BI) and (CI)) but in different scale range (−0.04 ≤ ɛ_yy ≤ 0) to provide details for the “jumps” of the optimum strained graphene structure at low strain ɛ_xx values. The curves presented in those plots correspond to constant strain ɛ_xx, for the ɛ_xx values shown in the legends. The ɛ_yy increment in these plots is 10^–4.

Inside the border strips, the system displays on average an opposite dependence of strain on stress, which can be roughly estimated as the slope of the strip itself, namely $\approx -250$ GPa for σ_xx and $\approx 450$ GPa for σ_yy. The negative and positive slopes along x and y directions, respectively, show the tendency of the PES inside that area to form a saddle point. In general, therefore, moving along the red lines in (panels B) and (C), one crosses the different ɛ_xx lines and can rebuilt plots of Figure 4. Thus, for 0 ≥ɛ_xx ≥ 0.03, the energy minimum falls in the region below that strip, exhibiting a linear-like behavior between stress and strain with a specific slope, as shown in Figure 4A, which is also depicted as a linear relation of ν versus strain in Figure 4B for that strain range. For 0.03 < ɛ_xx < 0.07, however, it falls inside that strip area and the slope of σ_xx versus ɛ_xx changes having an irregular (not linear) behavior, which is also depicted in the stress–strain plot of Figure 4A for that strain range. Thus, graphene in the lateral strain direction either enlarges or shrinks also irregularly, causing the irregular behavior of ν, which can be seen in Figure 4B for that strain range. For ɛ_xx ≥ 0.07 the energy minimum falls in the region above that strip, exhibiting again an almost linear behavior, as shown by the thick red line of Figure 5B and Figure 4A.

Beyond that anomalous behavior of graphene PES, panels (BII) and (CII) of Figure 5 also show some discontinuities in the stress–strain curves. These discontinuities are more pronounced in the stress–strain curves between σ_xx and σ_yy versus ɛ_xx for constant ɛ_yy values, as shown in Figures 6A,B, where different color curves correspond to different ɛ_yy values, as shown with the corresponding colored legends in panel (B). These stress discontinuities are caused as an effect of the discontinuity of the first derivative of the energy with respect to ɛ_xx, as Figure 6D shows for ɛ_yy = 0.13. In particular, for ɛ_yy = 0.13 (and strain values close to that), two minima of the energy curve as a function of strain appear, since σ_xx becomes zero twice (before and after the discontinuity), as Figure 6A shows. These minima can be also seen in Figure 6D.

FIGURE 6

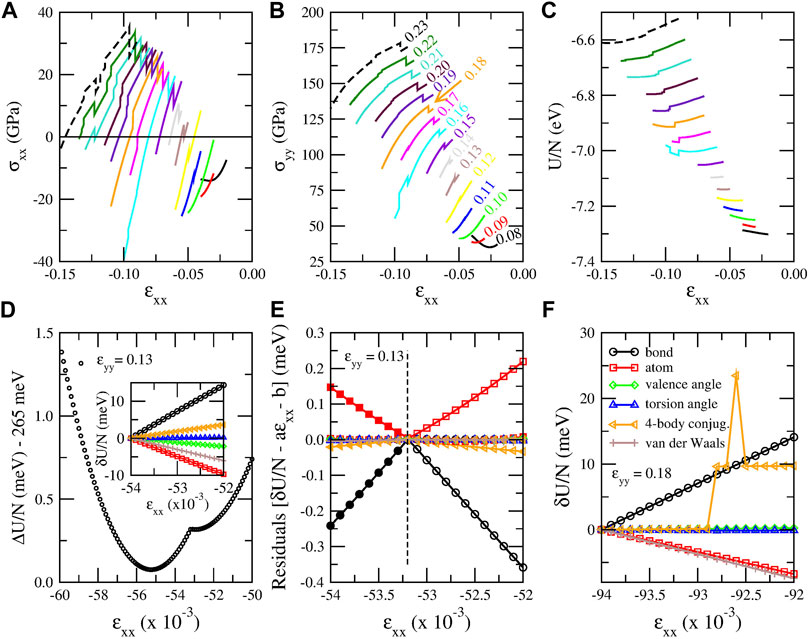
FIGURE 6. (A)–(C) “Jumps” (discontinuities) in stress and energy plots obtained using the CHON-2019 potential. (A) Stress along x direction (σ_xx), (B) stress along y direction (σ_yy) and (C) energy per atom (U/N) as a function of strain along x direction (ɛ_xx) for fixed ɛ_yy values indicated with different colors. The ɛ_yy value corresponding to each curve of panels (A), (B) and (C) is shown next to each curve in panel (B) with the same color. (D) Strain energy per atom ΔU/N = U/N − U_coh shifted by 265 meV versus ɛ_xx for ɛ_yy = 0.13, showing the discontinuous change in the energy slope. In the inset: energy per atom for the six terms constituting the energy of the system. Each energy term is shifted by the value it has for ɛ_xx = −0.0540. (E) Residuals between the energy per atom values of each energy term shown in the inset of panel (D) and their fitted linear functions for −0.0540 ≤ ɛ_xx ≤ −0.0532 (open symbols) and for −0.0532 ≤ ɛ_xx ≤ −0.0520 (solid symbols). The residuals are calculated for all the energy values in the [-0.0540, -0.0520] interval and not only for the values used for the fitting.(F) The six energy terms for ɛ_yy = 0.18 and −0.0940 ≤ ɛ_xx ≤ −0.0920. The legends of panel (F) apply both in panel (E) and the inset of panel (D). The ɛ_xx increment in all these plots is 10^–4.

The ɛ_xx values at which those discontinuities take place perfectly fit to a quadratic function of ɛ_yy, as Supplementary Figure S1 shows the interatomic distance distributions for the discontinuity strain values reveals that those discontinuities take place when some second nearest neighbor distances (which for the CHON-2019 potential take the value of 2.459 Å at equilibrium), cross the value of 2.45 Å, as ɛ_xx decreases taking negative values for a constant ɛ_yy value. This is a strong indication that these discontinuities are probably due to some cutoff distance, which is used either by LAMMPS implementation of the ReaxFFs or the ReaxFFs themselves to define the bonds, by eliminating the bond order contributions for interatomic distances beyond that cutoff value. This indication is amplified by the fact that the interatomic distance r_C−C dependence of the carbon–carbon bond order, which is used in ReaxFFs, practically vanishes for r_C−C > 2.5 Å (see Ref. van Duin et al. (2001)). Moreover, for the saddle point of the ci-CH potential, which was discussed earlier in section 3.1.1, the distance between second nearest neighbors is 2.505 Å, which is very close to the 2.445 Å distance, which is found here. This indicates that maybe that saddle point and the second minimum, which appear in that case, are of the same origin as the discontinuity of the first derivative of the energy curve and the second energy minimum, respectively, which are shown in Figure 6D.

Interestingly, it appears that not only the stress, but also the energy curves have discontinuities, as Figure 6C shows, where the energy per atom versus ɛ_xx is plotted for constant ɛ_yy values. Those discontinuities appear in different strain ɛ_xx values compared with those already described and it is expected that they are also associated with similar cutoff distances and are also shown in Supplementary Figure S1. These energy discontinuities should possibly be considered in further improvements.

Similar discontinuities of the stress and the energy were also obtained using the C-2013 and GR-RDX-2021 potentials, as shown in the corresponding Supplementary Figure S1,S3.

These observations are in agreement with the findings of Furman and Wales (Furman and Wales (2019)), who also studied those discontinuities of ReaxFFs. According to their observations in the dissociation of N₂, the bond energy term features a cusp at approximately 2.5Å, causing the first derivative of the bond energy to be discontinuous at this point. Those discontinuities were attributed to several bond order and bond distance cutoffs, in agreement with our suspicions. For the elimination of those discontinuities the authors proposed the use of tapering functions, which would allow a smooth transition between bonded and nonbonding environments. However, such tapering functions or any other way to eliminate those discontinuities are not yet included in the ReaxFFs.

To shed more light in those discontinuities, we examined which energy terms among those composing the CHON-2019 ReaxFF potential are responsible for those discontinuities. In the case of strained graphene six such terms exist, namely the atom, bond, valence angle, torsion angle, 4-body conjugation and van der Waals terms. We examined two cases, 1) one for which the energy is continuous and its first derivative ∂U/∂ɛ_xx discontinuous, and 2) one for which the energy itself is discontinuous in a ɛ_xx range for constant ɛ_yy. For the former we selected ɛ_yy = 0.13 and −0.054 ≤ ɛ_xx ≤ −0.052, corresponding to the energy curve shown in Figure 6D. For this case the discontinuity of ∂U/∂ɛ_xx occurs at ɛ_xx = −0.0532. For the later we selected ɛ_yy = 0.18 and −0.094 ≤ ɛ_xx ≤ −0.092, where the energy is discontinuous more than once between ɛ_xx = −0.0929 and -0.0925. For the former the six energy terms are shown in the inset of Figure 6D, shifted by the value they have for ɛ_xx = −0.0540. Due to the small ɛ_xx range, all terms which are not responsible for the ∂U/∂ɛ_xx discontinuity are expected to be linear functions of ɛ_xx. Although the curves shown in the inset of Figure 6D give the impression of a linear dependence of those terms on ɛ_xx, it is not linear for all terms. This can be seen in Figure 6E, which shows the residuals δU/N − aɛ_xx − b between the shifted energy values δU/N for each term and the fitting functions aɛ_xx + b of δU/N in the range before and after the discontinuity of ∂U/∂ɛ_xx, i.e. for −0.0540 ≤ ɛ_xx ≤ −0.0532 and for −0.0532 ≤ ɛ_xx ≤ −0.0520, respectively. If the dependence of δU/N on ɛ_xx is linear, then the two fitting functions should more or less coincide and the residuals, not only in the fitted interval, but also in the extrapolated interval should be practically zero. If, on the other hand, the residuals in the extrapolated interval is not zero, this means that the slope of the linear fitting function changes, indicating a discontinuous behavior of the derivative ∂U/∂ɛ_xx of that energy term. As one can see in Figure 6E, the slope of the bond and atom energy terms change significantly, with a smaller slope change for the 4-body conjugation term. Consequently, the discontinuity of ∂U/∂ɛ_xx is caused mainly due to the strain dependence of the bond and atom term of the energy, with a smaller contribution from the 4-body conjugation term. For the later the energy terms are depicted in Figure 6F, which shows that the discontinuity in that case clearly comes from the 4-body conjugation term. All other terms are continuous.

It is worth noting that the behavior described above is not associated to anomalous elongation of bonds, or rupture, which have been observed for large positive values of both ɛ_xx and ɛ_yy. For graphene under strain along x and/or y direction there are only two kind of bonds with different lengths, namely those aligned along x direction, with bond length a, and those belonging to the zig-zag chains along the y direction, with bond length b. Moreover, there are two different types of bond angles, namely the angles ϕ formed between the bonds of those zig-zag chains, and the angles θ formed by the bonds of those zig-zag chains and the bonds directed along the x direction. The angles ϕ and θ depend with each other through the relation θ = π − ϕ/2. The discontinuities of the derivative ∂U/∂ɛ_xx (i.e., the sharp change of the slope of the energy, like the one shown in Figure 6D) do not seem to affect the smooth change of a, b and ϕ as a function of strain ɛ_xx. However, the discontinuities of U(ɛ_xx) affects a, b and ϕ, which are also discontinuous as a function of ɛ_yy. As examples of those cases we show in Supplementary Figure S4 the a, b and ϕ values of the equilibrium structure of graphene under strain ɛ_xx = 0.13 (left panels) and 0.18 (right panels) as a function of ɛ_yy in a ɛ_yy range, where for the former U is continuous and ∂U/∂ɛ_yy discontinuous, and for the latter U is discontinuous.

3.1.4 Phonon dispersion relation

For the phonon dispersion relation we use an in-house code made by one of us, implementing the frozen phonons method²: The forces on all atoms of a 7 × 7 portion of the supercell, shown in Figure 7 (blue and red colored), are calculated for ± δx, ± δy and ± δz displacements of the atoms of the central unit cell (red colored). For our calculations, we chose δx = δy = δz = 0.0001 Å. Those forces are used to calculate numerically the second derivatives of the energy. E.g., for a displacement ± δy, one has

$\frac{{\partial }^{2}U}{\partial x_i\partial y_j}\approx \frac{f_{i,x}\left(y_j-\delta y\right)-f_{i,x}\left(y_j+\delta y\right)}{2\delta y},(11)$

where f_i,x(y_j ± δy) denotes the x component of the force f_i on ith atom. The k dependent dynamical matrix is then evaluated by discrete Fourier transform and diagonalized to get the different branches of dispersion relations.

FIGURE 7

FIGURE 7. The 98 atom 7 × 7 hexagonal supercell (blue colored atoms) as part of the 1,008 atom rectangular supercell of Figure 1. The red colored atoms in the center of the 7 × 7 hexagonal supercell are those corresponding to the two-atom primitive unit cell of graphene, which are displaced from equilibrium for the necessary force calculations.

The optimized 1008-atom rectangular supercell was used for the calculations. A smaller than a 7 × 7 force summation truncation introduces errors due to missing terms in the dynamic matrix, thus producing imaginary frequencies near the Γ point.

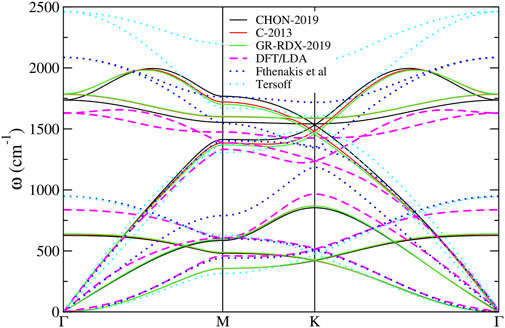
The phonon dispersion relations calculated for the potentials of the second group along the ΓMKΓ path in k-space are shown in Figure 8 and compared with 1) DFT results (Fthenakis et al. (2017)), 2) the results of the much simpler molecular mechanics potential of Fthenakis et al (Fthenakis et al. (2017)) and 3) the Tersoff potential (Tersoff (1988)). As one can see in that figure, the phonon dispersion relations provided by the three potentials are very similar. Quantitative agreement with DFT dispersion relations can also been observed at several parts of the ΓMKΓ path, indicating that these potentials are an improvement with respect to Tersoff and Fthenakis, especially for the representation of the in-plane optical branches. Conversely, the representation of the flexural modes at the zone boundary and of the optical out of plane modes is worse than in Tersoff and Fthenakis.

FIGURE 8

FIGURE 8. Phonon dispersion relation for the three ReaxFF potentials along ΓMKΓ path.

3.2 Carbon nanotubes

3.2.1 Energetics

It has been shown that the energy of single-wall carbon nanotubes (CNTs) depends on the diameter D of the CNT, as an effect of the CNT curvature as follows (Tibbetts (1984); Fthenakis et al. (2017); Kanamitsu and Saito (2002)).

$U/N=U_0+C_1/D^2+C_2/D^4(12)$

where U₀ is the energy of graphene corresponding to D = ∞. The C₁ term is dominant, but C₂ is not negligible. Depending on the method used for the energy calculations, the value of C₁ ranges between $\approx 5$ and $\approx 10$ eV⋅Ų (see Ref. Fthenakis et al. (2017) and references therein).

In Figure 9, we report the energy of the (n, n) and the (n, 0) CNTs as a function of their diameter D, obtained with the three ReaxFF potentials of the second group. The fit with Eq. 12 is reported in Table 2 showing that U₀ differs from the binding energy of graphene reported in Table 1 by less than 0.004%. The main differences between the curves in Figure 9 are due to this parameter, which differs by 0.03 eV in CHON-2019 potential with respect to others. The parameter C₁ ≈ 7 eV⋅Ų for all three potentials and for both (n, 0) and (n, n) CNTs. Moreover, C₂ turns out to be different for (n, 0) and (n, n) CNT’s ($\approx -25$ eV⋅Å⁴ and $\approx -30$ eV⋅Å⁴, respectively) without significant differences between the three potentials.

FIGURE 9

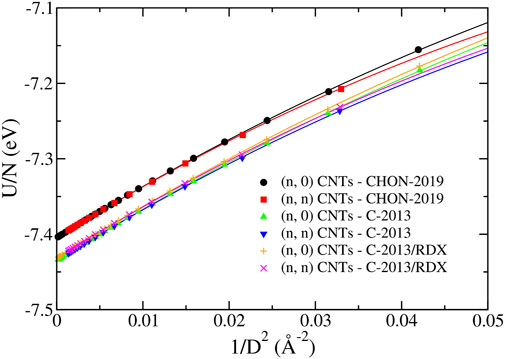
FIGURE 9. The energy per atom U/N of the (n, 0) and (n, n) CNTs predicted by the CHON-2019, C-2013 and GR-RDX-2021 potentials. The lines correspond to the fitting lines provided in Tab. 2.

TABLE 2

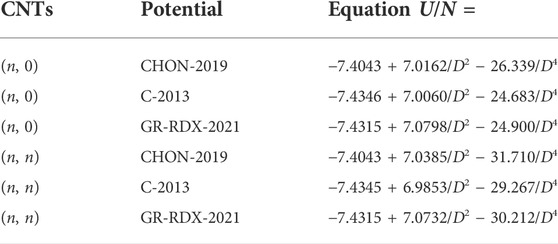
TABLE 2. Fitting functions of the energy per atom U/N of the (n, 0) and (n, n) CNTs for the three ReaxFF potentials. U/N and the CNT diameter D are given in eV and Å units, respectively.

3.2.2 Mechanical properties and response to strain

Figure 10 reports E and ν of the (n, 0) and (n, n) CNTs obtained with the ReaxFF potentials of the second group. For D > 10 Å, E and ν have a monotonic behavior ultimately leading to the “bulk” graphene values, and independent from the chirality, as expected, and also seen in DFT calculations (Ogata and Shibutani (2003); Qian et al. (2021)). Consequently, as in the “bulk”, E and ν are underestimated and overestimated, respectively, compared DFT calculations. On the other hand, they are coherent with the values obtained with molecular dynamics using C-2013 by Jensen et al (Jensen et al. (2015)) for the (20.0) (E = 777 GPa) and by Qian et al (Qian et al. (2021)) for the (5.5) (E = 764 GPa) and for the (10.0) (E = 825 GPa).

FIGURE 10

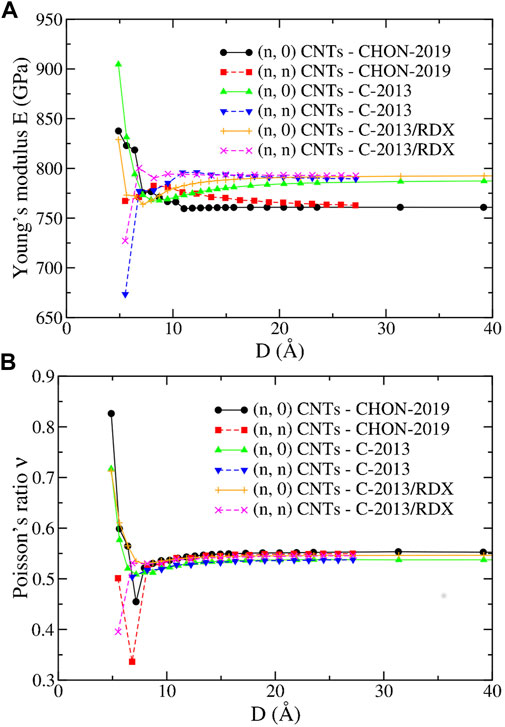
FIGURE 10. (A) The Young’s modulus E and (B) the Poisson’s ratio ν as a function of the diameter D for the (n, 0) and (n, n) CNTs of the present study predicted by the CHON-2019, C-2013 and GR-RDX-2021 potentials.

Conversely, the trend for D⪅10 Å is less clear displaying increasing or decreasing behavior and especially opposite divergences at small D depending on the potential, as previously observed (see Ref. Sakharova et al. (2017) and references therein). On the other hand, ν displays a regularly increasing behavior for all three potentials and for both (n, 0) and (n, n) CNTs, for D⪆10 Å, and a minimum at small D whose location and depth is dependent on the potential. However, both the dependence of E and ν on D > 10 Å is rather weak, in accordance with similar studies using other potentials (Fthenakis et al. (2017)).

Panels (A), (B) and (C) of Figure 11 show the energy per atom U/N, the stress σ_zz and the Poisson’s ratio ν, respectively, of (n, 0) and (n, n) CNTs, calculated using the three ReaxFF potentials, as a function of the strain ɛ_zz in the range [0, 0.5]. The “drops” shown in Figure 11B at ɛ_zz ≈ 0.05 are likely to be of the same origin as the corresponding ones discussed for graphene. Accordingly, the plots of ν shown in Figure 11C are very similar with their counterpart for graphene (Figure 4B). There are some differences due to the CNT curvature, mostly affecting CNTs with small diameter. These “drops” for the C-2013 potential can be also seen in the stress - strain plots of the study by Qian et al (Qian et al. (2021)) for the (5.5) and the (10.0) CNTs.

FIGURE 11

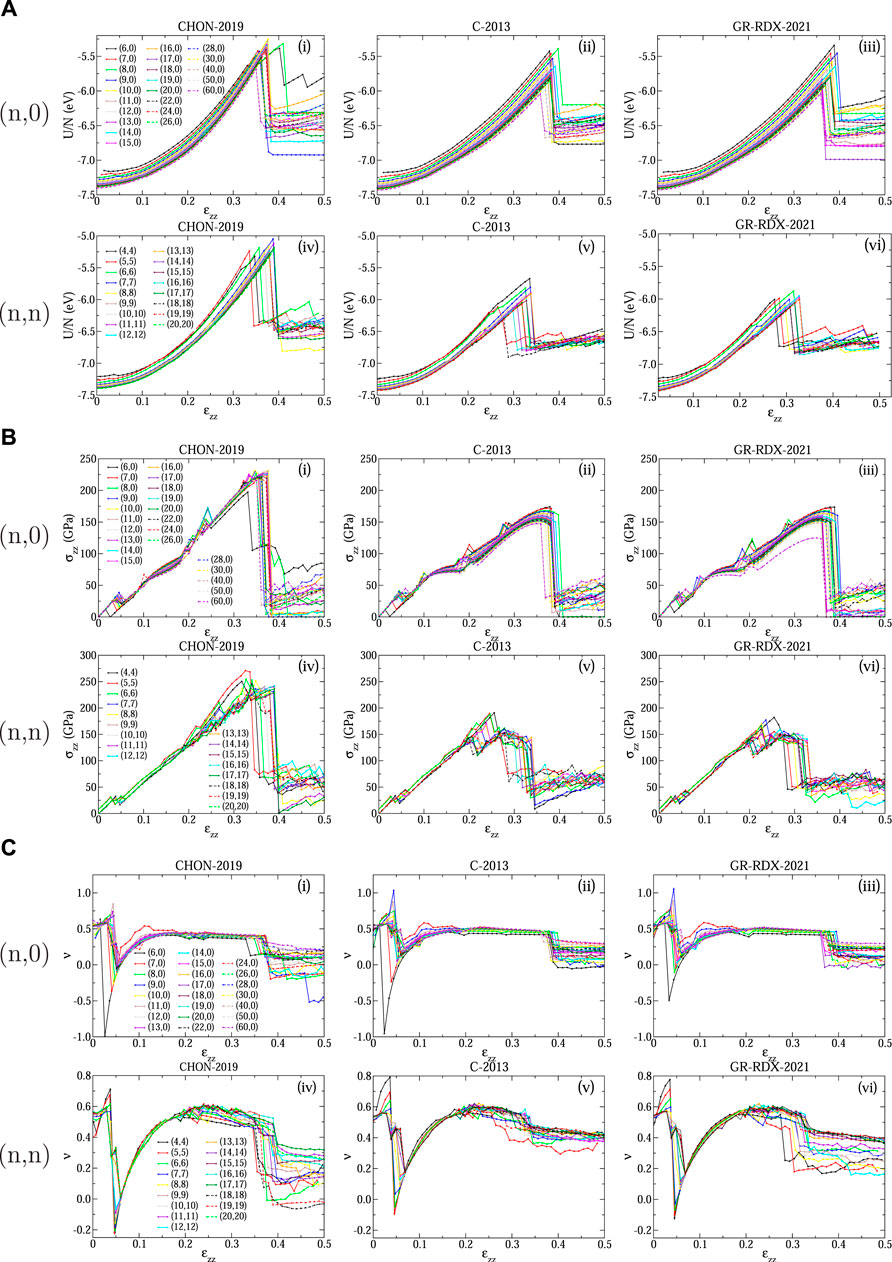
FIGURE 11. Response of CNTs to strain: (A) Energy per atom U/N, (B) stress σ_zz and (C) Poisson’s ratio ν as a function of strain ɛ_zz for (n, 0) (subpanels i, ii, iii) and (n, n) (subpanels iv, v, vi) CNTs predicted using the CHON-2019 (subpanels i, iv), C-2013 (subpanels ii, v) and GR-RDX-2021 (subpanels iii, vi) potential.

3.2.3 Ultimate tensile strength and fracture strain limits

The energy and stress drops shown in Figures 11A,B at high strain values indicate brittle fractures. The ultimate tensile strength σ_UTS (i.e., the maximum stress that can be reached as strain increases) and the corresponding strain ɛ_UTS, as well as the fracture strain limits ɛ_F, defined as the strain at which the energy drops occur, are shown in Figure 12 versus n of the (n, 0) and (n, n) CNTs.

FIGURE 12

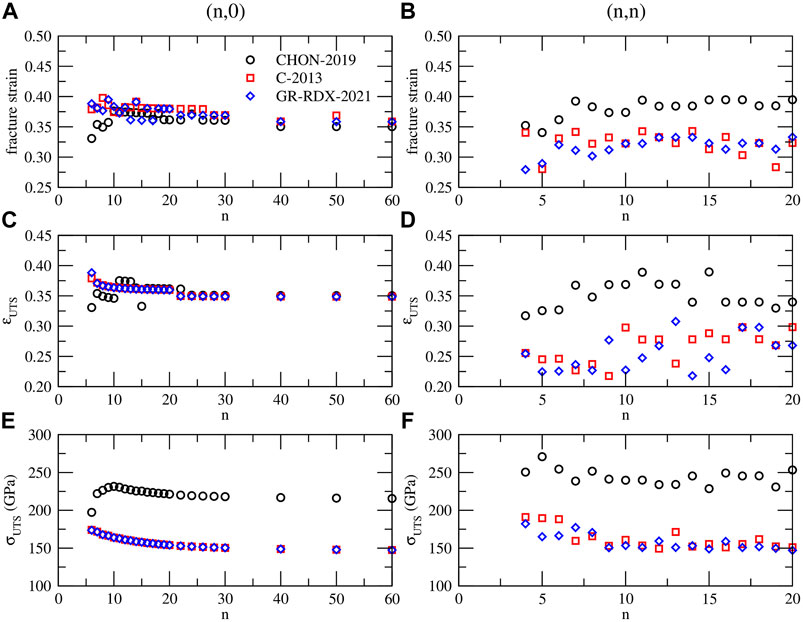
FIGURE 12. (A) and (B) fracture strain, (C) and (D) ultimate tensile strain ɛ_UTS, (E) and (F) ultimate tensile strength σ_UTS for (n, 0) (left panels - (A), (C) and (E)) and (n, n) (right panels - (B), (D) and (F)) CNTs, predicted by CHON-2019 (black circles), C-2013 (red squares) and GR-RDX-2021 (blue diamonds).

As shown in Figures 11A,B the two values ɛ_UTS and ɛ_F, coincide in many cases, or ɛ_F is slightly larger. For the (n, 0) CNTs they both range between 0.33 and 0.40, with most of the cases ranging between 0.36 and 0.38 for ɛ_F, and 0.35 and 0.37 for ɛ_UTS, with not significant differences between the three potentials. For the (n, n) CNTs the ɛ_F and ɛ_UTS values are more scattered. Those obtained with CHON-2019 fall in a similar strain range as those for the (n, 0) CNTs, i.e. 0.36–0.39 for ɛ_F and 0.32–0.39 for ɛ_UTS, while those from C-2013 and GR-RDX-2021 are smaller for ɛ_F (0.28–0.34) and much smaller for ɛ_UTS (0.22–0.31). Concerning σ_UTS, values predicted by CHON-2019 both for (n, 0) and (n, n) CNTs are higher than those predicted by C-2013 and GR-RDX-2021, and sligthly decreasing with n, although the values for (n, n) CNTs (panel f), are more scattered. Moreover, σ_UTS from CHON-2019 for (n, 0) CNTs ($\approx 230$ GPa) are smaller than those for the (n, n) ($\approx 250$ GPa), while those from C-2013 and GR-RDX-2021 appear almost independent from chirality (σ_UTS ≈ 160 GPa). These values of strain fall into the experimental range, which, on average is not larger than $\approx 20$ %, and can be as small as 2%, while σ_UTS does not exceed the value of $\approx 150$ GPa (Walters et al. (1999); Yu et al. (2000); Demczyk et al. (2002)), although in some specific experimental conditions much larger values (Bozovic et al. (2003); Troiani et al. (2003)) up to 280% (Huang et al. (2006)) have been reported for ɛ.

On the theoretical side, Ogata and Shibutani (Ogata and Shibutani (2003)) reported a study on (8,0), (9,0), (10,0) and (8,8) CNTs finding σ_UTS ∼ 86.8–95.6 GPa (with tight binding, (TB)) and 117.4–114.6 GPa (with DFT), and ɛ_UTS ∼0.170–0.211 (with TB) and 0.108–0.110 (with DFT). DFT calculations by Qian et al (Qian et al. (2021)) provide similar results, $\approx 100$ GPa for the (10.0), $\approx 92$ GPa for the (5.5) CNT, and ɛ_UTS = 0.22 for the (5.5) CNT, while for the (10.0) CNT the ɛ_UTS was found significantly larger (ɛ_UTS = 0.33). Indeed, the values obtained with classical potentials, are found, on average, larger than DFT values. Duan et al (Duan et al. (2007)) reported ɛ_UTS = 0.2736–0.4349 and σ_UTS = 99.89–134.01 GPa for (10,n) CNTs, n = 0, 1, 3, 5, 7, 9, 10, using four classical potentials (COMPASS, a modified Morse, REBO and Dumitrica potentials) while Qian et al (Qian et al. (2021)) found σ_UTS = 90–407.1 GPa, and ɛ_UTS 0.19–0.56 for (10.0) and (5.5) CNTs, using eight classical potentials (Tersoff and modified Tersoff, AIREBO and modified AIREBO, EDIP, LCBOP, C-2013 and GAP-20). Therefore the results provided by the three ReaxFF potentials of the present study are in line with those of other classical potentials, performing even slightly better in comparison to DFT. On the other hand, the comparison to experiment is very difficult given the large spread of values.

3.3 Fullerenes and the pentagon adjacency penalty rule

In this part, we calculate the energy U of the icosahedral C₆₀ fullerene and the energy of the 40 isomers of C₄₀ fullerene, which can be obtained with all possible arrangements of pentagonal and hexagonal rings of the C₄₀ fullerene structure (see Refs. Fowler and Manolopoulos (1995), Albertazzi et al. (1999) and Fthenakis et al. (2017)). Albertazzi et al (Albertazzi et al. (1999)) showed that a simple descriptor of the energy of those isomers is the number N_p of pentagon adjacencies and that the energy U of those isomers can be approximated by

$U=a{N}_p+b(13)$

the parameter a ranging between 20 and 100 kJ/mol for different calculations, while for the C₄₀ isomers N_p ranges between 10 and 20. Therefore, the maximum energy difference ΔU = aΔN_p of those isomers can be estimated for the maximum values ΔN_p = 10 and a = 100 kJ/mol and is of the order of 1,000 kJ/mol (10 eV or 0.25 eV/atom). Similarly, the energy difference between isomers for which the N_p value differs by one can be estimated as 0.025 eV/atom, or even smaller down to 5 meV/atom, which gives an idea of the required sensitivity of the used force field.

At variance with graphene, fullerenes have non-zero torsional angles. In a recent work (Fthenakis et al. (2017)), Fthenakis et al showed the importance of torsional terms in the energy expression of the molecular mechanics potential for sp² carbon systems. Neglecting those terms turns out in a poor dependence of the energy of the C₄₀ fullerene isomers on N_p, and a strong underestimation of the isomers’ energy differences. This may explain the small value of a found by Albertazzi et al with the Tersoff (a = 24.4 kJ/mol) and the Brenner (a = 36.1 kJ/mol) potentials, which do not explicitly include torsional terms. On the other hand, potentials which include torsional terms, like those by Fthenakis et al (Fthenakis et al. (2017)) or DTMM (Crabbe et al. (1994)) used by Albertazzi et al (Albertazzi et al. (1999)), return higher slope values, although not as high as those given by ab initio and semi-empirical methods, which are of the order of 80–100 kJ/mol (see Ref. Albertazzi et al. (1999)).

In Figure 13, we report the energy of the C₄₀ isomers as a function of N_p for the three ReaxFF potentials of the second group. The results are compatible with a linear behavior with a = 32.848, 34.023 and 34.066 kJ/mol for CHON-2019, C-2013 and GR-RDX-2021, respectively, with correlation coefficient R² values of 0.860, 0.918 and 0.922, respectively. These values of a are comparable with those found by the molecular mechanics potentials of Fthenakis et al (Fthenakis et al. (2017)) (a = 40.5 kJ/mol) and the DTMM potential (Crabbe et al. (1994)) (a = 42.2 kJ/mol), i.e., they are smaller than DFT values, which seems to be a problem, common to all classical potentials, as confirmed by a study (Aghajamali and Karton (2021)) comparing the energy of the 1812 C₆₀ isomers by DFT to those obtained using several potentials including the CHO and the C-2013.

FIGURE 13

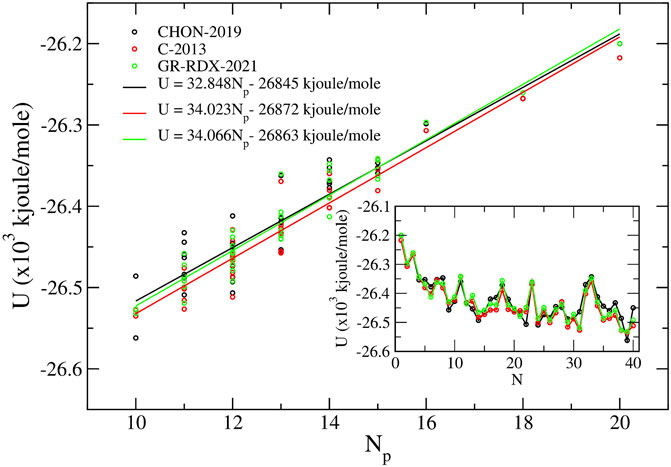
FIGURE 13. Binding energy U of the 40 C₄₀ fullerene isomers vs. the pentagon adjacencies N_p calculated using the three ReaxFF potentials. In the inset, we show the calculated energy values versus the standard C₄₀ isomer enumeration (Fowler and Manolopoulos (1995).

The inset of Figure 13 shows U as a function of standard isomers enumeration, N, used also in Refs. (Fowler and Manolopoulos (1995)), (Albertazzi et al. (1999)) and (Fthenakis et al. (2017)), clearly showing a high correlation among energies predicted by the three ReaxFF potentials of the second group. The optimized C₄₀ isomers using the GR-RDX-2021 potential are shown in Supplementary Figure S5. The isomer number (40:N) is shown below each structure. It is worth noting that energy differences among the three potentials are less than in graphene. The maximum energy difference per atom in any isomer evaluated with the three potential is of the order of at most 0.016 eV, and 0.003 eV on the average. The corresponding difference for graphene is 0.03 eV/atom (see above).

Among the 12 potentials used in the study by Albertazzi et al (Albertazzi et al. (1999)), all predict isomer no 38 to be the most stable, except Tersoff. Unfortunately, even the three ReaxFF potentials of the second group fail to predict isomer 38 as the most stable. CHON-2019 potential predicts isomer no 39 to be the most stable one, with no 30, 29, 24, 22 and 14 having energies between isomers no 39 and no 38. The energy difference between isomers no 39 and 38 is 76 kJ/mol, corresponding to 0.78 eV (or 20 meV/atom). C-2013 and GR-RDX-2021 potentials work better in this respect, predicting no 39 to be the most stable one, followed by isomer no 38 with a very small energy difference, 2.0 meV/atom for C-2013 and 1.4 meV/atom for GR-RDX-2021. For completeness, we report that Fthenakis et al (Fthenakis et al. (2017)) find isomer no 38 as the most stable one.

As a final validation check, we evaluated the energy of the icosahedral C₆₀ and its difference with respect to graphene using the three potentials of the second group. The values we find with CHON-2019, C-2013 and GR-RDX-2021 potentials, are 0.3625, 0.3759 and 0.3767 eV/atom, respectively, while the corresponding experimental value (Fthenakis (2013); Chen et al. (1991)) is 0.41 ± 0.02 and the one calculated with DFT at the GGA/PBE level (Wirz et al. (2016)) is 0.38 eV/atom. Therefore, the three ReaxFF potentials, although in some cases they fail to capture the very small energy differences between the C₄₀ fullerene isomers, they qualitative reproduce the linear increase of the fullerene energy with N_p and correctly predict the relative energy of the icosahedral C₆₀ fullerene with respect to graphene.

4 Conclusion

In this work, we study the performance of 11 ReaxFF potentials in reproducing the structural, vibrational and mechanical properties of fullerene, graphene and carbon nanotubes under strain up to the rupture limit. Ten of them are commonly used general reactive potentials. The 11th one, which we call GR-RDX-2021, is built in this work combining the C-2013 and RDX. The combination is realized defining two different types for carbon atoms belonging to graphene (C_g) or other molecules (C) which are treated with C-2013 and RDX, respectively, to exploit their capabilities to treat graphene and other molecules, respectively, so to optimize the overall performance of the representation. This procedure does not require any further reparameterization and can be easily generalized to any couple of potentials at least in the same class.

According to our findings, seven of these potentials predict unphysical values of the Poisson’s ratio describing practically unstretchable graphene bonds in comparison with bond angle deformation. These potentials are not indicated for studies of the elastic properties of sp² systems. We the focus our study on they four remaining potentials, C-2013, CHO-2016, CHON-2019 and the new one GR-RDX-2021 which do not suffer from such problems. We evaluated the structural and mechanical properties of graphene, its response to tensile stain and its phonon band structure. We studied the energetic and mechanical properties of the (n, 0) and (n, n) CNTs as a function of their diameter, as well as, their response on tensile strain and fracture. We studied the energetics of the 40 C₄₀ fullerene isomers and the predictions of the pentagon adjacency penalty rule, as well as, the energy of the icosahedral C₆₀ fullerene. The hybrid GR-RDX-2021 potential is tested here on its performances on stretched graphene-derived materials, and is intended to be used to explore the consequences of stretching on the reactivity of graphene with organic molecules including H, O and N, besides C, where it is expected to provide a description at least as good as its parent potential RDX. These aspects are the matter of a fortcoming paper.

Overall, the selected ReaxFF potentials predict practically the same values for graphene bond length (1.42 Å) and cohesive energy (-7.4 eV/atom), in agreement with experimental and DFT values. They also predict similar phonon dispersion relations for graphene, whose discrepancy from DFT is on average similar. Moreover, they all qualitatively and correctly predict: 1) The trend for the energy of CNTs as a function of diameter, 2) the increasing trend of the energy of fullerene isomers as a function of their pentagon adjacencies, and 3) the correct energy difference between the icosahedral C₆₀ fullerene with respect to graphene. On the other hand, they underestimate the Young’s modulus of both graphene and CNTs by $\approx 3/4$ and overestimate their Poisson’s ratio by $\approx 3$ times, compared to DFT. In terms of the bond stretching and bond angle bending “spring constants” of an equivalent sticks-spiral mechanical model, the bond stretching is stronger than that provided by DFT by a factor of $\approx 4/3$, while the bond angle bending is weaker by a factor of $\approx 1/2$.

We found unexpected drops and discontinuities in the stress–strain plots, both for graphene and CNT’s. We then performed an accurate analysis of the PES as a function of ɛ_xx and ɛ_yy. Our study revealed several irregularities of the PES (U), including 1) discontinuities of stresses due either to discontinuities of U or its gradients 2) the existence of more than one minimum of U at constant ɛ_xx or ɛ_yy and 3) changes of the “spring constant” of the equivalent stick-spiral model. Three different regions of the U landscape and corresponding regimes are identified, whose borders crossing is related to the “drops” in the stress–strain plots. Due to those drops, which significantly affect the structural behavior of graphene and CNTs under strain, the dependence of ν on ɛ, for ɛ > 0.03 is rather irregular.

The predictions of the three ReaxFF potentials for the fracture strain, the ultimate tensile strength and the corresponding strain values for the CNTs are overestimated with respect to DFT results. They are, however, in the range of the predictions of other potentials and even closer to the DFT, and fall within the experimental range, which displays a very large variability.

The overall conclusion, therefore, is that the studied ReaxFF potentials, for strain values ⪅0.05, provide quantitatively reliable results, for the energy and structural properties of graphene, the energetics of CNTs and fullerenes, as well as, the phonon band structure of graphene. Those results are comparable with the corresponding ones of other non-reactive potentials and DFT calculations. On the other hand, further studies are needed at larger stress values. On a qualitative level, reasonable behavior is reproduced displaying the onset of plasticity and rupture, while the quantitative aspects needs further investigations.

The present study, therefore, provides interesting information for the strengths and weakness of those potentials, which hopefully will be useful for their further improvement.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author contributions

ZF performed the calculations, had the idea for the hybrid ReaxFF and wrote the first draft of the paper. VT, NL and IP contributed to the conception and design of the study and to the manuscript revision. All authors read and approved the submitted version.

Funding

This research was funded by the projects (1) EU-H2020 FETPROACT LESGO (Agreement No. 952068), (2) MONSTRE-2D PRIN2017 KFMJ8E of the Italian Ministry of University and Research and (3) “nanoporous GrAphene membrane made without Transfer for gas Separation–GATES” (MIS 5041612), Operational Program “Competitiveness, Entrepreneurship and Innovation” (NSRF 2014–2020) co- financed by Greece and the European Union (European Regional Development Fund).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2022.951261/full#supplementary-material

Footnotes

¹For routine runs workstations. Thousands on High Performance Computing systems.

²The code is available upon request.

References

Abell, G. C. (1985). Empirical chemical pseudopotential theory of molecular and metallic bonding. Phys. Rev. B 31, 6184–6196. doi:10.1103/PhysRevB.31.6184

PubMed Abstract | CrossRef Full Text | Google Scholar

Aghajamali, A., and Karton, A. (2021). Can force fields developed for carbon nanomaterials describe the isomerization energies of fullerenes? Chem. Phys. Lett. 779, 138853. doi:10.1016/j.cplett.2021.138853

CrossRef Full Text | Google Scholar

Albertazzi, E., Domene, C., Fowler, W. P., Heine, T., Seifert, G., Van Alsenoy, C., et al. (1999). Pentagon adjacency as a determinant of fullerene stability. Phys. Chem. Chem. Phys. 1, 2913–2918. doi:10.1039/A901600G

CrossRef Full Text | Google Scholar

Allinger, N. L., Chen, K., and Lii, J.-H. (1996). An improved force field (mm4) for saturated hydrocarbons. J. Comput. Chem. 17, 642–668. doi:10.1002/(SICI)1096-987X(199604)17:5/6⟨642::AID-JCC6⟩3.0.CO;2-U

CrossRef Full Text | Google Scholar

Allinger, N. L. (1977). Conformational analysis. 130. mm2. a hydrocarbon force field utilizing v1 and v2 torsional terms. J. Am. Chem. Soc. 99, 8127–8134. doi:10.1021/ja00467a001

CrossRef Full Text | Google Scholar

Allinger, N. L., Yuh, Y. H., and Lii, J. H. (1989). Molecular mechanics. the mm3 force field for hydrocarbons. 1. J. Am. Chem. Soc. 111, 8551–8566. doi:10.1021/ja00205a001

CrossRef Full Text | Google Scholar

Ashraf, C., and van Duin, A. C. (2017). Extension of the reaxff combustion force field toward syngas combustion and initial oxidation kinetics. J. Phys. Chem. A 121, 1051–1068. doi:10.1021/acs.jpca.6b12429

PubMed Abstract | CrossRef Full Text | Google Scholar

Beardmore, K., and Smith, R. (1996). Empirical potentials for c[sbnd]si[sbnd]h systems with application to c60 interactions with si crystal surfaces. Philos. Mag. A 74, 1439–1466. doi:10.1080/01418619608240734

CrossRef Full Text | Google Scholar

Bellucci, L., and Tozzini, V. (2020). Engineering 3d graphene-based materials: State of the art and perspectives. Molecules 25, 339. doi:10.3390/molecules25020339

PubMed Abstract | CrossRef Full Text | Google Scholar

Berber, S., Kwon, Y.-K., and Tomanek, D. (2000). Unusually high thermal conductivity of carbon nanotubes. Phys. Rev. Lett. 84, 4613–4616. doi:10.1103/PhysRevLett.84.4613

PubMed Abstract | CrossRef Full Text | Google Scholar

Blakslee, O. L., Proctor, D. G., Seldin, E. J., Spence, G. B., and Weng, T. (1970). Elastic constants of compression-annealed pyrolytic graphite. J. Appl. Phys. 41, 3373–3382. doi:10.1063/1.1659428

CrossRef Full Text | Google Scholar

Bosak, A., Krisch, M., Mohr, M., Maultzsch, J., and Thomsen, C. (2007). Elasticity of single-crystalline graphite: Inelastic x-ray scattering study. Phys. Rev. B 75, 153408. doi:10.1103/PhysRevB.75.153408

CrossRef Full Text | Google Scholar

Bozovic, D., Bockrath, M., Hafner, J. H., Lieber, C. M., Park, H., and Tinkham, M. (2003). Plastic deformations in mechanically strained single-walled carbon nanotubes. Phys. Rev. B 67, 033407. doi:10.1103/PhysRevB.67.033407

CrossRef Full Text | Google Scholar

Brenner, D. W. (1990). Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. Phys. Rev. B 42, 9458–9471. doi:10.1103/PhysRevB.42.9458

PubMed Abstract | CrossRef Full Text | Google Scholar

Brenner, D. W., Shenderova, O. A., Harrison, J. A., Stuart, S. J., Ni, B., and Sinnott, S. B. (2002). A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Phys. Condens. Matter 14, 783–802. doi:10.1088/0953-8984/14/4/312

CrossRef Full Text | Google Scholar

Brooks, B. R., Bruccoleri, R. E., Olafson, B. D., States, D. J., Swaminathan, S., and Karplus, M. (1983). Charmm: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4, 187–217. doi:10.1002/jcc.540040211

CrossRef Full Text | Google Scholar

Budzien, J., Thompson, A. P., and Zybin, S. V. (2009). Reactive molecular dynamics simulations of shock through a single crystal of pentaerythritol tetranitrate. J. Phys. Chem. B 113, 13142–13151. doi:10.1021/jp9016695

PubMed Abstract | CrossRef Full Text | Google Scholar

Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S., and Geim, A. K. (2009). The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162. doi:10.1103/RevModPhys.81.109

CrossRef Full Text | Google Scholar

Chatzidakis, G. D., Kalosakas, G., Fthenakis, Z. G., and Lathiotakis, N. N. (2018). A torsional potential for graphene derived from fitting to dft results. Eur. Phys. J. B 91, 11. doi:10.1140/epjb/e2017-80444-5

CrossRef Full Text | Google Scholar

Chelikowsky, J. R. (1992). Formation of c₆₀ clusters via Langevin molecular dynamics. Phys. Rev. B 45, 12062–12070. doi:10.1103/PhysRevB.45.12062

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, H. S., Kortan, A. R., Haddon, R. C., Kaplan, M. L., Chen, C. H., Mujsce, A. M., et al. (1991). Reactivity of c60 in pure oxygen. Appl. Phys. Lett. 59, 2956–2958. doi:10.1063/1.105810

CrossRef Full Text | Google Scholar

Chenoweth, K., van Duin, A. C. T., and Goddard, W. A. (2008). Reaxff reactive force field for molecular dynamics simulations of hydrocarbon oxidation. J. Phys. Chem. A 112, 1040–1053. doi:10.1021/jp709896w

PubMed Abstract | CrossRef Full Text | Google Scholar

Chou, P. C., and Pagano, N. J. (1992). Elasticity: Tensor, dyadic and engineering approaches. New York: Dover.

Google Scholar

Côté, M., Grossman, J. C., Cohen, M. L., and Louie, S. G. (1998). Theoretical study of a three-dimensional all-sp² structure. Phys. Rev. B 58, 664–668. doi:10.1103/PhysRevB.58.664

CrossRef Full Text | Google Scholar

[Dataset] Crabbe, M. J. C., Appleyard, J. R., and Rees Lay, C. (1994). Dtmm3.0 : Desk-top molecular modeller.

Google Scholar

Crespi, V. H., Benedict, L. X., Cohen, M. L., and Louie, S. G. (1996). Prediction of a pure-carbon planar covalent metal. Phys. Rev. B 53, R13303–R13305. doi:10.1103/PhysRevB.53.R13303

PubMed Abstract | CrossRef Full Text | Google Scholar

Demczyk, B., Wang, Y., Cumings, J., Hetman, M., Han, W., Zettl, A., et al. (2002). Direct mechanical measurement of the tensile strength and elastic modulus of multiwalled carbon nanotubes. Mater. Sci. Eng. A 334, 173–178. doi:10.1016/S0921-5093(01)01807-X

CrossRef Full Text | Google Scholar

Duan, W., Wang, Q., Liew, K., and He, X. (2007). Molecular mechanics modeling of carbon nanotube fracture. Carbon 45, 1769–1776. doi:10.1016/j.carbon.2007.05.009

CrossRef Full Text | Google Scholar

Dyson, A., and Smith, P. (1996). Extension of the brenner empirical interatomic potential to c-si-h systems. Surf. Sci. 355, 140–150. doi:10.1016/0039-6028(96)00004-0

CrossRef Full Text | Google Scholar

Elstner, M., Porezag, D., Jungnickel, G., Elsner, J., Haugk, M., Frauenheim, T., et al. (1998). Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 58, 7260–7268. doi:10.1103/PhysRevB.58.7260

CrossRef Full Text | Google Scholar

Fonseca, A. F., Lee, G., Borders, T. L., Zhang, H., Kemper, T. W., Shan, T.-R., et al. (2011). Reparameterization of the rebo-cho potential for graphene oxide molecular dynamics simulations. Phys. Rev. B 84, 075460. doi:10.1103/PhysRevB.84.075460

CrossRef Full Text | Google Scholar

Fowler, P. W., and Manolopoulos, D. E. (1995). An atlas of fullerenes. Oxford: Clarendon Press.

Google Scholar

Fthenakis, Z., Andriotis, A. N., and Menon, M. (2003). Temperature evolution of structural and magnetic properties of transition metal clusters. J. Chem. Phys. 119, 10911–10916. doi:10.1063/1.1619931

CrossRef Full Text | Google Scholar

Fthenakis, Z. G. (2016). Ab initio investigation on the stability of h-6 carbon. RSC Adv. 6, 78187–78193. doi:10.1039/C6RA10809A

CrossRef Full Text | Google Scholar

Fthenakis, Z. G. (2017). Are the experimentally observed 3-dimensional carbon honeycombs all-sp2 structures? The dangling p-orbital instability. RSC Adv. 7, 9790–9794. doi:10.1039/C6RA27833G

CrossRef Full Text | Google Scholar

Fthenakis, Z. G. (2013). Energetics of graphene flakes. Mol. Phys. 111, 3289–3296. doi:10.1080/00268976.2013.782437

CrossRef Full Text | Google Scholar

Fthenakis, Z. G., Kalosakas, G., Chatzidakis, G. D., Galiotis, C., Papagelis, K., and Lathiotakis, N. N. (2017). Atomistic potential for graphene and other sp2 carbon systems. Phys. Chem. Chem. Phys. 19, 30925–30932. doi:10.1039/C7CP06362H

PubMed Abstract | CrossRef Full Text | Google Scholar

Fthenakis, Z. G., and Lathiotakis, N. N. (2015). Graphene allotropes under extreme uniaxial strain: An ab initio theoretical study. Phys. Chem. Chem. Phys. 17, 16418–16427. doi:10.1039/C5CP02412A

PubMed Abstract | CrossRef Full Text | Google Scholar

Fthenakis, Z. G., and Lathiotakis, N. N. (2017). Structural deformations of two-dimensional planar structures under uniaxial strain: The case of graphene. J. Phys. Condens. Matter 29, 175401. doi:10.1088/1361-648x/aa63d5

PubMed Abstract | CrossRef Full Text | Google Scholar

Fthenakis, Z. G., and Menon, M. (2019). Structural deformations and mechanical properties of si₂BN under uniaxial and uniform biaxial strain in comparison with graphene: An ab initio study. Phys. Rev. B 99, 205302. doi:10.1103/PhysRevB.99.205302

CrossRef Full Text | Google Scholar

Fthenakis, Z. G., and Tománek, D. (2012). Computational study of the thermal conductivity in defective carbon nanostructures. Phys. Rev. B 86, 125418. doi:10.1103/PhysRevB.86.125418

CrossRef Full Text | Google Scholar

Fthenakis, Z. G., Zhu, Z., and Tománek, D. (2014). Effect of structural defects on the thermal conductivity of graphene: From point to line defects to haeckelites. Phys. Rev. B 89, 125421. doi:10.1103/PhysRevB.89.125421

CrossRef Full Text | Google Scholar

Furman, D., and Wales, D. J. (2019). Transforming the accuracy and numerical stability of reaxff reactive force fields. J. Phys. Chem. Lett. 10, 7215–7223. doi:10.1021/acs.jpclett.9b02810

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoffmann, R. (1963). An extended hückel theory. i. hydrocarbons. J. Chem. Phys. 39, 1397–1412. doi:10.1063/1.1734456

CrossRef Full Text | Google Scholar

Huang, J. Y., Chen, S., Wang, Z. Q., Kempa, K., Wang, Y. M., Jo, S. H., et al. (2006). Superplastic carbon nanotubes. Nature 439, 281. doi:10.1038/439281a

PubMed Abstract | CrossRef Full Text | Google Scholar

Iijima, S. (1991). Helical microtubules of graphitic carbon. Nature 354, 56–58. doi:10.1038/354056a0

CrossRef Full Text | Google Scholar

Inagaki, M., Qiu, J., and Guo, Q. (2015). Carbon foam: Preparation and application. Carbon 87, 128–152. doi:10.1016/j.carbon.2015.02.021

CrossRef Full Text | Google Scholar

Ivanovskaya, V. V., Zobelli, A., Teillet-Billy, D., Rougeau, N., Sidis, V., and Briddon, P. R. (2010). Hydrogen adsorption on graphene: A first principles study. Eur. Phys. J. B 76, 481–486. doi:10.1140/epjb/e2010-00238-7

CrossRef Full Text | Google Scholar

Jang, I., and Sinnott, S. B. (2004). Molecular dynamics simulations of the chemical modification of polystyrene through C_xF_y⁺ beam deposition. J. Phys. Chem. B 108, 18993–19001. doi:10.1021/jp049283y

CrossRef Full Text | Google Scholar

Jensen, B. D., Wise, K. E., and Odegard, G. M. (2015). Simulation of the elastic and ultimate tensile properties of diamond, graphene, carbon nanotubes, and amorphous carbon using a revised reaxff parametrization. J. Phys. Chem. A 119, 9710–9721. doi:10.1021/acs.jpca.5b05889

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalosakas, G., Lathiotakis, N. N., Galiotis, C., and Papagelis, K. (2013). In-plane force fields and elastic properties of graphene. J. Appl. Phys. 113, 134307. doi:10.1063/1.4798384

CrossRef Full Text | Google Scholar

Kalosakas, G., Lathiotakis, N. N., and Papagelis, K. (2021). Width dependent elastic properties of graphene nanoribbons. Materials 14, 5042. doi:10.3390/ma14175042

PubMed Abstract | CrossRef Full Text | Google Scholar

Kamat, A. M., van Duin, A. C. T., and Yakovlev, A. (2010). Molecular dynamics simulations of laser-induced incandescence of soot using an extended reaxff reactive force field. J. Phys. Chem. A 114, 12561–12572. doi:10.1021/jp1080302

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanamitsu, K., and Saito, S. (2002). Geometries, electronic properties, and energetics of isolated single walled carbon nanotubes. J. Phys. Soc. Jpn. 71, 483–486. doi:10.1143/JPSJ.71.483

CrossRef Full Text | Google Scholar

Kański, M., Maciżek, D., Postawa, Z., Ashraf, C. M., van Duin, A. C. T., and Garrison, B. J. (2018). Development of a charge-implicit reaxff potential for hydrocarbon systems. J. Phys. Chem. Lett. 9, 359–363. doi:10.1021/acs.jpclett.7b03155

PubMed Abstract | CrossRef Full Text | Google Scholar

Khor, K. E., and Das Sarma, S. (1988). Proposed universal interatomic potential for elemental tetrahedrally bonded semiconductors. Phys. Rev. B 38, 3318–3322. doi:10.1103/PhysRevB.38.3318

PubMed Abstract | CrossRef Full Text | Google Scholar

Kowalik, M., Ashraf, C., Damirchi, B., Akbarian, D., Rajabpour, S., and van Duin, A. C. T. (2019). Atomistic scale analysis of the carbonization process for c/h/o/n-based polymers with the reaxff reactive force field. J. Phys. Chem. B 123, 5357–5367. doi:10.1021/acs.jpcb.9b04298

PubMed Abstract | CrossRef Full Text | Google Scholar

Krainyukova, N. V., and Zubarev, E. N. (2016). Carbon honeycomb high capacity storage for gaseous and liquid species. Phys. Rev. Lett. 116, 055501. doi:10.1103/PhysRevLett.116.055501

PubMed Abstract | CrossRef Full Text | Google Scholar

Kroto, H. W., Heath, J. R., O’Brien, S. C., Curl, R. F., and Smalley, R. E. (1985). C₆0: Buckminsterfullerene. Nature 318, 162–163. doi:10.1038/318162a0

CrossRef Full Text | Google Scholar

Lathiotakis, N. N., Andriotis, A. N., Menon, M., and Connolly, J. (1996). Tight binding molecular dynamics study of ni clusters. J. Chem. Phys. 104, 992–1003. doi:10.1063/1.470823

CrossRef Full Text | Google Scholar

Lebedeva, I. V., Minkin, A. S., Popov, A. M., and Knizhnik, A. A. (2019). Elastic constants of graphene: Comparison of empirical potentials and dft calculations. Phys. E Low-dimensional Syst. Nanostructures 108, 326–338. doi:10.1016/j.physe.2018.11.025

CrossRef Full Text | Google Scholar

Lee, C., Wei, X., Kysar, J. W., and Hone, J. (2008). Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 321, 385–388. doi:10.1126/science.1157996

PubMed Abstract | CrossRef Full Text | Google Scholar

Lindsay, L., and Broido, D. A. (2010). Optimized tersoff and brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene. Phys. Rev. B 81, 205441. doi:10.1103/PhysRevB.81.205441

CrossRef Full Text | Google Scholar

Liu, A. Y., and Cohen, M. L. (1992). Theoretical study of a hypothetical metallic phase of carbon. Phys. Rev. B 45, 4579–4581. doi:10.1103/PhysRevB.45.4579

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, H., Wu, S., Tian, N., Yan, F., You, C., and Yang, Y. (2020). Carbon foams: 3d porous carbon materials holding immense potential. J. Mat. Chem. A 8, 23699–23723. doi:10.1039/D0TA08749A

CrossRef Full Text | Google Scholar

Liu, L., Liu, Y., Zybin, S. V., Sun, H., and Goddard, W. A. (2011). Reaxff-lg: Correction of the reaxff reactive force field for London dispersion, with applications to the equations of state for energetic materials. J. Phys. Chem. A 115, 11016–11022. doi:10.1021/jp201599t

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Wang, G., Huang, Q., Guo, L., and Chen, X. (2012). Structural and electronic properties of t graphene: A two-dimensional carbon allotrope with tetrarings. Phys. Rev. Lett. 108, 225505. doi:10.1103/PhysRevLett.108.225505

PubMed Abstract | CrossRef Full Text | Google Scholar

Los, J. H., and Fasolino, A. (2003). Intrinsic long-range bond-order potential for carbon: Performance in Monte Carlo simulations of graphitization. Phys. Rev. B 68, 024107. doi:10.1103/PhysRevB.68.024107

CrossRef Full Text | Google Scholar

Los, J. H., Ghiringhelli, L. M., Meijer, E. J., and Fasolino, A. (2005). Improved long-range reactive bond-order potential for carbon. i. construction. Phys. Rev. B 72, 214102. doi:10.1103/PhysRevB.72.214102

CrossRef Full Text | Google Scholar

Lynch, R. W., and Drickamer, H. G. (1966). Effect of high pressure on the lattice parameters of diamond, graphite, and hexagonal boron nitride. J. Chem. Phys. 44, 181–184. doi:10.1063/1.1726442

CrossRef Full Text | Google Scholar

Mattsson, T. R., Lane, J. M. D., Cochrane, K. R., Desjarlais, M. P., Thompson, A. P., Pierce, F., et al. (2010). First-principles and classical molecular dynamics simulation of shocked polymers. Phys. Rev. B 81, 054103. doi:10.1103/PhysRevB.81.054103

CrossRef Full Text | Google Scholar

Mayo, S. L., Olafson, B. D., and Goddard, W. A. (1990). Dreiding: A generic force field for molecular simulations. J. Phys. Chem. 94, 8897–8909. doi:10.1021/j100389a010

CrossRef Full Text | Google Scholar

Ng, T. Y., Yeo, J., and Liu, Z. (2013). Molecular dynamics simulation of the thermal conductivity of shorts strips of graphene and silicene: A comparative study. Int. J. Mech. Mat. Des. 9, 105–114. doi:10.1007/s10999-013-9215-0

CrossRef Full Text | Google Scholar

Ni, B., Lee, K.-H., and Sinnott, S. B. (2004). A reactive empirical bond order (REBO) potential for hydrocarbon–oxygen interactions. J. Phys. Condens. Matter 16, 7261–7275. doi:10.1088/0953-8984/16/41/008

CrossRef Full Text | Google Scholar

Nilsson, L., and Karplus, M. (1986). Empirical energy functions for energy minimization and dynamics of nucleic acids. J. Comput. Chem. 7, 591–616. doi:10.1002/jcc.540070502

CrossRef Full Text | Google Scholar

Novoselov, K. S., Geim, A. K., Morozov, S. V., Jiang, D., Zhang, Y., Dubonos, S. V., et al. (2004). Electric field effect in atomically thin carbon films. Science 306, 666–669. doi:10.1126/science.1102896

PubMed Abstract | CrossRef Full Text | Google Scholar

O’Connor, T. C., Andzelm, J., and Robbins, M. O. (2015). Airebo-m: A reactive model for hydrocarbons at extreme pressures. J. Chem. Phys. 142, 024903. doi:10.1063/1.4905549

PubMed Abstract | CrossRef Full Text | Google Scholar

Ogata, S., and Shibutani, Y. (2003). Ideal tensile strength and band gap of single-walled carbon nanotubes. Phys. Rev. B 68, 165409. doi:10.1103/PhysRevB.68.165409

CrossRef Full Text | Google Scholar

Pastewka, L., Pou, P., Pérez, R., Gumbsch, P., and Moseler, M. (2008). Describing bond-breaking processes by reactive potentials: Importance of an environment-dependent interaction range. Phys. Rev. B 78, 161402. doi:10.1103/PhysRevB.78.161402

CrossRef Full Text | Google Scholar

Qian, C., McLean, B., Hedman, D., and Ding, F. (2021). A comprehensive assessment of empirical potentials for carbon materials. Apl. Mater. 9, 061102. doi:10.1063/5.0052870

CrossRef Full Text | Google Scholar

Rajasekaran, G., Kumar, R., and Parashar, A. (2016). Tersoff potential with improved accuracy for simulating graphene in molecular dynamics environment. Mat. Res. Express 3, 035011. doi:10.1088/2053-1591/3/3/035011

CrossRef Full Text | Google Scholar

Rappe, A. K., Casewit, C. J., Colwell, K. S., Goddard, W. A., and Skiff, W. M. (1992). Uff, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 114, 10024–10035. doi:10.1021/ja00051a040

CrossRef Full Text | Google Scholar

Rossi, A., Piccinin, S., Pellegrini, V., de Gironcoli, S., and Tozzini, V. (2015). Nano-scale corrugations in graphene: A density functional theory study of structure, electronic properties and hydrogenation. J. Phys. Chem. C 119, 7900–7910. doi:10.1021/jp511409b

CrossRef Full Text | Google Scholar

Sakharova, N. A., Antunes, J. M., Pereira, A. F. G., and Fernandes, J. V. (2017). Developments in the evaluation of elastic properties of carbon nanotubes and their heterojunctions by numerical simulation. AIMS Mat. Sci. 4, 706–737. doi:10.3934/matersci.2017.3.706

CrossRef Full Text | Google Scholar

Schuler, L. D., Daura, X., and van Gunsteren, W. F. (2001). An improved gromos96 force field for aliphatic hydrocarbons in the condensed phase. J. Comput. Chem. 22, 1205–1218. doi:10.1002/jcc.1078

CrossRef Full Text | Google Scholar

Sheng, X.-L., Cui, H.-J., Ye, F., Yan, Q.-B., Zheng, Q.-R., and Su, G. (2012). Octagraphene as a versatile carbon atomic sheet for novel nanotubes, unconventional fullerenes, and hydrogen storage. J. Appl. Phys. 112, 074315. doi:10.1063/1.4757410

CrossRef Full Text | Google Scholar

Shi, L., Ma, X., Li, M., Zhong, Y., Yang, L., Yin, W., et al. (2021). Molecular dynamics simulation of phonon thermal transport in nanotwinned diamond with a new optimized tersoff potential. Phys. Chem. Chem. Phys. 23, 8336–8343. doi:10.1039/D1CP00399B

PubMed Abstract | CrossRef Full Text | Google Scholar

Shin, H., Kang, S., Koo, J., Lee, H., Kim, J., and Kwon, Y. (2014). Cohesion energetics of carbon allotropes: Quantum Monte Carlo study. J. Chem. Phys. 140, 114702. doi:10.1063/1.4867544

PubMed Abstract | CrossRef Full Text | Google Scholar

Srinivasan, S. G., van Duin, A. C. T., and Ganesh, P. (2015). Development of a reaxff potential for carbon condensed phases and its application to the thermal fragmentation of a large fullerene. J. Phys. Chem. A 119, 571–580. doi:10.1021/jp510274e

PubMed Abstract | CrossRef Full Text | Google Scholar

Strachan, A., van Duin, A. C. T., Chakraborty, D., Dasgupta, S., and Goddard, W. A. (2003). Shock waves in high-energy materials: The initial chemical events in nitramine rdx. Phys. Rev. Lett. 91, 098301. doi:10.1103/PhysRevLett.91.098301

PubMed Abstract | CrossRef Full Text | Google Scholar

Stuart, S. J., Tutein, A. B., and Harrison, J. A. (2000). A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 112, 6472–6486. doi:10.1063/1.481208

CrossRef Full Text | Google Scholar

Sun, H. (1998). Compass: An ab initio force-field optimized for condensed-phase applications overview with details on alkane and benzene compounds. J. Phys. Chem. B 102, 7338–7364. doi:10.1021/jp980939v

CrossRef Full Text | Google Scholar

Takai, T., Lee, C., Halicioglu, T., and Tiller, W. A. (1990). A model potential function for carbon systems: Clusters. J. Phys. Chem. 94, 4480–4482. doi:10.1021/j100374a025

CrossRef Full Text | Google Scholar

Terrones, H., Terrones, M., Hernández, E., Grobert, N., Charlier, J.-C., and Ajayan, P. M. (2000). New metallic allotropes of planar and tubular carbon. Phys. Rev. Lett. 84, 1716–1719. doi:10.1103/PhysRevLett.84.1716

PubMed Abstract | CrossRef Full Text | Google Scholar

Tersoff, J. (1988). Empirical interatomic potential for carbon, with applications to amorphous carbon. Phys. Rev. Lett. 61, 2879–2882. doi:10.1103/PhysRevLett.61.2879

PubMed Abstract | CrossRef Full Text | Google Scholar

Thompson, A. P., Aktulga, H. M., Berger, R., Bolintineanu, D. S., Brown, W. M., Crozier, P. S., et al. (2022). Lammps - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171. doi:10.1016/j.cpc.2021.108171

CrossRef Full Text | Google Scholar

Tibbetts, G. G. (1984). Why are carbon filaments tubular? J. Cryst. Growth 66, 632–638. doi:10.1016/0022-0248(84)90163-5

CrossRef Full Text | Google Scholar

Tozzini, V., and Pellegrini, V. (2011). Reversible hydrogen storage by controlled buckling of graphene layers. J. Phys. Chem. C 115, 25523–25528. doi:10.1021/jp208262r

CrossRef Full Text | Google Scholar

Troiani, H. E., Miki-Yoshida, M., Camacho-Bragado, G. A., Marques, M. A. L., Rubio, A., Ascencio, J. A., et al. (2003). Direct observation of the mechanical properties of single-walled carbon nanotubes and their junctions at the atomic level. Nano Lett. 3, 751–755. doi:10.1021/nl0341640

CrossRef Full Text | Google Scholar

van Duin, A. C. T., Dasgupta, S., Lorant, F., and Goddard, W. A. (2001). Reaxff: A reactive force field for hydrocarbons. J. Phys. Chem. A 105, 9396–9409. doi:10.1021/jp004368u

CrossRef Full Text | Google Scholar

Walters, D. A., Ericson, L. M., Casavant, M. J., Liu, J., Colbert, D. T., Smith, K. A., et al. (1999). Elastic strain of freely suspended single-wall carbon nanotube ropes. Appl. Phys. Lett. 74, 3803–3805. doi:10.1063/1.124185

CrossRef Full Text | Google Scholar

Weiner, S. J., Kollman, P. A., Case, D. A., Singh, U. C., Ghio, C., Alagona, G., et al. (1984). A new force field for molecular mechanical simulation of nucleic acids and proteins. J. Am. Chem. Soc. 106, 765–784. doi:10.1021/ja00315a051

CrossRef Full Text | Google Scholar

Weiner, S. J., Kollman, P. A., Nguyen, D. T., and Case, D. A. (1986). An all atom force field for simulations of proteins and nucleic acids. J. Comput. Chem. 7, 230–252. doi:10.1002/jcc.540070216

PubMed Abstract | CrossRef Full Text | Google Scholar

Wirz, L. N., Tonner, R., Hermann, A., Sure, R., and Schwerdtfeger, P. (2016). From small fullerenes to the graphene limit: A harmonic force-field method for fullerenes and a comparison to density functional calculations for goldberg–coxeter fullerenes up to c980. J. Comput. Chem. 37, 10–17. doi:10.1002/jcc.23894

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, M.-F., Files, B. S., Arepalli, S., and Ruoff, R. S. (2000). Tensile loading of ropes of single wall carbon nanotubes and their mechanical properties. Phys. Rev. Lett. 84, 5552–5555. doi:10.1103/PhysRevLett.84.5552

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, X., Zhang, Y., Li, Y., and Liu, W. (2019). Molecular dynamics simulation of shear deformation of multi-layer graphene sheets with tersoff potential. Int. J. Nanomanuf. 15, 12–24. doi:10.1504/IJNM.2019.097235

CrossRef Full Text | Google Scholar

Zhu, Z., Fthenakis, Z. G., Guan, J., and Tománek, D. (2014). Topologically protected conduction state at carbon foam surfaces: An ab initio study. Phys. Rev. Lett. 112, 026803. doi:10.1103/PhysRevLett.112.026803

PubMed Abstract | CrossRef Full Text | Google Scholar