- 1School of Chemistry, Beihang University, Beijing, China
- 2Beijing Advanced Innovation Center for Biomedical Engineering, Beihang University, Beijing, China
- 3Beijing Shenyun Zhihe Technology Co., Ltd., Beijing, China
A holey carbon material with ordered sub-nanometer hole defects was synthesized from oxidative cyclodehydrogenation of a polyhexaphenylbenzene precursor. Band gap of around 2.2 eV is formed due to the narrow connection between the hexabenzocoronene subunits. It has weak interlayer interaction energy compared with graphene and shows easy dispersion in a wide range of solvents, surprisingly including water. Density functional theory calculations confirmd the excellent dispersion of this material in water. This new carbon material was then proved as effective support for various inorganic nanoparticles of small sizes. The supported iron nanoparticles showed enzyme-like catalysis behavior in nitrophenyl reduction reaction by NaBH4, exemplifying the great potential of this new material in catalysis.
Introduction
Graphene has garnered interest from people from all disciplines, because of its peculiar two-dimensional carbon-based conjugated structure (Geim and Novoselov, 2007). Graphene is a two-dimensional structure with sp2-honeycomb carbon lattice (Song et al., 2013). The formation of π bonds in the graphene honeycomb lattice creates a closed shell electron system. The superposition of multiple closed electronic shell systems produces an interaction dominated by repulsion, resulting in weak electronic coupling between the layers (Berashevich and Chakraborty, 2011). The weak interlayer interaction of graphene gives it a wide range of properties and applications (Lebedeva et al., 2011). The change of the force between graphene layers will have an important impact on its properties. Enhancing the interlayer interaction of bilayer graphene can effectively modulate the thermal transport (Sun et al., 2019). As the number of graphene layers increases, the interaction energy changes, and the room temperature thermal conductivity drops sharply (Ghosh et al., 2010). The interaction of bilayer graphene significantly changes the zero-field electronic structures, and has more abundant optical properties than monolayer graphene (Ho et al., 2010). Interlayer interaction will also affect the hydrogenation rate and selective etching (Imamura and Saiki, 2014). Exploring the interaction energy between graphene layers will help to prepare materials with novel functions.
The interlayer interaction of graphene is closely related to the dispersion of graphene. The energy barrier is introduced through electrostatic or steric repulsion to achieve electrostatically stability or steric stability and maintain a dispersion (Johnson et al., 2015; Hong et al., 2012). Many methods can be used to increase the dispersion of graphene. The graphite exfoliation (Yi et al., 2013; Bourlinos et al., 2009), microwave-assisted synthesis and functional modification methods can increase the dispersibility of graphene in water (Li et al., 2019; Long et al., 2011; Zuo et al., 2010; Wang et al., 2020; Jiang et al., 2019). By changing the solvent, graphite oxide can be stably dispersed in organic solvents (Mu et al., 2021), such as N,N-dimethylformamide (DMF) and tetrahydrofuran (THF). This can be explained as the polarity of the solvent molecules and graphene oxide sheets are comparable (Paredes et al., 2008). The selective adsorption of functional groups on graphene can increase its dispersibility in suitable solvents. The 1, 3-dipole cycloaddition can make graphene layers have higher dispersibility in water and DMF (Quintana et al., 2013). These methods affect the interlayer interaction of graphene, thereby improving the dispersion properties of graphene.
Graphene with sub-nanopores has a wide range of applications in ion transport (Suk and Aluru, 2014), selective ion sieving (van Deursen et al., 2019), seawater desalination (Xu et al., 2019), supercapacitors (Lee et al., 2016), etc., Graphene with nanopores has a strong water permeability and can be used as a reverse osmosis desalination membrane (Cohen-Tanugi and Grossman, 2014). The incorporate of three-dimensional nanopore crystals with sub-nano sized aperture size into the two-dimensional graphene laminate greatly improves the separation performance of water (Guan et al., 2017). Carbon materials with rich topological defects of high entropy have great potential in the field of electrocatalysis (Feng and Zhuang, 2020; Ding et al., 2021; Feng and Zhuang, 2021). Herein we would like to report our work of bulk synthesis of a graphene derivative with regular sub-nanometer defects. Correlation calculations confirm that its interlayer interaction energy is smaller than that of graphene, which leads to its unique dispersibility and electrocatalytic properties. Experiments and density functional theory (DFT) calculations confirmed that it can be dissolved in water well. Our work provides a new method for the dispersion and trapping of metal atoms in graphene in water.
Preparation and Bandgap of Polyhexabenzocoronene Network
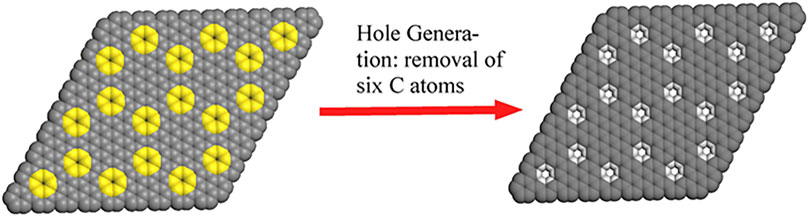
For bottom-up approach, the reaction condition in solution is much milder than that in previous top-down approaches, the formed small holes, which is found to self-heal under the high energy electron beam (Zan et al., 2012), are then expected to survive during the synthesis (Bieri et al., 2009). In addition, bottom-up approach offers structural precision and future tunability, since their structure follows deterministically from small-molecule precursors readily modified through organic synthesis. As shown in Figure 1, the removal of six adjacent carbons periodically from graphene layer will generate a holey graphene with sub-nanometer holes and hexabenzocoronene subunits. The hexabenzocoronene subunits are intentionally targeted due to the fact that relative hexaphenylbenzene precursors can be readily made. The careful design leads to extremely simple experimental procedure, and we surprisingly found that the designed holey graphene structure can be easily made in bulk through simple oxidation reaction of a topologically equivalent polyhexaphenylbenzene network (PHN). Upon be soaked in the CH2Cl2 solution of FeCl3 at room temperature, white PHN powder turned into dark brown immediately, which indicated the occurrence of the cyclodehydrogenation reaction. Finally, we obtained the anticipated polyhexabenzocoronene network (PBN). More synthetic details and structural confirmation are provided in our another manuscript (Liu et al., 2022).
PBN has a bandgap of around 2.2 eV, which matches very well with the calculated 2.1 eV at the HSE06 level and has a high accuracy in predicating bandgap energy. The bandgap is significantly reduced from those of hexabenzocoronene derivatives (2.7 ∼ 3 ev) (Hiszpanski et al., 2015; Hughes et al., 2012; Davy et al., 2016), again reflecting the highly conjugated nature of PBN. From the point view of holey graphene, the bandgap of this 2D hole-decorated graphene is justified by the narrow bridges between adjacent hexabenzocoronene units, whose width is inversely proportional to bandgap value (Son et al., 2006).
Interlayer Interaction Energy of Polyhexabenzocoronene Network
Non-covalent interactions, including π-π interactions and van der Waals forces, are related to the dispersion of graphene (Georgakilas et al., 2016). Studying the non-covalent interaction between graphene and PBN can help explain the difference in the properties of the two. Independent gradient model (IGM) analysis, a method based on electron density (ED), can identify and isolate the interaction between user-defined fragments, using pro-molecular density (Lefebvre et al., 2017; Lu and Chen, 2022). Three models of double-layer PBN, double-layer graphene, one-layer PBN and one-layer graphene were considered to explore the difference of non-covalent interaction between PBN and graphene layers, as shown in Figure 2. The AA stacking structures were employed to qualitatively analyze the differences between the different models, ignoring the effect of different stacking models. The structure of the model was optimized first, and then the optimized structure was analyzed by IGM.
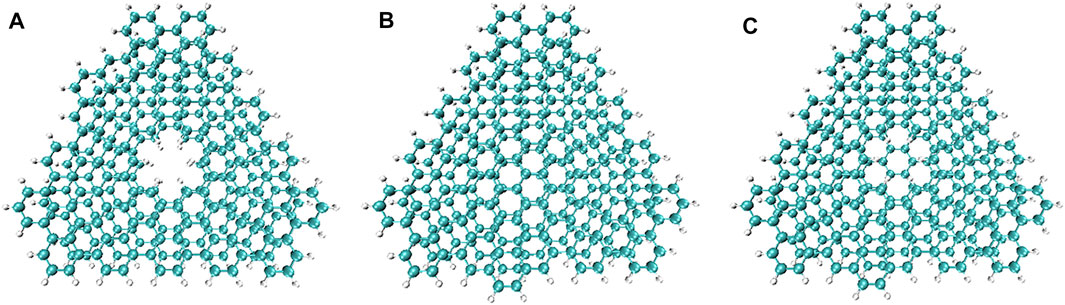
FIGURE 2. Structure diagram of (A) double-layer PBN, (B) double-layer graphene, and (C) one-layer PBN and one-layer graphene. The layer spacing is approximately 0.35 nm. Geometric structures were shown through VMD software (Humphrey et al., 1996).
The structure optimization and single point energy calculation were performed with the ORCA package (Neese, 2012; Neese, 2018). The calculation used the BLYP functional, the def2-SVP basis set and the def2-SVP/J auxiliary basis set. The DFT-D3 dispersion correction with the Becke-Johnson damping function and tight SCF convergence criteria were used for calculation (Grimme et al., 2010; Grimme, 2011; Grimme et al., 2011; Becke and Johnson, 2006). The calculation solved the basis set superposition error (BSSE) problem by performing the geometrical Counterpoise Correction (gCP) at the level of a compound of the DFT and the def2-SVP basis set. The final single point energies after gCP correction of the three models and the individual layers of each model were counted. In order to describe the interaction energy between PBN or graphene, we define the interaction energy
where
It can be seen from Table 1 that the interlayer interaction energy of double-layer PBN is smaller than that of double-layer graphene, indicating that the existence of pores has an impact on non-covalent interaction. The interaction energy between one-layer PBN and one-layer graphene is slightly smaller than that of a double layer of graphene, indicating that the non-covalent interaction between the two pores is more obvious. In order to further explore the influence of pores on non-covalent interactions, IGM analyses were performed on the three optimized models using Multiwfn software 3.7 (Lu and Chen, 2012). In IGM analyses, δginter is used to describe the interaction between molecules, which is defined as:
where
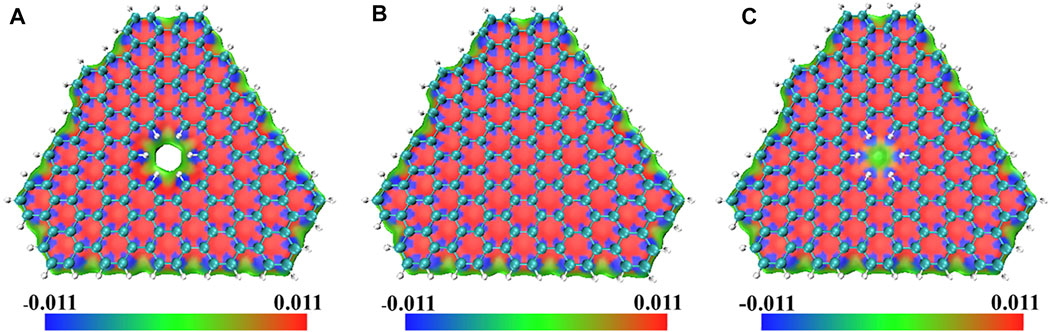
FIGURE 3. The sign
In the blue area in Figure 3, the value of the sign
Dispersion of Polyhexabenzocoronene Network
PBN can be readily dispersed in a wide range of solvents. Unlike graphene and most 2D materials, PBN spontaneously disperses in common organic solvents to form dark red dispersion upon sonication (Figure 4A). The stability of the dispersion is also adjustable by the choices of solvents, with the dispersant ability roughly following the order of DEF, CHCl3, H2O > Acetone > Ethanol > HOAc, DMSO, cyclohexane, toluene, EtOAc. AFM analysis on the aqueous dispersion show plates with the heights of 1∼2 nm and diameters of up to 200 nms (Figure 4B), reflecting the few-layer dispersion in water. As far as we know, PBN represents the first 2D material that form stable dispersion in both hydrophobic and hydrophilic solvents without any additives. The simple and easy dispersion of PBN in a wide range of solvents up to single-layer level represents a significant advance in dispersible 2D materials (Marco et al., 2017). We suspect that the presence of sub-nanometer holes reduces inter-layer interaction while providing strong interaction with some specific small molecules. DFT calculations were performed to understand the dispersion of PBN in water.
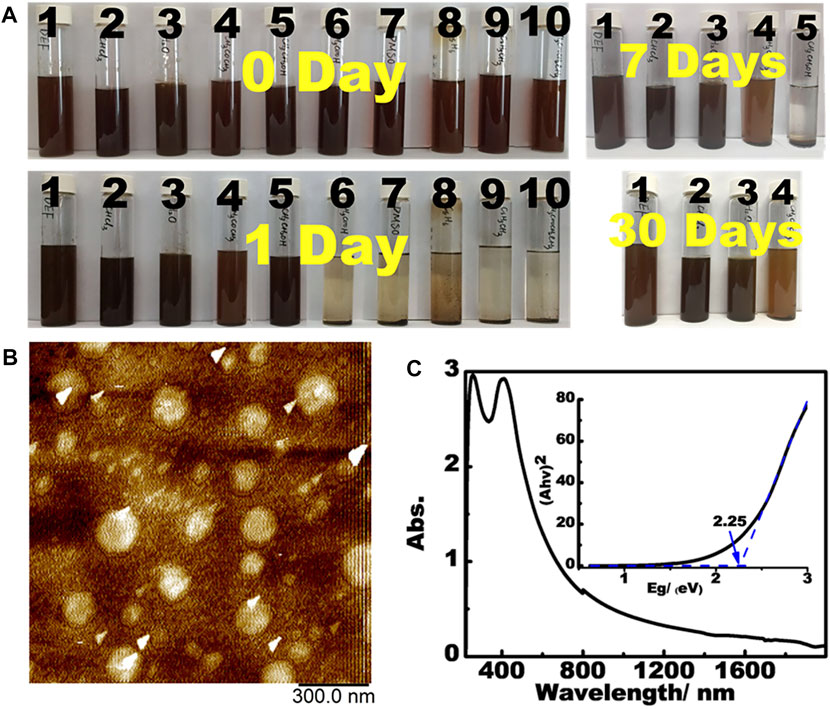
FIGURE 4. (A) The dispersion of PBN in various solvents (10 mg/20 ml). Solvent list: (1) diethylformamide, (2) chloroform, (3) water, (4) acetone, (5) ethanol, (6) acetic acid, (7) DMSO, (8) cyclohexane, (9) toluene, and (10) ethyl acetate. (B) AFM images of aqueous dispersion. (C) UV-Vis-Near IR spectra of PBN with the insert showing the band gap calculation.
All dispersion calculations of PBN were performed using the Vienna Ab initio Simulation Package (VASP) code (Kresse and Hafner, 1994; Kresse and Furthmüller, 1996). The Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA) functional and the projected augmented wave (PAW) potential were used to describe the exchange–correlation potential and the ion-electron interactions, respectively. (Perdew et al., 1996; Kresse and Joubert, 1999). The kinetic energy cutoff for the plane-wave base was set to 500 eV and a 2 × 2 × 1 Gamma k-point mesh was used to sample PBN and H2O molecules. In the case of a fixed unit cell volume, the convergence criterion of 10−4 eV for electron energy and convergence criterion of 10−2 eV/Å for the forces on each ion were used to optimize all structures. The Many-body dispersion energy method (MBD@rsSCS) was used to determine the interaction energy of PBN and water molecules to account for van der Waals interactions (Lebègue et al., 2010).
In the optimization process of PBN and H2O structure, we chose gaussian smearing to decide how to set the partial occupancies for each orbital. For the optimized structure, tetrahedron method with Blchl corrections was selected for accurate energy calculation, and the structures of PBN and H2O were extracted from it, and the same method was used for energy calculation. In order to describe the interaction energy between PBN and water, we define the adsorption energy
where
When PBN adsorbed a water molecule, the initial structure and the adsorption energy of the water molecule at different positions is shown in Figure 5. The Figures 5B–E are similar, indicating that the water molecules above the hole will automatically gather to the center of the hole during the optimization process. The holes may have a certain effect on the accumulation of water molecules. In comparison, the adsorption energy was only 0.06 eV when the adsorption site was nearby the center of hexabenzocoronene units, which was actually not unexpected given the bad solubility of large CH aromatics in water. Therefore, the presence of CH decorated holes is crucial to the strong interaction of PBN with water molecules.
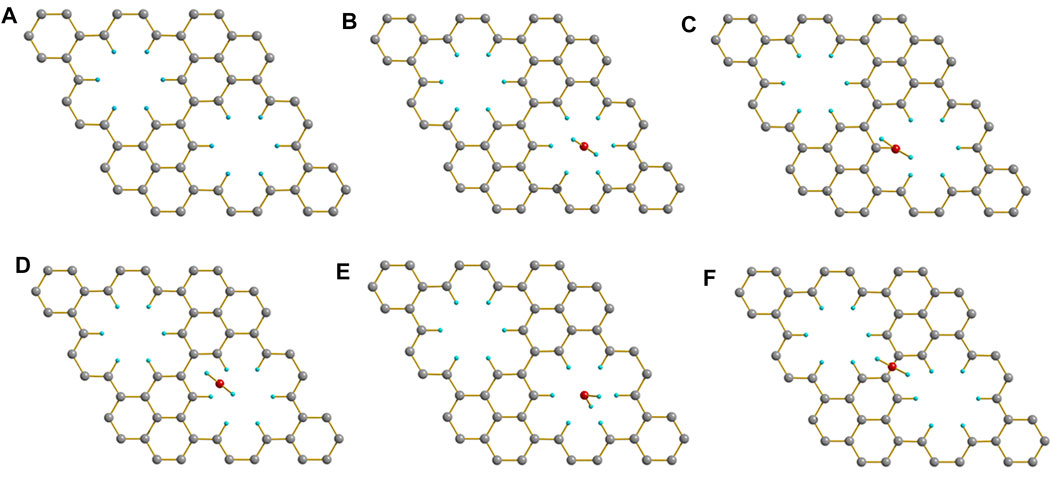
FIGURE 5. (A) The crystal structure of PBN. When the water molecule was initially located, (B) above the center of the hole, (C) above the H atom of the hole, (D) above the center of the H-H bond of the hole, (E) above the center of the hole, and (F) above the entire PBN, the optimized crystal structure. Geometric structures were shown through Diamond software.
The adsorption energy of PBN with different positions of water is shown in Table 2. The optimized results and the adsorption energy of the first four cases in Table 2 are similar, and they are all greater than the adsorption energy of the last case, indicating that when H2O is above the pores, PBN has a significant adsorption effect on water. In order to investigate the water solubility of PBN, the adsorption energy between PBN and multiple water molecules and double-layer PBN was calculated, as shown in Figure 6.
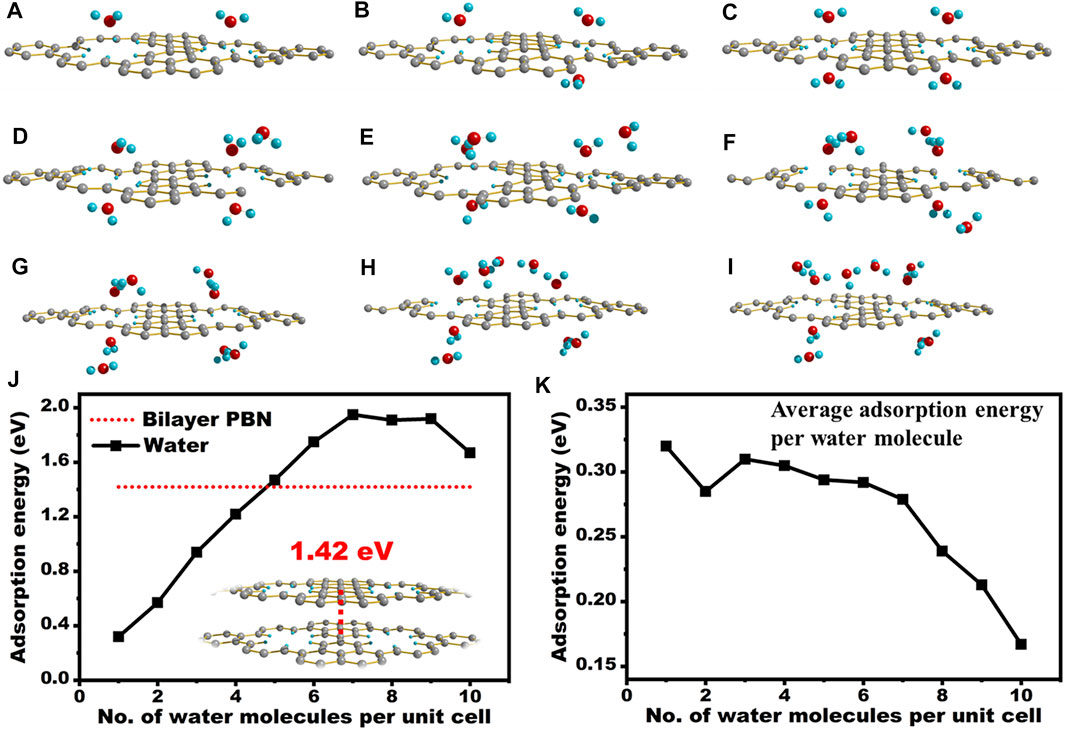
FIGURE 6. Calculation of the adsorption energy of water interacted with PBN. (A–I) The optimized structure of PBN and two water to ten water molecules, (J) The optimized structure of double-layer PBN and the absolute value of adsorption energy of different structures, (K) The absolute value of adsorption energy per water molecule when PBN interacts with different water molecules. Geometric structures were shown through Diamond software.
DFT investigation of the interaction of PBN layer with water molecules revealed the interesting role of these sub-nanometer holes. The adsorption energy of one water molecule nearby the holes was around 0.32 eV or 7.34 kcal/mol, which was comparable to or even stronger than common hydrogen bond. In fact, the hydrogen bonding between two water molecules was estimated to be around 0.2 eV. This strong interaction will withdraw water molecule to the vicinity of PBN from the bulk solution. We further increased the number of water molecules per unit cell to probe maximum interaction per hole with water. With the increased in the number of water molecules around the PBN pores, the adsorption energy of PBN gradually increased, but the increasing trend gradually became flat. When it increased to about five waters, the adsorption energy of PBN and water molecules was greater than the interaction energy of double-layer PBN molecules. As shown in Figure 6J, as more water molecules were place around the hole, the overall adsorption energy increased almost linearly to 1.9 eV. Excess water molecules may decrease the average adsorption energy per water molecule due to the formation of clusters (Figure 6K). We also computed the interlayer interaction of PBN, which was around 1.4 eV per unit cell, and it was actually smaller than the interaction between PBN and five water molecules. This explained the good dispersion of PBN in water.
Application of Polyhexabenzocoronene Network in Catalysis
Treatment of unwashed PBN, which is loaded with FeCl2, with excessive NaBH4 in ethanol leads PBN supported Fe NPs. The low atomic number of Fe prevents direct imaging, but galvanic replace of Fe2+ by Ru3+ leads to clear view of the extremely small nano Fe particles with sizes around 1 nm (Figure 7A) (Hudson et al., 2015), expected size value from the quantitative cyclodehydrogenation of polyhexaphenylbenzene network (PHN). We further take advantage of the feasible dispersion of PBN to combine with various metal precursors in solution in order to expand the scope of loaded NPs. Interestingly, various PBN-NPs can be easily prepared simply by chemical reduction of relative metal salts in ethanol in the presence of PBN. This simple procedure leads to preparation of supported Pt, Pd, Ru, Rh, and Ni NPs by PBN (Figure 7). The sizes of the NPs range from 2 to 5 nm, reflecting the effective confinement of the growth of inorganic NPs by PBN. The wide range of supported NPs is consistent with previous DFT calculation which predicates strong interaction between small graphene defects and different various clusters (Navalon et al., 2016).
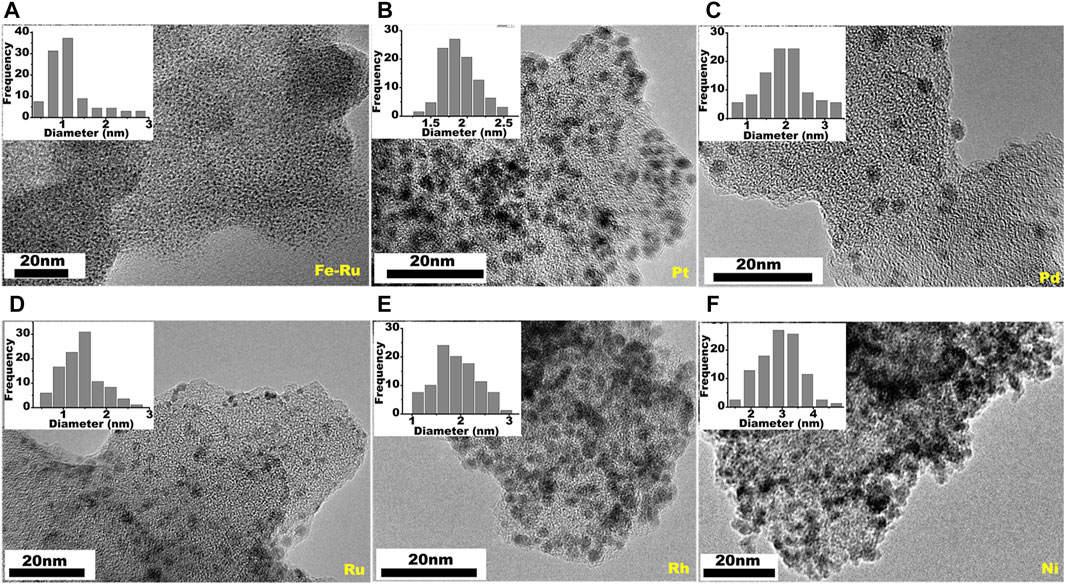
FIGURE 7. TEM images of PBN supported transition nanoparticles of (A) Fe-Ru, (B) Pt, (C) Pd, (D) Ru, (E) Rh, (F) Ni.
The use of these semiconducting PBN supported transition metal NPs was preliminarily tested on the reduction of nitrobenzene by NaBH4 by use of PBN-FeCl2 at room temperature. PBN-FeCl2 exhibits a remarkably different catalysis behavior compared to pure FeCl2, which show sluggish first-order reaction kinetics (Figure 8A) (MacNair et al., 2014). PBN-FeCl2 showed both greatly improved reaction yield and speed at the same 10 wt% loading. The formation of aniline product reaches quantitative within 20 min and the reaction speed remains constant up to around 95% yield, a phenomenon belonging to the zero-order reaction kinetics.
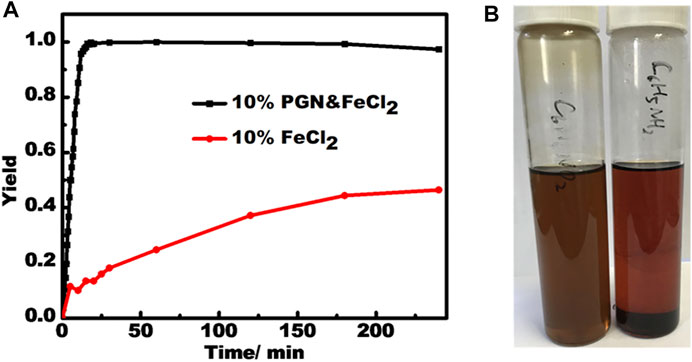
FIGURE 8. (A) The reaction kinetics for catalysts of PBN-FeCl2 and FeCl2. (B) The dispersion solutions of PBN in nitrobenzene and aniline respectively after 2 h.
The super performance of PBN-FeCl2 may be attributed to several factors associated with unique properties of PBN mentioned above. First, the zero-order kinetics indicates that there is a strong substrate binding prior to the occurrence of the catalysis on the surface of the Fe NPs, very similar to the enzyme-substrate binding in enzyme catalysis (Koerner et al., 1959). In fact, the PBN dispersion in nitrobenzene is stable up to months without significant settlement while PBN almost completely settles down in phenylaniline within a few hours (Figure 8B). This dispersion phenomenon indicates the strong binding of reactant and weak binding of the product, a prerequisite for efficient enzyme-like catalysis. Second, together with the small sizes of Fe NPs, their naked nature without any extra functional groups offers more reactive sites to interact with reactants, and therefore speeding up the reaction. Third, the semiconducting nature of PBN and its close contact with the Fe nanoparticles may change the electronic nature on the surface through the Mott-Schottky hetero junctions (Su et al., 2017). In addition, filtration test was conducted to validate the nature of heterogeneous catalysis by PBN-FeCl2.
In addition to its promise in next-generation graphene-based heterogenous catalysts, PBN is also attractable for application in gas-filtration (Jiang et al., 2009), water-desalination (Cohen-Tanugi and Grossman, 2012), semiconductor devices (Kim et al., 2011), electromechanical sensors et al. (Boland Conor et al., 2016). where sub-nanometer holes, band-gap or feasible dispersion is required, indicating a wide application space.
Conclusion
In conclusion, a holey carbon material with ordered sub-nanometer hole defects (polyhexabenzocoronene network, PBN) was synthesized by oxidative cyclodehydrogenation with polyhexaphenylbenzene as precursor. The IGM analyses of PBN and graphene show that PBN has weak interlayer interaction energy compared with graphene, which makes PBN has better dispersion performance than graphene. The DFT calculations show that the holes in PBN will attract water molecules nearby. With the number of water molecules increased, the interaction energy between PBN and water gradually increased, and when it reached saturation, the interaction energy of PBN and water was greater than that of double-layer graphene, which confirmed the excellent dispersion of PBN in water. It is proved experimentally that PBN can be dissolved in many other solvents in addition to water. PBN can effectively support various inorganic nanoparticles of small sizes, and when PBN supports iron nanoparticles, it has high catalytic activity in the reduction of nitrophenyl by NaBH4, indicating that it has great potential in catalysis.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
All the authors conceived the theme and method of the research, and discussed the data. NL, QL, GP, and CL wrote the manuscript. QL, GP, and CL carried out the experiments. NL carried out the theoretical calculations. YL reviewed and edited the manuscript. All authors approved the submitted version of the manuscript.
Funding
This work was supported by Beihang University Research Fund 74004601, Youth 1000 Talent Fund KZ37029501, and the 111 Project (B14009). This research was supported by the high performance computing (HPC) resources at Beihang University and the DeepChem platform from Shenyunzhihe Company.
Conflict of Interest
YL was employed by the company Beijing Shenyun Zhihe Technology Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2022.858154/full#supplementary-material
References
Becke, A. D., and Johnson, E. R. (2006). Exchange-hole Dipole Moment and the Dispersion Interaction: High-Order Dispersion Coefficients. J. Chem. Phys. 124, 014104. doi:10.1063/1.2139668
Berashevich, J., and Chakraborty, T. (2011). On the Nature of Interlayer Interactions in a System of Two Graphene Fragments. J. Phys. Chem. C 115, 24666–24673. doi:10.1021/jp2095032
Bieri, M., Treier, M., Cai, J., Aït-Mansour, K., Ruffieux, P., Gröning, O., et al. (2009). Porous Graphenes: Two-Dimensional Polymer Synthesis with Atomic Precision. Chem. Commun., 6919–6921. doi:10.1039/b915190g
Boland, C. S., Khan, U., Ryan, G., Barwich, S., Charifou, R., Harvey, A., et al. (2016). Sensitive Electromechanical Sensors Using Viscoelastic Graphene-Polymer Nanocomposites. Science 354, 1257–1260. doi:10.1126/science.aag2879
Bourlinos, A. B., Georgakilas, V., Zboril, R., Steriotis, T. A., Stubos, A. K., and Trapalis, C. (2009). Aqueous-phase Exfoliation of Graphite in the Presence of Polyvinylpyrrolidone for the Production of Water-Soluble Graphenes. Solid State. Commun. 149, 2172–2176. doi:10.1016/j.ssc.2009.09.018
Cohen-Tanugi, D., and Grossman, J. C. (2012). Water Desalination across Nanoporous Graphene. Nano Lett. 12, 3602–3608. doi:10.1021/nl3012853
Cohen-Tanugi, D., and Grossman, J. C. (2014). Mechanical Strength of Nanoporous Graphene as a Desalination Membrane. Nano Lett. 14, 6171–6178. doi:10.1021/nl502399y
Davy, N. C., Man, G., Kerner, R. A., Fusella, M. A., Purdum, G. E., Sezen, M., et al. (2016). Contorted Hexabenzocoronenes with Extended Heterocyclic Moieties Improve Visible-Light Absorption and Performance in Organic Solar Cells. Chem. Mater. 28, 673–681. doi:10.1021/acs.chemmater.5b04503
Ding, J., Wu, D., Zhu, J., Huang, S., Rodríguez-Hernández, F., Chen, Y., et al. (2021). High-entropy Carbons: From High-Entropy Aromatic Species to Single-Atom Catalysts for Electrocatalysis. Chem. Eng. J. 426, 131320. doi:10.1016/j.cej.2021.131320
Feng, B., and Zhuang, X. (2020). Carbon-Enriched Meso-Entropy Materials: from Theory to Cases. Acta Chim. Sinica 78, 833–847. doi:10.6023/A20050167
Feng, B., and Zhuang, X. (2021). The Philosophy of Carbon: Meso-Entropy Materials. Faraday Discuss. 227, 80–90. doi:10.1039/c9fd00115h
Geim, A. K., and Novoselov, K. S. (2007). The Rise of Graphene. Nat. Mater 6, 183–191. doi:10.1038/nmat1849
Georgakilas, V., Tiwari, J. N., Kemp, K. C., Perman, J. A., Bourlinos, A. B., Kim, K. S., et al. (2016). Noncovalent Functionalization of Graphene and Graphene Oxide for Energy Materials, Biosensing, Catalytic, and Biomedical Applications. Chem. Rev. 116, 5464–5519. doi:10.1021/acs.chemrev.5b00620
Ghosh, S., Bao, W., Nika, D. L., Subrina, S., Pokatilov, E. P., Lau, C. N., et al. (2010). Dimensional Crossover of thermal Transport in Few-Layer Graphene. Nat. Mater 9, 555–558. doi:10.1038/nmat2753
Grimme, S. (2011). Density Functional Theory with London Dispersion Corrections. Wires Comput. Mol. Sci. 1, 211–228. doi:10.1002/wcms.30
Grimme, S., Antony, J., Ehrlich, S., and Krieg, H. (2010). A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 132, 154104. doi:10.1063/1.3382344
Grimme, S., Ehrlich, S., and Goerigk, L. (2011). Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 32, 1456–1465. doi:10.1002/jcc.21759
Guan, K., Zhao, D., Zhang, M., Shen, J., Zhou, G., Liu, G., et al. (2017). 3D Nanoporous Crystals Enabled 2D Channels in Graphene Membrane with Enhanced Water Purification Performance. J. Membr. Sci. 542, 41–51. doi:10.1016/j.memsci.2017.07.055
Hiszpanski, A. M., Saathoff, J. D., Shaw, L., Wang, H., Kraya, L., Lüttich, F., et al. (2015). Halogenation of a Nonplanar Molecular Semiconductor to Tune Energy Levels and Bandgaps for Electron Transport. Chem. Mater. 27, 1892–1900. doi:10.1021/acs.chemmater.5b00329
Ho, Y. H., Wu, J. Y., Chiu, Y. H., Wang, J., and Lin, M. F. (2010). Electronic and Optical Properties of Monolayer and Bilayer Graphene. Phil. Trans. R. Soc. A. 368, 5445–5458. doi:10.1098/rsta.2010.0209
Hong, B. J., Compton, O. C., An, Z., Eryazici, I., and Nguyen, S. T. (2012). Successful Stabilization of Graphene Oxide in Electrolyte Solutions: Enhancement of Biofunctionalization and Cellular Uptake. ACS Nano 6, 63–73. doi:10.1021/nn202355p
Hudson, R., Chazelle, V., Bateman, M., Roy, R., Li, C.-J., and Moores, A. (2015). Sustainable Synthesis of Magnetic Ruthenium-Coated Iron Nanoparticles and Application in the Catalytic Transfer Hydrogenation of Ketones. ACS Sust. Chem. Eng. 3, 814–820. doi:10.1021/acssuschemeng.5b00206
Hughes, J. M., Hernandez, Y., Aherne, D., Doessel, L., Müllen, K., Moreton, B., et al. (2012). High Quality Dispersions of Hexabenzocoronene in Organic Solvents. J. Am. Chem. Soc. 134, 12168–12179. doi:10.1021/ja303683v
Humphrey, W., Dalke, A., and Schulten, K. (1996). VMD: Visual Molecular Dynamics. J. Mol. Graphics 14, 33–38. doi:10.1016/0263-7855(96)00018-5
Imamura, G., and Saiki, K. (2014). Interlayer Interaction in the UV Irradiated Defect Formation of Graphene. J. Phys. Chem. C 118, 11842–11848. doi:10.1021/jp503802d
Jiang, D.-e., Cooper, V. R., and Dai, S. (2009). Porous Graphene as the Ultimate Membrane for Gas Separation. Nano Lett. 9, 4019–4024. doi:10.1021/nl9021946
Jiang, H.-B., Liu, Y., Liu, J., Li, S.-Y., Song, Y.-Y., Han, D.-D., et al. (2019). Moisture-Responsive Graphene Actuators Prepared by Two-Beam Laser Interference of Graphene Oxide Paper. Front. Chem. 7, 464. doi:10.3389/fchem.2019.00464
Johnson, E. R., Keinan, S., Mori-Sánchez, P., Contreras-García, J., Cohen, A. J., and Yang, W. (2010). Revealing Noncovalent Interactions. J. Am. Chem. Soc. 132, 6498–6506. doi:10.1021/ja100936w
Johnson, D. W., Dobson, B. P., and Coleman, K. S. (2015). A Manufacturing Perspective on Graphene Dispersions. Curr. Opin. Colloid Interf. Sci. 20, 367–382. doi:10.1016/j.cocis.2015.11.004
Kim, K., Choi, J.-Y., Kim, T., Cho, S.-H., and Chung, H.-J. (2011). A Role for Graphene in Silicon-Based Semiconductor Devices. Nature 479, 338–344. doi:10.1038/nature10680
Koerner, J. F., Smith, M. S., and Buchanan, J. M. (1959). A DEOXYCYTIDINE TRIPHOSPHATE SPLITTING ENZYME AND THE SYNTHESIS OF THE DEOXYRIBOSENUCLEIC ACID OF T2 BACTERIOPHAGE1. J. Am. Chem. Soc. 81, 2594–2595. doi:10.1021/ja01519a076
Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 54, 11169–11186. doi:10.1103/PhysRevB.54.11169
Kresse, G., and Hafner, J. (1994). Ab Initiomolecular-Dynamics Simulation of the Liquid-Metal-Amorphous-Semiconductor Transition in Germanium. Phys. Rev. B 49, 14251–14269. doi:10.1103/PhysRevB.49.14251
Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59, 1758–1775. doi:10.1103/PhysRevB.59.1758
Lebedeva, I. V., Knizhnik, A. A., Popov, A. M., Lozovik, Y. E., and Potapkin, B. V. (2011). Interlayer Interaction and Relative Vibrations of Bilayer Graphene. Phys. Chem. Chem. Phys. 13, 5687–5695. doi:10.1039/c0cp02614j
Lebègue, S., Harl, J., Gould, T., Ángyán, J. G., Kresse, G., and Dobson, J. F. (2010). Cohesive Properties and Asymptotics of the Dispersion Interaction in Graphite by the Random Phase Approximation. Phys. Rev. Lett. 105, 196401. doi:10.1103/PhysRevLett.105.196401
Lee, K., Yoon, Y., Cho, Y., Lee, S. M., Shin, Y., Lee, H., et al. (2016). Tunable Sub-nanopores of Graphene Flake Interlayers with Conductive Molecular Linkers for Supercapacitors. ACS Nano 10, 6799–6807. doi:10.1021/acsnano.6b02415
Lefebvre, C., Rubez, G., Khartabil, H., Boisson, J.-C., Contreras-García, J., and Hénon, E. (2017). Accurately Extracting the Signature of Intermolecular Interactions Present in the NCI Plot of the Reduced Density Gradient versus Electron Density. Phys. Chem. Chem. Phys. 19, 17928–17936. doi:10.1039/c7cp02110k
Li, L., Zhou, M., Jin, L., Liu, L., Mo, Y., Li, X., et al. (2019). Research Progress of the Liquid-phase Exfoliation and Stable Dispersion Mechanism and Method of Graphene. Front. Mater. 6, 325. doi:10.3389/fmats.2019.00325
Liu, C., Pan, G., Liang, N., Hong, S., Ma, J., and Liu, Y. (2022). Ir Single Atom Catalyst Loaded on Amorphous Carbon Materials with High HER Activity. Adv. Sci. 9. doi:10.1002/advs.202105392
Long, J., Fang, M., and Chen, G. (2011). Microwave-assisted Rapid Synthesis of Water-Soluble Graphene. J. Mater. Chem. 21, 10421–10425. doi:10.1039/c0jm04564k
Lu, T., and Chen, F. (2012). Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 33, 580–592. doi:10.1002/jcc.22885
Lu, T., and Chen, Q. (2021). Interaction Region Indicator: A Simple Real Space Function Clearly Revealing Both Chemical Bonds and Weak Interactions**. Chem. Methods 1, 231–239. doi:10.1002/cmtd.202100007
Lu, T., and Chen, Q. (2022). Independent Gradient Model Based on Hirshfeld Partition: A New Method for Visual Study of Interactions in Chemical Systems. J. Comput. Chem. 43, 539–555. doi:10.1002/jcc.26812
MacNair, A. J., Tran, M.-M., Nelson, J. E., Sloan, G. U., Ironmonger, A., and Thomas, S. P. (2014). Iron-catalysed, General and Operationally Simple Formal Hydrogenation Using Fe(OTf)3 and NaBH4. Org. Biomol. Chem. 12, 5082–5088. doi:10.1039/C4OB00945B
Marco, A. B., Cortizo-Lacalle, D., Perez-Miqueo, I., Valenti, G., Boni, A., Plas, J., et al. (2017). Twisted Aromatic Frameworks: Readily Exfoliable and Solution-Processable Two-Dimensional Conjugated Microporous Polymers. Angew. Chem. Int. Ed. 56, 6946–6951. doi:10.1002/anie.201700271
Mu, S., Yue, J., Wang, Y., and Feng, C. (2021). Electrical, Piezoresistive and Electromagnetic Properties of Graphene Reinforced Cement Composites: A Review. Nanomaterials 11, 3220. doi:10.3390/nano11123220
Navalon, S., Dhakshinamoorthy, A., Alvaro, M., and Garcia, H. (2016). Metal Nanoparticles Supported on Two-Dimensional Graphenes as Heterogeneous Catalysts. Coord. Chem. Rev. 312, 99–148. doi:10.1016/j.ccr.2015.12.005
Neese, F. (2018). Software Update: the ORCA Program System, Version 4.0. Wires Comput. Mol. Sci. 8, e1327. doi:10.1002/wcms.1327
Paredes, J. I., Villar-Rodil, S., Martínez-Alonso, A., and Tascón, J. M. D. (2008). Graphene Oxide Dispersions in Organic Solvents. Langmuir 24, 10560–10564. doi:10.1021/la801744a
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865
Quintana, M., Vazquez, E., and Prato, M. (2013). Organic Functionalization of Graphene in Dispersions. Acc. Chem. Res. 46, 138–148. doi:10.1021/ar300138e
Son, Y.-W., Cohen, M. L., and Louie, S. G. (2006). Energy Gaps in Graphene Nanoribbons. Phys. Rev. Lett. 97, 216803. doi:10.1103/PhysRevLett.97.216803
Song, X., Hu, J., and Zeng, H. (2013). Two-dimensional Semiconductors: Recent Progress and Future Perspectives. J. Mater. Chem. C 1, 2952–2969. doi:10.1039/c3tc00710c
Su, H., Zhang, K.-X., Zhang, B., Wang, H.-H., Yu, Q.-Y., Li, X.-H., et al. (2017). Activating Cobalt Nanoparticles via the Mott-Schottky Effect in Nitrogen-Rich Carbon Shells for Base-free Aerobic Oxidation of Alcohols to Esters. J. Am. Chem. Soc. 139, 811–818. doi:10.1021/jacs.6b10710
Suk, M. E., and Aluru, N. R. (2014). Ion Transport in Sub-5-nm Graphene Nanopores. J. Chem. Phys. 140, 084707. doi:10.1063/1.4866643
Sun, Z., Yuan, K., Chang, Z., Zhang, X., Qin, G., and Tang, D. (2019). Efficient thermal Conductivity Modulation by Manipulating Interlayer Interactions: A Comparative Study of Bilayer Graphene and Graphite. J. Appl. Phys. 126, 125104. doi:10.1063/1.5115808
van Deursen, P. M. G., Tang, Z., Winter, A., Mohn, M. J., Kaiser, U., Turchanin, A. A., et al. (2019). Selective Ion Sieving through Arrays of Sub-nanometer Nanopores in Chemically Tunable 2D Carbon Membranes. Nanoscale 11, 20785–20791. doi:10.1039/c9nr05537a
Wang, B., Liu, Q., and Fan, Z. (2020). A Mini Review: Application Progress of Magnetic Graphene Three-Dimensional Materials for Water Purification. Front. Chem. 8, 595643. doi:10.3389/fchem.2020.595643
Xu, G.-R., Xu, J.-M., Su, H.-C., Liu, X.-Y., Lu-Li, L., Zhao, H.-L., et al. (2019). Two-dimensional (2D) Nanoporous Membranes with Sub-nanopores in Reverse Osmosis Desalination: Latest Developments and Future Directions. Desalination 451, 18–34. doi:10.1016/j.desal.2017.09.024
Yi, M., Shen, Z., Liang, S., Liu, L., Zhang, X., and Ma, S. (2013). Water Can Stably Disperse Liquid-Exfoliated Graphene. Chem. Commun. 49, 11059–11061. doi:10.1039/c3cc46457a
Zan, R., Ramasse, Q. M., Bangert, U., and Novoselov, K. S. (2012). Graphene Reknits its Holes. Nano Lett. 12, 3936–3940. doi:10.1021/nl300985q
Keywords: holey carbon material, hole defects, water-soluble, low bandgap, catalytic activity
Citation: Liang N, Li Q, Pan G, Liu C and Liu Y (2022) Carbon Material With Ordered Sub-Nanometer Hole Defects. Front. Chem. 10:858154. doi: 10.3389/fchem.2022.858154
Received: 20 January 2022; Accepted: 01 March 2022;
Published: 21 March 2022.
Edited by:
Zhuhua Zhang, Nanjing University of Aeronautics and Astronautics, ChinaReviewed by:
Jincheng Lei, Yale University, United StatesXiaodong Zhuang, Shanghai Jiao Tong University, China
Ruiqi Zhao, Henan Polytechnic University, China
Copyright © 2022 Liang, Li, Pan, Liu and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuzhou Liu, bGl1eXV6aG91QGJ1YWEuZWR1LmNu
†These authors have contributed equally to this work
 Nianjie Liang1†
Nianjie Liang1† Qiaosheng Li
Qiaosheng Li