Designing Special Nonmetallic Superalkalis Based on a Cage-like Adamanzane Complexant

In this study, to examine the possibility of using cage-like complexants to design nonmetallic superalkalis, a series of X@3⁶adz (X = H, B, C, N, O, F, and Si) complexes have been constructed and investigated by embedding nonmetallic atoms into the 3⁶adamanzane (3⁶adz) complexant. Although X atoms possess very high ionization energies, these resulting X@3⁶adz complexes possess low adiabatic ionization energies (AIEs) of 0.78–5.28 eV. In particular, the adiabatic ionization energies (AIEs) of X@3⁶adz (X = H, B, C, N, and Si) are even lower than the ionization energy (3.89 eV) of Cs atoms, and thus, can be classified as novel nonmetallic superalkalis. Moreover, due to the existence of diffuse excess electrons in B@3⁶adz, this complex not only possesses pretty low AIE of 2.16 eV but also exhibits a remarkably large first hyperpolarizability (β₀) of 1.35 × 10⁶ au, indicating that it can also be considered as a new kind of nonlinear optical molecule. As a result, this study provides an effective approach to achieve new metal-free species with an excellent reducing capability by utilizing the cage-like organic complexants as building blocks.

Introduction

Reducing agents with low ionization energies (IEs) play a crucial role in chemical synthesis. As is well-known, alkali metal atoms possess the lowest ionization energies (5.39–3.89 eV) (Lide, 2003) among all the elements in the periodic table. However, it is reported that a class of extraordinary compounds possesses even lower IEs than those of alkali metal atoms. Such species were termed “superalkalis” by Gutsev and Boldyrev (1982). Initially, superalkalis were designed by decorating an electronegative central atom with alkali-metal ligands, such as FLi₂, OLi₃, and NLi₄ following the formula ML_k+1 (L is an alkali-metal atom and M is an electronegative atom of valency k). In ML_k+1, one more alkali metal atom will bring an extra valence electron for the electronic shell of M according to the octet rule. Consequently, such an ML_k+1 complex has a great tendency to lose the extra valence electron and thus possess strong reducibility (Sun and Wu, 2019).

Owing to their excellent reducing ability, superalkalis can be used to synthesize unusual charge-transfer salts (Zintl and Morawietz, 1938; Jansen, 1976) with the counterpart possessing relatively low electron affinity and activate stable CO₂ and N₂ molecules (Park and Meloni, 2017; Zhao et al., 2017; Park and Meloni, 2018; Sun et al., 2019; Sikorska and Gaston, 2020) to produce high-value products (Zhang et al., 2021a; Zhang et al., 2021b). In particular, as a special subset of superatom (Reveles et al., 2009; Luo and Castleman, 2014), superalkalis can behave as alkali metal atoms and maintain their structural and electronic integrities when assembled into extended nanostructures (Reber et al., 2007). Hence, they offer an exciting prospect of serving as building blocks for nanomaterials with highly tunable properties (Jena and Sun 2018), such as supersalts (Giri et al., 2014), hydrogen storage materials (Merino et al., 2012), noble-gas-trapping agents (Pan et al., 2013), superbases (Srivastava and Misra, 2015), and nonlinear optical materials (Sun et al., 2014a; Sun et al., 2014b; Sun et al., 2016b; Sun et al., 2016c; Sun et al., 2018a).

In view of the great importance of superalkalis in chemistry, various superalkalis have been theoretically (Tong et al., 2009; Tong et al., 2011, Tong et al., 2012a,Tong et al., 2012b; Hou et al., 2013; Liu et al., 2014; Sun et al., 2013; Sun et al., 2016a; Giri et al., 2016; Zhao et al., 2017; Sun et al., 2018b; Sun et al., 2019; Park and Meloni, 2018; Sun and Wu, 2019; Tkachenko et al., 2019; Sikorska and Gaston, 2020) and experimentally (Lievens et al., 1999; Yokoyama et al., 2000, 2001; Hou and Wang, 2020) characterized in the past decades. To date, conventional mononuclear ML_k+1 superalkalis have been expanded to dinuclear (Tong et al., 2009; Tong et al., 2011) and polynuclear (Tong et al., 2012a; Tong et al., 2012b; Liu et al., 2014) superalkalis, aromatic superalkalis (Sun et al., 2013), Zintl-ion-based superalkalis (Giri et al., 2016; Sun et al., 2018b), hyperalkalis (Sun et al., 2016a), alkali-metal complexes (Tkachenko et al., 2019), and so on. More importantly, some alkali-metal-free superalkalis (Hou et al., 2014; Liu et al., 2016), particularly nonmetallic superalkalis (Hou et al., 2013; Srivastava, 2019a; Srivastava, 2019b), have been proposed in recent years. For example, Hou et al. (2013) designed a class of M₂H_2n+1⁺ (M = F, O, N, C for n = 1, 2, 3, 4, respectively) superalkali cations by using hydrogen atoms as ligands. Following a similar rule, the other two series of nonmetallic superalkali cations, namely, F_nH_n+1⁺ (n = 1–10) and C_xH_4x+1⁺ (x = 1–5), have been proposed by Srivastava (2019a, 2019b). These achievements demonstrate that the potential of designing superalkalis of new type is limitless and thereby motivate us to create more diverse superalkali species by using different rules and ligands to further enrich the superalkali family.

More recently, Tkachenko et al. (2019) reported the record low ionization potentials (1.70–1.52 eV) of alkali metal complexes with crown ethers and cryptands and defined them as superalkali species. In fact, such alkali metal complexes were previously named as electrides, a special kind of ionic solids with trapped electrons serving as anions (Dye, 2009). Hence, this work first built a bridge between superalkalis and electrides. However, it is known that crown ethers and cryptands are prone to be cleaved at the C-O bonds (Redko et al., 2002). Fortunately, analogous complexants, such as adamanzane (adz) (Redko et al., 2002) and aza-cage (aza222) (Kim et al., 1999) with only C-N linkages and no amine hydrogens are considerably stable to synthesize the crystalline salts, including alkalides (Kim et al., 1999; Redko et al., 2002) and electrides (Redko et al., 2005) at room temperature. Hence, it is highly expected that such complexants could also be used as excellent building blocks to design and synthesize new superalkalis.

To verify this hypothesis, the 3⁶adamanzane (3⁶adz) has been chosen as a representative to design a series of X@3⁶adz (X = H, B, C, N, O, F, and Si) by encapsulating nonmetallic atoms into the cavity of this cage-like complexant in this work (see Figure 1). The 3⁶adz complexant is composed of tricyclic tetra-amines with aliphatic chains (Springborg, 2003), which has been used to synthesize a stable alkalide [H@3⁶adz]⁺Na⁻ (Redko et al., 2002). In this complexant, all the lone pairs of 4 N atoms direct toward the center of the cage (see Supplementary Figure S1). Under the repulsion of the lone pairs of N atoms, the outmost valence electrons of X are destabilized to different degrees, leading to the obvious rise of HOMO level of X@3⁶adz as compared with the isolated 3⁶adz complexant. As a result, these proposed complexes exhibit extraordinarily low AIE values of 0.78–5.28 eV although X atoms possess very high ionization energies (IEs) of 8.15–17.42 eV (Lide, 2003). In particular, the B@3⁶adz complex also has the potential to serve as new nonlinear optical (NLO) molecule with a remarkably large first hyperppolarizability of 1.35 × 10⁶ au because the valence electron of boron atom is pushed out of cage to form diffuse excess electrons. We hope that this work will not only provide new nonmetallic members for the superatom family, but will also open the door to design strong reducing matters by embedding nonmetallic atoms into the various cage-like complexants.

FIGURE 1

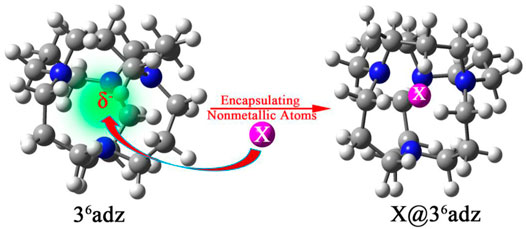
FIGURE 1. The schematic design strategy of X@3⁶adz (X = H, B, C, N, O, F, and Si) based on the cage-like 3⁶adz complexant.

Computational Details

In this work, all the calculations were carried out by using the coulomb-attenuated hybrid exchange-correlation functional (CAM-B3LYP) (Tawada et al., 2004; Yanai et al., 2004), which has been reported to be capable of providing not only the molecular geometries close to the experimentally observed structures but also the (hyper)polarizabilities close to those of the coupled cluster calculations (Limacher et al., 2009). Hence, this method has been widely used to calculate the (hyper)polarizabilities of NLO molecules in the previous works (Sun et al., 2014a; Sun et al., 2014b, Sun et al., 2016c). Also, a method test has also been carried out by sampling B@3⁶adz (see Supplementary Table S1) to verify the reliability of this method in calculating the properties of such systems. From Supplementary Table S1, it is found that CAM-B3LYP gives approximately equal VIE and β₀ to those obtained by several other functionals, which indicates that this method is reliable for these studied systems. Hence, all the optimized geometric structures of the studied species with real frequencies were obtained under the CAM-B3LYP/6-31+G(d) level. Based on the optimized structures, the single-point energies, nature population analysis (NPA) charges, and static electric properties were calculated at the CAM-B3LYP/6-311++G (d, p) level.

In this work, the vertical ionization energies (VIEs) of X@3⁶adz (X = H, B, C, N, O, F, and Si) were calculated as the energy difference between the optimized neutral complex and the cation in the geometry of the neutral complex, while their adiabatic ionization energies (AIEs) are defined as the energy difference between the neutral and cationic complex at their respective optimized structures. In addition, the TD-M06-2X calculations were performed to obtain the transition energies and oscillator strengths of the crucial excited states as well as the difference of the dipole moments between the ground state and crucial excited state of X@3⁶adz by using the 6-311++G (d, p) basis set. Herein, the dipole moments (µ₀), polarizabilities (α₀), and first hyperpolarizabilities (β₀) are defined as follows,

${\mu }_0={\left({\mu }_x^2+{\mu }_y^2+{\mu }_z^2\right)}^{1/2}(1)$

${\mathit{\alpha }}_0=\frac{1}{3}\left({\mathit{\alpha }}_{\mathit{xx}}+{\mathit{\alpha }}_{\mathit{yy}}+{\mathit{\alpha }}_{\mathit{zz}}\right)(2)$

${\beta }_0={\left({\beta }_x^2+{\beta }_y^2+{\beta }_z^2\right)}^{1/2}(3)$

where ${\beta }_i=\frac{1}{3}{\displaystyle \sum _j\left({\beta }_{ijj}+{\beta }_{jji}+{\beta }_{jij}\right)}$, i, j = {x, y, z}.

All the above calculations were performed by using the GAUSSIAN 16 program package (Frisch et al., 2016). The dimensional plots of the molecular structures were generated with the GaussView program (Dennington et al., 2016).

Results and Discussion

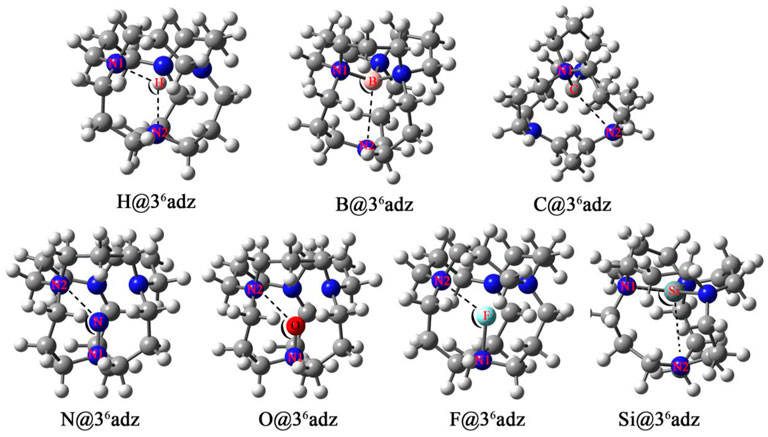
Initially, seven X@3⁶adz (X = H, B, C, N, O, F, and Si) compounds have been constructed by encapsulating one X atom into a 3⁶adz cage. After optimization, the geometric structures of X@3⁶adz are illustrated in Figure 2, while the corresponding cations are plotted in Supplementary Figure S2. Moreover, selected structural parameters of these resulting X@3⁶adz compounds are summarized in Table 1.

FIGURE 2

FIGURE 2. Optimized geometric structures of X@3⁶adz (X = H, B, C, N, O, F, and Si) compounds.

TABLE 1

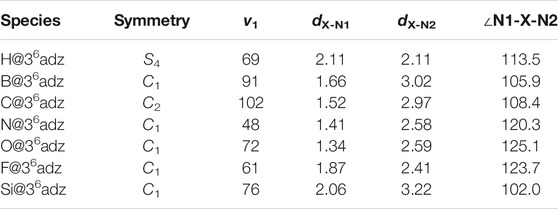
TABLE 1. Symmetry point group, the lowest vibrational frequencies v₁ (in cm⁻¹), the bond lengths of X-N1 and X-N2 bonds (d_X-N1 and d_X-N2, in Å), ∠N1-X-N2 angle (in deg) of X@3⁶adz (X = H, B, C, N, O, F, and Si) compounds.

As shown in Figure 1, 3⁶adz is a cage-like complexant with S₄ symmetry. From Figure 2, it is observed that the geometric integrity of 3⁶adz cage is well-preserved in these X@3⁶adz compounds. However, the geometric symmetries of these compounds are lowered to C₁ and C₂, except for H@3⁶adz, which maintains the S₄ symmetry of 3⁶adz. To be specific, the encapsulated hydrogen atom located at the central position of 3⁶adz in H@3⁶adz, yields the newly formed N-H bonds of 2.11 Å and ∠N1-H-N2 of 113.5°. As for B@3⁶adz, the boron atom tends to bind with 3 N atoms of the complexant, forming 3 N-B bonds of 1.63 Å ∼ 1.66 Å, while the distance between the uncombined N and B atoms is as long as 3.02 Å. The C@3⁶adz complex possesses a C₂-symmetric structure, where the introduced carbon atom prefers to bind with 2 N atoms of 3⁶adz by forming two N-C bonds of 1.52 Å. Differently, the more electronegative N, O, and F atoms are linked to only 1 N atom of the cage complexant via N-N, N-O, and N-F bonds of 1.41, 1.34, and 1.87 Å, respectively, generating the very similar structures of X@3⁶adz (X = N, O, and F). Similar to B@3⁶adz, the introduced silicon atom tends to bind with 3 N atoms of complexant via 3 N-Si bonds of 2.06–2.35 Å in Si@3⁶adz.

By turning to the cations of X@3⁶adz, it is found that only the optimized structure of [B@3⁶adz]⁺ cation almost coincides with the geometry of the corresponding neutral one (see Supplementary Figure S2). For instance, the critical geometric parameters of d_B-N1, d_B-N2, and ∠N1-B-N2 are hardly changed after one electron is lost from B@3⁶adz. However, for the rest of X@3⁶adz (X = H, C, N, O, F, and Si), quite different geometries of cationic and neutral complexes were found. For instance, the H⁺ is attached to 1 N atom of the complexant in the resulting [H@3⁶adz]⁺, while the doped N atom turns to combine with 2 N atoms of 3⁶adz in [N@3⁶adz]⁺ and Si atom almost moves to the center of the cage in [Si@3⁶adz]⁺. The geometry of C@3⁶adz is distorted from C₂ symmetry to C₁ with the changes of 0.29 Å for the C-N2 bond and 7.3° for ∠N1-C-N2. As for [F@3⁶adz]⁺, the N-F bond is shortened from 1.87 Å to 1.38 Å because the introduced F atom further loses 0.333e (see Supplementary Table S1) and thus tends to bind more tightly with the N atom of the complexant. Also, as shown in Table 2, the difference in the geometry can also be reflected by the difference of 0.29–3.06 eV between the vertical ionization energies (VIEs) and adiabatic ionization energies (AIEs) of these X@3⁶adz (X = H, C, N, O, F, and Si) species.

TABLE 2

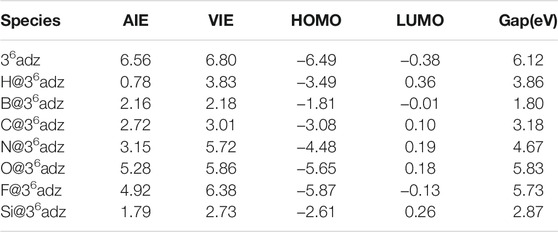
TABLE 2. Adiabatic ionization energies (AIEs, in eV), vertical ionization energies (VIEs, in eV), HOMO and LUMO energy levels (in eV), and the HOMO–LUMO gaps of 3⁶adz and X@3⁶adz (X = H, B, C, N, O, F, and Si) compounds.

More interestingly, as shown in Table 2, extraordinarily low AIE values of 0.78–5.28 eV were found for all the studied X@3⁶adz (X = H, B, C, N, O, F, and Si) complexes, although X atoms possess very high ionization energies (IEs) of 8.15–17.42 eV (Lide, 2003). Such low AIE values of X@3⁶adz are not only lower than that of 6.56 eV for the 3⁶adz complexant but also significantly lower than that of 5.39 eV (Lide, 2003) for lithium atom. In particular, the AIE values of H@3⁶adz (0.78 eV), B@3⁶adz (2.16 eV), C@3⁶adz (2.72 eV), N@3⁶adz (3.15 eV), and Si@3⁶adz (1.79 eV) are even lower than the IE of 3.89 eV (Lide, 2003) for Cs atoms. Hence, these compounds should be classified as novel nonmetallic superalkalis.

How to understand the low IE values of such X@3⁶adz complexes? We can find some clues from the frontier molecular orbital analysis. From Figure 3, a clear inverse correlation between the VIE values and HOMO levels of these studied compounds can be observed, that is, the higher the HOMO level is, the lower the VIE is. This is reasonable considering the fact that the valence electrons on the higher HOMOs are easier to be ionized. To be specific, all the HOMO energies (−1.81 ∼ −5.87 eV) of X@3⁶adz are much higher than that of −6.49 eV for 3⁶adz, because of the repulsion between the lone pairs of N atoms and the outmost valence electrons of X, resulting in the lower VIEs (2.18–6.38 eV) than that (6.80 eV) of 3⁶adz. In particular, B@3⁶adz exhibits the highest HOMO level of −1.81 eV, and thus possesses the lowest VIE of 2.18 eV among these X@3⁶adz complexes. This is because that the valence electron of embedded boron atom is pushed out of the cage by the lone pairs of N atoms of the complexant, forming a electride-like molecule [B⁺@3⁶adz](e^‒) with obvious diffuse electrons in the HOMO of B@3⁶adz (see Supplementary Figure S3). Thus, the existence of diffuse excess electrons in its high-lying HOMO level results in the high reducibility of this B@3⁶adz complex.

FIGURE 3

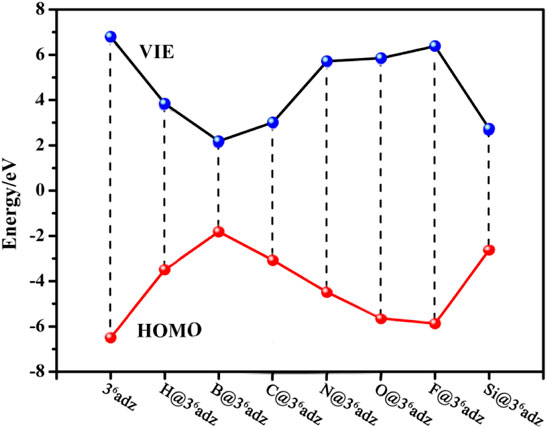
FIGURE 3. The relationship between the VIE values and HOMO levels of X@3⁶adz (X = H, B, C, N, O, F, and Si) compounds.

Differently, as shown in Supplementary Figure S3, the valence electrons are accommodated into the HOMOs mainly composed of the 1s atomic orbital of embedded hydrogen atom in H@3⁶adz, and the np orbitals of C and Si atoms in X@3⁶adz (X = C and Si), which show obvious antibonding character with respect to the central atom-complexant interaction. Such antibonding HOMOs destabilize the neutral structures of X@3⁶adz (X = H, C, and Si) and result in their low VIE values (Gutsev and Boldyrev, 1987; Tkachenko et al., 2019). Hence, these 3 species also have quite low VIE values of 2.73–3.83 eV. However, it should be mentioned that the VIEs of 5.72–6.38 eV for X@3⁶adz (X = N, O, and F) are larger than that of 5.39 eV for Li atom, although their HOMOs also possess obvious antibonding character. This is attributed to the larger elertonegativities of N, O, and F atoms than H, C, and Si atoms, which hinders the ionization of the valence electrons on their np orbitals in the HOMOs of X@3⁶adz (X = N, O, and F).

On the other hand, the difference between the VIE and AIE values are also related to the different electron distribution in the HOMOs of X@3⁶adz. To be specific, the geometric structure of B@3⁶adz is hardly changed after its diffuse excess electron of HOMO is lost, resulting in its nearly equal VIE (2.18 eV) and AIE (2.16 eV) values. However, the destabilization of antibonding HOMOs for the neutral X@3⁶adz (X = H, C, and Si) complexes drives the embedded X atom to lose nearly one valence electron (0.667 e ∼ 0.867 e, as shown in Supplementary Table S1), forming relatively stable [X@3⁶adz]⁺ cations. After losing one electron, the formed X⁺ ion changes its interaction mode with the cage complexant, which leads to the large structural distortion and considerable difference between the VIE and AIE values of X@3⁶adz (X = H, C, and Si). Note that the AIE of H@3⁶adz is as low as 0.78 eV because the formed [H@3⁶adz]⁺ is very stable and has been identified in various synthesized ionic compounds, such as [H@3⁶adz]⁺X^‒ (X = Cl, Br, I, and Na) (Kim et al., 1994; Springborg et al., 1996; Redko et al., 2002).

Finally, considering the diffuse excess electron in the HOMO of B@3⁶adz, it is highly expected that this superalkali also exhibits considerable nonlinear optical (NLO) response. Thus, the static electric properties of these studied X@3⁶adz compounds and 3⁶adz complexant were calculated and listed in Table 3. It is observed that B@3⁶adz has the largest dipole moment (3.326 au) and polarizability (1,599 au) among these X@3⁶adz complexes because of the existence of diffuse electrons in the HOMO of this superalkali. In particular, the first hyperpolarizability (β₀) of B@3⁶adz is as large as 1.35 × 10⁶ au, which is significantly larger than those of the reported superalkalis and superalkali-based NLO materials, such as the aromatic organometallic superalkali Au₃(Py)₃ (3.74 × 10⁴ au) (Parida et al., 2018), superalkali-based alkalide Li₃O⁺(calix [4]pyrrole)M^‒ (M = Li, Na, and K) (1.18 × 10⁴–3.33 × 10⁴ au) (Sun et al., 2014a), and superalkali-based electride Li₃O@Al₁₂N₁₂ (8.73 × 10⁵ au) (Sun et al., 2016b), indicating that this proposed superalkali species can indeed be considered as a new kind of NLO molecule of high performance.

TABLE 3

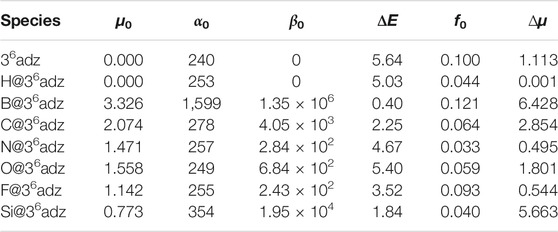
TABLE 3. Calculated dipole moments (µ₀, in au), polarizabilities (α₀, in au), first hyperpolarizabilities (β₀, in au), transition energies (ΔE, in eV), oscillator strength (f₀), and the difference in the dipole moments (∆µ, in Debye) between the ground and crucial excited states of 3⁶adz and X@3⁶adz (X = H, B, C, N, O, F, and Si) compounds.

To understand the eminently large β₀ value of B@3⁶adz, we focus our attention on the simple two-level model (Oudar, 1977; Oudar and Chemla, 1977),

${\beta }_{\mathrm{0}}\propto \frac{\mathrm{\Delta }\mu \cdot f_{\mathrm{0}}}{\mathrm{\Delta }{E}^3}(4)$

where ΔE, f₀, and Δµ are the transition energy, oscillator strength, and the difference in the dipole moment between the ground state and crucial excited state, respectively. According to this two-level expression, β₀ is proportional to f₀ and ∆µ, while is inversely proportional to the cube of ΔE, and therefore, the transition energy is considered to be the decisive factor in the first hyperpolarizability (Sun et al., 2014a,b, 2016b,c). Hence, the ΔE, f₀, and Δµ values of the crucial excited states with the largest oscillator strength of 3⁶adz and X@3⁶adz are summarized in Table 3. It is noted that B@3⁶adz possesses extremely smaller ΔE and much larger f₀ and ∆µ values than those of other X@3⁶adz (X = H, C, N, O, F, and Si) compounds, which rationalizes its largest β₀ value among these studied X@3⁶adz species. In addition, the proposed C@3⁶adz and Si@3⁶adz superalkalis also show considerable β₀ values of 4.05 × 10³ au and 1.95 × 10⁴ au, respectively, because of their relatively smaller ΔE values and larger Δµ values.

Conclusion

By using 3⁶adamanzane (3⁶adz) as a complexant, a series of X@3⁶adz (X = H, B, C, N, O, F, and Si) compounds were constructed and studied based on the density functional theory. It is interesting to find that the X@3⁶adz (X = H, B, C, N, and Si) complexes possess lower AIE values than the IE of Cs atoms though the X atoms and 3⁶adz possess very high IE values. Thereby, they can be regarded as a new kind of nonmetallic superalkalis. In particular, different from other complexes, the low IE of B@3⁶adz is derived from the diffuse excess electron formed by the repulsion between the valence electron of the embedded boron atom and lone pairs of N atoms of the complexant. Due to the existence of diffuse electrons, this superalkali also possesses a remarkably large β₀ of 1.35 × 10⁶ au, which can serve as a new kind of NLO molecule. Hence, it is highly hoped that the theoretical design and characterization of these nonmetallic superalkali species could provide meaningful references to further design novel reducing matters or NLO materials by using such cage-like molecules as complexants.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the Natural Science Foundation of Fujian Province (2021J01682) and the National Natural Science Foundation of China (21603032).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank the National Supercomputing Center in Shenzhen for providing computational resources.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2022.853160/full#supplementary-material

References

Dennington, R. D., Keith, T. A., and Millam, J. M. (2016). GaussView, Version 6. Shawnee Mission, KS: Semichem Inc.

Google Scholar

D. R. Lide (Editor) (2003). CRC Handbook of Chemistry and Physics (Boca Raton, Florida: CRC Press).

Google Scholar

Dye, J. L. (2009). Electrides: Early Examples of Quantum Confinementfinement. Acc. Chem. Res. 42, 1564–1572. doi:10.1021/ar9000857

PubMed Abstract | CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian 16, Revision A.03. Wallingford CT, USA: Gaussian, Inc.

Google Scholar

Giri, S., Behera, S., and Jena, P. (2014). Superalkalis and Superhalogens as Building Blocks of Supersalts. J. Phys. Chem. A. 118 (3), 638–645. doi:10.1021/jp4115095

CrossRef Full Text | Google Scholar

Giri, S., Reddy, G. N., and Jena, P. (2016). Organo-Zintl Clusters [P7R4]: A New Class of Superalkalis. J. Phys. Chem. Lett. 7, 800–805. doi:10.1021/acs.jpclett.5b02892

PubMed Abstract | CrossRef Full Text | Google Scholar

Gutsev, G. L., and Boldyrev, A. I. (1982). DVM Xα Calculations on the Electronic Structure of "superalkali" Cations. Chem. Phys. Lett. 92, 262–266. doi:10.1016/0009-2614(82)80272-8

CrossRef Full Text | Google Scholar

Gutsev, G. L., and Boldyrev, A. I. (1987). The Electronic Structure of Superhalogens and Superalkalies. Russ. Chem. Rev. 56 (6), 519–531. doi:10.1070/rc1987v056n06abeh003287

CrossRef Full Text | Google Scholar

Hou, G.-L., and Wang, X.-B. (2020). Potassium Iodide Cluster Based Superhalogens and Superalkalis: Theoretical Calculations and Experimental Confirmation. Chem. Phys. Lett. 741, 137094. doi:10.1016/j.cplett.2020.137094

CrossRef Full Text | Google Scholar

Hou, N., Li, Y., Wu, D., and Li, Z.-R. (2013). Do Nonmetallic Superalkali Cations Exist? Chem. Phys. Lett. 575, 32–35. doi:10.1016/j.cplett.2013.05.014

CrossRef Full Text | Google Scholar

Hou, N., Wu, D., Li, Y., and Li, Z.-R. (2014). Lower the Electron Affinity by Halogenation: an Unusual Strategy to Design Superalkali Cations. J. Am. Chem. Soc. 136 (7), 2921–2927. doi:10.1021/ja411755t

CrossRef Full Text | Google Scholar

Jansen, M. (1976). Na³NO₃-kein Orthonitrit. Angew. Chem. Int. Ed. 88, 411. doi:10.1002/ange.19760881205

CrossRef Full Text | Google Scholar

Jena, P., and Sun, Q. (2018). Super Atomic Clusters: Design Rules and Potential for Building Blocks of Materials. Chem. Rev. 118 (11), 5755–5870. doi:10.1021/acs.chemrev.7b00524

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, J., Ichimura, A. S., Huang, R. H., Redko, M., Phillips, R. C., and Jackson, J. E. (1999). Crystalline Salts of Na and K (Alkalides) that Are Stable at Room Temperature. J. Am. Chem. Soc. 121, 10666–10667. doi:10.1021/ja992667v

CrossRef Full Text | Google Scholar

Kim, R. D. H., Wilson, M., and Haseltine, H. (1994). Simple Preparations of Tricyclic Orthoamides and Macrocyclic Triamines. Synth. Commun. 24 (21), 3109–3114. doi:10.1080/00397919408011324

CrossRef Full Text | Google Scholar

Lievens, P., Thoen, P., Bouckaert, S., Bouwen, W., Vanhoutte, F., Weidele, H., et al. (1999). Ionization Potentials of Li_nO (2≤n≤70) Clusters: Experiment and Theory. J. Chem. Phys. 110 (21), 10316. doi:10.1063/1.478965

CrossRef Full Text | Google Scholar

Limacher, P. A., Mikkelsen, K. V., and Lüthi, H. P. (2009). On the Accurate Calculation of Polarizabilities and Second Hyperpolarizabilities of Polyacetylene Oligomer Chains Using the CAM-B3lyp Density Functional. J. Chem. Phys. 130 (19), 194114. doi:10.1063/1.3139023

CrossRef Full Text | Google Scholar

Liu, J. Y., Wu, D., Sun, W. M., Li, Y., and Li, Z. R. (2014). Trivalent Acid Radical-Centered YLi₄⁺ (Y = PO₄, AsO₄, VO₄) Cations: New Polynuclear Species Designed to Enrich the Superalkali Family. Dalton Trans. 43 (48), 18066–18073. doi:10.1039/c4dt02347a

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, J. Y., Xi, Y. J., Li, Y., Li, S. Y., Wu, D., and Li, Z. R. (2016). Does Alkaline-Earth-Metal-Based Superalkali Exist? J. Phys. Chem. A. 120 (51), 10281–10288. doi:10.1021/acs.jpca.6b10555

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, Z., and Castleman, A. W. (2014). Special and General Superatoms. Acc. Chem. Res. 47 (10), 2931–2940. doi:10.1021/ar5001583

PubMed Abstract | CrossRef Full Text | Google Scholar

Merino, G., Chattaraj, P. M., and Pan, S. (2012). Hydrogen Trapping Potential of Some Li-Doped Star-like Clusters and Super-alkali Systems. Phys. Chem. Chem. Phys. 14, 10345–10350. doi:10.1039/c2cp40794a

PubMed Abstract | CrossRef Full Text | Google Scholar

Oudar, J. L., and Chemla, D. S. (1977). Hyperpolarizabilities of the Nitroanilines and Their Relations to the Excited State Dipole Moment. J. Chem. Phys. 66 (6), 2664. doi:10.1063/1.434213

CrossRef Full Text | Google Scholar

Oudar, J. L. (1977). Optical Nonlinearities of Conjugated Molecules. Stilbene Derivatives and Highly Polar Aromatic Compounds. J. Chem. Phys. 67 (2), 446. doi:10.1063/1.434888

CrossRef Full Text | Google Scholar

Pan, S., Contreras, M., Romero, J., Reyes, A., Chattaraj, P. K., and Merino, G. (2013). C₅Li₇⁺ and O₂Li₅⁺ as Noble-Gas-Trapping Agents. Chem. Eur. J. 19 (7), 2322–2329. doi:10.1002/chem.201203245

CrossRef Full Text | Google Scholar

Parida, R., Reddy, G. N., Ganguly, A., Roymahapatra, G., Chakraborty, A., and Giri, S. (2018). On the Making of Aromatic Organometallic Superalkali Complexes. Chem. Commun. 54 (31), 3903–3906. doi:10.1039/c8cc01170b

CrossRef Full Text | Google Scholar

Park, H., and Meloni, G. (2018). Activation of Dinitrogen with a Superalkali Species, Li₃F₂. ChemPhysChem 19 (3), 256–260. doi:10.1002/cphc.201701232

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, H., and Meloni, G. (2017). Reduction of Carbon Dioxide with a Superalkali. Dalton Trans. 46 (35), 11942–11949. doi:10.1039/c7dt02331f

PubMed Abstract | CrossRef Full Text | Google Scholar

Reber, A. C., Khanna, S. N., and Castleman, A. W. (2007). Superatom Compounds, Clusters, and Assemblies: Ultra Alkali Motifs and Architectures. J. Am. Chem. Soc. 129, 10189–10194. doi:10.1021/ja071647n

CrossRef Full Text | Google Scholar

Redko, M. Y., Jackson, J. E., Huang, R. H., and Dye, J. L. (2005). Design and Synthesis of a Thermally Stable Organic Electride. J. Am. Chem. Soc. 127, 12416–12422. doi:10.1021/ja053216f

CrossRef Full Text | Google Scholar

Redko, M. Y., Vlassa, M., Jackson, J. E., Misiolek, A. W., Huang, R. H., and Dye, J. L. (2002). Inverse Sodium Hydride”: A Crystalline Salt that Contains H and Na-. J. Am. Chem. Soc. 124, 5928–5929. doi:10.1021/ja025655+

CrossRef Full Text | Google Scholar

Reveles, J. U., Clayborne, P. A., Reber, A. C., Khanna, S. N., Pradhan, K., Sen, P., et al. (2009). Designer Magnetic Superatoms. Nat. Chem. 1 (4), 310–315. doi:10.1038/nchem.249

PubMed Abstract | CrossRef Full Text | Google Scholar

Sikorska, C., and Gaston, N. (2020). N₄Mg₆M (M = Li, Na, K) Superalkalis for CO₂ Activation. J. Chem. Phys. 153, 144301. doi:10.1063/5.0025545

PubMed Abstract | CrossRef Full Text | Google Scholar

Springborg, J. (2003). Adamanzanes–Bi- and Tricyclic Tetraamines and Their Coordination Compounds. Dalton Trans. (9), 1653–1665. doi:10.1039/b300510k

CrossRef Full Text | Google Scholar

Springborg, J., Pretzmann, U., and Olsen, C. E. (1996). An Inert Proton Coordinated inside the Tetrahedral Cage [3⁶]Adamanzane. Synthesis of the inside Monoprotonated Amine 1,5,9,13-Tetraazatricyclo[7.7.3.3^5,13]docosane. Acta Chem. Scand. A. 50, 294–298. doi:10.3891/acta.chem.scand.50-0294

CrossRef Full Text | Google Scholar

Srivastava, A. K. (2019a). Ab Initio investigations on Non-metallic Chain-Shaped F_nH_n+1⁺ Series of Superalkali Cations. Chem. Phys. Lett. 721, 7–11. doi:10.1016/j.cplett.2019.02.021

CrossRef Full Text | Google Scholar

Srivastava, A. K. (2019b). C_xH_4x+1⁺ (X = 1–5): a Unique Series of Organic Superalkali Cations. Mol. Phys., 1–7.

Google Scholar

Srivastava, A. K., and Misra, N. (2015). Superalkali-hydroxides as Strong Bases and Superbases. New J. Chem. 39 (9), 6787–6790. doi:10.1039/c5nj01259g

CrossRef Full Text | Google Scholar

Sun, W.-M., Li, C.-Y., Kang, J., Wu, D., Li, Y., Ni, B.-L., et al. (2018a). Superatom Compounds under Oriented External Electric Fields: Simultaneously Enhanced Bond Energies and Nonlinear Optical Responses. J. Phys. Chem. C 122 (14), 7867–7876. doi:10.1021/acs.jpcc.8b01896

CrossRef Full Text | Google Scholar

Sun, W.-M., Li, X.-H., Li, Y., Liu, J.-Y., Wu, D., Li, C.-Y., et al. (2016a). On the Feasibility of Designing Hyperalkali Cations Using Superalkali Clusters as Ligands. J. Chem. Phys. 145 (19), 194303. doi:10.1063/1.4967461

CrossRef Full Text | Google Scholar

Sun, W.-M., Li, X.-H., Wu, D., Li, Y., He, H.-M., Li, Z.-R., et al. (2016b). A Theoretical Study on Superalkali-Doped Nanocages: Unique Inorganic Electrides with High Stability, Deep-Ultraviolet Transparency, and Considerable Nonlinear Optical Response. Dalton Trans. 45 (17), 7500–7509. doi:10.1039/c6dt00342g

CrossRef Full Text | Google Scholar

Sun, W.-M., Li, Y., Wu, D., and Li, Z.-R. (2013). Designing Aromatic Superatoms. J. Phys. Chem. C 117 (46), 24618–24624. doi:10.1021/jp408810e

CrossRef Full Text | Google Scholar

Sun, W.-M., Wu, D., Kang, J., Li, C.-Y., Chen, J.-H., Li, Y., et al. (2018b). Decorating Zintl Polyanions with Alkali Metal Cations: A Novel Strategy to Design Superatom Cations with Low Electron Affinity. J. Alloys Compd. 740 (5), 400–405. doi:10.1016/j.jallcom.2017.12.075

CrossRef Full Text | Google Scholar

Sun, W.-M., Zhang, X.-L., Pan, K.-Y., Chen, J.-H., Wu, D., Li, C.-Y., et al. (2019). On the Possibility of Using the Jellium Model as a Guide to Design Bimetallic Superalkali Cations. Chem. Eur. J. 25 (17), 4358–4366. doi:10.1002/chem.201806194

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, W. M., Fan, L. T., Li, Y., Liu, J. Y., Wu, D., and Li, Z. R. (2014a). On the Potential Application of Superalkali Clusters in Designing Novel Alkalides with Large Nonlinear Optical Properties. Inorg. Chem. 53 (12), 6170–6178. doi:10.1021/ic500655s

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, W. M., Li, Y., Li, X. H., Wu, D., He, H. M., Li, C. Y., et al. (2016c). Stability and Nonlinear Optical Response of Alkalides that Contain a Completely Encapsulated Superalkali Cluster. Chemphyschem 17 (17), 2672–2678. doi:10.1002/cphc.201600389

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, W. M., Wu, D., Li, Y., and Li, Z. R. (2014b). Theoretical Study on Superalkali (Li₃) in Ammonia: Novel Alkalides with Considerably Large First Hyperpolarizabilities. Dalton Trans. 43 (2), 486–494. doi:10.1039/c3dt51559a

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, W. M., and Wu, D. (2019). Recent Progress on the Design, Characterization, and Application of Superalkalis. Chem. Eur. J. 25 (41), 9568–9579. doi:10.1002/chem.201901460

PubMed Abstract | CrossRef Full Text | Google Scholar

Tawada, Y., Tsuneda, T., Yanagisawa, S., Yanai, T., and Hirao, K. (2004). A Long-Range-Corrected Time-dependent Density Functional Theory. J. Chem. Phys. 120, 8425–8433. doi:10.1063/1.1688752

CrossRef Full Text | Google Scholar

Tkachenko, N. V., Sun, Z. M., and Boldyrev, A. I. (2019). Record Low Ionization Potentials of Alkali Metal Complexes with Crown Ethers and Cryptands. Chemphyschem 20 (16), 2060–2062. doi:10.1002/cphc.201900422

PubMed Abstract | CrossRef Full Text | Google Scholar

Tong, J., Li, Y., Wu, D., Li, Z.-R., and Huang, X.-R. (2011). Ab Initio Investigation on a New Class of Binuclear Superalkali Cations M₂Li_2k+1⁺ (F₂Li₃⁺, O₂Li₅⁺, N₂Li₇⁺, and C₂Li₉⁺). J. Phys. Chem. A. 115 (10), 2041–2046. doi:10.1021/jp110417z

CrossRef Full Text | Google Scholar

Tong, J., Li, Y., Wu, D., Li, Z. R., and Huang, X. R. (2009). Low Ionization Potentials of Binuclear Superalkali B₂Li₁₁. J. Chem. Phys. 131 (16), 164307. doi:10.1063/1.3254835

CrossRef Full Text | Google Scholar

Tong, J., Li, Y., Wu, D., and Wu, Z.-J. (2012a). Theoretical Study on Polynuclear Superalkali Cations with Various Functional Groups as the Central Core. Inorg. Chem. 51 (11), 6081–6088. doi:10.1021/ic202675j

PubMed Abstract | CrossRef Full Text | Google Scholar

Tong, J., Wu, Z., Li, Y., and Wu, D. (2012b). Prediction and Characterization of Novel Polynuclear Superalkali Cations. Dalton Trans. 42, 577–584. doi:10.1039/c2dt31429k

PubMed Abstract | CrossRef Full Text | Google Scholar

Yanai, T., Tew, D. P., and Handy, N. C. (2004). A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3lyp). Chem. Phys. Lett. 393 (1-3), 51–57. doi:10.1016/j.cplett.2004.06.011

CrossRef Full Text | Google Scholar

Yokoyama, K., Haketa, N., Tanaka, H., Furukawa, K., and Kudo, H. (2000). Ionization Energies of Hyperlithiated Li₂F Molecule and Li_nF_n-1 (N= 3, 4) Clusters. Chem. Phys. Lett. 330, 339–346. doi:10.1016/s0009-2614(00)01109-x

CrossRef Full Text | Google Scholar

Yokoyama, K., Tanaka, H., and Kudo, H. (2001). Structure of Hyperlithiated Li₃O and Evidence for Electronomers. J. Phys. Chem. A. 105, 4312–4315. doi:10.1021/jp0037450

CrossRef Full Text | Google Scholar

Zhang, X.-L., Ye, Y.-L., Zhang, L., Li, X.-H., Yu, D., Chen, J.-H., et al. (2021a). Designing an Alkali-metal-like Superatom Ca₃B for Ambient Nitrogen Reduction to Ammonia. Phys. Chem. Chem. Phys. 23 (34), 18908–18915. doi:10.1039/d1cp01533h

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X.-L., Zhang, L., Ye, Y.-L., Li, X.-H., Ni, B.-L., Li, Y., et al. (2021b). On the Role of Alkali-metal-like Superatom Al₁₂P in Reduction and Conversion of Carbon Dioxide. Chem. Eur. J. 27 (3), 1039–1045. doi:10.1002/chem.202003733

CrossRef Full Text | Google Scholar

Zhao, T., Wang, Q., and Jena, P. (2017). Rational Design of Super-alkalis and Their Role in CO₂ Activation. Nanoscale 9 (15), 4891–4897. doi:10.1039/c7nr00227k

PubMed Abstract | CrossRef Full Text | Google Scholar

Zintl, E., and Morawietz, W. (1938). Orthosalze von Sauerstoffsäuren. Z. Anorg. Allg. Chem. 236, 372–410. doi:10.1002/zaac.19382360134

CrossRef Full Text | Google Scholar