- 1Institute for Advanced Study, Shenzhen University, Shenzhen, China
- 2Institute of Microscale Optoelectronics, Shenzhen University, Shenzhen, China
Catalytic activity of the colloids and chemotactic response to gradients of the chemicals in the solution leads to effective interaction between catalytic colloids. In this paper, we simulate mixtures of active and passive colloids via a Brownian dynamics algorithm. These particles interact via phoretic interactions, which are determined by two independent parameters, surface activity and surface mobility. We find rich dynamic structures by tuning passive colloids’ surface mobility, size, and area fractions, which include schools of active colloids with exclusion zone, yolk/shell cluster, and stable active–passive alloys to motile clusters. Dynamical cluster can also be formed due to the nonreciprocity of the phoretic interaction. Increasing the size ratio of passive colloids to active colloids favors the phase separation of active and passive colloids, resulting in yolk/shell structure. Increasing the area fraction of active colloids tends to transfer from dynamical clusters into stable alloys. The simulated binary active colloid systems exhibit intriguing nonequilibrium phenomena that mimic the dynamic organizations of active/passive systems.
1 Introduction
Active matter can harvest energy from the environment for mechanical motion, such as bacterial suspension (Ishikawa and Hota, 2006; Cates et al., 2010; McCarter, 2010; Marchetti et al., 2013; Singh et al., 2017), fish schools, and animal flocks (Ballerini et al., 2008; Moussaïd et al., 2009). These biological systems have inspired the design of artificial swimmers experimentally with different sources of energy, including chemical (Howse et al., 2007), electromagnetic (Creppy et al., 2016), acoustic (Ahmed et al., 2014), magnetic (Wang M. et al., 2013; Tierno, 2014; Wang et al., 2021), or thermal (Jiang et al., 2010) energy. Systems driven by chemicals have obvious advantages over others since they require no moving parts and can be free from external actuations (Varma et al., 2018). Chemically active colloids (Vicario et al., 2005; Niu et al., 2018; Yu et al., 2018; Shah et al., 2020; Zhang et al., 2021) can exhibit chemotaxis in response to gradients of chemicals that they themselves produce or consume. Concentration gradients of a solute along the surface of a chemotactic particle in a fluid produces pressure difference resulting in a slip flow parallel to the surface, so that the particle moves through the fluid in the direction opposite the slip velocity (Saha et al., 2019). This phenomenon is known as diffusiophoresis (Anderson, 1989).
Catalytic particles interact with each other through their influence and response on the chemical’s concentration field resulting in a wide variety of self-organization in heterogeneous populations of microorganisms (Keller and Surette, 2006), cell–cell communication (Friedl and Gilmour, 2009), aggregation of enzymes (Wu et al., 2015; Sun et al., 2017), and assembly of active materials from catalytical colloids (Palacci et al., 2013; Qin et al., 2017). Rich collective phenomena, such as flocking and schooling, have been observed in experiments and simulations (Mei et al., 2011; Lee et al., 2014; Choudhury et al., 2015; Agudo-Canalejo and Golestanian, 2019; Ouazan-Reboul et al., 2021). However, these studies have focused mostly on the mixture of active particles, while much less has been done for active/passive mixtures. Experimental results revealed that the active particles can collect the passive particles (Wang W. et al., 2013). Specifically, Ibele et al. (Ibele et al., 2009) have reported that photo-inactive silica particles surround active silver chloride (AgCl) particles while maintaining a small exclusion zone when the UV light is on. Meanwhile, some theoretical studies have predicted that a small fraction of active colloids can promote crystallization in passive hard-sphere glasses (Ni et al., 2014) or that a small fraction of active colloids can induce phase separation and self-assembly in passive colloids (Stenhammar et al., 2015), suggesting the crucial role of area fraction in controlling the collective behavior of the binary mixture. These studies also provide insights into the active–passive binary colloidal systems and demonstrate the importance of nonreciprocity in phase transitions (Fruchart et al., 2021). However, the role of surface properties and size of colloids on the dynamics and self-organization of the active–passive binary system remains unexplored.
In this work, we numerically investigated the collective behavior of binary active/passive colloids systems in which colloidal particles interact and respond via diffusiophoresis. Here the active colloids present the catalytic active colloids, such as Pt and hematite (Howse et al., 2007; Zhou et al., 2021), which will decompose the chemicals, for example, H2O2 in the solution, while the passive colloids will not decompose the chemicals, but they will respond to the chemical gradient, such as TPM particles (Zhou et al., 2021). By altering the surface parameters, size ratio, and area fractions of each component, we demonstrate that the binary mixtures can self-organize into structures, such as the yolk/shell, binary active/passive alloy, dynamical clusters, and moving clusters. Note that phoretic interactions between particles are not restricted to be reciprocal and are inherently non-equilibrium, which, therefore, may lead to binary colloidal systems with distinct structural diversities.
2 Methodology
Diffusiophoretic motion can be characterized by two distinct physicochemical properties of the colloids. The first one is the surface activity α, which refers to the colloid’s ability to generate (α > 0) or consume (α < 0) solute molecules through chemical reactions on their surface, and α = 0 corresponds to passive colloids. The second one is surface mobility, also termed as phoretic mobility μ, which describes the ability of colloids in generating an effective slip motion in response to chemical gradients near the surface (Soto and Golestanian, 2014). μ < 0 (μ > 0) corresponds to the colloid moving toward a high (low) chemical concentration. Experimentally, these two parameters can be manipulated by modifying the surface chemistry of the colloidal particles (Lyu et al., 2021; Zhou et al., 2021).
To introduce our model, we consider two colloidal particles, colloid (1) and colloid (2), randomly in a quasi two-dimensional domain, with a radius R1 and R2. The surface parameters are α1, α2 and μ1, μ2. The concentration field c(r) around colloid 1 in 3D can be obtained by solving the diffusion equation
with a boundary condition
where D is the diffusion coefficient of the solute chemicals. The resulting concentration field decays as
The diffusiophoretic motion applied to colloid 2 in this concentration field can be calculated by:
where r12 = r1 − r2 and r12 = |r12|. Similarly, the diffusiophoretic motion of colloid 1 induced by colloid 2 is
2.1 Equation of Motion
Based on the presented diffusiophoresis model, the equation of motion governing the movement of the colloids can be formulated as the following stochastic equation:
where ri is the position of colloid i, σj is the diameter of colloid j, and
3 Results and Discussion
In this study, we consider a binary mixture of active and passive colloids. The active colloids have nonzero surface activity

TABLE 1. Phoretic interaction applied to passive colloids by active colloids with different surface parameters (S. R., strong repulsion; W. R., weak repulsion; W. A., weak attraction; E. A., equal attraction; S. A., strong attraction.).
In this section, we first summarize the typical collective behavior of the binary mixture in Section 3.1. In Section 3.2, we present the results of active/passive mixtures of equal size and equal area fraction with varying surface mobilities of the passive colloids. In Section 3.3, we study the effect of relative area fraction with fixed total area fraction of the colloids. In Section 3.4, we alter the size ratio
3.1 Typical Collective Behavior
The general structure formed by the binary colloidal system is plotted in Figure 1, which can be categorized into four groups: 1) school of active colloids (active colloids aggregate together resulting in a region with higher active colloids concentration) with an exclusion zone that passive colloids cannot enter because of the strong repulsion applied to the passive colloids; 2) active colloids cluster surrounded by the passive colloids, in this scenario the phoretic force applied to passive colloids is weak repulsion which can be overcome by the Brownian motion; 3) yolk/shell structure with active cluster core and passive colloids shell are attached to the core due to the weak attraction applied to the passive colloids; 4) active–passive alloys formed when the attraction applied to the passive colloids are of the same magnitude compared to the active–active phoretic attraction.
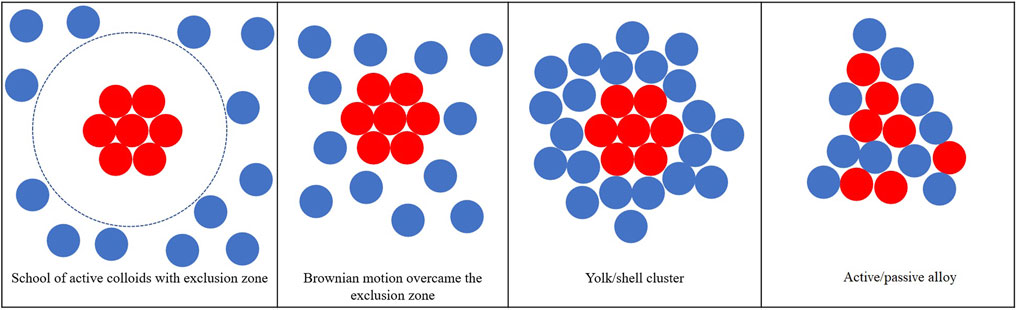
FIGURE 1. Typical collective behavior of active/passive mixture with different surface mobilities of the passive colloids.
3.2 Effect of Varying Surface Mobility of Passive Colloids
To investigate the effect of the surface mobility of passive colloids, we consider the case of β = Rp/Ra = 1 and ϕa = ϕp = 5%. Figure 2 shows the snapshots of the binary colloid systems’ collective behavior at different passive colloids’ surface mobility
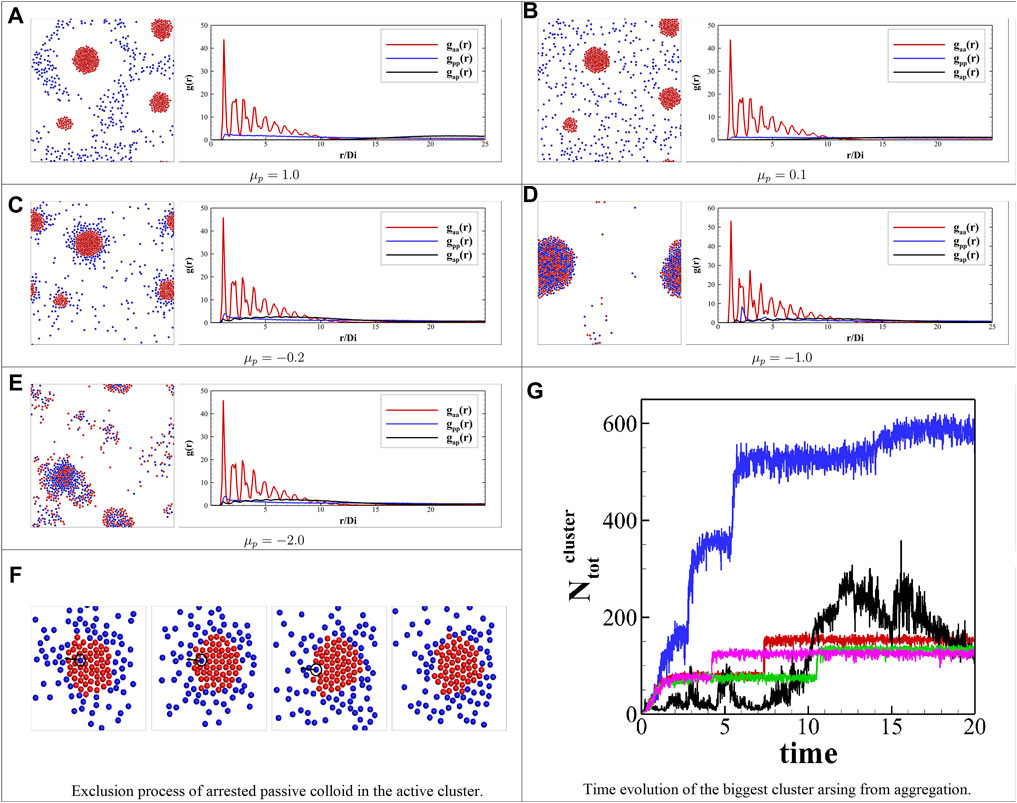
FIGURE 2. Self-organization observed in the simulation with different surface parameters of passive colloids’ mobility. The left side shows the snapshots of (A) a school of active colloids with an exclusion zone, (B) active colloid clusters surrounded by the passive colloids, (C) yolk/shell structure, (D) binary active/passive alloy, (E) dynamical clusters. The right side plots the corresponding pair correlation functions from a–e; the red line gaa(r) is the pair correlation function for active–active colloids; similarly, the blue line gpp(r) is for passive–passive colloids, and the black line gap(r) is for active–passive colloids. The distance is scaled by the diameter (2Ra) of the active colloid (F) exclusion of a single trapped passive colloid in the active cluster. (G) Time evolution of stoichiometry of the biggest cluster arising from aggregation for different cases;
3.3 Effects of Relative Area Fraction
Varying the area fraction of the active colloids ϕa while fixing the total area fraction ϕtot can also affect the collective behavior of the active/passive binary mixture. In this work, we keep the total area fraction ϕtot = 10% as a constant and increased the area fraction of active colloids from ϕa = 2% to ϕa = 8%. Figure 3 plots the results for different ϕa and
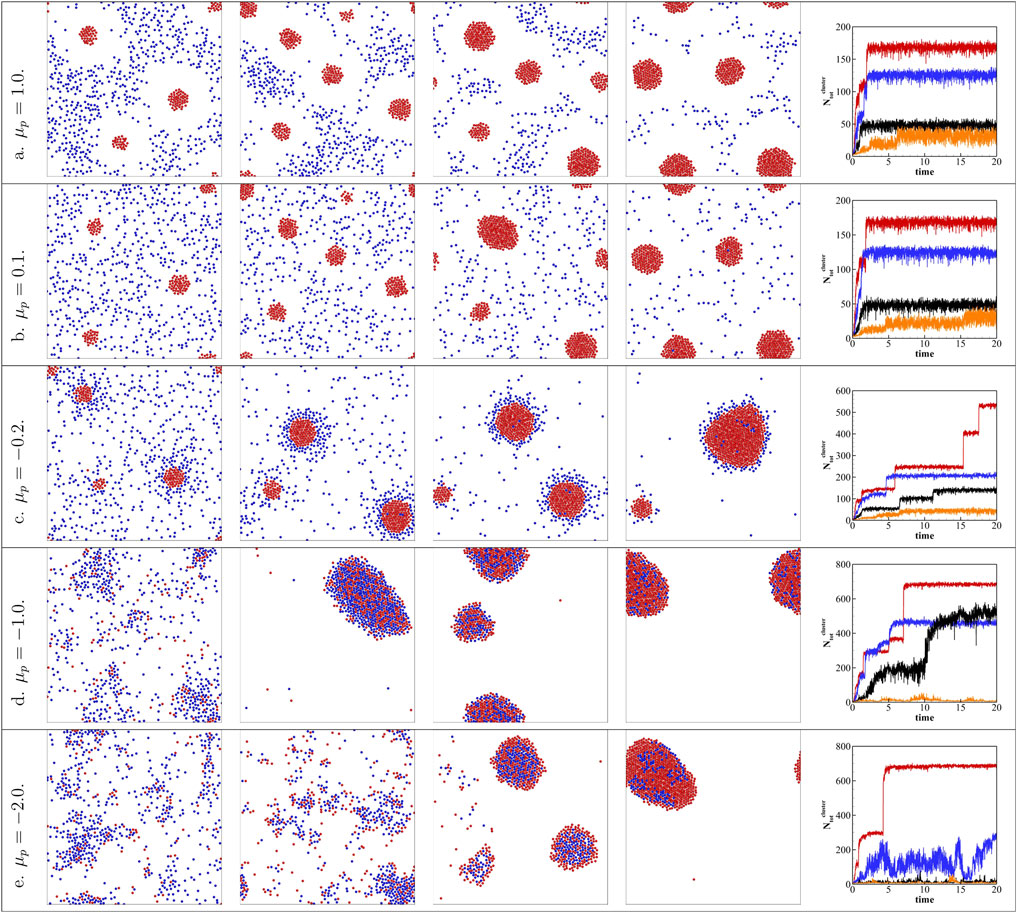
FIGURE 3. Keeping the total area fraction ϕtot = 10%, increasing ϕa = 2% to ϕa = 8% with different passive colloid surface mobilities
However, for
3.4 Effects of Size Ratio
Phoretic interactions also affected by the size of the colloids (Piazza and Parola, 2008; Ouazan-Reboul et al., 2021). Hence, we further investigate the effect of size ratio
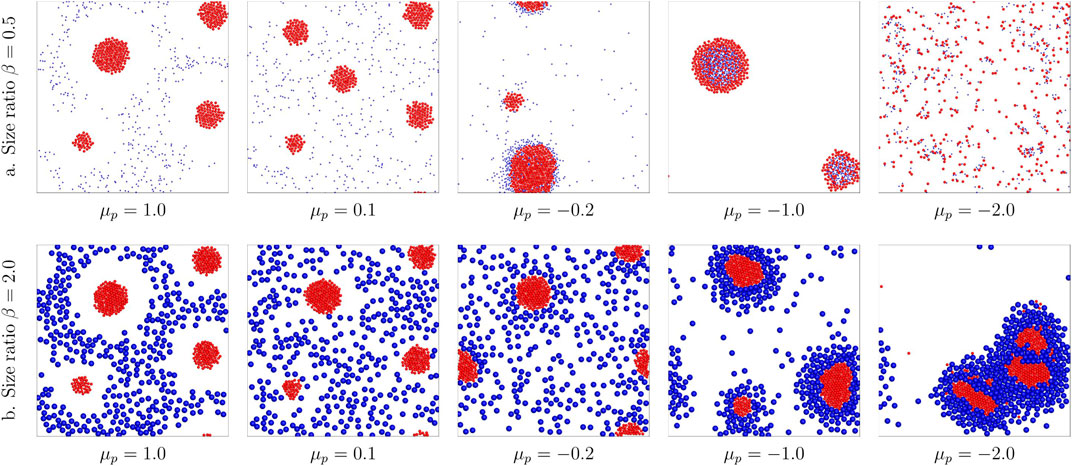
FIGURE 4. Comparison of binary structures formed by different size ratios β = 0.5, 2.0 with varying passive colloid mobilities
4 Concluding Remarks
We have presented a systematic investigation for mixtures of chemically active and passive colloids via a diffusiophoresis model, which not only captures collective behavior observed experimentally but also reveals some intriguing new self-organizations. We demonstrate that the binary active/passive colloids systems can self-organize into schools of active colloids with exclusion zone, active crystal core surrounded by passive colloids, yolk/shell structure, dynamical clusters, and motile clusters. Exclusion zone is formed when the passive colloids feel strong repulsion from the active colloids, which are in accordance with previous experiment results (Ibele et al., 2009). In addition, active colloids and passive colloids will separate into two phases when the attraction difference is large enough resulting in the yolk/shell structure. The binary mixture may collapse to a stable mixture when the attractive interaction strength is of comparable magnitude. Further increasing the phoretic attraction applied to the passive colloids will lead to the formation of dynamical clusters. We further investigate the effects of size ratios and specific fractions of the components. Increasing the size of passive colloids favors the formation of yolk/shell structures for the binary colloid system. We also showed that at low active colloid fraction, dynamical clusters may form due to the nonreciprocal interaction between these colloids, and increasing the fraction of active colloids results in the formation of motile clusters. These clusters can even further merge into a single big cluster collecting all the colloids. These predicted structures should be applicable to a wide variety of active–passive systems, for example, yolk/shell structures are reported to be useful in delivery and lithium-ion batteries for their tailorability and functionality in both the cores and hollow shells (Liu et al., 2011).
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
We acknowledge funding support from the Innovation Program of Guangdong Provincial Department of Education (Project no. 2019KTSCX148), the Science and Technology Innovation Commission of Shenzhen (Project no. JCYJ20170818141727254), and the Young Program of the National Natural Science Foundation of China (Grant no. 21902107).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2022.803906/full#supplementary-material
References
Agudo-Canalejo, J., and Golestanian, R. (2019). Active Phase Separation in Mixtures of Chemically Interacting Particles. Phys. Rev. Lett. 123, 018101. doi:10.1103/PhysRevLett.123.018101
Ahmed, S., Gentekos, D. T., Fink, C. A., and Mallouk, T. E. (2014). Self-assembly of Nanorod Motors into Geometrically Regular Multimers and Their Propulsion by Ultrasound. ACS Nano 8, 11053–11060. doi:10.1021/nn5039614
Anderson, J. L. (1989). Colloid Transport by Interfacial Forces. Annu. Rev. Fluid Mech. 21, 61–99. doi:10.1146/annurev.fl.21.010189.000425
Ballerini, M., Cabibbo, N., Candelier, R., Cavagna, A., Cisbani, E., Giardina, I., et al. (2008). Interaction Ruling Animal Collective Behavior Depends on Topological rather Than Metric Distance: Evidence from a Field Study. Proc. Natl. Acad. Sci. 105, 1232–1237. doi:10.1073/pnas.0711437105
Buttinoni, I., Bialké, J., Kümmel, F., Löwen, H., Bechinger, C., and Speck, T. (2013). Dynamical Clustering and Phase Separation in Suspensions of Self-Propelled Colloidal Particles. Phys. Rev. Lett. 110, 1–8. doi:10.1103/PhysRevLett.110.238301
Camargo, P. H. C., Li, Z.-Y., and Xia, Y. (2007). Colloidal Building Blocks with Potential for Magnetically Configurable Photonic Crystals. Soft Matter 3, 1215–1222. doi:10.1039/b706565e
Cates, M. E., Marenduzzo, D., Pagonabarraga, I., and Tailleur, J. (2010). Arrested Phase Separation in Reproducing Bacteria Creates a Generic Route to Pattern Formation. Proc. Natl. Acad. Sci. 107, 11715–11720. doi:10.1073/pnas.1001994107
Choudhury, U., Soler, L., Gibbs, J. G., Sanchez, S., and Fischer, P. (2015). Surface Roughness-Induced Speed Increase for Active Janus Micromotors. Chem. Commun. 51, 8660–8663. doi:10.1039/c5cc01607j
Creppy, A., Plouraboué, F., Praud, O., Druart, X., Cazin, S., Yu, H., et al. (2016). Symmetry-breaking Phase Transitions in Highly Concentrated Semen. J. R. Soc. Interf. 13, 20160575. doi:10.1098/rsif.2016.0575
Friedl, P., and Gilmour, D. (2009). Collective Cell Migration in Morphogenesis, Regeneration and Cancer. Nat. Rev. Mol. Cel Biol 10, 445–457. doi:10.1038/nrm2720
Fruchart, M., Hanai, R., Littlewood, P. B., and Vitelli, V. (2021). Non-reciprocal Phase Transitions. Nature 592, 363–369. doi:10.1038/s41586-021-03375-9
Howse, J. R., Jones, R. A. L., Ryan, A. J., Gough, T., Vafabakhsh, R., and Golestanian, R. (2007). Self-Motile Colloidal Particles: From Directed Propulsion to Random Walk. Phys. Rev. Lett. 99, 8–11. doi:10.1103/PhysRevLett.99.048102
Ibele, M., Mallouk, T. E., and Sen, A. (2009). Schooling Behavior of Light-Powered Autonomous Micromotors in Water. Angew. Chem. Int. Ed. 48, 3308–3312. doi:10.1002/anie.200804704
Ishikawa, T., and Hota, M. (2006). Interaction of Two Swimming Paramecia. J. Exp. Biol. 209, 4452–4463. doi:10.1242/jeb.02537
Jiang, S., Chen, Q., Tripathy, M., Luijten, E., Schweizer, K. S., and Granick, S. (2010). Janus Particle Synthesis and Assembly. Adv. Mater. 22, 1060–1071. doi:10.1002/adma.200904094
Keller, L., and Surette, M. G. (2006). Communication in Bacteria: An Ecological and Evolutionary Perspective. Nat. Rev. Microbiol. 4, 249–258. doi:10.1038/nrmicro1383
Lee, T.-C., Alarcón-Correa, M., Miksch, C., Hahn, K., Gibbs, J. G., and Fischer, P. (2014). Self-propelling Nanomotors in the Presence of strong Brownian Forces. Nano Lett. 14, 2407–2412. doi:10.1021/nl500068n
Lei, L., Wang, S., Zhang, X., Lai, W., Wu, J., and Gao, Y. (2021). Phoretic Self-Assembly of Active Colloidal Molecules*. Chin. Phys. B 30, 056112. doi:10.1088/1674-1056/abc2bd
Liu, J., Qiao, S. Z., Chen, J. S., Lou, X. W., Xing, X., and Lu, G. Q. (2011). Yolk/shell Nanoparticles: New Platforms for Nanoreactors, Drug Delivery and Lithium-Ion Batteries. Chem. Commun. 47, 12578–12591. doi:10.1039/c1cc13658e
Lyu, X., Liu, X., Zhou, C., Duan, S., Xu, P., Dai, J., et al. (2021). Active, yet Little Mobility: Asymmetric Decomposition of H2O2 Is Not Sufficient in Propelling Catalytic Micromotors. J. Am. Chem. Soc. 143, 12154–12164. doi:10.1021/jacs.1c04501
Marchetti, M. C., Joanny, J. F., Ramaswamy, S., Liverpool, T. B., Prost, J., Rao, M., et al. (2013). Hydrodynamics of Soft Active Matter. Rev. Mod. Phys. 85, 1143–1189. doi:10.1103/RevModPhys.85.1143
McCarter, L. L. (2010). Bacterial Acrobatics on a Surface: Swirling Packs, Collisions, and Reversals during Swarming. J. Bacteriol. 192, 3246–3248. doi:10.1128/JB.00434-10
Mei, Y., Solovev, A. A., Sanchez, S., and Schmidt, O. G. (2011). Rolled-up Nanotech on Polymers: From Basic Perception to Self-Propelled Catalytic Microengines. Chem. Soc. Rev. 40, 2109–2119. doi:10.1039/c0cs00078g
Mognetti, B. M., Šarić, A., Angioletti-Uberti, S., Cacciuto, A., Valeriani, C., and Frenkel, D. (2013). Living Clusters and Crystals from Low-Density Suspensions of Active Colloids. Phys. Rev. Lett. 111, 245702. doi:10.1103/PhysRevLett.111.245702
Moussaïd, M., Helbing, D., Garnier, S., Johansson, A., Combe, M., and Theraulaz, G. (2009). Experimental Study of the Behavioural Mechanisms Underlying Self-Organization in Human Crowds. Proc. R. Soc. B. 276, 2755–2762. doi:10.1098/rspb.2009.0405
Ni, R., Cohen Stuart, M. A., Dijkstra, M., and Bolhuis, P. G. (2014). Crystallizing Hard-Sphere Glasses by Doping with Active Particles. Soft Matter 10, 6609–6613. doi:10.1039/c4sm01015a
Niu, R., Fischer, A., Palberg, T., and Speck, T. (2018). Dynamics of Binary Active Clusters Driven by Ion-Exchange Particles. ACS Nano 12, 10932–10938. doi:10.1021/acsnano.8b04221
Ouazan-Reboul, V., Agudo-Canalejo, J., and Golestanian, R. (2021). Non-equilibrium Phase Separation in Mixtures of Catalytically-Active Particles: Size Dispersity and Screening Effects. The Eur. Phys. J. E 123. doi:10.1140/epje/s10189-021-00118-6
Palacci, J., Sacanna, S., Steinberg, A. P., Pine, D. J., and Chaikin, P. M. (2013). Living Crystals of Light-Activated Colloidal Surfers. Science 339, 936–940. doi:10.1126/science.1230020
Piazza, R., and Parola, A. (2008). Thermophoresis in Colloidal Suspensions. J. Phys. Condens. Matter 20, 153102. doi:10.1088/0953-8984/20/15/153102
Qin, W., Peng, T., Gao, Y., Wang, F., Hu, X., Wang, K., et al. (2017). Catalysis-Driven Self-Thermophoresis of Janus Plasmonic Nanomotors. Angew. Chem. Int. Ed. 56, 515–518. doi:10.1002/anie.201609121
Rapaport, D. C. (2004). The Art of Molecular Dynamics Simulation. 2 edn. Cambridge: Cambridge University Press. doi:10.1017/CBO9780511816581
Saha, S., Ramaswamy, S., and Golestanian, R. (2019). Pairing, Waltzing and Scattering of Chemotactic Active Colloids. New J. Phys. 21, 063006. doi:10.1088/1367-2630/ab20fd
Shah, Z. H., Wang, S., Xian, L., Zhou, X., Chen, Y., Lin, G., et al. (2020). Highly Efficient Chemically-Driven Micromotors with Controlled Snowman-like Morphology. Chem. Commun. 56, 15301–15304. doi:10.1039/d0cc06812h
Singh, D. P., Choudhury, U., Fischer, P., and Mark, A. G. (2017). Non-Equilibrium Assembly of Light-Activated Colloidal Mixtures. Adv. Mater. 29, 1701328. doi:10.1002/adma.201701328
Soto, R., and Golestanian, R. (2014). Self-Assembly of Catalytically Active Colloidal Molecules: Tailoring Activity through Surface Chemistry. Phys. Rev. Lett. 112, 68301. doi:10.1103/PhysRevLett.112.068301
Stenhammar, J., Wittkowski, R., Marenduzzo, D., and Cates, M. E. (2015). Activity-Induced Phase Separation and Self-Assembly in Mixtures of Active and Passive Particles. Phys. Rev. Lett. 114, 018301. doi:10.1103/PhysRevLett.114.018301
Sun, L., Gao, Y., Xu, Y., Chao, J., Liu, H., Wang, L., et al. (2017). Real-Time Imaging of Single-Molecule Enzyme Cascade Using a DNA Origami Raft. J. Am. Chem. Soc. 139, 17525–17532. doi:10.1021/jacs.7b09323
Tierno, P. (2014). Recent Advances in Anisotropic Magnetic Colloids: Realization, Assembly and Applications. Phys. Chem. Chem. Phys. 16, 23515–23528. doi:10.1039/C4CP03099K
Varma, A., Montenegro-Johnson, T. D., and Michelin, S. (2018). Clustering-induced Self-Propulsion of Isotropic Autophoretic Particles. Soft Matter 14, 7155–7173. doi:10.1039/c8sm00690c
Vicario, J., Eelkema, R., Browne, W. R., Meetsma, A., La Crois, R. M., and Feringa, B. L. (2005). Catalytic Molecular Motors: Fuelling Autonomous Movement by a Surface Bound Synthetic Manganese Catalase. Chem. Commun. 2005, 3936–3938. doi:10.1039/b505092h
Wang, M., He, L., and Yin, Y. (2013a). Magnetic Field Guided Colloidal Assembly. Mater. Today 16, 110–116. doi:10.1016/j.mattod.2013.04.008
Wang, S., Chen, Y., Zhou, X., Lei, L., Shah, Z. H., Lin, G., et al. (2021). Magnetic Manipulation and Assembly of Nonmagnetic Colloidal Rods in a Ferrofluid. Langmuir 37, 1429–1437. doi:10.1021/acs.langmuir.0c02891
Wang, W., Duan, W., Sen, A., and Mallouk, T. E. (2013b). Catalytically Powered Dynamic Assembly of Rod-Shaped Nanomotors and Passive Tracer Particles. Proc. Natl. Acad. Sci. 110, 17744–17749. doi:10.1073/pnas.1311543110
Watanabe, K., Ishii, H., Konno, M., Imhof, A., Van Blaaderen, A., and Nagao, D. (2017). Yolk/shell Colloidal Crystals Incorporating Movable Cores with Their Motion Controlled by an External Electric Field. Langmuir 33, 296–302. doi:10.1021/acs.langmuir.6b03116
Wu, F., Pelster, L. N., and Minteer, S. D. (2015). Krebs Cycle Metabolon Formation: Metabolite Concentration Gradient Enhanced Compartmentation of Sequential Enzymes. Chem. Commun. 51, 1244–1247. doi:10.1039/c4cc08702j
Yu, T., Chuphal, P., Thakur, S., Reigh, S. Y., Singh, D. P., and Fischer, P. (2018). Chemical Micromotors Self-Assemble and Self-Propel by Spontaneous Symmetry Breaking. Chem. Commun. 54, 11933–11936. doi:10.1039/c8cc06467a
Zhang, J., Alert, R., Yan, J., Wingreen, N. S., and Granick, S. (2021). Active Phase Separation by Turning towards Regions of Higher Density. Nat. Phys. 17, 961–967. doi:10.1038/s41567-021-01238-8
Keywords: Brownian dynamics, diffusiophoresis, self-assembly, active colloids, nonreciprocal interaction
Citation: Lei L, Wang S, Zhou X, Ghellab SE, Lin G and Gao Y (2022) Self Organization of Binary Colloidal Mixtures via Diffusiophoresis. Front. Chem. 10:803906. doi: 10.3389/fchem.2022.803906
Received: 28 October 2021; Accepted: 02 February 2022;
Published: 10 March 2022.
Edited by:
Lijuan Zhang, Shanghai Advanced Research Institute (CAS), ChinaCopyright © 2022 Lei, Wang, Zhou, Ghellab, Lin and Gao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yongxiang Gao, eW9uZ3hpYW5nLmdhb0BzenUuZWR1LmNu
 Lijie Lei
Lijie Lei Shuo Wang1
Shuo Wang1