Theoretical analysis of the thermoelectric properties of penta-PdX2 (X = Se, Te) monolayer

Based on the successful fabrication of PdSe₂ monolayers, the electronic and thermoelectric properties of pentagonal PdX₂ (X = Se, Te) monolayers were investigated via first-principles calculations and the Boltzmann transport theory. The results showed that the PdX₂ monolayer exhibits an indirect bandgap at the Perdew–Burke–Ernzerhof level, as well as electronic and thermoelectric anisotropy in the transmission directions. In the PdTe₂ monolayer, P-doping owing to weak electron–phonon coupling is the main reason for the excellent electronic properties of the material. The low phonon velocity and short phonon lifetime decreased the thermal conductivity (κ_l) of penta-PdTe₂. In particular, the thermal conductivity of PdTe₂ along the x and y transmission directions was 0.41 and 0.83 Wm⁻¹K⁻¹, respectively. Owing to the anisotropy of κ_l and electronic structures along the transmission direction of PdX₂, an anisotropic thermoelectric quality factor ZT appeared in PdX₂. The excellent electronic properties and low lattice thermal conductivity (κ_l) achieved a high ZT of the penta-PdTe₂ monolayer, whereas the maximum ZT of the p- and n-type PdTe₂ reached 6.6 and 4.4, respectively. Thus, the results indicate PdTe₂ as a promising thermoelectric candidate.

1 Introduction

Currently, the energy crisis is the greatest challenge facing the world today, and requires the rapid acquisition of technological alternatives to traditional energy sources (Tan et al., 2016; Yang et al., 2018). Based on the Seebeck and Peltier effects, thermoelectric materials can convert thermal and electrical energy, thereby providing an initial solution to address this problem (He and Tritt, 2017). We use the thermoelectric quality factor ZT (Zhao et al., 2016; Snyder and Snyder, 2017) to measure the conversion efficiency of a thermoelectric material, expressed as:

$\mathit{Z}\mathit{T}=\frac{{\mathit{S}}^{\mathbf{2}}\mathit{\sigma }\mathit{T}}{\mathit{\kappa }},(1)$

where S, σ, T, and κ are the Seebeck coefficient, electrical conductivity, absolute temperature, and thermal conductivity, respectively. The overall thermal conductivity (κ) is generated by the combined effect of the lattice (κ_l) and electronic (κ_e) thermal conductivity. Thus, a material with excellent electrical heating should achieve exceptional electrical properties [high Seebeck coefficient S, electronic conductivity σ, and power factor (PF) = S²σ] and thermal properties (low thermal conductivity κ). In addition, electrical conductivity is counter-correlated to S and directly proportional to κ_e (Jonson and Mahan, 1980), demonstrating the tradeoff in thermoelectric materials with a good ZT.

Low-dimensional materials can achieve local quantum pegging and polarization owing to the changes in their coordination environment and, thus, work well as thermoelectric materials (Dresselhaus et al., 2007). In particular, two-dimensional (2D) materials (Buscema et al., 2013; Kumar and Schwingenschlogl, 2015; Hong et al., 2016a; Gu et al., 2016; Yoshida et al., 2016; Hippalgaonkar et al., 2017; Hu et al., 2017; Huang et al., 2019; Zhu et al., 2019), especially transition metal dichalcogenides (TMDs) (Hippalgaonkar et al., 2017; Marfoua and Hong, 2019; Ding et al., 2020; Patel et al., 2020; Tao et al., 2020; Bilc et al., 2021; Wang et al., 2021), have garnered extensive attention owing to their thermoelectric properties. TMDs exhibit various crystal structures, mainly the H (p-6 m2) and T (p-3m1) phases, which are experimentally found to have good thermal conductivity and low ZT (Yan et al., 2014; Hong et al., 2016b; Ma et al., 2016; Zhang et al., 2017). After the discovery of pentagonal graphene (Zhang et al., 2015), the low symmetry of the pentagonal composition has elevated the study of 2D electrothermal materials, such as pentagonal Y₂N₄ (Y = Pd, Ni or Pt), pentagonal Y₂C (Y = Sb, As, P) and pentasilene (Tian et al., 2016; Liu et al., 2018a; Naseri et al., 2018; Gao et al., 2019; Gao and Wang, 2020; Liu et al., 2020; Liu et al., 2021). The discovery of the good structural stability and high carrier mobility of monoclinic pentagonal PdS₂ by Wang et al. (2015) led researchers to conduct extensive studies on the various properties and potential applications of pentaco-MY₂ (M = Pd, Pt; Y = Te, Se ) (Oyedele et al., 2017; Sun et al., 2018; Lan et al., 2019; Zhao et al., 2020; Raval et al., 2021; Tao et al., 2021). Lan et al. (2019) demonstrated that the κ_l along the x-(y-) transport direction for PdTe₂, PdSe₂, and PdS₂ are 1.42 (5.90), 2.91 (6.62), and 4.34 (12.48) Wm⁻¹K⁻¹, respectively. The maximum p-type ZT of penta-PdX₂ (X = S, Se, Te) along the x-direction are 0.85, 1.18, and 2.42, respectively, demonstrating the potential of penta-PdX₂ monolayers as thermoelectric materials. However, penta-PdTe₂ monolayers have not yet been synthesized experimentally. In particular, although several studies have investigated the thermoelectric properties of pristine penta-PdX₂, the conclusion are conflicting, and the principal discussions are controversial. Therefore, a systematic and detailed investigation should be conducted on the electronic and thermoelectric properties of pristine penta-PdX₂ (X = Se, Te).

In this study, we systematically investigated the electronic and thermoelectric transport properties of monolayer pentagonal PdSe₂ and PdTe₂ by combining first-principles calculations and the Boltzmann transport theory. PdX₂ exhibited the characteristics of an indirect bandgap semiconductor. The results show that the thermoelectric performance parameters of the penta-PdX₂ (X = Se, Te) monolayers, such as thermal conductivity, relaxation time, carrier mobility, and ZT, show strong anisotropy in the x and y directions due to their specific structural characteristics. Compared with PdSe₂, the heavier atomic mass and weaker chemical bonds of PdTe₂ achieved a lower κ_l and higher ZT.

2 Computational details

All calculations were performed based on the density functional theory with the projector-augmented plane wave method used in the Vienna ab initio simulation package (VASP) (Blöchl, 1994; Kresse and Furthmüller, 1996). The electron exchange-correlation energy was described by GGA-PBE (Perdew et al., 1996) and the cut-off energy was set to 500 eV (Monkhorst and Pack, 1976). The structural optimization was performed until the energy change per atom was less than 10^–5 eV, the forces on atoms were less than 10^–4 eV Å⁻¹, all the stress components were less than 0.02 GPa, and there was a maximum displacement of $5.0\times {10}^{-4}\mathrm{Å}$. The k-point meshes were set as 12 × 11 × 1 to ensure the energy convergence. We took a 20 Å thick vacuum slab insertion to model the periodic structure of the monolayers. We used the Boltzmann transport equation based on the relaxation time approximation to calculate the thermoelectric transport coefficients (Madsen and Singh, 2006).

κ_l is mainly dominated by anharmonic phonon–phonon scattering. According to the Boltzmann–Peierls theory and the relaxation time approximation, κ_l is computed by (Yue et al., 2022):

${\mathit{\kappa }}_{\mathit{L}}^{\mathit{\alpha }\mathit{\beta }}\left(\mathit{T}\right)=\frac{\mathbf{1}}{{\mathit{N}}_{\mathit{q}}\mathbf{\Omega }}{\displaystyle \sum }_{\mathit{q},\mathit{j}}{\mathit{C}}_{\mathit{q},\mathit{j}}\left(\mathit{T}\right){\mathit{\upsilon }}_{\mathit{q},\mathit{j}}^{\mathit{\alpha }}{\mathit{\upsilon }}_{\mathit{q},\mathit{j}}^{\mathit{\beta }}{\mathit{\tau }}_{\mathit{q},\mathit{j}}\left(\mathit{T}\right)(2)$

where N_q is the number of wave vectors, Ω is the unit cell volume, α and β are Cartesian coordinate directions, C_q,j is the specific heat capacity of the jth phonon branch at the crystal momentum q, υ_q,j is the phonon group velocity obtained from the harmonic phonon frequency, and τ_q,j is the phonon lifetime. The harmonic phonon frequency was calculated by constructing a 4 × 4 × 1 supercell based on the finite displacement method, as implemented in the Phonopy package (Togo et al., 2008). The anharmonic third-order interatomic force constants (3^rd-IFCs) were computed by constructing a 4 × 4 × 1 supercell with the cutoff value of the fifth nearest neighbor. By combining the 2^nd-IFCs and 3^rd-IFCs, κ_l was obtained through the ShengBTE code (Li et al., 2014).

3 Results and discussion

3.1 Structural models and electronic properties

The penta-PdX₂ monolayer with the P2₁/c space group (No. 14) consists entirely of pentagons. The schematic crystal structures of pentagonal PdX₂ (X = Se, Te) are shown in Figure 1A. The diagram shows that the Pd atom is linked to four X-atoms, and that the adjacent X-atoms are connected to each other to form an anisotropic pentagonal structure. The anisotropy of pentagonal structure determines the anisotropy of the electron and transport properties. After structural optimization, the lattice parameter a (b) of penta-PdSe₂ and penta-PdTe₂ are 5.71 (5.90) and 6.14 (6.44) Å, respectively, which are consistent with previous theoretical calculations (Bardeen and Shockley, 1950) (see Table 1).

FIGURE 1

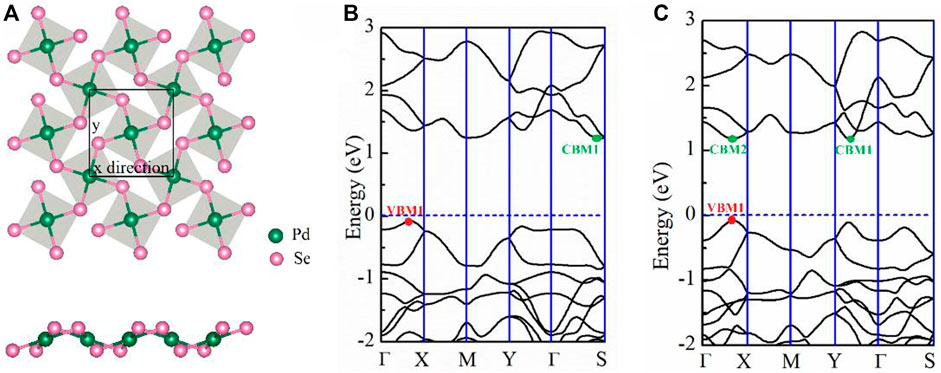
FIGURE 1. (A) Schematic of the top and side view of the penta-PdSe₂ monolayer; the unit cells are marked by the black line. (B) Band structure of the PdSe₂ and (C) PdTe₂ monolayers. The horizontal line indicates the Fermi level. The high symmetry k points are: Γ(0 0 0), X (0.5 0 0), M (0.5 0.5 0), Y (0 0.5 0), and S (0.39 0.5 0).

TABLE 1

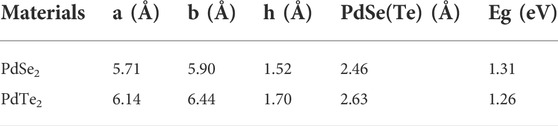
TABLE 1. Lattice parameters (a ,b), the thickness of monolayer materials (h), and bandgap (Eg) at the PBE level.

To determine the electronic properties of the PdSe₂ and PdTe₂ monolayers, we calculated the respective energy band structures and electronic density of states (DOS), as shown in Figure 1, Supplementary Figure S1 of the Supporting Information (SI). All materials exhibited semiconducting band structures with indirect bandgaps for the penta-PdSe₂ (1.31 eV) and PdTe₂ (1.26 eV) monolayers. Combined with the partial DOS (Supplementary Figure S1 of SI), the conduction and valence bands were mainly composed of Pd_d and X_p orbitals. In penta-PdSe₂, the valence band maximum (VBM) and conduction band minimum (CBM) occurred in the Γ-X and Γ-S paths, respectively, as shown in Figure 1B. In penta-PdTe₂, the CBM values were close to the degenerate minima in the Γ-Y and Γ-X paths with a difference of 2 meV only.

3.2 Electronic transport properties

The carrier mobility can be calculated using the deformation potential theory, which is based on the electron–acoustic phonon scattering mechanism, and can be expressed as follows (Bardeen and Shockley, 1950):

${\mathit{\mu }}_{\mathbf{2}\mathit{D}}=\frac{\mathit{e}{\mathit{ħ}}^{\mathbf{3}}{\mathit{C}}_{\mathbf{2}\mathit{D}}}{{\mathit{k}}_{\mathit{B}}\mathit{T}{\mathit{m}}^{*}{\mathit{m}}_{\mathit{d}}{\mathit{E}}_{\mathit{l}}^{\mathbf{2}}}(3)$

where ħ, k_B, T, and m* are the reduced Planck constant, Boltzmann constant, temperature, and effective mass along the transport direction, respectively. m_d is the average effective mass, decided by the effective masses along the x and y transport directions. C_2D represent the elastic modulus, which can be expressed as $C_{2D}=\frac{1}{s_0}\frac{{\partial }^{2}E}{\partial {\left(\frac{l}{l_0}\right)}^2}$, where E, l, l₀, and S₀ are the total energy, lattice constant after and before deformation, and area of the unit cell, respectively. By fitting the band-edge curve, we can obtained the deformation potential constant E_l.

The parameters calculated at 300 K are listed in Table 2 and include the effective mass neutrality, the elastic modulus, the deformation potential and the carrier mobility. As Table 2 shows, the anisotropy of the PdSe₂ and PdTe₂ structures causes them to exhibit anisotropy in all of the above parameters. In the x-direction, the effective mass of the holes was smaller than that of the electrons, particularly for the PdSe₂ monolayers, which is in good agreement with their dispersive band structures (Figure 1). In the y-direction, the effective mass of the electrons (0.51) of PdSe₂ was smaller than that of the holes (1.41), whereas the opposite results were found in the PdTe₂ monolayers. The deformation potential of the holes in the monolayer materials was smaller than that of the electrons in both directions, which reflects the lower scattering rate due to the hole–acoustic phonon interaction and larger carrier mobility. As listed in Table 1, the penta-PdX₂ monolayer exhibited high hole mobility at 300 K. For p-type doping, the small potential constant along the y transport direction indicates high hole mobility. The hole mobilities along the x(y) directions were 620 (1230) and 1063 (1817) cm² V⁻¹ s⁻¹ for the PdSe₂ and PdTe₂ monolayers, respectively which mark them as showing a great advantage in electron transport.

TABLE 2

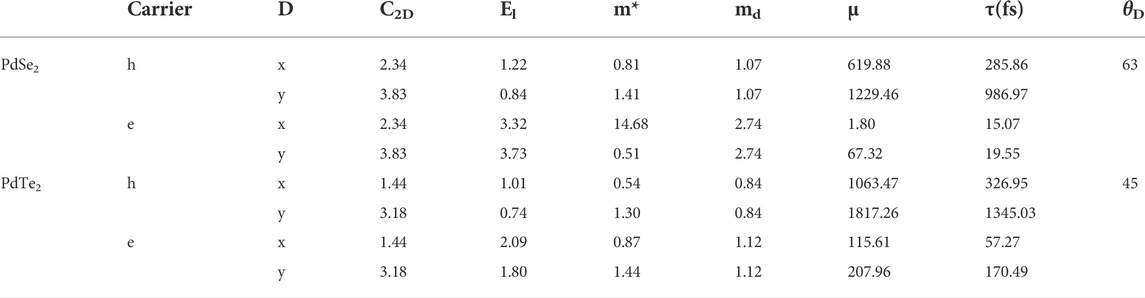
TABLE 2. Calculated deformation potential (E_l), elastic constant (C_2D), effective mass of carrier (m*), average effective mass (m_d), carrier mobility (μ), relaxation time (τ) of the electron (e) and hole (h) along different directions (D) at 300 K, and average Debye temperatureθ_D (K).

The relaxation time can be obtained using the following equation:

$\mathit{\tau }=\frac{\mathit{m}*\mathit{\mu }}{\mathit{e}}(4)$

The temperature-dependent relaxation times of electrons and holes along the x and y transport directions is shown in Figure 2. In agreement with our predictions, the relaxation times also exhibit significant anisotropy, and the holes lifetime (Figure 2A) was significantly longer than that of the electrons because of the weaker hole phonon scattering (Figure 2B). The results demonstrated that the individual anisotropy of the relaxation times was mainly due to differences in the effective masses in x and y transport directions. Among all p-type candidates, The PbTe₂ monolayer had the largest amount of relaxation time variation with temperature along the y-direction, which is mainly due to the smallest potential constant E_l and average effective mass m* at the VBM.

FIGURE 2

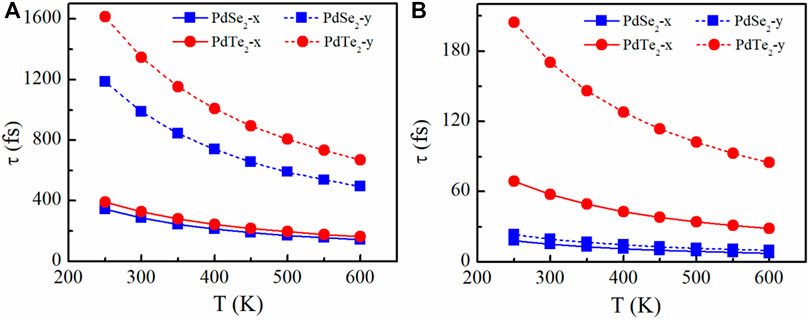
FIGURE 2. Relaxation time of the (A) holes and (B) electrons of the PdSe₂ and PdTe₂ monolayer along the x and y transport directions.

The calculated S and σ/τ along the x and y transport directions at 300 K as functions of the carrier concentration (n) of the PdSe₂ and PdTe₂ monolayer are plotted in Supplementary Figures S2, S3 of SI, respectively. With increasing n, S decreased while σ/τ increased. The transmission coefficients S and σ can be treated with the degenerate-doped single parabolic model, where S and σ were expressed as:

${\mathit{S}}_{\mathbf{2}\mathit{D}}=\frac{\mathbf{2}{\mathit{\pi }}^{\mathbf{3}}{\mathit{k}}_{\mathit{B}}^{\mathbf{2}}\mathit{T}}{\mathbf{3}\mathit{e}{\mathit{h}}^{\mathbf{2}}\mathit{n}}{\mathit{m}}^{*}(5)$

$\mathit{\sigma }=\frac{\mathit{n}{\mathit{e}}^{\mathbf{2}}\mathit{\tau }}{{\mathit{m}}^{*}}(6)$

In the single parabolic band, S decreased as n increased, whereas $\sigma$ linearly increased with n. Compared with p-type doping (Figure 3A), the S of n-type doping was higher for a fixed n (10¹³ cm⁻²). This is because the electron effective mass lies at the edge of conduction band. The isoenergy surfaces enabled analysis of the shape of the electron band. The isoenergy surfaces of the PdX₂ monolayer were plotted (Figure 4), and the results suggested that a single pocket appear only in the Γ-X path for p-type doping, whereas multiple degenerate isoenergy pockets occurs for n-type doping. These results are consistent with previous reports on the significant enhancement of S owing to multiple degenerate bands at the band extrema (Xing et al., 2016; Huang et al., 2021). In p-type doping, the two-pocket properties (Figure 1C) increased S for PdTe₂ in penta-PdX₂ at room temperature. S decreased from PdSe₂ to PdTe₂ at temperatures above 600 K, which can be ascribed to the dual polarization effect caused by the reduced bandgap. Meanwhile, a larger hole’s effective mass increased S along the y-direction for the PdSe₂ and PdTe₂ monolayers. The electrical conductivity during the relaxation time is inversely proportional to S, (as shown in Figure 3A and C) of the SI. In addition, the higher carrier pocket degeneracy and effective mass favor a higher S for n-type doping. Among them, n-type doped PdTe₂ obtained the largest S in the x- or y-direction.

FIGURE 3

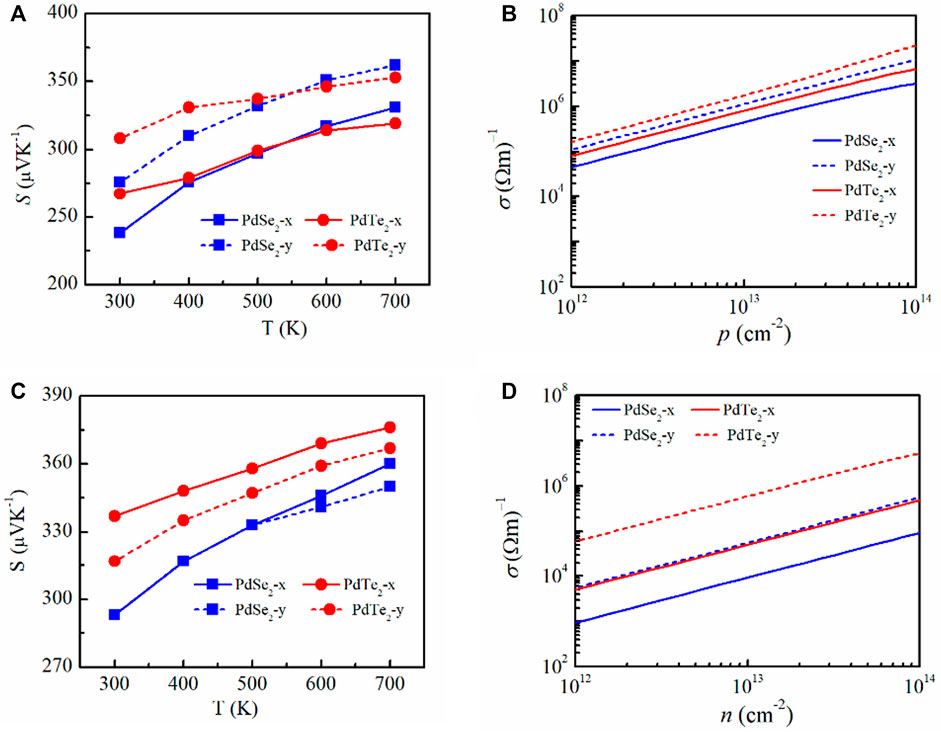
FIGURE 3. (A,C) Calculated Seebeck coefficient of penta-PdSe₂ and penta-PdTe₂ as a function of temperature and electrical conductivity. (B,D) Function of the carrier concentration at 300 K along the x and y directions under p-type (top panels) and n-type (bottom panels) doping.

FIGURE 4

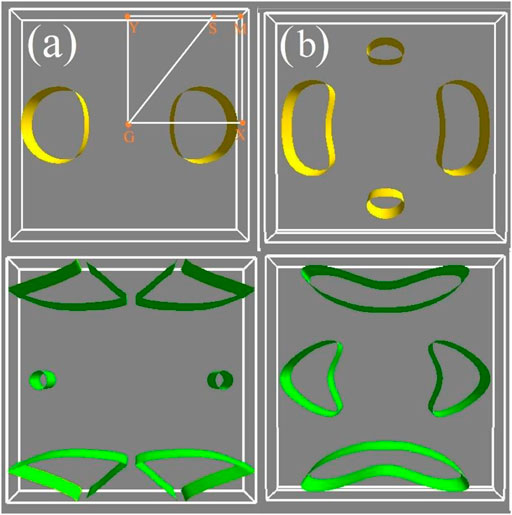
FIGURE 4. Constant energy surface of (A) penta-PdSe₂ and (B) penta-PdTe₂. The top images denote the highest valence with the energy of 0.1 eV less than the VBM, and the bottom images denote the lowest conduction band with the energy of 0.1 eV more than the CBM.

Electrical conductivity was determined based on the relaxation time τ. Figures 3B,D show the electrical conductivities of the PdSe₂ and PdTe₂ monolayers at 300 K in p-type and n-type doping. The p-type electrical conductivity was higher than the n-type electrical conductivity because of the higher carrier mobility and longer carrier lifetime. In p-type doping, the electrical conductivity along the y-direction was larger than that along the x-direction, although the effective mass of the holes in the y-direction was higher. Similar behavior was observed for n-type doping. This trend is mainly attributed to the significantly larger elastic constant in the y-direction, which increased τ in all temperature ranges.

PF is used to evaluate the ability of a material to convert electrical energy. The determined PF in this study is plotted in Figure 5. A higher electrical conductivity combined with a suitable S achieved a higher PF for p-type doping. In particular, for PdTe₂, the highest PF during p-type and n-type doping at 300 K reached 300 mWmK⁻² along the y-direction (Figure 5A) and 90 mW mK⁻² (Figure 5B), respectively.

FIGURE 5

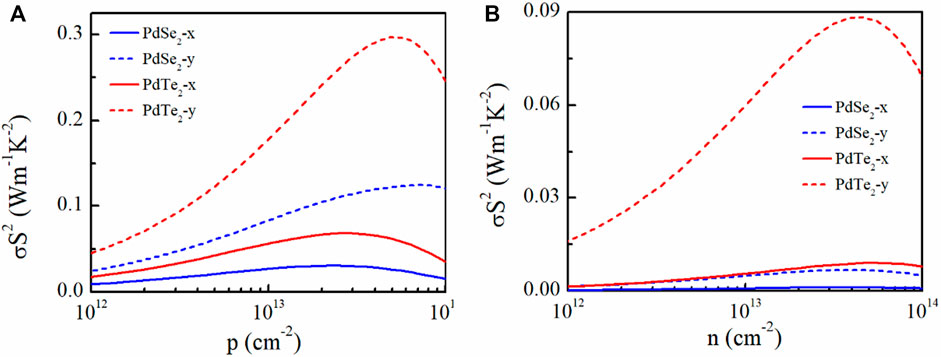
FIGURE 5. Calculated (A) p-type and (B) n-type power factor (σS²) of penta-PdSe₂ and penta-PdTe₂ as a function of the carrier concentration at 300 K along the x- (solid lines) and y- (dotted lines) directions.

3.3 Thermal transport properties

We analyzed the thermal transport properties of the PdX₂ (X = Se, Te) monolayer based on the harmonic and anharmonic effects. Phonon spectra were obtained from the harmonic interatomic force constants, as shown in Supplementary Figure S4 of SI. Heavier elements and a small force constant have lower vibration frequency. The maximum phonon vibrational frequency gradually decreased from the PdSe₂ to PdTe₂ monolayers, indicating the suppressed phonon vibrations and shift of the optical branches toward lower energies, thereby achieving strong interactions between the phonon modes and decreasing κ_l. Using the harmonic (2^nd) and anharmonic (3^rd) interatomic force constants, κ_l of the PdSe₂ and PdTe₂ monolayers were obtained, as shown in Figure 6A. In general, κ_l decreased with increasing temperature owing to the low-frequency phonons (Figure 6B) and demonstrate anisotropy along different directions. At 300 K, the calculated κ_l was 3.99 (10.58) and 0.41 (0.83) W m⁻¹K⁻¹ for PdSe₂ and PdTe₂, respectively, along the x(y) transport directions. These results are comparable to other thermoelectric materials with superior thermoelectric properties, such as monolayer SnSe (3 Wm⁻¹K⁻¹) (Zhang et al., 2016), bulk SnSe (0.62 Wm⁻¹K⁻¹) (Xiao et al., 2016), Ge₄Se₃Te (1.6 Wm⁻¹K⁻¹) (Huang et al., 2021), silicene (2.86 Wm⁻¹K⁻¹) (Peng et al., 2016), germanene (2.4 Wm⁻¹K⁻¹) (Peng et al., 2017), and GeSe (2.63 Wm⁻¹K⁻¹) (Liu et al., 2018b). Therefore, κ_e is a vital factor in the ZT evaluation owing to the low κ_l.

FIGURE 6

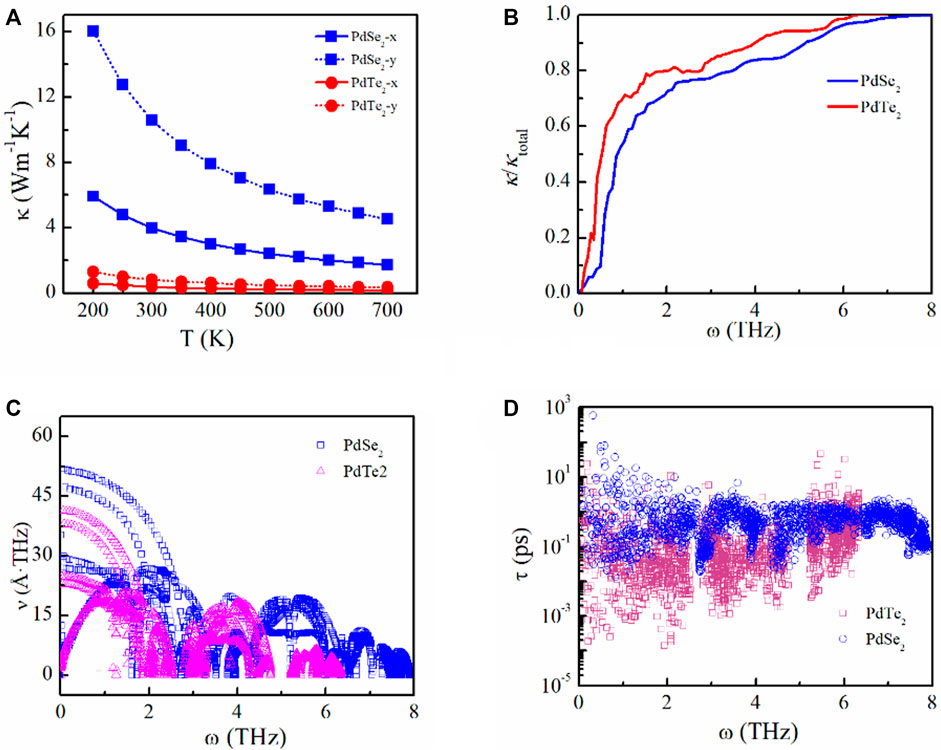
FIGURE 6. (A) Lattice thermal conductivity as a function of temperature, (B) phonon contributions toward the total lattice thermal conductivity, (C) phonon velocity, and (D) phonon lifetime of the penta-PdSe₂ and penta-PdTe₂ monolayers.

To analyze κ_l, we obtained the phonon group velocity and lifetime. The lower thermal conductivity is mainly attributed to the decreasing phonon velocity from PdSe₂ to PdTe₂, as shown in Figure 6C. Compared to the PdSe₂ monolayer, the PdTe₂ monolayer exhibited a shorter phonon lifetime, as shown in Figure 6D, indicating that the PdTe₂ monolayer exhibits a considerably higher scattering rate and anharmonic feature, which can also be obtained from the phonon spectra. The scattering probability of the emission and absorption processes can be described by the frequency-dependent scattering phase space. The scattering phase spaces of the emission and absorption processes at 300 K are shown in Supplementary Figure S5 in the SI. The suppressed phonons increased the scattering phase space and enhanced the anharmonic feature, resulting in decreased thermal conductivity from PdSe₂ to PdTe₂ in the low-frequency region.

To further analyze the anharmonic feature, the difference in the charge density was computed as:

$∆\mathit{\rho }={\mathit{\rho }}_{\mathit{M}\mathit{X}\mathbf{2}}-{\mathit{\rho }}_{\mathit{M}}-{\mathit{\rho }}_{\mathit{X}\mathbf{2}}(7)$

where ${\rho }_{MX2}$, ${\rho }_M$, and ${\rho }_{X2}$ are the total charge density, charge density of the metal atoms, and chalcogen atoms, respectively. Lower charge density was accumulated on the Pd–Te bonds of PdTe₂, compared to PdSe₂, suggesting that penta-PdTe₂ was significantly softer than PdSe₂ with a strong anharmonic effect, as shown in Figure 7. Furthermore, the average acoustic Debye temperature (θ_D) was evaluated using the formula:

$\frac{\mathbf{1}}{{\mathit{\theta }}_{\mathit{D}}^{\mathbf{3}}}=\frac{\mathbf{1}}{\mathbf{3}}\left(\frac{\mathbf{1}}{{\mathit{\theta }}_{\mathit{Z}\mathit{A}}^{\mathbf{3}}}+\frac{\mathbf{1}}{{\mathit{\theta }}_{\mathit{T}\mathit{A}}^{\mathbf{3}}}+\frac{\mathbf{1}}{{\mathit{\theta }}_{\mathit{L}\mathit{A}}^{\mathbf{3}}}\right)(8)$

where θ_i (i = ZA, TA, LA) is obtained by ${\theta }_i=h{v}_{i,\mathit{max}}/k_B$, where h, k_B, and v_i,max are the Planck constant, Boltzmann constant, and the maximal phonon frequency of the ith acoustic phonon mode, respectively. The θ_D values of the PdSe₂ and PdTe₂ monolayers were 63 and 45 K, respectively. The low Debye temperature is due to the weak interatomic bonding of the PdTe₂ monolayer, which suggested more phonons could participate in the scattering process, thereby reducing κ_l.

FIGURE 7

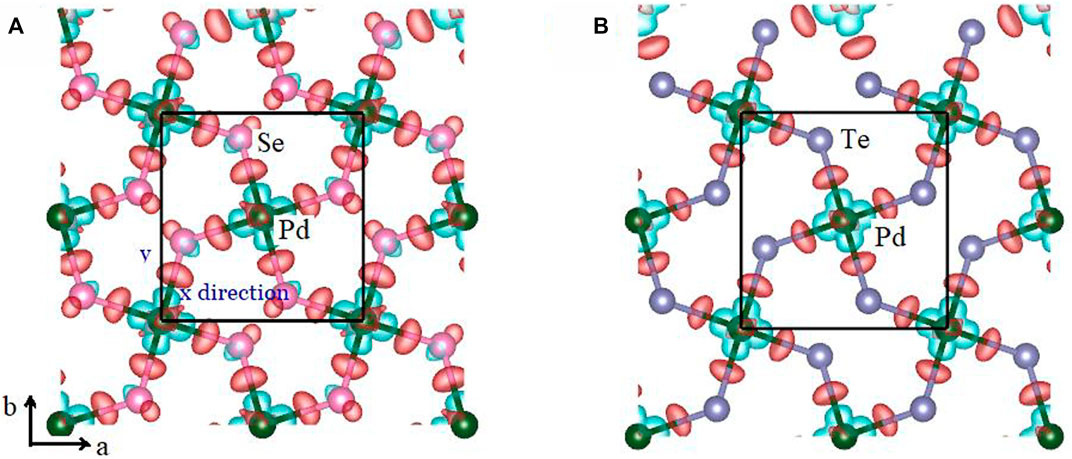
FIGURE 7. Difference of the charge density of the (A) penta-PdSe₂ and (B) penta-PdTe₂ monolayers, respectively. The red and green regions denote the charge accumulation and depletion, respectively. The charge density isosurfaces were set to 0.05 eÅ⁻³.

3.4 Quality factor

The dimensionless thermoelectric ZT was analyzed. κ_e was calculated using the Wiedemann–Franz law (Jonson and Mahan, 1980):

${\mathit{\kappa }}_{\mathit{e}}=\mathit{L}\mathit{\sigma }\mathit{T}(9)$

where L is the Lorenza number (L = 2.45 × 10^–8 WΩK⁻²). κ_e of the PdSe₂ and PdTe₂ monolayers at 300 K are shown in Supplementary Figure S6 of the SI, which was similar to κ_l. κ_e in the y-direction was larger than that in the x-direction owing to the high electronic conductivity in the y-direction. The larger κ_e and κ_l in the y-direction also prove that the thermoelectric properties were worse along the y-direction than along the x-direction.

The ZT values for p- and n-type doping of the monolayer materials at 300 K along the x and y directions are plotted in Figure 8. The ZT values of the p-type-doped PdSe₂ and PdTe₂ monolayers were larger than those with n-type doping because of the higher electronic conductivity. Owing to the smaller κ_l and higher PF, the PdTe₂ monolayer obtained the largest ZT values, regardless of the doping type. In particular, the calculated ZT of the p-type- and n-type-doped PdTe₂ monolayers along the x- (y-) direction were 5.2 (6.6) and 2.1 (4.4), demonstrating PdTe₂ as a promising thermoelectric candidate.

FIGURE 8

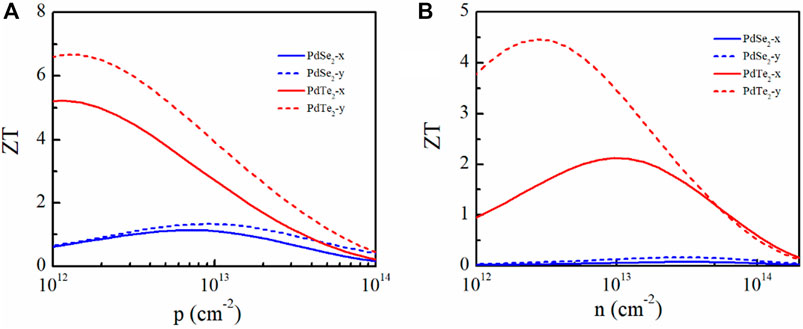
FIGURE 8. Figure of merit ZT of the penta-PdSe₂ and penta-PdTe₂ monolayers under (A) p-type and (B) n-type doping as a function of the carrier concentration at 300 K along the x and y directions.

4 Conclusion

In this study, we systematically investigated the electronic structures, electronic transport, and thermal transport properties of pentagonal PdX₂ (X = Se, Te) monolayers using first-principles calculations and with Boltzmann transport theory. The PdSe₂ and PdTe₂ monolayer semiconductors had bandgaps of 1.31 and 1.26 eV, respectively. The anisotropic crystal structure of penta-PdX₂ (X = Se, Te) achieved anisotropic transport properties. At the optimized doping concentration, the PdSe₂ and PdTe₂ monolayers with p-type and n-type doping along the x- (y-) directions obtained PF of up to 30 (120) and 70 (300) mW m⁻¹ K⁻², and 1 (7) and 9 (88) mW m⁻¹ K⁻², respectively. The shorter phonon lifetime of penta- PdX₂ decreased κ_l. In particular, the κ_l values were 3.99 (10.58) and 0.41 (0.83) Wm⁻¹K⁻¹ for PdSe₂ and PdTe₂ along the x- (y-) direction at 300 K, respectively. Owing to its smaller phonon group velocity and larger scattering space, PdTe₂ exhibited lower thermal conductivity. The reasonable PF and low κ_l imply that the optimal ZT values of p-type and n-type-doped PdTe₂ along the y-direction at the optimal doping concentrations of 6.6 and 4.4, respectively, indicating that the PdTe₂ monolayer is a thermoelectric material with excellent properties.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

LL and HH: Conceptualization, methodology, software; LL and HH: Writing—original draft preparation. LL, ZH, JX, and HH: Investigation; HH: Supervision; LL: Writing—review and editing.

Funding

Financial support was received from the National Natural Science Foundation of China (11904033 and 12204215), the Advanced Research Projects of Chongqing Municipal Science and Technology Commission (cstc2019jcyj-msxmX0674), and the Natural Science Foundation of Shandong Province of China (ZR2021QA026).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2022.1061703/full#supplementary-material

References

Bardeen, J., and Shockley, W. (1950). Deformation potentials and mobilities in non-polar crystals. Phys. Rev. 80, 72–80. doi:10.1103/physrev.80.72

CrossRef Full Text | Google Scholar

Bilc, D. I., Benea, D., Pop, V., Ghosez, P., and Verstraete, M. J. (2021). Electronic and thermoelectric properties of transition-metal dichalcogenides. J. Phys. Chem. C 125, 27084–27097. doi:10.1021/acs.jpcc.1c07088

CrossRef Full Text | Google Scholar

Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953–17979. doi:10.1103/physrevb.50.17953

CrossRef Full Text | Google Scholar

Buscema, M., Barkelid, M., Zwiller, V., van der Zant, H. S., Steele, G. A., and Castellanos-Gomez, A. (2013). Large and tunable photothermoelectric effect in single-layer MoS₂. Nano Lett. 13, 358–363. doi:10.1021/nl303321g

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, W., Li, X., Jiang, F., Liu, P., Liu, P., Zhu, S., et al. (2020). Defect modification engineering on a laminar MoS₂ film for optimizing thermoelectric properties. J. Mat. Chem. C 8, 1909–1914. doi:10.1039/c9tc06012j

CrossRef Full Text | Google Scholar

Dresselhaus, M. S., Chen, G., Tang, M. Y., Yang, R., Lee, H., Wang, D., et al. (2007). New directions for low‐dimensional thermoelectric materials. Adv. Mat. 19, 1043–1053. doi:10.1002/adma.200600527

CrossRef Full Text | Google Scholar

Gao, Z., and Wang, J.-S. (2020). Thermoelectric penta-silicene with a high room-temperature figure of merit. ACS Appl. Mat. Interfaces 12, 14298–14307. doi:10.1021/acsami.9b21076

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, Z., Zhang, Z., Liu, G., and Wang, J.-S. (2019). Ultra-low lattice thermal conductivity of monolayer penta-silicene and penta-germanene. Phys. Chem. Chem. Phys. 21, 26033–26040. doi:10.1039/c9cp05246a

PubMed Abstract | CrossRef Full Text | Google Scholar

Gu, X., Li, B., and Yang, R. (2016). Layer thickness-dependent phonon properties and thermal conductivity of MoS₂. J. Appl. Phys. 119, 085106. doi:10.1063/1.4942827

CrossRef Full Text | Google Scholar

He, J., and Tritt, T. M. (2017). Advances in thermoelectric materials research: Looking back and moving forward. Science 357, eaak9997. doi:10.1126/science.aak9997

PubMed Abstract | CrossRef Full Text | Google Scholar

Hippalgaonkar, K., Wang, Y., Ye, Y., Qiu, D. Y., Zhu, H., Wang, Y., et al. (2017). High thermoelectric power factor in two-dimensional crystals of MoS₂. Phys. Rev. B 95, 115407. doi:10.1103/physrevb.95.115407

CrossRef Full Text | Google Scholar

Hong, J., Lee, C., Park, J.-S., and Shim, J. H. (2016). Control of valley degeneracy in MoS₂ by layer thickness and electric field and its effect on thermoelectric properties. Phys. Rev. B 93, 035445. doi:10.1103/physrevb.93.035445

CrossRef Full Text | Google Scholar

Hong, Y., Zhang, J., and Zeng, X. C. (2016). Thermal conductivity of monolayer MoSe₂ and MoS₂. J. Phys. Chem. C 120, 26067–26075. doi:10.1021/acs.jpcc.6b07262

CrossRef Full Text | Google Scholar

Hu, Z.-Y., Li, K.-Y., Lu, Y., Huang, Y., and Shao, X.-H. (2017). High thermoelectric performances of monolayer SnSe allotropes. Nanoscale 9, 16093–16100. doi:10.1039/c7nr04766e

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, H., Fan, X., Zheng, W., and Singh, D. J. (2021). Improved thermoelectric transport properties of Ge₄Se₃ Te through dimensionality reduction. J. Mat. Chem. C 9, 1804–1813. doi:10.1039/d0tc04537c

CrossRef Full Text | Google Scholar

Huang, S., Wang, Z., Xiong, R., Yu, H., and Shi, J. (2019). Significant enhancement in thermoelectric performance of Mg₃Sb₂ from bulk to two-dimensional mono layer. Nano Energy 62, 212–219. doi:10.1016/j.nanoen.2019.05.028

CrossRef Full Text | Google Scholar

Jonson, M., and Mahan, G. (1980). Mott's formula for the thermopower and the Wiedemann-Franz law. Phys. Rev. B 21, 4223–4229. doi:10.1103/physrevb.21.4223

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mat. Sci. 6, 15–50. doi:10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

Kumar, S., and Schwingenschlogl, U. (2015). Thermoelectric response of bulk and monolayer MoSe₂ and WSe₂. Chem. Mat. 27, 1278–1284. doi:10.1021/cm504244b

CrossRef Full Text | Google Scholar

Lan, Y.-S., Chen, X.-R., Hu, C.-E., Cheng, Y., and Chen, Q.-F. (2019). Penta-PdX₂ (X= S, Se, Te) monolayers: Promising anisotropic thermoelectric materials. J. Mat. Chem. A 7, 11134–11142. doi:10.1039/c9ta02138h

CrossRef Full Text | Google Scholar

Li, W., Carrete, J., Katcho, N. A., and Mingo, N. (2014). ShengBTE: A solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 185, 1747–1758. doi:10.1016/j.cpc.2014.02.015

CrossRef Full Text | Google Scholar

Liu, P.-F., Bo, T., Xu, J., Yin, W., Zhang, J., Wang, F., et al. (2018). First-principles calculations of the ultralow thermal conductivity in two-dimensional group-IV selenides. Phys. Rev. B 98, 235426. doi:10.1103/physrevb.98.235426

CrossRef Full Text | Google Scholar

Liu, X., Ouyang, T., Zhang, D., Huang, H., Wang, H., Wang, H., et al. (2020). First-principles calculations of phonon transport in two-dimensional penta-X₂C family. J. Appl. Phys. 127, 205106. doi:10.1063/5.0004904

CrossRef Full Text | Google Scholar

Liu, X., Zhang, D., Wang, H., Chen, Y., Wang, H., and Ni, Y. (2021). Ultralow lattice thermal conductivity and high thermoelectric performance of penta-Sb₂C monolayer: A first principles study. J. Appl. Phys. 130, 185104. doi:10.1063/5.0065330

CrossRef Full Text | Google Scholar

Liu, Z., Wang, H., Sun, J., Sun, R., Wang, Z., and Yang, J. (2018). Penta-Pt₂N₄: An ideal two-dimensional material for nanoelectronics. Nanoscale 10, 16169–16177. doi:10.1039/c8nr05561k

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, J., Chen, Y., Han, Z., and Li, W. (2016). Strong anisotropic thermal conductivity of monolayer WTe₂. 2D Mat. 3, 045010. doi:10.1088/2053-1583/3/4/045010

CrossRef Full Text | Google Scholar

Madsen, G. K., and Singh, D. J. (2006). BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 175, 67–71. doi:10.1016/j.cpc.2006.03.007

CrossRef Full Text | Google Scholar

Marfoua, B., and Hong, J. (2019). High thermoelectric performance in hexagonal 2D PdTe₂ monolayer at room temperature. ACS Appl. Mat. Interfaces 11, 38819–38827. doi:10.1021/acsami.9b14277

PubMed Abstract | CrossRef Full Text | Google Scholar

Monkhorst, H. J., and Pack, J. D. (1976). Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192. doi:10.1103/physrevb.13.5188

CrossRef Full Text | Google Scholar

Naseri, M., Lin, S., Jalilian, J., Gu, J., and Chen, Z. (2018). Penta-P₂X (X= C, Si) monolayers as wide-bandgap semiconductors: A first principles prediction. Front. Phys. 13, 138102–138109. doi:10.1007/s11467-018-0758-2

CrossRef Full Text | Google Scholar

Oyedele, A. D., Yang, S., Liang, L., Puretzky, A. A., Wang, K., Zhang, J., et al. (2017). PdSe₂: Pentagonal two-dimensional layers with high air stability for electronics. J. Am. Chem. Soc. 139, 14090–14097. doi:10.1021/jacs.7b04865

PubMed Abstract | CrossRef Full Text | Google Scholar

Patel, A., Singh, D., Sonvane, Y., Thakor, P., and Ahuja, R. (2020). High thermoelectric performance in two-dimensional Janus monolayer material WS-X (X= Se and Te). ACS Appl. Mat. Interfaces 12, 46212–46219. doi:10.1021/acsami.0c13960

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, B., Zhang, D., Zhang, H., Shao, H., Ni, G., Zhu, Y., et al. (2017). The conflicting role of buckled structure in phonon transport of 2D group-IV and group-V materials. Nanoscale 9, 7397–7407. doi:10.1039/c7nr00838d

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, B., Zhang, H., Shao, H., Xu, Y., Zhang, R., Lu, H., et al. (2016). First-principles prediction of ultralow lattice thermal conductivity of dumbbell silicene: A comparison with low-buckled silicene. ACS Appl. Mat. Interfaces 8, 20977–20985. doi:10.1021/acsami.6b04211

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Raval, D., Babariya, B., Gupta, S. K., Gajjar, P., and Ahuja, R. (2021). Ultrahigh carrier mobility and light-harvesting performance of 2D penta-PdX₂ monolayer. J. Mat. Sci. 56, 3846–3860. doi:10.1007/s10853-020-05501-w

CrossRef Full Text | Google Scholar

Snyder, G. J., and Snyder, A. H. (2017). Figure of merit ZT of a thermoelectric device defined from materials properties. Energy Environ. Sci. 10, 2280–2283. doi:10.1039/c7ee02007d

CrossRef Full Text | Google Scholar

Sun, M., Chou, J.-P., Shi, L., Gao, J., Hu, A., Tang, W., et al. (2018). Few-layer PdSe₂ sheets: Promising thermoelectric materials driven by high valley convergence. ACS omega 3, 5971–5979. doi:10.1021/acsomega.8b00485

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, G., Zhao, L.-D., and Kanatzidis, M. G. (2016). Rationally designing high-performance bulk thermoelectric materials. Chem. Rev. 116, 12123–12149. doi:10.1021/acs.chemrev.6b00255

PubMed Abstract | CrossRef Full Text | Google Scholar

Tao, W.-L., Lan, J.-Q., Hu, C.-E., Cheng, Y., Zhu, J., and Geng, H.-Y. (2020). Thermoelectric properties of Janus MXY (M= Pd, Pt; X, Y= S, Se, Te) transition-metal dichalcogenide monolayers from first principles. J. Appl. Phys. 127, 035101. doi:10.1063/1.5130741

CrossRef Full Text | Google Scholar

Tao, W.-L., Zhao, Y.-Q., Zeng, Z.-Y., Chen, X.-R., and Geng, H.-Y. (2021). Anisotropic thermoelectric materials: Pentagonal PtM₂ (M = S, Se, Te). ACS Appl. Mat. Interfaces 13, 8700–8709. doi:10.1021/acsami.0c19460

PubMed Abstract | CrossRef Full Text | Google Scholar

Tian, H., Tice, J., Fei, R., Tran, V., Yan, X., Yang, L., et al. (2016). Low-symmetry two-dimensional materials for electronic and photonic applications. Nano Today 11, 763–777. doi:10.1016/j.nantod.2016.10.003

CrossRef Full Text | Google Scholar

Togo, A., Oba, F., and Tanaka, I. (2008). First-principles calculations of the ferroelastic transition between rutile-type and CaCl₂-type SiO₂ at high pressures. Phys. Rev. B 78, 134106. doi:10.1103/physrevb.78.134106

CrossRef Full Text | Google Scholar

Wang, N., Gong, H., Sun, Z., Shen, C., Li, B., Xiao, H., et al. (2021). Boosting thermoelectric performance of 2D transition-metal dichalcogenides by complex cluster substitution: The role of octahedral Au6 clusters. ACS Appl. Energy Mat. 4, 12163–12176. doi:10.1021/acsaem.1c01777

CrossRef Full Text | Google Scholar

Wang, Y., Li, Y., and Chen, Z. (2015). Not your familiar two dimensional transition metal disulfide: Structural and electronic properties of the PdS₂ monolayer. J. Mat. Chem. C 3, 9603–9608. doi:10.1039/c5tc01345c

CrossRef Full Text | Google Scholar

Xiao, Y., Chang, C., Pei, Y., Wu, D., Peng, K., Zhou, X., et al. (2016). Origin of low thermal conductivity in SnSe. Phys. Rev. B 94, 125203. doi:10.1103/physrevb.94.125203

CrossRef Full Text | Google Scholar

Xing, G., Sun, J., Ong, K. P., Fan, X., Zheng, W., and Singh, D. J. (2016). Perspective: n-Type oxide thermoelectrics via visual search strategies. Apl. Mat. 4, 053201. doi:10.1063/1.4941711

CrossRef Full Text | Google Scholar

Yan, R., Simpson, J. R., Bertolazzi, S., Brivio, J., Watson, M., Wu, X., et al. (2014). Thermal conductivity of monolayer molybdenum disulfide obtained from temperature-dependent Raman spectroscopy. ACS Nano 8, 986–993. doi:10.1021/nn405826k

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, L., Chen, Z. G., Dargusch, M. S., and Zou, J. (2018). High performance thermoelectric materials: Progress and their applications. Adv. Energy Mat. 8, 1701797. doi:10.1002/aenm.201701797

CrossRef Full Text | Google Scholar

Yoshida, M., Iizuka, T., Saito, Y., Onga, M., Suzuki, R., Zhang, Y., et al. (2016). Gate-optimized thermoelectric power factor in ultrathin WSe₂ single crystals. Nano Lett. 16, 2061–2065. doi:10.1021/acs.nanolett.6b00075

PubMed Abstract | CrossRef Full Text | Google Scholar

Yue, T., Sun, Y., Zhao, Y., Meng, S., and Dai, Z. (2022). Thermoelectric performance in the binary semiconductor compound A₂Se₂ (A= K, Rb) with host-guest structure. Phys. Rev. B 105, 054305. doi:10.1103/physrevb.105.054305

CrossRef Full Text | Google Scholar

Zhang, J., Liu, X., Wen, Y., Shi, L., Chen, R., Liu, H., et al. (2017). Titanium trisulfide monolayer as a potential thermoelectric material: A first-principles-based Boltzmann transport study. ACS Appl. Mat. Interfaces 9, 2509–2515. doi:10.1021/acsami.6b14134

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, L.-C., Qin, G., Fang, W.-Z., Cui, H.-J., Zheng, Q.-R., Yan, Q.-B., et al. (2016). Tinselenidene: A two-dimensional auxetic material with ultralow lattice thermal conductivity and ultrahigh hole mobility. Sci. Rep. 6, 19830. doi:10.1038/srep19830

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, S., Zhou, J., Wang, Q., Chen, X., Kawazoe, Y., and Jena, P. (2015). Penta-graphene: A new carbon allotrope. Proc. Natl. Acad. Sci. U. S. A. 112, 2372–2377. doi:10.1073/pnas.1416591112

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, L.-D., Tan, G., Hao, S., He, J., Pei, Y., Chi, H., et al. (2016). Ultrahigh power factor and thermoelectric performance in hole-doped single-crystal SnSe. Science 351, 141–144. doi:10.1126/science.aad3749

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y., Yu, P., Zhang, G., Sun, M., Chi, D., Hippalgaonkar, K., et al. (2020). Low‐symmetry PdSe₂ for high performance thermoelectric applications. Adv. Funct. Mat. 30, 2004896. doi:10.1002/adfm.202004896

CrossRef Full Text | Google Scholar

Zhu, X.-L., Hou, C.-H., Zhang, P., Liu, P.-F., Xie, G., and Wang, B.-T. (2019). High thermoelectric performance of new two-dimensional IV–VI compounds: A first-principles study. J. Phys. Chem. C 124, 1812–1819. doi:10.1021/acs.jpcc.9b09787

CrossRef Full Text | Google Scholar