- DBS&H, CEME, National University of Sciences and Technology, Islamabad, Pakistan
We analyze the steady laminar incompressible boundary-layer magnetohydrodynamic impacts on the nanofluidic flux over a static and mobile wedge in the existence of an applied magnetic field. The Falkner–Skan wedge flow model is taken into consideration. Reynolds’ model is considered to introduce temperature-dependent viscosity. As in real life, most fluids have variable viscosity. The executive partial differential equations are converted into a set-up of ordinary differential equations by means of a similarity conversion. Numerical solutions are computed for the converted set-up of equations subjected to physical boundary conditions. The specific flow dynamics like velocity profile, streamlines, temperature behavior, and coefficient of local skin friction are graphically analyzed through numerical solutions. It is concluded that the laminar boundary-layer separation from the static and moving wedge surface is altered by the applied external electric field, and the wedge (static or moving) angle improves the surface heat flux in addition to the coefficient of skin friction. Furthermore, it is found that the methanol-based nanofluid is a less-efficient cooling agent than the water-based nanofluid; therefore, the magnitude of the Nusselt number is smaller for the water-based nanofluid. It is also observed that the addition of only 1% of these nanoparticles in a base fluid results in an enhancement of almost 200% in the thermal conductivity.
Introduction
The fluid mechanical aspects of the boundary layer on the static and mobile wedges (Falkner–Skan flow) have received a lot of attention from researchers and scientists of fluid mechanics mainly because of their applications in diverse situations such as natural flow, mechanical flow, biological flow, and transport of fluids in industries. The laminar boundary-layer flow impacts for a fixed wedge engaged in the viscous incompressible fluid were first reported by Falkner and Skan (1931). It was the extension of Prandtl’s concept on the applications of boundary layers. In the review of the laminar boundary-layer flow over a wedge set at an angle (
The motivation behind the huge intriguing research on the topic of nanofluids in recent years is due to an open range of practical applications in both the engineering and pharmaceutical industries. The dispersion of nano-scale particles in a base fluid provides the combination of the nanofluid and in most cases nanotubes, nanofibers, nanosheets, nanowires, or droplets being used for this purpose. It is experimentally (Murshed et al., 2005; Wang and Mujumdar, 2007; Yu and Xie, 2012; Mahian et al., 2013; Bianco et al., 2015) proved that the addition of only 1% of these nanoparticles in a base fluid results in an enhancement of almost 200% in the thermal conductivity. Some of the most recent applications of nanofluids are reported by Tripathi and Bég (2014) and Akbar et al. (2016a). The carbon nanotube (CNT) is one of the nanoparticles which can be dispersed in base fluids, and it has a wide range of applications in various disciplines. The dispersion of the CNT in base fluids and its effects on the enhancement of thermal conductivity were analyzed through an experimental study performed by Kim and Peterson (2007). They observed that the addition of only 1% SWNT results in a thermal conductivity increase of 10%, while only 3.5% was achieved in the case of aluminum oxide. Some other experimental studies (Sastry et al., 2008; Garg et al., 2009) examining thermal conductivity and heat transfer performance are also reported. Furthermore, Kamali and Binesh (2010) presented a numerical study on fixed heat flux consequences of the addition of multi-wall nanotubes. They used the finite volume method (FVM) and considered the power law model of viscous fluids for base fluids. Most recently, Chai et al. (2016) used TEM imaging and FTIR analysis for the MWCNT structure and chemical compound. They have concluded that the hydrogenated oil containing multi-wall carbon nanotubes has a 9.8% increase in thermal conductivity at a concentration of 100 ppm, while an increase of 7.2% and 4.5% is noted at a concentration of 50 ppm and 25 ppm, respectively. There are many applications of MHD flows in the field of science and engineering. The combined effects of MHD and the nanofluid flow have huge applications in science, technology, and industries. Most recently, Chamkha (1996), Thameem Bash, Sivaraj, Takhar et al. (1999), Chamkha et al. (2006), Akbar et al. (2016b), Akbar et al. (2016), Akbar et al. (2016d), Animasaun et al. (2019), Kumaran et al. (2019), Thameem Basha et al. (2019), Ashraf et al. (2020), Basha et al. (2020), Hamad et al. (2022), and Rasool et al. (2022) reported the study of MHD, and the nanofluid flow is reported in the literature.
In all the aforementioned studies, the study of the nanofluid flow through a static and movable wedge is not reported. However, considering the immense count of practical applications in flow over the wedge, few investigators (Yacob et al., 2011a; Yacob et al., 2011b; Khan and Pop, 2013; Dennis et al., 2015; Khan et al., 2015) have reported. Yacob et al. (2011a) solved the Falkner–Skan problem by means of the Keller-box numerical technique for a fixed and mobile wedge, considering copper, titania, and alumina nanofluids. A higher coefficient of skin friction is observed for Cu–water than for other cases. In other studies, Yacob et al. (2011b) further extended their analysis by means of multiple numerical solution techniques like Keller box, shooting, and the Runge–Kutta–Fehlberg method. Khan and Pop (2013) investigated the boundary layer impacts on a mobile wedge with the nanofluid flow. Khan et al. (2015) extended their model by considering various effects like radiations, MHD, and chemical reactions on the boundary layer over a wedge. Daub et al. (Dennis et al., 2015) experimentally studied the effects of a mobile wedge on the shockwave boundary layer. Most recently, some important works (Javaherdeh and Ashorynejad, 2014; Malvandi et al., 2014; Sheikholeslami and Ganji, 2015; Kasmani et al., 2016; Madaki et al., 2016; Salama, 2016; Akram et al., 2020) have reported on the flow over the wedge moving in the second-grade nanofluid, highlighting the impacts of the Cu–water combination of nanofluids over a mobile wedge, the homotopy asymptotic technique for the Falkner–Skan flow problem. The fluid transport in composite membranes used in water desalination is presented in recent articles (Ezaier et al., 2022a; Ezaier et al., 2022b; Ezaier et al., 2022c).
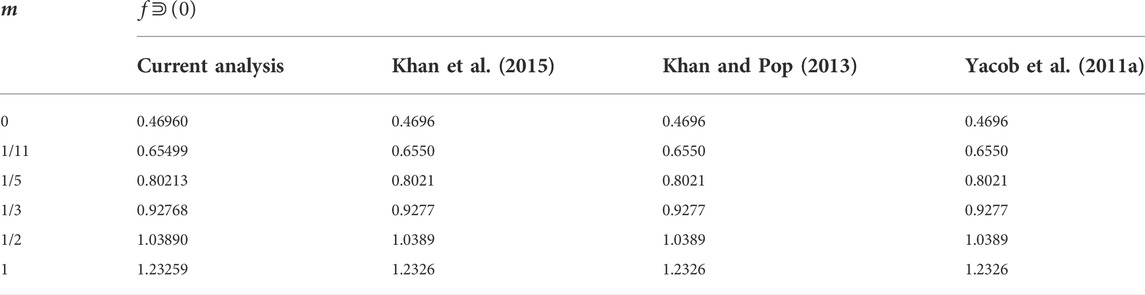
Motivated by the aforementioned studies and findings, we extend the work of Kuo (2005), Khan et al. (Yacob et al., 2011a), Yacob et al. (2011b), and Khan and Pop (2013) for the static and movable wedge to study the heat transfer properties of different nanofluids, that is, the water-based copper nanofluid and methanol-based copper nanofluid. The viscosity of the fluid is assumed to be temperature-dependent, and the effect of the magnetic field is also included. Similarity transformation is used to change a set of PDEs to a set of ODEs; then, the Runge–Kutta method is employed for the numerical solution. A comparative analysis is presented between the results of the current study and the previously published literature in the limited cases in the tabular form, and it is shown that a good agreement with existing results is noted. This study is applicable in aerodynamics and hydrodynamics, especially in enhancing oil refinement, industrial usage in geothermal sciences, generators working on MHD principles, multiple bearings and pumps, control effects on boundary layers, etc.
Formulation of the problem
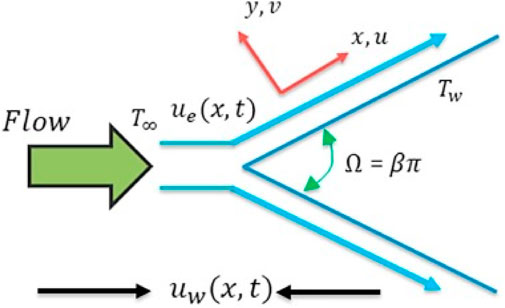
The numerical computations are performed for the boundary-layer impacts on a fixed or a mobile wedge flow problem considering the nanofluids’ case of copper nanoparticles and two different base fluids, that is, methanol and water. The geometrical diagram of this wedge flow problem is presented in Figure 1. A thermal equilibrium condition is maintained for the nanoparticles, and a temperature-dependent viscosity is conceded. The free stream velocity is considered to be u(x) = U∞ xm, while the mobile wedge has a velocity u(x) = Uwxm. The range of
The pertinent equations that govern this physical flow problem are given as (See Refs (Tsung and Lin, 1987; Ishak et al., 2006))
The relevant boundary conditions are imposed in the forms:
Static wedge
Moving wedge
The characteristics of the nanofluid model are taken (Kim and Peterson, 2007; Sastry et al., 2008; Garg et al., 2009; Kamali and Binesh, 2010; Akbar et al., 2016a; Chai et al., 2016) as follows:
The following similarity variables are introduced to convert the problem into a set-up of ordinary differential equations as determined in Ishak et al. (2006):
Here, ψ denotes the stream function and can be interpreted as u = ∂ψ/∂y and v = −∂ψ/∂x.
The following viscosity model known as Reynold’s model is considered (Akbar et al., 2016b):
On substituting (6, 7, and 8) into (2) to (4) with boundary conditions (4 and 5), the converted set-up of ordinary differential equations is given as follows:
Static Wedge
Moving Wedge
where
The coefficient of skin friction
Eq. 13 in non-dimensional form is
Numerical illustration
The shooting technique is utilized to numerically compute the solutions of Equations 9, 10 with boundary conditions (11 and 12). This boundary value problem is initially transformed into an initial value problem; then, initial guesses are set up for
Graphical results and discussion
The numerical computations are performed to present the graphical illustrations (see Figures 2–10) of numerous intrigued parameters on the velocity outline, temperature formation, skin friction coefficient,
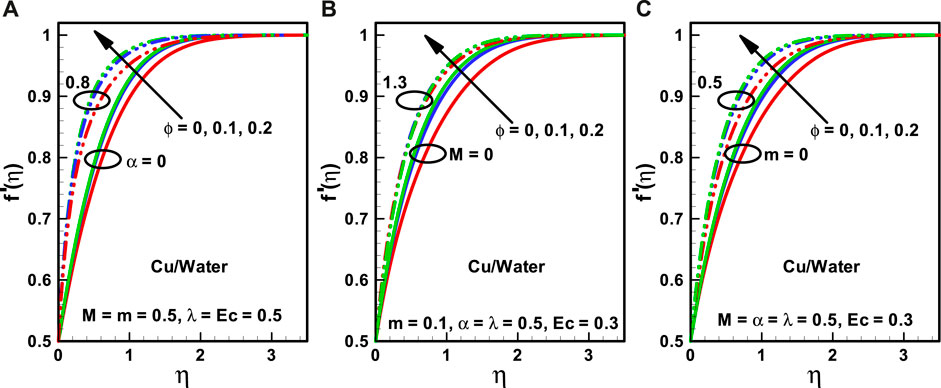
FIGURE 2. (A–C) Velocity profiles corresponding to multiple nanofluidic fractions: (A) (α), (B) (M), and (C) (m).
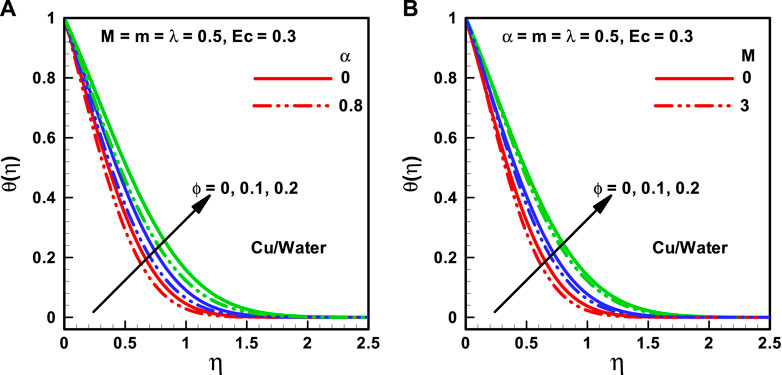
FIGURE 3. (A,B) Temperature profiles corresponding to multiple nanofluidic fractions: (A) (α) and (B) (M).
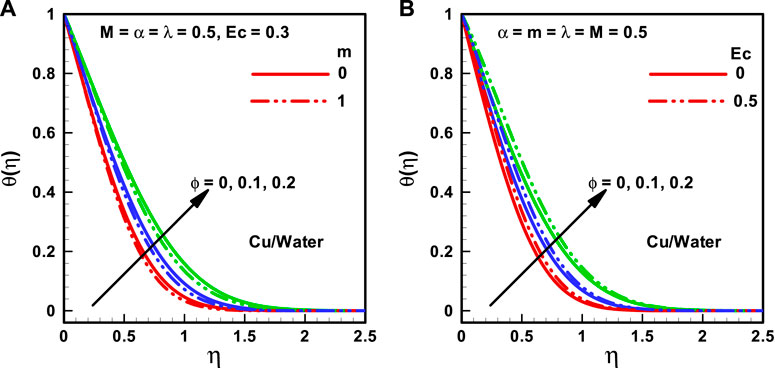
FIGURE 4. (A,B) Temperature profiles corresponding to multiple nanofluidic fractions: (A) (m) and (B) (Ec).
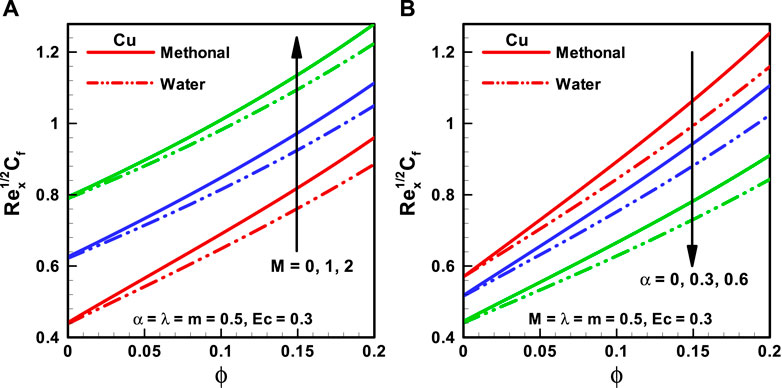
FIGURE 5. (A,B): Skin friction coefficient corresponding to different base fluids, that is, water and methanol for (A) (M). (B) (α).
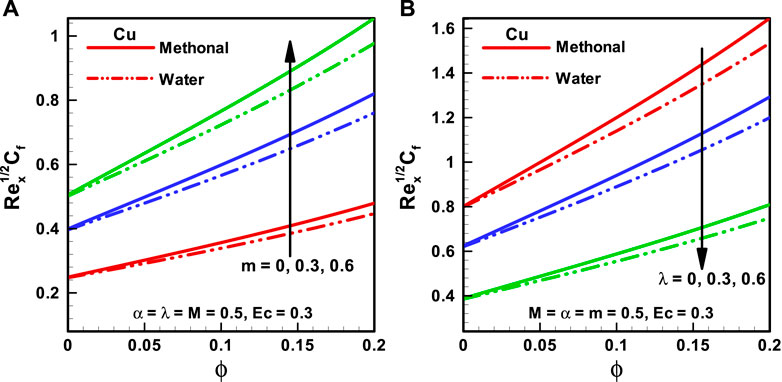
FIGURE 6. (A,B) Skin friction coefficient corresponding to different base fluids, that is, water and methanol for (A) wedge parameter (m) and (B) moving wedge parameter ( λ).
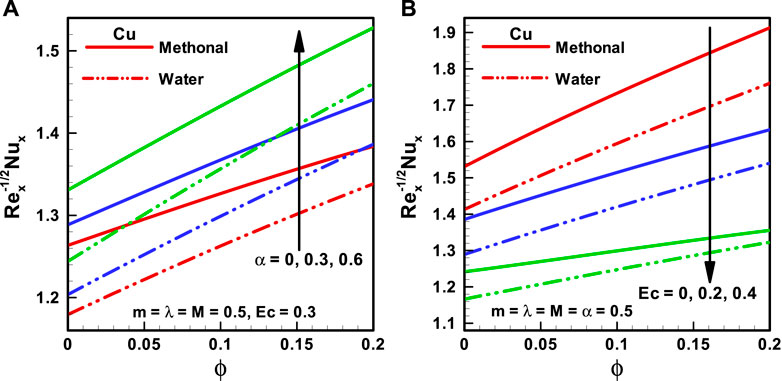
FIGURE 7. (A,B) Nusselt number corresponding to different base fluids, that is, water and methanol for (A) viscosity parameter (α) and (B) Eckert number (Ec).
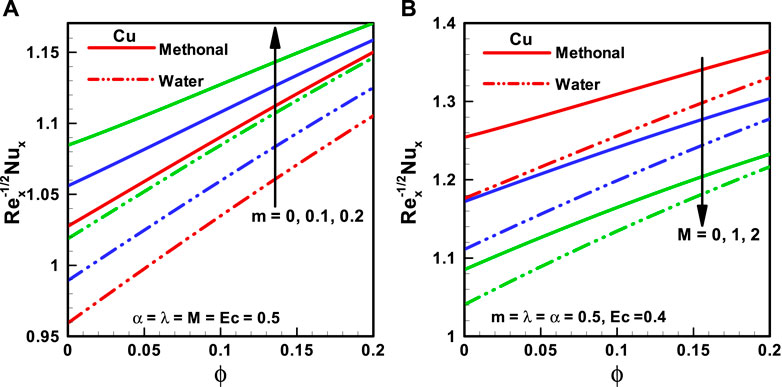
FIGURE 8. (A,B) Nusselt number corresponding to different base fluids, that is, water and methanol for (A) wedge parameter (m) and (B) Hartmann number (M).
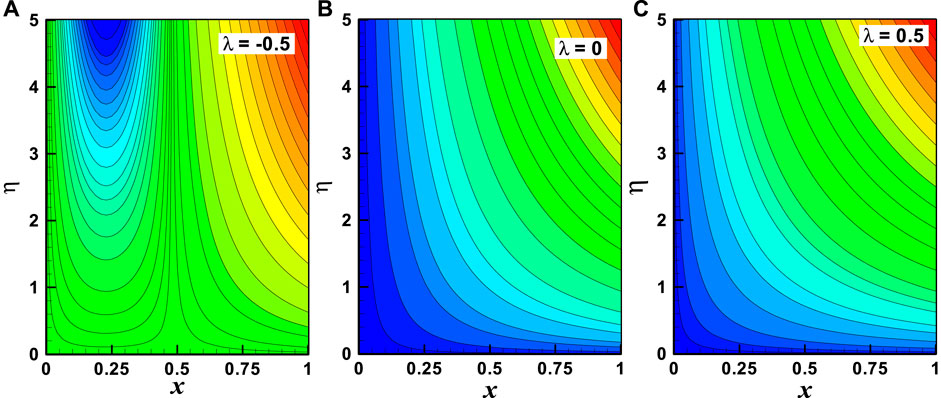
FIGURE 9. (A–C) Streamlines with the variation of the moving wedge parameter (λ). Other parameters are m = 1, M = 2, and α = 0.3.
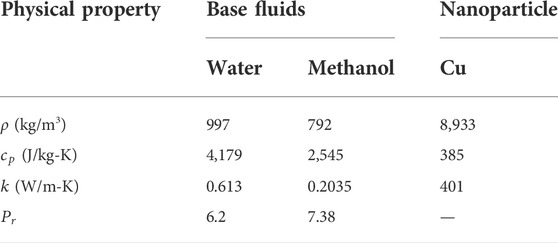
TABLE 1. Experimental values for the base fluid and nanoparticles (Sajjan et al., 2022).
The effects of nanoparticle volume fraction (
The behaviors of the viscosity parameter (
The variations of distinct quantities on
The characteristics of
Streamlines are the key characteristics of the fluid flow which are mathematically found when the stream function is constant. For different values of stream function, the variation of stream lines is illustrated in Figures 9A–C and Figures 10A–C accordingly. The variation of the moving wedge parameter (
Conclusion
The impacts of relevant variable parameters on the characteristics of the Falkner–Skan wedge flow of a temperature-dependent viscous effect with CNT nanofluids have been discussed. The concluding results are summarized as follows:
• The extent of the boundary layer reduces with an upsurging magnitude of
• The extent of the thermal boundary layer expands by enhancing the value of
•
•
• Nusselt number is more for methanol nanofluids than for water nanofluids.
• The Nusselt number is proportional to the viscosity parameter and wedge parameter; however, it is related in an inverse proportion to the Eckert number and Hartman number.
• The parabolic nature of streamlines reduces for the –ve value to +ve value of the moving wedge parameter, and it also decreases with the increasing value of the viscosity parameter.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akbar, N. S., Bintul Huda, A., and Tripathi, D. (2016). Thermally developing MHD peristaltic transport of nanofluids with velocity and thermal slip effects. Eur. Phys. J. Plus 131 (9), 332. doi:10.1140/epjp/i2016-16332-y
Akbar, N. S., Kazmi, N., Tripathi, D., and Mir, N. A. (2016). Study of heat transfer on physiological driven movement with CNT nanofluids and variable viscosity. Comput. Methods Programs Biomed. 136, 21–29. doi:10.1016/j.cmpb.2016.08.001
Akbar, N. S., Tripathi, D., Bég, O. A., and Khan, Z. H. (2016). MHD dissipative flow and heat transfer of Casson fluids due to metachronal wave propulsion of beating cilia with thermal and velocity slip effects under an oblique magnetic field. Acta Astronaut. 128, 1–12. doi:10.1016/j.actaastro.2016.06.044
Akbar, N. S., Tripathi, D., Khan, Z. H., and Bég, O. A. (2016). A numerical study of magnetohydrodynamic transport of nanofluids over a vertical stretching sheet with exponential temperature-dependent viscosity and buoyancy effects. Chem. Phys. Lett. 661, 20–30. doi:10.1016/j.cplett.2016.08.043
Akram, J., Akbar, N. S., and Tripathi, D. (2020). Numerical study of the electroosmotic flow of Al2O3-CH3OH Sisko nanofluid through a tapered microchannel in a porous environment. Appl. Nanosci. 10, 4161–4176. doi:10.1007/s13204-020-01521-9
Animasaun, I. L., Mahanthesh, B., Jagun, A. O., Bankole, T. D., Sivaraj, R., Shah, N. A., et al. (2019). Significance of lorentz force and thermoelectric on the flow of 29 nm CuO–water nanofluid on an upper horizontal surface of a paraboloid of revolution. J. Heat. Transf. 141 (2), 022402. (9 pages). doi:10.1115/1.4041971
Asaithambi, N. S. (1997). A numerical method for the solution of the Falkner-Skan equation. Appl. Math. Comput. 81 (2), 259–264. doi:10.1016/s0096-3003(95)00325-8
Ashraf, M. U., Qasim, M., Wakif, A., Afridi, M. I., and Animasaun, I. L. (2020). A generalized differential quadrature algorithm for simulating magnetohydrodynamic peristaltic flow of blood-based nanofluid containing magnetite nanoparticles: A physiological application. Numer. Methods Partial Differ. Equ. 27, 22676. doi:10.1002/num.22676
Basha, H. T., Sivaraj, R., Subramanyam Reddy, A., Chamkha, A. J., Tilioua, M., and Chamkha, A. J. (2020). Impacts of temperature-dependent viscosity and variable Prandtl number on forced convective Falkner–Skan flow of Williamson nanofluid. SN Appl. Sci. 2, 477. doi:10.1007/s42452-020-2216-3
Bianco, V., Manca, O., Nardini, S., and Vafai, K. (2015). Heat transfer enhancement with nanofluids. CRC 21, 58–64.
Chai, Y. H., Yusup, S., Chok, V. S., Arpin, M. T., and Irawan, S. (2016). Investigation of thermal conductivity of multi-walled carbon nanotube dispersed in hydrogenated oil-based drilling fluids. Appl. Therm. Eng. 107, 1019–1025. doi:10.1016/j.applthermaleng.2016.07.017
Chamkha, A. J., Al-Mudhaf, A. F., and Pop, I. (2006). Effect of heat generation or absorption on thermophoretic free convection boundary layer from a vertical flat plate embedded in a porous medium. Int. Commun. Heat Mass Transf. 33, 1096–1102. doi:10.1016/j.icheatmasstransfer.2006.04.009
Chamkha, A. J. (1996). Non-Darcy hydromagnetic free convection from a cone and a wedge in porous media. Int. Commun. Heat Mass Transf. 23, 875–887. doi:10.1016/0735-1933(96)00070-x
Dennis, D., Willems, S., and Gülhan, A. (2015). Experimental results on shock-wave/boundary-layer interaction induced by a movable wedge. 8th Eur. Symposium Aerothermodyn., 89557.
Ezaier, Y., Hader, A., Achik, I., Tarras, I., Moultif, R., and Bakir, R. (2022). Breaking process of composite membranes used in desalination phenomenon. Multidiscip. Model. Mater. Struct. 18, 249–261. doi:10.1108/mmms-12-2021-0203
Ezaier, Y., Hader, A., Latif, A., Amallah, L., Achik, I., and Boughaleb, Y. (2022). Morphological properties of the interfaces growth of composite membranes. Mater. Today Proc. 66, 238–243. in press. doi:10.1016/j.matpr.2022.03.729
Ezaier, Y., Hader, A., Latif, A., Touizi, R. E., Wakif, A., Boughaleb, Y., et al. (2022). Significance of deposition and diffusion retention on the performance of the composite membrane. Waves Random Complex Media, 1–14. the press. doi:10.1080/17455030.2022.2079758
Falkner, V. M., and Skan, S. W. (1931). Some approximate solutions of the boundary layer equations. Station. Office1930 12, 865–896.
Fang, T., Yao, S., Zhang, J., Zhong, Y., and Tao, H. (2012). Momentum and heat transfer of the falkner–skan flow with algebraic decay: An analytical solution. Commun. Nonlinear Sci. Numer. Simul. 17 (6), 2476–2488. doi:10.1016/j.cnsns.2011.10.021
Garg, P., Alvarado, J. L., Marsh, C., Carlson, T. A., Kessler, D. A., and Annamalai, K. (2009). An experimental study on the effect of ultrasonication on viscosity and heat transfer performance of multi-wall carbon nanotube-based aqueous nanofluids. Int. J. Heat Mass Transf. 52 (21), 5090–5101. doi:10.1016/j.ijheatmasstransfer.2009.04.029
Hamad, N. H., Wakif, A., and Alshehri, A. (2022). Towards the dynamics of a radiative-reactive magnetized viscoelastic nanofluid involving gyrotactic microorganisms and flowing over a vertical stretching sheet under multiple convective and stratification constraints. Waves Random And Complex Media, 1–31. doi:10.1080/17455030.2022.2100944
Hartree, D. R. (2008). On an equation occurring in Falkner and Skan's approximate treatment of the equations of the boundary layer. Math. Proc. Camb. Phil. Soc. 33, 223–239. doi:10.1017/s0305004100019575
Hsing, H. C., Chen, C. S., and Teng, J. T. (1997). Temperature and flow fields for the flow of a second-grade fluid past a wedge. Int. J. Non-Linear Mech. 32 (5), 933–946. doi:10.1016/s0020-7462(96)00086-8
Ishak, A., Nazar, R., and Pop, I. (2006). Moving wedge and flat plate in a micropolar fluid. Int. J. Eng. Sci. 44 (18), 1225–1236. doi:10.1016/j.ijengsci.2006.08.005
Javaherdeh, K., and Ashorynejad, H. R. (2014). Magnetic field effects on force convection flow of a nanofluid in a channel partially filled with porous media using Lattice Boltzmann Method. Adv. Powder Technol. 25, 666–675. doi:10.1016/j.apt.2013.10.012
Kamali, R., and Binesh, A. R. (2010). Numerical investigation of heat transfer enhancement using carbon nanotube-based non-Newtonian nanofluids. Int. Commun. Heat Mass Transf. 37 (8), 1153–1157. doi:10.1016/j.icheatmasstransfer.2010.06.001
Kasmani, R. M., Sivasankaran, S., Bhuvaneswari, M., and Siri, Z. (2016). Effect of chemical reaction on convective heat transfer of boundary layer flow in nanofluid over a wedge with heat generation/absorption and suction. J. Appl. Fluid Mech. 9 (1), 379–388. doi:10.18869/acadpub.jafm.68.224.24151
Khan, W. A., Culham, R., and Haq, R. U. (2015). Heat transfer analysis of MHD water functionalized carbon nanotube flow over a static/moving wedge. J. Nanomater. 2015, 1–13. doi:10.1155/2015/934367
Khan, W. A., and Pop, I. (2013). Boundary layer flow past a wedge moving in a nanofluid. Math. Problems Eng. 2013, 1–7. doi:10.1155/2013/637285
Kim, B. H., and Peterson, G. P. (2007). Effect of morphology of carbon nanotubes on thermal conductivity enhancement of nanofluids. J. Thermophys. heat Transf. 21 (3), 451–459. doi:10.2514/1.18341
Krishna, M. V., Ahamad, N. A., and Chamkha, A. J. (2020). Hall, and ion slip effects on unsteady MHD free convective rotating flow through a saturated porous medium over an exponential accelerated plate. Alexandria Eng. J. 59, 565–577. doi:10.1016/j.aej.2020.01.043
Krishna, M. V., and Chamkha, A. J. (2019). Hall, and ion slip effects on MHD rotating boundary layer flow of nanofluid past an infinite vertical plate embedded in a porous medium. Results Phys. 15, 102652. doi:10.1016/j.rinp.2019.102652
Kumaran, G., Sivaraja, R., Subramanyam Reddy, A., Rushi Kumar, B., and Ramachandra Prasad, V. (2019). Hydromagnetic forced convective flow of Carreau nanofluid over a wedge/plate/ stagnation of the plate. Eur. Phys. J. Spec. Top. 228, 2647–2659. doi:10.1140/epjst/e2019-900069-2
Kuo, B. L. (2005). Heat transfer analysis for the Falkner–Skan wedge flow by the differential transformation method. Int. J. Heat Mass Transf. 48 (23), 5036–5046. doi:10.1016/j.ijheatmasstransfer.2003.10.046
Madaki, A. G., Abdulhameed, M., Ali, M., and Roslan, R. (2016). Solution of the Falkner–Skan wedge flow by a revised optimal homotopy asymptotic method. SpringerPlus 5 (1), 513–518. doi:10.1186/s40064-016-2147-z
Mahian, O., Kianifar, A., Kalogirou, S. A., Pop, I., and Wongwises, S. A. (2013). A review of the applications of nanofluids in solar energy. Int. J. Heat Mass Transf. 57 (2), 582–594. doi:10.1016/j.ijheatmasstransfer.2012.10.037
Malvandi, A., Moshizi, S., and Ganji, D. (2014). Effect of magnetic fields on heat convection inside a concentric annulus filled with Al 2 O 3–water nanofluid. Adv. Powder Technol. 25, 1817–1824. doi:10.1016/j.apt.2014.07.013
Matsson, O. J. E. (2008). Görtler vortices in Falkner–Skan flows with suction and blowing. Int. J. Numer. Methods Fluids 56 (3), 257–277. doi:10.1002/fld.1516
Murshed, S. M., Leong, K. C., and Yang, C. (2005). Enhanced thermal conductivity of TiO 2—Water-based nanofluids. Int. J. Therm. Sci. 44 (4), 367–373. doi:10.1016/j.ijthermalsci.2004.12.005
Rasool, G., Shah, N. A., El-Zahar, E. R., and Wakif, A. (2022). numerical investigation of EMHD nanofluid flows over a convectively heated riga pattern positioned horizontally in a Darcy-forchheimer porous medium: Application of passive control strategy and generalized transfer laws. Waves Random Complex Media, 1–20. doi:10.1080/17455030.2022.2074571
Sajjan, K., Shah, N. A., Ahammad, N. A., Raju, C. S. K., Kumar, M. D., and Weera, W. (2022). Nonlinear Boussinesq and Rosseland approximations on 3D flow in an interruption of Ternary nanoparticles with various shapes of densities and conductivity properties. AIMS Math. 7 (10), 18416–18449. doi:10.3934/math.20221014
Salama, F. A. (2016). Effects of radiation on convection heat transfer of Cu-water nanofluid past a moving wedge. Therm. Sci. 20 (2), 437–447. doi:10.2298/tsci140719049s
Sastry, N. V., Bhunia, A., Sundararajan, T., and Das, S. K. (2008). Predicting the effective thermal conductivity of carbon nanotube based nanofluids. Nanotechnology 19 (5), 055704. doi:10.1088/0957-4484/19/05/055704
Sheikholeslami, M., and Ganji, D. D. (2015). Entropy generation of nanofluid in presence of magnetic field using Lattice Boltzmann Method. Phys. A Stat. Mech. its Appl. 417, 273–286. doi:10.1016/j.physa.2014.09.053
Takhar, H. S., Chamkha, A. J., and Nath, G. (1999). Unsteady flow and heat transfer on a semi-infinite flat plate with an aligned magnetic field. Int. J. Eng. Sci. 37, 1723–1736. doi:10.1016/s0020-7225(98)00144-x
Thameem Bash, H., and Sivaraj, R. (2022). Heat and mass transfer in stagnation point flow of cross nanofluid over a permeable extending/contracting surface: A stability analysis. J. Therm. Eng. 8, 38–51. doi:10.18186/thermal.1067004
Thameem Basha, H., Sivaraj, R., Subramanyam Reddy, A., and Chamkha, A. J. (2019). SWCNH/diamond-ethylene glycol nanofluid flow over a wedge, plate and stagnation point with induced magnetic field and nonlinear radiation – solar energy application. Eur. Phys. J. Spec. Top. 228, 2531–2551. doi:10.1140/epjst/e2019-900048-x
Tripathi, D., and Bég, O. A. (2014). A study on peristaltic flow of nanofluids: Application in drug delivery systems. Int. J. Heat Mass Transf. 70, 61–70. doi:10.1016/j.ijheatmasstransfer.2013.10.044
Tsung, L. H., and Lin, L. K. (1987). Similarity solutions for laminar forced convection heat transfer from wedges to fluids of any Prandtl number. Int. J. Heat And Mass Transf. 30 (6), 1111–1118. doi:10.1016/0017-9310(87)90041-x
Tuncer, C., and Keller, H. B. (1971). Shooting and parallel shooting methods for solving the Falkner-Skan boundary-layer equation. J. Comput. Phys. 72, 289–300. doi:10.1016/0021-9991(71)90090-8
Wang, X. Q., and Mujumdar, A. S. (2007). Heat transfer characteristics of nanofluids: A review. Int. J. Therm. Sci. 46 (1), 1–19. doi:10.1016/j.ijthermalsci.2006.06.010
Yacob, A., Ishak, A., Nazar, R., and Pop, I. (2011). Falkner–Skan problem for a static or moving wedge in nanofluids. Int. J. Therm. Sci. 50 (2), 133–139. doi:10.1016/j.ijthermalsci.2010.10.008
Yacob, N. A., Ishak, A., Nazar, R., and Pop, I. (2011). Falkner–Skan problem for a static and moving wedge with prescribed surface heat flux in a nanofluid. Int. Commun. Heat Mass Transf. 38 (2), 149–153. doi:10.1016/j.icheatmasstransfer.2010.12.003
Yang, G. C., and Lan, K. Q. (2011). Nonexistence of the reversed flow solutions of the Falkner–Skan equations. Nonlinear Analysis Theory, Methods & Appl. 74 (16), 5327–5339. doi:10.1016/j.na.2011.05.017
Yang, G. C., and Lan, K. Q. (2007). The velocity and shear stress functions of the Falkner–Skan equation arising in boundary layer theory. J. Math. analysis Appl. 328 (2), 1297–1308. doi:10.1016/j.jmaa.2006.06.042
Yih, K. A. (1998). Uniform suction/blowing effect on forced convection about a wedge uniform heat flux. Acta Mech. 128 (3-4), 173–181. doi:10.1007/bf01251888
Yu, W., and Xie, H. (2012). A review on nanofluids: Preparation, stability mechanisms, and applications. J. Nanomater. 2012, 1–17. doi:10.1155/2012/435873
Zaturska, M. B., and Banks, W. H. H. (2001). A new solution branch of the Falkner-Skan equation. Acta Mech. 152 (1), 197–201. doi:10.1007/bf01176954
Nomenclature
U∞, Uw free stream and wedge velocity
kf thermal conductivity of the base fluid
Tw wall temperature
knf nanofluid thermal conductivity
Keywords: magnetohydrodynamics, nanofluids, Runge–Kutta method, static and moving wedge, skin friction coefficient
Citation: Akbar NS (2022) Numerical study of the thermally stratified hemodynamic nanofluid flow with variable viscosity over a heated wedge. Front. Chem. 10:1021303. doi: 10.3389/fchem.2022.1021303
Received: 17 August 2022; Accepted: 22 September 2022;
Published: 11 October 2022.
Edited by:
Sivaraj R, United Arab Emirates University, United Arab EmiratesReviewed by:
Yassine Ezaier, University Hassan II, MoroccoNilankush Acharya, Jadavpur University, India
Copyright © 2022 Akbar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Noreen Sher Akbar, bm9yZWVuLnNoZXJAY2VtZS5udXN0LmVkdS5waw==
 Noreen Sher Akbar
Noreen Sher Akbar