Infrared Spectra of Hydrogen-Bonded Molecular Complexes Under Spatial Confinement

Infrared (IR) spectroscopy is commonly used in chemical laboratories to study the geometrical structure of molecules and molecular complexes. The analysis of experimental IR spectra can nowadays be reliably supported by the results of quantum-chemical computations as vibrational frequencies and corresponding vibrational transition intensities are routinely calculated using harmonic approximation by virtually all quantum chemistry packages. In the present study we combine the methodology of computing vibrational spectra using high-level electron correlation treatments with an analytical potential-based approach to take into account spatial confinement effects. Using this approach, we perform a pioneering analysis of the impact of the spatial confinement caused by a cylindrical harmonic oscillator potential on the harmonic vibrational transition intensities and frequencies of two hydrogen-bonded complexes: HCN…HCN and HCN…HNC. The emphasis is put on the largest-intensity bands, which correspond to the stretching vibrations. The obtained results demonstrate that embedding the molecular complexes in an external confining potential causes significant changes of transition intensities and vibrational frequencies.

1 Introduction

Studies of molecular structure using infrared spectroscopy have become a fairly routine task and nowadays IR spectrometers are part of virtually all chemical laboratories. This technique (as well as other complementary vibrational spectroscopies) allows to gain an insight into the geometrical structure of molecules and molecular complexes. In fact, changes in frequencies and intensities of some key vibrational transitions are used as fingerprints to monitor the hydrogen or halogen bonds of molecular complexes. The analysis of experimental IR spectra can nowadays be reliably supported by the results of quantum-chemical computations as vibrational frequencies and corresponding transition intensities are routinely calculated using harmonic approximation by practically all packages. High-level electron-correlation methods can be used for band assignments in vibrational spectra of small- and medium-sized molecules and molecular complexes. Moreover, they can also be used to map the changes in infrared vibrational spectroscopic signatures to structural changes. The present study contributes to these theoretical efforts and its goal is to apply the methodology to compute the harmonic infrared vibrational spectra using high-level electron correlation treatments to spatially confined hydrogen-bonded molecular complexes.

The term “spatial confinement” is used throughout this work to refer to atoms and molecules trapped inside chemical cages (such as zeolites, mesoporous silica/organosilica, metal-organic frameworks, nanotubes and fullerenes), matter under high pressure, quantum wells, wires and dots as well as other constraining environments (Jaskólski (1996); Sen (2014)). On the theoretical basis, the spatial confinement is often simulated by external repulsive potentials, which reproduce the effect of orbital compression (connected with valence repulsion). This approach describes the interaction of objects with chemically and electronically inert environments (Jaskólski (1996)). Over the years, much effort has been devoted to the studies of the spatial confinement phenomenon, demonstrating its significant effects on the physical and chemical properties of atomic and molecular systems (Bartkowiak et al. (2021); Buchachenko (2001); Kozłowska et al. (2014); Chattaraj and Sarkar (2003); Cammi et al. (2008, 2012); Zaleśny et al. (2013); Góra et al. (2012); Lo and Klobukowski (2006)). Numerous interesting results were obtained, e.g., it was shown that the spatial confinement, in the form of analytical potential, causes an increase of the total energy (Buchachenko (2001); Bartkowiak and Strasburger (2010); Bielińska-Wa̧ż et al. (2001)) and the separation of HOMO and LUMO orbitals (Borgoo et al. (2008, 2009); Kozłowska et al. (2014)). Upon increasing the confinement strength, the polarizability of the spatially restricted systems decreases (Holka et al. (2005); Góra et al. (2012); Lo and Klobukowski (2006); Zaleśny et al. (2015); Kozłowska et al. (2015); Zaleśny et al. (2017)). Moreover, a shortening of the bond lengths was reported for molecules and molecular complexes embedded in confining potentials (Cammi et al. (2008, 2012); Zaleśny et al. (2013); Zaleśny et al. (2015)). Nevertheless, despite recent progress, there are still many aspects of spatial confinement which have not received sufficient attention yet. One of them is the modeling of IR spectra of spatially confined molecules and molecular complexes. In this context, one should not overlook the paper by Bonfim and Pilling who studied the effect of chemical environment on some properties of “trapped molecules” by using Polarizable Continuum Model (Bonfim and Pilling (2017)). These authors considered the effect of dielectric constant (3 < ϵ < 180) on vibrational frequencies and transition intensities. It was demonstrated that in the case of all analyzed molecules, i.e., CO, CO₂, H₂O—components of the astrophysical ices matrix, the increase of the value of dielectric constant is accompanied by larger band strengths. Other literature reports are largely limited to the analysis of the spatial confinement effect on shifts of vibrational frequencies (Shameema et al. (2006); Jana and Bandyopadhyay (2011); Song et al. (2005); Pagliai et al. (2014); Cammi et al. (2012); Boccalini et al. (2021)). Therefore, the goal of this project is to fill this gap by performing a pioneering analysis of the impact of spatial restriction, modeled by confining cylindrical analytical harmonic potential, on the infrared spectra (vibrational frequencies and transition intensities) of hydrogen-bonded molecular complexes.

2 Methods

In this work, the effect of spatial confinement on the vibrational properties of HCN…HCN and HCN…HNC complexes, with symmetry axis parallel to Cartesian z direction, was modeled by the cylindrical harmonic oscillator potential:

$V_{conf}\left({\vec{r}}_i\right)=\frac{1}{2}{\omega }^2\left(x_i^2+y_i^2\right),(1)$

where the ω parameter controls the strength of spatial confinement, which is obtained by changing the curvature of the harmonic potential and the ${\vec{r}}_i$ refer only to the electronic coordinates. Thus, the effect of confinement on nuclei is accounted for indirectly by its effect on the electrons. Because of its symmetry, the cylindrical harmonic oscillator potential can be used as simplified representation of nanotube-like confining cages. V_conf as given by Eq. 1 was added to the Hamiltonian of the isolated complexes and subsequently vibrational-structure calculations were performed. In particular, the calculations of the infrared intensity for i-th mode (I_i) under the influence of spatial confinement were performed based on the following equation:

$I_i=\frac{N\pi }{3c^2}\sum _{j=x,y,z}{\left(\frac{\partial {\mu }_j}{\partial Q_i}\right)}^2(2)$

where N is Avogadro’s number, c is speed of light and $\frac{\partial {\mu }_j}{\partial Q_i}$ is derivative of j-th Cartesian component of dipole moment with respect to normal mode Q_i.

Vibrational-structure computations were performed using MP2 and CCSD(T) methods and aug-cc-pVTZ basis set. MP2 method was used to determine gas-phase equilibrium geometries, vibrational frequencies and transition intensities analytically, as implemented in the GAUSSIAN 2009 package (Frisch et al. (2009)). On the other hand, at the CCSD(T)/aug-cc-pVTZ level the geometries of the studied complexes were optimized in vacuum and in the presence of cylindrical harmonic oscillator potential using custom computer routines based on total energies computed with the aid of the GAUSSIAN 2009 package (Frisch et al. (2009)). The calculations of infrared intensities of the spatially confined molecular complexes were performed at the CCSD(T)/aug-cc-pVTZ level using custom computer routines. To that end, we employed double numerical differentiation, i.e., the dipole moment components were computed numerically for a mesh of electric fields F (±2ⁿ × F, where n = 0, …, 8, F = 0.000 2 au) at a set of displaced geometries (with mesh ±2^m ×Δ, where m = 0, …, 4, Δ = 0.01 bohr). The numerical accuracy of both numerical diffferentiation procedures was controlled with the aid of Romberg-Rutishauser scheme (Medved et al. (2007)).

3 Results and Discussion

To investigate the effect of spatial confinement on vibrational transition intensities, we chose two hydrogen-bonded complexes, i.e., HCN…HCN and HCN…HNC. The rationale behind selection of these two complexes stems from the results presented in the earlier studies by some of the present authors, devoted to the analysis of the effect of spatial confinement on the electronic and nuclear relaxation polarizability as well as first and second hyperpolarizability of molecules and molecular complexes (Zaleśny et al. (2015); Zaleśny et al. (2017)). The nuclear relaxation (hyper) polarizabilities are the major contribution to the vibrational (hyper) polarizabilities and include all their low-order corrections (Bishop (1998); Kirtman et al. (2000)). There are two main conclusions of these studies. Firstly, the effect of spatial confinement increases with the order of electrical property, both for electronic and vibrational counterparts, and it is much more pronounced for the former. In other words, the least significant effect was observed for electronic and nuclear relaxation polarizability. Secondly, the decrease of vibrational first hyperpolarizability was largely due to the harmonic part. The nuclear relaxation polarizability can be directly linked with infrared intensity given by Eq. 2 as both involve electric dipole moment (μ) derivatives with respect to normal modes (Q). Average nuclear relaxation polarizability is given by:

$\langle {\alpha }^{\text{nr}}\rangle =\frac{1}{3}\sum _{j=x,y,z}{\alpha }_{jj}^{\text{nr}}=\frac{1}{3}\sum _{i=1}\frac{1}{{\omega }_i^2}\left[\sum _{j=x,y,z}{\left(\frac{\partial {\mu }_j}{\partial Q_i}\right)}^2\right]=\sum _{i=1}{\langle {\alpha }^{\text{nr}}\rangle }_i(3)$

where i labels normal modes with angular frequencies ω_i. We may re-write the equation defining the nuclear relaxation polarizability in terms of the IR intensity I_i:

$\langle {\alpha }^{\text{nr}}\rangle =\sum _i{\langle {\alpha }^{\text{nr}}\rangle }_i=\frac{c^2}{N\pi }\sum _i\frac{I_i}{{\omega }_i^2}(4)$

Then for each mode we have the following relationship between the nuclear relaxation contribution to mode i and the corresponding intensity I_i:

$I_i\sim {\omega }_i^2{⟨{\alpha }^{\text{nr}}⟩}_i(5)$

It follows from the above relations that the effect of spatial confinement on nuclear relaxation polarizabilities can be predominantly manifested by the contributions from low-frequency normal modes, provided that corresponding dipole moment derivatives are significant. These expressions also allow for rationalizing why the absolute value of α^nr is more than order of magnitude larger for HCN…HCN than for HCN (Zaleśny et al. (2015); Zaleśny et al. (2017)). In the case of hydrogen-bonded complexes there are X-H stretching modes corresponding to significant dipole moment changes which give rise to large-intensity bands. One may thus expect a significant effect of spatial confinement on vibrational intensities for such modes. Taken together, these evidences support the choice of HCN…HCN and HCN…HNC for the pioneering analysis performed in this study.

In what follows we will analyze the effect of confinement by choosing two values of ω parameter, i.e., 0.1 and 0.2 au. It was shown that these values approximately correspond to the realistic chemical environment, i.e., they reproduce exchange repulsion for linear weakly-bound complexes enclosed in carbon nanotubes (Zaleśny et al. (2017)). Such link can be established by comparison of the Hartree-Fock interaction energies between both studied complexes and the (4,4) carbon natotube with the results obtained using the analytic cylindrical confining potential. The results presented in Ref (Zaleśny et al. (2017)) demonstrate that the HF interaction energy between the (4,4) nanotube and HCN…HCN (HCN…HNC) is 133 kcal/mol (134 kcal/mol). The amplitude of the confining potential (ω) can be adjusted to represent this repulsive interaction:

$\mathrm{\Delta }{E}_{\text{int}}^{\text{HF}}\approx E\left(\omega \right)-E\left(\omega =0.0\right)$

The amplitude ω = 0.1 a.u., through the above equation, roughly corresponds to Hartree-Fock interaction energy of HCN…HCN and HCN…HNC complexes trapped inside (4,4) carbon nanotube. The second chosen value of the amplitude thus corresponds to much larger confining environment caused by a carbon nanotube with smaller diameter.

In order to shed light on the vibrational structure of isolated complexes, we evaluated the infrared intensities for all vibrational modes of HCN…HCN and HCN…HNC complexes, hereafter shortly referred to as (A(i)) and (B(i)). The results of calculations, performed at the cost-effective MP2/aug-cc-pVTZ level of theory, are presented in Table 1. Modes 12 and 13 have the largest IR intensities among all vibrations and this holds for both studied complexes. In particular, the IR intensities of the C-H and N-H stretching vibrations involving the hydrogen of hydrogen bond (A (12) and B (13)) are equal to 389 and 1,190 km/mol, respectively, and dominate the IR spectrum. In the reminder of the analysis, we will use highly accurate CCSD(T)/aug-cc-pVTZ level of theory to analyze the effect of confinement on four stretching modes presented in Figure 1, corresponding to the two C-N stretchings (A (10,11) and B (10,11)) and to the C-H (A (12,13), B (12)) and N-H stretchings vibrations (B (13)). We will start with the analysis of the influence of spatial confinement on the vibrational frequencies. Table 2 reports the computed vibrational frequencies of HCN…HCN and HCN…HNC complexes in vacuum and in the presence of confinement represented by the cylindrical harmonic oscillator potential. It is clear from these data that ν_i for modes 10-13 of both complexes are shifted to higher values by the spatial confinement, which agrees with the fact that the energy of a chemical systems increases under confinement. The increase of all ν_i values upon growing confinement strength from ω = 0.0 to ω = 0.1 au falls in between 33.7 and 56.1 cm⁻¹. On the other hand, the changes caused by the confinement when its strength is equal to 0.2 au are much more pronounced, as the increase of ν_i ranges from 117.7 to 198.1 cm⁻¹. Although the absolute shift of the frequencies caused by the spatial restriction is larger for the C-H and N-H stretchings (modes A (12,13) and B (12,13)) than the frequencies of the other two modes (A (10,11) and B (10,11)), analyzing the relative shift respect to the vacuum frequency is very similar for the four vibrations (i.e., 1.4–1.7% for ω = 0.1 au and 4.9–5.8% for ω = 0.2 au). Similar findings, i.e., an increase of vibrational frequencies under pressure, were reported for various molecular systems, such as diborane (Cammi et al. (2012)), C₆₀ and C₇₀ fullerenes (Pagliai et al. (2014)) and SF₆ molecule (Boccalini et al. (2021)).

TABLE 1

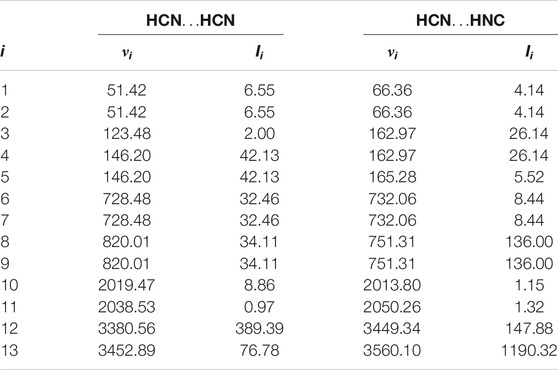
TABLE 1. Harmonic frequencies (ν_i, in cm⁻¹) and infrared intensities (I_i, in km/mol) for vibrational normal modes i of HCN…HCN and HCN…HNC complexes computed at the MP2/aug-cc-pVTZ level of theory.

FIGURE 1

FIGURE 1. Stretching vibrations of HCN…HCN (A) and HCN…HNC (B) complexes and their labeling.

TABLE 2

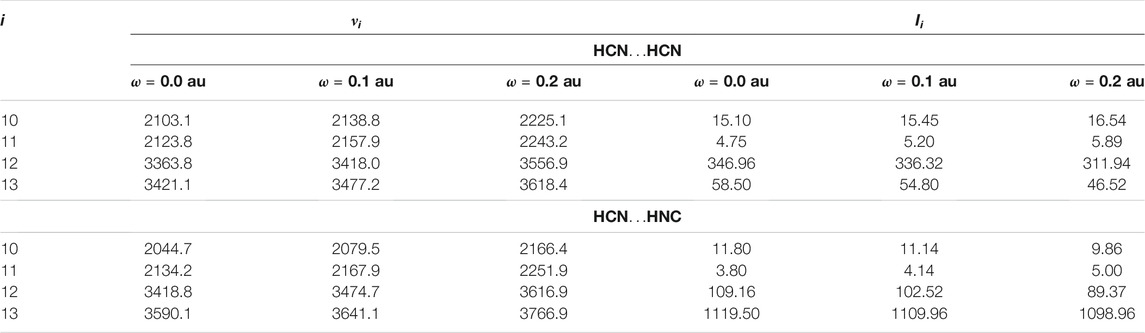
TABLE 2. Frequencies (ν_i, in cm⁻¹) and infrared intensities (I_i, in km/mol) for vibrational normal modes i of HCN…HCN and HCN…HNC complexes computed at the CCSD(T)/aug-cc-pVTZ level of theory.

We will now turn to the infrared intensities (see Table 2). Similarly to what we reported for vibrational frequencies, there is a monotonic perturbation in I_i for all four modes as the amplitude of confinement increases. The absolute changes in the IR intensities of modes A (10,11) and B (10,11) are very small and do not exceed 2 km/mol. Nevertheless, we highlight that for HCN…HCN the intensities of modes 10 and 11 increase on passing from ω = 0 through ω = 0.1 to ω = 0.2 au. The same is observed for mode 11 for HCN…HNC complex. In contrast, the modes A (12,13) and B (12,13) suffer a much stronger impact due to the spatial confinement, as there is a quite substantial decrease in I_i computed for unconfined and confined complexes that ranges from 3.7 to 20.54 km/mol. The largest-intensity bands in infrared spectra of the studied molecular complexes are the C-H and N-H stretchings which hydrogens are involved in the hydrogen bond (modes A (12) and B (13)). These two bands are the most significantly influenced by the spatial confinement. These observations can be further elucidated based on simple geometrical arguments. For ω = 0.1 a.u. there is shortening of all covalent bonds in HCN…HCN and HCN…HNC approximately by 0.006 Å, while the N…H bond length is shorter by 0.011 Å. Larger strength of confinement, i.e., ω = 0.2 a.u., leads to further shortening of covalent bonds (ranging from 0.020 to 0.022 Å with respect to the unconfined systems). Moreover, there is a significant decrease in the N…H bond length ranging from 0.035 Å (HCN…HCN) to 0.039 Å (HCN…HNC). The latter data explain the significant changes in intensities for modes A (12) and B (13). The confinement-induced geometrical changes observed for HCN…HCN and HCN…HNC complexes are in line with reports for other systems, e.g., CO₂, C₂H₂, HCN and HCCCN (Zaleśny et al. (2013); Zaleśny et al. (2015)) Similar trends were also observed for the hydrogen bond length in other theoretical as well as experimental works concerning the effect of spatial confinement on the HB complexes (Lipkowski et al. (2014); Roztoczyńska et al. (2014); Ajami et al. (2011); Dougherty (1998)). As highlighted by Cammi et al. the bond shortening upon confinement can be linked with the deformation of the molecular electronic charge density, due to the Pauli repulsive interaction with the environment (Cammi et al. (2008; 2012)).

4 Summary

In summary, in the present study we demonstrated that the spatial confinement simulated by a cylindrical harmonic oscillator potential significantly affects vibrational spectra of hydrogen-bonded molecular complexes. Based on the obtained results we can draw several conclusions concerning the impact of spatial confinement on four stretching vibrations along molecular axis of HCN…HCN and HCN…HNC complexes:

• the changes in the vibrational transition intensities and corresponding frequencies are monotonic, and yet they are much more pronounced upon increasing the confinement strength from ω = 0.0 to ω = 0.2 au than on passing from ω = 0.0 to ω = 0.1 au;

• the presence of cylindrical harmonic oscillator potential leads to an increase of vibrational frequencies for all studied stretching vibrations;

• the vibrational transition intensities of modes corresponding to the C-H and N-H stretchings significantly decrease when the strength of the spatial confinement grows;

• the spatial confinement causes very small absolute changes in the IR intensities of C-N stretching vibrations and in the case of HCN…HCN complex the increase of confinement leads to increase in the corresponding vibrational transition intensities.

We believe that our results will not only contribute to broadening the knowledge on the spatial confinement phenomenon but they will also complement and support the experimental efforts in this field, by giving valuable insight into the nature of changes in the infrared spectra caused by spatial confinement. Our findings are particularly important from the point of view of astrochemistry, as the astrochemical measurements probe molecular species that experience extreme conditions, such as high pressure, and one of the most fundamental techniques used for exploration of cosmic space is the infrared spectroscopy. Finally, we highlight that in order to predict IR spectra of confined species with high accuracy it is mandatory to account for anharmonicity effects.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

The analysis and design of data and the writing of the article was carried out predominantly by MC. RZ performed the calculations. RZ, WB, and JML helped in the design and review of data. All authors contributed to the writing and review of the article.

Funding

This work was supported by MINECO-Spain for project PGC 2018-098212-B-C22 and Generalitat de Catalunya for project 2017SGR264 to JML.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors gratefully acknowledge Wroclaw Centre for Networking and Supercomputing for the generous allotment of computer time.

References

Ajami, D., Tolstoy, P. M., Dube, H., Odermatt, S., Koeppe, B., Guo, J., et al. (2011). Encapsulated Carboxylic Acid Dimers with Compressed Hydrogen Bonds. Angew. Chem. Int. Ed. 50, 528–531. doi:10.1002/anie.201002182

CrossRef Full Text | Google Scholar

Bartkowiak, W., Chołuj, M., and Kozłowska, J. (2021). “Effect of Confinement on the Optical Response Properties of Molecules,” in Chemical Reactivity in Confined Systems: Theory, Modelling and Applications. Editors P. K. Chattaraj, and D. Chakraborty (Wiley). doi:10.1002/9781119683353.ch12

CrossRef Full Text | Google Scholar

Bartkowiak, W., and Strasburger, K. (2010). Linear and Nonlinear Electric Properties of Spatially Confined LiH Molecule, Studied with the Finite Field Method. J. Mol. Struct. THEOCHEM 960, 93–97. doi:10.1016/j.theochem.2010.08.028

CrossRef Full Text | Google Scholar

Bielińska-Wa̧ż, D., Diercksen, G. H. F., and Klobukowski, M. (2001). Quantum Chemistry of Confined Systems: Structure and Vibronic Spectra of a Confined Hydrogen Molecule. Chem. Phys. Lett. 349, 215–219. doi:10.1016/S0009-2614(01)01226-X

CrossRef Full Text | Google Scholar

Bishop, D. M. (1998). Molecular Vibration and Nonlinear Optics. Adv. Chem. Phys. 104, 1–40.

Google Scholar

Boccalini, M., Cammi, R., Pagliai, M., Cardini, G., and Schettino, V. (2021). Toward an Understanding of the Pressure Effect on the Intramolecular Vibrational Frequencies of Sulfur Hexafluoride. J. Phys. Chem. A. 125, 6362–6373. doi:10.1021/acs.jpca.1c02595

CrossRef Full Text | Google Scholar

Bonfim, V. S., and Pilling, S. (2017). The Influence of Chemical Environment on the Infrared Spectra of Embedded Molecules in Astrophysical Ices. Proc. IAU 13, 346–352. doi:10.1017/s1743921317008110

CrossRef Full Text | Google Scholar

Borgoo, A., Tozer, D. J., Geerlings, P., and De Proft, F. (2009). Confinement Effects on Excitation Energies and Regioselectivity as Probed by the Fukui Function and the Molecular Electrostatic Potential. Phys. Chem. Chem. Phys. 11, 2862–2868. doi:10.1039/b820114e

PubMed Abstract | CrossRef Full Text | Google Scholar

Borgoo, A., Tozer, D. J., Geerlings, P., and De Proft, F. (2008). Influence of Confinement on Atomic and Molecular Reactivity Indicators in DFT. Phys. Chem. Chem. Phys. 10, 1406–1410. doi:10.1039/b716727j

PubMed Abstract | CrossRef Full Text | Google Scholar

Buchachenko, A. L. (2001). Compressed Atoms. J. Phys. Chem. B 105, 5839–5846. doi:10.1021/jp003852u

CrossRef Full Text | Google Scholar

Cammi, R., Cappelli, C., Mennucci, B., and Tomasi, J. (2012). Calculation and Analysis of the Harmonic Vibrational Frequencies in Molecules at Extreme Pressure: Methodology and Diborane as a Test Case. J. Chem. Phys. 137, 154112. doi:10.1063/1.4757285

CrossRef Full Text | Google Scholar

Cammi, R., Verdolino, V., Mennucci, B., and Tomasi, J. (2008). Towards the Elaboration of a QM Method to Describe Molecular Solutes under the Effect of a Very High Pressure. Chem. Phys. 344, 135–141. doi:10.1016/j.chemphys.2007.12.010

CrossRef Full Text | Google Scholar

Chattaraj, P. K., and Sarkar, U. (2003). Chemical Reactivity of the Spherically Confined Atoms. Chem. Phys. Lett. 372, 805–809. doi:10.1016/s0009-2614(03)00516-5

CrossRef Full Text | Google Scholar

Dougherty, R. C. (1998). Temperature and Pressure Dependence of Hydrogen Bond Strength: A Perturbation Molecular Orbital Approach. J. Chem. Phys. 109, 7372–7378. doi:10.1063/1.477343

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (20092009). Gaussian 09 Revision D.01. Wallingford CT: Gaussian Inc [Dataset].

Google Scholar

Góra, R. W., Zaleśny, R., Kozłowska, J., Nacia̧żek, P., Roztoczyńska, A., Strasburger, K., et al. (2012). Electric Dipole (Hyper)Polarizabilities of Spatially Confined LiH Molecule. J. Chem. Phys. 137, 094307. doi:10.1063/1.4748144

CrossRef Full Text | Google Scholar

Holka, F., Neogrády, P., Kellö, V., Urban, M., and Diercksen, G. H. F. (2005). Polarizabilities of Confined Two-Electron Systems: the 2-Electron Quantum Dot, the Hydrogen Anion, the Helium Atom and the Lithium Cation. Mol. Phys. 103, 2747–2761. doi:10.1080/00268970500181160

CrossRef Full Text | Google Scholar

Jana, M., and Bandyopadhyay, S. (2011). Vibrational Spectrum of Water Confined in and Around Cyclodextrins. Chem. Phys. Lett. 509, 181–185. doi:10.1016/j.cplett.2011.04.103

CrossRef Full Text | Google Scholar

Jaskólski, W. (1996). Confined Many-Electron Systems. Phys. Rep. 27, 1–66.

Google Scholar

K. D. Sen (Editor) (2014). Electronic Structure of Quantum Confined Atoms and Molecules (Springer International Publishing).

Google Scholar

Kirtman, B., Champagne, B., and Luis, J. M. (2000). Efficient Treatment of the Effect of Vibrations on Electrical, Magnetic, and Spectroscopic Properties. J. Comput. Chem. 21, 1572–1588. doi:10.1002/1096-987x(200012)21:16<1572:aid-jcc14>3.0.co;2-8

CrossRef Full Text | Google Scholar

Kozłowska, J., Roztoczyńska, A., and Bartkowiak, W. (2015). About Diverse Behavior of the Molecular Electric Properties upon Spatial Confinement. Chem. Phys. 456, 98–105. doi:10.1016/j.chemphys.2014.12.003

CrossRef Full Text | Google Scholar

Kozłowska, J., Zaleśny, R., and Bartkowiak, W. (2014). On the Nonlinear Electrical Properties of Molecules in Confined Spaces - from Cylindrical Harmonic Potential to Carbon Nanotube Cages. Chem. Phys. 428, 19–28. doi:10.1016/j.chemphys.2013.10.007

CrossRef Full Text | Google Scholar

Lipkowski, P., Kozłowska, J., Roztoczyńska, A., and Bartkowiak, W. (2014). Hydrogen-Bonded Complexes upon Spatial Confinement: Structural and Energetic Aspects. Phys. Chem. Chem. Phys. 16, 1430–1440. doi:10.1039/c3cp53583e

PubMed Abstract | CrossRef Full Text | Google Scholar

Lo, J. M. H., and Klobukowski, M. (2006). Computational Studies of One-Electron Properties of Lithium Hydride in Confinement. Chem. Phys. 328, 132–138. doi:10.1016/j.chemphys.2006.06.019

CrossRef Full Text | Google Scholar

Medved, M., Stachovà, M., Jacquemin, D., Andrè, J. M., and Perpeté, E. A. (2007). A Generalized Romberg Differentiation Procedure for Calculation of Hyperpolarizabilities. J. Mol. Struc. (Theochem) 847, 39–46. doi:10.1016/j.theochem.2007.08.028

CrossRef Full Text | Google Scholar

Pagliai, M., Cardini, G., and Cammi, R. (2014). Vibrational Frequencies of Fullerenes C60 and C70 under Pressure Studied with a Quantum Chemical Model Including Spatial Confinement Effects. J. Phys. Chem. A. 118, 5098–5111. doi:10.1021/jp504173k

CrossRef Full Text | Google Scholar

Roztoczyńska, A., Kozłowska, J., Lipkowski, P., and Bartkowiak, W. (2014). Does the Spatial Confinement Influence the Electric Properties and Cooperative Effects of the Hydrogen Bonded Systems? HCN Chains as a Case Study. Chem. Phys. Lett. 608, 264–268. doi:10.1016/j.cplett.2014.05.102

CrossRef Full Text | Google Scholar

Shameema, O., Ramachandran, C. N., and Sathyamurthy, N. (2006). Blue Shift in X−H Stretching Frequency of Molecules Due to Confinement. J. Phys. Chem. A. 110, 2–4. doi:10.1021/jp056027s

CrossRef Full Text | Google Scholar

Song, Y., Liu, Z., Mao, H.-k., Hemley, R. J., and Herschbach, D. R. (2005). High-Pressure Vibrational Spectroscopy of Sulfur Dioxide. J. Chem. Phys. 122, 174511. doi:10.1063/1.1883405

CrossRef Full Text | Google Scholar

Zaleśny, R., Góra, R. W., Kozłowska, J., Luis, J. M. J., Ågren, H., and Bartkowiak, W. (2013). Resonant and Nonresonant Hyperpolarizabilities of Spatially Confined Molecules: A Case Study of Cyanoacetylene. J. Chem. Theor. Comput. 9, 3463–3472. doi:10.1021/ct400410m

CrossRef Full Text | Google Scholar

Zaleśny, R., Góra, R. W., Luis, J. M., and Bartkowiak, W. (2015). On the Particular Importance of Vibrational Contributions to the Static Electrical Properties of Model Linear Molecules under Spatial Confinement. Phys. Chem. Chem. Phys. 17, 21782–21786. doi:10.1039/c5cp02865e

PubMed Abstract | CrossRef Full Text | Google Scholar

Zaleśny, R., Chołuj, M., Kozłowska, J., Bartkowiak, W., and Luis, J. M. (2017). Vibrational Nonlinear Optical Properties of Spatially Confined Weakly Bound Complexes. Phys. Chem. Chem. Phys. 19, 24276–24283. doi:10.1039/C7CP04259K

PubMed Abstract | CrossRef Full Text | Google Scholar