Fine-Tuning of Nonlinear Optical Contrasts of Hexaphyrin-Based Molecular Switches Using Inverse Design

In the search for new nonlinear optical (NLO) switching devices, expanded porphyrins have emerged as ideal candidates thanks to their tunable chemical and photophysical properties. Introducing meso-substituents to these macrocycles is a successful strategy to enhance the NLO contrasts. Despite its potential, the influence of meso-substitution on their structural and geometrical properties has been scarcely investigated. In this work, we pursue to grasp the underlying pivotal concepts for the fine-tuning of the NLO contrasts of hexaphyrin-based molecular switches, with a particular focus on the first hyperpolarizability related to the hyper-Rayleigh scattering (β_HRS). Building further on these concepts, we also aim to develop a rational design protocol. Starting from the (un)substituted hexaphyrins with various π-conjugation topologies and redox states, structure-property relationships are established linking aromaticity, photophysical properties and β_HRS responses. Ultimately, inverse molecular design using the best-first search algorithm is applied on the most favorable switches with the aim to further explore the combinatorial chemical compound space of meso-substituted hexaphyrins in search of high-contrast NLO switches. Two definitions of the figure-of-merit of the switch performance were used as target objectives in the optimization problem. Several meso-substitution patterns and their underlying characteristics are identified, uncovering molecular symmetry and the electronic nature of the substituents as the key players for fine-tuning the β_HRS values and NLO contrasts of hexaphyrin-based switches.

1 Introduction

Scientists’ searching for new and innovative materials with promising properties often finds their way back to the roots and fundamentals of nature. Porphyrins, for example, are engaged in many essential and complex processes of nature, such as photosynthesis or oxygen fixation in blood cells. Hence, porphyrins are excellent candidates as natural products to design novel compounds with a high adaptability to their environment (Kadish et al., 2000; Dolphin, 2012; Auwärter et al., 2015). Based on these tetrapyrrolic macrocycles, expanded porphyrins have been synthesized with an array of interesting properties, including a high conformational flexibility, novel coordination behaviours, versatile aromaticity and exceptional optical properties (Tanaka and Osuka, 2016). Expanded porphyrins are macrocycles containing more than four pyrrole rings (or analogous heterocyclic subunits), which are connected directly or by methine groups, keeping an internal pathway of at least 17 atoms (Sessler and Seidel, 2003). Different modifications to the core structure of expanded porphyrins can be introduced, either by 1) replacing one or more pyrrole rings with other five-membered heterocycles such as furan, thiophene or tellurophene (Chandrashekar and Venkatraman, 2003; Rath et al., 2005; Kumar et al., 2007; Chatterjee et al., 2017), or by 2) introducing different substituents at the meso-positions of the macrocycle (Marcos et al., 2014; Tanaka and Osuka, 2016; Woller et al., 2016; Torrent-Sucarrat et al., 2017b). These variations in the core structures have recently drawn a lot of attention as the modified structures exhibit outstanding properties for multidisciplinary applications such as bio-sensors, photodynamic therapy, photochemistry, catalysis and molecular electronics (Saito and Osuka, 2011; Sung et al., 2017; Cárdenas-Jirón et al., 2019).

The field of molecular electronics involves the use of individual molecules as active elements in the electronic circuit, such as diodes, rectifiers, transistors, or memory devices (Sun et al., 2014; Su et al., 2016; Xiang et al., 2016). Besides their potential to meet the ever-increasing demand for the miniaturization of electronics, more importantly, molecular electronics opens up the possibility of devices with novel functionalities beyond the complementary silicon-based technologies, such as molecular switches (Zhang et al., 2015). A considerable advantage over silicon-based electronics is that molecular electronics can be tailor-made using the concepts from self-assembly and thus becomes highly compatible with a large number of substrates (Su et al., 2016). As a consequence, the chemical and physical properties are easily tunable resulting in applications ranging from photopharmacology and drug delivery to imaging, spectroscopy and optoelectronics (Feringa and Browne, 2011; Feringa, 2017).

The switching devices consist of a molecular building block that can be reversibly shifted between two or more stable states upon application of an external stimulus, including light, temperature, bias voltage, chemical reactions and even mechanical forces (Zhang et al., 2015; Ladenthin et al., 2016). The prerequisite of a molecular switch is that the two or more states are separable and show a distinct difference in the property of interest (Zhang et al., 2015). Regarding optical switches, organic materials with commutable nonlinear optical responses are sought for optoelectronic applications, such as molecular-scale memory devices with multiple storage and non-destructive reading capacity (Kawata and Kawata, 2000). Interesting nonlinear (NLO) optical properties are second harmonic generation (SHG), two-photon absorption (TPA), and third harmonic generation (THG), among others. At the molecular level, the first hyperpolarizability (β) is a noteworthy quantity as this property is intimately connected to a variety of optical phenomena like SHG or the Hyper-Rayleigh Scattering (HRS). The potential of single molecules as nonlinear optical switches is mainly determined by the amplitude of the NLO contrast and thus large differences in first hyperpolarizability between the different states are required for high-performance optical switches (Castet et al., 2013; Kariduraganavar et al., 2021).

Expanded porphyrins are highly desirable for near-infrared dyes and nonlinear optical applications (Rath et al., 2005; Pawlicki et al., 2009; Mori et al., 2013; Shimomura et al., 2020; Wang et al., 2020). Thanks to their extended π-system, expanded porphyrins experience a red-shift of absorption bands and exhibit a much larger TPA cross section compared to regular porphyrins. As expanded porphyrins can easily switch between different redox states and π-conjugation topologies induced by diverse external stimuli, they are an ideal test bed for molecular optical switches (Tanaka and Osuka, 2016). Indeed, recent computational studies have shown that the interconversion between different π-conjugation topologies, more precisely, Hückel and Möbius structures, induces dramatic changes in first and second hyperpolarizabilities, acting therefore as a novel type of efficient nonlinear optical switches (Torrent-Sucarrat et al., 2017b; Woller et al., 2019). Importantly, the performance of these optical switches can be improved by introducing different types of functionalizations (Torrent-Sucarrat et al., 2017b; Pino-Rios and Cárdenas-Jirón, 2019; Woller et al., 2019). For example, it has been demonstrated that the NLO contrast in [28]hexaphyrin topological switches can be enhanced by introducing push-pull substitution patterns, which incorporate electron-withdrawing and electron-donating substituents on meso-positions located on the opposite sides of the macrocycles (Torrent-Sucarrat et al., 2017b).

However, exploring the entire region of synthetically accessible expanded porphyrins in the chemical compound space (CCS) remains an immense challenge. Hence, a rational approach is needed to help in the design of new high-potential molecular switches. In traditional molecular design procedures, one directly introduces the desired functionalizations into the chemical structure and subsequently evaluates for the altered structure the NLO quantities (Torrent-Sucarrat et al., 2012; Torrent-Sucarrat et al., 2017b; Tonnelé et al., 2018; Woller et al., 2019). One thus mainly relies on the chemist’s intuition to design derivatives with favorable NLO properties, which can become a cumbersome task when multiple chemical modifications are demanded. Alternatively, inverse molecular design approaches target the optimization of the property of interest as a function of the chemical structure (Wang et al., 2006; Balamurugan et al., 2008; De Vleeschouwer et al., 2012; De Vleeschouwer et al., 2015; De Vleeschouwer et al., 2016; Teunissen et al., 2017; Freeze et al., 2019). Only modifications are made that effectuate property enhancement. A big advantage of these inverse design approaches is that only a small subset of all possible expanded porphyrin derivatives needs to be evaluated to devise high-performing chemical structures for a particular application. Recent advances in computational inverse design approaches have already impacted the pool of structures available to nanophotonics (Molesky et al., 2018; Su et al., 2020).

In this paper, we take up the challenge to design efficient molecular NLO switches by means of an inverse design algorithm. In this way, the discovery of new functionalized expanded porphyrins with improved NLO contrasts can be accelerated. In particular, we focus on hexaphyrins, which are very effective platforms to realize versatile electronic states including Möbius and Hückel aromatic and antiaromatic species (Sankar et al., 2008; Ahn et al., 2005; Ishida et al., 2011; Kim et al., 2009; Sun et al., 2016). Two types of hexaphyrin-based molecular switches are considered here, namely redox (28R → 26R) and topology (28R → 28M) switches, the latter involving Hückel-to-Möbius transformations while keeping the number of π-electrons constant (Scheme 1). Among the different porphyrinoids investigated so far in our research group, the redox-triggered aromaticity switches based on hexapyrrolic macrocycles exhibit the largest ON/OFF transmission ratios in conductance switching applications (Alonso et al., 2012, 2014; Alonso et al., 2013a; Alonso et al., 2013b; Woller et al., 2016; Woller et al., 2018; Stuyver et al., 2018). In addition, topology switches based on [28]hexaphyrin exhibit dramatic variations in the second- and third-order NLO properties, as shown by Torrent-Sucarrat et al. (2017b).

SCHEME 1

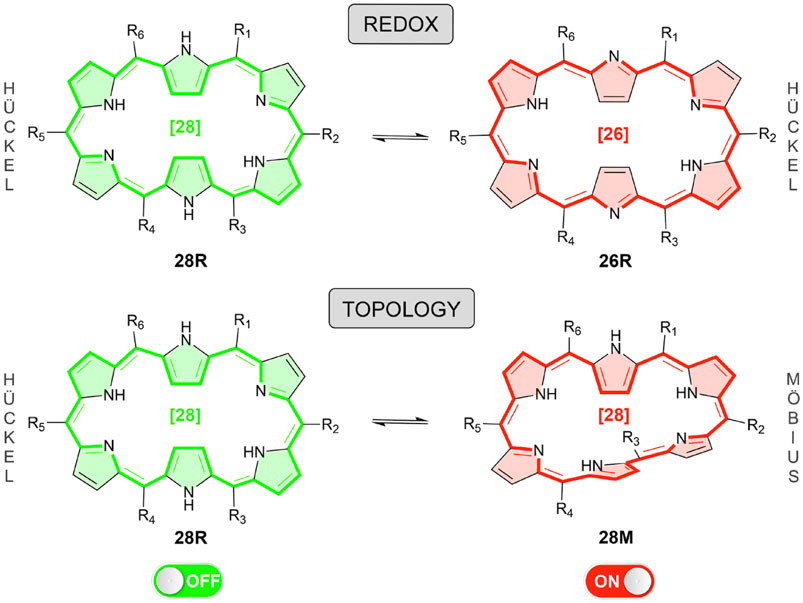
SCHEME 1. Overview of the redox and topology switches based on hexaphyrins. Inverse design is applied to optimize the functionalization of both molecular switches by maximizing the NLO contrasts. Red five-membered rings are linked to aromatic structures, whereas green ones to antiaromatic configurations.

Our objectives are threefold. First, we aim to establish the structure-property relationships between molecular topology, aromaticity, and optoelectronic properties for different unsubstituted hexaphyrins, labelled as the parent structures. Second, we investigate the effect of selected electron-withdrawing and electron-donating meso-substituents on the macrocyclic aromaticity and nonlinear optical properties. Lastly, we perform the inverse molecular design procedure with the Best-First Search (BFS) algorithm (Wang et al., 2006; Balamurugan et al., 2008; De Vleeschouwer et al., 2012, 2015; De Vleeschouwer et al., 2016; Teunissen et al., 2017) to find meso-substitution functionalizations of hexaphyrins inducing a maximum NLO contrast. By applying the inverse design protocol, only a fraction of all possible structures is calculated. Different substitution patterns as previously described in literature are considered, involving multiple sites to be modified, from a library of possible substituents.

2 Theoretical Background: Inverse Molecular Design

The Best-First Search (BFS) algorithm consists of a site-by-site optimization during which chemical modifications from a fragment library are introduced into a predefined molecular scaffold (Wang et al., 2006; Balamurugan et al., 2008; De Vleeschouwer et al., 2012; De Vleeschouwer et al., 2015; Teunissen et al., 2017; De Vleeschouwer et al., 2016). For each site, the modification’s impact on the target property of interest is evaluated and the most favourable substituent is selected based on the largest improvement in property value. The algorithm relies on the independent site approximation (ISA), which assumes that the sites can be optimized one by one, yielding the optimum after a single iteration over all sites and regardless of the site sequence used. Nevertheless, for most properties, the ISA is not fully valid as sites are affected by the type of functionalization on other positions in the structure. Therefore, several site iterations are carried out to ensure that intersite influences are evaluated as well. Figure 1 shows an example of the BFS algorithm on the 28R ⇆ 26R redox switch with 3 pairs of sites (R_1,4, R_2,5 and R_3,6) and 3 substituents (-F, -CN and -OH) available for functionalization. The three pairs of sites consist of combinations of 2 meso-positions that face each other on the macrocycle. First, the algorithm generates a random initial structure within the hexaphyrin CCS, with the CCS magnitude defined by the number of sites and the size of the substituent library. To this end, the algorithm randomly selects for each site a substituent from the fragment library. In the example of Figure 1, the randomly chosen substituents are a cyano group for the first (R_1,4), a hydroxyl group for the second (R_2,5), and a fluoro group for the third site (R_3,6). Next, the algorithm starts to optimize site 1 (R_1,4), while keeping all other sites (R_2,5 and R_3,6) fixed, i.e. the substituents on all sites, but site 1, remain unaltered. Optimizing site 1 involves placing each of the substituents from its fragment library on that position and evaluating the property for each generated structure. The substituent with the largest improvement in β_HRS contrast (here: -F) is then introduced into the initial structure. This altered structure is subsequently used as the starting point for the next step in the algorithm, corresponding to the optimization of site 2 while keeping the other two positions fixed. The same procedure is repeated until all sites have been visited. Convergence is reached when a single site modification does not result anymore in an improved property value. Even though there exist more recently introduced inverse design methods that may outperform the BFS method based on efficacy or larger CCS exploration (Elward and Rinderspacher, 2015; Strasser et al., 2016; Häse et al., 2018), BFS has the key advantage of systematically delivering essential information on how the type and location of each possible substituent influences our property of interest, since in every global iteration all substituents are tested on all available sites (Teunissen et al., 2017).

FIGURE 1

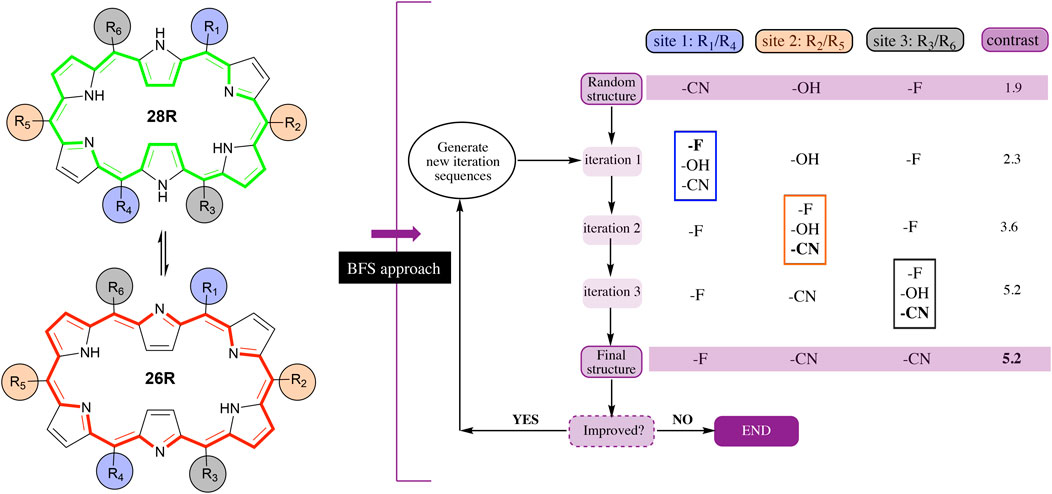
FIGURE 1. Example of the best-first search algorithm applied on the hexaphyrin-based redox switch (26R → 28R) with six modifiable sites, considered pairwise, and three substituents. Note that the desired target property, i.e. the NLO contrast, adds to the complexity of the inverse design problem. The contrast optimization requires the evaluation of the first hyperpolarizability of the two states involved in the switching. Thus, for each functionalization, two structure optimizations are needed before evaluating the target property, increasing the computational time. Therefore, the application of an inverse design approach to the discovery of high-performance optical switches remains a challenging task.

The figure-of-merit of the performance of an NLO switch is the NLO contrast as defined by Eq. 1. This contrast considers the ratio of the first HRS hyperpolarizabilities of both the ON and OFF state structures having the same meso-substitution pattern and has a high value for a well-performing NLO switch.

$contrast=\frac{{\beta }_{HRS}\left(\text{O}\text{N}\right)}{{\beta }_{HRS}(\text{O}\text{F}\text{F})}(1)$

In the literature, this contrast expression has been widely used for the evaluation of the performance of molecular switches (Plaquet et al., 2008; Castet et al., 2013; Tonnelé et al., 2018; Woller et al., 2019). The contrast is maximized during the BFS procedures, but the maximization of the ratio entails one problem. If the denominator becomes zero, the entire contrast reaches a value of infinity making it impossible to compare other structures facing the same issue. This widely used contrast definition may therefore not be an ideal target objective in the inverse design maximizations. To circumvent this complication, we implemented the following condition within the BFS procedure. If the β_HRS of the OFF state becomes lower than 10 a.u., the denominator is set to a value of 0.001 a.u.

Another measure of NLO contrast has been presented, among others, in the work of Torrent-Sucarrat et al. (2017b), taking the difference of the NLO responses between the ON and OFF state (Eq. 2). A high difference is connected to a high and low β_HRS response for the ON and OFF state, respectively, and reflects similar behaviour as our previous contrast definition. Note that a value of zero for the OFF state does not pose any optimization issues. The main difference between both contrast definitions is that high β_HRS differences can also appear from molecular switches in which the OFF state’s β_HRS response is far away from zero a.u. In this work, we carried out additional BFS searches in which the β_HRS difference is maximized. The best performing switches are then compared with the optimal structures connected to the ratio in β_HRS.

$contrast={\beta }_{HRS}(\text{O}\text{N})-{\beta }_{HRS}(\text{O}\text{F}\text{F})(2)$

3 Methodology

All quantum-chemical calculations were executed with the Gaussian16 software package (Frisch et al., 2016). The geometry optimizations and frequency calculations were performed using the Minnesota hybrid functional M06-2X (Zhao and Truhlar, 2008) with the cc-pVDZ basis set (Dunning, 1989). In recent benchmark studies (Marcos et al., 2012; Torrent-Sucarrat et al., 2017a; Sylvetsky et al., 2020; Woller et al., 2020), the M06-2X functional emerges among the best contemporary density functionals to describe the relative energies of Hückel and Möbius expanded porphyrins. Although singly-twisted Möbius topologies are a challenging test for electronic structure methods, M06-2X provides errors close to chemical accuracy relative to the golden-standard canonical CCSD(T) calculations. Harmonic vibrational analyses show that all optimized structures are exclusively characterized by positive eigenvalues and thus represent minima on the potential energy surface. To obtain more accurate electronic energies, subsequent single-point energy calculations on the optimized geometries were performed at the M06-2X/cc-pVTZ level of theory.

For all unsubstituted hexaphyrins, several aromaticity descriptors were computed, including the magnetic susceptibility exaltation (Λ) (Dauben et al., 1968), the nucleus-independent chemical shifts (NICS) (Lazzeretti, 2004; Chen et al., 2005; Fallah-Bagher-Shaidaei et al., 2006), the relative chemical hardness (Δη) (De Proft and Geerlings, 2004), and the recently introduced AV1245 and AV_min (Casademont-Reig et al., 2018; Matito, 2016). This set of aromaticity descriptors are rooted in magnetic, reactivity and electronic criteria in order to take the multidimensional character of the aromaticity into account (Solà, 2017; Woller et al., 2016; Wu et al., 2013). For the evaluation of the aromaticity descriptors, we employed the long-range corrected functional CAM-B3LYP (Yanai et al., 2004), in combination with 6–311+G(d,p) (Hehre et al., 1986), due to the relevance of the delocalization error in these measures. It has been recently found that the amount of Hartree-Fock exchange in DFT functionals largely influences the value of the aromaticity descriptors in expanded porphyrin systems, although aromaticity trends remain (Casademont-Reig et al., 2018, 2020; Szczepanik et al., 2017). The global aromaticity indices, Λ and Δη, were computed on the basis of the isomerization scheme (Figure 2), which involves the comparison of the magnetic susceptibilities and hardness values of a methyl and methylene isomer of each hexaphyrin structure (Schleyer and Pühlhofer, 2002; Alonso et al., 2012).

FIGURE 2

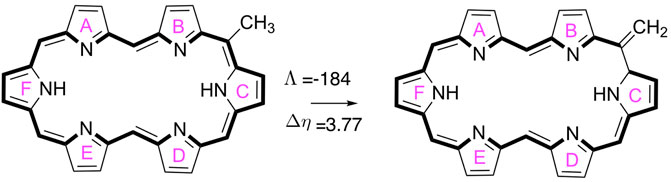
FIGURE 2. A schematic overview of the isomerization reaction used to evaluate the magnetic susceptibility exaltation (Λ in ppm cgs) and relative hardness (Δη in kcal mol⁻¹) for the 26D macrocycle.

Magnetic susceptibilities were evaluated with the Continuous Set of Gauge Transformations (CGST) method (Keith and Bader, 1993), whereas the hardness of the methyl and methylene isomers was computed as the HOMO and LUMO energy difference. The Gauge-Independent Atomic Orbital (GIAO) method (Wolinski et al., 1990) was applied to obtain the NICS values at three different positions: the geometrical center of the macrocycle’s heavy atoms and at 1Å above and below the ring center, together with their respective out-of-plane tensor components. The anisotropy of the induced current density (AICD) method (Herges and Geuenich, 2001; Geuenich et al., 2005) was applied to visualize the induced delocalization of π-electrons. In both the NICS and AICD methods, an external magnetic field is applied perpendicular to the molecular plane for expanded porphyrins with a Hückel or Möbius topology. Recently, extensive studies have been performed on the aromaticity of both unsubstituted and substituted expanded porphyrins by means of the ring current criterion and current density analysis (Fliegl et al., 2010, 2011; Fliegl and Sundholm, 2012; Valiev et al., 2013; Valiev et al., 2017; Valiev et al., 2018; Foroutan-Nejad et al., 2018; Foroutan-Nejad and Ghosh, 2018; Ghosh et al., 2018; Conradie et al., 2019). The electronic delocalization indices AV1245 and AV_min indices were computed with the ESI-3D program (Matito, 2006; Casademont-Reig et al., 2018) at the CAM-B3LYP/6-311+G(d,p) level of theory. The calculation of these electronic indices relies on Quantum Theory of Atoms in Molecules (QTAIM) atomic partition performed with the AIMAll software (Keith, 2017). AV1245 consists of the average of the 4-center multicenter index (MCI) values along the ring that keeps a positional relationship of 1, 2, 4, 5, whereas AV_min corresponds to the minimal absolute value of the aforementioned 4-center MCI values along the conjugation pathway (Matito, 2016; Casademont-Reig et al., 2018).

Next to the aromaticity descriptors, two geometrical descriptors, i.e., the torsional ring strain (Φ_p) (Alonso et al., 2012) and the π-conjugation index (Π) (Stępień et al., 2011; Alonso et al., 2012), were computed to gain insight into the factors governing the relative energies of Hückel and Möbius conformations. Φ_p corresponds to the average dihedral angle between neighboring pyrrole rings, whereas Π measures the effectiveness of the overlap of neighboring p-orbitals. Π is positive for Hückel conformations and negative for Möbius structures. Macrocyclic aromaticity in porphyrinoids corresponds to values of Π above a threshold of 0.30 (Stępień et al., 2011).

Hyperpolarizabilities related to the nonlinear optical responses in the static and dynamic regimes were obtained at the coupled-perturbed Kohn-Sham and TD-DFT levels of theory, respectively, with the CAM-B3LYP functional and a Pople basis set 6-311G+(d,p). Different benchmark studies highlight the dependency of extended organic dyes’ NLO properties on the exchange-correlation functional and basis set. However, recent research has shown that range-separated hybrid functionals, such as CAM-B3LYP, are the best choice for the calculation of first order hyperpolarizabilities (Garza et al., 2015; Lescos et al., 2020). For the particular case of Hückel and Möbius π-conjugation topologies, Torrent-Sucarrat et al. showed that the hybrid M05-2X and the long-range corrected CAM-B3LYP provide a semi-quantitative description of the NLO properties at a reasonable computational cost (Torrent-Sucarrat et al., 2011; Torrent-Sucarrat et al., 2012; Torrent-Sucarrat et al., 2017b). In Torrent-Sucarrat’s work on designing topological switches based on meso-substituted [28]hexaphyrins with high NLO properties, both functionals together with the 6-31G basis set were employed (Torrent-Sucarrat et al., 2017b). While the good performance of M05-2X on the NLO properties can be ascribed to the large percentage of exact HF exchange (56%), the success of CAM-B3LYP is based on the introduction of a growing fraction of exact HF exchange at larger inter-electronic distances. Regarding the basis set dependency, split-valence double- or triple-ζ basis sets including one set of diffuse and polarization functions were shown to be generally sufficient to describe the dominant β tensor components and the depolarization ratios (Plaquet et al., 2008; de Wergifosse and Champagne, 2011; Castet et al., 2013). In particular, for the evaluation of the nonlinear optical properties of a Hückel-Möbius aromaticity switch of a closely related porphyrinoid A,D-di-para-benzi[28]hexaphyrin(1.1.1.1.1.1), Torrent-Sucarrat et al. showed that the increment of basis set from 6-31G to 6-311G(d) does not provoke a large variation of α and γ values (Torrent-Sucarrat et al., 2012). As such, the 6-311+G(d,p) basis set employed in our study is adequate to compute the β_HRS values of the Hückel and Möbius conformers of hexaphyrins. Indeed, in a very recent benchmark study on the influence of the amount of exact Hartree–Fock exchange included in the DFT functional on the magnitude of the static HRS responses, a similar basis set 6-311+G(d) was employed (Lescos et al., 2020).

In this study, we mainly focus on the first hyperpolarizability associated to the Hyper-Rayleigh scattering phenomenon, termed as β_HRS (Clays and Persoons, 1991; Hendrickx et al., 1998; Verbiest et al., 2009). The incoherent scattered light is at twice the optical frequency (2ω) of the incident laser pulse (ω) and its intensity is related to the first hyperpolarizability. The entire HRS intensity can be written as Eq. 3, when the incoherent scattered light is observed perpendicular to the laser’s propagation plane.

${\beta }_{HRS}(-2\omega ;\omega ,\omega )=\sqrt{\langle {\beta }_{ZZZ}^2\rangle +\langle {\beta }_{ZXX}^2\rangle }(3)$

$⟨{\beta }_{ZZZ}^2⟩$ and $⟨{\beta }_{ZXX}^2⟩$ represent the orientational averages of β and describe the isotropic distribution of molecular orientations. The full descriptions of these tensor components are written in Eqs. 4, 5.

$\begin{array}{ll}\hfill ⟨{\beta }_{ZZZ}^2⟩=& \frac{1}{7}\sum _i^{x,y,z}{\beta }_{iii}^2+\frac{4}{35}\sum _{i\ne j}^{x,y,z}{\beta }_{iij}^2+\frac{2}{35}\sum _{i\ne j}^{x,y,z}{\beta }_{iii}{\beta }_{ijj}+\frac{4}{35}\sum _{i\ne j}^{x,y,z}{\beta }_{jii}{\beta }_{iij}\hfill \\ \hfill +& \frac{4}{35}\sum _{i\ne j}^{x,y,z}{\beta }_{iii}{\beta }_{jji}+\frac{1}{35}\sum _i^{x,y,z}{\beta }_{jii}^2+\frac{4}{105}\sum _{i\ne j\ne k}^{x,y,z}{\beta }_{iij}{\beta }_{jkk}+\frac{1}{105}\sum _{i\ne j\ne k}^{x,y,z}{\beta }_{jii}{\beta }_{jkk}\hfill \\ \hfill +& \frac{4}{105}\sum _{i\ne j\ne k}^{x,y,z}{\beta }_{iij}{\beta }_{kkj}+\frac{2}{105}\sum _{i\ne j\ne k}^{x,y,z}{\beta }_{ijk}^2+\frac{4}{105}\sum _{i\ne j\ne k}^{x,y,z}{\beta }_{ijk}{\beta }_{jik}\hfill \end{array}(4)$

$\begin{array}{ll}\hfill ⟨{\beta }_{ZXX}^2⟩=& \frac{1}{35}\sum _i^{x,y,z}{\beta }_{iii}^2+\frac{4}{105}\sum _{i\ne j}^{x,y,z}{\beta }_{iii}{\beta }_{ijj}-\frac{2}{35}\sum _{i\ne j}^{x,y,z}{\beta }_{iii}{\beta }_{jji}+\frac{8}{105}\sum _{i\ne j}^{x,y,z}{\beta }_{iij}^2\hfill \\ \hfill +& \frac{3}{35}\sum _{i\ne j}^{x,y,z}{\beta }_{ijj}^2-\frac{2}{35}\sum _i^{x,y,z}{\beta }_{ijj}{\beta }_{jii}+\frac{1}{35}\sum _{i\ne j\ne k}^{x,y,z}{\beta }_{ijj}{\beta }_{jkk}-\frac{2}{105}\sum _{i\ne j\ne k}^{x,y,z}{\beta }_{iik}{\beta }_{jjk}\hfill \\ \hfill -& \frac{2}{105}\sum _{i\ne j\ne k}^{x,y,z}{\beta }_{iij}{\beta }_{jkk}+\frac{2}{35}\sum _{i\ne j\ne k}^{x,y,z}{\beta }_{ijk}^2-\frac{2}{105}\sum _{i\ne j\ne k}^{x,y,z}{\beta }_{ijk}{\beta }_{jik}\hfill \end{array}(5)$

Lastly, an inverse design procedure was executed using the best-first search (BFS) algorithm (Pearl, 1984) as implemented in our in-house program CINDES (Teunissen, 2019; Teunissen, 2016). Both definitions for the contrast are considered for each substitution pattern. The fragment library consists of -NO₂, -CN, -F, -H, -CH₃, -OH and -NH₂. For all BFS optimizations, the computational approach and level of theory for the geometry optimization, frequency and NLO calculations are kept the same as aforementioned.

4 Results and Discussion

4.1 Structure-Property Relationships in the Parent Macrocycles

In order to establish a relationship between molecular topology, aromaticity and NLO properties in hexaphyrin-based macrocycles, we first investigate the optoelectronic properties of unsubstituted [26] and [28]hexaphyrins. The most stable configurations for each redox state were selected based on our extensive conformational study of hexaphyrin macrocycles (Scheme 2) (Alonso et al., 2012). Each structure is labelled according to its redox state (i.e. the number of π-electrons along the annulene-type conjugation pathway) and conformation (D: dumbbell, R: rectangular and M: Möbius). For example, the 26D(H) has 26 π-electrons and a dumbbell conformation with H-atoms on the meso-positions. In the case of unsubstituted macrocycles, the lowest-energy conformations for the [26] and [28]hexaphyrins correspond to 26D(H) and 28R(H), respectively, which are characterized by the lowest torsional ring strain and a high degree of π-conjugation (Table 1). Hence, the more planar conformations are the most stable for each redox state. It is interesting to note that the 26R(H) and 28R(H) structures exhibit similar structural parameters despite the difference in number of π-electrons. Appealingly, Hückel and Möbius conformations coexist in dynamic equilibrium for the [28]hexaphyrin (Sankar et al., 2008; Kim et al., 2009) as can be inferred from the small Gibbs free energy difference between 28R(H) and 28M(H) (Scheme 2).

SCHEME 2

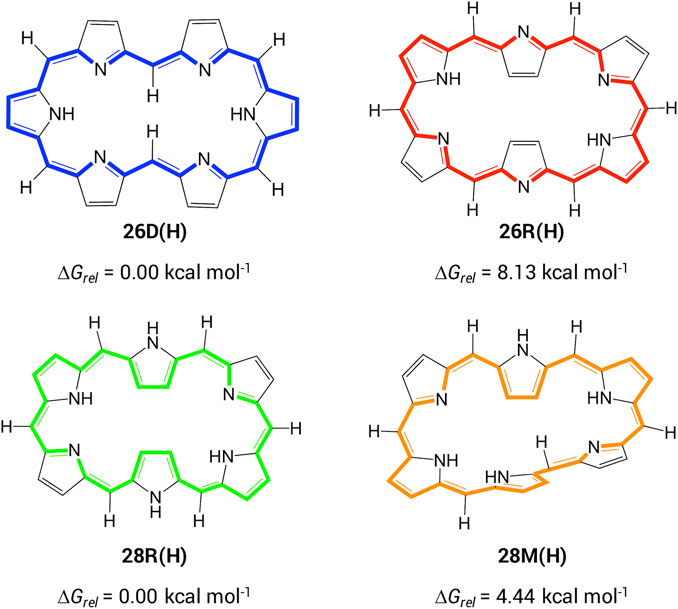
SCHEME 2. Selected conformations of [26] and [28]hexaphyrins with the corresponding relative Gibbs free energies. The classical annulene-type conjugation pathway is depicted with bold bonds.

TABLE 1

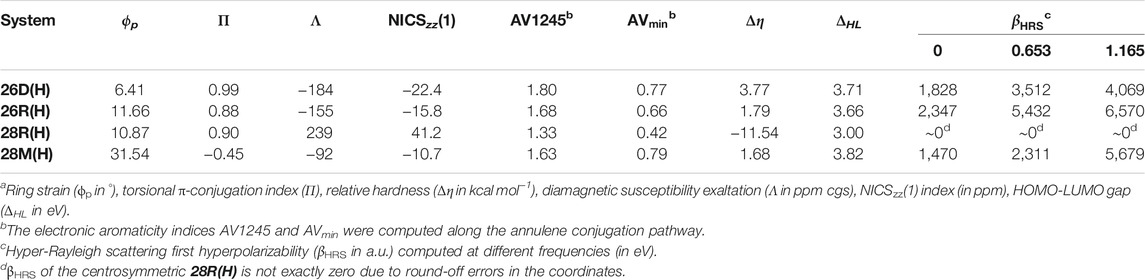
TABLE 1. Structural parameters, aromaticity descriptors and static and dynamic HRS first hyperpolarizability of the unsubstituted hexaphyrins^a.

The aromaticity of the unsubstituted conformations is quantified by means of several aromaticity indices rooted in reactivity, magnetic and energetic criteria (Table 1). Aromatic systems, such as 26D(H), 26R(H) and 28M(H), are characterized by a positive relative hardness, a negative diamagnetic susceptibility exaltation and negative NICS indices and larger values for AV1245 and AV_min. On the other hand, the 28R(H) conformation shows a clear antiaromatic character with a negative relative hardness, positive magnetic descriptors and reduced values for the electronic indices. The Anisotropy of the Induced Current Density (AICD) plots (Herges and Geuenich, 2001; Geuenich et al., 2005) confirm the (anti)aromatic character of the parent structures (Figure 3). While the direction of the induced current through the aromatic structures is clockwise, the antiaromatic system 28R(H) shows a counterclockwise current. Nicely, all the indices confirm the reversal of macrocyclic aromaticity upon redox reactions (i.e., 28R(H) → 26R(H)) and topology interconversions (i.e., 28R(H) → 28M(H)). The arrangement of the molecular frontier orbitals and the magnitude of the HOMO-LUMO gap (Δ_HL) clearly depend on the aromaticity of the system (Figure 4). Aromatic systems (26D(H), 26R(H) and 28M(H)) show quasi-degenerate H/H-1 and L/L+1 energy levels with larger Δ_HL gaps. On the other hand, the H-1/H-2 and L+1/L+2 energy levels are almost degenerate in the antiaromatic 28R(H), whereas the Δ_HL value is significantly reduced.

FIGURE 3

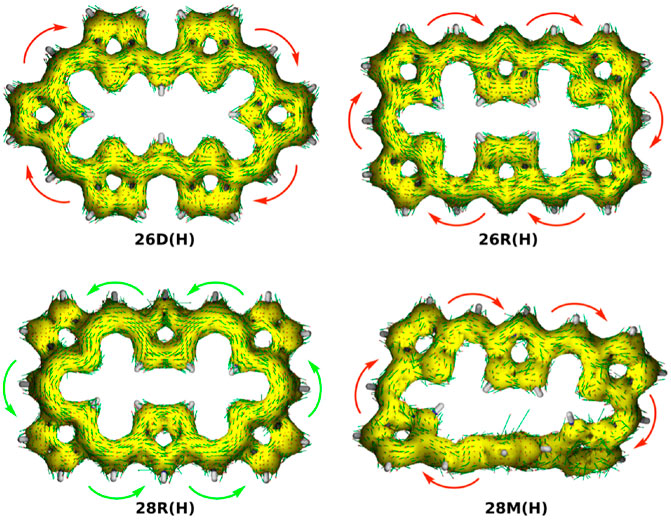
FIGURE 3. AICD isosurface plots (isocontour value 0.05) of unsubstituted [26] and [28]hexaphyrins with different conformations computed at the CAM-B3LYP/6-311+G(d,p) level of theory. The arrows denote the direction of the current density vectors.

FIGURE 4

FIGURE 4. Molecular orbital diagrams computed at the CAM-B3LYP/6-311+G(d,p) level of theory.

Regarding the nonlinear optical (NLO) properties, we focus on the first hyperpolarizability related to the Hyper-Rayleigh Scattering (β_HRS). The β_HRS is evaluated in both the static and dynamic regime at two different wavelengths, 1,064 nm and 1,907 nm, corresponding to the Nd:YAG and Ho:YAG lasers, respectively. The β_HRS values for the unsubstituted hexaphyrins in static and dynamic regime at the two laser frequencies are tabulated in Table 1. It should be noted that the β_HRS is highly dependent on the centrosymmetry of the system (Woller et al., 2019). If the structure is centrosymmetric, the β_HRS value is zero. This is the case for the 28R(H) conformation, which contains an inversion point and belongs to the C_i point group. All other conformations are within the C₁ point group. On top of the centrosymmetry, the torsional strain of the molecular topology is also an underlying factor regulating the β_HRS response. When the topology shifts from Hückel (28R(H)) to Möbius (28M(H)) topology, a large increase of about 1,500 a.u. in the β_HRS value is observed. By changing the oxidation state while keeping constant the topology, and thus the ring strain, an increase of 2,347 a.u. in β_HRS is observed (28R(H) → 26R(H)). The large changes in β_HRS demonstrate the potential of redox and topology interconversions in hexaphyrins as a novel type of optical switches. Overall, molecular symmetry, particularly the presence or absence of an inversion point, remains the most influencing property determining the β_HRS, followed by the macrocyclic planarity and aromaticity.

The first hyperpolarizability contrast, defined as the ratio (definition 1, see Eq. 1) or the difference (definition 2, see Eq. 2) between the β_HRS of the ON state (the highest value of β_HRS) and the OFF state (the lowest value of β_HRS) involved in the switching, is the figure of merit for identifying efficient NLO switches. The larger is the β_HRS contrast, the more efficient becomes the switch. The values of the NLO contrasts for all possible interconversions can be found in Supplementary Tables S1, S2 and Supplementary Figure S3. As expected, when the OFF state is assigned to the centrosymmetric 28R(H) structure, the highest NLO contrasts are found. Focusing on static β_HRS ratio-based contrast values, the redox switch 28R(H) → 26R(H) exhibits the largest contrast, followed by 28R(H) → 26D(H) and then the topological switch 28R(H) → 28M(H), although all the contrasts are of the same order of magnitude (10⁶, since the β_HRS value of 28R was set to 0.001 a.u.). The higher the variation of the symmetry and aromaticity between the OFF and ON states, the larger the NLO contrasts. The redox interconversion 28R(H) → 26R(H) yields higher NLO contrasts than the topological switch 28R(H) → 28M(H), presumably due to larger variation in aromaticity involved in the former switch. Note that the Hückel configuration (26R(H)) is slightly more aromatic than the Möbius one (28M(H)) according to the majority of aromaticity descriptors (Table 1). When we have a look at the second contrast definition, the β_HRS difference, the most efficient NLO switches coincide with the ones found using the β_HRS ratio, with 28R(H) as the OFF state. However, additional interconversions can be identified for which the contrast differs by less than an order of magnitude from the best performing switches. The ratio definition of the contrast motivates the selection of the centrosymmetric 28R as the ultimate OFF state for NLO-type molecular switching applications, whereas for the difference definition more than one potential OFF-state candidate is put forward.

Finally, it is observed that the β_HRS values and the β_HRS contrasts are generally enhanced in the dynamic regime, indicating that the switch performance can be further fine-tuned with the wavelength of the incident light (see also Supplementary Figure S2). Remarkably, the values in Table 1 denote that the ON and OFF states of the 26D(H)/28M(H) interconversion interchange when a frequency of 1.165 eV is applied for the first hyper-Rayleigh scattering in the dynamic regime, most clearly demonstrated by the opposite sign of the contrast value in Supplementary Table S2. A plausible explanation is that the 28M(H) system is close to resonance. Generally, systems close to resonance are characterized by exalted magnitudes of β_HRS in the dynamic regime at certain wavelengths. Half of the Q-band’s excitation energy and half of the B-band’s excitation energy correspond to the first and the second resonance energy, respectively. In Supplementary Figure S1, the β_HRS is plotted against the incident energy of the photon for the different unsubstituted hexaphyrins. It is observed that, besides 28M(H), none of the systems are close to resonance in the dynamic regime.

4.2 Effect of the Meso-Substituent in the Hexaphyrin-Based Switches

As a proof of concept, we concentrate on the effect of meso-substitution on the NLO responses of hexaphyrins, in particular, the β_HRS. Since the 28R(H) → 26R(H) redox-based switch and the 28R(H) → 28M(H) topological interconversion showed high NLO contrasts, these two switches are selected for further investigation. We consider five distinct substitution patterns (Scheme 3), the first three based on currently synthesizable [26] and [28] hexaphyrins (Suzuki and Osuka, 2003; Plamont et al., 2017) and the final two taken from a previous computational study on efficient optical topological switches of [28]hexaphyrin (Torrent-Sucarrat et al., 2017b).

SCHEME 3

SCHEME 3. Overview and labelling of the meso-substituted structures based on the 26R topology.

The experimental substitution patterns are based on synthetically available routes towards meso-substituted hexaphyrins (Tanaka and Osuka, 2016). At present, the A₃B₃-type [26]hexaphyrins (Scheme 3, exp_a) with a range of meso-aryl substituents can be synthesized via acid-catalysed condensation of meso-substituted dipyrromethene and aryl aldehydes (Suzuki and Osuka, 2003). More recently, a two-step synthesis of meso-substituted [28]hexaphyrins was discovered for the preparation of unprecedented A₂BC₂D-hexaphyrins (Scheme 3, exp_b) containing up to four different kinds of meso-appended aryl groups (Plamont et al., 2017). A variety of meso-substituents including electron-donating groups (EDG) and electron-withdrawing groups (EWG), inducing different electronic and steric effects, are considered. For each state of the molecular switch, the most relevant geometric, electronic, and optical properties are summarized in Table 2.

TABLE 2

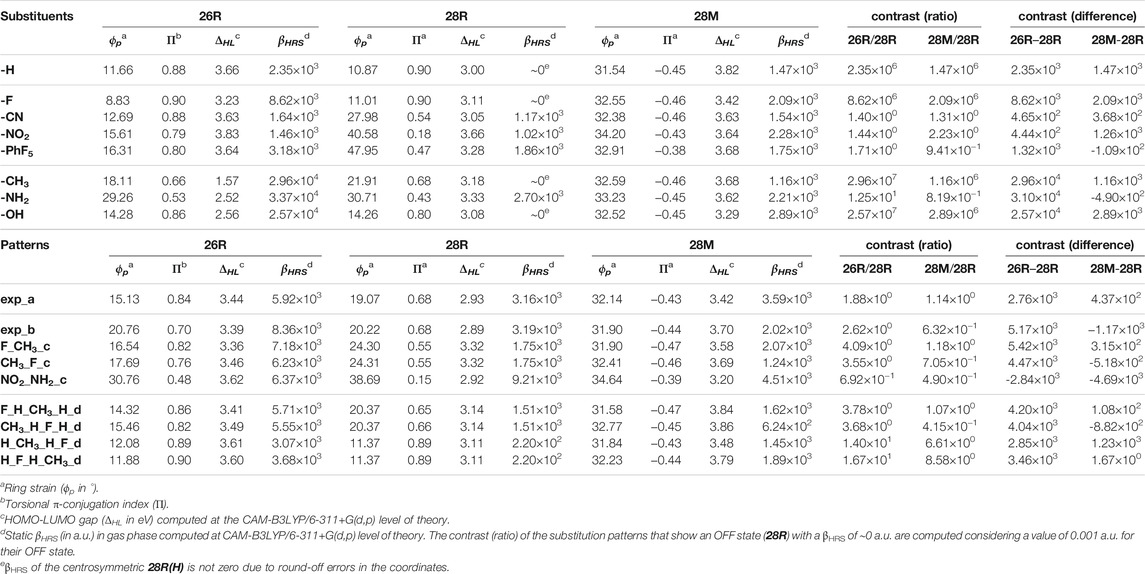
TABLE 2. Most relevant structural, energetic and optical properties of the meso-substituted hexaphyrins.

Depending on the bulkiness of the substituent and the topology of the π-system, the introduction of meso-substituents distorts the macrocyclic planarity in different degrees. In the 26R structures bearing the same substituent, all substituents except F reduce the planarity of the macrocycle, thus decreasing the effective π-overlap, as shown by the reduced values of the Π descriptor. This effect is particularly large for the CH₃ and NH₂ substituents, in which ϕ_p increases by 6.5° and 17.6° and Π decreases by 0.22 and 0.35, respectively. The planarity distortion increases considerably the β_HRS response of the 26R state, up to an order of magnitude. In addition, the electronic nature of the meso-substituent plays an important role with EDGs leading to larger β_HRS responses than EWGs. It is interesting to further note that the presence of EDGs significantly reduces the Δ_HL of the 26R structures, while this effect is less pronounced for EWGs. Accordingly, lowering the Δ_HL results in higher first hyperpolarizabilities and other NLO properties in line with previous studies (Suslick et al., 1992; Yoon et al., 2008).

In the case of the 28R structures, the symmetry of the conformation is a key factor in tuning the NLO response. Either a centrosymmetric meso-substituted 28R is found, or a more stable C₂ or C₁-symmetric structure. Recall that centrosymmetric structures produce null β_HRS responses. The introduction of several meso-substituents such as NO₂, CN and PhF₅ breaks the centrosymmetry to either a C₁ or C₂ symmetry by disturbing the planarity of the system. The more pronounced becomes the geometrical distortion (higher ϕ_p, lower Π), the higher becomes the NLO response of the 28R state. For example, the NO₂ substituent significantly distorts the macrocyclic planarity making the π-conjugation rather ineffective with a concomitant huge increase in the β_HRS response of 28R(NO₂).

A change in topology from Hückel to Möbius also affects the β_HRS response of [28]hexaphyrins. The singly-twisted 28M conformation allows for a better arrangement of the meso-substituents and, consequently, meso-substitution does not induce a significant change in the torsional or structural descriptors. Compared to their Hückel 28R counterparts, most meso-substituted Möbius structures show a (much) larger β_HRS response of the order of 10³ and this response can be tuned by the inclusion of electron-withdrawing and electron-donating groups, however without any clear trend.

Several push-pull substitution patterns were also investigated to assess the influence of the number and position of the substituents. Similar conclusions can be drawn regarding the structural parameters, i.e., slight to moderate increase and decrease for their ϕ_p and Π values, respectively. The tabulated meso-substituted structures taken from literature lend themselves to several interesting observations. First, the two synthetically available substitution patterns exp_a (A₃B₃) and exp_b (A₂BC₂D), have significantly enhanced β_HRS responses with respect to the unsubstituted structures, especially the 28R conformation. We also point out that the 26R(exp_a) and 26R(exp_b) are outperformed by several of the previously discussed meso-substituted structures leaving room for improvement in terms of the NLO response. Second, we have computed some of the push-pull structures suggested by Torrent-Sucarrat et al. (2017b), which can be compartmentalized into two distinct substitution patterns, indicated in their name by _c and _d. Structures F_CH₃_c and CH₃_F_c patterns are very similar, but the substituents are differently positioned on the macrocycle. Nonetheless the F_CH₃_c shows a higher NLO response for 26R and 28M than its CH₃_F_c counterpart. Intensifying the electronic character of this pattern by replacing the CH₃ and F by NH₂ and NO₂, respectively, results in more distorted structures for all hexaphyrins. For 28R(NO₂_NH₂_c) and 28M(NO₂_NH₂_c), this leads to significantly larger β_HRS values compared to the F_CH₃_c equivalents. However, this geometrical distortion does not necessarily result in a higher NLO response as observed for 26R(NO₂_NH₂_c). Lastly, the number and orientation of the substituents also influence the NLO response. For substitution pattern d, we compare disubstituted with quadruply substituted hexaphyrins, again introducing push-pull functionalization via fluoro and methyl groups. Putting the CH₃ or F at the R₁/R₆ and R₃/R₄ results in higher NLO responses for the 26R and 28R conformation with a lower planarity and higher ring strain with respect to the substitution of the R₂/R₅. This demonstrates that the number of meso-substitutions can be a determining factor in magnifying the β_HRS response. In addition, the orientation of the push-pull components has a clear effect, though to a lesser degree. Conversely, the 28M conformation shows more similar NLO responses for the different positions, with the exception of 28M(CH₃_H_F_H_d).

From this table, it becomes clear that EDGs (CH₃, NH₂, OH) give the highest β_HRS values for the 26R state and that push-pull substitution is not essential for this configuration. Conversely, the β_HRS response of the 28M conformations varies to a much smaller extent upon meso-substitution as compared to the Hückel topologies. The most pronounced changes in the NLO response, however, are observed for the 28R state, where the structural symmetry, more precisely the absence of presence of an inversion point, dominates the effect of the chemical modifications on the β_HRS response. As the lowest β_HRS responses usually correspond to the 28R structures, they are selected as the OFF state in the evaluation of the switch contrast. Both the ratio and the difference based definitions are considered. We observe that the presence of a centrosymmetric OFF state influences the ratio based contrast immensely yielding contrasts up to 10⁶-10⁷. In absence of a centrosymmetric OFF state, push-pull patterns compete with fully EDG substituted 28R → 26R switches. In line with the parent structures, the redox switch outperforms the topology switch upon meso-substitution. Moreover, for several topology switches a reversal of the ON and OFF state has occurred, as witnessed from the ratio values below 1 and the negative contrast differences. Inclusion of push-pull functional groups can play a major role in improving the switching efficiency of 28R → 28M but the positioning of these groups is of vital importance.

We finally would like to note that overall both contrast definitions correlate well. For centrosymmetric OFF states, the ratio and the difference are linearly dependent (Figure 5). As mentioned before, these coincide with a high and low NLO response for the ON and OFF state, respectively. Most switches with a non-centrosymmetric OFF state display a relatively high NLO response and are therefore characterized by a low ratio-based contrast between 0.69 and 14, but a high difference-based contrast (see purple box in Figure 5). Upon removal of 2 outliers (28R(H_CH₃_H_F_d) → 26R(H_CH₃_H_F_d) and 28R(H_CH₃_H_F_d) → 28M(H_CH₃_H_F_d), a strong linear correlation between the two contrast definitions is found with a correlation coefficient (R²) of 0.96. We therefore expect similar results when both definitions are optimized for substitution patterns for which centrosymmetric OFF states are not accessible.

FIGURE 5

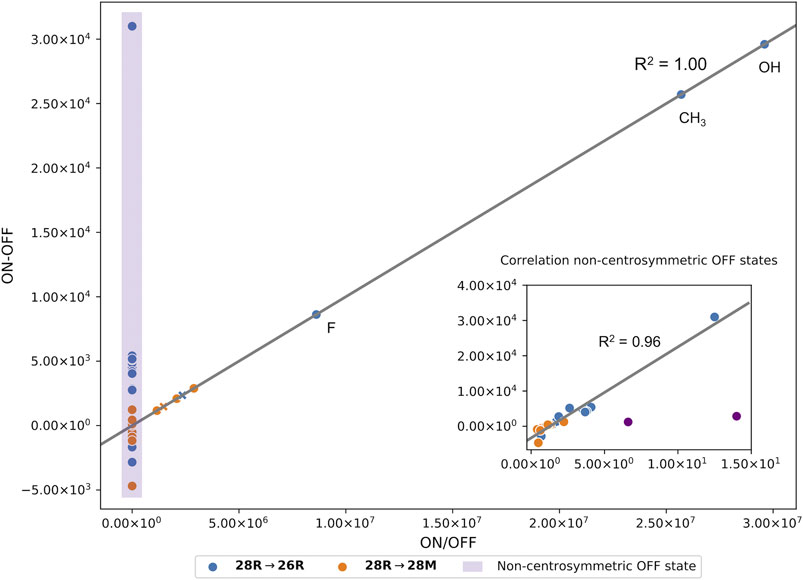
FIGURE 5. Correlation plot between the two contrast definitions based on the ratio and the difference of the β_HRS responses of all meso-substituted structures with a centrosymmetric OFF state (R² of 1.00). The datapoints marked with an X are the unsubstituted hexaphyrins. All switches with a non-centrosymmetric OFF state are highlighted in the purple box. A separate plot in the right corner shows the correlation of these systems (R² of 0.96).

4.3 Inverse Design of Hexaphyrin-Based Optical Switches

4.3.1 Prestudy

Before we start our inverse design optimizations, a small prestudy is conducted in which the most favorable functional groups are determined when substituting each pair of meso-positions facing each other diagonally on the macrocycle (R₁/R₄, R₂/R₅ and R₃/R₆). For each site combination, the β_HRS responses of the 26R, 28R and 28M conformations and the resulting contrasts of both switches are summarized in Table 3. This prestudy is of particular interest since we observed that the most stable¹ 28R conformation of some of the fully substituted hexaphyrins has C_i symmetry, largely impacting the β_HRS contrasts of both the topological and redox switches.

TABLE 3

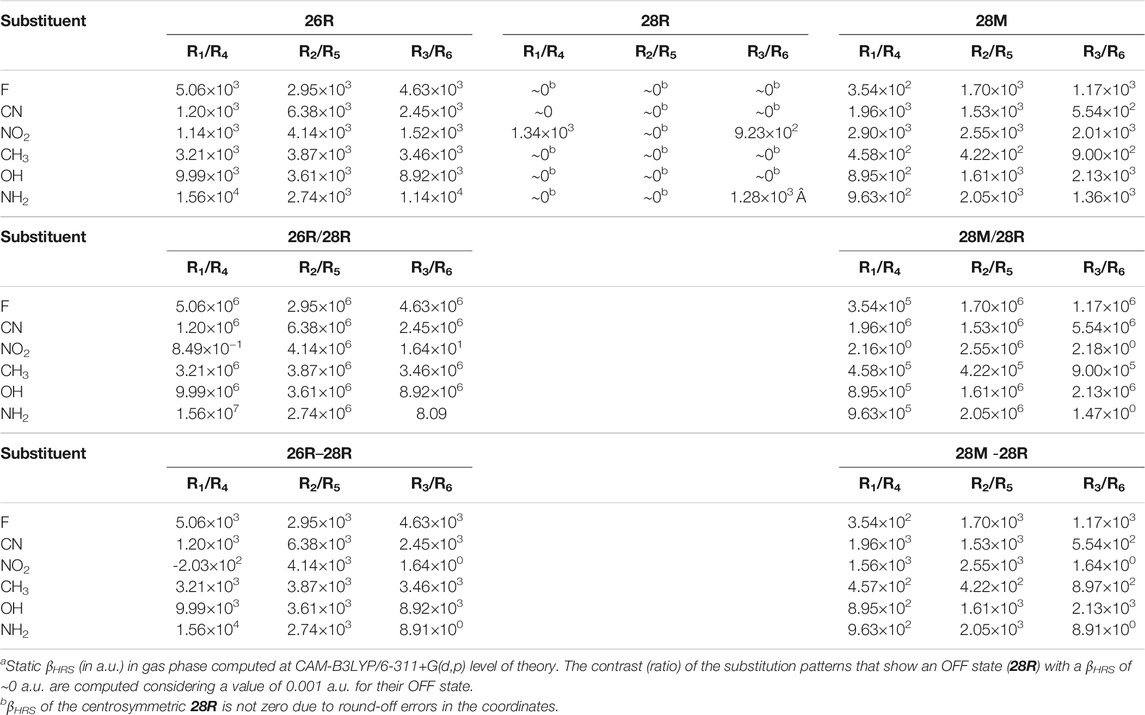
TABLE 3. The β_HRS response^a of meso-substituted hexaphyrins’ individual sites (R₁/R₄, R₂/R₅ and R₃/R₆) and their corresponding contrasts using both the ratio and difference definition.

For the 26R conformation, the highest responses are retrieved for EDGs (NH₂ and OH) substituted on the R₁/R₄ and R₃/R₆ site combinations and EWGs (CN and NO₂) on the R₂/R₅ positions. Substituents with an opposite electronic character on the aforementioned site combinations exhibit two to even thirteen times lower β_HRS responses. The NH₂ functional group outperforms other substituents from 30% to around an order of magnitude, except for the R₂/R₅ positions where it shows the lowest HRS response of all. A different trend is obtained for the 28M conformation, where only EWGs (CN and NO₂) on R₁/R₄ reveal a high β_HRS response with respect to the other substituents, while on other positions both EWGs and EDGs (NO₂, NH₂ and OH) perform about equally well. Note that for both the 26R and 28M conformations, the greatest impact can be achieved by substituting sites R₁/R₄, however, where for 26R an almost sevenfold enhancement in β_HRS can be gained, functionalization of 28M induces only a twofold improvement compared to the parent conformation. Finally, 28R, typically the OFF state, shows for all substituents a nearly zero β_HRS response due to its centrosymmetry. The only exceptions are the NO₂ substituents positioned on the R₁/R₄ and R₃/R₆ site combinations and the NH₂ substituted R₃/R₆ conformation, which all have C₂ symmetry. Because most functionalized 28R structures have a very low NLO response, the discussed trends apply to both the ratio-based and difference-based contrasts of the associated redox (28R → 26R) and topological switches (28R → 28M).

Building on our previous proof of concept and the additional disubstitutions, we expand our search for well-performing functionalized redox and topological switches, i.e. connected to a high NLO contrast, by means of the BFS algorithm. Three sets of BFS runs are executed considering three substitution patterns and a fragment library containing seven substituents (-NH₂ (amino-), -OH (hydroxyl-), -CH₃ (methyl-), -H, -F (fluoro-), -CN (cyano-) and -NO₂ (nitro-)). We introduce a new substitution pattern, called A₂B₂C₂ (Scheme 4A). It considers all meso-positions, but fixes the same substituent on the diagonal sites (R₁ = R₄ versus R₂ = R₅ versus R₃ = R₆). The other examined substitution patterns are the two synthesizable ones as described in the proof of concept section, indicated as A₃B₃ (Scheme 4B) and A₂BC₂D (Scheme 4C) containing up to two and four, respectively, different kinds of functional groups (Plamont et al., 2017). In the next part, we discuss a series of β_HRS contrast maximizations to identify the most optimal functionalizations of the three substitution patterns showing enhanced NLO contrasts.

SCHEME 4

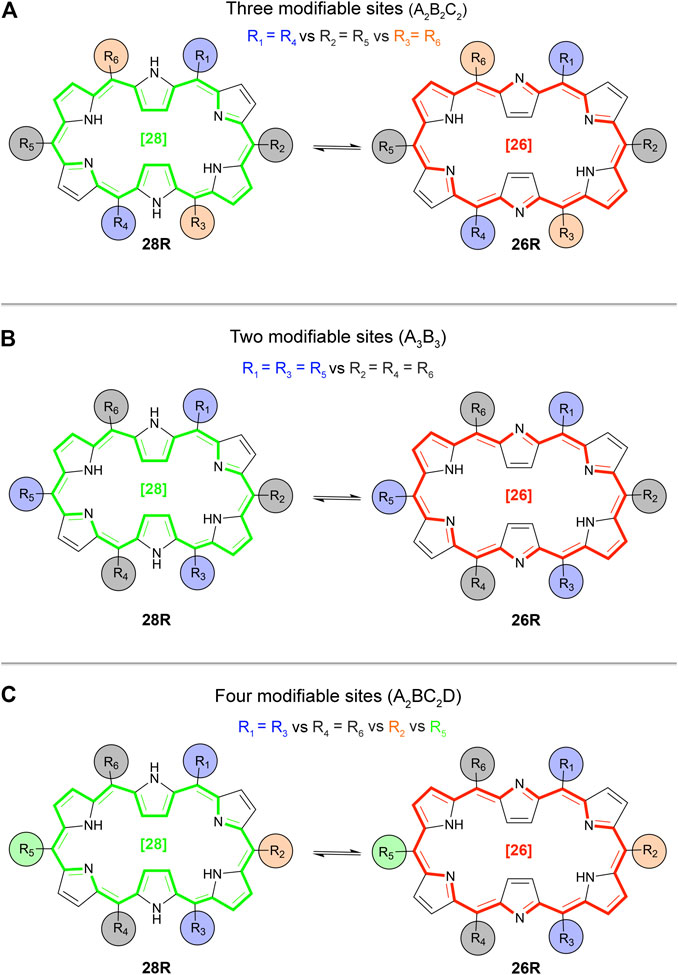
SCHEME 4. Overview of the studied substitution patterns: (A) A₂B₂C₂ type hexaphyrins, (B) A₃B₃ type hexaphyrins and (C) A₂BC₂D type hexaphyrins. Example given for the redox switch 28R → 26R.

4.3.2 Redox Switches

The meso-substituted redox switches with the highest β_HRS ratio and difference obtained through the BFS algorithm are summarized for all three substitution patterns in Figure 6. In short, the best performing macrocycles either involve only EDGs (NH₂ and OH) or a combination of 4 EDGs (NH₂ and OH) and 2 EWGs (NO₂ and CN), with the EWGs placed on sites R₂/R₅. In the following paragraphs, a more detailed analysis of the BFS results is provided.

FIGURE 6

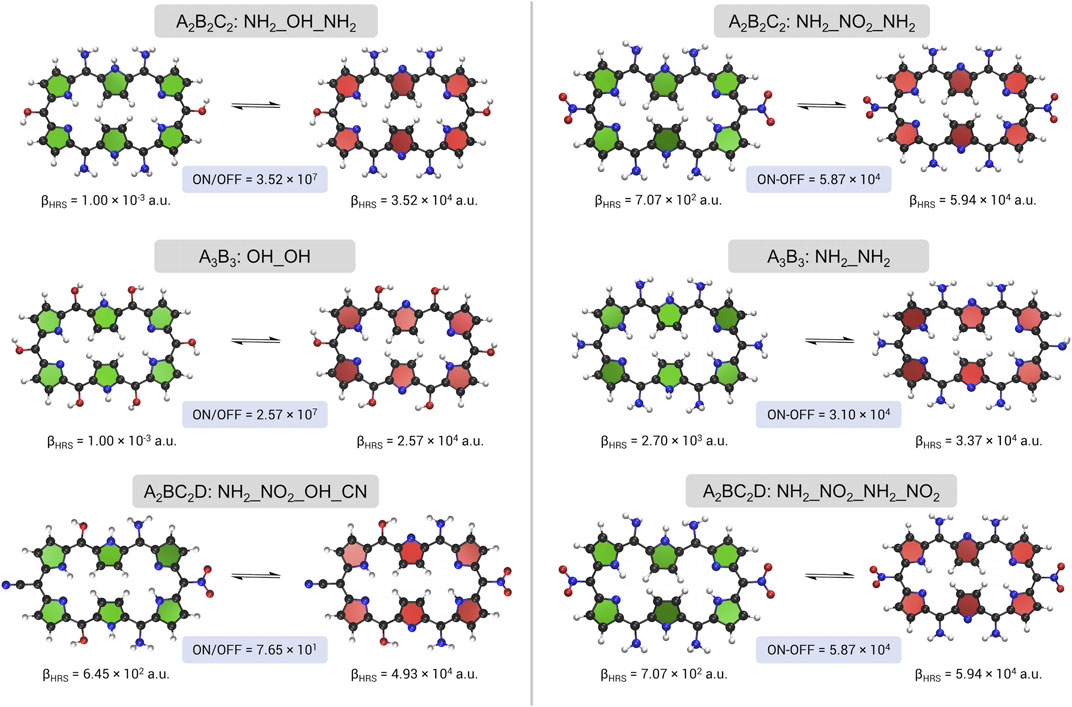
FIGURE 6. A schematic overview of the redox switches with the highest NLO contrast, β_HRS ratio on the left and β_HRS difference on the right, upon meso-substitution for the three substitution patterns.

The optimum molecular switches for the first substitution pattern A₂B₂C₂ contain 4 amino groups, located at sites R₁/R₄ and R₃/R₆, and have either an EDG (OH) or EWG (NO₂) positioned on R₂/R₅, with the former obtained for the ratio and the latter for the difference contrast maximization. Both switches are encountered during both BFS optimizations. The choice of one or the other is directly related to the contrast definitions. On the one hand, we have the ON state of the most optimal switch retrieved from the β_HRS difference maximization, which leads to a more enhanced NLO response in comparison to that of the β_HRS ratio optimization (β_HRS(26R(NH₂_NO₂_NH₂)) = 5.94 ×10⁴ a.u. versus β_HRS(26R(NH₂_OH_NH₂)) = 3.52 ×10⁴ a.u.), for which a push-pull configuration is responsible. On the other hand, there is the magnitude of the OFF state’s NLO response, which becomes more dominant when optimizing the ratio compared to the difference, especially when the OFF state has a near-zero β_HRS value due to centrosymmetry (β_HRS(28R(NH₂_OH_NH₂)) = $\sim 0$ a.u. versus β_HRS(28R(NH₂_NO₂_NH₂)) = 7.07 ×10² a.u.) inherently amplifying the ratio contrast. Surprisingly, the push-pull configuration (NH₂_CN_NH₂), conjectured based on our pairwise prestudy, was not selected as the optimum, despite having a centrosymmetric OFF state. The cyano groups on sites R₂/R₅ underperform, with a β_HRS value even lower than for the unsubstituted R₂ and R₅ positions . This low value can probably be traced back to the structural parameters for this macrocycle. The 26R(NH₂_OH_NH₂) conformation has a higher ring strain and lower planarity (ϕ_p: 13.60° and Π: 0.77) than the predicted 26R(NH₂_CN_NH₂) conformation (ϕ_p: 12.22° and Π: 0.80). Compared to our parent switch, the switching efficiency increases by a factor of 15–25 (depending on which contrast definition is used), with site combination R₁/R₄ being the most and R₂/R₅ the least influential meso-positions, in line with the findings of the pairwise disubstitution study.

Optimization of the second substitution pattern A₃B₃ results for both definitions in a very similar structure. All positions are substituted with the same EDG (OH for the contrast and NH₂ for the difference). Whereas for the ratio optimum a centrosymmetric OFF state is acquired, 28R(NH₂_NH₂) has C₂ symmetry with a β_HRS value of the order of 10³. These meso-substituted structures were already designated in our proof of concept as high-potential switches, although it was shown that the sixfold methyl-substituted hexaphyrin performs even better than the OH-substituted one. Nonetheless, the A₃B₃ pattern does not achieve the same efficiency as the A₂B₂C₂ pattern with a 27% lower ratio for OH_OH and a 47% lower difference for NH₂_NH₂ compared to the A₂B₂C₂ optima. The best performing push-pull switch in the A₃B₃ setting, according to the difference-based contrast, is 28R(F_NH₂) → 26R(F_NH₂), having a NLO contrast of approximately two third of the BFS optimum and 7 times larger than the currently synthesizable exp_a (β_HRS difference = 2.76 × 10³ a.u.).

Finally, the A₂BC₂D pattern optimizations using both contrast definitions are discussed. Two different optima are obtained, but both contain a combination of EWGs and EDGs. The best redox switch of the ratio optimization is 28R(NH₂_NO₂_OH_CN) → 26R(NH₂_NO₂_OH_CN) and contains 4 distinct functional groups. The switch combines a C₁-symmetric OFF state with a relatively low response of the order of 10² with a significantly enhanced response of the ON state. On the R₂ and R₅ sites two different EWGs (CN and NO₂) are positioned while for the other sites (R₁, R₃, R₄ and R₆) EDGs (OH and NH₂) are preferred. The BFS optimum for the difference maximization is macrocycle NH₂_NO₂_NH₂_NO₂, which is the same optimum as found for the A₂B₂C₂ pattern. The difference based contrast is more than 10 times larger than exp_b (5.17 × 10³). In fact, its 26R structure has the highest NLO response of all visited redox switches. Hence, combining strongly EDGs with strongly EWGs, with a preference for more EDGs, is a good recipe to magnify the switching efficiency of hexaphyrin-based redox switches, which is in agreement with the findings in our proof of concept. Nonetheless, the OFF state’s symmetry remains a key player for improving the contrast when the original contrast definition is employed.

4.3.3 Topological Switch

Figure 7 gives an overview of all optimal topological switches obtained from six BFS runs with the ratio or difference in β_HRS as the target function. Nearly all optima contain combinations of EWGs and EDGs with various electronic characters (inductive versus mesomeric). Again, the centrosymmmetry of the OFF state plays a major role in maximizing the NLO response ratio, but to a lesser extent than for the difference. On the other hand, much higher β_HRS responses are found for the 28M and 28R states of the difference optima, compared to the best ratio switches. In general, the NLO contrasts are lower in value than the redox switches. In the following paragraphs, the contrast maximizations are briefly discussed.

FIGURE 7

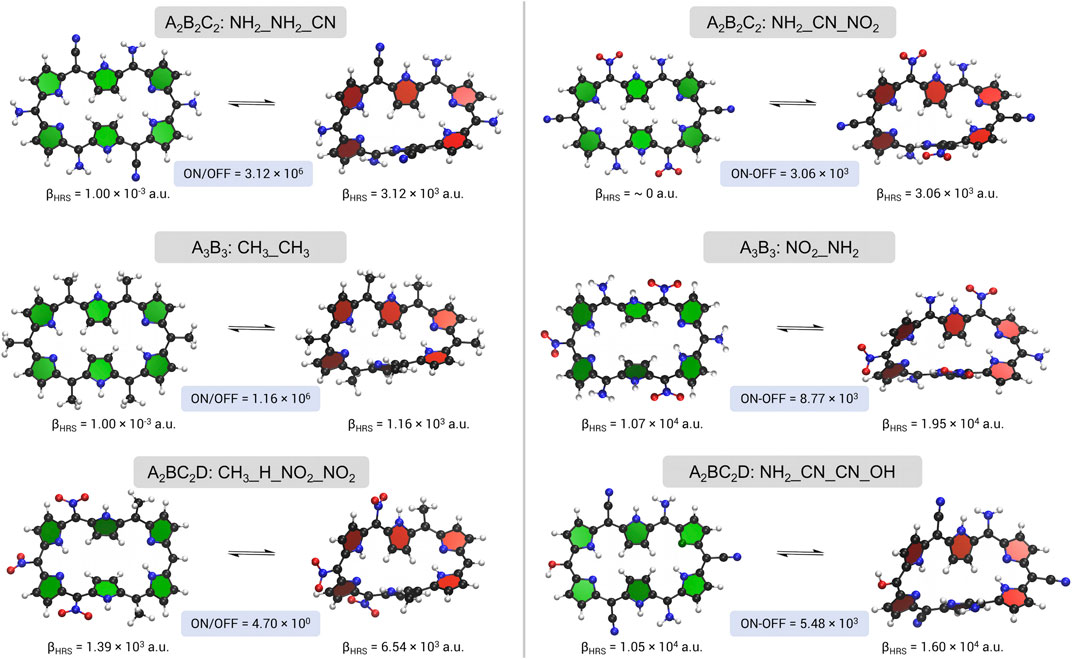
FIGURE 7. A schematic overview of the topological switches with the highest NLO contrast, β_HRS ratio on the left and β_HRS difference on the right, upon meso-substitution for the three substitution patterns.

The two figure of merit maximizations of the A₂B₂C₂ pattern result in relatively different optima. The topological switch for the ratio maximization contains 4 mesomerically EDGs (NH₂), on sites R₁/R₄ and R₂/R₅, and 2 EWGs (CN) positioned on R₃/R₆: 28R(NH₂_NH₂_CN) → 28M(NH₂_NH₂_CN). In contrast, the EWGs outnumber the EDGs in the difference optimum, with amino groups placed on R₁/R₄, cyano groups on R₂/R₅ and nitro groups on R₃/R₆. Note, however, that the ratio optimum is performing slightly better than the difference optimum, also when the difference-based contrast is considered (3.12 × 10³ versus 3.06 × 10³ a.u.). Once again, the OFF states are centrosymmetric structures with zero HRS responses, whereas the ON states have improved NLO responses, among the largest we have encountered so far for the 28R → 28M topological switch. Surprisingly, none of the functional groups emerge from our two-site prestudy as one of the best performing substituents on their respective positions in the ratio and difference optima, which is particularly the case for CN on sites R₂/R₅ or R₃/R₆. The synergetic effect between the different functionalizations may be attributed to the formation of a push-pull configuration. Overall, this substitution pattern leads to a twofold enhancement with respect to the parent switch and even more compared to the synthesized macrocycles exp_a and exp_b.

The contrast optimizations for the A₃B₃ pattern end up in two distinct structures. On the one hand, we obtain a switch fully functionalized with a relatively weak EDG (CH₃) and on the other hand, a combination of strong EWGs (NO₂) and strong EDGs (NH₂) is discovered. Even though the fully methyl substituted topological switch (28R(CH₃_CH₃) → 28M(CH₃_CH₃)) shows a fairly high β_HRS ratio, our proof of concept puts forward other fully substituted candidate switches (e.g., OH, F) with a higher contrast than this switch. What is more, no improvement over the parent topological switch is seen. During the BFS run, multiple 28M structures are generated for which a considerably more enhanced NLO response is registered, examples being CH₃_CN, CH₃_OH and NO₂_CH₃. However, none of these 28M structures can be associated with a low response of the 28R. Therefore, the same guiding features are encountered here: the ratio-based contrast optimizes, when possible, to a centrosymmetric OFF state and an enhanced ON state. Consequently, the optimization pathway can get stuck in such a topological switch, if it is the only one present having C_i symmetry. The difference-based contrast maximization is, however, a whole different story. The 28R(NO₂_NH₂) → 28M(NO₂_NH₂) maximum displays very different characteristics from the ratio-based optimum. The OFF state’s β_HRS now has the same order of magnitude as the ON state (1.07 × 10⁴ versus 1.95 × 10⁴ a.u.) but the switch still displays a difference of 8.77 × 10³ a.u., the highest difference-based contrast in this study. These augmented β_HRS responses are again due to a push-pull configuration. In contrast to the redox interconversion, where switches fully substituted with the same EDG, regardless of the presence of a centrosymmetric OFF state, displayed a significant difference-based contrast, a similar topological switch performs an order of magnitude worse due to a lower β_HRS response of the Möbius ON state. The 28R → 28M topological switch in substitution pattern A₃B₃ benefits more from push-pull functionalization than the 28R → 26R redox switch. Lastly, we observe that for some of the functionalized structures the 28R becomes the ON state for both the ratio and difference contrast optimization, generally because of reduced β_HRS values for the 28M conformation, examples being CH₃_H, CH₃_F, and H_CH₃ with difference-based contrast values up until 10³ a.u.

Similarly to the redox interconversion, the topological switches visited during the inverse design procedures using the last substitution pattern A₂BC₂D do not have a high NLO ratio contrast, mainly because none of the OFF states belong to the C_i point group. In contrast, some of the switches show a high NLO difference, even though the ON and OFF states are of the same order of magnitude, as we also noted for the A₃B₃ substitution pattern. Both switches present a push-pull design with substituents ranging in electronic character, from the mesomerically EWGs, NO₂ and CN, over the neutral H and rather weak inductive EDG, CH₃, to mesomerically EDGs, OH and NH₂. The ratio-optimized switch, 28R(CH₃_H_NO₂_NO₂) → 28M(CH₃_H_NO₂_NO₂), combines a strongly electron-withdrawing side with a moderately electron-donating side. The presence of EWGs on positions R₄/R₆ is vital to get a ratio above 1, as these functional groups give rise to the highest response for the 28M as well as the lowest response for the 28R. The same is observed for the nitro group on site R₅. Strangely, no functionalization is preferred over the hydrogen atom on position R₂. Placing a strongly EWG (significantly) augments the β_HRS of the ON state; compare, for example, the 1.43 × 10⁴ a.u. of 28M(CH₃_NO₂_NO₂_NO₂) with the 6.54 × 10³ a.u. of the optimum (28R(CH₃_NO₂_NO₂_NO₂) → 28M(CH₃_NO₂_NO₂_NO₂). Unfortunately, the OFF state’s NLO response increases as well, resulting in a ratio-based contrast that is about half of the contrast of the optimum. Finally, the methyl groups on R₁/R₃ seem to provide a good trade-off between a β_HRS that is low enough for 28R and enhanced enough for 28M. The optimal 28R(NH₂_CN_OH_CN) → 28M(NH₂_CN_OH_CN) switch for the difference optimization has a analogous type of motif as the A₃B₃ pattern optimum, in which 3 mesomerically EDGs are combined with 3 mesomerically EWGs. Despite the larger flexibility in the switch design of A₂BC₂D hexaphyrins, i.e., 4 (pairs of) sites are optimized versus 2 site combinations in A₃B₃, the A₃B₃ optimum performs 60% better. Nonetheless, during the NLO ratio optimization, another switch was found with a higher NLO difference than the best switch of our A₂BC₂D difference optimization: 28R(CH₃_NO₂_NO₂_NO₂) → 28M(CH₃_NO₂_NO₂_NO₂) with a difference of 8.35 × 10³ a.u. With respect to the fully NO₂ substituted structure from our proof of concept, this switch has a 7 times larger difference. Hence, changing two positions (here R₁ and R₃) within the substitution pattern can drastically change the NLO difference. An even more convincing illustration of the large impact of the peripheral functionalization is the interchange of ON and OFF state when the strongly EWGs are replaced by one of the other possible functionalizations on the R₄/R₆ positions in the final BFS iterations. Strikingly, by placing two hydroxyl groups on those sites, the topological switch 28M(CH₃_H_OH_NO₂) → 28R(CH₃_H_OH_NO₂) is, displaying a β_HRS difference of 7.92 × 10³ a.u., which is at the same level of our most improved 28R → 28M switches. These findings corroborate that the positioning, the type, and the number of functionalizations are all indisputably key players in the design of efficient NLO hexaphyrin switches.

5 Conclusion

In this work, we discovered efficient nonlinear optical (NLO) switches with high β_HRS contrasts by applying the Best-First Search (BFS) algorithm. These innovative switches are based on meso-substituted hexaphyrins with different oxidation states and π-conjugation topologies and contain various electron-donating and electron-withdrawing substituents. Initially, we unveiled the structure-property relationships involving their aromaticity and NLO properties. As a proof of concept, we investigated the substituent effect on the geometry and (nonlinear) optical properties of different meso-substituted hexaphyrins previously reported in the literature. With the help of an inverse molecular design algorithm, the NLO contrasts (for which two definitions were taken into account, namely the ratio and the differences of the β_HRS responses of the ON and OFF states) of the most promising redox and topological switches were maximized by chemically modifying the ON and OFF states.

Unsubstituted [26] and [28] hexaphyrins prefer planar conformations driven by the low ring strain and high π-conjugation. A close relationship is found between the number of π-electrons, the topology and aromaticity as revealed by magnetic, electronic and reactivity aromaticity descriptors. While 26D, 26R and 28M are aromatic macrocycles, 28R is highly antiaromatic. The aromaticity is also reflected in their molecular orbital diagrams. Symmetry is the dominating factor in tweaking the β_HRS response of the parent structures. Other, contributing factors are the planarity and the ring strain of the macrocycle. The highest NLO contrasts are associated to redox or topological switches consisting of an OFF state (28R) and ON state (26R and 28M) with low and high β_HRS values, respectively. Changes in topology, aromaticity and symmetry are responsible for the high NLO contrasts.

The effect of meso-substitution on the β_HRS response of hexaphyrins was explored in detail. A proof of concept was included in which fully substituted macrocycles and 4 additional substitution patterns were evaluated, carefully selected from currently synthesizable hexaphyrins and a previous computational study. In general, meso-substituents distort the planarity of the macrocycle. As a consequence, the ring strain increases leading to an enhanced β_HRS response. The degree of the distortion depends on the number of introduced functional groups as well as their electronic character. Nonlinear optical properties (β_HRS) can be enhanced by the introduction of different types of meso-substituents, especially by EDGs and push-pull combinations of substituents. A high difference in symmetry between the ON and OFF state of the switch significantly increases the NLO ratio. The results for the difference-based contrast are more subtle.

Multiple inverse molecular design procedures were performed, starting from three distinct substitution patterns, to design redox (28R → 26R) and topological (28R → 28M) switches with maximal NLO contrasts. Depending on the number, type and position of meso-substituents, ratio-based β_HRS contrasts up to 15 times larger for the redox switch and 2 times larger for the topological switch, compared to the unsubstituted versions, were discovered. For the difference-based contrast definition, the improvement is even more pronounced, reaching values 25 times larger for the redox switch and 6 times for the topological switch. Hence, the efficiency of the 28R → 26R redox switch can be enhanced upon meso-substitution to a much greater extent than for the 28R → 28M Hückel-Möbius switch. When the NLO response ratio is considered, both the optimal meso-substituted redox and topology switches show a preference for EDGs in combination with a centrosymmetric OFF state. Symmetry, more precisely the presence or absence of an inversion center, plays a pivotal role in tweaking the OFF state’s β_HRS as it can vary to a larger extent than the ON state’s response, from zero when in C_i symmetry to the order of 10³ a.u. Meso-substitution can induce profound changes in the symmetry resulting in a wide spectrum of different NLO responses. When centrosymmetry is far less likely due to the selected substitution pattern, e.g. A₂BC₂D, push-pull functionalizations take the upper hand. Nonetheless, the absence of low-response OFF states significantly reduces the ratio, despite higher ON state values. The difference-based contrast maximizations tend to almost always converge to push-pull configurations with OFF states showing a minimal NLO response. The main difference between the redox and topology switches is that EDGs generally outnumber EWGs for the former, while the reverse is true for the latter. On a final note, we would like to point out that replacing functional groups by substituents of the opposite nature can in some cases lead to a reversal of ON/OFF switching behaviour of the redox and especially topological switch, displaying more or less equivalent NLO contrasts.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

MA and FDV conceived the project. ED and TW conducted the numerical calculations for the proof of concept. JT implemented the in-house program CINDES for the BFS procedures and provided support for ED in case of technical issues of the program. ED, TW, MA and FDV analyzed the data and ED, FDV and MA wrote the paper.

Funding

FDV wishes to thank the VUB for the Strategic Research Program awarded to the ALGC research group. MA thanks the Fund for Scientific Research–Flanders (FWO-12F4416N) for a postdoctoral fellowship and the Vrije Universiteit Brussel (VUB) for financial support. ED thanks the Fund for Scientific Research–Flanders (FWO-11E0321N) for a predoctoral fellowship.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Computational resources and services were provided by the shared ICT Services Centre funded by the Vrije Universiteit Brussel, the Flemish Supercomputer Center (VSC) and FWO.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2021.786036/full#supplementary-material

Footnotes

¹Even though we did not carry out a full conformational analysis, multiple conformations were computed, retaining only the energetically most stable ones for the subsequent NLO calculations.

References

Ahn, T. K., Kwon, J. H., Kim, D. Y., Cho, D. W., Jeong, D. H., Kim, S. K., et al. (2005). Comparative Photophysics of [26] and [28]hexaphyrins(1.1.1.1.1.1): Large Two-Photon Absorption Cross Section of Aromatic [26]hexaphyrins(1.1.1.1.1.1). J. Am. Chem. Soc. 127, 12856–12861. doi:10.1021/ja050895l

PubMed Abstract | CrossRef Full Text | Google Scholar

Alonso, M., Geerlings, P., and De Proft, F. (2013a). Conformational Control in [22]- and [24]Pentaphyrins(1.1.1.1.1) by Meso Substituents and Their N-Fusion Reaction. J. Org. Chem. 78, 4419–4431. doi:10.1021/jo4003823

CrossRef Full Text | Google Scholar

Alonso, M., Geerlings, P., and . De Proft, F. (2014). Exploring the Structure-Aromaticity Relationship in Hückel and Möbius N-Fused Pentaphyrins Using DFT. Phys. Chem. Chem. Phys. 16, 14396–14407. doi:10.1039/C3CP55509G

PubMed Abstract | CrossRef Full Text | Google Scholar

Alonso, M., Geerlings, P., and De Proft, F. (2013b). Topology Switching in [32]Heptaphyrins Controlled by Solvent, Protonation, Andmeso Substituents. Chem. Eur. J. 19, 1617–1628. doi:10.1002/chem.201203295

CrossRef Full Text | Google Scholar

Alonso, M., Geerlings, P., and de Proft, F. (2012). Viability of Möbius Topologies in [26] and [28]Hexaphyrins. Chem. Eur. J. 18, 10916–10928. doi:10.1002/chem.201200511

PubMed Abstract | CrossRef Full Text | Google Scholar

Auwärter, W., Écija, D., Klappenberger, F., and Barth, J. V. (2015). Porphyrins at Interfaces. Nat. Chem 7, 105–120. doi:10.1038/nchem.2159

PubMed Abstract | CrossRef Full Text | Google Scholar

Balamurugan, D., Yang, W., and Beratan, D. N. (2008). Exploring Chemical Space with Discrete, Gradient, and Hybrid Optimization Methods. J. Chem. Phys. 129, 174105. doi:10.1063/1.2987711

CrossRef Full Text | Google Scholar

Cárdenas‐Jirón, G., Borges‐Martínez, M., Mera‐Adasme, R., and Pino‐Rios, R. (2019). Quantum Chemical Studies of Porphyrin‐ and Expanded Porphyrin‐based Systems and Their Potential Applications in nanoscience.Latin America Research Review. Int. J. Quan. Chem. 119, e25821. doi:10.1002/qua.25821

CrossRef Full Text | Google Scholar

Casademont-Reig, I., Ramos-Cordoba, E., Torrent-Sucarrat, M., and Matito, E. (2020). How Do the Hückel and Baird Rules Fade Away in Annulenes. Molecules 25, 711. doi:10.3390/molecules25030711

PubMed Abstract | CrossRef Full Text | Google Scholar

Casademont-Reig, I., Woller, T., Contreras-García, J., Alonso, M., Torrent-Sucarrat, M., and Matito, E. (2018). New Electron Delocalization Tools to Describe the Aromaticity in Porphyrinoids. Phys. Chem. Chem. Phys. 20, 2787–2796. doi:10.1039/C7CP07581B

PubMed Abstract | CrossRef Full Text | Google Scholar

Castet, F., Rodriguez, V., Pozzo, J.-L., Ducasse, L., Plaquet, A., and Champagne, B. (2013). Design and Characterization of Molecular Nonlinear Optical Switches. Acc. Chem. Res. 46, 2656–2665. doi:10.1021/ar4000955

PubMed Abstract | CrossRef Full Text | Google Scholar

Chandrashekar, T. K., and Venkatraman, S. (2003). Core-modified Expanded Porphyrins: New Generation Organic Materials. Acc. Chem. Res. 36, 676–691. doi:10.1021/ar020284n

PubMed Abstract | CrossRef Full Text | Google Scholar

Chatterjee, T., Shetti, V. S., Sharma, R., and Ravikanth, M. (2017). Heteroatom-containing Porphyrin Analogues. Chem. Rev. 117, 3254–3328. doi:10.1021/acs.chemrev.6b00496

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Z., Wannere, C. S., Corminboeuf, C., Puchta, R., and Schleyer, P. v. R. (2005). Nucleus-independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 105, 3842–3888. doi:10.1021/cr030088

PubMed Abstract | CrossRef Full Text | Google Scholar

Clays, K., and Persoons, A. (1991). Hyper-rayleigh Scattering in Solution. Phys. Rev. Lett. 66, 2980–2983. doi:10.1103/PhysRevLett.66.2980

PubMed Abstract | CrossRef Full Text | Google Scholar

Conradie, J., Foroutan-Nejad, C., and Ghosh, A. (2019). Norcorrole as a Delocalized, Antiaromatic System. Sci. Rep. 9, 4852. doi:10.1038/s41598-019-39972-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Dauben, H. J., Wilson, J. D., and Laity, J. L. (1968). Diamagnetic Susceptibility Exaltation as a Criterion of Aromaticity. J. Am. Chem. Soc. 90, 811–813. doi:10.1021/ja01005a059

CrossRef Full Text | Google Scholar

De Proft, F., and Geerlings, P. (2004). Relative Hardness as a Measure of Aromaticity. Phys. Chem. Chem. Phys. 6, 242–248. doi:10.1039/B312566C

CrossRef Full Text | Google Scholar

De Vleeschouwer, F., Chankisjijev, A., Geerlings, P., and De Proft, F. (2015). Designing Stable Radicals with Highly Electrophilic or Nucleophilic Character: Thiadiazinyl as a Case Study. Eur. J. Org. Chem. 2015, 506–513. doi:10.1002/ejoc.201403198

CrossRef Full Text | Google Scholar

De Vleeschouwer, F., Yang, W., Beratan, D. N. D., Geerlings, P., and De Proft, F. (2012). Inverse Design of Molecules with Optimal Reactivity Properties: Acidity of 2-naphthol Derivatives. Phys. Chem. Chem. Phys. 14, 16002–16013. doi:10.1039/C2CP42623D

PubMed Abstract | CrossRef Full Text | Google Scholar

de Wergifosse, M., and Champagne, B. (2011). Electron Correlation Effects on the First Hyperpolarizability of Push-Pull π-conjugated Systemsπ-Conjugated Systems. J. Chem. Phys. 134, 074113. doi:10.1063/1.3549814

CrossRef Full Text | Google Scholar

De Vleeschouwer, F., Geerlings, P., and De Proft, F. (2016). Molecular Property Optimizations with Boundary Conditions through the Best First Search Scheme. ChemPhysChem 17, 1391. doi:10.1002/cphc.201600402

CrossRef Full Text | Google Scholar

Dolphin, D. (2012). The Porphyrins V7: Biochemistry. Elsevier.

Google Scholar

Dunning, T. H. (1989). Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms boron through Neon and Hydrogen. J. Chem. Phys. 90, 1007–1023. doi:10.1063/1.456153

CrossRef Full Text | Google Scholar

Elward, J. M., and Rinderspacher, B. C. (2015). Smooth Heuristic Optimization on a Complex Chemical Subspace. Phys. Chem. Chem. Phys. 17, 24322–24335. doi:10.1039/C5CP02177D

PubMed Abstract | CrossRef Full Text | Google Scholar

Fallah-Bagher-Shaidaei, H., Wannere, C. S., Corminboeuf, C., Puchta, R., and Schleyer, P. v. R. (2006). Which NICS Aromaticity Index for Planar π Rings Is Best?π Rings Is Best. Org. Lett. 8, 863–866. doi:10.1021/ol0529546

PubMed Abstract | CrossRef Full Text | Google Scholar

Feringa, B. L., and Browne, W. R. (2011). Molecular Switches, 2 Volume Set. John Wiley & Sons.

Google Scholar

Feringa, B. L. (2017). The Art of Building Small: from Molecular Switches to Motors (Nobel Lecture). Angew. Chem. Int. Ed. 56, 11060–11078. doi:10.1002/anie.201702979

PubMed Abstract | CrossRef Full Text | Google Scholar

Fliegl, H., and Sundholm, D. (2012). Aromatic Pathways of Porphins, Chlorins, and Bacteriochlorins. J. Org. Chem. 77, 3408–3414. doi:10.1021/jo300182b

CrossRef Full Text | Google Scholar

Fliegl, H., Sundholm, D., and Pichierri, F. (2011). Aromatic Pathways in Mono- and Bisphosphorous Singly Möbius Twisted [28] and [30]hexaphyrins. Phys. Chem. Chem. Phys. 13, 20659–20665. doi:10.1039/C1CP21935A

PubMed Abstract | CrossRef Full Text | Google Scholar

Fliegl, H., Sundholm, D., Taubert, S., and Pichierri, F. (2010). Aromatic Pathways in Twisted Hexaphyrins. J. Phys. Chem. A. 114, 7153–7161. doi:10.1021/jp1021517

CrossRef Full Text | Google Scholar

Foroutan-Nejad, C., and Ghosh, A. (2018). Magnetic Diversity in Heteroisocorroles: Aromatic Pathways in 10-Heteroatom-Substituted Isocorroles. ACS Omega 3, 15865–15869. doi:10.1021/acsomega.8b02626

PubMed Abstract | CrossRef Full Text | Google Scholar

Foroutan-Nejad, C., Larsen, S., Conradie, J., and Ghosh, A. (2018). Isocorroles as Homoaromatic Nir-Absorbing Chromophores: A First Quantum Chemical Study. Sci. Rep. 8, 11952. doi:10.1038/s41598-018-29819-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Freeze, J. G., Kelly, H. R., and Batista, V. S. (2019). Search for Catalysts by Inverse Design: Artificial Intelligence, Mountain Climbers, and Alchemists. Chem. Rev. 119, 6595–6612. doi:10.1021/acs.chemrev.8b00759

PubMed Abstract | CrossRef Full Text | Google Scholar

[Dataset] Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian 16 Revision A.01. Gaussian Inc. Wallingford CT.

Google Scholar

Garza, A. J., Osman, O. I., Asiri, A. M., and Scuseria, G. E. (2015). Can gap Tuning Schemes of Long-Range Corrected Hybrid Functionals Improve the Description of Hyperpolarizabilities. J. Phys. Chem. B 119, 1202–1212. doi:10.1021/jp507226v

CrossRef Full Text | Google Scholar

Geuenich, D., Hess, K., Köhler, F., and Herges, R. (2005). Anisotropy of the Induced Current Density (ACID), a General Method to Quantify and Visualize Electronic Delocalization. Chem. Rev. 105, 3758–3772. doi:10.1021/cr0300901

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghosh, A., Larsen, S., Conradie, J., and Foroutan-Nejad, C. (2018). Local versus Global Aromaticity in Azuliporphyrin and Benziporphyrin Derivatives. Org. Biomol. Chem. 16, 7964–7970. doi:10.1039/C8OB01672K

PubMed Abstract | CrossRef Full Text | Google Scholar

Häse, F., Roch, L. M., Kreisbeck, C., and Aspuru-Guzik, A. (2018). Phoenics: a Bayesian Optimizer for Chemistry. ACS Cent. Sci. 4, 1134–1145. doi:10.1021/acscentsci.8b00307

PubMed Abstract | CrossRef Full Text | Google Scholar

Hehre, W. J., Radom, L., Schleyer, P. v. R., and Pople, J. A. (1986). Ab Initio Molecular Orbital Theory. Wiley.

Google Scholar

Hendrickx, E., Clays, K., and Persoons, A. (1998). Hyper-Rayleigh Scattering in Isotropic Solution. Acc. Chem. Res. 31, 675–683. doi:10.1021/ar960233o

CrossRef Full Text | Google Scholar

Herges, R., and Geuenich, D. (2001). Delocalization of Electrons in Molecules. J. Phys. Chem. A. 105, 3214–3220. doi:10.1021/jp0034426

CrossRef Full Text | Google Scholar

Ishida, M., Shin, J.-Y., Lim, J. M., Lee, B. S., Yoon, M.-C., Koide, T., et al. (2011). Neutral Radical and Singlet Biradical Forms of Meso-free, -keto, and -diketo hexaphyrins(1.1.1.1.1.1): Effects on Aromaticity and Photophysical Properties. J. Am. Chem. Soc. 133, 15533–15544. doi:10.1021/ja204626t

PubMed Abstract | CrossRef Full Text | Google Scholar

Kadish, K., Smith, K. M., and Guilard, R. (2000). The Porphyrin Handbook, vol, 1. Elsevier.

Google Scholar

Kariduraganavar, M. Y., Doddamani, R. V., Waddar, B., and Reddy Parne, S. (2021). Nonlinear Optical Responsive Molecular Switches, Nonlinear Optics - From Solitons to Similaritons, İlkay Bakirtas and Nalan Antar. IntechOpen. doi:10.5772/intechopen.92675

CrossRef Full Text | Google Scholar

Kawata, S., and Kawata, Y. (2000). Three-dimensional Optical Data Storage Using Photochromic Materials. Chem. Rev. 100, 1777–1788. doi:10.1021/cr980073p

PubMed Abstract | CrossRef Full Text | Google Scholar

[Dataset] Keith, T. A. (2017). Aimall. Overland Park KS, USA: TK Gristmill Software.

Google Scholar

Keith, T. A., and Bader, R. F. W. (1993). Calculation of Magnetic Response Properties Using a Continuous Set of Gauge Transformations. Chem. Phys. Lett. 210, 223–231. doi:10.1016/0009-2614(93)89127-4

CrossRef Full Text | Google Scholar

Kim, K. S., Yoon, Z. S., Ricks, A. B., Shin, J.-Y., Mori, S., Sankar, J., et al. (2009). Temperature-Dependent Conformational Change of Meso-Hexakis(pentafluorophenyl) [28]Hexaphyrins(1.1.1.1.1.1) into Möbius Structures. J. Phys. Chem. A. 113, 4498–4506. doi:10.1021/jp8111205

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, R., Misra, R., Chandrashekar, T. K., Nag, A., Goswami, D., Suresh, E., et al. (2007). One-pot Synthesis of Core-Modified Rubyrin, Octaphyrin, and Dodecaphyrin: Characterization and Nonlinear Optical Properties. Eur. J. Org. Chem. 2007, 4552–4562. doi:10.1002/ejoc.200700466

CrossRef Full Text | Google Scholar

Ladenthin, J. N., Frederiksen, T., Persson, M., Sharp, J. C., Gawinkowski, S., Waluk, J., et al. (2016). Force-induced Tautomerization in a Single Molecule. Nat. Chem 8, 935–940. doi:10.1038/nchem.2552

PubMed Abstract | CrossRef Full Text | Google Scholar

Lazzeretti, P. (2004). Assessment of Aromaticity via Molecular Response Properties. Phys. Chem. Chem. Phys. 6, 217–223. doi:10.1039/B311178D

CrossRef Full Text | Google Scholar

Lescos, L., Sitkiewicz, S. P., Beaujean, P., Blanchard-Desce, M., Champagne, B., Matito, E., et al. (2020). Performance of DFT Functionals for Calculating the Second-Order Nonlinear Optical Properties of Dipolar Merocyanines. Phys. Chem. Chem. Phys. 22, 16579–16594. doi:10.1039/D0CP02992K

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcos, E., Anglada, J. M., and Torrent-Sucarrat, M. (2014). Effect of the Meso-Substituent in the Hückel-To-Möbius Topological Switches. J. Org. Chem. 79, 5036–5046. doi:10.1021/jo500569p

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcos, E., Anglada, J. M., and Torrent-Sucarrat, M. (2012). Theoretical Study of the Switching between Hückel and Möbius Topologies for Expanded Porphyrins. J. Phys. Chem. C 116, 24358–24366. doi:10.1021/jp3083612

CrossRef Full Text | Google Scholar

[Dataset] Matito, E. (2006). ESI-3D: Electron Sharing Indexes Program for 3D Molecular Space Partitioning. Girona: Institut de Química Computacional i Catàlisi (IQCC), Universitat de Girona.

Google Scholar

Matito, E. (2016). An Electronic Aromaticity index for Large Rings. Phys. Chem. Chem. Phys. 18, 11839–11846. doi:10.1039/C6CP00636A

PubMed Abstract | CrossRef Full Text | Google Scholar

Molesky, S., Lin, Z., Piggott, A. Y., Jin, W., Vucković, J., and Rodriguez, A. W. (2018). Inverse Design in Nanophotonics. Nat. Photon 12, 659–670. doi:10.1038/s41566-018-0246-9

CrossRef Full Text | Google Scholar

Mori, H., Tanaka, T., and Osuka, A. (2013). Fused Porphyrinoids as Promising Near-Infrared Absorbing Dyes. J. Mater. Chem. C 1, 2500–2519. doi:10.1039/C3TC00932G

CrossRef Full Text | Google Scholar

Pawlicki, M., Collins, H. A., Denning, R. G., and Anderson, H. L. (2009). Two-photon Absorption and the Design of Two-Photon Dyes. Angew. Chem. Int. Ed. 48, 3244–3266. doi:10.1002/anie.200805257

CrossRef Full Text | Google Scholar

Pearl, J. (1984). Heuristics: Intelligent Search Strategies for Computer Problem Solving. Boston, MA, USA: Addison-Wesley Longman Publishing Co., Inc.

Google Scholar

Pino-Rios, R., and Cárdenas-Jirón, G. (2019). Effect of the Meso/beta Halogenation in the Photoelectronic Properties and Aromaticity of Expanded Porphyrins. J. Photochem. Photobiol. A: Chem. 385, 112052. doi:10.1016/j.jphotochem.2019.112052

CrossRef Full Text | Google Scholar

Plamont, R., Balaban, T. S., and Canard, G. (2017). Straightforward Syntheses that Avoid Scrambling of Meso -Substituted [28]Hexaphyrins. Eur. J. Org. Chem. 2017, 593–599. doi:10.1002/ejoc.201601342

CrossRef Full Text | Google Scholar

Plaquet, A., Guillaume, M., Champagne, B., Castet, F., Ducasse, L., Pozzo, J.-L., et al. (2008). In Silico optimization of Merocyanine-Spiropyran Compounds as Second-Order Nonlinear Optical Molecular Switches. Phys. Chem. Chem. Phys. 10, 6223–6232. doi:10.1039/B806561F

PubMed Abstract | CrossRef Full Text | Google Scholar

Rath, H., Sankar, J., PrabhuRaja, V., Chandrashekar, T. K., Nag, A., and Goswami, D. (2005). Core-modified Expanded Porphyrins with Large Third-Order Nonlinear Optical Response. J. Am. Chem. Soc. 127, 11608–11609. doi:10.1021/ja0537575

CrossRef Full Text | Google Scholar

Saito, S., and Osuka, A. (2011). Expanded Porphyrins: Intriguing Structures, Electronic Properties, and Reactivities. Angew. Chem. Int. Ed. 50, 4342–4373. doi:10.1002/anie.201003909

CrossRef Full Text | Google Scholar

Sankar, J., Mori, S., Saito, S., Rath, H., Suzuki, M., Inokuma, Y., et al. (2008). Unambiguous Identification of Möbius Aromaticity for Meso-Aryl-Substituted [28]Hexaphyrins(1.1.1.1.1.1). J. Am. Chem. Soc. 130, 13568–13579. doi:10.1021/ja801983d

CrossRef Full Text | Google Scholar

Schleyer, P. v. R., and Pühlhofer, F. (2002). Recommendations for the Evaluation of Aromatic Stabilization Energies. Org. Lett. 4, 2873–2876. doi:10.1021/ol0261332

PubMed Abstract | CrossRef Full Text | Google Scholar

Sessler, J. L., and Seidel, D. (2003). Synthetic Expanded Porphyrin Chemistry. Angew. Chem. Int. Ed. 42, 5134–5175. doi:10.1002/anie.200200561

CrossRef Full Text | Google Scholar

Shimomura, K., Kai, H., Nakamura, Y., Hong, Y., Mori, S., Miki, K., et al. (2020). Bis-metal Complexes of Doubly N-Confused Dioxohexaphyrins as Potential Near-Infrared-II Photoacoustic Dyes. J. Am. Chem. Soc. 142, 4429–4437. doi:10.1021/jacs.9b13475

PubMed Abstract | CrossRef Full Text | Google Scholar

Solà, M. (2017). Why Aromaticity Is a Suspicious Concept? Why. Front. Chem. 5, 22. doi:10.3389/fchem.2017.00022

PubMed Abstract | CrossRef Full Text | Google Scholar

Stępień, M., Sprutta, N., and Latos-Grażyński, L. (2011). Figure Eights, Möbius Bands, and More: Conformation and Aromaticity of Porphyrinoids. Angew. Chem. Int. Ed. 50, 4288–4340. doi:10.1002/anie.201003353

CrossRef Full Text | Google Scholar

Strasser, S., Goodman, R., Sheppard, J., and Butcher, S. (2016). “A New Discrete Particle Swarm Optimization Algorithm,” in Proceedings of the Genetic and Evolutionary Computation Conference 2016; GECCO ’16, Denver, Colorado, USA, 20–24 July, 2016 (New York: ACM), 53–60. doi:10.1145/2908961

CrossRef Full Text | Google Scholar

Stuyver, T., Perrin, M., Geerlings, P., De Proft, F., and Alonso, M. (2018). Conductance Switching in Expanded Porphyrins through Aromaticity and Topology Changes. J. Am. Chem. Soc. 140, 1313–1326. doi:10.1021/jacs.7b09464

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, L., Vercruysse, D., Skarda, J., Sapra, N. V., Petykiewicz, J. A., and Vučković, J. (2020). Nanophotonic Inverse Design with SPINS: Software Architecture and Practical Considerations. Appl. Phys. Rev. 7, 011407. doi:10.1063/1.5131263

CrossRef Full Text | Google Scholar

Su, T. A., Neupane, M., Steigerwald, M. L., Venkataraman, L., and Nuckolls, C. (2016). Chemical Principles of Single-Molecule Electronics. Nat. Rev. Mater. 1, 1–15. doi:10.1038/natrevmats.2016.2

CrossRef Full Text | Google Scholar

Sun, G., Lei, E., Liu, X.-S., Yu, C.-H., Duan, X.-X., and Liu, C.-G. (2016). Theoretical Investigation of Structure Diversity and Electronic Properties in the Series Isomeric [26]hexaphyrin (1.1.1.1.1.1) and [28]hexaphyrin (1.1.1.1.1.1). Comput. Theor. Chem. 1087, 18–25. doi:10.1016/j.comptc.2016.04.020

CrossRef Full Text | Google Scholar

Sun, L., Diaz-Fernandez, Y. A., Gschneidtner, T. A., Westerlund, F., Lara-Avila, S., and Moth-Poulsen, K. (2014). Single-molecule Electronics: from Chemical Design to Functional Devices. Chem. Soc. Rev. 43, 7378–7411. doi:10.1039/C4CS00143E

PubMed Abstract | CrossRef Full Text | Google Scholar

Sung, Y. M., Oh, J., Cha, W.-Y., Kim, W., Lim, J. M., Yoon, M.-C., et al. (2017). Control and Switching of Aromaticity in Various All-Aza-Expanded Porphyrins: Spectroscopic and Theoretical Analyses. Chem. Rev. 117, 2257–2312. doi:10.1021/acs.chemrev.6b00313

PubMed Abstract | CrossRef Full Text | Google Scholar

Suslick, K. S., Chen, C. T., Meredith, G. R., and Cheng, L. T. (1992). Push-pull Porphyrins as Nonlinear Optical Materials. J. Am. Chem. Soc. 114, 6928–6930. doi:10.1021/ja00043a055

CrossRef Full Text | Google Scholar

Suzuki, M., and Osuka, A. (2003). Improved Synthesis of Meso-Aryl-Substituted [26]hexaphyrins. Org. Lett. 5, 3943–3946. doi:10.1021/ol035650x

PubMed Abstract | CrossRef Full Text | Google Scholar

Sylvetsky, N., Banerjee, A., Alonso, M., and Martin, J. M. L. (2020). Performance of Localized Coupled Cluster Methods in a Moderately Strong Correlation Regime: Hückel-Möbius Interconversions in Expanded Porphyrins. J. Chem. Theor. Comput. 16, 3641–3653. doi:10.1021/acs.jctc.0c00297

PubMed Abstract | CrossRef Full Text | Google Scholar

Szczepanik, D. W., Solà, M., Andrzejak, M., Pawełek, B., Dominikowska, J., Kukułka, M., et al. (2017). The Role of the Long-Range Exchange Corrections in the Description of Electron Delocalization in Aromatic Species. J. Comput. Chem. 38, 1640–1654. doi:10.1002/jcc.24805

CrossRef Full Text | Google Scholar

Tanaka, T., and Osuka, A. (2016). Chemistry of Meso-Aryl-Substituted Expanded Porphyrins: Aromaticity and Molecular Twist. Chem. Rev. 117, 2584–2640. doi:10.1021/acs.chemrev.6b00371

PubMed Abstract | CrossRef Full Text | Google Scholar

[Dataset] Teunissen, J. L. (2016). CINDES. Available at: https://gitlab.com/jlteunissen/CINDES (Accessed on June 14, 2021).

Google Scholar

Teunissen, J. L. (2019). “Inverse Molecular Design: Optimization and Application of Combinatorial and Stochastic Approaches,” (Brussel: Vrije Universteit). Ph.D. thesis.

Google Scholar

Teunissen, J. L., De Proft, F., and De Vleeschouwer, F. (2017). Tuning the HOMO-LUMO Energy gap of Small Diamondoids Using Inverse Molecular Design. J. Chem. Theor. Comput. 13, 1351–1365. doi:10.1021/acs.jctc.6b01074

PubMed Abstract | CrossRef Full Text | Google Scholar

Tonnelé, C., Champagne, B., Muccioli, L., and Castet, F. (2018). Second-order Nonlinear Optical Properties of Stenhouse Photoswitches: Insights from Density Functional Theory. Phys. Chem. Chem. Phys. 20, 27658–27667. doi:10.1039/C8CP05843A

PubMed Abstract | CrossRef Full Text | Google Scholar

Torrent-Sucarrat, M., Anglada, J. M., and Luis, J. M. (2012). Evaluation of the Nonlinear Optical Properties for an Expanded Porphyrin Hückel-Möbius Aromaticity Switch. J. Chem. Phys. 137, 184306. doi:10.1063/1.4765667

CrossRef Full Text | Google Scholar

Torrent-Sucarrat, M., Anglada, J. M., and Luis, J. M. (2011). Evaluation of the Nonlinear Optical Properties for Annulenes with Hückel and Möbius Topologies. J. Chem. Theor. Comput. 7, 3935–3943. doi:10.1021/ct2005424

PubMed Abstract | CrossRef Full Text | Google Scholar

Torrent-Sucarrat, M., Navarro, S., Cossío, F. P., Anglada, J. M., and Luis, J. M. (2017a). Relevance of the DFT Method to Study Expanded Porphyrins with Different Topologies. J. Comput. Chem. 38, 2819–2828. doi:10.1002/jcc.25074

CrossRef Full Text | Google Scholar

Torrent-Sucarrat, M., Navarro, S., Marcos, E., Anglada, J. M., and Luis, J. M. (2017b). Design of Hückel-Möbius Topological Switches with High Nonlinear Optical Properties. J. Phys. Chem. C 121, 19348–19357. doi:10.1021/acs.jpcc.7b05900

CrossRef Full Text | Google Scholar

Valiev, R. R., Benkyi, I., Konyshev, Y. V., Fliegl, H., and Sundholm, D. (2018). Computational Studies of Aromatic and Photophysical Properties of Expanded Porphyrins. J. Phys. Chem. A. 122, 4756–4767. doi:10.1021/acs.jpca.8b02311

PubMed Abstract | CrossRef Full Text | Google Scholar

Valiev, R. R., Fliegl, H., and Sundholm, D. (2017). Closed-shell Paramagnetic Porphyrinoids. Chem. Commun. 53, 9866–9869. doi:10.1039/C7CC05232D

CrossRef Full Text | Google Scholar

Valiev, R. R., Fliegl, H., and Sundholm, D. (2013). Insights into Magnetically Induced Current Pathways and Optical Properties of Isophlorins. J. Phys. Chem. A. 117, 9062–9068. doi:10.1021/jp404828n

CrossRef Full Text | Google Scholar

Verbiest, T., Clays, K., and Rodriguez, V. (2009). Second-order Nonlinear Optical Characterization Techniques: An Introduction. Boca Raton: CRC Press.

Google Scholar

Wang, M., Hu, X., Beratan, D. N., and Yang, W. (2006). Designing Molecules by Optimizing Potentials. J. Am. Chem. Soc. 128, 3228–3232. doi:10.1021/ja0572046

CrossRef Full Text | Google Scholar

Wang, Y., Kai, H., Ishida, M., Gokulnath, S., Mori, S., Murayama, T., et al. (2020). Synthesis of a Black Dye with Absorption Capabilities across the Visible-To-Near-Infrared Region: a MO-mixing Approach via Heterometal Coordination of Expanded Porphyrinoid. J. Am. Chem. Soc. 142, 6807–6813. doi:10.1021/jacs.0c01824

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolinski, K., Hinton, J. F., and Pulay, P. (1990). Efficient Implementation of the Gauge-independent Atomic Orbital Method for NMR Chemical Shift Calculations. J. Am. Chem. Soc. 112, 8251–8260. doi:10.1021/ja00179a005

CrossRef Full Text | Google Scholar

Woller, T., Banerjee, A., Sylvetsky, N., Santra, G., Deraet, X., De Proft, F., et al. (2020). Performance of Electronic Structure Methods for the Description of Hückel-Möbius Interconversions in Extended π-Systems. J. Phys. Chem. A. 124, 2380–2397. doi:10.1021/acs.jpca.9b10880

PubMed Abstract | CrossRef Full Text | Google Scholar

Woller, T., Contreras-García, J., Geerlings, P., De Proft, F., and Alonso, M. (2016). Understanding the Molecular Switching Properties of Octaphyrins. Phys. Chem. Chem. Phys. 18, 11885–11900. doi:10.1039/C5CP07413D

PubMed Abstract | CrossRef Full Text | Google Scholar

Woller, T., Geerlings, P., De Proft, F., Champagne, B., and Alonso, M. (2018). Aromaticity as a Guiding Concept for Spectroscopic Features and Nonlinear Optical Properties of Porphyrinoids. Molecules 23, 1333. doi:10.3390/molecules23061333

PubMed Abstract | CrossRef Full Text | Google Scholar

Woller, T., Geerlings, P., De Proft, F., Champagne, B., and Alonso, M. (2019). Fingerprint of Aromaticity and Molecular Topology on the Photophysical Properties of Octaphyrins. J. Phys. Chem. C 123, 7318–7335. doi:10.1021/acs.jpcc.8b10908

CrossRef Full Text | Google Scholar

Wu, J. I., Fernández, I., and Schleyer, P. v. R. (2013). Description of Aromaticity in Porphyrinoids. J. Am. Chem. Soc. 135, 315–321. doi:10.1021/ja309434t

CrossRef Full Text | Google Scholar

Xiang, D., Wang, X., Jia, C., Lee, T., and Guo, X. (2016). Molecular-scale Electronics: from Concept to Function. Chem. Rev. 116, 4318–4440. doi:10.1021/acs.chemrev.5b00680

PubMed Abstract | CrossRef Full Text | Google Scholar

Yanai, T., Tew, D. P., and Handy, N. C. (2004). A New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3lyp). Chem. Phys. Lett. 393, 51–57. doi:10.1016/j.cplett.2004.06.011

CrossRef Full Text | Google Scholar

Yoon, Z. S., Cho, D.-G., Kim, K. S., Sessler, J. L., and Kim, D. (2008). Nonlinear Optical Properties as a Guide to Aromaticity in Congeneric Pentapyrrolic Expanded Porphyrins: Pentaphyrin, Sapphyrin, Isosmaragdyrin, and Orangarin. J. Am. Chem. Soc. 130, 6930–6931. doi:10.1021/ja801395y

CrossRef Full Text | Google Scholar

Zhang, J. L., Zhong, J. Q., Lin, J. D., Hu, W. P., Wu, K., Xu, G. Q., et al. (2015). Towards Single Molecule Switches. Chem. Soc. Rev. 44, 2998–3022. doi:10.1039/C4CS00377B

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y., and Truhlar, D. G. (2008). The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Account. 120, 215–241. doi:10.1007/s00214-007-0310-x

CrossRef Full Text | Google Scholar