The Interplay of Interstitial and Substitutional Copper in Zinc Oxide

Cu impurities are reported to have significant effects on the electrical and optical properties of bulk ZnO. In this work, we study the defect properties of Cu in ZnO using hybrid quantum mechanical/molecular mechanical (QM/MM)–embedded cluster calculations based on a multi-region approach that allows us to model defects at the true dilute limit, with polarization effects described in an accurate and consistent manner. We compute the electronic structure, energetics, and geometries of Cu impurities, including substitutional and interstitial configurations, and analyze their effects on the electronic structure. Under ambient conditions, Cu_Zn is the dominant defect in the d⁹ state and remains electronically passive. We find that, however, as we approach typical vacuum conditions, the interstitial Cu defect becomes significant and can act as an electron trap.

Introduction

ZnO, with a wide bandgap of 3.44 eV (Reynolds et al., 1999), is one of the most widely studied transparent semiconductors, with applications in solar cells (Keis et al., 2002), light-emitting diodes (Tsukazaki et al., 2005a; Tsukazaki et al., 2005b), photocatalysts (Barick et al., 2010), and piezoelectric devices (Wang and Song, 2006). To optimize its performance in applications, it is important to understand and control the properties of impurities in ZnO. The Cu/ZnO system is a very important industrial methanol catalyst (Waugh, 1992; Baltes et al., 2008). Substitution of copper into ZnO (Cu_Zn^q) (here and elsewhere in this article, we denote the effective charge of the defect, q, with respect to the lattice site explicitly with the superscript) has been reported to improve the photocatalytic activity (Mohan et al., 2012), ferromagnetism (Xing et al., 2008), and gas sensitivity (Gong et al., 2006) of ZnO. By admittance spectroscopy experiments, Cu_Zn^q is found to possess an (0/−) acceptor level at 0.17 eV below the bottom of the conduction band (CBM) in ZnO (McCluskey et al., 2015). Doping with copper has been proposed as a route for producing stable p-type ZnO (Özgür et al., 2005), which, however, has not been successful to date and which partly inspired our current investigation. Moreover, although there are many investigations both experimental and computational on the effects of CuZn on the electrical and optical properties of ZnO, information about Cu interstitials (Cu_i^q) in ZnO is limited.

In this article, we report the properties of Cu in both substitutional and interstitial forms in ZnO using a hybrid quantum mechanical/molecular mechanical (QM/MM)–embedded cluster approach. For the description of point defects in crystals, the commonly used implementation of density functional theory (DFT) with periodic boundary conditions suffers from finite-size effects (Freysoldt et al., 2014). In contrast, the QM/MM method defines the vacuum reference level unambiguously and describes accurately the short- and long-range polarization effects of a charged defect in a host material. The approach allows us to compare the energetics of different defect configurations and charge states on an equal footing. We focus here on isolated defects, but copper impurities may also form complexes in a variety of ways, an investigation into which is underway and will be reported elsewhere.

Computational Techniques

In this work, the QM region containing 86 atoms is treated with DFT using a triple zeta plus polarization Gaussian basis set for oxygens (Def2-TZVPP) (Weigend and Ahlrichs, 2005) and a double zeta plus polarization set for Zn cations (cc-pVDZ-PP) (Peterson, 2003; Figgen et al., 2005) (relevant input files can be found in the git repository “https://github.com/qhou1/chemshell.git”). To reduce the computational load, we have removed f functions from the oxygen basis set and some of the highly diffuse functions from the cation basis sets, which do not contribute to the bonding in these ionic solids.

For electron exchange and correlation, we have employed the BB1k functional (Zhao et al., 2004), which has been fitted to both thermochemical and kinetic data including 42% exact exchange, and the PBE0 functional (Adamo and Barone, 1999), which is frequently used in plane-wave basis calculations including 25% exact exchange for comparison. In order to embed the QM cluster within a polar environment, the MM region containing 10,460 atoms is treated with a previously derived interatomic potential (Catlow et al., 2008).

The hybrid QM/MM-embedded cluster approach used is implemented in the ChemShell (Sherwood et al., 2003) package. The QM/MM energy is obtained in an additive approach as a sum of QM and MM terms with the interaction energy between the two regions accounted for the QM term whose Hamiltonian includes the embedding potential. The GAMESS-UK (Guest et al., 2005) code is employed in the QM calculations, while the GULP package has been used to calculate the MM contributions.

The formation energies of the Cu substitution with charge q are calculated according to the following reactions:

$C{u}_{\left(s\right)}+Z{n}_{\mathbf{Zn}}^0\to C{u}_{\mathbf{Zn}}^{\mathit{q}-}+Z{n}_{\left(s\right)}+\mathit{q}{h}^{+},(1)$

under Zn-rich/O-poor condition and

$\mathbf{Cu}{O}_{\left(s\right)}+Z{n}_{\mathbf{Zn}}^0\to C{u}_{\mathbf{Zn}}^{\mathit{q}-}+\mathbf{Zn}{O}_{\left(s\right)}+\mathit{q}{h}^{+},(2)$

under Zn-poor/O-rich condition.

The formation energies of the Cu interstitial are calculated according to the following reaction:

$\mathbf{C}{\mathbf{u}}_{\left(\mathbf{s}\right)}\to \mathbf{C}{\mathbf{u}}_{\mathbf{i}}^{\mathit{q}+}+\mathit{q}{\mathbf{e}}^{-},(3)$

under Zn-rich/O-poor condition and

$\mathbf{Cu}{O}_{\left(s\right)}\to C{u}_i^{\mathit{q}+}+\frac{1}{2}{O}_{2\left(\mathbf{g}\right)}+\mathit{q}{e}^{-},(4)$

Under Zn-poor/O-rich condition.

The chemical potentials of O₂ molecular and single Zn atoms are calculated using GAMESS-UK with the corresponding basis set and density functional; the standard state energy of ZnO is derived from the experimental heat of formation (Haynes, 2014).

Results and Discussion

We first present the local geometries as well as the defect formation of the Cu interstitial Cu_i^q and Cu substitutional Cu_Zn^q; we next calculate the self-consistent Fermi energies and charge carrier and defect concentrations of Cu-doped ZnO. Finally, we report on the equilibrium between Cu_Zn^q and Cu_i^q.

Positions of Cu

As noted, Cu impurities have been widely studied due to their possible influence on the optical properties of ZnO. Moreover, by using the emission channeling technique, 60–70% of the Cu atoms are found to occupy the substitutional Zn site with root-mean-square displacements from the site of 0.16–0.17 Å (Wahl et al., 2004).

In our calculation, for the singly negatively charged state of Cu_Zn⁻, the four nearest O neighbors of Cu are displaced outward by 0.11–0.14 Å (using the BB1k functional) as shown in Figure 1A. After an electron is removed from this negatively charged system, the neutrally charged state Cu_Zn is formed. As shown by the spin density in Figure 1B, the resulting d⁹ Cu impurity drives a Jahn–Teller distortion, with the axial neighbor O relaxing inward by 0.06 Å and the other three non-axial O ions relaxing outward by 0.03 Å. In the +1 charge state, four neighbor O ions all relax inward by 0.04–0.07 Å around the d¹⁰ Cu ion (Figure 1C).

FIGURE 1

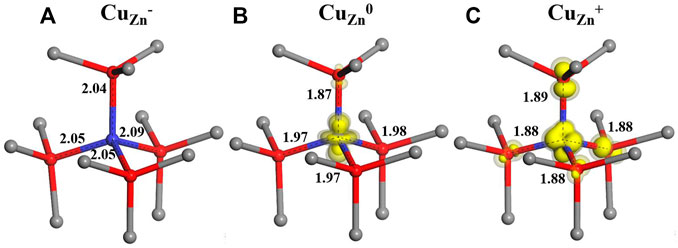
FIGURE 1. Calculated local structures for three charge states ( (A)-1, (B)0 and (C) +1) of the Cu_Zn defect in ZnO, with zinc ions represented by grey spheres, oxygen ions by red spheres and copper ions by blue spheres.

The Cu impurities could also be present as interstitials in ZnO, in two possible positions: octahedral and tetrahedral sites. As discussed in previous studies by Janotti and Van de Walle (Janotti and Van de Walle, 2007) and Sokol et al. (Sokol et al., 2007), the Zn interstitial is expected to be more stable at the octahedral site than at the tetrahedral site. Hence, here, we only consider the interstitial at the octahedral site.

The calculated configurations are illustrated in Figure 2B. The Cu⁺ interstitial has a lower coordination by electron-rich O^2- ions and forms a trigonal pyramid with the closest Cu_i–O separation distance of 1.98 Å and the two other distances of 2.01 and 2.05 Å (BB1k structures are shown in Figure 2A). On ionization, this nearly symmetric configuration is broken, with the Cu²⁺ ion moving toward one of the lattice oxygens (1.97, 1.98, and 2.11 Å). The next nearest O ions move now toward the interstitial Cu (by 0.16, 0.50, and 0.38 Å) but do not approach close enough to coordinate to this ion directly by a dative bond.

FIGURE 2

FIGURE 2. Local structures of Cu_i in +1 (A) and 2+(B) charge states.

Formation Energies

The calculated formation energies of both Cu_Zn and Cu_i are plotted in Figure 3. The (0/−) transition level of Cu_Zn^q is found to lie at 3.54 eV (PBE0) above the valence band maximum (VBM), which is in agreement with previous calculations by Lany and Zunger (Lany and Zunger, 2009), who reported 3.46 eV using generalized gradient approximation (GGA)+U with an additional hole-state correction for the Cu d state, and close to the calculations by Lyons et al. (Lyons et al., 2017), who reported 3.27 eV using the Heyd–Scuseria–Ernzerhof (HSE) hybrid functional. Our results contrast with Yan et al. (Yan et al., 2006), who reported 0.7 eV using local density approximation (LDA), and Gallino and Valentin (Gallino and Di Valentin, 2011), who reported 2.48 eV using B3LYP. The computed ε(0/−) using BB1k is, however, 4.40 eV. The (+/0) transition level of Cu_Zn^q is found to lie at 1.14 eV (BB1k) and 1.07 eV (PBE0) above the VBM, which yields a deep donor level, which is shallower than that of Lany and Zunger (Lany and Zunger, 2009), who reported 0.37 eV, and Lyons et al. (Lyons et al., 2017), who reported 0.46 eV.

FIGURE 3

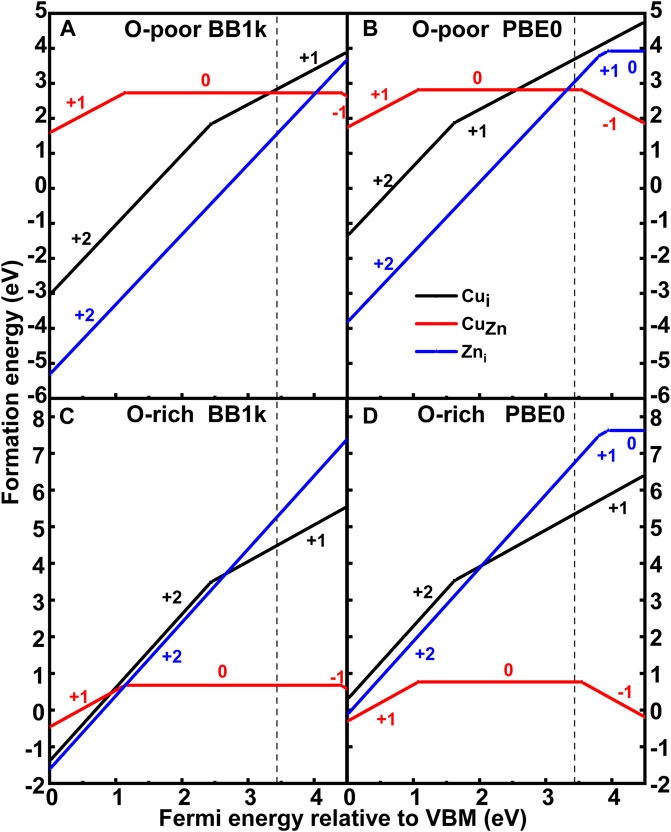
FIGURE 3. Formation energy of Cu_Zn and Cu_i in ZnO as a function of the Fermi level relative to the valence band maximum (VBM) under O-poor ((A) BB1k and (B) PBE0) and O-rich ((C) BB1k and (D) PBE0) conditions.

In O-poor conditions, we observe that the Cu_i^q is more stable than Cu_Zn^q using BB1k until the Fermi level is very close to the CB from the calculated formation energies. In O-rich conditions, when the Fermi level is near the VBM, the interstitial Cu is still more stable than substitutional Cu. While for PBE0 results, the substitutional Cu becomes more stable than the interstitial Cu for the Fermi level greater than 2.56 eV under the Zn-rich condition. Under O-rich conditions, the substitutional Cu is the most stable defect type in the d⁹ state as a donor.

Charge Carrier and Defect Concentrations

From the computed formation energies, the self-consistent Fermi energy and equilibrium defect and carrier concentrations can be determined. Here, we use the code “SC-FERMI” (Buckeridge, 2019). We focus on the results obtained using the BB1k functional, which reproduces the localization of holes on the oxygen sublattice more accurately than that on other functionals we have tested.

The concentration of each defect $X$ in each charge state $q$ is given by:

${\mathit{C}}_{{\mathit{X}}^{\mathit{q}}}={\mathit{N}}_{\mathit{X}}{\mathit{g}}_{{\mathit{X}}^{\mathit{q}}}\mathit{exp}\left(-\frac{{\mathit{E}}_{\mathit{f}}\left({\mathit{X}}^{\mathit{q}}\right)}{\mathit{kT}}\right),(7)$

where N_X is the density of sites in which the defect may form, g_X^q is the degeneracy of the charge state, E_F is the self-consistent Fermi energy, and k is the Boltzmann constant.

The electron (n₀) and hole (p₀) carrier concentrations can be determined by integrating the density of states weighed by the appropriate Fermi–Dirac function:

${\mathit{n}}_0=\underset{{\mathit{E}}_{\mathit{g}}}{\overset{\infty }{{\displaystyle \int }}}{\mathit{f}}_{\mathit{e}}\left(\mathit{E}\right)\mathit{\rho }\left(\mathit{E}\right)\mathit{dE;}(8)$

${\mathit{p}}_0=\underset{-\mathbf{\infty }}{\overset{0}{{\displaystyle \int }}}{\mathit{f}}_{\mathit{h}}\left(\mathit{E}\right)\mathit{\rho }\left(\mathit{E}\right)\mathit{dE,}(9)$

where $f_{\text{e}}\left(E\right)$ = [exp ((E_F-E)/kT) +1]⁻¹ is the Fermi–Dirac distribution function and $f_{\text{h}}\left(E\right)$ = 1- $f_{\text{e}}\left(E\right)$.

The computed self-consistent E_F and equilibrium carrier and equilibrium concentrations of Cu impurities with native defects in ZnO as a function of T are shown in Figure 4. The range of temperatures is 0–1500 K, which encompasses common synthesis temperatures of ZnO and a majority of device operational temperatures.

FIGURE 4

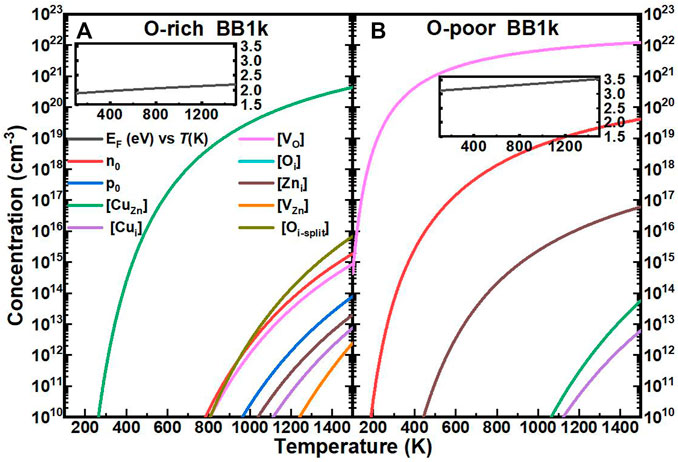
FIGURE 4. Calculated self-consistent Fermi energy (E_F, relative to the CBM, black line) and equilibrium concentrations of electrons (n₀, red line), holes (p₀, blue line), Cu substitutionals ([Cu_Zn], green line), Cu interstitials ([Cu_i], purple line), oxygen vacancies ([V_O], magenta line), oxygen interstitials ([O_i], cyan line), zinc interstitials ([Zn_i], brown line), zinc vacancies ([V_Zn], orange line), and oxygen split interstitials ([O_i], dark yellow line)in ZnO as a function of temperature, determined using the BB1k hybrid density functional, under O-rich (A) and O-poor (B) conditions.

In O-rich conditions, the E_F remains deep in the bandgap, between 1.9 and 2.2 eV above the VBM as T is increased, as shown in the inset of Figure 4A. The carrier concentrations remain below 10¹⁶ cm⁻³ for T ≤ 1500 K, with the Cu interstitial concentration [Cu_i] three-order of magnitude below. The [Cu_Zn] in the neutrally charged state is the dominant defect in this range of E_F, with the concentration above 10¹⁸ cm⁻³ for T > 600 K, which is close to the experimental result of ∼10¹⁸ cm⁻³ at room temperature (Kanai, 1991).

In O-poor conditions, due to the lower formation energies, E_F moves closer to the CB and even above the CBM as shown in the inset of Figure 4B. From our analysis, ZnO is found to be n-type with electron concentrations n₀ of 10¹⁶ cm⁻³ for T > 453 K (Hou, 2021) (details of the properties of native defects in ZnO will be published in the future).

We next investigated the equilibrium defect concentrations of Cu impurities in ZnO with fixed E_F as a function of T (Figures 5, 6). We mainly considered four conditions of E_F at: (A) 0.1 eV above the VBM, (B) 0.1 eV below the CBM, (C) 0.1 eV above the CBM, and (D) 1 eV above the CBM. We note here that the concentrations are not available when the formation energies of the defects are negative based on Eq. 7. In O-rich conditions, the [Cu_Zn] in the neutrally charged state is the dominant defect for all four conditions. In O-poor conditions, when the E_F is near to the CBM, the [Cu_i⁺] is close to [Cu_Zn⁰], but both are in relatively low concentrations.

FIGURE 5

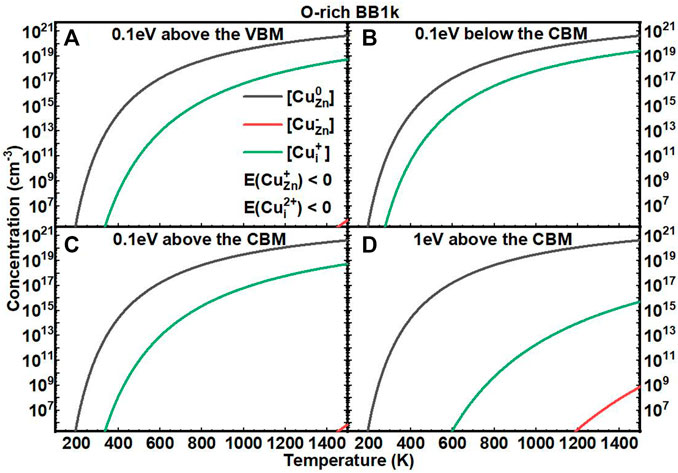
FIGURE 5. Calculated equilibrium concentrations of Cu substitutional in the 0 charge state ([Cu_Zn⁰], black line), Cu substitutional in the −1 charge state ([Cu_Zn⁻], red line), Cu substitutional in the +1 charge state ([Cu_Zn⁺], blue line), Cu interstitial in the +1 charge state ([Cu_Zn⁺], green line), and Cu interstitial in the +2 charge state ([Cu_Zn²⁺], purple line) in ZnO as a function of temperature at a fixed fermi level ((A) 0.1eV above the VBM, (B) 0.1eV below the CBM, (C) 0.1eV above the CBM, (D) 1eV above the CBM), determined using the BB1k hybrid density functional, under O-rich conditions.

FIGURE 6

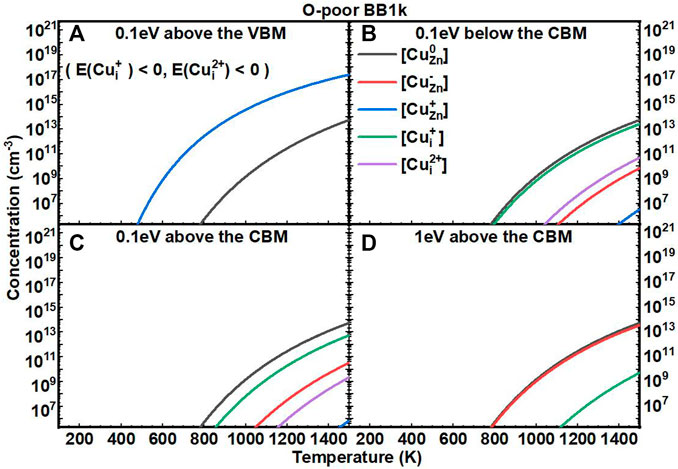
FIGURE 6. Calculated equilibrium concentrations of Cu substitutional in the 0 charge state ([Cu_Zn⁰], black line), Cu substitutional in the −1 charge state ([Cu_Zn⁻], red line), Cu substitutional in the +1 charge state ([Cu_Zn⁺], blue line), Cu interstitial in the +1 charge state ([Cu_Zn⁺], green line), and Cu interstitial in the +2 charge state ([Cu_Zn²⁺], purple line) in ZnO as a function of temperature at a fixed fermi level ((A) 0.1eV above the VBM, (B) 0.1eV below the CBM, (C) 0.1eV above the CBM, (D) 1eV above the CBM), determined using the BB1k hybrid density functional, under O-poor conditions.

O Partial Pressure Variation

To compare our results to the experiment, it is important to relate the theoretically defined O-rich and O-poor condition to the oxygen chemical potential under different temperature and partial pressure conditions. The chemical potential of oxygen gas at varying oxygen partial pressures at a given temperature is expressed by:

${\mathit{\mu }}_{\mathrm{O}}\left(\mathit{T},\mathit{p}\right)={\mathit{\mu }}_{\mathrm{O}}\left(\mathit{T},{\mathit{p}}^0\right)+\frac{1}{2}\mathit{kT}\mathit{ln}\frac{\mathit{p}}{{\mathit{p}}^0}.(10)$

By setting the zero state of ${\mu }_{\text{O}}\left(T,p\right)$ to be the total energy of oxygen at T = 0 K, which is ${\mathit{\mu }}_O\left(0,p^0\right)=1/2{\mathit{E}}_{O_2}^{\mathrm{total}}=0$, the temperature dependence of the oxygen chemical potential at a constant oxygen pressure p⁰ is defined as:

${\mathit{\mu }}_{\mathbf{O}}\left(\mathit{T},{\mathit{p}}^0\right)=\frac{1}{2}\left[\mathit{H}\left(\mathit{T},{\mathit{p}}^0,{\mathbf{O}}_2\right)-\mathit{H}\left(0,{\mathit{p}}^0,{\mathbf{O}}_2\right)\right]-\frac{1}{2}\mathit{T}\left[\mathit{S}\left(\mathit{T},{\mathit{p}}^0,{\mathbf{O}}_2\right)-\mathit{S}\left(0,{\mathit{p}}^0,O_2\right)\right] ,(11)$

where H is the enthalpy, and S is the entropy. Based on the data from thermochemical tables (Stull and Prophet, 1971), ${\mu }_{\text{O}}\left(T,p^0\right)$ at $p^0=1 \text{atm}$ was calculated by Taylor et al. (Taylor et al., 2016) and Reuter and Scheffler (Reuter and Scheffler, 2001) (${\mu }_O\left(300,p^0\right)=-0.27\mathrm{eV}$; ${\mu }_{\text{O}}\left(1000,p^0\right)=-1.01\text{ eV}$).

Our procedure then follows the method by Reuter and Scheffler (Reuter and Scheffler, 2001). The formation energies of Cu impurities in ZnO as a function of the O partial pressure from 10^–22 to 1 atm at 300 and 1000 K are shown in Figure 7. At 300 K, the Cu_Zn in the neutrally charged state remains as the dominant defect for O partial pressures from 10^–22 to 1 atm, which is consistent with the defect concentration results. At high temperatures of 1000 K, the Cu_i⁺ becomes the dominant defect under very low O partial pressures, with the crossover from Cu_Zn⁰ to Cu_i⁺ at 6.5*10^–9 atm.

FIGURE 7

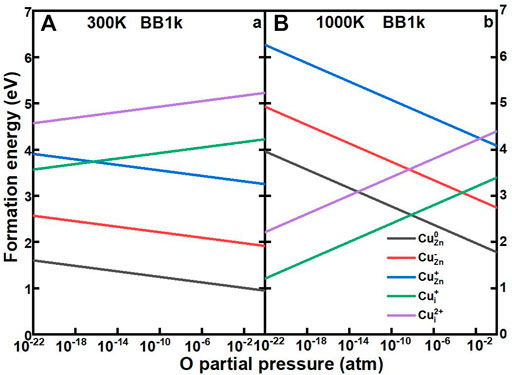
FIGURE 7. Calculated formation energies of Cu_Zn⁰ (black line), Cu_Zn⁻ (red line), Cu_Zn⁺ (blue line), Cu_Zn⁺ (green line), and Cu_Zn²⁺ (purple line) in ZnO as a function of oxygen partial pressures, determined using the BB1k hybrid density functional, under 300K (A) and 1000 K (B)>.

Balance Between Cu Substitutional and Interstitial

Bulk ZnO contains significant concentrations of intrinsic defects, to which are attributed the intrinsic n-type conductivity in ZnO (Harrison, 1954; Thomas, 1957; Hagemark, 1976). In the presence of the Cu dopants, there can be interchange of electrons or holes between Cu substitutional with extrinsic defects and Cu interstitial with intrinsic defect Zn vacancy or interstitial, for e.g.,

$C{u}_{\mathbf{Zn}}^0+V_i^0\to C{u}_i^{\mathit{q}+}+V_{\mathbf{Zn}}^{\mathit{p}-}+\left(\mathit{q}-\mathit{p}\right)e^{-};(12)$

$C{u}_{\mathbf{Zn}}^0+Z{n}_i^{\mathit{r}+}\to C{u}_i^{\mathit{q}+}+Z{n}_{\mathbf{Zn}}^0+\left(\mathit{r}-\mathit{q}\right)h^{+}.(13)$

The corresponding processes and their reaction energies ΔE_f (in eV) are listed in Table 1, with the electron in the CB and the hole in the VB. In general, Cu_Zn⁰ remains energetically preferable. Cu will not migrate directly from the substitutional to the interstitial site under ambient conditions, owing to the high reaction energy at 6.21 and 6.15 eV. However, under O-poor/Zn-rich conditions, in the presence of the native defect Zn interstitial, Cu will spontaneously migrate to the interstitial site with a reaction energy of −0.45 eV; the Cu_i can trap electrons from CB.

TABLE 1

TABLE 1. Reaction energies (eV) for Cu_Zn and Cu_i with intrinsic defect V_Zn or Zn_i.

Summary and Conclusion

We have investigated the copper dopants in both substitutional and interstitial forms in ZnO from embedded cluster calculations. By computing defect formation energies, we find that the Cu substitutional in the neutrally charged state is the dominant defect under O-rich conditions, which acts as a deep donor, while under Zn-rich conditions Cu interstitial becomes more stable than the Cu substitutional, which is consistent with the results of the equilibrium carrier and effect concentrations as a function of temperature. The Cu will not migrate directly from the substitutional to the interstitial site under ambient conditions, but under Zn-rich conditions Cu will spontaneously migrate to the interstitial site and trap electrons in the presence of Zn interstitial.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

All authors contributed to the components of the science and techniques used in the work and to the development and revision of the manuscript.

Funding

QH thanks the China Scholarship Council-UCL Joint Research Scholarship.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors acknowledge the use of the YOUNG, ARCHER, and ARCHER2 UK National Supercomputing Service (http://www.archer2.ac.uk) via membership of UK’s HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/R029431 and EP/T022213).

References

Adamo, C., and Barone, V. (1999). Toward Reliable Density Functional Methods Without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 110 (13), 6158–6170. doi:10.1063/1.478522

CrossRef Full Text | Google Scholar

Baltes, C., Vukojevic, S., and Schuth, F. (2008). Correlations Between Synthesis, Precursor, and Catalyst Structure and Activity of a Large Set of CuO/ZnO/Al2O3 Catalysts for Methanol Synthesis. J. Catal. 258 (2), 334–344. doi:10.1016/j.jcat.2008.07.004

CrossRef Full Text | Google Scholar

Barick, K., Singh, S., Aslam, M., Bahadur, D. J. M., and Materials, M. (2010). Porosity and Photocatalytic Studies of Transition Metal Doped ZnO Nanoclusters. 134(1-3), 195–202. doi:10.1016/j.micromeso.2010.05.026

CrossRef Full Text | Google Scholar

Buckeridge, J. (2019). Equilibrium point Defect and Charge Carrier Concentrations in a Material Determined Through Calculation of the Self-Consistent Fermi Energy. Comp. Phys. Commun. 244, 329–342. doi:10.1016/j.cpc.2019.06.017

CrossRef Full Text | Google Scholar

Catlow, C. R. A., French, S. A., Sokol, A. A., Al-Sunaidi, A. A., and Woodley, S. M. (2008). Zinc Oxide: A Case Study in Contemporary Computational Solid State Chemistry. J. Comput. Chem. 29 (13), 2234–2249. doi:10.1002/jcc.21051

CrossRef Full Text | Google Scholar

Figgen, D., Rauhut, G., Dolg, M., and Stoll, H. (2005). Energy-consistent Pseudopotentials for Group 11 and 12 Atoms: Adjustment to Multi-Configuration Dirac-Hartree-Fock Data. Chem. Phys. 311 (1-2), 227–244. doi:10.1016/j.chemphys.2004.10.005

CrossRef Full Text | Google Scholar

Freysoldt, C., Grabowski, B., Hickel, T., Neugebauer, J., Kresse, G., Janotti, A., et al. (2014). First-principles Calculations for Point Defects in Solids. Rev. Mod. Phys. 86 (1), 253–305. doi:10.1103/revmodphys.86.253

CrossRef Full Text | Google Scholar

Gallino, F., and Di Valentin, C. (2011). Copper Impurities in Bulk ZnO: A Hybrid Density Functional Study. J. Chem. Phys. 134 (14), 144506. doi:10.1063/1.3575198

CrossRef Full Text | Google Scholar

Gong, H., Hu, J. Q., Wang, J. H., Ong, C. H., Zhu, F. R., and Chemical, A. B. (2006). Nano-crystalline Cu-Doped ZnO Thin Film Gas Sensor for CO. Sensors Actuators B: Chem. 115 (1), 247–251. doi:10.1016/j.snb.2005.09.008

CrossRef Full Text | Google Scholar

Guest*, M. F., Bush, I. J., Van Dam, H. J., Sherwood, P., Thomas, J. M., Van Lenthe, J. H., et al. (2005). The GAMESS-UK Electronic Structure Package: Algorithms, Developments and Applications. Mol. Phys. 103 (6-8), 719–747. doi:10.1080/00268970512331340592

CrossRef Full Text | Google Scholar

Hagemark, K. (1976). Defect Structure of Zn-Doped ZnO. J. Solid State. Chem. 16 (3-4), 293–299. doi:10.1016/0022-4596(76)90044-x

CrossRef Full Text | Google Scholar

Harrison, S. E. (1954). Conductivity and Hall Effect of ZnO at Low Temperatures. Phys. Rev. 93 (1), 52–62. doi:10.1103/physrev.93.52

CrossRef Full Text | Google Scholar

Haynes, W. M. (2014). CRC Handbook of Chemistry and Physics. Boca Raton, FL: CRC Press.

Google Scholar

Hou, Q. (2021). Theory of Defects in N-type Transparent Conducting Oxides. London: UCL (University College London).

Google Scholar

Janotti, A., and Van de Walle, C. G. (2007). Native Point Defects in ZnO. Phys. Rev. B 76 (16), 165202. doi:10.1103/physrevb.76.165202

CrossRef Full Text | Google Scholar

Kanai, Y. (1991). Admittance Spectroscopy of Cu-Doped ZnO Crystals. Jpn. J. Appl. Phys. 30 (4R), 703. doi:10.1143/jjap.30.703

CrossRef Full Text | Google Scholar

Keis, K., Magnusson, E., Lindström, H., Lindquist, S.-E., and Hagfeldt, A. (2002). A 5% Efficient Photoelectrochemical Solar Cell Based on Nanostructured ZnO Electrodes. Solar Energ. Mater. solar Cell 73 (1), 51–58. doi:10.1016/s0927-0248(01)00110-6

CrossRef Full Text | Google Scholar

Lany, S., and Zunger, A. J. P. R. B. (2009). Polaronic Hole Localization and Multiple Hole Binding of Acceptors in Oxide Wide-gap Semiconductors. 80(8), 085202. doi:10.1103/physrevb.80.085202

CrossRef Full Text | Google Scholar

Lyons, J. L., Alkauskas, A., Janotti, A., and Van de Walle, C. G. (2017). Deep Donor State of the Copper Acceptor as a Source of green Luminescence in ZnO. Appl. Phys. Lett. 111 (4), 042101. doi:10.1063/1.4995404

CrossRef Full Text | Google Scholar

McCluskey, M. D., Corolewski, C. D., Lv, J., Tarun, M. C., Teklemichael, S. T., Walter, E. D., et al. (2015). Acceptors in ZnO. J. Appl. Phys. 117 (11), 112802. doi:10.1063/1.4913827

CrossRef Full Text | Google Scholar

Mohan, R., Krishnamoorthy, K., and Kim, S.-J. (2012). Enhanced Photocatalytic Activity of Cu-Doped ZnO Nanorods. Solid State. Commun. 152 (5), 375–380. doi:10.1016/j.ssc.2011.12.008

CrossRef Full Text | Google Scholar

Özgür, Ü., Alivov, Y. I., Liu, C., Teke, A., Reshchikov, M., Doğan, S., et al. (2005). A Comprehensive Review of ZnO Materials and Devices. J. Appl. Phys. 98 (4), 11. doi:10.1063/1.1992666

CrossRef Full Text | Google Scholar

Peterson, K. A. (2003). Systematically Convergent Basis Sets with Relativistic Pseudopotentials. I. Correlation Consistent Basis Sets for the Post-d Group 13-15 Elements. J. Chem. Phys. 119 (21), 11099–11112. doi:10.1063/1.1622923

CrossRef Full Text | Google Scholar

Reuter, K., and Scheffler, M. (2001). Composition, Structure, and Stability of RuO₂ (110) as a Function of Oxygen Pressure. Phys. Rev. B 65 (3), 035406. doi:10.1103/physrevb.65.035406

CrossRef Full Text | Google Scholar

Reynolds, D. C., Look, D. C., Jogai, B., Litton, C. W., Cantwell, G., and Harsch, W. C. (1999). Valence-band Ordering in ZnO. Phys. Rev. B 60 (4), 2340–2344. doi:10.1103/physrevb.60.2340

CrossRef Full Text | Google Scholar

Sherwood, P., de Vries, A. H., Guest, M. F., Schreckenbach, G., Catlow, C. R. A., French, S. A., et al. (2003). QUASI: A General Purpose Implementation of the QM/MM Approach and its Application to Problems in Catalysis. J. Mol. Struct. THEOCHEM 632 (1-3), 1–28. doi:10.1016/s0166-1280(03)00285-9

CrossRef Full Text | Google Scholar

Sokol, A. A., French, S. A., Bromley, S. T., Catlow, C. R. A., van Dam, H. J. J., and Sherwood, P. (2007). Point Defects in ZnO. Faraday Discuss. 134, 267–282. doi:10.1039/b607406e

PubMed Abstract | CrossRef Full Text | Google Scholar

Stull, D., and Prophet, H. (1971). JANAF Thermochemical Tables. 2nd Edn., 37. Washington, DC: US National Bureau of Standards.

Google Scholar

Taylor, F. H., Buckeridge, J., and Catlow, C. R. A. (2016). Defects and Oxide Ion Migration in the Solid Oxide Fuel Cell Cathode Material LaFeO3. Chem. Mater. 28 (22), 8210–8220. doi:10.1021/acs.chemmater.6b03048

CrossRef Full Text | Google Scholar

Thomas, D. (1957). Interstitial Zinc in Zinc Oxide. J. Phys. Chem. Sol. 3 (3-4), 229–237. doi:10.1016/0022-3697(57)90027-6

CrossRef Full Text | Google Scholar

Tsukazaki, A., Kubota, M., Ohtomo, A., Onuma, T., Ohtani, K., Ohno, H., et al. (2005a). Blue Light-Emitting Diode Based on ZnO. Jpn. J. Appl. Phys. 44 (5L), L643. doi:10.1143/jjap.44.l643

CrossRef Full Text | Google Scholar

Tsukazaki, A., Ohtomo, A., Onuma, T., Ohtani, M., Makino, T., Sumiya, M., et al. (2005b). Repeated Temperature Modulation Epitaxy for P-type Doping and Light-Emitting Diode Based on ZnO. Nat. Mater. 4 (1), 42–46. doi:10.1038/nmat1284

CrossRef Full Text | Google Scholar

Wahl, U., Rita, E., Correia, J., Alves, E., and Soares, J., (2004). Lattice Location and Stability of Implanted Cu in ZnO. 69 (1), 012102. doi:10.1103/physrevb.69.012102

CrossRef Full Text | Google Scholar

Wang, Z. L., and Song, J. (2006). Piezoelectric Nanogenerators Based on Zinc Oxide Nanowire Arrays. Science 312 (5771), 242–246. doi:10.1126/science.1124005

PubMed Abstract | CrossRef Full Text | Google Scholar

Waugh, K. C. (1992). Methanol Synthesis. Catal. Today 15 (1), 51–75. doi:10.1016/0920-5861(92)80122-4

CrossRef Full Text | Google Scholar

Weigend, F., and Ahlrichs, R. (2005). Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 7 (18), 3297–3305. doi:10.1039/b508541a

PubMed Abstract | CrossRef Full Text | Google Scholar

Xing, G. Z., Yi, J. B., Tao, J. G., Liu, T., Wong, L. M., Zhang, Z., et al. (2008). Comparative Study of Room-Temperature Ferromagnetism in Cu-Doped ZnO Nanowires Enhanced by Structural Inhomogeneity. Adv. Mater. 20 (18), 3521–3527. doi:10.1002/adma.200703149

CrossRef Full Text | Google Scholar

Yan, Y., Al-Jassim, M. M., and Wei, S.-H. (2006). Doping of ZnO by Group-IB Elements. Appl. Phys. Lett. 89 (18), 181912. doi:10.1063/1.2378404

CrossRef Full Text | Google Scholar

Zhao, Y., Lynch, B. J., and Truhlar, D. G. (2004). Development and Assessment of a New Hybrid Density Functional Model for Thermochemical Kinetics. J. Phys. Chem. A. 108 (14), 2715–2719. doi:10.1021/jp049908s

CrossRef Full Text | Google Scholar