Unraveling the Effect of Aromatic Groups in Mn(I)NNN Pincer Complexes on Carbon Dioxide Activation Using Density Functional Study

Carbon dioxide utilization is necessary to reduce carbon footprint and also to synthesize value-added chemicals. The transition metal pincer complexes are attractive catalysts for the hydrogenation of carbon dioxide to formic acid. There is a need to understand the factors affecting the catalytic performance of these pincer complexes through a structure–activity relationship study using computational methods. It is a well-established fact that aromatic functionalities offer stability and selectivity to transition metal catalysts. However, their impact on the performance of the catalysts is lesser known in the case of metal pincer complexes. Hence, it is necessary to investigate the catalytic performance of Mn(I)NNN pincer complexes with variably activated aromatic functionalities. In this context, 15 catalysts are designed by placing different types of aromatic rings at the pincer carbons and two terminal nitrogen of Mn(I)NNN pincer complexes. A benzene moiety, placed at C2–C3 carbons of Mn(I)NNN pincer complex with identical aromatic groups at the terminal nitrogen, is found to be most efficient toward CO₂ hydrogenation than the rest of the catalysts. On the other hand, when N,N-dimethyl aniline is placed at C2–C3 carbons of Mn(I)NNN pincer complexes, then the catalytic performance is significantly decreased. Thus, the present study unravels the impact of aromatic groups in Mn(I)NNN pincer complexes toward the catalytic hydrogenation of carbon dioxide.

Introduction

The burning of fossil fuels continuously increases CO₂ concentration in the atmosphere, leading to a substantial and negative impact on the world climate. About 33,890.8 million tons of CO₂ was released into the atmosphere in 2018, and the global CO₂ concentration in the atmosphere reached 407.65 (BP Statistical Review of World Energy, 2019; Global Monitoring Division, 2019) Nearly ∼35 GT of CO₂ is being added to the atmosphere per year, and there is a considerable gap between the amount of CO₂ produced and utilized. Therefore, carbon dioxide utilization becomes a necessity to save the world from global warming. CO₂ utilization would not only help to remove CO₂ from the atmosphere but also helps to get alternate fuels and to reduce dependence on petrochemicals and, thus, restricts CO₂ expulsion in the atmosphere (Centi and Perathoner, 2009; Balaraman et al., 2011). Apart from forming fuels from carbon dioxide, many synthetically useful chemicals are being synthesized from carbon dioxide (Aresta, 2010). The conversion of formic acid from carbon dioxide has manyfold benefits to the environment and economy. Formic acid is considered to be potential chemical hydrogen storage material because of its stability, nontoxicity, and easy accessibility (Dörthe et al., 2016; Jörg et al., 2017; Miriam et al., 2019; Ganesh, 2014; Kassem et al., 2020). The global formic acid market is growing at a CAGR of 1.3%, and it is expected to reach US$828.1 million by 2025 due to its wide applications in agriculture, leather, textile, rubber, chemical and pharmaceuticals, and industries (https://dataintelo.com/report/formic-acid-market). Therefore, developing an energy-efficient and environmentally benign protocol to get formic acid from CO₂ becomes significant.

GRAPHICAL ABSTRACT

GRAPHICAL ABSTRACT. TOC for paper.

In carbon dioxide activation and formation of formic acid or formate derivatives, the use of rhodium, ruthenium, and iridium pincer complexes have made remarkable progress in recent years (Wen, et al., 2021; Wang et al., 2013; Huff and Sanford, 2011, Wesselbaum et al., 2012; Kothandaraman et al., 2016; Wesselbaum et al., 2015; Campos et al., 2014). However, the high price and limited availability of these metals restrict their wide applications to an industrial scale. Therefore, the development of new catalytic technologies based on earth-abundant metals such as Fe, Mn, Ni, and Co is of considerable interest (Figure 1) (Zell and Milstein, 2015; Furstner, 2016; Langer et al., 2011; Zhang et al., 2015; Ge et al., 2016; Choi and Lee., 2020; Curley et al., 2018). The transition metal pincer complexes of these earth-abundant metals are of particular importance due to their thermal stability, cost efficiency, and flexibility for modification. The flexibility in the modification could be useful to fine-tune structural and electronic properties of the metal pincer complexes to make them more reactive as well as more selective (Peris and Crabtree, 2018). In this context, Mn pincer complexes in catalytic carbon dioxide hydrogenation have seen much progress over a much shorter time (Bertini et al., 2017; Garbe et al., 2017; Kar et al., 2017). The PNP, PCP PNN pincer complexes have been commonly used to develop transition metal pincer complexes (Kumar et al., 2019; Bernskoetter and Hazari, 2017; Irina et al., 2016; Bertini et al., 2016; Jan et al., 2020). It is necessary to understand the donor–acceptor strength of the ligand during the rational ligand designing for new catalyst development. In all the cases, the metal–ligand interaction will depend highly on the choice of the transition metal, oxidation state, coordinating sites of the ligands, and the substituents on ligands. Steric bulk is also an extremely important aspect not only for enhancing the stability of the complexes but also for providing stereoselectivity (Garbe et al., 2019; Wen et al., 2021; Jessica et al., 2017). The NNN pincer ligands are of particular importance due to their accessibility, scalability, stability, and affordability. In the recent review, Crabtree mentioned that there is a necessity to explore transition metal NNN pincer complexes and to understand their catalytic performance (Peris and Crabtree, 2018). Herein, 15 Mn(I)NNN pincer complexes are designed to understand steric and electronic factor ligands on the catalytic efficacy toward carbon dioxide hydrogenation (Figure 2). However, it would be difficult to understand the efficacy of these 15 Mn(I)NNN complexes and also to throw light on the impact of aromatic and heterocyclic rings present in the NNN pincer ligands by using experimental methods. Therefore, the use of computational methods to assess a large number of complexes by evaluating the mechanistic pathway and energetics of the reaction is highly desirable.

FIGURE 1

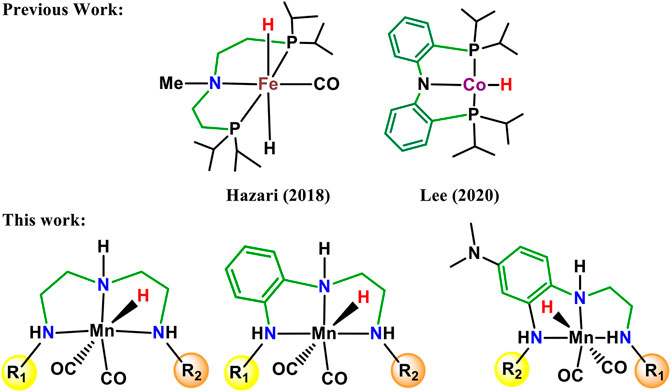
FIGURE 1. Recently developed NNN pincer ligands with varying electron withdrawing and donating moieties.

FIGURE 2

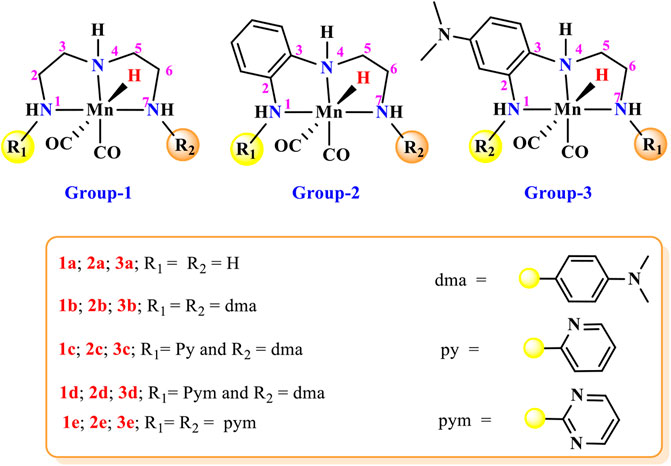
FIGURE 2. Mn(I)NNN complexes designed for the computational study of the impact of aromatic substituents on carbon dioxide hydrogenation.

Computational Details

The Gaussian-16 program package was used to perform the computational calculations (Frisch et al., 2016). The meta-GGA hybrid M06 functional with dispersion corrections without the imposition of any symmetry constraints were used to optimize reactants and intermediates (Zhao and Truhlar, 2008a). M06 is the accurate, economical functional for transition metals than B3LYP functional (Hehre et al., 1972). The SDD basis set was used for manganese, and Pople’s 6-31G(d,p) basis set was used for all the main group elements (Hariharan and Pople, 1973; Hay and Wadt, 1985). All complexes were treated as neutral species to compute optimized energies. The ground states of intermediates and transition states were confirmed as singlets through the comparison with optimized high-spin analogs. All transition states exhibited a single imaginary frequency, corresponding to the eigenvector along the reaction path. Frequency analysis of all the stationary points was performed at the same level of theory to confirm stationary points as minima or first-order saddle points along with the reaction coordinate (Liu et al., 2012; Jain et al., 2018; Zhao and Truhlar, 2008b). Intrinsic reaction coordinates (IRCs) were carried out on the transition states to endorse that such structures were indeed connecting the two minima, reactant, and product (Fukui, 1970; Fukui, 1981). All the calculations presented in this work were performed in the presence of water (dielectric constant = 78.39) using the integral equation formalism variant-like solvation model based on density (SMD) (Aleksandr et al., 2009; Aleksandr et al., 2009).

NBO analysis was carried out using the NBO 3.1 suite as implemented in Gaussian-16 (Foster and Weinhold, 1980; Reed et al., 1985; Reed and Weinhold, 1985; Glendening et al., 1987; Carpenter et al., 1988; Reed et al., 1988). The second-order perturbative estimation of donor–acceptor stabilization energy (E_s) was calculated using the following equation,

$E_s=\Delta E_{ij}=q_i\frac{F_{ij}^2}{\Delta {\epsilon }_{ji}}(1)$

where q_i is the donor orbital occupancy number, and F_ij is the off-diagonal element of the Fock matrix in the NBO basis. Δε_ji = ε_j − ε_i is the orbital energy difference between the acceptor (j) and donor (i) NBO.

The solvent-corrected relative Gibbs free energies (ΔG) for the transition states and intermediate as well as overall activation Gibbs free energies (ΔG^⧧) for the catalytic cycle was calculated at 1 atm pressure and 298.15 K temperature. Visualization of all optimized structures was performed using the CYLview software (CYLview, 2020), and imaging of all NBO structures and orbitals was performed using the Chemcraft Visualization software (Chemcraft, 2021).

Catalyst Designing

A large number of pincer catalysts have been developed for various catalytic applications. (Bernskoetter and Hazari, 2017; Irina et al., 2016; Garbe et al., 2019; Kumar et al., 2019; Kar et al., 2020; Wen et al., 2021). However, PNP and PCP pincer complexes have been studied mostly than NNN pincer complexes (Bernskoetter and Hazari, 2017; Bertini et al., 2016; Kar et al., 2019; Tang et al., 2019). Therefore, it is necessary to explore the efficacy of Mn(I)NNN pincer complexes toward the activation of carbon dioxide. In many instances, aromatic systems are commonly used during the designing of metal pincer complexes with limited combinations (Figure 1) (Choi and Lee., 2020; Jessica et al., 2015; Talukdar et al., 2019). The aromatic systems are known to provide better thermal stability to the catalyst complex by offering steric bulk and hydrophobic groups to minimize the leaching of the metals. However, it is very important to understand the impact of the position and the nature of the aromatic rings present in the pincer complexes on their catalytic performances. It would be impossible to study all these parameters using any experimental study, and hence, the DFT (density functional theory) would play an important role to throw light on the effect of aromatic rings on the efficacy of the catalysts. Herein, 15 catalysts were designed by changing the position and reactivity of the aromatic ring attached to pincer ligands. These 15 catalysts were further studied to understand the impact of the position and nature of the aromatic rings on carbon dioxide hydrogenation (Figure 2). The computationally designed catalysts are classified into three groups: 1) Group 1: No aromatic ring is placed on pincer ring carbons. 2) Group 2: The benzene ring is inserted at the C2—C3 carbons of the pincer ring. 3) Group 3: The N,N-dimethyl aniline ring is inserted at the C2—C3 carbons of the pincer ring in such a way that the N,N-dimethyl group is para to the C3 nitrogen. All three groups are further subdivided into a, b, c, d, and e classes based on the substituents attached to the terminal nitrogens of the pincer ligands. The hydrogens attached to both the terminal nitrogens are replaced with differently activated aromatic rings in all the three groups like N,N-dimethyl aniline, pyridine, and pyrimidine (Figure 2). Catalysts 1a, 2a, and 3a contain all unsubstituted pincer nitrogen. The hydrogens of both the terminal nitrogen are replaced by an electron-donating group, N,N-dimethyl aniline, in 1b, 2b, and 3b catalysts, whereas catalysts 1c, 2c, and 3c contain pyridine and N,N-dimethyl aniline groups attached to both the terminal nitrogen of the Mn(I)NNN pincer complex. Catalysts 1d, 2d, and 3d are designed to have pyrimidine and N,N-dimethyl aniline groups attached to each terminal nitrogen of the pincer complexes. The two strong electrons withdrawing the pyrimidine groups are attached to the Mn(I)NNN pincer ring nitrogen in catalysts 1e, 2e, and 3e (Figure 2). All these 15 Mn(I)NNN pincer complexes are further used to explore their catalytic performance toward carbon dioxide hydrogenation (Figure 3).

FIGURE 3

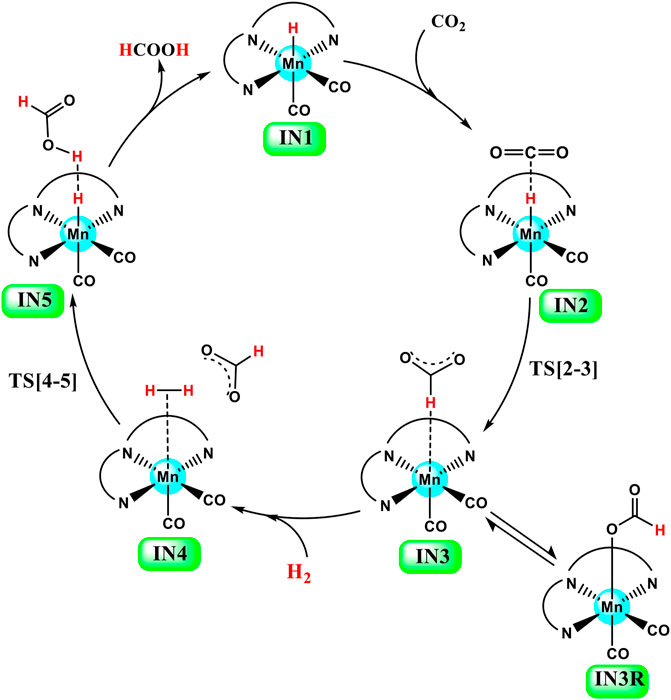
FIGURE 3. General catalytic cycle of Mn(I)NNN-catalyzed hydrogenation of carbon dioxide to formic acid through the NC pathway for Groups 1, 2, and 3 catalysts.

Result and Discussion

Hydrogenation of Carbon Dioxide to Formic Acid Catalyzed by Group 1 Catalysts, 1a–1e

Catalysts 1a–1e are designed to explore the impact of donating and withdrawing groups on the catalytic performance in the absence of any aromatic rings on the pincer ring carbons toward CO₂ hydrogenation (Figure 2). The intermediate IN2 is obtained after the addition of CO₂ to the active catalyst complex IN1 of the catalysts 1a–1e. The relative Gibbs free energies of the transition state and the intermediate states are calculated by considering the relative Gibbs free energy of the IN2 as 0.0 kcal/mol (Figure 4). The IN2 is further converted into the IN3 by transferring the hydride from the Mn center to the carbon dioxide carbon through the transition state TS[2-3].

FIGURE 4

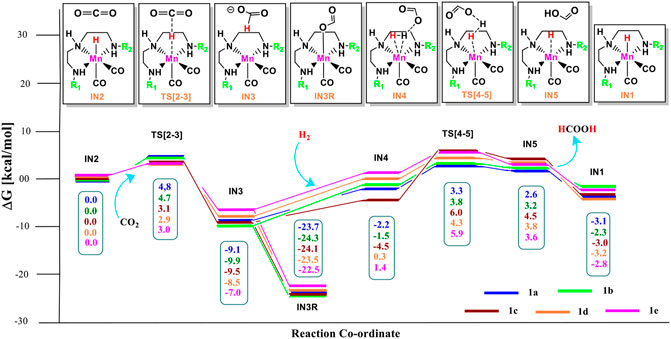
FIGURE 4. Solvent-corrected relative Gibbs free energy profile for Mn(I)NNN-catalyzed formation of formic acid through the NC pathway for catalysts 1a–1e. Calculations were carried out at the M06/6-31G(d,p)-SDD(Mn), SMD(H₂O) level of theory.

The relative Gibbs free energies for the TS[2-3] are ∼3.0 kcal/mol for the catalyst complexes 1c, 1d, and 1e and ∼4.8 kcal/mol for the catalyst complexes 1a and 1b. The IN3 of all three catalysts groups are stabilized with the relative Gibbs free energy of approximately ∼−7.0 to −10.0 kcal/mol. The relative Gibbs free energy of IN3 is minimum for 1b (−9.9 kcal/mol) and maximum for 1e (−7.0 kcal/mol). The IN3 further isomerizes to the IN3R (−22.5 to −24.3 kcal/mol) by forming an Mn—OCHO bond. This is the most stable state TDI (Turn-over Determining Intermediate), and hence, it is also a rate-determining state of the reaction. The IN3R again isomerizes to IN3 with an energy barrier of ∼15.0 kcal/mol, and then, the protonation takes place. The hydrogen molecule adds to IN3 to provide the IN4 comprising formic acid. The relative Gibbs free energy of the IN4 is minimum for 1c (−4.5 kcal/mol) and maximum for 1e (1.4 kcal/mol) (Figure 5).

FIGURE 5

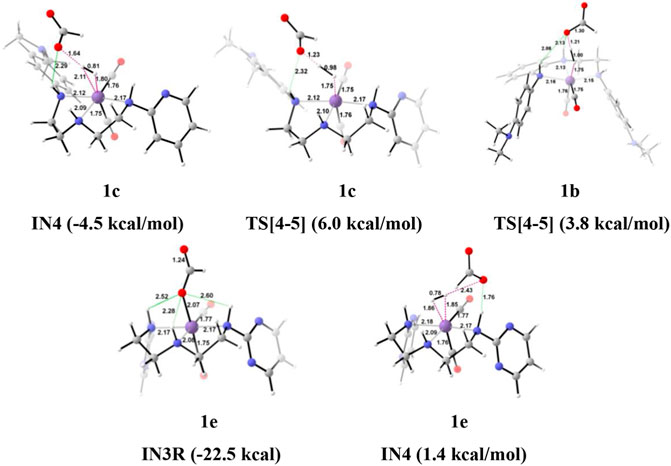
FIGURE 5. The optimized geometries of the intermediates in the formation of formic acid from carbon dioxide. The bond lengths are in Å, and the relative Gibbs free energies are in parentheses (Figures are shown in Supplementary Data Sheet S1 for all the optimized geometries of all the transition states and intermediates).

Interestingly, we found that in Group 1, the catalyst with a shorter Mn—N (1a, Mn—N = 2.13 Å) distance performs better than the catalyst with a longer Mn—N bond (1e, Mn—N = 2.20 Å) distance (Figure 6). However, there is no significant change in the Mn—N bond distance during the catalytic reaction. The presence of a strong H-bond (HCOO—H₂ = 1.64 Å) in 1c than in 1e (HCOO—H₂ = 2.43 Å) lowers the relative Gibbs free energy in 1c (−4.5 kcal/mol) than 1e (1.36 kcal/mol) in IN4. However, TS[4-5] of 1c is found to have higher Gibbs free energy than 1b, due to strong H₂ polarization and strong bond-forming interactions in 1b (1.00 Å) than in 1c (0.98 Å).

FIGURE 6

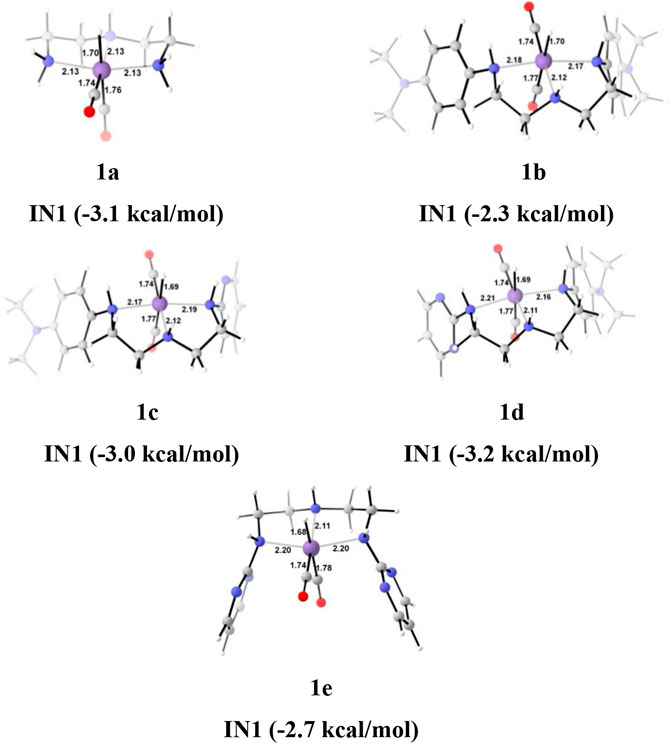
FIGURE 6. The optimized geometries of the Group 1 IN1 catalysts. The bond lengths are in Å, and relative Gibbs free energies are in parentheses (The optimized geometries of all the transition states and intermediates are disclosed in Supplementary Data Sheet S1).

A similar dihydrogen polarization is found to be efficient in the M—H₂ σ-complex of 1c (0.81 Å) than in 1e (0.78 Å). The IN4 is further converted into IN5, the regenerated catalyst and formic acid complex through the TS[4-5] with the relative Gibbs free energy of 3.3–6.0 kcal/mol for all the catalysts. However, the activation energy barrier for this step is the lowest for 1a (3.3 kcal/mol) and the highest for 1c (6.0 kcal/mol). In this entire mechanism, the dihydrogen dissociation and catalyst regeneration steps are more energy demanding by 1–3 kcal/mol than the hydride transfer transition state for the catalyst complexes 1c, 1d, and 1e. On the other hand, the catalysts complexes 1a and 1b show facile protonation via dihydrogen polarization than the hydride transfer from the Mn center to carbon dioxide. In overall CO₂ to formic acid formation, catalysts 1a and 1d have almost the same catalytic efficiency as the rest of the catalysts with ΔG^⧧ of 23.9 and 24.6 kcal/mol (Table 1), whereas catalyst complex 1c is most sluggish toward carbon dioxide hydrogenation. This indicates that unsubstituted carbon centers of Mn(I)NNN with unsubstituted nitrogen pincer ligands of Group 1 show better catalytic performance than the one with electron-withdrawing groups. The donating groups and moderate withdrawing groups at terminal nitrogen make 1b and 1c catalysts less reactive than the Mn(I)NNN complex 1a and 1d. However, there is no drastic change in the reactivity when we change the N substituents in Group 1 Mn(I)NNN pincer complexes.

TABLE 1

TABLE 1. Catalytic performance of Group 1 catalyst, 1a–1e.

Hydrogenation of carbon dioxide to formic acid catalyzed by Group 2 catalysts 2a–2e

The unsubstituted pincer ring carbons provided exciting results; therefore, we decided to investigate the effect of aromatic substituents of the pincer carbons (C2 and C3) on the catalytic performance (Curley et al., 2018; Kumar et al., 2019; Luca et al., 2020) (Figure 2). Herein, C2 and C3 carbons of catalysts 1a-1e are used to attach the unsubstituted aromatic ring to form the new pincer complexes 2a-2e (Figure 7). After the addition of carbon dioxide to these pincer complexes, IN2 is formed. The relative Gibbs free energy of the IN2 is considered as 0.0 kcal/mol to calculate the relative Gibbs free energies of the transition state and the intermediate states (Figure 8). The intermediate IN2 converts into the IN3 through the transition state TS[2-3]. The activation energy barrier for the TS[2-3] is found to be maximum for catalyst 2b (4.3 kcal/mol) and minimum for catalyst 2e (1.9 kcal/mol). The TS[2-3] (1.9 kcal/mol) has the lowest relative Gibbs free energy among all the Group 2 catalysts. This could be due to a strong H-bond [N(1) H…OCO = 2.7 Å, N(4) H…OCO = 2.3 Å, and N(7) H…OCO = 2.9 Å] among the Group 2 catalysts (Figure 9). The IN3 of 2a (−11.2 kcal/mol) is the most stable, and 2b (−8.1 kcal/mol) is less stable among all the catalysts. It has been reported in papers that IN3 isomerizes to a more stable metal formate intermediate, IN3R (Boodsarin et al., 2018; Kumar et al., 2019). Herein, all the IN3R intermediates are stabilized by three strong H-bonds with a relative Gibbs free energy of ∼ −24.0 to −27.0 kcal/mol (All energies are added in the table in Supplementary Data Sheet S1). However, strong H-bonds [N(1) H…OCHO = 2.26 Å, N(4) H…OCHO = 2.28 Å, and N(7) H…OCHO = 1.93 Å] stabilize the IN3R of catalyst 2d more effectively than the rest of the catalysts (Figure 9). The isomerization energy barrier for IN3R to IN3 is ∼15 kcal/mol for all the catalysts except 2d (18.0 kcal/mol). When IN3R changes to IN3, then the hydrogen molecule adds to the IN3 to provide the intermediate IN4. In the IN4, there is an increase in the Gibbs free energy by 2–9 kcal/mol than IN3.

FIGURE 7

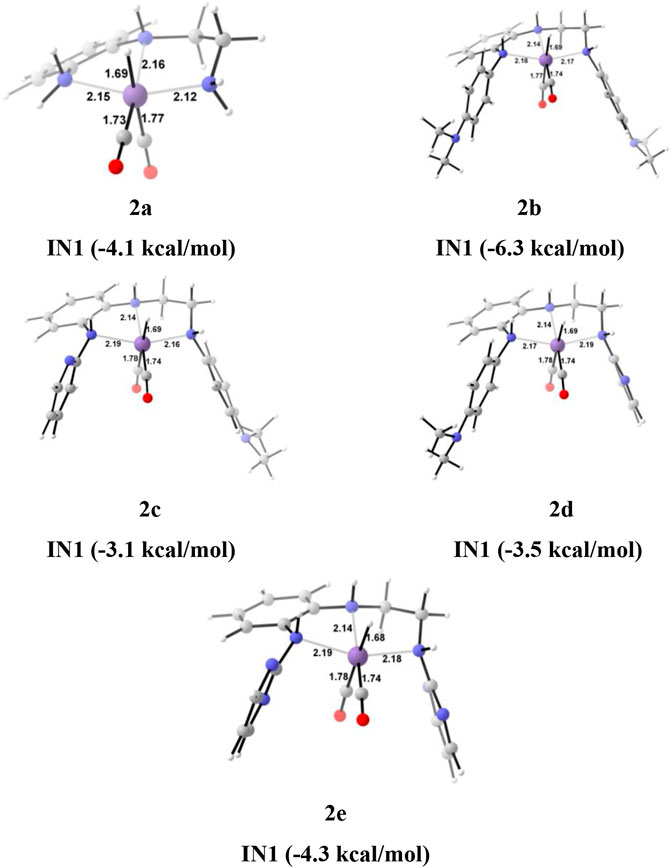
FIGURE 7. The optimized geometries of the Group 2 IN1 catalysts. The bond lengths are in Å, and relative Gibbs free energies are in parentheses (The optimized geometries of all the transition states and intermediates are disclosed in Supplementary Data Sheet S1).

FIGURE 8

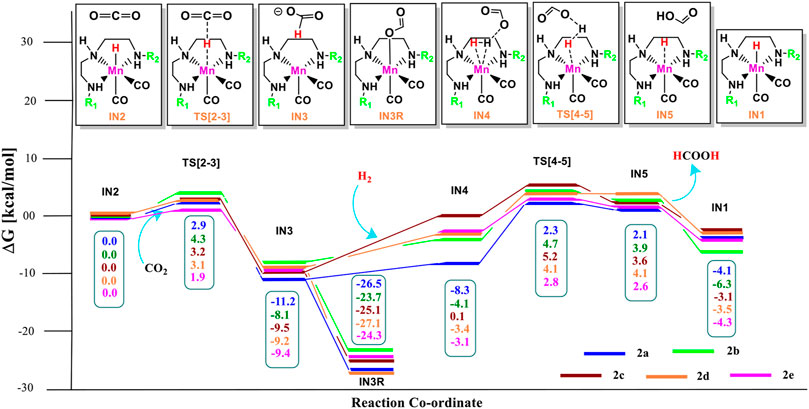
FIGURE 8. Solvent-corrected relative Gibbs free energy profile for Mn(I)NNN-catalyzed formation of formic acid through the NC pathway for catalysts 2a–2e. Calculations were carried out at the M06/6-31G(d,p)-SDD(Mn), SMD(H₂O) level of theory.

FIGURE 9

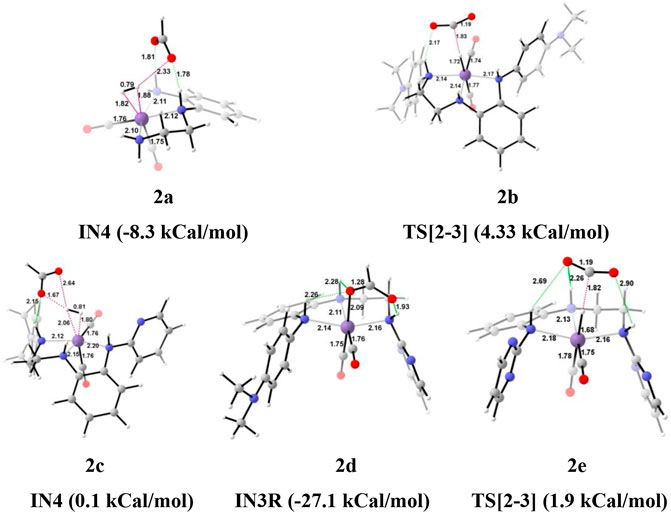
FIGURE 9. The optimized geometries of the transition state in the formation of formic acid from carbon dioxide for catalysts 2a–2e. The bond lengths are in Å, and relative Gibbs free energies are in parentheses (Figures are shown in Supplementary Data Sheet S1 for all the optimized geometries of all the transition states and intermediates).

In the Mn—H₂ σ-complex, the IN4 of catalyst 2a is most stable (−8.3 kcal/mol), whereas 2c is the least stable (0.1 kcal/mol) (Figure 9) among all the catalysts. The presence of stronger H-bonds [N(1) H…OCHO = 1.8 Å and N(4) H…OCHO = 1.78 Å] offer better stability than all the catalysts (∼0 to −4 kcal/mol). The IN4 of 2a shows an Mn-H₂ σ-complex with an Mn center, and the remaining catalysts show a distorted Mn-H₂ σ-complex, where one Mn—H_a (1.88 Å) is longer than the other Mn—H_b (1.82 Å) bond (Structure in Supplementary Data Sheet S1). These distortions in the Mn—H bond could be due to strong dihydrogen polarization. The IN4 converts into IN5 through the TS[4-5], where the strong dissociation of a dihydrogen bond is observed in all the catalysts. The H-bond stabilizes the TS[4-5] with the relative Gibbs free energy of 2.0 to 5.0 kcal/mol. The IN5 contains the product, formic acid, and the regenerated catalyst complex. The IN5 further expels formic acid and provides regenerated catalysts, 2a–2e. The ΔG for the entire catalytic reaction is found to be minimum for catalysts 2b (22.1 kcal/mol) and 2e (22.8 kcal/mol) and maximum for catalysts 2c (27.2 kcal/mol) and 2d (27.7 kcal/mol) (Table 2). This indicates that in Group 2, catalysts show better catalytic performance when both the terminal nitrogen are attached to either electron-donating groups, N,N-dimethyl aniline, or strong electron-withdrawing groups, pyrimidine. On the other hand, the catalytic performance slows down when these two terminal nitrogens carry mixed electron-withdrawing and donation groups 2a and 2c. However, catalyst 2a with an unsubstituted terminal nitrogen shows average performance toward carbon dioxide hydrogenation.

TABLE 2

TABLE 2. Catalytic performance of Group 2 catalyst, 2a–2e.

Hydrogenation of carbon dioxide to formic acid catalyzed by Group 3 catalysts, 3a–3e

The unsubstituted Group 1, as well as benzene, substituted Group 2 manganese pincer complexes provided a deeper insight into their catalytic performances toward carbon dioxide hydrogenation reaction. Therefore, we also investigated the effect of the activated aromatic ring by placing N,N-dimethyl aniline at the C2—C3 of the pincer ligands of the Mn(I)NNN complex in Group 3 (Figures 2 and 10) (Smith et al., 2018). Complexes 3a–3e are designed to understand the effect of Mn(I)NNN complexes on carbon dioxide hydrogenation. After the addition of carbon dioxide to these pincer complexes, the IN2 is formed. The relative Gibbs free energy of the IN4 is considered as 0.0 kcal/mol to calculate the relative Gibbs free energies of the transition and the intermediate states (Figure 11). The IN2 converts into the IN3 through the transition state TS[2-3]. The relative Gibbs free energy of the TS[2-3] of all the catalysts is in the range of 3.0–4.0 kcal/mol except for catalyst 3c (9.7 kcal/mol). The TS[2-3] [N(1) H…OCHO = 2.9 Å, N(4) H…OCHO = 2.4 Å, and N(7) H…OCHO = 2.5 Å] and IN3R [N(1) H…OCHO = 2.29 Å, N(4) H…OCHO = 2.25 Å, and N(7) H…OCHO = 1.95 Å] show moderate H-bonds in all the catalysts (Figure 12). After careful evaluation, it is observed that the IN1 of 3c has higher energy than the rest of the catalysts, and hence, the entire catalytic cycle, transitions states, and intermediates associated with this catalyst have higher relative Gibbs free energy than the other catalysts of Group 3. The formation of IN3 is found to be exergonic by 12.0–13.0 kcal/mol in all the catalysts of Group 3. The IN3 isomerizes to the resting state, IN3R. The relative Gibbs free energy of the resting state IN3R is in the range of −24.0 to −27.0 kcal/mol except for catalyst 3c (−20.5 kcal/mol). The IN3R is the rate-controlling state in the entire catalytic conversion. The IN3R again isomerizes to IN3 to undergo further reaction to form product IN5. The dihydrogen molecule adds to the IN3 to give the intermediate IN4. The IN4 forms a classical σ-complex with an Mn center. Similar to Group 2, a strong Mn—H₂ σ-complex is formed in IN4 of 3a, while the remaining catalysts show a distorted Mn-H₂ σ-complex, where one Mn—H_a (1.88 Å) is longer than the other Mn—H_b (1.82 Å) bond (Structure in Supplementary Data Sheet S1). A strong polarization must have led to this distortion.

FIGURE 10

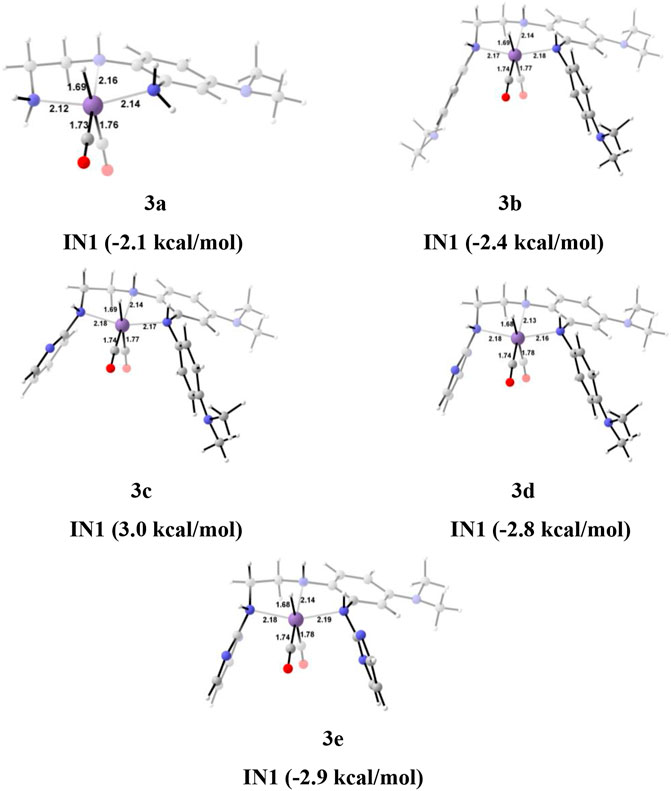
FIGURE 10. The optimized geometries of the Group 3 IN1 catalysts. The bond lengths are in Å, and relative Gibbs free energies are in parentheses (The optimized geometries of all the transition states and intermediates are disclosed in Supplementary Data Sheet S1).

FIGURE 11

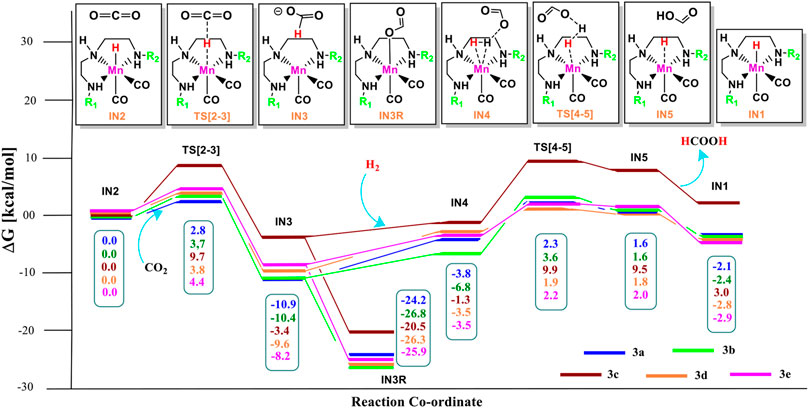
FIGURE 11. Solvent-corrected relative Gibbs free energy profile for Mn(I)NNN-catalyzed formation of formic acid through the NC pathway for catalysts 3a–3e. Calculations were carried out at the M06/6-31G(d,p)-SDD(Mn), SMD(H₂O) level of theory.

FIGURE 12

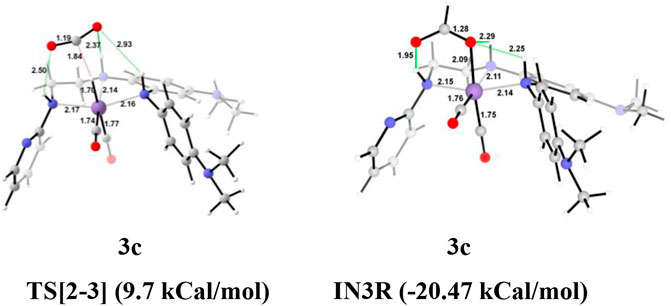
FIGURE 12. The optimized geometries of the transition states TS[2-3] in the formation of formic acid from carbon dioxide for catalysts 3a–3e. The bond lengths are in Å, and relative Gibbs free energies are in parentheses (The optimized geometries of all the transition states and intermediates are disclosed in Supplementary Data Sheet S1).

The IN4 of the 3b (−6.8 kcal/mol) is the most stable, and 3c (−1.3 kcal/mol) is the least stable among all the catalysts of Group 3. The IN4 further converts to the IN5 through the transition state TS[4-5] with a maximum relative Gibbs free energy for catalyst 3c (9.9 kcal/mol) and minimum for catalyst 1a, 1d, and 1e (∼2.0 kcal/mol). The entire CO₂ hydrogenation is found to be thermodynamically favorable for all the catalysts except for catalyst 3c. This indicates that electron-donating and weak-withdrawing groups at an Mn center make dihydrogen polarization and catalyst generation sluggish. On the other hand, unsubstituted terminal nitrogen and terminal nitrogen with strong withdrawing groups facilitate the dihydrogen polarization and carbon dioxide to the formic acid formation (Table 3).

TABLE 3

TABLE 3. The catalytic performance of Group 3 catalyst, 3a–3e.

Natural Bond Orbital

Natural bond orbital (NBO) analysis is performed to gain a mechanistic insight into the carbon dioxide hydrogenation reaction mechanism (Chemcraft, 2021). The Lewis acid–base pair present in the chemical species can be predicted from the second-order perturbative estimation of donor–acceptor stabilization energy ($E_s$). The NBO analysis of the transition states TS[2-3] provides the picture of relevant orbital interactions for the bond formation based on the second-order perturbative interaction energy. At the transition state TS[2-3], prominent bond-forming interactions are observed for the C—H(a) bond. (Figure 13).

FIGURE 13

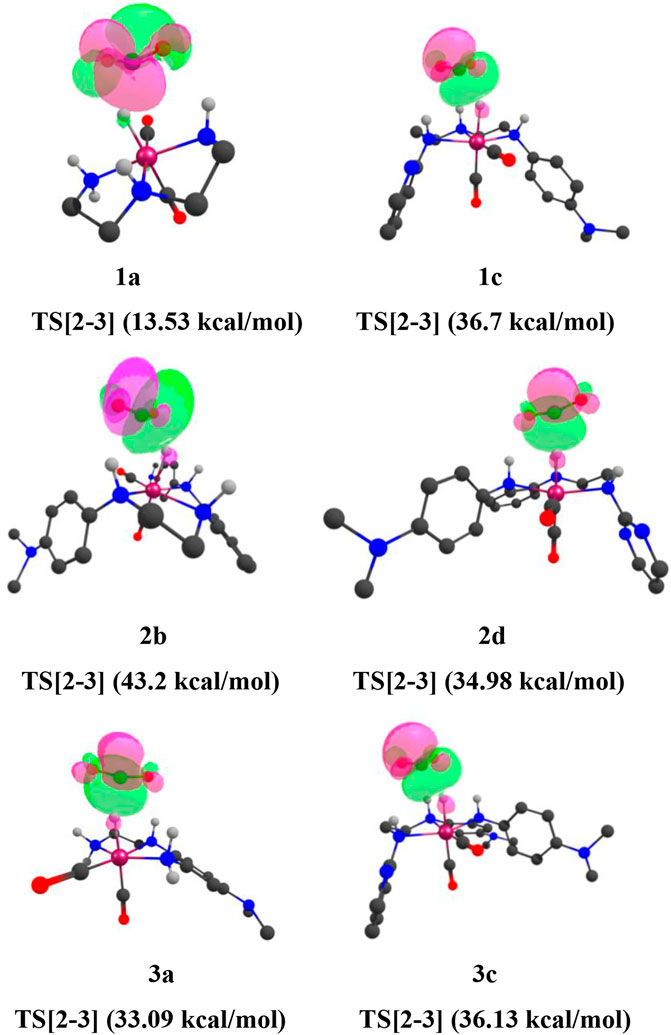
FIGURE 13. (Mn)H—CO₂ interaction of natural bond orbitals (NBOs) of TS[2-3] of catalysts 1a, 1d, 1e, 2a, 2b, 2e, and 3a (isovalue = 0.0174). Interaction energies are indicated in parentheses. The structures are visualized using the Chemcraft software (Chemcraft, 2021) (NBO for all catalysts are given in Supplementary Data Sheet S1).

Here, the TS[2-3] of 1e has stronger bond-forming interaction energy (45.01 kcal/mol) and lower relative Gibbs free energy(3.0 kcal/mol), whereas the TS[2-3] of 1a shows weaker bond-forming interaction energy of (13.53 kcal/mol) and higher relative Gibbs free energy (4.8 kcal/mol). A similar trend is observed when NBO analysis is performed for the IN4 of all the catalysts (Figure 14).

FIGURE 14

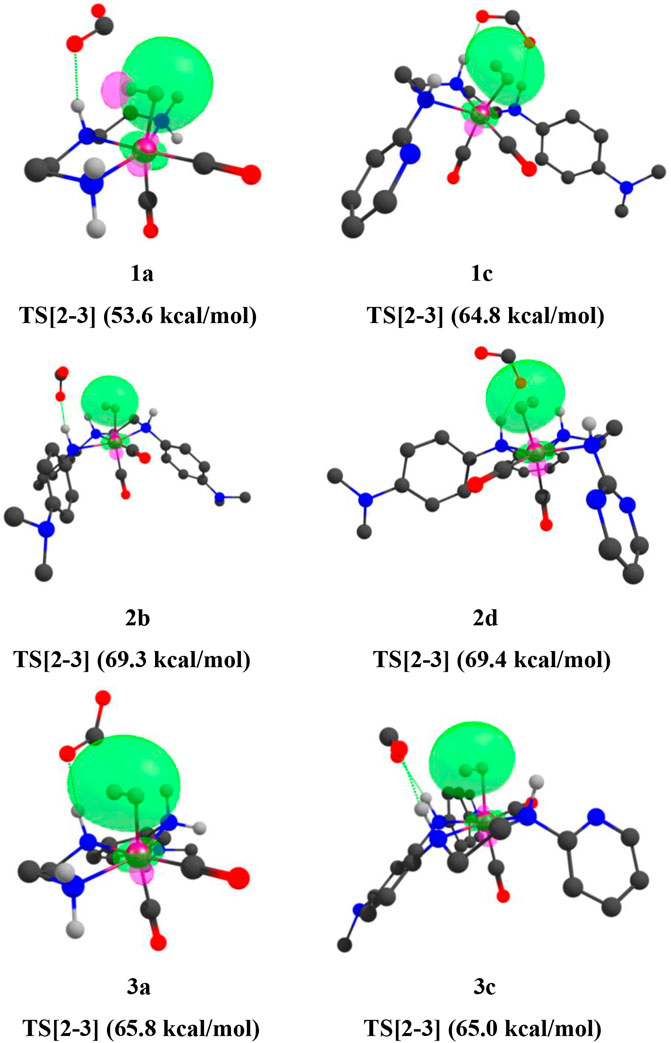
FIGURE 14. Mn—H₂ interaction NBOs of IN4 of catalysts 1a, 1d, 1e, 2a, 2b, 2e, and 3a (isovalue = 0.03). Interaction energies are indicated in parentheses. The structures are visualized using the Chemcraft software (Chemcraft, 2021) (NBO for all catalysts are given in Supplementary Data Sheet S1).

Conclusion

The structure–activity relationship study of computationally modeled Mn(I)NNN pincer complexes emphasize that the position and nature of the aromatic rings attached to the pincer ligands affect the catalytic performance to a considerable amount for carbon dioxide hydrogenation reaction. The Group 2 Mn(I)NNN pincer complexes with benzene substituent at C2—C3 and identical substituents at both the terminal nitrogen are superior to all the catalysts from the three groups, whereas Group 1 catalysts without any aromatic substituents at C2—C3 show moderate catalytic performance, and Group 3 catalysts with N,N-dimethyl aniline at C2—C3 are sluggish toward carbon dioxide hydrogenation.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors.

Author Contributions

SP and VA conceived the project. SVP carried out the computational calculations and analysis of data. All authors were involved in the manuscript writing and revision. All authors have made substantial, direct and intellectual contributions to the work, and approved it for publication.

Funding

This research was supported by SERB-DST for the research grant under the IMPRINT II project (File no. IMP/2018/001208/EN).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

VA and SVP acknowledge the Department of Chemistry, SP College, Pune, DST-FIST, and Dr. TR Ingle research foundation for the infrastructure and facilities.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2021.778718/full#supplementary-material

References

Aleksandr, V. M., Christopher, J. C., and Truhlar, D. G. (2009). Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B. 113, 6378–6396. doi:10.1021/jp810292n

CrossRef Full Text | Google Scholar

Aleksandr, V. M., Christopher, J. C., and Truhlar, D. G. (2009). Universal Solvation Model Based on the Generalized Born Approximation with Asymmetric Descreening. J. Chem. Theor. Comput. 5, 2447–2464. doi:10.1021/ct900312z

CrossRef Full Text | Google Scholar

Aresta, M. (2010). Carbon Dioxide Recovery and Utilization. Dordrecht: Kluwer Academic Publishers.

Google Scholar

Balaraman, E., Gunanathan, C., Zhang, J., Shimon, L. J. W., and Milstein, D. (2011). Efficient Hydrogenation of Organic Carbonates, Carbamates and Formates Indicates Alternative Routes to Methanol Based on CO₂ and CO. Nat. Chem. 3, 609–614. doi:10.1038/nchem.1089

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernskoetter, W. H., and Hazari, N. (2017). Reversible Hydrogenation of Carbon Dioxide to Formic Acid and Methanol: Lewis Acid Enhancement of Base Metal Catalysts. Acc. Chem. Res. 50, 1049–1058. doi:10.1021/acs.accounts.7b00039

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertini, F., Glatz, M., Gorgas, N., Stöger, B., Peruzzini, M., Veiros, L. F., et al. (2017). Veiros, Karl Kirchner and Luca GonsalviCarbon Dioxide Hydrogenation Catalysed by Well-Defined Mn(I) PNP Pincer Hydride Complexes. Chem. Sci. 8, 5024–5029. doi:10.1039/c7sc00209b

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertini, F., Gorgas, N., Stöger, B., Peruzzini, M., Veiros, L. F., Kirchner, K., et al. (2016). Efficient and Mild Carbon Dioxide Hydrogenation to Formate Catalyzed by Fe(II) Hydrido Carbonyl Complexes Bearing 2,6-(Diaminopyridyl)diphosphine Pincer Ligands. ACS Catal. 6 (5), 2889–2893. doi:10.1021/acscatal.6b00416

CrossRef Full Text | Google Scholar

Boodsarin, S., Wodrich, M. D., and Corminboeuf, C. (2018). Unraveling Metal/Pincer Ligand Effects in the Catalytic Hydrogenation of Carbon Dioxide to Formate. Organometallics 37 (24), 4568–4575. doi:10.1021/acs.organomet.8b00490

CrossRef Full Text | Google Scholar

BP Statistical Review of World Energy (2019).BP Statistical Review of World Energy. 68th ed. London, United Kingdom: BPp.l.c.

Google Scholar

Campos, J., Hintermair, U., Brewster, T. P., Takase, M. K., and Crabtree, R. H. (2014). Catalyst Activation by Loss of Cyclopentadienyl Ligands in Hydrogen Transfer Catalysis with Cp*IrIII Complexes. ACS Catal. 4 (3), 973–985. doi:10.1021/cs401138f

CrossRef Full Text | Google Scholar

Carpenter, J. E., and Weinhold, F. (1988). Analysis of the Geometry of the Hydroxymethyl Radical by the "different Hybrids for Different Spins" Natural Bond Orbital Procedure. J. Mol. Struct. THEOCHEM. 169, 41–62. doi:10.1016/0166-1280(88)80248-3

CrossRef Full Text | Google Scholar

Centi, G., and Perathoner, S. (2009). Opportunities and Prospects in the Chemical Recycling of Carbon Dioxide to Fuels. Catal. Today. 148, 191–205. doi:10.1016/j.cattod.2009.07.075

CrossRef Full Text | Google Scholar

Chemcraft (2021). Chemcraft - Graphical Software for Visualization of Quantum Chemistry Computations. Available at: https://www.chemcraftprog.com.

Google Scholar

Choi, J., and Lee, Y. (2020). Catalytic Hydrogenation of CO2 at a Structurally Rigidified Cobalt center. Inorg. Chem. Front. 7, 1845–1850. doi:10.1039/c9qi01431d

CrossRef Full Text | Google Scholar

Curley, J. B., Smith, N. E., Bernskoetter, W. H., Hazari, N., and Mercado, B. Q. (2018). Catalytic Formic Acid Dehydrogenation and CO2 Hydrogenation Using Iron PNRP Pincer Complexes with Isonitrile Ligands. Organometallics. 37 (21), 3846–3853. doi:10.1021/acs.organomet.8b00534

CrossRef Full Text | Google Scholar

CYLview. (2020). Université de Sherbrooke. Available at: http://www.cylview.org.

Google Scholar

Dörthe, M., Peter, S., Henrik, J., and Beller, M. (2016). Formic Acid as a Hydrogen Storage Material - Development of Homogeneous Catalysts for Selective Hydrogen Release. Chem. Soc. Rev. 45, 3954–3988. doi:10.1039/c5cs00618j

PubMed Abstract | CrossRef Full Text | Google Scholar

Foster, J. P., and Weinhold, F. (1980). Natural Hybrid Orbitals. J. Am. Chem. Soc. 102, 7211–7218. doi:10.1021/ja00544a007

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian 16, Revision C.01. Wallingford C. T: Gaussian, Inc.

Google Scholar

Fukui, K. (1970). Formulation of the Reaction Coordinate. J. Phys. Chem. 74, 4161–4163. doi:10.1021/j100717a029

CrossRef Full Text | Google Scholar

Fukui, K. (1981). The Path of Chemical Reactions - the IRC Approach. Acc. Chem. Res. 14, 363–368. doi:10.1021/ar00072a001

CrossRef Full Text | Google Scholar

Furstner, A. (2016). Iron Catalysis in Organic Synthesis: A Critical Assessment of what it Takes to Make This Base Metal a Multitasking Champion. ACS Cent. Sci. 2 (11), 778–789.

PubMed Abstract | CrossRef Full Text | Google Scholar

Ganesh, I. (2014). Conversion of Carbon Dioxide into Methanol - a Potential Liquid Fuel: Fundamental Challenges and Opportunities (A Review). Renew. Sustain. Energ. Rev. 31, 221–257. doi:10.1016/j.rser.2013.11.045

CrossRef Full Text | Google Scholar

Garbe, M., Junge, K., and Beller, M. (2017). Homogeneous Catalysis by Manganese-Based Pincer Complexes. Eur. J. Org. Chem. 2017, 4344–4362. doi:10.1002/ejoc.201700376

CrossRef Full Text | Google Scholar

Garbe, M., Wei, Z., Tannert, B., Spannenberg, A., Jiao, H., Bachmann, S., et al. (2019). Enantioselective Hydrogenation of Ketones Using Different Metal Complexes with a Chiral PNP Pincer Ligand. Adv. Synth. Catal. 361 (8), 1913–1920. doi:10.1002/adsc.201801511

CrossRef Full Text | Google Scholar

Ge, H., Chen, X., and Yang, X. (2016). A Mechanistic Study and Computational Prediction of Iron, Cobalt and Manganese Cyclopentadienone Complexes for Hydrogenation of Carbon Dioxide. Chem. Commun. 52, 12422–12425. doi:10.1039/c6cc05069g

CrossRef Full Text | Google Scholar

Glendening, E. D., Reed, A. E., Carpenter, J. E., and Weinhold, F. (1987). “Extension of Lewis Structure Concepts to Open-Shell and Excited-State Molecular Species,” Ph.D. Thesis. (Madison, WI: University of Wisconsin).

Google Scholar

Global Monitoring Division (2019). “Global Greenhouse Gas Reference Network-Trends in Atmospheric Carbon Dioxide. National Oceanic and Atmospheric Administration,” in Earth System Research Laboratory (Mauna Loa, Hawaii, U.S.December: U.S. Department of Commerce), 5.

Google Scholar

Hariharan, P. C., and Pople, J. A. (1973). The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Theoret. Chim. Acta. 28, 213–222. doi:10.1007/bf00533485

CrossRef Full Text | Google Scholar

Hay, P. J., and Wadt, W. R. (1985). Ab Initio effective Core Potentials for Molecular Calculations. Potentials for K to Au Including the Outermost Core Orbitals. J. Chem. Phys. 82, 299–310. doi:10.1063/1.448975

CrossRef Full Text | Google Scholar

Hehre, W. J., Ditchfield, R., and Pople, J. A. (1972). Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 56, 2257–2261. doi:10.1063/1.1677527

CrossRef Full Text | Google Scholar

Huff, C. A., and Sanford, M. S. (2011). Cascade Catalysis for the Homogeneous Hydrogenation of CO2 to Methanol. J. Am. Chem. Soc. 133, 18122–18125. doi:10.1021/ja208760j

CrossRef Full Text | Google Scholar

Irina, O., Tamm, T., Ahlquist, M. S. G., and Ahlquist, G. (2016). Reduced State of Iridium PCP Pincer Complexes in Electrochemical CO2 Hydrogenation. ACS Catal. 6 (6), 3834–3839. doi:10.1021/acscatal.6b01233

CrossRef Full Text | Google Scholar

Jain, P., Pal, S., and Avasare, V. (2018). Ni(COD)2-Catalyzed Ipso-Silylation of 2-Methoxynaphthalene: A Density Functional Theory Study. Organometallics. 37, 1141–1149. doi:10.1021/acs.organomet.8b00046

CrossRef Full Text | Google Scholar

Jan, P., Eder, W., Stöger, B., Realista, S., Martinho, P. N., Calhorda, M. J., et al. (2020). Synthesis, Characterization, and Catalytic Reactivity of {CoNO}8 PCP Pincer Complexes. Organometallics 39 (14), 2594–2601. doi:10.1021/acs.organomet.0c00167

PubMed Abstract | CrossRef Full Text | Google Scholar

Jessica, D. C., Dekarske, J. R., McCulloch, B. J., and Ozerov, O. V. (2015). Cyclometallation of the NNN Pincer Ligand in Complexes of Platinum. Inorg. Chem. Front. 2, 912–916. doi:10.1039/c5qi00102a

CrossRef Full Text | Google Scholar

Jessica, S. F., Wan, K. Y., Sues, P. E., and Morris, R. H. (2017). Ketone Asymmetric Hydrogenation Catalyzed by P-NH-P′ Pincer Iron Catalysts: An Experimental and Computational Study. ACS Catal. 7 (1), 316–326. doi:10.1021/acscatal.6b02489

CrossRef Full Text | Google Scholar

Jörg, E., and Huang, K.-W. (2017). Formic Acid as a Hydrogen Energy Carrier. ACS Energ. Lett. 2 (1), 188–195. doi:10.1021/acsenergylett.6b00574

CrossRef Full Text | Google Scholar

Kar, S., Goeppert, A., Kothandaraman, J., and Prakash, G. K. S. (2017). Manganese-Catalyzed Sequential Hydrogenation of CO2 to Methanol via Formamide. ACS Catal. 7, 6347–6351. doi:10.1021/acscatal.7b02066

CrossRef Full Text | Google Scholar

Kar, S., Rauch, M., Kumar, A., Leitus, G., Ben-David, Y., and Milstein, D. (2020). Selective Room-Temperature Hydrogenation of Amides to Amines and Alcohols Catalyzed by a Ruthenium Pincer Complex and Mechanistic Insight. ACS Catal. 10, 5511–5515. doi:10.1021/acscatal.0c01406

PubMed Abstract | CrossRef Full Text | Google Scholar

Kar, S., Sen, R., Kothandaraman, J., Goeppert, A., Chowdhury, R., Munoz, S. B., et al. (2019). Mechanistic Insights into Ruthenium-Pincer-Catalyzed Amine-Assisted Homogeneous Hydrogenation of CO2 to Methanol. J. Am. Chem. Soc. 141 (7), 3160–3170. doi:10.1021/jacs.8b12763

PubMed Abstract | CrossRef Full Text | Google Scholar

Kassem, B., Thenert, K., Wiesenthal, J., Hoppe, C., and Klankermayer, J. (2020). Utilization of Formic Acid as C1 Building Block for the Ruthenium‐Catalyzed Synthesis of Formaldehyde Surrogates. ChemCatChem 12 (7), 1944–1947. doi:10.1002/cctc.201902332

CrossRef Full Text | Google Scholar

Kothandaraman, J., Goeppert, A., Czaun, M., Olah, G. A., and Prakash, G. K. S. (2016). Conversion of CO2 from Air into Methanol Using a Polyamine and a Homogeneous Ruthenium Catalyst. J. Am. Chem. Soc. 138, 778–781. doi:10.1021/jacs.5b12354

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, A., Daw, P., Espinosa-Jalapa, N. A., Leitus, G., Shimon, L. J. W., Ben-David, Y., et al. (2019). CO2 Activation by Manganese Pincer Complexes through Different Modes of Metal-Ligand Cooperation. Dalton Trans. 48, 14580–14584. doi:10.1039/c9dt03088c

PubMed Abstract | CrossRef Full Text | Google Scholar

Langer, R., Diskin-Posner, Y., Leitus, G., Shimon, L. J. W., Ben-David, Y., and Milstein, D. (2011). Low-Pressure Hydrogenation of Carbon Dioxide Catalyzed by an Iron Pincer Complex Exhibiting Noble Metal Activity. Angew. Chem. Int. Ed. 50, 9948–9952. doi:10.1002/anie.201104542

CrossRef Full Text | Google Scholar

Liu, P., Xu, X., Dong, X., Keitz, B. K., Herbert, M. B., Grubbs, R. H., et al. (2012). Z-selectivity in Olefin Metathesis with Chelated Ru Catalysts: Computational Studies of Mechanism and Selectivity. J. Am. Chem. Soc. 134, 1464–1467. doi:10.1021/ja2108728

CrossRef Full Text | Google Scholar

Luca, P., Danielle, L., Justo, P., and Nielsen, M. (2020). Recent Progress with Pincer Transition Metal Catalysts for Sustainability. Catalysts 10 (7), 773. doi:10.3390/catal10070773

CrossRef Full Text | Google Scholar

Miriam, N., Mori, K., Salinas-Torres, D, Kuwahara, Y., and Yamashita, H. (2019). New Approaches toward the Hydrogen Production from Formic Acid Dehydrogenation over Pd-Based Heterogeneous Catalysts. Front. Mater. 6, 2296–8016. doi:10.3389/fmats.2019.00044

CrossRef Full Text | Google Scholar

Peris, E., and Crabtree, R. H. (2018). Key Factors in Pincer Ligand Design. Chem. Soc. Rev. 47, 1959–1968. doi:10.1039/c7cs00693d

PubMed Abstract | CrossRef Full Text | Google Scholar

Reed, A. E., Curtiss, L. A., and Weinhold, F. (1988). Intermolecular Interactions from a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 88, 899–926. doi:10.1021/cr00088a005

CrossRef Full Text | Google Scholar

Reed, A. E., and Weinhold, F. (1985). Natural Localized Molecular Orbitals. J. Chem. Phys. 83, 1736–1740. doi:10.1063/1.449360

CrossRef Full Text | Google Scholar

Reed, A. E., Weinstock, R. B., and Weinhold, F. (1985). Natural Population Analysis. J. Chem. Phys. 83, 735–746. doi:10.1063/1.449486

CrossRef Full Text | Google Scholar

Smith, J. D., Chih, E., Piers, W. E., and Spasyuk, D. M. (2018). Tuning Iridium (I) PCcarbeneP Frameworks for Facile Cooperative N2O Reduction. Polyhedron 155, 281–290. doi:10.1016/j.poly.2018.08.054

CrossRef Full Text | Google Scholar

Talukdar, K., Issa, A., and Jurss, J. W. (2019). Synthesis of a Redox-Active NNP-type Pincer Ligand and its Application to Electrocatalytic CO2 Reduction with First-Row Transition Metal Complexes. Front. Chem. 7 (330), 330–2646. doi:10.3389/fchem.2019.00330

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, S., von Wolff, N., Diskin-Posner, Y., Leitus, G., Ben-David, Y., and Milstein, D. (2019). Pyridine-Based PCP-Ruthenium Complexes: Unusual Structures and Metal-Ligand Cooperation. J. Am. Chem. Soc. 141, 7554–7561. doi:10.1021/jacs.9b02669

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W.-H., Muckerman, J. T., Fujita, E., and Himeda, Y. (2013). Mechanistic Insight through Factors Controlling Effective Hydrogenation of CO2 Catalyzed by Bioinspired Proton-Responsive Iridium(III) Complexes. ACS Catal. 3, 856–860. doi:10.1021/cs400172j

CrossRef Full Text | Google Scholar

Wen, J., Wang, F., and Zhang, X. (2021). Asymmetric Hydrogenation Catalyzed by First-Row Transition Metal Complexes. Chem. Soc. Rev. 50, 3211–3237. doi:10.1039/d0cs00082e

PubMed Abstract | CrossRef Full Text | Google Scholar

Wesselbaum, S., Moha, V., Meuresch, M., Brosinski, S., Thenert, K. M., Kothe, J., et al. (2015). Hydrogenation of Carbon Dioxide to Methanol Using a Homogeneous Ruthenium-Triphos Catalyst: from Mechanistic Investigations to Multiphase Catalysis. Chem. Sci. 6, 693–704. doi:10.1039/c4sc02087a

PubMed Abstract | CrossRef Full Text | Google Scholar

Wesselbaum, S., vom Stein, T., Klankermayer, J., and Leitner, W. (2012). Hydrogenation of Carbon Dioxide to Methanol by Using a Homogeneous Ruthenium-Phosphine Catalyst. Angew. Chem. Int. Ed. 51, 7499–7502. doi:10.1002/anie.201202320

CrossRef Full Text | Google Scholar

Zell, T., and Milstein, D. (2015). Hydrogenation and Dehydrogenation Iron Pincer Catalysts Capable of Metal-Ligand Cooperation by Aromatization/Dearomatization. Acc. Chem. Res. 48, 1979–1994. doi:10.1021/acs.accounts.5b00027

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., MacIntosh, A. D., Wong, J. L., Bielinski, E. A., Williard, P. G., Mercado, B. Q., et al. (2015). Iron Catalyzed CO2hydrogenation to Formate Enhanced by Lewis Acid Co-catalysts. Chem. Sci. 6, 4291–4299. doi:10.1039/c5sc01467k

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y., and Truhlar, D. G. (2008a). Density Functionals with Broad Applicability in Chemistry. Acc. Chem. Res. 41, 157–167. doi:10.1021/ar700111a

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y., and Truhlar, D. G. (2008b). The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Account. 120, 215–241. doi:10.1007/s00214-007-0310-x

CrossRef Full Text | Google Scholar