Excellent Ultracold Molecular Candidates From Group VA Hydrides: Whether Do Nearby Electronic States Interfere?

By means of highly accurate ab initio calculations, we identify two excellent ultracold molecular candidates from group VA hydrides. We find that NH and PH are suitable for the production of ultracold molecules, and the feasibility and advantage of two laser cooling schemes are demonstrated, which involve different spin-orbit states ($A^3{\Pi }_2$ and $X^3{\Sigma }_1^{-}$ ). The internally contracted multireference configuration interaction method is applied in calculations of the six low-lying Λ-S states of NH and PH with the spin-orbit coupling effects included, and excellent agreement is achieved between the computed and experimental spectroscopic data. We find that the locations of crossing point between the $A^3\Pi$ and ${}^5{\Sigma }^{-}$ states of NH and PH are higher than the corresponding v′ = 2 vibrational levels of the $A^3\Pi$ state indicating that the crossings with higher electronic states would not affect laser cooling. Meanwhile, the extremely small vibrational branching loss ratios of the $A^3{\Pi }_2$ → $a^1{\Delta }_2$ transition for NH and PH (NH: 1.81 × 10^–8; PH: 1.08 × 10^–6) indicate that the $a^1{\Delta }_2$ intermediate electronic state will not interfere with the laser cooling. Consequently, we construct feasible laser-cooling schemes for NH and PH using three lasers based on the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition, which feature highly diagonal vibrational branching ratio $R_{00}$ (NH: 0.9952; PH: 0.9977), the large number of scattered photons (NH: 1.04×10⁵; PH: 8.32×10⁶) and very short radiative lifetimes (NH: 474 ns; PH: 526 ns). Our work suggests that feasible laser-cooling schemes could be established for a molecular system with extra electronic states close to those chosen for laser-cooling.

Introduction

Searching for promising laser cooling candidates to produce ultracold polar molecules has attracted considerable research interests in recent years owing to their importance for a lot of promising applications in various fields such as precision measurements, quantum computing and quantum information (Hudson et al., 2011; Yan et al., 2013; Baron et al., 2014). One of the most remarkable successes is direct laser cooling of SrF to the µK level in 2010 (Shuman et al., 2010), which has initiated many research interests in molecular laser cooling. However, up to now only a very limited number of molecules have been successfully cooled to the ultracold temperatures experimentally. So there is an urgent necessity to search for more promising laser cooling candidates, and some theoretical efforts have been made to identify more candidates for laser cooling (Wells and Lane, 2011; Fu et al., 2017; Cao et al., 2019; Moussa et al., 2021). It is known (Fu et al., 2016; Yuan et al., 2019; Li et al., 2021) that, a suitable candidate for laser cooling needs to satisfy three criteria: highly diagonal Franck-Condon factors (FCFs), an extremely short radiative lifetime, and no interference from the intermediate electronic states. In our recent work, the fourth criterion for molecular laser cooling was proposed, that is, no electronic-state crossing, or the crossing point between the two states was high enough in energy (Li et al., 2020). Consequently, all electronic states close to those chosen for laser-cooling should be calculated and checked beforehand in selecting laser-cooling candidates.

Many studies have been performed for NH and PH over the past decades. Experimentally, most previous studies were based upon spectroscopic techniques. In 1959, Dixon (1959) observed the emission spectra of the $A^3\Pi$ → $X^3{\Sigma }^{-}$ transition of NH and photographed the (0, 0) and (1, 0) bands. In 1976, Smith et al. (1976) observed weak predissociation from the $A^3\Pi$ state of NH via high resolution lifetime measurements using the high-frequency deflection technique. In 1986, the emission spectra of the $A^3\Pi$ → $X^3{\Sigma }^{-}$ transition of NH were observed by Brazier et al. (1986) using a high-resolution Fourier transform spectrometer. They reported the vibrational, fine structure and rotational constants of the two states. In 1999, the high-resolution emission spectra of the $A^3\Pi$ → $X^3{\Sigma }^{-}$ transition of NH were observed using a Fourier transform spectrometer, and five vibration-rotation bands were measured (Ram et al., 1999). On the other hand, in 1974, the emission spectra of the $A^3\Pi$ → $X^3{\Sigma }^{-}$ transition of PH were photographed with high resolution, and the (0, 0) and (0, 1) bands were obtained (Rostas et al., 1974). In 1985, Gustafsson et al. (1985) recorded the emission spectra of the $A^3\Pi$ → $X^3{\Sigma }^{-}$ transition of PH and measured the fluorescence lifetimes of individual rotational fine structure levels for the v' = 0 level of the $A^3\Pi$ state by the high frequency deflection technique; they detected weak predissociations from the $A^3\Pi$ state. In 2002, Fitzpatrick et al. (2002) observed the emission spectra of the $A^3\Pi$ → $X^3{\Sigma }^{-}$ transition of PH, reported the fluorescence lifetimes of the (1, 0) (2, 0) and (2, 1) bands, and investigated the predissociation dynamics of the $A^3\Pi$ state. Later, Fitzpatrick et al. (2003) recorded Sub-Doppler spectra of the $A^3\Pi$ → $X^3{\Sigma }^{-}$ transition of PH and reported measurements of the hyperfine coupling constants of the $A^3\Pi$ state.

Theoretically, in 1987, Gustafsson et al. (1987) performed ab initio calculations on NH using the complete active space self-consistent field (CASSCF) method, and reported the radiative lifetimes of various rovibrational levels in the $A^3\Pi$ state. In 2007, Owono et al. (2007) calculated the potential energy curves (PECs), spectroscopic constants and dipole moment functions for the excited and Rydberg states of NH with the internally contracted multireference configuration interaction (icMRCI) approach. Subsequently, Owono et al. (2008) computed various radiative characteristics for the $A^3\Pi$ → $X^3{\Sigma }^{-}$ transition of NH including Einstein coefficients, radiative lifetimes and oscillator strengths at the MRCI level. In 2016, Song et al. (2016) obtained the PECs of the twelve Λ-S states and corresponding Ω states for NH using the icMRCI approach including the Davidson correction (+Q). They also calculated the allowed transition dipole moments of four transitions and the lifetimes of the corresponding vibrational levels. On the other hand, seven low-lying Λ-S states of PH were calculated at the MRCI level by Bruna et al. (1981) in 1981; they supposed that the ${}^5{\Sigma }^{-}$ repulsive state was responsible for the predissociation of the $A^3\Pi$ state. In 1992, the transition moments of the $A^3\Pi$ → $X^3{\Sigma }^{-}$ transition and dipole moments of the first five low-lying states of PH were computed by an ab initio effective valence shell Hamiltonian method (Park and Sun, 1992). In 2014, Gao and Gao (2014) investigated the spectroscopic properties of six low-lying Λ-S states and predissociation mechanisms of the $A^3\Pi$ state for PH using the icMRCI + Q method.

Molecular laser cooling is achieved by a continuous scattering of a large number of photons, with each cycle of absorption and emission slowing down its translational motion by a small amount. In each cooling cycle, molecules are excited to their higher electronic state, and then return to the initial ground state through spontaneous emission. Photons are emitted in random directions with a symmetric average distribution, so their contribution to the molecule’s momentum averages to zero. Consequently, a molecule is slowed using the transfer of momentum that occurs when it absorbs a colliding photon. The emission in a molecule may populate different vibrational levels, and thus additional repump lasers must be used to bring the population back to continue the photon cycling.

So far, there have not been theoretical investigations reported on laser cooling of PH to the best of our knowledge. Very recently, the $A^3{\Pi }_1$ → $X^3{\Sigma }^{-}$ transition of NH has been used to establish a laser cooling scheme based on the ab initio calculation by Yan et al. (2021), however, the spin-orbit coupling (SOC) effects on the PECs and vibrational structures were not considered, and the influences of higher electronic states and the spin-orbit splitting of the $X^3{\Sigma }^{-}$ state were not studied. In the present work, by means of highly accurate ab initio and dynamical calculations with the SOC effects included, two excellent ultracold molecular candidates from group VA hydrides are identified, which satisfy all known criteria of molecular laser cooling. The paper is organized as follows. The theoretical methods and computational details are briefly described in section 2. In section 3, we present the calculational results, outline the effects of the extra electronic states on laser cooling, and construct two feasible schemes for promising ultracold molecular candidates from group VA hydrides. The conclusions are given in section 4.

Methods and Computational Details

In the present work, all the ab initio calculations of NH and PH are performed in the C_2v point group using the MOLPRO 2012.1 program package (Werner et al., 2012). The energies of six Λ-S states of NH and PH are calculated using the CASSCF (Werner and Knowles, 1985) method followed by the icMRCI + Q (Langhoff and Davidson, 1974; Knowles and Werner, 1988; Werner and Knowles, 1988) method.

Choosing a proper active space is crucial in the CASSCF and MRCI + Q calculations (Liu et al., 2009; Yu and Bian, 2011; Yu and Bian, 2012). The full valence space is inadequate from our test calculations, thus we add additional orbitals into active space for NH and PH. The inner shell orbitals are included to account for the core-valence correlation effects, and the outer virtual orbitals are involved to give a better description on the dissociation behavior as well as Rydberg character, especially for excited electronic states (Shen et al., 2017). The best balance accuracy and computational performance is to distribute the eight electrons in ten active orbitals corresponding to N 1s2s2p3s3p and H 1s, and we use the aug-cc-pV6Z basis sets for N and H (Dunning and Peterson, 2000; van Mourik et al., 2000). The active space of PH is denoted as CAS (6e, 7o) including the P 3s3p3d_π and H 1s orbitals, and the aug-cc-pV6Z basis sets are used for P and H. In the SOC computations, the SOC effect was included by the state interaction approach with the Breit-Pauli Hamiltonian (H_BP) (Berning et al., 2000), and the SO eigenstates were obtained by diagonalizing Ĥ^el + Ĥ^SO in a basis of eigenfunctions of Ĥ^el. Moreover, the Ĥ^el matrix elements are obtained from the icMRCI + Q calculations, and the Ĥ^SO matrix elements are acquired from the icMRCI + Q waves functions.

The Einstein spontaneous emission coefficient $A_{{\nu }^{\prime },J^{\prime }\to \nu ,J}$ from the initial-state (ν′, J′) to the final-state (ν, J) is defined by the following expression (Herzberg, 1950):

$A_{{\nu }^{\prime },J^{\prime }\to \nu ,J}=3.1361861\times {10}^{-7}\frac{S\left(J^{\prime },J\right)}{2J^{\prime }+1}{v}^3{\left|{\Psi }_{{\nu }^{\prime },J^{\prime }}\left|M\left(r\right)\right|{\Psi }_{\nu ,J}\right|}^2(1)$

where $A_{{\nu }^{\prime },J^{\prime }\to \nu ,J}$ is in s⁻¹ unit, $S\left(J^{\prime },J\right)$ is the Hönl-London rotational intensity factor, v is emission frequency in cm⁻¹ unit, M (r) is the transition dipole function in Debye unit, ${\Psi }_{\nu ,J}$ and ${\Psi }_{{\nu }^{\prime },J^{\prime }}$ are the unit normalized radial wave functions.

For a given vibrational level ν′, the radiative lifetime $\left({\tau }_{{\nu }^{\prime }}\right)$ is obtained by the following expression:

${\tau }_{{\nu }^{\prime }}=\frac{1}{{\displaystyle {\sum }_v{A}_{v^{\prime }v}}}(2)$

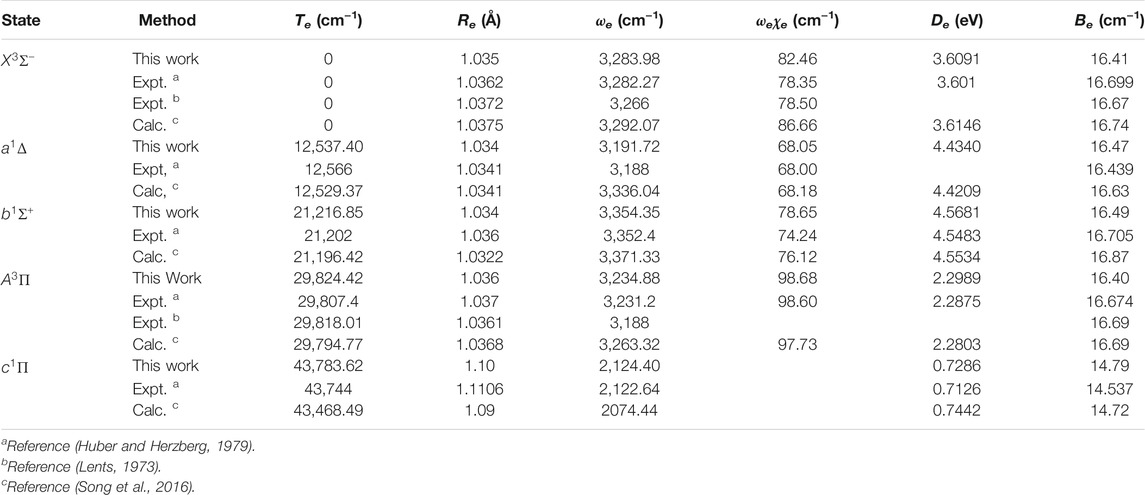
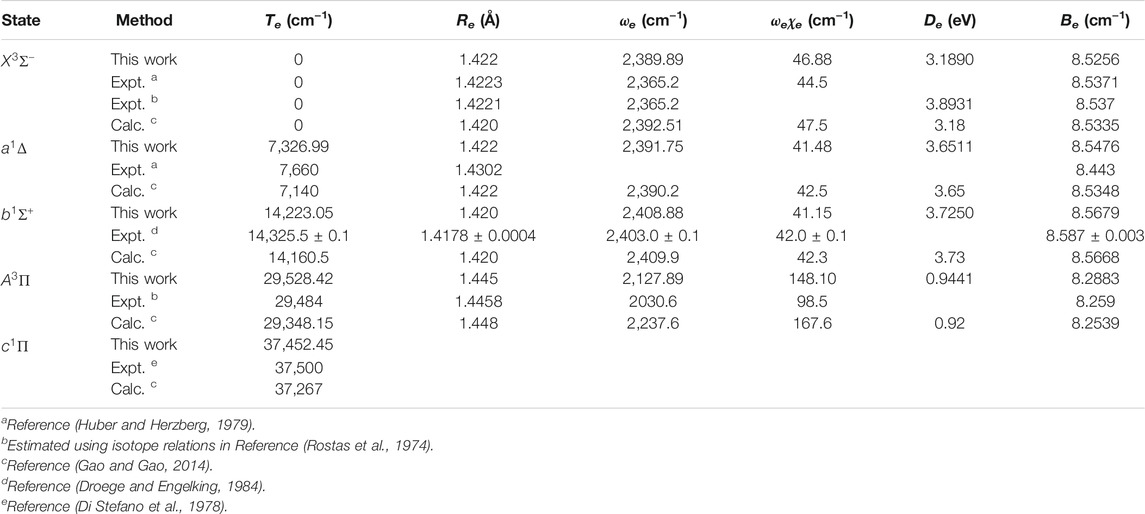
The spectroscopic constants of NH and PH, including the adiabatic relative electronic energy referred to the ground state (T_e), equilibrium interatomic distance (R_e), dissociation energy (D_e), the rotational constant (B_e), the harmonic and anharmonic vibrational constants (ω_e and ω_eχ_e) are determined by solving the nuclear Schrӧdinger equation using the LEVEL 8.0 program (Le Roy, 2007).

Results and Discussion

PECs and Molecular Spectroscopic Constants

In this work, the PECs of six Λ-S electronic states of NH and PH are computed with the icMRCI + Q method. The first three low-lying electronic states ( $X^3{\Sigma }^{-}$, $a^1\Delta$ and $b^1{\Sigma }^{+}$ ) of NH and PH have the same electronic configuration σ²π². The electronic configurations of the excited states $A^3\Pi$ and $c^1\Pi$ are σ¹π³, which could be considered as involving a pσ → pπ transition within the N/P atom. The electronic configuration of the repulsive state ${}^5{\Sigma }^{-}$ is σ¹π²σ^∗. The PECs of six Λ-S electronic states of NH and PH are depicted in Figures 1 and 2, respectively. As seen in Figures 1 and 2, the $X^3{\Sigma }^{-}$ and ${}^5{\Sigma }^{-}$ states of NH and PH correlate to the lowest neutral atomic N/PH $\left({}^4\text{S}\right)$ +$\text{H}\left({}^2\text{S}\right)$ limit, the $a^1\Delta$, $A^3\Pi$ and $c^1\Pi$ states correlate adiabatically to the N/PH $\left({}^2\text{D}\right)+\text{H}\left({}^2\text{S}\right)$ limit, and the $b^1{\Sigma }^{+}$ state corresponds to the N/PH $\left({}^2\text{P}\right)+\text{H}\left({}^2\text{S}\right)$ limit. Since the spectroscopic constants of the $X^3{\Sigma }^{-}$ and $A^3\Pi$ states have been measured in experiment for NH and PH, comparing with the available experimental measurements could give an indicator of the accuracy and reliability of our computations. Our calculated spectroscopic constants of five Λ-S states for NH and PH are tabulated in Tables 1 and 2, respectively, comparing with previous experimental and theoretical values.

FIGURE 1

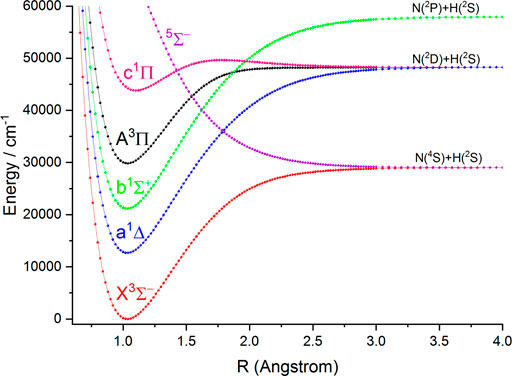
FIGURE 1. Potential energy curves of NH as a function of the interatomic distance (R) for the six Λ-S states at the icMRCI(8e, 10o)+Q/aug-cc-pV6Z level.

FIGURE 2

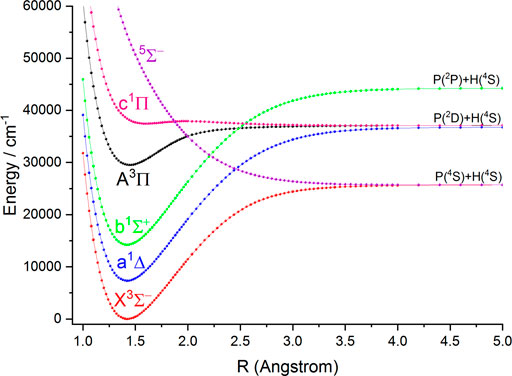
FIGURE 2. Potential energy curves of PH as a function of the interatomic distance (R) for the six Λ-S states at the icMRCI (6e, 7o) + Q/aug-cc-pV6Z level.

TABLE 1

TABLE 1. Spectroscopic constants of the five Λ-S states for NH.

TABLE 2

TABLE 2. Spectroscopic constants of the five Λ-S states for PH.

As seen in Table 1, for the ground state $X^3{\Sigma }^{-}$ of NH, our computed R_e, ω_e and ω_eχ_e values (1.035 Å, 3,283.98 and 82.46 cm⁻¹) reproduce the experimental data (1.0362 Å, 3,282.27 and 78.35 cm⁻¹) very well (Huber and Herzberg, 1979). It is also encouraging to see that our calculated D_e value of 3.6091 eV for the $X^3{\Sigma }^{-}$ state of NH is in excellent agreement with the experimental result of 3.601 eV (Huber and Herzberg, 1979). Concerning the first excited state $a^1\Delta$ of NH, our computed T_e, ω_e and ω_eχ_e values are 12,537.40, 3,191.72 and 68.05 cm⁻¹, respectively, which are in excellent accordance with the experimental data (12,566, 3,188 and 68.00 cm⁻¹) (Huber and Herzberg, 1979) and much improved compared with the previous calculations (12,529.37, 3,336.04 and 68.18 cm⁻¹) (Song et al., 2016). The calculated R_e and B_e values (1.034 Å and 16.47 cm⁻¹) of the $a^1\Delta$ state are in excellent accordance with the measurements (1.0341 Å and 16.439 cm⁻¹) (Huber and Herzberg, 1979). Next in energy is the $b^1{\Sigma }^{+}$ state of NH. Our calculated T_e value of the $b^1{\Sigma }^{+}$ state (21,216.85 cm⁻¹) is in excellent agreement with the experimental data (21,202 cm⁻¹) (Huber and Herzberg, 1979) and theoretical value (21,196.42 cm⁻¹) (Song et al., 2016). The R_e and ω_e values of the $b^1{\Sigma }^{+}$ state computed by us (1.034 Å and 3,354.35 cm⁻¹) are much closer to the experimental results (1.036 Å and 3352.4 cm⁻¹) compared with the previous theoretical values (1.0322 Å and 3,371.33 cm⁻¹). Besides, our computed ω_eχ_e, D_e and B_e values of the $b^1{\Sigma }^{+}$ state agree well with the experimental results. The experimental T_e value of the $A^3\Pi$ state of NH is (29,818.01 cm⁻¹) (Lents, 1973), whereas our calculated T_e value is 29,824.42 cm⁻¹, which is better than the previous computational value (29,794.77 cm⁻¹) (Song et al., 2016). The R_e, ω_e, ω_eχ_e and D_e values of the $A^3\Pi$ state computed by us (1.036 Å, 3,234.88 cm⁻¹, 98.68 cm⁻¹ and 2.2989 eV) agree very well with the corresponding experimental data (1.037 Å, 3,231.2 cm⁻¹, 98.60 cm⁻¹ and 2.2875 eV) (Huber and Herzberg, 1979). For the $c^1\Pi$ state of NH, the excitation energy is calculated to be 43,783.62 cm⁻¹, noticeably higher than that obtained in the previous calculations (43,468.49 cm⁻¹) (Song et al., 2016), and thus in much better agreement with the measured value of 43,744 cm⁻¹(Huber and Herzberg, 1979). The calculated R_e, ω_e and D_e values of the $c^1\Pi$ state of NH are 1.10 Å, 2,124.40 cm⁻¹ and 0.7286 eV, respectively, which agree excellently with the experimental results (1.1106 Å, 2,122.64 cm⁻¹ and 0.7126 eV). In Figure 1, for the $c^1\Pi$ state of NH, the bump of the PEC may result from an avoided crossing between the $c^1\Pi$ state and a higher ${}^1\Pi$ state. The resultant potential barrier is 1,293.26 cm⁻¹ at 1.80 Å relative to the dissociation limit in this work, which is in very good agreement with the value of 1,292.12 cm⁻¹ calculated by Song et al. (2016)

In Table 2, our calculated R_e and B_e values of the $X^3{\Sigma }^{-}$ state of PH are 1.422 Å and 8.5256 cm⁻¹, respectively, which agree perfectly with the experimental measurements (1.4223 Å and 8.5371 cm⁻¹) (Huber and Herzberg, 1979). The present calculated ω_e and ω_eχ_e values of the $X^3{\Sigma }^{-}$ state are 2,389.89 cm⁻¹ and 46.88 cm⁻¹, respectively, which are in very good agreement with the previous theoretical results (2,392.51 cm⁻¹ and 47.5 cm⁻¹) (Gao and Gao, 2014). For the $a^1\Delta$ state of PH, our calculated T_e value (7,326.99 cm⁻¹) is much closer to the experimental value (7,660 cm⁻¹) (Huber and Herzberg, 1979) than the old one (7,140 cm⁻¹) (Gao and Gao, 2014). The R_e, ω_e, ω_eχ_e, D_e and B_e values of the $a^1\Delta$ state are computed to be 1.422 Å, 2,391.75 cm⁻¹, 41.48 cm⁻¹, 3.6511 eV and 8.5476 cm⁻¹, respectively, which agree very well with the corresponding theoretical results (1.422 Å, 2,390.2 cm⁻¹, 42.5 cm⁻¹, 3.65 eV and 8.5348 cm⁻¹) (Gao and Gao, 2014). The excitation energy of the present work for the $b^1{\Sigma }^{+}$ state of PH is computed to be 14,223.05 cm⁻¹, which is much closer to the experimental result of 14,325.5 ± 0.1 cm⁻¹ (Droege and Engelking, 1984) than the previous calculation (14,160.5 cm⁻¹) (Gao and Gao, 2014). It is also encouraging to see that the present values of R_e and ω_e values for the $b^1{\Sigma }^{+}$ state are 1.420 Å and 2,408.88 cm⁻¹, respectively, which are in excellent agreement with those derived experimentally, 1.4178 ± 0.0004 Å and 2,403.0 ± 0.1 cm⁻¹ (Droege and Engelking, 1984). In addition, the calculated value (41.15 cm⁻¹) for ω_eχ_e of the $b^1{\Sigma }^{+}$ state agrees very well with the experimental value of 42.0 ± 0.1 cm⁻¹ (Droege and Engelking, 1984). Besides, the computed D_e and B_e values of the $b^1{\Sigma }^{+}$ state (3.7250 eV and 8.5679 cm⁻¹) are in very good agreement with the theoretical results (3.73 eV and 8.5668 cm⁻¹) (Gao and Gao, 2014). The experimental excitation energy to the $A^3\Pi$ state of PH is 29,484 cm⁻¹ (Rostas et al., 1974), while the present value is 29,528.42 cm⁻¹, which is much improved compared with the previous theoretical value 29,348.15 cm⁻¹ (Gao and Gao, 2014). For the $A^3\Pi$ state, the agreement between our computed R_e, D_e and B_e values (1.445 Å, 0.9441 eV and 8.2883 cm⁻¹) and the theoretical data (1.448 Å, 0.92 eV and 8.2539 cm⁻¹) (Gao and Gao, 2014) is very good. There are some deviations between the calculational and experimental (Rostas et al., 1974) results for the ω_e and ω_eχ_e values of the $A^3\Pi$ state, although the experimental values were estimated based on the isotopic relation, and may have large uncertainties (Rostas et al., 1974). The experimental T_e value of the $c^1\Pi$ state of PH is 37,500 cm⁻¹(Di Stefano et al., 1978), whereas our calculated T_e value is 37,452.45 cm⁻¹, which is much better than the previous computational value of 37,267 cm⁻¹. (Gao and Gao, 2014).

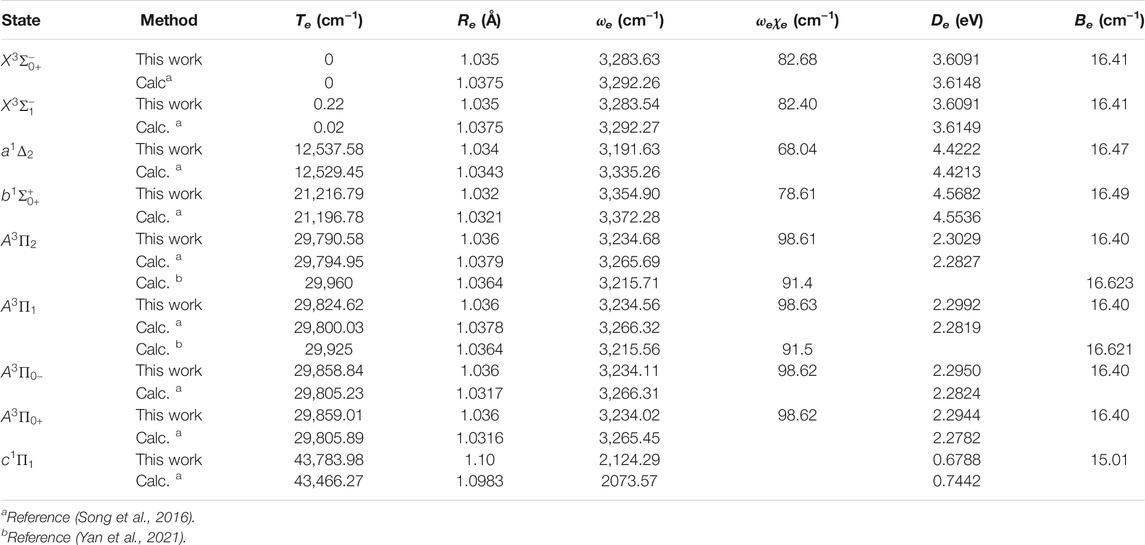
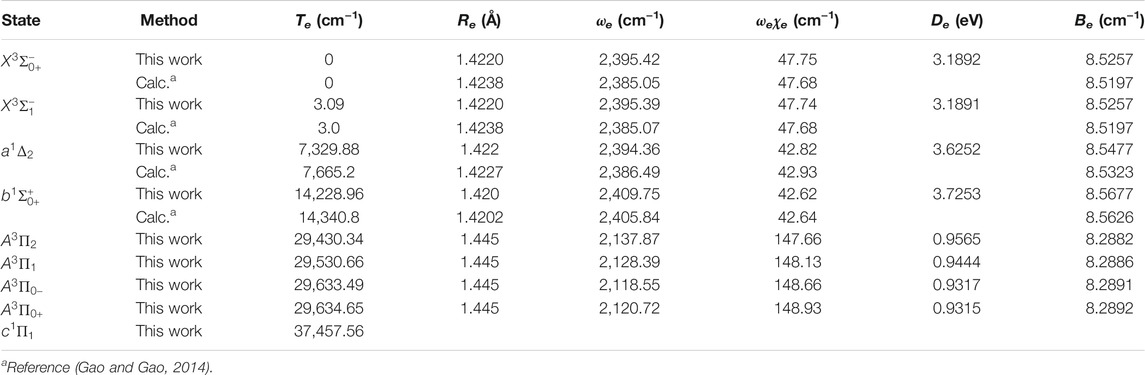
The six Λ-S states $X^3{\Sigma }^{-}$, $a^1\Delta$ , $b^1{\Sigma }^{+}$, $A^3\Pi$, $c^1\Pi$ and ${}^5{\Sigma }^{-}$ of NH and PH split into 12 Ω states when the SOC effects are taken into account, including three states with Ω = $0^{+}$ ( $X^3{\Sigma }_{0+}^{-}$, $b^1{\Sigma }_{0+}^{+}$ and $A^3{\Pi }_{0+}$ ), two states with Ω = $0^{-}$ ( $A^3{\Pi }_{0-}$ and ⁵${\Sigma }_{0-}^{-}$ ), four states with Ω = 1 ($X^3{\Sigma }_1^{-}$, $A^3{\Pi }_1$, $c^1{\Pi }_1$ and ⁵${\Sigma }_1^{-}$), and three states with Ω = 2 ($a^1{\Delta }_2$, $A^3{\Pi }_2$ and ⁵${\Sigma }_2^{-}$ ). The PECs of 12 Ω states of NH and PH are depicted in Figures 3 and 4, respectively. The spectroscopic constants of the 9 Ω states of NH and PH including the $X^3{\Sigma }_{0+}^{-}$, $X^3{\Sigma }_1^{-}$, $a^1{\Delta }_2$, $b^1{\Sigma }_{0+}^{+}$, $A^3{\Pi }_{0+}$, $A^3{\Pi }_{0-}$, $A^3{\Pi }_1$, $A^3{\Pi }_2$ and $c^1{\Pi }_1$ states are displayed in Tables 3 and 4, respectively. As seen in Table 3, the spectroscopic constants T_e, R_e, ω_e, ω_eχ_e, D_e and B_e values of the four Λ-S states $X^3{\Sigma }^{-}$, $a^1\Delta$ , $b^1{\Sigma }^{+}$ and $c^1\Pi$ of NH are nearly same to those of the corresponding Ω states. For the four Λ-S states of NH, the energy difference between the four Λ-S states and the corresponding Ω states is less than 1 cm⁻¹. While the SO splitting values of the $A^3{\Pi }_1-A^3{\Pi }_2$, $A^3{\Pi }_{0-}-A^3{\Pi }_1$ and $A^3{\Pi }_{0+}-A^3{\Pi }_{0-}$ states are 34.04, 34.22 and 0.17 cm⁻¹, respectively, which are in excellent accordance with the computational values (the splitting values of the $A^3{\Pi }_1-A^3{\Pi }_2$ and $A^3{\Pi }_{0-}-A^3{\Pi }_1$ states are 34.06 and 34.00 cm⁻¹, respectively) (Yan et al., 2021). In Table 4, the energy difference between the four Λ-S states ($X^3{\Sigma }^{-}$, $a^1\Delta$, $b^1{\Sigma }^{+}$ and $c^1\Pi$ ) and the corresponding Ω states of PH is less than 6 cm⁻¹, whereas the SO splitting values of the $A^3{\Pi }_1-A^3{\Pi }_2$, $A^3{\Pi }_{0-}-A^3{\Pi }_1$ and $A^3{\Pi }_{0+}-A^3{\Pi }_{0-}$ states are 100.32, 102.83 and 1.16 cm⁻¹, respectively. In view of the above, the SOC effects should be taken into account for the spectroscopic study of excited states for NH and PH and thus are important for laser cooling of NH and PH.

FIGURE 3

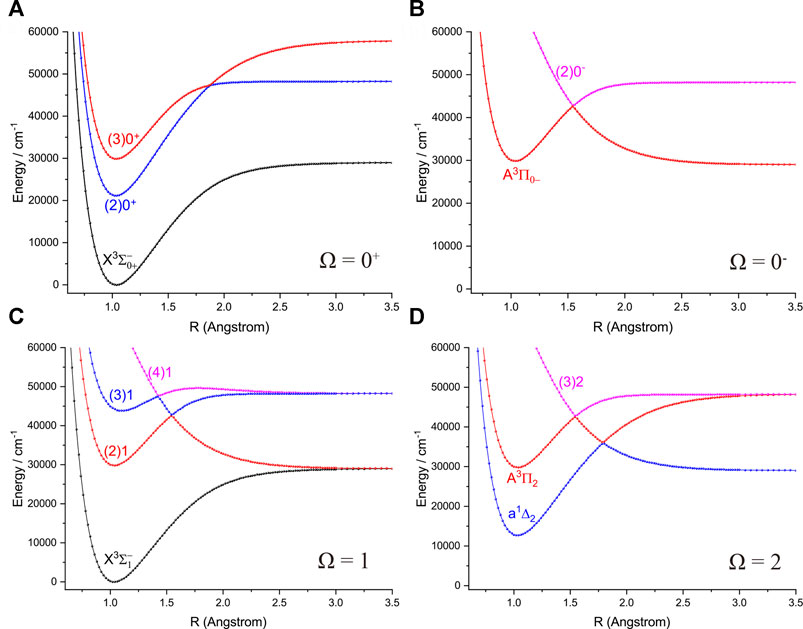
FIGURE 3. Potential energy curves of NH as a function of the interatomic distance (R) for (A) Ω = 0⁺, (B) Ω = 0⁻, (C) Ω = 1 and (D) Ω = 2 at the icMRCI + Q level.

FIGURE 4

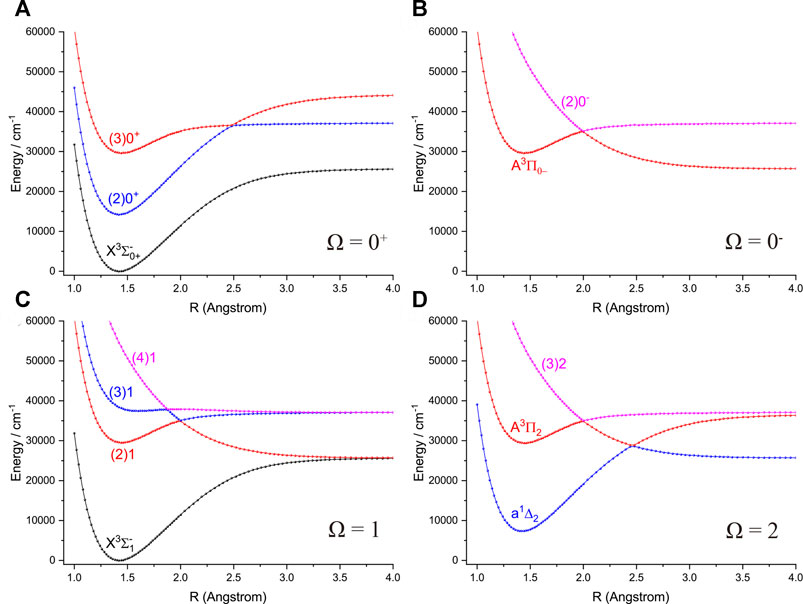
FIGURE 4. Potential energy curves of PH as a function of the interatomic distance (R) for (A) Ω = 0⁺, (B) Ω = 0⁻, (C) Ω = 1 and (D) Ω = 2 at the icMRCI + Q level.

TABLE 3

TABLE 3. Spectroscopic constants of the 9 Ω states for NH.

TABLE 4

TABLE 4. Spectroscopic constants of the 9 Ω states for PH.

Accurate determination of T_e is very important for evaluating the pump and repump wavelengths in laser-cooling cycles, and our computed T_e values, which agree very well with the corresponding experimental ones, give us confidence in the subsequent investigation on molecular laser cooling of NH and PH.

The Effects of the Extra Electronic States on Laser Cooling

Here, we discuss the effects of the extra electronic states on direct laser cooling of NH and PH. An amplified view of crossing regions of PECs of the $A^3\Pi$ and ${}^5{\Sigma }^{-}$ states for NH and PH is depicted in Figure 5. We can see that the dissociation energies of the $A^3\Pi$ state of NH and PH are 18,541.92 and 7,614.34 (Di Stefano et al., 1978)cm⁻¹, respectively. The $A^3\Pi$ and ${}^5{\Sigma }^{-}$ states of NH and PH have a crossing point, which can lead to nonradiative transition (Wu et al., 2019), and may cause predissociation. In the polyatomic molecule cases, this kind of electronic state crossing in a diatomic molecule will become potential energy surface intersections including multiple electronic states (Liu et al., 2003; Zhao et al., 2006). We find that the locations of crossing point between the $A^3\Pi$ and ${}^5{\Sigma }^{-}$ states of NH and PH are higher than the corresponding ν′ = 2 vibrational levels of the $A^3\Pi$ state (4,163 and 989 cm⁻¹, respectively) indicating that the crossings with higher electronic states would not affect laser cooling. The large $f_{00}$ values of the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition for NH and PH (NH: 0.9994; PH: 0.9675) suggest that the two molecules are promising candidates for efficient and rapid laser cooling. This conclusion can be backed up by experimentalists, since the (1, 1) band of the $A^3\Pi$ → $X^3{\Sigma }^{-}$ transition for NH and PH has been observed (Funke, 1935; Fitzpatrick et al., 2002). Generally speaking, a larger atomic mass difference for the diatomic candidate is desirable by experimentalists, and in this respect, PH is a better laser cooling candidate than NH.

FIGURE 5

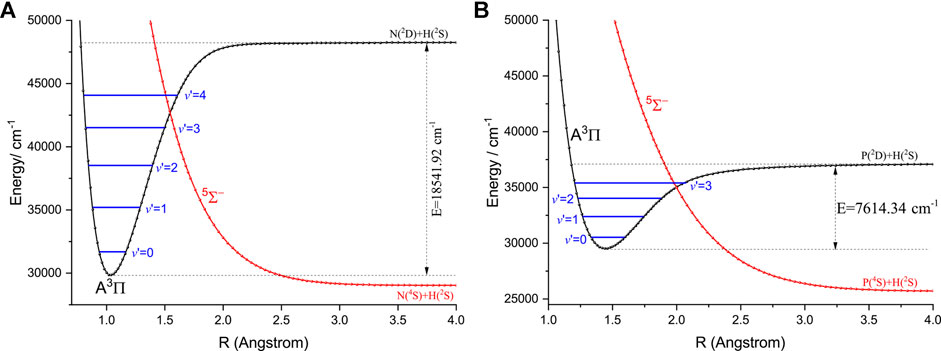
FIGURE 5. An amplified view of crossing regions of the $A^3\Pi$ and ${\hspace{0.17em}}^5{\Sigma }^{-}$ potential energy curves for NH (A) and PH (B) as a function of the interatomic distance (R).

It should be noted that the transitions between the singlet and triplet states are allowed when the SOC effects are considered. The effects of the intermediate electronic states $\left(a^1{\Delta }_2\text{and}{b}^1{\Sigma }_{0+}^{+}\right)$ of NH and PH on laser cooling are discussed below. There are two intermediate electronic states $a^1{\Delta }_2$ and $b^1{\Sigma }_{0+}^{+}$ in the constructed laser cooling schemes for NH/PH based on the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition, where NH/PH molecules are excited from the $X^3{\Sigma }_1^{-}$ (v = 0) state to the $A^3{\Pi }_2$ (v′ = 0) state, then they may decay to the $X^3{\Sigma }_1^{-}$ or $a^1{\Delta }_2$ state rather than the $b^1{\Sigma }_{0+}^{+}$ state since the $A^3{\Pi }_2$ → $b^1{\Sigma }_{0+}^{+}$ transition is forbidden according to the selection rules. So the intermediate electronic state $b^1{\Sigma }_{0+}^{+}$ does not interfere with the laser-cooling. In addition, the absolute transition dipole moments (TDMs) of the $A^3{\Pi }_2$ → $a^1{\Delta }_2$ transition for NH and PH are shown in Supplementary Figure S1. As seen, the TDMs values of the $A^3{\Pi }_2$ → $a^1{\Delta }_2$ transition for NH and PH are 0.000495 and 0.000793 debye (0.082% and 0.1169% of the corresponding $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition) at corresponding R_e. The vibrational branching loss ratios $\left({\eta }_i\right)\left[{\eta }_i=A_{A^3{\Pi }_2\to a^1{\Delta }_2}/\left(A_{A^3{\Pi }_2\left(v^{\prime }=0\right)\to X^3{\displaystyle {\Sigma }_1^{-}\left(v\right)}}+A_{A^3{\Pi }_2\to a^1{\Delta }_2}\right)\right]$ of the $A^3{\Pi }_2$ → $a^1{\Delta }_2$ $\left({\eta }_1\right)$ transition for NH and PH are extremely small (NH: 1.81 × 10^–8; PH: 1.08 × 10^–6), and much smaller than the experimental value of YO ( $\eta$ (YO) $<$ 4 × 10^–4) (Hummon et al., 2013). The extremely small vibrational branching loss ratios of the $A^3{\Pi }_2$ → $a^1{\Delta }_2$ transition for NH and PH indicate that the $a^1{\Delta }_2$ intermediate electronic state will not interfere with the laser-cooling. Hence, we will construct feasible three-laser cooling schemes for NH and PH on the basis of the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition in the next section, which satisfy all known criteria including the fourth one proposed in our recent work (Li et al., 2020).

Laser Cooling Schemes Proposed for NH and PH Using Specific Spin-Orbit States

Since the SOC effects are important as shown above, we construct the schemes for laser cooling of NH and PH using the spin-orbit states $A^3{\Pi }_2$ and $X^3{\Sigma }_1^{-}$. We find that only the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition can ensure a closed-loop cooling cycles in the six possible transitions ($A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$, $A^3{\Pi }_1$ → $X^3{\Sigma }_1^{-}$, $A^3{\Pi }_1$ → $X^3{\Sigma }_{0+}^{-}$, $A^3{\Pi }_{0+}$ → $X^3{\Sigma }_1^{-}$, $A^3{\Pi }_{0+}$ → $X^3{\Sigma }_{0+}^{-}$ and $A^3{\Pi }_{0-}$ → $X^3{\Sigma }_1^{-}$) from the $A^3{\Pi }_{\Omega }$. The $A^3{\Pi }_2$ → $X^3{\Sigma }_{0+}^{-}$ and $A^3{\Pi }_{0-}$ → $X^3{\Sigma }_{0+}^{-}$ transitions for NH and PH are forbidden according to the selection rules of transitions between the Ω states. In addition, the $A^3{\Pi }_2$ state of NH and PH is the energetically lowest-lying state in the 4 Ω states ($A^3{\Pi }_{0+}$, $A^3{\Pi }_{0-}$, $A^3{\Pi }_1$ and $A^3{\Pi }_2$), which can avoid the interference from the other $A^3{\Pi }_{\Omega }$ states ($A^3{\Pi }_{0+}$, $A^3{\Pi }_{0-}$ and $A^3{\Pi }_1$) and ensure a closed-loop cooling cycles. In the constructed laser cooling schemes for NH/PH molecules based on the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition, NH/PH molecules are excited from the $X^3{\Sigma }_1^{-}$ (v = 0) state to the $A^3{\Pi }_2$ (v′ = 0) state, then they will decay to the $X^3{\Sigma }_1^{-}$ state rather than the $X^3{\Sigma }_{0+}^{-}$ state according to the selection rules, and the ultracold NH/PH will be produced through the constructed schemes when the process of cooling cycles repeats constantly. Consequently, the $A^3{\Pi }_2$ (v') → $X^3{\Sigma }_1^{-}$ (v) transition of NH and PH is used to establish corresponding laser cooling schemes in this work.

The permanent dipole moments (PDMs) and TDMs for the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition of NH and PH at the icMRCI + Q level are shown in Supplementary Figure S2. The TDMs of NH and PH decrease with the increasing interatomic distance and are 0.6059 and 0.6788 debye, respectively, at corresponding R_e. The FCFs $\left(f_{{\nu }^{\prime }\nu }\right)$ values of the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition for NH and PH are computed and plotted in Figures 6 and 7, respectively. We can clearly see that the $f_{{\nu }^{\prime }\nu }$ values of $\Delta \nu =0$ vibrational levels of the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition for NH and PH are remarkably higher than those for the off-diagonal terms. The $f_{00}$ values of the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition for NH (0.9994) and PH (0.9675) are so large that the spontaneous decays to ν = 1, 2 vibrational levels of the corresponding $X^3{\Sigma }_1^{-}$ state are highly restricted. We will use the v' = 0, 1 levels of the corresponding $A^3{\Pi }_2$ state of NH and PH with three lasers to establish laser cooling cycles on the basis of the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition. Owing to the relative strengths of the photon loss pathways are more directly related to the vibrational branching ratios $R_{{\nu }^{\prime }\nu }$ than the $f_{{\nu }^{\prime }\nu }$ in the laser cooling cycle, the Einstein spontaneous emission coefficient $A_{{\nu }^{\prime }\nu }$ and $R_{{\nu }^{\prime }\nu }$ of the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition for NH and PH are calculated and presented in Tables 5 and 6, respectively. As seen, a very large $A_{00}$ (NH: 2.10×10⁶ s⁻¹, PH: 1.90×10⁶ s⁻¹) and very low scattering probabilities into off-diagonal bands of NH and PH contribute to a desirable condition for efficient and rapid optical cycles.

FIGURE 6

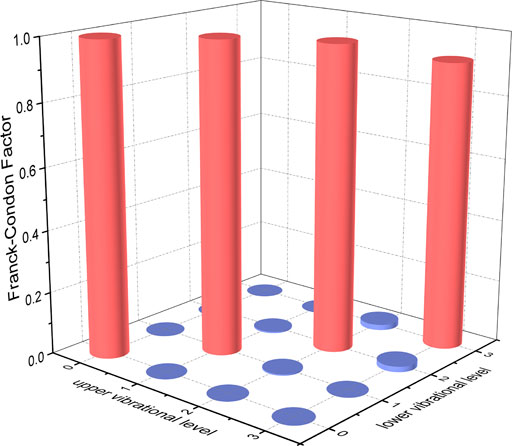
FIGURE 6. Franck-Condon factors of the $A^3{\Pi }_2$ (v' ≤ 3) → $X^3{\Sigma }_1^{-}$ (v ≤ 3) transitions for NH, calculated at the icMRCI + Q level.

FIGURE 7

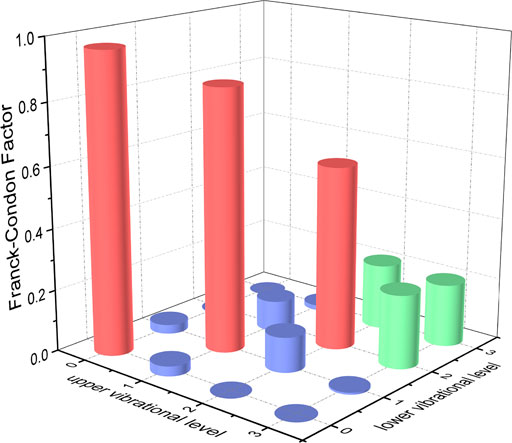
FIGURE 7. Franck-Condon factors of the $A^3{\Pi }_2$ (v' ≤ 3) → $X^3{\Sigma }_1^{-}$ (v ≤ 3) transitions for PH, calculated at the icMRCI + Q level.

TABLE 5

TABLE 5. Calculated Einstein A coefficients $A_{{\nu }^{\prime }\nu }$ and vibrational branching ratio $R_{{\nu }^{\prime }\nu }$ of the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition for NH.

TABLE 6

TABLE 6. Calculated Einstein A coefficients $A_{{\nu }^{\prime }\nu }$ and vibrational branching ratio $R_{{\nu }^{\prime }\nu }$ of the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition for PH.

The $R_{{\nu }^{\prime }\nu }$ are assessed using the following expression:

$R_{{\nu }^{\prime }\nu }=\frac{A_{{\nu }^{\prime }\nu }}{{\displaystyle {\sum }_v{A}_{{\nu }^{\prime }\nu }}}(3)$

In addition, the Doppler temperatures ( $T_{Doppler}=h/\left(4k_B\pi \tau \right)$, where h is Planck’s constant, k_B is Boltzmann’s constant, and τ is the radiative lifetime) of the $A^3{\Pi }_2$ (ν′ = 0) → $X^3{\Sigma }_1^{-}$ (ν = 0) transition of NH and PH are 8.06 and 7.27 µK, respectively, the radiative lifetimes $\left({\tau }_{{\nu }^{\prime }}\right)$ for main cooling transition of NH and PH are 474 and 526 ns, respectively, and the recoil temperatures $\left(T_{recoil}=h^2/\left(m{k}_B{\lambda }^2\right),\text{where}\text{λ}\text{is}\text{the}\text{laser}\text{wavelength}\right)$ for main cooling transition of NH and PH are 1.13 and 5.12 µK, respectively.

The constructed laser-cooling schemes for the production of ultracold NH and PH are presented in Figures 8 and 9, respectively. As seen in Figure 8, the laser for the main cycling may drive the $X^3{\Sigma }_1^{-}$ (ν = 0, J = 1) → $A^3{\Pi }_2$ (ν′ = 0, J′ = 0) transition of NH at the wavelength ${\lambda }_{00}$ of 336.1 nm (here J represents the rotational quantum number). According to the angular momentum and parity selection rules, the $A^3{\Pi }_2$ (J′ = 0) state can only decays to the initial $X^3{\Sigma }_1^{-}$ (J = 1) state, leading to the elimination of the rotational branching. In addition, another two lasers of 382.8 and 382.6 nm are used to recover the molecules falling to the $X^3{\Sigma }_1^{-}$ (ν = 1, 2) states of NH, further reducing the vibrational branching loss. So quasi-closed optical cycling can be achieved by using the scheme shown in Figure 8. Similarly, in Figure 9, the constructed scheme for PH take the $X^3{\Sigma }_1^{-}$ (ν = 0, J = 1) → $A^3{\Pi }_2$ (ν′ = 0, J′ = 0) transition as the main pump, the $X^3{\Sigma }_1^{-}$ (v = 1) → $A^3{\Pi }_2$ (v′ = 0) and $X^3{\Sigma }_1^{-}$ (v = 2) → $A^3{\Pi }_2$ (ν′ = 1) transitions as the first and second vibrational repump, respectively. The computed pump and repump wavelengths ${\lambda }_{00}$, ${\lambda }_{01}$ and ${\lambda }_{12}$ are 341.9, 370.8 and 375.4 nm, respectively, which are all in the range of ultraviolet A (320 ∼ 400 nm) and can be produced with the frequency doubled Ti: sapphire semiconductor laser (Xing et al., 2018). The large $R_{00}$ values of NH (0.9952) and PH (0.9977) suggest that the $A^3{\Pi }_2$ (ν′ = 0) → $X^3{\Sigma }_1^{-}$ (ν = 0) transition of NH and PH has the largest possibilities, and the vibrational branching loss can be addressed through a reasonable laser cooling cycle process. The off-diagonal $R_{{\nu }^{\prime }\nu }$ of NH and PH have also been computed, and we use $R_{{03}^{+}}$ (here $3^{+}$ means ν $\ge$ 3) to evaluate the possibilities of unwanted decay channels for NH and PH. The negligible values of 9.64 × 10^–6 (NH) and 1.20 × 10^–7 (PH) mean that NH and PH can scatter at least 1.04 × 10⁵ (NH) and 8.32 × 10⁶ (PH) photons on average using the present schemes, respectively, which are enough to decelerate NH and PH in a cryogenic beam, in principle (Shuman et al., 2010).

FIGURE 8

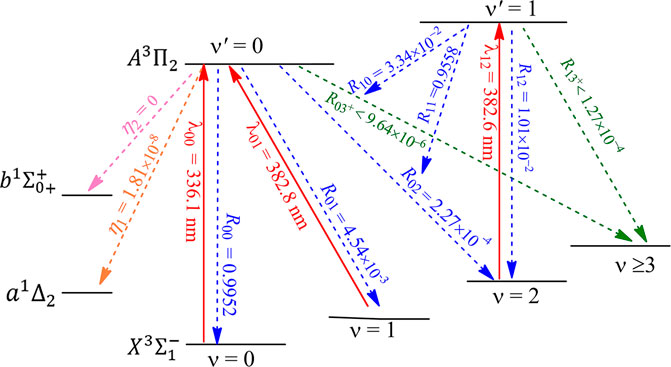
FIGURE 8. Constructed three-laser cooling scheme for NH using the $X^3{\Sigma }_1^{-}$ (ν) → $A^3{\Pi }_2$ (ν′) transitions. Solid arrows indicate laser-driven transitions at certain wavelengths ${\lambda }_{{\nu }^{\prime }\nu }$. Dashed arrows indicate spontaneous decays from the $A^3{\Pi }_2$ (v′ = 0, 1) states with the calculated vibrational branching ratios. The rotational branching can be eliminated by driving the J = 1 → J' = 0 type transition (J is the rotational quantum number) for each vibrational level.

FIGURE 9

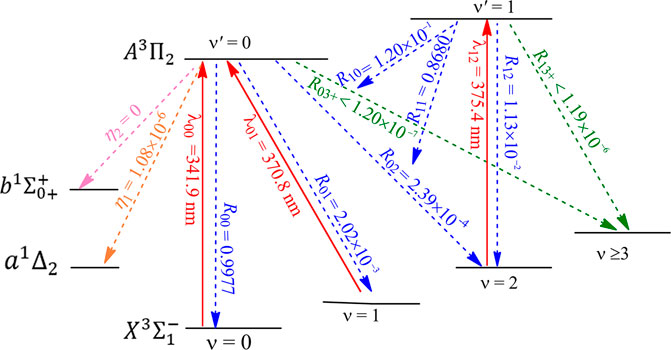
FIGURE 9. Constructed three-laser cooling scheme for PH using the $X^3{\Sigma }_1^{-}$ (ν) → $A^3{\Pi }_2$ (ν′) transitions. Solid arrows indicate laser-driven transitions at certain wavelengths ${\lambda }_{{\nu }^{\prime }\nu }$. Dashed arrows indicate spontaneous decays from the $A^3{\Pi }_2$ (v′ = 0, 1) states with the calculated vibrational branching ratios. The rotational branching can be eliminated by driving the J = 1 → J' = 0 type transition (J is the rotational quantum number) for each vibrational level.

After initial cooling and trapping stages, evaporative cooling is often used to bring molecules to quantum degeneracy or Bose-Einstein condensation. The possibility of evaporative cooling of NH has been investigated (Janssen et al., 2011; Janssen et al., 2013), however, recent accurate quantum calculations (Janssen et al., 2013) indicate that chemical reactions can cause more trap loss than inelastic NH + NH collisions, and evaporative cooling is not favorable for NH. As mentioned above, the laser cooling scheme constructed here allows for 1.04 × 10⁵ photons scattered for NH, which are sufficient for cooling to µK temperatures. In addition, PH seems to be a better candidate than NH for laser cooling. So the present work indicates that the direct laser cooling method can be used to produce magnetically trapped ultracold NH/PH molecules, and it is expected that the subsequent evaporative cooling can be avoided.

Conclusion

In this work, we identify two excellent ultracold molecular candidates from group VA hydrides using highly accurate ab initio method; in particular, NH and PH are identified as very promising laser cooling candidates, which satisfy all known criteria including the fourth one proposed in our recent work. Six low-lying Λ-S states of NH and PH are investigated with the SOC effects included. The agreement between our calculated spectroscopic constants and the available experimental data is excellent. We find that the locations of crossing point between the $A^3\Pi$ and ${}^5{\Sigma }^{-}$ states of NH and PH are higher than the corresponding v′ = 2 vibrational levels of the $A^3\Pi$ state indicating that the crossings with higher electronic states would not affect laser cooling. Meanwhile, the extremely small vibrational branching loss ratios of the $A^3{\Pi }_2$ → $a^1{\Delta }_2$ transition for NH and PH (NH: 1.81 × 10^–8; PH: 1.08 × 10^–6) indicate that the $a^1{\Delta }_2$ intermediate electronic state will not interfere with the laser cooling. Besides, the $b^1{\Sigma }_{0+}^{+}$ intermediate electronic state does not interfere since the $A^3{\Pi }_2$ → $b^1{\Sigma }_{0+}^{+}$ transition is forbidden. Consequently, we construct practical and efficient laser-cooling schemes for NH and PH on the basis of the $A^3{\Pi }_2$ → $X^3{\Sigma }_1^{-}$ transition. The calculated excitation energies to the $A^3\Pi$ state of NH and PH are 29,824.42 and 29,528.42 cm⁻¹, respectively, which are in excellent accordance with the corresponding experimental data (NH: 29,807.4 cm⁻¹; PH: 29,498.0 cm⁻¹) (Huber and Herzberg, 1979). This enables us accurately predict the pump and repump wavelengths in laser cooling cycles. The Doppler temperatures for the main transition of NH and PH are 8.06 and 7.27 µK, respectively, whereas the recoil temperatures are 1.13 and 5.12 µK, respectively. The vibrational branching ratios $R_{{\nu }^{\prime }\nu }$ for the $A^3{\Pi }_2$ (v′ = 0) → $X^3{\Sigma }_1^{-}$ transition of NH and PH are shown to be highly diagonally distributed with $R_{00}$ being 0.9952 and 0.9977, respectively. The radiative lifetimes for the $A^3{\Pi }_2$ (v′ = 0) → $X^3{\Sigma }_1^{-}$ (v = 0) transition of NH and PH are extremely short (NH: 474 ns; PH: 526 ns). The constructed schemes allow for 1.04 × 10⁵ and 8.32 × 10⁶ photons scattered for NH and PH, respectively, which are sufficient for cooling to ultracold temperatures. Generally speaking, PH is a better candidate than NH for laser cooling. It is our hope that the present theoretical study will stimulate experimental interests in laser cooling NH and PH to the ultracold regime.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

DL carried out the ab initio and dynamical calculations. DL and WB analyzed the data, interpreted the results, developed the theoretical schemes and wrote the paper. WB supervised the research.

Funding

This work was supported by the National Natural Science Foundation of China (Nos. 21773251, 21973098).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2021.778292/full#supplementary-material

References

Baron, J., Baron, J., Campbell, W. C., DeMille, D., Doyle, J. M., Gabrielse, G., et al. (2014). Order of Magnitude Smaller Limit on the Electric Dipole Moment of the Electron. Science 343, 269–272. doi:10.1126/science.1248213

PubMed Abstract | CrossRef Full Text | Google Scholar

Berning, A., Schweizer, M., Werner, H.-J., Knowles, P. J., and Palmieri, P. (2000). Spin-orbit Matrix Elements for Internally Contracted Multireference Configuration Interaction Wavefunctions. Mol. Phys. 98, 1823–1833. doi:10.1080/00268970009483386

CrossRef Full Text | Google Scholar

Brazier, C. R., Ram, R. S., and Bernath, P. F. (1986). Fourier Transform Spectroscopy of the A³Π-X³Σ⁻ Transition of NH. J. Mol. Spectrosc. 120, 381–402. doi:10.1016/0022-2852(86)90012-3

CrossRef Full Text | Google Scholar

Bruna, P. J., Hirsch, G., Peyerimhoff, S. D., and Buenker, R. J. (1981). Non-empirical CI Potential Curves for the Ground and Excited States of PH and its Positive Ion. Mol. Phys. 42, 875–898. doi:10.1080/00268978100100681

CrossRef Full Text | Google Scholar

Cao, J., Li, F., Xia, W., and Bian, W. (2019). van der Waals Interactions in Bimolecular Reactions. Chin. J. Chem. Phys. 32, 157–166. doi:10.1063/1674-0068/cjcp1901007

CrossRef Full Text | Google Scholar

Di Stefano, G., Lenzi, M., Margani, A., and Xuan, C. N. (1978). The (B¹Σ⁺) State of PH in the Vacuum Ultraviolet Photolysis of Phosphine. J. Chem. Phys. 68, 959–963. doi:10.1063/1.435834

CrossRef Full Text | Google Scholar

Dixon, R. N. (1959). The 0-0 and 1-0 Bands of the A³Π_i - X³Σ⁻ System of NH. Can. J. Phys. 37, 1171–1186. doi:10.1139/p59-134

CrossRef Full Text | Google Scholar

Droege, A. T., and Engelking, P. C. (1984). The b¹Σ⁺ → X³Σ⁻ Transition in PH: A Measurement of the Term Energy, Bond Length, and Vibrational Frequency of a Phosphinidene Metastable. J. Chem. Phys. 80, 5926–5929. doi:10.1063/1.446698

CrossRef Full Text | Google Scholar

Dunning, T. H., and Peterson, K. A. (2000). Approximating the Basis Set Dependence of Coupled Cluster Calculations: Evaluation of Perturbation Theory Approximations for Stable Molecules. J. Chem. Phys. 113, 7799–7808. doi:10.1063/1.1316041

CrossRef Full Text | Google Scholar

Fitzpatrick, J. A. J., Chekhlov, O. V., Morgan, D. R., Burrows, R. W., and Western, C. M. (2002). Predissociation Dynamics in the A³Π State of PH: An Experimental and Ab Initio investigationElectronic Supplementary Information (ESI) Available: 6 Tables of Supporting Material. See http://www.rsc.Org/suppdata/cp/b1/b111198c/. Phys. Chem. Chem. Phys. 4, 1114–1122. doi:10.1039/b111198c

CrossRef Full Text | Google Scholar

Fitzpatrick, J. A. J., Chekhlov, O. V., Western, C. M., and Ashworth, S. H. (2003). Sub-Doppler Spectroscopy of the PH Radical: Hyperfine Structure in the A³Π State. J. Chem. Phys. 118, 4539–4545. doi:10.1063/1.1543946

CrossRef Full Text | Google Scholar

Fu, M., Ma, H., Cao, J., and Bian, W. (2016). Extensive Theoretical Study on Electronically Excited States of Calcium Monochloride: Molecular Laser Cooling and Production of Ultracold Chlorine Atoms. J. Chem. Phys. 144, 184302. doi:10.1063/1.4948631

CrossRef Full Text | Google Scholar

Fu, M., Ma, H., Cao, J., and Bian, W. (2017). Laser Cooling of CaBr Molecules and Production of Ultracold Br Atoms: A Theoretical Study Including Spin-Orbit Coupling. J. Chem. Phys. 146, 134309. doi:10.1063/1.4979566

CrossRef Full Text | Google Scholar

Funke, G. S. W. (1935). The NH Bands at λ 3360. Z. Physik 96, 787–798. doi:10.1007/bf01337920

CrossRef Full Text | Google Scholar

Gao, Y., and Gao, T. (2014). A Theoretical Study on Low-Lying Electronic States and Spectroscopic Properties of PH. Spectrochimica Acta A: Mol. Biomol. Spectrosc. 118, 308–314. doi:10.1016/j.saa.2013.07.009

CrossRef Full Text | Google Scholar

Gustafsson, O., Kindvall, G., Larsson, M., Olsson, B. J., and Sigray, P. (1987). An Experimental and Theoretical Investigation of the Radiative Properties of the A³Π State of NH. Chem. Phys. Lett. 138, 185–194. doi:10.1016/0009-2614(87)80366-4

CrossRef Full Text | Google Scholar

Gustafsson, O., Kindvall, G., Larsson, M., Senekowitsch, J., and Sigray, P. (1985). An Experimental Investigation of Predissociation Effects in the A³Π-X³Σ⁻ Transition of PH. Mol. Phys. 56, 1369–1380. doi:10.1080/00268978500103101

CrossRef Full Text | Google Scholar

Herzberg, G. (1950). Spectra of Diatomic Molecules. second ed. New York: Van Nostrand Reinhold.

Google Scholar

Huber, K. P., and Herzberg, G. (1979). Molecular Spectra and Molecular Structure IV: Constants of Diatomic Molecules. New York, NY: Van Nostrand Reinhold.

Google Scholar

Hudson, J. J., Kara, D. M., Smallman, I. J., Sauer, B. E., Tarbutt, M. R., and Hinds, E. A. (2011). Improved Measurement of the Shape of the Electron. Nature 473, 493–496. doi:10.1038/nature10104

PubMed Abstract | CrossRef Full Text | Google Scholar

Hummon, M. T., Yeo, M., Stuhl, B. K., Collopy, A. L., Xia, Y., and Ye, J. (2013). 2D Magneto-Optical Trapping of Diatomic Molecules. Phys. Rev. Lett. 110, 143001. doi:10.1103/PhysRevLett.110.143001

PubMed Abstract | CrossRef Full Text | Google Scholar

Janssen, L. M. C., van der Avoird, A., and Groenenboom, G. C. (2013). Quantum Reactive Scattering of Ultracold NH(X³Σ⁻) Radicals in a Magnetic Trap. Phys. Rev. Lett. 110, 063201. doi:10.1103/PhysRevLett.110.063201

PubMed Abstract | CrossRef Full Text | Google Scholar

Janssen, L. M. C., Żuchowski, P. S., van der Avoird, A., Groenenboom, G. C., and Hutson, J. M. (2011). Cold and Ultracold NH-NH Collisions in Magnetic fields. Phys. Rev. A. 83, 022713. doi:10.1103/PhysRevA.83.022713

CrossRef Full Text | Google Scholar

Knowles, P. J., and Werner, H.-J. (1988). An Efficient Method for the Evaluation of Coupling Coefficients in Configuration Interaction Calculations. Chem. Phys. Lett. 145, 514–522. doi:10.1016/0009-2614(88)87412-8

CrossRef Full Text | Google Scholar

Langhoff, S. R., and Davidson, E. R. (1974). Configuration Interaction Calculations on the Nitrogen Molecule. Int. J. Quan. Chem. 8, 61–72. doi:10.1002/qua.560080106

CrossRef Full Text | Google Scholar

Le Roy, R. J. (2007). LEVEL 8.0: A Computer Program for Solving the Radial Schrӧdinger Equation for Bound and Quasibound Levels. Chemical Physics Research Report CPRR-663. Waterloo, Canada: University of Waterloo. Available online at: http://leroy.uwaterloo.ca.

Google Scholar

Lents, J. M. (1973). An Evaluation of Molecular Constants and Transition Probabilities for the NH Free Radical. J. Quantitative Spectrosc. Radiative Transfer 13, 297–310. doi:10.1016/0022-4073(73)90061-7

CrossRef Full Text | Google Scholar

Li, D., Yang, C., Sun, Z., Wang, M., and Ma, X. (2021). Theoretical Study on the Spectroscopic Properties of the Low-Lying Electronic States and the Laser Cooling Feasibility of the CaI Molecule. J. Quantitative Spectrosc. Radiative Transfer 270, 107709. doi:10.1016/j.jqsrt.2021.107709

CrossRef Full Text | Google Scholar

Li, D., Fu, M., Ma, H., Bian, W., Du, Z., and Chen, C. (2020). A Theoretical Study on Laser Cooling Feasibility of Group IVA Hydrides XH (X = Si, Ge, Sn, and Pb): The Role of Electronic State Crossing. Front. Chem. 8, 20. doi:10.3389/fchem.2020.00020

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, C., Zhang, D., and Bian, W. (2003). Theoretical Investigation of the Reaction of Co⁺ with OCS. J. Phys. Chem. A. 107, 8618–8622. doi:10.1021/jp034693s

CrossRef Full Text | Google Scholar

Liu, K., Yu, L., and Bian, W. (2009). Extensive Theoretical Study on Various Low-Lying Electronic States of Silicon Monochloride Cation Including Spin−Orbit Coupling. J. Phys. Chem. A. 113, 1678–1685. doi:10.1021/jp809618y

CrossRef Full Text | Google Scholar

Moussa, A., El-Kork, N., and Korek, M. (2021). Laser Cooling and Electronic Structure Studies of CaK and its Ions CaK^±. New J. Phys. 23, 013017. doi:10.1088/1367-2630/abd50d

CrossRef Full Text | Google Scholar

Owono, L. C., Ben Abdallah, D., Jaidane, N., and Ben Lakhdar, Z. (2008). Theoretical Radiative Properties between States of the Triplet Manifold of NH Radical. J. Chem. Phys. 128, 084309. doi:10.1063/1.2884923

CrossRef Full Text | Google Scholar

Owono, L. C., Jaidane, N., Kwato Njock, M. G., and Ben Lakhdar, Z. (2007). Theoretical Investigation of Excited and Rydberg States of Imidogen Radical NH: Potential Energy Curves, Spectroscopic Constants, and Dipole Moment Functions. J. Chem. Phys. 126, 244302. doi:10.1063/1.2741260

CrossRef Full Text | Google Scholar

Park, J. K., and Sun, H. (1992). Dipole and Transition Moments of SiH, PH and SH by Ab Initio Effective Valence Shell Hamiltonian Method. Chem. Phys. Lett. 195, 469–474. doi:10.1016/0009-2614(92)85546-m

CrossRef Full Text | Google Scholar

Ram, R. S., Bernath, P. F., and Hinkle, K. H. (1999). Infrared Emission Spectroscopy of NH: Comparison of a Cryogenic Echelle Spectrograph with a Fourier Transform Spectrometer. J. Chem. Phys. 110, 5557–5563. doi:10.1063/1.478453

CrossRef Full Text | Google Scholar

Rostas, J., Cossart, D., and Bastien, J. R. (1974). Rotational Analysis of the PH and PD A³Π_i-X³Σ⁻ Band Systems. Can. J. Phys. 52, 1274–1287. doi:10.1139/p74-172

CrossRef Full Text | Google Scholar

Shen, Z., Ma, H., Zhang, C., Fu, M., Wu, Y., Bian, W., et al. (2017). Dynamical importance of van der Waals saddle and excited potential surface in C(¹D)+D₂ complex-forming reaction. Nat. Commun. 8, 14094. doi:10.1038/ncomms14094

PubMed Abstract | CrossRef Full Text | Google Scholar

Shuman, E. S., Barry, J. F., and DeMille, D. (2010). Laser Cooling of a Diatomic Molecule. Nature 467, 820–823. doi:10.1038/nature09443

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, W. H., Brzozowski, J., and Erman, P. (1976). Lifetime Studies of the NH Molecule: New Predissociations, the Dissociation Energy, and Interstellar Diatomic Recombination. J. Chem. Phys. 64, 4628–4633. doi:10.1063/1.432046

CrossRef Full Text | Google Scholar

Song, Z., Shi, D., Sun, J., and Zhu, Z. (2016). Accurate Spectroscopic Calculations of the 12 Λ-S and 25 Ω States of the NH Radical Including the Spin-Orbit Coupling Effect. Comput. Theor. Chem. 1093, 81–90. doi:10.1016/j.comptc.2016.08.017

CrossRef Full Text | Google Scholar

van Mourik, T., Dunning, T. H., and Peterson, K. A. (2000). Ab Initio Characterization of the HCO^x (x = −1, 0, +1) Species: Structures, Vibrational Frequencies, CH Bond Dissociation Energies, and HCO Ionization Potential and Electron Affinity. J. Phys. Chem. A. 104, 2287–2293. doi:10.1021/jp9925583

CrossRef Full Text | Google Scholar

Wells, N., and Lane, I. C. (2011). Electronic States and Spin-Forbidden Cooling Transitions of AlH and AlF. Phys. Chem. Chem. Phys. 13, 19018–19025. doi:10.1039/c1cp21313j

PubMed Abstract | CrossRef Full Text | Google Scholar

Werner, H.-J., Knowles, P. J., Lindh, R., Manby, F. R., Schütz, M., Celani, P., et al. (2012). Molpro, Version 2012.1, A Package of Ab Initio Programs. Available online at: http://www.molpro.net.

Google Scholar

Werner, H.-J., and Knowles, P. J. (1985). A Second Order Multiconfiguration SCF Procedure with Optimum Convergence. J. Chem. Phys. 82, 5053–5063. doi:10.1063/1.448627

CrossRef Full Text | Google Scholar

Werner, H.-J., and Knowles, P. J. (1988). An Efficient Internally Contracted Multiconfiguration-Reference Configuration Interaction Method. J. Chem. Phys. 89, 5803–5814. doi:10.1063/1.455556

CrossRef Full Text | Google Scholar

Wu, Y., Cao, J., Ma, H., Zhang, C., Bian, W., Nunez-Reyes, D., et al. (2019). Conical Intersection-Regulated Intermediates in Bimolecular Reactions: Insights from C(¹D)+HD Dynamics. Sci. Adv. 5, eaaw0446. doi:10.1126/sciadv.aaw0446

PubMed Abstract | CrossRef Full Text | Google Scholar

Xing, W., Sun, J., Shi, D., and Zhu, Z. (2018). Theoretical Study of Spectroscopic Properties of 5 Λ-S and 10 Ω States and Laser Cooling for AlH⁺ Cation. Acta Phys. Sin. 67, 193101. doi:10.7498/aps.67.20180926

CrossRef Full Text | Google Scholar

Yan, B., Moses, S. A., Gadway, B., Covey, J. P., Hazzard, K. R. A., Rey, A. M., et al. (2013). Observation of Dipolar Spin-Exchange Interactions with Lattice-Confined Polar Molecules. Nature 501, 521–525. doi:10.1038/nature12483

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, N., Yang, C., Sun, Z., Wang, M., and Ma, X. (2021). Direct Laser Cooling the NH Molecule with the Pseudo-closed Loop Triplet-Triplet Transition Including Intervening Electronic States. Spectrochimica Acta Part A: Mol. Biomol. Spectrosc. 250, 119229. doi:10.1016/j.saa.2020.119229

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, L., and Bian, W. (2012). Electronically Excited-State Properties and Predissociation Mechanisms of Phosphorus Monofluoride: A Theoretical Study Including Spin-Orbit Coupling. J. Chem. Phys. 137, 014313. doi:10.1063/1.4731635

CrossRef Full Text | Google Scholar

Yu, L., and Bian, W. (2011). Extensive Theoretical Study on Electronically Excited States and Predissociation Mechanisms of Sulfur Monoxide Including Spin-Orbit Coupling. J. Comput. Chem. 32, 1577–1588. doi:10.1002/jcc.21737

CrossRef Full Text | Google Scholar

Yuan, X., Guo, H., Wang, Y., Xue, J., Xu, H., and Yan, B. (2019). Laser-cooling with an Intermediate Electronic State: Theoretical Prediction on Bismuth Hydride. J. Chem. Phys. 150, 224305. doi:10.1063/1.5094367

CrossRef Full Text | Google Scholar

Zhao, H., Bian, W., and Liu, K. (2006). A Theoretical Study of the Reaction of O(³P) with Isobutene. J. Phys. Chem. A. 110, 7858–7866. doi:10.1021/jp060583k

CrossRef Full Text | Google Scholar