Ab Initio Study of the Large Amplitude Motions of Various Monosubstituted Isotopologues of Methylamine (CH3-NH2)

CCSD(T)-F12 theory is applied to determine electronic ground state spectroscopic parameters of various isotopologues of methylamine (CH₃-NH₂) containing cosmological abundant elements, such as D, ¹³C and ¹⁵N. Special attention is given to the far infrared region. The studied isotopologues can be classified in the G₁₂, G₆ and G₄ molecular symmetry groups. The rotational and centrifugal distortion constants and the anharmonic fundamentals are determined using second order perturbation theory. Fermi displacements of the vibrational bands are predicted. The low vibrational energy levels corresponding to the large amplitude motions are determine variationally using a flexible three-dimensional model depending on the NH₂ bending and wagging and the CH₃ torsional coordinates. The model has been defined assuming that, in the amine group, the bending and the wagging modes interact strongly. The vibrational levels split into six components corresponding to the six minima of the potential energy surface. The accuracy of the kinetic energy parameters has an important effect on the energies. Strong interactions among the large amplitude motions are observed. Isotopic effects are relevant for the deuterated species.

Introduction

Methylamine (CH₃-NH₂) plays important roles in the gas phase chemistry in the terrestrial and extraterrestrial atmospheres. The presence in the Earth’s atmosphere has both natural and anthropogenic causes (Ge et al., 2011). In air quality studies, it is considered to be a Volatile Organic Compound (VOC) that can be a precursor of secondary organic aerosols (SOA) in the presence of glyoxal (De Haan et al., 2009). In 1974, it was detected in the interstellar medium and it is contemplated as a relatively abundant species (Kaifu et al., 1974) (Fourikis et al., 1974). Recent studies consider it a precursor of glycine and a building block of life (Ohoshi et al., 2019). Recently, methylamine has been detected in the quasar PKS 1830-211 (Muller et al., 2011) and together with other simple N-bearing species, it has been observed in the hot cores NGC 6334I MM1-3 (Bøgelund et al., 2019). Fourikis et al. (1977) have reported the probable detection of deuterated methylamine (CH₃NHD) in Sgr B2.

The aim of the present work is the theoretical study of probably detectable methylamine isotopologues. Monosubstituted isotopologues were detected for many astrophysical molecules such as dimethyl-ether and methyl-formate as it is described in the references provided by the papers of Fernández et al. (2019) and Gámez et al. (2019). In a recent study of the methylamine main isotopologue, highly correlated ab initio methods were employed to simulate the far infrared spectra (Senent 2018). The low-lying vibrational energy levels in and their tunneling splitting components were computed, providing relevant information for rotational spectrum assignments, which are mandatory for the detection using radio-astronomy. Very accurate results were obtained by comparing with previous experimental data. A detailed review of previous theoretical and experimental works can be found in Senent (2018).

The motivation of many previous studies of methylamine concerns more to the peculiar molecular structure than to its applications (Hamada et al., 1982) (Ohashi & Hougen 1987), because it is contemplated as a prototype small non-rigid molecule where two interacting large amplitude motions, the torsion of the methyl group and the NH₂ wagging, govern its internal dynamics (Ohashi & Hougen 1987) (Kreglewski 1978, 1989) (Ohashi & Toriyama 1994 (Kleiner and Hougen, 2015). High resolution rovibrational spectra have been measured for the ground and various excited vibrational states, given a special attention to the far infrared region (Belorgeot et al., 1982) (Diallo et al., 1985) (Ohashi et al., 1987, 1988, 1989, 1992) (Ilyushin et al., 2005) (Kreglewski & Winther 1992) (Kreglewski & Wlodarczak 1992) (Motiyenko et al., 2014) (Nguyen et al., 2021) (Dawadi et al., 2013a; 2013b).

Whereas publications about the methylamine main isotopologue are recurrent, less studies attend to other isotopic species. The microwave spectrum of the monosubstituted species CH₃NHD (Ohashi et al., 1991), CH₂DNH₂ (Tamagake & Tsuboi 1974), and ¹³CH₃NH₂ (Motiyenko et al., 2016), and the deuterated species, CH₃ND₂, CD₃NH₂, CD₃ND₂ (Lide 1954) (Sastry 1960) (Takagi & Kojima 1971) (Kreglewski et al., 1990a; 1990b) were measured and assigned. The infrared absorption spectrum of ¹⁵N-methylamine was inspected in the gas phase (Hirakawa et al., 1972). Mass resolved excitation spectroscopy and ab initio calculations were employed to analyze the low-lying excited states of CH₃NH₂, CH₃NH2, CD₃NH₂, CH₃ND₂, and CD₃ND2 (Taylor & Bernstein 1995). The A←X excitation spectra of six different deuterated isotopologues including the CH₃NHD monosubstituted species, were explored (Park et al., 2006).

Previous studies devoted to n-methyl amines describe theoretical techniques and symmetry concepts useful for the present work (Senent & Smeyers 1996) (Smeyers et al., 1996, 1998) (Senent 2018)On the basis of previous ab initio results (Senent 2018), performed using explicitly correlated coupled cluster theory, CCSD(T)-F12 (Adlet et al., 2007) (Knizia et al., 2009), in this new paper, we attend to several monosubstituted isotopologues containing abundant cosmological elements. Although, to our knowledge, a unique isotopologue CH₃NHD has been probably detected (Fourikis et al., 1977), other species are considered to be detectable species. Four isotopic species, ¹³CH₃NH₂, CH₃¹⁵NH₂, CH₃NHD, and CH₂DNH₂, are studied and compared with the main isotopologue for predicting theoretically isotopic shifts. Recently, interstellar amines and their fragments have been studied using quantum-chemical computations (Salta et al., 2020) (Puzzarini et al., 2020).

An earliest CCSD(T)-F12 three-dimensional potential energy surface is revisited in the present work (Senent 2018) because it is mass independent. It is employed for constructing mass dependent effective potential energy surfaces for the different isotopologues. The surfaces present six minima separated by relatively low potential energy barriers. If the minimum interconversion is taken into consideration, the most abundant isotopologue can be classified in the G₁₂ molecular symmetry group (Ohashi & Hougen 1987). The isotopic substitutions carry out changes in the symmetry. Details concerning the followed procedure can be found in our previous paper devoted to the acetone isotopologues (Dalbouha et al., 2021). The effective surfaces allow to construct Hamiltonians depending on three interacting coordinates, two interacting large amplitude motions, the NH₂ wagging and the CH₃ torsion, and the HNH bending. Then, both the bending and wagging of the amine group are treated together. The final levels are computed variationally.

Results and Discussion

Electronic Structure Calculations

The theoretical study of methylamine isotopologues was started from the results of a previous work devoted to the main isotopologue CH₃NH₂ (Senent 2018). In this earlier paper, the structural parameters of the minimum energy structure and a three-dimensional ab initio potential energy surface (3D-PES) were computed using explicitly correlated coupled cluster theory with single and double substitutions augmented by a perturbative treatment of triple excitations (CCSD(T)-F12b) (Adlet et al., 2007) (Knizia et al., 2009) using the MOLPRO package default options (Werner et al., 2012). The procedure was applied in connection with the AVTZ-F12 basis set, which contains the Dunning’s type aug-cc-pVTZ atomic orbitals (AVTZ) (Kendall et al., 1992) and the corresponding functions for the density fitting and the resolutions of the identity. These previous computed data are mass independent properties that can be used for the different isotopic species.

To determine the core-valence electron correlation effects on the rotational constants, the structure was optimized using CCSD(T) (coupled-cluster theory with single and double substitutions, augmented by a perturbative treatment of triple excitations) (Hampel et al., 1992) and the cc-pCVTZ basis set (CVTZ) (Woon and Dunning Jr 1995).

The full-dimensional anharmonic force field and the vibrational corrections of the potential energy surface are mass dependent properties that must be computed for each isotopologue. For this reason, new electronic structure calculations have been performed in the present work. That properties were determined using second order Möller-Plesset theory (MP2) (Møller & Plesset 1934) implemented in GAUSSIAN (Frisch et al., 2016). Anharmonic force fields allow obtain spectroscopic properties using second order perturbation theory (VPT2) (Barone 2005) (Bloino et al., 2012). The vibrationally corrected surfaces were employed to construct Hamiltonians for the isotopologues. The energy levels corresponding to the large amplitude vibrations and to the HNH bending mode were computed using a variational procedure implemented in ENEDIM (Senent 1998a; 1998b, 2001).

The Symmetry of the Isotopologues

The main isotopologue, as well as ¹³CH₃NH₂ and CH₃¹⁵NH₂, can be classified in the G₁₂ molecular symmetry group (MSG) (Ohashi & Hougen 1987) and in the C_s point group. However, the H →D substitution carries out changes in the symmetry properties. CH₃NDH must be classified in the C₁ point group and in the G₆ MSG, due to the absence of the symmetry plane. In CDH₂NH_2, the D atom can replace the in-plane H atom (C_s-CDH₂NH₂) or one out-of plane H atom (C₁-CDH₂NH₂). If VPT2 is applied and a unique minimum is considered, the molecule is assumed to be semi-rigid and all the vibrations are described as small displacements around the equilibrium. Two different point groups C₁ and C_s are used. However, if the internal rotation is taken into account, C_s-CDH₂NH₂ and C₁-CDH₂NH₂ represent different minima of the same potential energy surface and they can be inter-converted. Then, both are classified in the same G₄ MSG.

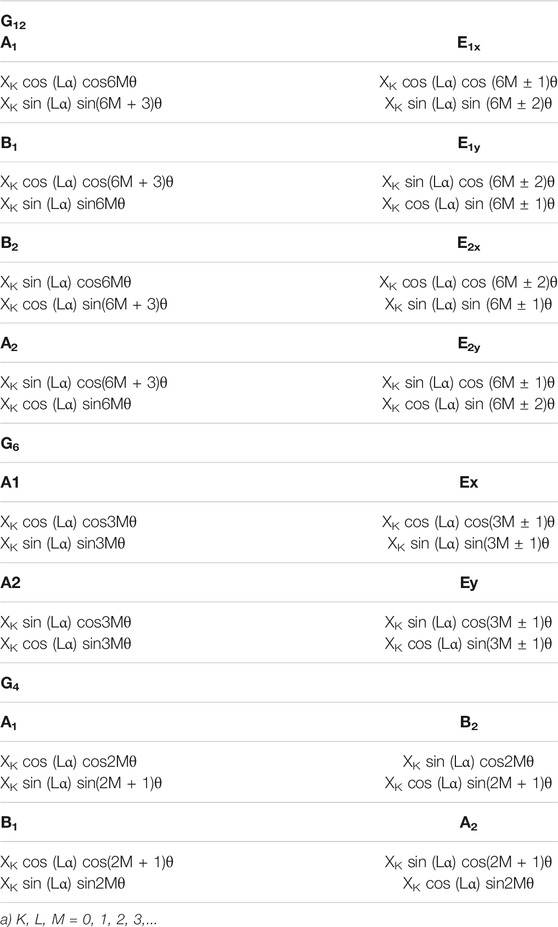
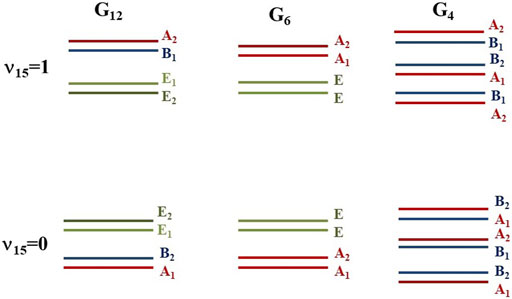
The G₁₂ MSG contains six irreducible representations, four non-degenerate, A₁, A₂, B₁ and B₂, and two double-degenerate E₁ and E₂. The G₆ MSG contains three irreducible representations, two non-degenerate, A₁, and A₂, and one double-degenerate E. The G₄ MSG contains four non-degenerate irreducible representations, A₁, A₂, B₁, and B₂.

Rovibrational Parameters

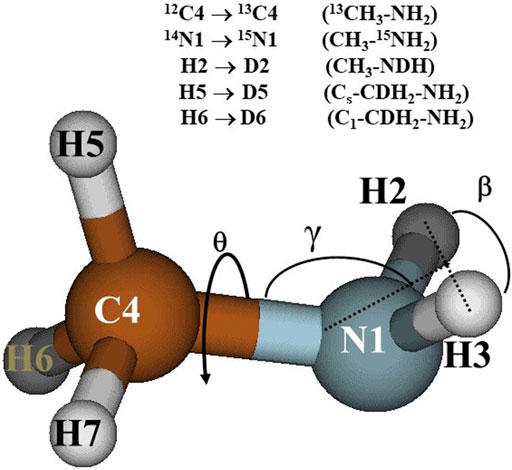
In the earlier paper (Senent 2018), the CCSD(T)-F12/AVTZ structural parameters of the methylamine equilibrium geometry, are detailed. The structure is shown in Figure 1, that helps to understand the atom labelling and the isotopic substitutions.

FIGURE 1

FIGURE 1. Methylamine equilibrium structure.

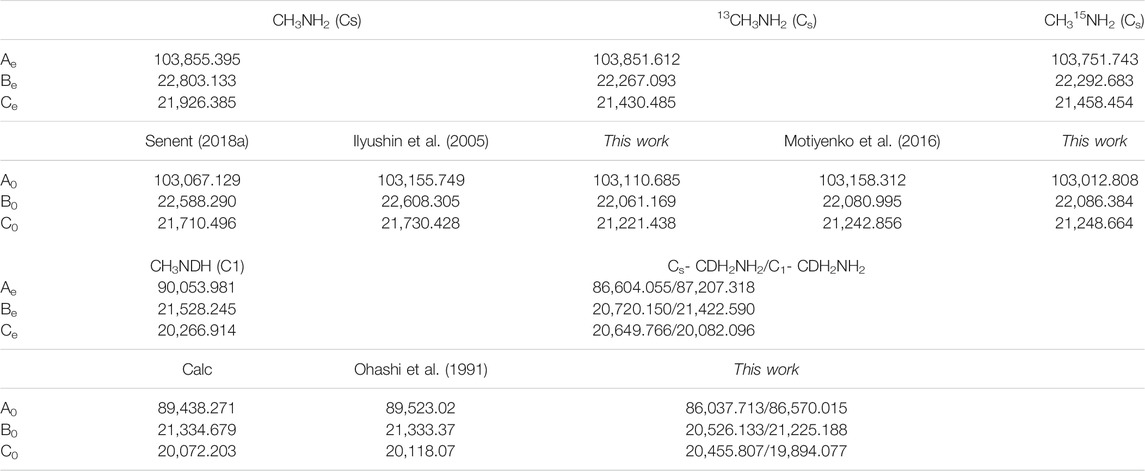
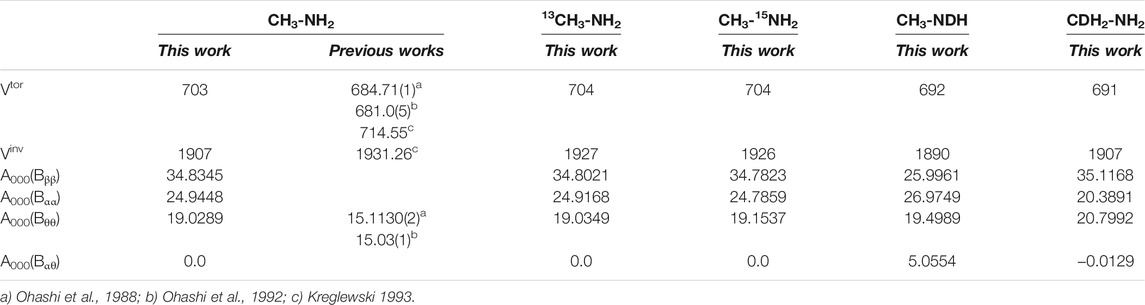
For all the isotopologues, the vibrational ground state rotational constants shown in Table 1, were computed from the CCSD(T)-F12 equilibrium rotational constants using the following equation:

${\text{B}}_{\text{0}}{=\text{ B}}_{\text{e}}\left(\text{CCSD}\left(\text{T}\right)-\text{F}12/\text{AVTZ}-\text{F}12\right)+△{\text{B}}_{\text{e}}{}^{\text{core}}\left(\text{CCSD}\left(\text{T}\right)/\text{CVTZ}\right)+△{\text{B}}^{\text{vib}}\left(\text{MP}2/\text{AVTZ}\right)(1)$

TABLE 1

TABLE 1. Rotational constants (in MHz).

Here, ΔB_e^core collects the core-valence electron correlation effects on the equilibrium structure and ΔB^vib represents the vibrational contribution derived from the second order perturbation theory (VPT2) α_rⁱ vibration-rotation interaction parameters. These last were determined using the MP2/AVTZ cubic force fields and vibrational second order perturbation theory. ΔB_e^core was determined from the CCSD(T)/CVTZ parameters B_e (CV) and B_e(V), calculated correlating both core and valence electrons (CV) or just the valence electrons (V) in the post-SCF process. Then:

$\Delta {\text{B}}_{\text{e}}^{\text{core}}{=\text{ B}}_{\text{e}}\left(\text{CV}\right){-\text{ B}}_{\text{e}}\left(\text{V}\right)(2)$

This approximation has been corroborated in previous studies of other non-rigid molecules providing really accurate parameters, whose deviations with respect available experimental data, represent few MHz (Boussesi et al., 2016) (Dalbouha et al., 2016, 2021). In Table 1, the computed rotational constants of CH₃NH₂, ¹³CH₃NH_2, and CH₃NDH are compared with available experimental parameters (Ilyushin et al., 2005) (Motiyenko et al., 2016) (Ohashi et al., 1991). The MP2/AVTZ quartic centrifugal distortion constants corresponding to the asymmetrically reduced Hamiltonian, are shown in Table 2 where they are compared with previous experimental data (Ilyushin et al., 2005) (Motiyenko et al., 2016) (Ohashi et al., 1991). Disagreements between experimental and computed data can be correlated with the level of ab initio calculations used to compute the anharmonic force field. In addition, in methyl amine, the interaction between the internal and global rotation causes deviations. Isotopic shifts are more reliable.

TABLE 2

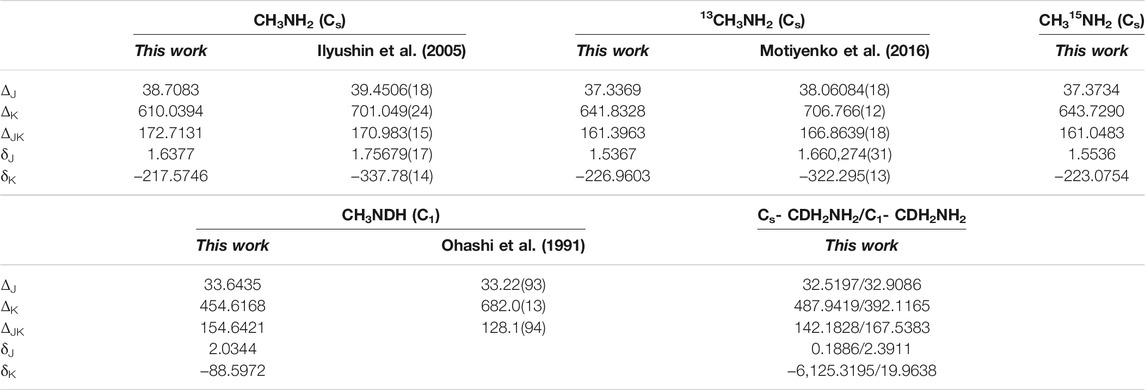
TABLE 2. MP2/AVTZ quartic (in KHz) centrifugal distortion constants^a computed using the MP2/AVTZ cubic force fields.

The anharmonic fundamental frequencies shown in Table 3, were computed using VPT2 theory (Barone 2005) (Bloino et al., 2012) implemented in Gaussian (Frisch et al., 2016) and the MP2/AVTZ force fields. The modes are ordered following the criteria used for the main isotopologue that helps to make visible the isotopic shifts. Although VPT2 does not represent the proper treatment for the study of the vibrations responsible for the non-rigidity, it provides a good description of the mid- and near-infrared regions and a useful first description of the far-infrared region. In addition, it allows predict possible band displacements due to Fermi resonances. VPT2 theory ignores the inter-conversion of minima and treats the molecule as a semi-rigid species with a single minimum. If the existence of a single minimum is assumed, the resulting VPT2 properties are different for C_s-CDH₂NH₂ than for C₁-CDH₂NH₂.

TABLE 3

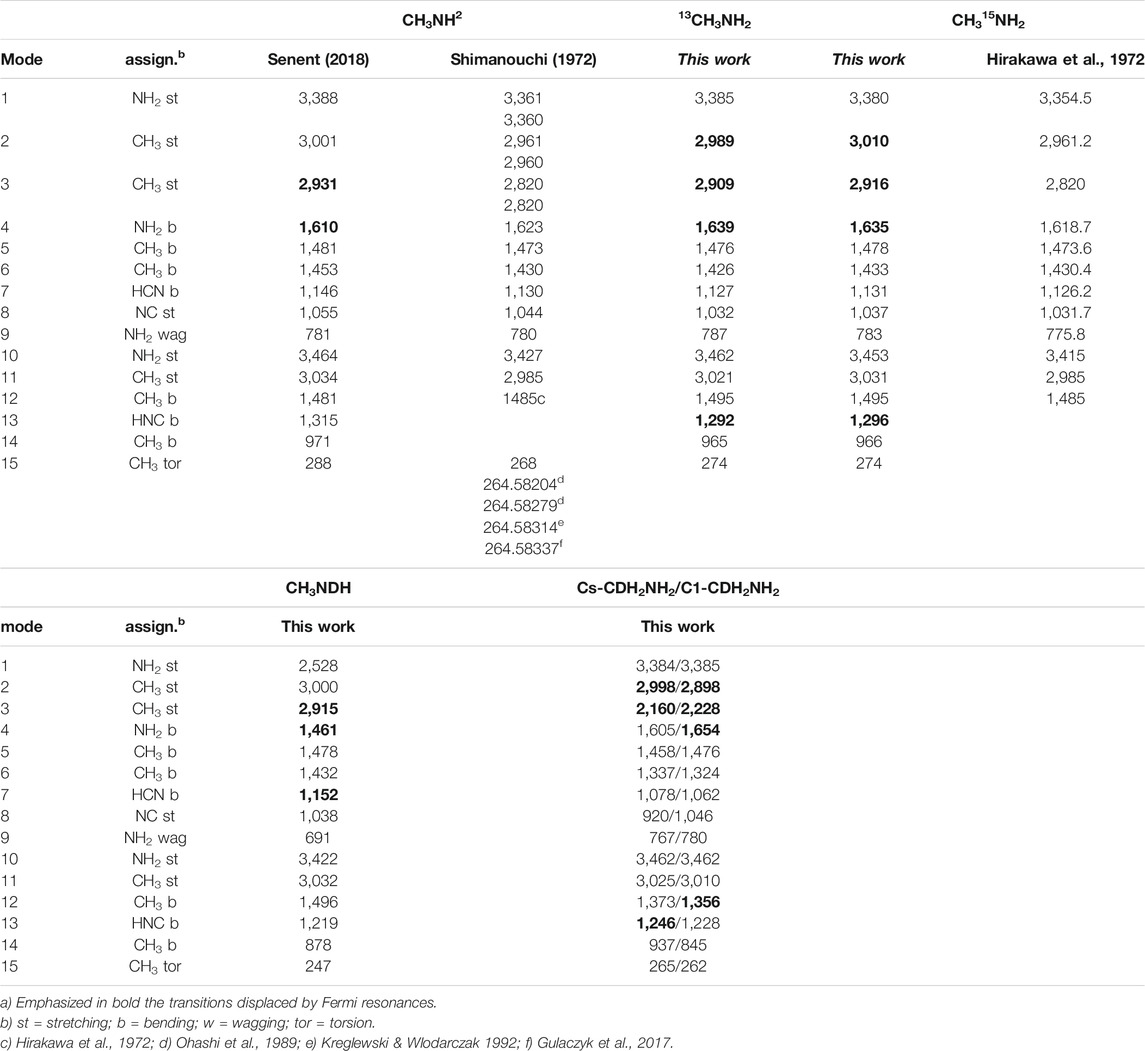
TABLE 3. Anharmonic fundamental frequencies (in cm⁻¹) calculated in this work and measured in previous experiments in the gas phase^a.

The frequencies corresponding to the main isotopologue are compared with experimental data measured in the gas phase (Ohashi et al., 1989) (Kreglewski & Wlodarczak 1992) (Gulaczyk et al., 2017) (Hirakawa et al., 1972) [58]. Previous results are available for CH₃¹⁵NH₂ (Hirakawa et al., 1972). Deviation for several modes are significant, whereas the isotopic shits computed at the MP2 level of theory are reliable.

In Table 3, emphasized in bold, are the fundamental frequencies for which resonances can be relevant. Displacements due to the Fermi interactions were found to be relevant for the ν₃ fundamental (CH₃ st), that interacts with two overtones (2ν₆ and 2ν₁₂). The NH₂ bending fundamental is predicted to interact strongly with the NH₂ wagging overtone. Since both amine vibrations behave as inseparable modes, the variational model used for exploring the far infrared region, includes explicitly the bending coordinate.

The far Infrared Spectrum

As was assumed in the previous paper devoted to the main isotopologue (Senent 2018), the low-lying vibrational energy levels corresponding to the two large amplitude motions, the methyl torsion (θ) and the amine NH₂ wagging (α) can be determined by solving variationally a three-dimensional Hamiltonian where a third coordinate, the HNH bending angle (β), is considered to be an independent variable. The Hamiltonian obeys the formula:

$H\left(\text{β},\alpha ,\theta \right)=-{\displaystyle \sum }_{i=1}^3{\displaystyle \sum }_{j=1}^3\left(\frac{\partial }{\partial q_i}\right)B_{q_i{q}_j}\left(\text{β},\alpha ,\theta \right)\left(\frac{\partial }{\partial q_j}\right)+V^{eff}\left(\text{β},\alpha ,\theta \right)(3)$

This Hamiltonian was defined by taking into consideration the predictions of the test of resonances described in the previous section and in the previous paper (Senent 2018). Significant interactions between the NH₂ bending and wagging vibrational modes were predicted. This fact suggests the prerequisite of a 3D-model. In Eq. 3, $B_{qiqj}$ and V^eff represent the kinetic energy parameters and the effective potential defined as the sum of three contributions:

${\text{V}}^{\text{eff}}\left(\beta \text{,}\alpha \text{,}\theta \right)=\text{V}\left(\beta \text{,}\alpha \text{,}\theta \right)+\text{ V}\prime \left(\beta \text{,}\alpha \text{,}\theta \right){+\text{V}}^{\text{ZPVE}}\left(\beta \text{,}\alpha \text{,}\theta \right)(4)$

Here, V($\text{β},\alpha ,{\theta }_{ }$) is the mass independent ab initio three-dimensional potential energy surface; V’($\text{β},\alpha ,{\theta }_{ }$) and V^ZPVE($\text{β},\alpha ,{\theta }_{ }$) represent the Podolsky pseudopotential and the zero point vibrational energy correction (Dalbouha et al., 2021). The two last contributions must be computed for all the isotopologues because they are mass dependent properties. β, α, and θ, the HNH bending, the NH2 wagging and the torsional coordinates, are defined using curvilinear internal coordinates:

$\begin{array}{c}\beta {=\text{HNH}-\text{HNH}}^{\text{e}}\\ \alpha =180\text{.0}-\mathrm{\gamma }\\ \mathrm{\theta }=\left(\text{H}5\text{C}4\text{N}1\text{X}+\text{H6C4N1X}+\text{H7C4N1X }-2\Pi \right)/3\end{array}(5)$

HNH^e is the value of the HNH bending angle corresponding to the equilibrium geometry; γ represents the angle between the C-N bond and the HNH plane (see Figure 1); X denotes a ghost atom lying in the HNH plane perpendicular to the HNH angle bisector. The set of internal coordinates were chosen taking into consideration the procedure for the determination of the 3D-PES which demands a partial optimization of the geometry. Three internal coordinates, NHN, γ and H5C4N1X distinguish the selected conformations whereas twelve “dependent coordinates” are allowed to be relaxed in all the structures.

The ab initio three-dimensional potential energy surface, V($\text{β},\alpha ,{\theta }_{ }$), was computed for the study of the main isotopologue (Senent 2018). It was constructed using the CCSD(T)-F12/AVTZ energies of 131 geometries defined for selected values of the independent coordinates that were fitted to the following series:

$V\left(\beta ,\alpha ,\theta \right)= {\displaystyle \sum _{K,L,M}{A}_{KML}^{CC}{\beta }^K\cos L\alpha \cos 6M\theta +A_{KML}^{SS}{\beta }^K\sin L\alpha \sin 3(2M+1)\theta }(6)$

This analytical expression transforms as the totally symmetric representation of the G₁₂ MSG. Formally identical expressions can be employed for V’, V^ZPVE, V^eff($\text{β},\alpha ,{\theta }_{ }$) and the diagonal kinetic energy parameters B_qiqi of the main isotopologue, ¹³CH₃NH₂ and CH₃¹⁵NH₂. However, since the H →D substitution carries out symmetry changes, the effective potential V^eff($\text{β},\alpha ,{\theta }_{ }$) and the diagonal kinetic parameters must be expressed using less-symmetric analytical expressions. For CH₃NDH (G₆):

$V^{eff}\left(\beta ,\alpha ,\theta \right)= {\displaystyle \sum _{K,L,M}{A}_{KML}^{CC}{\beta }^K\cos L\alpha \cos 3M\theta +A_{KML}^{SS}{\beta }^K\sin L\alpha \sin 3M\theta }(7)$

and for CDH₂NH₂ (G₄)

$V^{eff}\left(\beta ,\alpha ,\theta \right)= {\displaystyle \sum _{K,L,M}{A}_{KML}^{CC}{\beta }^K\cos L\alpha \cos 2M\theta +A_{KML}^{SS}{\beta }^K\sin L\alpha \sin (2M+1)\theta }(8)$

To construct the effective potential using Eq. 4, two mass-dependent properties V′ and V^ZPVE must be computed for all the isotopologues and for all the geometries. The V’ pseudopotential is very small. However, V^ZPVE has important effects on the levels. It was determined within the harmonic approximation at the MP2/AVTZ level of theory. To obtain the mass-dependent properties of the low-symmetry varieties, more than 131 geometries and more than 131 sets of harmonic frequencies need to be computed. For example, in the case of CDH₂NH₂, 131x3 geometries are required because the three hydrogen atoms of the methyl group are not identical.

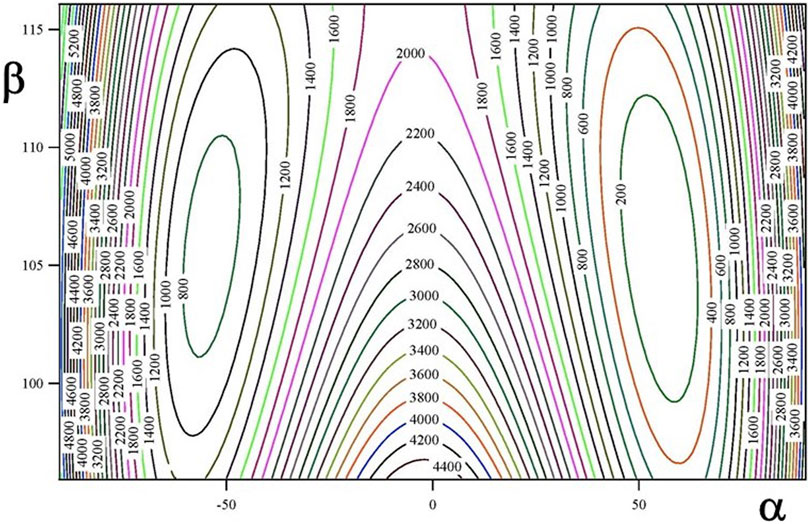
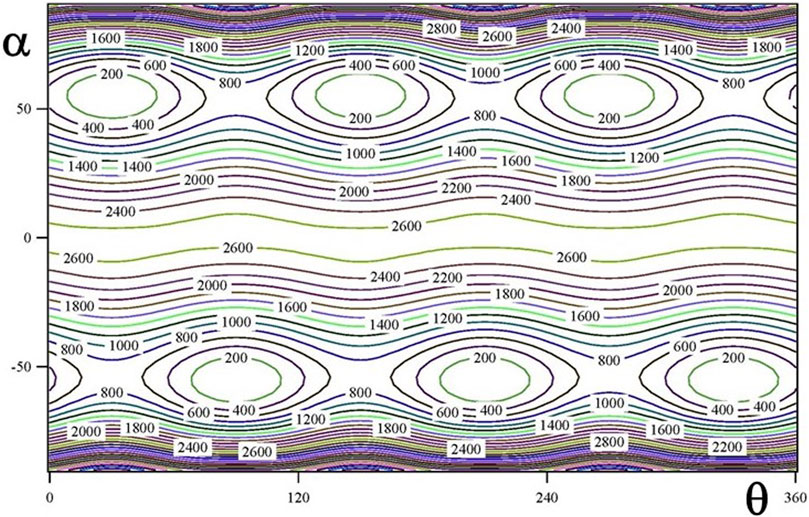
The ground vibrational state potential energy surface contains six equivalent minima corresponding to a single conformer. The contours of Figures 2, 3 represents layers of the 3D-surface of the main isotopologue containing the minimum energy structure. Figure 2 corresponds to V^eff (α, β; θ = 270°) and Figure 3 to V^eff (α, θ; β = 106°). Figures emphasize the coupling between coordinates.

FIGURE 2

FIGURE 2. V^eff (α, β; θ = 270°) two dimensional potential energy surface (in cm⁻¹).

FIGURE 3

FIGURE 3. V^eff (α, θ; β = 106°) two dimensional potential energy surface (in cm⁻¹).

The kinetic energy parameters were also computed for all the selected geometries and for all the isotopologues. The number of selected geometries required for their computation in the deuterated forms was 171 and 393 for CH₃NDH and CDH₂NH₂, respectively. For all the symmetries, the diagonal terms B_ββ, B_αα, and B_θθ transform as the totally symmetric representation A₁. However, the symmetry properties of the off-diagonal elements vary with the MSG:

B_αθ transforms as B₁ (G₁₂, G₄) and A₁(G₆)

B_αβ transforms as B₂ (G₁₂, G₄) and A₂(G₆)

B_θβ transforms as A₂ (G₁₂, G₄, G₆)

The non-zero coefficients A₀₀₀(B_qiqz) of the kinetic energy expressions are shown in Table 4. For the main isotopologue, they are compared with previous data (Ohashi et al., 1988, 1992), although in works based in experiments, these coefficients are considered to be constants. The potential energy barriers, V^tor and V^inv were estimated using the effective potentials. For the main isotopologue, they are in reasonable good agreement with previous data (Ohashi et al., 1988, 1992) (Kreglewski 1993). Isotopic shifts of all the potential parameters are only important for the deuterated forms.

TABLE 4

TABLE 4. CCSD(T)-F12/AVTZ potential energy barriers (in cm⁻¹).

Symmetry adapted series were employed as trial functions for the variational calculations. Products of harmonic oscillator solutions X_K (for the bending coordinate) and double Fourier series (for the wagging and torsional coordinates) were employed. Table 5 shows the symmetry eigenvectors. The convergence of the low energy levels requires long basis sets leading to Hamiltonian matrices of 18,755 x18,755 elements. In the case of the G₁₂ species, the matrices factorize by symmetry into eight blocks which dimensions are 1815 (A₁, B₂), 1,518 (B₁), 1,507 (A₂), and 3,025 (E_1x, E_1y, E_2x and E_2y). For the G₆ species, the corresponding submatrix dimensions were 3,333 (A₁), 3,322 (A₂), and 6,050 (E), whereas for the G₄ species, the dimensions were 4,840 (A₁, B₂), 4,543 (B₁), and 4,532 (A₂).

TABLE 5

TABLE 5. Symmetry eigenvectors.^a.

The resulting energy levels are shown in Table 6 and they are classified using symmetry and the v₇, v₉ and v₁₅ quantum numbers. For the main isotopologue, the energies are compared with those of Kreglewski (1989) obtained from experimental parameters. The computed levels denote a slight improvement with respect to the work of Senent (2018), after using longer expansions for the kinetic energy parameters. The aim was to increase precision considering that isotopic shifts are relatively small. We observed that the vibrational energies are very sensitive to the kinetic contributions. It can be pointed out that their computations in the deuterated forms is not straightforward.

TABLE 6

TABLE 6. CCSD(T)-F12 energy levels corresponding to the large amplitude vibration and to the HNH bending mode (in cm⁻¹). For the main isotopologue, the energies compared with previous data obtained using a two-dimensional model.

Each energy level splits into six components corresponding to the six minima of the potential energy surface. Their distributions are represented in Figure 4. In the G₁₂ species, the levels split into two non-degenerate and two double-degenerated sublevels. The components of the ground vibrational state were computed to lie at 0.000 (A₁), 0.163 (B₂), 0.325 (E₁), and 0.407 (E₂) cm⁻¹. Very small shifts are found for ¹³CH₃-NH₂, whereas for CH₃-¹⁵NH₂, the subcomponents are close in energy (0.000 (A₁), 0.153 (B₂), 0.322 (E₁), and 0.398 (E₂)). The non-degenerated components B₁ and A₂ of the ʋ₁₅ fundamental (0 0 1) were obtained to lie at 265.572 and 266.117 cm⁻¹ in the main isotopologue and at 264.441 and 264.995 cm−1 in ¹³CH₃-NH₂, and at 264.428 and 264.936 cm⁻¹ in CH₃-¹⁵NH_2. For ʋ_9, the corresponding components of the (0 1 0) level were obtained to lie at 771.083 and 775.011 in the main isotopologue and at 776.413 and 777.617 cm−1 in ¹³CH₃-NH₂, and at 763.413 and 769.602 cm−1 in CH₃-¹⁵NH_2. It may be concluded that the effects of isotopic substitutions on the heavy atoms are less relevant for the torsional excitation than for inversion excitations.

FIGURE 4

FIGURE 4. Subcomponents of the (0 0 0) and (0 01) energy levels.

As was expected, isotopic effects on the low-lying energies are more noticeable for the deuterated species. For CH₃-NDH, the nondegenerate components of the ʋ₉ and ʋ₁₅ fundamentals have been computed to be 236.260 and 236.470 cm⁻¹, and to be 715.178 and 718.848 cm⁻¹. The gaps among subcomponents of the ground vibrational state are smaller than in the hydrogenated species. The isotopic substitution in one methyl group hydrogen breaks ten the degeneracy of the CDH₂NH₂ levels. The ground vibrational state splits into two A₁, two B₂, one B₁ and one A₂ components lying in the 0.000–1.672 cm⁻¹ range.

Conclusion

This work describes the shifts of spectroscopic parameters and the symmetry changes due to the isotopic substitutions for various probably detectable methylamine isotopologues, ¹³CH₃NH₂, CH₃¹⁵NH₂, CH₃NHD, and CDH₂ND₂. A variational procedure and VPT2 theory are employed for describing rovibrational properties with a special attention to the far infrared region. For all the isotopologues, the levels up to 1,500 cm⁻¹ over the ground vibrational state are determine variationally and classified using the G₁₂, G₆ and G₄ MSG properties. For the main isotopologue, the ground vibrational state splits into six components computed to lie at 0.000 (A₁), 0.163 (B₂), 0.325 (E₁), and 0.407 (E₂) cm⁻¹. Very small differences are found for ¹³CH₃-NH₂, whereas for CH₃-¹⁵NH₂, the computed subcomponents are close in energy (0.000 (A₁), 0.153 (B₂), 0.322 (E₁), and 0.398 (E₂)). Isotopic shifts are relevant for the deuterated forms, whereas the effects of substitution of heavy atoms are less relevant for the torsional excitation than for inversion excitations. Small variations of the kinetic energy parameters carry out substantial displacements of the levels. It can be pointed out that their computations in the deuterated forms is not straightforward.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

MA has performed the new ab initio calculations. MS was responsible for the variational calculations, the assignments of the levels, and for writing the manuscript.

Funding

The authors would like to extend their sincere appreciation to the Deanship of Scientific Research at King Saud University for funding the research through the Research Group Project No. RG-333. This research was supported by the Ministerio de Ciencia, Innovación y Universidades of Spain through the grants EIN 2019-103072 and FIS 2016-76418-P. The author acknowledges the “Red Española de Computación” for the grants AECT-2020-2-0008 and RES-AECT-2020-3-0011.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The author acknowledges the CTI (CSIC) and CESGA for computing facilities.

References

Adler, T. B., Knizia, G., and Werner, H.-J. (2007). A Simple and Efficient CCSD(T)-F12 Approximation. J. Chem. Phys. 127, 221106. doi:10.1063/1.2817618

CrossRef Full Text | Google Scholar

Barone, V. (2005). Anharmonic Vibrational Properties by a Fully Automated Second-Order Perturbative Approach. J. Chem. Phys. 122, 014108. doi:10.1063/1.1824881

CrossRef Full Text | Google Scholar

Belorgeot, C., Stern, V., Goff, N., Kachmarsky, J., and Möller, K. D. (1982). Far-infrared Spectrum of the Internal Rotation in Methylamine. J. Mol. Spectrosc. 92, 91–100. doi:10.1016/0022-2852(82)90085-6

CrossRef Full Text | Google Scholar

Bloino, J., Biczysko, M., and Barone, V. (2012). General Perturbative Approach for Spectroscopy, Thermodynamics, and Kinetics: Methodological Background and Benchmark Studies. J. Chem. Theor. Comput. 8, 1015–1036. doi:10.1021/ct200814m

PubMed Abstract | CrossRef Full Text | Google Scholar

Bøgelund, E. G., McGuire, B. A., Hogerheijde, M. R., van Dishoeck, E. F., and Ligterink, N. F. W. (2019). Methylamine and Other Simple N-Bearing Species in the Hot Cores NGC 6334I MM1-3. Astron&Astrophys 624, A82–A100. doi:10.1051/0004-6361/201833676

CrossRef Full Text | Google Scholar

Boussesi, R., Senent, M. L., and Jaïdane, J. (2016). Weak Intramolecular Interaction Effects on the Low Temperature Spectra of Ethylene Glycol, an Astrophysical Species. J.Chem.Phys. 144, 164110. doi:10.1063/1.4947088

PubMed Abstract | CrossRef Full Text | Google Scholar

Dalbouha, S., Al-Mogren, M. M., and Senent, M. L. (2021). Rotational and Torsional Properties of Various Monosubstituted Isotopologues of Acetone (CH3-CO-CH3) from Explicitly Correlated Ab Initio Methods. ACS Earth Space Chem. 5, 890–899. doi:10.1021/acsearthspacechem.1c00010

CrossRef Full Text | Google Scholar

Dalbouha, S., Senent, M. L., Komiha, N., and Domínguez-Gómez, R. (2016). Structural and Spectroscopic Characterization of Methyl Isocyanate, Methyl Cyanate, Methyl Fulminate, and Acetonitrile N-Oxide Using Highly Correlated Ab Initio Methods. J. Chem. Phys. 145, 124309. doi:10.1063/1.4963186

CrossRef Full Text | Google Scholar

Dawadi, M. B., Bhatta, R. S., and Perry, D. S. (2013b). Torsion-Inversion Tunneling Patterns in the CH-Stretch Vibrationally Excited States of the G12 Family of Molecules Including Methylamine. J. Phys. Chem. A. 117, 13356–13367. doi:10.1021/jp406668w

CrossRef Full Text | Google Scholar

Dawadi, M. B., Michael Lindsay, C., Chirokolava, A., Perry, D. S., and Xu, L.-H. (2013a). Novel Patterns of Torsion-Inversion-Rotation Energy Levels in the ν11 Asymmetric CH-Stretch Spectrum of Methylamine. J. Chem. Phys. 138, 104305. doi:10.1063/1.4794157

CrossRef Full Text | Google Scholar

De Haan, D. O., Tolbert, M. A., and Jimenez, J. L. (2009). Atmospheric Condensed-phase Reactions of Glyoxal with Methylamine. Geophys. Res. Lett. 36, L11819–L118823. doi:10.1029/2009gl037441

CrossRef Full Text | Google Scholar

Diallo, A. O., van Thanh, N., and Rossi, I. (1985). Further Resolution of the Infrared Amino Wagging Band of Methylamine. Spectrochimica Acta A: Mol. Spectrosc. 41, 1485–1489. doi:10.1016/0584-8539(85)80209-9

CrossRef Full Text | Google Scholar

Fernández, J. M., Tejeda, G., Carvajal, M., and Senent, M. L. (2019). New Spectral Characterization of Dimethyl Ether Isotopologues CH 3 OCH 3 and 13 CH 3 OCH 3 in the THz Region. ApJS 241, 13–21. doi:10.3847/1538-4365/ab041e

CrossRef Full Text | Google Scholar

Fourikis, N., Takagi, K., and Morimoto, M. (1974). Detection of Interstellar Methylamine by its 2_{02}->1_{10} A_{a^{-}} State Transition. ApJ 191, L139–L141. doi:10.1086/181570

CrossRef Full Text | Google Scholar

Fourikis, N., Takagi, K., and Saito, S. (1977). Probable Detection of Interstellar Methylamine-D/CH3NHD/. ApJ 212, L33–L37. doi:10.1086/182369

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian 16, Revision, C.01. Wallingford, CT, USA: Gaussian, Inc.

Gámez, V., Senent, M. L., Carvajal, M., and Galano, A. (2019). Competitive Gas Phase Reactions for the Production of Isomers C2O2H4. Spectroscopic Constants of Methyl Formate. J. Phys. Chem. A. 123, 9658–9668. doi:10.1021/acs.jpca.9b07270

CrossRef Full Text | Google Scholar

Ge, X., Wexler, A. S., and Clegg, S. L. (2011). Atmospheric Amines - Part I. A Review. Atmos. Environ. 45, 524–546. doi:10.1016/j.atmosenv.2010.10.012

CrossRef Full Text | Google Scholar

Gulaczyk, I., Kręglewski, M., and Horneman, V.-M. (2017). Accurate Rovibrational Energies for the First Excited Torsional State of Methylamine. J. Mol. Spectrosc. 342, 25–30. doi:10.1016/j.jms.2016.12.007

CrossRef Full Text | Google Scholar

Hamada, Y., Tanaka, N., Sugawara, Y., Hirakawa, A. Y., Tsuboi, M., Kato, S., et al. (1982). Force Field in the Methylamine Molecule from Ab Initio MO Calculation. J. Mol. Spectrosc. 96, 313–330. doi:10.1016/0022-2852(82)90195-3

CrossRef Full Text | Google Scholar

Hampel, C., Peterson, K. A., and Werner, H.-J. (1992). A Comparison of the Efficiency and Accuracy of the Quadratic Configuration Interaction (QCISD), Coupled Cluster (CCSD), and Brueckner Coupled Cluster (BCCD) Methods. Chem. Phys. Lett. 190, 1–12. doi:10.1016/0009-2614(92)86093-w

CrossRef Full Text | Google Scholar

Hirakawa, A. Y., Tsuboi, M., and Shimanouchi, T. (1972). Force Constants in Methylamine‐A Determination by the Use of 15N Isotope Shifts. J. Chem. Phys. 57, 1236–1247. doi:10.1063/1.1678381

CrossRef Full Text | Google Scholar

Ilyushin, V. V., Alekseev, E. A., Dyubko, S. F., Motiyenko, R. A., and Hougen, J. T. (2005). The Rotational Spectrum of the Ground State of Methylamine. J. Mol. Spectrosc. 229, 170–187. doi:10.1016/j.jms.2004.08.022

CrossRef Full Text | Google Scholar

Kaifu, N., Morimoto, M., Nagane, K., Akabane, K., Iguchi, T., and Takagi, K. (1974). Detection of Interstellar Methylamine. ApJ 191, L135–L137. doi:10.1086/181569

CrossRef Full Text | Google Scholar

Kendall, R. A., Dunning, T. H., and Harrison, R. J. (1992). Electron Affinities of the First‐row Atoms Revisited. Systematic Basis Sets and Wave Functions. J. Chem. Phys. 96, 6796–6806. doi:10.1063/1.462569

CrossRef Full Text | Google Scholar

Kleiner, I., and Hougen, J. T. (2015). A Hybrid Program for Fitting Rotationally Resolved Spectra of Floppy Molecules with One Large-Amplitude Rotatory Motion and One Large-Amplitude Oscillatory Motion. J. Phys. Chem. A. 119, 10664–10676. doi:10.1021/acs.jpca.5b08437

PubMed Abstract | CrossRef Full Text | Google Scholar

Knizia, G., Adler, T. B., and Werner, H.-J. (2009). Simplified CCSD(T)-F12 Methods: Theory and Benchmarks. J. Chem. Phys. 130, 054104. doi:10.1063/1.3054300

PubMed Abstract | CrossRef Full Text | Google Scholar

Kreglewski, M. (1993). Structure and Conformations of Non-rigid moleculesNATO/ASI Series. (Dordecht: Kluwer), 23–43.

Kreglewski, M. (1989). The Geometry and Inversion-Internal Rotation Potential Function of Methylamine. J.Mol.Spectrosc. 133, 10–21.

Google Scholar

Kreglewski, M. (1978). Vibration-inversion-internal Rotation-Rotation Hamiltonian for Methylamine. J.Mol.Spectrosc. 78, 1–19.

Google Scholar

Kreglewski, M., Jäger, W., and Dreizler, H. (1990). The Rotational Spectrum of Methylamine-D₃. J. Mol. Spec. 144, 334–343.

Google Scholar

Kreglewski, M., Stryjewski, D., and Dreizler, H. (1990). Hyperfine Quadrupole Structure of the Rotational Spectrum of Methylamine-D₅. J. Mol. Spec. 139, 182–190.

Google Scholar

Kreglewski, M., and Winther, F. (1992). High-resolution Infrared Spectrum of Methyl Amine: Assignment and Analysis of the Wagging State. J.Mol.Spectrosc. 156, 261–291.

Google Scholar

Kréglewski, M., and Wlodarczak, G. (1992). The Rotational Spectrum of Methylamine in a Submillimeter-Wave Range. J. Mol. Spectrosc. 156, 383–389. doi:10.1016/0022-2852(92)90239-k

CrossRef Full Text | Google Scholar

Lide, D. R. (1954). Effects of Internal Motion in the Microwave Spectrum of Methyl Amine. J. Chem. Phys. 22, 1613–1614. doi:10.1063/1.1740473

CrossRef Full Text | Google Scholar

Møller, Chr., and Plesset, M. S. (1934). Note on an Approximation Treatment for many-electron Systems. Phys. Rev. 46, 618–622.

Google Scholar

Motiyenko, R. A., Ilyushin, V. V., Drouin, B. J., Yu, S., and Margulès, L. (2014). Rotational Spectroscopy of Methylamine up to 2.6 THz. A&A 563, A137–A142. doi:10.1051/0004-6361/201323190

CrossRef Full Text | Google Scholar

Motiyenko, R. A., Margulès, L., Ilyushin, V. V., Smirnov, I. A., Alekseev, E. A., Halfen, D. T., et al. (2016). Millimeter and Submillimeter Wave Spectra of13C Methylamine. A&A 587, A152–A157. doi:10.1051/0004-6361/201526924

CrossRef Full Text | Google Scholar

Muller, S., Beelen, A., Guélin, M., Aalto, S., Black, J. H., Combes, F. F., et al. (2011). Molecules Atz= 0.89. A&A 535, A103–A134. doi:10.1051/0004-6361/201117096

CrossRef Full Text | Google Scholar

Nguyen, H. V. L., Gulaczyk, I., Kręglewski, M., and Kleiner, I. (2021). Large Amplitude Inversion Tunneling Motion in Ammonia, Methylamine, Hydrazine, and Secondary Amines: From Structure Determination to Coordination Chemistry. Coord. Chem. Rev. 436, 213797–213817. doi:10.1016/j.ccr.2021.213797

CrossRef Full Text | Google Scholar

Ohashi, N., and Hougen, J. T. (1987). The Torsional-Wagging Tunneling Problem and the Torsional-Wagging-Rotational Problem in Methylamine. J. Mol. Spectrosc. 121, 474–501. doi:10.1016/0022-2852(87)90064-6

CrossRef Full Text | Google Scholar

Ohashi, N., Oda, M., and Takagi, K. (1991). Microwave Spectrum of Methylamine-D1: Analysis of the Ground State. J. Mol. Spectrosc. 145, 180–191. doi:10.1016/0022-2852(91)90361-d

CrossRef Full Text | Google Scholar

Ohashi, N., Shimada, H., Olson, W. B., and Kawaguchi, K. (1992). Fourier Transform Spectrum in the Second Torsional Band Region of Methylamine. J. Mol. Spectrosc. 152, 298–306. doi:10.1016/0022-2852(92)90070-5

CrossRef Full Text | Google Scholar

Ohashi, N., Takagi, K., Hougen, J. T., Olson, W. B., and Lafferty, W. J. (1987). Far-infrared Spectrum and Ground State Constants of Methyl Amine. J. Mol. Spectrosc. 126, 443–459. doi:10.1016/0022-2852(87)90249-9

CrossRef Full Text | Google Scholar

Ohashi, N., Takagi, K., Hougen, J. T., Olson, W. B., and Lafferty, W. J. (1988). Far-infrared Spectrum of Methyl Amine. J. Mol. Spectrosc. 132, 242–260. doi:10.1016/0022-2852(88)90072-0

CrossRef Full Text | Google Scholar

Ohashi, N., and Toriyama, Y. (1994). Treatment of Tunneling Motions in Methylamine Using the Generalized IAM-like Method: Analysis of the Ground Vibrational State. J. Mol. Spectrosc. 165, 265–276. doi:10.1006/jmsp.1994.1128

CrossRef Full Text | Google Scholar

Ohashi, N., Tsunekawa, S., Takagi, K., and Hougen, J. T. (1989). Microwave Spectrum of Methyl Amine: Assignment and Analysis of the First Torsional State. J. Mol. Spectrosc. 137, 33–46. doi:10.1016/0022-2852(89)90266-x

CrossRef Full Text | Google Scholar

Ohishi, M., Suzuki, T., Hirota, T., Saito, M., and Kaifu, N. (2019). Detection of a New Methylamine (CH₃NH₂) Source: Candidate for Future glycine Surveys. Pub. Astron.Soc.Japan 71, 86. doi:10.1093/pasj/psz068

CrossRef Full Text | Google Scholar

Park, M. H., Choi, K.-W., Choi, S., Kim, S. K., and Choi, Y. S. (2006). Vibrational Structures of Methylamine Isotopomers in the Predissociative à States: CH3NHD, CD3NH2, CD3NHD, and CD3ND2. J. Chem. Phys. 125, 084311. doi:10.1063/1.2338322

PubMed Abstract | CrossRef Full Text | Google Scholar

Puzzarini, C., Salta, Z., Tasinato, N., Lupi, J., Cavallotti, C., and Barone, V. (2020). A Twist on the Reaction of the CN Radical with Methylamine in the Interstellar Medium: New Hints from a State-Of-The-Art Quantum-Chemical Study. MNRAS 496, 4298–4310. doi:10.1093/mnras/staa1652

CrossRef Full Text | Google Scholar

Salta, Z., Tasinato, N., Lupi, J., Boussessi, R., Balbi, A., Puzzarini, C., et al. (2020). Exploring the Maze of C2N2H5 Radicals and Their Fragments in the Interstellar Medium with the Help of Quantum-Chemical Computations. ACS Earth Space Chem. 4, 774–782. doi:10.1021/acsearthspacechem.0c00062

CrossRef Full Text | Google Scholar

Sastry, K. V. L. N. (1960). Microwave Spectrum of Methyl Amine. Proc. Indian Acad. Sci. 51, 301–309. doi:10.1007/bf03045786

CrossRef Full Text | Google Scholar

Senent, M. L. (1998b). Ab InitioDetermination of the Roto-Torsional Energy Levels Oftrans-1,3-Butadiene. J. Mol. Spectrosc. 191, 265–275. doi:10.1006/jmsp.1998.7638

PubMed Abstract | CrossRef Full Text | Google Scholar

Senent, M. L. (1998a). Determination of the Kinetic Energy Parameters of Non-rigid Molecules. Chem. Phys. Lett. 296, 299–306. doi:10.1016/s0009-2614(98)01052-5

CrossRef Full Text | Google Scholar

Senent, M. L. (2001). ENEDIM, “A Variational Code for Non-rigid Molecules”. (seefor more details) Available at: http://tct1.iem.csic.es/PROGRAMAS.htm.

Google Scholar

Senent, M. L., and Smeyers, Y. G. (1996). Ab Initio calculations and Analysis of the Torsional Spectra of Dimethylamine and Dimethylphosphine. J. Chem. Phys. 105, 2789–2797. doi:10.1063/1.472141

CrossRef Full Text | Google Scholar

Senent, M. L. (2018). The Large Amplitude Motions of Methylamine from the Perspective of the Highly Correlated Ab Initio Methods. J. Mol. Spectrosc. 343, 28–33. doi:10.1016/j.jms.2017.06.009

CrossRef Full Text | Google Scholar

Shimanouchi, T. (1972). Tables of Molecular Vibrational Frequencies Consolidated Volume I. National Bureau of Standards, 1–160.

Smeyers, Y. G., Villa, M., and Senent, M.-L. (1998). Ab InitioDetermination of the Torsion-Wagging and Wagging-Bending Infrared Band Structure Spectrum of Methylamine. J. Mol. Spectrosc. 191, 232–238. doi:10.1006/jmsp.1998.7626

PubMed Abstract | CrossRef Full Text | Google Scholar

Smeyers, Y. G., Villa, M., and Senent, M. L. (1996). Ab InitioDetermination of the Torsional and Wagging FIR Spectrum of Methylamine. J. Mol. Spectrosc. 177, 66–73. doi:10.1006/jmsp.1996.0118

CrossRef Full Text | Google Scholar

Takagi, K., and Kojima, T. (1971). Microwave Spectrum of Methylamine. J. Phys. Soc. Jpn. 30, 1145–1157. doi:10.1143/jpsj.30.1145

CrossRef Full Text | Google Scholar

Tamagake, K., and Tsuboi, M. (1974). Inversion and Internal Rotation in Methyl-D-Amine: Microwave Spectrum. J. Mol. Spectrosc. 53, 204–220. doi:10.1016/0022-2852(74)90127-1

CrossRef Full Text | Google Scholar

Taylor, D. P., and Bernstein, E. R. (1995). On the Low Lying Excited States of Methyl Amine. J. Chem. Phys. 103, 10453–10464. doi:10.1063/1.469895

CrossRef Full Text | Google Scholar

Werner, H.-J., Knowles, P. J., Manby, F. R., Schütz, M., Celani, P., Knizia, G., et al. (2012). MOLPRO, Version 2012.1, a Package of Ab Initio Programs. Available at: http://www.molpro.net.

Google Scholar

Woon, D. E., and Dunning, T. H. T. H. (1995). Gaussian Basis Sets for Use in Correlated Molecular Calculations. V. Core‐valence Basis Sets for boron through Neon. J. Chem. Phys. 103, 4572–4585. doi:10.1063/1.470645

CrossRef Full Text | Google Scholar