Promising Thermoelectric Performance in Two-Dimensional Semiconducting Boron Monolayer

A heavy element is a special character for high thermoelectric performance since it generally guarantees a low lattice thermal conductivity. Here, we unexpectedly found a promising thermoelectric performance in a two-dimensional semiconducting monolayer consisting of a light boron element. Using first-principles combined with the Boltzmann transport theory, we have shown that in contrast to graphene or black phosphorus, the boron monolayer has a low lattice thermal conductivity arising from its complex crystal of hexagonal vacancies. The conduction band with an intrinsic camelback shape leads to the high DOS and a high n-type Seebeck coefficient, while the highly degenerate valence band along with the small hole effective mass contributes to the high p-type power factor. As a result, we obtained the p-type thermoelectric figure of merit up to 0.96 at 300 K, indicating that the boron monolayer is a promising p-type thermoelectric material.

Introduction

In the past decade, people devoted themselves to improve the thermoelectric efficiency by trying to individually control the thermoelectric coefficients through low-dimensional crystals such as single layers, nanowires, 2D heterostructures, and nanotubes. The thermoelectric performance of a material is usually characterized by the dimensionless figure of merit ZT = S²σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity including both electronic and lattice contributions, and T is the absolute temperature, respectively (Mohanraman et al., 2015; Hu et al., 2021). High ZT requires a superior electronic transport but a minimized phonon transport at the same time, the latter usually arises from heavy elements (Ding et al., 2016). For instance, the lattice thermal conductivity of traditional commercial bulk thermoelectric materials such as Bi₂Te₃ and PbTe are lower than 1 W/mK (Pei and Liu, 2012; Hellman and Broido, 2014). Although the thermoelectric coefficient in some cases can be individually controlled in a low-dimensional crystal, the high lattice thermal conductivity still prevents a striking improvement of ZT (Kumar and Schwingenschlögl, 2015).

Balandin et al. (2008) experimentally reported that the thermal conductivity of single-layer graphene is higher than 4000 W/mK at room temperature. For monolayer MoS₂, it is about 100 W/mK at 300 K based on Yang’s report (Jin et al., 2015). Using a molecular dynamics simulation, Xu et al. (2015) obtained the lattice thermal conductivity of phosphorene along the zigzag direction that is higher than 150 W/mK at 300 K. Among these popular single-layer crystals, it was found that an extremely high thermal conductivity leads to poor ZT, which can be ascribed to the following two factors: 1) light elements with high vibration frequency and 2) large atomic weight difference forbids the anharmonic scattering. In this regard, we intended to think that is there possibility to achieve promising thermoelectric transport in other single-layer crystal consisting of light elements? In recent years, boron, one of the carbon’s nearest neighbors, demonstrated the polymorphism in two-dimensional crystals, which are called borophene. However, most of the boron monolayers were found to be metallic by experiment or theory. Interestingly, Hu et al. recently proposed a series of semiconducting boron monolayers formulated by the connected network of hexagonal vacancies (Xu et al., 2017). Such semiconducting phases of the boron monolayer are expected to achieve in experiments since the controlled synthesis of the boron monolayer is a mature technology (Kong et al., 2018; Kiraly et al., 2019).

The semiconducting ${\beta }_1^s$ boron monolayer has an indirect bandgap of 0.74 eV based on HSE06 functional (Xu et al., 2017), and the multi-valley character of both conduction and valence band near the Fermi level indicates the promising electronic transport performance. In addition, the complex crystal consisting of twelve boron atoms and hexagonal vacancies leads to large number of coupled phonon branches, which points to possible low lattice thermal conductivity in the crystal. To explore the potential of the semiconducting ${\beta }_1^s$ boron monolayer as a thermoelectric material, we studied its thermoelectric transport performance by first-principles combined with Boltzmann transport equations. We found that the lattice thermal conductivity is 20.2 W/mK at 300 K, and highly degenerate hole pockets with small effective mass lead to the high p-type power factor. Finally, the optimal ZT reaches 0.96 at 300 K for p-type doping, which is a recorded value among two-dimensional monolayers.

Computational Details

The first-principles calculations were performed within the framework of density function theory (DFT) using projector-augmented wave (PAW) (Perdew et al., 1997) pseudopotentials and Perdew–Burke–Ernzerhof (PBE) (Kresse and Furthmüller, 1996) exchange correlation functionals as implemented in VASP (Tran and Blaha, 2009). To construct the single-layer crystal, a 15-Å-thick vacuum slab was added along the z-direction. The plane-wave cutoff energy was set to 400 eV and the Monkhorst–Pack k mesh was 15 × 15 × 1. Geometry optimization was converged until the force acting on the ions become smaller than 10⁻³ eV/Å. When we calculated the electronic structure, a modified Becke–Johnson (mBJ) (Tran and Blaha, 2009) functional was also considered to yield the accurate effective mass and bandgap.

The electronic transport properties were calculated using the Boltzmann transport equation (BTE) under a constant relaxation time approximation as implemented in BoltzTraP (Madsen and Singh, 2006). A rigid band approximation is used to treat doping, and the Fermi level shifts up for n-type doping while down for the p-type. However, within this approximation, the Seebeck coefficient can be calculated independent of carrier relaxation time τ, while the evaluation of electrical conductivity still requires the knowledge of τ. In this regard, we employed deformation potential theory based on effective mass approximation to calculate τ (Herring and Vogt, 1956). At last, we performed phonon BTE solution as implemented in the ShengBTE (Li et al., 2014) package to calculate lattice thermal conductivity. Second- and third-order interatomic force constants (IFCs) are quite necessary inputs for pBTE, which were obtained from DFT calculations using a converged 4 × 4 × 1 supercell. The phonon spectrum was obtained from the Phonopy code (Togo et al., 2008), and a converged cutoff distance of 0.4 nm for interactive distance was used in calculating anharmonic IFCs.

Results and Discussion

Figure 1A shows the crystal structure of the ${\beta }_1^s$ semiconducting boron monolayer, which consists of a connected network of hexagonal vacancies that can be divided into triangle regions and heptagon regions, according to Hu et al (Xu et al., 2017). The space group is Amm2 and the lattice parameter 6.12 Å after relaxation is consistent with Hu’s result (Xu et al., 2017). Figure 1B shows the Brillouin zone path, that is, Γ-Y-P₁-Γ-N-P₁. Based on Hu et al (Xu et al., 2017), the HSE06 band structure indicates that the ${\beta }_1^s$ boron monolayer is an indirect semiconductor with a bandgap of 0.74 eV, and also, the phonon spectrum and molecular dynamics simulation confirm the thermal stability of this boron monolayer. In contrast to monolayer TMDCs with a large bandgap, the moderate bandgap of the boron monolayer may possess better electronic transport performance.

FIGURE 1

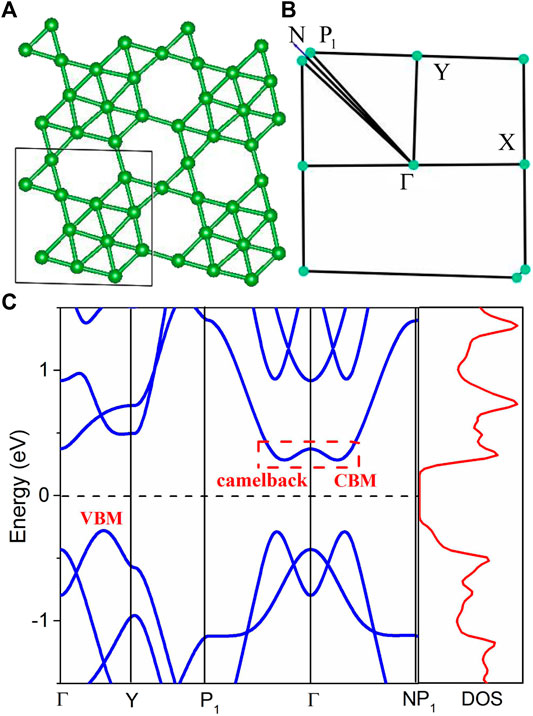
FIGURE 1. The atomic structure (A) and the Brillouin zone path (B) of the ${\beta }_1^s$ boron monolayer and (C) shows the calculated band structure and density of states.

As shown in Figure 1C, the calculated band structure of the ${\beta }_1^s$ boron monolayer displays an indirect bandgap of 0.68 eV based on mBJ modification, which is very close to the result of HSE06 (Xu et al., 2017). The mBJ functional has been shown to yield the accurate bandgap, effective mass, and frontier-band ordering. The conduction band minimum (CBM) is located in the interval between Γ and P₁ points, while the valence band maximum (VBM) is located in the interval between Γ and Y points. In consistent with previous calculation, the VBM is dominated by the out-of-plane p_z orbitals while the CBM is attributed to the in-plane s+p_x,y orbitals (Xu et al., 2017), and this semiconducting ${\beta }_1^s$ boron monolayer was realized by modulating the in-plane s+p_x,y orbitals and p_z-derived bands through the connected network of hexagonal vacancies, according to Hu et al (Xu et al., 2017).

Interestingly, the band structure of the ${\beta }_1^s$ boron monolayer possesses several advantages of electronic transport performance. First, the lowest conduction band, shown in Figure 1C, exhibits a camelback shape along the P₁-Γ-N direction. The camelback shape is known in topological materials where the spin-orbital coupling is not large enough to cause inversion between the frontier bands (Eremeev et al., 2010). Here, this interesting band dispersion is obtained in the light ${\beta }_1^s$ boron monolayer. The importance of the camelback shape in electronic transport is that it can increase the number of degenerate carrier pockets, which thereby increases the density of states (DOS) effective mass (Ding et al., 2019a; Ding et al., 2019b). As one can see in the right panel of Figure 1C, the DOS at the CBM is markedly higher than that at VBM. As a result, a higher n-type Seebeck coefficient can be achieved in this boron monolayer. In addition to CBM, there are these band extremes of VBM along Γ-Y, P₁-Γ, and Γ-N, respectively, which are highly degenerate in energy and indicate more carrier pockets joining in hole transport. The carrier effective mass near the Fermi level dominates the carrier mobility and relaxation time and plays an important role in thermoelectric transport (Peng et al., 2014). As one can see, the band near the VBM is more dispersive than that near the CBM, yielding a hole effective mass 0.57 m₀ smaller than the 0.998 m₀ of an electron.

Calculated electronic transport properties including the Seebeck coefficient, electrical conductivity, and the power factor at room temperature are shown in Figure 2. The Seebeck coefficient decreases while the electrical conductivity increases with the increase of carrier density since they are inversely related to carrier density. In this regard, the power factor cannot be improved infinitely but can be optimized by modulating carrier density. In Figure 2A, the higher n-type Seebeck coefficient can be attributed to the camelback-shaped band, as discussed above. To obtain the electrical conductivity as shown in Figure 2B, we employed deformation potential theory (Herring and Vogt, 1956) to calculate the carrier relaxation time. Calculated results are shown in Table 1. It is crucial to find that the lower deformation potential constant of holes reflects the minimal sensitivity of valence band maximum to deformation. Along with the smaller hole effective mass, a high hole mobility and long hole relaxation time were obtained, as compared to an electron. As a result, the p-type power factor is much higher than n-type, as shown in Figure 2C. The maximum power factor of the p-doped semiconducting boron monolayer reaches 121 mW/mK² at an optimal carrier density of 3.14 × 10¹² cm⁻², while it is only about 17mW/mK² in monolayer MoS₂ (Jin et al., 2015). The Seebeck coefficient under this optimal carrier density for n- and p-type are 263 µV/K and 175 µV/K, respectively, which are the standard values of thermoelectric materials (Sun and Singh, 2016).

FIGURE 2

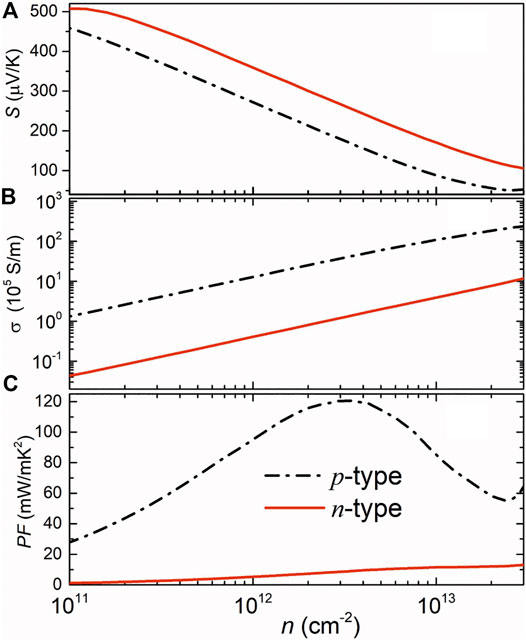
FIGURE 2. Calculated Seebeck coefficient (A), electrical conductivity (B), and the power factor (C) of the ${\beta }_1^s$ boron monolayer at 300 K.

TABLE 1

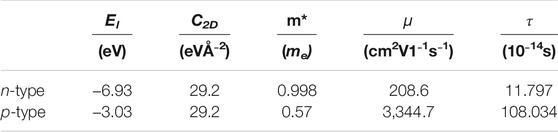
TABLE 1. Calculated DP constant, elastic modulus, carrier effective mass, carrier mobility, and carrier relaxation time at 300 K.

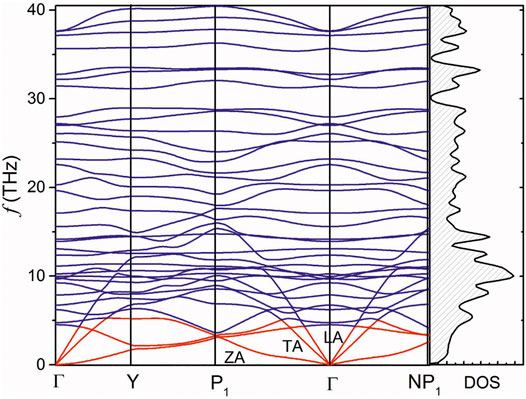
Calculated phonon dispersion of the ${\beta }_1^s$ boron monolayer is shown in Figure 3. First, in contrast to graphene, in phosphorene and monolayer MoS₂, the twelve atoms in the unit cell leads to thirty-six phonon branches. It was found that a complex crystal with many optical modes is usually associated with low lattice thermal conductivity (Ding et al., 2018; Hu et al., 2020a; Hu et al., 2020b). A number of optical modes gather in frequency about 10 THz. High-frequency phonons with low velocity often do little contribution to lattice thermal conductivity. One can also see that the low-lying optical modes are coupled with acoustic modes, which is different from phosphorene or monolayer MoS₂ where there is a wide frequency gap among optical branches or between acoustic and optical branches (Fei et al., 2014; Jin et al., 2015). A strong coupling of phonon modes will increase the anharmonic scattering processes and leads to the low lattice thermal conductivity. Although the allowed phonon frequency of about 40 THz is higher than that of phosphorene and monolayer MoS₂ due to the light element, the allowed acoustic frequency of about 5 THz of phonon modes is quite lower than graphene, phosphorene, and monolayer MoS₂ (Fei et al., 2014; Jin et al., 2015; Ge et al., 2016). These advantages of low lattice thermal conductivity in the ${\beta }_1^s$ boron monolayer are probably associated with its complex crystal of hexagonal vacancies.

FIGURE 3

FIGURE 3. The phonon dispersion and density of states of the ${\beta }_1^s$ boron monolayer.

Figure 4A shows the calculated lattice thermal conductivity of the boron monolayer with respect to temperature. It can be seen that the BTE results are well fitted with κ∝1/T. The lattice thermal conductivity at room temperature is about 20 W/mK, which is much lower than that of graphene (above 4000 W/mK) (Balandin et al., 2008), phosphorene (above 150 W/mK along zigzag) (Xu et al., 2015) consisting of light element, and also monolayer MoS₂ (about 100 W/mK) (Jin et al., 2015). Thus, the ${\beta }_1^s$ boron monolayer with a light boron element in the crystal also exhibits low lattice thermal conductivity, as compared to previous light monolayers. Such a low lattice thermal conductivity can be ascribed to the large number of optical modes and the strongly coupled phonon modes as arising from the complex unit cell with a network of hexagonal vacancies, as discussed above. The low group velocity of optical modes, as shown in Figure 4B, indicates that the acoustic and low-lying optical modes do most of the contribution to phonon transport. One can see from Figure 4C that the anharmonic scattering rate increases with the increase in temperature, and such scattering rate is much higher than monolayer MoS₂ in which the scattering rates of phonons almost lie below 1ps⁻¹ (Ding et al., 2018). Figure 4D shows the cumulative lattice thermal conductivity as a function of mean free path at 300 K, which points to the well convergence of the lattice thermal conductivity.

FIGURE 4

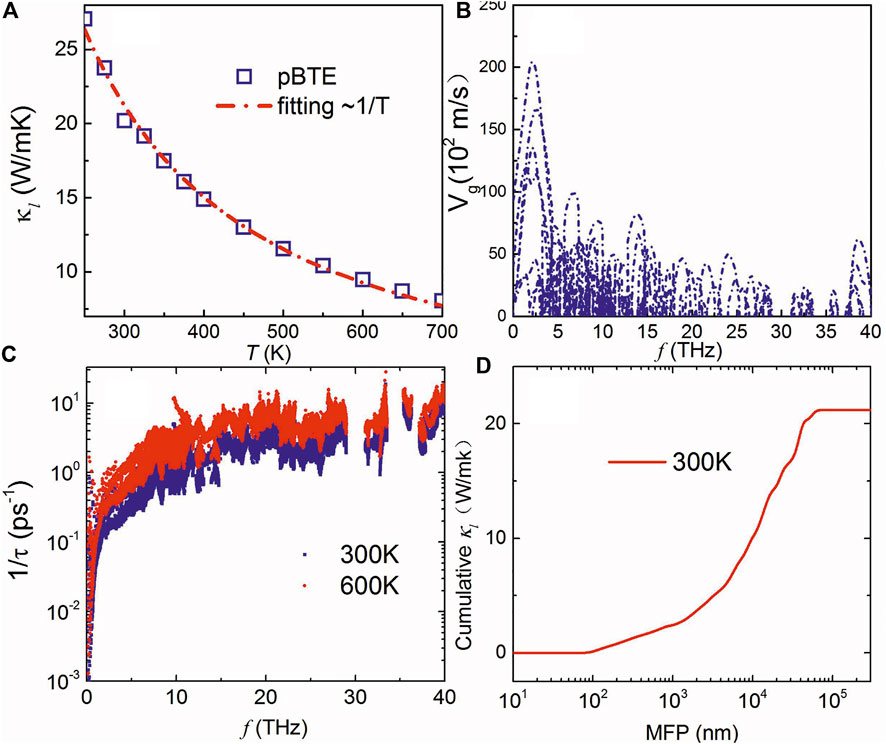
FIGURE 4. (A) Calculated lattice thermal conductivity with respect to temperature, phonon group velocity (B), and anharmonic scattering (C) of the ${\beta }_1^s$ boron monolayer. (D) shows the cumulative lattice thermal conductivity with respect to the mean free path at 300 K.

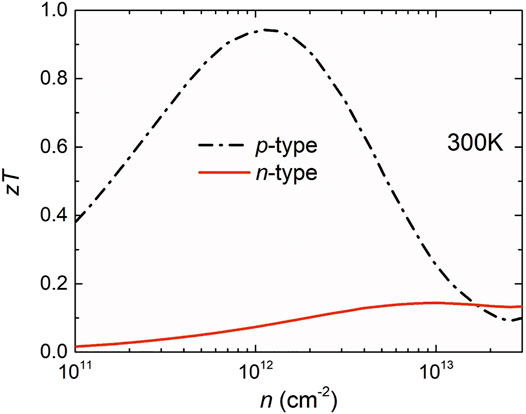
Combining the electronic and phonon transport properties, we evaluated the thermoelectric performance of the ${\beta }_1^s$ boron monolayer. Figure 5 shows the figure of merit ZT values for both the n- and p-doped boron monolayer as a function of the carrier concentration at room temperature. Obviously, the p-type thermoelectric performance is superior to n-type due to the excellent p-type power factor. Combined with the relatively low lattice thermal conductivity, the optimal p-type ZT value of the boron monolayer reaches 0.96 at an optimal carrier concentration of about 1 × 10¹² cm⁻², which is a recorded value among single-layer materials consisting of light elements. Our results indicate that the semiconducting ${\beta }_1^s$ boron monolayer has a potential application in thermoelectric devices.

FIGURE 5

FIGURE 5. Calculated thermoelectric figure of merit at 300 K.

Conclusion

We have investigated the thermoelectric performance of a semiconducting ${\beta }_1^s$ boron monolayer using first-principles combined with Boltzmann transport equations. We have shown that the high n-type Seebeck coefficient arises from the camelback shape of the lowest conduction band, while the highly degenerate valence band with small effective mass leads to the high hole mobility and long relaxation time, which contributes to the superior hole transport performance. Importantly, we found relatively low lattice thermal conductivity in the boron monolayer, ∼20 W/mK at 300 K, as compared with graphene or phosphorene also consisting of a light element. This is primarily ascribed to the complex unit cell with the hexagonal vacancy. Finally, we obtained an optimal p-type ZT of about 0.96 at 300 K in this boron monolayer, indicating its potential as p-type thermoelectric materials.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author Contributions

GD developed the idea for the study. YH and GD did the analyses and wrote the study. DL, RL, SL, CF, and DFL conceived and designed the study. All authors analyzed the data and were involved in writing the manuscript.

Funding

This work is supported by the National Natural Science Foundation of China (Grant No.11804040).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer (HY) declared a past coauthorship with one of the authors (GD) to the handling editor.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Balandin, A. A., Ghosh, S., Bao, W., Calizo, I., Teweldebrhan, D., Miao, F., et al. (2008). Superior thermal Conductivity of Single-Layer Graphene. Nano Lett. 8, 902–907. doi:10.1021/nl0731872

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, G., Carrete, J., Li, W., Gao, G. Y., and Yao, K. (2016). Ultralow Lattice thermal Conductivity in Topological Insulator TlBiSe2. Appl. Phys. Lett. 108, 233902. doi:10.1063/1.4953588

CrossRef Full Text | Google Scholar

Ding, G., He, J., Gao, G. Y., and Yao, K. (2018). Two-dimensional MoS2-MoSe2 Lateral Superlattice with Minimized Lattice thermal Conductivity. J. Appl. Phys. 124, 165101. doi:10.1063/1.5051067

CrossRef Full Text | Google Scholar

Ding, G., Hu, Y., Li, D., and Wang, X. (2019). A Comparative Study of Thermoelectric Properties between Bulk and Monolayer SnSe. Results Phys. 15, 102631. doi:10.1016/j.rinp.2019.102631

CrossRef Full Text | Google Scholar

Ding, G., Li, S., and He, J. (2019). Origins of Promising Thermoelectric Performance in Quaternary Selenide BaAg2SnSe4. Appl. Phys. Express 12, 071006. doi:10.7567/1882-0786/ab29e1

CrossRef Full Text | Google Scholar

Eremeev, S. V., Koroteev, Y. M., and Chulkov, E. V. (2010). Ternary Thallium-Based Semimetal Chalcogenides Tl-V-VI2 as a New Class of Three-Dimensional Topological Insulators. JETP Lett. 91, 594–598. doi:10.1134/S0021364010110111

CrossRef Full Text | Google Scholar

Fei, R., Faghaninia, A., Soklaski, R., Yan, J.-A., Lo, C., and Yang, L. (2014). Enhanced Thermoelectric Efficiency via Orthogonal Electrical and thermal Conductances in Phosphorene. Nano Lett. 14, 6393–6399. doi:10.1021/nl502865s

PubMed Abstract | CrossRef Full Text | Google Scholar

Ge, X.-J., Yao, K.-L., and Lü, J.-T. (2016). Comparative Study of Phonon Spectrum and thermal Expansion of Graphene, Silicene, Germanene, and Blue Phosphorene. Phys. Rev. B. 94, 165433. doi:10.1103/PhysRevB.94.165433

CrossRef Full Text | Google Scholar

Hellman, O., and Broido, D. A. (2014). Phonon thermal Transport inBi2Te3from First Principles. Phys. Rev. B. 90, 134309. doi:10.1103/PhysRevB.90.134309

CrossRef Full Text | Google Scholar

Herring, C., and Vogt, E. (1956). Transport and Deformation-Potential Theory for many-valley Semiconductors with Anisotropic Scattering. Phys. Rev. 101, 944–961. doi:10.1103/PhysRev.101.944

CrossRef Full Text | Google Scholar

Hu, Y., Li, D., Yin, Y., Li, S., Ding, G., Zhou, H., et al. (2020). The Important Role of Strain on Phonon Hydrodynamics in diamond-like Bi-layer Graphene. Nanotechnology 31, 335711. doi:10.1088/1361-6528/ab8ee1

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, Y., Yang, T., Li, D., Ding, G., Dun, C., Wu, D., et al. (2021). Origins of Minimized Lattice thermal Conductivity and Enhanced Thermoelectric Performance in WS2/WSe2 Lateral Superlattice. ACS Omega 6, 7879–7886. doi:10.1021/acsomega.1c00457

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, Y., Yin, Y., Li, S., Zhou, H., Li, D., and Zhang, G. (2020). Three-Fold Enhancement of In-Plane Thermal Conductivity of Borophene through Metallic Atom Intercalation. Nano Lett. 20, 7619–7626. doi:10.1021/acs.nanolett.0c03135

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, Z., Liao, Q., Fang, H., Liu, Z., Liu, W., Ding, Z., et al. (2015). A Revisit to High Thermoelectric Performance of Single-Layer MoS2. Sci. Rep. 5, 1–7. doi:10.1038/srep18342

PubMed Abstract | CrossRef Full Text | Google Scholar

Kiraly, B., Liu, X., Wang, L., Zhang, Z., Mannix, A. J., Fisher, B. L., et al. (2019). Borophene Synthesis on Au(111). ACS Nano 13, 3816–3822. doi:10.1021/acsnano.8b09339

PubMed Abstract | CrossRef Full Text | Google Scholar

Kong, L., Wu, K., and Chen, L. (2018). Recent Progress on Borophene: Growth and Structures. Front. Phys. 13, 138105. doi:10.1007/s11467-018-0752-8

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B. 54, 11169–11186. doi:10.1103/PhysRevB.54.11169

CrossRef Full Text | Google Scholar

Kumar, S., and Schwingenschlögl, U. (2015). Thermoelectric Response of Bulk and Monolayer MoSe2 and WSe2. Chem. Mater. 27, 1278–1284. doi:10.1021/cm504244b

CrossRef Full Text | Google Scholar

Li, W., Carrete, J., A. Katcho, N., and Mingo, N. (2014). ShengBTE: A Solver of the Boltzmann Transport Equation for Phonons. Comp. Phys. Commun. 185, 1747–1758. doi:10.1016/j.cpc.2014.02.015

CrossRef Full Text | Google Scholar

Madsen, G. K. H., and Singh, D. J. (2006). BoltzTraP. A Code for Calculating Band-Structure Dependent Quantities. Comp. Phys. Commun. 175, 67–71. doi:10.1016/j.cpc.2006.03.007

CrossRef Full Text | Google Scholar

Mohanraman, R., Lan, T.-W., Hsiung, T.-C., Amada, D., Lee, P.-C., Ou, M.-N., et al. (2015). Engineering Nanostructural Routes for Enhancing Thermoelectric Performance: Bulk to Nanoscale. Front. Chem. 3, 63. doi:10.3389/fchem.2015.00063

PubMed Abstract | CrossRef Full Text | Google Scholar

Pei, Y.-L., and Liu, Y. (2012). Electrical and thermal Transport Properties of Pb-Based Chalcogenides: PbTe, PbSe, and PbS. J. Alloys Comp. 514, 40–44. doi:10.1016/j.jallcom.2011.10.036

CrossRef Full Text | Google Scholar

Peng, H., Kioussis, N., and Snyder, G. J. (2014). Elemental Tellurium as a Chiralp-type Thermoelectric Material. Phys. Rev. B. 89, 195206. doi:10.1103/PhysRevB.89.195206

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1997). Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)]. Phys. Rev. Lett. 78, 1396. doi:10.1103/PhysRevLett.77.386510.1103/physrevlett.78.1396

CrossRef Full Text | Google Scholar

Sun, J., and Singh, D. J. (2016). Thermoelectric Properties ofMg2(Ge,Sn): Model and Optimization ofZT. Phys. Rev. Appl. 5, 024006. doi:10.1103/PhysRevApplied.5.024006

CrossRef Full Text | Google Scholar

Togo, A., Oba, F., and Tanaka, I. (2008). First-principles Calculations of the Ferroelastic Transition between Rutile-type andCaCl2-typeSiO2at High Pressures. Phys. Rev. B. 78, 134106. doi:10.1103/PhysRevB.78.134106

CrossRef Full Text | Google Scholar

Tran, F., and Blaha, P. (2009). Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential. Phys. Rev. Lett. 102, 226401. doi:10.1103/PhysRevLett.102.226401

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, S.-G., Li, X.-T., Zhao, Y.-J., Liao, J.-H., Xu, W.-P., Yang, X.-B., et al. (2017). Two-Dimensional Semiconducting Boron Monolayers. J. Am. Chem. Soc. 139, 17233–17236. doi:10.1021/jacs.7b08680

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, W., Zhu, L., Cai, Y., Zhang, G., and Li, B. (2015). Direction Dependent thermal Conductivity of Monolayer Phosphorene: Parameterization of Stillinger-Weber Potential and Molecular Dynamics Study. J. Appl. Phys. 117, 214308. doi:10.1063/1.4922118

CrossRef Full Text | Google Scholar