
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Chem. , 13 September 2021
Sec. Theoretical and Computational Chemistry
Volume 9 - 2021 | https://doi.org/10.3389/fchem.2021.737579
Developing models for predicting molecular properties of organic compounds is imperative for drug development and environmental safety; however, development of such models that have high predictive power and are independent of the compounds used is challenging. To overcome the challenges, we used a thermodynamics-based theoretical derivation to construct models for accurately predicting molecular properties. The free energy change that determines a property equals the sum of the free energy changes (ΔGFs) caused by the factors affecting the property. By developing or selecting molecular descriptors that are directly proportional to ΔGFs, we built a general linear free energy relationship (LFER) for predicting the property with the molecular descriptors as predictive variables. The LFER can be used to construct models for predicting various specific properties from partition coefficients. Validations show that the models constructed according to the LFER have high predictive power and their performance is independent of the compounds used, including the models for the properties having little correlation with partition coefficients. The findings in this study are highly useful for applications in drug development and environmental safety.
The rapid development of new organic compounds in various chemical-related laboratories and industries has increased the difficulty in measuring the physicochemical, and absorption, distribution, metabolism, excretion, and toxicity (ADME/Tox) properties of all possible compounds. Therefore, the development of techniques for predicting these properties via computational tools is imperative (Sarkar et al., 2012; Li et al., 2019; Sun et al., 2019; Suay-Garcia et al., 2020). Quantitative structure–property relationships (QSPRs) with multiple predictive variables are widely used for predicting various properties of organic compounds. QSPR employs regression statistics using algorithms, such as artificial neural networks, (Deeb et al., 2011; Song et al., 2017), machine learning (Bushdid et al., 2018; Cheng and Ng, 2019; Zheng et al., 2019), and partial least square (Deeb et al., 2011; T. Stanton, 2012), with predictive variables usually selected from a few thousand molecular descriptors based on mathematical and statistical tools (Mansouri et al., 2018; Lee et al., 2019; Fioressi et al., 2020). A large number of articles related to QSPR were published per year and QSPR has gained importance in a wide range of fields, such as drug design, pesticide design, and environmental toxicology (Roy et al., 2018; Yang et al., 2018; Zhu et al., 2018; He et al., 2019; Khan et al., 2019; Zhu et al., 2020a). For example, predicting the ADME/Tox of drug candidates before synthesis can significantly reduce the cost and time of drug development and increase the success rate (Cheng et al., 2013; Dickson et al., 2017; Zhu et al., 2018). Predicting soil/water partition coefficients and the toxicities of organic compounds is vital for environmental risk assessments (Freitas et al., 2014; Sabour et al., 2017; Khan et al., 2019). Some properties can be predicted accurately with hydrophobicity (logPoct, the logarithm of the partition coefficient between n-octanol and water) and/or other commonly used molecular descriptors, e.g., electrophilicity index (ω) (Raevsky, 2004; Pal et al., 2019; Jana et al., 2020). For example, logPoct has been used to predict the water solubility with high accuracy, (Raevsky, 2004), Robust multiple linear regression (MLR) models for toxicity prediction can be constructed by using the combinations of electronic factor (ω, ω2, or ω3) and hydrophobicity factor [logPoct, (logPoct)2] as predictors (Pal et al., 2019; Jana et al., 2020). The robustness of the models were ascertained by neural networks. However, for many properties, constructing QSPR models with high predictive accuracy and reliability remains a challenge. The performance of QSPR models greatly depends on the compounds used for investigation, quality of the data, and modelling methodology employed (Song et al., 2017; Mansouri et al., 2018; Zhang et al., 2020). For a given property, the predictive variables would be different if the data in the training set are different. In addition, QSAR models usually work well only for the compounds within their applicability domains and do not have good predictive accuracy for other compounds (Kaneko, 2017; Liu and Wallqvist, 2019). However, it is difficult to define the accurate applicability domains for QSPR models because there is no general agreement for quantifying compound similarity (Carrió et al., 2016). It is thus important to develop a new methodology for constructing models that have high predictive power and the performance of the models is independent of the compounds used.
The quantitative formula and quantitative relationships that are developed via theoretical derivation in physical chemistry are absolutely correct and are independent of the compounds used. For example, the partition coefficient between water and an organic solvent (logPow) for a solute is directly proportional to the standard free energy change for transferring the solute from water to the organic solvent (ΔGtr). The ΔGtr in turn depends on the standard enthalpy change (ΔHtr) and entropy change (ΔStr) of the phase-transferring process. Thus, at a given temperature, the model logPow = b1ΔHtr + b2ΔStr + c (b1, b2, and c are constants) is absolutely correct and has high predictive power for predicting logPow. This example indicates that the models developed via thermodynamics-based theoretical derivations may overcome the shortages of the models developed by using mathematical and statistical tools. A large number of physicochemical properties, ADME/Tox qualities, and many other properties of organic compounds depend on the changes in free energy caused by the intermolecular noncovalent interactions of the compounds with their environments. The enormous catalytic power of many enzymes depends on the noncovalent interactions between substrates and enzymes (Warshel et al., 2006; Chen et al., 2019). It is thus expected that models with high predictive power for many properties can be developed by considering the free energy changes related to the properties. In this study, we used a thermodynamics-based theoretical derivation to develop a general linear free energy relationship (LFER) for predicting various properties of organic compounds. The LFER can be used to construct models for many specific properties. Validation shows that the models for specific properties have high predictive power and their performance is independent of the compounds used.
In this study, all experimental data of logPoct, logP16 (the logarithm of the partition coefficient between hexadecane and water), logPchl (the logarithm of the partition coefficient between chloroform and water), logPaln (the logarithm of the partition coefficient between aniline and water), logKbrain (the logarithm of the partition coefficient from air to human brain) and logKp(logarithm of experimental human skin permeability) are collected from literatures (Abraham et al., 1994; Abraham et al., 1999; Abraham and Martins, 2004; Abraham et al., 2006; Abraham et al., 2015; Zhang et al., 2017). Hydrogen bond acceptors (HBAs) include very weak H-bond acceptors. For example, the sp2 carbon atoms from carbon-carbon double bonds and aromatic rings are weak HBAs. Hydrogen bond donors (HBDs) include very weak H-bond donors. For example, the hydrogen atoms in CHCl3 and CH3NO2 are weak HBDs.
Sm is a molecular descriptor developed in this study. The Sm values of organic compounds were calculated based on the formula of the compounds. Assume the formula of a neutral organic compound is CcHhOoNnSsFfClclBrbrIi, the Sm of this compound is
In Eq. 1, c, h, o, n, s, f, cl, br and i are the numbers of carbon, hydrogen, oxygen, nitrogen, sulfur, fluoride, chloride, bromide and iodide atoms in the solute, Nc3 is the number of sp3 carbons connecting three heavy atoms (fluoride is not included), Nc4 is the number of sp3 carbons connecting four heavy atoms (fluoride is not included).
HM_HBD values of solutes were calculated based on the approach reported in a previous study (Chen et al., 2020).
In this study, the flexibility of a solute is calculated by summarizing the flexibilities of the bonds of the solute. If a bond is not rotatable or if the rotation of a bond does not change the conformation of the solute, the flexibility of the bond is set to zero (note: hydrogen atoms are not included for determining conformations). The flexibility of the C—C bond in R1CH2—CH2R2 is set to one. If the energy barrier for rotating a bond is obviously higher than that for rotating the R1CH2—CH2R (Sun et al., 2019) bond, the flex value is set to zero. For example, the C—N bond in RCO—NH and the C—C bond in Ar—CO are set to zero. If the energy barrier for rotating a bond is obviously lower than that for rotating the R1CH2—CH2R2 bond, the flex value is set to 1.5. For example, the energy barrier for rotating the R1O—CH2R2 bond is lower than that for R1CH2—CH2R (Sun et al., 2019) and thus the Flex value of the C—O bond is set to 1.5. Also, the flexibility of C—C in R1CH2—C6H5 is set to 0.5 because of the symmetry of phenyl ring.
The free energy changes for transferring depolarized solutes from water to hexadecane (ΔGtr_depol) were calculated based on the method reported in previous study (Chen et al., 2020). Based on the logPoct (or logPchl) and ΔGtr_depol values of nonpolar compounds, the model for the regression of logPoct (or logPchl) against ΔGtr_depol was developed. This model was then used to calculate the logPoct (or logPchl) values for depolarized solutes. For a solute containing HBAs but no HBDs, the difference between the calculated logPoct (or logPchl) for the depolarized solute and the experimental logPoct (or logPchl) of the solute is the effect of HBAs on the logPoct (or logPchl) of the solute.
All the models and the statistical reliabilities of the models were obtained by performing the multiple linear regressions implemented in Excel.
In the theoretical derivation, we used “Y” to represent a property and the symbol “ΔGY” to represent the free energy change that determines Y. The ΔGY values for many properties are not easy to be calculated directly. Thus, we decomposed ΔGY into the free energy changes that are caused by the factors affecting Y. The free energy change caused by a factor is denoted by “ΔGF”. Thus, ΔGY equals the summarization of the ΔGFs for all the factors affecting Y.
For the properties depending on the noncovalent interactions of solutes, they are affected by the molecular sizes, hydrogen-bond acceptors (HBAs), and hydrogen-bond donors (HBDs) of the solutes, which was demonstrated in a previous study (Chen et al., 2020). Many properties are also affected by the flexibilities of solutes. For example, the partition coefficients of organic compounds between a flexible environment (e.g., blood) and a much less flexible environment (e.g., muscle) are obviously affected by the flexibilities of the compounds. It is challenging to accurately quantify the ΔGFs for various properties. However, it is possible to develop molecular descriptors that are directly proportional to ΔGFs. We used DF to represent the molecular descriptor that is directly proportional to ΔGF. Then, ΔGY can be expressed as:
The kF values are constant for a given property. Theoretically, if the molecular descriptors apply to various properties, Eq. 3 can be used to construct models with high predictive power for the properties. Many properties are mainly affected by the molecular sizes, HBAs, HBDs and flexibilities of solutes. Thus, in this study, we developed or selected molecular descriptors for quantifying the effects of molecular size, HBAs, HBDs and flexibility on the properties.
The molecular descriptor we developed for quantifying the effects of molecular size on properties is denoted by “Sm”. The Sm values of organic compounds represent the relative molecular sizes of the compounds and can be easily calculated from their molecular formulas (see Computational Methods). For example, the Sm for catechol (formula: C6H6O2) is 9.8 (num. for C + 0.3
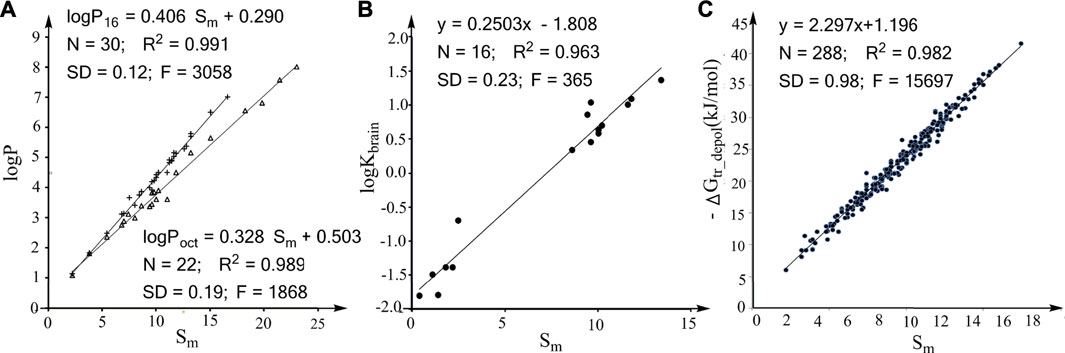
FIGURE 1. Correlations between the molecular descriptor Sm and the effects of molecular size on various properties. (A) Linear associations between logP16/logPoct and Sm for alkanes. (B) Linear association between logKbrain (log of the partition coefficient from air to human brain) and Sm for nonpolar compounds. (C) Plot of the water to hexadecane phase-transferring free energy for depolarized solutes (ΔGtr_depol) against the Sm values of the solutes.
In previous studies, we defined the water to hexadecane phase transferring free energy contributed by the electrostatic interactions of the HBAs of a solute as the overall H-bonding capability of the HBAs of the solute (Chen et al., 2019; Chen et al., 2020; Chen et al., 2016) and this overall H-bonding capability is donated by “HM_HBA.” The definition indicates that HM_HBA is an ideal molecular descriptor for quantifying the effects of HBAs on logP16. We next explored whether HM_HBA is an ideal molecular descriptor for logPoct and logPchl. The strong linear associations between the effect of HBAs on logPoct and HM_HBA (Figure 2A) and between the effect of HBAs on logPchl and HM_HBA (Figure 2B) suggest that HM_HBA is an ideal molecular descriptor for quantifying the effects of HBAs on various properties. Similarly, we defined the water to hexadecane phase transferring free energy contributed by the electrostatic interactions of the HBDs of a solute as the overall H-bonding capability of the HBDs of the solute (HM_HBD) (Chen et al., 2016; Chen et al., 2019; Chen et al., 2020). In a previous study, we revealed that the contribution of a protein-ligand H-bond to the protein-ligand binding free energy is directly proportional to the H-bonding capability of the HBA and the H-bonding capability of the HBD (Chen et al., 2016). We also found that the effect of an enzyme-substrate H-bond interaction on the free energy barrier of the enzymatic reaction is directly proportional to the H-bonding capability of the atom from the enzyme (Chen et al., 2019). Thus, we believe that the effects of HBAs and HBDs of solutes on the properties related to noncovalent interactions are directly proportional to the HM_HBA and HM_HBD values of the solutes. HM_HBA and HM_HBD are ideal molecular descriptors for quantifying the effect of HBAs and HBDs on the properties related to noncovalent interactions.
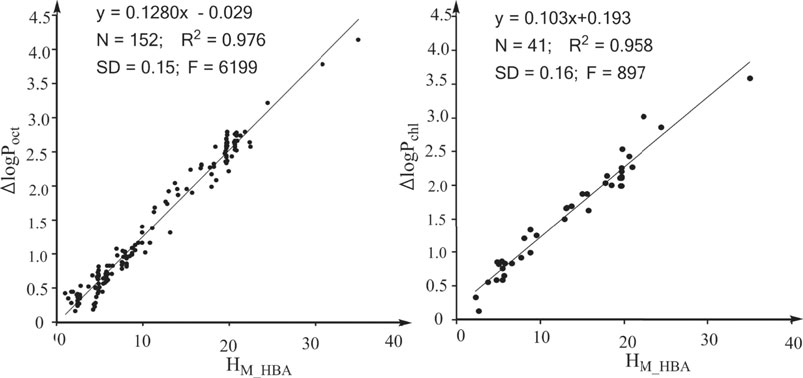
FIGURE 2. Strong linear associations between the effects of HBAs on properties and HM_HBA. HM_HBA: overall H-bonding capabilities of the HBAs of a solute. (A) For the property logPoct (log of the partition coefficient between n-octanol and water). (B) For the property logPchl (log of the partition coefficient between chloroform and water).
The molecular descriptor for quantifying the effect of molecular flexibility on properties is denoted by “Flex.” The effects of molecular flexibility on properties mainly result from rotatable bonds of the solutes because the rotatable bonds of the solutes can rotate more freely in some environments than in other environments. The flexibilities of solutes are calculated from the rotatable bonds of the solutes, especially the rotatable bonds that change the conformations of solutes (see Computational Methods). Thus, for many properties that are affected by molecular size, HBAs, HBDs and flexibility, they can be quantified with the following equation
where k1, k2, k3, k4 and c are constants for a give property. Organic compounds usually contain multiple HBAs and the HBAs affect each other. The accurate calculation of HM_HBA for many organic compounds is not easy. Eq. 4 would become simpler and easier to use if HM_HBA is replaced by logPow because logPow is a well-known molecular descriptor for predicting properties (Liu et al., 2019; Zhu et al., 2020b) and can be obtained accurately via experimental and/or computational approaches. Based on the fact that logPow is a property and Eq. 4 also applies to logPow, we can convert Eqs. 4 to 5 (see Supplementary Text S1 for the detail of the process of the conversion).
where b1, b2, b3, and b4 are constants, logPow is logP16 or logPoct. Eq. 5 is identical to Eq. 4. Both equations are correct for the properties that are determined by the noncovalent interactions of solutes with flexible environments. All the factors related to effects of noncovalent interactions on phase-transferring free energies, including electrostatic interaction, desovation, van der Waals interactions, entropy change, etc. are considered in Eq. 5. Eq. 5 is the general LFER we developed for predicting the properties that depends on the noncovalent interactions of solutes with flexible environments. Although Sm and HM_HBD may be strongly correlated with logPow for some properties, none of the molecular descriptors can be omitted because Eq. 4 is a general LFER for various different properties.
To prove that this general LFER can be used to construct models with high predictive power for various specific properties, we first demonstrated that it can be used to predict an organic solvent/water partition coefficient from another organic solvent/water partition coefficient with high accuracy. Eighty-nine compounds with experimental logPoct, logP16, and logPchl values (Abraham et al., 1994; Abraham et al., 1999) (Supplementary Table S1) were used for this investigation. Among the compounds, 45 compounds contain HBAs but no HBDs and 41 compounds containing HBDs. The equations and statistical results of the simple regressions of logP16 against logPoct and logPchl against logPoct for various types of compounds are shown in Supplementary Text S2. The R2 (squared correlation coefficient) values of the regressions range from 0.501 to 0.972 (gray columns, Figures 3A,B) and the SD (standard deviation) values of the regressions range from 0.241 to 0.965, indicating that the strength of the linear associations between two partition coefficients largely depends on compounds used for investigation. Then the same data for constructing the simple regressions were used to construct models according to the general LFER and the results are also shown in Supplementary Text S2 (note: the model descriptor Flex is not used because Flex has little effect on logPow). The R2 values of the models range from 0.947 to 0.992 (black columns, Figures 3A,B) and the SD values range from 0.183 to 0.248. The results indicate that the models constructed according to the LFER have a high statistical reliability and the performance of the models is independent of the compounds for investigation.
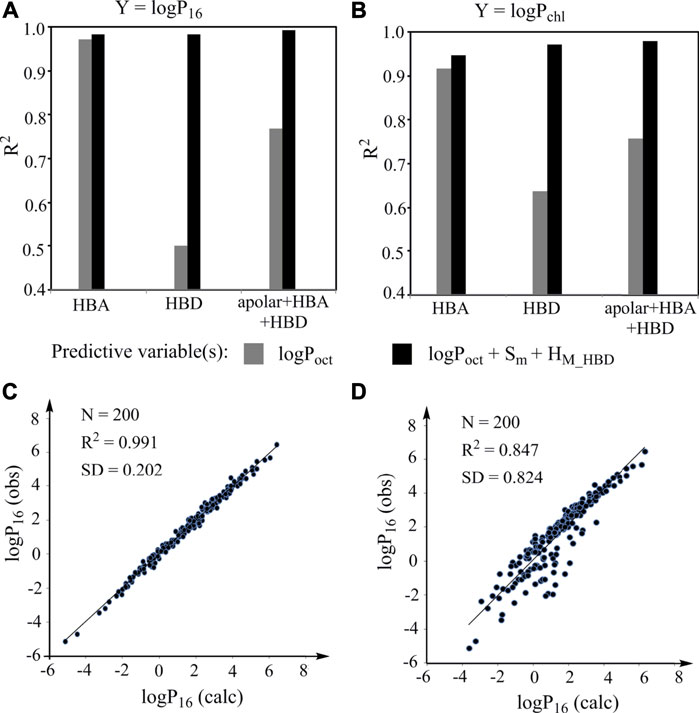
FIGURE 3. Prediction of organic solvent/water partition coefficients for validating the general LFER. (A, B) R2 values of the simple regressions (gray columns) of logP16(A)/logPchl(B) against logPoct and of the corresponding models constructed according to the LFER (black columns). HBA: compounds containing HBAs but no HBDs; HBD: compounds containing HBDs; apolar: nonpolar compounds; (C) Plot of observed logP16 against the logP16 calculated from the model constructed according to the LFER; (D) Plot of observed logP16 against the logP16 calculated from the model with logPoct as predictive valuable.
To demonstrate whether the models have high predictive power, we compared the experimental logP16 values of 200 organic compounds [from Supplementary Table S1 of a previous study (Chen et al., 2020)] and the logP16 values calculated from the model constructed according to the LFER by using an external validation approach (Figure 3C and Supplementary Text S3). The result shows that the model has high predictive power. For comparison, the predictive power of the corresponding simple regression was also investigated (Figure 3D), which is much worse than that for the model constructed according to the LFER. Thus, the LFER is powerful for constructing models with high predictive power.
We next used the LFER to construct a model for predicting the human skin permeability of neutral organic molecules. Supplementary Table S2 shows the logKp (Abraham and Martins, 2004; Zhang et al., 2017) values of 51 organic compounds. Thirty-two of the compounds were used as training set to develop the model with logPoct as a predictive valuable and the other 19 compounds as a test set to validate the model. The model constructed according to the LFER is shown below.
This model is characterized by high statistical reliability according to the R2 and SD values. It is used to calculate the logKp values of the 19 solutes in the test set. The plot of the experimental logKp values versus the calculated logKp values is characterized by statistically robust linearity (Figure 4A). The accurate prediction of logKp can provide a rapid and accurate prediction of human skin permeability of organic compounds, which is very useful for evaluating environmental risks due to contact with skin.
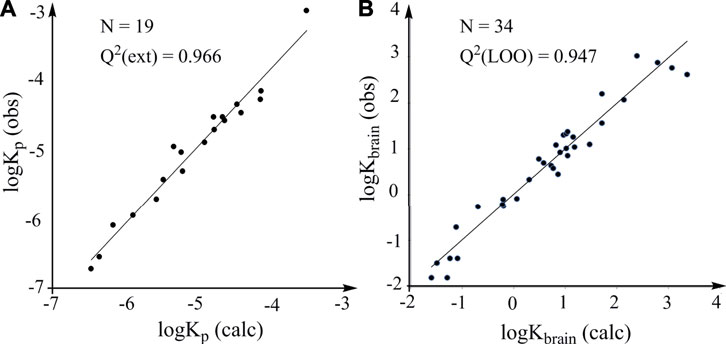
FIGURE 4. Predictive power of models constructed according to the LFER. (A) External validation. Plots of observed logKp (log of human skin permeability) against the logKp calculated from the model constructed according to the LFER (logPoct is used). (B) LOO cross-validation. Plots of observed logKbrain against the logKbrain calculated from the model constructed according to the LFER.
To further illustrate the reliability and accuracy of the LFER, we used the LFER to construct models for the properties that have little correlation with logPow. The strength of the linear association between logKbrain and logPoct (or logP16) is weak (R2 < 0.1) (Chen et al., 2020). Supplementary Table S3 lists the compounds that were used to demonstrate the weak linear association between logKbrain and logP16 (or logPoct) in a previous study (Chen et al., 2020). Based on the experimental logKbrain, logP16 and logPoct data of the compounds, we constructed two models according to the LFER.
Results indicate that both models have high predictive power and the model with logP16 as predictive variable is better than the model with logPoct as predictive variable. The predicted logKbrain obtained from the LOO cross-validation (logP16 is used) and the observed logKbrain show a robust linear association (Figure 4B). Thus, the general LFER works well for the properties that have little correlation with partition coefficients, supporting the reliability and efficacy of the general LFER in the accurate prediction of the properties related to noncovalent interactions. We believe that the thermodynamics-based theoretical derivation is a powerful methodology for developing robust models and will be useful in many fields, including drug design, environmental safety and human health.
In some cases, not all the molecular descriptors in the LFER are required for specific models with high predictive power. Some models still have high predictive power without using the molecular descriptor HM_HBD. For example, if the HBAs and HBDs of an organic solvent are obviously weaker than the HBAs and HBDs of water, the partition coefficient between water and the organic solvent can be predicted accurately from the model with logP16 and Sm as predictive variables. Eq. 9 is the model for predicting the aniline/water partition coefficient (logPaln) with logP16 and Sm as predictive variables (see Supplementary Table S4 for the data). Its statistical reliability is high and is obviously better than that for the simple regression (Eq. 10).
Without using HM_HBD, the model for predicting logKbrain from logP16, Sm, and Flex still has high predictive power.
Because the calculation of Sm and Flex is easy, the accurate prediction of some properties from logP16 or logPoct is easy for the researchers across various fields. For example, logKbrain can be accurately predicted from logP16, without the need for additional experimental data or complicated calculations. Without using the LFER, the accurate prediction of logKbrain from logP16 or another organic solvent/water partition coefficient is difficult because there is little correlation between logKbrain and organic solvent/water partition coefficients. For the models containing HM_HBD, the HM_HBD values of solutes are calculated with computer software. All the molecular descriptors in the LFER are easy to be understood and used by the researchers in various research fields. However, when constructing QSPR models by using mathematical and statistical tools, the predictive variables are usually selected from a few thousand molecular descriptors. The meanings of many predictive variables, e.g., the 3D-MoRSE descriptors, (Zapadka et al., 2019), are not easy to be understood or used by many researchers in various research fields.
Because logPoct and logP16 can be calculated accurately from the structures of solutes (Chen et al., 2020), it is expected that this method still performs well when all of the molecular descriptors in the LFER are calculated from solute structures. For example, the R2, Q2ext and SD of the model for predicting human skin permeability, in which all predictive variables are calculated from solute structures, are 0.940, 0.957, and 0.202 (see Supplementary Text S4). Thus, the general LFER developed in this study has obvious advantages in predicting many properties related to noncovalent interactions.
Above examples indicate that the models constructed according to the LFER for many specific properties have high predictive power. Moreover, the performance of the models is independent of the compounds for investigation, suggesting that the models can provide guidance for improving properties of organic compounds and designing compounds with optimal properties. The merits of the LFER result from the theoretical derivation, which ensures that the quantitative relationships in the models constructed according to the LFER are correct in the aspect of thermodynamics. For the QSPR models developed using mathematical and statistical tools, the predictive variables are selected from a few thousand molecular descriptors based on the data of the compounds in training sets. The relationships between the properties and molecular descriptors in the QSPR models are statistical relationships for the compounds in training sets. The QSPR models usually work well only for the compounds in the training set and similar compounds, but may do not work well for other compounds. Thus, for the properties determined by the noncovalent interactions of solutes with flexible environments, the models developed according to the proposed LFER performs better than the QSPR models developed by using mathematical and statistical tools, including robust artificial neural networks. Developing models according to the proposed LFER is faster and computationally cheap than developing traditional QSPR models because the process of the variable selection is not required. Moreover, the proposed LFER is quite simple and can be easily used by the researchers across various fields, while expert knowledge is required for developing robust artificial neural networks, such as the knowledge in choosing the most appropriate approach. Thus, the method developed in study has obvious advantages over the traditional QSPR construction method. Thermodynamics-based theoretical derivation can be used to solve many problems that are hard to be solved by using mathematical and statistical tools. In addition, results in this study demonstrate that there are quantitative relationships between the properties related to thermodynamics, suggesting that many properties can be accurately predicted from other properties.
The theoretical derivation in this study is based on the assumption that solutes have similar interactions with their environments, which requires that the environments for the properties are flexible or the properties have little relationship with the conformation or orientations of solutes. Thus, the present LFER may not work well in predicting the binding affinities of ligands because the binding sites of proteins are not flexible. If the environment for a property is rigid (e.g., the binding sites of proteins), the model for predicting the property should consider H-bond interactions individually, rather than the overall H-bond interactions. In our further study, we will explore how to develop models for the properties related to rigid environments, which can be used to develop scoring functions for predicting protein-ligand binding affinities and develop QSAR models for screening databases of ligands. Furthermore, in this study, we demonstrated to effectiveness of the LFER for predicting the properties of neutral organic compounds. If a dataset contains ionizable compounds, it will be necessary to include molecular descriptors for the ionized forms. Although several approaches currently exist for considering the effects of ionization on various molecular properties (Li et al., 2006; Zhang et al., 2017), our future work with involve attempts to adapt the proposed LFER for use in these situations.
In this study, we used a thermodynamics-based theoretical derivation to develop a general LFER for accurately predicting various properties from partition coefficients. The theoretical derivation ensures that many specific properties can be accurately quantified with the molecular descriptors in the LFER. It overcomes the shortages of constructing QSPR models by using mathematical and statistical tools. It is expected that the thermodynamics-based theoretical derivation can be used to solve many difficult problems, including the accurate prediction of protein-ligand binding affinities.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
DC and XH conceived and designed the study. YF and XH built their models, validated the models. DC and YF wrote the first draft of the manuscript. All authors read, revised and approved the submitted version.
This work is supported by grants from the National Natural Science Foundation of China (21763002, 21473041) and the Natural Science Foundation of Jiangxi Province (20202ACBL203008).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. At the time of publication a provisional patent was filed on the findings.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2021.737579/full#supplementary-material
Abraham, M. H., Chadha, H. S., Whiting, G. S., and Mitchell, R. C. (1994). Hydrogen Bonding. 32. An Analysis of Water-Octanol and Water-Alkane Partitioning and the Δlog P Parameter of Seiler. J. Pharm. Sci. 83, 1085–1100. doi:10.1002/jps.2600830806
Abraham, M. H., Ibrahim, A., and Acree, W. E. (2006). Air to Brain, Blood to Brain and Plasma to Brain Distribution of Volatile Organic Compounds: Linear Free Energy Analyses. Eur. J. Med. Chem. 41, 494–502. doi:10.1016/j.ejmech.2006.01.004
Abraham, M. H., and Martins, F. (2004). Human Skin Permeation and Partition: General Linear Free‐Energy Relationship Analyses. J. Pharm. Sci. 93, 1508–1523. doi:10.1002/jps.20070
Abraham, M. H., Platts, J. A., Hersey, A., Leo, A. J., and Taft, R. W. (1999). Correlation and Estimation of Gas-Chloroform and Water-Chloroform Partition Coefficients by a Linear Free Energy Relationship Method. J. Pharm. Sci. 88, 670–679. doi:10.1021/js990008a
Abraham, M. H., Zad, M., and Acree, W. E. (2015). The Transfer of Neutral Molecules from Water and from the Gas Phase to Solvents Acetophenone and Aniline. J. Mol. Liquids 212, 301–306. doi:10.1016/j.molliq.2015.09.033
Bushdid, C., de March, C. A., Fiorucci, S., Matsunami, H., and Golebiowski, J. (2018). Agonists of G-Protein-Coupled Odorant Receptors Are Predicted from Chemical Features. J. Phys. Chem. Lett. 9, 2235–2240. doi:10.1021/acs.jpclett.8b00633
Carrió, P., Sanz, F., and Pastor, M. (2016). Toward a Unifying Strategy for the Structure-Based Prediction of Toxicological Endpoints. Arch. Toxicol. 90, 2445–2460. doi:10.1007/s00204-015-1618-2
Chen, D., Li, Y., Li, X., Guo, W., Li, Y., Savidge, T., et al. (2019). Quantitative Effects of Substrate-Environment Interactions on the Free Energy Barriers of Reactions. J. Phys. Chem. C 123, 13586–13592. doi:10.1021/acs.jpcc.9b01094
Chen, D., Oezguen, N., Urvil, P., Ferguson, C., Dann, S. M., and Savidge, T. C. (2016). Regulation of Protein-Ligand Binding Affinity by Hydrogen Bond Pairing. Sci. Adv. 2, e1501240. doi:10.1126/sciadv.1501240
Chen, D., Wang, Q., Li, Y., Li, Y., Zhou, H., and Fan, Y. (2020). A General Linear Free Energy Relationship for Predicting Partition Coefficients of Neutral Organic Compounds. Chemosphere 247, 125869. doi:10.1016/j.chemosphere.2020.125869
Cheng, F., Li, W., Liu, G., and Tang, Y. (2013). In Silico ADMET Prediction: Recent Advances, Current Challenges and Future Trends. Ctmc 13, 1273–1289. doi:10.2174/15680266113139990033In
Cheng, W., and Ng, C. A. (2019). Using Machine Learning to Classify Bioactivity for 3486 Per- and Polyfluoroalkyl Substances (PFASs) from the OECD List. Environ. Sci. Technol. 53, 13970–13980. doi:10.1021/acs.est.9b04833
Deeb, O., Khadikar, P. V., and Goodarzi, M. (2011). Prediction of Gas/Particle Partitioning Coefficients of Semi Volatile Organic Compounds via QSPR Methods: PC-ANN and PLS Analysis. Jics 8, 176–192. doi:10.1007/bf03246214
Dickson, C. J., Hornak, V., Pearlstein, R. A., and Duca, J. S. (2017). Structure-Kinetic Relationships of Passive Membrane Permeation from Multiscale Modeling. J. Am. Chem. Soc. 139, 442–452. doi:10.1021/jacs.6b11215
Fioressi, S. E., Bacelo, D. E., Aranda, J. F., and Duchowicz, P. R. (2020). Prediction of the Aqueous Solubility of Diverse Compounds by 2D-QSPR. J. Mol. Liquids 302, 112572. doi:10.1016/j.molliq.2020.112572
Freitas, M. R., Freitas, M. P., and Macedo, R. L. G. (2014). Aug-MIA-QSPR Modeling of the Soil Sorption of Carboxylic Acid Herbicides. Bull. Environ. Contam. Toxicol. 93, 489–492. doi:10.1007/s00128-014-1356-9
He, L., Xiao, K., Zhou, C., Li, G., Yang, H., Li, Z., et al. (2019). Insights into Pesticide Toxicity against Aquatic Organism: QSTR Models on Daphnia Magna. Ecotoxicology Environ. Saf. 173, 285–292. doi:10.1016/j.ecoenv.2019.02.014
Jana, G., Pal, R., Sural, S., and Chattaraj, P. K. (2020). Quantitative Structure-Toxicity Relationship: An "In Silico Study" Using Electrophilicity and Hydrophobicity as Descriptors. Int. J. Quan. Chem. 120, e26097. doi:10.1002/qua.26097
Kaneko, H. (2017). A New Measure of Regression Model Accuracy that Considers Applicability Domains. Chemometrics Intell. Lab. Syst. 171, 1–8. doi:10.1016/j.chemolab.2017.09.018
Khan, K., Benfenati, E., and Roy, K. (2019). Consensus QSAR Modeling of Toxicity of Pharmaceuticals to Different Aquatic Organisms: Ranking and Prioritization of the DrugBank Database Compounds. Ecotoxicology Environ. Saf. 168, 287–297. doi:10.1016/j.ecoenv.2018.10.060
Lee, J., Kumar, S., Lee, S.-Y., Park, S. J., and Kim, M.-h. (2019). Development of Predictive Models for Identifying Potential S100A9 Inhibitors Based on Machine Learning Methods. Front. Chem. 7, 779. doi:10.3389/fchem.2019.00779
Li, J., Sun, J., Cui, S., and He, Z. (2006). Quantitative Structure-Retention Relationship Studies Using Immobilized Artificial Membrane Chromatography I: Amended Linear Solvation Energy Relationships with the Introduction of a Molecular Electronic Factor. J. Chromatogr. A 1132, 174–182. doi:10.1016/j.chroma.2006.07.073
Li, L., Arnot, J. A., and Wania, F. (2019). How Are Humans Exposed to Organic Chemicals Released to Indoor Air?. Environ. Sci. Technol. 53, 11276–11284. doi:10.1021/acs.est.9b02036
Liu, K., Fu, H., Zhu, D., and Qu, X. (2019). Prediction of Apolar Compound Sorption to Aquatic Natural Organic Matter Accounting for Natural Organic Matter Hydrophobicity Using Aqueous Two-phase Systems. Environ. Sci. Technol. 53, 8127–8135. doi:10.1021/acs.est.9b00529
Liu, R., and Wallqvist, A. (2019). Molecular Similarity-Based Domain Applicability Metric Efficiently Identifies Out-Of-Domain Compounds. J. Chem. Inf. Model. 59, 181–189. doi:10.1021/acs.jcim.8b00597
Mansouri, K., Grulke, C. M., Judson, R. S., and Williams, A. J. (2018). OPERA Models for Predicting Physicochemical Properties and Environmental Fate Endpoints. J. Cheminform 10. doi:10.1186/s13321-018-0263-1
Pal, R., Jana, G., Sural, S., and Chattaraj, P. K. (2019). Hydrophobicity versus Electrophilicity: A New Protocol toward Quantitative Structure-Toxicity Relationship. Chem. Biol. Drug Des. 93, 1083–1095. doi:10.1111/cbdd.13428
Raevsky, O. (2004). Physicochemical Descriptors in Property-Based Drug Design. Mrmc 4, 1041–1052. doi:10.2174/1389557043402964
Roy, K., Ambure, P., Kar, S., and Ojha, P. K. (2018). Is it Possible to Improve the Quality of Predictions from an "intelligent" Use of Multiple QSAR/QSPR/QSTR Models?. J. Chemometr. 32, 2992. doi:10.1002/cem.2992
Sabour, M. R., Moftakhari Anasori Movahed, S., and Movahed, A. (2017). Application of Radial Basis Function Neural Network to Predict Soil Sorption Partition Coefficient Using Topological Descriptors. Chemosphere 168, 877–884. doi:10.1016/j.chemosphere.2016.10.122
Sarkar, A., Anderson, K. C., and Kellogg, G. E. (2012). Computational Analysis of Structure-Based Interactions and Ligand Properties Can Predict Efflux Effects on Antibiotics. Eur. J. Med. Chem. 52, 98–110. doi:10.1016/j.ejmech.2012.03.008
Song, R., Keller, A. A., and Suh, S. (2017). Rapid Life-Cycle Impact Screening Using Artificial Neural Networks. Environ. Sci. Technol. 51, 10777–10785. doi:10.1021/acs.est.7b02862
Suay-Garcia, B., Ignacio Bueso‐Bordils, J., Falcó, A., Pérez‐Gracia, M. T., Antón‐Fos, G., and Alemán‐López, P. (2020). Quantitative Structure-Activity Relationship Methods in the Discovery and Development of Antibacterials. Wires Comput. Mol. Sci. 10, e1472. doi:10.1002/wcms.v10.6
Sun, Y., Shi, S., Li, Y., and Wang, Q. (2019). Development of Quantitative Structure-Activity Relationship Models to Predict Potential Nephrotoxic Ingredients in Traditional Chinese Medicines. Food Chem. Toxicol. 128, 163–170. doi:10.1016/j.fct.2019.03.056
T. Stanton, D. (2012). QSAR and QSPR Model Interpretation Using Partial Least Squares (PLS) Analysis. Cad 8, 107–127. doi:10.2174/157340912800492357
Warshel, A., Sharma, P. K., Kato, M., Xiang, Y., Liu, H., and Olsson, M. H. M. (2006). Electrostatic Basis for Enzyme Catalysis. Chem. Rev. 106, 3210–3235. doi:10.1021/cr0503106
Yang, H., Sun, L., Li, W., Liu, G., and Tang, Y. (2018). In Silico Prediction of Chemical Toxicity for Drug Design Using Machine Learning Methods and Structural Alerts. Front. Chem. 6, 30. doi:10.3389/fchem.2018.00030In
Zapadka, M., Kaczmarek, M., Kupcewicz, B., Dekowski, P., Walkowiak, A., Kokotkiewicz, A., et al. (2019). An Application of QSRR Approach and Multiple Linear Regression Method for Lipophilicity Assessment of Flavonoids. J. Pharm. Biomed. Anal. 164, 681–689. doi:10.1016/j.jpba.2018.11.024
Zhang, K., Abraham, M. H., and Liu, X. (2017). An Equation for the Prediction of Human Skin Permeability of Neutral Molecules, Ions and Ionic Species. Int. J. Pharmaceutics 521, 259–266. doi:10.1016/j.ijpharm.2017.02.059
Zhang, K., Zhong, S., and Zhang, H. (2020). Predicting Aqueous Adsorption of Organic Compounds onto Biochars, Carbon Nanotubes, Granular Activated Carbons, and Resins with Machine Learning. Environ. Sci. Technol. 54, 7008–7018. doi:10.1021/acs.est.0c02526
Zheng, S., Chang, W., Xu, W., Xu, Y., and Lin, F. (2019). E-Sweet: A Machine-Learning Based Platform for the Prediction of Sweetener and its Relative Sweetness. Front. Chem. 7, 35. doi:10.3389/fchem.2019.00035
Zhu, L., Zhao, J., Zhang, Y., Zhou, W., Yin, L., Wang, Y., et al. (2018). ADME Properties Evaluation in Drug Discovery: In Silico Prediction of Blood-Brain Partitioning. Mol. Divers. 22, 979–990. doi:10.1007/s11030-018-9866-8
Zhu, T., Jiang, Y., Cheng, H., Singh, R. P., and Yan, B. (2020). Development of Pp-LFER and QSPR Models for Predicting the Diffusion Coefficients of Hydrophobic Organic Compounds in LDPE. Ecotoxicology Environ. Saf. 190, 110179. doi:10.1016/j.ecoenv.2020.110179
Keywords: computational chemistry, linear free energy relationships, molecular properties, partition coefficient, noncovalent interactions, quantitative structure-property relationships
Citation: Chen D, Huang X and Fan Y (2021) Thermodynamics-Based Model Construction for the Accurate Prediction of Molecular Properties From Partition Coefficients. Front. Chem. 9:737579. doi: 10.3389/fchem.2021.737579
Received: 07 July 2021; Accepted: 20 August 2021;
Published: 13 September 2021.
Edited by:
Sudip Pan, University of Marburg, GermanyReviewed by:
Santanab Giri, Haldia Institute of Technology, IndiaCopyright © 2021 Chen, Huang and Fan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Deliang Chen, ZGVsaWFuZzIyMTFAaG90bWFpbC5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.