Conformational Change of H64 and Substrate Transportation: Insight Into a Full Picture of Enzymatic Hydration of CO2 by Carbonic Anhydrase

The enzymatic hydration of CO₂ into HCO₃⁻ by carbonic anhydrase (CA) is highly efficient and environment-friendly measure for CO₂ sequestration. Here extensive MM MD and QM/MM MD simulations were used to explore the whole enzymatic process, and a full picture of the enzymatic hydration of CO₂ by CA was achieved. Prior to CO₂ hydration, the proton transfer from the water molecule (WT1) to H64 is the rate-limiting step with the free energy barrier of 10.4 kcal/mol, which leads to the ready state with the Zn-bound OH⁻. The nucleophilic attack of OH⁻ on CO₂ produces HCO₃⁻ with the free energy barrier of 4.4 kcal/mol and the free energy release of about 8.0 kcal/mol. Q92 as the key residue manipulates both CO₂ transportation to the active site and release of HCO₃⁻. The unprotonated H64 in CA prefers in an inward orientation, while the outward conformation is favorable energetically for its protonated counterpart. The conformational transition of H64 between inward and outward correlates with its protonation state, which is mediated by the proton transfer and the product release. The whole enzymatic cycle has the free energy span of 10.4 kcal/mol for the initial proton transfer step and the free energy change of −6.5 kcal/mol. The mechanistic details provide a comprehensive understanding of the entire reversible conversion of CO₂ into bicarbonate and roles of key residues in chemical and nonchemical steps for the enzymatic hydration of CO₂.

Introduction

CO₂ reduction and carbon neutral have been constantly drawing attention in human societies. In order to alleviate and finally solve the ecological and environmental problems caused by the increased emissions of the industrial byproduct CO₂, lots of efforts to its capture, sequestration, and conversion (Jo et al., 2014; Sanz-Pérez et al., 2016; Darunte et al., 2016; Kim et al., 2018; Kar et al., 2018) have been made in both academic and industry communities. Carbonic anhydrase (CA), as the first recognized zinc-containing enzyme, can efficiently catalyze the interconversion between CO₂ and bicarbonate (HCO₃⁻), which has been widely used in biological capture and sequestration of CO₂. (Krishnamurthy et al., 2008; Vinoba et al., 2011; Vinoba et al., 2013; Alvizo et al., 2014). As shown in Figure 1, the active site of CA contains a zinc ion coordinated by three histidine residues (H94, H96, and H119) and one water molecule (WT1) (Håkansson et al., 1992) and a stable hydrogen bond network responsible for the proton transfer between WT1 and H64. (Avvaru et al., 2010; Mikulski et al., 2013; Singh et al., 2019). The deprotonation/protonation of the imidazole side chain of H64 mediated by the water chain is generally considered as the rate-determining step, and the corresponding free energy barrier is ∼10 kcal/mol in the reaction cycle. (Silverman and Vincent, 1983; Duda et al., 2001; Maupin et al., 2009; Riccardi et al., 2010; Aggarwal et al., 2014).

FIGURE 1

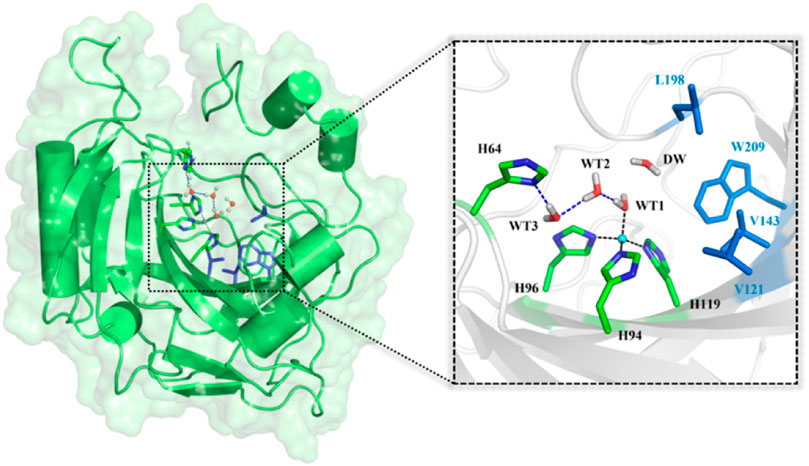
FIGURE 1. Structures of CA and the selected active domain highlighted in the dotted box, where the zinc ion is coordinated with H94, H96, H119, and WT1, and the residues colored in blue represent the hydrophobic pocket in the active site of the equilibrated ready state of CA prepared based on the X-ray crystal structure (PDB code: 2CBA).

It was widely accepted that the hydration of CO₂ is triggered by the proton transfer from WT1 to H64 through a water chain, along with the rotation of H64 side chain from inward to outward orientation. The previous studies suggest that the protonation state of H64 and WT1 in the water bridge is related to the conformational dynamics of H64 in the proton transfer and CO₂ hydration. (Cui and Karplus, 2003; Riccardi et al., 2008; Maupin et al., 2011; Taraphder et al., 2016; Paul et al., 2018). As shown in Figure 2, the enzymatic coversion of CO₂ into bicarbonate by CA can be described by using five states, denoted as E₁, E₂, E₃, E₄, and E₅. H64, as the proton accepter, is found to have two different conformations in the crystal structure, i.e. inward and outward configurations, corresponding to HIE64 and HIP64. (Tu et al., 1989; An et al., 2002; Silverman and Mckenna, 2007). Based on some mutants of the wild-type CA, the proton transfer step and the role of the conformational change of H64 in the enzymatic hydration of CO₂ by CA have been investigated in the past decades (Loferer et al., 2003; Roy and Taraphder, 2008; Roy and Taraphder, 2009; Piazzetta et al., 2014; Chen et al., 2017; Chen et al., 2018a; Chen et al., 2018b), and the dynamical interconversion between inward and outward conformations of H64, detected in the experiment, was not observed during the MD simulations.

FIGURE 2

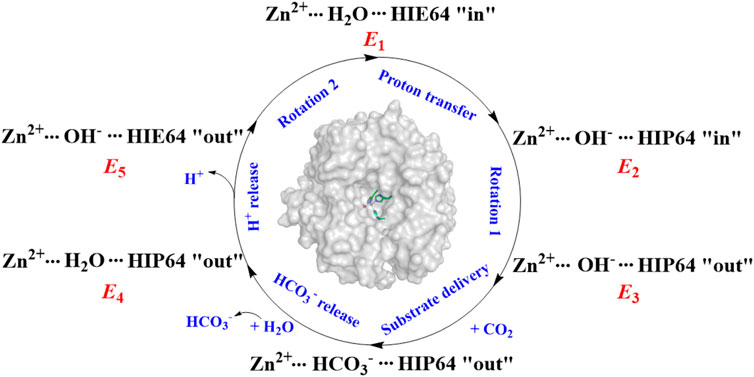
FIGURE 2. The enzymatic hydration cycle of CO₂ by CA, where “in” and “out” stand for inward and outward conformations, respectively.

Despite all these important contributions, a comprehensive understanding of the whole biological seguestration process of CO₂ by CA and roles of key residues in CO₂ transportation and binding to the active site, the catalytic reversible hydration of CO₂, and the bicarbonate release, is still required. Here the entire enzymatic catalysis is divided into five chemical and nonchemical steps, where the chemical steps include the proton transfer between WT1 and H64 and the formation of HCO₃⁻ from the nucleophilic attack of the Zn-bound OH⁻ on CO₂, and the nonchemical steps consist of the conformational transition of H64 between inward to outward, the CO₂ transportation from the bulk solution to the active site, and the release of HCO₃⁻.

To build a full picture of the enzymatic hydration of CO₂ by CA, extensive QM/MM and MM MD simulations have been carried out, and the following issues will be discussed in the present study 1) the hydrogen transfer mechanism 2) the plausible channels for CO₂/HCO₃⁻ transportation 3) the role of key residues and water in the conformational transition of H64, CO₂/HCO₃⁻ transportation, and CO₂ hydration 4) mechanisms and corresponding dynamical and thermodynamic properties for key chemical and non-chemical steps. Here the global simulation may provide a comprehensive understanding of this enzymatic catalysis and open up an avenue to further improve the biological capture of CO₂ by CA.

Computational Details

Setup of Enzyme-Substrate Complex Model

The initial enzyme model was prepared on the basis of the X-ray crystal structure of the human carbonic anhydrase II (PDB code: 2CBA) (Håkansson et al., 1992), and the initial enzyme-substrate complex was built by replacing DW (the water molecule, see Figure 1) with CO₂. Both models with and without substrate were equilibrated by using 200 ns MM MD simulations, respectively. The protonation states of all ionizable residues were determined by using the PROPKA software (Olsson et al., 2011) at PH 7.0 and the hydrogen bond network in the X-ray crystal structure. (Fan et al., 2019a; Fan et al., 2019b). The zinc ions and its coordination sphere were parametrized by using the “MCPB.py” modeling tool. (Li and Merz, 2016; Li and Merz, 2017). The substrate and protein were described by the AMBER14SB (Gao et al., 2017) and AMBER GAFF force fields (Wang et al., 2004), respectively. The partial atomic charges of CO₂ were determined by the restrained electrostatic potential (RESP) (Bayly et al., 1993) charge at the HF/6-31G* level with Gaussian 09. (Frisch et al., 2013). The computational model was solvated into a 95 × 93 × 101 Å cuboid TIP3P (Sun and Kollman, 1995) water box, with 10 Å buffer distances between protein atoms and the edge (Chen et al., 2018a) of the box. The whole system was neutralized by a chloride ion. The topology parameters and initial coordinates were produced by Amber tleap tools. The molecular dynamics simulation contains four steps, including the energy minimization to adjust poor interatomic distances, the system heating up from 0 to 300 K with a constant pressure for 1,000 ps, the equilibration under the NVT ensemble for 1,000 ps to relax the system density to about 1.0 g/cm³, and the final 200 ns MD simulation under the NPT ensemble with a timescale of 2 fs for the enzyme-CO₂ complex and the enzyme system separately. The SHAKE algorithm (Miyamoto and Kollman, 1992) was used to constrain all hydrogen bonds and the cut off value was set to 10.0 Å for both van der Waals and electrostatic interactions. The root-mean-square deviation (RMSD) was applied to evaluate the stability of the enzyme backbone during MD simulations. All the above processes are accomplished by Amber18 (Case et al., 2005; Götz et al., 2012; Le Grand et al., 2013) and Gaussian 09 software. (Frisch et al., 2013).

Umbrella Sampling

The umbrella sampling and the weighted Histogram analysis method (WHAM) (Kumar et al., 1992; Souaille and Roux, 2001) were applied to estimate thermodynamic and dynamic properties of CO₂ delivery in different channels and release of HCO₃⁻, as well as the conformational transition of H64. The initial structure was selected from the stable configuration equilibrated by MD simulations. For the CO₂ transportation, the distance between W209@CH2 and CO₂@C was defined as the reaction coordinate (RC1, see Figure 3A), which varies from 3.4 to 18.0 Å with a 0.2 Å interval for two adjacent windows. Finally, 25 ns MD simulations with the biasing harmonic potential of 50 kcal/mol were performed for each window. According to the high-resolution crystal structure and the previous studies (Roy and Taraphder, 2009), the dihedral angle χ (N–C_α–C_β–C_γ) was defined as the reaction coordinate (RC2, see Figure 3B), which changes from 43.87° to −38.40° with a 3° interval for two adjacent windows in the 25 ns MD simulation with a force constant of 200 kcal/mol rad (Sanz-Pérez et al., 2016), describing the conformational transition of H64 from inward to outward orientation. In order to explore the conformational change of H64, umbrella samplings under different conditions were performed: 1) the side chain of the protonated H64 rotates from inward to outward conformation without CO₂ in the active site; 2) the side chain of deprotonated H64 rotates back from outward to inward conformation after the detachment of HCO₃⁻. The distance between H119@ND1 and HCO₃⁻@C was defined as the reaction coordinate to identify the release channel of HCO₃⁻ (RC3) (see Figure 3C), which varies from 4.6 Å to 17.0 Å with a 0.2 Å interval for two adjacent windows, and 35 ns MD simulation was carried out for each window with the appropriate biasing harmonic potential. And the last 10 ns MD simulations of all above samplings were collected to generate free energy profiles by using WHAM. (Kumar et al., 1992; Souaille and Roux, 2001).

FIGURE 3

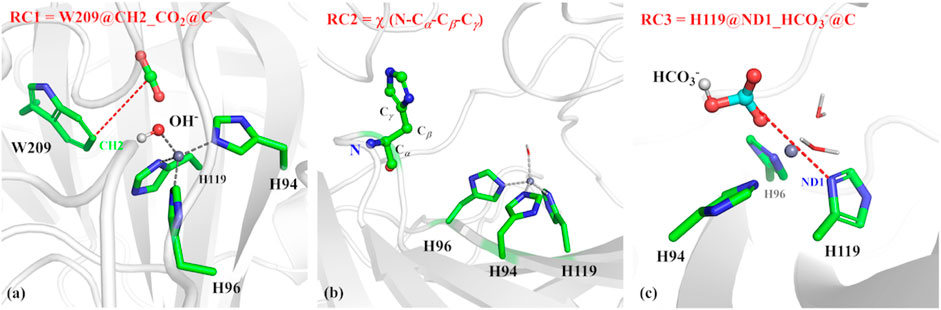
FIGURE 3. (A) Reaction coordinate (RC1) defined by the distance between CO₂@C and W209@CH2 for the delivery of CO₂, (B) Reaction coordinate (RC2) defined as the dihedral angle χ(N–C_α–C_β–C_γ), (C) Reaction coordinate (RC3) defined by the distance between H119@ND1 and HCO₃^-@C.

QM/MM and QM/MM MD Simulations

QM/MM calculations were employed to explore the plausible mechanism for the proton transfer between WT1 and H64. The QM/MM calculations were performed by using the ChemShell package (Sherwood et al., 2003; Metz et al., 2014), combining Orca (Neese, 2018) and DL_POLY (Smith and Forester, 1996) for QM and MM subsystems, respectively, and the AMBER GAFF force field was employed throughout this study for the MM region. The QM/MM system consists of ∼74,000 atoms, and the QM subsystem consists of more than 120 atoms, including Y7, H64, H94, H96, E106, H119, T199, T200, zinc ion, WT1, WT2, WT3, and DW, which was described by the B3LYP functional with the Def2/TZVP and def2/J auxiliary basis set, dispersion corrections were computed with Grimme’s D3 method. (Grimme, 2006; Grimme et al., 2011). The MM subsystem was described by the AMBER force field, and the boundary was described by the charge-shift model. (Sherwood et al., 2003; Metz et al., 2014). Then a 21 psWell-Tempered Adaptively Biased Molecular Dynamics (WT-ABMD) method was carried out to get the thermodynamic characteristics and free energy profile for the hydration of CO₂. (Barducci et al., 2008). The initial structure for WT-ABMD was obtained from 1.5 ps QM(B3LYP/6-31G**)/MM MD simulation without any restrain, the QM region for QM/MM MD and WT-ABMD consists of more than 70 atoms, including H94, H96, H119, E106, T199, hydroxyl ion, zinc ion, CO₂ and one water molecule around the hydroxyl ion, the QM region and MM region for both of them were describe by Gaussian 09 and Amber force field, respectively. The distance between Zn-bound OH⁻@O and CO₂@C was defined as the reaction coordinate (RC4) to describe the formation of HCO₃⁻. The mode was set to FLOODING, with a timescale of 0.05 ps The resolution of reaction is set to 0.25 Å, and the reaction coordinate RC4 changes from 0.9 Å to 3.2 Å. All above calculations were carried out by the modified Orca 4.0,⁵² Gaussian 09⁴² and Amber 18 programs. (Case et al., 2005; Götz et al., 2012; Le Grand et al., 2013).

Results and Discussions

Equilibrium Configurations

To explore the delivery channel of CO₂ and the reaction mechanism of carbonic anhydrase, a 200 ns MM MD simulation without substrate was carried out. On the basis of the root-mean-square deviation (RMSD) (see Supplementary Figure 1), it can be noted that the CA system may become stable after 140 ns during MD simulations, and thus we choose the snapshot after 140 ns as the initial structure for the further study. The representative structure selected from the MD simulation and the QM region highlighted in the stick model are displayed in Figure 4, where the zinc ion is coordinated with three histidines (H94, H96, and H119) and one water molecule, and the residue H64 is stable at the inward conformation. Besides that, there is a stable hydrogen network in the active site, which may mediate the proton transfer from WT1 to H64 through a water chain containing two water molecules (WT2 and WT3). To evaluate the stability of the water chain, we counted the probability of water molecules appearing within 1.8 Å and 2.2 Å of T199@OG1, T200@H and H64@ND1, and there is a relatively high probability of 76% to form the hydrogen bond (see Supplementary Table 1). At the same time, the deeper water molecule (DW), as shown in Figure 1, surrounded by the side chain residues of V121, V143, L198, and W209 (hydrophobic pocket), will be squeezed out during the CO₂ delivery from the bulk water to the active site. Such desolvation free energy from the displacement of the water molecule solvating the protein pocket into the bulk water may facilitate the substrate binding. In order to study the hydration of CO₂, the water molecule (DW, refer to Figure 1) is replaced by CO₂, and a 200 ns MM MD simulation for the enzyme-substrate system was also performed to achieve its equilibrium configuration. As shown in Supplementary Figure 2, the CA-CO₂ complex system becomes stable after 100 ns, where CO₂ survives in the active site with the Zn⋅⋅⋅CO₂@C distance ranging from 3.5 to 4.5 Å, as shown in Supplementary Figure 3.

FIGURE 4

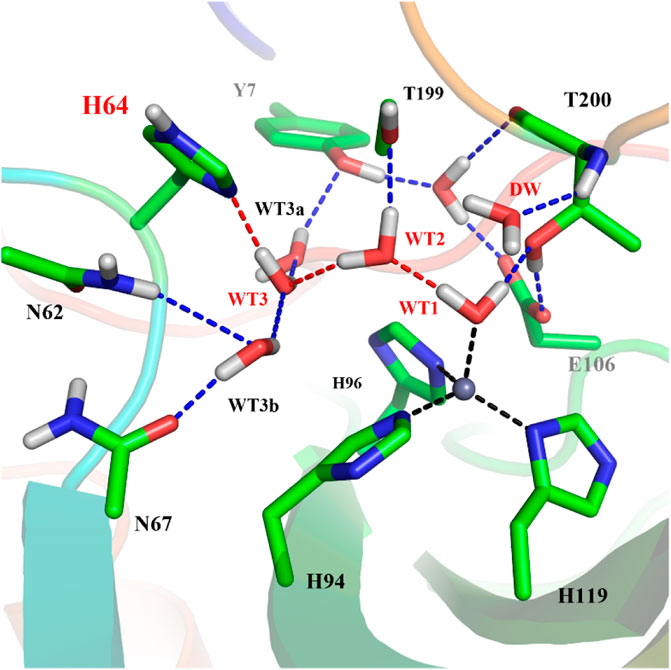
FIGURE 4. The represent structure of the active site from the MD simulation, where the blue dotted lines represent hydrogen bonds and the red dotted lines show the proton transfer pathway between WT1 and H64.

Proton Transfer for the Ready State Formation

It is generally assumed that the proton transfer from WT1 to H64 through a water chain is responsible for formation of the ready state of CA for CO₂ hydration, and this key step has been studied by using QM(B3LYP)/MM calculations and MD simulations. As shown in Figure 5, the distance of r₁—r₂—r₃ is defined as the reaction coordinate (RC) to explore the proton transfer, and the predicted free energy barrier is ∼10.4 kcal/mol, consistent with the experimental result. (Silverman and Mckenna, 2007). Selected representative conformations of the active domain, involved in the proton transfer, are shown in Figure 6. The initial proton transfer from WT1 to WT2 leads to the formation of H₃O⁺ at RC = −1.48 Å, then WT3 accepts the proton from WT2 to reach the transition state, and finally, the proton transfers to H64 at RC = −0.43 Å. We note that Mulliken gross atomic charges of zinc maintain less changed during the proton transfer process, although it appears to fluctuate to some extent, from 0.44 to 0.42 and then to 0.48, as shown in Supplementary Figure 4. The excess negative charges from the proton transfer mainly populate the Zn-bound OH⁻. Our QM/MM results reveal that the hydrogen-bonded water chain plays a vital role in the proton transfer, as shown in previous study. (Mikulski et al., 2013). The whole proton tranfer process is in accord with the Grotthus mechanism (Agmon, 1995; Riccardi et al., 2006), and it is endothermic by 7.0 kcal/mol.

FIGURE 5

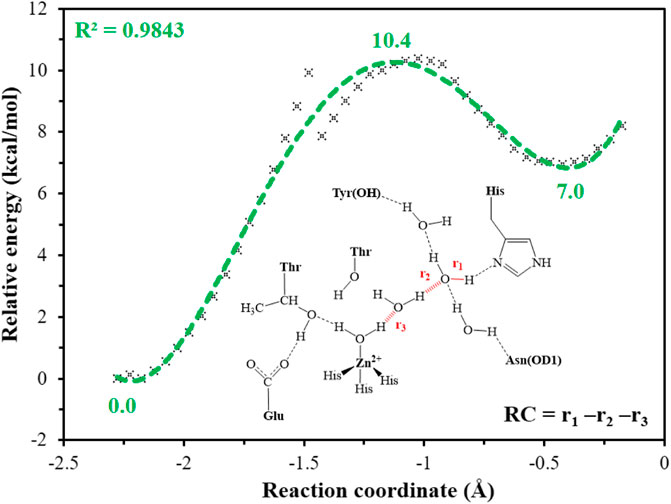
FIGURE 5. QM(B3LYP/TZVP–D3)/MM-predicted relative energy profiles for the proton transfer between H64 and WT1, where the reaction coordinate is defined as r₁—r₂—r₃ (in red).

FIGURE 6

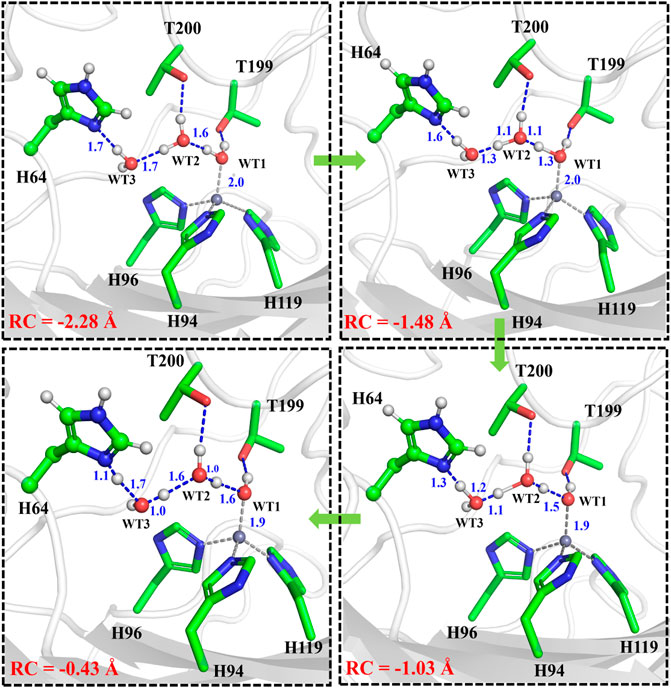
FIGURE 6. Representative structures of the active site during the proton transfer between WT1 and the residue H64.

Rotation of the Protonated H64 and Transportation of CO₂

The umbrella sampling and the WHAM technology were used to calculate the potential of mean force (PMF) for the rotation of H64 and the transportation of CO₂. At first, in order to describe the rotation of the protonated H64, the dihedral angle χ (N–C_α–C_β–C_γ) was selected as the reaction coordinate (RC2), and the inward and outward conformations correspond to the dihedral angles of 40.0° and −52.0°, respectively, as shown in Figure 7. The protonated H64 rotates within a narrow channel between W5 and N62, and the driving force of the rotation may come from the hydrogen bond interaction between H64 and H4. As Figure 7 shows, the residue H4 gradually approaches to H64 and forms a hydrogen bond during the rotation, while H4 is back to the initial position and H64 evolves into its outward orientation when χ = −53.0°. The outward conformation of H64 can be stabilized by the π-π stacking interaction with the residue W5 and hydrogen bond interaction with the residue N62. As Figure 9A shows, the conformational change of the protonated H64 from inward to outward is quite facile with a free energy barrier of 0.5 kcal/mol and an energy release of 3.9 kcal/mol. The protonated H64 will maintains the outward conformation until the product release from the active site (vide infra).

FIGURE 7

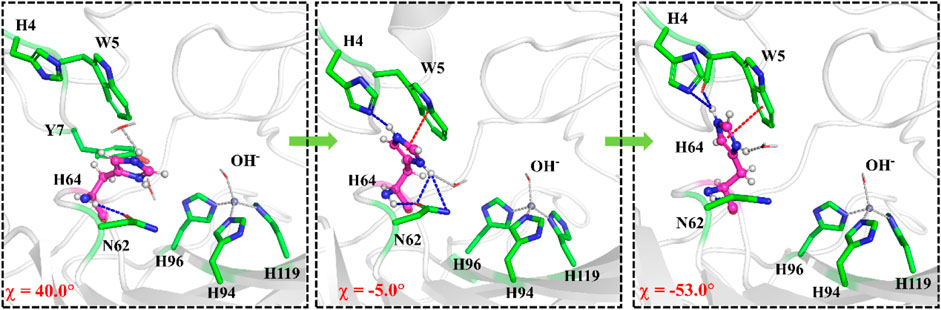
FIGURE 7. Representative structures and conformational changes for the rotation of H64 from inward to outward conformation, where the reaction coordinate is defined as the dihedral angle χ(N–C_α–C_β–C_γ).

The next step is CO₂ delivery from the bulk water to the active site of CA, and here the distance between CO₂@C and W209@CH2 was defined as the reaction coordinate (RC1) (see Figure 3A). According to the position evolution of CO₂ and the relative free energy changes depicted in Figure 8 and Figure 9B, the whole CO₂ transportation process can be subdivided into three stages: 1) The initial stage (RC1 ≥ 10.4 Å). CO₂, surrounded by water molecules through the hydrogen bond interaction, is outside of the protein; 2) The second stage (6.6 Å ≤ RC1 < 10.4 Å). CO₂ is getting into the protein gradually, while it is still out of the hydrophobic pocket, composed by V121, V143, L198 and W209. Besides that, as shown in Figure 8, during the stage I, Q92 is parallel to the β-sheet protein at before, however, Q92 is “activated” at this stage, and to drive CO₂ delivery into the hydrophobic pocket through its hydrogen bond interaction with CO₂. CO₂ transportation during this stage needs to overcome a free energy barrier of ∼1.5 kcal/mol; 3) The third stage (10.4 Å ≤ RC1 ≤ 6.6 Å). CO₂ is getting into the hydrophobic pocket and squeezes out the water molecule (DW), in which a hydrogen bond between CO₂ and T200 is formed, and at the same time, Q92 is back to the initial state. There is the energy release of about −4.8 kcal/mol at this stage.

FIGURE 8

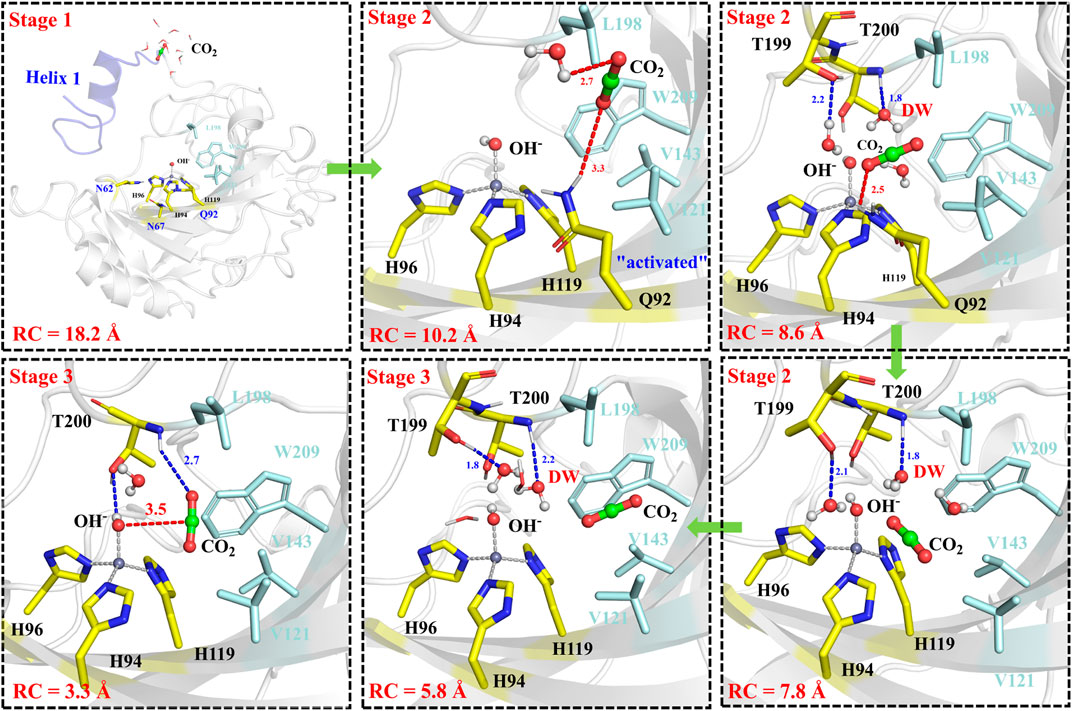
FIGURE 8. Representative structures and conformational changes for the delivery of CO₂, where the reaction coordinate is defined as the distance between W209@CH2 and CO₂@C.

FIGURE 9

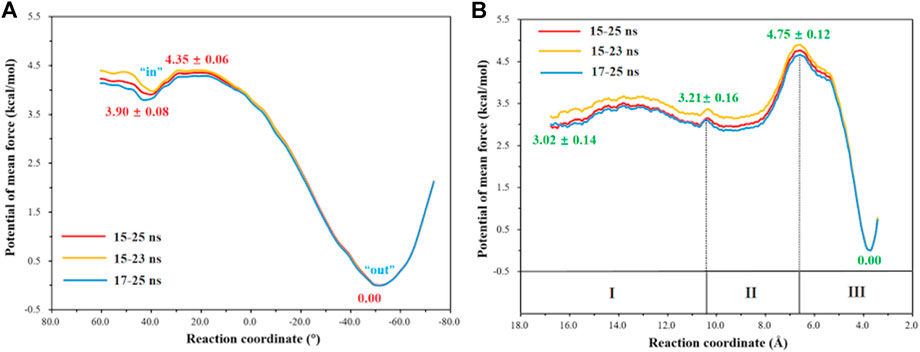
FIGURE 9. (A) Free energy profiles for the rotation of the protonated H64 from inward to outward conformation. (B) Free energy profiles for the CO₂ delivery to the active site of CA.

The whole process of CO₂ delivery to the active site is exothermic by 3.0 kcal/mol with a free energy barrier of 1.7 kcal/mol, where the residue Q92 plays a crucial role in this process. Note that the number of water molecules within 3 Å of CO₂ decreases gradually during the CO₂ delivery, as shown in Supplementary Figure 5, although there is a short-term fluctuation during CO₂ entry into the hydrophobic pocket. And the desolvation effect from the squeezing out of water molecules solvating the active-site protein is conducive to enhancing the binding affinity of CO₂.

Mechanisms for the Enzymatic Hydration of CO₂

After another 200 ns MD simulation, the equilibrium configuration of the CA-CO₂ complex system is obtained. The Well-Tempered Adaptively Biased Molecular Dynamics (WT-ABMD) method was used to explore the free energy profile for the hydration of CO₂. The corresponding reaction coordinate (RC4) is defined as the distance between CO₂@C and OH⁻@O (see Figure 10A), and the nucleophilic attack of OH⁻@O on CO₂@C produces bicarbonate, which is coordinated to the zinc ion in a bidentate mode. As Figure 10 shows, the enzymatic CO₂ hydration has the reaction ΔG of −12.4 kcal/mol and the free energy barrier of about 4.4 kcal/mol, suggesting that the CO₂ hydration is quite facile, both thermodynamically and kinetically. Clearly, the notable energy release may facilitate the release of HCO₃⁻ and the rotation of H64. The evolution of selected distances depicted in Figure 10C reveals that the distance between CO₂@O1 and the zinc ion decreases as the RC4 decreases, while the distance between OH⁻@O and the zinc ion slightly increases to ∼ 2.1 Å, leading to a stable pentacoordinate Zn²⁺ configuration after the HCO₃⁻ formation, where the newly-generated bicarbonate is bound to Zn²⁺ in a bidentate coordination. Besides that, as shown in Figures 10B,C, the distance between OH⁻@O and the zinc ion increases to more than 3 Å, corresponding to the configuration change from the bidentate to monodentate coordination directly, and there is a sharp rise of the free energy.

FIGURE 10

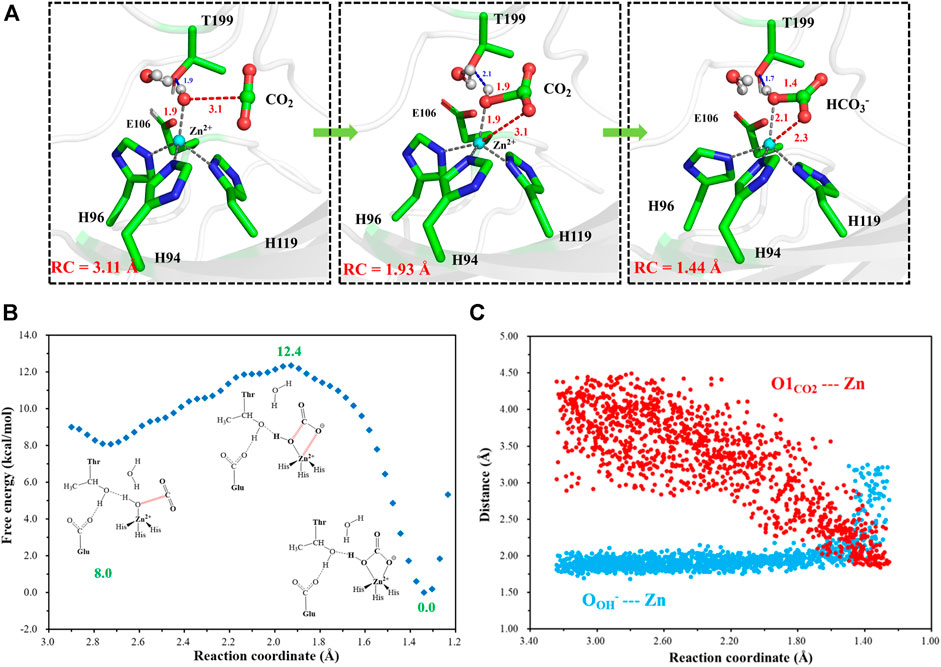
FIGURE 10. (A) Selected representative structures of the active site in the enzymatic hydration of CO₂. The distance between OH⁻@O and CO₂@C is defined as RC4. (B) The predicted free energy profile for the hydration of CO₂ by metadynamics simulations at the QM(B3LYP/6-31G**)/MM level. The reaction coordinate is defined as the distance between OH⁻@O and CO₂@C. (C) Evolution of selected interatomic distances along the reaction coordinate.

Release of HCO₃⁻ and Deprotonation of H64

To have an insight into the release of HCO₃⁻, the representative snapshot from the 50 ns MM MD simulation was selected as the initial structure for subsequent investigation of the product release. The umbrella sampling and WHAM methods were applied to predict the relative free energy profile for the product release, based on the reaction coordinate (RC5) defined by the distance between H119@NE2 and HCO₃⁻@C. According to conformational features and free energy profiles, the process of HCO₃⁻ release could be subdivided into three stages. At the first stage, HCO₃⁻ is initially bound to Zn²⁺ through the electrostatic interactions, and then it dissociates from the zinc coordination shell. The zinc-unbound HCO₃⁻ has relative strong hydrogen bond interactions with the active-site residues L198, T199, T200, Q92 and surrounding water molecules, as shown in Figure 11. Importantly, Q92 as the key residue is also involved in the release of HCO₃⁻. In the second stage, HCO₃⁻ is pulled out of the protein with the guide of residues H64, Y5, and N62. As shown in Figure12A, there is a free energy barrier of ∼8.4 kcal/mol for the first two stages including dissociation of HCO₃⁻ and ligand exchange around Zn²⁺. In the third stage, HCO₃⁻ gets into the bulk water through helix 1 and builds hydrogen interactions with H4, W5, H64 and Lys168. The release process of HCO₃⁻ requires a free energy of about 2.7 kcal/mol. Compared with the results of Markov-state model (Chen et al., 2018a; Chen et al., 2018b), as shown in Figure 9B and Figure 12A, our results also found that the diffuses of HCO₃^- release is more difficult than CO₂ delivery, besides that, we obtain free energy profile through umbrella sampling, and observed the influences of the key residues such as H64, Q92, and T200 on substrates delivery and product release.

FIGURE 11

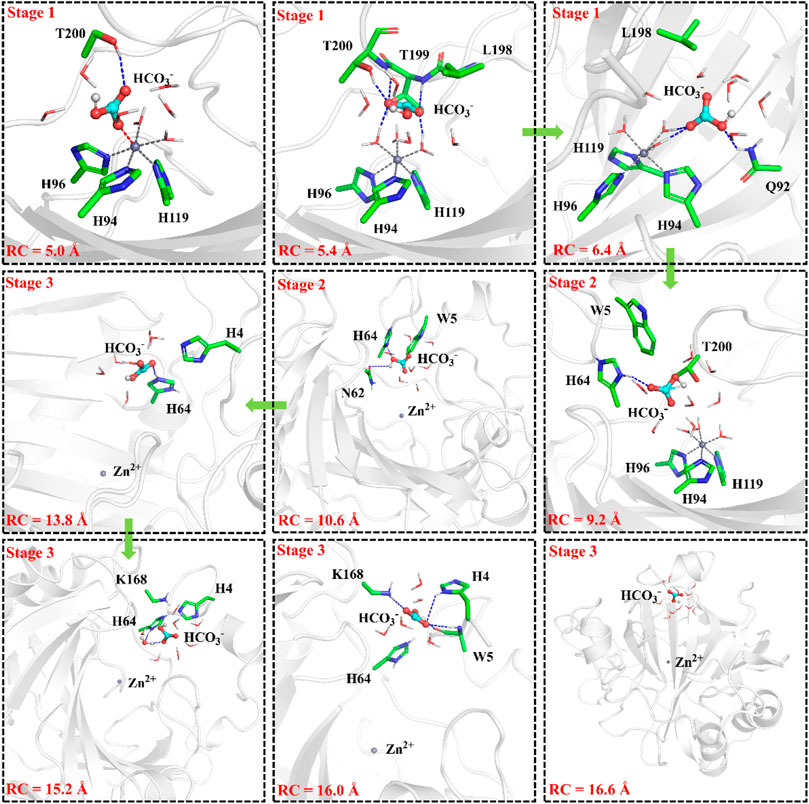
FIGURE 11. Representative structures and conformational changes of the transportation channel for the release of HCO₃^-, where the distance between H119@NE2 and HCO₃^-@C is defined as RC5.

FIGURE 12

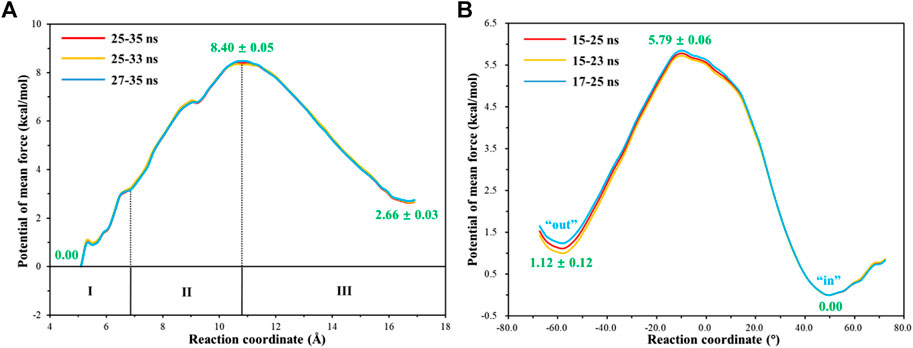
FIGURE 12. (A) Free energy profile for the release of HCO₃^- from the active site to the bulk water. (B) Free energy profile for the rotation of the unprotonated H64 from outward to inward conformation.

With the departure of HCO₃⁻, the protonated H64 may release one proton to the medium and rotates back to the inward conformation, recovering to the ready state of CA for the next cycle. Previous studies proposed that the rate-limiting step might be related to external buffers. (Tu and Silverman, 1975; Silverman et al., 1979; Lindskog et al., 1991; Lu and Voth, 1998). At high buffer concentrations, the proton transfer between the zinc-bound water and H64 is the rate-limiting step, while the proton release to the medium is the rate-limiting step at low buffer concentrations. (Tu and Silverman, 1975; Silverman et al., 1979; Lindskog et al., 1991). Here primary QM/MM and QM calculations were performed to explore the deprotonation of H64, and test calculations indicate that the proton abstractions from H64 by the nearby residue N62 and water molecule are quite difficult (see Supplemenatary Figures 6, 7). On the contrary, the proton transfer from H64 to a phosphate group with the aid of one water molecule is predicted to be barrier free by QM calculations with a cluster model, and the full geometry optimization directly converges to the proton-transfer product with the energy release of 112 kcal/mol, suggesting that the deprotonation of H64 by the phosphate group, which approximately mimics the presence of external buffers as the proton acceptor or donor, is quite facile. As Figure 13 shows, the hydrogen-bond interaction between H4 and H64 disappears after the deprotonation of H64, while W5 still maintains the hydrogen bond and π-π stacking interactions with H64 in the outward conformation. Afterward, H64 recovers to the inward conformation through the narrow channel between W5 and N62, and the water chain of two molecules connecting H64 to Zn²⁺ is again formed, as observed in the initial configuration of CA. The narrow channel for the rotation of H64 was proposed in previous transition path sampling study. (Roy and Taraphder, 2009). As Figure 12B shows, the H64 rotation back to the inward conformation along with its deprotonation experiences about a free energy barrier of 4.7 kcal/mol with the free energy release of about 1.1 kcal/mol, leading to that CA evolves to its initial state and completion of the enzymatic cycle for CO₂ hydration. The free energy profiles for the whole catalytic hydration process of CO₂ are summarized in Figure 14, and this enzymatic capture of CO₂ is favorable, both thermodynamically and kinetically.

FIGURE 13

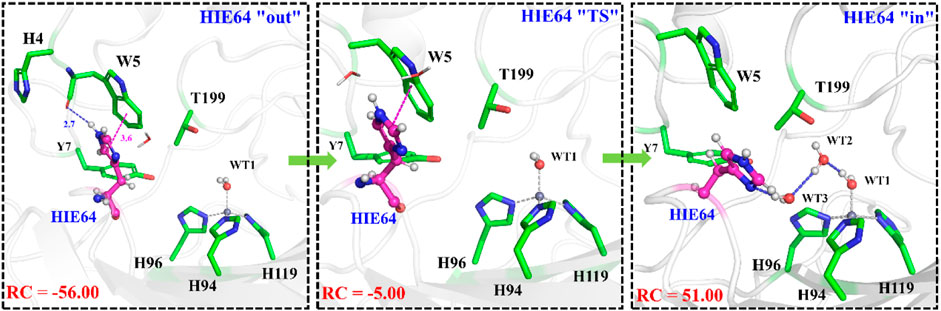
FIGURE 13. Representative structures and conformational changes of the rotation of H64 from outward to inward conformation, where the reaction coordinate is defined as the dihedral angle χ(N–C_α–C_β–C_γ).

FIGURE 14

FIGURE 14. Free energy profiles for the entire enzymatic catalytic process.

Conclusion

Extensive QM(B3LYP)/MM MD and MM MD simulations with the umbrella sampling have been used to study the whole enzymatic hydration of CO₂ by carbonic anhydrase, including the CO₂ delivery to the active site, the catalytic mechanisms for proton transfer and CO₂ hydration, the dissociation and release of HCO₃⁻, the conformational change of H64 side chain, and the role of key residues. The present results reveal that Q92 plays role in CO₂ transportation and the release of HCO₃⁻. Besides that, H4, N62 and W5 also show nonnegligible effects, as they stabilize the protonated H64 and provide the driving force for the rotation of H64 and the release of HCO₃⁻. The proton transfer from the water molecule (WT1) to H64, leading to formation of the Zn-bound OH⁻, is the rate-limiting step with an energy barrier of about 10.4 kcal/mol, in line with previous experiments and calculations. The conformational transition of the protonated H64 from inward to outward mediates CO₂ entry into the active site, which squeezes out the water molecules from the hydrated active-site with an energy release of 7.0 kcal/mol. After the entrance of CO₂ into the hydrophobic pocket, the nucleophilic attack of OH⁻@O on CO₂@C forms HCO₃⁻, which is bound to the zinc ion in the bidentate coordination, with a free energy span of 4.4 kcal/mol and the free energy release of 8.0 kcal/mol. The release of HCO₃⁻ from the active site has the free-energy span of 8.4 kcal/mol. During the release of HCO₃⁻, H64 may be deprotonated with the aid of H4 and K168 and then rotates back from outward to inward conformation with the free energy barrier of 4.7 kcal/mol. The present study provides a comprehensive understanding of enzymatic hydration CO₂ by carbonic anhydrase, which is important for rational enzyme engineering of biological capture and sequestration of CO₂.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

YF: performed calculations; YF, FF, and YZ: analysed data; YF, BW, and ZC: designed research; YF, FF, BW, and ZC: wrote the paper. All authors have approved the final version of the article.

Funding

This work is supported by the National Science Foundation of China (21873078, 21673185, and 21933009).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2021.706959/full#supplementary-material.

References

Aggarwal, M., Kondeti, B., Tu, C., Maupin, C. M., Silverman, D. N., and McKenna, R. (2014). Structural Insight into Activity Enhancement and Inhibition of H64A Carbonic Anhydrase II by Imidazoles. Int. Union Crystallogr. J. 1, 129–135. doi:10.1107/s2052252514004096

CrossRef Full Text | Google Scholar

Agmon, N. (1995). The Grotthuss Mechanism. Chem. Phys. Lett. 244 (5-6), 456–462. doi:10.1016/0009-2614(95)00905-j

CrossRef Full Text | Google Scholar

Alvizo, O., Nguyen, L. J., Savile, C. K., Bresson, J. A., Lakhapatri, S. L., Solis, E. O. P., et al. (2014). Directed Evolution of an Ultrastable Carbonic Anhydrase for Highly Efficient Carbon Capture from Flue Gas. Proc. Natl. Acad. Sci. USA 111 (46), 16436–16441. doi:10.1073/pnas.1411461111

PubMed Abstract | CrossRef Full Text | Google Scholar

An, H., Tu, C., Duda, D., Montanez-Clemente, I., Math, K., Laipis, P. J., et al. (2002). Chemical rescue in Catalysis by Human Carbonic Anhydrases II and III. Biochemistry 41 (9), 3235–3242. doi:10.1021/bi0120695

PubMed Abstract | CrossRef Full Text | Google Scholar

Avvaru, B. S., Kim, C. U., Sippel, K. H., Gruner, S. M., Agbandje-McKenna, M., Silverman, D. N., et al. (2010). A Short, Strong Hydrogen Bond in the Active Site of Human Carbonic Anhydrase II. Biochemistry 49 (2), 249–251. doi:10.1021/bi902007b

PubMed Abstract | CrossRef Full Text | Google Scholar

Barducci, A., Bussi, G., and Parrinello, M. (2008). Well-tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method. Phys. Rev. Lett. 100 (2), 020603. doi:10.1103/PhysRevLett.100.020603

PubMed Abstract | CrossRef Full Text | Google Scholar

Bayly, C. I., Cieplak, P., Cornell, W., and Kollman, P. A. (1993). A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: the RESP Model. J. Phys. Chem. 97 (40), 10269–10280. doi:10.1021/j100142a004

CrossRef Full Text | Google Scholar

Case, D. A., Cheatham, T. E., Darden, T., Gohlke, H., Luo, R., Merz, K. M., et al. (2005). The Amber Biomolecular Simulation Programs. J. Comput. Chem. 26 (16), 1668–1688. doi:10.1002/jcc.20290

CrossRef Full Text | Google Scholar

Chen, G., Kong, X., Lu, D., Wu, J., and Liu, Z. (2017). Kinetics of CO2 Diffusion in Human Carbonic Anhydrase: a Study Using Molecular Dynamics Simulations and the Markov-State Model. Phys. Chem. Chem. Phys. 19 (18), 11690–11697. doi:10.1039/c7cp00887b

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, G., Lu, D., Wu, J., and Liu, Z. (2018). Detachment of HCO3- from the Active Site of Carbonic Anhydrase: Molecular Dynamics Simulation and Machine Learning. J. Phys. Chem. C 122 (35), 20539–20549. doi:10.1021/acs.jpcc.8b05298

CrossRef Full Text | Google Scholar

Chen, G., Xu, W. N., Lu, D. N., Wu, J. Z., and Liu, Z. (2018). Markov-state Model for CO2 Binding with Carbonic Anhydrase under Confinement. J. Chem. Phys. 148 (3). doi:10.1063/1.5003298

CrossRef Full Text | Google Scholar

Cui, Q., and Karplus, M. (2003). Is a "proton Wire" Concerted or Stepwise? A Model Study of Proton Transfer in Carbonic Anhydrase. J. Phys. Chem. B 107 (4), 1071–1078. doi:10.1021/jp021931v

CrossRef Full Text | Google Scholar

Darunte, L. A., Oetomo, A. D., Walton, K. S., Sholl, D. S., and Jones, C. W. (2016). Direct Air Capture of CO2 Using Amine Functionalized MIL-101(Cr). ACS Sustain. Chem. Eng. 4 (10), 5761–5768. doi:10.1021/acssuschemeng.6b01692

CrossRef Full Text | Google Scholar

Duda, D., Tu, C., Qian, M., Laipis, P., Agbandje-McKenna, M., Silverman, D. N., et al. (2001). Structural and Kinetic Analysis of the Chemical Rescue of the Proton Transfer Function of Carbonic Anhydrase II†. Biochemistry 40 (6), 1741–1748. doi:10.1021/bi002295z

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, F., Zhao, Y., and Cao, Z. (2019). Insight into the Delivery Channel and Selectivity of Multiple Binding Sites in Bovine Serum Albumin towards Naphthalimide-Polyamine Derivatives. Phys. Chem. Chem. Phys. 21 (14), 7429–7439. doi:10.1039/c9cp00527g

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, F., Zheng, Y., Zhang, Y., Zheng, H., Zhong, J., and Cao, Z. (2019). A Comprehensive Understanding of Enzymatic Degradation of the G-type Nerve Agent by Phosphotriesterase: Revised Role of Water Molecules and Rate-Limiting Product Release. ACS Catal. 9 (8), 7038–7051. doi:10.1021/acscatal.9b01877

CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2013). Gaussian 09, Revision E.01, Wallingford, CT: Gaussian Inc.

Gao, Y., Zhang, C., Wang, X., and Zhu, T. (2017). A Test of AMBER Force fields in Predicting the Secondary Structure of α-helical and β-hairpin Peptides. Chem. Phys. Lett. 679, 112–118. doi:10.1016/j.cplett.2017.04.074

CrossRef Full Text | Google Scholar

Götz, A. W., Williamson, M. J., Xu, D., Poole, D., Le Grand, S., and Walker, R. C. (2012). Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born. J. Chem. Theor. Comput. 8 (5), 1542–1555. doi:10.1021/ct200909j

CrossRef Full Text | Google Scholar

Grimme, S., Ehrlich, S., and Goerigk, L. (2011). Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 32 (7), 1456–1465. doi:10.1002/jcc.21759

CrossRef Full Text | Google Scholar

Grimme, S. (2006). Semiempirical GGA-type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 27 (15), 1787–1799. doi:10.1002/jcc.20495

CrossRef Full Text | Google Scholar

Håkansson, K., Carlsson, M., Svensson, L. A., and Liljas, A. (1992). Structure of Native and Apo Carbonic Anhydrase II and Structure of Some of its Anion-Ligand Complexes. J. Mol. Biol. 227 (4), 1192–1204. doi:10.1016/0022-2836(92)90531-n

CrossRef Full Text | Google Scholar

Jo, B. H., Seo, J. H., Yang, Y. J., Baek, K., Choi, Y. S., Pack, S. P., et al. (2014). Bioinspired Silica Nanocomposite with Autoencapsulated Carbonic Anhydrase as a Robust Biocatalyst for CO2 Sequestration. ACS Catal. 4 (12), 4332–4340. doi:10.1021/cs5008409

CrossRef Full Text | Google Scholar

Kar, S., Goeppert, A., Galvan, V., Chowdhury, R., Olah, J., and Prakash, G. K. S. (2018). A Carbon-Neutral CO2 Capture, Conversion, and Utilization Cycle with Low-Temperature Regeneration of Sodium Hydroxide. J. Am. Chem. Soc. 140 (49), 16873–16876. doi:10.1021/jacs.8b09325

CrossRef Full Text | Google Scholar

Kim, H. S., Hong, S.-G., Woo, K. M., Teijeiro Seijas, V., Kim, S., Lee, J., et al. (2018). Precipitation-Based Nanoscale Enzyme Reactor with Improved Loading, Stability, and Mass Transfer for Enzymatic CO2 Conversion and Utilization. ACS Catal. 8 (7), 6526–6536. doi:10.1021/acscatal.8b00606

CrossRef Full Text | Google Scholar

Krishnamurthy, V. M., Kaufman, G. K., Urbach, A. R., Gitlin, I., Gudiksen, K. L., Weibel, D. B., et al. (2008). Carbonic Anhydrase as a Model for Biophysical and Physical-Organic Studies of Proteins and Protein−Ligand Binding. Chem. Rev. 108 (3), 946–1051. doi:10.1021/cr050262p

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, S., Rosenberg, J. M., Bouzida, D., Swendsen, R. H., and Kollman, P. A. (1992). THE Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method. J. Comput. Chem. 13 (8), 1011–1021. doi:10.1002/jcc.540130812

CrossRef Full Text | Google Scholar

Le Grand, S., Götz, A. W., and Walker, R. C. (2013). SPFP: Speed without Compromise-A Mixed Precision Model for GPU Accelerated Molecular Dynamics Simulations. Comput. Phys. Commun. 184 (2), 374–380. doi:10.1016/j.cpc.2012.09.022

CrossRef Full Text | Google Scholar

Li, P., and Merz, K. M. (2016). MCPB.py: A Python Based Metal Center Parameter Builder. J. Chem. Inf. Model. 56 (4), 599–604. doi:10.1021/acs.jcim.5b00674

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, P., and Merz, K. M. (2017). Metal Ion Modeling Using Classical Mechanics. Chem. Rev. 117 (3), 1564–1686. doi:10.1021/acs.chemrev.6b00440

PubMed Abstract | CrossRef Full Text | Google Scholar

Lindskog, S. B. G., Engstrant, C., Forsman, C., Jonsson, B., Liang, Z., et al. (1991). Carbonic Anhydrase: From Biochemistry and Genetics to Physiology and Clinical Medicine. Biochem. Genet. Physiol. Clin. Med. 306 (2-3), 277. doi:10.1016/0014-5793(9281019)-I

CrossRef Full Text | Google Scholar

Loferer, M. J., Tautermann, C. S., Loeffler, H. H., and Liedl, K. R. (2003). Influence of Backbone Conformations of Human Carbonic Anhydrase II on Carbon Dioxide Hydration: Hydration Pathways and Binding of Bicarbonate. J. Am. Chem. Soc. 125 (29), 8921–8927. doi:10.1021/ja035072f

CrossRef Full Text | Google Scholar

Lu, D., and Voth, G. A. (1998). Proton Transfer in the Enzyme Carbonic Anhydrase: Anab InitioStudy. J. Am. Chem. Soc. 120 (16), 4006–4014. doi:10.1021/ja973397o

CrossRef Full Text | Google Scholar

Maupin, C. M., Castillo, N., Taraphder, S., Tu, C., McKenna, R., Silverman, D. N., et al. (2011). Chemical Rescue of Enzymes: Proton Transfer in Mutants of Human Carbonic Anhydrase II. J. Am. Chem. Soc. 133 (16), 6223–6234. doi:10.1021/ja1097594

CrossRef Full Text | Google Scholar

Maupin, C. M., McKenna, R., Silverman, D. N., and Voth, G. A. (2009). Elucidation of the Proton Transport Mechanism in Human Carbonic Anhydrase II. J. Am. Chem. Soc. 131 (22), 7598–7608. doi:10.1021/ja8091938

CrossRef Full Text | Google Scholar

Metz, S., Kästner, J., Sokol, A. A., Keal, T. W., and Sherwood, P. (2014). C Hem S Hell-A Modular Software Package for QM/MM Simulations. Wires Comput. Mol. Sci. 4 (2), 101–110. doi:10.1002/wcms.1163

CrossRef Full Text | Google Scholar

Mikulski, R., West, D., Sippel, K. H., Avvaru, B. S., Aggarwal, M., Tu, C., et al. (2013). Water Networks in Fast Proton Transfer during Catalysis by Human Carbonic Anhydrase II. Biochemistry 52 (1), 125–131. doi:10.1021/bi301099k

PubMed Abstract | CrossRef Full Text | Google Scholar

Miyamoto, S., and Kollman, P. A. (1992). Settle: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comput. Chem. 13 (8), 952–962. doi:10.1002/jcc.540130805

CrossRef Full Text | Google Scholar

Neese, F. (2018). Software Update: the ORCA Program System, Version 4.0. Wires Comput. Mol. Sci. 8 (1). doi:10.1002/wcms.1327

CrossRef Full Text | Google Scholar

Olsson, M. H. M., Søndergaard, C. R., Rostkowski, M., and Jensen, J. H. (2011). PROPKA3: Consistent Treatment of Internal and Surface Residues in Empirical pKa Predictions. J. Chem. Theor. Comput. 7 (2), 525–537. doi:10.1021/ct100578z

PubMed Abstract | CrossRef Full Text | Google Scholar

Paul, S., Paul, T. K., and Taraphder, S. (2018). Reaction Coordinate, Free Energy, and Rate of Intramolecular Proton Transfer in Human Carbonic Anhydrase II. J. Phys. Chem. B 122 (11), 2851–2866. doi:10.1021/acs.jpcb.7b10713

PubMed Abstract | CrossRef Full Text | Google Scholar

Piazzetta, P., Marino, T., and Russo, N. (2014). Promiscuous Ability of Human Carbonic Anhydrase: QM and QM/MM Investigation of Carbon Dioxide and Carbodiimide Hydration. Inorg. Chem. 53 (7), 3488–3493. doi:10.1021/ic402932y

PubMed Abstract | CrossRef Full Text | Google Scholar

Riccardi, D., König, P., Guo, H., and Cui, Q. (2008). Proton Transfer in Carbonic Anhydrase Is Controlled by Electrostatics rather Than the Orientation of the Acceptor. Biochemistry 47 (8), 2369–2378. doi:10.1021/bi701950j

PubMed Abstract | CrossRef Full Text | Google Scholar

Riccardi, D., König, P., Prat-Resina, X., Yu, H., Elstner, M., Frauenheim, T., et al. (2006). "Proton Holes" in Long-Range Proton Transfer Reactions in Solution and Enzymes: A Theoretical Analysis. J. Am. Chem. Soc. 128 (50), 16302–16311. doi:10.1021/ja065451j

CrossRef Full Text | Google Scholar

Riccardi, D., Yang, S., and Cui, Q. (2010). Proton Transfer Function of Carbonic Anhydrase: Insights from QM/MM Simulations. Biochim. Biophys. Acta (Bba) - Proteins Proteomics 1804 (2), 342–351. doi:10.1016/j.bbapap.2009.07.026

CrossRef Full Text | Google Scholar

Roy, A., and Taraphder, S. (2008). A Theoretical Study on the Detection of Proton Transfer Pathways in Some Mutants of Human Carbonic Anhydrase II. J. Phys. Chem. B 112 (43), 13597–13607. doi:10.1021/jp0757309

CrossRef Full Text | Google Scholar

Roy, A., and Taraphder, S. (2009). Transition Path Sampling Study of the Conformational Fluctuation of His-64 in Human Carbonic Anhydrase II. J. Phys. Chem. B 113 (37), 12555–12564. doi:10.1021/jp9010982

CrossRef Full Text | Google Scholar

Sanz-Pérez, E. S., Murdock, C. R., Didas, S. A., and Jones, C. W. (2016). Direct Capture of CO2 from Ambient Air. Chem. Rev. 116 (19), 11840–11876. doi:10.1021/acs.chemrev.6b00173

PubMed Abstract | CrossRef Full Text | Google Scholar

Sherwood, P., de Vries, A. H., Guest, M. F., Schreckenbach, G., Catlow, C. R. A., French, S. A., et al. (2003). QUASI: A General Purpose Implementation of the QM/MM Approach and its Application to Problems in Catalysis. J. Mol. Struct. THEOCHEM 632, 1–28. doi:10.1016/s0166-1280(03)00285-9

CrossRef Full Text | Google Scholar

Silverman, D. N., and Mckenna, R. (2007). Solvent-mediated Proton Transfer in Catalysis by Carbonic Anhydrase. Acc. Chem. Res. 40 (8), 669–675. doi:10.1021/ar7000588

PubMed Abstract | CrossRef Full Text | Google Scholar

Silverman, D. N., Tu, C. K., Lindskog, S., and Wynns, G. C. (1979). Rate of Exchange of Water from the Active Site of Human Carbonic Anhydrase C. J. Am. Chem. Soc. 101, 6734. doi:10.1021/ja00516a040

CrossRef Full Text | Google Scholar

Silverman, D. N., and Vincent, S. H. (1983). Proton Transfer in the Catalytic Mechanism of Carbonic Anhydrase. Crit. Rev. Biochem. 14 (3), 207–255. doi:10.3109/10409238309102794

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, H., Vasa, S. K., Jangra, H., Rovó, P., Päslack, C., Das, C. K., et al. (2019). Fast Microsecond Dynamics of the Protein-Water Network in the Active Site of Human Carbonic Anhydrase II Studied by Solid-State NMR Spectroscopy. J. Am. Chem. Soc. 141 (49), 19276–19288. doi:10.1021/jacs.9b05311

CrossRef Full Text | Google Scholar

Smith, W., and Forester, T. R. (1996). DL_POLY_2.0: A General-Purpose Parallel Molecular Dynamics Simulation Package. J. Mol. Graphics 14 (3), 136–141. doi:10.1016/s0263-7855(96)00043-4

CrossRef Full Text | Google Scholar

Souaille, M., and Roux, B. (2001). Extension to the Weighted Histogram Analysis Method: Combining Umbrella Sampling with Free Energy Calculations. Comput. Phys. Commun. 135 (1), 40–57. doi:10.1016/s0010-4655(00)00215-0

CrossRef Full Text | Google Scholar

Sun, Y., and Kollman, P. A. (1995). Hydrophobic Solvation of Methane and Nonbond Parameters of the Tip3p Water Model. J. Comput. Chem. 16 (9), 1164–1169. doi:10.1002/jcc.540160910

CrossRef Full Text | Google Scholar

Taraphder, S., Maupin, C. M., Swanson, J. M. J., and Voth, G. A. (2016). Coupling Protein Dynamics with Proton Transport in Human Carbonic Anhydrase II. J. Phys. Chem. B 120 (33), 8389–8404. doi:10.1021/acs.jpcb.6b02166

PubMed Abstract | CrossRef Full Text | Google Scholar

Tu, C. K., and Silverman, D. N. (1975). The Mechanism of Carbonic Anhydrase Studied by13C and 180 Labeling of Carbon Dioxide. J. Am. Chem. Soc. 97, 5935. doi:10.1021/ja00853a060

CrossRef Full Text | Google Scholar

Tu, C., Silverman, D. N., Forsman, C., Jonsson, B. H., and Lindskog, S. (1989). Role of Histidine 64 in the Catalytic Mechanism of Human Carbonic Anhydrase II Studied with a Site-specific Mutant. Biochemistry 28 (19), 7913–7918. doi:10.1021/bi00445a054

PubMed Abstract | CrossRef Full Text | Google Scholar

Vinoba, M., Bhagiyalakshmi, M., Grace, A. N., Kim, D. H., Yoon, Y., Nam, S. C., et al. (2013). Carbonic Anhydrase Promotes the Absorption Rate of CO2in Post-Combustion Processes. J. Phys. Chem. B 117 (18), 5683–5690. doi:10.1021/jp401622c

CrossRef Full Text | Google Scholar

Vinoba, M., Bhagiyalakshmi, M., Jeong, S. K., Yoon, Y. I., and Nam, S. C. (2011). Capture and Sequestration of CO2 by Human Carbonic Anhydrase Covalently Immobilized onto Amine-Functionalized SBA-15. J. Phys. Chem. C 115 (41), 20209–20216. doi:10.1021/jp204661v

CrossRef Full Text | Google Scholar

Wang, J., Wolf, R. M., Caldwell, J. W., Kollman, P. A., and Case, D. A. (2004). Development and Testing of a General Amber Force Field. J. Comput. Chem. 25 (9), 1157–1174. doi:10.1002/jcc.20035

CrossRef Full Text | Google Scholar