
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Chem. , 12 March 2021
Sec. Theoretical and Computational Chemistry
Volume 9 - 2021 | https://doi.org/10.3389/fchem.2021.637286
This article is part of the Research Topic Atomic Clusters: Theory & Experiments View all 10 articles
The structural characterization of clusters or nanoparticles is essential to rationalize their size and composition-dependent properties. As experiments alone could not provide complete picture of cluster structures, so independent theoretical investigations are needed to find out a detail description of the geometric arrangement and corresponding properties of the clusters. The potential energy surfaces (PES) are explored to find several minima with an ultimate goal of locating the global minima (GM) for the clusters. Optimization algorithms, such as genetic algorithm (GA), basin hopping method and its variants, self-consistent basin-to-deformed-basin mapping, heuristic algorithm combined with the surface and interior operators (HA-SIO), fast annealing evolutionary algorithm (FAEA), random tunneling algorithm (RTA), and dynamic lattice searching (DLS) have been developed to solve the geometrical isomers in pure elemental clusters. Various model or empirical potentials (EPs) as Lennard–Jones (LJ), Born–Mayer, Gupta, Sutton–Chen, and Murrell–Mottram potentials are used to describe the bonding in different type of clusters. Due to existence of a large number of homotops in nanoalloys, genetic algorithm, basin-hopping algorithm, modified adaptive immune optimization algorithm (AIOA), evolutionary algorithm (EA), kick method and Knowledge Led Master Code (KLMC) are also used. In this review the optimization algorithms, computational techniques and accuracy of results obtained by using these mechanisms for different types of clusters will be discussed.
Nanoclusters are considered as a collection of ∼10 to 106 atoms or molecules within a nanometre size range (Lesley and Johnston, 2000; Johnston, 2002) such as fullerenes, metal clusters, molecular clusters and ionic clusters (Jellinek, 1999; Baletto and Ferrando, 2005). Nanometre-size clusters are both crystalline (face-centred cubic (fcc), octahedra or truncated octahedral (TO)) and noncrystalline (icosahedra, decahedra, polytetrahedra and polyicosahedra) structures. The small size nanoclusters exist in noncrystalline shapes. The noble and transition metals are dominated with icosahedra and Marks truncated decahedra structures (Martin, 1996). These structures are not favourable for large clusters due to the strain arising from their noncrystalline packing (Baletto and Ferrando, 2005). However the strain can be released by placing a smaller atom in the core of the nanoalloy (Rossi et al., 2004) as the strain is proportional to the cluster volume. The quantized electronic energy levels of clusters give rise to atomic-like character (Halperin, 1986; Ralph et al., 1995) and this phenomenon is used to enhance the optical and electrical properties of some clusters (Heath, 1995; Papavassiliou, 1979). Advancement in modern research occur with nanoalloy composition (Ferrando et al., 2008; Oderji and Ding, 2011; Liu et al., 2005) and chemical ordering patterns (Scott et al., 2004; Chen et al., 2005; Knudsen et al., 2007; Maksimuk et al., 2007; Ye and Crooks, 2007; Teng and Yang, 2003) in addition to the size, atomic order and structure. Chemical ordering depends upon structure, size and composition, among others (Johnston, 2003). See Figure 1. The theoretical studies for clusters are far cheaper than the experimental trial-and-error approaches, and led to conclusion by following parameters; heat of formation, energies, structural mechanisms, transition states (TS) mechanisms, and molecular spectra analysis (Foresman and Frisch, 1996). Various groups have explored these properties for the generation and characterization of the atomic clusters (Cabaleiro-Lago et al., 2000; Marques and Pereira, 2010a; Marques and Pereira, 2013; Marques and Pereira, 2013, Marques et al., 2018; Bartolomei et al., 2015).
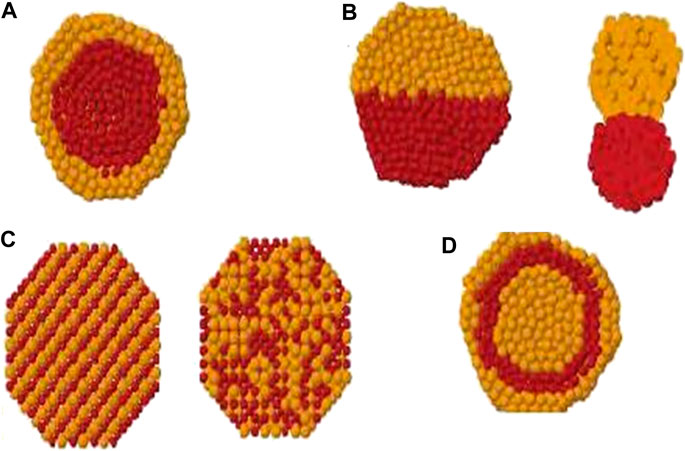
FIGURE 1. Cross section view of (A) core-shell, (B) subcluster segregated, (C) mixed and (D) multishell patterns. (Ismail, 2012).
The PES is explored to locate the GM for the smaller clusters by different approaches. Electronic structure of these clusters can be defined by either ab initio Molecular Orbital (MO) or semi-empirical atomistic potentials (Wales and Scheraga, 1999; Johnston, 2002). GM structure is the most preferred structure though other metastable structures are also observed due to kinetic effects. Ab initio method are feasible for the smaller systems (tens of atoms) as it is based on the laws of quantum mechanics, atomic, electronic properties and few other physical constants. In this method, the system is studied either by short single-point energy calculation or by geometrically relax the system for more stable configuration. The empirical or semi-empirical methods are used for the medium sized systems. As ab initio methods are computationally demanding so empirical methods are used as an alternative, but empirical methods are not found to be accurate to encounter hydrogen-bonding, chemical transitions or nitrated compounds (Akutsu et al., 1991; Cook, 2005). Further compared to pure elemental clusters, the existence of homotops complicates nanoalloys studies. The conformational stability of clusters is carried out by the global minima and transition states being stationary points with zero potential gradients. Local minima is obtained by the rise in potential energy for any infinitesimal displacement of internal coordinates, where there is a Hessian with positive (second derivative matrix) eigenvalue for the transition states.
GA is considered as a better and popular choice in clusters compared to Monte Carlo (MC) and Molecular Dynamics (MD) Simulated Annealing method. The other techniques are evolution strategies, differential evolution, genetic programming, evolutionary programming, gene expression programming, neuro-evolution, learning classifier systems. Xiao and Williams (Xiao and Williams, 1993) used the GA approach for the molecular clusters (benzene, naphthalene and anthracene) in 1990’s. Then Hartke (Hartke, 1993) reported the genetic algorithms for global optimization of molecular clusters. The binary encoded geometries and bitwise acting genetic operators on binary strings were reported by Xiao et al. (Xiao and Williams, 1993). Further these binary encoding and decoding were replaced by applying cartesian coordinates on GA approach (Zeiri, 1995). A significant contribution was made by Deaven and Ho (Deaven and Ho, 1995) in which gradient-driven local minimization was implemented for the cluster energy. Birmingham Cluster Genetic Algorithm (BCGA) in house GA was developed by Wales group for Morse clusters (Roberts et al., 2000), fullerenes (Johnston, 2003), ionic clusters (Roberts and Johnston, 2001), water clusters (Guimaraes et al., 2002), metal clusters (Lloyd et al., 2002) and bimetallic clusters (Bailey et al., 2003; Lordeiro et al., 2003). BHMC algorithm is based on the MC minimization or BH algorithm (Li and Scheraga, 1987) in which PES is simplified by the transformation of energy which results in a smoother landscape. So these methods are also known as hypersurface deformation (Stillinger and Weber, 1988). In 2005 Karaboga (Karaboga, 2005) proposed artificial bee colony (ABC) algorithm which was very efficient in locating global minima for long range potentials. The ABC algorithm was successfully applied to the atomic clusters (Zhang and Dolg, 2015) and rigid molecules with corresponding ABCluster software (Zhang and Dolg, 2016). Particle swarm optimization (Call et al., 2007), stochastic surface walking (Shang and Liu, 2013), kick method (Saunders, 1987; Bera et al., 2007; Addicoat and Metha, 2009; Zhai et al., 2015) and GIGA (Jäger et al., 2019) have shown good performance for various chemical systems.
Various model or empirical potentials (EPs) are used to describe the bonding in these clusters. It was observed that global minimum configurations show different symmetries for Sutton Chen potentials and Lennard-Jones potentials. The Sutton-Chen potential is a Finnis-Sinclair type potential with two terms providing the pair-wise repulsive and approximate many-body cohesive contributions separately. Gupta potential is a semi-empirical potential derived within the tight-binding second-moment approximation. It is highly recommended for metallic systems (Gupta, 1981) with inter-atomic interactions. This potential function is applied to describe homonuclear and heteronuclear interactions. The parameters used for this potential is given in Table 1 from the work carried out by Srivastava (Srivastava, 2017a) for (Aum-Agn-Pdo-Ptp) (m = 10 and n + o + p = 10) tetrametallic clusters. A, ξ, p and q potential parameters are used to fit the experimental properties as cohesive energy, lattice parameters, elastic constants, among others), while r0 can either be average of the pure bulk distances or can be taken by specific ordered bulk alloy. See Figure 2.
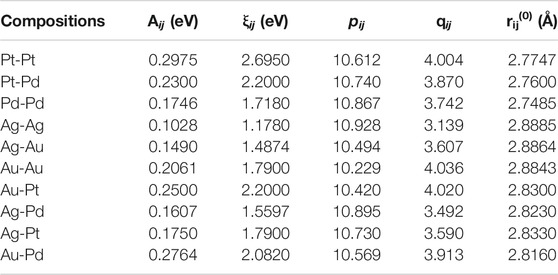
TABLE 1. Gupta potential parameters used for the four (Pt, Pd, Ag, Au) coinage metals. (Srivastava, 2017b).
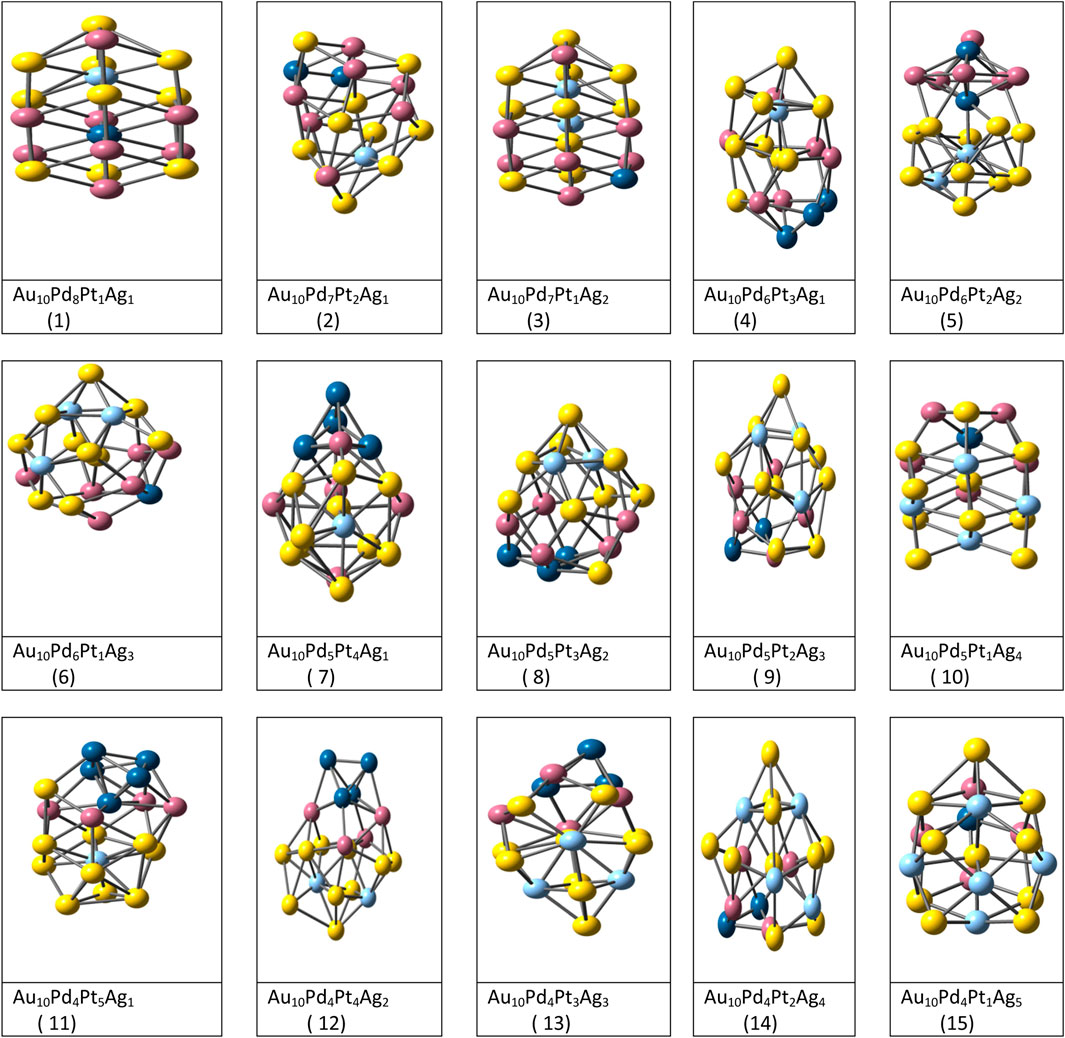
FIGURE 2. Optimized structures of Fifteen tetrametallic clusters complexes by DFT method. (Srivastava, 2017b).
Due to high computational costs, a combined empirical-ab initio approach is used to carry out the unbiased searches at empirical level for global and local minima structures. These structures were optimized at ab initio level and GO technique was used at EP level to build a database of structural motifs. Global searches were performed with the BCGA and BHMC algorithms by employing Gupta and Gupta-derives potentials. Then the selected minima are locally optimized at the DFT level using various softwares as the Northwest Computational Chemistry (NWChem) (Aprà et al., 2020), Quantum ESPRESSO (QE) (Giannozzi et al., 2020), Gaussian 09 package (Frisch, 2009), VASP (Kresse and Furthmüller, 1996) and ADF (TeVelde et al., 2001; Baerends et al., 2003) etc.
OGOLEM (Hartke, 1993; Dieterich and Hartke, 2017), GMIN (Wales and Scheraga, 1999; Wales, 2010), BCGA (Johnston, 2003; Shayeghi et al., 2015), Gradient Embedded Genetic Algorithm or GEGA (Alexandrova and Boldyrev, 2005), Global Reaction Route Mapping (GRRM) (Ohno and Maeda, 2006; Ohno and Maeda, 2019), Evolutionary Algorithm for Molecular Clusters or EA_MOL (Llanio-Trujillo et al., 2011; Marques and Pereira, 2011), Automated Mechanisms and Kinetics (AutoMeKin) (Martínez-Núñez, 2015a; Martínez-Núñez, 2015b; Martínez-Núñez et al., 2020), ABCluster (Zhang and Dolg, 2015), Genetic Algorithm fitting (GAFit) (Rodríguez-Fernández et al., 2017; Rodríguez-Fernández et al., 2020), AUTOMATON (Yañez et al., 2019; Yañez et al., 2020) and NWPEsSe (Zhang et al., 2020) are some of the computational tools which have included many of these methods.
The energetic analysis of clusters is carried out by average binding energy (pure clusters), second difference in binding energy and excess (or mixing) energy for nanoalloys by both EP and DFT levels. The mixing effect is studied by various factors as size, cohesive energy, surface energy, electronegativity among many others. Radial distribution function (RDF), pair distribution function (PDF) and average nearest-neighbour distance (ANND) are also calculated for bonding analysis. Further chemical ordering and symmetry are studied for the cluster structure analysis. Compositional Mixing Degree is calculated to give emphasis to the mixed bonds (Srivastava, 2017a; Srivastava, 2018a).
In next section, we will discuss the use of these optimization algorithms in various types of clusters.
Spherical shell model was used to determine the electronic structures of “magic numbers” in Nan and Kn alkali-metal clusters (Brack, 1993; de Heer, 1993). Åkeby et al. (Åkeby et al., 1990) used the configuration interaction (CI) method with an effective core potential for small clusters (n ≤ 10). Full-potential muffin-tin orbitals (FP-LMTO) technique was used for small Cun clusters (Kabir et al., 2003). Tight-binding (TB) approach with quasi-empirical potential was used to study the molecular dynamics for nearly 1,300 atoms (D’Agostino, 1993). A minimal parameter TBMD method was used for transition metal (Nin and Fen) clusters (Menon et al., 1994; Lathiotakis et al., 1996). Random search method has been adopted by Johnston group on (Al, Ca, Fe, Ni, Pd and Pt) bound 17–19 atoms clusters by Murrell–Mottram 2 + 3 body potentials. Results indicated similar structural patterns but different positions of elements for both Murrell–Mottram and Sutton–Chen potentials.
A previous studies indicated amorphous structures for 13 atoms (Au, Ag, Cu) clusters (Oviedo and Palmer, 2002) and large Aun clusters (n = 38, 55, 75) (Michaelian et al., 1999; Li et al., 2000; Wilson and Johnston, 2000). Ab initio studies showed that most of the copper clusters adopt icosahedral structure for (10 ≤ n ≤ 55), derived from the 13 atom icosahedron; polyicosahedral (19, 23, and 26) atom; and icosahedron (55 atoms) clusters by adding or removing atoms (Moore, 2013). Small anionic gold clusters were studied by Häkkinen et al. (Häkkinen et al., 2002) with PBE (Perdew et al., 1996) functional in which Au7− formed a planar structure, whereas both Cu7− and Ag7− form 3D structure. Furche et al. (Furche et al., 2002) found planar structures for Aun− up to n = 15. DFT calculations find stable planar gold clusters (Jain, 2005), while Fa et al. (Fa et al., 2005) predicted 2D→3D transition between n = 13 and n = 15 for neutral gold clusters.
Large magic number Cu clusters tend to adopt close-packed structures such as icosahedron or cuboctahedron (Massobrio et al., 1998). Jackson used local-spin-density approximation for even-numbered Cu clusters, while other study (Winter et al., 1991) predicted jellium model like icosahedral geometrical closure effects for small copper clusters. Density functional theory (DFT) within generalized gradient approximation and BFGS algorithm on Cu20, Ag20, and Au20 clusters study also showed tetrahedral structures with Td symmetry for Ag20 and Au20 clusters (Wang et al., 2003). Li et al. (Li et al., 2003) predicted tetrahedral structure with Td symmetry for Au20; similar to alkali-metal cluster Na20 (Solov’yov et al., 2002). Recently Asenjo et al. (Asenjo et al., 2013) showed that L-BFGS as well as FIRE algorithm is also a fastest minimizer and it led to less fragmented basins of attraction. As these magic number clusters are stable and have closed electronic and/or geometric shell, they can be used as building block in nanoscale materials and devices.
38, 75, and 98 atom Lennard-Jones clusters, truncated octahedron for LJ38 (Doye et al., 1999), tetrahedral symmetry for LJ98 (Leary and Doye, 1999a), Marks decahedra for LJ75–77 (Doye et al., 1995) and LJ102–104 (Doye and Wales, 1995) which are all multiple-funnel systems of the corresponding energy landscapes (Wales et al., 1998, Wales, 2004; Doye et al., 1999) were studied by GMIN optimization code by Wales Group (Wales, 2012; Oakley et al., 2013). Adaptive immune optimization algorithm (AIOA) search algorithm has been used for the structural optimization of monatomic LJ clusters (up to 200 atoms) (Ye et al., 2011; Cheng et al., 2004). Studies on the geometrical optimization of Lennard-Jones clusters within 250 atoms and Ag clusters (within 150 atoms) were carried out by adaptive immune optimization algorithm (AIOA) with dynamic lattice searching (DLS) operation (AIOA-DLS) using many-body Gupta potential (Wu and Wu, 2014a). Dynamic searching approach reduces the searching space and runs at a very high efficiency, especially for larger size clusters. This approach can be effectively used for other molecular or atomic clusters. The performance of DLS for the optimization of LJ clusters with 13 ≤ N ≤ 309 with different parameters are listed in Table 2. DLS method showed a very fast convergence speed compared with monotonic sequence basin-hopping (MSBH). Recently KLMC method is used to locate and explore double funnel landscape of LJ38 atom system (Lazauskas et al., 2017).
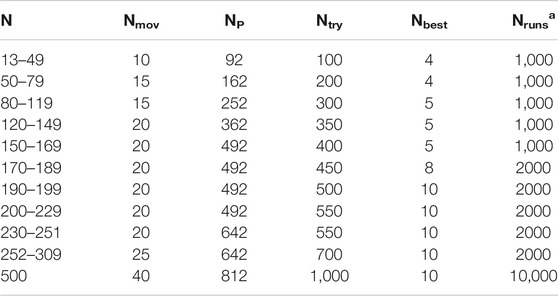
TABLE 2. Parameters Used in Dynamic Lattice Searching Method. For the magic numbers (38, 75–77, 98, 102–104). Nruns 10,000. (Shao et al., 2004b).
The Gupta potential parameters with GMIN code were used for the gold and silver clusters for Cystene-coinage metal interactions (Srivastava, 2017a). The clusters were optimized using basin hopping algorithms within higher temperature and the structures validated the experimental studies. Results indicated that basin hopping algorithm based on the Monte Carlo minimization is appropriate for these clusters. The same GMIN code has been used for the structural optimization of silver clusters (Ag8, Ag10 and Ag12) in Agn-A,T/WC complexes interactions (Srivastava, 2018a). See Figure 3. In Mutagen-Au8 complexes, the gold clusters were optimized using Gupta potential parameters and BH algorithm and the electronic and optical properties of the Mutagen-Au8 complexes (Srivastava 2017c) were studied with G09 software. See Figure 4.
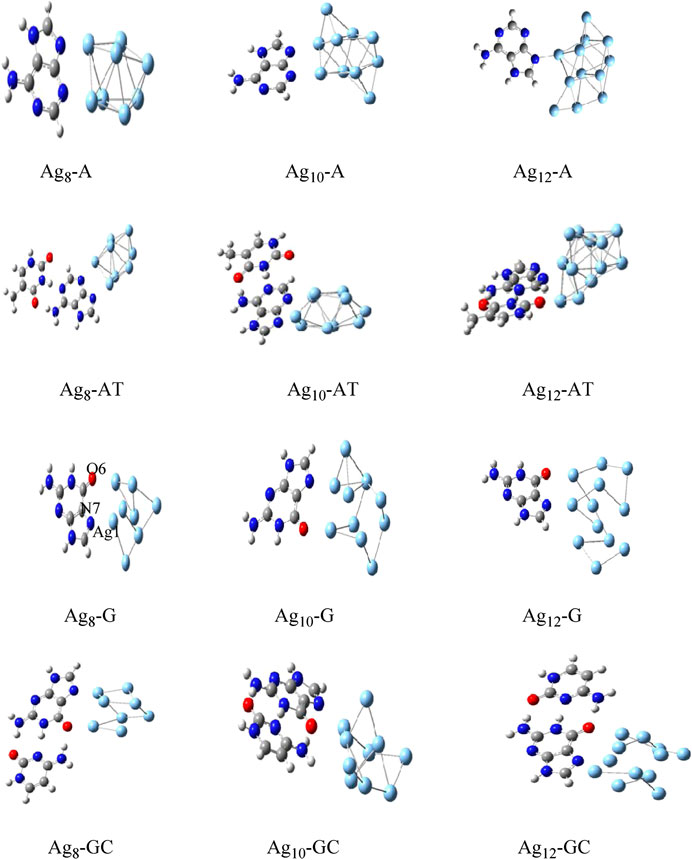
FIGURE 3. Optimized structures of Agn-A,T/WC complexes for n = 8, 10 and 12 by DFT method (Srivastava, 2018a).
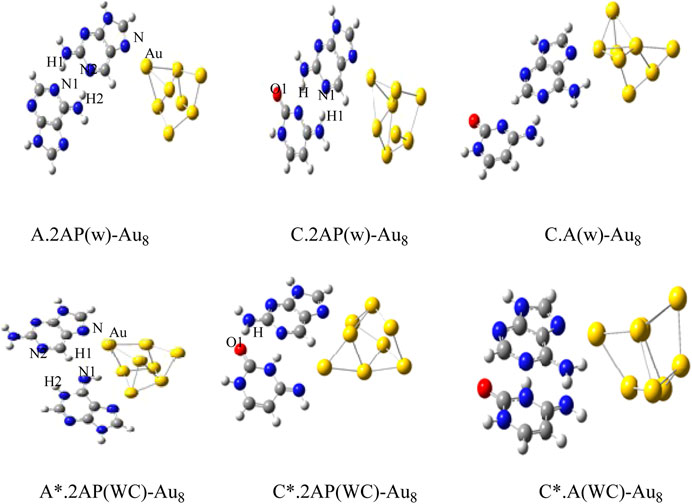
FIGURE 4. Optimized structures of Au8-wobble/WC mispair Complexes by DFT method. (Srivastava, 2018a).
In bimetallic clusters, four different types of chemical ordering are possible as core-shell, subcluster segregated (Janus nanoparticles), mixed and multiple shells. See Figure 1. The design of nanoalloys can be changed by fine tuning the mixing pattern. The chemical arrangement of these clusters are influenced by many factors as relative strengths of homo and heteronuclear bonds, atomic sizes, electronic/magnetic effects and many others (Ferrando et al., 2008; Oderji and Ding, 2011).
The highly efficient unbiased optimization methods used for nanoalloys are the genetic algorithm (GA) (Daven et al., 1996; Xiang et al., 2004; Curley et al., 2007), basin hopping (BH) method and its variants (Wales and Doye, 1997; Wales et al., 1998; Leary and Doye, 1999b), self-consistent basin-to-deformed-basin mapping, heuristic algorithm (Leary and Doye, 1999b) with surface and interior operators (HA-SIO) (Takeuchi, 2006), fast annealing evolutionary algorithm (FAEA) (Cai and Shao, 2002), evolutionary algorithm (EA) (Hartke, 2000), random tunneling algorithm (RTA) (Shao et al., 2004a), dynamic lattice searching (DLS) methods (Pillardy et al., 1999; Shao et al., 2004b), modified adaptive immune optimization algorithm (AIOA) (Shao et al., 2004c) and Knowledge Led Master Code (KLMC) (Woodley, 2013) due to larger number of homotops. In a previous study Spin polarized density-functional theory (SP-DFT) (Pant and Rajagopal, 1972) with B3 (Becke, 1993) exchange functional and PW91 (Perdew and Wang, 1992) correlation functional was used to investigate small AgxPt10-x (1 ≤ x ≤ 10) nanoalloys and global reactivity descriptors were used to determine the activity of these bimetallic clusters (Erlinda del et al., 2009). The LANL2DZ pseudo-potential with corresponding double- ζ basis set was used for Ag and Pt atoms (Hay and Wadt, 1985). Nanoalloys as iron and silver are of immense interest as they have distinct properties compared to the pure elemental clusters and corresponding bulk alloys due to finite size effects. These nanoalloys may show both magic sizes and magic compositions (Baletto and Ferrando, 2005). Paz Borbón et al. (Paz Borbón et al., 2008) used combined empirical potential (EP)/density functional (DF) method to study the structural properties and segregation effects for 38 atom binary clusters (combination of Pt-Ag, Ag-Au, Pd-Au and Ag-Pt) metals. Results favored mixed five-fold-symmetric/close-packed or decahedral arrangements for Pt-Pd, Ag-Pt and Ag-Au pairs. We have also used the combined EP-DF approach for structural optimization of nineteen bimetallic Au38-xPtx and Au38-xAgx clusters. The basin-hopping procedures with accept/reject strategies (10,000 Steps) were used and the studied structures were compared to the reference Au38 (theoretical and experimental) structure. Further the geometrical, thermal and other properties were studied for these binary structures (Srivastava, 2018b). See Figure 5.
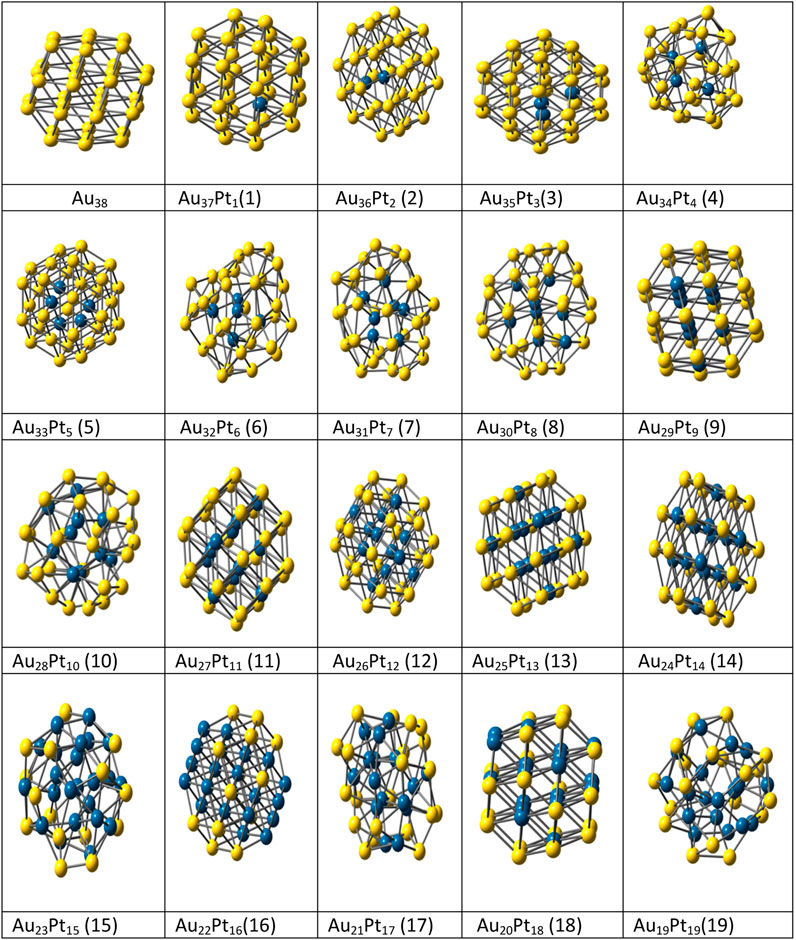
FIGURE 5. Optimized structures of Au38-xPt x bimetallic (x = 1–19) clusters. (Srivastava, 2018b).
A general tight-binding (TB) total energy scheme has been used to calculate the structural properties of the smaller bimetallic coinage metal compounds: Cu3Au, CuAu, CuAu2, CuAu3, and Cu6Au8 clusters (Metadjer et al., 2001). The structural and electronic properties of bimetallic gold-silver clusters (Bonacic et al., 2002) and AunXm+ (X = Cu, Al, Y, In) (Bouwen et al., 1999) were studied by the TB energy scheme. Heinebrodt el al. (Heinebrodt el al., 1999) used DFT method for AunXm (X = Cu, Al, Y, In, Cs) clusters and found the electronic shell effects separately in the clusters. Yuan et al. investigated the geometric and electronic structures of AunM (n = 1–7, M = Ni, Pd, Pt) by employing the first-principles method (Yuan et al., 2005). The structures and electronic properties of CunOn (n = 1–8) clusters (Bae et al., 2011) were also carried out by DFT.
The structural stability and electronic properties of PdnSiq (n = 1–7 and q = 0, 1, −1) clusters were studied by DFT within GGA (Begum et al., 2014) framework. The chemical ordering in magic-size Ag–Pd clusters were carried out for global optimization searches with DFT based atomistic potential developed within the second-moment approximation to the tight-binding model (Cyrot-Lackmann and Ducastelle, 1971) using the BH algorithm (Wales and Doye, 1997; Rossi and Ferrando, 2009). BH algorithm consists of Metropolis Monte Carlo simulations in which local minimization are performed after each move. In this study exchange moves were only allowed to search the best homotops for the most favourable chemical ordering patterns. Thermodynamic parameters of surface configurations for the corresponding bulk alloys were studied by Strohl and King et al. (Strohl and King, 1989). In another study different chemical ordering patterns were analyzed for Ag–Pd nanoparticles up to 60 atoms (Bochicchio et al., 2014).
The embedded-atom method was used to study the structural stability of CumAgn nanoalloys with BH algorithm for all (m,n) with N = m + n from 2 to 60 atoms. Most of the structures were icosahedra, polyicosahedra, truncated octahedral and 5-fold pancakes (Molayem et al., 2010). The studies were compared to the NimAgn (Molayem et al., 2011) clusters using the similar approaches. Electronic shell closure effects have been observed for magic size N = 40 for Cu-Ag nanoalloys (Barcaro et al., 2006).
The second moment approximation to the tight binding (SMATB) method with Gupta potential and genetic algorithms (GA) were employed for the global optimization (Rossi et al., 2004; Barcaro et al., 2006; Nu_nez and Johnston, 2010) for CuAg clusters using three different algorithms; basin-hopping (BH) method, the energy-landscape paving method, and the parallel excitable walkers method. The predicted most stable clusters have core shell polyicosahedra structures (Rossi et al., 2004; Nu_nez and Johnston, 2010). Another study has been carried out for Au19X doped (X = Li, Na, K, Rb, Cs, Ag and Cu) clusters by ab initio scalar relativistic DFT method using ADF package based on zero-order regular approximation (ZORA) (vanLenthe et al., 1993; vanLenthe et al., 1994). Perdew-Wang 1991 (PW91) (Perdew, 1991) exchange-correlation (XC) functional within GGA with triple-STO basis set added with two polarization functions at the frozen core approximation level were used for the studies (Ghanty et al., 2010).
KLMC method (Woodley, 2013; Farrow et al., 2014) was used to study the nanocluster structures of binary heteropolar compounds; ZnO, MgO, KF, and CdSe, (Farrow et al., 2014) using interatomic potentials (IP) (within GULP (Gale, 1997; Gale and Rohl, 2003) and density functional theory (DFT) (within FHI-aims (Blum et al., 2009) respectively. The study showed that improved Lamarckian evolutionary algorithm within KLMC proves to be a useful tool for structural prediction for nanoclusters (Woodley, 2013). These algorithms were used for (BaO)n nanoclusters (Escher et al., 2017) and it showed great resemblance for (KF)n clusters, while (MgO)n nanoclusters have barrel shape LM for n = 6. Interestingly (BaO)n for n = (4, 6, 8, 10, 16) were considered to be the magic number clusters (Lazauskas et al., 2017). The similar code has been used to study the ionic semiconductor (ZnO)1–32 and CdSe (Farrow et al., 2014) to explore the energy landscape using interatomic potentials.
Trimetallic (or ternary) coinage metal clusters have shown potential applications in optics, electronics, magnetic, and catalytic field (Stucky et al., 1989; Teo et al., 1993; Hungria et al., 2006; Fang et al., 2011). These clusters are highly catalytic and selective, yet the studies are very complex (Toshima and Yonezawa, 1998). Various global optimization techniques are used for the structural analysis for these clusters. (See Introduction section paragraph 3).
The interactions of Cu-Ag-Au trimetallic clusters were described by the second-moment approximation of the tight-binding (TB) potentials (N-body Gupta potential) with AIOA method. AIOA is an adaptive heuristic GA based algorithm which is used in the biological applications also. Another modified algorithm, MAIOA is used for the structural optimization of bimetallic (Wu et al., 2009; Wu et al., 2017) and ternary clusters. The immune clone selection and a mutation operation were the basic steps of MAIOA algorithms (Wu et al., 2011). AIOA method was also approved for A(l)B(m)C(n) (l + m + n = 9–55) clusters and A(l)B(m)C(n) (l = 13, m + n = 42) clusters (Wu et al., 2011). Further an improved adaptive immune optimization algorithm (AIOA-IC method) was found to be suitable for Cu8AunPt30-n (n = 1–29), Cu8AunPt47-n (n = 1–46), and partial 75, 79, 100, and 147 atom clusters (Wu et al., 2017). The structures, properties and interatomic interactions of trimetallic M–Pd–Pt (M = Ag and Au) upto 75 atoms were optimized using AIOA with the tight-binding Gupta potential (Wu et al., 2015). The Stacking fault (sf) and twin defects in Pd, Au–Pd, and Au–Pd–Pt clusters were studied with Gupta potential using DFT and fitted averaged parameters (Wu and Dong, 2014b). It was seen that the Gupta and Murrell Mottram potentials (Lloyd and Johnston, 2000) were found to be a good choice for the 19 atom trimetallic Double-icosahedra (DI) clusters (Farges et al., 1985). In another studies, random selection of bimetallic atom pairs were made with their exchanged location (Calvo and Yurtsever, 2004) based on the fact that the atoms with lower number of nearest neighbor contacts have higher potential energies in energy based mutations. Mutation and updating operation were performed for MAIOA runs till the achievement of maximal iteration number (LOOP), as the larger LOOP is needed for the structural optimization of unknown clusters. Limited memory quasi-Newton algorithm (L-BFGS) (Liu and Nocedal, 1989b) was used for local minimization (LM) for the clusters.
Au@Pd@Pt NPs were studied by DFT total-energy with VASP software (Zhou and Lee, 2007). The projector augmented wave method (PAW) and the Perdew–Burke–Ernzerhof generalized gradient approximation (GGA-PBE) was used for the exchange–correlation functional with an energy cut-off of 400 eV. A dipole correction (Neugebauer and Scheffler, 1992; Makov and Payne, 1995) was employed to use the induced dipole moment. Interestingly the theoretical results match well with the experimental values. In one of the Agpdpt alloys study, both empirical investigation and the theoretical analysis has given strong evidence that these nanoparticles are composed by an AgPd alloy core with Pt atoms lied on the surface (Wang and Yamauchi, 2011).
The structural optimization of (Aum-Agn-Pdo-Ptp) (m = 10 and n + o + p = 10) tetrametallic coinage metal clusters (Srivastava, 2017b) were carried out using combined EP-DF method. Completely random starting configuration was taken subjected to the lowest DF energy minimizations within GMIN code. In this work, the thermal and chemical stability of thirty eight tetrametallic clusters were measured by various parameters. Mixing/segregation effect results indicated that the surface sites are occupied by Au and Ag atoms while inner and middle shell are occupied by Pt and Pd atoms. See Figure 2.
The stability, electronic and mechanical properties of fullerenes has been used broadly in nanotechnological and biomedical applications. The discovery of buckyball C60 (Kroto et al., 1985) has launched a new era and stimulated the search for other related allotropes of carbon as nanotubes, nanopeapods, nanocones, etc. Detailed information about the structure, synthesis, and properties of carbon fullerenes are published in books and reviews (Dresselhaus et al., 1996; Hirsch, 1999, 2002; Hirsch and Brettreich, 2005). In 1970s, the first articles about C20 and C60 cages and their boron derivatives using quantum-mechanical method was published by Bochvar et al. (Bochvar and Galpern, 1973; Bochvar and Galpern, 1974). There are other well-known fullerene-like and fullerenic allotropes, chalcogenides, halides and oxides (Bar-Sadan et al., 2007; Tenne and Seifert, 2009). Small cage-like clusters Sin (n < 60) doped by endohedral metal atoms (Kumar, 2003) showed stable cage structures. The elemental fullerenes based on boron particles form pure boron and mixed borocarbide structures (Albert, 2009). In 1912 Stock reported his pioneering work on boranes (Stock and Massanez, 1912), which led to the identification of neutral boron hydrides (B2H6, B4H10, B5H9, B5H11, and B6H10). Further, Lipscomb and co-workers (Eberhardt et al., 1954) introduced the concept of three-center two-electron (3c-2e) bonding B2H6 diborane. The existence of regular octahedra of boron atoms in several metal hexaborides with general formula MB6 was demonstrated experimentally by Allard et al. (Allard, 1932; Pauling et al., 1934). Longuet-Higgins and Roberts show that the [B6]2− unit has a highly stable closed-shell electronic arrangement (Longuet-Higgins and Roberts, 1954) and B12 icosahedron is a dominant structure of various allotropes of boron (Longuet-Higgins and Roberts, 1955). The existence of other deltahedral boranes, B11H112−, B9H92−, B8H82−, B7H72−, and B6H62− were demonstrated in experimental studies (Klanberg and Muetterties, 1966; Klanberg et al., 1967; Boone, 1964). In another study to search global minima for the BnHn+2 (n = 2–5) series, it was found that classical structures composed of 2c-2e B—H and B—B bonds become progressively less stable. The reason for this might be that the boron atoms are trying to avoid sp2 hybridization and trigonal structure at the boron atoms, which is highly unfavourable as in that case one 2p-AO is empty (Osorio et al., 2012). These studies play a very important role to emulate structures analogous to the C allotropes (i.e., C60), such as in systems containing N-B replacing an isoelectronic C-C fragment. A lot more about boron cluster studies is covered in an extensive review by Alexandrova et al. (Alexandrova et al., 2006). The most stable allotropes of boron exists as B12 (boron polyhedral) while sandwich-like hexagonal-structured “metal” atoms between boron atomic structure is seen in layered borides MgB2, AlB2, and TiB2 (Chernozatonskii, 2001; Ivanovskaya et al., 2004). The most stable crystalline form of binary boron nitride is the hexagonal one, which is held by weak van der Waals interaction. Semi-empirical Hückel Austin Model (AM1) and ab initio Hartree–Fock (HF) methods have predicted possible configurations for BN nanoalloys. Similar approach with coupled-cluster theory (CCSD) method showed stable cage structures for (BN)n (n = 8–11) clusters. DFT tight-binding method (DFTB) was performed to study the structural stability of (BN)n fullerenes with n = 4–30 (Fowler et al., 1996) and (BN)n fullerenes with n = 13–35 (Rogers et al., 2000). Octahedron-like fullerenes structures were found for B12N12, B16N16, and B28N28 (Seifert et al., 1997). Ab initio calculations have been performed for energetically stable small cages B13N13, B14N14, B16N16 clusters (Strout, 2004) and BnNm fullerenes for 20 < (n + m) < 288 (Alexandre et al., 2001; Batista et al., 2006). Semi-empirical PM5 and discrete-variational calculations were carried out for B12N12, B28N28, B36N36 (Oku et al., 2004a; Oku et al., 2004b; Oku et al., 2004c) and B24N24 (Oku et al., 2003) clusters, while semi-empirical AM1 and discrete-variational (DV) calculations were used to study the stability of single atom doped B36N36 fullerene clusters (Nishiwaki et al., 2004). First principle calculations were carried out for boron-carbon nanocages (B12C48, B12C50) and it was found that these structural motifs showed aggregated boron atoms at one location in the form of a patch. These studies have violated all the other previous suggested empirical rules for constructing low-energy fullerenes. Also the energetic stabilities of these two clusters predicted that the structures derived from the C60 (buckminsterfullerene) are not necessarily magic sizes for heterofullerene structures (Mohr et al., 2014).
Ab initio projector-augmented wave (PAW) spin-polarized calculations were performed on La@B36N36 endofullerene, tetrahedral Fe4, Co4, and Ni4 clusters encapsulated into B36N36 fullerene (Nigam and Majumder, 2007), while spin polarized DFT–GGA pseudo-potential calculations were performed for B36N36 fullerene doped by (Fe, Co, and W) and FeO molecule (Batista et al., 2007). The stability of BN tubular structures were studied by DFT calculations, while the sphericity of BN cap models (squares, and pentagon–pentagon and pentagon–heptagon pairs) (Fowler et al., 1999) and octahedral fullerenes B12N12 inside (14,0), (8,8), and (12,4) BN nanotubes (Enyashin and Ivanovskii, 2008) were studied by DFTB method. Different lattice parameters of B12N12 and B24N24 (Pokropivny and Bekenev, 2006, 2007) have been studied by semi-empirical MNDO and ab initio FLAPW methods (Pokropivny et al., 2000) and the results indicated that B12N12 fullerites were the most stable diamond-like lattice structure.
In a latest study entirely unusual derivatives of boron clusters doped with lithium, LiBn0/− (n = 10–20) clusters were studied through Crystal structure AnaLYsis by Particle Swarm Optimization (CALYPSO) structural search approach alongwith the DFT calculations. Three (half-sandwich-type, quasi-planar and drum-type) structures were found for the studied clusters (Shi et al., 2020). The lowest-energy minima of the pure B22 cluster and the capacity of its isomers to form endohedrally doped cages with two transition metal atoms M (M = Sc and Ti) were carried out with genetic search algorithm using DFT calculations (Celaya et al., 2020). Recent reviews on boron clusters (Yan et al., 2020; Axtell et al., 2018; Zhu and Hosmane, 2018; Núñez et al., 2016a; Núñez et al., 2016b) are recommended for the interested readers.
DFTB method was used to investigate the properties of sulfide fullerene-like particles and sulfide MoS2 nanotubes, while DFTB calculations with a derived continuum approach (Bar-Sadan et al., 2006.; Enyashin et al., 2007) was used to investigate WS2, MoS2, and MoSe2 polyhedral nanoclusters (Margulis et al., 1996; Parilla et al., 2004). The semi-empirical Extended Hückel Theory (EHT) level was used to study (MoS2)n upto (n = 64), (MoS2)n upto (n = 576), imperfect MoS2 fullerenes and nanoseashells (Enyashin et al., 2009). Halide fullerenes was studied by ab initio spin-polarized DV method without geometry optimization for (NiCl2)48, (FeCl2)48, and (CdCl2)48 clusters (Enyashin and Ivanovskii, 2005a; Enyashin et al., 2005b), while (TiO2)n nanooctahedra with n upto 108 (Enyashin and Seifert, 2007) were studied by DFTB method. Recently KLMC is used to investigate the metallic Ni13 and covalently bonded C60 (buckminsterfullerene) potential energy surfaces (Lazauskas et al., 2017).
P, As, Sb, and Bi, are the few elements among all the variety of periodic table which can appear as hexagonal atomic layers assembled using covalently bounded sp3 hybridized atoms. The possibility of stable non-carbon fullerenes as phosphorus fullerene-like cage structures was studied on the basis of Density Functional Tight Binding calculations (Seifert et al., 2001). DFT calculations showed that P20 (dodecahedron) is the most stable structure and Pn hollow cages corresponds to the metastable structures. It was observed that with increasing nuclearity these metastable structures become less stable with respect to separate molecular P4 units.
Dipolar interactions form chains with a low coordination number, while spherical particle clusters with isotropic attraction form close-packed structures. The dipolar clusters favor strongly distinguished nearest-neighbour interactions. The combination of both isotropic and dipolar interactions form intricate knot, link and coil structures. The global minima of these interconverted self-organize structures are bound by the Stockmayer potential (Lennard-Jones plus point dipole). The Stockmayer model with dipolar fluids has been summarized in a good review (Teixeira et al., 2000). For these particles, the energy landscape for low-lying minima was obtained by the basin-hopping global optimization. The isotropic Lennard-Jones part of the potential is used to drive the compact structures toward highly-coordinated arrangements for the frustrated Stockmayer clusters, while chain-like motifs are favored by dipolar interactions. The studies of these idealized model systems are useful as it give insight for the knot systems as biomolecules and synthetic organic molecules.
The global optimization calculations for the Stockmayer particle have been carried out for the energetically favorable structures (knots, links, and coils) with a permanent dipole plus anisotropic soft core and alluring tail by Miller et al. (Miller and Wales, 2005). These particles have anisotropic point dipole with five degrees of freedom and cylindrical symmetry. Further, the PES is characterized by scaling out local minima which corresponds to the locally stable structures, connected via first-order saddle points (transition states). The clusters of spherical particles are bound by Lennard-Jones and Morse type of simple isotropic potentials, while the anisotropic Stockmayer potential differs from these potentials as the particles' have the tendency to form chains (Farrell et al., 2013).
Studies were carried out for the energetically stabilized kagome structures, which are the simple model of triblock Janus particles based on the discoidal building blocks. Basin-hopping global optimization was used for these particles. The three nearest neighbors were detected by an algorithm based on the interparticle distances. Further it was seen that the energetic stabilization is enhanced with the occurrence of sedimentation. The interaction of each ellipsoid of two building blocks occured via the Paramonov–Yaliraki (PY) potential (Paramonov and Yaliraki, 2005). The Paramonov-Yaliraki (PY) potential is used to study the collection of both homomolecular and heteromolecular pyrene, coronene, and circumcoronene below 1000 K within a stochastic Monte Carlo framework (Hernandez-Rojas and Calvo, 2019). This elliptic potential is also applicable for mixtures of any (size, orientation) ellipsoids and/or spheres, hard and soft particles.
Short-ranged pairwise Morse potential is more appropriate method to study the structural optimization of colloidal clusters with planar morphologies. The PES, global minima, rearrangement paths with discrete path sampling and free energy landscapes are visualized by the disconnectivity graphs. Here the number of nearest neighbor contacts control the short range potential. It was found that the free energy global minimum differs from the potential energy GM in quasi-degeneracy state due to the symmetry effects, which results in higher entropic lower symmetry structures. BH steps were taken as random Cartesian displacements (Wales, 2004) and the possible nominee for the transition states are selected between the minima’s by the doubly-nudged (Trygubenko and Wales, 2004; Carr et al., 2005) elastic band (Henkelman et al., 2000a; Henkelman and Jónsson, 2000b; Henkelman and Jónsson, 2001) method.
The understanding of the structure and thermodynamics of water is very important as water is used in the wide range of applications from biomolecular solvation to the atmospheric chemistry. The angle axis framework with TIP4P potential was used for the water clusters containing eight molecules. In these clusters the energy landscape was mapped with the basin-hopping global optimization and a modified limited-memory Broyden-Fletcher-Goldfarb Shanno (L-BFGS) algorithm to find the global minima and a database for the low energy minima. The combined doubly-nudged elastic band and a hybrid eigenvector-following method (Henkelman and Jónsson, 2000b; Kumeda et al., 2001.) was used to obtain minimum-transition state-minimum triplets. The intermolecular and intramolecular forces were studied over the larger amplitudes to get a connectivity PES graph by exploring the local minima. Recently artificial bee colony (ABC) algorithm with “ABCluster” was used to find the successful location of global minima for TIP4P water clusters (H2O)N (N ≤ 20). The similar methodology was further applied to various clusters of different chemical nature: 10 microhydration clusters, 4 methanol microsolvation clusters, 4 nonpolar clusters and 2 ion–aromatic clusters (Zhang and Dolg, 2016).
These clusters were optimized using BHMC simulations with a rigid-body EP and a move set, which included the cycle inversions to inquire the hydrogen bond topologies with the sulfate ion, belonging to the Hofmeister series. As the system has large size so the bond parameters (length, angle) of the sulfate clusters were held rigid. The water molecules were described by four-site rigid-body TIP4P water potential (Jorgensen et al., 1983a; Jorgensen et al., 1983b; Jorgensen et al., 1983c; Kazachenko and Thakkar, 2010) to describe the water phase diagram with certain modifications. The TS connecting the minima on the PES were located by doubly nudged elastic band method. Translational (linear interpolation) and rotational coordinates (spherical interpolation) were used for the endpoints interpolation and the artificial frustration was removed by connecting the minima to the global minimum (Małolepsza et al., 2010) with the visualization of disconnectivity graphs (Becker and Karplus, 1997; Morgan and Wales, 2014; Smeeton et al., 2014).
The rise of machine learning (ML) has explored the use of these algorithms in atomistic modeling and inference techniques and led it toward the data-driven approaches in the recent years. The machine learning landscape can easily analyze the most fitted functions that exhibit multiple solutions as local minima. Supervised as well as the unsupervised learning methods in combination to the fundamental mathematical concepts are mostly used for the machine learning techniques (Ceriott, 2019). These studies are mainly focused toward clusters, biomaterials, crystals and self-organized structures (Ballard et al., 2017). ML can use the algorithms more effectively to get a new and useful insight about the corresponding predictions, so that the directions for new interdisciplinary research will be explored. Though certain limitations regarding the use of machine-learning techniques in atomistic modeling are still needed to be rectified for materials, chemical, and biomolecular clusters, we hope that machine learning techniques and computational chemical physics will collaborate in highly efficient manner to show great productivity for different models in near future.
The author confirms being the sole contributor of this work and has approved it for publication.
RS acknowledges the financial assistance by DST WOSA project (SR/WOS-A/CS-69/2018). This work is funded by DST WOSA project (SR/WOS-A/CS-69/2018). The author is thankful to Dr Shrish Tiwari, Bioinformatics, CSIR-Centre for Cellular and Molecular Biology and Dr G. Narahari Sastry, Director, CSIR-NEIST for the technical support.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Addicoat, M. A., and Metha, G. F. (2009). Kick: constraining a stochastic search procedure with molecular fragments. J. Comput. Chem. 30, 57–64. doi:10.1002/jcc.21026 |
Åkeby, H., Panas, I., Pettersson, L. G., Seigbahn, M. P., and Wahlgren, U. (1990). Electronic and geometric structure of the copper (Cun) cluster anions (n ≤ 10). J. Chem. Phys. 94, 5471–5477. doi:10.1021/j100377a010
Akutsu, Y., Tahara, S.-Y., Tamura, M., and Yoshida, T. (1991). Calculations of heats of formation for nitro compounds by semi-empirical mo methods and molecular mechanics. J. Energetic Mat. 1991 (9), 161–171. doi:10.1080/07370659108019862
Albert, B. (2009). Boron: elementary challenge for experimenters and theoreticians. Angew. Chem. Int. Ed. 48 (46), 8640–8668. doi:10.1002/anie.200903246 |
Alexandre, S. S., Chacham, H., and Nunes, R. W. (2001). Structure and energetics of boron nitride fullerenes: the role of stoichiometry. Phys. Rev. B 63, 045402. doi:10.1103/PhysRevB.63.045402
Alexandrova, A. N., and Boldyrev, A. I. (2005). Search for the Lin0/+1/-1 (n = 5−7) lowest-energy structures using the ab initio gradient embedded genetic algorithm (GEGA). Elucidation of the chemical bonding in the lithium clusters. J. Chem. Theor. Comput. 1, 566–580. doi:10.1021/ct050093g
Alexandrova, A. N., Boldyrev, A. I., Zhai, H.-J., and Wang, L.-S. (2006). All-boron aromatic clusters as potential new inorganic ligands and building blocks in chemistry. Coord. Chem. Rev. 250, 2811–2866. doi:10.1016/j.ccr.2006.03.032
Allard, A. (1932). X-ray study of some borides, bull. Soc. Chim. Fr. 51, 1213–1215. doi:10.1361/105497199770335974
Aprà, E., Bylaska, E. J., de Jong, W. A., Govind, N., Kowalski, K., Straatsma, T. P., et al. (2020). NWChem: past, present, and future. J. Chem. Phys. 152, 184102. doi:10.1063/5.0004997 |
Asenjo, D., Stevenson, J. D., Wales, D. J., and Frenkel, D. (2013). Visualizing basins of attraction for different minimization algorithms, J. Phys. Chem. B 117, 12717–12723. doi:10.1021/jp312457a |
Axtell, J. C., Saleh, L. M. A., Qian, E. A., Wixtrom, A. I., and Spokoyny, A. M. (2018). Synthesis and applications of perfunctionalized boron clusters. Inorg. Chem. 57, 2333–2350. doi:10.1021/acs.inorgchem.7b02912 |
Bae, G.-T., Dellinger, B., and Hall, R. W. (2011). Density functional calculation of the structure and electronic properties of CunOn(n= 1−8) clusters. J. Phys. Chem. A. 115 (11), 2087–2095. doi:10.1021/jp104177q |
Baerends, E. J., Autscbach, J., and Berces, A. (2003). Amsterdam density functional. Amsterdam, Netherlands: VirjeUniversiteit.
Bailey, M. S., Wilson, N. T., Roberts, C., and Johnston, R. L. (2003). Structures, stabilities and ordering in Ni-Al nanoalloy clusters. Eur. Phys. J. D 25, 41–55. doi:10.1140/epjd/e2003-00218-2
Baletto, F., and Ferrando, R. (2005). Structural properties of nanoclusters: energetic, thermodynamic, and kinetic effects. Rev. Mod. Phys. 77, 371–423. doi:10.1103/RevModPhys.77.371
Ballard, A. J., Das, R., Martiniani, S., MehtaD., , Sagun, L., Stevenson, J. D., et al. (2017). Energy landscapes for machine learning. Phys. Chem. Chem. Phys. 19, 12585–12603. doi:10.1039/c7cp01108c |
Bar-Sadan, M., Enyashin, A. N., Gemming, S., Popovitz- Biro, R., Hong, S. Y., Prior, Y., et al. (2006). Structure and stability of molybdenum sulfide fullerenes†. J. Phys. Chem. B 110, 25399–25410. doi:10.1021/jp0644560 |
Bar-Sadan, M., Kaplan-Ashiri, I., and Tenne, R. (2007). Inorganic fullerenes and nanotubes: wealth of materials and morphologies. Eur. Phys. J. Spec. Top. 149, 71–101. doi:10.1140/epjst/e2007-00245-1
Barcaro, G., Fortunelli, A., Rossi, G., Nita, F., and Ferrando, R. (2006). Electronic and structural shell closure in AgCu and AuCu nanoclusters. J. Phys. Chem. B 110, 23197. doi:10.1021/jp064593x |
Bartolomei, M., Pirani, F., and Marques, J. M. C. (2015). Low-energy structures of benzene clusters with a novel accurate potential surface. J. Comput. Chem. 36 (31), 2291–2301. doi:10.1002/jcc.24201 |
Batista, R. J. C., Mazzoni, M. S. C., and Chacham, H. (2007). Boron nitride fullerene B36N36 doped with transition metal atoms: first-principles calculations. Phys. Rev. B 75, 035417. doi:10.1103/PhysRevB.75.035417
Batista, R. J. C., Mazzoni, M. S. C., and Chacham, H. (2006). A theoretical study of the stability trends of boron nitride fullerenes. Chem. Phys. Lett. 421, 246–250. doi:10.1016/j.cplett.2005.12.097
Becke, A. D. (1993). A new mixing of Hartree-Fock and local density‐functional theories. J. Chem. Phys. 98 (1372), 1372. doi:10.1063/1.464304
Becker, O. M., and Karplus, M. (1997). The topology of multidimensional potential energy surfaces: theory and application to peptide structure and kinetics. J. Chem. Phys. 106, 1495. doi:10.1063/1.473299
Begum, P., Bhattacharjee, D., Mishra, B. K., and Deka, R. C. (2014). Density functional study on structures, stabilities, and electronic properties of size-selected PdnSiq (n 5 1–7 and q 5 0, +1, 21) clusters. TheorChemAcc 133, 1418. doi:10.1007/s00214-013-1418-9
Bera, P. P., Schleyer, P. v. R., and Schaefer, H. F. (2007). Periodane: a wealth of structural possibilities revealed by the kick procedure. Int. J. Quan. Chem. 107, 2220–2223. doi:10.1002/qua.21322
Blum, V., Gehrke, R., Hanke, F., Havu, P., Havu, V., Ren, X., et al. (2009). Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 2009 (180), 2175–2196. doi:10.1016/j.cpc.2009.06.022
Bochicchio, D., Ferrando, R., Novakovic, R., Panizona, E., and Rossia, G. (2014). Chemical ordering in magic-size Ag-Pd nanoparticles. Phys. Chem. Chem. Phys. 16, 26478–26484. doi:10.1039/C4CP02143F |
Bochvar, D. A., and Galpern, E. G. (1974). Calculation of hypothetical systems: carbododecahedron (C20) and various diboracarbododecahedrons (B2C18) by the expanded Huckel method. Russ. Chem. Bull. 23, 2282–2284. doi:10.1007/BF00921307
Bochvar, D. A., and Galpern, E. G. (1973). Hypothetical systems carbododecahedron, s-icosahedrone and carbo-s-icosahedron. Proc. Acad. Sci. USSR 209, 610–612.
Bonacic, K. V., Burda, J., Mitric, R., Ge, M., Zampella, G., and Fantucci, P. (2002). Density functional study of structural and electronic properties of bimetallic silver–gold clusters: comparison with pure gold and silver clusters, J. Chem. Phys 117, 3120–3131. doi:10.1063/1.1492800
Boone, J. L. (1964). Isolation of the hexahydroclovohexaborate(2−) anion, B6H62−. J. Am. Chem. Soc. 86, 5036. doi:10.1021/ja01076a082
Bouwen, W., Vanhoutte, F., Despa, F., Bouckaert, S., Neukermans, S., Kuhn, L. T., et al. (1999). Stability effects of AunXm+ (X=Cu, Al, Y, In) clusters. Chem. Phys. Lett. 314, 227–233. doi:10.1016/S0009-2614(99)01150-1
Brack, M. (1993). The physics of simple metal clusters: self-consistent jellium model and semiclassical approaches. Rev. Mod. Phys. 65, 677–732. doi:10.1103/RevModPhys.65.677
Cabaleiro-Lago, E. M., Hermida-Ramón, J. M., and Pena-Gallego, A. (2000). Intermolecular interactions and cooperative effects in acetonitrile clusters. An ab initio molecular orbital study. J. Mol. Struct. Theochem 498 (1-3), 21–28. doi:10.1016/S0166-1280(99)00207-9
Cai, W., and Shao, X. (2002). A fast annealing evolutionary algorithm for global optimization. J. Comput. Chem. 23, 427–435. doi:10.1002/jcc.10029 |
Call, S. T., Zubarev, D. Y., and Boldyrev, A. I. (2007). Global minimum structure searches via particle swarm optimization. J. Comput. Chem. 28, 1177–1186. doi:10.1002/jcc.20621 |
Calvo, F., and Yurtsever, E. (2004). Composition-induced structural transitions in mixed rare-gas clusters. Phys. Rev. B 70, 045423. doi:10.1103/PhysRevB.70.045423
Carr, J. M., Trygubenko, S. A., and Wales, D. J. (2005). Finding pathways between distant local minima. J. Chem. Phys. 122, 234903. doi:10.1063/1.1931587 |
Celaya, C. A., Buendía, F., Miralrio, A., Paz-Borbón, L. O., Beltran, M., Nguyen, M. T., et al. (2020). Structures, stabilities and aromatic properties of endohedrally transition metal doped boron clusters M@B22, M = Sc and Ti: a theoretical study. Phys. Chem. Chem. Phys. 22, 8077–8087. doi:10.1039/D0CP00307G |
Ceriott, M. (2019). Unsupervised machine learning in atomistic simulations, between predictions and understanding. J. Chem. Phys. 150, 150901. doi:10.1063/1.5091842 |
Chen, M., Kumar, D., Yi, C.-W., and Goodman, D. W. (2005). The promotional effect of gold in catalysis by palladium-gold. Science 310, 291–293. doi:10.1126/science.1115800 |
Cheng, L., Cai, W., and Shao, X. (2004). A connectivity table for cluster similarity checking in the evolutionary optimization method. Chem. Phys. Lett. 389, 309–314. doi:10.1016/j.cplett.2004.03.125
Chernozatonskii, L. A. (2001). Diboride bifullerenes and binanotubes. JETP Lett. 74, 335–339. doi:10.1134/1.1421411
Cook, D. B. (2005). Handbook of computational quantum Chemistry (dover books on Chemistry). Mineola, NY: Dover Publications.
Curley, B. C., Johnston, R. L., YoungP.Li, N., Di Vece, Z., Palmer, Y. M. R. E., et al. (2007). Combining theory and experiment to characterize the atomic structures of surface-deposited Au309 clusters. J. Phys. Chem. C 2007 (111), 17846–17851. doi:10.1021/jp0713099
Cyrot-Lackmann, F., and Ducastelle, F. (1971). Self-consistent theory of clusters in disordered alloys. Phys. Rev. Lett. 27, 429–431. doi:10.1103/PhysRevLett.27.429
Daven, D. M., Tit, N., Morris, J. R., and Ho, K. M. (1996). Structural optimization of Lennard-Jones clusters by a genetic algorithm. Chem. Phys. Lett. 256, 195–200. doi:10.1016/0009-2614(96)00406-X
De Heer, W. A. (1993). The physics of simple metal clusters: experimental aspects and simple models. Rev. Mod. Phys. 65, 611–676. doi:10.1103/RevModPhys.65.611
Deaven, D. M., and Ho, K. M. (1995). Molecular geometry optimization with a genetic algorithm. Phys. Rev. Lett. 75, 288–291. doi:10.1103/PhysRevLett.75.288 |
Dieterich, J. M., and Hartke, B. (2017). OGOLEM: framework for GA-based global optimization. Available at: https://www.ogolem.org/ (Accessed March 13, 2020).
Doye, J. P. K., Miller, M. A., and Wales, D. J. (1999). The double-funnel energy landscape of the 38-atom Lennard-Jones cluster. J. Chem. Phys. 110, 6896–6906. doi:10.1063/1.480217
Doye, J. P. K., Wales, D. J., and Berry, R. S., (1995). The effect of the range of the potential on the structures of clusters. J. Chem. Phys. 103, 4234–4249. doi:10.1063/1.470729
Doye, J. P. K., and Wales, D. J. (1995). Magic numbers and growth sequences of small face-centered-cubic and decahedral clusters. Chem. Phys. Lett. 247, 339–347. doi:10.1016/S0009-2614(95)01223-0
Dresselhaus, M. S., Dresselhaus, G., and Eklund, P. C. (1996). Science of fullerenes and carbon nanotubes. San Diego, CA: Academic Press, 965.
D’Agostino, G. (1993). Copper clusters simulated by a many-body tight-binding potential. Philos. Mag. B 68, 903–911. doi:10.1080/13642819308217948
Eberhardt, W. H., Crawford, B., and Lipscomb, W. N. (1954). The valence structure of the boron hydrides. J. Chem. Phys. 22, 989–1001. doi:10.1063/1.1740320
Enyashin, A. N., and Ivanovskii, A. L. R. (2005a). Calculating the atomic and electronic structure and magnetic properties of inorganic fullerenes. Russian J. Phys. Chem. 79, 940–945.
Enyashin, A. N., Bar-Sadan, M., Sloan, J., Houben, L., and Seifert, G. (2009). Nanoseashells and nanooctahedra of MoS2: routes to inorganic fullerenes. Chem. Mater. 21, 5627–5636. doi:10.1021/am404843b
Enyashin, A. N., Gemming, S., Bar-SadanPopovitz-Biro, M., Hong, R., Y.Prior, S., Tenne, Y., et al. (2007). Struktur und Stabilität von Molybdänsulfid-Fullerenen. Angew. Chem. 119 (119), 631–635. doi:10.1002/ange.200602136
Enyashin, A. N., and Ivanovskii, A. L. (2008). Atomic and electronic structures and thermal stability of boron-nitrogen nanopeapods: B12N12 fullerenes in BN nanotubes. Phys. Solid State 50, 390–396. doi:10.1134/S1063783408020285
Enyashin, A. N., Medvedeva, N. I., Medvedeva, Y. E., and Ivanovskii, A. L. (2005b). Electronic structure and magnetic states of crystalline and fullerene-like forms of nickel dichloride NiCl[sub 2]. Phys. Solid State 47, 527–530. doi:10.1134/1.1884717
Enyashin, A. N., and Seifert, G. (2007). Titanium oxide fullerenes: electronic structure and basic trends in their stability. Phys. Chem. Chem. Phys. 9, 5772–5775. doi:10.1039/B712094J |
Erlinda del, V. O., María, B., Lópeza, B., and Castroc, E. A. (2009). Spin polarized density functional theory applied to the study of nanoalloys. Mecánica Computacional XXVIII, 2435–2443.
Escher, S. G. E. T., Lazauskas, T., Zwijnenburg, M. A., and Woodley, S. M. (2017). Structure prediction of (BaO) n nanoclusters forn⩽24using an evolutionary algorithm. Comput. Theor. Chem. 1107, 74–81. doi:10.1016/j.comptc.2017.01.010
Fa, W., Luo, C., and Dong, J. (2005). Bulk fragment and tube like structures of AuN (N=2−26). Phys. Rev. B 72, 205428. doi:10.1103/PhysRevB.72.205428
Fang, P. P., Duan, S., Lin, X. D., Anema, J. R., Li, J. F., et al. (2011). Tailoring Au-core Pd-shell Pt-cluster nanoparticles for enhanced electrocatalytic activity. Chem. Sci. 2, 531–539. doi:10.1039/C0SC00489H
Farges, J., Feraudy De, M. F., Raoult, B., and Torchet, G. (1985). Cluster models made of double icosahedron units. Surf. Sci. 156, 370–378. doi:10.1016/0039-6028(85)90596-5
Farrell, J. D., Lines, C., Shepherd, J. J., Chakrabarti, D., Miller, M. A., and Wales, D. J. (2013). Energy landscapes, structural topologies and rearrangement mechanisms in clusters of dipolar particles. Soft Matter 9 (22), 5407–5416. doi:10.1039/C3SM50711D
Farrow, M. R., Chow, Y., and Woodley, S. M. (2014). Structure prediction of nanoclusters; a direct or a pre-screened search on the DFT energy landscape? Phys. Chem. Chem. Phys. 16, 21119–21134. doi:10.1039/C4CP01825G |
Ferrando, R., Jellinek, J., and Johnston, R. L. (2008). Nanoalloys: from theory to applications of alloy clusters and nanoparticles. Chem. Rev. 108 (108), 845–910. doi:10.1021/cr040090g |
Foresman, J. B., and Frisch, A. (1996). Exploring chemistry with electronic structure methods. Wallingford, CT: Gaussian Inc.
Fowler, P. W., Heine, T., Mitchell, D., Schmidt, R., and Seifert, G. (1996). Boron-nitrogen analogues of the fullerenes: the isolated-square rule. J. Chem. Soc. Faraday Trans. 92 (92), 2197–2201. doi:10.1039/FT9969202197
Fowler, P. W., Rogers, K. M., Seifert, G., Terrones, M., and Terrones, H. (1999). Pentagonal rings and nitrogen excess in fullerene-based BN cages and nanotube caps. Chem. Phys. Lett. 299, 359–367. doi:10.1016/S0009-2614(98)01265-2
Furche, F., Ahlrichs, R., Weis, P. J., Gilb, C., Bierweiler, S. T., and Kappes, M. (2002). The structures of small gold cluster anions as determined by a combination of ion mobility measurements and density functional calculations. J. Chem. Phys. 117, 6982–6990. doi:10.1063/1.1507582
Gale, J. D. J. (1997). GULP: a computer program for the symmetry-adapted simulation of solids. Faraday Trans. 93, 629–637. doi:10.1039/A606455H
Gale, J. D., and Rohl, A. L. (2003). The general utility lattice program (GULP). Mol. Simul. 29, 291–341. doi:10.1080/0892702031000104887
Ghanty, T. K., Banerjee, A., and Chakrabarti, A. (2010). Structures and the electronic properties of Au19X clusters (X = Li, Na, K, Rb, Cs, Cu, and Ag). J. Phys. Chem. C 114, 20–27. doi:10.1021/jp906400t
Giannozzi, P., Baseggio, O., Bonfà, P., Brunato, D., Car, R., Carnimeo, I., et al. (2020). Quantum ESPRESSO toward the exascale. Chem. Phys. 152, 154105. doi:10.1063/5.0005082 |
Guimaraes, F. F., Belchior, J. C., Johnston, R. L., and Roberts, C. (2002). Global optimization analysis of water clusters (H2O)n (11⩽n⩽13) through a genetic evolutionary approach. J. Chem. Phys. 116, 8327–8333. doi:10.1063/1.1471240
Gupta, R. P. (1981). Lattice relaxation at a metal surface. Phys. Rev. B 23, 6265–6270. doi:10.1103/PhysRevB.23.6265
Häkkinen, H., Moseler, M., and Landman, U. (2002). Bonding in Cu, Ag, and Au clusters: relativistic effects, trends, and surprises. Phys. Rev. Lett. 89, 033401. doi:10.1103/PhysRevLett.89.033401 |
Halperin, W. P. (1986). Quantum size effects in metal particles. Rev. Mod. Phys. 58, 533–606. doi:10.1103/RevModPhys.58.533
Hartke, B. (2000). Global geometry optimization of molecular clusters: TIP4P water. Z. Phys. Chem. 214, 1251–1264. doi:10.1002/(SICI)1096-987X10.1524/zpch.2000.214.9.1251
Hartke, B. (1993). Global geometry optimization of clusters using genetic algorithms J. Phys. Chem. 97, 9973–9976. doi:10.1021/j100141a013
Hay, P. J., and Wadt, W. R. (1985). Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 82, 270. doi:10.1063/1.448799
Heath, J. R. (1995). Monolayer/bilayer transition in Langmuir films of derivatized gold nanoparticles at the gas/water interface: an x-ray scattering study. Science 270, 1315. doi:10.1063/1.1640334
Heinebrodt, M., Malinowski, N., Tast, F., Branz, W., Billas, I. M. L., and Martin, T. P. (1999). Bonding character of bimetallic clusters AunXm (X=Al, In, Cs). J. Chem. Phys. 110, 9915–9921. doi:10.1063/1.478865
Henkelman, G., and Jónsson, H. (2000b). Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 113, 9978–9985. doi:10.1063/1.1323224
Henkelman, G., and Jónsson, H. (2001). Long time scale kinetic Monte Carlo simulations without lattice approximation and predefined event table. J. Chem. Phys. 115, 9657–9666. doi:10.1063/1.1415500
Henkelman, G., Uberuaga, B. P., and Jónsson, H. (2000a). A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904. doi:10.1063/1.1329672
Hernandez-Rojas, J., and Calvo, F. (2019). Coarse-grained modeling of the nucleation of polycyclic aromatic hydrocarbons into soot precursors. Phys. Chem. Chem. Phys. 21 (9), 5123–5132. doi:10.1039/C8CP07724J |
Hirsch, H., and Brettreich, M. (2005). Fullerenes: Chemistry and reactions. Weinheim, Germany: Wiley-VCH, 440.
Hungria, A. B., Raja, R., Adams, R. D., Captain, B., Thomas, J. M., Midgley, P. A., et al. (2006). Single-step conversion of dimethyl terephthalate into cyclohexanedimethanol with Ru5PtSn, a trimetallic nanoparticle catalyst. Angew. Chem. 118, 4900–4903. doi:10.1002/anie.200702407
Ismail, R. (2012). Theoretical studies of free and supported nanoalloy clusters. PhD thesis. Birmingham (England): The University of Birmingham.
Ivanovskaya, V. V., Enyashin, A. N., and Ivanovskii, A. L. (2004). Structure, electronic spectrum, and chemical bonding of fullerene-like nanoparticles based on MB2(M = Mg, Al, Sc, Ti) layered diborides. Inorg. Mater. Struct. 40, 134–143. doi:10.1023/B:INMA.0000016087.31732.b0
Jäger, M., Schafer, R., and Johnston, R. L. (2019). GIGA: a versatile genetic algorithm for free and supported clusters and nanoparticles in the presence of ligands. Nanoscale 11, 9042–9052. doi:10.1039/C9NR02031D |
Jain, P. K. (2005). A DFT-based study of the low-energy electronic structures and properties of small gold clusters. Struct. Chem. 16, 421–426. doi:10.1007/s11224-005-6350-8
Jellinek, J. (1999). Theory of atomic and molecular clusters: with a glimpse at experiments. Berlin, Germany: Springer.
Johnston, R. L. (2003). Evolving better nanoparticles: genetic algorithms for optimising cluster geometries. Dalton Trans. 22, 4193–4207. doi:10.1039/B305686D
Jorgensen, W. L., Chandrasekhar, J., and Klein, M. L. (1983c). Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79, 926–935. doi:10.1063/1.445869
Jorgensen, W. L., Chandrasekhar, J., Madura, J. D., Impey, R. W., and Klein, M. L. (1983a). Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79, 926–935. doi:10.1063/1.445869
Jorgensen, W. L., Chandrasekhar, J., Madura, J. D., Impey, R. W., and Klein, M. L. (1983b). Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79, 926–935. doi:10.1063/1.445869
Kabir, M., Mookerjee, A., Datta, R., Banerjea, A., and Bhattacharya, A. K. (2003). Study of small metallic nanoparticles an ab-initio full-potential muffin-tin orbitals based molecular dynamics study of small Cu clusters. Int. J. Mod. Phys. B 17, 2061–2075. doi:10.1142/S0217979203018181
Karaboga, D. (2005). An idea based on honey bee swarm for numerical optimization: technical report TR06. Kayseri, Turkey: Erciyes University.
Kazachenko, S., and Thakkar, A. J. (2010). Are there any magic numbers for water nanodroplets, (H2O)n, in the range 36 ≤n≤ 50? Mol. Phys. 108, 2187–2193. doi:10.1063/1.445869
Klanberg, F., Eaton, D. R., Guggenberger, L. J., and Muetterties, E. L. (1967). Chemistry of boranes. XXVIII. New polyhedral borane anions, B8H82-, B8H8-, and B7H72-. Inorg. Chem. 6, 1271–1281. doi:10.1016/S0040-4020(01)90682-9
Klanberg, F., and Muetterties, E. L. (1966). Chemistry of boranes. XXVII. new polyhedral borane anions, B9H92-and B11H112-. Inorg. Chem. 5, 1955–1960. doi:10.1021/ic50045a027
Knudsen, J., Nilekar, A. U., Vang, R. T., Schnadt, J., Kunkes, E. L., and Dumesic, J. A. (2007). A Cu/PtNear-Surface alloy for Water−Gas shift catalysis. J. Am. Chem. Soc. 129, 6485–6490. doi:10.1021/ja0700855 |
Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 54 (16), 11169–11186. doi:10.1103/physrevb.54.11169
Kroto, H. W., Heath, J. R., OBrien, S. C., Curl, R. F., and Smalley, R. E. (1985). C60: buckminsterfullerene. Nature 318, 162–163. doi:10.1038/318162a0
Kumar, V. (2003). Novel metal-encapsulated caged clusters of silicon and germanium. Eur. Phys. J. D-At. Mol. Opt. Phys. 24, 227–232. doi:10.1140/epjd/e2003-00194-5
Kumeda, Y., Munro, L. J., and Wales, D. J. (2001). Transition states and rearrangement mechanisms from hybrid eigenvector-following and density functional theory. Chem. Phys. Lett. 341, 185–194. doi:10.1016/S0009-2614(01)00334-7
Lathiotakis, N. N., Andriotis, A. N., Menon, M., and Connolly, J. (1996). Tight binding molecular dynamics study of Ni clusters. J. Chem. Phys. 104, 992–1003. doi:10.1063/1.470823
Lazauskas, T., Sokol, A. A., and Woodley, S. M. (2017). An efficient genetic algorithm for structure prediction at the nanoscale. Nanoscale 9, 3850–3864. doi:10.1039/C6NR09072A |
Leary, R. H., and Doye, J. P. K. (1999a). Tetrahedral global minimum for the 98-atom Lennard-Jones cluster. Phys. Rev. E 60, R6320–R6322. doi:10.1063/1.480465
Leary, R. H., and Doye, J. P. K. (1999b). Tetrahedral global minimum for the 98-atom Lennard-Jones cluster. Phys. Rev. E 60, R6320–R6322. doi:10.1103/PhysRevE.60.R6320
Lesley, D. L., and Johnston, R. L. (2000). Theoretical analysis of 17–19-atom metal clusters using many-body potentials. J. Chem. Soc. Dalton Trans., 307–316. doi:10.1039/A908003A
Li, J., Li, X., Zhai, H., and Wang, L. (2003). Au20: a tetrahedral cluster. Science 299, 864–867. doi:10.1126/science.1079879 |
Li, T., Yin, S., Ji, Y., Wang, G., and Zhao, J. (2000). A genetic algorithm study on the most stable disordered and ordered configurations of Au38-55. Phys. Lett. A 267, 403–407. doi:10.1016/S0375-9601(00)00120-1
Li, Z., and Scheraga, H. A. (1987). Monte Carlo-minimization approach to the multiple-minima problem in protein folding. Proc. Natl. Acad. Sci. U.S.A. 84, 6611–6615. doi:10.1073/pnas.84.19.6611 |
Liu, D. C., and Nocedal, J. (1989b). On the limited memory BFGS method for large scale optimization. Math. Programming 45, 503–528. doi:10.1007/BF01589116
Liu, H. B., Pal, U., Medina, A., Maldonado, C., and Ascencio, J. A. (2005). Structural incoherency and structure reversal in bimetallicAu−Pdnanoclusters. Phys. Rev. B 71, 075403–2. doi:10.1103/PhysRevB.71.075403
Llanio-Trujillo, J. L., Marques, J. M. C., and Pereira, F. B. (2011). An evolutionary algorithm for the global optimization of molecular clusters: application to water, benzene, and benzene cation. J. Phys. Chem. A. 115, 2130–2138. doi:10.1021/jp1117695 |
Lloyd, L. D., Johnston, R. L., Roberts, C., and Mortimer-Jones, T. V. (2002). Geometry Optimisation of Aluminium Clusters Using a Genetic Algorithm. ChemPhysChem 3, 408–415. doi:10.1002/1439-7641(20020517)3 |
Lloyd, L. D., and Johnston, R. L. (2000). Theoretical analysis of 17-19-atom metal clusters using many-body potentials †. J. Chem. Soc. Dalton Trans. 2000, 307–316. doi:10.1039/A908003A
Longuet-Higgins, H. C., and Roberts, M. D. (1955). The electronic structure of an icosahedron of boron atoms. Proc. R. Soc. 230A, 110–119. doi:10.1098/rspa.1955.0115
Longuet-Higgins, H. C., and Roberts, M. D. (1954). The electronic structure of the borides MB 6. Proc. R. Soc. 224A, 336–347. doi:10.1098/rspa.1954.0162
Lordeiro, R. A., Guimaraes, F. F., Belchior, J. C., and Johnston, R. L. (2003). Determination of main structural compositions of nanoalloy clusters of CuxAuy (x + y ≤ 30) using a genetic algorithm approach. Int. J. Quan. Chem. 95, 112–125. doi:10.1002/qua.10660
Makov, G., and Payne, M. C. (1995). Periodic boundary conditions inab initiocalculations. Phys. Rev. B 51, 4014–4022. doi:10.1103/PhysRevB.51.4014
Maksimuk, S., Yang, S., Peng, Z., and Yang, H. (2007). Synthesis and Characterization of Ordered Intermetallic PtPb Nanorods. J. Am. Chem. Soc. 129, 8684–8685. doi:10.1021/ja071980r |
Margulis, L., Tenne, R., and Iijima, S. (1996). Nucleation of WS2Fullerenes at Room Temperature. Microsc. Microanal. Microstruct. 7, 87–89. doi:10.1051/mmm:1996107
Marques, J. M. C., Jesus, W. S., Prudente, F. V., and Pereira, F. B. (2018). Revealing Energy Landscapes of Atomic Clusters by Applying Adaptive Bioinspired Algorithms. Phys. Chem. Chemist. Chem. Enginee. 3, 28. doi:10.1201/b22413
Marques, J. M. C., and Pereira, F. B. (2010a). An evolutionary algorithm for global minimum search of binary atomic clusters. Chem. Phys. Lett. 485 (1–3), 211–221. doi:10.1016/j.cplett.2009.11.059
Marques, J. M. C., and Pereira, F. B. (2011). EA_MOL: evolutionary algorithm for the global minimum search of molecular clusters. Available at: https://apps.uc.pt/mypage/faculty/qtmarque/en/software/ (Accessed Feburary 20, 2020).
Marques, J. M. C., and Pereira, F. B. (2013). A detailed investigation on the global minimum structures of mixed rare-gas clusters: Geometry, energetics, and site occupancy. J. Comput. Chem. 34 (6), 505–517. doi:10.1002/jcc.23161 |
Marques, J. M. C., and Pereira, F. B. (2015). Colloidal clusters from a global optimization perspective. J. Mol. Liquids 210, 51–63. doi:10.1016/j.molliq.2015.03.009
Martínez-Núñez, E., Barnes, G. L., Glowacki, D. R., Kopec, S., Pelaez-Ruiz, D., Rodriguez, A., et al. (2020). AutoMeKin: automated mechanisms and kinetics. Available at: https://rxnkin.usc.es/index.php/AutoMeKin (Accessed January 14, 2020).
Martínez-Núñez, E. (2015a). An automated method to find transition states using chemical dynamics simulations. J. Comput. Chem. 36, 222–234. doi:10.1002/jcc.23790
Martínez-Núñez, E. (2015b). An automated transition state search using classical trajectories initialized at multiple minima. Phys. Chem. Chem. Phys. 17, 14912. doi:10.1039/C5CP02175H
Massobrio, C., PasquarelloDal Corso, A., and Dal Corso, A. (1998). Structural and electronic properties of small CunCun clusters using generalized-gradient approximations within density functional theory. J. Chem.Phys. 109, 6626–6630. doi:10.1063/1.477313
Małolepsza, E., Strodel, B., Khalili, M., Trygubenko, S., Fejer, S. N., and Wales, D. J. (2010). Symmetrization of the AMBER and CHARMM force fields. J. Comput. Chem. 31, 1402–1409. doi:10.1002/jcc.21425 |
Menon, M., Connolly, J., Lathiotakis, N., and Andriotis, A. (1994). Tight-binding molecular-dynamics study of transition-metal clusters. Phys. Rev. B 50, 8903–8906. doi:10.1103/PhysRevB.50.8903
Metadjer, N., Laref, A., and Khelifa, B. (2001). TightTight-binding calculation of structural properties of bulk Cu3Au and its corresponding clusters. Superlatti. Microstru. 30, 21–28. doi:10.1006/spmi.2001.0988
Michaelian, K., Rendon, N., and Garz_on, I. L. (1999). Structure and energetics of Ni, Ag, and Au nanoclusters. Phys. Rev. B 60, 2000–2010. doi:10.1103/PhysRevB.60.2000
Miller, M. A., and Wales, D. J. (2005). Novel structural motifs in clusters of dipolar spheres: knots, links, and coils. J. Phys. Chem. B 109, 23109. doi:10.1021/jp0549632 |
Mohr, S., Pochet, P., Amsler, M., Schaefer, B., Sadeghi, A., Genovese, L., et al. (2014). Boron aggregation in the ground states of boron-carbon fullerenes. Phys. Rev. B 89, 041404(R). doi:10.1103/PhysRevB.89.041404
Molayem, M., Grigoryan, V. G., and Springborg, M. (2010). Theoretical studies of structural and electronic properties of clusters. J. Phys. Chem. C 115, 7179–7192. doi:10.1021/jp1094678
Molayem, M., Grigoryan, V. G., and Springborg, M. (2011). Global Minimum Structures and Magic Clusters of CumAgn Nanoalloys. J. Phys. Chem. C 115, 22148–22162. doi:10.1021/jp2050417
Moore, J. M. (2013). molecular dynamics simulations of supported Pt nanoclusters with sutton-chen potentials. J. Phys. Chem 120, 14883–14891. doi:10.1021/acs.jpcc.6b03074
Morgan, J. W. R., and Wales, D. J. (2014). Energy landscapes of planar colloidal clusters. Nanoscale. 6, 10717–10726. doi:10.1039/C4NR02670E |
Neugebauer, J., and Scheffler, M. (1992). Adsorbate-substrate and adsorbate-adsorbate interactions of Na and K adlayers on Al(111). Phys. Rev. B 46, 16067. doi:10.1103/physrevb.46.16067
Nigam, S., and Majumder, C. (2007). Magnetic needles encapsulated inside (BN)36 cage: Prediction of atomic, electronic, and magnetic structure from first principle calculations. Appl. Phys. Lett. 91, 223112. doi:10.1063/1.2815922
Nishiwaki, A., Oku, T., and Suganuma, K. (2004). Atomic and electronic structures of endohedral B36N36 clusters with doping elements studied by molecular orbital calculations. Physica B: Condensed Matter 349, 254–259. doi:10.1016/j.physb.2004.03.308
Nu_nez, S., and Johnston, R. L. (2010). Structures and Chemical Ordering of Small Cu−Ag Clusters.J. Phys. Chem. C 114, 13255–13266. doi:10.1021/jp1048088
Núñez, R., Tarrés, M., Ferrer-Ugalde, A., de Biani, F. F., and Teixidor, F. (2016a). Electrochemistry and photoluminescence of icosahedral carboranes, boranes, metallacarboranes, and their derivatives. Chem. Rev. 116, 14307–14378. doi:10.1021/acs.chemrev.6b00198
Núñez, R., Romero, I., Teixidor, F., and Viñas, C. (2016b). Icosahedral boron clusters: A perfect tool for the enhancement of polymer features. Chem. Soc. Rev. 45, 5147–5173. doi:10.1039/C6CS00159A
Oakley, M. T., Johnston, R. L., and Wales, D. J. (2013). Symmetrisation schemes for global optimisation of atomic clusters. Phys. Chem. Chem. Phys. 15, 3965–3976. doi:10.1039/C3CP44332A |
Oderji, H. Y., and Ding, H. (2011). Determination of melting mechanism of Pd24Pt14 nanoalloy by multiple histogram method via molecular dynamics simulations. Chem. PhysicsChem. Phys. 388, 23–30. doi:10.1016/j.chemphys.2011.07.011
Ohno, K., and Maeda, S. (2019). Distribution of GRRM. Available at: https://iqce.jp/GRRM/index_e.shtml (Accessed October 5, 2020).
Ohno, K., and Maeda, S. (2006). global reaction route mapping on potential energy surfaces of formaldehyde, formic acid, and their metal-substituted analogues. J. Phys. Chem. A. 110, 8933–8941. doi:10.1021/jp061149l |
Oku, T., Nishiwaki, A., and Narita, I. (2004a). Formation and atomic structure of B12N12 nanocage clusters studied by mass spectrometry and cluster calculation. Sci. Tech. Adv. Mater. 5, 635–638. doi:10.1016/j.stam.2004.03.017
Oku, T., Nishiwaki, A., and Narita, I. (2004b). Formation and structure of B28N28 clusters studied by mass spectrometry and molecular orbital calculation. Solid State. Commun. 130, 171–173. doi:10.1016/j.ssc.2004.02.004
Oku, T., Nishiwaki, A., and Narita, I. (2004c). Formation and structures of B36N36 and Y@B36N36 clusters studied by high-resolution electron microscopy and mass spectrometry clusters studied by high-resolution electron microscopy and mass spectrometry. J. Phys. Chem. Sol. 65, 369–372. doi:10.1016/j.jpcs.2003.09.010
Oku, T., Nishiwaki, A., Narita, I., and Gonda, M. (2003). Formation and structure of. B24N24 clusters. Chem. Phys. Lett. 380, 620–623. doi:10.1016/j.stam.2004.03.017
Osorio, E., Olson, J. K., Tiznado, W., and Boldyrev, A. I. (2012). Analysis of why boron avoids sp2 hybridization and classical structures in the BnHn+2 Series. Chem. Eur. J. 18 (31), 9677–9681. doi:10.1002/chem.201200506 |
Oviedo, J., and Palmer, R. E. (2002). Amorphous structures of Cu, Ag, and Au nanoclusters from first principles calculations. J. Chem. Phys. 117, 9548–9551. doi:10.1063/1.1524154
Pant, M. M., and Rajagopal, A. K. (1972). Theory of inhomogeneous magnetic electron gas. Solid State. Commun. 10, 1157–1160. doi:10.1016/0038-1098(72)90934-9
Papavassiliou, G. C. (1979). Optical properties of small inorganic and organic metal particles. Prog. Solid State. Chem. 12, 185–271. doi:10.1016/0079-6786(79)90001-3
Paramonov, L., and Yaliraki, S. N. (2005). The directional contact distance of two ellipsoids: coarse-grained potentials for anisotropic interactions. J. Chem. Phys. 123, 194111–194122. doi:10.1063/1.2102897 |
Parilla, P. A., Dillon, A. C., Parkinson, B. A., Jones, K. M., Alleman, J., Riker, G., et al. (2004). Formation of nanooctahedra in molybdenum disulfide and molybdenum diselenide using pulsed laser vaporization. J. Phys. Chem. B 108, 6197–6207. doi:10.1021/jp036202 |
Pauling, L., and Weinbaum, S. (1934). The structure of calcium boride. Z. Kristallogr. 87, 181–183. doi:10.1007/BF00802582
Paz Borbón, L. O., Johnston, R. L., Barcaro, G., and Fortunelli, A. (2008). Structural motifs, mixing, and segregation effects in 38-atom binary clusters. J. Chem. Phys. 128, 134517. doi:10.1063/1.2897435 |
Perdew, J. P. (1991). ” in Electronic structure of solids ’91. Editors P. Ziesche, and H. Eschriq (Berlin, Germany: AkademieVerlag), 11–20.
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865 |
Perdew, J. P., and Wang, Y. (1992). Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 45, 13244–13249. doi:10.1103/PhysRevB.45.13244
Pillardy, J., Liwo, A., and Scheraga, H. A. (1999). An efficient deformation-based global optimization method (self-consistent basin-to-deformed-basin mapping (SCBDBM)). application to lennard-jones atomic clusters. J. Phys. Chem. A. 103, 9370–9377. doi:10.1021/jp992741w
Pokropivny, V. V., and Bekenev, V. L. (2006). Electronic properties and bulk moduli of new boron nitride polymorphs, i.e., hyperdiamond B12N12 and simple cubic B24N24, B12N12 fulborenites. Semiconductors 40, 636–641. doi:10.1134/S1063782606060042
Pokropivny, V. V., Skorokhod, V. S., Oleinik, G. S., Kurdyumov, A. V., Bartnitskaya, T. S., Pokropivny, A. V., et al. (2000). Boron nitride analogs of fullerenes (the Fulborenes), nanotubes, and fullerites (the fulborenites. J. Solid State. Chem. 154, 214–222. doi:10.1006/jssc.2000.8838
Pokropivny, V. V., Smolyar, A. S., and Pokropivny, A. V. (2007). Fluid synthesis and structure of a new boron nitride polymorph-hyperdiamond fulborenite B12N12 (E phase). Phys. Solid State 49, 591–598. doi:10.1134/S1063783407030365
Ralph, D. C., Black, C. T., and Tinkham, M. (1995). Spectroscopic measurements of discrete electronic states in single metal particles. Phys. Rev. Lett. 74, 3241–3244. doi:10.1103/PhysRevLett.74.3241 |
Roberts, C., and Johnston, R. L. (2001). Investigation of the structures of MgO clusters using a genetic algorithm. Phys. Chem. Chem. Phys. 2001 (3), 5024–5034. doi:10.1039/B106507F
Roberts, C., Johnston, R. L., and Wilson, N. T. (2000). A genetic algorithm for the structural optimization of Morse clusters. Theor. Chem. Acc. 104, 123–130. doi:10.1007/s002140000117
Rodríguez-Fernández, R., Pereira, F. P., Marques, J. M. C., Vázquez-Rodríguez, S., and Martinez-Nunez, E. (2020). GAFit, version 1.6. Available at: https://rxnkin.usc.es/index.php/GAFit (Accessed January 29, 2020).
Rodríguez-Fernández, R., Pereira, F. B., Marques, J. M. C., Martínez-Núñez, E., and Vázquez, S. A. (2017). GAFit: A general-purpose, user-friendly program for fitting potential energy surfaces. Comput. Phys. Commun. 217, 89. doi:10.1016/j.cpc.2017.02.008
Rogers, K. M., Fowler, P. W., and Seifert, G. (2000). Chemical versus steric frustration in boron nitride heterofullerene polyhedra. Chem. Phys. Lett. 332, 43–50. doi:10.13005/ojc/300247
Rossi, G., and Ferrando, R. (2009). Searching for low-energy structures of nanoparticles: a comparison of different methods and algorithms. J. Phys. Condens. Matter 21, 084208. doi:10.1088/0953-8984/21/8/084208 |
Rossi, G., Rapallo, A., Mottet, C., Fortunelli, A., Baletto, F., and Ferrando, R. (2004). Magic polyicosahedral core-shell clusters. Phys. Rev. Lett. 93, 105503–105507. doi:10.1103/PhysRevLett.93.105503 |
Saunders, M. (1987). stochastic exploration of molecular mechanics energy surfaces. hunting for the global minimum. J. Am. Chem. Soc. 109, 3150–3152. doi:10.1021/ja00244a051
Scott, R. W. J., Wilson, O. M., Oh, S.-K., Kenik, E. A., and Crooks, R. M. (2004). Bimetallic palladium−gold dendrimer-encapsulated Catalysts. J. Am. Chem. Soc. 126, 15583–15591. doi:10.1021/ja0475860 |
Seifert, G., Fowler, P. W., Mitchell, D., Porezag, D., and Frauenheim, T. (1997). Boron-nitrogen analogues of the fullerenes: electronic and structural properties. Chem. Phys. Lett. 268, 352–358. doi:10.1016/S0009-2614(97)00214-5
Seifert, G., Heine, T., and Fowler, P. W. (2001). Inorganic nanotubes and fullerenes - Structure and properties of hypothetical phosphorus fullerenes. Eur. Phys. J. D 16 (1–3), 341–343. doi:10.1007/s100530170125
Shang, C., and Liu, Z.-P. (2013). Stochastic Surface Walking Method for Structure Prediction and Pathway Searching. J. Chem. Theor. Comput. 9, 1838–1845. doi:10.1021/ct301010b
Shao, X., Jiang, H., and Cai, W. (2004a). Parallel Random Tunneling Algorithm for Structural Optimization of Lennard-Jones Clusters up toN= 330. J. Chem. Inf. Comput. Sci. 44 (1), 193–199. doi:10.1021/ci0340862
Shao, X., Cheng, L., and Cai, W. (2004b). A dynamic lattice searching method for fast optimization of Lennard-Jones clusters. J. Comput. Chem. 25, 1693–1698. doi:10.1002/jcc.20096 |
Shao, X., Cheng, L., and Cai, W. (2004c). An adaptive immune optimization algorithm for energy minimization problems. J. Chem. Phys. 120, 11401–11406. doi:10.1063/1.1753257 |
Shayeghi, A., Götz, D., Davis, J. B. A., Schäfer, R., and Johnston, R. L. (2015). Pool-BCGA: a parallelised generation-free genetic algorithm for the ab initio global optimisation of nanoalloy clusters. Phys. Chem. Chem. Phys. 17, 2104–2112. doi:10.1039/C4CP04323E |
Shi, H., Kuang, X., and Lu, C. (2020). LiB13: a new member of tetrahedral-typed B13 ligand half-surround cluster. Sci. Rep. 10, 1642–1651. doi:10.1038/s41598-020-57769-2 |
Smeeton, L. C., Oakley, M. T., and Johnston, R. L. (2014). Visualizing energy landscapes with metric disconnectivity graphs. J. Comput. Chem. 35, 1481–1490. doi:10.1002/jcc.23643 |
Solov’yov, I. A., Solov'yov, A. V., and Greiner, W. (2002). Structure and properties of small sodium clusters. Phys. Rev. B 65, 053203–053222. doi:10.1103/PhysRevA.65.053203
Srivastava, R. (2018b). Theoretical analysis of Au38-xPtx and Au38−xAgx (x=1−19) bimetallic clusters. AASCIT J. Mater. 4 (2), 33–42.
Srivastava, R. (2018a). Complexes of DNA bases and Watson-Crick base pairs interaction with neutral silver Agn (n = 8, 10, 12) clusters: a DFT and TDDFT study. J. Biomol. Struct. Dyn. 36 (4), 1050–1062. doi:10.1080/07391102.2017.1310059 |
Srivastava, R. (2017a). Interaction of cysteine with Aun (n =8, 10, 12) even neutral clusters: a theoretical study. ChemistrySelect 2, 2789–2796. doi:10.1002/slct.201700041
Srivastava, R. (2017b). Structural Optimization of (Aum-Agn-Pdo-Ptp) (m=10 and n+o+p=10) Tetrametallic Clusters Using a Combined Empirical Potential-Density Functional (EP-DF) Approach. ChemistrySelect 2, 8063–8071. doi:10.1002/slct.201701145
Srivastava, R. (2017c). Theoretical studies on the electronic and optoelectronic properties of [A.2AP(w)/A*.2AP(WC)/C.2AP(w)/C*.2AP(WC)/C.A(w)/C*.A(WC)]-Au8 mismatch nucleobase complexes. Mol. Phys. 116 (2), 263–272. doi:10.1080/00268976.2017.1382737
Stillinger, F. H., and Weber, T. A. (1988). Nonlinear optimization simplified by hypersurface deformation. J. Stat. Phys. 52, 1429–1445. doi:10.1007/bf01011658
Stock, A., and Massanez, C. (1912). Borwasserstoffe. Chem. Ber 45 (1912), 3539–3568. doi:10.1002/cber.191204503113
Strohl, J., and King, T. (1989). A multicomponent, multilayer model of surface segregation in alloy catalysts. J. Catal. 118, 53–67. doi:10.1016/0021-9517(89)90300-X
Strout, D. L. (2004). Fullerene-like cages versus alternant cages: isomer stability of B13N13, B14N14, and B16N16. Chem. Phys. Lett. 383, 95–98. doi:10.1016/j.cplett.2003.10.141
Stucky, G. D., Herron, N., Wang, Y., Eddy, M., Cox, D., Moller, K., et al. (1989). Structure and optical properties of cadmium sulfide superclusters in zeolite hosts. J. Am. Chem. Soc. 111, 530–540. doi:10.1021/ja00184a021
Takeuchi, H. (2006). Clever and efficient method for searching optimal geometries of Lennard-Jones clusters. J. Chem. Inf. Model. 46, 2066–2070. doi:10.1021/ci600206k |
Teixeira, P. I. C., Tavares, J. M., and Gama, M. M. T. d. (2000). The effect of dipolar forces on the structure and thermodynamics of classical fluids. J. Phys. Condens. Matter 12, R411–R434. doi:10.1088/0953-8984/12/33/201
Teng, X., and Yang, H. (2003). Synthesis of face-centered tetragonal FePt nanoparticles and granular films from Pt@Fe2O3 core−shell nanoparticless. J. Am. Chem. Soc. 125, 14559–14563. doi:10.1021/ja0376700 |
Tenne, R., and Seifert, G. (2009). Recent Progress in the Study of Inorganic Nanotubes and Fullerene-Like Structures. Annu. Rev. Mater. Res. 39, 387–413. doi:10.1146/annurev-matsci-082908-145429
Teo, B. K., Zhang, H., and Shi, X. (1993). Design, synthesis, and structure of the largest trimetallic cluster, [(Ph3P)10Au12Ag12PtCl7]Cl: the first example of a trimetallic biicosahedral supracluster and its implication for the vertex-sharing polyicosahedral growth of the gold/silver/platinum ternary cluster system. J. Am. Chem. Soc. 115, 8489–8490. doi:10.1021/ja00071a085
TeVelde, G., Bickelhaupt, F. M., Baerends, E. J., Fonseca Guerra, C., van Gisbergen, S. J. A., Snijders, J. G., et al. (2001). Chemistry with ADF. J. Comput. Chem. 22, 931–967. doi:10.1002/jcc.1056
Toshima, N., and Yonezawa, T. (1998). Bimetallic nanoparticles-novel materials for chemical and physical applications. New J. Chem. 22, 1179–1201. doi:10.1039/A805753B
Trygubenko, S. A., and Wales, D. J. (2004). A doubly nudged elastic band method for finding transition states. J. Chem. Phys. 120, 2082–2094. doi:10.1063/1.1636455 |
vanLenthe, E., Baerends, E. J., and Snijders, J. G. (1993). Relativistic regular two‐component Hamiltonians. J. Chem. Phys. 99, 4597–4610. doi:10.1063/1.466059
vanLenthe, E., Baerends, E. J., and Snijders, J. G. (1994). Relativistic total energy using regular approximations. Chem. Phys. 101, 9783–9792. doi:10.1063/1.467943
Wales, D. J. (2004). Some further applications of discrete path sampling to cluster isomerization. Mol. Phys. 102, 891–908. doi:10.1080/00268970410001703363
Wales, D. J. (2012). Decoding the energy landscape: extracting structure, dynamics and thermodynamics. Phil. Trans. R. Soc. A. 370, 2877–2899. doi:10.1021/acs.jctc.5b00962 |
Wales, D. J., and Doye, J. P. K. (1997). Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms. J. Phys. Chem. A. 101, 5111–5116. doi:10.1021/jp970984n
Wales, D. J. (2010). Energy landscapes of clusters bound by short-ranged potentials. Chem. Eur. J. Chem. Phys. 11, 2491–2494. doi:10.1002/cphc.201000233
Wales, D. J., Miller, M. A., and Walsh, T. R. (1998). Archetypal energy landscapes. Nature 394, 758–760. doi:10.1038/29487
Wales, D. J., and Scheraga, H. A. (1999). Global optimization of clusters, crystals, and biomolecules. Science 285, 1368–1372. doi:10.1126/science.285.5432.1368 |
Wang, J., Wang, G., and Zhao, J. (2003). Structures and electronic properties of Cu20, Ag20, and Au20 clusters with density functional method. Chem. Phys. Lett. 380, 716–720. doi:10.1016/j.cplett.2003.09.062
Wang, L., and Yamauchi, Y. (2011). Tailoring Au-core Pd-shell Pt-cluster nanoparticles for enhancedelectrocatalytic activity. Chem. Sci. 2, 531–539. doi:10.1039/C0SC00489H
Wilson, N. T., and Johnston, R. L. (2000). Modelling gold clusters with an empirical many-body potential. Eur. Phys. J. D 12, 161–169. doi:10.1007/s100530070053
Winter, B. J., Parks, E. K., and Riley, S. J. (1991). Copper clusters: The interplay between electronic and geometrical structure. J. Chem. Phys. 94, 8618–8621. doi:10.1063/1.460046
Woodley, S. M. (2013). knowledge led master code search for atomic and electronic structures of LaF3 nanoclusters on hybrid rigid ion–shell model–DFT landscapes. J. Phys. Chem. C 117, 24003–24014. doi:10.1021/jp406854j
Wu, G., Sun, Y., Wu, X., Chen, R., and Wang, Y. (2017). Large scale structural optimization of trimetallic Cu-Au-Pt clusters up to 147 atoms. Chem. Phys. Lett. 686, 103–110. doi:10.1016/j.cplett.2017.08.049
Wu, X., Wu, G., and Youcun, C. (2011). structural optimization of Cu-Ag-Au trimetallic clusters by adaptive immune optimization algorithmstructural optimization of CuAgAu trimetallic clusters by adaptive immune optimization algorithm. J. Phys. Chem. A. 115, 13316–13323. doi:10.1021/jp208514m |
Wu, X., Cai, W., and Shao, X. (2009). Optimization of bimetallic Cu-Au and Ag-Au clusters by using a modified adaptive immune optimization algorithm. J. Comput. Chem. 30, 1992–2000. doi:10.1063/1.4896152 |
Wu, X., and Dong, Y. (2014b). Theoretical studies of structures and energies of Pd, Au-Pd, and Au-Pd-Pt clusters. New J. Chem. 38, 4893–4900. doi:10.1039/C4NJ00984C
Wu, X., Liu, Q., Sun, Y., and Wu, G. (2015). Structural characterization of metal dopants (M = Ag or Au) in trimetallic M-Pd-Pt clusters. RSC Adv. 5, 51142–51148. doi:10.1039/C5RA06457K
Wu, X., and Wu, G. (2014a). An adaptive immune optimization algorithm with dynamic lattice searching operation for fast optimization of atomic clusters. Chem. Phys. 440, 94–98. doi:10.1016/j.chemphys.2014.06.002
Xiang, Y., Cheng, L., Cai, W., and Shao, X. (2004). structural distribution of lennard-jones clusters containing 562 to 1000 atoms. J. Phys. Chem. A. 108, 9516–9520. doi:10.1021/jp047807o |
Xiao, Y., and Williams, D. E. (1993). Genetic algorithm: a new approach to the prediction of the structure of molecular clusters. Chem. Phys. Lett. 215, 17–24. doi:10.1016/0009-2614(93)89256-H
Yan, J., Yang, W., Zhang, Q., and Yan, Y. (2020). Introducing borane clusters into polymeric frameworks: architecture, synthesis, and applications. Chem. Commun. 56, 11720–11734. doi:10.1039/D0CC04709K |
Yañez, O., Báez-Grez, R., Inostroza, D., Rabanal-León, W. A., Pino-Rios, R., Garza, J., et al. (2019). Automaton: a program that combines a probabilistic cellular automata and a genetic algorithm for global minimum search of clusters and molecules. J. Chem. Theor. Comput. 15, 1463–1475. doi:10.1021/acs.jctc.8b00772
Yañez, O., Inostroza, D., Usuga-Acevedo, B., Pino-Rios, R., Tabilo-Sepulveda, M., Garza, J., et al. (2020). Evaluation of restricted probabilistic cellular automata on the exploration of the potential energy surface of Be6B11−. Theor. Chem. Acc. 139, 41. doi:10.1007/s00214-020-2548-5
Ye, H., and Crooks, R. M. (2007). effect of elemental composition of PtPd bimetallic nanoparticles containing an average of 180 atoms on the kinetics of the electrochemical oxygen reduction reaction. J. Am. Chem. Soc. 129 (129), 3627–3633. doi:10.1021/ja068078o |
Ye, T., Xu, R., and Huang, W. (2011). global optimization of binary lennard-jones clusters using three perturbation operators. J. Chem. Inf. Model. 51 (3), 572–577. doi:10.1021/ci1004256 |
Yuan, D. W., Wang, Y., and Zeng, Z. (2005). Geometric, electronic, and bonding properties of AuNM (N=1–7, M=Ni, Pd, Pt) clusters. J. Chem. Phys. 122, 114310. doi:10.1063/1.1862239 |
Zeiri, Y. (1995). Prediction of the lowest energy structure of clusters using a genetic algorithm. Phys. Rev. E 51, R2769. doi:10.1103/PhysRevE.51.R2769
Zhai, H., Ha, M.-A., and Alexandrova, A. N. (2015). AFFCK: adaptive force-field-assistedab initiocoalescence kick method for global minimum search. J. Chem. Theor. Comput. 11, 2385–2393. doi:10.1021/acs.jctc.5b00065
Zhang, J., and Dolg, M. (2015). ABCluster: the artificial bee colony algorithm for cluster global optimization. Phys. Chem. Chem. Phys. 17, 24173–24181. doi:10.1039/c5cp04060d |
Zhang, J., and Dolg, M. (2016). Global optimization of clusters of rigid molecules using the artificial bee colony algorithm. Phys. Chem. Chem. Phys. 18, 3003–3010. doi:10.1039/c5cp06313b |
Zhang, J., Glezakou, V.-A., Rousseau, R., and Nguyen, M.-T. (2020). NWPEsSe: an adaptive-learning global optimization algorithm for nanosized cluster systems. J. Chem. Theor. Comput. 16 (6), 3947–3958. doi:10.1021/acs.jctc.9b01107
Zhou, W., and Lee, J. Y. (2007). Highly active core-shell Au@Pd catalyst for formic acid electrooxidation. Electrochemistry Commun. 9 (9), 1725–1729. doi:10.1016/j.elecom.2007.03.016
Keywords: global optimization, potential energy landscape, clusters, empirical potentials, homotops
Citation: Srivastava R (2021) Application of Optimization Algorithms in Clusters. Front. Chem. 9:637286. doi: 10.3389/fchem.2021.637286
Received: 03 December 2020; Accepted: 21 January 2021;
Published: 12 March 2021.
Edited by:
Suzana Velickovic, University of Belgrade, SerbiaCopyright © 2021 Srivastava. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ruby Srivastava, YW1pdHJ1YnkxQGdtYWlsLmNvbQ==
†ORCID: Ruby Srivastava orcid.org/0000-0002-2367-0176
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.