- College of Science, North China University of Science and Technology, Tangshan, China
Realizing rich topological elements in topological materials has attracted increasing attention in the fields of chemistry, physics, and materials science. Topological semimetals/metals are classified into three main types: nodal-point, nodal-line, and nodal-surface types with zero-, one-, and two-dimensional topological elements, respectively. This study reports that XPt (X = Sc, Y, La) intermetallic compounds are topological metals with opened and closed nodal lines, and triply degenerate nodal points (TNPs) when the spin–orbit coupling (SOC) is ignored. Based on the calculated phonon dispersions, one can find that ScPt and YPt are dynamically stable whereas LaPt is not. When SOC is added, the one-dimensional nodal line and zero-dimensional TNPs disappear. Interestingly, a new zero-dimensional topological element, that is, Dirac points with 4-fold degenerate isolated band crossings with linear band dispersion appear. The proposed materials can be considered a good platform to realize zero- and one-dimensional topological elements in a single compound and to study the relationship between zero- and one-dimensional topological elements.
Introduction
In the last decade, with the discovery of topological insulators (Cava et al., 2013; Kou et al., 2013; Zhao et al., 2013; Shen and Cha, 2014; Wang et al., 2014; Luo et al., 2015; Zhou et al., 2015; Liu et al., 2016; Chen et al., 2017a; Loïc and Izmaylov, 2017; Pan et al., 2017; Pielnhofer et al., 2017; Politano et al., 2017; Andrey et al., 2018; Hu et al., 2018, 2019; Gao et al., 2019; Mal et al., 2019; Qiao et al., 2019; Narimani et al., 2020), topologically non-trivial materials have attracted significant interest in the chemistry, physics, and materials science communities. Recently, studies have increasingly focused on topological semimetals/metals (Bin et al., 2018; Chenguang et al., 2018; Zhou et al., 2018; He et al., 2019, 2020; Jin et al., 2019a, 2020b; Li et al., 2019; Qie et al., 2019; Xie et al., 2019; Yi et al., 2019; Zhong et al., 2019; Ma and Sun, 2020; Meng et al., 2020b; Wang et al., 2020a,c,d; Yang and Zhang, 2020; Zhang et al., 2020; Zhao et al., 2020) with non-trivial band topology. For example, in 2018, Schoop et al. (2018) described the key features of the electronic structures of topological semimetals/metals and how these structures can be realized based on chemical principles.
Topological semimetals/metals can be roughly classified into three main parts: nodal-point (Chen et al., 2015; Yuan et al., 2017; Zhang et al., 2017a,c, 2018c; Jing and Heine, 2018; Ma et al., 2018; Tsipas et al., 2018; Khoury et al., 2019), nodal-line (Chang et al., 2016; Liu et al., 2018b; Guo et al., 2019; Sankar et al., 2019; Tang et al., 2019; Xu et al., 2019; Zhang et al., 2019; Jin et al., 2020a; Kirby et al., 2020; Zhou et al., 2020), and nodal-surface (Türker and Sergej, 2018; Wu et al., 2018; Zhang et al., 2018b,d; Fu et al., 2019; Yang et al., 2019b, 2020; Chen et al., 2020; Wang et al., 2020e; Xiao et al., 2020) semimetals/metals enjoying zero-, one-, and two-dimensional topological elements, respectively. The main examples of nodal-point semimetals/metals are Weyl and Dirac semimetals/metals with 2- and 4-fold degenerate band-crossing points with linear dispersion. In addition, 3-, 6-, and 8-fold (Cano and Vergniory, 2016; Lu et al., 2016; Weng et al., 2016b) band degenerates also exist. Among them, nodal-point semimetals/metals with 3-fold band degenerates [i.e., triply degenerate nodal point (TNP)] are of importance owing to their special properties. Many investigations have been conducted to predict and confirm new TNP semimetals/metals (Weng et al., 2016a; Xia and Li, 2017; Zhang et al., 2017b,d; Guo et al., 2018; Owerre, 2018; Jin et al., 2019b; Yang et al., 2019a). For example, in 2019, Jin et al. (2019b) reported that centrosymmetric Li2NaN is a topological material with critical-type TNPs. A critical-type TNP is an interesting topological metal phase that lies between type-I and type-II TNPs. In 2018, Guo et al. (2018) proposed that YRh6Ge4, LaRh6Ge4, and LuRh6Ge4 are TNP materials, and what is more, Zhu et al. (2020) performed transport measurements and confirmed TNP fermions in YRh6Ge4. In 2019, Yang et al. (2019a) experimentally demonstrated TNP as well as double Fermi arc surface states in a three-dimensional phononic crystal.
Nodal-line semimetals/metals with one-dimensional topological elements may show various forms according to the shape of the nodal lines, such as nodal link (Yan et al., 2017), nodal chain (Yan et al., 2018), nodal box (Sheng et al., 2017), nodal ring (Zhang et al., 2018a; Wang et al., 2020b), nodal knot (Bi et al., 2017; Lee et al., 2018), and nodal net (Feng et al., 2018). For example, in 2018, Zhou et al. (2018) proposed that two-dimensional B2C hosts opened and closed nodal-line states based on first-principles calculation. In 2020, Yi et al. (2019) predicted that NaAlGe and NaAlSi nodal-line materials would be good cathode materials for sodium ion batteries. In 2020, Wang et al. (2020d) proposed that a two-dimensional Nb3GeTe6 monolayer is a topological nodal-line material with a nearly flat nodal line around the Fermi level and that it led to a remarkable thermoelectric power factor platform. In 2018, Liu et al. (2018a) proposed that graphene monolith, a three-dimensional nodal-line semimetal, is a candidate lithium ion battery anode material. In 2019, Yan et al. (2019) proposed that the Cu2Si monolayer is a topological material with possible superconductivity and nodal-line fermions.
The electronic structure, dynamical stability, and topological signatures of ScPt, YPt, and LaPt, a cubic-type family of materials with space group are investigated in the present study. This study shows that opened and closed nodal lines and 3-fold degenerate nodal-point states can be realized in ScPt, LaPt, and LuPt when the spin-orbit coupling is ignored. Moreover, the effect of spin-orbit coupling on the topological signatures of these systems is also considered. A 3- to 4-fold degenerate nodal-point transition can be found in these systems when spin-orbit coupling is added.
Materials
The topological signatures of cubic-type ScPt, YPt, and LaPt are investigated. As an example, Figure 1A shows the structural model of cubic ScPt. This primitive ScPt cell contains one Sc atom and one Pt atom at the (0.5, 0.5, 0.5) and (0, 0, 0) sites, respectively. Using first-principles calculation, the structural models of ScPt, YPt, and LaPt are fully optimized; Table 1 lists the calculated results.
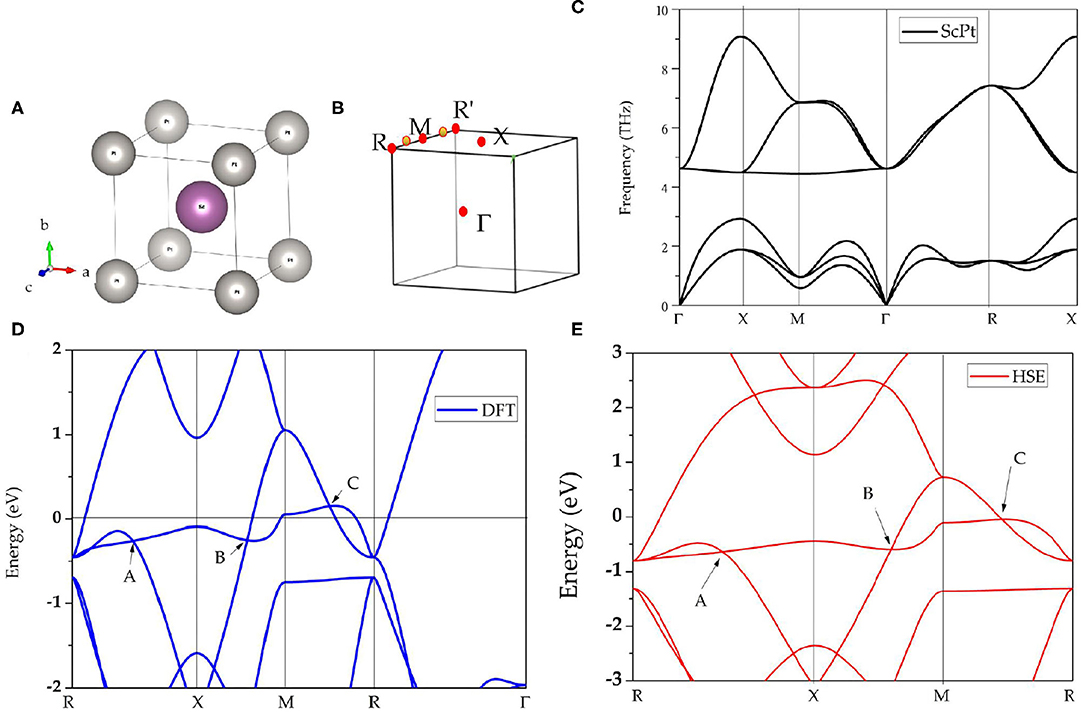
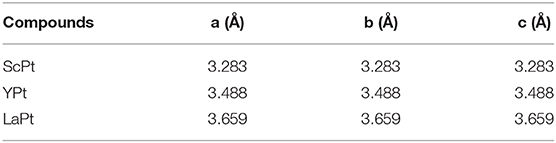
Figure 1. (A) Crystal structures of cubic ScPt; (B) Brillouin zone and the considered high-symmetry points Γ-X-M-Γ-R-X; (C) calculated phonon dispersion of cubic ScPt at its optimized lattice constant; (D) calculated band structure of cubic ScPt with PBE method, where (A–C) indicate the band-crossing points around the Fermi level; and (E) calculated band structure of ScPt with Heyd–Scuseria–Ernzerhof (HSE) screened hybrid functional.
The phonon dispersions of cubic-type ScPt, YPt, and LaPt are calculated using the force-constants method with Phonopy code (Togo and Tanaka, 2015). For these three compounds, 2 × 2 × 2 supercells are built to calculate the phonon dispersions. The considered high-symmetry points are Γ-X-M-Γ-R-X, as shown in Figure 1B. Figures 1C, 2A exhibit the calculated phonon dispersions of ScPt and YPt; one can find that ScPt and YPt are dynamically stable owing to the absence of the imaginary frequency (Han et al., 2019; Wu et al., 2019). However, the obtained phonon dispersion shown in Figure 2B indicates that LaPt is not dynamically stable.
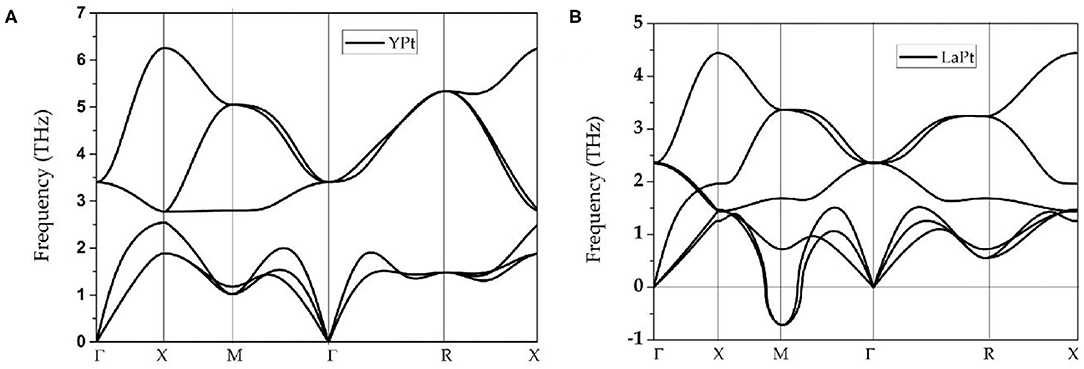
Figure 2. (A,B) Calculated phonon dispersion of cubic YPt and LaPt, respectively, at their optimized lattice constants. The phonon dispersions of both intermetallic compounds are obtained using the force-constants method with Phonopy code.
Computational Methods
In this study, first-principles calculations are used, and the generalized gradient approximation (GGA) (Perdew et al., 1996) of the Perdew–Burke–Ernzerhof (PBE) (Perdew et al., 1998) functional is adopted for the exchange-correlation potential. In the calculations, the cutoff energy is set as 600 eV, and the Brillouin zone is sampled using a Monkhorst-Pack k-mesh with a size of 9 × 9 × 9. To ensure good convergence, the calculations continue until the energy deviation is <10−6 eV/atom. The atomic positions and lattice constants of the structures were totally relaxed until all the force components were smaller than 10−3 eV/Å.
Results and Discussion
First, the physical natures of ScPt, YPt, and LaPt are determined. Figures 1D, 3A,C, respectively, show the band structures of ScPt, YPt, and LaPt along the R-X-M-R-Γ paths. The spin–orbit coupling (SOC) is not added for the band structures in these figures; the effect of SOC on the electronic structures of these compounds will be discussed later in this paper. These three figures show that the bands and the Fermi level overlap each other, indicating common metallic behaviors.
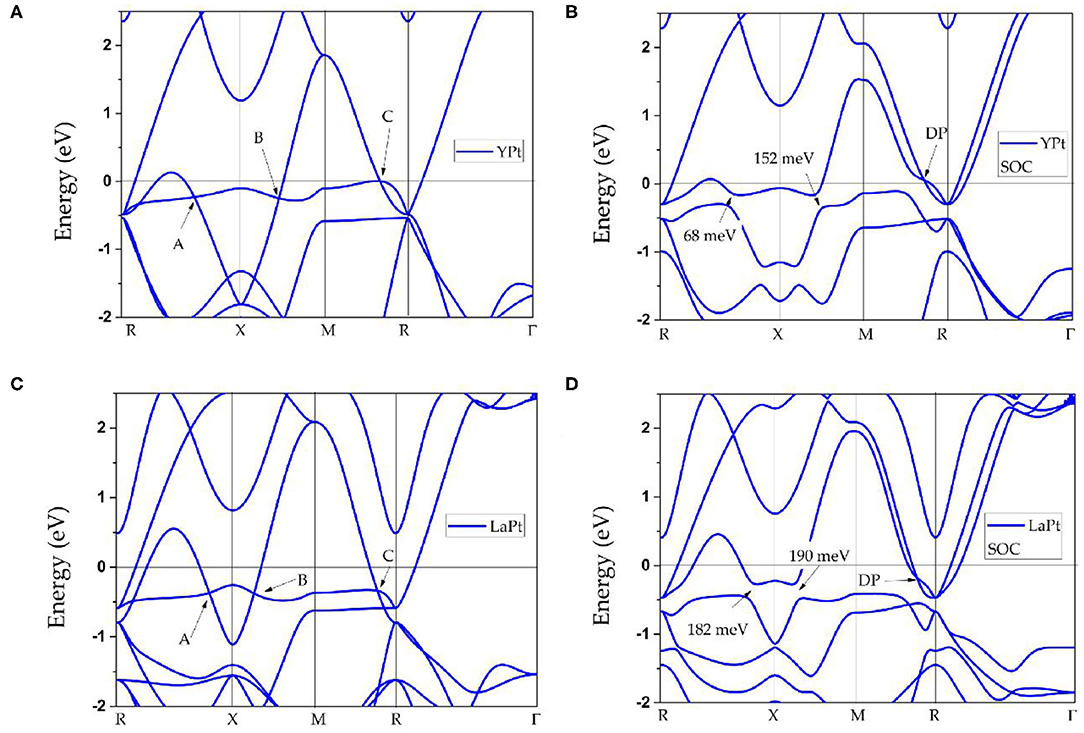
Figure 3. (A–D) Calculated band structures of cubic YPt and LaPt with their optimized lattice constants. The spin–orbit coupling effect is neglected for (A,C) and added for (B,D).
Moreover, some obvious band crossings are seen around the Fermi level, namely, point A along the R-X path, point B along the X-M path, and point C along the M-R path. A careful study of these three band-crossing points indicates that points A and B are doubly degenerate band-crossing points, whereas point C is a 3-fold degenerate band-crossing point formed by a doubly degenerate band and a non-degenerate band. Apart from these three clear band-crossing points, the band structure near the Fermi level is very clean; therefore, these three points dominate the topological signatures of these compounds. For clarity, hereafter, ScPt is used as an example to investigate the band topology considering that the band structures of ScPt, YPt, and LaPt are almost the same near the Fermi level.
Figure 1E shows the band structure of ScPt with the revised Heyd–Scuseria–Ernzerhof (HSE) (Heyd and Scuseria, 2004) screened hybrid functional. The HSE method is well-known to be accurate for describing the band gap of topological materials. In particular, for some d-orbital-dominated systems, the GGA method cannot provide a fair evaluation of the band gap around the Fermi level. Figures 1D,E show that the band-crossing points A, B, and C are still maintained under the HSE method; this confirms that the GGA method is suitable for investigating the electronic structure of the ScPt system.
In addition to SOC, the ScPt system enjoys time reversal (T) and spatial inversion (P) symmetries. Basically, doubly degenerate band crossings like points A and B should not be isolated (Weng et al., 2016b; Zhang et al., 2018b). Instead, they should belong to one type of nodal structure; they most commonly belong to a nodal-line structure. As shown in Figures 1D, 3A,C, two bands cross each other and form two band-crossing points A and B along the R-X and X-M paths. Symmetry analysis shows that these two bands belong to irreducible representations A1g and A2u of D4h symmetry, respectively.
Figure 4A shows the X-centered 3D band dispersion of the kz = π plane. The two above-mentioned bands form a closed nodal line in the kz = π plane (highlighted by a white line), and points A and B belong to this closed nodal line. The crystal symmetry of the ScPt cubic system implies three closed nodal lines in the kx/y/z = π planes. The nodal lines are located in the mirror-invariant plane, and they protect the mirror symmetry Mx,y,z. As an example, Figure 4B shows the shape of the X-centered closed nodal line in the kz = π plane.
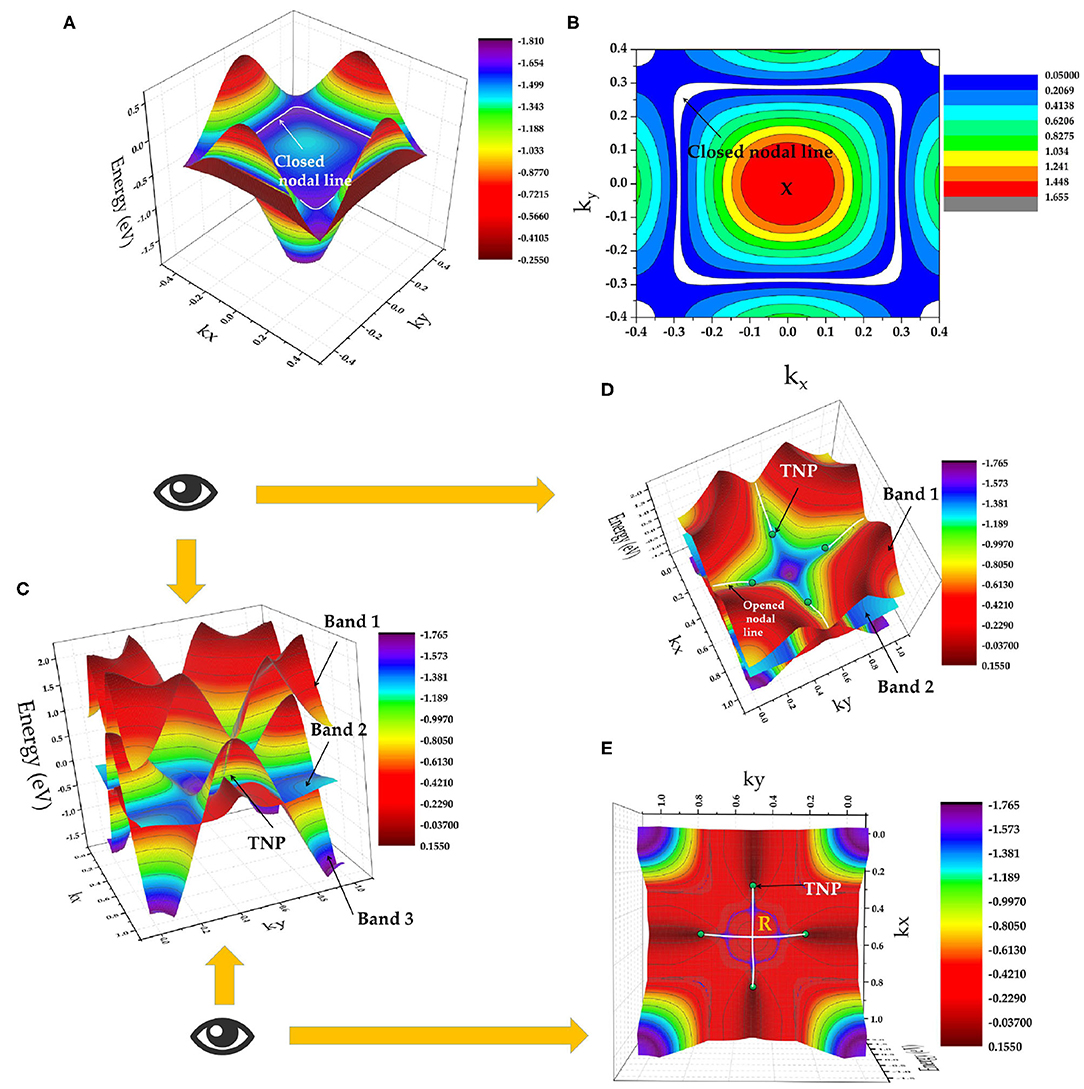
Figure 4. (A) X-centered 3D band dispersion in the kz = π plane; (B) shape of closed X-nodal line in the kz = π plane (nodal line is indicated by white lines and marked by arrows); (C) R-centered 3D band dispersion in the kz = π plane, where TNPs and bands 1, 2, and 3 are marked by arrows; (D) top view of (C); and (E) bottom view of (C). The TNPs and the opened nodal lines (formed by degenerate bands 1 and 2) are indicated by green balls and white lines, respectively.
Figure 4C shows the R-centered 3D band dispersion in the kz = π plane; here, TNPs are indicated by green balls. As shown in Figures 1D, 3A,C, the band-crossing point C is formed by a 2-fold degenerate band and a non-degenerate band along the M-R path. This 2-fold degenerate band can be seen as two independent bands that are completely degenerated along the whole M-R path. Therefore, this 2-fold degenerate band (named as band 1 and band 2) should contain a series of band-crossing points along the whole M-R path and form an opened nodal line along the M-R path. To clearly present the opened nodal lines and the TNPs in ScPt, Figures 4D,E, respectively, show top and bottom views of Figure 4C. These figures clearly show the opened nodal lines formed from bands 1 and 2 along the R-M path as well as the TNPs. Therefore, ScPt, YPt, and LaPt are topological metals that co-exhibit opened and closed nodal lines when the spin-orbit coupling is ignored. Based on the above-mentioned results, the ScPt family of materials is a good platform to study the relationship of closed and opened nodal lines.
Moreover, band-crossing point C along the M-R path is a TNP. Normally, TNP can not only occur in isolation but also be linked by nodal lines in the momentum space. One pair of TNPs exists in ScPt, YPt, and LaPt. Figure 1B shows a schematic of the pair of TNPs (indicated by yellow balls) along the R-M-R′ path. As shown in Figure 4C, the TNPs are located at the crossing of band 3 (non-degenerate band) and bands 1 and 2 (2-fold degenerate band). Therefore, ScPt is concluded to have one-dimensional topological elements, namely, opened and closed nodal lines (in the kx/y/z = π plane) and a zero-dimensional topological element, namely, TNP, along the R-M-R′ path when the spin-orbit coupling is ignored. Therefore, ScPt, LaPt, and YPt are excellent target materials for studying the entanglement between nodal-line and nodal-point fermions.
Finally, the effect of SOC on the band structures of ScPt, YPt, and LaPt is investigated. The corresponding results are shown in Figures 5A, 3B,D, respectively. The gaps induced by SOC for band-crossing points A and B are 53.9 and 83.2 meV, 68 and 152 meV, and 182 and 190 meV for ScPt, YPt, and LaPt, respectively. In comparison, the gaps induced by SOC in the well-known nodal-line materials Cu2NPd (Yu et al., 2015), CaAgBi (Chen et al., 2017b), and BaSn2 (Huang et al., 2016) are 60–100 meV, 80–140 meV, and 60–160 meV, respectively. Therefore, ScPt and YPt are comparable to these reference materials.
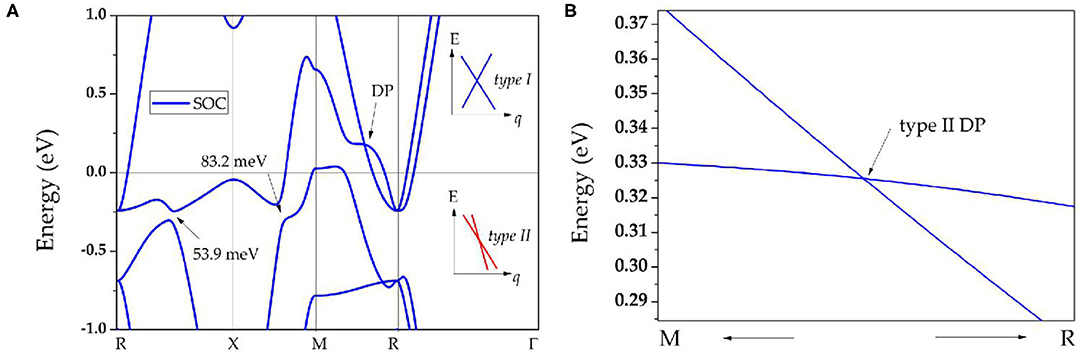
Figure 5. (A) Band structure of ScPt with spin–orbit coupling; the insets show schematics of types I and II nodal points, indicated by blue and red lines, respectively; for type I nodal points, they are conventional type band dispersion, however, for type II nodal points, they enjoy a tilted band dispersion; (B) enlarged band structure of ScPt along the M-R path slightly above the Fermi level.
Moreover, Figures 5B, 3B,D show that the TNPs disappear in ScPt, YPt, and LaPt systems. However, a new topological signature reveals a nodal point with linear band dispersion around the Fermi level. When the SOC effect was considered, each band was doubly degenerate. Therefore, the newly occurring nodal point along the along R-M path should be a Dirac nodal point (DP) with 4-fold degeneracy. Specifically, a pair of DPs with 4-fold degeneracy is found along the R-M-R′ path. Notably, similar SOC-induced TNP–DP transitions have also been reported in ErAs (Meng et al., 2020a), TiB2 (Zhang et al., 2017d), and Li2NaN (Jin et al., 2019b) topological materials. However, unlike the type-I DP predicted for ErAs, this is a type-II DP that may show strong anisotropy (Zhang et al., 2018b).
Summary
In summary, cubic-type ScPt, YPt, and LaPt are shown to be newly designed topological materials through the use of density functional theory. ScPt and YPt are dynamically stable whereas LaPt is not. Without SOC, XPt (X = Sc, Y, La) metals show closed and opened nodal-line states and one pair of TNPs. With SOC, the TNPs (along the R-M-R′ path) change to type-II DPs and the nodal-line states in kx/y/z = π planes are gapped. A series of interesting topological signatures has been predicted in XPt (X = Sc, Y, La), and it is hoped that these proposed topological elements can be confirmed through experiments in the future.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author/s.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This work was funded by the Science and Technology Research Project of Hebei Province Colleges and Universities (Grant No. QN2020113) and Tangshan Applied Basic Research Project (Grant No. 19130227g).
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a past co-authorship with one of the authors, HX.
References
Andrey, V., Sánchez-Barriga, J., Maria, B., Carolien, C., Joke, H., and Anna, S. (2018). Can surface reactivity of mixed crystals be predicted from their counterparts? A case study of (Bi1−−xSbx)2Te3 topological insulators. J. Mater. Chem. C 6, 8941–8949. doi: 10.1039/C8TC02235F
Bi, R., Yan, Z., Lu, L., and Wang, Z. (2017). Nodal-knot semimetals. Phys. Rev. B 96:201305. doi: 10.1103/PhysRevB.96.201305
Bin, Q., Tang, F., Ruan, Y. R., Yong, F., and Han, Z. D. (2018). Extremely large magnetoresistance in the nonmagnetic semimetal YBi. J. Mater. Chem. C 6, 10020–10029. doi: 10.1039/C8TC02839G
Cano, J., and Vergniory, M. G. (2016). Beyond dirac and Weyl fermions: unconventional quasiparticles in conventional crystals. Science 353:aaf5037. doi: 10.1126/science.aaf5037
Cava, R. J., Ji, H., Fuccillo, M. K., Gibson, Q. D., and Hor, Y. S. (2013). Crystal structure and chemistry of topological insulators. J. Mater. Chem. C 1, 3176–3189. doi: 10.1039/c3tc30186a
Chang, G., Xu, S. Y., Zheng, H., Singh, B., Hsu, C. H., and Bian, G. (2016). Room-temperature magnetic topological Weyl fermion and nodal line semimetal states in half-metallic Heusler Co2TiX (X= Si, Ge, or Sn). Sci. Rep. 6:38839. doi: 10.1038/srep38839
Chen, C., Wang, S. S., Liu, L., Yu, Z. M., and Yang, S. A. (2017b). Ternary wurtzite CaAgBi materials family: A playground for essential and accidental, type-I and type-II Dirac fermions. Phys. Rev. Mater. 1:044201. doi: 10.1103/PhysRevMaterials.1.044201
Chen, K. X., Lyu, S. S., Luo, Z. Y., Fu, Y. X., Heng, Y., and Mo, D. C. (2017a). Theoretical design of a new family of two-dimensional topological insulators. Phys. Chem. Chem. Phys.19, 7481–7485. doi: 10.1039/C6CP08670E
Chen, S. Z., Li, S., Chen, Y., and Duan, W. (2020). Nodal flexible-surface semimetals: case of carbon nanotube networks. Nano Lett. 20:5400. doi: 10.1021/acs.nanolett.0c01786
Chen, Z., Zhang, C., Zhou, Y., Zhang, E., Yang, L., Hong, M., et al. (2015). Scalable growth of high mobility dirac semimetal Cd3As2 microbelts. Nano Lett. 15, 5830–5834. doi: 10.1021/acs.nanolett.5b01885
Chenguang, F., Narayan, G. S., June, W. S., Guowei, L., Enke, L., and Nitesh, K. (2018). Large Nernst power factor over a broad temperature range in polycrystalline Weyl semimetal NbP. Energy Environ. Sci. 11, 2813–2820. doi: 10.1039/C8EE02077A
Feng, X., Yue, C., Song, Z., Wu, Q. S., and Wen, B. (2018). Topological dirac nodal-net fermions in AlB2-type TiB2 and ZrB2. Phys. Rev. Mater. 2:014202. doi: 10.1103/PhysRevMaterials.2.014202
Fu, B.-B., Yi, C., Zhang, T., Caputo, M., Ma, Z., Gao, X., et al. (2019). Dirac nodal surfaces and nodal lines in ZrSiS. Sci. Adv. 5:eaau6459. doi: 10.1126/sciadv.aau6459
Gao, L., Sun, J., Sethi, G., Zhang, Y., Du, S., and Liu, F. (2019). Orbital design of topological insulators from two-dimensional semiconductors. Nanoscale 11, 22743–22747. doi: 10.1039/C9NR06859G
Guo, L., Chen, T. W., Chen, C., Chen, L., Zhang, Y., and Gao, G. Y. (2019). Electronic transport evidence for topological nodal-line semimetals of ZrGeSe single crystals. ACS Appl. Electr. Mater. 1, 869–876. doi: 10.1021/acsaelm.9b00061
Guo, P. J., Yang, H. C., Liu, K., and Lu, Z. Y. (2018). Triply degenerate nodal points in RRh6Ge4 (R = Y, La, Lu). Phys. Rev. B 98:045134. doi: 10.1103/PhysRevB.98.045134
Han, Y., Wu, M., Feng, Y., Cheng, Z. X., and Wang, X. T. (2019). Competition between cubic and tetragonal phases in all-d-metal Heusler alloys, X2−xMn1+xV (X = Pd, Ni, Pt, Ag, Au, Ir, Co; x= 1, 0): a new potential direction of the Heusler family. IUCrJ 6, 465–472. doi: 10.1107/S2052252519004007
He, T., Zhang, X., Liu, Y., Dai, X., Liu, G., Liu, Z., et al. (2020). Ferromagnetic hybrid nodal loop and switchable type-I and type-II Weyl fermions in two dimensions. Phys. Rev. B 102:075133. doi: 10.1103/PhysRevB.102.075133
He, T., Zhang, X., Meng, W., Jin, L., Dai, X., and Liu, G. (2019). Topological nodal lines and nodal points in the antiferromagnetic material β-Fe2PO5. J. Mater. Chem. C 7, 12657–12663. doi: 10.1039/C9TC04046C
Heyd, J., and Scuseria, G. (2004). Efficient hybrid density functional calculations in solids: Assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional. J. Chem. Phys. 121, 1187–1192. doi: 10.1063/1.1760074
Hu, X., Pang, Z., Chen, X., Ren, M., and Li, P. (2018). Two-dimensional topological insulators of Pb/Sb honeycombs on a Ge (111) semiconductor surface. RSC Adv. 8, 34999–35004. doi: 10.1039/C8RA06316H
Hu, X. K., Pang, Z. X., Zhang, C. W., Wang, P. J., Li, P., and Ji, W. X. (2019). A two-dimensional robust topological insulator with coexisting ferroelectric and valley polarization. J. Mater. Chem. C 7, 9406–9412. doi: 10.1039/C8TC06252H
Huang, H., Liu, J., Vanderbilt, D., and Duan, W. (2016). Topological nodal-line semimetals in alkaline-earth stannides, germanides, and silicides. Phys. Rev. B 93:201114. doi: 10.1103/PhysRevB.93.201114
Jin, L., Zhang, X., Dai, X., Liu, H., Chen, G., and Liu, G. (2019b). Centrosymmetric Li2NaN: a superior topological electronic material with critical-type triply degenerate nodal points. J. Mater. Chem. C 7, 1316–1320. doi: 10.1039/C8TC05930F
Jin, L., Zhang, X., He, T., Meng, W., and Liu, G. (2020a). Ferromagnetic two-dimensional metal-chlorides MCl (M= Sc, Y, and La): candidates for Weyl nodal line semimetals with small spin-orbit coupling gaps. Appl. Surf. Sci. 520:146376. doi: 10.1016/j.apsusc.2020.146376
Jin, L., Zhang, X., Liu, Y., Dai, X., Shen, X., and Wang, L. (2020b). Two-dimensional Weyl nodal-line semimetal in a d0 ferromagnetic K2N monolayer with a high Curie temperature. Phys. Rev. B 102:125118. doi: 10.1103/PhysRevB.102.125118
Jin, L., Zhang, X. M., Dai, X. F., Wang, L. Y., and Liu, G. D. (2019a). Screening topological materials with a CsCl-type structure in crystallographic databases. IUCrJ 6, 688–694. doi: 10.1107/S2052252519007383
Jing, Y., and Heine, T. (2018). Two-dimensional kagome lattices made of hetero triangulenes are Dirac semimetals or single-band semiconductors. J. Am. Chem. Soc. 141, 743–747. doi: 10.1021/jacs.8b09900
Khoury, J. F., Rettie, A. J. E., Khan, M. A., Ghimire, N. J., and Kanatzidis, M. G. (2019). A new three-dimensional subsulfide Ir2In8S with Dirac semimetal behavior. J. Am. Chem. Soc. 141, 19130–19137. doi: 10.1021/jacs.9b10147
Kirby, R. J., Ferrenti, A., Weinberg, C., Klemenz, S., and Schoop, L. M. (2020). Transient drude response dominates near-infrared pump–probe reflectivity in nodal-line semimetals ZrSiS and ZrSiSe. J. Phys. Chem. Lett. 11, 6105–6111. doi: 10.1021/acs.jpclett.0c01377
Kou, L., Yan, B., Hu, F., Wu, S. C., Wehling, T. O., and Felser, C. (2013). Graphene-based topological insulator with an intrinsic bulk band gap above room temperature. Nano Lett. 13, 6251–6255. doi: 10.1021/nl4037214
Lee, C. H., Li, G., Liu, Y., Tai, T., Thomale, R., and Zhang, X. (2018). Tidal surface states as fingerprints of non-hermitian nodal knot metals. arXiv [Preprint] arXiv:1812.02011
Li, G., Xu, Q., Shi, W. J., Fu, C., and Felser, C. (2019). Surface states in bulk single crystal of topological semimetal Co3Sn2S2 toward water oxidation. Sci. Adv. 5:eaaw9867. doi: 10.1126/sciadv.aaw9867
Liu, C., Zhang, H., Sun, Z., Ding, K., and Jie, J. (2016). Topological insulator Bi2Se3 nanowire/Si heterostructure photodetectors with ultrahigh responsivity and broadband response. J. Mater. Chem. C 4, 5648–5655. doi: 10.1039/C6TC01083K
Liu, J., Li, X., Wang, Q., Kawazoe, Y., and Jena, P. (2018a). A new 3D Dirac nodal-line semi-metallic graphene monolith for lithium ion battery anode materials. J. Mater. Chem. A 6, 13816–13824. doi: 10.1039/C8TA04428G
Liu, Z., Xin, H., Fu, L., Liu, Y., Song, T., and Cui, X. (2018b). All-silicon topological semimetals with closed nodal line. J. Phys. Chem. Lett. 10, 244–250. doi: 10.1021/acs.jpclett.8b03345
Loïc, J., and Izmaylov, A. F. (2017). Molecular “topological insulators”: a case study of electron transfer in the bis (methylene) adamantyl carbocation. Chem. Commun. 53, 7365–7368. doi: 10.1039/C7CC02275A
Lu, L., Fang, C., Fu, L., Johnson, S. G., Joannopoulos, J. D., and Solja, I. M. (2016). Symmetry-protected topological photonic crystal in three dimensions. Nat. Phys. 12, 337–340. doi: 10.1038/nphys3611
Luo, L., Zheng, K., Zhang, T., Liu, Y. H., Yu, Y., and Lu, R. (2015). Optoelectronic characteristics of a near infrared light photodetector based on a topological insulator Sb2Te3 film. J. Mater. Chem. C 3, 9154–9160. doi: 10.1039/C5TC01772F
Ma, H., Chen, P., Li, B., Li, J., Ai, R., Zhang, Z., et al. (2018). Thickness-tunable synthesis of ultrathin type-II Dirac semimetal PtTe2 single crystals and their thickness-dependent electronic properties. Nano Lett. 18, 3523–3529. doi: 10.1021/acs.nanolett.8b00583
Ma, L., and Sun, Q. (2020). A topological semimetal Li2CrN2 sheet as a promising hydrogen storage material. Nanoscale 12, 12106–12113. doi: 10.1039/D0NR02180F
Mal, P., Bera, G., Turpu, G. R., Srivastava, S. K., and Das, P. (2019). Vibrational spectra of Pb2Bi2Te3, PbBi2Te4, and PbBi4Te7 topological insulators: temperature-dependent Raman and theoretical insights from DFT simulations. Phys. Chem. Chem. Phys. 21, 15030–15039. doi: 10.1039/C9CP01494B
Meng, W., Zhang, X., He, T., Jin, L., and Liu, G. (2020a). Multiple fermionic states with clear nontrivial surface signature in CsCl-type compound ErAs. Comput. Mater. Sci. 183:109815. doi: 10.1016/j.commatsci.2020.109815
Meng, W., Zhang, X., He, T., Jin, L., and Liu, G. (2020b). Ternary compound HfCuP: An excellent Weyl semimetal with the coexistence of type-I and type-II Weyl nodes. J. Adv. Res. 24:523. doi: 10.1016/j.jare.2020.05.026
Narimani, M., Shahram, Y., and Zahra, N. (2020). High thermoelectric efficiency of LaX (X = Sb, Bi) two dimensional topological insulators. J. Phys. Conden. Matter. 32:255501. doi: 10.1088/1361-648X/ab6046
Owerre, S. A. (2018). Magnonic triply-degenerate nodal points. Europhys. Lett. 120:57002. doi: 10.1209/0295-5075/120/57002
Pan, Z., Xue, L., and Sun, L. (2017). Large gap two dimensional topological insulators: the bilayer triangular lattice TlM (M = N, P, As, Sb). J. Mater. Chem. C 5, 4268–4274. doi: 10.1039/C7TC00634A
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77:3865. doi: 10.1103/PhysRevLett.77.3865
Perdew, J. P., Burke, K., and Ernzerhof, M. (1998). Perdew, burke, and ernzerhof reply. Phys. Rev. Lett. 80:891. doi: 10.1103/PhysRevLett.80.891
Pielnhofer, F., Menshchikova, T. V., Rusinov, I. P., Zeugner, A., Sklyadneva, I. Y., and Heid, R. (2017). Designing 3D topological insulators by 2D-Xene (X = Ge, Sn) sheet functionalization in GaGeTe-type structures. J. Mater. Chem. C 5, 4752–4762. doi: 10.1039/C7TC00390K
Politano, A., Vitiello, M. S., Viti, L., Boukhvalov, D. W., and Chiarello, G. (2017). The role of surface chemical reactivity in the stability of electronic nanodevices based on two-dimensional materials “beyond graphene” and topological insulators. FlatChem 1, 60–64. doi: 10.1016/j.flatc.2016.11.003
Qiao, J., Chuang, M. Y., Lan, J. C., Lin, Y. Y., Sung, W. H., and Fan, R. (2019). Two-photon absorption within layered Bi2Te3 topological insulators and the role of nonlinear transmittance therein. J. Mater. Chem. C 7, 7027–7034. doi: 10.1039/C9TC01885A
Qie, Y., Liu, J., Wang, S., Sun, Q., and Jena, P. (2019). Tetragonal C24, a topological nodal-surface semimetal with potential as an anode material for sodium ion batteries. J. Mater. Chem. A 7, 5733–5739. doi: 10.1039/C8TA11276B
Sankar, R., Muthuselvam, I. P., Babu, K. R., Murugan, G. S., and Chou, F. C. (2019). Crystal growth and magnetic properties of topological nodal-line semimetal gdsbte with antiferromagnetic spin ordering. Inorg. Chem. 58, 11730–11737. doi: 10.1021/acs.inorgchem.9b01698
Schoop, L. M., Pielnhofer, F., and Lotsch, B. V. (2018). Chemical principles of topological semimetals. Chem. Mater. 30, 3155–3176. doi: 10.1021/acs.chemmater.7b05133
Shen, J., and Cha, J. J. (2014). Topological crystalline insulator nanostructures. Nanoscale 6, 14133–14140. doi: 10.1039/C4NR05124F
Sheng, X. L., Yu, Z. M., Yu, R., Weng, H., and Yang, S. A. (2017). d orbital topological insulator and semimetal in the antifluorite Cu2S family: contrasting spin Helicities, nodal box, and hybrid surface states. J. Phys. Chem. Lett. 8, 3506–3511. doi: 10.1021/acs.jpclett.7b01390
Tang, M., Shen, H., Qie, Y., Xie, H., and Sun, Q. (2019). Edge-state-enhanced CO2 electroreduction on topological nodal-line semimetal Cu2Si nanoribbons. J. Phys. Chem. C 123, 2837–2842. doi: 10.1021/acs.jpcc.8b08871
Togo, A., and Tanaka, I. (2015). First principles phonon calculations in materials science. Scr. Mater. 108, 1–5. doi: 10.1016/j.scriptamat.2015.07.021
Tsipas, P., Tsoutsou, D., Fragkos, S., Sant, R., Alvarez, C., and Okuno, H. (2018). Massless dirac fermions in ZrTe2 semimetal grown on InAs (111) by van der Waals epitaxy. ACS Nano 12, 1696–1703. doi: 10.1021/acsnano.7b08350
Türker, O., and Sergej, M. (2018). Weyl nodal surfaces. Phys. Rev. B 97:075120. doi: 10.1103/PhysRevB.97.075120
Wang, A., Zhang, X., and Zhao, M. (2014). Topological insulator states in a honeycomb lattice of s-triazines. Nanoscale 6, 11157–11162. doi: 10.1039/C4NR02707H
Wang, X., Cheng, Z., Zhang, G., Wang, B., Wang, X. L., and Chen, H. (2020c). Rich novel zero-dimensional (0D), 1D, and 2D topological elements predicted in the P63/m type ternary boride HfIr3B4. Nanoscale 12, 8314–8319. doi: 10.1039/D0NR00635A
Wang, X., Ding, G., Khandy, S., Cheng, Z., Zhang, G., Wang, X., et al. (2020d). Unique topological nodal line states and associated exceptional thermoelectric power factor platform in Nb3GeTe6 monolayer and bulk. Nanoscale 12, 16910–16916. doi: 10.1039/D0NR03704D
Wang, X., Zhou, F., and Chen, H. (2020e). Organic-inorganic hybrid coordination polymer C3H9CdCl3N co-exhibiting superior Dirac point and nodal surface states. Results Phys. 17:103159. doi: 10.1016/j.rinp.2020.103159
Wang, X. T., Ding, G., Cheng, Z. X., Surucu, G., and Yang, T. (2020a). Novel topological nodal lines and exotic drum-head-like surface states in synthesized CsCl-type binary alloy TiOs. J. Adv. Res. 22, 137–144. doi: 10.1016/j.jare.2019.12.001
Wang, X. T., Ding, G., Cheng, Z. X., Wang, X. L., and Yang, T. (2020b). Intersecting nodal rings in orthorhombic-type BaLi2Sn compound. J. Mater. Chem. C 8, 5461–5466. doi: 10.1039/D0TC00504E
Weng, H., Fang, C., Fang, Z., and Dai, X. (2016a). Coexistence of Weyl fermion and massless triply degenerate nodal points. Phys. Rev. B 94:165201. doi: 10.1103/PhysRevB.94.165201
Weng, H., Fang, C., Fang, Z., and Dai, X. (2016b). Topological semimetals with triply degenerate nodal points in θ-phase tantalum nitride. Phys. Rev. B 93:241202. doi: 10.1103/PhysRevB.93.241202
Wu, M., Han, Y., Bouhemadou, A., Cheng, Z., and Wang, X. (2019). Site preference and tetragonal distortion in palladium-rich Heusler alloys. IUCrJ 6, 218–225. doi: 10.1107/S2052252518017578
Wu, W., Liu, Y., Li, S., Zhong, C., Yu, Z. M., and Sheng, X. L. (2018). Nodal surface semimetals: Theory and material realization. Phys. Rev. B 97:115125. doi: 10.1103/PhysRevB.97.115125
Xia, Y., and Li, G. (2017). Triply degenerate nodal points and topological phase transitions in NaCu3Te2. Phys. Rev. B 96:241204. doi: 10.1103/PhysRevB.96.241204
Xiao, M., Ye, L., Qiu, C., He, H., Liu, Z., and Fan, S. (2020). Experimental demonstration of acoustic semimetal with topologically charged nodal surface. Sci. Adv. 6:eaav2360. doi: 10.1126/sciadv.aav2360
Xie, H., Qie, Y., Imran, M., and Sun, Q. (2019). Topological semimetal porous carbon as a high-performance anode for Li-ion batteries. J. Mater. Chem. A 7, 14253–14259. doi: 10.1039/C9TA03587G
Xu, S. G., Zheng, B., Xu, H., and Yang, X. B. (2019). Ideal nodal line semimetal in a two-dimensional boron bilayer. J. Phys. Chem. C 123, 4977–4983. doi: 10.1021/acs.jpcc.8b12385
Yan, L., Liu, P. F., Bo, T., Zhang, J., Tang, M. H., and Xiao, Y. G. (2019). Emergence of superconductivity in a Dirac nodal-line Cu2Si monolayer: ab initio calculations. J. Mater. Chem. C 7, 10926–10932. doi: 10.1039/C9TC03740C
Yan, Q., Liu, R., Yan, Z., Liu, B., Chen, H., Wang, Z., et al. (2018). Experimental discovery of nodal chains. Nat. Phys. 14, 461–464. doi: 10.1038/s41567-017-0041-4
Yan, Z., Bi, R., Shen, H., Lu, L., Zhang, S. C., and Wang, Z. (2017). Nodal-link semimetals. Phys. Rev. B 96:041103. doi: 10.1103/PhysRevB.96.041103
Yang, T., Khenata, R., and Wang, X. (2020). Predicted remarkably topological nodal surface states in P63/m type Sr3WN3 from first-principles. Results Phys. 17:103026. doi: 10.1016/j.rinp.2020.103026
Yang, T., and Zhang, X. (2020). Nearly flat nodal surface states in pseudo-one-dimensional molybdenum monochalcogenides X(MoS)3 (X = K, Rb, and Cs). J. Mater. Chem. C 8, 9046–9054. doi: 10.1039/D0TC01978J
Yang, Y., Sun, H. X., Xia, J. P., Xue, H., Gao, Z., Ge, Y., et al. (2019a). Topological triply degenerate point with double Fermi arcs. Nat. Phys. 15, 645–649. doi: 10.1038/s41567-019-0502-z
Yang, Y., Xia, J. P., Sun, H. X., Ge, Y., and Zhang, B. (2019b). Observation of a topological nodal surface and its surface-state arcs in an artificial acoustic crystal. Nat. Commun. 10, 1–7. doi: 10.1038/s41467-019-13258-3
Yi, X., Li, W., Li, Z., Zjou, P., Ma, Z., and Sun, L. (2019). Topological dual double node-line semimetals NaAlSi (Ge) and their potential as cathode material for sodium ion batteries. J. Mater. Chem. C 7, 15375–15381. doi: 10.1039/C9TC04096J
Yu, R., Weng, H., Fang, Z., Dai, X., and Hu, X. (2015). Topological node-line semimetal and Dirac semimetal state in antiperovskite Cu3PdN. Phys. Rev. Lett. 115:036807. doi: 10.1103/PhysRevLett.115.036807
Yuan, X., Cheng, P., Zhang, L., Zhang, C., and Xiu, F. (2017). Direct observation of Landau level resonance and mass generation in dirac semimetal Cd3As2 thin films. Nano Lett. 17, 2211–2219. doi: 10.1021/acs.nanolett.6b04778
Zhang, C., Zhang, E., Wang, W., Liu, Y., Chen, Z. G., and Lu, S. (2017a). Room-temperature chiral charge pumping in dirac semimetals. Nat. Commun. 8, 1–9. doi: 10.1038/ncomms13741
Zhang, L., Zhang, S., Ji, W., Zhang, C., Li, P., Wang, P., et al. (2018a). Discovery of a novel spin-polarized nodal ring in a two-dimensional HK lattice. Nanoscale 10, 20748–20753. doi: 10.1039/C8NR05383A
Zhang, M. H., Zhang, S. F., Wang, P. J., and Zhang, C. W. (2020). Emergence of a spin-valley Dirac semimetal in a strained group-VA monolayer. Nanoscale 12, 3950–3957. doi: 10.1039/C9NR09545D
Zhang, T. T., Yu, Z. M., Guo, W., Shi, D., Zhang, G., and Yao, Y. (2017b). From type-II triply degenerate nodal points and three-band nodal rings to type-II Dirac points in centrosymmetric zirconium oxide. J. Phys. Chem. Lett. 8, 5792–5797. doi: 10.1021/acs.jpclett.7b02642
Zhang, X., Fu, B., Jin, L., Dai, X., and Yao, Y. (2019). Topological nodal line electrides: realization of an ideal nodal line state nearly immune from spin–orbit coupling. J. Phys. Chem. C 123, 25871–25876. doi: 10.1021/acs.jpcc.9b08446
Zhang, X., Jin, L., Dai, X., and Liu, G. (2017c). Topological type-II nodal line semimetal and Dirac semimetal state in stable kagome compound Mg3Bi2. J. Phys. Chem. Lett. 8, 4814–4819. doi: 10.1021/acs.jpclett.7b02129
Zhang, X., Jin, L., Dai, X., and Liu, G. (2018b). Highly anisotropic type-II nodal line state in pure titanium metal. Appl. Phys. Lett. 112:122403. doi: 10.1063/1.5023320
Zhang, X., Liu, Q., Xu, Q., Dai, X., and Zunger, A. (2018c). Topological insulators versus topological Dirac semimetals in honeycomb compounds. J. Am. Chem. Soc. 140, 13687–13694. doi: 10.1021/jacs.8b06652
Zhang, X., Yu, Z., Sheng, X., Yang, H., and Yang, S. A. (2017d). Coexistence of four-band nodal rings and triply degenerate nodal points in centrosymmetric metal diborides. Phys. Rev. B 95:235116. doi: 10.1103/PhysRevB.95.235116
Zhang, X., Yu, Z. M., Zhu, Z., Wu, W., and Yang, S. A. (2018d). Nodal loop and nodal surface states in the Ti 3 Al family of materials. Phys. Rev. B 97:235150. doi: 10.1103/PhysRevB.97.235150
Zhao, M., Dong, W., and Wang, A. (2013). Two-dimensional carbon topological insulators superior to graphene. Sci. Rep. 3:3532. doi: 10.1038/srep03532
Zhao, Z., Zhang, Z., and Guo, W. (2020). A family of all sp 2-bonded carbon allotropes of topological semimetals with strain-robust nodal-lines. J. Mater. Chem. C 8, 1548–1555. doi: 10.1039/C9TC05470G
Zhong, C., Wu, W., He, J., Ding, G., Liu, Y., and Li, D. (2019). Two-dimensional honeycomb borophene oxide: strong anisotropy and nodal loop transformation. Nanoscale 11, 2468–2475. doi: 10.1039/C8NR08729F
Zhou, P., Ma, Z., and Sun, L. (2018). Coexistence of open and closed type nodal line topological semimetals in two dimensional B2C. J. Mater. Chem. C 6, 1206–1214. doi: 10.1039/C7TC05095J
Zhou, Q., Wang, J., Chwee, T. S., Wu, G., Wang, X., and Ye, Q. (2015). Topological insulators based on 2D shape-persistent organic ligand complexes. Nanoscale 7, 727–735. doi: 10.1039/C4NR05247A
Zhou, T., Tong, M., Xie, X., Yu, Y., Zhu, X., Wang, Z. Y., et al. (2020). Quantum transport signatures of a close candidate for a type II nodal-line semimetal. J. Phys. Chem. Lett. 11, 6475–6481. doi: 10.1021/acs.jpclett.0c01726
Keywords: 4-fold degenerate nodal point, triply degenerate nodal point (TNP), spin-orbit coupling (SOC), topological element, phonon dispersion
Citation: Xu H (2020) Realization of Opened and Closed Nodal Lines and Four- and Three-fold Degenerate Nodal Points in XPt (X = Sc, Y, La) Intermetallic Compound: A Computational Modeling Study. Front. Chem. 8:609118. doi: 10.3389/fchem.2020.609118
Received: 22 September 2020; Accepted: 12 October 2020;
Published: 05 November 2020.
Edited by:
Xiaotian Wang, Southwest University, ChinaReviewed by:
Jiangchao Han, Beihang University, ChinaXiaoming Zhang, Hebei University of Technology, China
Copyright © 2020 Xu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Heju Xu, eHVoZWp1QG5jc3QuZWR1LmNu
 Heju Xu
Heju Xu