Slow Transition Path Times Reveal a Complex Folding Barrier in a Designed Protein

De-novo designed proteins have received wide interest as potential platforms for nano-engineering and biomedicine. While much work is being done in the design of thermodynamically stable proteins, the folding process of artificially designed proteins is not well-studied. Here we used single-molecule force spectroscopy by optical tweezers to study the folding of ROSS, a de-novo designed 2x2 Rossmann fold. We measured a barrier crossing time in the millisecond range, much slower than what has been reported for other systems. While long transition times can be explained by barrier roughness or slow diffusion, we show that isotropic roughness cannot explain the measured transition path time distribution. Instead, this study shows that the slow barrier crossing of ROSS is caused by the population of three short-lived high-energy intermediates. In addition, we identify incomplete and off-pathway folding events with different barrier crossing dynamics. Our results hint at the presence of a complex transition barrier that may be a common feature of many artificially designed proteins.

Introduction

The protein-folding problem has fascinated scientists for more than half a century (Anfinsen et al., 1961). To learn and understand more about the reaction that takes place when an unfolded polypeptide chain tries to “find” its correctly folded protein structure, the concept of energy landscapes is a powerful theoretical framework (Onuchic et al., 1997). Within this framework, three key parameters govern the typical timescales of an observed reaction: the height of a free energy barrier, which needs to be overcome, the curvature or stiffness at the top of that barrier, and the diffusion coefficient (Hänggi et al., 1990).

Experimentally, various techniques have been used to verify the applicability of energy landscape theory to protein folding. Besides single-molecule Förster resonance energy transfer (smFRET) (Borgia et al., 2012; Chung et al., 2012; Soranno et al., 2012; Chung and Eaton, 2013), another well-established tool to measure the folding of individual proteins is single-molecule force spectroscopy (SMFS), where force can act as both a denaturant and a readout of protein conformational changes (Rief et al., 1997; Junker et al., 2009; Gebhardt et al., 2010; Yu et al., 2012). In the case of optical tweezers, specific attachment strategies and stable setups have provided access to a large range of timescales and enabled measurements of single molecules over tens of minutes (Stigler et al., 2011; Rognoni et al., 2014) at a temporal resolution to resolve timescales of only a few tens of microseconds (Žoldák et al., 2013; Neupane et al., 2016). Recent studies have shown that with this technique it is possible to extract and evaluate transition paths [i.e., the rare events of actual barrier crossing, which allow the direct estimation of diffusion coefficients or the determination of transition path velocities (Neupane et al., 2017, 2018)]. In addition, the theoretical foundation used to analyze and correctly interpret experimentally measured transition paths is constantly improving (Hummer, 2004; Cossio et al., 2015, 2018; Covino et al., 2019).

A complementary approach to understanding protein folding tackles the problem from the opposite end (i.e., by de-novo designing protein sequences that fold into the desired shape). Because of their far-reaching potential in pharmaceutical applications, these artificial proteins have received wide interest from science and industry (Kuhlman and Bradley, 2019). In general, the de-novo design of proteins is an optimization problem where candidate sequences of amino acids are scored according to an energy model and a target fold. The optimization often comes at a high computational cost, as different side-chain packing can yield the same general fold, but widely different energy scores. While designers have been very successful in creating thermodynamically stable proteins as building blocks, there is little known about how these proteins compare to natural counterparts in terms of folding or conformational dynamics.

In this study, we characterize the timescales of folding and barrier crossing of one of the first fully designed artificial proteins with a topology that is abundantly found in nature, the 2x2 Rossmann fold, which can serve as a scaffold for designed enzymes (Koga et al., 2012).

Materials and Methods

Protein Expression and Sample Preparation

The sequence of the 2x2 Rossmann fold protein (ROSS) was based on the Di-II-10 sequence of Koga et al. (2012) where the part of the designed protein comprises 100 amino acids (bold in sequences below). We modified this sequence with additional n- and c-terminal cysteines and a c-terminal His₆-tag. The variant S49Cc lacked the n-terminal cysteine and harbored two cysteines at position 49 and the c-terminus. Protein expression and purification were performed as described previously (Fang et al., 2013).

ROSS: MACK MLLYVLIISN DKKLIEEARK MAEKANLELR TVKTEDELKK YLEEFRKESQ NIKVLILVSN DEELDKAKEL AQKMEIDVRT RKVTSPDEAK RWIKEFSEEG GSKCLE HHHHHH.

S49Cc: MASKGS MLLYVLIISN DKKLIEEARK MAEKANLELR TVKTEDELKK YLEEFRKECQ NIKVLILVSN DEELDKAKEL AQKMEIDVRT RKVTSPDEAK RWIKEFSEEG GSSGKCLE HHHHHH.

Bead-DNA-protein-bead-DNA dumbbells were generated as described previously (Mehlich et al., 2015). In short, maleimide-modified oligonucleotides were attached to the cysteines of the purified protein via a disulfide bond to form a protein-oligonucleotide construct. Next, biotin or digoxigenin modified DNA handles equipped with a single-stranded overhang complementary to the maleimide-modified oligonucleotides on their 3′ end were hybridized to this protein-oligonucleotide. The resulting DNA-protein-DNA hybrid was then bound to streptavidin or anti-digoxigenin functionalized 1 μm diameter silica beads for optical tweezers measurements.

Optical Trap Setup and Measurement Modes

A custom-built dual optical trap setup with back-focal plane detection was used for all force spectroscopic measurements (von Hansen et al., 2012). The two measurement modes comprise either stretch-relax cycles in constant-velocity mode or measurements at constant trap distances in passive-mode.

Before recording, signals were filtered with an eighth order Butterworth filter with a 3 dB-frequency set at 100 kHz. Data were acquired at 200 kHz. The stiffness of each trap was typically set to about 0.2 pN/nm. Constant-velocity measurements were performed at 500 nm/s.

Polymer Models and Length Coordinates

To model the force compliance of the polymer linkers that connect the protein to the beads we used previously published polymer models (Bustamante et al., 1994; Wang et al., 1997). Upon stretching and while the protein remains folded, the mechanical response of a trapping construct is dominated by stretching of the DNA handles which were modeled using an extensible Worm-Like Chain (eWLC) model (Wang et al., 1997)

$\begin{array}{ll}\begin{array}{l}F({\xi }_D)=\frac{k_{\text{B}}T}{p_D}\left(\frac{1}{4}{\left(1-\frac{{\xi }_D}{L_D}+\frac{F}{K}\right)}^{-2}-\frac{1}{4}+\frac{{\xi }_D}{L_D}-\frac{F}{K}\right)\end{array}& (1)\end{array}$

with DNA extension ξ_D, force F, thermal energy k_BT, DNA persistence length p_D, DNA contour length L_D, and stretch modulus K.

The additional force-extension of unfolded protein was modeled using a Worm-Like Chain (WLC) model in series with the above response of the DNA handles;

$\begin{array}{ll}\begin{array}{l}F({\xi }_p)=\frac{k_{\text{B}}T}{p_p}\left(\frac{1}{4}{\left(1-\frac{{\xi }_p}{L_p}\right)}^{-2}-\frac{1}{4}+\frac{{\xi }_p}{L_p}\right)\end{array}& (2)\end{array}$

where ξ_p is the additional extension of the unfolded amino acid chain of the protein, p_p is the protein persistence length, and L_p is the protein contour length.

To fit our experimental data, p_p was fixed at 0.7 nm. Typical values for the DNA fits were p_D ≈ 31 nm, L_D ≈ 364 nm, and K ≈ 200 pN. Experiments were conducted at a temperature of T ≈ 298 K.

Instead of the molecular extension ξ_p, which depends on the applied force, we used the force-independent contour length of the unfolded polypeptide L_p as a reaction coordinate. At a trap distance d, omitting the comparatively small extension of the folded protein, the extension of the unfolded polypeptide is given by ${\xi }_p=d-\frac{F}{k_c}-{\xi }_D(F)$, where $k_c={\left(k_1^{-1}+k_2^{-1}\right)}^{-1}$ is the combined spring constant of the two beads and $x=\frac{F}{k_c}$ is the combined bead deflection (see Supplementary Figure 1). The contour length L_p was then obtained from ξ_p using Equation (2). This conversion allowed us to compare events at different forces in a more straightforward manner (Puchner et al., 2008).

Integrals over the polymer models were used to convert energy profiles at different force biases as described (Ramm et al., 2014).

Experimental Rate Constants and Lifetime Distributions

Rate constants for unfolding and refolding from constant-velocity experiments were determined using cycles with 500 nm/s pulling speed and applying the method by Oberbarnscheidt et al. (2009).

Folding/unfolding rate constants from passive-mode measurements were obtained from hidden Markov models (HMMs) as described previously (Geier et al., 2007; Stigler et al., 2011; Stigler and Rief, 2012). In brief, HMMs were used to determine the likeliest sequence of hidden states that describes the observed trajectory of bead deflections. The lifetimes for each detected state were well-described by a single exponential distribution. Transition rate constants between states i and j were then determined using $k_{ij}=N_{ij}/({\tau }_i·\sum _k{N}_{ik})$, where τ_i is the average lifetime of state i and N_ij is the number of detected transitions between states i and j.

Force-dependent folding/unfolding rate constants were fitted to a model (Equation (S6), see Supplementary Information) that incorporates the energetic contributions of the non-linear polymer linkers to yield transition state positions and extrapolate force-free transition rate constants (Schlierf et al., 2007; Stigler et al., 2011).

The Relation Between Rates and Shape Parameters of an Energy Landscape

A relation between the transition rate k_ij from state i to j and the shape of the barrier with a height ΔG^iTS separating these two states is given by Kramers' rate theory in the Smoluchowski limit [i.e., the overdamped case where ${(D·\beta )}^{-1}\gg {\omega }_{\text{TS}}$ (Kramers, 1940; Hänggi et al., 1990)]:

$\begin{array}{ll}\begin{array}{l}{k}_{ij}=\frac{D·\beta ·{\omega }_i·{\omega }_{\text{TS}}}{2\pi }·exp\left(-\beta ·\Delta G^{i\text{TS}}\right)\end{array}& (3)\end{array}$

Here, D is the diffusion coefficient, β is the inverse thermal energy (${\beta }^{-1}=k_{\text{B}}T$), and ω_i and ω_TS represent the oscillation frequencies around the minimum of state i and around the barrier top of the transition state which needs to be passed to reach state j. We used this relation for barrier height reconstruction or expected rate calculation under the assumption of symmetric and harmonic barrier shapes. This assumption implies that ω_i = ω_TS and ${\omega }_{\text{TS}}^2$ = $\left|{\partial }_x^{2}G\right|$ = $4·\frac{{\Delta G}^{i\text{TS}}}{{\left({\Delta x}^{\mathit{\text{i}}\text{TS}}\right)}^2}$, where x^iTS is the distance between a state i and its adjoining transition state TS (Mehlich, 2018).

Deconvolution of Equilibrium Distributions

For deconvolution (i.e., the removal of thermal noise-broadening) of measured bead deflection distributions P_msmt(x), we used the same algorithm as described in Ramm et al. (2014). In brief, we numerically minimized the function

$\begin{array}{r}{O}={\langle |ln\left({\widehat{P}}_{\text{prot}}(x)\otimes {\Psi }_x(x)\right)-ln(P_{\text{msmt}}(x))|\rangle }_x+\lambda ·\\ {\displaystyle \sum _i}{\left[\beta ·{\partial }_x^2\hat{G}(x){|}_{{\widehat{x}}_i}\right]}^2& (4)\end{array}$

where ⊗ represents the convolution operator and Ψ_x(x) is the force-dependent point-spread function (PSF) to estimate the true probability distribution ${\widehat{P}}_{\text{prot}}(x)=exp\left(-\beta ·\hat{G}(x)\right)$. The only unknown quantity was the deconvolved energy landscape Ĝ(x) of the protein. The smoothing penalty parameter was set to λ = 10⁻²nm⁴.

The shape of the PSF was determined from equilibrium thermodynamics calculations (see Ramm et al., 2014 for a detailed description). In brief, at a given trap distance d, the mechanical free energy of stretching the polymer linkers and displacing the beads from their traps is

$\begin{array}{ll}\begin{array}{l}{H}(x)={\int }_0^{d-x}{F}_{D+p}(\xi )d\xi +\frac{1}{2}{k}_c{x}^2,\end{array}& (5)\end{array}$

where F_D+p(ξ) is the inverse of ξ_D(F) + ξ_p(F) (Equations (1), (2)). The theoretical PSF of deflection values for a given trap distance and a given unfolded contour length was then determined by

$\begin{array}{ll}\begin{array}{c}{\Psi }_x(x)=\frac{e^{-\beta {H}(x)}}{\int e^{-\beta {H}(x)}dx}\end{array}& (6)\end{array}$

Because of the nonlinearity of the eWLC and WLC linkers, the theoretical PSF is asymmetric and well-approximated by a skewed Gaussian distribution (See Azzalini, 1985 for a description of the skewed Gaussian distribution). Supplementary Figure 2 shows the theoretical PSF in contour-length space for the states N and U, at typical forces in passive-mode experiments and in stretch-relax experiments, which we parameterized by a scale parameter σ and a skewness parameter γ. Because the force is not constant in passive-mode experiments, σ = σ(x) and γ = γ(x) are position-dependent (Gebhardt et al., 2010). In our analysis, σ(x) and γ(x) were determined by linear interpolation between values obtained from fits to the distribution of the folded state and the unfolded state.

Determination of Transition Path Time

Hidden Markov models (HMM) were used to identify state positions, state occupancies, and dwell times for transitions between folded (N) and unfolded (U) states of ROSS as described elsewhere (Stigler et al., 2011). To assess the actual duration of these identified transitions, we applied a 3-state model where the two outer states were fixed at the identified N and U positions and a third obligatory intermediate state T was introduces and fixed right in the middle between N and U, similar to an approach already used elsewhere (Chung et al., 2012; Sturzenegger et al., 2018). The dwell times measured for T were interpreted as the required transition path time to cross the barrier between the folded and unfolded state.

For validation, the HMM method was also applied with, instead of one central intermediate T, two intermediates at the positions of I₁ and I₂. Here, transition path times were derived as the sum of the dwell times spent within I₁ and I₂ along each transition between N and U. The two methods resulted in practically identical estimates of the transition path time (TPT) from passive-mode measurements ($\langle {\tau }^{{\text{I}}_1+{\text{I}}_2}\rangle$ = 1.6 ± 0.1 ms and 〈τ^T〉 = 1.5 ± 0.1 ms). Supplementary Figures 3A,B shows a comparison between results obtained from both methods. We note that the HMM method does not strictly prohibit boundary re-crossing. When imposing absorbing boundaries, we found that the detected transition paths often excluded stretches that lie visibly on a path (Supplementary Figure 3C) and the corresponding TPTs were consequently underestimated. This underestimation was due to random bead fluctuation noise that did not reflect changes in the molecular length and was especially prominent at high bandwidth. Filtering to lower bandwidth suppressed this noise and resulted in TPTs that agreed with both the HMM method (see above) and the method of transition averaging (see below).

Alternatively, transition path times were determined by selecting individual transitions and fitting the high-bandwidth bead relaxation data to a sigmoidal equation $f(t)=A/\left(1+exp\left(\frac{t-t_0}{{\tau }_s}\right)\right)$, to determine the time t₀ at which a transition occurred. The transitions were then aligned according to their t₀ values and averaged. The characteristic timescale τ_s of the transition was then obtained from a sigmoidal fit to the aligned and averaged data (Supplementary Figures 4B,C). To be able to compare the characteristic timescales of the obligatory intermediate model and the sigmoidal model, we performed simulations of transitions between two states with an obligatory intermediate in the center (Supplementary Figure 4D, inset). The duration of the intermediate dwell was chosen from an exponential distribution with a time constant τ. Mimicking experiments, the transitions were then aligned, averaged, and fitted to a sigmoidal equation to determine the characteristic timescale of the sigmoidal model τ_s. A conversion factor between the two timescales τ and τ_s was then obtained by repeating the simulation for different intermediate durations (Supplementary Figure 4E).

Transition Path Time Analysis

An approximation for the average transition path time 〈τ_TP〉 which is required to cross a harmonic barrier of height $\Delta G^{‡}>2k_{\text{B}}T$ by one-dimensional diffusion is given by Chung et al. (2009):

$\begin{array}{ll}\begin{array}{l}\langle {\tau }_{\text{TP}}\rangle \approx \frac{ln\left(2e^{{\gamma }_E}·\beta ·\Delta G^{‡}\right)}{\beta ·D·{\omega }_{\text{TS}}^2}\end{array}& (7)\end{array}$

where γ_E ≈ 0.577 is Euler's constant.

The following model approximates the cumulative distribution function of transition path times over a harmonic barrier (Zhang et al., 2007; Chaudhury and Makarov, 2010):

$\begin{array}{ll}\begin{array}{l}P({\tau }_{\text{TP}})\approx {\int }_0^{{\tau }_{\text{TP}}}\frac{{\omega }_K·\sqrt{\beta ·\Delta G^{‡}}}{1-erf\left(\sqrt{\beta ·\Delta G^{‡}}\right)}·\frac{exp\left[-\beta ·\Delta G^{‡}·coth\left({\omega }_K·\frac{\tau }{2}\right)\right]}{sinh\left({\omega }_K·\frac{\tau }{2}\right)·\sqrt{2\pi ·sinh\left({\omega }_K·\tau \right)}}d\tau \end{array}& (8)\end{array}$

where ${\omega }_K=\beta ·D·{\omega }_{\text{TS}}^2$ and erf() represents the error function.

Off-rates from intermediates were determined by fitting dwell time distributions to a model that describes the escape rate with two determinant rates (Rief et al., 2000):

$\begin{array}{ll}\begin{array}{l}p({\tau }_{1+2})=\frac{k_1·k_2}{k_1-k_2}·\left[exp\left(-k_2·{\tau }_{1+2}\right)-exp\left(-k_1·{\tau }_{1+2}\right)\right]\end{array}& (9)\end{array}$

where, in our use case k₁ and k₂ represent off-rates out of two adjoining and predominant high-energy intermediate states located along a transition path and τ₁₊₂ reflects the combined dwell time of these two intermediates measured as an effective overall transition path time.

All diffusion coefficients reported are represented with contour length as a reaction coordinate.

Simulation of Transition Path Time Distributions

Simulations of transition path trajectories were performed by integrating the discrete-time Langevin equation in a 1D potential as described previously (Ramm et al., 2014). To gather statistics, transition path times were collected using a flux sampling scheme (Zhang et al., 2007; Laleman et al., 2017).

Results

Low-Bandwidth Stretch-Relax Experiments of an Artificial Protein Suggest Two-State Behavior

To study the folding and unfolding transition path times of an artificially designed globular protein, we introduced terminal cysteines into the sequence of ROSS, a 100 amino acid (aa), fully artificially designed protein that adopts a 2x2 Rossmann fold (Koga et al., 2012) (Figure 1A, inset). We then fused the protein termini to DNA handles and assembled bead-DNA-protein-DNA-bead dumbbells for force spectroscopic measurements in a custom-built optical tweezer instrument.

FIGURE 1

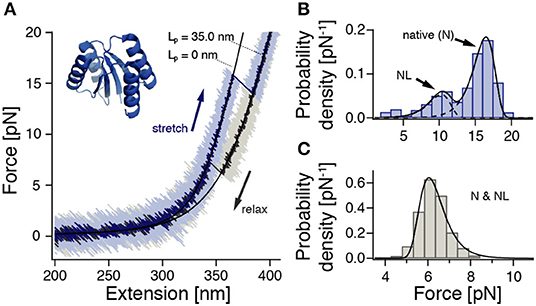
Figure 1. ROSS shows apparent two-state folding with minor populations of a native-like (NL) configuration. Cf. Supplementary Figure 10 for a zoom into the unfolding transition. (A) Stretch-relax cycle of ROSS recorded in a 500 nm/s constant-velocity experiment. Black lines are polymer model fits to the stretches of the folded and unfolded conformations. (B) Unfolding force distribution (500 nm/s, n = 691) with fits [Equation (S1)] to two distinct populations. (C) Refolding force distribution (500 nm/s, n = 651). Fit according to Equation (S2).

To characterize the mechanical behavior of ROSS, we subjected the protein-DNA dumbbell to stretch-relax cycles at 500 nm/s (Figure 1A). In the majority of cycles, ROSS displays apparent two-state unfolding behavior with unfolding forces at ≈17 pN and a contour length increase of 34.7 ± 0.9 nm, in excellent agreement with an expected length of 34.5 nm for the unfolding of 100 aa. Upon relaxation, ROSS readily refolds at a force of ≈ 6 pN back to the native contour length of 0 nm. In addition to the described behavior, we also observed, in 23% of cycles, a population of unfolding events at reduced forces of ≈ 10 pN, with a similar contour length increase of 33.8 ± 0.9 nm. An unfolding force histogram (Figure 1B) shows the occurrence of this second mechanically weaker state, which we call the native-like (NL) conformation. Refolding forces followed the expected behavior of a single pathway (Figure 1C). To obtain the equilibrium free energy difference between the native and unfolded states, we employed the Crooks fluctuation theorem (Crooks, 1999; Collin et al., 2005) (Supplementary Figure 5). We found a stability of the native state of −27 ± 2 k_BT, in good agreement with a reported value of −25.2 k_BT in chemical denaturation (Koga et al., 2012).

Transition Path Times Suggest a Rough Transition Barrier

We sought to investigate the transition path times (TPTs) for the unfolding and folding in greater detail. To this end, we held the tethered protein under tension in passive mode and followed the folding/unfolding transitions at high bandwidth over several minutes (Figure 2A). ROSS displayed long dwells in the native (N, 0 nm contour length) and unfolded (U, 34.7 nm contour length) states of up to a minute in duration. In addition, we also observed transient short-lived excursions from U toward the native structure, which we attribute to unsuccessful folding events. Using a model that incorporates the energetic contributions of linker stretching (see Methods) we determined a free energy difference between the N and U states of −28 ± 3 k_BT, confirming our earlier result from stretch-relax cycles (−27 ± 2 k_BT) and reported values from chemical denaturation (−25.2 k_BT) (Koga et al., 2012).

FIGURE 2

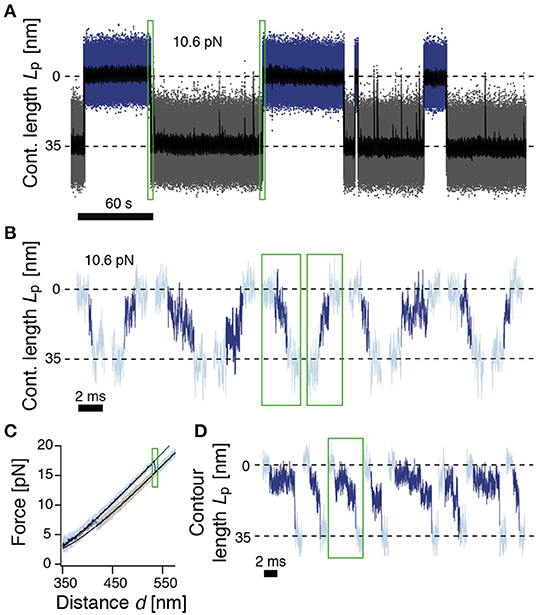
Figure 2. ROSS shows slow transitions between the native and unfolded states. (A) Passive-mode trajectory of equilibrium fluctuations between the native (blue, 0 nm) and unfolded states (gray, 35 nm of unfolded contour length). Black: Filtered trace to guide the eye. The indicated force is acting on the native state. (B) Extracted transitions between the native and unfolded states from passive-mode experiments. Dark colors show the identified trajectories during barrier crossing. Green boxes highlight exemplary positions in trace (A). (C) Force-distance curve at a pulling speed of 500 nm/s. Black solid lines are polymer model fits to the folded and unfolded conformations. (D) Unfolding transitions from force-distance curves. Dark colors indicate trajectories during barrier crossing. The trajectory in the green box corresponds to the trajectory shown in (C).

We next took a closer look into the transitions between the N and U states (Figure 2B). To identify parts of the trajectory on a barrier-crossing transition path, we used hidden Markov modeling with a transient state between N and U and considered parts of the trajectory that were classified into this transient state as barrier crossing events. We observed a diverse ensemble of trajectories, ranging from 140 μs to 5.5 ms in duration. The average folding duration (1.4 ± 0.2 ms) and unfolding duration (1.5 ± 0.2 ms) were identical, as expected (Neupane et al., 2016). Interestingly, the transitions were generally not unidirectional but showed frequent changes in direction and velocity as well as discernible pauses. Notably, the measured transition path times for ROSS were much slower than values obtained for a DNA hairpin (≈ 27 μs) (Neupane et al., 2016), the artificial protein α₃D (≈ 15 μs) (Chung and Eaton, 2013), or dimeric prion protein PrP (≈ 500 μs) (Neupane et al., 2016). The transition path duration of ROSS was also much slower than the predicted speed limit for the folding of a protein of 100 aa (≈ 1 μs) (Kubelka et al., 2004). To validate the resulting exceptionally slow barrier crossing time, we averaged aligned folding or unfolding transitions and fitted the resulting average relaxation response to a sigmoidal function (Supplementary Figure 4). The equivalent durations from this method were (0.7 ± 0.1 ms) for folding and (1.1 ± 0.1 ms) for unfolding, close to our previous results. Interestingly, transitions into non-native conformations were much faster and averaged ≈ 0.2 ms (Supplementary Figure 4C). Taken together, our observation of an exceptionally slow folding/unfolding time hint at the presence of a rugged barrier.

We suspected that the observed barrier crossing trajectories may be convoluted by thermal fluctuations of the beads that do not directly reflect changes in the protein end-to-end distance. We reasoned that this effect may be minimized at higher forces when the tension in the tether is higher and force fluctuations are thus minimized. To this end, we deliberately drove the system out of equilibrium with constant-velocity stretch-relax cycles and recorded the relaxation of the beads back to their equilibrium position at high bandwidth (Figure 2C). We note that during folding/unfolding, the trap position movement was ≈2 nm, much smaller than the observed bead relaxation amplitudes (≈15 nm). Hence, we do not anticipate significant bias from the active pulling protocol. Figure 2D shows representative relaxation trajectories of unfolding transitions that occurred at forces higher than 15 pN, thus fully excluding transitions that originate from the NL state. Contrary to expectations from a two-state model, and confirming our results from passive mode, the beads did not rapidly settle back into their relaxed position but displayed complicated trajectories for several milliseconds until relaxation, again hinting at a rugged barrier separating states N and U.

Transition Path Times of ROSS Depend on the Applied Force

The transition path times obtained from stretch-relax cycles probe the barrier at a different force bias and are thus not necessarily the same as those obtained from passive mode (Gladrow et al., 2019). Whereas, the N and U basins in our passive-mode experiments are approximately at the same energetic level, the U basin in typical stretch unfoldings lies ≈32 k_BT lower than the N basin. We, therefore, investigated whether the transition path times at higher forces, where the equilibrium is shifted toward the unfolded state, differs from the situation at low forces.

In the case of a symmetric harmonic barrier of significant height, the average transition path time is $\langle {\tau }_{\text{TP}}\rangle \approx \frac{ln\left(2e^{{\gamma }_E}·\beta ·\Delta G^{‡}\right)}{\beta ·D·{\omega }_{\text{TS}}^2}$ (Chung et al., 2009; Chaudhury and Makarov, 2010). Even though under increased force bias the approximation of a symmetric harmonic barrier no longer holds, the model predicts that 〈τ_TP〉 is largely unaffected by a shift to higher forces due to its logarithmic dependency on the barrier height, a result that was also confirmed experimentally for a DNA hairpin (Neupane et al., 2016).

We collected a dataset of the transition path times of ROSS folding/unfolding from passive-mode experiments and stretch-relax cycles where transitions occurred in a range between 5 and 20 pN (Figure 3A, also see Supplementary Figure 6 for an annotated and expanded version that also contains NL transitions). Surprisingly, we observed a clear correlation of increasing τ_TP with higher force (r = 0.53 ± 0.06, 99 % CI from bootstrapping), in stark disagreement with predictions from a harmonic barrier model. N → U transitions that occurred at ≈17 pN were much slower (3.9 ± 0.2 ms) than passive-mode N → U transitions at ≈10 pN (1.5 ± 0.2 ms, see above) or the corresponding reverse reaction U → N at ≈6 pN (0.9 ± 0.1 ms) (Supplementary Figure 6). To understand the significance of this observation, we performed diffusion simulations in a 1D potential for the case of a smooth harmonic barrier and the case of a barrier harboring a weakly stable intermediate (Supplementary Figure 7). Corroborating our suspicion, 〈τ_TP〉 was largely independent of force bias in the case of a harmonic barrier (Supplementary Figure 7B), but was force-dependent in the case of a barrier containing a weak intermediate (Supplementary Figure 7D). Together, these results confirmed our previous observation that ROSS folds over a rough barrier.

FIGURE 3

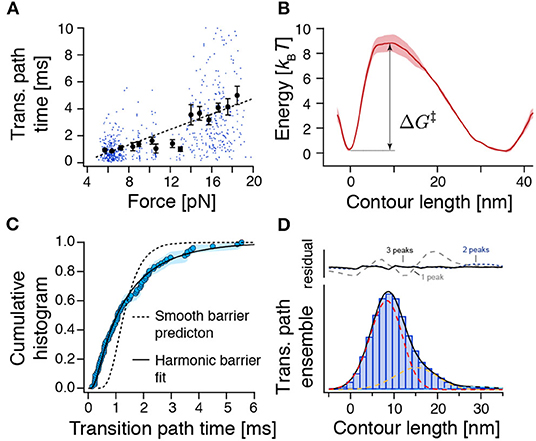
Figure 3. The force-dependence and distribution of transition path times as well as the transition path ensemble show unexpected results for crossing a single and smooth barrier. (A) Transition path time (TPT) versus force plot for measured TPTs between N and U from both constant-velocity and passive-mode experiments (n = 654). While dots represent individual data points, points with error bars represent average transition path times within their respective force range. The dashed line is a linear fit to guide the eye. The related Supplementary Figure 6 shows all detected transitions color coded according to their experimental origin. (B) Reconstructed free energy landscape from deconvolution of bead fluctuation histograms obtained from passive-mode experiments. (C) The distribution of experimental transition path times from passive-mode experiments (circles, n = 77) can be fitted to an approximation model for a central harmonic barrier [Equation (8), continuous line], albeit with unrealistic fit parameters (see text). Flux sampling simulations of one-dimensional diffusion over the deconvolved barrier shown in (B) predict a much narrower distribution (dashed line) that is incompatible with the experimental data (p = 5 × 10⁻⁶, KS test). (D) Position histogram of transition paths extracted from force-ramp experiments (bars, n = 85 transitions). Dashed lines represent fitted point-spread functions of three intermediates (see Methods). Black line: the sum of fitted point-spread functions. Upper panel: Fitting residuals scenarios of one, two, or three intermediates. ΔG^‡ represents the height of the energy barrier as in Equation (7).

Transition Path Times Are Incompatible With a Smooth Barrier

To get a more detailed picture of the folding barrier, we reconstructed the free energy landscape by deconvolving the bead fluctuation histograms obtained from passive-mode (constant-trap-separation) trajectories (Woodside et al., 2006; Gebhardt et al., 2010; Hinczewski et al., 2013; Ramm et al., 2014) (Figure 3B). However, because the time spent transitioning is an order of magnitude smaller than the time spent in the folded and unfolded states (≈0.01 %), the reconstructed energy landscape emphasized the N and U basins but failed to pick up any deviations from a smooth barrier profile. We found a single asymmetric barrier with $\Delta G^{‡}=8.8\pm 0.8k_{\text{B}}T$. Our measured barrier crossing time allowed us to estimate the diffusion constant of the reaction using (Hummer, 2004)

$\begin{array}{ll}\begin{array}{l}D=\frac{1}{\langle {\tau }_{\text{TP}}\rangle }{\int }_{x_A}^{x_B}{e}^{-\beta G(x)}{\Phi }_A(x){\Phi }_B(x)dx{\int }_{x_A}^{x_B}{e}^{\beta G(x)}dx,\end{array}& (10)\end{array}$

where Φ_A and Φ_B are committor functions (Hummer, 2004). We found D = 10^4.6±0.1nm²/s. A comparable value (D = 10^4.3±0.1nm²/s) was obtained when we used the approximation of a central harmonic barrier $D\approx \frac{ln\left(2e^{{\gamma }_E}·\beta ·\Delta G^{‡}\right)}{\beta ·\langle {\tau }_{\text{TP}}\rangle ·{\omega }^2}$ (Chung et al., 2009; Chaudhury and Makarov, 2010). An estimation of the diffusion constant based on the barrier height and the measured equilibrium transition rate constants between N and U using Kramers' theory (Kramers, 1940) ($D\approx 2\pi k\frac{e^{\Delta G^{‡}}}{\beta {\omega }^2}$) yielded a similar value of D = 10^4.6±0.4 nm²/s. Notably, this experimental diffusion constant is several orders of magnitude lower than the value expected for a protein that folds at its speed limit (τ_TP ≈ 1 μs, D ≈ 10^7.7 nm²/s) (Kubelka et al., 2004). Slowed diffusion can be interpreted in terms of a rough energy landscape (Zwanzig, 1988) $D=D_0{e}^{-{\left(\frac{{\epsilon }_{\text{RMS}}}{k_{\text{B}}T}\right)}^2}$, where ε_RMS is a measure of the roughness of the energy profile. Based on our measurements, we estimate ε_RMS ≈ 2.7 k_BT, which amounts to a sizeable ≈10% of the folding free energy.

The previous analysis only considered the average transition path time 〈τ_TP〉 and predicted a slow diffusion coefficient. We next also tested if the distribution of experimental transition path times is compatible with a one-dimensional diffusion model for the deconvolved barrier profile (Figure 3C). However, we found that the model (flux sampling calculation with D = 10^4.6nm²/s, dashed line) predicts a much narrower distribution than the experimental data. An approximation model for a central harmonic barrier [Equation (8), continuous line] could be fitted to the data. Nevertheless, the obtained parameters of D ≈ 10^3.8 nm²/s and $\Delta G^{‡}\approx 0.2k_{\text{B}}T$ were incompatible with the smooth-barrier estimations obtained earlier (D = 10^4.6±0.1nm²/s, $\Delta G^{‡}=8.8\pm 0.8k_{\text{B}}T$). Notably, a similar discrepancy has been observed also for PrP (Neupane et al., 2016). We conclude that the smooth barrier obtained from deconvolution (Figure 3B) is incompatible with the wide distribution of observed transition path times.

Weak Transient Intermediates Cause Slow Transition Paths

To understand the extraordinarily slow TPTs of ROSS, we took a closer look at the ensemble of trajectories during barrier crossing p(x|TP). Figure 3D shows a position histogram of transition paths obtained from force-ramp experiments as shown in Figure 2D. Interestingly, the measured histogram was peaked at ≈9 nm, which is unexpected for a symmetric barrier (Hummer, 2004) but is in good agreement with the location of the identified barrier position from deconvolution (Figure 3B). The same indication of an asymmetric barrier was found in passive-mode experiments (Supplementary Figure 8).

We suspected that the protein populates weakly metastable on-pathway intermediates that slow down the overall transition and thus give rise to the notion of a rough energy landscape. We reasoned that the population of intermediates may produce elongated pauses at certain positions along the reaction coordinate of unfolded contour length that should be visible in transition path ensembles. Indeed, when comparing p(x|TP) with the point-spread function (PSF) for intermediates, we noticed that at least three intermediates are necessary to fit the experimental p(x|TP) (Figure 3D). While it is technically not possible to assign thermodynamically correct population densities to the intermediates, because of the non-equilibrium way the transition paths to produce p(x|TP) are selected, the described procedure nevertheless clearly hints at the population of intermediates.

While intermediates were hidden in deconvolution of the equilibrium distribution (Figure 3B), the intermediates can be readily seen when the deconvolution procedure was applied to the transition path ensemble p(x|TP) (Supplementary Figure 9), where the selection emphasizes parts of the trajectory that cross the barrier. However, because of this selection, the obtained probability distribution cannot be Boltzmann inverted to obtain a reconstruction of the barrier.

Reconstruction of the Energy Barrier

We, therefore, reverted to approximating the energy barrier based on force-dependent transition rate constants between N and U. WLC-model fits to high-force unfolding trajectories revealed the positions of three high-energy intermediates I₁-I₃ (Figures 4A,B, Supplementary Figure 10). We obtained L_p(I₁) = 8.3 ± 1.1 nm, L_p(I₂) = 17.6 ± 1.9 nm, L_p(I₃) = 26.5 ± 2.1 nm, where L_p(N) = 0 nm.

FIGURE 4

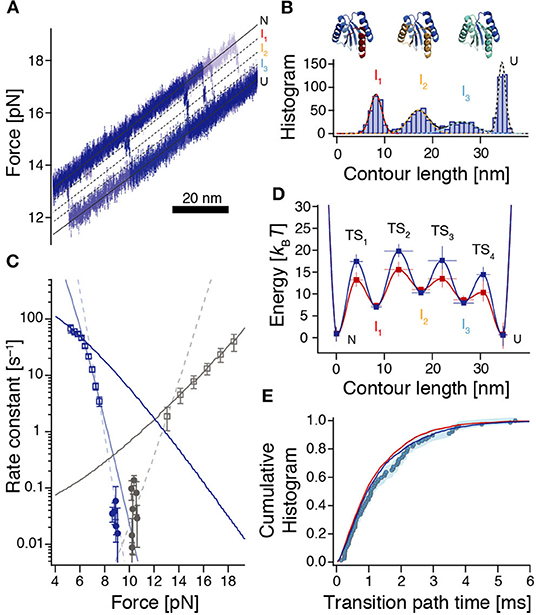
Figure 4. Reconstruction of the rough energy landscape of ROSS. (A) Example of six high-resolution unfolding trajectories from constant-velocity experiments used to reveal positions of high-energy intermediates. Black lines indicate the corresponding positions. (B) Contour length gain histogram based on WLC-fits to unfolding events from force-ramp experiments (n = 1010 from 304 unfolding events). Colored dashed lines are fits to the individual peaks resulting from a Gaussian multi-peak fit to the entire histogram. Top: Assignment of unfolded structural elements of ROSS to the intermediates. (C) Force-dependent rates for folding (dark blue) and unfolding (gray) of ROSS extracted from constant-velocity (squares) and passive-mode experiments (circles). Continuous lines are local fits [Equation (S6)] to the data. Dashed lines interpolate between the accessible force ranges of constant-velocity and passive-mode experiments and illustrate the notion of switches of the dominant transition barrier in different force regimes. (D) Reconstructed energy landscape for ROSS. For the dark blue landscape, we assumed that folding transitions are fundamentally limited by speed limit protein folding (D ≈ 10^7.7 nm²/s); for the dark red landscape, we assumed that the speed of our observation is fundamentally limited by the bead diffusion in our optical trap (D ≈ 10⁶ nm²/s). See Supplementary Tables 1, 2 for parameters of the energy landscapes. (E) The experimentally derived transition path time distribution (circles, same data as in Figure 3C) is well-reproduced by the distributions predicted from the energy landscapes shown in (D) [dark blue (p = 0.22, KS test) and red (p = 0.12, KS test) lines, respectively].

To identify the position of the dominant transition barrier we determined the force-dependent rate constants for folding and unfolding (Figure 4C), where we used both data from passive-mode and stretch-relax experiments, and fitted a model that incorporates the energetic contributions of all compliances in the system (Schlierf et al., 2007). Notably, this model assumes that transition state positions are independent of the applied force. Therefore, kinks in the force-dependent rate plots or corresponding deviations from the model indicate a switch of the dominant transition barrier (Schlierf et al., 2010; Rico et al., 2019). Based on unfolding and refolding events observed during constant-velocity measurements, we identified three force ranges where extracted rates could be fitted locally (Figure 4C, continuous lines). In addition, rate constants extracted from passive-mode experiments suggest that there must be at least one more force range with a different predominant transition state since these rates are substantially lower than any of the three fits would suggest. Taken together, this yields four required transition states to interpret our data, in agreement with our finding of three intermediate states I₁, I₂, and I₃ between N and U. The force at which the TS₃:TS₄ transition state switch occurs, lies at around 6.3 pN (force of U), which is directly given by the intersection of the respective rate fits. The transition state switches TS₂:TS₃ and TS₁:TS₂ occur around 7.5 pN and 13 pN, respectively. The slopes from the fitted rate constants indicate transition state positions TS₁ = 3.1 ± 0.3 nm between N and I₁, TS₃ = 19.4 ± 1.1 nm between I₂ and I₃, as well as TS₄ = 30.5 ± 1.3 nm between I₃ and U. Due to the very slow folding kinetics and the narrow accessible force range for measurements in passive-mode, no position could directly be derived from our data for TS₂. However, interpolations between rate constants obtained from stretch-relax cycles and passive-mode experiments suggest that the TS₂ position is situated at ≈ 10 – 12 nm which is right between I₁ and I₂ (Figure 4C, dashed fits).

To obtain values for the energies of the intermediates and transition states, we employed a piecewise reconstruction method where we determined individual effective barrier heights for each dominant barrier position [i.e., at different force biases, based on the measured dwell time distribution and Kramers' rate equation (Hänggi et al., 1990, Supporting Methods)]. Reasoning that the experimentally determined transition path times are likely dominated by metastable dwells in high-energy intermediates, we fitted the transition path time distribution to a model where the barrier crossing time is determined by the sequential population of the three intermediates I₁, I₂, and I₃. The corresponding rate constants for the escape rates from I₁, I₂, and I₃ were then translated into barrier heights using Kramers' rate equation, where we assigned the longest dwell to I₁ and the shortest dwell to I₃, in line with our observations (Figures 2B,D, 3D). Finally, we used the experimentally determined rate constants between N and U and the switch of the dominant transition barrier at different force bias to determine the missing barrier heights (Supplementary Figure 11 and Supporting Methods).

All reconstruction steps depend on an assumption of the diffusion constant D. Since bumps in the energy profile slow down the observed transitions, our experiments imply that a realistic intrinsic D must be higher than the smooth barrier estimation of D ≈ 10^4.6 nm²/s. Here we did the reconstruction for two cases: The assumption that folding is fundamentally limited by the folding speed limit (D ≈ 10^7.7 nm²/s) and the assumption that the speed of our observations is fundamentally limited by the diffusion of the beads in the optical trap (D ≈ 10⁶ nm²/s). The resulting barrier reconstructions mostly only differ in the barrier heights and are shown in Figure 4D.

A Barrier Harboring High-Energy Intermediates Agrees With Pulling Variants and Reproduces Experimental Transition Path Time Distributions

To verify our barrier reconstruction, we again used flux sampling simulations to determine the distribution of transition path times, based on the reconstructions shown in Figure 4D. In contrast to the smooth barrier case, this barrier profile yielded a much wider transition path time distribution that matched the experimental data very well (Figure 4E). In addition, we also performed Langevin dynamics simulations within the energy landscapes of Figure 4D to show that the ensembles of transition paths predicted from the reconstructions agree with experimental distributions (Supplementary Figure 12).

Corroborating evidence for the validity of our energy landscape reconstruction comes from a directional pulling mutant of ROSS, S49Cc, where force was only applied between residue 49 and the c-terminus. This variant also harbored an intermediate, which matched the I₁ intermediate of ROSS both in length (8.0 ± 0.9 nm) and in energy (−15 ± 2 k_BT) (ROSS: 8.3 ± 1.1 nm and −15 ± 3 k_BT, respectively; see Supplementary Figures 13, 14). In addition, the obligatory intermediate of S49Cc attains its maximal population at ≈13 pN, with an average dwell time of ≈2 ms. This closely resembles the properties of the corresponding I₁ intermediate of ROSS, which also reaches its maximum population at ≈13 pN, with a comparable lifetime (Supplementary Figure 15). Taken together, these results suggest that typical ROSS unfolding occurs via the unfolding of the c-terminal half of the protein, where the length of the first intermediate is compatible with the unraveling of the c-terminal helix.

As shown earlier, metastable intermediates in the barrier may cause a shift in the average transition path time with varying force (cf. Supplementary Figure 7). We determined the predicted variation of 〈τ_TP〉, based on the energy landscapes of Figure 4D analytically and with simulations. While both energy profiles correctly predicted an increase of 〈τ_TP〉 with increasing force, both also predict a subsequent decrease above about 13 pN (Supplementary Figure 15). While this behavior was directly observed in the variant S49Cc (Supplementary Figure 14C), the same trend reversal was not apparent in experimental data of ROSS (Figure 3A), suggesting that perhaps, a one-dimensional description of the energy barrier may not be adequate for ROSS, or the non-equilibrium protocol used for obtaining transition path times at high forces may probe different transition paths (Gladrow et al., 2019).

Discussion

In summary, ROSS exhibits remarkably slow transitions over the barrier between the folded and unfolded states, much slower than the transitions of other systems observed in optical tweezers (Neupane et al., 2016; Hoffer et al., 2019). FRET experiments generally have yielded even faster transition path times (Chung et al., 2012; Chung and Eaton, 2013). However, timescales are not directly comparable between different experimental techniques, because of the time-limiting effect of the measurement apparatus (Cossio et al., 2015, 2018; De Sancho et al., 2018). The best-characterized system in optical tweezers, DNA hairpins, generally displays much faster transitions than proteins (Neupane et al., 2016), likely because their transitions, owing to the experimental unzipping geometry, are well-described by a one-dimensional diffusion model (Neupane et al., 2012).

Slow transition path times have been discussed in the context of internal friction, frustration, or energy profile roughness (Liu et al., 2009; Wensley et al., 2010; Borgia et al., 2012; Chung et al., 2015), but our analysis revealed that none of these can explain the wide transition path time distribution of ROSS. Instead, we found evidence of a series of on-pathway intermediates that are briefly populated during barrier crossing. A similar mechanism has been observed for the coupled folding and binding of IDPs (Sturzenegger et al., 2018).

The slow transition path times of ROSS raise the interesting possibility that its impeded folding may be a consequence of its origin in artificial design. Indeed, most design algorithms, such as Rosetta optimize an equilibrium low energy state of the native target structure, compared to non-native interactions (Koga et al., 2012), but not the pathway of folding. The high-energy intermediates observed in our measurements may be caused by improper packing of individual alpha or beta secondary structures. The population of these non-native contacts, especially under denaturing conditions, may effectively hinder efficient folding. On the other hand, high-energy intermediates may also act as “checkpoints” in the folding landscape that can aid folding along a specific pathway, at the expense of overall cooperativity.

Notably, Rosetta structure prediction simulations indicate that ROSS may indeed adopt a non-native fold that is energetically very close to the native design structure (Koga et al., 2012). It is unclear if we observe this conformation in our experiments. However, possible candidates are the NL states and fast probing events observed in both variants. Interestingly, the fraction of NL states in the pulling variant S49Cc, where force is only applied across the c-terminal half, is significantly reduced from ≈23 to ≈7% (p < 0.01, binomial test), suggesting that NL states may be caused by non-native interactions between the n-terminal and the c-terminal halves.

Interestingly, the extremely slow transition path time of ROSS was only apparent in transitions between the native and unfolded conformations. Other transitions, such as incomplete folding events (Supplementary Figure 4C), were faster by almost an order of magnitude. In the context of a one-dimensional energy landscape, these probing events may correspond to partial barrier crossings from U to I₁. Indeed, our model predicts that such a partial crossing of the barrier lasts ≈150 μs, close to experimental values. However, this scenario fails to explain why under passive-mode conditions, there appear to be more probing events than successful folding transitions, requiring that the barrier TS₁ must be higher than TS₂. Therefore, an alternative explanation may be that the energy landscape of ROSS is multi-dimensional and our reconstruction only captures a projection of the true energy landscape.

A scenario of multidimensionality may result in position-dependent diffusion along the projected experimentally accessible energy landscape and, under certain circumstances, also result in a distribution of TPTs that is compatible with experiments. Supplementary Figure 16 illustrates this at the example of the smooth barrier of Figure 3B, where the diffusion coefficient was set to D = 10^7.7 nm²/s everywhere except in a close neighborhood around I₁ where we set D = 10^3.4 nm²/s. However, while this model can also reproduce the experimental TPT distribution (Supplementary Figure 16B), it fails to explain the experimentally observed force dependence of 〈τ_TP〉 (Supplementary Figure 16C). While it may be possible to build a position-dependent diffusivity model that also reproduces a force-dependent 〈τ_TP〉 (e.g., by requiring a force-dependent change of D), the basis for this is rather speculative. On the contrary, the reconstructions of Figure 4D reproduce both the distribution and force-dependence of TPTs, without the need for additional assumptions.

Finally, our results allow us to infer a structural interpretation of the rearrangements during barrier crossing (Figure 4B, top). Unfolding of ROSS starts via I₁ which can be attributed to the unfolding of the c-terminal α-helix., while the proximate β-sheet remains bound to the hydrophobic core. After I₁, unfolding continues via I₂ which can be attributed to the unfolding of the first three structural elements αβα starting from the c-terminus. The last and very weak intermediate I₃ most likely represents a conformation where only the n-terminal β-sheet and the successive α-helix remain folded, a possible folding seed for ROSS.

In summary, here we have presented a single-molecule folding study of the artificially designed protein ROSS. The protein showed exceptionally slow transition path times that are incompatible with a smooth transition barrier but could be explained by the presence of high-energy intermediates. Our results illustrate that high-energy folding intermediates slow the barrier crossing of all reaction systems and raise the question of whether uncharacteristically slow transition path times may be a trait of many protein structures that have been optimized for folding stability instead of folding speed (Basak et al., 2019).

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

AM conducted experiments. JS and AM analyzed data. BP, JF, and HL contributed reagents and methods. JS conceived of the study and wrote the paper with input from all authors. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The gene for 2x2 ROSS was a kind gift by David Baker. JS acknowledges the support by the LMU Center for Nanoscience CeNS and a DFG Emmy Noether grant STI673/2-1. HL acknowledges the support of an Alexander von Humboldt fellowship.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2020.587824/full#supplementary-material

References

Anfinsen, C. B., Haber, E., Sela, M., and White, F. H. (1961). The kinetics of formation of native ribonuclease during oxidation of the reduced polypeptide chain. PNAS 47, 1309–1314. doi: 10.1073/pnas.47.9.1309

PubMed Abstract | CrossRef Full Text | Google Scholar

Azzalini, A. (1985). A class of distributions which includes the normal ones. Scand. J. Statist. 12, 171–178.

Google Scholar

Basak, S., Nobrega, R. P., Tavella, D., Deveau, L. M., Koga, N., Tatsumi-Koga, R., et al. (2019). Networks of electrostatic and hydrophobic interactions modulate the complex folding free energy surface of a designed βα protein. PNAS 116, 6806–6811. doi: 10.1073/pnas.1818744116

PubMed Abstract | CrossRef Full Text | Google Scholar

Borgia, A., Wensley, B. G., Soranno, A., Nettels, D., Borgia, M. B., Hoffmann, A., et al. (2012). Localizing internal friction along the reaction coordinate of protein folding by combining ensemble and single-molecule fluorescence spectroscopy. Nat. Commun. 3, 1195–1199. doi: 10.1038/ncomms2204

PubMed Abstract | CrossRef Full Text | Google Scholar

Bustamante, C., Marko, J. F., Siggia, E. D., and Smith, S. (1994). Entropic elasticity of lambda-phage DNA. Science 265, 1599–1600. doi: 10.1126/science.8079175

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaudhury, S., and Makarov, D. E. (2010). A harmonic transition state approximation for the duration of reactive events in complex molecular rearrangements. J. Chem. Phys. 133, 034118–034112. doi: 10.1063/1.3459058

PubMed Abstract | CrossRef Full Text | Google Scholar

Chung, H. S., and Eaton, W. A. (2013). Single-molecule fluorescence probes dynamics of barrier crossing. Nature 502, 685–688. doi: 10.1038/nature12649

PubMed Abstract | CrossRef Full Text | Google Scholar

Chung, H. S., Louis, J. M., and Eaton, W. A. (2009). Experimental determination of upper bound for transition path times in protein folding from single-molecule photon-by-photon trajectories. PNAS 106, 11837–11844. doi: 10.1073/pnas.0901178106

PubMed Abstract | CrossRef Full Text | Google Scholar

Chung, H. S., McHale, K., Louis, J. M., and Eaton, W. A. (2012). Single-molecule fluorescence experiments determine protein folding transition path times. Science 335, 981–984. doi: 10.1126/science.1215768

PubMed Abstract | CrossRef Full Text | Google Scholar

Chung, H. S., Piana-Agostinetti, S., Shaw, D. E., and Eaton, W. A. (2015). Structural origin of slow diffusion in protein folding. Science 349, 1504–1510. doi: 10.1126/science.aab1369

PubMed Abstract | CrossRef Full Text | Google Scholar

Collin, D., Ritort, F., Jarzynski, C., Smith, S. B., Tinoco, I., and Bustamante, C. (2005). Verification of the Crooks fluctuation theorem and recovery of RNA folding free energies. Nature 437, 231–234. doi: 10.1038/nature04061

PubMed Abstract | CrossRef Full Text | Google Scholar

Cossio, P., Hummer, G., and Szabo, A. (2015). On artifacts in single-molecule force spectroscopy. PNAS 112, 14248–14253. doi: 10.1073/pnas.1519633112

PubMed Abstract | CrossRef Full Text | Google Scholar

Cossio, P., Hummer, G., and Szabo, A. (2018). Transition paths in single-molecule force spectroscopy. J. Chem. Phys. 148, 123309–123311. doi: 10.1063/1.5004767

PubMed Abstract | CrossRef Full Text | Google Scholar

Covino, R., Woodside, M. T., Hummer, G., Szabo, A., and Cossio, P. (2019). Molecular free energy profiles from force spectroscopy experiments by inversion of observed committors. J. Chem. Phys. 151:154115. doi: 10.1063/1.5118362

PubMed Abstract | CrossRef Full Text | Google Scholar

Crooks, G. E. (1999). Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E. 60, 2721–2726. doi: 10.1103/PhysRevE.60.2721

PubMed Abstract | CrossRef Full Text | Google Scholar

De Sancho, D., Schönfelder, J., Best, R. B., Perez-Jimenez, R., and Muñoz, V. (2018). Instrumental effects in the dynamics of an ultrafast folding protein under mechanical force. J. Phys. Chem. B 122, 11147–11154. doi: 10.1021/acs.jpcb.8b05975

PubMed Abstract | CrossRef Full Text | Google Scholar

Fang, J., Mehlich, A., Koga, N., Huang, J., Koga, R., Gao, X., et al. (2013). Forced protein unfolding leads to highly elastic and tough protein hydrogels. Nat. Commun. 4:2974. doi: 10.1038/ncomms3974

PubMed Abstract | CrossRef Full Text | Google Scholar

Gebhardt, J. C., Bornschlögl, T., and Rief, M. (2010). Full distance-resolved folding energy landscape of one single protein molecule. PNAS 107, 2013–2018. doi: 10.1073/pnas.0909854107

PubMed Abstract | CrossRef Full Text | Google Scholar

Geier, F., Fengos, G., Felizzi, F., and Iber, D. (2007). Numerical Recipes 3rd Edition: The Art of Scientific Computing. 3rd ed. Cambridge: Cambridge University Press.

Google Scholar

Gladrow, J., Ribezzi-Crivellari, M., Ritort, F., and Keyser, U. F. (2019). Experimental evidence of symmetry breaking of transition-path times. Nat. Commun. 10:55. doi: 10.1038/s41467-018-07873-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Hänggi, P., Talkner, P., and Borkovec, M. (1990). Reaction-rate theory: fifty years after Kramers. Rev. Modern Phys. 62:251. doi: 10.1103/RevModPhys.62.251

CrossRef Full Text | Google Scholar

Hinczewski, M., Gebhardt, J. C., Rief, M., and Thirumalai, D. (2013). From mechanical folding trajectories to intrinsic energy landscapes of biopolymers. PNAS 110, 4500–4505. doi: 10.1073/pnas.1214051110

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoffer, N. Q., Neupane, K., Pyo, A. G. T., and Woodside, M. T. (2019). Measuring the average shape of transition paths during the folding of a single biological molecule. PNAS 116, 8125–8130. doi: 10.1073/pnas.1816602116

PubMed Abstract | CrossRef Full Text | Google Scholar

Hummer, G. (2004). From transition paths to transition states and rate coefficients. J. Chem. Phys. 120, 516–523. doi: 10.1063/1.1630572

PubMed Abstract | CrossRef Full Text | Google Scholar

Junker, J. P., Ziegler, F., and Rief, M. (2009). Ligand-dependent equilibrium fluctuations of single calmodulin molecules. Science 323, 633–637. doi: 10.1126/science.1166191

PubMed Abstract | CrossRef Full Text | Google Scholar

Koga, N., Tatsumi-Koga, R., Liu, G., Xiao, R., Acton, T. B., Montelione, G. T., et al. (2012). Principles for designing ideal protein structures. Nature 491, 222–227. doi: 10.1038/nature11600

PubMed Abstract | CrossRef Full Text | Google Scholar

Kramers, H. (1940). Brownian motion in a field of force and the diffusion model of chemical reactions. Physica 7, 284–304. doi: 10.1016/S0031-8914(40)90098-2

CrossRef Full Text | Google Scholar

Kubelka, J., Hofrichter, J., and Eaton, W. A. (2004). The protein folding “speed limit.” Curr. Opin. Struct. Biol. 14, 76–88. doi: 10.1016/j.sbi.2004.01.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuhlman, B., and Bradley, P. (2019). Advances in protein structure prediction and design. Nat. Rev. Mol. Cell Biol. 20, 681–697. doi: 10.1038/s41580-019-0163-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Laleman, M., Carlon, E., and Orland, H. (2017). Transition path time distributions. J. Chem. Phys. 147, 214103–214110. doi: 10.1063/1.5000423

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, F., Nakaema, M., and Gruebele, M. (2009). The transition state transit time of, W. W. domain folding is controlled by energy landscape roughness. J. Chem. Phys. 131, 195101–195110. doi: 10.1063/1.3262489

PubMed Abstract | CrossRef Full Text | Google Scholar

Mehlich, A. (2018). Transition Paths of Protein-Folding Probed With Optical Tweezers (Aachen: Shaker Verlag).

Google Scholar

Mehlich, A., Austen, K., Ringer, P., Grashoff, C., and Rief, M. (2015). Evaluation of molecular tension sensors using single-molecule force spectroscopy and live cell FRET imaging. Protocol Exchange. doi: 10.1038/protex.2015.095. [Epub ahead of print].

CrossRef Full Text | Google Scholar

Neupane, K., Foster, D. A., Dee, D. R., Yu, H., Wang, F., and Woodside, M. T. (2016). Direct observation of transition paths during the folding of proteins and nucleic acids. Science 352, 239–242. doi: 10.1126/science.aad0637

PubMed Abstract | CrossRef Full Text | Google Scholar

Neupane, K., Hoffer, N. Q., and Woodside, M. T. (2018). Measuring the local velocity along transition paths during the folding of single biological molecules. Phys. Rev. Lett. 121:018102. doi: 10.1103/PhysRevLett.121.018102

PubMed Abstract | CrossRef Full Text | Google Scholar

Neupane, K., Ritchie, D. B., Yu, H., Foster, D. A., Wang, F., and Woodside, M. T. (2012). Transition path times for nucleic Acid folding determined from energy-landscape analysis of single-molecule trajectories. Phys. Rev. Lett. 109:068102. doi: 10.1103/PhysRevLett.109.068102

PubMed Abstract | CrossRef Full Text | Google Scholar

Neupane, K., Wang, F., and Woodside, M. T. (2017). Direct measurement of sequence-dependent transition path times and conformational diffusion in DNA duplex formation. PNAS 114, 1329–1334. doi: 10.1073/pnas.1611602114

PubMed Abstract | CrossRef Full Text | Google Scholar

Oberbarnscheidt, L., Janissen, R., and Oesterhelt, F. (2009). Direct and model free calculation of force-dependent dissociation rates from force spectroscopic data. Biophys. J. 97, L19–L21. doi: 10.1016/j.bpj.2009.08.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Onuchic, J. N., Luthey-Schulten, Z., and Wolynes, P. G. (1997). Theory of protein folding: the energy landscape perspective. Ann. Rev. Phys. Chem. 48, 545–600. doi: 10.1146/annurev.physchem.48.1.545

PubMed Abstract | CrossRef Full Text | Google Scholar

Puchner, E. M., Franzen, G., Gautel, M., and Gaub, H. E. (2008). Comparing proteins by their unfolding pattern. Biophys. J. 95, 426–434. doi: 10.1529/biophysj.108.129999

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramm, B., Stigler, J., Hinczewski, M., Thirumalai, D., Herrmann, H., Woehlke, G., et al. (2014). Sequence-resolved free energy profiles of stress-bearing vimentin intermediate filaments. PNAS 111, 11359–11364. doi: 10.1073/pnas.1403122111

PubMed Abstract | CrossRef Full Text | Google Scholar

Rico, F., Russek, A., González, L., Grubmüller, H., and Scheuring, S. (2019). Heterogeneous and rate-dependent streptavidin-biotin unbinding revealed by high-speed force spectroscopy and atomistic simulations. PNAS 116, 6594–6601. doi: 10.1073/pnas.1816909116

PubMed Abstract | CrossRef Full Text | Google Scholar

Rief, M., Gautel, M., Oesterhelt, F., Fernandez, J. M., and Gaub, H. E. (1997). Reversible unfolding of individual titin immunoglobulin domains by AFM. Science 276, 1109–1112. doi: 10.1126/science.276.5315.1109

PubMed Abstract | CrossRef Full Text | Google Scholar

Rief, M., Rock, R. S., Mehta, A. D., Mooseker, M. S., Cheney, R. E., and Spudich, J. A. (2000). Myosin-V stepping kinetics: a molecular model for processivity. PNAS 97, 9482–9486. doi: 10.1073/pnas.97.17.9482

PubMed Abstract | CrossRef Full Text | Google Scholar

Rognoni, L., Möst, T., Zoldák, G., and Rief, M. (2014). Force-dependent isomerization kinetics of a highly conserved proline switch modulates the mechanosensing region of filamin. PNAS 111, 5568–5573. doi: 10.1073/pnas.1319448111

PubMed Abstract | CrossRef Full Text | Google Scholar

Schlierf, M., Berkemeier, F., and Rief, M. (2007). Direct observation of active protein folding using lock-in force spectroscopy. Biophys. J. 93, 3989–3998. doi: 10.1529/biophysj.107.114397

PubMed Abstract | CrossRef Full Text | Google Scholar

Schlierf, M., Yew, Z. T., Rief, M., and Paci, E. (2010). Complex unfolding kinetics of single-domain proteins in the presence of force. Biophys. J. 99, 1620–1627. doi: 10.1016/j.bpj.2010.06.039

PubMed Abstract | CrossRef Full Text | Google Scholar

Soranno, A., Buchli, B., Nettels, D., Cheng, R. R., Müller-Späth, S., Pfeil, S. H., et al. (2012). Quantifying internal friction in unfolded and intrinsically disordered proteins with single-molecule spectroscopy. PNAS 109, 17800–17806. doi: 10.1073/pnas.1117368109

PubMed Abstract | CrossRef Full Text | Google Scholar

Stigler, J., and Rief, M. (2012). Hidden markov analysis of trajectories in single-molecule experiments and the effects of missed events. Chemphyschem 13, 1079–1086. doi: 10.1002/cphc.201100814

PubMed Abstract | CrossRef Full Text | Google Scholar

Stigler, J., Ziegler, F., Gieseke, A., Gebhardt, J. C., and Rief, M. (2011). The complex folding network of single calmodulin molecules. Science 334, 512–516. doi: 10.1126/science.1207598

PubMed Abstract | CrossRef Full Text | Google Scholar

Sturzenegger, F., Zosel, F., Holmstrom, E. D., Buholzer, K. J., Makarov, D. E., Nettels, D., et al. (2018). Transition path times of coupled folding and binding reveal the formation of an encounter complex. Nat. Commun. 9:4708. doi: 10.1038/s41467-018-07043-x

PubMed Abstract | CrossRef Full Text | Google Scholar

von Hansen, Y., Mehlich, A., Pelz, B., Rief, M., and Netz, R. R. (2012). Auto- and cross-power spectral analysis of dual trap optical tweezer experiments using Bayesian inference. Rev. Sci. Instr. 83:095116. doi: 10.1063/1.4753917

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, M. D., Yin, H., Landick, R., Gelles, J., and Block, S. M. (1997). Stretching DNA with optical tweezers. Biophys. J. 72, 1335–1346. doi: 10.1016/S0006-3495(97)78780-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Wensley, B. G., Batey, S., Bone, F. A., Chan, Z. M., Tumelty, N. R., Steward, A., et al. (2010). Experimental evidence for a frustrated energy landscape in a three-helix-bundle protein family. Nature 463, 685–688. doi: 10.1038/nature08743

PubMed Abstract | CrossRef Full Text | Google Scholar

Woodside, M. T., Anthony, P. C., Behnke-Parks, W. M., Larizadeh, K., Herschlag, D., and Block, S. M. (2006). Direct measurement of the full, sequence-dependent folding landscape of a nucleic acid. Science 314:1001. doi: 10.1126/science.1133601

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, H., Liu, X., Neupane, K., Gupta, A. N., Brigley, A. M., Solanki, A., et al. (2012). Direct observation of multiple misfolding pathways in a single prion protein molecule. PNAS 109, 5283–5288. doi: 10.1073/pnas.1107736109

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, B. W., Jasnow, D., and Zuckerman, D. M. (2007). Transition-event durations in one-dimensional activated processes. J. Chem. Phys. 126, 074504–074519. doi: 10.1063/1.2434966

PubMed Abstract | CrossRef Full Text | Google Scholar

Žoldák, G., Stigler, J., Pelz, B., Li, H., and Rief, M. (2013). Ultrafast folding kinetics and cooperativity of villin headpiece in single-molecule force spectroscopy. PNAS 110, 18156–18161. doi: 10.1073/pnas.1311495110

PubMed Abstract | CrossRef Full Text | Google Scholar

Zwanzig, R. (1988). Diffusion in a rough potential. PNAS 85, 2029–2030. doi: 10.1073/pnas.85.7.2029

PubMed Abstract | CrossRef Full Text | Google Scholar