- 1Department of Physics, Chongqing University of Arts and Sciences, Chongqing, China
- 2Faculty of Mechanical and Electrical Engineering, Kunming University of Science and Technology, Kunming, China
Very recently, topological semimetals with nontrivial band crossing and associated topological surface states have received widespread attention. Various types of topological semimetals, including nodal point semimetals, nodal line semimetals, and nodal surface semimetals, have been predicted from first principles. In absence of spin-orbit coupling (SOC) effect, we propose that cubic-type hafnium nitride (HfN) with a space group is a novel topological semimetal hosting a rare 0-D triple nodal point and a 1-D topological nodal ring. More importantly, the interesting 0-D and 1-D topological states all occur near the Fermi level, and these topological states are not disturbed by other extraneous bands. When the SOC effect is taken into consideration, 0-D triple nodal point was gapped and a new 0-D topological element, namely, Dirac point appears along Γ-R path. Finally, the dynamical and mechanical stabilities of this semimetal and its associated mechanical properties are discussed in order to provide a reference for future investigations. Our work promises that HfN can serve as a superior topological semimetal with high stability, excellent mechanical properties, and rich topological states.
Introduction
After the discovery of topological insulators (Zhang et al., 2009; Hasan and Kane, 2010; Yu et al., 2010; Qi and Zhang, 2011; Rechtsman et al., 2013), topological semimetals (Jiang et al., 2015; Fang et al., 2016; Chang et al., 2017; Yan and Felser, 2017; Gao et al., 2019) with topological band inversion and exotic topological boundary states have attracted widespread attention. To date, many types of topological semimetals have been proposed, including topological nodal point semimetals (Liu et al., 2013, 2019; Li et al., 2014; Xu et al., 2014, 2016, 2020; Dvorak and Wu, 2015; Cheng et al., 2017; Zhong et al., 2017; Gao et al., 2019; Zhang et al., 2019), topological nodal line semimetals (Cai et al., 2018; Chen et al., 2018; Gao et al., 2018; Zhou et al., 2018; He et al., 2019; Jin et al., 2019a; Pham et al., 2019; Yi et al., 2019; Zou et al., 2019; Zhao et al., 2020), and topological nodal surface semimetals (Qie et al., 2019; Yang and Zhang, 2020).
For nodal point semimetals, the most studied members among them are Weyl and Dirac semimetals. Weyl semimetals (Hosur and Qi, 2013; Soluyanov et al., 2015; Zheng et al., 2016; Lin et al., 2017; Zhang M. et al., 2018; Bedoyapinto et al., 2020; Geishendorf et al., 2020; Thakur et al., 2020) possess twofold degenerate 0-D Weyl nodes, which are protected by inversion (P) or time-reversal (T) symmetries. However, Dirac semimetals (Chen et al., 2015; Gong et al., 2017; Yuan et al., 2017; Zhang X. et al., 2018; Jing and Heine, 2019) host quadruple-degenerate 0-D Dirac points, and these massless Dirac points are protected by the crystalline symmetry. In addition to the Weyl and Dirac semimetals generated by twofold- or quadruple-degenerate nodal points, topological nodal point semimetals with triple-degenerate 0-D nodal points have also become a new focus of research due to their novel topological states and related physics properties. Among inversion-asymmetric and centrosymmetric systems, some members are proposed to be triple point-type semimetals (He et al., 2017; Lv et al., 2017).
Moreover, topological nodal line semimetals (Cai et al., 2018; Chen et al., 2018; Zhou et al., 2018; Pham et al., 2019; Yi et al., 2019) possess 1-D topological elements, which are formed by band crossing along a line in momentum space. Compared to the topological nodal point semimetals with 0-D topological elements, topological nodal line semimetals feature more subtypes due to the fact that the 1-D line can deform into many different geometries. Topological nodal ring semimetals with a 1-D nodal loop in momentum space form one well-known type of topological nodal line semimetal. Topological nodal ring semimetals have emerged as a hot research topic very recently because these topological materials have intriguing electronic band behaviors and interesting drum-head-like surface states.
Topological materials are suitable for a range of potential applications, such as superconductivity (Das et al., 2012), chemical sensors (Schoop et al., 2018), and thermoelectricity (Sung et al., 2014). However, the candidates for such topological semimetals that possess more than one topological element are quite limited, which greatly restricts further investigations into those topological semimetals with rich topological elements. We would like to point out that materials with CsCl-type enjoy many interesting properties, such as simple in crystal structure, easy of synthesis and high phase stability, and thus, CsCl-type materials are a good target for searching for now functional materials. In this study, we propose, from first principles, that cubic (CsCl type) hafnium nitride (HfN), which is a phase-stable material, can serve as an interesting topological semimetal exhibiting both 0-D and 1-D topological elements. Furthermore, these topological elements all appear around the Fermi level. We hope the 0-D and 1-D topological elements, as well as the nontrivial surface states in cubic HfN, will soon be confirmed experimentally.
Computational Details
All atomic and electronic structure calculations were performed by means of the Vienna Ab initio Simulation Package (VASP) (Sun et al., 2003) within the generalized gradient approximation (Perdew et al., 1996) using the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional. The projector augmented wave (PAW) (Perdew et al., 1998) pseudo-potential was employed with a cutoff energy of 600 eV for plane-wave expansions. The whole Brillouin zone is sampled with the Γ- centered k mesh of 11 × 11 × 11. The convergence criteria for energy and force were set at 10−6 eV per atom and 0.0005 eV/Å, respectively. The surface states of HfN were investigated in this study on a basis of a slab model built by WannierTools package (http://www.wanniertools.com) (Mostofi et al., 2008), according to the method of maximally localized Wannier functions. The value of NSlab, i.e., Number of slabs for slab band was set as 20 in this work.
Results and Discussion
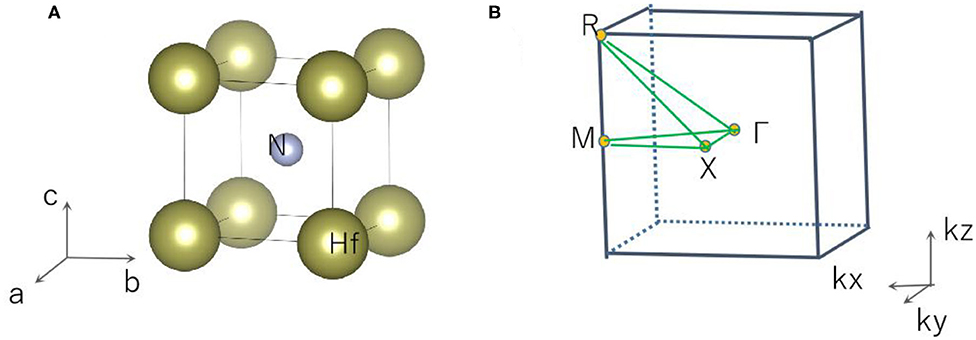
Cubic phase HfN with space group and ICSD: 1834201 was chosen for this study. The crystal structure of HfN was optimized and is shown in Figure 1A. The optimized lattice constants are a = b = c = 2.803 Å, which are in good agreement with the calculated results shown in the materials project database1 (a = b = c = 2.816 Å). Subsequently, we will study the electronic structure, topological elements, and surface states using the lattice constants obtained from the crystal structure.
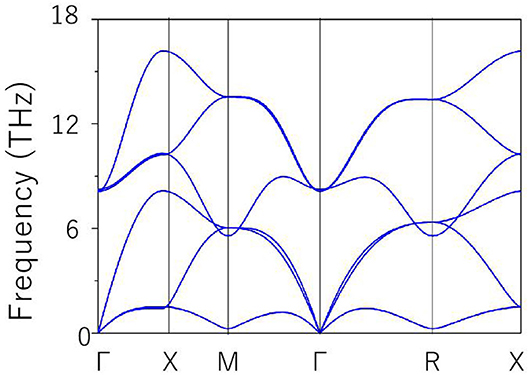
The 3-D bulk Brillouin zone (BZ) is shown in Figure 1B. Based on the 3-D BZ, the phonon dispersion was determined in order to examine the dynamical stability of cubic HfN material with this space group. It is noted that materials are dynamically stable when there exist no imaginary phonon modes in their phonon dispersion curves. The phonon dispersion obtained along the Γ-X-M-Γ-R-X direction is shown in Figure 2. The absence of a negative frequency in the figure confirms the dynamical stability of the HfN material.
Because HfN is a cubic system, the mechanical behavior of HfN can be achieved using three elastic constants: C11, C12, and C44. The results for these are as follows: C11 = 551.16 GPa, C12 = 92.96 GPa, and C44 = 24.31 GPa. The mechanical stability of cubic HfN can be examined based on the Born–Huang criteria as follows:
HfN is mechanically stable based on the above-mentioned Born–Huang criteria. Some other important mechanical parameters can also be obtained, such as the bulk modulus (B = 245.68 GPa), shear modulus (G = 72.03 GPa), Poisson's ratio (ν = 0.366), and Pugh's index (B/G = 3.41), based on C11, C12, and C44. B/G and ν are normally used to examine the brittleness and ductility of materials, with critical values of 1.75 and 0.26, respectively. For HfN, it is elastically ductile. Furthermore, the value of ν is also used to examine the nature of the chemical bonds of materials, with a critical value of 0.25; a value of ν greater (or less) than 0.25 implies an ionic (or covalent) nature. The chemical bonds of HfN are mainly ionic.
The calculated anisotropy parameter A value of 0.106 deviates from unity, reflecting the fact that HfN is elastically anisotropic. Furthermore, the directional-dependence anisotropy of Young's modulus, the shear modulus, and Poisson's ratio for HfN were obtained by means of the ELATE (Gaillac et al., 2016) program, as shown in Figures S1–S3, respectively. Young's modulus, the shear modulus, and Poisson's ratio in Figures S1–S3 all show obvious anisotropy. We would like to point out that the mechanical anisotropy of HfN is very important for its practical applications.
Based on the values of the equilibrium lattice constants obtained, we studied the electronic band structures of cubic HfN. The Γ-X-M-Γ-R-X high symmetry points (Figure 1B) in the first BZ were selected to describe the band structure of HfN. Using the generalized gradient approximation (GGA) method, the calculated band structure is shown in Figure 3A. When the spin-orbit coupling effect is ignored, we can see that HfN manifests a semimetallic band structure with conduction and valence bands overlapping each other. Interestingly, one can see that HfN possesses several band crossing points located close to the Fermi energy. We divided these band crossing points into two parts, i.e., regions R1 and R2, and we discuss these in detail separately. Before discussing the band crossing points in regions R1 and R2, the state-of-the-art Heyd–Scuseria–Ernzerhof (HSE) 06 method (Heyd and Scuseria, 2004), which can be seen as a better way of describing the band crossing points than the GGA method, was also selected to further prove the occurrence of the band crossing points in regions R1 and R2. The results of the calculated band structure of HfN with HSE 06 along the X-M-Γ-R directions are shown in Figure 3B.
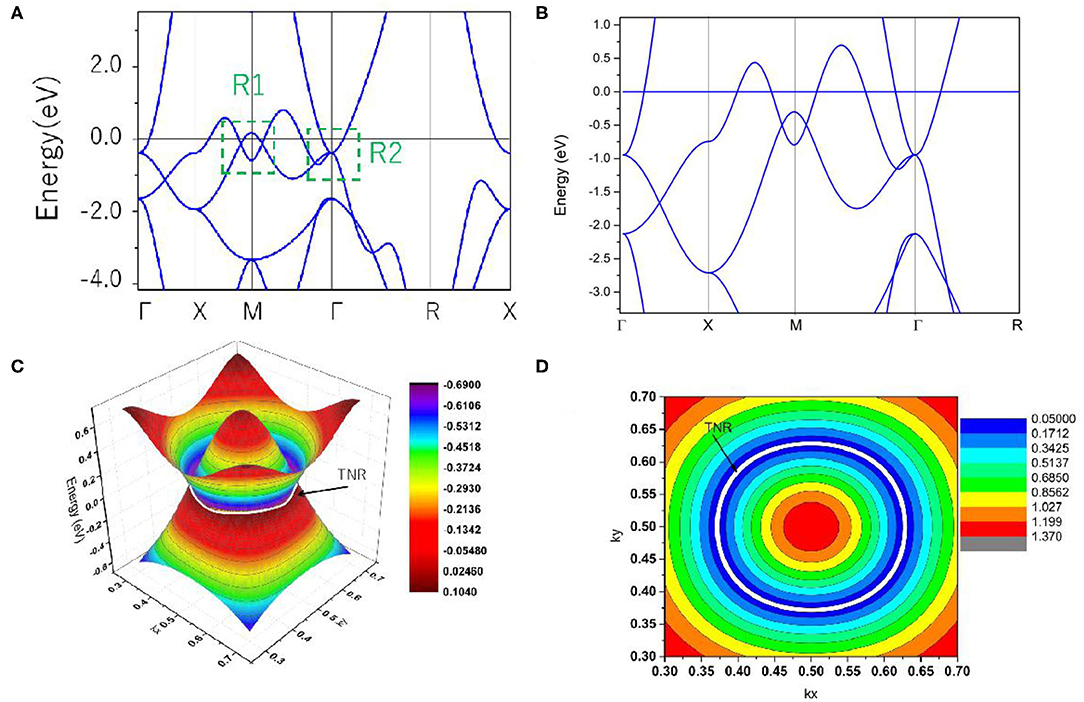
Figure 3. (A) Band structure of HfN via the GGA method; (B) Band structure of HfN via the HSE 06 method; (C) 3-D plot of both bands in the kz = 0 plane in region R1; (D) 2-D plot of both bands in the kz = 0 plane in region R1.
First, we study the band crossing point in region R2, which indicates a band crossing point at the Γ point. This band crossing point was generated by one non-degenerate band and one doubly degenerate band. That is to say, this band crossing point is a triple nodal point, as shown in Figures 3A,B.
Next, we discuss the band crossing points along the X-M-Γ directions in region R1. Here, one can see that there are two band crossing points in total, generated by the crossing of two non-degenerate bands. Because this cubic HfN system possesses both P and T symmetries, both band crossing points in this system cannot be regarded as isolated points. Normally, both points should reside on the nodal line. To further verify that these two band crossing points in region R1 belong to a nodal line, a 3-D plot of both bands in the kz = 0 plane is shown in Figure 3C. One can see that there is a closed nodal line, i.e., nodal ring, in the kz = 0 plane, and the two band crossing points in region R1 belong to the closed nodal line (marked as a white ring). To confirm the shape of the closed nodal line in the kz = 0 plane, we show the 2-D plot of both bands in the kz = 0 plane in Figure 3D. A near-ring shape can be seen in this figure. It is well-known that the nodal ring (Wang et al., 2020) can be classified into three types: type I, type II, and a hybrid type, according to the degree of tilting of the band crossing points in the nodal ring. Type I (or II) nodal rings are formed only by type I (or II) band crossing points, while the hybrid rings simultaneously host type I and type II band crossing points [more details about the three types of nodal ring can be found in (Wang et al., 2020)]. As shown in Figure 3C, the nodal ring in the kz = 0 plane belongs to type I.
Figure 4 shows the HfN (001) surface state without the effect of SOC, which clearly shows that topological surface states can be found around the triple nodal point at the points marked by the arrows. However, the surface state near the nodal ring is only faintly visible inside the projected topological nodal ring (see the arrow along the direction).
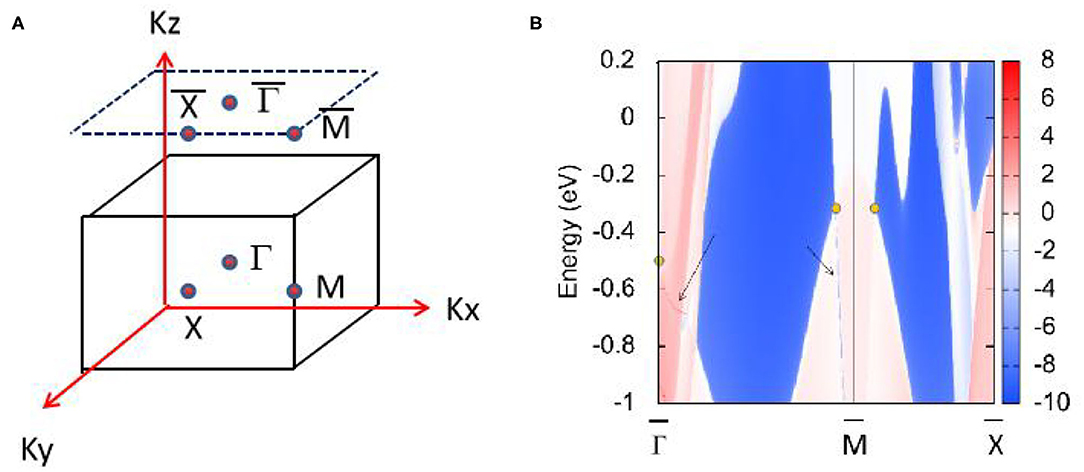
Figure 4. (A) (0 0 1) surface Brillouin zone of HfN; (B) Projection spectrum on the (001) surface state of HfN near the 1-D nodal ring and 0-D triple nodal point. The band crossing points are highlighted by yellow circles and the surface states are marked by black arrows.
In the final, the effect of SOC on the electronic structure has been discussed and results are given in Figure 5. At the Γ point, an energy band gap of 0.25 eV can be found, reflecting that the triple nodal point is gapped under SOC. However, along Γ-R direction, two bands now cross with each other at−0.235 eV below the Fermi level. In this cubic HfN, the time-reversal and inversion symmetries retain, thus each band is twofold degenerate when the SOC is taken into consideration. This band-crossing point at −0.235 eV along Γ-R direction (see the insert figure in Figure 5) is a Dirac point with fourfold degeneracy. We would like to point out that similar triple nodal point - Dirac point transition can also be observed in TiB2 (Zhang et al., 2017) and Li2NaN (Jin et al., 2019b) materials.
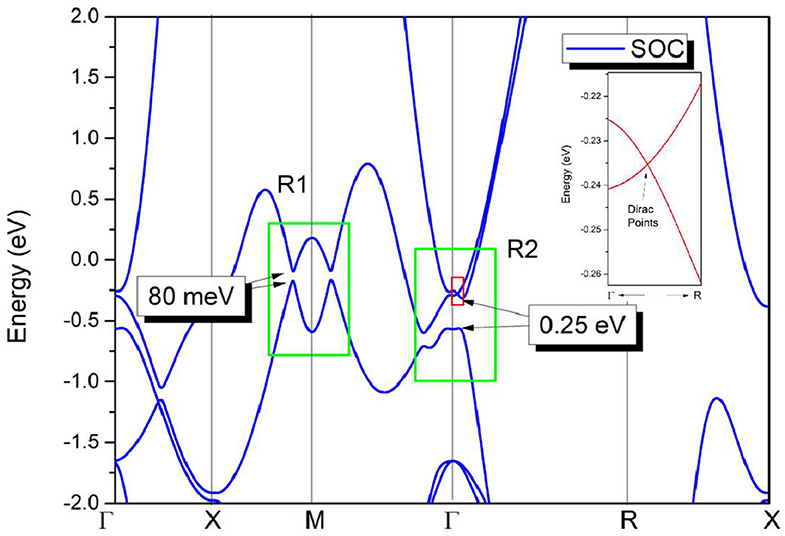
Figure 5. Band structure of HfN via the GGA method; The SOC effect was taken into consideration during the calculation. Insert figure: Enlarged band structure of HfN along Γ-R direction.
In R1, two band crossing points are also gapped due to the SOC effect. The SOC gaps are calculated to be ~80 meV, as shown in Figure 5. We would like to point out that most nodal lines proposed so far will be gapped under the effect of SOC. The SOC-induced gaps in HfN are comparable with those in typical nodal line semimetals, such as Cu3NPd (Yu et al., 2015) (60–100 meV), CaAgBi (Yamakage et al., 2016) (80–140 meV), and BaSn2 (Huang et al., 2016) (60–160 meV).
Conclusions
In this study, we report that cubic HfN is a newly designed topological semimetal with rich topological elements, i.e., 0-D and 1-D band crossing points. When the spin-orbit coupling (SOC) effect is ignored, near the Fermi level, HfN possesses a triple nodal point at the Γ point and a nodal ring in the kz = 0 plane. The topological surface states around the 0-D and 1-D band crossing points were determined. When the SOC effect is taken into consideration, 0-D triple nodal point disappears, however, new topological signature, i.e., 0-D Dirac point occurs along Γ-R direction. The computational results also suggest that cubic HfN possesses mechanical stability, dynamical stability, elastic ductility, and anisotropy. Our investigation has revealed that HfN is a good topological semimetal with rich topological elements, high stability, and important mechanical properties.
Data Availability Statement
All datasets generated for this study are included in the article/Supplementary Material.
Author Contributions
YL: software, methodology, writing, and supervisor. JX: reviewing. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the first batch of postdoctoral research fund research projects in Yunnan Province (Serial No. 9), the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJQN201801346), and the Chongqing University of Arts and Sciences Foundation (Grant No. Z2011Rcyj05).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2020.00727/full#supplementary-material
Footnotes
References
Bedoyapinto, A., Pandeya, A. K., Liu, D., Deniz, H., Chang, K., Tan, H., et al. (2020). Realization of epitaxial NbP and TaP weyl semimetal thin films. ACS Nano. 14, 4405–4413. doi: 10.1021/acsnano.9b09997
Cai, J., Xie, Y., Chang, P., Kim, H., and Chen, Y. (2018). Nodal-chain network, intersecting nodal rings and triple points coexisting in nonsymmorphic Ba3Si4. Phys. Chem. Chem. Phys. 20, 21177–21183. doi: 10.1039/C8CP02810A
Chang, T., Xu, S., Sanchez, D., Tsai, W., Huang, S., Chang, G., et al. (2017). Type-II symmetry-protected topological dirac semimetals. Phys. Rev. Lett. 119, 026404. doi: 10.1103/PhysRevLett.119.026404
Chen, H., Zhang, S., Jiang, W., Zhang, C., Guo, H., Liu, Z., et al. (2018). Prediction of two-dimensional nodal-line semimetals in a carbon nitride covalent network. J. Mater. Chem. C 6, 11252–11259. doi: 10.1039/C8TA02555J
Chen, Z., Zhang, C., Zou, Y., Zhang, E., Yang, L., Hong, M., et al. (2015). Scalable growth of high mobility dirac semimetal Cd3As2 microbelts. Nano Lett. 15, 5830–5834. doi: 10.1021/acs.nanolett.5b01885
Cheng, T., Lang, H., Li, Z., Liu, Z., and Liu, Z. (2017). Anisotropic carrier mobility in two-dimensional materials with tilted Dirac cones: theory and application. Phys. Chem. Chem. Phys. 19, 23942–23950. doi: 10.1039/C7CP03736H
Das, A., Ronen, Y., Most, Y., Oreg, Y., Heiblum, M., and Shtrikman, H. (2012). Zero-bias peaks and splitting in an Al–InAs nanowire topological superconductor as a signature of Majorana fermions. Nat. Phys. 8, 887–895. doi: 10.1038/nphys2479
Dvorak, M., and Wu, Z. (2015). Dirac point movement and topological phase transition in patterned graphene. Nanoscale 7, 3645–3650. doi: 10.1039/C4NR06454B
Fang, C., Lu, L., Liu, J., and Fu, L. (2016). Topological semimetals with helicoid surface states. Nat. Phys. 12, 936–941. doi: 10.1038/nphys3782
Gaillac, R., Pullumbi, P., and Coudert, F. (2016). ELATE: an open-source online application for analysis and visualization of elastic tensors. J. Phys. Cond. Matter. 28:275201. doi: 10.1088/0953-8984/28/27/275201
Gao, H., Venderbos, J. W., Kim, Y., and Rappe, A. M. (2019). Topological Semimetals from first-principles. Annu. Rev. Mater. Res. 49, 153–183. doi: 10.1146/annurev-matsci-070218-010049
Gao, Y., Xie, Y., Chen, Y., Gu, J., and Chen, Z. (2018). Spindle nodal chain in three-dimensional α′ boron. Phys. Chem. Chem. Phys. 20, 23500–23506. doi: 10.1039/C8CP03874K
Geishendorf, K., Vir, P., Shekhar, C., Felser, C., Facio, J. I., Den Brink, J. V., et al. (2020). Signatures of the magnetic entropy in the thermopower signals in nanoribbons of the magnetic weyl semimetal Co3Sn2S2. Nano Lett. 20, 300–305. doi: 10.1021/acs.nanolett.9b03822
Gong, P., Deng, B., Huang, L., Hu, L., Wang, W., Liu, D., et al. (2017). Robust and pristine topological dirac semimetal phase in pressured two-dimensional black phosphorus. J. Phys. Chem. C 121, 20931–20936. doi: 10.1021/acs.jpcc.7b08926
Hasan, M. Z., and Kane, C. L. (2010). Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067. doi: 10.1103/RevModPhys.82.3045
He, J. B., Chen, D., Zhu, W. L., Zhang, S., Zhao, L., Ren, Z., et al. (2017). Magnetotransport properties of the triply degenerate node topological semimetal tungsten carbide. Phys. Rev. B 95:195165. doi: 10.1103/PhysRevB.95.195165
He, T., Zhang, X., Meng, W., Jin, L., Dai, X., and Liu, G. (2019). Topological nodal lines and nodal points in the antiferromagnetic material β-Fe2PO5. J. Mater. Chem. C 7, 12657–12663. doi: 10.1039/C9TC04046C
Heyd, J., and Scuseria, G. E. (2004). Efficient hybrid density functional calculations in solids: assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional. J. Chem. Phys. 121, 1187–1192. doi: 10.1063/1.1760074
Hosur, P., and Qi, X. (2013). Recent developments in transport phenomena in Weyl semimetals. Comp Rend Phys. 14, 857–870. doi: 10.1016/j.crhy.2013.10.010
Huang, H., Liu, J., Vanderbilt, D., and Duan, W. (2016). Topological nodal-line semiemtals in alkaline-earth stannides, germanides, and silicides, Phys. Rev. B 93:201114. doi: 10.1103/PhysRevB.93.201114
Jiang, Q., Jiang, H., Liu, H., Sun, Q., and Xie, X. C. (2015). Topological imbert-fedorov shift in weyl semimetals. Phys. Rev. Lett. 115, 156602. doi: 10.1103/PhysRevLett.115.156602
Jin, L., Zhang, X., Dai, X., Liu, H., Chen, G., and Liu, G. (2019b). Cemtrosymmetric Li2NaN: a superior topological electronic material with critical-type triply degenerate nodal points. J. Mater. Chem. C 7, 1316–1320. doi: 10.1039/C8TC05930F
Jin, L., Zhang, X., He, T., Meng, W., Dai, X., and Liu, G. (2019a). Topological nodal line state in superconducting NaAlSi compound. J. Mater. Chem. C 7, 10694–10699. doi: 10.1039/C9TC03464A
Jing, Y., and Heine, T. (2019). Two-dimensional kagome lattices made of hetero triangulenes are dirac semimetals or single-band semiconductors. J. Am. Chem. Soc. 141, 743–747. doi: 10.1021/jacs.8b09900
Li, X., Dai, Y., Ma, Y., and Huang, B. (2014). Electronic and magnetic properties of honeycomb transition metal monolayers: first-principles insights. Phys. Chem. Chem. Phys. 16, 13383–13389. doi: 10.1039/C4CP01512F
Lin, C., Arafune, R., Liu, R., Yoshimura, M., Feng, B., Kawahara, K., et al. (2017). Visualizing type-II weyl points in tungsten ditelluride by quasiparticle interference. ACS Nano 11, 11459–11465. doi: 10.1021/acsnano.7b06179
Liu, Z., Feng, W., Xin, H., Gao, Y., Liu, P., Yao, Y., et al. (2019). Two-dimensional spin–valley-coupled Dirac semimetals in functionalized SbAs monolayers. Mater. Horizons 6, 781–787. doi: 10.1039/C8MH01588K
Liu, Z., Wang, J., and Li, J. (2013). Dirac cones in two-dimensional systems: from hexagonal to square lattices. Phys. Chem. Chem. Phys. 15, 18855–18862. doi: 10.1039/c3cp53257g
Lv, B. Q., Feng, Z., Xu, Q., Gao, X., Ma, J., Kong, L., et al. (2017). Observation of three-component fermions in the topological semimetal molybdenum phosphide. Nature 546, 627–631. doi: 10.1038/nature22390
Mostofi, A. A., Yates, J. R., Lee, Y., Souza, I., Vanderbilt, D., and Marzari, N. (2008). Wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685–699. doi: 10.1016/j.cpc.2007.11.016
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77:3865. doi: 10.1103/PhysRevLett.77.3865
Perdew, J. P., Burke, K., and Ernzerhof, M. (1998). Perdew, burke, and ernzerhof reply. Phys. Rev. Lett. 80:891. doi: 10.1103/PhysRevLett.80.891
Pham, A., Klose, F., and Li, S. (2019). Robust topological nodal lines in halide carbides. Phys. Chem. Chem. Phys. 21, 20262–20268. doi: 10.1039/C9CP04330F
Qi, X., and Zhang, S. (2011). Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110. doi: 10.1103/RevModPhys.83.1057
Qie, Y., Liu, J., Wang, S., Sun, Q., and Jena, P. (2019). Tetragonal C24: a topological nodal-surface semimetal with potential as an anode material for sodium ion batteries. J. Mater. Chem. A 7, 5733–5739. doi: 10.1039/C8TA11276B
Rechtsman, M. C., Zeuner, J. M., Plotnik, Y., Lumer, Y., Podolsky, D. K., Dreisow, F., et al. (2013). Photonic Floquet topological insulators. Nature 496, 196–200. doi: 10.1038/nature12066
Schoop, L. M., Pielnhofer, F., and Lotsch, B. V. (2018). Chemical principles of topological semimetals. Chem. Mater. 30, 3155–3176. doi: 10.1021/acs.chemmater.7b05133
Soluyanov, A. A., Gresch, D., Wang, Z., Wu, Q., Troyer, M., Dai, X., et al. (2015). Type-II Weyl semimetals. Nature 527, 495–498. doi: 10.1038/nature15768
Sun, G., Kurti, J., Rajczy, P., Kertesz, M., Hafner, J., and Kresse, G. (2003). Performance of the Vienna ab initio simulation package (VASP) in chemical applications. J. Mol. Struct. Theochem. 624, 37–45. doi: 10.1016/S0166-1280(02)00733-9
Sung, J. H., Heo, H., Hwang, I., Lim, M., Lee, D., Kang, K., et al. (2014). Atomic layer-by-layer thermoelectric conversion in topological insulator bismuth/antimony tellurides. Nano Lett. 14, 4030–4035. doi: 10.1021/nl501468k
Thakur, G. S., Vir, P., Guin, S. N., Shekhar, C., Weihrich, R., Sun, Y., et al. (2020). Intrinsic anomalous hall effect in Ni-substituted magnetic weyl semimetal Co3Sn2S2. Chem. Mater. 32, 1612–1617. doi: 10.1021/acs.chemmater.9b05009
Wang, X., Cheng, Z., Zhang, G., Kuang, M., Wang, X.-L., and Chen, H. (2020). Strain tuning of closed topological nodal lines and opposite pockets in quasi-two-dimensional α-phase FeSi2. Phys. Chem. Chem. Phys. 22, 13650–13658. doi: 10.1039/D0CP02334E
Xu, L., Du, A., and Kou, L. (2016). Hydrogenated borophene as a stable two-dimensional Dirac material with an ultrahigh Fermi velocity. Phys. Chem. Chem. Phys. 18, 27284–27289. doi: 10.1039/C6CP05405F
Xu, L., Wang, R., Miao, M., Wei, X., Chen, Y., Yan, H., et al. (2014). Two dimensional Dirac carbon allotropes from graphene. Nanoscale 6, 1113–1118. doi: 10.1039/C3NR04463G
Xu, S., Chen, Z., Zhao, Y., Zhang, X., Xu, H., and Yang, X. (2020). Realizing graphene-like Dirac cones in triangular boron sheets by chemical functionalization. J. Mater. Chem. C 8, 2798–2805. doi: 10.1039/C9TC06464H
Yamakage, A., Tamakawa, Y., Tanaka, Y., and Okamoto, Y. (2016). Line-node Dirac semiemtal and topological insulating phase in noncentrosymmetric pnictides CaAgX (X = P, As), J. Phys. Soc. Jpn. 85:013708. doi: 10.7566/JPSJ.85.013708
Yan, B., and Felser, C. (2017). Topological materials: weyl semimetals. Ann Rev Conden Matt Phys. 8, 337–354. doi: 10.1146/annurev-conmatphys-031016-025458
Yang, T., and Zhang, X. (2020). Nearly flat nodal surface states in pseudo-one-dimensional molybdenum monochalcogenides X(MoS)3 (X = K, Rb, Cs). J. Mater. Chem. C, doi: 10.1039/D0TC01978J
Yi, X., Li, W. Q., Li, Z. H., Zhou, P., Ma, Z., and Sun, L. Z. (2019). Topological dual double node-line semimetals NaAlSi(Ge) and their potential as cathode material for sodium ion batteries. J. Mater. Chem. C 7, 15375–15381. doi: 10.1039/C9TC04096J
Yu, R., Weng, H., Fang, Z., Dai, X., and Hu, X. (2015). Topological nodal-line semimetal and Dirac semiemtal state in antiperovskite Cu3PdN, Phys. Rev. B 115:036807. doi: 10.1103/PhysRevLett.115.036807
Yu, R., Zhang, W., Zhang, H., Zhang, S., Dai, X., and Fang, Z. (2010). Quantized anomalous hall effect in magnetic topological insulators. Science 329, 61–64. doi: 10.1126/science.1187485
Yuan, X., Cheng, P., Zhang, L., Zhang, C., Wang, J., Liu, Y., et al. (2017). Direct observation of landau level resonance and mass generation in dirac semimetal Cd3As2 thin films. Nano Lett. 17, 2211–2219. doi: 10.1021/acs.nanolett.6b04778
Zhang, B., Li, Y., Zhang, C., and Wang, J. (2019). Two-dimensional ZrB2C2 with multiple tunable Dirac states. Phys. Chem. Chem. Phys. 21, 24212–24217. doi: 10.1039/C9CP04913D
Zhang, H., Liu, C., Qi, X., Dai, X., Fang, Z., and Zhang, S. (2009). Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442. doi: 10.1038/nphys1270
Zhang, M., Yang, Z. C., and Wang, G. (2018). Coexistence of type-I and type-II weyl points in the weyl-semimetal OsC2. J. Phys. Chem. C 122, 3533–3538. doi: 10.1021/acs.jpcc.8b00920
Zhang, X., Liu, Q., Xu, Q., Dai, X., and Zunger, A. (2018). Topological insulators versus topological dirac semimetals in honeycomb compounds. J. Am. Chem. Soc. 140, 13687–13694. doi: 10.1021/jacs.8b06652
Zhang, X., Yu, Z., Sheng, X., and Yang, H., Yang, S. (2017). Coexistance of four-band nodal rings and triply degenerate nodal points in centrosymmetric metal diborides. Phys. Rev. B 95:235116. doi: 10.1103/PhysRevB.95.235116
Zhao, Z., Zhang, Z., and Guo, W. (2020). A family of all sp2-bonded carbon allotropes of topological semimetals with strain-robust nodal-lines. J. Mater. Chem. C 8, 1548–1555. doi: 10.1039/C9TC05470G
Zheng, H., Xu, S., Bian, G., Guo, C., Chang, G., Sanchez, D. S., et al. (2016). Atomic-scale visualization of quantum interference on a weyl semimetal surface by scanning tunneling microscopy. ACS Nano 10, 1378–1385. doi: 10.1021/acsnano.5b06807
Zhong, C., Chen, Y., Xie, Y., Sun, Y., and Zhang, S. B. (2017). Semi-Dirac semimetal in silicene oxide. Phys. Chem. Chem. Phys. 19, 3820–3825. doi: 10.1039/C6CP08439G
Zhou, P., Ma, Z., and Sun, L. Z. (2018). Coexistence of open and closed type nodal line topological semimetals in two dimensional B2C. J. Mater. Chem. C 6, 1206–1214. doi: 10.1039/C7TC05095J
Keywords: topological nodal ring, triple point, density functional theory, phonon dispersion, mechanical behaviors
Citation: Li Y and Xia J (2020) Cubic Hafnium Nitride: A Novel Topological Semimetal Hosting a 0-Dimensional (0-D) Nodal Point and a 1-D Topological Nodal Ring. Front. Chem. 8:727. doi: 10.3389/fchem.2020.00727
Received: 19 June 2020; Accepted: 14 July 2020;
Published: 26 August 2020.
Edited by:
Xiaotian Wang, Southwest University, ChinaReviewed by:
Jiangchao Han, Beihang University, ChinaYongmao Cai, Northeast Electric Power University, China
Copyright © 2020 Li and Xia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yang Li, bGl5YW5nQGNxd3UuZWR1LmNu; bGl5YW5nX3BoeXNpY3NAMTI2LmNvbQ==; Jihong Xia, amh4aWFAY3F3dS5lZHUuY24=; amh4aWExMDEwQDEyNi5jb20=
 Yang Li
Yang Li Jihong Xia1*
Jihong Xia1*