The Influence of Halide Substituents on the Structural and Magnetic Properties of Fe6Dy3 Rings

Introduction

Cyclic coordination clusters (CCCs) consisting of paramagnetic ions are of interest since these can show unusual physical and chemical properties arising from the cyclisation of a short chain of metal ions to give a finite molecular species (Larsen et al., 2003; Cador et al., 2004, 2005; Tang et al., 2006; Timco et al., 2009; Whitehead et al., 2013; Ungur et al., 2014; Ferrando-Soria et al., 2015; Gysler et al., 2016; Langley et al., 2019). For 4f containing cycles this includes stabilization of toroidal moments (Waldmann, 2005; Chibotaru et al., 2008; Ungur et al., 2012), whereas for 3d heterometallic cycles it has been shown that these can function as qubits and even be incorporated into logic gates (Troiani et al., 2005). Cyclic 3d/4f clusters where 3d = Fe(III) offer new opportunities in chiral separation (Baniodeh et al., 2013), magnetic resonance imaging (MRI) (Guthausen et al., 2015; Ranzinger et al., 2016) and the magnetocaloric effect (Botezat et al., 2017; Schmidt et al., 2017b). The Fe/4f cyclic coordination clusters show perhaps the most exotic behavior and can be produced in different nuclearities, such as [Fe₂Ln₂] (Song et al., 2013; Pugh et al., 2016; Alexandru et al., 2018), [Fe₃Ln₂] (Baniodeh et al., 2013), [Fe₄Dy₄] (Schray et al., 2010; Chen et al., 2015), [Fe₄Ln₂] (Schmidt et al., 2012, 2017a; Baniodeh et al., 2013; Botezat et al., 2017, 2019b; Chen et al., 2017), [Fe₅Ln₃] (Baniodeh et al., 2013), [Fe₆Ln₃] (Kühne et al., 2016; Botezat et al., 2019a), [Fe₆Ln₄] (Botezat et al., 2019b), [Fe₈Ln₈] (Zhang et al., 2020), [Fe₁₀Ln₁₀] (Baniodeh et al., 2013, 2014), [Fe₁₆Ln₄] (Baniodeh et al., 2011), and [Fe₁₈Ln₆] (Botezat et al., 2017). The Fe₁₀Gd₁₀ system demonstrated the potential of cyclized systems to show solid state properties on a molecular length scale—in this case, a quantum critical point tipping the system toward a ferromagnetic ultra-high spin state of S = 60 with a choice of at least 10,000 ground state configurations, making this a system with polynary rather than binary prospects (Baniodeh et al., 2018). A particularly fascinating aspect to these systems is provided by examples where the components of the chain are not simply alternating iron and 4f ions (Schmidt et al., 2012, 2017a; Baniodeh et al., 2013; Botezat et al., 2017, 2019b). This behavior was recently reported for the family of Fe₆Ln₃ clusters (Kühne et al., 2016) where the repeating unit can be regarded as {Fe₂Ln}₃ and three of these give an {Fe₆Ln₃} cycle. The repeating units within big clusters can vary, but it is also possible to have a situation where there is no true cyclisation of a fundamental building block. This can be seen for example in the arrangement within [Fe₄Ln₂] clusters where some structures can be described in terms of a {FeLn₂}₂ cycle as shown by Schmidt et al. (2012), Botezat et al. (2019b), and Schmidt et al. (2017a) which is very different from the cyclized strand of {FeLn₄Fe} described in Baniodeh et al. (2013). Other repeating units, such as {Fe₃Dy} have been reported in the largest example of Fe/4f coordination cluster where the basic unit is repeated six times to give an {Fe₁₈Dy₆} cycle (Botezat et al., 2017).

Odd-numbered rings are rare, with only a few examples (Baniodeh et al., 2013; Kühne et al., 2016; Botezat et al., 2019a), such as provided by our non-anuclear Fe₆Ln₃ clusters (Kühne et al., 2016), but they hold promise for discovering new exotic magnetic phenomena including single molecule magnetism, magnetocaloric effect, MRI contrast reagents, and toroidal arrangements of anisotropic 4f spin centers. It has previously been shown that electron-withdrawing/donating substituents on the phenyl ring of benzoic acids can lead to small changes in the structural environment and therefore have an impact on the magnetic properties of Single Molecule Magnets (SMMs) (Mereacre et al., 2011; Habib et al., 2013). Even small variations in the ligand field of lanthanide ions can have a significant influence on the slow relaxation process responsible for SMM behavior (Peng et al., 2016).

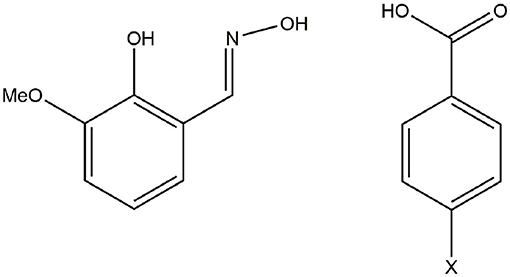
Here, we investigate the influence of para-substituents of the coordinated benzoate ligand on the structural and magnetic properties of [Fe₆Dy₃] cyclic coordination clusters. This systematic study led to three new crystal structures of cyclic [Fe₆Dy₃] clusters, with a core motif of [Fe₆Dy₃(μ-OMe)₉(vanox)₆(X-benz)₆] where vanox⁻² is doubly-deprotonated o-vanillinoxime, and the benzoate ligands are para-substituted with X = F (1), Cl (2), Br (3) (Scheme 1). The subtle changes in the non-coordinating part of the ligand, give insights into the structure-directing properties of the ligand as well as the magnetic properties of the clusters. The change of the coordination preferences of the bridging benzoate with para-substituent variation was monitored by magnetic susceptibility measurements. We compare the static and dynamic susceptibility data of the para-substituted 1-3 and the unsubstituted cyclic coordination clusters to determine the role of the electron-withdrawing group.

SCHEME 1

Scheme 1. H₂vanox (left) and 4-parasubstituted benzoic acid (right).

Results

Synthetic Route

The synthesis of 1-3 was achieved in a one pot reaction; for full synthetic details see section Materials and Methods. A ligand solution containing o-vanillinoxime, H₂vanox, and sodium methoxide, NaOMe, dissolved in methanol was added to a solution of FeCl₂·4H₂O and Dy(NO₃)₃·6H₂O in methanol with the respective para-halide-substituted benzoic acid as depicted in Scheme 1. Small adjustments in terms of solvents and amount of base to allow for the different pK_a of the para-substituted benzoic acids were made as outlined in section Materials and Methods. In this way, dark red single crystals of three nine-membered [Fe₆Dy₃(μ-OMe)₉(vanox)₆(X-benz)₆] cyclic coordination clusters 1-3 were obtained for the 4-fluorobenzoate, [Fe₆Dy₃(μ-OMe)₉(vanox)₆(F-benz)₆]^.12MeOH^.H₂O (1), the 4-chlorobenzoate, [Fe₆Dy₃(μ-OMe)₉(vanox)₆(Cl-benz)₆]^.13MeOH (2), and the 4-bromobenzoate, [Fe₆Dy₃(μ-OMe)₉(vanox)₆(Br-benz)₆(MeOH)]^. 9MeOH (3).

Structural Details

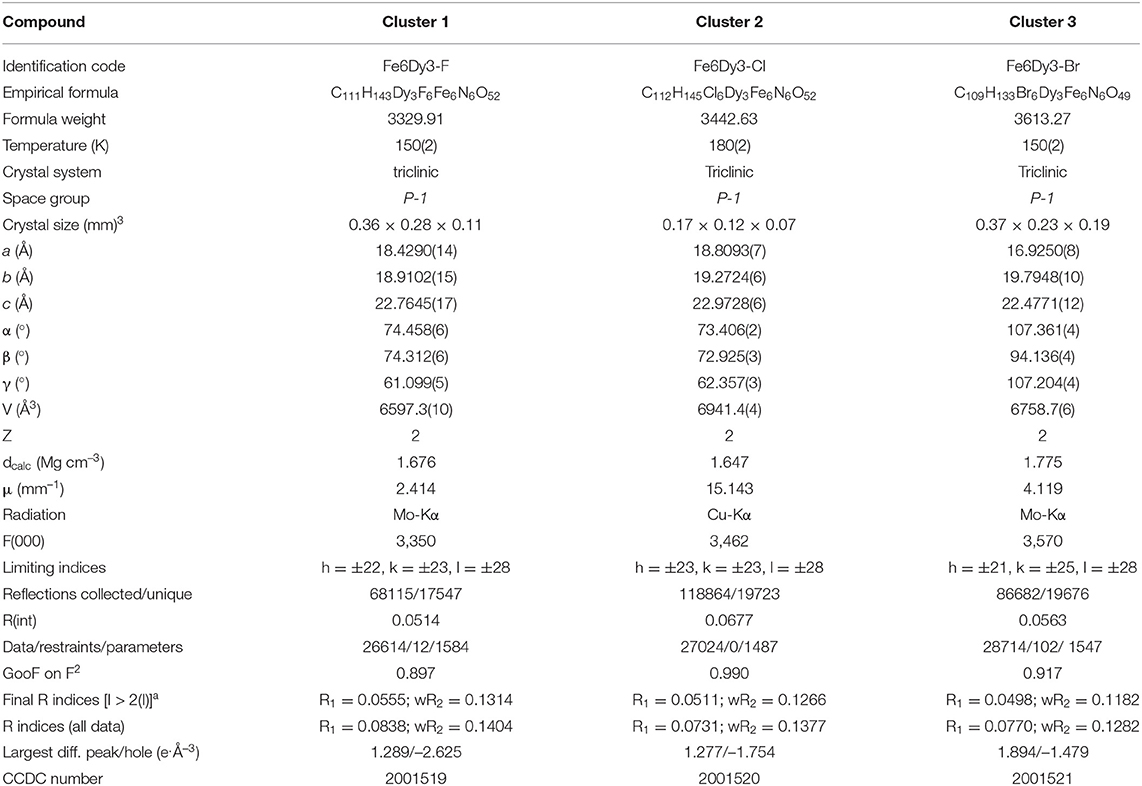
1-3 crystallize in the triclinic space group P1̄, where 1 and 2 crystallize isomorphically with 13 solvent molecules found in the crystal lattice. For 1, there are 12 methanol molecules and one water molecule and for 2, there are 13 methanol molecules. In contrast, 3 crystallizes with 9 molecules of methanol in the unit cell and incorporates a tenth methanol within an iron coordination sphere of the cluster as outlined below. A table summarizing the crystallographic details can be found in section Materials and Methods. The structure of the coordination cluster within 1 is taken as a representative of the isomorphous structures 1 and 2. The structures of 1 and 3 are shown in Figure 1. The nonanuclear metal core of 1-3 consists of three Fe(III) dimeric units which are linked together through single Dy(III) ions to form a ring and this core motif has been previously reported for the Dy(III) and other Ln(III) compounds where the unsubstituted benzoate was used as a bridging co-ligand (Kühne et al., 2016).

FIGURE 1

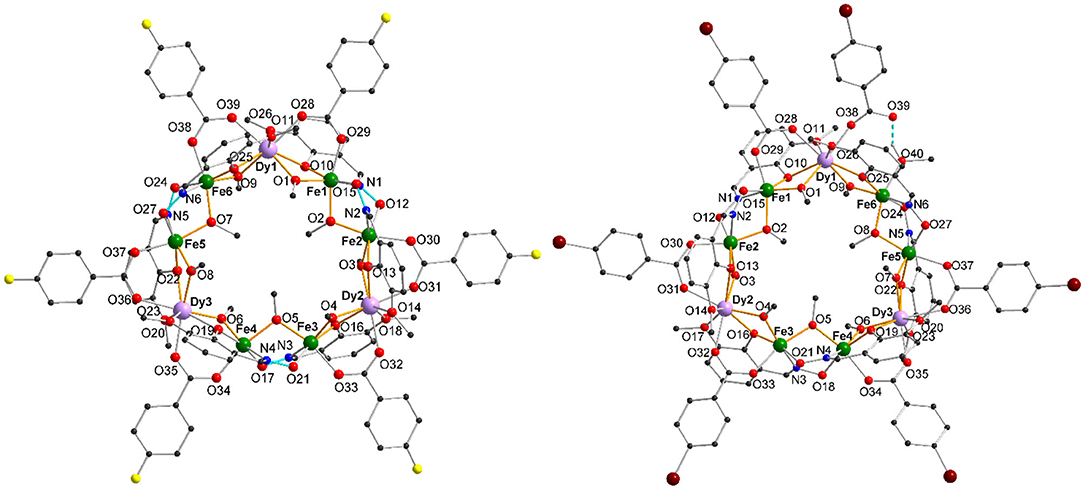
Figure 1. Molecular structure of [Fe₆Dy₃(μ-OMe)₉(vanox)₆(F-benz)₆] cyclic coordination clusters (1) (left) and of [Fe₆Dy₃(μ-OMe)₉(vanox)₆(Br-benz)₆(MeOH)] (3) (right) with H-bonds highlighted as turquoise dashed lines, (solvents and H atoms omitted for clarity).

1 and 2 are analogous to the previously reported structure, with the six substituted benzoates in a 1,1′-μ-bridging mode, linking together each end of the dinuclear iron units to the intervening Dy(III) centers. Within 3 one of the Br-benzoates does not bridge between the Fe(III) and Dy(III) ions anymore, but coordinates only to the Dy(III) ion (Figure 1). The vacant coordination site on the Fe(III) center, Fe(6), is filled by O(40) of the methanol ligand. The hydrogen of this methanol forms a hydrogen-bond to the non-coordinated Br-benzoate O(39), which is highlighted as a turquoise dashed bond in Figure 1.

Even though 1 and 2 crystallize isomorphously and show similar bond lengths and angles, the differences become more pronounced by overlapping the structures in Figure 2, where 1-3 are shown as capped stick models with 1 in yellow, 2 in green, and 3 in purple. The metal centers of all clusters almost overlap, highlighting the similarity of the M^...M distances (Table S1) within 1-3 (Figure S1). While the vanox²⁻ and the μ₂-bridging methoxy groups of 1 and 2 do overlap, there are some differences visible, especially for the coordinating benzoate ligands, which become more pronounced in the side view (Figure 2). By increasing the halide radius from F via Cl to Br, it becomes clear, that the benzoate ligands bend out of the metal plane, and this bending seems to be too much in case of 3, which then leads to the break in connectivity observed in this structure. Additionally, the steric demand of the intramolecular H-bond of the unidentate bromobenzoate forces the latter out of the metal plane, which is defined by all nine Fe(III) and Dy(III) centers (Figure 2). The tilting angles of the benzoate ligands within 1-3 are summarized in Table S2, with small angles in the range 2–20° for the isomorphous clusters 1 and 2, while 3 exhibits stronger tilting of 9.4–34.2° for the μ₂-coordinated benzoates. The monodentate bromobenzoate Br6, exhibits the largest tilting out of the metal plane with an angle of 38.9°.

FIGURE 2

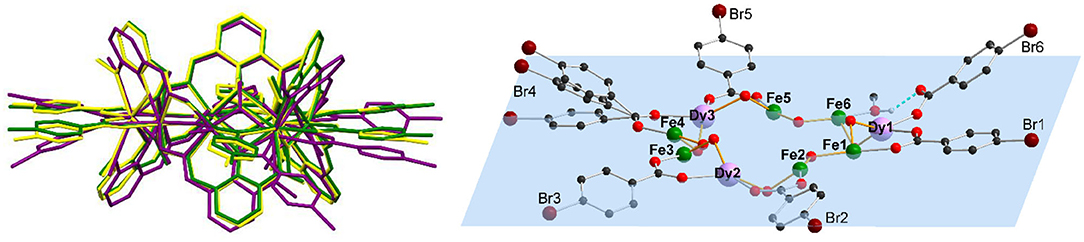
Figure 2. Structure overlap of 1-3 by superposition of all nine metal centers (left) (1: 4-fluorobenzoate (yellow), 2: 4-chlorobenzoate (green) and 3: 4-bromobenzoate (purple)), and plane through all nine metal centers (blue) of 3, [Fe₆Dy₃(μ-OMe)₉(vanox)₆(Br-benz)₆(MeOH)], (right), highlighting the deviation of the benzoate rings tilted out of the plane (all other ligands omitted for clarity, except for the 4-bromobenzoates and bridging methoxy groups).

In order to see the differences between the structures which can lead to the tuning of the magnetic behavior, the bond lengths around the Fe(III) centers are summarized in Table S3. Table S4 summarizes all Dy-O bond lengths, and both sets of data are compared to the unsubstituted Fe₆Dy₃ cluster. All Fe(III) centers are hexa-coordinate with five oxygen atoms and one nitrogen atom in the coordination sphere. The Fe-O bond lengths within 1-3 are 1.93–2.08 Å and the Fe-N bond lengths are 2.09-2.13 Å, similar to those for the unsubstituted cluster. Although, 3 shows the disorder of one benzoate ligand, where the carboxylate oxygen of one of the Fe(III) centers, Fe6, is replaced by a coordinating methanol, this Fe-O bond length is in the same range as the respective Fe-O_carboxylate bonds within this cluster as well as compared to 1 and 2.

Taken together, the Dy-O bond lengths are in a rather wide range, 2.23–2.56 Å. But if they are classified according to the nature of the coordinated oxygen, they now form four non-overlapping ranges, and Table 1 shows the ranges and mean values for the different Dy-O types in 1-3 and the unsubstituted Fe₆Dy₃ cluster. These clearly highlight the relative hardness of the different oxygen species coordinated to the Dy(III) centers, with the μ₂-bridging methoxides exhibiting the shortest Dy-O distances, followed by those involving oxygens from the bridging carboxylates, the bridging phenoxides, while the neutral vanox methoxy groups unsurprisingly form the longest Dy-O bonds. The corresponding bond length for the monodentate bromobenzoate in 3 (Dy1-O38: 2.234 Å) was not included within the data for the bridging carboxylates in Table 1 as it is much shorter, and in fact it falls toward the lower end of the methoxide Dy-O range. This indicates that the “unplugging” of that benzoate from the Fe(III) center has increased the negative charge and hardness of O38, and this may have a significant effect on the electrostatic field around Dy1 in 3.

TABLE 1

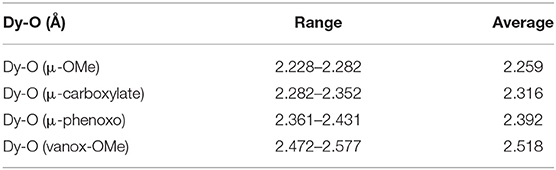
Table 1. Dy-O bond length ranges and averages (in Å) in 1-3 and the unsubstituted cluster (Kühne et al., 2016).

Angular Distortion Analysis of Fe(III) Centers

As previously shown in [Fe₆Ln₃(μ-OMe)₉(vanox)₆(benz)₆] (Kühne et al., 2016), the magnetic behavior of the clusters is dominated by the three dimeric Fe(III) units within the cluster which are antiferromagnetically coupled and the strength of the coupling can be influenced by the bridging angle between the Fe(III) centers as well as the distortion from the octahedral environment (Gorun and Lippard, 1991; Werner et al., 2001). The angular distortion from the octahedral environment around the Fe(III) centers also has an impact on the strength of the magnetic coupling. Therefore the overall distortion of the Fe(III) centers can be described by the angular distortion Σ and the torsional distortion Θ which are defined by formulas (1) and (2) by McKee (Drew et al., 1995), which is a common procedure to describe spin crossover compounds (Marchivie et al., 2005; Halcrow et al., 2019; Kühne et al., 2020).

$\begin{array}{ll}\Sigma ={\sum }_{i=1}^{12}|90-{\varphi }_i|& (1)\end{array}$

$\begin{array}{ll}\Theta ={\sum }_{j=1}^{24}|60-{\theta }_j|& (2)\end{array}$

The degree of trigonal distortion can be described on the one hand by Σ, which shows the local angular deviation from the octahedral angle of 90° and, on the other hand, by Θ which is the sum of the deviation of the triangular faces from 60°, measured by the torsion angle between two adjacent coordinated oxygen atoms of the two triangles. Σ describes the sum of all 12 cis octahedral angles which should be ideally 90° and Θ describes the sum of all 24 unique torsion angles which define the degree of twist from octahedral toward trigonal prismatic geometry. The twist angle, θ, is defined between opposite triangular faces where θ = 0° for a trigonal prism and θ = 60° for an octahedron, leading to Θ = 1440.0° for a trigonal prism. For an octahedron, both Σ and Θ would be 0. Both Σ and Θ have been calculated for 1-3 as well as for the unsubstituted Fe₆Dy₃ cluster, using OctaDist 2.6.1 (Ketkaew et al., 2019) and the results are summarized in Table 2.

TABLE 2

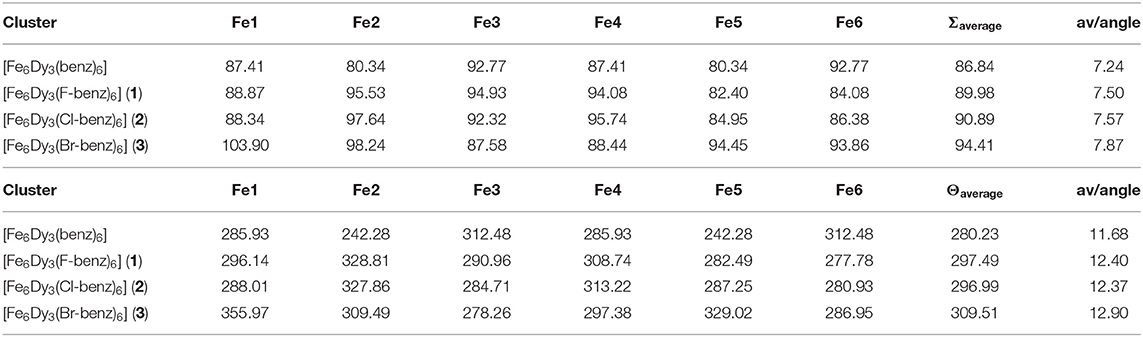
Table 2. Calculated Σ (top) and Θ (bottom) values (in °), together with the average values within one cluster and the average deviation per angle using OctaDist 2.6.1 (Ketkaew et al., 2019) for the hexacoordinated Fe(III) ions within 1–3 in comparison to the unsubstituted Fe₆Dy₃ cluster.

The Σ values were found to increase stepwise from the unsubstituted Fe₆Dy₃ cluster to the 4-bromobenzoate cluster 3 by 8.7%. While the Σ values for the unsubstituted compound were found to be 80.3°-92.8°, these values increase and widen by substituting the benzoate, and the values are found to be 82.4°-103.9°. These values are similar to the ones reported for mononuclear octahedrally coordinated high-spin Fe(III) systems (Halcrow, 2011). This distortion from the octahedral environment leads to an average deviation of 7–8° for each of the expected 90° angles within 1-3. The average Σ values within one cluster were found to be similar for the isostructural clusters 1 and 2, where the average only changes by <1°. Cluster 3 shows that the average value is higher due to the high distortion around Fe1. Interestingly, Fe6, the Fe(III) center with the benzoate distortion, exhibits a smaller and a more close to average distortion from the octahedral environment in comparison to Fe1.

A similar trend of stepwise increase is observed for the Θ values, from an average angle of 280° for the unsubstituted Fe₆Dy₃ cluster, to 297° in 1 and 2 to the highest deviation of 309° within 3, which is again an increase by 10.4% from the unsubstituted cluster to 3. The Θ values vary between 278° and 355° (242°-312° for the unsubstituted Fe₆Dy₃) with similar average values for 1 and 2, while 3 shows again a greater distortion for all Fe(III) centers. Fe1 within 3 exhibits the highest deviation from an octahedral environment. This shows that the deviation for each of the 24 torsion angles averages to 11°-13°, which highlights that the system is far from being trigonal prismatic and can be better described as a distorted octahedron. For comparison, Θ values in mononuclear and octahedrally coordinated high-spin Fe(III) coordination complexes (Halcrow, 2011) as well as Jahn-Teller active Mn(III) high-spin complexes (Gildea et al., 2014; Kühne et al., 2020) were found to be 130°-230°. The angles within 1-3 are slightly higher than these values but are indicative of an octahedral environment.

SHAPE Analysis of Fe(III) and Dy(III) Ions

The unsubstituted cluster, [Fe₆Ln₃(μ-OMe)₉(vanox)₆(benz)₆] (Kühne et al., 2016), exhibits antiferromagnetic exchange between the Fe-Fe centers. Therefore, the main SMM behavior arises from the three anisotropic Dy(III) ions. The magnetic behavior of 4f-ions is related to the interaction between the single-ion electron density and the crystal field environment (Rinehart and Long, 2011; Sorace et al., 2011; Feltham and Brooker, 2014). The coordination geometry can be analyzed using the software SHAPE (Llunell et al., 2013). For SMMs containing the oblate Dy(III), the square antiprismatic (SAP) configuration was found to be a good geometry to support SMM properties, especially for mononuclear Ln-SMMs where small changes in the coordination environment (Rinehart and Long, 2011; Sorace et al., 2011; Feltham and Brooker, 2014), ligand field strength and the complicated inter-molecular interactions could regulate the anisotropy and tune the magnetic dynamics of the mononuclear SMM systems (Neese and Pantazis, 2011). In order to describe the geometries of the lanthanide ions within the structures, they were analyzed using the software SHAPE (Llunell et al., 2013), which evaluates each geometry and assesses how far it deviates from an idealized polyhedron with zero being ideal. Table 3 summarizes the best geometry for the octacoordinated Dy(III) ions as well as the deviation from the square antiprism. For the Dy(III) centers within 1 and 2, there are two Dy(III) centers best described as having a triangular dodecahedral environment, which is a common geometry found in multinuclear SMMs (Langley et al., 2019). The other Dy(III) center, Dy2 in both clusters, is closer to a square antiprismatic environment. This behavior is not observed in 3, where all Dy(III) centers show small deviations from the triangular dodecahedral geometry, which is similar to that of the unsubstituted Fe₆Dy₃ cluster.

TABLE 3

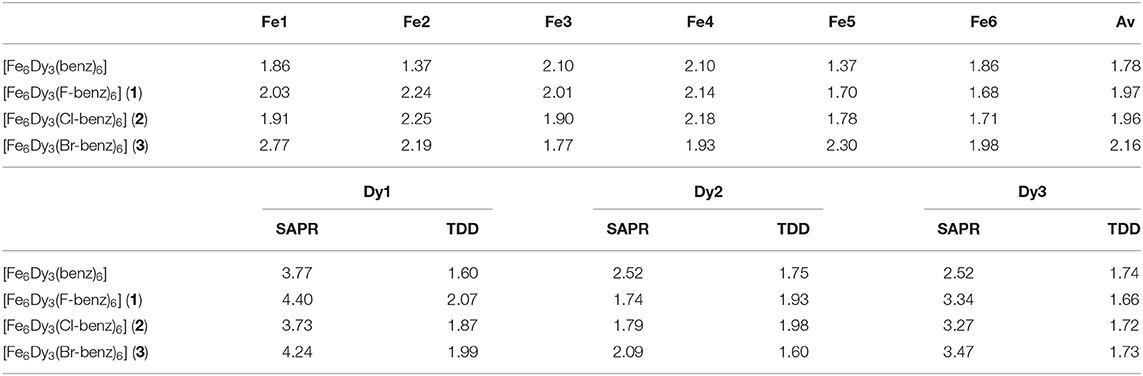
Table 3. SHAPE analysis of Fe(III) ions within 1–3, highlighting the deviation from the octahedral coordination geometry, OC-6 (top) and SHAPE analysis for all Dy(III) ions (bottom), highlighting the deviation from the square antiprismatic (SAPR) and the triangular dodecahedral (TDD) environment.

The six “best” suggested geometries for the hexacoordinated Fe(III) ions are given in Table 3. This clearly shows that all Fe(III) ions exhibit a small deviation from an octahedral environment even though the angular distortion Σ and the torsional distortion Θ seem rather large. The SHAPE analysis clearly highlights that the Fe(III) centers within the unsubstituted Fe₆Dy₃ cluster exhibit smaller deviations from octahedral than within the clusters with the para-substituted benzoates. Trigonal prismatic coordination geometry is the second-best choice with an average deviation of 9.97% for 1 and 10.18% for 2 and 9.88% for 3. As expected, within 3, the Fe(III) center with the largest deviation from an octahedron, Fe1, shows a smaller deviation from a trigonal prism than the other Fe(III) centers.

Packing Arrangement

In the solid state, 1 and 2 exhibit a similar packing arrangement within the crystal lattice as expected for isomorphous clusters, such that the discrete molecules are arranged in layers which are slightly tilted out of the ab-plane (Figure S3). It is not possible for cluster 3, with the bigger bromo substituent, to pack in a similar way (Figure S4) as observed within 1 and 2. The disarray of the coordinated 4-bromobenzoates does not allow the molecules to form sheets and layers like within 1 and 2, but leads to a packing arrangement with slightly shifted molecules. The packing arrangement of all clusters shows that there are intermolecular short contacts between the neighboring molecules, formed by hydrogen bonds to the electronegative halides. These H^..X hydrogen bonds within 1-3 (Figure S5) lead to the formation of a 1D chain of molecules along one preferred axis. This seems to be the dominating packing factor, which might be the reason for the change of the coordination mode of one benzoate ligand observed in 3.

In addition to the H^..X bonds, two substituted benzoate ligands of adjacent molecules of 1 and 2 are in close proximity to each other (Figure S6), leading to sheets of molecules within the ab-plane. This is not possible for 3 due to the disorder of benzoate ligands, where the steric demand of the intramolecular hydrogen bond of the unidentate bromobenzoate, Br6 (Figure 2), forces the latter out of the Fe₆Dy₃ plane by 39° and therefore it cannot form short contacts to neighboring molecules.

Although 3, with one of its benzoates being monodentate, is clearly not isostructural to 1 and 2, and its unit cell parameters are also different, there still seems to be a relationship between these crystal structures. Transformation of the unit cell of 2 (Table A1), using the matrix [1/2 1/2 0 1 −1 0 0 0 −1] results in a non-conventional cell with parameters a = 16.308 Å, b = 19.724 Å, c = 22.941 Å, α = 90.06°, β = 109.83°, and γ = 91.56°, which shows a more obvious relationship to the unit cell of 3, and in which the rings would be nearly parallel to the new ab plane, as is the case in 3. It is possible to imagine that the partial disconnection of the bromobenzoate then leads to a shearing which brings the three angles into line with those for the unit cell of 3.

Magnetic Properties

DC Magnetic Properties

The direct current (dc) magnetic properties were studied on freshly filtered crystalline samples (in order to avoid lattice solvent loss) in a temperature range 1.9–300 K under an applied field of 1,000 Oe and are shown as χ_MT vs. T plots in Figure 3. 1-3 show a similar behavior to the unsubstituted cluster with a steady decrease on lowering the temperature. The χ_MT value for each compound measured at room temperature is lower than the expected spin-only value of 68.76 cm³K/mol for six non-interacting Fe(III) ions and three non-interacting Dy(III) ions. The obtained values at room temperature are 56.77 cm³K/mol for 1 (fluorobenzoate), 57.72 cm³K/mol for 2 (chlorobenzoate) and 58.39 cm³K/mol for 3 (bromobenzoate), which is in good agreement with the unsubstituted Fe₆Dy₃ where a χ_MT value of 58.8 cm³K/mol was observed at room temperature (Kühne et al., 2016). The data show a similar curvature for all compounds and initially decrease slowly in an almost linear fashion upon lowering the temperature to 30 K. Below this temperature the curves bend downwards and reach their minimal values at 1.9 K of 33.25 cm³K/mol for 1 (32.73 cm³K/mol for 2 and 36.89 cm³K/mol for 3), indicating the presence of dominant antiferromagnetic interactions within the three Fe(III)₂ dinuclear units. The slow and steady decrease in χ_MT values from room temperature on, highlights the dominating antiferromagnetic coupling of the dimeric Fe₂ units within the ring structure, which is present even at room temperature. The arrangement of these dimeric Fe(III) units in a cyclic cluster can lower the expected χ_MT value due to the spin arrangement within the ring.

FIGURE 3

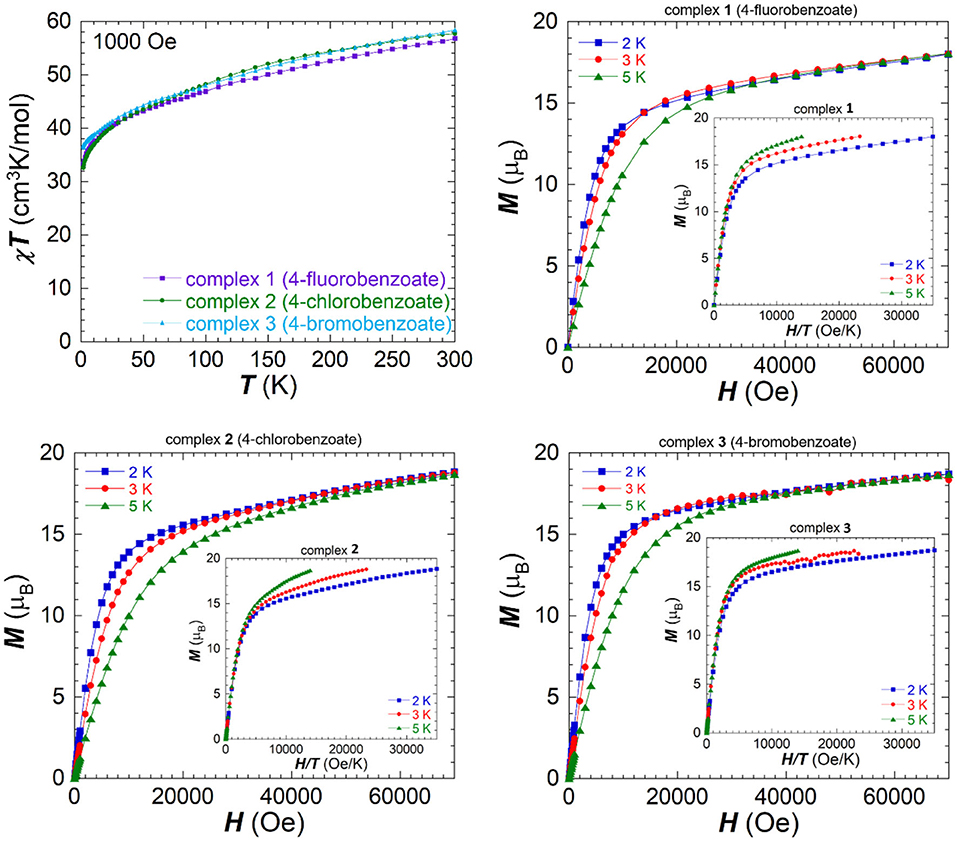
Figure 3. Temperature dependence of the χ_MT product measured under an applied field of 1,000 Oe for 1-3 (top left), field dependence of magnetization for 1 (top right), 2 (bottom left), and 3 (bottom right) measured between 0 and 7 T at different temperatures and the reduced magnetization as inset for each.

Field dependence of the magnetization was measured between 2.0 and 5.0 K and the plots are shown in Figure 3, as M vs. H curves. The lack of saturation in the magnetization values for all clusters indicates the presence of magnetic anisotropy and/or low-lying excited states. The values of the isotherms rapidly increase in all cases at low field, before following a more gradual linear increase after 1.4 T. None of the compounds show saturation of magnetization up to 7.0 T at a temperature of 2.0 K and these values of 18.0 μ_B for 1 (18.84 μ_B for 2 and 18.71 μ_B for 3) are lower than the expected value for six non-interacting or ferromagnetically coupled Fe(III) centers and three Dy(III) centers. The first derivatives of the magnetization isotherms with respect to the applied field are shown in Figure S7, ESI, since such plots can be indicative of a transition between two different magnetic states (Kühne et al., 2014), or a toroidal behavior (Novitchi et al., 2012), but no maxima were observed in these plots.

The reduced magnetization curves plotted as M vs. H/T (Figure 3, inset) show at lower fields, up to 1,000 Oe (0.1 T), only small deviations from an almost perfect superposition of the three isotherms on to one master curve, which is indicative of an isotropic system within this range. On increasing the magnetic field strength, there is an increased deviation from this superposition, compatible with the presence of anisotropy and/or low-lying excited states within 1-3.

AC Magnetic Properties

Given that all χ_MT vs. T and M vs. H curves have similar shapes with similar slopes, it is likely that the coupling between the metal centers should be in a similar range. This enables us to compare 1-3 to see the effect of the different para-substituents on the dynamic magnetic behavior using ac susceptibility measurements, which previously showed slow relaxation and thus likely SMM behavior for the unsubstituted Fe₆Dy₃ cluster (Kühne et al., 2016). As a means to suppress any quantum tunneling of the magnetization (QTM), frequency-dependent ac susceptibility was measured at 1.8 K for all clusters with applied fields between 0 Oe and 3,000 Oe (Figure S8). The in-phase and out-of-phase ac susceptibility measurements show field-dependent signals for all compounds. Although 1 and 2 showed rather similar behavior in the dc magnetic properties, their behavior in the ac component is distinctly different. Only 2 shows weak frequency-dependent behavior in the in phase and out-of-phase ac susceptibility under zero applied field, but without visible maxima within the measured parameter set. On application of higher dc fields, it is possible to suppress the quantum tunneling component within 1-3 with the maxima in the out-of-phase component shifted to lower frequencies. At fields higher than 2,500 Oe, the frequency-dependent maxima in the out-of-phase susceptibility start to become very broad and/or vanish (Figure S8). The optimum dc fields where the quantum tunneling is the smallest are 1,500 Oe for 1, 2,000 Oe for 2 and 1,000 Oe for 3.

For the fluorobenzoate cluster 1, the ac measurements under an applied field of 1,500 Oe, show frequency-dependent in-phase and out-of-phase signals (Figure 4), with the temperature-shifting maxima in the out-of-phase component. The Cole-Cole plots (Figure S9) were used to extract the τ and α values (Table S5) and fit the in-phase and out-of-phase susceptibility data (Figure 4) by using a generalized Debye model.

FIGURE 4

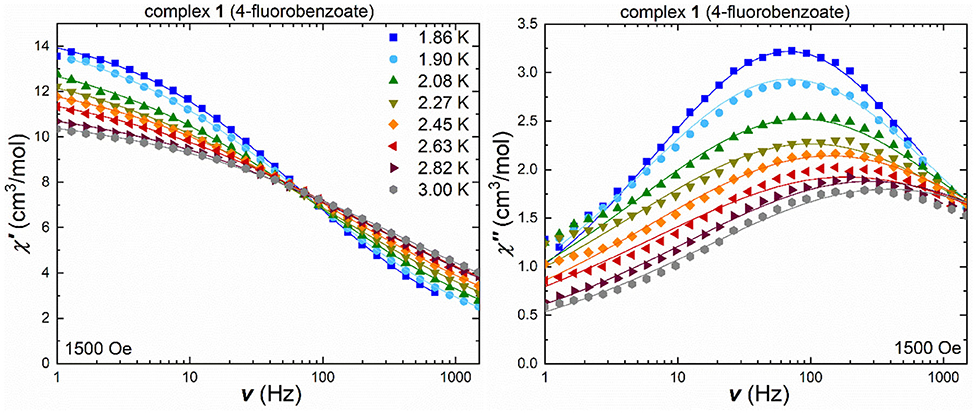
Figure 4. Frequency-dependent in-phase (left) and out-of-phase susceptibility (right) under an applied field of 1,500 Oe for 1 in a temperature range 1.8–3.0 K [the lines are the best fit using CCFit (Reta and Chilton, 2019)].

The obtained α-values are around 0.6 in the higher temperature range of 2.26–3.0 K, indicating a broad distribution of relaxation pathways most likely involving more than one relaxation process. For a single relaxation process, the Cole-Cole plot would show a perfect semi-circular profile leading to an α-value of zero. For 1, the high deviation from this behavior is expected given the very broad maxima which spread over almost the whole frequency range. In order to check for secondary relaxation processes, especially at higher temperatures, the in-phase and out-of-phase susceptibilities were also measured in terms of their temperature-dependency under a variety of frequencies (Figure S10). The out-of-phase susceptibility component clearly highlights that the magnetic relaxation processes are limited to temperatures below 10 K, and that no secondary relaxation processes are expected beyond this temperature, since the out-of-phase susceptibility is now at zero. The temperature-dependent in-phase susceptibility (Figure S10) clearly exhibits a change in slope at low temperatures, from negative for small frequencies (1–100 Hz) to positive at frequencies beyond 200 Hz, which is indicative of multiple relaxation processes.

The isostructural chlorobenzoate cluster 2 shows frequency-dependent in-phase and out-of-phase signals in the ac susceptibility measurements under an applied field of 2,000 Oe, (Figure 5), with the temperature-dependent maxima in the out-of-phase component. The maxima located at low temperatures and small frequencies appear to be frequency-independent and only start shifting at temperatures beyond 3.1 K. The Cole-Cole plot of the 2.5 K ac susceptibility data clearly shows the presence of two relaxation processes (Figure S11) and these were fitted using CCFit (Reta and Chilton, 2019) highlighting that a second process is thermally activated while the frequency-independent QTM process becomes less dominant. This is more pronounced in the temperature-dependent out-of-phase susceptibility (Figure S12), where at small frequencies and temperatures, a crossover point at 2.5 K can be observed. While the out-of-phase susceptibility curves at low frequencies display a rather sharp profile, without visible maxima, the curves become more broad at frequencies beyond 40 Hz, and no clear maxima are found due to the broadened curves, which indicates secondary magnetic relaxation processes over the measured temperature range. On the other hand, the shift of the frequency- and temperature-dependent signals at temperatures higher than 2.5 K in the out-of-phase susceptibility is easier to detect in Figure 5 due to the logarithmic x-axis. Cole-Cole plots (Figure S11) were used in the measured temperature range between 3.1 and 6.0 K, to calculate the τ and α values (Table S6). The α values decrease from 0.6 at 3.4 K to 0.2 at 5.5 K, highlighting that even at 3.4 K, the relaxation pathway is most likely a combination of several magnetic relaxation processes.

FIGURE 5

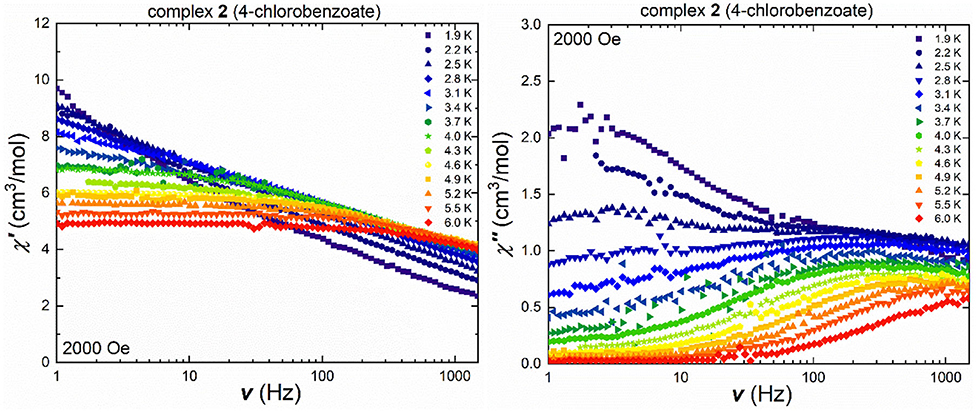
Figure 5. Frequency-dependent in-phase (left) and out-of-phase susceptibility (right) under an applied field of 2,000 Oe of 2 in a temperature range between 1.9 and 6.0 K.

Cluster 3, containing the bromobenzoate ligand, which led to the structural change in coordination mode, shows frequency-dependent in-phase and out-of-phase signals in the ac measurements under an applied field of 1,000 Oe (Figure 6), as well as without an externally applied magnetic field (Figure S13) with temperature-dependent maxima in the out-of-phase component over the measured temperature range up to 5.0 K. The in-phase and out-of-phase susceptibilities were also measured in terms of their temperature-dependency under a variety of frequencies (Figures S14, S15), in order to check for secondary relaxation processes at higher temperatures and these were found to be absent. The Cole-Cole plots (Figure S1) of the ac susceptibility data at 1,000 Oe were used to extract the τ and α values (Table S7). The obtained α-values decrease on increasing the temperature from 0.5 at 1.8 K to 0.3 at 5.0 K, indicating a narrower distribution of relaxation processes and possibly corresponding to only one pathway.

FIGURE 6

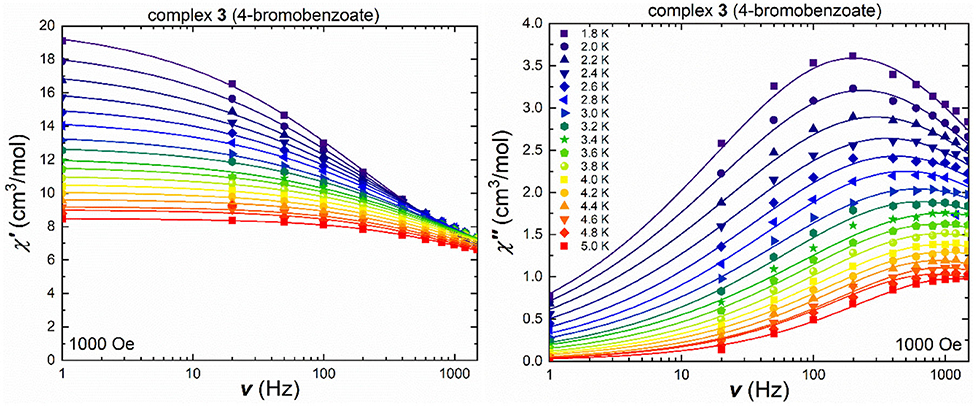
Figure 6. Frequency-dependent in-phase (left) and out-of-phase susceptibility (right) under an applied field of 1,000 Oe for 3 in a temperature range between 1.8 and 5.0 K [the lines show the best fit using CCFit (Reta and Chilton, 2019)].

The energy barrier for spin reversal for 1-3 was fitted using the extracted τ values from the Cole-Cole plots which are then plotted against the reciprocal temperature, 1 /T. In contrast to 1 and 2, cluster 3 could be fitted using the Arrhenius law for all τ values (Figure 7), since a distinct linear trend can be observed by plotting τ against 1/T, which leads to U_eff = 4.9 K and τ₀ = 5.2^.10⁻⁵ s. Considering not just thermally induced relaxation processes, but also other relaxation mechanisms such as Raman and QTM (which seems to be fully suppressed) processes, and fitting combinations or all of them simultaneously, using Equation (1), does not lead to any improvement (Figure S17).

$\begin{array}{l}{\tau }^{-1}={\tau }_0^{-1}exp\left(-\frac{U_{eff}}{T}\right)+C{T}^n+{\tau }_{QTM}^{-1}\end{array}$

1 and 2 show a noticeably different behavior in their magnetic relaxation mechanism compared to 3 (Figure 8). It is not possible to fit all data points of the τ values with one single slope over the measured temperature range. It has been shown in the literature, that by ignoring the overall slope of the extracted τ values and constraining a linear regime at higher temperatures, in which the data could be fitted to the Arrhenius law, can lead to an erroneously large U_eff value (Lampropoulos et al., 2009). Therefore, the spin relaxation was simultaneously fitted using Equation (1) (Reta and Chilton, 2019), considering all three possible relaxation processes, including a tunneling process, QTM, at low temperatures, followed by a Raman and an Orbach processes. This approach was only applied to 2 (Figure S18), since more data in form of τ values are available for 2 than for 1 and it is thus not possible to get a reasonable fit for the τ values of 1 as a result of the poor data:parameter ratio.

FIGURE 7

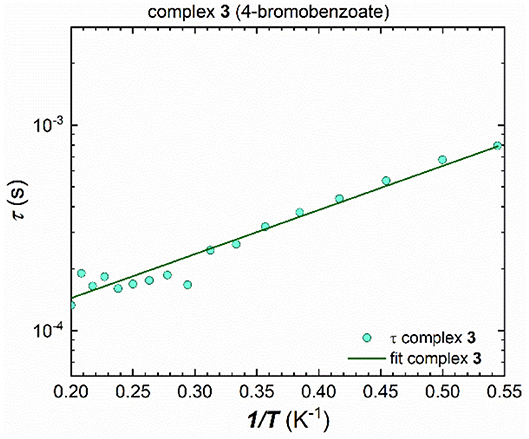
Figure 7. Extracted τ values plotted against 1/T for 3, fitted to an Arrhenius law over the whole measured temperature range, leading to U_eff = 4.9 K and τ₀ = 5.2^.10⁻⁵ s.

FIGURE 8

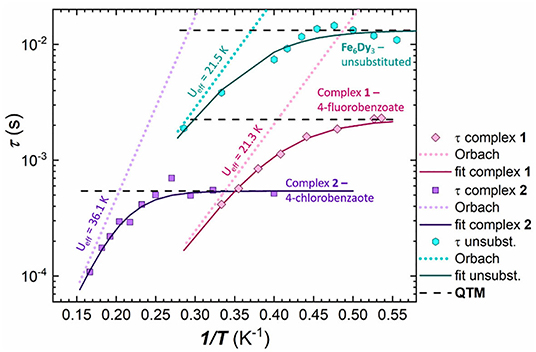
Figure 8. Extracted τ values plotted against 1/T for 1 (4-fluorobenzoate; pink) 2 (4-chlorobenzoate; purple) and the unsubstituted Fe₆Dy₃ cluster (turquoise), with the respective simultaneous Orbach-QTM fit (solid line) (Orbach process—dotted lines; QTM factor—dashed black lines).

The best simultaneous fit of Equation (1), for 2, shows that the magnetic relaxation is dominated by quantum tunneling at low temperatures, followed by an Orbach process at higher temperatures as indicated by the almost linear dependence. Thus the relaxation process of 1 was fitted according to this outcome from the isostructural cluster 2 (i.e. without a Raman process), in order to avoid overparameterization. In case of 1, the quantum tunneling parameter was determined as τ_QTM = 2.3^.10⁻³ s, which includes only the points at very low temperatures up to 2.0 K, whilst for 2 the QTM process is the dominant process up to 3.4 K with a faster τ_QTM factor of 5.4^.10⁻³ s. The exponential fit of the Orbach processes leads to energy barriers of U_eff = 21.3 K for 1 and U_eff = 36.1 K for 2, with τ₀ = 4.1^.10⁻⁷ s for 1 and τ₀ = 3.4^.10⁻⁷ s for 2, respectively, indicating similar relaxation processes and energy barriers for both.

In order to compare this result with the unsubstituted cluster, we used the published ac data (Kühne et al., 2016) and ran new simulations to fit the in-phase and out-of-phase susceptibilities of the Cole-Cole plot (Figure S19 and Table S8) using CCFit (Reta and Chilton, 2019). The energy barrier was then fitted using the extracted τ values and Equation (1) (Figure S20) in a similar way as for 1 and 2, leading to an Orbach process with an energy barrier of U_eff = 21.5 K and τ₀ = 4.5^.10⁻⁶ s and a QTM process below 2.2 K. This illustrates that the fluorosubstituted cluster 1 shows a similar behavior to that of the unsubstituted Fe₆Dy₃ cluster (Figure 8), where the complete fit of both clusters exhibits a nearly parallel performance, leading to almost identical energy barriers in the Orbach component of U_eff = 21.5 K for the unsubstituted cluster and U_eff = 21.3 K for 1. This is reasonable due to the similarity of the 4-fluorobenzoic acid and the benzoic acid in terms of their acidity.

In 2011, Mereacre et al. established a correlation between the energy barrier U_eff and the Hammett parameters of the coordinated substituted benzoic acids in a butterfly Fe₂Dy₂ compound (Mereacre et al., 2011). In these compounds, each Dy(III) is coordinated by four carboxylate oxygens that are all well-aligned around the Dy(III) centers on the direction of the local Dy anisotropy axis. In the system shown here, each Dy(III) ion is only ligated by two carboxylate oxygens that bridge to an Fe(III) center on either side, which therefore can be seen as cis to each other. The pk_a value of benzoic acid (4.19) is similar to that of 4-fluorobenzoic acid (4.15) and therefore the Hammett parameters for both are similar too, with 4-fluorobenzoate = −0.03 (Hansch et al., 1991). By increasing the strength of the acid toward 4-chlorobenzoate (pk_a = 3.98; = +0.19) (Hansch et al., 1991) an increase in the energy barrier, U_eff = 36.1 K for 2 was observed. Since the Hammett parameter of 4-bromobenzoate (= +0.25) (Hansch et al., 1991) is bigger than that of 4-chlorobenzoate, while the pk_a of both acids are in a similar range (3.98 for Cl vs. 3.97 for Br), a comparison between 3 and the other compounds should show whether the trend of the increase of U_eff tracks the Hammett parameters or the pk_a values of the ligand. Unfortunately, as cluster 3 features a different structure, a direct comparison cannot be made.

Conclusions

We report the structural and magnetic properties of three nonanuclear Fe₆Dy₃ cyclic coordination clusters with para-halosubstituted benzoate ligands. 1 and 2, the fluoro- and chlorobenzoate clusters, are isostructural and can be regarded as the cyclisation of three {Fe₂Ln} units. In the case of the bromo substituent within 3, we can no longer use this model, since one of its benzoates is monodentate: it does not bridge between one Fe(III) and one Dy(III) ion anymore, but coordinates only to a single Dy(III) ion. The change in pK_a/Hammett constants for these benzoic acids on moving from para-Cl to para-Br results in this “carboxylate shift” from the bridging to monodentate coordination. A second influence is the size of the halo-substituent forcing the benzoate ligands of the cyclic coordination clusters out of the metal plane in order to keep the packing arrangement similar. This results in one oxygen of a 4-bromobenzoate carboxylate group maintaining its coordination to the Dy(III) ion, but with the other oxygen now losing its grip on the neighboring Fe(III) ion and becoming just a hydrogen-bond acceptor; this switch to monodentate coordination by the carboxylate requires the ligation of a methanol molecule to the Fe(III) to maintain its 6 coordination. This coordinative flexibility opens possibilities for future applications such as MRI contrast agents or catalytic activities.

These considerations are also relevant to the dynamic magnetic properties within these antiferromagnetically coupled coordination clusters. Whereas, 1 and 2 show similar behavior in their magnetic relaxation processes, with a combination of QTM and Orbach mechanisms, the QTM part can be completely suppressed within 3 by application of a small dc field. Furthermore, 1, which has the para-fluorobenzoate as a ligand, shows behavior similar to that of the unsubstituted Fe₆Dy₃ cluster, as shown by the complete fit of the data for both clusters being almost parallel. The energy barrier, U_eff, increases significantly on going to the para-chlorobenzoate within 2 from U_eff = 21.3 K for 1 to U_eff = 36.1 K for 2. This reflects the changes in pK_a and Hammett constants, but a clear trend cannot be identified due to the structural break observed on going to the 4-bromobenzoate within 3.

Materials and Methods

Materials and Instrumentation

All chemicals and solvents unless otherwise stated were of reagent grade and used as received from commercial suppliers. They were used without further purification or drying. Dy(NO₃)${}_3^{.}$6H₂O was synthesized from Dy₂O₃ by treatment with nitric acid, HNO₃. o-Vanillinoxime (H₂vanox) was prepared according to the literature (Hewitt et al., 2009). Elemental analysis (C, H, N) was recorded on dried polycrystalline samples using an Exeter Analytical CE-440 CHN analyzer. Infrared spectra were recorded using a Bruker Alpha Platinum ATR (attenuated total reflection) spectrometer. PXRD pattern were recorded on dried samples using a Stoe STADI-4 XRD diffractometer equipped with a Cu-Kα source.

Synthesis of Compounds 1-3

The synthesis of 1-3 is straightforward, and the compounds were recovered in varying yields. All reactions are modified versions of the published work on the unsubstituted benzoate Fe₆Ln₃ compounds (Kühne et al., 2016). The elemental analysis was performed on dried polycrystalline samples. Due to the volatility of the methanol molecules within the crystal lattice, the elemental analysis was fitted using water molecules in the crystal lattice replacing the methanol molecules. The IR spectra of 2 and 3 are shown in Figure S21, and highlight the structural similarities of the clusters, including the carboxylate C-O stretching bands [~1,540 cm⁻¹ (antisymmetric) and ~1,410 cm⁻¹ (symmetric)] and the oxime bands (C=N ~1,590 cm⁻¹). No differences resulting from a monodentate 4-bromobenzoate in 3 are found in the IR spectra. PXRD patterns of 2 and 3 were recorded on dried samples (Figure S23), highlighting the presence of the main peaks in the correct positions. The relative intensities of the peaks show some differences with the predicted pattern likely caused by the loss of solvent. However, despite this the extracted unit cell parameters are in good agreement with the single crystal data.

Compound 1: [Fe₆Dy₃(μ-OMe)₉(vanox)₆(F-benz)₆]^.12MeOH^.H₂O: H₂vanox (0.4 mmol; 0.066 g) and NaOMe (1.0 mmol; 0.054 g) were dissolved in 10 ml MeOH and were added to a solution of ${\text{FeCl}}_2^{.}$4H₂O (0.2 mmol; 0.040 g), Dy(NO₃)${}_3^{.}$6H₂O (0.2 mmol; 0.092 g) and 4-fluorobenzoic acid (0.4 mmol; 0.056 g) in 10 ml MeOH. The dark red, almost black, solution was stirred for 10 min at room temperature, and left to stand for crystallization without filtration. After 1 week, 1 crystallized as dark red-black blocks suitable for single crystal X-ray analysis.

Yield of [Fe₆Dy₃(μ-OMe)₉(vanox)₆(F-benz)₆]^.12MeOH^. H₂O: 55 mg (50% related to Fe)

Elemental analysis for [C₉₉H₉₃Fe₆Dy₃N₆O₃₉F₆]^.10.6H₂O (%): calculated: C: 38.13, H: 3.69; N: 2.69; found: C: 38.11; H: 3.67; N: 2.71.

IR (KBr):/cm⁻¹ = 3,441 (m), 2,822 (w), 1,606 (s), 1,591 (s), 1,543 (s), 1,508 (w), 1,459 (s), 1,439 (m), 1,410 (s), 1,354 (w), 1,269 (m), 1,239 (w), 1,221 (m), 1,153 (m), 1,094 (w), 1,056 (s), 965 (m), 856 (m), 783 (m), 764 (m), 737 (w), 691 (w), 657 (m), 618 (m), 555 (w), 500 (w), 461 (m).

Compound 2: [Fe₆Dy₃(μ-OMe)₉(vanox)₆(Cl-benz)₆]^. 13MeOH: H₂vanox (0.4 mmol; 0.066 g) and NaOMe (1.5 mmol; 0.081 g) were dissolved in 10 ml MeOH and were added to a solution of ${\text{FeCl}}_2^{.}$4H₂O (0.2 mmol; 0.040 g), Dy(NO₃)${}_3^{.}$6H₂O (0.2 mmol; 0.092 g) and 4-chlorobenzoic acid (0.4 mmol; 0.063 g) in 10 ml MeOH. The dark red, almost black, solution was stirred for 10 min at room temperature, and left to stand for crystallization without filtration. After 1 week, 2 crystallized as dark red-black blocks suitable for single crystal X-ray analysis.

Yield of [Fe₆Dy₃(μ-OMe)₉(vanox)₆(Cl-benz)₆]^.13MeOH: 51 mg (44% related to Fe)

Elemental analysis for [C₉₉H₉₃Fe₆Dy₃N₆O₃₉Cl₆]^.4.6MeOH^. 5.9H₂O (%): calculated: C: 37.94, H: 3.78; N: 2.56; found: C: 37.73; H: 3.57; N: 2.35.

IR (KBr):/cm⁻¹ = 3,439 (m), 2,991 (w), 2,927 (m), 2,821 (m), 1,592 (s), 1,537 (s), 1,459 (s), 1,407 (s), 1,268 (s), 1,221 (s), 1,171 (m), 1,093 (s), 1,056 (s), 964 (s), 853 (m), 776 (m), 737 (m), 656 (s), 584 (w), 540 (m), 458 (m).

Compound 3: [Fe₆Dy₃(μ-OMe)₉(vanox)₆(Br-benz)₆ (MeOH)]^.9MeOH: H₂vanox (0.4 mmol; 0.066 g) and NaOMe (1.5 mmol; 0.081 g) were dissolved in 10 ml MeOH and were added to a solution of ${\text{FeCl}}_2^{.}$4H₂O (0.2 mmol; 0.040 g), Dy(NO₃)${}_3^{.}$6H₂O (0.2 mmol; 0.092 g), and 4-bromobenzoic acid (0.4 mmol; 0.080 g) in 10 ml MeOH and 5 ml CH₂Cl₂. The dark red, almost black, solution was stirred for 10 min at room temperature, then filtered and left to stand for crystallization. After 2 weeks, 3 crystallized as dark red-black blocks suitable for single crystal X-ray analysis.

Yield of [Fe₆Dy₃(μ-OMe)₉(vanox)₆(Br-benz)₆(MeOH)]^. 9MeOH: 43 mg (36% related to Fe)

Elemental analysis for [C₁₀₀H₉₇Fe₆Dy₃N₆O₄₀Br₆]^.0.9 MeOH^.13.2H₂O (%): calculated: C: 33.74, H: 3.56; N: 2.34; found: C: 33.52; H: 3.79; N: 2.57.

IR (KBr):/cm⁻¹ = 3,437 (m), 2,943 (w), 2,822 (w), 1,588 (s), 1,537 (s), 1,459 (s), 1,438 (w), 1,406 (s), 1,356 (w), 1,270 (m), 1,222 (m), 1,171 (m), 1,057 (s), 1,013 (m), 966 (m), 854 (m), 771 (s), 736 (m), 657 (m), 572 (w), 504 (m), 460 (m).

Single Crystal X-Ray Structure Determination

X-ray crystallography was carried out on suitable single crystals using an Oxford Supernova diffractometer (Oxford Instruments, Oxford, United Kingdom). Datasets were measured using monochromatic Cu-Kα (2) or Mo-Kα (1 and 3) radiation and corrected for absorption. The temperature was controlled with an Oxford Cryosystem instrument. All structures were solved by dual-space direct methods (SHELXT) and refined by full matrix least-squares on F2 for all data using SHELXL-2016 (Sheldrick, 2015). All hydrogen atoms were added at calculated positions and refined using a riding model. Their isotropic displacement parameters were fixed to 1.2 times the equivalent one of the parent atom. Anisotropic displacement parameters were used for all ordered non-hydrogen atoms. Crystallographic details for 1-3 are summarized in Table A1 and crystallographic data for the structures reported in this paper have been deposited with the Cambridge Crystallographic Data Center as supplementary publication numbers CCDC2001519-2001521.

Magnetic Measurements

The magnetic susceptibility measurements were obtained using a Quantum Design SQUID magnetometer MPMS-XL (Quantum Design, San Diego, USA) operating between 1.8 and 300 K. DC (direct current) measurements were performed on freshly filtered polycrystalline samples to avoid loss of lattice solvent. Each sample was wrapped in a polyethylene membrane, and susceptibility data were collected at 0.1 T between 1.8 and 300 K in cooling mode. The magnetization data was collected at 2, 3, and 5 K. Diamagnetic corrections were applied to correct for contribution from the sample holder, and the inherent diamagnetism of the sample was estimated with the use of Pascal's constants. AC (alternating current) measurements were carried out in with frequencies between 1 and 1,500 Hz.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material. Crystallographic data have been deposited with the CCDC (Cambridge Crystallographic Data Centre) Numbers: 2001519–2001521. Copies of the data can be obtained free of charge from https://www.ccdc.cam.ac.uk/structures/.

Author Contributions

IK and AP were responsible for the conceptualization of the project. IK was responsible for the synthesis and standard characterizations, performed the analysis of the magnetic data, and drafted the initial manuscript. CA collected and refined the single crystal data whilst IK and CA performed the structural analysis. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Funding

AP acknowledges the DFG (SFB/TRR 88-3MET) and the Helmholtz Gemeinschaft POF STN for funding.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge Dr. Yanhua Lan and Dr. Valeriu Mereacre for collecting the magnetic data. IK acknowledges Blue Carter for help with proofreading of the final manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2020.00701/full#supplementary-material

References

Alexandru, M.-G., Visinescu, D., Shova, S., Oliveira, W. X. C., Lloret, F., and Julve, M. (2018). Design of 3d-4f molecular squares through the [Fe{(HB(pz)₃)}(CN)₃]⁻ metalloligand. Dalton Trans. 47, 6005–6017. doi: 10.1039/C8DT00895G

PubMed Abstract | CrossRef Full Text | Google Scholar

Baniodeh, A., Anson, C. E., and Powell, A. K. (2013). Ringing the changes in Feiii/Ybiii cyclic coordination clusters. Chem. Sci. 4:4354. doi: 10.1039/c3sc52041b

CrossRef Full Text | Google Scholar

Baniodeh, A., Hewitt, I. J., Mereacre, V., Lan, Y., Novitchi, G., Anson, C. E., et al. (2011). Heterometallic 20-membered {Fe₁₆Ln₄} (Ln = Sm, Eu, Gd, Tb, Dy, Ho) metallo-ring aggregates. Dalton Trans. 40:4080. doi: 10.1039/c0dt01742f

PubMed Abstract | CrossRef Full Text | Google Scholar

Baniodeh, A., Liang, Y., Anson, C. E., Magnani, N., Powell, A. K., Unterreiner, A.-N., et al. (2014). Unraveling the influence of lanthanide ions on intra- and inter-molecular electronic processes in Fe₁₀Ln₁₀ Nano-Toruses. Adv. Funct. Mater. 24, 6280–6290. doi: 10.1002/adfm.201400336

CrossRef Full Text | Google Scholar

Baniodeh, A., Magnani, N., Lan, Y., Buth, G., Anson, C. E., Richter, J., et al. (2018). High spin cycles: topping the spin record for a single molecule verging on quantum criticality. npj Quantum Mater. 3:10. doi: 10.1038/s41535-018-0082-7

CrossRef Full Text | Google Scholar

Botezat, O., van Leusen, J., Hauser, J., Decurtins, S., Liu, S.-X., Kögerler, P., et al. (2019a). A spontaneous condensation sequence from a {Fe₆Dy₃} wheel to a {Fe₇Dy₄} globe. Cryst. Growth Des. 19, 2097–2103. doi: 10.1021/acs.cgd.8b01668

CrossRef Full Text | Google Scholar

Botezat, O., van Leusen, J., Kögerler, P., and Baca, S. G. (2019b). Ultrasound-assisted formation of {Fe₆Ln/Y₄} wheel-shaped clusters and condensed {Fe₄Ln/Y₂} aggregates. Eur. J. Inorg. Chem. 2019, 2236–2244. doi: 10.1002/ejic.201900175

CrossRef Full Text | Google Scholar

Botezat, O., van Leusen, J., Kravtsov, V. C., Kögerler, P., and Baca, S. G. (2017). Ultralarge 3d/4f coordination wheels: from carboxylate/amino alcohol-supported {Fe₄Ln/Y₂} to {Fe₁₈Ln/Y₆} rings. Inorg. Chem. 56, 1814–1822. doi: 10.1021/acs.inorgchem.6b02100

PubMed Abstract | CrossRef Full Text | Google Scholar

Cador, O., Gatteschi, D., Sessoli, R., Barra, A. L., Timco, G. A., and Winpenny, R. E. P. (2005). Spin frustration effects in an odd-member antiferromagnetic ring and the magnetic Möbius strip. J. Magn. Magn. Mater. 290–291 PA, 55–60. doi: 10.1016/j.jmmm.2004.11.159

CrossRef Full Text | Google Scholar

Cador, O., Gatteschi, D., Sessoli, R., Larsen, F. K., Overgaard, J., Barra, A.-L., et al. (2004). The Magnetic möbius strip: synthesis, structure, and magnetic studies of odd-numbered antiferromagnetically coupled wheels. Angew. Chem. 116, 5308–5312. doi: 10.1002/ange.200460211

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, S., Mereacre, V., Kostakis, G. E., Anson, C. E., and Powell, A. K. (2017). Systematic studies of hexanuclear {${\text{M}}_4^{\text{III}}$${\text{Ln}}_2^{\text{III}}$} complexes (M = Fe, Ga; Ln = Er, Ho): structures, magnetic properties and SMM behavior. Inorg. Chem. Front. 4, 927–934. doi: 10.1039/C7QI00091J

CrossRef Full Text | Google Scholar

Chen, S., Mereacre, V., Prodius, D., Kostakis, G. E., and Powell, A. K. (2015). Developing a “Highway Code” to steer the structural and electronic properties of Fe^III/Dy^III coordination clusters. Inorg. Chem. 54, 3218–3227. doi: 10.1021/ic502809y

PubMed Abstract | CrossRef Full Text | Google Scholar

Chibotaru, L. F., Ungur, L., and Soncini, A. (2008). The origin of nonmagnetic kramers doublets in the ground state of dysprosium triangles: evidence for a toroidal magnetic moment. Angew. Chem. Int. Ed. 47, 4126–4129. doi: 10.1002/anie.200800283

PubMed Abstract | CrossRef Full Text | Google Scholar

Drew, M. G. B., Harding, C. J., Mckee, V., Morgan, G. G., and Nelson, J. (1995). Geometric control of manganese redox state. J. Chem. Soc. Chem. Commun. 1035–1038. doi: 10.1039/C39950001035

CrossRef Full Text | Google Scholar

Feltham, H. L. C., and Brooker, S. (2014). Review of purely 4f and mixed-metal nd-4f single-molecule magnets containing only one lanthanide ion. Coord. Chem. Rev. 276, 1–33. doi: 10.1016/j.ccr.2014.05.011

CrossRef Full Text | Google Scholar

Ferrando-Soria, J., Fernandez, A., Moreno Pineda, E., Varey, S. A., Adams, R. W., Vitorica-Yrezabal, I. J., et al. (2015). Controlled synthesis of nanoscopic metal cages. J. Am. Chem. Soc. 137, 7644–7647. doi: 10.1021/jacs.5b04664

CrossRef Full Text | Google Scholar

Gildea, B., Harris, M. M., Gavin, L. C., Murray, C. A., Ortin, Y., Müller-Bunz, H., et al. (2014). Substituent effects on spin state in a series of mononuclear manganese(III) complexes with hexadentate schiff-base ligands. Inorg. Chem. 53, 6022–6033. doi: 10.1021/ic5003012

CrossRef Full Text | Google Scholar

Gorun, S. M., and Lippard, S. J. (1991). Magnetostructural correlations in magnetically coupled (.mu.-oxo)diiron(III) complexes. Inorg. Chem. 30, 1625–1630. doi: 10.1021/ic00007a038

CrossRef Full Text | Google Scholar

Guthausen, G., Machado, J. R., Luy, B., Baniodeh, A., Powell, A. K., Krämer, S., et al. (2015). Characterisation and application of ultra-high spin clusters as magnetic resonance relaxation agents. Dalton Trans. 44, 5032–5040. doi: 10.1039/C4DT02916J

PubMed Abstract | CrossRef Full Text | Google Scholar

Gysler, M., El Hallak, F., Ungur, L., Marx, R., Hakl, M., Neugebauer, P., et al. (2016). Multitechnique investigation of Dy₃ - implications for coupled lanthanide clusters. Chem. Sci. 7, 4347–4354. doi: 10.1039/C6SC00318D

PubMed Abstract | CrossRef Full Text | Google Scholar

Habib, F., Brunet, G., Vieru, V., Korobkov, I., Chibotaru, L. F., and Murugesu, M. (2013). Significant enhancement of energy barriers in dinuclear dysprosium single-molecule magnets through electron-withdrawing effects. J. Am. Chem. Soc. 135, 13242–13245. doi: 10.1021/ja404846s

PubMed Abstract | CrossRef Full Text | Google Scholar

Halcrow, M. A. (2011). Structure:function relationships in molecular spin-crossover complexes. Chem. Soc. Rev. 40:4119. doi: 10.1039/c1cs15046d

PubMed Abstract | CrossRef Full Text | Google Scholar

Halcrow, M. A., Capel Berdiell, I., Pask, C. M., and Kulmaczewski, R. (2019). Relationship between the molecular structure and switching temperature in a library of spin-crossover molecular materials. Inorg. Chem. 58, 9811–9821. doi: 10.1021/acs.inorgchem.9b00843

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansch, C., Leo, A., and Taft, R. W. (1991). A survey of Hammett substituent constants and resonance and field parameters. Chem. Rev. 91, 165–195. doi: 10.1021/cr00002a004

CrossRef Full Text | Google Scholar

Hewitt, I. J., Lan, Y., Anson, C. E., Luzon, J., Sessoli, R., and Powell, A. K. (2009). Opening up a dysprosium triangle by ligand oximation. Chem. Commun. 3, 6765–7. doi: 10.1039/b908194a

PubMed Abstract | CrossRef Full Text | Google Scholar

Ketkaew, R., Tantirungrotechai, Y., Harding, D. J., Harding, P., and Marchivie, M. (2019). OctaDist-2.6.1. Available online at: https://octadist.github.io

Google Scholar

Kühne, I. A., Barker, A., Zhang, F., Stamenov, P., O'Doherty, O., Müller-Bunz, H., et al. (2020). Modulation of Jahn-Teller distortion and electromechanical response in a Mn³⁺ spin crossover complex. J. Phys. Condens. Matter. 32:404002. doi: 10.1088/1361-648X/ab82d1

PubMed Abstract | CrossRef Full Text | Google Scholar

Kühne, I. A., Magnani, N., Mereacre, V., Wernsdorfer, W., Anson, C. E., and Powell, A. K. (2014). An octanuclear {${\text{Cu}}_4^{\text{II}}$${\text{Dy}}_4^{\text{III}}$} coordination cluster showing single molecule magnet behaviour from field accessible states. Chem. Commun. 50, 1882–1885. doi: 10.1039/c3cc46458j

PubMed Abstract | CrossRef Full Text | Google Scholar

Kühne, I. A., Mereacre, V., Anson, C. E., and Powell, A. K. (2016). Nine members of a family of nine-membered cyclic coordination clusters; Fe₆Ln/Y₃ wheels (Ln = Gd to Lu and Y). Chem. Commun. 52, 1021–1024. doi: 10.1039/C5CC08887A

PubMed Abstract | CrossRef Full Text | Google Scholar

Lampropoulos, C., Hill, S., and Christou, G. (2009). A caveat for single-molecule magnetism: non-linear arrhenius plots. ChemPhysChem. 10, 2397–2400. doi: 10.1002/cphc.200900420

PubMed Abstract | CrossRef Full Text | Google Scholar

Langley, S. K., Vignesh, K. R., Moubaraki, B., Rajaraman, G., and Murray, K. S. (2019). Oblate versus prolate electron density of lanthanide ions: a design criterion for engineering toroidal moments? A Case Study on {${\text{Ln}}_6^{\text{III}}$} (Ln=Tb, Dy, Ho and Er) wheels. Chem. Eur. J. 25, 4156–4165. doi: 10.1002/chem.201805765

PubMed Abstract | CrossRef Full Text | Google Scholar

Larsen, F. K., McInnes, E. J. L., El Mkami, H., Overgaard, J., Piligkos, S., Rajaraman, G., et al. (2003). Synthesis and characterization of heterometallic {Cr₇M} wheels. Angew. Chem. Int. Ed. 42, 101–105. doi: 10.1002/anie.200390034

PubMed Abstract | CrossRef Full Text | Google Scholar

Llunell, M., Casanova, D., Cirera, J., Alemany, P., and Alvarez, S. (2013). SHAPE 2.1: Program for the Stereochemical Analysis of Molecular Fragments by Means of Continuous Shape Measures and Assosciated Tools, ver 2.1. Barcelona.

Google Scholar

Marchivie, M., Guionneau, P., Létard, J.-F., and Chasseau, D. (2005). Photo-induced spin-transition: the role of the iron(II) environment distortion. Acta Crystallogr. Sect. B Struct. Sci. 61, 25–28. doi: 10.1107/S0108768104029751

PubMed Abstract | CrossRef Full Text | Google Scholar

Mereacre, V., Baniodeh, A., Anson, C. E., and Powell, A. K. (2011). Effect of ligand substitution on the interaction between anisotropic Dy(III) ions and ⁵⁷Fe nuclei in Fe₂Dy₂ coordination clusters. J. Am. Chem. Soc. 133, 15335–15337. doi: 10.1021/ja206941e

PubMed Abstract | CrossRef Full Text | Google Scholar

Neese, F., and Pantazis, D. A. (2011). What is not required to make a single molecule magnet. Faraday Discuss. 148, 229–238. doi: 10.1039/C005256F

PubMed Abstract | CrossRef Full Text | Google Scholar

Novitchi, G., Pilet, G., Ungur, L., Moshchalkov, V. V., Wernsdorfer, W., Chibotaru, L. F., et al. (2012). Heterometallic Cu^II/Dy^III 1D chiral polymers: chirogenesis and exchange coupling of toroidal moments in trinuclear Dy₃ single molecule magnets. Chem. Sci. 3:1169. doi: 10.1039/c2sc00728b

CrossRef Full Text | Google Scholar

Peng, Y., Mereacre, V., Baniodeh, A., Lan, Y., Schlageter, M., Kostakis, G. E., et al. (2016). Effect of ligand field tuning on the SMM behavior for three related alkoxide-bridged dysprosium dimers. Inorg. Chem. 55, 68–74. doi: 10.1021/acs.inorgchem.5b01793

PubMed Abstract | CrossRef Full Text | Google Scholar

Pugh, T., Chilton, N. F., and Layfield, R. A. (2016). A Low-Symmetry dysprosium metallocene single-molecule magnet with a high anisotropy barrier. Angew. Chem. Int. Ed. 55, 11082–11085. doi: 10.1002/anie.201604346

PubMed Abstract | CrossRef Full Text | Google Scholar

Ranzinger, F., Herrling, M. P., Lackner, S., Grande, V. W., Baniodeh, A., Powell, A. K., et al. (2016). Direct surface visualization of biofilms with high spin coordination clusters using magnetic resonance imaging. Acta Biomater. 31, 167–177. doi: 10.1016/j.actbio.2015.12.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Reta, D., and Chilton, N. F. (2019). Uncertainty estimates for magnetic relaxation times and magnetic relaxation parameters. Phys. Chem. Chem. Phys. 21, 23567–23575. doi: 10.1039/C9CP04301B

PubMed Abstract | CrossRef Full Text | Google Scholar

Rinehart, J. D., and Long, J. R. (2011). Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2:2078. doi: 10.1039/c1sc00513h

CrossRef Full Text | Google Scholar

Schmidt, S., Prodius, D., Novitchi, G., Mereacre, V., Kostakis, G. E., and Powell, A. K. (2012). Ferromagnetic heteronuclear {Fe₄ (Er,Lu)₂} cyclic coordination clusters based on ferric wheels. Chem. Commun. 48, 9825. doi: 10.1039/c2cc34361d

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmidt, S. F. M., Koo, C., Mereacre, V., Park, J., Heermann, D. W., Kataev, V., et al. (2017a). A three-pronged attack to investigate the electronic structure of a family of ferromagnetic Fe₄Ln₂ cyclic coordination clusters: a combined magnetic susceptibility, high-field/high-frequency electron paramagnetic resonance, and ⁵⁷Fe mössbauer study. Inorg. Chem. 56, 4796–4806. doi: 10.1021/acs.inorgchem.6b02682

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmidt, S. F. M., Merkel, M. P., Kostakis, G. E., Buth, G., Anson, C. E., and Powell, A. K. (2017b). SMM behaviour and magnetocaloric effect in heterometallic 3d-4f coordination clusters with high azide : metal ratios. Dalton Trans. 46, 15661–15665. doi: 10.1039/C7DT03149A

PubMed Abstract | CrossRef Full Text | Google Scholar

Schray, D., Abbas, G., Lan, Y., Mereacre, V., Sundt, A., Dreiser, J., et al. (2010). Combined magnetic susceptibility measurements and ⁵⁷Fe mössbauer spectroscopy on a ferromagnetic {${\text{Fe}}_4^{\text{III}}$Dy₄} ring. Angew. Chem. Int. Ed. 49, 5185–5188. doi: 10.1002/anie.201001110

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheldrick, G. M. (2015). Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 71, 3–8. doi: 10.1107/S2053229614024218

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, X.-J., Xu, J.-J., Chen, Y., Muddassir, M., Cao, F., Wei, R.-M., et al. (2013). Synthesis, structures and magnetic properties of cyano-bridged 3d-4f rectangular tetranuclear [${\text{Fe}}_2^{\text{III}}$${\text{Ln}}_2^{\text{III}}$] (Ln = Y, Tb, Dy) compounds containing [Fe^III(bpy)(CN)₄]⁻ unit. Polyhedron 66, 212–217. doi: 10.1016/j.poly.2013.04.037

CrossRef Full Text | Google Scholar

Sorace, L., Benelli, C., and Gatteschi, D. (2011). Lanthanides in molecular magnetism: old tools in a new field. Chem. Soc. Rev. 40:3092. doi: 10.1039/c0cs00185f

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, J., Hewitt, I., Madhu, N. T., Chastanet, G., Wernsdorfer, W., Anson, C. E., et al. (2006). Dysprosium triangles showing single-molecule magnet behavior of thermally excited spin states. Angew. Chem. Int. Ed. 45, 1729–1733. doi: 10.1002/anie.200503564

PubMed Abstract | CrossRef Full Text | Google Scholar

Timco, G. A., Carretta, S., Troiani, F., Tuna, F., Pritchard, R. J., Muryn, C. A., et al. (2009). Engineering the coupling between molecular spin qubits by coordination chemistry. Nat. Nanotechnol. 4, 173–178. doi: 10.1038/nnano.2008.404

PubMed Abstract | CrossRef Full Text | Google Scholar

Troiani, F., Ghirri, A., Affronte, M., Carretta, S., Santini, P., Amoretti, G., et al. (2005). Proposal for quantum gates in permanently coupled antiferromagnetic spin rings without need of local fields. Phys. Rev. Lett. 94:207208. doi: 10.1103/PhysRevLett.94.190501

PubMed Abstract | CrossRef Full Text | Google Scholar

Ungur, L., Langley, S. K., Hooper, T. N., Moubaraki, B., Brechin, E. K., Murray, K. S., et al. (2012). Net toroidal magnetic moment in the ground state of a {Dy₆}-triethanolamine ring. J. Am. Chem. Soc. 134, 18554–18557. doi: 10.1021/ja309211d

PubMed Abstract | CrossRef Full Text | Google Scholar

Ungur, L., Lin, S.-Y., Tang, J, and Chibotaru, L. F. (2014). Single-molecule toroics in Ising-type lanthanide molecular clusters. Chem. Soc. Rev. 43, 6894–6905. doi: 10.1039/C4CS00095A

PubMed Abstract | CrossRef Full Text | Google Scholar

Waldmann, O. (2005). Magnetic molecular wheels and grids - the need for novel concepts in “zero-dimensional” magnetism. Coord. Chem. Rev. 249, 2550–2566. doi: 10.1016/j.ccr.2004.12.019

CrossRef Full Text | Google Scholar

Werner, R., Ostrovsky, S., Griesar, K., and Haase, W. (2001). Magnetostructural correlations in exchange coupled phenoxo-, alkoxo-, and hydroxo-bridged dinuclear iron(III) compounds. Inorganica Chim. Acta 326, 78–88. doi: 10.1016/S0020-1693(01)00604-1

CrossRef Full Text | Google Scholar

Whitehead, G. F. S., Moro, F., Timco, G. A., Wernsdorfer, W., Teat, S. J., and Winpenny, R. E. P. (2013). A ring of rings and other multicomponent assemblies of cages. Angew. Chem. Int. Ed. 52, 9932–9935. doi: 10.1002/anie.201304817

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, H.-L., Zhai, Y.-Q., Qin, L., Ungur, L., Nojiri, H., and Zheng, Y.-Z. (2020). Single-molecule toroic design through magnetic exchange coupling. Matter. 2, 1481–1493. doi: 10.1016/j.matt.2020.02.021

CrossRef Full Text | Google Scholar

Appendix

TABLE A1

Table A1. Crystallographic Data for the cyclic coordination clusters 1-3.