Changes in Structure and Reactivity of Ng2 Encapsulated in Fullerenes: A Density Functional Theory Study

Introduction

Regarded as the most unreactive elements in the periodic table, noble gas atoms could indeed be reactive and no noble at all under certain circumstances, [e.g., high temperature, high pressure, special conditions (e.g., confinement, etc.)]. The first successful experimental realization was the synthesis of xenon hexafluoro platinate XePtF₆ in 1962 (Bartlett, 1962; Graham et al., 2000). Since then many more compounds with noble gas elements included have been reported (Turner and Pimentel, 1963; Nelson and Pimentel, 1967; Bondybey, 1971; Stein, 1973; Holloway and Hope, 1999) and a brand new discipline of noble gas chemistry has emerged thereafter.

In this contribution, we explore the possibility of fullerene encapsulation as another feasible way to make noble gas elements no longer noble. In specific, we consider the impact of the encapsulation by fullerene molecules on geometrical structure and chemical reactivity for noble gas species. Previously, by heating fullerenes at 650°C under 3,000 atmosphere, helium (Saunders et al., 1993), neon (Saunders et al., 1993), argon (DiCamillo et al., 1996), krypton (Yamamoto et al., 1999), and xenon (Syamala et al., 2002) noble gas atoms were experimentally introduced into the fullerene cage. This experimental realization of fullerene encapsulation demonstrates the feasibility, and there were reports of experimental realization of noble gas dimers encapsulation in fulerenes (Saunders et al., 1996; Laskin et al., 1998; Peres et al., 2001; Popov et al., 2013; Saha et al., 2019). Also, earlier, Krapp and Frenking performed a computational study on Ng₂@C₆₀ (Ng = He, Ne, Ar, Kr, and Xe) systems from the bonding perspective and concluded that He₂@C₆₀ and Ne₂@C₆₀ were weakly bonded van der Waals complexes (Krapp and Frenking, 2007). On the other hand, Solà et al. explored the same systems from the reactivity perspective and they attributed the changes in reactivity to the stabilized LUMO, increased fullerene strain energy, and compressed Ng₂ unit (Osuna et al., 2009). There are other theoretical and computational studies on the encapsulation of either noble gas or other species in the literature (Osuna et al., 2011; Cheng and Sheng, 2013; Dolgonos and Peslherbe, 2014; Khatua et al., 2014; Bickelhaupt et al., 2015; Kryachko et al., 2015; Nikolaienko and Kryachko, 2015; Jalife et al., 2016; Srivastava et al., 2016; Nikolaienko et al., 2017; Foroutan-Nejad et al., 2018; Jaroš et al., 2018; Gómez and Restrepo, 2019; Das et al., 2020).

In this work, we reconsider the likelihood of these species from the computational perspective using a few newly developed theoretical tools. To that end, we examine noble gas dimers, He₂, Ne₂, and Ar₂, inside a few fullerene systems, C₅₀, C₆₀, and C₇₀, as illustrative examples in this work. In addition, to pinpoint the nature and origin of these structure and reactivity changes, we make use of a few analytical tools available in the literature, including density functional theory, conceptual density functional theory, information-theoretic approach, energy decomposition analysis, bonding energy analysis, natural population analysis, and noncovalent interaction analysis. In information theory, Shannon introduced a measure of information content or a lack of it as an entropy through an analogy with the statistical mechanical variant of thermodynamic entropy as proposed by Boltzmann. Hence the stability of a system and spontaneous evolution toward an equilibrium state can be understood by following the variation of the entropy during the thermodynamic process. These analyses should provide better understanding from the viewpoint of changing the perspectives of noble gas reactivity.

Computational Details

Models

Nine model systems were built to examine the impact of fullerene encapsulation on structure and reactivity properties for noble gas dimers (Ng₂) using three fullerenes C₅₀, C₆₀, and C₇₀ and three Ng₂ species, He₂, Ne₂, and Ar₂. They are represented by following notations: He₂@C₅₀, He₂@C₆₀, He₂@C₇₀, Ne₂@C₅₀, Ne₂@C₆₀, Ne₂@C₇₀, Ar₂@C₅₀, Ar₂@C₆₀, and Ar₂@C₇₀. Also, as the reference, the structural and reactivity properties of these three fullerene molecules and three Ng₂ dimers in vacuum were also simulated and compared.

Analyses

Structure, bonding and reactivity properties for these species were analyzed through a number of well-established analytical tools available in the literature. They include analyses of the total energy decomposition (Parr and Yang, 1989; Liu, 2007), interaction energy decomposition (Bickelhaupt and Baerends, 2000), natural population (Glendening et al., 2012), non-covalent interactions (Johnson et al., 2010), conceptual density functional theory (Geerlings et al., 2003, 2020; Liu, 2009, 2013), and informational-theoretic approach (Liu, 2016; Rong et al., 2019). These analyses enable in-depth understanding about the origin and nature of the changes in structure, bonding, and reactivity. Formulations as well as the details of how to perform these analyses are available elsewhere.

Methodologies

Structure optimizations and natural population analyses were performed with the Gaussian 16 (Frisch et al., 2016) package (versionA03), with ultrafine integration grids and tight self-consistent field (SCF) convergence. To obtain the most stable orientation of Ng₂ dimer in a fullerene cage, quantum molecular dynamics simulations were performed for each species at the DFT B3LYP/3-21G (Lee et al., 1988; Becke, 1993) level of theory at 3,000 K for 300 ps with a step size of 1 fs. A total of 20 structures with the lowest total energy were selected as the possible structure candidates from the trajectory and then optimized at the DFT M06-2X/6-311G(d) (Zhao and Truhlar, 2008) level of theory. The structure with the lowest total energy from these 20 candidates was selected as the global minimum for the species. The full structure optimization was followed by a single-point frequency calculation to ensure that the final optimized structure has no imaginary frequency. As a measure of quality control, we conducted a benchmark test on the impact of different choices of basis sets and approximate DFT functionals (Ma et al., 2014). The Multiwfn 3.6.1 program (Lu and Chen, 2012) was utilized to calculate the information-theoretic quantities by using the checkpoint file from the Gaussian calculations as the input file. The total energy components were obtained from Gaussian calculations with the keyword of iop(5/33 = 1). The ADF (Amsterdam Density Functional) (Lee et al., 1988) package was employed to perform the bond energy decomposition (BED) analysis. The BED analysis was conducted using the previously optimized structure and the DFT BP86 approximate functional with the double zeta basis set, zero order regular approximation for relativistic correction, and Grimme4 dispersion correction (Te Velde et al., 2001).

Results and Discussion

Table 1 is the benchmark results using Ar₂@C₆₀ as an example with 14 basis sets and 14 DFT functionals as well as HF and MP2 methods to examine their impact on the Ar-Ar bond distance. It is compared with Ar-Ar length in vacuum. As can be seen from the table, the bond length in Ar2@C₆₀ is not significantly dependent on the choice of basis sets and functionals, which is unsurprising because the Ng₂ molecule is confined. As a reference, the experimental Ar-Ar length in vacuum is 3.758 Å (Computational Chemistry Comparison Benchmark DataBase, 2019). There are a handful of computational results for the Ar-Ar length (Colburn and Douglas, 1976). In all analyses below, we chose M06-2X/6-311G(d).

TABLE 1

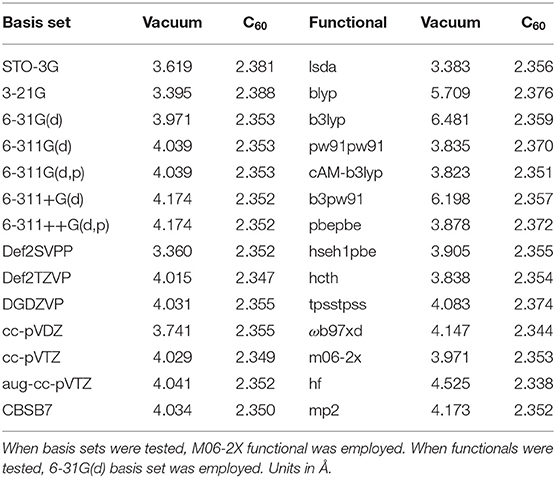
Table 1. Benchmark tests for Ar₂@C₆₀ with 14 basis sets and 14 functionals/methods to examine the impact of the methodology dependence on the Ar-Ar bond distance in both vacuum and C₆₀ fullerene.

Figure 1 shows the final structure obtained for Ng₂@C₅₀, Ng₂@C₆₀, and Ng₂@C₇₀ with both top and side views. With a given fullerene, the binding mode is the same for different Ng₂ dimers, but for different fullerenes, as shown in Figure 1, the same Ng₂ dimer prefers to bind differently. This is not surprising either. This is because, for instance, C₇₀ is elongated so the dimer aligns with the long axis, as one would expect from a simple steric argument. These similarity and difference illustrate the fact that the size and nature of fullerene molecules play more important role during the encapsulation process of Ng₂ dimers.

FIGURE 1

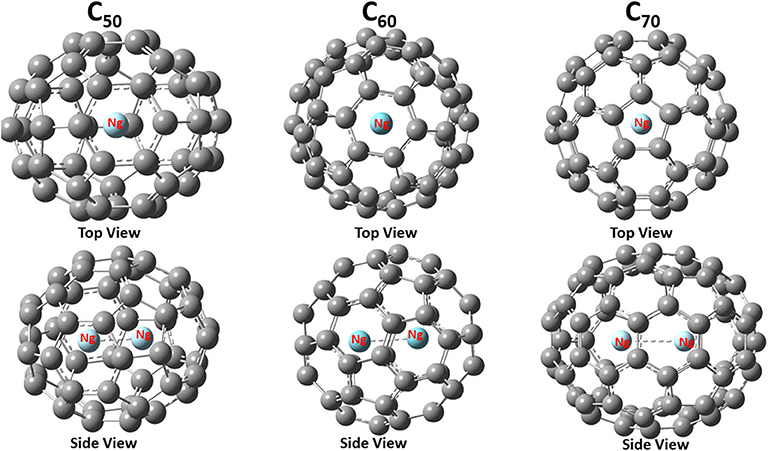
Figure 1. Optimized structures of noble gas dimers encapsulated in fullerene cages with Ng = Ar as an illustrative example. The point group for these three encapsulated systems are C_2v, D_3d, and D_5h, respectively.

Table 2 exhibits a few selected structural and electronic properties of these species. As can be seen from the table, the bond length of Ng₂ dimers becomes smaller when encapsulated in fullerenes, and the smaller the fullerene cage the shorter the Ng-Ng distance. This latter trend was resulted from the fact that a smaller fullerene has a smaller cage inside so Ng₂ dimers are forced to have shorter bond distance. Energetically, both BSSE (basis set superposition error; Boys and Bernardi, 1970; Simon et al., 1996)-corrected and uncorrected interaction energy results show that for He₂, all three fullerene molecules yield negative (favorable) interaction energies, whereas for larger Ng₂ dimers, (e.g., Ne₂ and Ar₂, it appears that only larger-sized fullerenes such as C₇₀ are able to yield attractive interactions between Ng₂ and fullerene, albeit with the limitations of the method of computation used). This is because larger Ng₂ dimers tend to occupy more space within the fullerene molecule, making it harder for smaller-sized fullerenes to compensate the energetic cost from electrostatic and other repulsions. We are, however, interested in analyzing the qualitative trends only.

TABLE 2

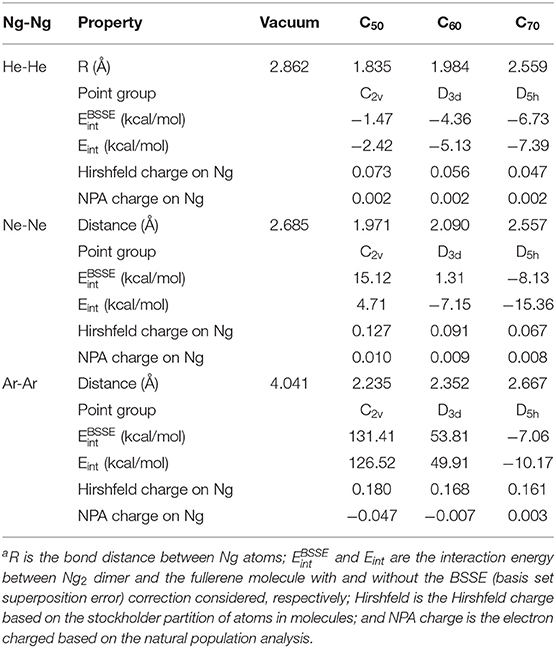
Table 2. A few selected structure and electronic properties at the DFT M06-2X/6-311G(d) level of theory for Ng₂ (Ng = He, Ne, and Ar) dimers encapsulated in C₅₀, C₆₀, and C₇₀ fullerenes^a.

Shown in Table 2 are two charge results for Ng atoms encapsulated in fullerene molecules. The first one is the NPA (natural population analysis) charge from NBO (natural bond orbital) analysis (Glendening et al., 2012), and the other is the Hirshfeld charge based on the shareholder partition of atoms in molecules (Hirshfeld, 1977). NPA charges for Ng atoms could be either positive or negative, but the Hirshfeld charge value is always positive for Ng atoms. According to the reference literature on the Hirshfeld charge (Liu et al., 2014), which is a good descriptor of electrophilicity and nucleophilicity, a positive Hirshfeld charge is an indication that the atom is electrophilic. The larger value of a positive Hirshfeld charge indicates that it is more electrophilic, able to accept more electrons from a nucleophile. Hirshfeld charge results in Table 2 displays that Ng₂ in smaller fullerenes tend to be more electrophilic.

Shown in Figure 2 are frontier molecular orbitals from both top and side views for Ar₂@C₇₀ as an illustrative example, from which one can see that they are both delocalized over the entire molecule. Notice that in both orbitals, we do not see discernible contributions from the Ng₂ dimer overlapping with any of the atomic orbitals from the fullerene, suggesting that atomic orbitals from Ng atoms are not involved in the frontier molecular orbital delocalization. In Table 3, using the information from these frontier orbitals, we calculated a few global reactivity descriptors from conceptual DFT, including chemical potential μ (Parr et al., 1978), chemical hardness η (Parr and Pearson, 1983), and electrophilicity index ω (Parr et al., 1999) for the nine systems studied in this work. A larger value in hardness is usually an indication of being more stable, while a larger value in electrophilicity index suggests that the species is more reactive. From the results in Table 2, we can see that numerical values of these reactivity indices are slightly changed after Ng₂ encapsulation. This should be mainly due to the charge transfer between Ng₂ and fullerene. Ng₂ in smaller fullerenes are more reactive with a larger ω value, whereas in larger fullerenes it becomes often more stable with a larger η value. These results agree well with the conventional chemical wisdom.

FIGURE 2

Figure 2. HOMO and LUMO contour surfaces of Ar₂@C₇₀ molecule.

TABLE 3

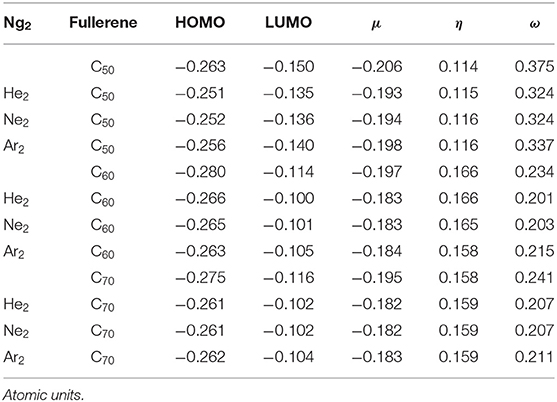
Table 3. Global descriptors from Conceptual DFT, including HOMO, LUMO, chemical potential μ, chemical hardness η, and electrophilicity index ω for the systems studied in this work.

Figure 3 shows the contour surface of the molecular electrostatic potential mapped onto the van der Waals surface for Ne₂ and Ar₂ dimers encapsulated in C₆₀ fullerene. It shows that the carbon atoms perpendicular to the Ng-Ng bond is more electronegative. This result is consistent with our Hirshfeld charge result, showing that Ng atoms become more positive and the neighboring carbon atoms in fullerene become more negative. Since Hirshfeld charges are reliable descriptors of electrophilicity and nucleophilicity, Figure 3 also shows that carbon atoms of the fullerene molecule become more nucleophilic, capable of donating more electrons to an electrophile.

FIGURE 3

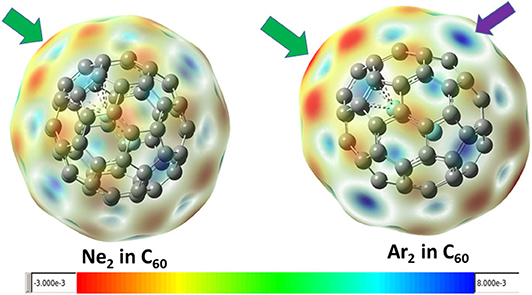
Figure 3. The mapped contour surface of the molecular electrostatic potential onto the van der Waals surface for Ne₂ and Ar₂ dimers encapsulated in C₆₀ fullerene.

In conceptual DFT, Fukui functions (Yang et al., 1984) can also be employed as local descriptors to predict nucleophilic and electrophilic attacks. Shown in Figure 4 are these local functions, where both electrophilic (Figures 4A,B) and nucleophilic (Figures 4C,D) Fukui functions for Ar₂ dimer encapsulated in C₆₀ fullerene are exhibited. From the figure, we found that (i) carbon atoms in fullerene can be both electrophilic (dark blue areas in Figures 4A,B) and nucleophilic (dark blue regions in Figures 4C,D), and (ii) nucleophilic regions in Figures 4C,D are drastically different from those of Figure 3 (red areas), suggesting that using Hirshfeld charge and Fukui charge, we obtain different results. According our recent findings, this discrepancy is not unusual. As our recent study demonstrated (Wang et al., 2019), results from the Hirshfeld charge should be more robust and reliable. Notice that Krapp and Frenking (2007) also observed that Ng₂ molecules were oxidized inside fullerenes, implying that Ng₂ became more electrophilic in return as electrons were transferred to C₆₀, and this also made fullerenes more nucleophilic. This result was confirmed by Solà et al. (Osuna et al., 2009, 2011), also who unveiled that the combination of the LUMO stabilization, increased fullerene strain energy, and greater compression of the encapsulated Ng₂ contributed to the reactivity change.

FIGURE 4

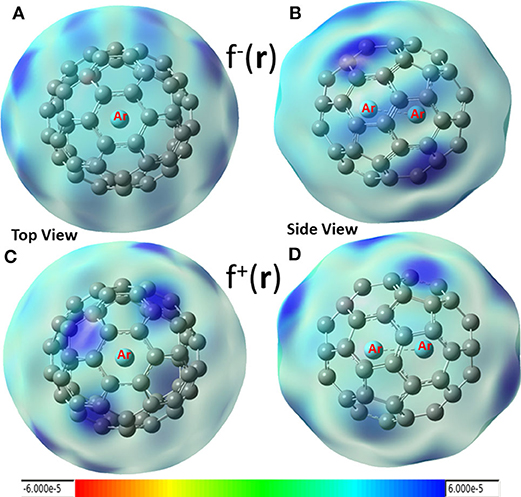
Figure 4. Electrophilic (A,B) and nucleophilic (C,D) Fukui functions for Ar₂ dimer encapsulated in C₆₀ fullerene.

To qualitatively identify and distinguish weak interactions between Ng₂ and fullerene molecules, noncovalent interaction (NCI) analysis (Johnson et al., 2010) was employed, whose results are shown in Figure 5. The reduced density gradient is large and positive in the regions far from the molecule, but it becomes small in the vicinity of both covalent and non-covalent interactions. To identify different types of interactions, the sign of Laplacian of the density is utilized and compared. Plotting low-gradient isosurfaces subject to a further low-density constraint enables real-space visualization of non-covalent interactions. Results in Figure 5 show that when He₂ encapsulated from C₅₀ to C₇₀, a “spike” area becomes more apparent from −0.02 to 0 a.u., indicating that there existed more attractive interactions within the complexes as the fullerene cage becomes larger. The same trend is also observed for Ne₂ and Ar₂. These results are also in qualitative agreement with the total energy difference result as shown in Table 2.

FIGURE 5

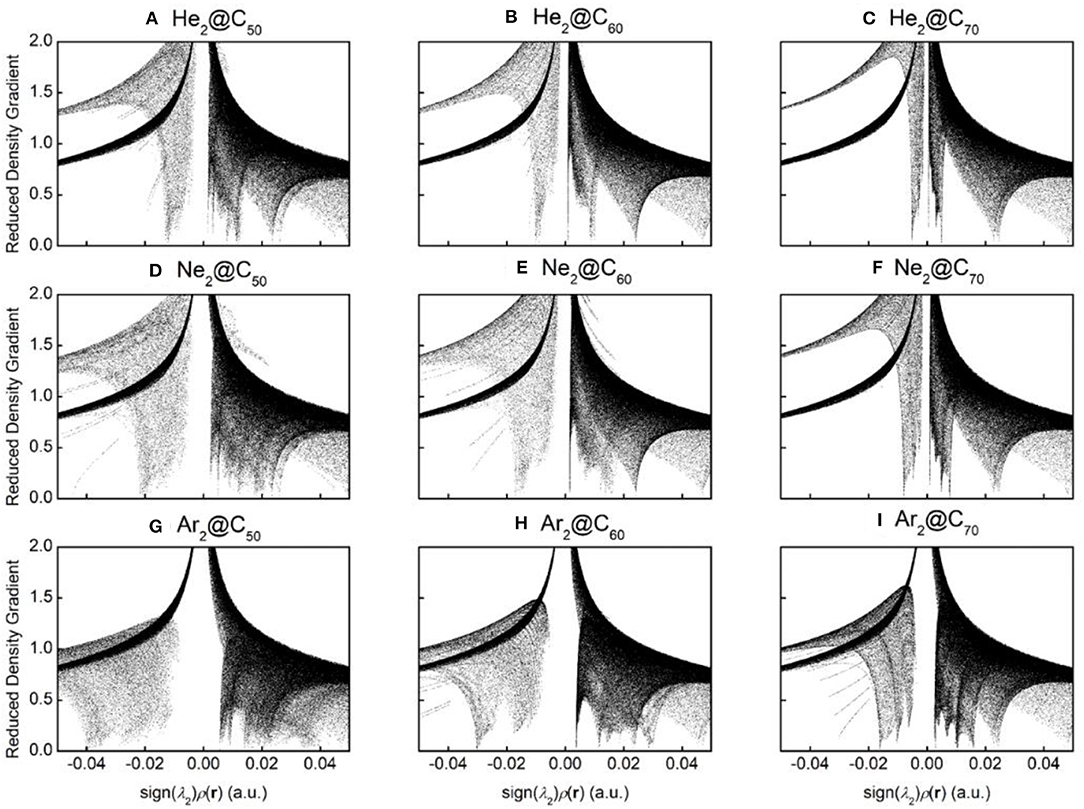
Figure 5. Diagrams of the reduced density gradient (RDG) vs. sign(λ₂)ρ(r) for nine endohedral fullerenes: (A) He₂@C50; (B) He₂@C60; (C) He₂@C70; (D) Ne₂@C50; (E) Ne₂@C60; (F) Ne₂@C70; (G) Ar₂@C50; (H) Ar₂C60; and (I) Ar₂@C70.

Table 4 is the results from the two schemes (Parr and Yang, 1989; Liu, 2007) of the total energy partition for the nine Ng₂-fullerene systems studied in this work. Different from the traditional binding energy or interaction energy partition, the total energy partition decomposes the total energy E of a molecular system in terms of a few components that are physiochemically meaningful. In DFT (Parr and Yang, 1989), we have E = T_S + E_xc + E_e, where T_S, E_xc, and E_e are the non-interacting kinetic energy, exchange-correlation energy, and electrostatic interaction energy, respectively. An alternative scheme was proposed by one of us (Liu, 2007), where E = E_S + E_e + E_q, where E_S, E_e, and E_q stand for the energetic contribution from three physiochemical effects, steric, electrostatic, and quantum (due to the exchange-correlation effects). There is a common component in these two partition schemes, the electrostatic energy E_e. Considering the energy difference ΔE between two chemical processes sharing the same molecular fragments, we have ΔE = ΔT_S + ΔE_xc + ΔE_e, and ΔE = ΔE_S + ΔE_e + ΔE_q. Table 4 shows the values of these five components from the above two partition schemes using Ng₂ and fullerene in vacuum as the reference. From the table, we found that in the first scheme (Parr and Yang, 1989; Liu, 2007), both ΔT_s and ΔE_xc contribute positively to ΔE <0, and it is the electrostatic contribution ΔE_e that contributes negatively to their stability, in order to make ΔE <0. Since E_e itself is negative in value (Liu, 2007), this result suggests that to put Ng₂ dimer in the fullerene cage, one has to overcome the large electrostatic repulsion between Ng₂ and fullerene. This result is further verified by the second total energy partition scheme (Liu, 2007), where we found that in this case both electrostatic and quantum (due to exchange-correlation effects) contribute negatively to ΔE <0 but the steric contribution ΔE_S is positive. This result shows that after Ng₂ dimer is put into the cage, smaller space is occupied, but to do so, large electrostatic and Fermionic quantum repulsions have to be overcome. Notice that this total energy difference is different from the BSSE corrected interaction energy in Table 2 and our present results are consistent with what we observed elsewhere for other systems.

TABLE 4

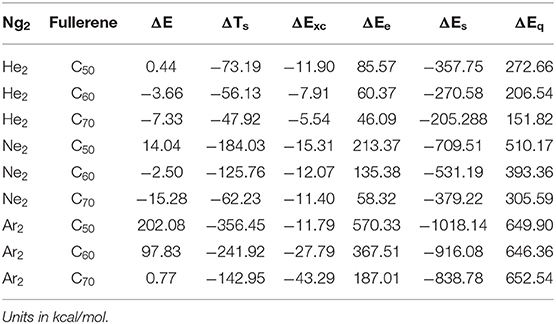
Table 4. Numerical results of the two total energy partition schemes using Ng₂ and fullerene in vacuum as the references for the nine Ng₂-fullerene systems studied in this work.

Figure 6 illustrates the total energy partition analysis to elucidate which energy component is dominant over others in contributing to the total energy difference. A strong linear correlation of the total energy difference ΔE with the electrostatic energy difference ΔE_e is shown in Figure 6A, suggesting that it is the electrostatic repulsion that dominates the energetic contribution, which agrees well with the numerical results in Table 4. If the strategy of two-variable fitting is employed, shown in Figures 6B,C, we found that ΔE_e combining with either ΔE_xc and ΔE_S yields even stronger correlations, indicating that contributions from the exchange-correlation and steric effects are minor yet indispensable.

FIGURE 6

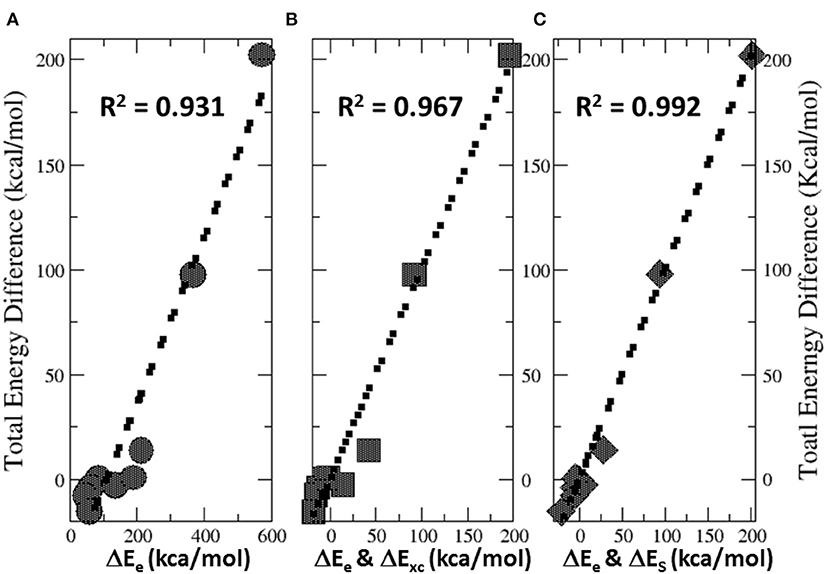
Figure 6. Strong linear correlations of the total energy difference ΔE with (A) the electrostatic energy difference ΔE_e, (B) two-variable fitting with ΔE_e and ΔE_xc, and (C) two-variable fitting with ΔE_e and ΔE_S.

To confirm the results in Tables 4, 5 shows the total bonding energy ΔE_bond analysis (Bickelhaupt and Baerends, 2000) results using the ADF package. In this analysis, ΔE_bond consists of contributions from the Pauli repulsion ΔE_Pauli, steric interaction ΔE_steric, electrostatic attraction ΔE_elstat, orbital interactions ΔE_orb, and dispersion Pauli repulsion ΔE_disp, ΔE_bond = ΔE_Pauli + ΔE_steric + ΔE_orb + ΔE_disp + ΔE_elstat. From the results in Table 5, it can be seen that the steric effect (even though its definition is substantially different) contributes favorably and the major opposite contribution is from the electrostatic interaction, agreeing well with our results in Table 4.

TABLE 5

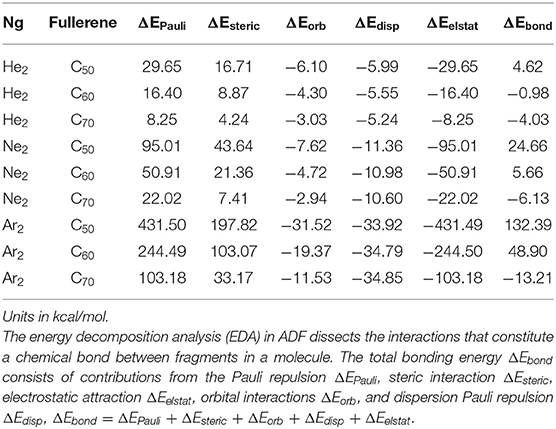
Table 5. The chemical bonding analysis results using the ADF package to analyze the bond energy between the Ng₂dimer and fullerene fragments.

Lastly, we examine the results of eight quantities from the information-theoretic approach, which are shown in Table 6, including Shannon entropy (Shannon, 1948), Fisher information (Fisher, 1925), Ghosh-Berkowitz-Parr entropy (Ghosh et al., 1984), information gain (Kullback and Leibler, 1951), 2nd and 3rd orders of absolute Rényi and relative Rényi entropy (Rényi, 1970; Nagy and Romera, 2015). These quantities each have their own physio-chemical meaning and thus representing different yet intrinsic properties of molecular systems. For example, Shannon entropy is a measure of the electron density distribution uniformity, Fisher information gauges the heterogeneity of the same electron density distribution, and information gain is a robust measurement of regioselectivity, electrophilicity, and nucleophilicity, with its first-order approximation yielding the Hirshfeld charge (Liu et al., 2014). To make sense of these ITA results, Table 7 lists the correlation coefficient of these quantities with respect to either Ng₂ or fullerene types, and Figure 7 displays illustrative example of strong linear relationships of the total energy difference ΔE with Shannon entropy, Fisher information, and information gain for He₂, Ne₂, and Ar₂ encapsulated in three fullerenes. Strong correlations are seen in most cases, as shown in the figure, but as highlighted in Table 7, these strong correlations are true only for Ng₂ dimers cross different fullerenes. If one fits a fullerene with three Ng₂ dimers, no such strong correlation is often observed. Also, we tried to put all data points in one plot, and no significant correlation was observed either. Strong correlations in Figure 7 show that ITA quantities could be good descriptors of change trends for Ng₂ dimers encapsulated in fullerene cages. For instance, for He₂ encapsulated in from C₅₀ to C₇₀, binding energy increases, so does the Shannon entropy, due to the more delocalization of the electron density distribution. Another example is the information gain, which is a direct measure of the Hirshfeld charge. Again, for He₂ dimer, from C₅₀ to C₇₀, the difference in information gain decreases, leading to the decrease in Hirshfeld charge, which is in good agreement with the result in Table 2. We noticed the abnormality of Shannon entropy for Ar₂ dimer in Figure 7, whose trend is opposite to that of He₂ and Ne₂. The reason is unknown. More studies are in need.

TABLE 6

Table 6. Numerical results of eight ITA quantities.

TABLE 7

Table 7. Correlation coefficients R² values between ΔE and eight ITA quantities for three Ng₂ dimers with different fullerene systems (first three rows) and for three fullerenes with different Ng₂ dimers (last three rows).

FIGURE 7

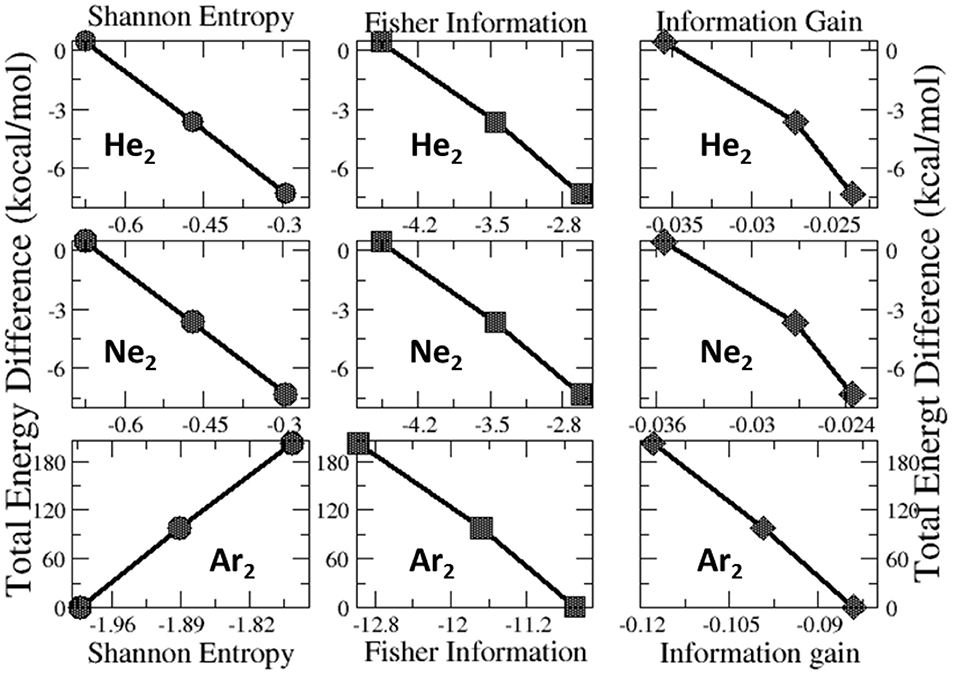
Figure 7. Strong linear relationships of the total energy difference ΔE with ITA quantities such as Shannon entropy, Fisher information, and information gain for He₂, Ne₂, and Ar₂ encapsulated in C₅₀, C₆₀, and C₇₀ fullerenes.

Conclusions

To summarize, in this work, we investigated the possibility of making noble gas reactive through the means of fullerene encapsulation. To that end, we built a total of nine model systems, with three Ng₂ dimers (He₂, Ne₂, and Ar₂) encapsulated in three fullerene (C₅₀, C₆₀, and C₇₀) cages. Quantum molecular dynamics simulations were employed to explore the potential energy surface of Ng₂ inside the fullerene molecule. To obtain the lowest energy structure it was further examined through a few well-established analytical tools such as conceptual density functional theory, information-theoretic approach, total energy decomposition, bonding energy decomposition, and others. Our results show that bond distances of Ng₂ inside fullerene become substantially smaller and noble gas atoms become more electrophilic. In return, these noble gas dimers make fullerene molecules more nucleophilic. Using these analytical tools, we appreciate the nature and origin of these structure and reactivity changes. Our results and conclusions drawn from the present study should provide more understanding and new insights from the viewpoint of changing the perspectives of noble gas reactivity.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation, to any qualified researcher.

Author Contributions

ML performed the calculations and analyses and prepared the draft. XH and BW helped in calculations and analyses. DZ and CR managed progression of the project. PC initiated the project and revised the draft. SL worked on the plan, assisted the calculations and analyses, and revised the manuscript. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

ML and CR acknowledge support from the Excellent Undergraduate Research Fund of Haoqing Experimental Class, Hunan Normal University and the National Natural Science Foundation of China (No. 21503076). PC would like to thank the DST, New Delhi for the J. C. Bose National Fellowship.

References

Bartlett, N. (1962). Xenon hexafluoroplatinate(V) Xe+[PtF 6]-. Proc. Chem. Soc. 115:218. doi: 10.1039/ps9620000197

CrossRef Full Text | Google Scholar

Becke, A. D. (1993). Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652. doi: 10.1063/1.464913

CrossRef Full Text | Google Scholar

Bickelhaupt, F. M., and Baerends, E. J. (2000). “Kohn-Sham density functional theory: predicting and understanding chemistry,” in Rev. Comput. Chem., eds K. B. Lipkowitz and D. B. Boyd (New York, Ny: Wiley-VCH), 1–86. doi: 10.1002/9780470125922.ch1

PubMed Abstract | CrossRef Full Text | Google Scholar

Bickelhaupt, F. M., Solà, M., and Fernández, I. (2015). Understanding the reactivity of endohedral metallofullerenes: C₇₈ versus Sc₃N@C₇₈. Chem. Eur. J. 21, 5760–5768. doi: 10.1002/chem.201500067

PubMed Abstract | CrossRef Full Text | Google Scholar

Bondybey, V. E. (1971). Matrix Isolation Search for Transient Species. (Thesis). University of California, Berkeley, CA, United States.

Google Scholar

Boys, S. F., and Bernardi, F. (1970). Calculation of small molecular interactions by differences of separate total energies—some procedures with reduced errors. Mol. Phys. 19, 553–566. doi: 10.1080/00268977000101561

CrossRef Full Text | Google Scholar

Cheng, C., and Sheng, L. (2013). Ab-Initio study of Helium-small carbon cage systems. Int. J. Quantum Chem. 113, 35–38. doi: 10.1002/qua.24303

CrossRef Full Text | Google Scholar

Colburn, E. Q., and Douglas, A. E. (1976). The spectrum and ground state potential curve of Ar2. J. Chem. Phys. 65:1741. doi: 10.1063/1.433319

CrossRef Full Text | Google Scholar

Computational Chemistry Comparison Benchmark DataBase (2019). NIST Chemistry Webbook. Available online at: https://cccbdb.nist.gov/exp2x.asp?casno=12595594, https://cccbdb.nist.gov/geom2x.asp (accessed June 23, 2020).

Google Scholar

Das, P., Saha, R., and Chattaraj, P. K. (2020). Encapsulation of Mg₂ inside a C₆₀ cage forms an electride. J. Comput. Chem. 41, 1645–1653. doi: 10.1002/jcc.26207

CrossRef Full Text | Google Scholar

DiCamillo, B. A., Hettich, R. L., Guiochon, G., Compton, R. N., Saunders, M., Jimenez-Vazquez, H. A., et al. (1996). Enrichment and characterization of a noble gas fullerene: Ar@C₆₀. J. Phys. Chem. 100, 9197–9201. doi: 10.1021/jp960049k

CrossRef Full Text | Google Scholar

Dolgonos, G. A., and Peslherbe, G. H. (2014). Encapsulation of diatomic molecules in fullerene C₆₀: implications for their main properties. Phys. Chem. Chem. Phys. 16, 26294–26305. doi: 10.1039/C4CP04069D

CrossRef Full Text | Google Scholar

Fisher, R. A. (1925). Theory of statistical estimation. Proc. Cambridge Philos. Soc. 22, 700–725. doi: 10.1017/S0305004100009580

CrossRef Full Text | Google Scholar

Foroutan-Nejad, C., Straka, M., Fernández, I., and Frenking, G. (2018). Buckyball difluoride ${\text{F}}_2^{-}$@${\text{C}}_{60}^{+}$–a single-molecule crystal. Angew. Chem. Int. Ed. 57, 13931–13934. doi: 10.1002/anie.201809699

PubMed Abstract | CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian Inc., Wallingford, CT.

Google Scholar

Geerlings, P., Chamorro, E., Chattaraj, P. K., De Proft, F., Gazquez, J. L., Liu, S. B., et al. (2020). Conceptual density functional theory: status, prospects, issues. Theor. Chem. Acc. 139:36. doi: 10.1007/s00214-020-2546-7

CrossRef Full Text | Google Scholar

Geerlings, P., De Proft, F., and Langenaeker, W. (2003). Conceptual density functional theory. Chem. Rev. 103, 1793–1847. doi: 10.1021/cr990029p

CrossRef Full Text | Google Scholar

Ghosh, S. K., Berkowitz, M., and Parr, R. G. (1984). Transcription of ground-state density-functional theory into a local thermodynamics. Proc. Natl. Acad. Sci. U. S. A. 81, 8028–8031. doi: 10.1073/pnas.81.24.8028

CrossRef Full Text | Google Scholar

Glendening, E. D., Landis, C. R., and Weinhold, F. (2012). Natural bond orbital methods. WIREs Comput. Mol. Sci. 2, 1–42. doi: 10.1002/wcms.51

CrossRef Full Text | Google Scholar

Gómez, S., and Restrepo, A. (2019). Noble gas dimers confined inside C₇₀. Phys. Chem. Chem. Phys. 21, 15815–15822. doi: 10.1039/C9CP03015H

CrossRef Full Text | Google Scholar

Graham, L., Graudejus, O., Jha, N. K., and Bartlett, N. (2000). Concerning the nature of XePtF₆. Coord. Chem. Rev. 197, 321–334. doi: 10.1016/S0010-8545(99)00190-3

CrossRef Full Text | Google Scholar

Hirshfeld, F. (1977). Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acc. 44, 129–138. doi: 10.1007/BF00549096

CrossRef Full Text | Google Scholar

Holloway, J. H., and Hope, E. G. (1999). Recent advances in noble-gas chemistry. Adv. Inorg. Chem. 46, 51–100. doi: 10.1016/S0898-8838(08)60149-X

CrossRef Full Text | Google Scholar

Jalife, S., Mondal, S., Cabellos, J. L., Pan, S., Méndez-Rojas, M. Á., Fernández, I., et al. (2016). Breaking the isolated pentagon rule by encapsulating Xe₂ in C₆₀: the guest defines the shape of the host. Chemistry Select 1, 2405–2408. doi: 10.1002/slct.201600525

CrossRef Full Text | Google Scholar

Jaroš, A., Badri, Z., Bora, P. L., Bonab, E. F., Marek, R., Straka, M., et al. (2018). How does a container affect acidity of its content: charge-depletion bonding inside fullerenes. Chem. Eur. J. 24, 4245–4249. doi: 10.1002/chem.201706017

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, E. R., Keinan, S., Mori-Sánchez, P., Contreras-García, J., Cohen, A. J., and Yang, W. (2010). Revealing noncovalent interactions. J. Am. Chem. Soc. 132, 6498–6506. doi: 10.1021/ja100936w

PubMed Abstract | CrossRef Full Text | Google Scholar

Khatua, M., Pan, S., and Chattaraj, P. K. (2014). Movement of Ng₂ molecules confined in a C₆₀ cage: an ab initio molecular dynamics study. Chem. Phys. Lett. 610–611, 351–356. doi: 10.1016/j.cplett.2014.06.052

CrossRef Full Text | Google Scholar

Krapp, A., and Frenking, G. (2007). Is this a chemical bond? A theoretical study of Ng₂@C₆₀ (Ng=He, Ne, Ar, Ke, Xe). Chem. Eur. J. 13, 8256–8270. doi: 10.1002/chem.200700467

PubMed Abstract | CrossRef Full Text | Google Scholar

Kryachko, E. S., Nikolaienko, T., and Yu. (2015). He₂@C₆₀: thoughts of the concept of a molecule and of the concept of a bond in quantum chemistry. Int. J. Quantum Chem. 115, 859–867. doi: 10.1002/qua.24916

CrossRef Full Text | Google Scholar

Kullback, S., and Leibler, R. A. (1951). On information and sufficiency. Ann. Math. Stat. 22, 79–86. doi: 10.1214/aoms/1177729694

CrossRef Full Text | Google Scholar

Laskin, J., Peres, T., Lifshitz, C., Saunders, M., Cross, R. J., and Khong, A. (1998). An artificial molecule of Ne₂ inside C₇₀. Chem. Phys. Lett. 285, 7–9. doi: 10.1016/S0009-2614(97)01473-5

CrossRef Full Text | Google Scholar

Lee, C., Yang, W., and Parr, R. G. (1988). Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. B 37, 785–789. doi: 10.1103/PhysRevB.37.785

CrossRef Full Text | Google Scholar

Liu, S. B. (2007). Steric effect: a quantitative description from density functional theory. J. Chem. Phys. 126:244103. doi: 10.1063/1.2747247

CrossRef Full Text | Google Scholar

Liu, S. B. (2009). Conceptual density functional theory and some recent developments. Acta Phys. Chim. Sin. 25, 590–600. doi: 10.3866/PKU.WHXB20090332

CrossRef Full Text | Google Scholar

Liu, S. B. (2013). Origin and nature of bond rotation barriers: a unified view. J. Phys. Chem. A 17, 962–965. doi: 10.1021/jp312521z

CrossRef Full Text | Google Scholar

Liu, S. B. (2016). Information-theoretic approach in density functional reactivity theory. Acta Phys. Chim. Sin. 32, 98–118. doi: 10.3866/PKU.WHXB201510302

CrossRef Full Text | Google Scholar

Liu, S. B., Rong, C. Y., and Lu, T. (2014). Information conservation principle determines electrophilicity, nucleophilicity, and regioselectivity. J. Phys. Chem. A 118, 3698–3704. doi: 10.1021/jp5032702

CrossRef Full Text | Google Scholar

Lu, T., and Chen, F. (2012). Multiwfn: a multifunctional wavefunction analyzer. J. Comput. Chem. 33, 580–592. doi: 10.1002/jcc.22885

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, Y., Ai, Y., Song, X., Wang, C., and Luo, Y. (2014). The equilibrium geometry of A@C₆₀: a test case for conventional density functional theory. Chem. Phys. Lett. 591, 312–316. doi: 10.1016/j.cplett.2013.11.050

CrossRef Full Text | Google Scholar

Nagy, Á., and Romera, E. (2015). Relative Rényi entropy and fidelity susceptibility. Europhys. Lett. 109:60002. doi: 10.1209/0295-5075/109/60002

CrossRef Full Text | Google Scholar

Nelson, L. Y., and Pimentel, G. C. (1967). Infrared detection of xenon dichloride. Inorg. Chem. 6, 1758–1759. doi: 10.1021/ic50055a038

CrossRef Full Text | Google Scholar

Nikolaienko, T., Yu Kryachko, E. S., and Dolgonos, G. A. (2017). On the existence of He–He bond in the endohedral fullerene H?₂@C₆₀. J. Comput. Chem. 39, 1090–1102. doi: 10.1002/jcc.25061

CrossRef Full Text | Google Scholar

Nikolaienko, T. Y., and Kryachko, E. S. (2015). Formation of dimers of light noble atoms under encapsulation within fullerene's voids. Nanoscale Res. Lett. 30:185. doi: 10.1186/s11671-015-0871-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Osuna, S., Swart, M., and Solà, M. (2009). Reactivity and regioselectivity of noble gas endohedral fullerenes Ng@C₆₀ and Ng₂@C₆₀ (Ng=He–Xe). Chem. Eur. J. 15, 13111–13123. doi: 10.1002/chem.200901224

CrossRef Full Text | Google Scholar

Osuna, S., Swart, M., and Solà, M. (2011). The reactivity of endohedral fullerenes. What can be learnt from computational studies? Phys. Chem. Chem. Phys. 13, 3585–3603. doi: 10.1039/C0CP01594F

PubMed Abstract | CrossRef Full Text | Google Scholar

Parr, R. G., Donnelly, R. A., Levy, M., and Palke, W. E. (1978). Electronegativity: the density functional viewpoint. J. Chem. Phys. 68, 3801–3807. doi: 10.1063/1.436185

CrossRef Full Text | Google Scholar

Parr, R. G., and Pearson, R. G. (1983). Absolute hardness: companion parameter to absolute electronegativity. J. Am. Chem. Soc. 105, 7512–7516. doi: 10.1021/ja00364a005

CrossRef Full Text | Google Scholar

Parr, R. G., Szentpaly, L. V., and Liu, S. B. (1999). Electrophilicity index. J. Am. Chem. Soc. 121, 1922–1924. doi: 10.1021/ja983494x

CrossRef Full Text | Google Scholar

Parr, R. G., and Yang, W. (1989). Density Functional Theory of Atoms and Molecules. Oxford: Oxford University Press.

Google Scholar

Peres, T., Cao, B., Cui, W., Khong, A., Cross, R. J. Jr., Saunders, M., et al. (2001). Some new diatomic molecule containing endohedral fullerenes. Int. J. Mass Spec. 210–211, 241–247. doi: 10.1016/S1387-3806(01)00420-1

CrossRef Full Text | Google Scholar

Popov, A. A., Yang, S., and Dunsch, L. (2013). Endohedral fullerenes. Chem. Rev. 113, 5989–6113. doi: 10.1021/cr300297r

PubMed Abstract | CrossRef Full Text | Google Scholar

Rényi, A. (1970). Probability Theory. Amsterdam: North-Holland.

Google Scholar

Rong, C., Wang, B., Zhao, D., and Liu, S. (2019). Information-theoretic approach in density functional theory and its recent applications to chemical problems. WIREs Comput. Mol. Sci. 10:e1461. doi: 10.1002/wcms.1461

CrossRef Full Text | Google Scholar

Saha, R., Jana, G., Pan, S., Merino, G., and Chattaraj, P. K. (2019). How far can one push the noble gases towards bonding?: a personal account. Molecules 24:2933. doi: 10.3390/molecules24162933

PubMed Abstract | CrossRef Full Text | Google Scholar

Saunders, M., Cross, R. J., Jiménez-Vázquez, H. A., Shimshi, R., and Khong, A. (1996). Noble gas atoms inside fullerenes. Science 271, 1693–1697. doi: 10.1126/science.271.5256.1693

CrossRef Full Text | Google Scholar

Saunders, M., Jiménez-Vázquez, H. A., Cross, R. J., and Poreda, R. J. (1993). Stable compounds of helium and neon: He@C₆₀ and Ne@C₆₀. Science 259, 1428–1430. doi: 10.1126/science.259.5100.1428

CrossRef Full Text | Google Scholar

Shannon, C. E. (1948). A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x

CrossRef Full Text | Google Scholar

Simon, S., Duran, M., and Dannenberg, J. J. (1996). How does basis set superposition error change the potential surfaces for hydrogen bonded dimers? J. Chem. Phys. 105, 11024–11031. doi: 10.1063/1.472902

CrossRef Full Text | Google Scholar

Srivastava, A. K., Pandey, S. K., and Misra, N. (2016). (CH₃Br?NH₃)@C₆₀: the effect of nanoconfinement on halogen bonding. Chem. Phys. Lett. 662, 240–243. doi: 10.1016/j.cplett.2016.09.036

CrossRef Full Text | Google Scholar

Stein, L. (1973). Removal of xenon and radon from contaminated atmospheres with dioxygenyl hexafluoroantimonate, O₂SbF₆. Nature 243, 30–32. doi: 10.1038/243030a0

CrossRef Full Text | Google Scholar

Syamala, M. S., Cross, R. J., and Saunders, M. (2002). ¹²⁹Xe NMR spectrum of Xenon inside C₆₀. J. Am. Chem. Soc. 124, 6216–6219. doi: 10.1021/ja012676f

PubMed Abstract | CrossRef Full Text | Google Scholar

Te Velde, G. T., Bickelhaupt, F. M., Baerends, E. J., Fonseca Guerra, C., van Gisbergen, S. J., Snijders, J. G., et al. (2001). Chemistry with ADF. J. Comput. Chem. 22, 931–967. doi: 10.1002/jcc.1056

CrossRef Full Text | Google Scholar

Turner, J. J., and Pimentel, G. C. (1963). Krypton fluoride: preparation by the matrix isolation technique. Science 140, 974–975. doi: 10.1126/science.140.3570.974-a

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, B., Rong, C. Y., Chattaraj, P. K., and Liu, S. B. (2019). A comparative study to predict regioselectivity, electrophilicity and nucleophilicity with Fukui function and Hirshfeld charge. Theor. Chem. Acc. 138:124. doi: 10.1007/s00214-019-2515-1

CrossRef Full Text | Google Scholar

Yamamoto, K., Saunders, M., Khong, A., Cross, R. J., Grayson, M., Gross, M. L., et al. (1999). Isolation and spectral properties of Kr@C₆₀, a stable van der Waals molecule. J. Am. Chem. Soc. 121, 1591–1596. doi: 10.1021/ja9831498

CrossRef Full Text | Google Scholar

Yang, W., Parr, R. G., and Pucci, R. (1984). Electron density, Kohn–Sham frontier orbitals, and Fukui functions. J. Chem. Phys. 81, 2862–2863. doi: 10.1063/1.447964

CrossRef Full Text | Google Scholar

Zhao, Y., and Truhlar, D. G. (2008). The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 120, 215–241. doi: 10.1007/s00214-007-0310-x

CrossRef Full Text | Google Scholar