Systematic Theoretical Study on Structural, Stability, Electronic, and Spectral Properties of Si2MgnQ (Q = 0, ±1; n = 1–11) Clusters of Silicon-Magnesium Sensor Material

By using CALYPSO searching method and Density Functional Theory (DFT) method at the B3LYP/6-311G (d) level of cluster method, a systematic study of the structures, stabilities, electronic and spectral properties of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material, is performed. According to the calculations, it was found that when n > 4, most stable isomers in Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material are three-dimensional structures. Interestingly, although large size Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ clusters show cage-like structures, silicon atoms are not in the center of the cage, but tend to the edge. The Si₂${\text{Mg}}_{1,5,6,8}^{-1}$ and Si₂${\text{Mg}}_{13,4,7,9,10}^{+1}$ clusters obviously differ to their corresponding neutral structures, which are in good agreement with the calculated values of VIP, AIP, VEA, and AEA. |VIP-VEA| values reveal that the hardness of Si₂Mg_n clusters decreases with the increase of magnesium atoms. The relative stabilities of neutral and charged Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material is analyzed by calculating the average binding energy, fragmentation energy, second-order energy difference and HOMO-LUMO gaps. The results reveal that the Si₂${\text{Mg}}_3^0$, Si₂${\text{Mg}}_3^{-1}$, and Si₂${\text{Mg}}_3^{+1}$clusters have stronger stabilities than others. NCP and NEC analysis results show that the charges in Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material transfer from Mg atoms to Si atoms except for Si₂${\text{Mg}}_1^{+1}$, and strong sp hybridizations are presented in Si atoms of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ clusters. Finally, the infrared (IR) and Raman spectra of all ground state of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon magnesium sensor material are also discussed.

Introduction

Silicon and magnesium are abundant elements on the earth and are widely used in sensor industry. In particular, silicon, as the main material of semiconductor sensors, has always been the research frontier in the field of sensors. As the only stable compound in Mg-Si binary system, Mg₂Si, which has the characteristics of high melting point, high hardness, high modulus of elasticity and environmentally friendly, is an n-type semiconductor material with a band gap of 0.68–1.03 eV (Atanassov and Baleva, 2007). There are many experimental and theoretical studies on silicon-magnesium sensor materials. For example, theoretically, Morris et al. (1958) first used graphite crucible to melt stoichiometric components to prepare high purity single crystal Mg₂Si materials, they found the band gap of Mg₂Si is 0.78 eV. Aymerich and Mula (2010) and Imai et al. (2003) studied the band structure of Mg₂Si using empirical and first-principles pseudopotentials, respectively. Chen et al. (2010) studied the band structure of Mg₂Si and doped Ag, Al elements by using the first-principles pseudopotential plane wave method based on density functional theory (DFT). By using DFT, they obtained the real part, imaginary part and Photoconductivity of Mg₂Si dielectric function as a function of photon energy. Experimentally, the main work on Mg₂Si is focused on the preparation of thin film materials. Wittmer et al. (1979) was the first to fabricate Mg₂Si semiconductor thin films on Si (111) substrates by evaporating Mg atoms films with different thicknesses using an electron gun at a speed of about 40Å/s in vacuum. Boher et al. (1992) used radio frequency magnetron sputtering technology to sputter Mg₂Si targets onto glass materials and Si (111) substrates, and obtained amorphous Mg₂Si films. Song et al. (2003) used pulsed laser deposition (PLD) method to grow Mg₂Si crystal semiconductor thin films nearly 380 nanometers thick on stainless steel substrates at 500° annealing temperature.

All the above theoretical and experimental studies have greatly enriched the research results on the properties of silicon-magnesium sensor material. However, these studies have not touched the fundamental problem, how do the physical and chemical properties of silicon-magnesium compounds change from small systems (several or dozens of atoms) to large systems? Fortunately, small clusters provide a new way to study this system, which can provide insight into the strength and properties of metal bonds (Ju et al., 2015; Sun et al., 2017, 2018; Bole et al., 2018). Cluster material scale is a concept of nanomaterials. It is a relatively stable micro or sub-micro aggregate composed of several or even thousands of atoms, molecules or ions. Its physical and chemical properties usually vary with the number of atoms contained. Cluster studies have successfully helped us to in-depth understand the structure, stability, electronic states and spectral properties of many materials (Jin et al., 2015a,b; Xia et al., 2015; Xing et al., 2016a,b). There are many reports about sensor material study by using cluster method. For example, Yang et al. (2006) used full-muffin-tin-orbital molecular-dynamics (FP-LMTO-MD) method to study the electronic and geometric structures of Ga_nAs_n (n = 4, 5, 6) cluster ions. They found that some of the lowest energy structures for the cluster ions are different from those of the corresponding neutral clusters. Dmytruk et al. (2009) produced zinc oxide clusters by laser ablation of bulk powder zinc peroxide in vacuum and studied them by time-of-flight mass spectrometry. By comparing the experimental results with the theoretical calculations of clusters, the most stable structure of (ZnO)n clusters was verified at n = 34, 60, and 78.

However, most of the studies on sensor material clusters are carried out in a crystal growth mode, such as AsGa and ZnO, where the number of different atoms increases in harmony. In this paper, doped clusters will be used to study the materials of silicon-magnesium sensors. To be exact, we doped a small amount of silicon into magnesium element, which increased the number of magnesium atoms around two silicon atoms from 1 to 11, and made them neutral charged, negative charged and positive charged, respectively. Then, we will study the structure, stability, electronic and spectral properties of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicide-magnesium materials in detail. The paper is organized as follows: Section Computation Methods describes the computational details, the results are presented and completely discussed in section Results and discussions, and the final conclusions are summarized in section Conclusion.

Computation Methods

All structural optimization and infrared Raman spectrum analysis are carried out by using DFT at B3LYP/6-311G (d) basis set level in Gauss 09 program package (Frisch et al., 2014). In order to find the lowest energy state structure of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material, it is necessary to prepare enough initial configurations of Si₂Mg_n clusters. We used the particle swarm optimization (CALYPSO) method (Wang et al., 2010, 2012; Lv et al., 2012) to get the initial structures of pure magnesium clusters. Then, replacing any two Mg atoms with Si atom in the initial Mg_n clusters' structures. CALYPSO method has successfully predicted structures for various systems ranging from clusters to crystal structures (Lu et al., 2013, 2017, 2018; Lu and Chen, 2018; Xiao et al., 2019). In the process of geometric optimization in Gauss 09 package, for neutral clusters, the spin multiplicity of electrons takes into account 1, 3, 5 states, while for charged clusters, it is 2, 4, 6 states, and there is no constraint on the symmetry. Finally, if the optimization results include virtual frequencies, the coordinates of the virtual mode are relaxed until the real local minimum is obtained. On the basis of eliminating imaginary frequency, the potential energy of all optimized ground state structures will reach absolute local minimum.

In order to prove the reliability of the selected B3LYP/6-311G (d) basis set level, the calculated bond length, vibrational frequency, vertical ionization potential (VIP) and vertical electron affinity (VEA)of the neutral Mg₂, Si₂, SiMg clusters by using different methods at the same 6-311G (d) basis set are shown in Table 1. As showed in Table 1, the calculated values r(Mg₂) = 3.93 Å, ω(Mg₂) = 44.96 cm⁻¹, r(Si₂) = 2.17 Å, ω(Si₂) = 540.82 cm⁻¹, VIP(Si₂) = 9.13 eV, and VEA(Si₂) = 2.02 eV, these conclusions are quite agree with the existed experimental results (Huber, 1979; de Heer et al., 1987; Kitsopoulos et al., 1991; Ruette et al., 2005).

TABLE 1

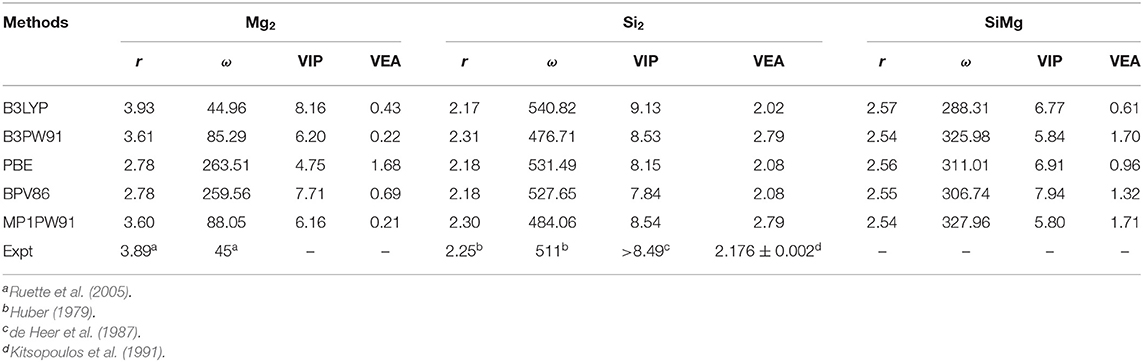
Table 1. Calculated values of bond length r (Å), frequency ω (cm⁻¹), vertical ionization potential VIP (eV) and vertical electron affinity VEA (eV) for the Mg₂, Si₂, and SiMg clusters by different methods.

Results and Discussions

Geometrical Structures of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$(n = 1–11; Q = 0, ±1) Clusters of Silicon-Magnesium Sensor Material

The geometries of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material are optimized by using the computational method in section Computation Methods. Due to the existence of so many initial structures, the relative energies of all the initial isomers with different spin multiplicities are optimized, but only the lowest energies and a few low-lying energy isomers are given in Figures 1–3. In addition, in Figures 1–3, in order to compare the effect of Si-doped Mg clusters on the original structure of pure Mg clusters, we also list the lowest energy state structure Mg_n+2 (n = 1–11) of pure Mg clusters optimized by the same method, while the lowest energy state and two metastable structures of neutral Si₂${\text{Mg}}_{\text{n}}^0$, anionic Si₂${\text{Mg}}_{\text{n}}^{-1}$, cationic Si₂${\text{Mg}}_{\text{n}}^{+1}$ (n = 1–11) clusters are given. Under each isomer structure, there are three information about the energy difference between the metastable structure and the lowest energy state structure, the symmetry, and the electronic spin state. So, the first structure of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ clusters are all labeled as 0.00 eV, indicating that this structure is the lowest energy state. The latter two are two metastable structures, and the energy difference with the lowest energy state is directly expressed as a non-zero value. It is noteworthy that when n is determined, there are three energy differences on the right side of the lowest energy structure of Mg_n+2, they are ΔE₁ = E(Si₂${\text{Mg}}_{\text{n}}^0$)–E(Mg_n+2), ΔE₂ = E(Si₂${\text{Mg}}_{\text{n}}^{-1}$)–E(Mg_n+2), and ΔE₃ = E(Si₂${\text{Mg}}_{\text{n}}^{+1}$)–E(Mg_n+2), notably, E means the ground state energy. Since there are too many structures, we first give a brief introduction to each structure, and then analyze and discuss their growth patterns shortly below.

FIGURE 1

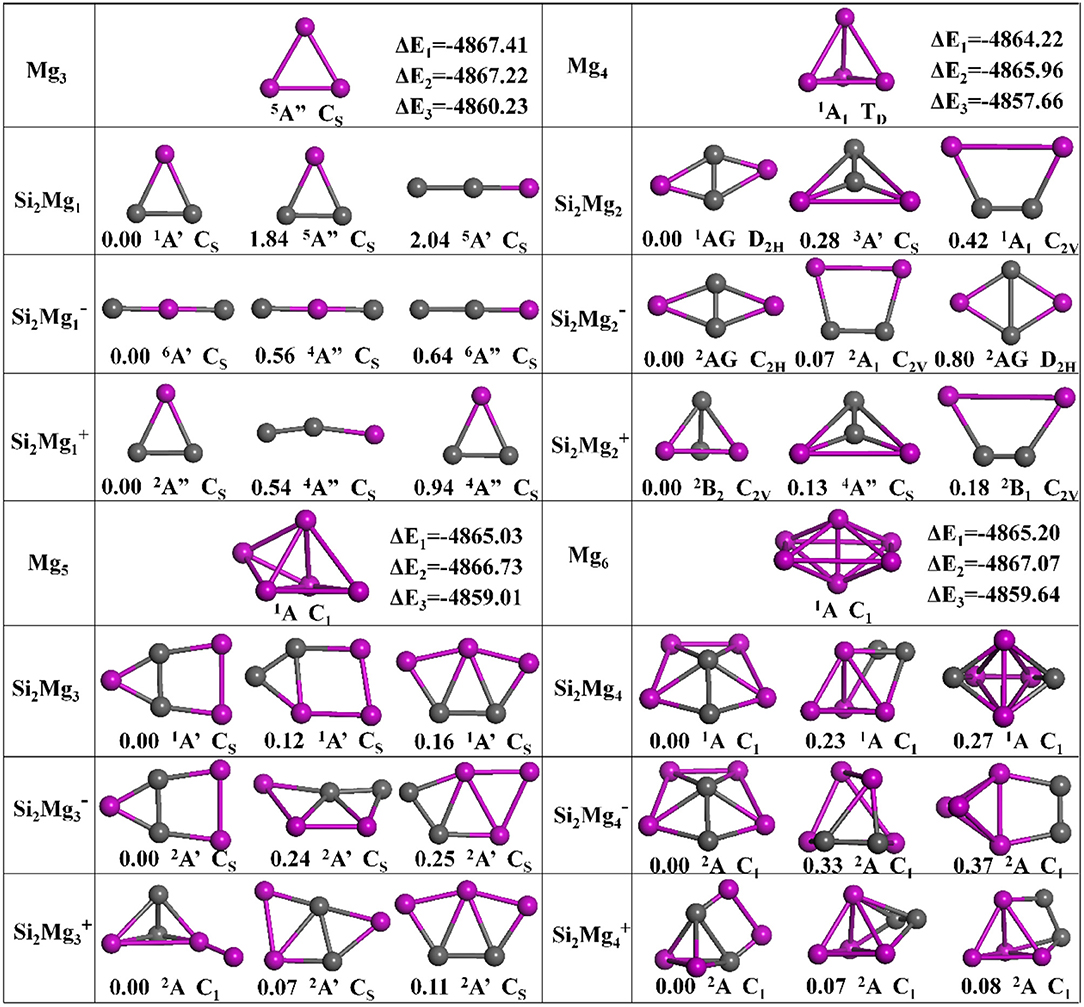
Figure 1. Optimized geometries of Mg_n+2 and Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–4; Q = 0, ±1) clusters of silicon-magnesium sensor material at B3LYP/6-311+G(d) level. The pink and gray balls present the Mg and Si atoms, respectively.

FIGURE 2

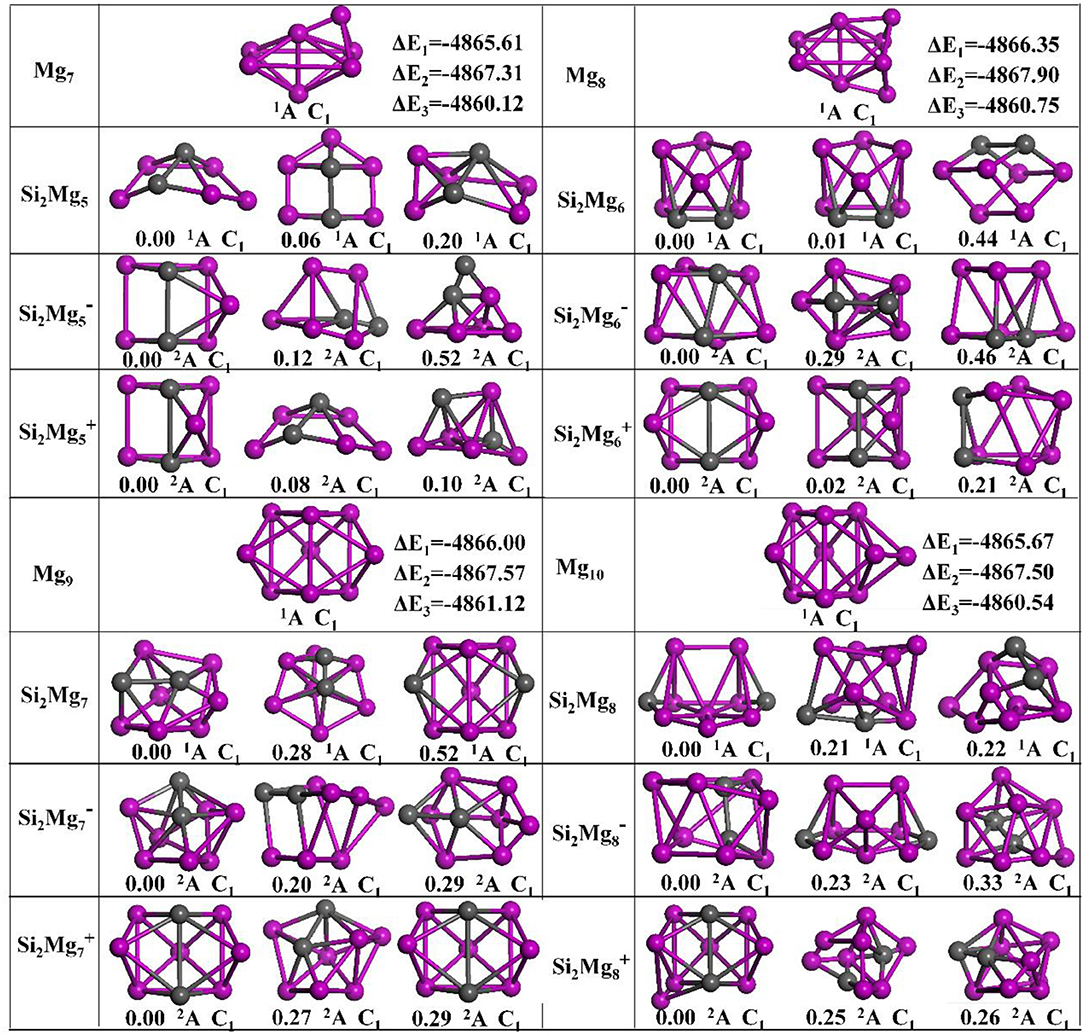
Figure 2. Optimized geometries of Mg_n+2 and Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 5–8; Q = 0, ±1) clusters of silicon-magnesium sensor material at B3LYP/6-311+G(d) level. The pink and gray balls present the Mg and Si atoms, respectively.

FIGURE 3

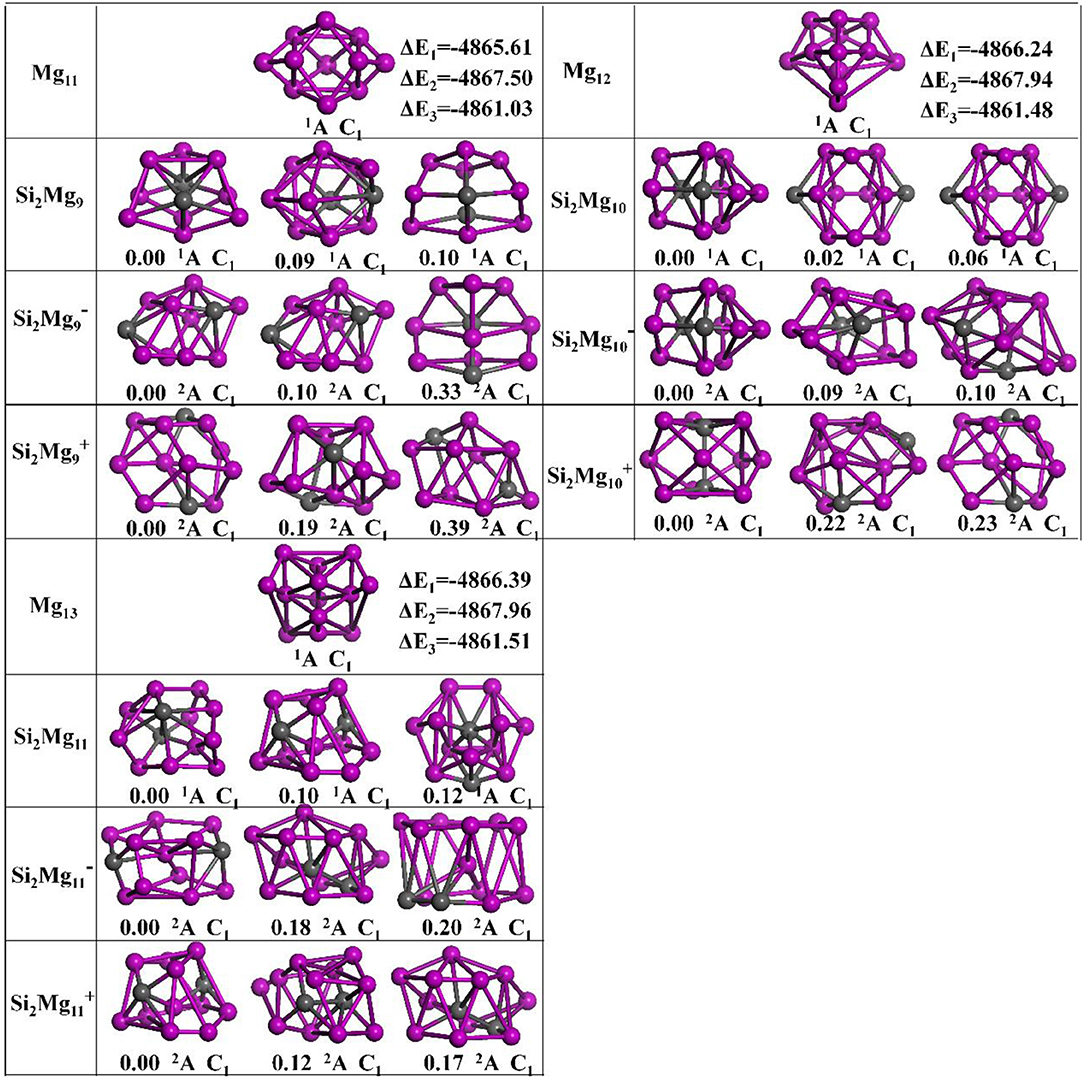
Figure 3. Optimized geometries of Mg_n+2 and Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 9–11; Q = 0, ±1) clusters of silicon-magnesium sensor material at B3LYP/6-311+G(d) level. The pink and gray balls present the Mg and Si atoms, respectively.

n = 1: Si₂Mg₁, Si₂${Mg}_1^{-1}$, Si₂${Mg}_1^{+1}$, and Mg₃

The lowest energy structure of neutral Si₂Mg1 with spin singlet and C_S symmetry is an isosceles triangle, which are the similar as the ground state of cationic Si₂${\text{Mg}}_1^{+1}$ and pure Mg₃ clusters. For anionic Si₂${\text{Mg}}_1^{-1}$, the linear chain (C_S, ⁶A') in which the Mg atom is in the middle position is found to be the most stable isomer. For metastable isomers, two triangular structures for Si₂${\text{Mg}}_1^{+1}$, two linear chain structures for Si₂${\text{Mg}}_1^{-1}$, and one triangular, one linear chain structures for neutral Si₂Mg1.

n = 2: Si₂Mg₂, Si₂${Mg}_2^{-1}$, Si₂${Mg}_2^{+1}$, and Mg₄

The ground states of Si₂Mg2 (D_2H, ¹AG) and Si₂${\text{Mg}}_2^{-1}$ (C_2H, ²AG) are parallelograms with a little different shapes. Replacing any two Mg atoms with Si atoms in the tetrahedral structure of Mg₄ (T_D, ¹A₁) forms the lowest energy isomer structure of Si₂${\text{Mg}}_2^{+1}$ (C_2V, ²B₂). All metastable isomers are planar structures, such as trapezoids, triangles and parallelograms.

n = 3: Si₂Mg₃, Si₂${Mg}_3^{-1}$, Si₂${Mg}_3^{+1}$, and Mg₅

It is impossible to replace two magnesium atoms in the ground state structure of Mg₅ (C₁, ¹A) with silicon atoms to directly form any Si₂MgQ 3 (Q = 0, ±1) cluster structure. But the lowest energy isomer structures of Si₂Mg3 (C_S, ¹A') and Si₂${\text{Mg}}_3^{-1}$ (C_S, ²A') can be formed by the second metastable isomer structure of Si₂Mg2, in where attracting a Mg atom in the same plane outside the trapezoidal silicon-silicon bond. The lowest energy isomer structure of Si₂${\text{Mg}}_3^{+1}$ (C₁, ²A) is formed by the ground state of Si₂${\text{Mg}}_2^{+1}$ with a magnesium cap at the top of a magnesium atom. In addition, all metastable isomers exhibit planar structures.

n = 4: Si₂Mg₄, Si₂${Mg}_4^{-1}$, Si₂${Mg}_4^{+1}$, and Mg₆

The lowest energy structure of Mg₆ (C₁, ¹A) is an octahedron. When the two magnesium atoms at the octahedron vertex are replaced by silicon atoms and the lower silicon atoms float up to the plane where the four magnesium atoms are located, the lowest energy state structures of Si₂Mg₄ (C₁, ¹A) and Si₂${\text{Mg}}_4^{-1}$ (C₁, ²A) are formed. The ground state structure of Si₂${\text{Mg}}_4^{+1}$ (C₁, ²A) can be formed by the ground state of Si₂${\text{Mg}}_2^{+1}$attrcating a Mg-Mg bond parallel to the Si-Si bond. All metastable isomers are three-dimensional structures and are directly related to the structure of isomers with small n values.

n = 5: Si₂Mg₅, Si₂${Mg}_5^{-1}$, Si₂${Mg}_5^{+1}$, and Mg₇

The ground state structure of Mg₇ (C₁, ¹A) can be directly formed from Mg₆ with a magnesium atom cap on one side of the octahedron. The ground state structures of Si₂${\text{Mg}}_5^{-1}$ (C₁, ²A) and Si₂${\text{Mg}}_5^{+1}$ (C₁, ²A) are similar, their main body is a triangular prism with a magnesium-silicon-magnesium triangle at the top and bottom, and then a magnesium atom cap at different distances from the side. The lowest energy structure of neutral Si₂Mg₅ (C₁, ²A) is formed when the ground sate structure of Si₂Mg₄ attracting one magnesium atom. It is easy to see that the first metastable structure of cationic Si₂${\text{Mg}}_5^{+1}$ is the lowest energy state structure of neutral Si₂Mg₅. Interestingly, the difference between the first metastable state structure of neutral Si₂Mg₅ and the lowest energy state structure of anionic Si₂${\text{Mg}}_5^{-1}$ is the orientation of the cap with magnesium atom, the former at the bottom and the latter at the side.

n = 6: Si₂Mg₆, Si₂${Mg}_6^{-1}$, Si₂${Mg}_6^{+1}$, and Mg₈

The lowest energy structure of Mg₈ (C₁, ¹A) is formed by adding a Mg atom cap to the up down mirror symmetry of Mg₇. When adding a Mg atom cap to the right left mirror symmetry of the lowest energy structure of Si₂${\text{Mg}}_5^{+1}$, the ground state structures of Si₂${\text{Mg}}_6^{+1}$ (C₁, ²A) is formed. The lowest energy structure of neutral Si₂Mg₆ (C₁, ¹A) is as the same as its first metastable structure. The ground state of Si₂${\text{Mg}}_6^{-1}$(C₁, ²A) is an irregular polyhedral cylinder, but its metastable state structures show certain irregularity.

n = 7: Si₂Mg₇, Si₂${Mg}_7^{-1}$, Si₂${Mg}_7^{+1}$, and Mg₉

The lowest energy state structure of the cationic Si₂${\text{Mg}}_7^{+1}$ (C₁, ²A), which is as the same as its second metastable state structure, can be formed by substituting the upper and lower mirror symmetrical Mg atoms for the silicon atoms in the lowest energy state Mg₉ (C₁, ¹A) structure. The ground state of Si₂${\text{Mg}}_7^{-1}$ (C₁, ²A) is similar as the first metastable state structure Si₂${\text{Mg}}_7^{+1}$. The lowest energy structure of the neutral Si₂Mg₇ (C₁, ²A) has the same main body as the ground state structure of Si₂Mg₄. Interestingly, the second metastable state structure of Si₂Mg₇ is similar as the ground state structure of Si₂${\text{Mg}}_7^{+1}$, the only difference is the two silicon atoms are bonded from top to bottom to left.

n = 8: Si₂Mg₈, Si₂${Mg}_8^{-1}$, Si₂${Mg}_8^{+1}$, and Mg₁₀

The lowest energy state structure of the Mg₁₀ (C₁, ¹A) is formed by Mg₉ with a magnesium atom on right side. The ground state structure of Si₂${\text{Mg}}_8^{+1}$ (C₁, ²A) can be formed by ground state structure of Si₂${\text{Mg}}_7^{+1}$ with a magnesium cap on left-down side. The lowest energy state structure of neutral Si₂Mg₈ (C₁, ²A) is similar as the first metastable state structure of Si₂${\text{Mg}}_8^{-1}$. The ground state of Si₂${\text{Mg}}_8^{-1}$(C₁, ²A) is cage-like structure with one silicon atom trapped on the upper surface. Interestingly, other metastable state structures also present cage-like structures.

n = 9: Si₂Mg₉, Si₂${Mg}_9^{-1}$, Si₂${Mg}_9^{+1}$, and Mg₁₁

When Mg₁₀ attracting a magnesium on the left side, it is the lowest energy structure of Mg₁₁ (C₁, ¹A). From n = 9, it is easy found that no structure of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (Q = 0, ±1) can be formed by substituting two magnesium atoms for silicon atoms in Mg_n+2. The ground state of Si₂${\text{Mg}}_9^{-1}$ (C₁, ²A) is similar as its first metastable state structure. They can be formed based on the first metastable structure of Si₂${\text{Mg}}_8^{+1}$ with a Mg atomic cap. The ground state structure of neutral Si₂Mg₉ (C₁, ²A) is similar as its second metastable structure and the second metastable structure of Si₂${\text{Mg}}_9^{-1}$. The lowest energy state structure of Si₂${\text{Mg}}_9^{+1}$ (C₁, ²A) is a complex 3D cage-like structure based on the second metastable state of Si₂Mg₄ with attracting more five Mg atoms.

n = 10: Si₂Mg₁₀, Si₂${Mg}_1^{-1}$0, Si₂${Mg}_1^{+1}$0, and Mg₁₂

The ground state structures of neutral Si₂Mg₁₀ (C₁, ¹A) and Si₂${\text{Mg}}_1^{-1}$0 (C₁, ²A) are the same and can be formed by the lowest energy state structure of Si₂${\text{Mg}}_9^{+1}$ with a magnesium cap. The lowest energy state structure of Si₂${\text{Mg}}_1^{+1}$0 (C₁, ²A) is formed by the ground state structure of Si₂${\text{Mg}}_8^{-1}$ with adding two magnesium atoms. All the metastable structures present 3D structures, and some of them can easily be found to be associated with the cluster structure discussed earlier. For example, the metastable structure of neutral Si₂Mg₁₀ can be formed by the ground state of neutral Si₂Mg₈ with adding two Mg atoms.

n = 11: Si₂Mg₁₁, Si₂${Mg}_1^{-1}$1, Si₂${Mg}_1^{+1}$1, and Mg₁₃

The lowest energy structures of Si₂Mg₁₁ (C₁, ¹A), Si₂${\text{Mg}}_1^{-1}$1(C₁, ²A), Si₂${\text{Mg}}_1^{+1}$1(C₁, ²A) show cage structures, but no silicon atom located the cage center. By using the ground state structure of Si₂${\text{Mg}}_9^{-1}$ with adding two magnesium atoms, the lowest energy structure of Si₂${\text{Mg}}_1^{-1}$1(C₁, ²A) is got. The ground state structure of Si₂Mg₁₁ (C₁, ¹A) can be formed by the first metastable structure of Si₂Mg₉ with two more magnesium attracted. The lowest energy structure of Si₂${\text{Mg}}_1^{+1}$1(C₁, ²A) is the same as the first metastable structure of Si₂Mg₁₁, and they are quite similar as the first metastable structure of Si₂${\text{Mg}}_9^{+1}$. Other metastable structures exhibit 3D cage-like structure.

Energy Difference Between Structures

As shown in Figures 1–3, the energy differences ΔE₁ (from −4867.41 to −4864.22 eV), ΔE₂ (from −4867.96 to −4865.96 eV), and ΔE₃ (from −4861.51 to −4857.66 eV) are quite stable and reasonable. Because the energy difference between the free neutral Si₂ and Mg₂, E(Si₂)–E(Mg₂) = −4864.42 eV, is quite near to the ΔE_1. In addition, ΔE₂ < ΔE₁ < ΔE₃ is consistent with the following conclusion: if the neutral charged cluster is negatively charged, the cluster will lose energy, and if the neutral charged cluster is positively charged, the cluster will get energy. In addition, the energy differences between all metastable state structures and their corresponding ground state structures are also listed under each metastable state structure, they are all very small (from 0.01 to 2.04 eV) and reasonable.

Growth Pattern

According to the structural characteristics of the lowest energy state structures mentioned above, the growth mechanism of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material can be summarized as following: (i) The lowest energy state Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ clusters favor 3D and low spin multiplicity for n = 4–11. (ii) Compared with neutral Si₂Mg_n clusters, charged Si₂${\text{Mg}}_{\text{n}}^{\pm 1}$ clusters formed when they get or lose electrons will change their structures in most cases. (iii) Larger size clusters Si₂${\text{Mg}}_{\text{n}}^{0\pm 1}$ show cage-like geometries, but silicon atoms are not in the center of the cage, but tend to the edge, which is different from some reports (Zhang et al., 2015). This may be related to the distribution of electrons outside the nucleus of magnesium and silicon atoms. Through the above structure optimization, we can find that the shortest chemical bond length of clusters tends to be smaller when silicon doped with magnesium. Table 2 shows the shortest chemical bond lengths of Mg-Mg, Si-Si, Si-Mg for all Si₂Mg_n clusters as the number of magnesium atoms increases. For comparison, Table 2 also lists the shortest chemical bond lengths of Mg-Mg clusters with corresponding atomic numbers of pure magnesium clusters. From Table 2, it can be seen clearly that silicon doping into magnesium can indeed make the cluster structure more compact when the total number of atoms is the same.

TABLE 2

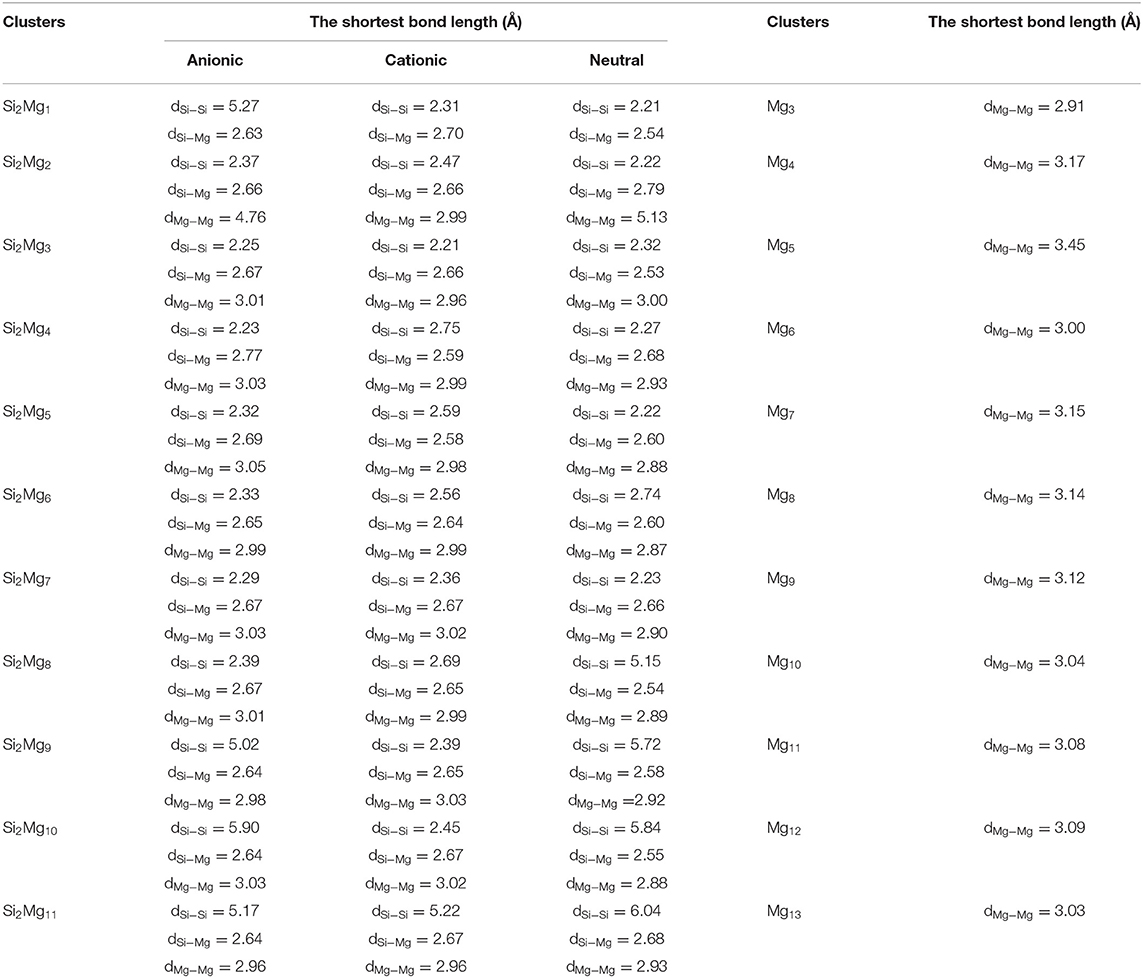
Table 2. The shortest bond length (Å) of Mg_n+2, neutral and charged Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters.

The Relative Stabilities of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$(n = 1–11; Q = 0, ±1) Clusters of Silicon-Magnesium Sensor Material

In order to study the relativity stabilities of neutral and charged Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material, the average binding energy E_b, fragmentation energy E_f, the second-order energy differences Δ₂E, and the HOMO-LUMO energy gap E_gap are calculated, which can be read as below:

$\begin{array}{ll}{E}_b(S{i}_{2}M{g}_n)=\left[n{E}_k(Mg)+2E_k(Si)-E_k(S{i}_{2}M{g}_n)\right]/\text{(}n+2)& (1)\end{array}$

$\begin{array}{l}{E}_b(S{i}_{2}M{g}_n^{\pm 1})=[(n-1)E_k(Mg)+E_k(M{g}^{\pm })\hfill \\ +2E_k(Si)-E_k(S{i}_{2}M{g}_n^{\pm 1})]/\text{(}n\text{+2)}\hfill & (2)\end{array}$

$\begin{array}{ll}{E}_f(S{i}_{2}M{g}_n^{0,\pm 1})=E_k(S{i}_{2}M{g}_{n-1}^{0,\pm 1})+E_k(Mg)-E_k(S{i}_{2}M{g}_n^{0,\pm 1})& (3)\end{array}$

$\begin{array}{l}{\Delta }_{2}E(S{i}_{2}M{g}_n^{0,\pm 1})=E_k(S{i}_{2}M{g}_{n-1}^{0,\pm 1})+E_k(S{i}_{2}M{g}_{n+1}^{0,\pm 1})\hfill \\ -2E_k(S{i}_{2}M{g}_n^{0,\pm 1})\hfill & (4)\end{array}$

$\begin{array}{ll}{E}_{gap}(S{i}_{2}M{g}_n^{0,\pm 1})=E_{LUMO}(S{i}_{2}M{g}_n^{0,\pm 1})-E_{HOMO}(S{i}_{2}M{g}_n^{0,\pm 1})& (5)\end{array}$

E_k in Equations (1–4) are the total energy of the corresponding atom and ground state clusters. E_HOMO and E_LUMO in Equation (5) are the energies of highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO).

The motivation for comparing pure magnesium clusters must be explained here. Physically, the most ideal (simplest) silicon doping is to replace two magnesium atoms with silicon atoms in pure magnesium clusters, and then to optimize the structure. Therefore, comparing some properties of silicon-doped magnesium clusters, we always habitually compare pure magnesium clusters with the total number of corresponding atoms in our research. The size-dependent properties of E_b, E_f, Δ₂E, and E_gap for the lowest energy state Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material are presented in Figure 4. We can summarize the properties as the following:

1) The E_b values of all Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material decrease followed by same tendency with the size increases, but the E_b values of pure Mg_n+2 clusters are gradually increase. In addition, the E_b values of cationic Si₂${\text{Mg}}_{\text{n}}^{+1}$ are always the highest, while the E_b values of neutral Si₂${\text{Mg}}_{\text{n}}^0$ are the lowest all the time. It means that electron removal can enhance the chemical properties of Si₂Mg_n clusters.

2) The E_f curves of neutral and charged Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material have a similar oscillating tendency. For neutral Si₂${\text{Mg}}_{\text{n}}^0$ clusters, the stronger relative stability clusters are Si₂${\text{Mg}}_3^0$, Si₂${\text{Mg}}_6^0$, and Si₂${\text{Mg}}_{10}^0$ based on the maxim of E_f values. For anionic Si₂${\text{Mg}}_{\text{n}}^{-1}$ clusters, three significant maxima are found at n = 3, 7, 9, which indicate that Si₂${\text{Mg}}_3^{-1}$, Si₂${\text{Mg}}_7^{-1}$, and Si₂${\text{Mg}}_9^{-1}$ clusters are the most stable clusters. For cationic Si₂${\text{Mg}}_{\text{n}}^{+1}$ clusters, three local peaks can be found from the E_f curve, it means that Si₂${\text{Mg}}_3^{+1}$, Si₂${\text{Mg}}_6^{+1}$, Si₂ ${\text{Mg}}_8^{+1}$ clusters are more stable than their neighbors.

3) The irregular oscillation behaviors are the most prominent feature of Δ₂E curves of all Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material. The maxima are found at n = 3 for all Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ clusters, n = 6 and 8 for both neutral Si₂${\text{Mg}}_{\text{n}}^0$ and anionic Si₂${\text{Mg}}_{\text{n}}^{-1}$ clusters, n = 7 for cationic Si₂${\text{Mg}}_{\text{n}}^{+1}$ clusters. It means that the Si₂${\text{Mg}}_3^{-1}$, Si₂${\text{Mg}}_6^{-1}$, Si₂${\text{Mg}}_8^{-1}$, Si₂${\text{Mg}}_3^{+1}$, Si₂Mg+1 6, and Si₂${\text{Mg}}_7^{+1}$ clusters have slightly stronger relative stabilities and have large abundances in mass spectroscopy in comparison with the corresponding neighbors. For neutral clusters, Si₂${\text{Mg}}_3^0$, Si₂${\text{Mg}}_6^0$, and Si₂${\text{Mg}}_8^0$ clusters are more stable than other clusters.

4) The pure Mg_n+2 clusters have the highest E_gap is an unexpected conclusion, because pure magnesium has higher chemical stability than silicon magnesium. For Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters, the E_gap of cationic Si₂${\text{Mg}}_{\text{n}}^{+1}$ clutters is always the higher one. It means that Si₂${\text{Mg}}_{\text{n}}^{+1}$ clusters have higher chemical stability than the neutral and anionic Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ clusters. The curves of E_gap show that the maxima values appear at n = 3 for all Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (Q = 0, ±1) clusters, n = 7 for both neutral Si₂${\text{Mg}}_{\text{n}}^0$ and cationic Si₂${\text{Mg}}_{\text{n}}^{+1}$, and n = 8 for anionic Si₂${\text{Mg}}_{\text{n}}^{-1}$ clusters, which implies that the higher chemical stability clusters are Si₂${\text{Mg}}_3^0$, Si₂${\text{Mg}}_3^{-1}$, Si₂${\text{Mg}}_3^{+1}$, Si₂${\text{Mg}}_7^0$, Si₂${\text{Mg}}_7^{+1}$, and Si₂${\text{Mg}}_8^{-1}$.

FIGURE 4

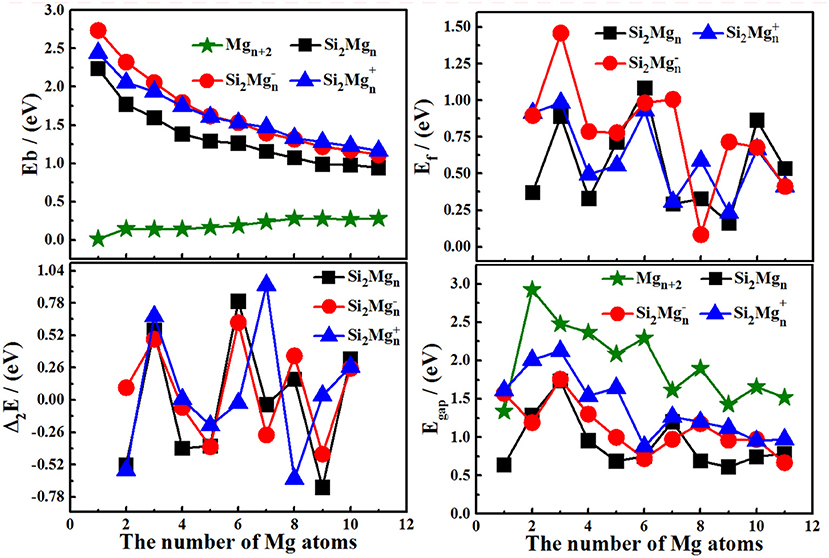
Figure 4. The size-dependent properties of E_b, Δ₂E, E_f, and E_gap of the lowest-energy Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$(n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material.

Based on the discussions about E_b, E_f, Δ₂E, and E_gap, we can conclude that the magic numbers of neutral and charged Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material are Si₂${\text{Mg}}_3^0$, Si₂${\text{Mg}}_3^{-1}$, Si₂${\text{Mg}}_3^{+1}$.

The Charge Transfer of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$(n = 1–11; Q = 0, ±1) Clusters of Silicon-Magnesium Sensor Material

Natural charge population (NCP) and natural electron population (NEC) of clusters are two important parameters to study the localization of charges in clusters (Trivedi et al., 2014). In order to study internal charge transfer of neutral and charged Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material, we calculate NCP and NEC for the ground state structures of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1), and the results are summarized in the Tables 3–6. We can find that the charges of silicon atoms in Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters is very significant from the Tables 3–5. Specifically, except for Si₂${\text{Mg}}_1^{+1}$, silicon atoms are negatively charged in the range of −0.34 to −2.06 electrons, and most magnesium atoms are positively charged in the range of 0.02–0.99 electrons. This result is consistent with expectation, because electrons are always transferred from magnesium atoms to silicon atoms in Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ clusters. In short, the NCP of Si atoms indicates that silicon atoms are electron acceptors in Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ clusters. The NEC of silicon atoms can be found in the Table 6, the electronic configuration for silicon atoms (3s¹3p³) shows that 3p orbital get 0.10–2.28 electrons, while 3s orbital loses 0.11–0.47 electrons. Obviously, charge transfer occurs only in the outermost electron orbit, and strong s-p hybridizations are presented in silicon atoms of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ clusters. Notably, the contributions of 4s and 5d orbitals are almost zero and can be ignored. Moreover, the charges of 3s and 3p orbitals for two silicon atoms in the ground state of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ clusters are equal except for ${\text{Si}}_2{\text{Mg}}_{3-5}^{-}$, ${\text{Si}}_2{\text{Mg}}_7^{-}$, ${\text{Si}}_2{\text{Mg}}_{9-11}^{-}$ ${\text{Si}}_2{\text{Mg}}_4^{-}$, ${\text{Si}}_2{\text{Mg}}_{7-11}^{-}$, Si₂${\text{Mg}}_5^{+}$, and Si₂${\text{Mg}}_{8-9}^{+}$.

TABLE 3

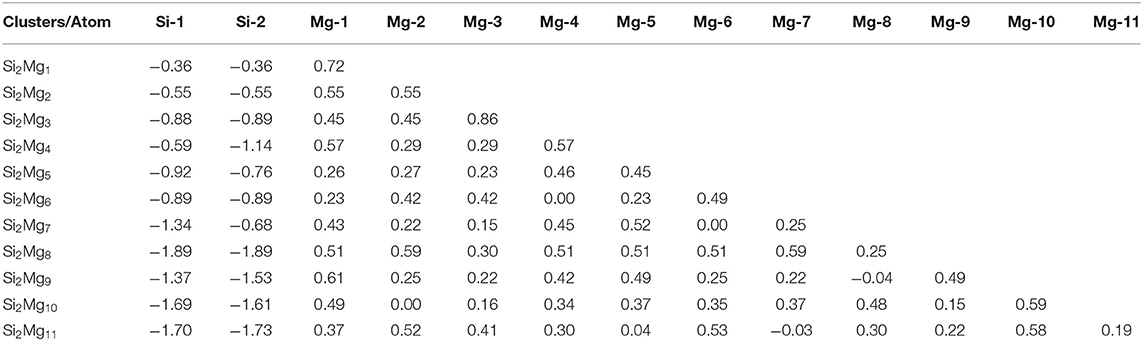
Table 3. NCP of the lowest-energy structures for neutral SiMg_n (n = 1–11) clusters of silicon-magnesium sensor material.

TABLE 4

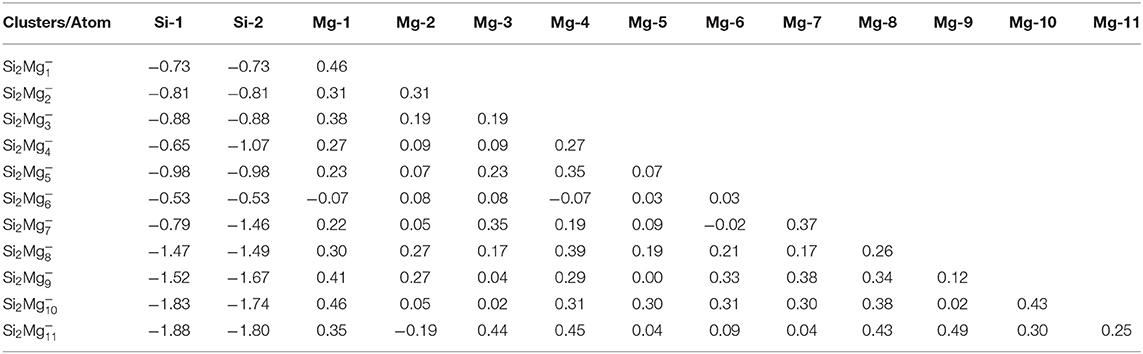
Table 4. NCP of the lowest-energy structures for anionic Si₂${\text{Mg}}_{\text{n}}^{-1}$ (n = 1–11) clusters of silicon-magnesium sensor material.

TABLE 5

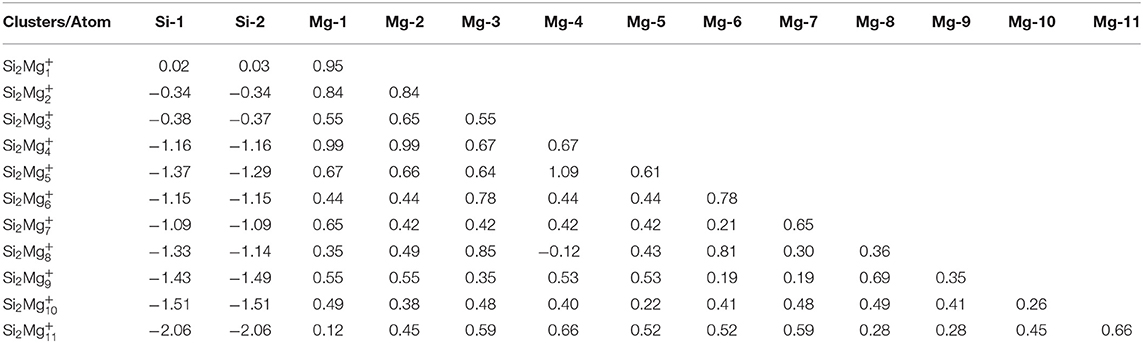
Table 5. NCP of the lowest-energy structures for cationic Si₂${\text{Mg}}_n^{+1}$ (n = 1–11) clusters of silicon-magnesium sensor material.

TABLE 6

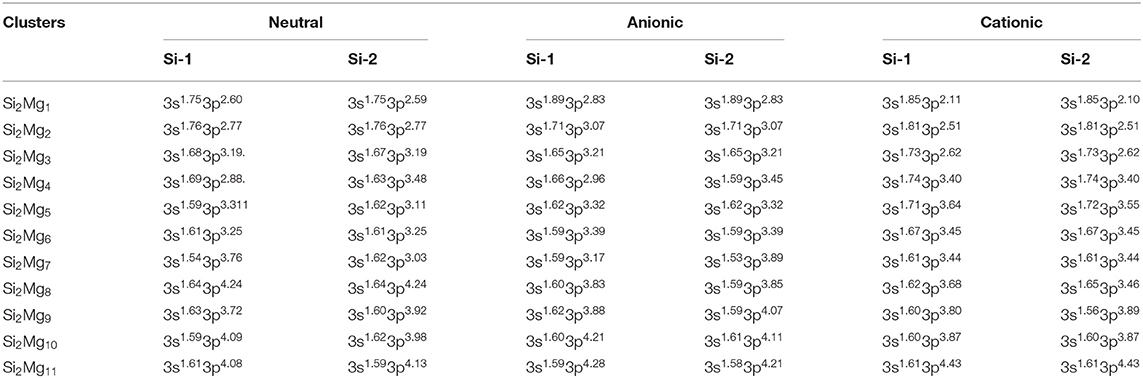
Table 6. NEC of the lowest-energy structures for neutral and charged Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$(n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material.

Ionization Potential and Electron Affinity of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$(n = 1–11; Q = 0, ±1) Clusters of Silicon-Magnesium Sensor Material

Adiabatic ionization potential (AIP), vertical ionization potential (VIP), adiabatic electron affinity (AEA), and vertical electron affinity (VEA) are important characteristics of the electronic properties for clusters. On the basis of optimizing the structure, AIP, VIP, AEA, and VEA are calculated and listed in the Table 7 with the following formulas (Deka et al., 2014):

$\begin{array}{ll}AIP=E_{\text{(optimized cation)}}-E_{(\text{optimized neutral})}& (6)\end{array}$

$\begin{array}{ll}VIP=E_{\text{(cation at optimized neutral geometry)}}-E_{(\text{optimized neutral})}& (7)\end{array}$

$\begin{array}{ll}AEA=E_{(\text{optimized neutral})}-E_{\text{(optimized anion)}}& (8)\end{array}$

$\begin{array}{ll}VEA=E_{(\text{optimized neutral})}-E_{\text{(anion at optimized neutral geometry)}}& (9)\end{array}$

It should be pointed out that the properties of neutral clusters are related to the values of VIP and VEA, while the properties of anionic and cationic clusters are related to AEA and AIP. Figures 5A,B show the size dependence of the AIP, VIP, AEA, and VEA. As Figure 5A showed, the curves of AIP and VIP have the same tendencies as the cluster size increases except n = 3, 8, 10. This result means that most cations are similar to the corresponding neutrals. In addition, from the Table 7, we can find that except for n = 3, 4, 7, 9, 10, the |AIP-VIP| values are in the range of 0.07–0.29 eV, which implies that the deformation of these structures corresponding to their neutral clusters are not big. The relation between AEA and VEA is showed in the Figure 5B, one can find that they also have the same tendencies and the |AEA-VEA| values are all small except for n = 1, 2, 5, 6, and 8, which means that these structures of Si₂${\text{Mg}}_{\text{n}}^{-1}$ clusters do not differ greatly from the corresponding Si₂Mg_n clusters. In addition, as one knows that |VIP-VEA| can present the chemical hardness and is always used to characterize the stability of clusters (Pearson, 1997). Table 7 also shows the hardness of Si₂Mg_n (n = 1–11) clusters, and one can find that the hardness of Si₂Mg_n clusters decreases with the increase of magnesium atoms. It is noteworthy that when n = 6, the hardness of the corresponding clusters is obviously larger than that of the adjacent clusters, which indicates that the stability of Si₂Mg₆ is higher. This conclusion is consistent with that of the Δ₂E in Figure 4.

FIGURE 5

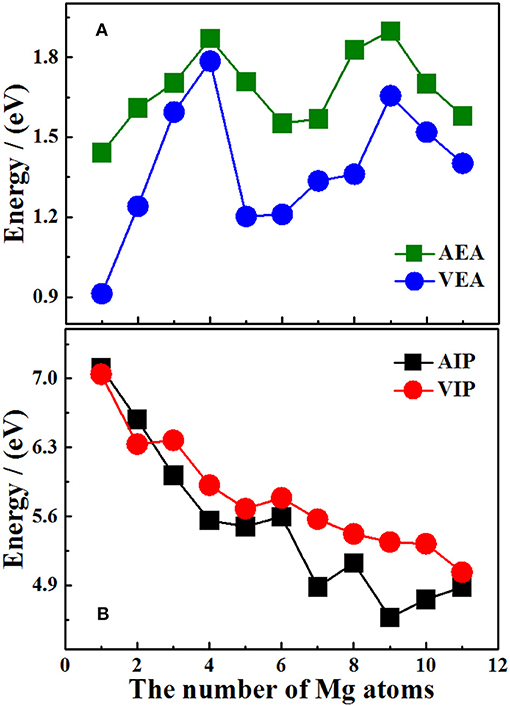
Figure 5. Size dependence of AIP, VIP, AEA, and VEA of ground state Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material. (A) Size dependent properties of AEA and VEA of the ground state of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (Q = 0, ±1; n = 1–11) clusters. (B) Size dependent properties of AIP and VIP of the ground state of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$(Q = 0, ±1; n = 1–11) clusters.

TABLE 7

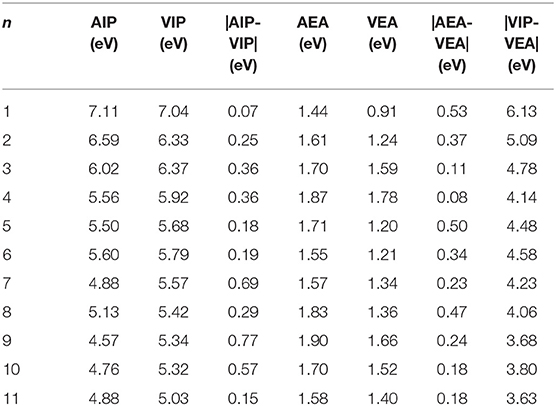
Table 7. AIP, VIP, AEA, VEA of ground state Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium sensor material.

Infrared and Raman Spectra of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$(n = 1–11; Q = 0, ±1) Clusters of Silicon-Magnesium Sensor Material

In order to further determine the stability of silicon-magnesium semiconductor sensor material, we calculate the infrared and Raman spectra of ground state of pure Mg_n+2 and all Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters at B3LYP/6-311G (d) level, and present them in Figures 6–9. Figure 6 presents the infrared spectra of the lowest energy structure of Mg_n+2 (n = 1–11) and Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–5; Q = 0, ±1) clusters. It is necessary to point out that the vibration spectra (intensity ratio, line width, wave number, and location) are related to the calculation methods and basis groups. For example, the IR spectra of Mg₂₋₃₁ clusters are calculated and showed by two different basis sets under B3PW1 function (Belyaev et al., 2016), but the overall trend of the spectra is similar. By our calculation, the main absorption bands of Mg_n+2 clusters (n = 1–11) are located at 60–230 cm⁻¹, which is similar as the results of the existing report (Belyaev et al., 2016). From Figures 6, 7, one can find that the IR strong peaks frequencies are in the range of 40–500 cm⁻¹ for neutral Si₂${\text{Mg}}_{\text{n}}^0$ clusters, 80–460 cm⁻¹ for anionic Si₂${\text{Mg}}_{\text{n}}^{-1}$ clusters and 30–540 cm⁻¹. In small size (n ≤ 5) clusters, the IR strong vibration spectra of neutral, anionic and cationic Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$(n = 1–11; Q = 0, ±1) clusters are easily distinguished from each other. While, in large size (n = 6–11) clusters, the frequency of IR strong vibration spectra of these clusters is relatively close from mid-frequency to the high-frequency region. As we know that the electron-absorbing base moves the infrared absorption peak to the high frequency region, and the electron-supplying base moves the infrared absorption peak to the low frequency region. In addition, the tension property of materials shows that the larger the tension of structures, the higher the infrared absorption frequency. Therefore, we can find that two interesting conclusions from Figures 6, 7. (i) The electron-absorbing base structure of neutral cluster materials is stronger than that of charged clusters, and this trend decreases with the increase of the number of magnesium atoms. (ii) With the increase of magnesium atoms around silicon atoms, the peak infrared absorption frequency shifts from relative high frequency to relative low frequency. This indicates that the tension properties of cluster materials with high Mg atoms are not good. The vibration modes of IR spectra of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$(n = 1–11; Q = 0, ±1) clusters are very numerous and complex, and as the results discussed above show that magic number clusters of Si₂${\text{Mg}}_3^0$, Si₂${\text{Mg}}_3^{-1}$, Si₂${\text{Mg}}_3^{+1}$ are more stable than other clusters. Therefore, here we only focus on these three clusters' vibration modes. As Figure 6 showed, the highest intensity IR frequency of neutral Si₂${\text{Mg}}_3^0$ locates at 425.28 cm⁻¹, and its vibration mode is assigned as stretching of Si2-Si1 bond. The frequency of the strongest peak of anionic Si₂${\text{Mg}}_3^{-1}$ cluster at 465.87 cm⁻¹, and its vibrational mode is as the same as the highest peak of neutral Si₂${\text{Mg}}_3^0$. The strong peaks of IR spectra of cationic Si₂${\text{Mg}}_3^{+1}$ cluster at 516.55 cm⁻¹ resulted from the stretching of Si2-Si1 bond.

FIGURE 6

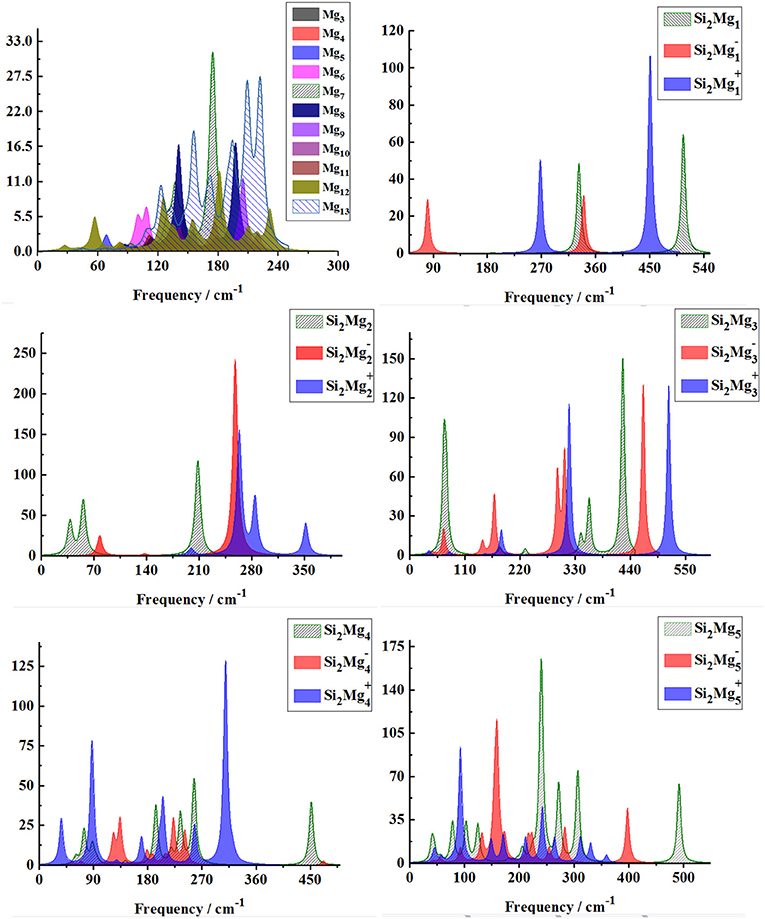
Figure 6. Infrared spectra of the lowest-energy structure of Mg_n+2 clusters (n = 1–11) and Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–5; Q = 0, ±1) clusters of silicon-magnesium sensor material calculated at B3LYP/6-311G (d) level. Horizontal axes is wave number; vertical axes is IR intensity, km/mol.

FIGURE 7

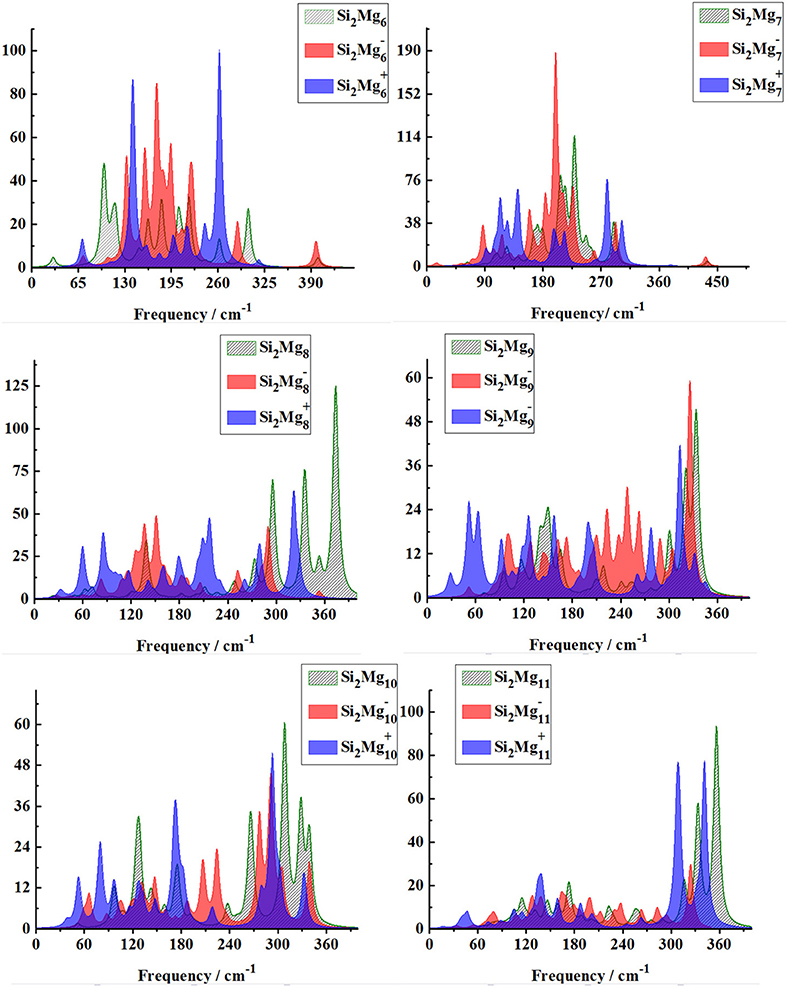
Figure 7. Infrared spectra of the lowest-energy structure of Si2${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 6–11; Q = 0, ±1) clusters of silicon-magnesium sensor material calculated at B3LYP/6-311G (d) level. Horizontal axes is wave number; vertical axes is IR intensity, km/mol.

From Figures 8, 9, one can find Raman spectra of Mg_n+2 and Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters. Raman spectra activity of Mg_n+2 (n = 1–11) clusters show a fairly low frequency (in the range of 25–180 cm⁻¹) nature except for Mg₃. Raman spectra activity properties of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters are rather different from their IR absorption properties. In small size clusters (n = 1–3), the Raman activity of cationic Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ clusters is fairly high in Mid-frequency and high-frequency regions. When n = 4, 5, the Raman activity of the clusters is widely distributed, and it is easy to distinguish them from each other. However, after n > 5, the Raman activity of the clusters begin to shift slowly from the high-frequency region to the mid-frequency region and close to each other. The Raman activity frequency of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (Q = 0, ±1) clusters are 50–480 cm⁻¹ for neutral Si₂${\text{Mg}}_{\text{n}}^0$, 40–480 cm⁻¹ for anionic Si₂${\text{Mg}}_{\text{n}}^{-1}$ and 40–450 cm⁻¹, respectively. When studying the vibration information of Raman spectra with specific magic number structure, we can find that the maximum Raman activity of neutral Si₂${\text{Mg}}_3^0$ cluster at the frequency of 179.66 cm⁻¹ with the stretching of Mg3-Mg4 bond, the frequency of the highest peak of anionic Si₂${\text{Mg}}_3^{-1}$ cluster at 308.76 cm⁻¹ is assigned as stretching of Si1-Mg3 and Si2-Mg3 bonds and the highest Raman activity frequency peak of cationic Si₂${\text{Mg}}_3^{+1}$ cluster at 182.25 cm⁻¹ vibrated as stretching of Si1-Mg4, Si2-Mg4 bonds.

FIGURE 8

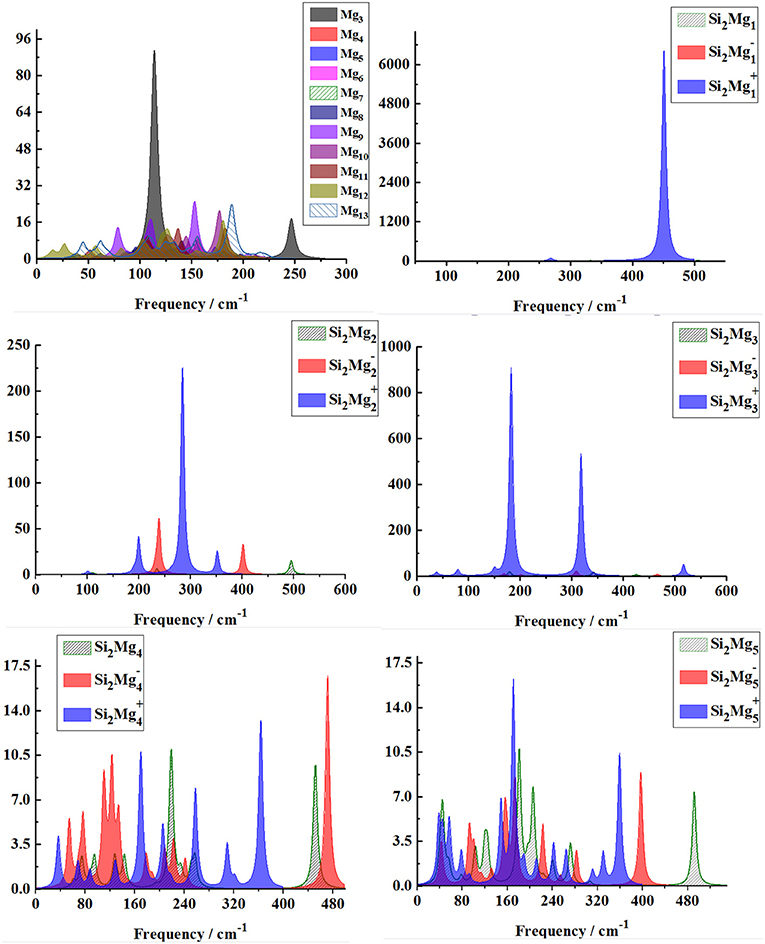
Figure 8. Raman spectra of the lowest-energy structure of Mg_n+2 clusters (n = 1–11) and Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–5; Q = 0, ±1) clusters of silicon-magnesium sensor material calculated at B3LYP/6-311G (d) level. Horizontal axes is wave number; vertical axes is Raman activity, A⁴/AMU.

FIGURE 9

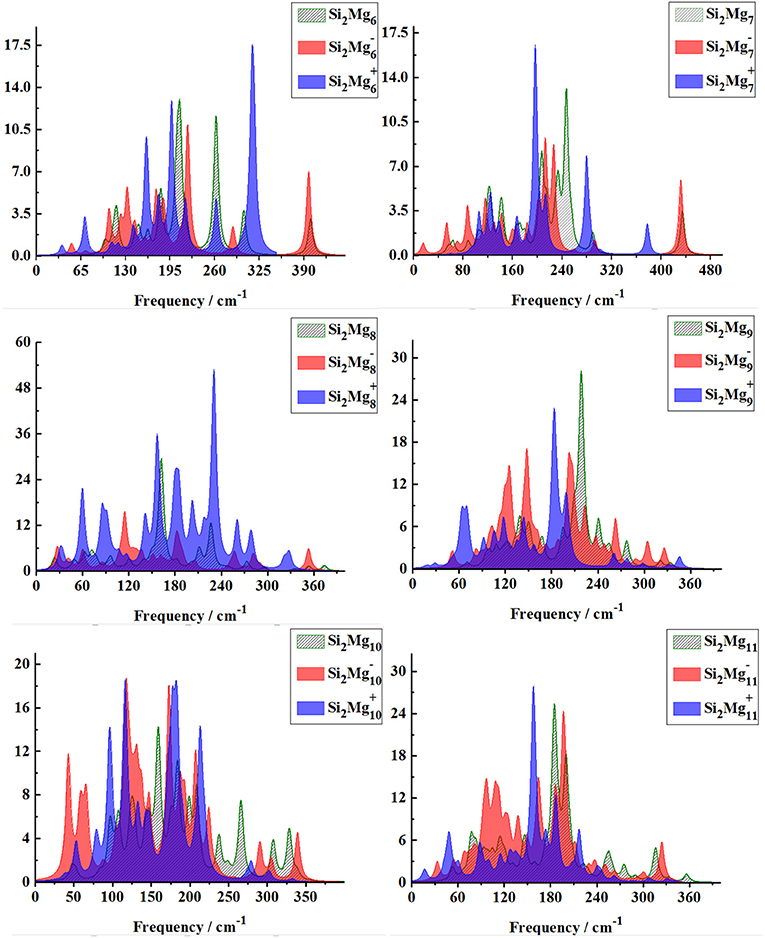
Figure 9. Raman spectra of the lowest-energy structure of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 6–11; Q = 0, ±1) clusters of silicon-magnesium sensor material calculated at B3LYP/6-311G (d) level. Horizontal axes is wave number; vertical axes is Raman activity, A⁴/AMU.

Conclusion

The structural, stability, electronic structure and spectral properties of silicon-magnesium semiconductor sensor materials are systematically studied by Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters in this paper. By using the CALYPSO searching method and B3LYP at 6-311G (d) basis set of DFT, the results can be summarized below:

(i) The results of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters' structure of silicon-magnesium semiconductor sensor material reveal that only a few of the lowest-energy anionic and cationic geometries are similar as their corresponding neutral ones, most of them are deformation. This conclusion is in good agreement with the changes of their AIP, VIP, AEA, and VEA. |VIP-VEA| values reveal that the hardness of Si₂Mg_n clusters decreases with the increase of magnesium atoms.

(ii) For the stability of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium semiconductor sensor materials, the average bonding energy of neutral Si₂${\text{Mg}}_{\text{n}}^0$ clusters are always smaller than the anionic and cationic ones show that attachment or detachment of one electron can enhance chemical stabilities of Si₂${\text{Mg}}_{\text{n}}^0$ clusters. Based on the calculations of E_b, E_f, Δ₂E, and E_gap, we find that Si₂${\text{Mg}}_3^0$, Si₂${\text{Mg}}_3^{-1}$, Si₂${\text{Mg}}_3^{+1}$, clusters have stronger stabilities than other clusters.

(iii) The cluster electronic structure of silicon-magnesium semiconductor sensor materials is analyzed. The results of NCP and NEC show that the charges in Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters transfer from Mg atoms to Si atoms, and the sp hybridization is existed in Si atoms in the clusters.

(iv) The infrared (IR) and Raman spectra of Si₂${\text{Mg}}_{\text{n}}^{\text{Q}}$ (n = 1–11; Q = 0, ±1) clusters of silicon-magnesium semiconductor sensor materials show different properties. Both IR and Raman spectra can be easily distinguished each other in small size clusters, however, in large clusters, IR spectra converge and concentrate at high frequencies, while Raman spectra converge and concentrate at mid-frequency region.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work was partly supported by the Cultivating Project for Young Scholar at Hubei University of Medicine (No. 2013QDJZR03), partly supported by the Basic Science and Preface Technology Project of Chongqing (cstc2017jcyjAX0315). The project of Fundamental Research Funds for the Central Universities (No. 2019CDYGYB011).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Atanassov, A., and Baleva, M. (2007). On the band diagram of Mg₂Si/Si heterojunction as deduced from optical constants dispersions. Thin Solid Films 515, 3046–3051. doi: 10.1016/j.tsf.2006.08.015

CrossRef Full Text | Google Scholar

Aymerich, F., and Mula, G. (2010). Pseudopotential band structures of Mg₂Si, Mg₂Ge, Mg₂Sn, and of the solid solution Mg₂(Ge, Sn). Phys. Status Solidi 42, 697–704. doi: 10.1002/pssb.19700420224

CrossRef Full Text | Google Scholar

Belyaev, S. N., Panteleev, S. V., Ignatov, S. K., and Razuvaev, A. G. (2016). Structural, electronic, thermodynamic and spectral properties of Mg_n (n = 2-31) clusters. A DFT study. Comput. Theor. Chem. 1079, 34–46. doi: 10.1016/j.comptc.2016.01.011

CrossRef Full Text | Google Scholar

Boher, P., Houdy, P., Kühne, M., Müller, P., Barchewitz, R., Delaboudiniere, J. P., et al. (1992). Tungsten/magnesium silicide multilayers for soft x-ray optics. J. Xray. Sci. Technol. 3, 118–132. doi: 10.1016/0895-3996(92)90004-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Bole, C., Weiguo, S., Xiao-Yu, K., Cheng, L., Xinxin, X., Hongxiao, S., et al. (2018). Structural stability and evolution of medium-sized tantalum-doped boron clusters: a half-sandwich-structured tab12– cluster. Inorg. Chem. 57, 343–350. doi: 10.1021/acs.inorgchem.7b02585

CrossRef Full Text | Google Scholar

Chen, Q., Xie, Q., Zhao, F., Cui, D., and Li, X. (2010). First-principles calculations of electronic structure and optical properties of strained Mg₂Si. Chin. Sci. Bull. 55, 2236–2242. doi: 10.1007/s11434-010-3280-7

CrossRef Full Text | Google Scholar

de Heer, W. A., Knight, W. D., Chou, M. Y., and Cohen, M. L. (1987). Electronic shell structure and metal clusters. Solid State Phys. 40. 93–181. doi: 10.1016/S0081-1947(08)60691-8

CrossRef Full Text | Google Scholar

Deka, R. C., Bhattacharjee, D., Chakrabartty, A. K., and Mishra, B. K. (2014). Catalytic oxidation of NO by ${\text{Au}}_2^{-}$ dimers: a DFT study. RSC Adv. 4, 5399–5404. doi: 10.1039/c3ra42240b

CrossRef Full Text | Google Scholar

Dmytruk, A., Dmitruk, I., Blonskyy, I., Belosludov, R., Kawazoe, Y., and Kasuya, A. (2009). ZnO clusters: laser ablation production and time-of-flight mass spectroscopic study. Microelectron. J. 40, 218–220. doi: 10.1016/j.mejo.2008.07.010

CrossRef Full Text | Google Scholar

Frisch, M., Trucks, G., Schlegel, H., Scuseria, G., Robb, M., Cheeseman, J., et al. (2014). Gaussian 09. Wallingford, CT: Gaussian, Inc., 481.

Huber, K. P. (1979). “Constants of diatomic molecules,” in Molecular Spectra and Molecular Structure.

Google Scholar

Imai, Y., Watanabe, A., and Mukaida, M. (2003). Electronic structures of semiconducting alkaline-earth metal silicides. J. Alloys Comp. 358, 257–263. doi: 10.1016/S0925-8388(03)00037-9

CrossRef Full Text | Google Scholar

Jin, Y., Maroulis, G., Kuang, X., Ding, L., Lu, C., Wang, J., et al. (2015a). Geometries, stabilities and fragmental channels of neutral and charged sulfur clusters: Sn(q) (n = 3-20, q = 0, ±1). Phys. Chem. Chem. Phys. 17, 13590–13597. doi: 10.1039/C5CP00728C

CrossRef Full Text | Google Scholar

Jin, Y., Tian, Y., Kuang, X., Zhang, C., Lu, C., Wang, J., et al. (2015b). Ab initio search for global minimum structures of pure and boron doped silver clusters. J. Phys. Chem. A 119, 6738–6745. doi: 10.1021/acs.jpca.5b03542

PubMed Abstract | CrossRef Full Text | Google Scholar

Ju, M., Lv, J., Kuang, X. Y., Ding, L. P., Lu, C., Wang, J. J., et al. (2015). Systematic theoretical investigation of geometries, stabilities and magnetic properties of iron oxide clusters (FeO) n μ (n = 1–8, μ = 0, ±1): insights and perspectives. RSC Adv. 5, 6560–6570. doi: 10.1039/C4RA12259C

CrossRef Full Text | Google Scholar

Kitsopoulos, A., Chick, C. J., Zhao, Y., and Neumark, D. M. (1991). Study of the low-lying electronic states of Si₂ and ${\text{Si}}_2^{-}$ using negative ion photodetachment techniques. J. Chem. Phys. 95, 1441–1448. doi: 10.1063/1.461057

CrossRef Full Text | Google Scholar

Lu, C., and Chen, C. (2018). High-pressure evolution of crystal bonding structures and properties of feooh. J. Phys. Chem. Lett. 9, 2181–2185. doi: 10.1021/acs.jpclett.8b00947

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, C., Li, Q., Ma, Y., and Chen, C. (2017). Extraordinary indentation strain stiffening produces superhard tungsten nitrides. Phys. Rev. Lett. 119:115503. doi: 10.1103/PhysRevLett.119.115503

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, C., Maximilian, A., and Changfeng, C. (2018). Unraveling the structure and bonding evolution of the newly discovered iron oxide FeO₂. Phys. Rev. B 98:054102. doi: 10.1103/PhysRevB.98.054102

CrossRef Full Text | Google Scholar

Lu, C., Miao, M., and Ma, Y. (2013). Structural evolution of carbon dioxide under high pressure. J. Am. Chem. Soc. 135, 14167–14171. doi: 10.1021/ja404854x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lv, J., Wang, Y., Zhu, L., and Ma, Y. (2012). Particle-swarm structure prediction on clusters. J. Chem. Phys. 137:084104. doi: 10.1063/1.4746757

PubMed Abstract | CrossRef Full Text | Google Scholar

Morris, R. G., Redin, R. D., and Danielson, G. C. (1958). Semiconducting properties of Mg₂Si single crystals. Phys. Rev. B 109:1916. doi: 10.1103/PhysRev.109.1909

CrossRef Full Text | Google Scholar

Pearson, R. G. (1997). Chemical Hardness - Applications From Molecules to Solids. Weinheim: Wiley-VCH), 198.

Ruette, F., Sánchez, M., Anez, R., Bermúdez, A., and Sierraalta, A. (2005). Diatomic molecule data for parametric methods. I. J. Mol. Struct. THEOCHEM 729, 19–37. doi: 10.1016/j.theochem.2005.04.024

CrossRef Full Text | Google Scholar

Song, S. W., Striebel, K., and Cairns, E. (2003). Electrochemical studies of the Mg₂Si thin films prepared with pulsed laser deposition. J. Electrochem. Soc. 153, A12–A19. doi: 10.1149/1.1527937

CrossRef Full Text | Google Scholar

Sun, W., Xia, X., Lu, C., Kuang, X., and Hermann, A. (2018). Probing the structural and electronic properties of zirconium doped boron clusters: Zr distorted B 12 ligand framework. Phys. Chem. Chem. Phys. 20, 23740–23746. doi: 10.1039/C8CP03384F

CrossRef Full Text | Google Scholar

Sun, W. G., Wang, J. J., Lu, C., Xia, X. X., Kuang, X. Y., and Hermann, A. (2017). Evolution of the structural and electronic properties of medium-sized sodium clusters: a honeycomb-like na\r, 20\r, cluster. Inorg. Chem. 56, 1241–1248. doi: 10.1021/acs.inorgchem.6b02340

CrossRef Full Text | Google Scholar

Trivedi, R., Dhaka, K., and Bandyopadhyay, D. (2014). Study of electronic properties, stabilities and magnetic quenching of molybdenum-doped germanium clusters: a density functional investigation. RSC Adv. 4, 64825–64834. doi: 10.1039/C4RA11825A

CrossRef Full Text | Google Scholar

Wang, Y., Lv, J., Zhu, L., and Ma, Y. (2010). Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82:094116. doi: 10.1103/PhysRevB.82.094116

CrossRef Full Text | Google Scholar

Wang, Y., Lv, J., Zhu, L., and Ma, Y. (2012). CALYPSO: a method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070. doi: 10.1016/j.cpc.2012.05.008

CrossRef Full Text | Google Scholar

Wittmer, M., Lüthy, W., and Allmen, M. V. (1979). Laser induced reaction of magnesium with silicon. Phys. Lett. A 75, 127–130. doi: 10.1016/0375-9601(79)90300-1

CrossRef Full Text | Google Scholar

Xia, X. X., Hermann, A., Kuang, X. Y., Jin, Y. Y., Lu, C., and Xing, X. D. (2015). Study of the structural and electronic properties of neutral and charged niobium-doped silicon clusters: niobium encapsulated in silicon cages. J. Phys. Chem. C 120, 677–684. doi: 10.1021/acs.jpcc.5b09453

CrossRef Full Text | Google Scholar

Xiao, T., Weiguo, S., Yuantong, G., Lu, C., Liangzhi, K., and Changfeng, C. (2019). CoB₆ monolayer: a robust two-dimensional ferromagnet. Phys. Rev. B 99:045445. doi: 10.1103/PhysRevB.99.045445

CrossRef Full Text | Google Scholar

Xing, X., Hermann, A., Kuang, X., Ju, M., Lu, C., Jin, Y., et al. (2016a). Insights into the geometries, electronic and magnetic properties of neutral and charged palladium clusters. Sci. Rep. 6:19656. doi: 10.1038/srep19656

PubMed Abstract | CrossRef Full Text | Google Scholar

Xing, X., Wang, J., Kuang, X., Xia, X., Lu, C., and Maroulis, G. (2016b). Probing the low-energy structures of aluminum–magnesium alloy clusters: a detailed study. Phys. Chem. Chem. Phys. 18, 26177–26183. doi: 10.1039/C6CP05571K

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, J., Li, B., and Zhan, S. (2006). Study of gaas cluster ions using fp-lmto md method. Phys. Lett. A 348, 416–423. doi: 10.1016/j.physleta.2005.08.071

CrossRef Full Text | Google Scholar

Zhang, S., Zhang, Y., Yang, X., Lu, C., Li, G., and Lu, Z. (2015). Systematic theoretical investigation of structures, stabilities, and electronic properties of rhodium-doped silicon clusters: Rh 2 Si n q (n = 1–10; q = 0, ±1). J. Mater. Sci. 50, 6180–6196. doi: 10.1007/s10853-015-9175-x

CrossRef Full Text | Google Scholar