
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Chem. , 03 April 2019
Sec. Inorganic Chemistry
Volume 7 - 2019 | https://doi.org/10.3389/fchem.2019.00197
This article is part of the Research Topic Inorganic Chemistry Editor’s Pick 2021 View all 20 articles
 Yaqi Ji1,2
Yaqi Ji1,2 Piotr M. Kowalski1,2*
Piotr M. Kowalski1,2* Philip Kegler1,2
Philip Kegler1,2 Nina Huittinen3
Nina Huittinen3 Nigel A. Marks4
Nigel A. Marks4 Victor L. Vinograd1,2
Victor L. Vinograd1,2 Yulia Arinicheva1,2,5
Yulia Arinicheva1,2,5 Stefan Neumeier1,2
Stefan Neumeier1,2 Dirk Bosbach1,2
Dirk Bosbach1,2Lanthanide phosphates (LnPO4) are considered as a potential nuclear waste form for immobilization of Pu and minor actinides (Np, Am, and Cm). In that respect, in the recent years we have applied advanced atomistic simulation methods to investigate various properties of these materials on the atomic scale. In particular, we computed several structural, thermochemical, thermodynamic and radiation damage related parameters. From a theoretical point of view, these materials turn out to be excellent systems for testing quantum mechanics-based computational methods for strongly correlated electronic systems. On the other hand, by conducting joint atomistic modeling and experimental research, we have been able to obtain enhanced understanding of the properties of lanthanide phosphates. Here we discuss joint initiatives directed at understanding the thermodynamically driven long-term performance of these materials, including long-term stability of solid solutions with actinides and studies of structural incorporation of f elements into these materials. In particular, we discuss the maximum load of Pu into the lanthanide-phosphate monazites. We also address the importance of our results for applications of lanthanide-phosphates beyond nuclear waste applications, in particular the monazite-xenotime systems in geothermometry. For this we have derived a state-of-the-art model of monazite-xenotime solubilities. Last but not least, we discuss the advantage of usage of atomistic simulations and the modern computational facilities for understanding of behavior of nuclear waste-related materials.
Lanthanide phosphates (LnPO4) are ceramic materials of interest in various research fields, including geochronology (Williams et al., 2007), geothermometry (Andrehs and Heinrich, 1998; Mogilevsky, 2007), and nuclear waste management (Ewing and Wang, 2002; Neumeier et al., 2017a; Schlenz et al., 2017). Occurring in nature, these are also important ores for thorium, lanthanum, and cerium (McGill, 2000; Stoll, 2000). Most of the potential applications come from high durability and radiation damage resistance of these materials (Neumeier et al., 2017a). There exist large varieties of phosphate-based ceramics of different crystalline structures [e.g., cheralite, apatites, kosnarite, see Neumeier et al. (2017a)], but anhydrous lanthanide orthophosphates form two structures called monazite and xenotime. Anhydrous lanthanide orthophosphates crystallize in the monazite form with the P22/n space group for light lanthanides, from La to Gd. In this structure, Ln cations are 9-fold coordinated. For heavier lanthanides, from Tb to Lu, LnPO4 compounds adopt a zircon type tetragonal structure called xenotime which has I41/amd symmetry and 8-fold coordinated Ln cations. Both these materials are considered in nuclear waste management as potential immobilization matrices for minor actinides and plutonium because of enhanced radiation damage resistance and durability of these materials (Ewing and Wang, 2002; Clavier et al., 2011; Schlenz et al., 2013, 2017; Neumeier et al., 2017a; Seydoux-Guillaume et al., 2018). Their natural analogues can contain significant amounts of actinides [up to ~50%wt of Th and U, see Stoll (2000); Ewing and Wang (2002); Lumpkin and Geisler-Wierwille (2012)] and still preserve their crystalline structure over geological time scales (Ewing and Wang, 2002). The aim is a potential usage of these materials as an immobilization matrix for radionuclides, such as the already mentioned Pu and minor actinides. The immobilization of Pu could reduce the proliferation risk associated with large stockpiles of weapons grade plutonium (Ewing, 1999; Macfarlane, 1999).
In the last two decades, atomistic modeling became a very popular research tool in various research fields, including nuclear materials (Chroneos et al., 2013). This is because steady advancements in supercomputing facilities and computational software, especially ab initio methods, allows nowadays for simulation and investigation of systems containing hundreds of atoms using first principle simulation methods (Jahn and Kowalski, 2014). Monazite became a topic of atomistic simulations effort in the last decade. Computational studies have been used to deliver information on: the structural (Rustad, 2012; Feng et al., 2013; Blanca-Romero et al., 2014; Beridze et al., 2016; Huittinen et al., 2017), the elastic (Wang et al., 2005; Feng et al., 2013; Ali et al., 2016; Kowalski and Li, 2016; Ji et al., 2017a; Kowalski et al., 2017b), the thermodynamic (Mogilevsky, 2007; Feng et al., 2013; Li et al., 2014; Kowalski et al., 2015, 2016; Ji et al., 2017b; Neumeier et al., 2017b; Eremin et al., 2019), the thermochemical (Rustad, 2012; Beridze et al., 2016), the radiation damage resistance (Kowalski et al., 2016; Li et al., 2016; Ji et al., 2017c; Jolley et al., 2017) parameters, the electronic structure (Blanca-Romero et al., 2014; Kowalski et al., 2017a) as well as high-pressure behavior (López-Solano et al., 2010; Stavrou et al., 2012; Ali et al., 2016; Shein and Shalaeva, 2016; Gomis et al., 2017). There is a steadily increasing relevant simulation effort with most of the papers published just recently.
In this contribution we provide an overview of the recent atomistic modeling activities on the lanthanide-phosphates, focusing on the information that have been delivered by atomistic modeling activities at Forschungszentrum Jülich and that allowed for better characterization of these materials, including long-term thermodynamic stability in the context of using them as a nuclear waste form. Besides this overview, we present results of computation of thermochemical parameters of La1-xPuxPO4 solid solution and the first ab initio-based evaluation of the relative solubilities in the monazite-xenotime system. These studies aim at the assessment of the maximum Pu load in LaPO4 and the long-term thermodynamic stability of such solid solution. The results of our studies are not limited to the field of nuclear waste management and in a general science aspect could be used to improve computational methods (Blanca-Romero et al., 2014) or the monazite-xenotime geothermometry (Mogilevsky, 2007). We especially highlight a cross-linking, interdisciplinary character of our research, from which the general science community could highly benefit.
In the ab initio1 investigation of the lanthanide phosphate systems we presented here we apply a density functional theory (DFT)-based quantum chemistry approach. For that purpose we utilize Quantum-ESPRESSO simulation package (Giannozzi et al., 2009). We apply the PBESol exchange-correlation functional (Perdew et al., 2008), the plane-wave energy cutoff of 50 Ryd and ultrasoft pseudopotentials to represent the core electrons of the atoms (Vanderbilt, 1990). Following our broad experience on computation of lanthanide phosphates (Blanca-Romero et al., 2014; Beridze et al., 2016) we apply two methods: (1) with 4f electrons included into the pseudopotential core and (2) with 4f electrons computed explicitly, which we use for DFT+U calculations. The DFT+U calculations were performed with the Hubbard U parameter values computed from first principles using the linear response method of Cococcioni and de Gironcoli (2005). These computational setups were extensively tested and proved to give very good results for monazite-xenotime systems (Blanca-Romero et al., 2014; Beridze et al., 2016).
Besides quantum chemistry methods, force-field-based molecular modeling has been also used in the investigation of lanthanide phosphates. In this approach, the interatomic interactions are described by an analytical function, for instance by the pair interaction potentials such as Buckingham type (Buckingham, 1938). The advantage of this method is that it allows for simulations of systems containing thousands and even millions of atoms, as opposite to more computationally intensive DFT-based methods, which is currently suitable for simulations of up to a few hundred atoms (Jahn and Kowalski, 2014). The force-field methods are used for the large scale simulations of processes such as radiation cascades (Ji et al., 2017c) or computationally intensive computation of statistical distributions, like different possibilities of incorporating doping elements (Huittinen et al., 2017, 2018). For that purpose, there has been some development in the force fields for lanthanide phosphates (Ji et al., 2017c; Jolley et al., 2017). Nevertheless, these methods do not guarantee to deliver information on the level of quantum-chemical methods. Interaction potentials are also not guaranteed to be transferable, even between the system of identical chemical composition like monazite and xenotime.
The first test of a computational method is its ability to reproduce the measured lattice parameters of the computed crystalline solid. The lattice parameters of lanthanide phosphates were measured by different studies and are known for all the Ln cations, except Pm (Ni et al., 1995; Clavier et al., 2011). These could be also accurately estimated from the values of ionic radii of Ln cations (Shannon, 1976; Ni et al., 1995). The first DFT-based computational studies of structural parameters of lanthanide phosphates were performed for LaPO4 monazite (Wang et al., 2005). In these studies the applied PW91 exchange-correlation functional (Perdew and Wang, 1992) resulted in slight overestimation of lattice parameters (by ~1% on average). Rustad (2012) used the PBE exchange-correlation functional (Perdew et al., 1996) to compute structural and thermochemical parameters of all lanthanide phosphates and obtained lattice parameters that are also ~1% too large. In similar, extensive studies of LnPO4 monazite compounds, Feng et al. (2013) applied local spin approximation, but obtained lattice parameters that are far smaller than the experimental values (up to 10% underestimation of volume). These studies show that the structural parameters of lanthanide-phosphates are very sensitive to the applied computational method, especially to the exchange-correlation functional. A correct treatment of strongly correlated 4f electrons also plays an important role here.
Blanca-Romero et al. (2014) performed extensive tests of the ability of different DFT-based approaches to reproduce the measured lattice parameters and bond-distances of monazite-type lanthanide-phosphates and the related lanthanide-oxides. In that paper, they found that the standard DFT method with explicitly computed 4f electrons overestimates the lattice parameters and bond-lengths by up to 3%, consistent with previous studies (Wang et al., 2005; Rustad, 2012). A very good match to the experimental values of structural parameters was obtained with the DFT+U method, in which the PBEsol exchange-correlation functional was applied (Perdew et al., 2008) and the Hubbard U parameters that represent the strength of the on-site Coulomb repulsion between 4f electrons (thus electronic correlations), were derived ab initio. In Figure 1 we present the Ln-O bond lengths computed with this method vs. the measured data for monazite and xenotime systems. The match is excellent and the key to get such a good result was to compute the Hubbard U parameters for each Ln case. As demonstrated in Figure 1, this parameter varies a lot for the different Ln cations (from ~3 to ~10eV). Having an improved description of structures using the PBEsol exchange-correlation functional is also expected, as by recovering the exact charge density limit for slowly varying densities, it improves the description of structural parameters over the widely used PBE functional [see discussion by Perdew et al. (2008)]. Another practice in computation of 4f elements is to include the 4f electrons into the pseudopotential core and to not compute them explicitly [as done, for instance, by Rustad (2012)]. This is due to the fact that these do not participate in the chemistry (bonding). Blanca-Romero et al. (2014) and Beridze et al. (2016) illustrated this for lanthanide phosphates. They found that such a “f in the core" approach results in the formation enthalpies (energies) that are consistent with the ones derived with the DFT+U method (see discussion in section 3.2). This method, although not that accurate for the structural parameters as the aforementioned DFT+U approach (Beridze et al., 2016), was shown to be accurate for prediction of the thermodynamic and elastic parameters of lanthanide phosphates, which is discussed in the following sections.
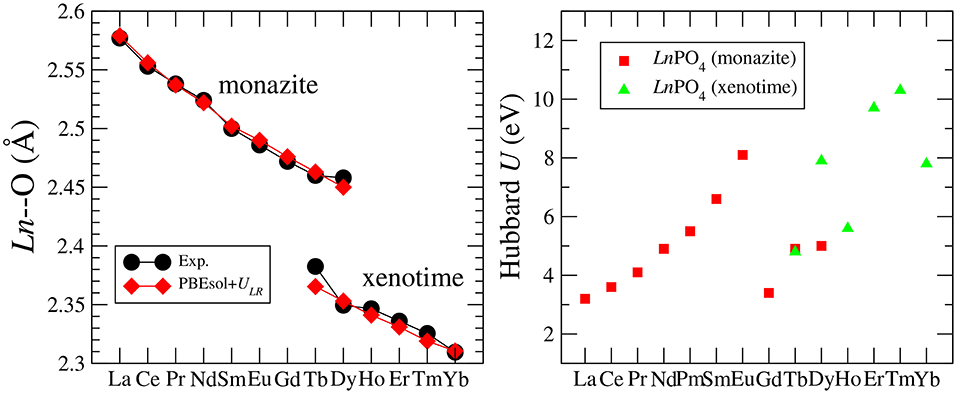
Figure 1. (Left) The measured and computed Ln-O bond-length in LnPO4 compounds. (Right) The Hubbard U parameter computed for LnPO4 compounds. The data come from Blanca-Romero et al. (2014) and Beridze et al. (2016).
The formation enthalpies of series of monazites and xenotimes have been measured by Ushakov et al. (2001). These were first computed at the DFT level by Rustad (2012). He noticed that there is a systematic offset between the computed and measured values of ~40kJ/mol, with the computed enthalpies being less exothermic. Blanca-Romero et al. (2014) have shown that this offset is present also in the DFT+U calculations and is to a large extent Ln-cation independent, which rules out the 4f electrons correlations as the underlying reason for it. They attributed this to the overestimation of P-O bond lengths, and thus volumes, of the LnPO4 and P2O5 compounds. Beridze et al. (2016) have found an identical offset for xenotimes. When a constant shift of ~30kJ/mol is applied to the computed formation enthalpies the measured values are nicely reproduced. The final result for series of LnPO4 compounds is given in Figure 2. The computed formation enthalpies reproduce well the experimental trend for most of the compounds. The only significant discrepancies are observed for GdPO4 and TbPO4, which however is crucial for the discussion of the relative solubilities provided in section 3.7.
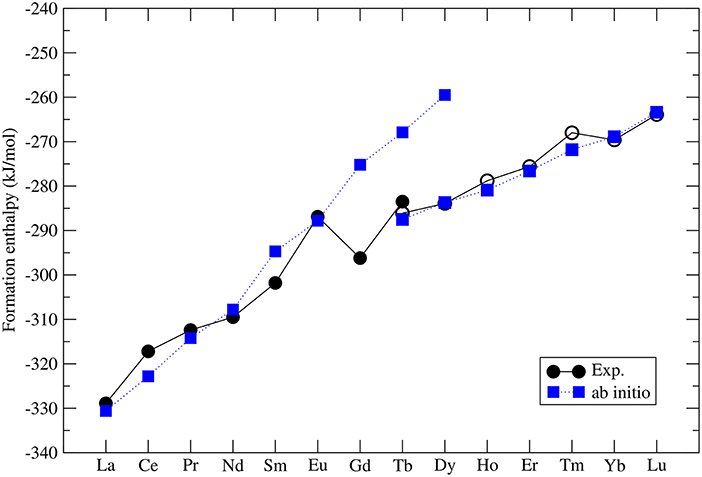
Figure 2. The computed (blue filled squares) and measured (black filled (monazite) and open (xenotime) circles) (Ushakov et al., 2001) formation enthalpy from oxides for LnPO4 compounds. The following Ln2O3 oxides were taken into account: A-type (La-Nd), B-type (Sm), and C-type (Eu-Lu). The data comes from Beridze et al. (2016).
The correct prediction of the formation enthalpies of monazite and xenotime phases is essential to properly model the relative solubilities in the monazite-xenotime system. Mogilevsky (2007) in his estimations used an extrapolation of the experimentally measured values for TbPO4 (Ushakov et al., 2001) - the only system for which formation enthalpies of both phases have been measured. Mogilevsky (2007) extrapolated these values by the following formula:
where Rtr is the ionic radius of a hypothetical ion located between Gd and Tb for which energies in the monazite and xenotime structures are identical, Rm, x is the ionic radius of Ln cations, which at normal conditions form monazite (m) or xenotime (x), respectively. He assumed that Rtr = 1.0516Å and derived Δhm, x which is the enthalpy difference between the standard phase and the other phase (e.g., for LaPO4 the enthalpy difference between monazite and xenotime phase of LaPO4). His result is given in Figure 3. In order to check these values we performed ab initio calculations of series of monazite and xenotimes counterparts of the existent phases. The advantage of atomistic simulations is that even non existing phases could be modeled (e.g., LaPO4 xenotime). The result is given in Figure 3. The computed Δhm−x is significantly different from the estimation of Mogilevsky (2007), with the differences for LaPO4 of ~20kJ/mol. We note that our ab initio data could be reproduced assuming Rtr = 1.507Å. Having a good match to the experimental values of the measured compounds (see Figure 2) there is no reason to believe that our prediction for the non-existing phases could be that much wrong. We thus assume that the values computed here are correct.
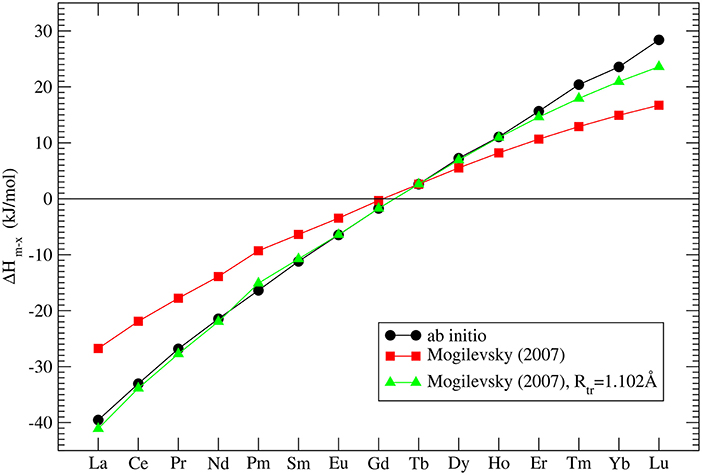
Figure 3. The computed enthalpy difference between monazite and xenotime LnPO4 compounds. The three data series represent our ab initio calculations (black filled circles), the model of Mogilevsky (2007) (red filled squares) and the model of Mogilevsky (2007) (Equations 1, 2) assuming the ionic radius of the 9-fold coordinated transition Ln cation is 1.102Å.
The elastic properties of lanthanide phosphates have been a topic of several experimental studies (Thomä et al., 1974; Harley and Manning, 1978; Nipko et al., 1996; Mogilevsky et al., 2006; Du et al., 2009; Thust et al., 2015). Also on the computational side these have been extensively investigated. Wang et al. (2005), Feng et al. (2013), and Kowalski and Li (2016) computed elastic constants and moduli for a series of monazites. We note that the later study gave the best match to the measured values. The key factor to obtain accurate results has been a good reproduction of structural parameters of the investigated materials. For instance, Kowalski and Li (2016) obtained volumes that are within 1% of the measured values, while in the earlier studies by Feng et al. (2013) the differences were as large as 10%. In the follow-up studies, Kowalski et al. (2017b) computed the variation of the Young's modulus along the La1-xEuxPO4 solid solution, which reproduced the experimental trend (Thust et al., 2015) and allowed for better interpretation of these data. Computational methods were also applied to study the pressure effect on the elastic moduli and the relevant elastic anisotropy (Ali et al., 2016; Gomis et al., 2017).
The computed elastic moduli were also used to derive some related thermodynamic parameters. Feng et al. (2013) and Ji et al. (2017b) used the Slack model (Slack, 1973), and derived thermal conductivities of monazite and xenotime compounds, respectively. According to Slack (1973) the thermal conductivity can be estimated as:
where A=3.12·10−8Wmolkg−1m−2K−3 is a constant, is the average atomic mass, δ3 is the average volume per atom in the system, ΘD is the Debye temperature, n is the number of atoms per primitive unit cell and γ is the acoustic Grüneisen parameter. Here, using the same approach as by Ji et al. (2017b) we computed the standard thermal conductivity of LaPO4. The obtained value of room temperature thermal conductivity of 4.0Wm−1K−1 is consistent with the measured value of 3.6Wm−1K−1 (Du et al., 2009) and the data computed by Feng et al. (2013). The data for LaPO4 (m) and LuPO4 (x) are reported in Table 1. Interestingly, both experiment and simulation show significant differences in the thermal conductivity of the monazite and xenotime phases. This comes mainly from the different number of atoms in the primitive cell of both phases, 12 for xenotime and 24 for monazite (see Equation 3).

Table 1. The thermal conductivity in (W m−1K−1) simulated and measured for LaPO4 (monazite) and LuPO4 (xenotime).
Mogilevsky (2007) used the Young's modulus to estimate the excess energy of mixing [the Margules interaction parameter (Prieto, 2009)] in monazite-xenotime solid solution systems. By a combination of fitting to the existing data on solubilities and so computed mixing energies he proposed an accurate model to describe the maximum solubilities and miscibility gap in the monazite-xenotime system. Kowalski and Li (2016) have shown that this Young's modulus-based approximation of elastic strain energy leads to a good description of the ab initio Margules interaction parameters. These issues will be discussed in details in sections 3.6 and 3.7. Nevertheless, Mogilevsky (2007) used an approximation for the variation of Young's modulus along lanthanide series. According to his derivation, for monazite compounds the Young's modulus decreases along the series, while the computation of Kowalski and Li (2016) and the aforementioned measurements show an increase (from 140GPa for La to ~160GPa for Gd). In Figure 4 we present the collection of measured and computed Young's moduli together with the Mogilevsky (2007) approximation. These results are important in the context of estimation of excess enthalpies of mixing and solubilities in the monazite-xenotime system (sections 3.6 and 3.7).
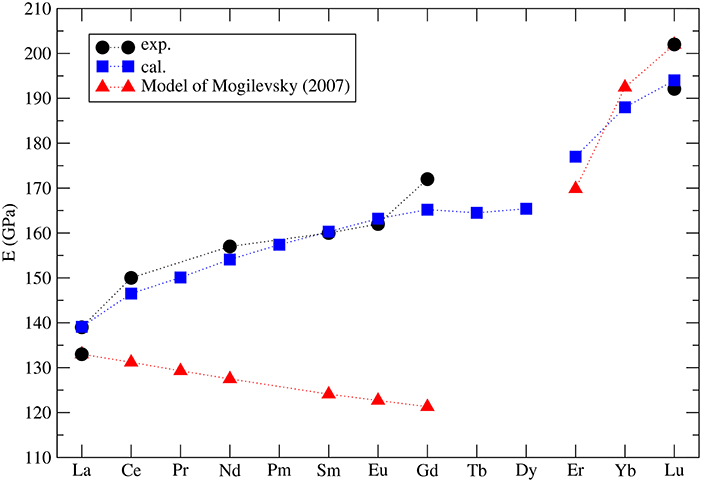
Figure 4. The computed (blue filled squares) (Kowalski and Li, 2016; Ji et al., 2017a) and measured (black filled circles) Young's modulus for selected lanthanide phospahtes monazites and xenotimes. Red triangles represent the model used by Mogilevsky (2007).
In the next section we will discuss that a careful selection of the computational method, which results in good description of the structural and elastic parameters, is also important to obtain good predictions for thermodynamic parameters such as the heat capacity and the thermal conductivity.
Besides the thermal conductivity, the heat capacity is the most widely investigated thermodynamic parameter of lanthanide phosphates. There is a series of experimental papers on measurements of this parameter for different monazite compositions (Thiriet et al., 2004, 2005a; Popa and Konings, 2006; Popa et al., 2006a,b; Gavrichev et al., 2008, 2009; Bauer et al., 2016), including Pu-rich compounds (Thiriet et al., 2005b; Popa et al., 2007a; Benes et al., 2011), and xenotime (Gavrichev et al., 2006, 2010, 2012, 2013; Nikiforova et al., 2012; Gysi et al., 2016). These measurements revealed a quasi-random-like variation of the standard heat capacity and the standard entropy along the lanthanide series. This is illustrated in Figure 5. For instance, the standard values are largest for EuPO4 and smallest for GdPO4 with no visible trend. The first systematic computational studies of Feng et al. (2013) were unable to match the experimental data and tried to explain these discrepancies by the large difference between computed constant volume (Cv) and measured (Cp) heat capacities. In order to shed the light on this variation, Kowalski et al. (2015) and Ji et al. (2017a) performed accurate ab initio calculations of the heat capacity of monazites and xenotimes, respectively. They accounted for two effects: (1) the lattice vibration and (2) the thermal excitation of 4f electrons, which had been known from experimental studies to significantly influence the heat capacity of monazites [e.g., Thiriet et al. (2005a,b)]. By doing so, Kowalski et al. (2015) were able to accurately reproduce the measured values for all the investigated cases. Using the same computational approach, Kowalski et al. (2017b) were able to explain the low temperature variation of heat capacity in the La1−xEuxPO4 monazite-type solid solution system (Thust et al., 2015). By applying a theoretically justified extrapolation, Kowalski et al. (2015) could also account for high temperature (T > 800K) anharmonic effects in monazites. We note however, that such a procedure was not that successful for xenotime phases, as here the anharmonic effects become important at a much lower temperature of ~400K (Ji et al., 2017a). Computational studies of the heat capacity of xenotime by Ji et al. (2017a) allowed also for the verification of the slightly conflicting experimental data sets published recently in the literature (Gavrichev et al., 2010, 2012, 2013; Gysi et al., 2016).
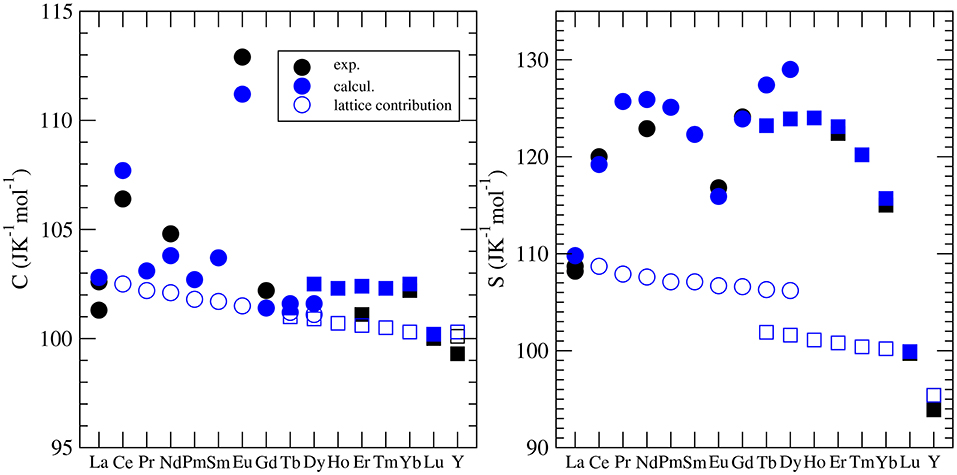
Figure 5. The variation of the standard heat capacity and standard entropy from LnPO4. The different symbols represent the computed Cv [filled blue cirlces (monazite) and squares (xenotime)] and measured (Cp) values [see Kowalski et al. (2015); Ji et al. (2017a)]. The open blue symbols represent the lattice vibration contribution to the heat capacity and entropy. The difference between the filled and open blue circles is due to the thermal excitation of 4f electrons (Schottky effect).
The thermodynamics of lanthanide phosphate solid solutions is discussed in section 3.6.
Incorporation of actinides into lanthanide phosphates ceramic is an important topic in terms of using these materials as potential nuclear waste forms. It is well known that the trivalent actinides such as Pu, Am and Cm could form monazite phases (e.g., PuPO4 Thiriet et al., 2005b; Clavier et al., 2011) and that the tetra-valent actinides such as U or Np can be introduced into the monazite lattice jointly with divalent cations [e.g., Ca, Clavier et al. (2011)]. However, an important aspect of the formation of such a solid solution is its homogeneity. In that respect, Huittinen et al. (2017) and Huittinen et al. (2018) investigated incorporation of Eu3+ into monazite and Cm3+ into monazite and rhabdophane phases, respectively. The latter compound is a hydrated lanthanide-phosphate which is a stable phase at lower temperatures (below T ~ 400K) (de Kerdaniel et al., 2007; Clavier et al., 2011). By a combination of time-resolved laser fluorescence spectroscopy (TRLFS) and atomistic modeling, Huittinen et al. (2017) have shown that monazite-type solid solutions are homogeneous. This conclusion was reached by explanation of the increased broadening of TRLFS profiles for the La1-xGdxPO4 solid solutions by the broad distribution of the dopant-O bond lengths in the measured mixed compounds. In these studies force-field methods were used to describe the interatomic interactions and special quasi-random structures (SQS) (Zunger et al., 1990) were used to model the ideal, homogeneous solid solutions. The same approach was used by Huittinen et al. (2018) to show homogeneous incorporation of Cm3+ into monazite. On the other hand, rhabdophane-type La1−xGdxPO4 solid solutions were found to be very selective in terms of actinides incorporation, with the anhydrous cation site (i.e., not coordinated to H2O molecules) being preferred by the Cm dopant, and the preference increasing toward larger and lighter lanthanides [greater for LaPO4 · 0.67H2O than GdPO4 · 0.67H2O, Huittinen et al. (2018)]. This selectivity was confirmed by the computation of the Cm solution (incorporation) energies.
Formation and thermodynamic stability of solid solutions of radionuclides-bearing lanthanide phosphates ceramic waste forms is a topic of extensive studies in the context of nuclear waste management (Popa et al., 2007a; Li et al., 2014; Kowalski and Li, 2016; Arinicheva et al., 2017; Hirsch et al., 2017; Neumeier et al., 2017b; Eremin et al., 2019). This is because the information gained allows for the assessment of long term stability of ceramic nuclear waste forms against phase separation. In that aspect there are two streams of research: (1) the investigation of homogeneity of a solid solution discussed in section 3.5 and (2) the investigation of its long-term thermodynamic stability. The second problem is a key issue for nuclear waste disposal because any desired waste form should be stable against formation of the miscibility gap. It was shown experimentally (Popa et al., 2007b) and by ab initio simulations (Li et al., 2014) that monazite-type solid solutions are highly regular. The excess enthalpy of mixing, HE, of a (A1−xBxPO4) could be described by a simple equation (Popa et al., 2007b):
where W is a Margules interaction parameter (Prieto, 2009). A solid solution is stable against formation of a miscibility gap if W < 2RT, where R is the gas constant. It is thus of interest to nuclear waste management strategies to characterize W for the considered solid solutions, especially for the mixture of actinides with the host matrix cations like Pu with La in a La1-xPuxPO4 solid solution.
The first systematic ab initio calculations of W parameters for monazite-type solid solutions were performed by Li et al. (2014). They found that for the La1−xLnxPO4 solid solutions, W = 0.618(ΔV(cm3/mol))2, where ΔV is the difference in the volume of solid solution endmembers. The obtained results suggest thermodynamic instability, characterized with W > 5kJ/mol at ambient conditions, of various solid solutions [e.g., (La1−xGdxPO4)]. In follow-up studies, Kowalski and Li (2016) explained the quadratic dependence of W parameter on the volumes difference by a strain energy-based model, in which
where E is the Young's modulus and V is the volume. These studies show that ΔV is an important parameter that determines the value of the W parameter.
Neumeier et al. (2017b) compared the derived ab initio W parameters with the calorimetric measurements of La1−xLnxPO4 (Ln = Eu, Gd) solid solutions. The measured values are smaller than the computed ones. The reason for this discrepancy is the difference in the value of measured and computed ΔV. These are summarized in Table 2. When Neumeier et al. (2017b) used the measured ΔV values and rescaled the ab initio computed values according to Equation 5, namely:
as provided in Table 2, they obtained a good match to the measured values.
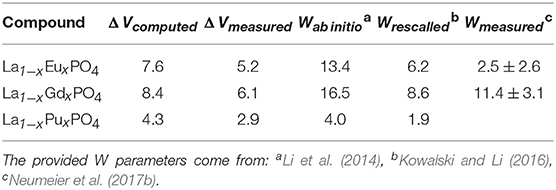
Table 2. The Margules interaction parameters W and the difference in volumes of endmembers (ΔV) for La1−xLnxPO4 (Ln = Eu, Gd, Pu) monazite-type solid solutions.
The most important outcome of these studies is their implication for immobilization of actinides, for instance Pu. The obtained Margules interaction parameter for La1−xPuxPO4 solid solution case is W = 1.8kJ/mol (Table 2), thus indicating thermodynamic stability of this solid solution against formation of a miscibility gap (as W is < 5kJ/mol). On the other hand, although synthesis of the pure PuPO4 monazite has been successful (Thiriet et al., 2005b; Clavier et al., 2011), the experimental studies suggest a maximum content of Pu in La1−xPuxPO4 solid solution at x ~ 0.15 (Popa et al., 2007a; Arinicheva et al., 2017). In particular, recent experimental investigation by Arinicheva et al. (2017) indicates formation of Pu-oxides (PuO2) for x > 0.15. In order to understand this contradiction, we computed the formation enthalpy of La1−xPuxPO4 solid solution from oxides. We consider the following reaction:
Because PuO2 is the most stable Pu-oxide at ambient conditions, we also account for the enthalpy of oxidation of Pu2O3 of 285kJ/mol (Konings et al., 2014). The result is given in Figure 6. Interestingly, the formation enthalpy becomes positive, and the solid solution becomes unstable against formation of PuO2 for x ~ 0.15. We thus conclude that the experimentally observed maximum load of Pu in LaPO4 results from the positive formation enthalpies, and thus thermodynamic instability of La1−xPuxPO4 compounds for x > 0.152.
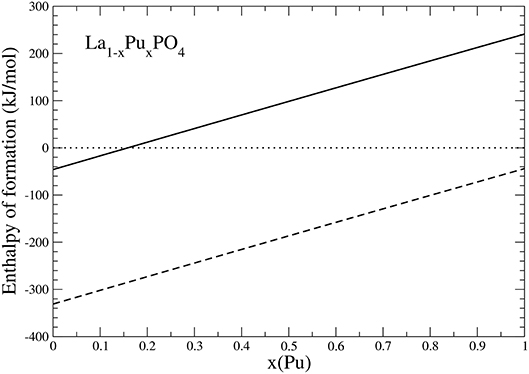
Figure 6. The formation enthalpy from oxides of La1−xPuxPO4 solid solution compounds. The lines represent results taking Pu2O3 (dashed) and PuO2 (solid) as a reference.
The thermodynamic parameters of mixing, such as the W parameter, are very important for assessment of thermodynamic stability of monazite-type nuclear waste forms. Therefore, it is of high importance to validate the model presented in section 3.6 against all the available data. Interestingly, the Margules interaction parameters are equally important for the description of the miscibility gap, and the maximum solubilities, in the naturally occurring monazite-xenotime systems. The monazite-xenotime system has been proposed as a potential geothermometer and some relevant data on solubilities have been measured (Andrehs and Heinrich, 1998; Mogilevsky, 2007). Monazite-xenotime system shows a large miscibility gap, which is associated with a large difference between the formation enthalpies of monazite and xenotime (Figure 3). Nevertheless, the measured maximum solubilities can be good indicators of temperature and this phenomenon have been investigated “in situ” experimentally (Andrehs and Heinrich, 1998), and by thermodynamic modeling (Mogilevsky, 2007). In order to model the maximum solubility of one phase in another we have to know the Margules interaction parameters W and the difference in the formation enthalpies between monazite and xenotime phases. The first is discussed in section 3.6 and as we concluded there, we have a good model for it. The latter is discussed in section 3.2.
The maximum solubilities of xenotime in monazite (x1) and monazite in xenotime (x2) are obtained by solving self-consistently two equations (Mogilevsky, 2007):
where Ωx,m = −Δhm,x + Wm,x. Δhm,x is given by Equations 1, 2 (see also section 3.2) and Wm, x are the Margules interaction parameters for monazite (m)- and xenotime (x)-type solid solutions. The self-consistent solution of Equations 8 and 9 can be easily done in a numerical way. The resulted maximum solubilities for the selected solid solution compositions at T = 1453K are given in Figure 7. The solubility of xenotime in monazite is much larger than monazite in xenotime (Mogilevsky, 2007), so here we focus on the former phenomenon. For the solubility of Y-xenotime (YPO4) in monazite there is a maximum at Sm - Nd. We note that the match to in situ data (Andrehs and Heinrich, 1998) is not perfect and is not that good as the empirically-based thermodynamic modeling of Mogilevsky (2007), but the trend is well described on the qualitative level. The main discrepancy comes from the ΔHm−x, which we have reasons to think are quite accurate by the ab initio calculations. Therefore, more testing against larger data sets would be required to work out and validate a more accurate model for the maximum solubilities in the monazite-xenotime system. This example also shows the importance of correct thermodynamic modeling of monazite-xenotime system, which could be performed and validated by a joint atomistic modeling and experimental effort.
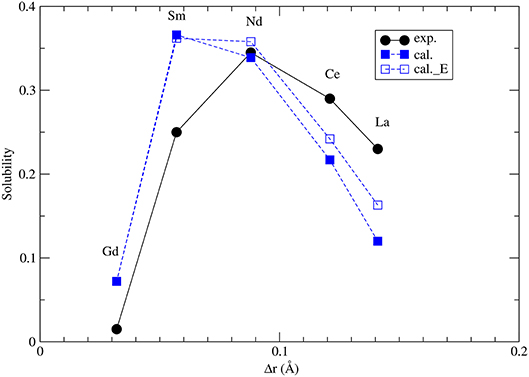
Figure 7. The computed maximum solubility of Y-xenotime in monazite at T = 1473K. Different sets represent our ab initio prediction (filled blue squares), prediction using Equation 5 [open blue squares, Kowalski and Li (2016)] and measurements [filled black circles, Andrehs and Heinrich (1998); Mogilevsky (2007)]. Δr is the difference in ionic radius of Ln and Y cations.
In this contribution we presented recent atomistic modeling contribution to the research on lanthanide phosphates, focusing on the studies performed at Forschungszentrum Jülich. We have shown that on many occasions joint atomistic modeling and experimental work resulted in the enhanced description of the investigated materials. Examples of such joint studies are investigations of homogeneity and thermodynamic parameters of solid solutions and incorporation of actinides into lanthanide phosphate ceramics. With the improved understanding and description of the 4f electrons, achieved with the parameter free DFT+U approach, we were able to obtain very accurate description of the local Ln − O bonding environments and the formation enthalpies. This allowed us to obtain better estimates of the relative solubilities in the monazite-xenotime system, elastic and thermodynamic parameters for pure phases and solid solutions. The joint modeling and experimental investigation of the excess enthalpies of mixing in monazite-type solid solutions provided solid arguments for the long-term thermodynamic stability of the plutonium-lanthanum monazite-type ceramic waste form. With respect to our previously published studies, the novel contribution discussed here is the investigation of incorporation of Pu into LaPO4 ceramics, which shows that the experimentally observed maximum load limit for La1-xPuxPO4 is governed by the formation enthalpy from oxides, which becomes positive at ~x = 0.15. This value is consistent with the experimental observations. In addition, we reinvestigated the thermodynamics of monazite-xenotime system. We provide accurate values of the enthalpy difference between monazite and xenotime phases and estimates of maximal solubilities computed from the best available ab initio data. These results are of great importance for monazite/xenotime-based geothermometry. However, the obtained slight discrepancies between theoretical prediction and the available in situ data show a need for more in-depth experimental and theoretical studies of solubilities in the monazite-xenotime system.
The assortment of results provided here shows that atomistic modeling is a valuable research tool for the investigation of lanthanide phosphates. The best results have been obtained by a joint computational and experimental approach, or at least by extensive testing and comparison to the available experimental data. With the steady increase in the availability of computational power we expect that atomistic modeling research will be applied to tackle more complex problems, such as dissolution or corrosion kinetics, an important aspects of nuclear waste performance.
All datasets generated for this study are included in the manuscript and/or the supplementary files.
YJ and PMK contributed equally to computing the data, analysis and editing the manuscript. PK, NH, and YA contributed experimental support and expertise. VV contributed to the computation of thermodynamic parameters of solid solutions. NM contributed to the computation of thermal conductivity and force-field simulations. SN and DB contributed expertise on ceramic waste forms.
We gratefully acknowledge the funding from the German Federal Ministry for Education and Research (BMBF, Grant 02NUK021A).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We thank Sergey Yudintsev and another reviewer for very positive and constructive comments on the manuscript. YJ is thankful to the China Scholarship Council (CSC) for providing financial support for her PhD study in Germany at Forschungszentrum Jülich/RWTH Aachen. Funded by the Excellence Initiative of the German federal and state governments and the Jülich Aachen Research Alliance – High-Performance Computing. We thank the JARA-HPC awarding body for time on the RWTH and Forschungszentrum Jülich computing resources awarded through JARA-HPC Partition.
1. ^In this contribution we call DFT methods an ab initio approach as the exchange-correlation functionals utilized in our studies were designed based on pure-theoretical considerations.
2. ^We notice that in order to correctly quantify the thermodynamics of this process, the free energies should be considered. However, the consideration of the entropy terms (main contributor to the difference between the enthalpies and the free energies of the reaction 7) in the reaction 7 would slightly increase the threshold x value but on qualitative level, the outlined picture will not change.
Ali, K., Arya, A., Ghosh, P. S., and Dey, G. K. (2016). “A first principle study of the pressure dependent elastic properties of monazite LaPO4,” AIP Conference Proceedings 1728:020090. doi: 10.1063/1.4946141
Andrehs, G. and Heinrich, W. (1998). Experimental determination of REE distributions between monazite and xenotime: potential for temperature-calibrated geochronology. Chem. Geol. 149, 83–96.
Arinicheva, Y., Popa, K., Scheinost, A. C., Rossberg, A., Dieste-Blanco, O., Raison, P., et al. (2017). Structural investigations of (La,Pu)PO4 monazite solid solutions: XRD and XAFS study. J. Nucl. Mater., 493, 404–411. doi: 10.1016/j.jnucmat.2017.06.034
Bauer, J., Hirsch, A., Bayarjargal, L., Peters, L., Roth, G., and Winkler, B. (2016). Schottky contribution to the heat capacity of monazite type (La, Pr)PO4 from low temperature calorimetry and fluorescence measurements. Chem. Phys. Lett. 654, 97–102. doi: 10.1016/j.cplett.2016.05.012
Benes, O., Popa, K., Reuscher, V., Zappia, A., Staicu, D., and Konings, R. J. M. (2011). High temperature heat capacity of PuPO4 monazite-analogue. J. Nucl. Mater. 418, 182–185. doi: 10.1016/j.jnucmat.2011.06.037
Beridze, G., Birnie, A., Koniski, S., Ji, Y., and Kowalski, P. M. (2016). DFT+U as a reliable method for efficient ab initio calculations of nuclear materials. Prog. Nucl. Energ. 92, 142–146. doi: 10.1016/j.pnucene.2016.07.012
Blanca-Romero, A., Kowalski, P. M., Beridze, G., Schlenz, H., and Bosbach, D. (2014). Performance of DFT+U method for prediction of structural and thermodynamic parameters of monazite-type ceramics. J. Comput. Chem. 35, 1339–1346. doi: 10.1002/jcc.23618
Buckingham, R. (1938). The classical equation of state of gaseous helium, neon and argon. Proc. Roy. Soc. A: Math. Phys. Eng. Sci. 168, 264–283.
Chroneos, A., Rushton, M., Jiang, C., and Tsoukalas, L. (2013). Nuclear wasteform materials: atomistic simulation case studies. J. Nucl. Mater. 441, 29–39. doi: 10.1016/j.jnucmat.2013.05.012
Clavier, N., Podor, R., and Dacheux, N. (2011). Crystal chemistry of the monazite structure. J. Eur. Ceram. Soc. 31, 941–976. doi: 10.1016/j.jeurceramsoc.2010.12.019
Cococcioni, M., and de Gironcoli, S. (2005). Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 71:035105. doi: 10.1103/PhysRevB.71.035105
de Kerdaniel, E. D. F., Clavier, N., Dacheux, N., Terra, O., and Podor, R. (2007). Actinide solubility-controlling phases during the dissolution of phosphate ceramics. J. Nucl. Mater. 362, 451–458. doi: 10.1016/j.jnucmat.2007.01.132
Du, A., Wan, C., Qu, Z., and Pan, W. (2009). Thermal conductivity of monazite-type repo4 (Re=La, Ce, Nd, Sm, Eu, Gd). J. Am. Ceram. Soc. 92, 2687–2692. doi: 10.1111/j.1551-2916.2009.03244.x
Eremin, N. N., Marchenko, E. I., Petrov, V. G., Mitrofanov, A. A., and Ulanova, A. S. (2019). Solid solutions of monazites and xenotimes of lanthanides and plutonium: atomistic model of crystal structures, point defects and mixing properties. Comput. Mater. Sci. 157, 43–50. doi: 10.1016/j.commatsci.2018.10.025
Ewing, R., and Wang, L. (2002). Phosphates as nuclear waste forms. Rev. Mineral. and Geochem. 48, 673–699. doi: 10.2138/rmg.2002.48.18
Feng, J., Xiao, B., Zhou, R., and Pan, W. (2013). Anisotropy in elasticity and thermal conductivity of monazite-type repo4 (re=la, ce, nd, sm, eu and gd) from first-principles calculations. Acta Mater. 61, 7364–7383. doi: 10.1016/j.actamat.2013.08.043
Gavrichev, K. S., Ryumin, M. A., Tyurin, A. V., Gurevich, V. M., Khoroshilov, A. V., and Komissarova, L. N. (2012). Thermodynamic functions of erbium orthophosphate ErPO4 in the temperature range of 0-1600 K. Thermochim. Acta 535, 1–7. doi: 10.1016/j.tca.2012.02.002
Gavrichev, K. S., Ryumin, M. A., Tyurin, A. V., Gurevich, V. M., and Komissarova, L. N. (2008). Refined heat capacity of LaPO4 in the temperature range 0-1600 K. Thermochim. Acta 474, 47–51. doi: 10.1016/j.tca.2008.05.004
Gavrichev, K. S., Ryumin, M. A., Tyurin, A. V., Gurevich, V. M., and Komissarova, L. N. (2009). The heat capacity and thermodynamic functions of EuPO4 over the temperature range 0-1600 K. Russ. J. Phys. Chem. A 83, 901–906. doi: 10.1134/S0036024409060053
Gavrichev, K. S., Ryumin, M. A., Tyurin, A. V., Gurevich, V. M., and Komissarova, L. N. (2010). Heat capacity and thermodynamic functions of xenotime YPO4(c) at 0-1600 K. Geochem. Int. 48, 932–939. doi: 10.1134/S0016702910090065
Gavrichev, K. S., Ryumin, M. A., Tyurin, A. V., Gurevich, V. M., Nikiforova, G. E., and Komissarova, L. N. (2013). Heat capacity and thermodynamic functions of YbPO4 from 0 to 1800 K. Inorg. Mater. 49, 701–708. doi: 10.1134/S0020168513070042
Gavrichev, K. S., Smirnova, N. N., Gurevich, V. M., Danilov, V. R., Tyurin, A. V., Ryumin, M. A., et al. (2006). Heat capacity and thermodynamic functions of LuPO4 in the range 0-320 K. Thermochim. Acta 448, 63–65. doi: 10.1016/j.tca.2006.05.019
Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., et al. (2009). Quantum espresso: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21:395502. doi: 10.1088/0953-8984/21/39/395502
Gomis, O., Lavina, B., Rodríguez-Hernández, P., Muñoz, A., Errandonea, R., Errandonea, D., et al. (2017). High-pressure structural, elastic, and thermodynamic properties of zircon-type HoPO4 and TmPO4. J. Phys. Condens. Matter 29:095401. doi: 10.1088/1361-648X/aa516a
Gysi, A. P., Harlov, D., Costa Filho, D., and Williams-Jones, A. E. (2016). Experimental determination of the high temperature heat capacity of a natural xenotime-(Y) solid solution and synthetic DyPO4 and ErPO4 endmembers. Thermochim. Acta 627, 61–67. doi: 10.1016/j.tca.2016.01.016
Harley, R. T., and Manning, D. I. (1978). Jahn-Teller induced elastic constant changes in TmPO4. J. Phys. C Solid State Phys.. 11:L633.
Hikichi, Y., Ota, T., Daimon, K., Hattori, T., and Mizuno, M. (1998). Thermal, mechanical, and chemical properties of sintered xenotime-type RPO4 (R = Y, Er, Yb, or Lu). J. Am. Ceram. Soc. 81, 2216–2218.
Hirsch, A., Kegler, P., Alencar, I., Ruiz-Fuertes, J., Shelyug, A., Peters, L., et al. (2017). Structural, vibrational, and thermochemical properties of the monazite-type solid solution La1−xPrxPO4. J. Solid State Chem. 245, 82–88. doi: 10.1016/j.jssc.2016.09.032
Huittinen, N., Arinicheva, Y., Kowalski, P., Vinograd, V., Neumeier, S., and Bosbach, D. (2017). Probing structural homogeneity of La1−xGdxPO4 monazite-type solid solutions by combined spectroscopic and computational studies. J. Nucl. Mater. 486, 148–157. doi: 10.1016/j.jnucmat.2017.01.024
Huittinen, N., Scheinost, A. C., Ji, Y., Kowalski, P. M., Arinicheva, Y., Wilden, A., et al. (2018). A spectroscopic and computational study of Cm3+ incorporation in lanthanide phosphate rhabdophane (LnPO4·0.67H2O) and monazite (LnPO4). Inorg. Chem. 57, 6252–6265. doi: 10.1021/acs.inorgchem.8b00095
Jahn, S. and Kowalski, P. M. (2014). Theoretical approaches to structure and spectroscopy of earth materials. Rev. Mineral. Geochem. 78, 691–743. doi: 10.2138/rmg.2014.78.17
Ji, Y., Beridze, G., Bosbach, D., and Kowalski, P. M. (2017a). Heat capacities of xenotime-type ceramics: An accurate ab initio prediction. J. Nucl. Mater. 494, 172–181. doi: 10.1016/j.jnucmat.2017.07.026
Ji, Y., Beridze, G., Li, Y., and Kowalski, P. M. (2017b). Large scale simulation of nuclear waste materials. Energy Procedia 127, 416–424. doi: 10.1016/j.egypro.2017.08.108
Ji, Y., Kowalski, P. M., Neumeier, S., Deissmann, G., Kulriya, P. K., and Gale, J. D. (2017c). Atomistic modeling and experimental studies of radiation damage in monazite-type LaPO4 ceramics. Nucl. Instrum. Methods Phys. Res. Sect. B 393, 54–58. doi: 10.1016/j.nimb.2016.09.031
Jolley, K., Asuvathraman, R., and Smith, R. (2017). Inter-atomic potentials for radiation damage studies in CePO4 monazite. Nucl. Instrum. Methods Phys. Res. B 393, 93–96. doi: 10.1016/j.nimb.2016.10.016
Konings, R. J. M., Beneš, O., Kovács, A., Manara, D., Sedmidubské, D., Gorokhov, L., et al. (2014). The thermodynamic properties of the f-elements and their compounds. Part 2: The lanthanide and actinide oxides. J. Phys. Chem. Ref. Data 43:013101. doi: 10.1063/1.4825256
Kowalski, P. M., Beridze, G., Ji, Y., and Li, Y. (2017a). Towards reliable modeling of challenging f electrons bearing materials: experience from modeling of nuclear materials. MRS Advances 2, 491–497. doi: 10.1557/adv.2017.46
Kowalski, P. M., Beridze, G., Li, Y., Ji, Y., Friedrich, C., Sasioglu, E., et al. (2016). Feasible and reliable ab initio approach to computation of materials relevant for nuclear waste management. Ceram. Trans. 258, 205–217. doi: 10.1002/9781119236016.ch21
Kowalski, P. M., Beridze, G., Vinograd, V. L., and Bosbach, D. (2015). Heat capacities of lanthanide and actinide monazite-type ceramics. J. Nucl. Mater. 464, 147–154. doi: 10.1016/j.jnucmat.2015.04.032
Kowalski, P. M., Ji, Y., Li, Y., Arinicheva, Y., Beridze, G., Neumeier, S., et al. (2017b). Simulation of ceramic materials relevant for nuclear waste management: Case of La1−xEuxPO4 solid solution. Nucl. Instrum. Methods Phys. Res. Sect. B, 393, 68–72. doi: 10.1016/j.nimb.2016.09.029
Kowalski, P. M. and Li, Y. (2016). Relationship between the thermodynamic excess properties of mixing and the elastic moduli in the monazite-type ceramics. J. Eur. Ceram. Soc. 36, 2093–2096. doi: 10.1016/j.jeurceramsoc.2016.01.051
Li, Y., Kowalski, P. M., Beridze, G., Blanca-Romero, A., Ji, Y., Vinograd, V. L., et al. (2016). Atomistic simulations of ceramic materials relevant for nuclear waste management: cases of monazite and pyrochlore. Ceram. Trans. 255:165. doi: 10.1002/9781119234531.ch15
Li, Y., Kowalski, P. M., Blanca-Romero, A., Vinograd, V., and Bosbach, D. (2014). Ab initio calculation of excess properties of solid solutions. J. Solid State Chem. 220, 137–141. doi: 10.1016/j.jssc.2014.08.005
López-Solano, J., Rodríguez-Hernández, P., Muñoz, A., Gomis, O., Santamaría-Perez, D., Errandonea, D., et al. (2010). Theoretical and experimental study of the structural stability of TbPO4 at high pressures. Phys. Rev. B 81:144126. doi: 10.1103/PhysRevB.81.144126
Lumpkin, G. and Geisler-Wierwille, T. (2012). Comprehensive Nuclear Materials: Minerals and Natural Analogues, Vol 5. Oxford: Elsevier.
Macfarlane, A. (1999). Immobilization of excess weapon plutonium: a better alternative to glass. Sci. Glob. Secur. 7, 271–309. doi: 10.1080/08929889808426463
Mogilevsky, P. (2007). On the miscibility gap in monazite–xenotime systems. Phys. Chem. Miner. 34, 201–214. doi: 10.1007/s00269-006-0139-1
Mogilevsky, P., Zaretsky, E. B., Parthasarathy, T. A., and Meisenkothen, F. (2006). Composition, lattice parameters, and room temperature elastic constants of natural single crystal xenotime from novo horizonte. Phys. Chem. Miner. 33, 691–698. doi: 10.1007/s00269-006-0118-6
Neumeier, S., Arinicheva, Y., Ji, Y., Heuser, J. M., Kowalski, P. M., Kegler, P., et al. (2017a). New insights into phosphate based materials for the immobilisation of actinides. Radiochim. Acta 105, 961–984. doi: 10.1515/ract-2017-2819
Neumeier, S., Kegler, P., Arinicheva, Y., Shelyug, A., Kowalski, P. M., Schreinemachers, C., et al. (2017b). Thermochemistry of La1−xLnxPO4 monazites (ln=gd, eu). J. Chem. Thermodyn. 105, 396–403. doi: 10.1016/j.jct.2016.11.003
Ni, Y., Hughes, J., and Mariano, A. (1995). Crystal-chemistry of the Monazite and Xenotime Structures. Am. Mineral. 80, 21–26.
Nikiforova, G. E., Ryumin, M. A., Gavrichev, K. S., and Gurevich, V. M. (2012). High-temperature thermodynamic properties of LuPO4. Inorg. Mater. 48, 841–844. doi: 10.1134/S0020168512080122
Nipko, J., Grimsditch, M., Loong, C.-K., Kern, S., Abraham, M. M., and Boatner, L. A. (1996). Elastic-constant anomalies in YbPO4. Phys. Rev. B 53, 2286–2290.
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77:3865.
Perdew, J. P., Ruzsinszky, A., Csonka, G. I., Vydrov, O. A., Scuseria, G. E., Constantin, L. A., et al. (2008). Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100:136406. doi: 10.1103/PhysRevLett.100.136406
Perdew, J. P. and Wang, Y. (1992). Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 45, 13244–13249.
Popa, K., Colineau, E., Wastin, F., and Konings, R. J. M. (2007a). The low-temperature heat capacity of (Pu0.1La0.9)PO4. Solid State Commun. 144, 74–77. doi: 10.1016/j.ssc.2007.07.011
Popa, K., Jutier, F., Wastin, F., and Konings, R. J. M. (2006a). The heat capacity of NdPO4. J. Chem. Thermodyn. 38, 1306–1311. doi: 10.1016/j.jct.2006.02.006
Popa, K., and Konings, R. J. M. (2006). High-temperature heat capacities of eupo4 and smpo4 synthetic monazites. Thermochim. Acta 445, 49–52. doi: 10.1016/j.tca.2006.03.023
Popa, K., Konings, R. J. M., and Geisler, T. (2007b). High-temperature calorimetry of (La1−xLnx)PO4 solid solutions. J. Chem. Thermodyn. 39, 236–239. doi: 10.1016/j.jct.2006.07.010
Popa, K., Sedmidubsky, D., Benes, O., Thiriet, C., and Konings, R. J. M. (2006b). The high-temperature heat capacity of LnPO4 (Ln=La, Ce, Gd) by drop calorimetry. J. Chem. Thermodyn. 38, 825–829. doi: 10.1016/j.jct.2005.08.019
Prieto, M. (2009). “Thermodynamics of solid solution-aqueous solution systems,” 19th Annual V M Goldschmidt Conference, Davos.
Rustad, J. R. (2012). Density functional calculations of the enthalpies of formation of rare-earth orthophosphates. Am. Mineral. 97, 791–799. doi: 10.2138/am.2012.3948
Schlenz, H., Heuser, J., Neumann, A., Schmitz, S., and Bosbach, D. (2013). Monazite as a suitable actinide waste form. Z. Kristallogr. 228, 113–123. doi: 10.1524/zkri.2013.1597
Schlenz, H., Neumeier, S., Hirsch, A., Peters, L., and Roth, G. (2017). “Phosphates as safe containers for radionuclides,” in Highlights in Applied Mineralogy, eds S. Heuss-Aßbichler, G. Amthauer, and M. John (Berlin; Boston: De Gruyter), 171–195.
Seydoux-Guillaume, A.-M., Deschanels, X., Baumier, C., Neumeier, S., Weber, W. J., and Peuget, S. (2018). Why natural monazite never becomes amorphous: experimental evidence for alpha self-healing. Am. Mineral. 103, 824–827. doi: 10.2138/am-2018-6447
Shannon, R. D. (1976). Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. A 32, 751–767.
Shein, I. R., and Shalaeva, E. V. (2016). Pressure-induced zircon to monazite phase transition in Y1−xLaxPO4: First-principles calculations. J. Struct. Chem. 57, 1513–1518. doi: 10.1134/S0022476616080047
Slack, G. (1973). Nonmetallic crystals with high thermal-conductivity. J. Phys. Chem. Solids 34, 321–335.
Stavrou, E., Tatsi, A., Raptis, C., Efthimiopoulos, I., Syassen, K., Muñoz, A., et al. (2012). Effects of pressure on the structure and lattice dynamics of TmPO4: experiments and calculations. Phys. Rev. B 85:024117. doi: 10.1103/PhysRevB.85.024117
Thiriet, C., Konings, R. J. M., Javorsky, P., Magnani, N., and Wastin, F. (2005a). The low temperature heat capacity of LaPO4 and GdPO4, the thermodynamic functions of the monazite-type LnPO4 series. J. Chem. Thermodyn. 37, 131–139. doi: 10.1016/j.jct.2004.07.031
Thiriet, C., Konings, R. J. M., Javorsky, P., and Wastin, F. (2004). The heat capacity of cerium orthophosphate CePO4, the synthetic analogue of monazite. Phys. Chem. Miner. 31, 347–352. doi: 10.1007/s00269-004-0397-8
Thiriet, C., Konings, R. J. M., and Wastin, F. (2005b). Low temperature heat capacity of PuPO4. J. Nucl. Mater. 344, 56–60. doi: 10.1016/j.jnucmat.2005.04.016
Thomä, R., Wehrle, H., and Armbruster, A. (1974). Measurement of the elastic constants of luaso4 and lupo4 by brillouin scattering and determination of the debye temperatures. Phys. Status Solidi A 24, K71–K73.
Thust, A., Arinicheva, Y., Haussühl, E., Ruiz-Fuertes, J., Bayarjargal, L., Vogel, S. C., et al. (2015). Physical properties of La1-xEuxPO4, 0 ≤ x ≤ 1, Monazite-Type Ceramics. J. Am. Ceram. Soc. 98, 4016–4021. doi: 10.1111/jace.13841
Ushakov, S., Helean, K., and Navrotsky, A. (2001). Thermochemistry of rare-earth orthophosphates. J. Mater. Res. 16:2623–2633. doi: 10.1557/JMR.2001.0361
Vanderbilt, D. (1990). Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41:7892. doi: 10.1103/PhysRevB.41.7892
Wang, J., Zhou, Y., and Lin, Z. (2005). First-principles elastic stiffness of LaPO4 monazite. Appl. Phys. Lett. 87:051902. doi: 10.1063/1.2005392
Williams, M. L., Jercinovic, M. J., and Hetherington, C. J. (2007). Microprobe monazite geochronology: understanding geologic processes by integrating composition and chronology. Annu. Rev. Earth Planet. Sci. 35, 137–175. doi: 10.1146/annurev.earth.35.031306.140228
Keywords: rare-earth phosphates, atomistic simulations, monazite, xenotime, nuclear waste management, ceramics, thermodynamics, solid solutions
Citation: Ji Y, Kowalski PM, Kegler P, Huittinen N, Marks NA, Vinograd VL, Arinicheva Y, Neumeier S and Bosbach D (2019) Rare-Earth Orthophosphates From Atomistic Simulations. Front. Chem. 7:197. doi: 10.3389/fchem.2019.00197
Received: 12 November 2018; Accepted: 14 March 2019;
Published: 03 April 2019.
Edited by:
Nicolas J. Dacheux, Université de Montpellier, FranceReviewed by:
Zhong Jin, Nanjing University, ChinaCopyright © 2019 Ji, Kowalski, Kegler, Huittinen, Marks, Vinograd, Arinicheva, Neumeier and Bosbach. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Piotr M. Kowalski, cC5rb3dhbHNraUBmei1qdWVsaWNoLmRl
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.