Oxygen Vacancies in Oxide Nanoclusters: When Silica Is More Reducible Than Titania

Oxygen vacancies are related to specific optical, conductivity and magnetic properties in macroscopic SiO₂ and TiO₂ compounds. As such, the ease with which oxygen vacancies form often determines the application potential of these materials in many technological fields. However, little is known about the role of oxygen vacancies in nanosized materials. In this work we compute the energies to create oxygen vacancies in highly stable nanoclusters of (TiO₂)_N, (SiO₂)_N, and mixed (Ti_xSi_1−xO₂)_N for sizes between N = 2 and N = 24 units. Contrary to the results for bulk and surfaces, we predict that removing an oxygen atom from global minima silica clusters is energetically more favorable than from the respective titania species. This unexpected chemical behavior is clearly linked to the inherent presence of terminal unsaturated oxygens at these nanoscale systems. In order to fully characterize our findings, we provide an extensive set of descriptors (oxygen vacancy formation energy, electron localization, density of states, relaxation energy, and geometry) that can be used to compare our results with those for other compositions and sizes. Our results will help in the search of novel nanomaterials for technological and scientific applications such as heterogeneous catalysis, electronics, and cluster chemistry.

Introduction

Metal oxides are an important class of materials in many scientific and technological fields. Silica and titania are abundant compounds and play crucial roles in geology (Howie, 1964; Lakshtanov et al., 2007; Lyle et al., 2015), astrochemistry (Lambert et al., 2012; Lee et al., 2015; Komatsu et al., 2018), environmental and chemical sciences (Joo et al., 2014; Kapilashrami et al., 2014), biology and medicine (Mal et al., 2003; Nguyen et al., 2005; Das et al., 2009; Bawazer et al., 2012; Lucky et al., 2016; Saroj and Rajput, 2018). Their ability to exchange oxygen drastically determines their properties. In the case of TiO₂, the loss of lattice oxygen results in a change of color from white to blue, the appearance of magnetism, and is connected with photocatalytic properties (Houlihan et al., 1975; Diebold, 2003; Di Valentin et al., 2006; Na-Phattalung et al., 2006; Vásquez et al., 2016; Li et al., 2018). On the other hand, oxygen vacancies present in amorphous silica have been reported to modify its electronic and optical properties (Rudra and Fowler, 1987; Skuja, 1998; Manveer et al., 2017). Oxygen substoichiometry in silica-based materials is linked to dielectric breakdown and electroforming in resistive random access memory devices (McPherson and Mogul, 1998; Yao et al., 2010; Wang et al., 2014; Mehonic et al., 2018). Whereas, the effect of creating an oxygen vacancy in bulk and surfaces of both titania and silica is well-reported, little is known about the role these defects may play in nanosized materials and clusters. By means of density functional theory (DFT) based calculations, we characterise the energetics of creating an oxygen vacancy in silica, titania and titanosilicate clusters recently derived from global optimization studies. Low energy clusters can be generated with cluster beam experiments and stabilized by soft landing techniques. Such studies are increasingly looking into the reactivity of the cluster species formed for technologically important reactions (Yin and Bernstein, 2014; Vajda and White, 2015; Sun et al., 2016). With our work we hope to elucidate the reactivity of such nanoclusters as estimated through their reduction by oxygen removal.

From a computational point of view, the energetic cost of removing a neutral oxygen atom from a stoichiometric metal oxide can be calculated with the following equation:

$\begin{array}{rcl}{\text{M}}_{\text{n}}{\text{O}}_{2\text{n}}& \to & {\text{M}}_{\text{n}}{\text{O}}_{2\text{n}-1}+1/2{\text{O}}_2\end{array}$

$\begin{array}{rcll}{\text{E}}_{\text{vac}}& =& \text{E}{\text{M}}_{\text{n}}{\text{O}}_{2\text{n}-1}+1/2\text{E}{\text{O}}_2-\text{E}{\text{M}}_{\text{n}}{\text{O}}_{2\text{n}}& (1)\end{array}$

A reducible oxide like titania tends to have small (positive) E_vac values, while the energy to form an oxygen vacancy in an irreducible oxide like silica is relatively higher. E_vac values can thus be used to compare different systems and provide an initial ranking of reducibility (Ganduglia-Pirovano et al., 2007; Deml et al., 2015; Helali et al., 2017). Typical values for bulk and surface E_vac values in rutile and anatase TiO₂ are 3.7–4.5 eV whereas for SiO₂ the values are much higher, 5–8 eV (see Sushko et al., 2005). In addition, the localization of the electrons remaining after the removal of the oxygen in the lattice provides crucial information related to the electronic structure of the defective material (Helali et al., 2017):

$\begin{array}{rc}{M}^{\mathrm{\text{n+}}}-O^{2-}-M^{\mathrm{\text{n+}}}\to M^{\mathrm{\text{n+}}}-2e^{-}-M^{\mathrm{\text{n+}}}+\frac{1}{2}{O}_2& (2)\end{array}$

It is commonly accepted that removing an oxygen atom from TiO₂ leads to the formation of paramagnetic Ti³⁺ sites in both bulk and surfaces (Houlihan et al., 1975; Di Valentin et al., 2006; Li et al., 2018). The electronic state of reduced titania systems is typically open-shell. In amorphous SiO₂ and quartz the removal of a lattice oxygen results in the formation of a Si-Si covalent bond where the electron pair is stabilized by two Si sites (Sushko et al., 2005). In the quartz surface the removal of an oxygen atom leads to an electron pair localized on a surface silicon site (Silvi and D'Arco, 2006; Causà et al., 2015). This typically leads to electronic states that are closed-shell.

We focus on the effects that the system size reduction to the nanoscale has on the type of oxygen defects exhibited and their resultant E_vac values. As has been previously reported for ZrO₂ (Ruiz Puigdollers et al., 2016a,b), CeO₂ (Kozlov et al., 2015), TiO₂ (Morales-García et al., 2018), this may result in a significant change in the materials' properties. Specifically, in this work we investigate the energetic, structural and electronic properties of silica, titania and mixed titanosilicates as regards their tendency to lose neutral oxygen atoms. These properties are then compared between the different oxides and with respect to the system size, including up to the bulk. At the nanoscale level, we consider a set of globally optimized silica and titania clusters with sizes between 2 and 24 MO₂ units. Moreover, we compare our results for these pure oxides with a comparative set of titanosilicate clusters for the size of 10 MO₂ units. At the bulk level, we consider alpha quartz and rutile phases, respectively, for silica and titania, which are the two most stable phases under ambient conditions. Such systems are then reduced by a single and neutral oxygen vacancy and the results are analyzed to elucidate the role of cluster size, structure and oxide type with respect to the formation of oxygen vacancies.

Methodology

All nanocluster structures selected in this study correspond to the lowest energy global minima candidates currently reported in the literature as derived by us and/or other authors: SiO₂ systems are derived from Flikkema and Bromley (2003, 2004), Lu et al. (2003), Bromley and Flikkema (2005), TiO₂ systems from Hamad et al. (2005), Woodley et al. (2006), Calatayud et al. (2008a), Syzgantseva et al. (2011), Chen and Dixon (2013), Bhattacharya et al. (2015), Aguilera-Granja et al. (2016), Lamiel-Garcia et al. (2017), and finally mixed titanosilicates are taken from Cuko et al. (2018). A two-step procedure is followed to compute E_vac (Equation 1): (i) a selected oxygen atom is removed from a structurally frozen stoichiometric nanocluster and the pre-removal/post-removal energy difference is defined as E_unrel, (ii) the post-removal non-stoichiometric nanocluster structure is then fully optimized, with the pre-optimized/post-optimized energy difference defined as E_vac. The relaxation energy E_rel is then derived as the difference between E_unrel and E_vac. For the smaller sizes, N = 2–10, every symmetrically distinct oxygen site was tested and only the most representative ones were reported. For larger sizes, an exhaustive approach was found to be too computationally demanding and a sampling of approximately 10 oxygen sites was performed, always including all symmetrically non-equivalent terminating oxygens. All DFT based calculations involving reduced nanoclusters were carried out using a spin-polarized formalism, employing the PBE0 functional (Adamo and Barone, 1999) and a tier-1/tight numerical basis set as implemented in the FHI-AIMS code (Blum et al., 2009). In most of the calculations, we did not force the spin multiplicity of the system. However, in a few cases, especially for TiO₂ systems, in order to overcome convergence problems, we forced the spin multiplicity to be either an open shell singlet or a triplet. Recently, room temperature ferromagnetism has been reported for zirconia nanoparticles (Rahman et al., 2016; Albanese et al., 2018). This effect might also take place in titania and could be studied by considering multiple vacancies in future works.

Results and Discussion

Pure (SiO₂)_N Nanoclusters

Figure 1 shows the calculated values of E_vac for the lowest energy SiO₂ nanoclusters together with some selected nanocluster structures. Figure S1 shows the structures of all stoichiometric silica nanoclusters used in this work and Table S1 includes the corresponding values of E_vac, E_unrel, and E_rel for the most stable reduced systems. Generally, stoichiometric silica global minimum nanoclusters tend to possess quite open symmetric structures and typically have between 2 and 4 unsaturated (terminal) oxygen sites. The majority of these structures present silanone centers, which are triply-coordinated planar Si centers involving a terminal oxygen atom (i.e., formally >Si=O, but arguably more accurately >Si⁺-O⁻) (Avakyan et al., 2006; Zwijnenburg et al., 2009). For nearly all the silica nanoclusters considered, the terminal oxygen atoms at these sites are found to cost the least energy to be removed, 2.6–2.8 eV, with E_vac increasing slightly and monotonically with the size. The (SiO₂)₁₂ nanocluster is the only exception as it only displays non-bridging oxygen (NBO) terminal species (i.e., ≡Si–O species where Si is 4-fold coordinated) rather than silanones. Removing the terminal oxygen atom of an NBO center results in a higher E_vac value (3.60 eV) as compared with silanone defects (2.6–2.8 eV). We note that the values of E_vac for the removal of oxygen atoms at both silanone and NBO defects are much lower than those for the removal of 2-fold coordinated oxygen atoms in the corresponding bulk systems. From our calculations, for example, we obtained E_vac values between 5.06–5.39 eV for a-quartz with a range of vacancy concentrations between 1/24 and 1/3 vacancies per SiO₂ units. These values are also consistent with other work where an E_vac value of 5.15 eV was obtained using plane-wave based DFT calculations at the PBE level for the alpha-quartz structure with a vacancy concentration of 1/48 (Helali et al., 2017). We note that, removing a 2-fold oxygen atom in our nanoclusters typically costs between 4.2 and 5.7 eV (see Figure S2 which shows selected values for Si₁₀O₂₀), which is comparable to the E_vac values obtained for bulk alpha quartz. This confirms that the terminal silanone oxygens are least energetically costly in silica nanoclusters. From a structural point of view, reducing a silanone defective site in a nanocluster leads to a 2-fold Si site displaying a Si-O distance of 1.71 Å. This is slightly longer than the Si-O bond length of 1.62 Å as calculated by Pacchioni and Ferrario (1998) for a 2-fold coordinated Si defect in alpha quartz using a cluster approach at both wave function theory level employing unrestricted Hartree Fock, and DFT level employing the hybrid B3LYP functional. Further comparing our results with these bulk cluster calculations, in our clusters the O-Si-O angle of a reduced silanone site is found to be between 87 and 111°, depending on whether the defect is part of a two or three membered ring. This compares with a value of 102° found from bulk cluster calculations. Also, the vicinal Si-O-Si^II angle (where Si^II corresponds to the 2-fold coordinated silicon atom) is found to be between 90 and 133° in our nanoscale clusters against the corresponding values for the same defective site of 141–161° from bulk cluster calculations.

FIGURE 1

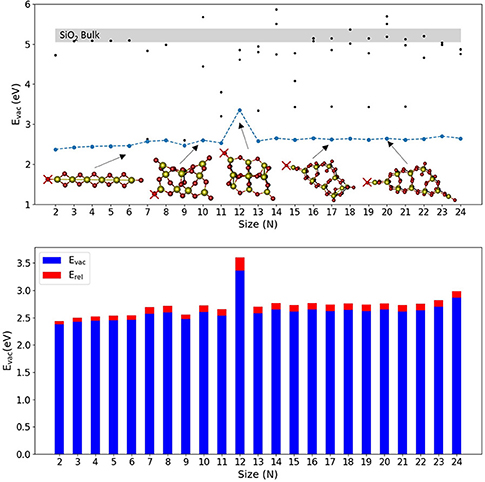
Figure 1. Top: E_vac vs. N plot of global minimum isomers for selected (SiO₂)_N nanocluster sizes. Blue line is relative to lowest E_vac obtained associated with the removal of O atoms indicated with red crosses. Black points indicate a selection of E_vac values obtained from the removal of different sites of O atoms. Light gray region indicates the range of E_vac values calculated for α-quartz SiO₂ bulk. Bottom, the corresponding oxygen vacancy formation energy values, E_vac (blue), and relaxation energy values, E_rel (red), with respect to nanocluster size.

We note that for silica nanoclusters, relaxation is found to have little impact on the energetics of oxygen removal. An analysis of Figure 1 (see Table S1 for the values) shows that E_rel is generally between 0.06 and 0.12 eV, and is thus < 5% of the corresponding E_vac. The structures of the relaxed O-deficient nanoclusters are very similar to the original stoichiometric structures. The only exception is the nanocluster structure for N = 12 that possesses two NBO sites. Oxygen vacancies originating from 2-fold coordinated oxygen atoms, which at nanoscale are less energetically favored than those generated from mono-coordinated oxygen sites, are also well-studied for bulk silica in the literature (Skuja et al., 1984; Skuja, 1998; Sulimov et al., 2002). Specifically, the ≡Si-Si≡ equilibrium distance is reported to be 2.3–2.5 Å in α-quartz (Skuja et al., 1984; Skuja, 1998; Sulimov et al., 2002). At the nanoscale, after removal of two-coordinated oxygens we find the ≡Si-Si≡ equilibrium distance to be between 2.12–2.37 Å, slightly lower with respect to the range reported for the bulk. Moreover, bulk oxygen removal is known to induce a long range structural distortion and asymmetric relaxation of atoms surrounding the vacancy (Sulimov et al., 2002). Such long-range effects are more difficult to evaluate for clusters for which the sizes range between 5 and 20 Å. However, generally we observe a relatively strong local relaxation for the neighboring atoms, whereas no significant long-range relaxation is observed (usually < 0.1 Å of total displacement for distances >3 Å from the vacancy).

The electronic structure of the oxygen-deficient non-stoichiometric silica clusters is consistently found to be a singlet, as expected. The electron density of the highest occupied state is mainly located on the O-deficient silicon site and has the shape of a sp orbital, see Figure S3.

Pure (TiO₂)_N Nanoclusters

Figure 2 shows the calculated values of E_vac for the lowest energy (TiO₂)_N nanoclusters together with selected nanocluster structures. Table S1 shows the corresponding values of E_vac, E_unrel, and E_rel obtained and Figure S4 shows the (TiO₂)_N structures used. It can be observed that the (TiO₂)_N nanocluster structures are more compact and less symmetric than silica clusters for the range selected, with titanium atoms being in 4-, 5-, and 6-fold coordinated environments. Many of these nanocluster structures, especially for sizes smaller than N = 20, possess terminal oxygen sites bonded to a Ti atom in a tetrahedral environment (≡Ti–O species). If present, these terminal oxygens are generally the least energetically costly to remove. In some cases (e.g., N = 4, 9, 11, 12), although the removal of a terminal oxygen does not have the lowest associated E_unrel value, removing a 2-fold oxygen atom nearby can lead to a reduced nanocluster with the same topology as the one that results from removing the terminal oxygen itself. E_vac values for (TiO₂)_N nanoclusters are found to oscillate between 2.48 and 5.01 eV and display no clear size-dependent trend, contrary to the case of silica nanoclusters. The energetic cost to remove an oxygen atom seems to depend critically on the structure of each cluster. In very few cases (i.e., N = 17, 22), the E_vac values for TiO₂ nanoclusters was found to be comparable with that found for SiO₂ nanoclusters. In such cases, after the relaxation, the TiO₂ nanocluster structure was found to have neither terminal oxygen sites (usually the site of the oxygen atom removal) nor 3-fold coordinated Ti defective centers, known to be highly destabilizing when left after the removal of a terminal site. We were not able to obtain a E_vac value for bulk systems with the computational setup used for the nanoclusters due to severe convergence problems associated with the presence of Ti³⁺ centers. Other authors have calculated E_vac for bulk and surfaces of anatase and rutile using DFT-based calculations employing hybrid functionals incorporating between 20 and 25% Hartree Fock exchange, obtaining values between 4.8 eV (Finazzi et al., 2008; Yamamoto and Ohno, 2012; Deák et al., 2014) and 5.4 eV (Islam et al., 2007; Janotti et al., 2010; Lee et al., 2012). We also note that the E_vac value for a terminal oxygen in an anatase bulk cut (TiO₂)₃₅ nanoparticle was calculated to be 3.95 eV, using the same methodology as employed herein (Kim et al., 2016). This value is similar to the average value of 3.65 eV, calculated for the lowest E_vac values over our set of nanoclusters. Interestingly, for the (TiO₂)₃₅ nanoparticle, the removal of an internal bulk-like three-coordinated oxygen resulted in a lower E_vac (i.e., 3.65 eV) with respect to that for removing a terminal oxygen atom. This behavior probably derives from the strong geometrical relaxation induced from the vacancy to the already metastable anatase bulk cut structure.

FIGURE 2

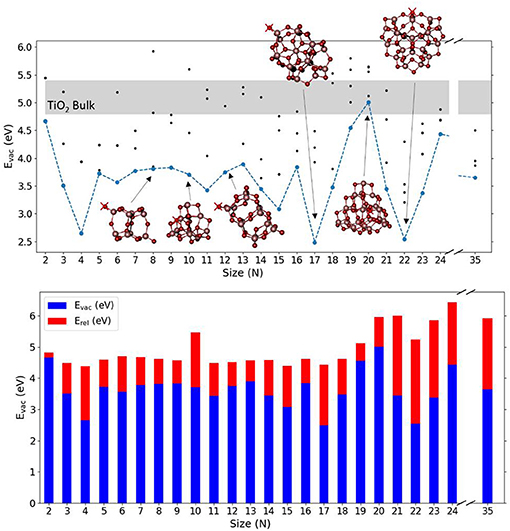
Figure 2. Top: E_vac as a function of the system size (N) for the considered (TiO₂)_N nanoclusters. Blue line is relative to lowest E_vac obtained associated with the removal of O atoms. Black points indicate a selection of E_vac values obtained from the removal of different sites of O atoms. Light gray region indicates the range of calculated TiO₂ bulk E_vac values reported in literature (see text). A selection of nanocluster structures is also shown where red crosses indicate the oxygen site that, upon removal, leads to the lowest E_vac value. Values of E_vac and E_rel for the nanoparticle with N = 35 are obtained from Kim et al. (2016). Bottom: the corresponding oxygen vacancy formation energies, E_vac (blue), and relaxation energies, E_rel (red), with respect to nanocluster size.

The relaxation of the TiO₂ nanoclusters after oxygen removal is found to involve more energy than in the case of silica nanoclusters. Specifically, the average E_rel value for the lowest energy clusters is found to be 1.50 eV, and in some cases it accounts for more than 2.5 eV (N = 21, 23). With a few exceptions, such as for N = 4, 17, 22, the removal of terminal oxygens induces a moderate degree of local relaxation. However, when 2-fold coordinated oxygen atoms are removed, significant structural rearrangements take place (i.e., N = 10, 20, 21, 23, 24). In Figure S3 we show the O-deficient structure for N = 11 where a 2-fold oxygen atom is removed in the presence of a terminal oxygen, which then subsequently moves during the relaxation to fill the vacancy.

The electronic structure of the O-deficient clusters is either a triplet with two unpaired electrons occupying two titanium sites or an open shell singlet with unpaired electrons equally delocalized around three Ti centers neighboring the vacancy. Figure S3 displays the electron density associated with the highest occupied state of the (TiO₂)₁₀ and (TiO₂)₁₁ nanocluster after the removal of an oxygen atom, which is localized on Ti³⁺ sites that carry the electrons left in the vacancy.

Mixed (Si_xTi_1–xO₂)_N Nanoclusters

In order to study the effect of mixing SiO₂ and TiO₂ on E_vac values, we have selected (Ti_xSi_1−xO₂)₁₀ nanoclusters and a Ti content x between 0 and 1. The nanocluster structures used are taken from the global optimized structures reported in Cuko et al. (2018) (see also Figure S5). The nanoclusters exhibit different isomers for pure and mixed structures. All the structures possess terminal ≡Ti-O oxygen sites, with the exception of the pure (TiO₂)₁₀ nanocluster. The pure silica (SiO₂)₁₀ nanocluster displays only silanone terminations, whereas mixed systems display typically two terminal oxygen centers bonded with titanium atoms. The presence of titanium thus seems to allow for relatively more energetically stable terminal oxygen sites than silicon (Cuko et al., 2018). Figure 3 shows that the E_vac values obtained for the mixed nanocluster systems oscillate around 3.7 eV, with the lowest value being found for x = 0.1 (E_vac = 3.29 eV) and the highest value for x = 0.3 (E_vac = 4.54 eV). The mixed nanocluster structure with x = 0.1 possesses two terminal oxygen sites bound to a Si and Ti atom. The removal of the terminal oxygen is more energetically facile (i.e., E_vac is relatively lower) when it is bound to a silicon atom rather than a titanium atom. As the content of TiO₂ increases, the E_vac values are found to initially increase up to x = 0.30, and afterwards decrease and oscillate with no obvious trend.

FIGURE 3

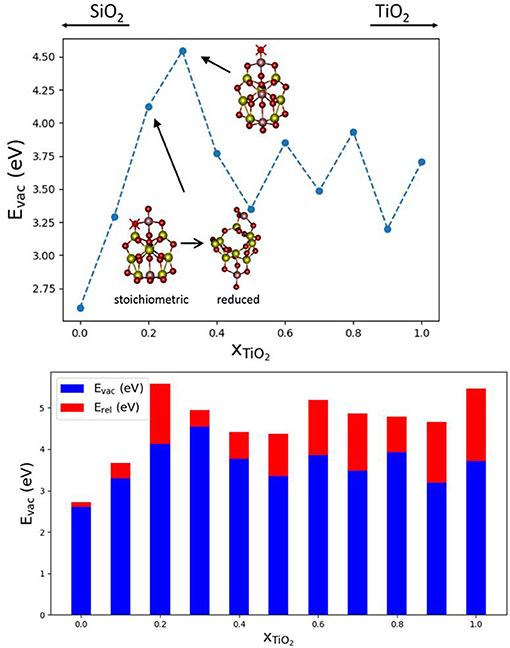
Figure 3. Top: E_vac vs. x plot; global minima isomers for (Ti_xSi_1−xO₂)₁₀ with 0 < x < 1, the red crosses indicate the O atom that, after removal, leads to the lowest E_vac. Bottom, the corresponding oxygen vacancy formation energies, E_vac (blue), and relaxation energies, E_rel (red), with respect to nanocluster composition.

Over the range of (Ti_xSi_1−xO₂)₁₀ nanoclusters, relaxation effects are relatively less significant for clusters with titania contents of x = 0.0, 0.1, 0.3. In the first two cases, indeed, the less energetically costly oxygen to be removed is from a silanone or a Si-NBO site, and therefore, the local structural relaxation effects are similar to those of pure silica systems. The system with x = 0.2 is a special case since lowest E_vac value we could find is related to the removal of a two coordinated oxygen as shown. The removal of this oxygen atom leads to a significant structural change during the geometry optimization with a consequent relatively large associated E_rel value (see Figure 3). For higher Ti content, E_rel energies are found to be in the range of 0.6–1.5 eV which is typical for pure TiO₂ nanoclusters. Overall, the mixed (Ti_xSi_1−xO₂)₁₀ nanocluster systems tend to behave more like titania nanoclusters rather than silica nanoclusters in terms of reduction through O-vacancy formation.

Discussion

The results obtained point to a (sub)nanosize dependency of the formation of oxygen vacancies in silica- and titania-based structures. Firstly, the removal of singly-coordinated terminal oxygen atoms is often associated with low E_vac values. This is explained by the low energetic cost of breaking an M-O bond compared with the energy required to break two M–O bonds for oxygen atoms in 2-fold coordinated sites. This is observed in the three types of nanoclusters studied in this work and has been reported in the literature for other oxides, especially in systems exhibiting structural stable dangling bonds. For instance, V₂O₅ in bulk, surface and clusters exhibit structurally stable terminal oxygen sites. The coordination of oxygen sites in vanadia is commonly associated with chemical reactivity (Calatayud and Minot, 2006; Ganduglia-Pirovano et al., 2007; Calatayud et al., 2008b). The lower E_vac found for nanoclusters compared to bulk values indicates higher reducibility of the nanosized materials as has been reported for other oxide systems like CeO₂ and ZrO₂ (Bruix and Neyman, 2016; Ruiz Puigdollers et al., 2016b).

It is, however, worth noting that the lowest E_vac values found for silica clusters, 2.3–3.6 eV, are generally lower than for titania clusters, 2.48–5.01 eV as also shown from Figures 1, 2 and Table S1. A direct comparison between bulk SiO₂ and bulk TiO₂ was not possible in this study due to the high computational cost and convergence problems with TiO₂ systems. However, there are several studies on O vacancy defects formation in metal oxides (Pacchioni, 2008; Deml et al., 2015; Helali et al., 2017) that agree on associating a higher reducibility to titania (either rutile and anatase phases) with respect to silica bulk (mainly α-quartz). Our results suggest that silica becomes more reducible than titania at the nanoscale, which is contrary to the properties observed for respective bulk materials. The reason for such inverted behavior seems to be connected to the presence of terminal silanone oxygen atoms in low energy silica nanoclusters. The electronic structure (projected density of states) of this site is displayed in Figure 4, showing that the energy levels are highly localized in two sharp peaks (one between −9 and −10 eV, and the other between −10.5 and −11.5 eV) associated to higher reactivity. In comparison, the oxygen levels of the 2-fold oxygen in (TiO₂)₁₀ are distributed over a 3 eV range of energies (between −9 and −12 eV). In the (TiO₂)₁₁ cluster, the electronic energy levels associated with the dangling oxygen lay closer to the Fermi level, between −9 and −11 eV, and those associated with the 2-fold coordinated site levels spread between −9 and −13 eV. The electronic structure of the dangling silanone oxygen in silica is consistent with an enhanced reactivity of this site and with the low E_vac values shown. Interestingly, the oxygen vacancy in bulk silica has been reported to exhibit specific electronic transitions associated with the electron pair localized on the silicon atom after reduction (Cannizzo and Leone, 2004; Sushko et al., 2005). We also observe the highest occupied electronic level of O-deficient (SiO₂)₁₀ cluster localized on the resulting Si < site (Figure S3 top right), which is consistent with the presence of an electron pair localized on the silicon site.

FIGURE 4

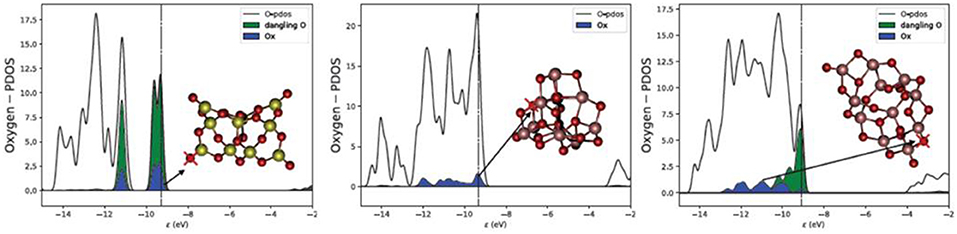
Figure 4. Projected density of states (PDOS) on for oxygen atoms for (SiO₂)₁₀ (left), (TiO₂)₁₀ (middle), and (TiO₂)₁₁ (right). Ox indicates the projection on the oxygen center marked with a cross (blue). Dangling O indicates the projection on all single terminal oxygen sites (green). Vertical lines indicate the position of the Fermi level. The PDOS plot has been smeared for clarity.

A second important point is the structure-dependency of the E_vac values. In the case of silica nanoclusters, the E_vac value is almost constant and related to the presence of Si sites with dangling silanone oxygen sites. However, titania nanoclusters display a greater range of E_vac values, depending on the structure near to the removed oxygen atom. Relaxation effects can also be significantly stronger in titania nanoclusters than in silica nanoclusters, which is consistent with the greater variety of E_vac sites and values found. The size dependency of E_vac values is also different for each nanomaterial. For the system sizes considered here, the majority of silica nanoclusters exhibit a near constant value of E_vac ~ 2.6 eV associated with silanone sites, and exceptionally an E_vac value of 3.6 eV associated with the NBO in the (SiO₂)₁₂ nanocluster. For larger sizes, silica nanoclusters are predicted to become fully-coordinated (Flikkema and Bromley, 2009), which will result in a jump of E_vac to near bulk values ~5 eV. As can be seen in Figure S2, 2-fold coordinated oxygens cost 4.4–5.5 eV. In the case of pure titania nanoclusters there seems to be no clear trend with size.

Finally, mixing nanosilica and nanotitania results in chemically and structurally rich nanocluster systems displaying a variety of oxygen sites. Interestingly the presence of titanium induces the disappearance of silanone sites in favor of pyramidal ≡Ti–O species. Whereas terminal oxygen sites are relatively unstable when bonded to silicon, they are stabilized when bonded to titanium. As for pure titania nanoclusters, the values of E_vac are found to strongly depend on the structure, the coordination of the oxygen removed, and the degree of relaxation after oxygen removal.

In order to further study the role of the chemical nature of Si and Ti in the oxygen vacancy energy, we consider a set of (Ti_xSi_1−xO₂)₁₀ structural isomers with the same topology (Figure 5), with selected compositions between x = 0–1. Such isomer structures are global minima for titanosilicates with x = 0.1, 0.2, and 0.3, and are slightly less stable than the global minima for pure systems. They have been geometrically optimized in their stoichiometric composition. We then remove each non-equivalent oxygen atom keeping the initial geometry frozen. In Figure 5 we report the resulting unrelaxed oxygen vacancy formation energies (E_unrel).

FIGURE 5

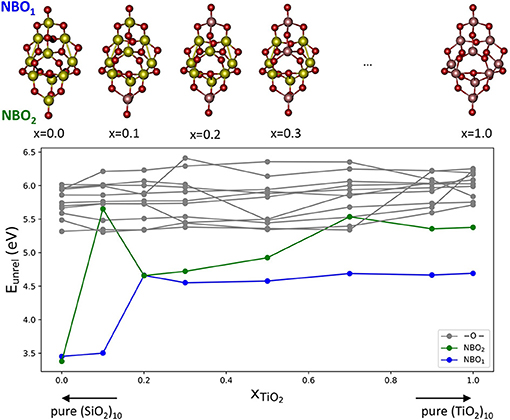
Figure 5. Top: a set of (Ti_xSi_1−xO₂)₁₀ cluster structures exhibiting the same structural isomer for pure silica (x = 0), pure titania (x = 1) and all intermediate compositions. Bottom: the corresponding oxygen formation energy without relaxation (E_unrel) in eV for all non-equivalent oxygen sites. Vacancies are generated after removing a 2-fold coordinated oxygen (gray), terminal NBO₁ (blue), and terminal NBO₂ (green).

Figure 5 shows E_unrel as a function of the mixing composition x_TiO2 of the cluster. In the plot there are three families of oxygen vacancies according of the type of oxygen removed: the vacancies originating from the removal of two-coordinated oxygen atoms are denoted in gray, whereas those originating from removing the terminal oxygen sites labeled NBO₁ and NBO₂, respectively, are denoted in blue and green. In most of the cases, vacancies at terminal position are found to provide the lowest E_unrel value. For the pure silica cluster isomer, the E_unrel values for the NBO₁ and NBO₂ are 3.38 and 3.45 eV, respectively, which values are significantly lower than the corresponding values for pure titania systems, 4.69 and 5.38 eV. This result further confirms that the oxygen vacancy formation energy is driven by the presence of unsaturated O centers and, particularly when such centers are bonded to Si atoms, are more easily removed than when they are bonded to Ti atoms. This is clearly seen in the x = 0.1 isomer that possesses one terminal oxygen on Si and one on Ti: the E_unrel for the Si-bonded oxygen NBO₁ is 3.50 eV whereas for the Ti-bonded oxygen NBO₂ it is 5.65 eV. Although relaxation effects have not been considered, based on the results discussed above, they are not expected to be significant. Therefore, the nature of the cationic site, Si or Ti, seems to critically determine the stabilization of the terminal oxygen deficient systems.

Conclusions

In this work we use DFT-based calculations employing the PBE0 hydrid functional to explore oxygen vacancy formation in globally optimized TiO₂, SiO₂, and mixed Ti_xSi_1−xO₂ nanoclusters for sizes between 2 and 24 stoichiometric oxide units. The properties computed (oxygen vacancy formation energies, electronic structure, nanocluster structure, relaxation effects) are found to critically depend on the nature of the oxide. The behavior of silica nanoclusters is found to be rather constant and dominated by the presence of dangling oxygens in silanone >Si = O sites. In titania and titanosilicate nanoclusters; however, we find a strong dependence of the properties with respect to the local geometry. When unsaturated oxygen centers are present in the system, removing such centers is energetically less costly than removing two-coordinated oxygen atoms. Since at the nanoscale such unsaturated centers are naturally present in low energy systems, contrary to the bulk and extended surfaces, we can predict that the reduction of nanosized silica clusters is energetically more favorable than in the bulk. Furthermore, we found that the oxygen vacancy formation in silica nanoclusters is also more favorable than from similar-sized low energy titania nanoclusters. This demonstrates the emergence of an unexpected chemical behavior induced by the small size of the systems considered. We hope that our results will help in the search of novel materials for applications in scientific and technological fields such as heterogeneous catalysis, electronics, and cluster chemistry.

Author Contributions

AC performed all the calculations, figures, tables, analyzed the data, discussed results, and participated in the elaboration of the manuscript. SB and MC directed the work, discussed the data, and wrote the manuscript.

Funding

This research was supported by the H2020 project ITN-EJD-642294 (TCCM: Theoretical Chemistry and Computational Modeling). The Spanish MINECO/AEI-FEDER grant: CTQ2015-64618-R and, in part, Generalitat de Catalunya grants: 2017SGR13 and XRQTC are acknowledged.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We also acknowledge support from the Spanish MCIU Maria de Maeztu award MDM-2017-0767. The GENCI-CINES/IDRIS (Grant 2016-x2016082131, 2017-x2017082131, 2018-x2018082131) and the Red Española de Supercomputación provided valuable computing time.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2019.00037/full#supplementary-material

Supplementary Data Sheet 1. Oxygen vacancy formation energies with and without relaxation (E_vac, E_unrel, E_rel), nanocluster structures employed, E_vac values for different O-vacancies, electron density plots of selected O-deficient structures.

References

Adamo, C., and Barone, V. (1999). Toward reliable density functional methods without adjustable parameters: the PBE0 model. J. Chem. Phys. 110, 6158–6170. doi: 10.1063/1.478522

CrossRef Full Text | Google Scholar

Aguilera-Granja, F., Vega, A., and Balbás, L. C. (2016). New structural and electronic properties of (TiO₂)₁₀. J. Chem. Phys. 144, 234312–234312. doi: 10.1063/1.4954060

PubMed Abstract | CrossRef Full Text | Google Scholar

Albanese, E., Ruiz Puigdollers, A., and Pacchioni, G. (2018). Theory of ferromagnetism in reduced ZrO_2−x nanoparticles. ACS Omega 3, 5301–5307. doi: 10.1021/acsomega.8b00667

CrossRef Full Text | Google Scholar

Avakyan, V. G., Sidorkin, V. F., Belogolova, E. F., Guselnikov, S. L., and Gusel'nikov, L. E. (2006). AIM and ELF electronic structure/G2 and G3 π-bond energy relationship for doubly bonded silicon species, H₂Si_X (X = E¹⁴H₂, E¹⁵H, E¹⁶)¹. Organometallics 25, 6007–6013. doi: 10.1021/om0605478

CrossRef Full Text | Google Scholar

Bawazer, L. A., Izumi, M., Kolodin, D., Neilson, J. R., Schwenzer, B., and Morse, D. E. (2012). Evolutionary selection of enzymatically synthesized semiconductors from biomimetic mineralization vesicles. Proc. Nat. Acad. Sci. 109, E1705–E1714. doi: 10.1073/pnas.1116958109

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhattacharya, S., Sonin, B. H., Jumonville, C. J., Ghiringhelli, L. M., and Marom, N. (2015). Computational design of nanoclusters by property-based genetic algorithms: tuning the electronic properties of (TiO₂)_n clusters. Phys. Rev. B 91, 241115–241115. doi: 10.1103/PhysRevB.91.241115

CrossRef Full Text | Google Scholar

Blum, V., Gehrke, R., Hanke, F., Havu, P., Havu, V., Ren, X., et al. (2009). Ab initio molecular simulations with numeric atom-centered orbitals. Computer Phys. Commun. 180, 2175–2196. doi: 10.1016/j.cpc.2009.06.022

CrossRef Full Text | Google Scholar

Bromley, S. T., and Flikkema, E. (2005). Columnar-to-disk structural transition in nanoscale (SiO₂)_N clusters. Phys. Rev. Lett. 95:185505. doi: 10.1103/physrevlett.95.185505

CrossRef Full Text | Google Scholar

Bruix, A., and Neyman, K. M. (2016). Modeling ceria-based nanomaterials for catalysis and related applications. Catalysis Lett. 146, 2053–2080. doi: 10.1007/s10562-016-1799-1

CrossRef Full Text | Google Scholar

Calatayud, M., Maldonado, L., and Minot, C. (2008a). Reactivity of (TiO₂)_N clusters (N = 1-10): probing gas-phase acidity and basicity properties. J. Phys. Chem. C 112, 16087–16095. doi: 10.1021/jp802851q

CrossRef Full Text | Google Scholar

Calatayud, M., and Minot, C. (2006). Reactivity of the V₂O₅-TiO₂-anatase catalyst: role of the oxygen sites. Top. Catalysis 41, 17–26. doi: 10.1007/s11244-006-0090-x

CrossRef Full Text | Google Scholar

Calatayud, M., Tielens, F., and De Proft, F. (2008b). Reactivity of gas-phase, crystal and supported V₂O₅ systems studied using density functional theory based reactivity indices. Chem. Phys. Lett. 456, 59–63. doi: 10.1016/j.cplett.2008.03.007

CrossRef Full Text | Google Scholar

Cannizzo, A., and Leone, M. (2004). Conformational disorder and optical properties of point defects in vitreous silica. Philos. Mag. A 84, 1651–1657. doi: 10.1080/14786430310001644440

CrossRef Full Text | Google Scholar

Causà, M., D'Amore, M., Gentile, F., Menendez, M., and Calatayud, M. (2015). Electron localization function and maximum probability domains analysis of semi-ionic oxides crystals, surfaces and surface defects. Comput. Theor. Chem. 1053, 315–321. doi: 10.1016/j.comptc.2014.11.001

CrossRef Full Text | Google Scholar

Chen, M., and Dixon, D. A. (2013). Tree growth—Hybrid genetic algorithm for predicting the structure of small (TiO₂)_n, n = 2–13, nanoclusters. J. Chem. Theor. Comput. 9, 3189–3200. doi: 10.1021/ct400105c

PubMed Abstract | CrossRef Full Text | Google Scholar

Cuko, A., Calatayud, M., and Bromley, S. T. (2018). Stability of mixed-oxide titanosilicates: dependency on size and composition from nanocluster to bulk. Nanoscale 10, 832–842. doi: 10.1039/C7NR05758J

PubMed Abstract | CrossRef Full Text | Google Scholar

Das, K., Bose, S., and Bandyopadhyay, A. (2009). TiO₂ nanotubes on Ti: influence of nanoscale morphology on bone cell–materials interaction. J. Biomed. Mater. Res. Part A 90A, 225–237. doi: 10.1002/jbm.a.32088

CrossRef Full Text | Google Scholar

Deák, P., Kullgren, J., and Frauenheim, T. (2014). Polarons and oxygen vacancies at the surface of anatase TiO₂. Phys. Status Solidi Rapid Res. Lett. 8, 583–586. doi: 10.1002/pssr.201409139

CrossRef Full Text | Google Scholar

Deml, A. M., Holder, A. M., O'Hayre, R. P., Musgrave, C. B., and Stevanovic, V. (2015). Intrinsic material properties dictating oxygen vacancy formation energetics in metal oxides. J. Phys. Chem. Lett. 6, 1948–1953. doi: 10.1021/acs.jpclett.5b00710

PubMed Abstract | CrossRef Full Text | Google Scholar

Di Valentin, C., Pacchioni, G., and Selloni, A. (2006). Electronic structure of defect states in hydroxylated and reduced rutile TiO₂(110) surfaces. Phys. Rev. Lett. 97:166803. doi: 10.1103/PhysRevLett.97.166803

CrossRef Full Text | Google Scholar

Diebold, U. (2003). The surface science of titanium dioxide. Surf. Sci. Rep. 48, 53–229. doi: 10.1016/S0167-5729(02)00100-0

CrossRef Full Text | Google Scholar

Finazzi, E., Valentin, C. D., Pacchioni, G., and Selloni, A. (2008). Excess electron states in reduced bulk anatase TiO₂: comparison of standard GGA, GGA+U, and hybrid DFT calculations. J. Chem. Phys. 129:154113. doi: 10.1063/1.2996362

CrossRef Full Text | Google Scholar

Flikkema, E., and Bromley, S. T. (2003). A new interatomic potential for nanoscale silica. Chem. Phys. Lett. 378, 622–629. doi: 10.1016/j.cplett.2003.07.017

CrossRef Full Text | Google Scholar

Flikkema, E., and Bromley, S. T. (2004). Dedicated global optimization search for ground state silica nanoclusters:~ (SiO₂)_N (N = 6–12). J. Phys. Chem. B 108, 9638–9645. doi: 10.1021/jp049783r

CrossRef Full Text | Google Scholar

Flikkema, E., and Bromley, S. T. (2009). Defective to fully coordinated crossover in complex directionally bonded nanoclusters. Phys. Rev. B 80:035402. doi: 10.1103/PhysRevB.80.035402

CrossRef Full Text | Google Scholar

Ganduglia-Pirovano, M. V., Hofmann, A., and Sauer, J. (2007). Oxygen vacancies in transition metal and rare earth oxides: current state of understanding and remaining challenges. Surface Sci. Rep. 62, 219–270. doi: 10.1016/j.surfrep.2007.03.002

CrossRef Full Text | Google Scholar

Hamad, S., Catlow, C. R. A., Woodley, S. M., Lago, S., and Mejias, J. A. (2005). Structure and stability of small TiO₂ nanoparticles. J. Phys. Chem. B 109, 15741–15748. doi: 10.1021/jp0521914

PubMed Abstract | CrossRef Full Text | Google Scholar

Helali, Z., Jedidi, A., Syzgantseva, O. A., Calatayud, M., and Minot, C. (2017). Scaling reducibility of metal oxides. Theor. Chem. Accounts 136:100. doi: 10.1007/s00214-017-2130-y

CrossRef Full Text | Google Scholar

Houlihan, J. F., Danley, W. J., and Mulay, L. N. (1975). Magnetic susceptibility and EPR spectra of titanium oxides: correlation of magnetic parameters with transport properties and composition. J. Solid State Chem. 12, 265–269. doi: 10.1016/0022-4596(75)90317-5

CrossRef Full Text | Google Scholar

Howie, R. A. (1964). Pleochroism of orthopyroxenes. Nature 204:279. doi: 10.1038/204279a0

CrossRef Full Text | Google Scholar

Islam, M. M., Bredow, T., and Gerson, A. (2007). Electronic properties of oxygen-deficient and aluminum-doped rutile TiO₂ from first principles. Phys. Rev. B 76:045217. doi: 10.1103/PhysRevB.76.045217

CrossRef Full Text | Google Scholar

Janotti, A., Varley, J. B., Rinke, P., Umezawa, N., Kresse, G., and Van de Walle, C. G. (2010). Hybrid functional studies of the oxygen vacancy in TiO₂. Phys. Rev. B 81:085212. doi: 10.1103/PhysRevB.81.085212

CrossRef Full Text | Google Scholar

Joo, J. B., Dillon, R., Lee, I., Yin, Y., Bardeen, C. J., and Zaera, F. (2014). Promotion of atomic hydrogen recombination as an alternative to electron trapping for the role of metals in the photocatalytic production of H₂. Proc. Nat. Acad. Sci. 111, 7942–7947. doi: 10.1073/pnas.1405365111

PubMed Abstract | CrossRef Full Text | Google Scholar

Kapilashrami, M., Zhang, Y., Liu, Y.-S., Hagfeldt, A., and Guo, J. (2014). Probing the optical property and electronic structure of TiO₂ nanomaterials for renewable energy applications. Chem. Rev. 114, 9662–9707. doi: 10.1021/cr5000893

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, S., Ko, K. C., Lee, J. Y., and Illas, F. (2016). Single oxygen vacancies of (TiO₂)₃₅ as a prototype reduced nanoparticle: implication for photocatalytic activity. Phys. Chem. Chem. Phys. 18, 23755–23762. doi: 10.1039/C6CP04515D

PubMed Abstract | CrossRef Full Text | Google Scholar

Komatsu, M., Fagan, T. J., Krot, A. N., Nagashima, K., Petaev, M. I., Kimura, M., et al. (2018). First evidence for silica condensation within the solar protoplanetary disk. Proc. Nat. Acad. Sci. 115, 7497–7502. doi: 10.1073/pnas.1722265115

PubMed Abstract | CrossRef Full Text | Google Scholar

Kozlov, S. M., Demiroglu, I., Neyman, K. M., and Bromley, S. T. (2015). Reduced ceria nanofilms from structure prediction. Nanoscale 7, 4361–4366. doi: 10.1039/C4NR07458K

PubMed Abstract | CrossRef Full Text | Google Scholar

Lakshtanov, D. L., Sinogeikin, S. V., Litasov, K. D., Prakapenka, V. B., Hellwig, H., Wang, J., et al. (2007). The post-stishovite phase transition in hydrous alumina-bearing SiO₂ in the lower mantle of the earth. Proc. Nat. Acad. Sci. 104, 13588–13590. doi: 10.1073/pnas.0706113104

PubMed Abstract | CrossRef Full Text | Google Scholar

Lambert, J.-F., Sodupe, M., and Ugliengo, P. (2012). Prebiotic chemistry. Chem. Soc. Rev. 41, 5373–5374. doi: 10.1039/C2CS90061K

PubMed Abstract | CrossRef Full Text | Google Scholar

Lamiel-Garcia, O., Cuko, A., Calatayud, M., Illas, F., and Bromley, S. T. (2017). Predicting size-dependent emergence of crystallinity in nanomaterials: titania nanoclusters versus nanocrystals. Nanoscale 9, 1049–1058. doi: 10.1039/C6NR05788H

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, G., Helling, C., Giles, H., and Bromley, S. T. (2015). Dust in brown dwarfs and extra-solar planets. A&A 575:A11. doi: 10.1051/0004-6361/201424621

CrossRef Full Text | Google Scholar

Lee, H.-Y., Clark, S. J., and Robertson, J. (2012). Calculation of point defects in rutile TiO₂ by the screened-exchange hybrid functional. Phys. Rev. B 86:075209. doi: 10.1103/PhysRevB.86.075209

CrossRef Full Text | Google Scholar

Li, J., Lazzari, R., Chenot, S., and Jupille, J. (2018). Contributions of oxygen vacancies and titanium interstitials to band-gap states of reduced titania. Phys. Rev. B 97:041403. doi: 10.1103/PhysRevB.97.041403

CrossRef Full Text | Google Scholar

Lu, W. C., Wang, C. Z., Nguyen, V., Schmidt, M. W., Gordon, M. S., and Ho, K. M. (2003). Structures and fragmentations of small silicon oxide clusters by ab initio calculations. J. Phys. Chem. A 107, 6936–6943. doi: 10.1021/jp027860h

CrossRef Full Text | Google Scholar

Lucky, S. S., Idris, N. M., Huang, K., Kim, J., Li, Z., Thong, P. S., et al. (2016). In vivo biocompatibility, biodistribution and therapeutic efficiency of titania coated upconversion nanoparticles for photodynamic therapy of solid oral cancers. Theranostics 6, 1844–1865. doi: 10.7150/thno.15088

PubMed Abstract | CrossRef Full Text | Google Scholar

Lyle, M. J., Pickard, C. J., and Needs, R. J. (2015). Prediction of 10-fold coordinated TiO₂ and SiO₂ structures at multimegabar pressures. Proc. Nat. Acad. Sci. 112, 6898–6901. doi: 10.1073/pnas.1500604112

PubMed Abstract | CrossRef Full Text | Google Scholar

Mal, N. K., Fujiwara, M., and Tanaka, Y. (2003). Photocontrolled reversible release of guest molecules from coumarin-modified mesoporous silica. Nature 421, 350. doi: 10.1038/nature01362

PubMed Abstract | CrossRef Full Text | Google Scholar

Manveer, S. M., David, Z. G., and Alexander, L. S. (2017). Diffusion and aggregation of oxygen vacancies in amorphous silica. J. Phys. Condensed Matter 29:245701. doi: 10.1088/1361-648x/aa6f9a

CrossRef Full Text | Google Scholar

McPherson, J. W., and Mogul, H. C. (1998). Underlying physics of the thermochemical E model in describing low-field time-dependent dielectric breakdown in SiO₂ thin films. J. Appl. Phys. 84, 1513–1523. doi: 10.1063/1.368217

CrossRef Full Text | Google Scholar

Mehonic, A., Shluger, A. L., Gao, D., Valov, I., Miranda, E., Ielmini, D., et al. (2018). Silicon oxide (SiOx): a promising material for resistance switching? Adv. Mater. 30:1801187. doi: 10.1002/adma.201801187

CrossRef Full Text | Google Scholar

Morales-García, Á., Lamiel-García, O., Valero, R., and Illas, F. (2018). Properties of single oxygen vacancies on a realistic (TiO₂)₈₄ nanoparticle: a challenge for density functionals. J. Phys. Chem. C 122, 2413–2421. doi: 10.1021/acs.jpcc.7b11269

CrossRef Full Text | Google Scholar

Na-Phattalung, S., Smith, M. F., Kim, K., Du, M.-H., Wei, S.-H., Zhang, S. B., et al. (2006). First-principles study of native defects in anatase TiO₂. Phys. Rev. B 73:125205. doi: 10.1103/PhysRevB.73.125205

CrossRef Full Text | Google Scholar

Nguyen, T. D., Tseng, H.-R., Celestre, P. C., Flood, A. H., Liu, Y., Stoddart, J. F., et al. (2005). A reversible molecular valve. Proc. Nat. Acad. Sci. U.S.A. 102, 10029–10034. doi: 10.1073/pnas.0504109102

PubMed Abstract | CrossRef Full Text | Google Scholar

Pacchioni, G. (2008). Modeling doped and defective oxides in catalysis with density functional theory methods: room for improvements. J. Chem. Phys. 128:182505. doi: 10.1063/1.2819245

CrossRef Full Text | Google Scholar

Pacchioni, G., and Ferrario, R. (1998). Optical transitions and EPR properties of two-coordinated Si, Ge, Sn and related $H(mathrm{I}),$ $H(mathrm{II}),$ and $H(mathrm{III})$ centers in pure and doped silica from ab initio calculations. Phys. Rev. B 58, 6090–6096. doi: 10.1103/PhysRevB.58.6090

CrossRef Full Text | Google Scholar

Rahman, M. A., Rout, S., Thomas, J. P., McGillivray, D., and Leung, K. T. (2016). Defect-rich dopant-free ZrO₂ nanostructures with superior dilute ferromagnetic semiconductor properties. J. Am. Chem. Soc. 138, 11896–11906. doi: 10.1021/jacs.6b06949

PubMed Abstract | CrossRef Full Text | Google Scholar

Rudra, J. K., and Fowler, W. B. (1987). Oxygen vacancy and the E${}_1^{{}^{\text{′}}}$ center in crystalline SiO₂. Phys. Rev. B 35, 8223–8230. doi: 10.1103/PhysRevB.35.8223

CrossRef Full Text | Google Scholar

Ruiz Puigdollers, A., Illas, F., and Pacchioni, G. (2016a). Structure and properties of zirconia nanoparticles from density functional theory calculations. J. Phys. Chem. C 120, 4392–4402. doi: 10.1021/acs.jpcc.5b12185

CrossRef Full Text | Google Scholar

Ruiz Puigdollers, A., Tosoni, S., and Pacchioni, G. (2016b). Turning a nonreducible into a reducible oxide via nanostructuring: opposite behavior of bulk ZrO₂ and ZrO₂ nanoparticles toward H₂ adsorption. J. Phys. Chem. C 120, 15329–15337. doi: 10.1021/acs.jpcc.6b05984

CrossRef Full Text | Google Scholar

Saroj, S., and Rajput, S. J. (2018). Composite smart mesoporous silica nanoparticles as promising therapeutic and diagnostic candidates: recent trends and applications. J. Drug Deliv. Sci. Technol. 44, 349–365. doi: 10.1016/j.jddst.2018.01.014

CrossRef Full Text | Google Scholar

Silvi, B., and D'Arco, P. (Eds.). (2006). Modelling of Minerals and Silicated Materials. New York, NY; Boston, MA; Dordrecht; London; Moscow: Kluwer Academic Publishers.

Google Scholar

Skuja, L. (1998). Optically active oxygen-deficiency-related centers in amorphous silicon dioxide. J. Non-Crystalline Solids 239, 16–48. doi: 10.1016/S0022-3093(98)00720-0

CrossRef Full Text | Google Scholar

Skuja, L. N., Streletsky, A. N., and Pakovich, A. B. (1984). A new intrinsic defect in amorphous SiO₂: two-fold coordinated silicon. Solid State Commun. 50, 1069–1072. doi: 10.1016/0038-1098(84)90290-4

CrossRef Full Text | Google Scholar

Sulimov, V. B., Sushko, P. V., Edwards, A. H., Shluger, A. L., and Stoneham, A. M. (2002). Asymmetry and long-range character of lattice deformation by neutral oxygen vacancy in ensuremath{alpha}-quartz. Phys. Rev. B 66:024108. doi: 10.1103/PhysRevB.66.024108

CrossRef Full Text | Google Scholar

Sun, X., Zhou, S., Schlangen, M., and Schwarz, H. (2016). Thermal methane activation by [Si₂O₅].+ and [Si₂O₅H₂].+: reactivity enhancement by hydrogenation. Angew. Chem. Int. Ed. 55, 13345–13348. doi: 10.1002/anie.201607864

CrossRef Full Text | Google Scholar

Sushko, P. V., Mukhopadhyay, S., Stoneham, A. M., and Shluger, A. L. (2005). Oxygen vacancies in amorphous silica: structure and distribution of properties. Microelectron. Eng. 80, 292–295. doi: 10.1016/j.mee.2005.04.083

CrossRef Full Text | Google Scholar

Syzgantseva, O. A., Gonzalez-Navarrete, P., Calatayud, M., Bromley, S., and Minot, C. (2011). Theoretical investigation of the hydrogenation of (TiO₂)_N clusters (N = 1–10). J. Phys. Chem. C 115, 15890–15899. doi: 10.1021/jp2050349

CrossRef Full Text | Google Scholar

Vajda, S., and White, M. G. (2015). Catalysis applications of size-selected cluster deposition. ACS Catalysis 5, 7152–7176. doi: 10.1021/acscatal.5b01816

CrossRef Full Text | Google Scholar

Vásquez, G. C., Karazhanov, S. Z., Maestre, D., Cremades, A., Piqueras, J., and Foss, S. E. (2016). Oxygen vacancy related distortions in rutile TiO₂ nanoparticles: a combined experimental and theoretical study. Phys. Rev. B 94:235209. doi: 10.1103/PhysRevB.94.235209

CrossRef Full Text | Google Scholar

Wang, G., Raji, A.-R. O., Lee, J.-H., and Tour, J. M. (2014). Conducting-interlayer SiOx memory devices on rigid and flexible substrates. ACS Nano 8, 1410–1418. doi: 10.1021/nn4052327

PubMed Abstract | CrossRef Full Text | Google Scholar

Woodley, S. M., Hamad, S., Mejías, J. A., and Catlow, C. R. A. (2006). Properties of small TiO₂, ZrO₂ and HfO₂ nanoparticles. J. Mater. Chem. 16, 1927–1933. doi: 10.1039/B600662K

CrossRef Full Text | Google Scholar

Yamamoto, T., and Ohno, T. (2012). A hybrid density functional study on the electron and hole trap states in anatase titanium dioxide. Phys. Chem. Chem. Phys. 14, 589–598. doi: 10.1039/C1CP21547G

PubMed Abstract | CrossRef Full Text | Google Scholar

Yao, J., Sun, Z., Zhong, L., Natelson, D., and Tour, J. M. (2010). Resistive switches and memories from silicon oxide. Nano Lett. 10, 4105–4110. doi: 10.1021/nl102255r

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, S., and Bernstein, E. R. (2014). Experimental and theoretical studies of H₂O oxidation by neutral Ti₂O_{4, 5} clusters under visible light irradiation. Phys. Chem. Chem. Phys. 16, 13900–13908. doi: 10.1039/C4CP00097H

PubMed Abstract | CrossRef Full Text | Google Scholar

Zwijnenburg, M. A., Sokol, A. A., Sousa, C., and Bromley, S. T. (2009). The effect of local environment on photoluminescence: a time-dependent density functional theory study of silanone groups on the surface of silica nanostructures. J. Chem. Phys. 131:034705. doi: 10.1063/1.3155083

CrossRef Full Text | Google Scholar