An Experimental Validated Computational Method for pKa Determination of Substituted 1,2-Dihydroxybenzenes

Introduction

1,2-dihydroxybenzenes (DHBs) are organic compounds that exhibit antioxidant and/or pro-oxidant activities in several biological systems (Iwahashi et al., 1989; Moran et al., 1997; Nakamura et al., 2000; Schweigert et al., 2001; Gomes et al., 2003; Zang et al., 2003; Ohara et al., 2006; Prousek, 2007) depending on the reaction conditions (Salgado et al., 2013; Melin et al., 2015). These compounds have actively participate in important biochemical processes, which are shown in Figure 1.

FIGURE 1

Figure 1. Applications and biochemical processes in which 1,2-DHB have been studied.

The antioxidant properties of DHBs are based on its radical scavenging properties (disrupting the radical chain reaction propagation) or iron chelating (disrupting the initiation step of the radical chain reaction) (Perron and Brumaghim, 2009). This role is important in plants' defense mechanisms against pathogens (Lukasik, 2007) and these antioxidant properties are present in different kinds of food, such as wine, honey, tea and blueberries (Ricci et al., 2018; Santhakumar et al., 2018; Yang et al., 2018).

Pro-oxidant activities of DHBs have also been widely studied in wood biodegradation caused by brown and white rot fungi. DHBs are produced by fungi as a type of non-enzymatic degradation mechanism that could penetrate through the wood cell wall matrix and degrade the wood by redox reactions (Goodell et al., 2006). In humans, dopamine, a kind of DHB, has been related to the progression of Parkinson's disease due to oxidative stress (Kuhn et al., 1999). In addition, the oxidation of catecholamines by reperfusion could generate oxidative stress and increase the cellular damage at cardiac level (Bindoli et al., 1992; Schweigert et al., 2001). Pro-oxidant properties of these compounds are based on their ability to reduce Fe(III) and O₂ to Fe(II) and HO₂, respectively. In the same way, DHBs have been used to increase the oxidant properties of Fenton's reagent on recalcitrant compound; thus, these compounds also have potential applications in advanced oxidation processes (AOPs) (Rodríguez et al., 1999; Rodriguez et al., 2003; Rodríguez et al., 2004).

The pro-oxidant and antioxidant activities of the DHBs are closely related to the formation of complexes with metals, which require the deprotonation of the hydroxyl groups (Avdeef et al., 1978; Hynes and Ó Coinceanainn, 2001; Hynes and O'Coinceanainn, 2004). Moreover, the kind of complex formed between DHB and metals is related to the pKa values of DHB (Jameson and Wilson, 1972; Pizer and Babcock, 1977; McBride et al., 1988). Considering this, and the wide application of DHBs, knowledge of the pKa values of each hydroxyl group becomes necessary.

For some commercially available DHB, pKa values have been reported under different methods or experimental conditions. This leads to situations where the reported pKa values show significant differences. Table 1 shows that in the case of catechol, there are several reports of pKa. These works assign values between 9.14 (Nurchi et al., 2009) and 9.43 (Park, 1963) pH units for the first pKa, and values between 11.49 (Pizer and Babcock, 1977) and 13.8 pH units (Nurchi et al., 2009) for the second pKa. Compounds such as 3,4-dihydroxybenzoic acid, 4-nitrocatechol, caffeic acid, and dopamine are also under similar situations.

TABLE 1

Table 1. pKa values for the hydroxyl group reported for different DHBs.

There are different methods used to calculate the pKa value for a compound. In general, these can be divided into experimental or computational methods. The experimental methods involve the monitoring of a physical property that varies with protonation of the molecule (Reijenga et al., 2013). Computational methods generally determine the pKa values by using thermodynamic cycles (Pliego, 2003). Computational methods have the advantage of having relatively good accuracy, low cost (Pathare et al., 2014), and facilitate determinations of pKa values at pH ranges where the compound lose solubility. However, to obtain good results, it is highly important to perform calculations using an adequate model of solvation (Sharma and Kaminski, 2012) and possess experimental data to validate the computational results.

It is interesting to obtain the pKa values of DHBs by reproducible and validated methods in aqueous solution, since these compounds have a wide range of applications in biological systems. In the literature, it is possible to find calculated pKa values for these molecules in dimethyl sulphoxide (DMSO) (Zhu et al., 2010), however, it is not possible to infer the same behavior in aqueous solution. Hence, in this work, a DFT calculation was implemented to predict pKa values of a group of 24 DHBs, which were validated through experimental determination using spectrophotometric methods.

Furthermore, in this work, the pKa values of DHBs were systematically determined in order to obtain reproducible values in aqueous solution. The pKa values for each hydroxyl group in the DHB were determined by computational methods and associated with experimental values.

Methodology

Reagents

All reagents were purchased from Sigma-Aldrich (Sigma-Aldrich, Germany) at their highest available purity and were used without any further purification steps. The DHBs studied are detailed in Figure 2. The H₃BO₃, H₃PO₄, and CH₃COOH used for the Britton-Robinson buffer preparation were supplied by Merck (Merck, Germany).

FIGURE 2

Figure 2. 1,2-dihydroxybenzenes studied.

Spectrophotometric pKa Determination

The DHBs were prepared in Britton-Robinson buffer at a pH value between 2.0 and 14.0, because this pH range is useful for biological systems and AOPs studies. The pH of each solution was adjusted just before each reaction with NaOH using a 3 Start Thermo Orion pH meter (Thermo Fisher Scientific, USA). The final concentration in the cuvette was 1.0 mmol L⁻¹ for each DHB.

The absorption spectrum of the solution with the DHB at different pH was determined using a UV-Vis diode array spectrophotometer, Agilent 8453 (Agilent Technologies, USA). All the experimental data were performed by triplicate under argon atmosphere at room temperature (approximately 25°C).

The spectrum obtained at different pH were plotted and analyzed to determine the pKa from the isosbestic points where the Henderson-Hasselbach equation (Equation 1) can be applied (Fernandes Previdello et al., 2006). When an isosbestic point was detected in the plot, the wavelengths with maximum absorbance near but at different sides of this point were selected. Then the absorbance obtained at the selected wavelengths and at different pH was plotted. The point where both lines intersect determines the value of pKa.

$\begin{array}{ll}\text{pH}=\text{p}{\text{K}}_{\text{a}}+\text{log}(\left[{\text{HL}}^{-}\right]/\left[{\text{H}}_2\text{L}\right])& \left(1\right)\end{array}$

Derivative spectrophotometry (D.S) was used when the isosbestic point was not found in the data obtained directly from the spectrophotometer. For finding the derivative of each spectra, the software ChemStation (Agilent Technologies, USA) was used. The first and second spectrum derivative were previously analyzed before applying any of the methods described below to determine the pKa value.

If the isosbestic point was not found in the original or derivative data, zero-crossing line method was used (Seleim et al., 2009). For this, two wavelengths were searched with the derivatives of the spectra. The first wavelength corresponds to a zero signal at pH “X” while at another, pH “Y” was obtained as a high absorbance signal. Afterwards, in another wavelength, the value of absorbance for pH “Y” was zero while the high absorbance was obtained for pH “X.” Then, the absorbance of the solution at different pH at each selected wavelength was plotted and the pKa value was determined from the point where both lines intersect.

If the pKa value cannot be calculated using a zero-crossing line, a baseline to peak method was applied, which searched for a wavelength related to a maximum where the absorbance signal was increasing as the pH increased (Erskine and Bobbitt, 1989). In that case, the relative amount of the basic form of a DHB at that wavelength (M) was obtained by subtracting the signal of the solution with DHB at a specific pH from the blank signal, whereas the relative amount of the acid form of the same DHB (N) was determined by subtracting the signal obtained for M with the signal of the most basic solution with DHB. From the Y axis intercept of the plot, log(M/N) v/s pH was obtained pKa (Equation 2) (Erskine and Bobbitt, 1989).

$\text{p}{\text{H}}_{\left[\text{X}\right]}=\text{p}{\text{K}}_{\text{a }}+\text{ log }\left(\frac{\text{M}}{\text{N}}\right)\left(2\right)$

$\text{p}{K}_a=\text{p}{\text{H}}_1-\text{ log}\frac{\left({10}^b-{10}^a\right)A_1+\left(1-{10}^b\right)A_2+({10}^a-1)A_3}{\left({10}^a-{10}^b\right)A_1+\left({10}^{a+b}-{10}^a\right)A_2+\left({10}^b-{10}^{a+b}\right)A_3}\left(3\right)$

The Seok method (Seok et al., 1995) was used if the pKa could not be determined by any previously detailed method. For this, search a wavelength related to a maximum where the absorbance signal was increasing as the pH increased. At that wavelength, three different pH and their respective absorbance (A_i) were selected. The pKa was calculated using Equation (3).

Where pH₁ was the lowest pH and pH₃ the highest pH selected, “a” was the difference between pH₂ and pH₁, “b” the difference between pH₃ and pH₁, A₁ was the absorbance at pH₁ at the selected wavelength, A₂ was the absorbance at pH₂ and A₃ was the absorbance for pH₃.

Computational pKa Determination

The pKa values were determined based on the thermodynamic cycle proposed by Pliego (2003) as shown in Figure 3.

FIGURE 3

Figure 3. Thermodynamic cycle used to determine pKa value for different DHBs.

The electronic structures of all species in the thermodynamic cycle were optimized using Gaussian 09 (Frisch and Trucks, 2009). According to previous reports for catechol, the density functional theory (DFT) with B3LYP function and 6-311+G(d,p) basis set was used (Altarawneh et al., 2010). The absence of imaginary frequencies in the optimized structure verified that the structure represented a local minimum. All calculations were performed at 298.15 K and 1.000 atm, according to the default conditions by Gaussian. To obtain the solvation free energies, CPCM, IPCM, and PCM models were tested (Liptak et al., 2002). The pKa values were determined using Equations (4) and (5) and were corrected according to Pliego using Equation (6) (Pliego, 2003).

$\begin{array}{l}\Delta {\text{G}}_{sol}=\Delta {\text{G}}_g+\Delta {\text{G}}_{solv}\left({\text{A}}^{-}\right)\\ +\Delta {\text{G}}_{solv}\left(H_3{O}^{+}\right)-\Delta {\text{G}}_{solv}\left(HA\right)\\ -{\text{G}}_{solv}\left(H_{2}O\right)& \left(4\right)\end{array}$

$p{K}_a=\frac{\Delta G_{sol}}{1.364}-log\left[H_{2}O\right]\left(5\right)$

$\text{pKa}(\mathrm{corrected})=\mathrm{pKa}(\mathrm{calculated})-4.54\left(6\right)$

Results and Discussion

Spectrophotometric pKa Determination

From the DHB spectra obtained at different pH (Figure S1 in Supplementary Information), we searched for an isosbestic point where the pKa was determined. For most of the DHBs, it was not possible to observe the isosbestic points directly from the data obtained by the spectrophotometer (C.S). Derivative spectrophotometry (D.S) must have been applied to the data to find the isosbestic points. Even different methods were used in combination with C.S or D.S to determine the pKa values. The method used to determine each pKa reported in this work is detailed in Table 2, and examples of the isosbestic points found for some DHBs are in Figure S2 in Supplementary Information.

TABLE 2

Table 2. Method and wavelength used to determine each pKa value for all the DHBs studied.

The pKa values for the first and second dissociations for all the DHBs studied are detailed in Table 3. The results were obtained by spectrophotometric methods and these are in agreement with the results obtained by other researchers despite using different methodologies (Taulier et al., 1987; Erskine and Bobbitt, 1989; El-Sayed and El-Salem, 2005; Fernandes Previdello et al., 2006). For the nordihydroguaiaretic acid, only the first pKa value was determined because at high pH values a precipitate was formed.

TABLE 3

Table 3. pKa values obtained by spectrophotometric method.

Computational pKa Determination

The computational calculations were obtained using the 6-311+G(d,p) basis set. In the present work, the basis set used for catechol (Altarawneh et al., 2010) was extrapolated for the structure optimization of different DHBs substituted in 4-position. On the other hand, to obtain computational pKa values (comparable with the experimental data), different solvation models in water were tested and are showed in Table 4. From the comparison of these values, the relative error was determined. The relative error was higher when the pKa was calculated using IPCM model (2.83% error in catechol and 13.5% error in 4-nitrocatechol determination). The smallest relative error was observed with the CMPC solvation model and this was not higher than 3%.

TABLE 4

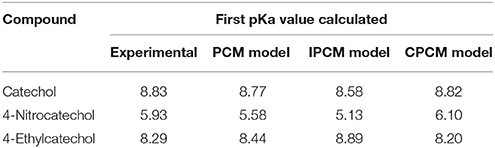
Table 4. Comparison of pKa values obtained experimentally and computationally with different solvation models.

For all the DHBs under the study, the pKa values in aqueous solution were calculated at DFT level with the CPCM solvation model, and this was in agreement with calculations in similar compounds (Liptak et al., 2002). Figure 4 shows that the calculated pKa values exhibited good accuracy with those pKa determined experimentally. The correlation (r²) for each pKa determined was higher than 0.87. Also, it was possible to calculate the pKa₂ for nordihydroguaiaretic acid through computational calculation, which was not possible to determine experimentally due to limitations of the technique.

FIGURE 4

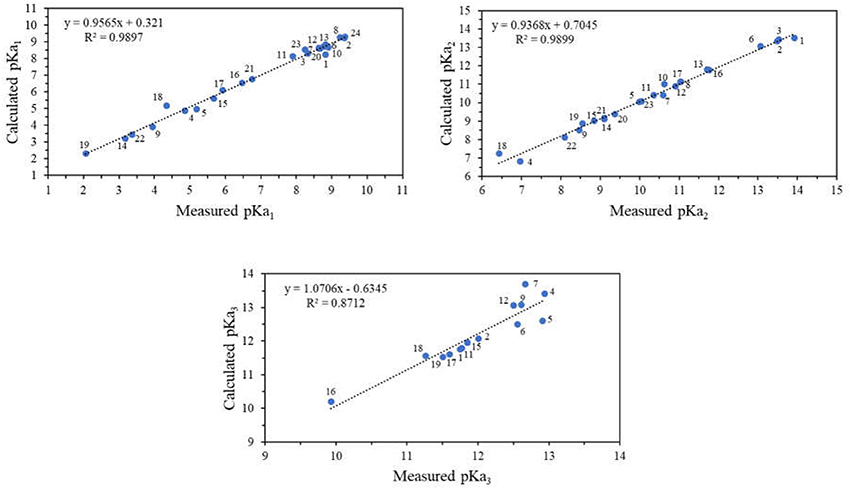
Figure 4. Correlation diagram of pKa values for different DHBs substituted on 4-position obtained experimentally and computationally.

The determination of each computational pKa allows the identification of the outgoing proton for each value, respectively. To simplify the analysis, Figure 5 shows that the pKa values determined were classified as part of one of the neighboring hydroxyls being the hydroxyl group in meta position (OH_m) or para position (OH_p) with respect to the substituent or as part of the substituent group (RH).

FIGURE 5

Figure 5. DHBs labels used in this paper.

The pKa whose value was less than 5.0 corresponds to the deprotonation equilibrium of carboxylic acids (RH). These results agree with the greater stability expected for these unprotoned groups (Clayden et al., 2012). In this context, different acidity influence was obtained in the DHBs studied due to their different substituent on 4-position. Hence, some of them can be classified as a donor of electron density (EDG) or as an electron density withdrawing group (EWG).

The Hammett constants (σ) reported for these groups are shown in Table 5. The DHBs with EDG have σ < 0 and are over the catechol, and below the catechol are the DHBs with EWG, which have σ > 0.

TABLE 5

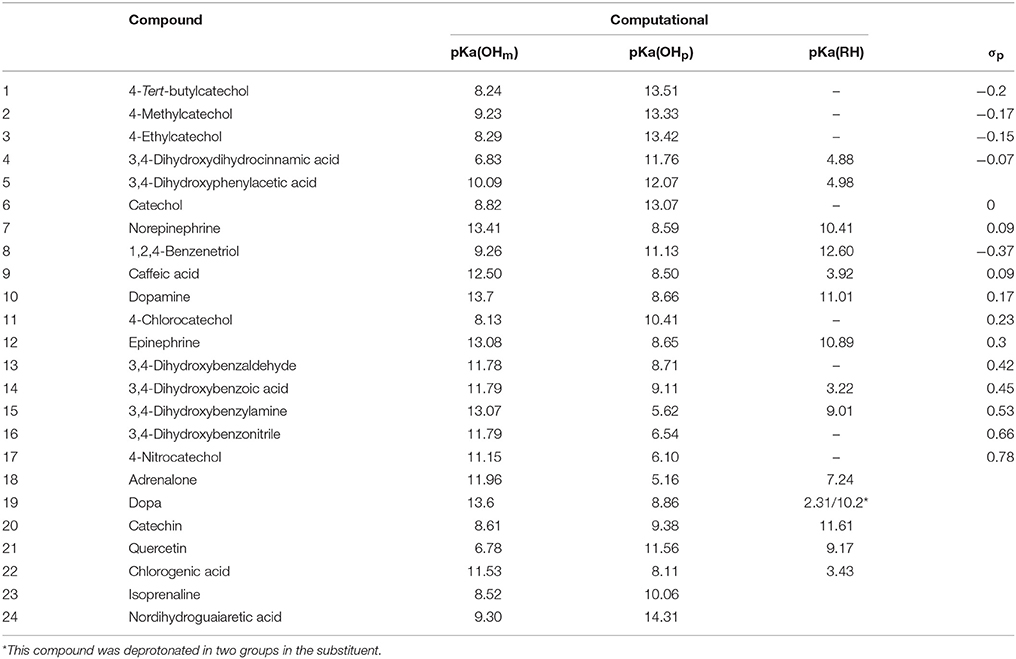
Table 5. pKa values obtained for different DHBs determined by computational method and the Hammett constant (σ) of each substituent on 4 position.

Figure 6 shows that according to the computational calculations, the more acidic proton was the OH_m for DHBs with EDG. Otherwise, in the DHBs with EWG, the more acidic proton was in the OH_p. The substituent can contribute to the charge stabilization of the anion that is formed by losing a proton. For DHBs with EWG, the anion formed is stabilized by resonance. In consequence, the OH_p shows lower pKa values than the DHBs with EDG.

FIGURE 6

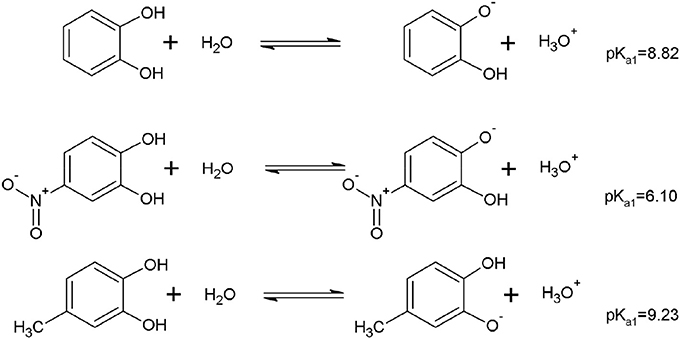
Figure 6. Example of the equilibrium associated to the pKa for the first hydroxyl deprotonation of DHBs substituted with EDG and EWG.

Moreover, it is well-known that in the optimization of a DHB structure, an intramolecular hydrogen bond must be considered between the neighboring hydroxyl groups to achieve good results (Zhu et al., 2010). As an example, Figure 7 shows that when the hydrogen bond was not considered in the computational pKa determination, the values were significantly different than the experimentally determined pKa. The difference between the calculated pKa with or without hydrogen bonding is higher for DHBs substituted by EDG than DHBs substituted by EWG, and this is explained by the charge stabilization of the molecule with substituents with higher electronegativity.

FIGURE 7

Figure 7. Effect of the intramolecular hydrogen bond in the pKa calculations.

In general, for the DHBs substituted by a EWG, the first deprotonated hydroxyl group is OH_p. On the other hand, if the DHBs are substituted by EDG (and for catechol), then the first deprotonated hydroxyl group is OH_m.

It has been noted that 4-chlorocatechol and 1,2,4-benzenotriol do not conform to this trend. This behavior could be explained because both chlorine and hydroxyl groups are electron-withdrawing, because of their electronegativity, but they are electron-donating by resonance. This effect is higher for hydroxyl groups because the overlapping between 2p and 2p orbitals is higher than the overlapping between 2p and 3p orbitals of chlorine (Clayden et al., 2012). In this way, the hydroxyl and chlorine are considered weak deactivating substituents. Therefore, for the 4-chlorocatechol and 1,2,4-benzenetriol, the first deprotonation of hydroxyl groups was OH_m.

Conclusion

In this work, an experimental validated computational method was implemented in aqueous solution for pKa determination of different DHBs, which are high value compounds and have had a great attention for its use as versatile platforms for the design of different materials. Also, it is well-known for its metal ligands properties with pro-oxidant and antioxidant performance in biological systems. In this framework, the knowledge of pKa is useful to explain the differences in the reactivity of DHBs compounds in their metallic complexing and subsequent activity in AOPs and biological systems.

Therefore, the pKa were calculated at DFT level with CPCM solvation model due to its relative error which was lower than 3% compared to the obtained experimental data. Furthermore, it was possible to predict the pKa value for each outgoing proton in the DHB structure, which was explained based on donor of electron density (EDG) or electron density withdrawing group (EWG) of each substituent in the DHB structure.

Author Contributions

RR performed the computational calculation of pKa values. PS performed the experimental determination of pKa values. CS supervised the experiments and the data treatment to determine the pKa values experimentally. VM and DC wrote the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors gratefully acknowledge FONDECYT (Grant no. 1160100 and 3180202), Basal CONICYT PFB-27 and FONDAP Solar Energy Research Center, SERC-Chile (Grant No. 151110019) for financial assistance.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fchem.2018.00208/full#supplementary-material

References

Adams, M. L., Sullivan, B. O., Downard, A. J., and Powell, K. J. (2002). Stability constants for Aluminum(III) Complexes with the 1,2-dihydroxyaryl ligands caffeic acid, chlorogenic acid, DHB, and DASA in aqueous solution. J. Chem. Eng. Data 47, 289–296. doi: 10.1021/je010279e

CrossRef Full Text | Google Scholar

Altarawneh, M., Dlugogorski, B. Z., Kennedy, E. M., and Mackie, J. C. (2010). Theoretical study of unimolecular decomposition of catechol. J. Phys. Chem. A 114, 1060–1067. doi: 10.1021/jp909025s

PubMed Abstract | CrossRef Full Text | Google Scholar

Antikainen, P. J., and Witikainen, U. (1973). A comparative study on the ionization of catechol amines in aqueous solutions. Acta Chem. Scand. 27, 2075–2082. doi: 10.3891/acta.chem.scand.27-2075

PubMed Abstract | CrossRef Full Text | Google Scholar

Avdeef, A., Sofen, S. R., Bregante, T. L., and Raymond, K. N. (1978). Coordination chemistry of microbial iron transport compounds. 9.1 stability constants for catechol models of enterobactin. J. Am. Chem. Soc. 100, 5362–5370. doi: 10.1021/ja00485a018

CrossRef Full Text | Google Scholar

Aydin, R., Ozer, U., Turkel, N. (1997). Potentiometric and spectroscopic determination of acid dissociation constants of some phenols and salicylic acids. Turkish J. Chem. 21, 428–436.

Google Scholar

Bindoli, A., Rigobello, M. P., and Deeble, D. J. (1992). Biochemical and toxicological properties of the oxidation products of catecholamines. Free Radic. Biol. Med. 13, 391–405. doi: 10.1016/0891-5849(92)90182-G

PubMed Abstract | CrossRef Full Text | Google Scholar

Beltran, J. L., Sanli, N., Fonrodona, G., Barron, D., Özkan, G., and Barbosa, J. (2003). Spectrophotometric, potentiometric and chromatographic pKa values of polyphenolic acids in water and acetonitrile-water media. Analytica chimica acta 484, 253–264. doi: 10.1016/S0003-2670(03)00334-9

CrossRef Full Text | Google Scholar

Charkoudian, L. K., Franz, K. J., Box, P. O., and Carolina, N. (2006). Fe (III) -coordination properties of neuromelanin components . Society 45, 3657–3664. doi: 10.1021/ic060014r

PubMed Abstract | CrossRef Full Text | Google Scholar

Clayden, J., Greeves, N., and Warren, S. (2012). Organic Chemistry. Oxford, NY: Oxford University Press.

Google Scholar

El-Sayed, A.-A. Y., and El-Salem, N. A (2005). Recent developments of derivative spectrophotometry and their analytical applications. Anal. Sci. 21, 595–614. doi: 10.2116/analsci.21.595

PubMed Abstract | CrossRef Full Text | Google Scholar

Erdemgil, F. Z., Sanli, S., Sanli, N., Özkan, G., Barbosa, J., Guiteras, J., et al. (2007). Determination of pKa values of some hydroxylated benzoic acids in methanol-water binary mixtures by LC methodology and potentiometry. Talanta 72, 489–496. doi: 10.1016/j.talanta.2006.11.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Erskine, S. R., and Bobbitt, D. R. (1989). Determination of the pK of an indicator by thermal lens spectroscopy: a laser experiment for instrumental analysis laboratory. J. Chem. Educ. 66:354. doi: 10.1021/ed066p354

CrossRef Full Text | Google Scholar

Evanko, C. R., and Dzombak, D. A (1998). Influence of structural features on sorption of NOM-analogue ornacic acids to goethite. Environ. Sci. Technol. 32, 2846–2855. doi: 10.1021/es980256t

CrossRef Full Text | Google Scholar

Fazary, A. E., and Ju, Y. H. (2008). Nonaqueous solution studies on the protonation equilibria of some phenolic acids. J. Solut. Chem. 37, 1305–1319. doi: 10.1007/s10953-008-9305-z

CrossRef Full Text | Google Scholar

Fernandes Previdello, B. A., De Carvalho, F. R., Tessaro, A. L., De Souza, V. R., and Hioka, N. (2006). O pKa de indicadores acido-base e os efeitos de sistemas coloidais. Quim. Nova 29, 600–606. doi: 10.1590/S0100-40422006000300032

CrossRef Full Text | Google Scholar

Frisch, M. J., and Trucks, G. W. (2009). Gaussian 09. Wallingford, CT: Gaussian Inc.

Gomes, C. A., Girão Da Cruz, T. G., Andrade, J. L., Milhazes, N., Borges, F., and Marques, M. P. M. (2003). Anticancer activity of phenolic acids of natural or synthetic origin: a structure-activity study. J. Med. Chem. 46, 5395–5401. doi: 10.1021/jm030956v

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodell, B., Daniel, G., Jellison, J., and Qian, Y. (2006). Iron-reducing capacity of low-molecular-weight compounds produced in wood by fungi. Holzforschung 60, 630–636. doi: 10.1515/HF.2006.106

CrossRef Full Text | Google Scholar

Hynes, M. J., and O'Coinceanainn, M. (2004). The kinetics and mechanisms of reactions of iron(III) with caffeic acid, chlorogenic acid, sinapic acid, ferulic acid and naringin. J. Inorg. Biochem. 98, 1457–1464. doi: 10.1016/j.jinorgbio.2004.05.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Hynes, M. J., and Ó Coinceanainn, M. (2001). The kinetics and mechanisms of the reaction of iron(III) with gallic acid, gallic acid methyl ester and catechin. J. Inorg. Biochem. 85, 131–142. doi: 10.1016/S0162-0134(01)00205-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Iwahashi, H., Morishita, H., Ishii, T., Sugata, R., and Kido, R. (1989). Enhancement by catechols of hydroxyl-radical formation in the presence of ferric ions and hydrogen peroxide. J. Biochem. 105, 429–34.

PubMed Abstract | Google Scholar

Jameson, R. F., and Wilson, M. F. (1972). Thermodynamics of the interactions of catechol with transition metals. part III. the effect of 4-chloro- and 4-nitro-substitution on proton and metal catechol complex formation. Dalt. Trans. 1972, 2617–2621. doi: 10.1039/dt9720002617

CrossRef Full Text | Google Scholar

Jovanovic, S. V., Steenken, S., Tosic, M., Marjanovic, B., and Simic, M. G. (1994). Flavonoids as antioxidants. J. Am. Chem. Soc. 116, 4846–4851. doi: 10.1021/ja00090a032

CrossRef Full Text | Google Scholar

Kiss, T., Sóvágó, I., and Martin, R. B. (1989). Complexes of 3,4-dihydroxyphenyl derivatives. 9. A13+ binding to catecholamines and tiron. J. Am. Chem. Soc. 111, 3611–3614. doi: 10.1021/ja00192a019

CrossRef Full Text | Google Scholar

Kuhn, D. M., Arthur, R. E., Thomas, D. M., and Elferink, L. A. (1999). Tyrosine hydroxylase is inactivated by catechol-quinones and converted to a redox-cycling quinoprotein: possible relevance to Parkinson's disease. J. Neurochem. 73, 1309–1317.

PubMed Abstract | Google Scholar

Liptak, M. D., Gross, K. C., Seybold, P. G., Feldgus, S., and Shields, G. C. (2002). Absolute pKa determinations for substituted phenols. J. Am. Chem. Soc. 124, 6421–6427. doi: 10.1021/ja012474j

CrossRef Full Text | Google Scholar

Lukasik, I. (2007). Changes in activity of superoxide dismutase and catalase within cereal aphids in response to plant o-dihydroxyphenols. J. Appl. Entomol. 131, 209–214. doi: 10.1111/j.1439-0418.2006.01136.x

CrossRef Full Text | Google Scholar

McBride, M. B., Sikora, F. J., and Wesselink, L. G. (1988). Complexation and catalyzed oxidative polymerization of catechol by aluminum in acidic solution. Soil Sci. Soc. Am. J. 52, 985–993. doi: 10.2136/sssaj1988.03615995005200040016x

CrossRef Full Text | Google Scholar

Melin, V., Henríquez, A., Freer, J., and Contreras, D. (2015). Reactivity of catecholamine-driven Fenton reaction and its relationships with iron(III) speciation. Redox Rep. 20, 89–96. doi: 10.1179/1351000214Y.0000000119

PubMed Abstract | CrossRef Full Text | Google Scholar

Moran, J. F., Klucas, R. V., Grayer, R. J., Abian, J., and Becana, M. (1997). Complexes of iron with phenolic compounds from soybean nodules and other legume tissues: prooxidant and antioxidant properties. Free Radic. Biol. Med. 22, 861–870. doi: 10.1016/S0891-5849(96)00426-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakamura, Y., Torikai, K., Ohto, Y., Murakami, A., Tanaka, T., and Ohigashi, H. (2000). A simple phenolic antioxidant protocatechuic acid enhances tumor promotion and oxidative stress in female ICR mouse skin: dose-and timing-dependent enhancement and involvement of bioactivation by tyrosinase. Carcinogenesis 21, 1899–1907. doi: 10.1093/carcin/21.10.1899

PubMed Abstract | CrossRef Full Text | Google Scholar

Nurchi, V. M., Pivetta, T., Lachowicz, J. I., and Crisponi, G. (2009). Effect of substituents on complex stability aimed at designing new iron(III) and aluminum(III) chelators. J. Inorg. Biochem. 103, 227–236. doi: 10.1016/j.jinorgbio.2008.10.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohara, K., Fujii, A., Ichimura, Y., Sato, K., and Mukai, K. (2006). Kinetic study of radical-scavenging and vitamin E-regenerating actions of edaravone (3-methyl-1-phenyl-2-pyrazolin-5-one). Bull. Chem. Soc. Jpn. 79, 421–426. doi: 10.1246/bcsj.79.421

CrossRef Full Text | Google Scholar

Ozkorucuklu, S. P., Beltrán, J. L., Fonrodona, G., Barrón, D., Alsancak, G., and Barbosa, J. (2009). Determination of dissociation constants of some hydroxylated benzoic and cinnamic acids in water from mobility and spectroscopic data obtained by CE-DAD. J. Chem. Eng. Data 54, 807–811. doi: 10.1021/je800595x

CrossRef Full Text | Google Scholar

Park, M. V. (1963). Complexes of ferric ion with salicylic acid and related substances. Nature 197:283. doi: 10.1038/197283a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Pathare, B., Tambe, V., and Patil, V. (2014). A review on various analytical methods used in determination of dissociation constant. Int. J. Pharm. Pharm. Sci. 6, 26–34.

Google Scholar

Perron, N. R., and Brumaghim, J. L. (2009). A review of the antioxidant mechanisms of polyphenol compounds related to iron binding. Cell Biochem. Biophys. 53, 75–100. doi: 10.1007/s12013-009-9043-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Pizer, R., and Babcock, L. (1977). Mechanism of the complexation of boron acids with catechol and substituted catechols. Inorg. Chem. 16, 1677–1681. doi: 10.1021/ic50173a021

CrossRef Full Text | Google Scholar

Pliego, J. R. (2003). Thermodynamic cycles and the calculation of pKa. Chem. Phys. Lett. 367, 145–149. doi: 10.1016/S0009-2614(02)01686-X

CrossRef Full Text | Google Scholar

Prousek, J. (2007). Fenton chemistry in biology and medicine. Pure Appl. Chem. 79, 2325–2338. doi: 10.1351/pac200779122325

CrossRef Full Text | Google Scholar

Rajan, K. S., Davis, J. M., Colburn, R. W., and Jarke, F. H. (1972). Metal chelates in the storage and transport of neurotransmitters: formation of mixed ligand chelates of Mg2+ -ATP with biogenic amines. J. Neurochem. 19, 1099–1116. doi: 10.1111/j.1471-4159.1972.tb01430.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Reijenga, J., van Hoof, A., van Loon, A., and Teunissen, B. (2013). Development of methods for the determination of pKa values. Anal. Chem. Insights 8, 53–71. doi: 10.4137/ACI.S12304

PubMed Abstract | CrossRef Full Text | Google Scholar

Ricci, A., Parpinello, G. P., and Versari, A. (2018). The nutraceutical impact of polyphenolic composition in commonly consumed green tea, green coffee and red wine beverages: a review. Food Nutr. J. 2017, 2575–7091. doi: 10.29011/2575-7091.100038

CrossRef Full Text | Google Scholar

Rodríguez, J., Contreras, D., Oviedo, C., Freer, J., and Baeza, J. (2004). Degradation of recalcitrant compounds by catechol-driven Fenton reaction. Water Sci. Technol. 49, 81–84. doi: 10.2166/wst.2004.0226

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodríguez, J., Contreras, D., Parra, C., Freer, J., Baeza, J., and Durán, N. (1999). Pulp mill effluent treatment by Fenton-type reactions catalyzed by iron complexes. Water Sci. Technol. 40, 351–355. doi: 10.2166/wst.1999.0732

CrossRef Full Text | Google Scholar

Rodriguez, M. L., Timokhin, V. I., Contreras, S., Chamarro, E., and Esplugas, S. (2003). Rate equation for the degradation of nitrobenzene by “Fenton-like” reagent. Adv. Environ. Res. 7, 583–595. doi: 10.1016/S1093-0191(02)00024-2

CrossRef Full Text | Google Scholar

Salgado, P., Melin, V., Contreras, D., Moreno, Y., and Mansilla, H. D. (2013). Fenton reaction driven by iron ligands. J. Chil. Chem. Soc. 58, 2096–2101. doi: 10.4067/S0717-97072013000400043

CrossRef Full Text | Google Scholar

Santhakumar, A. B., Battino, M., and Alvarez-Suarez, J. M. (2018). Dietary polyphenols: structures, bioavailability and protective effects against atherosclerosis. Food Chem. Toxicol. 113, 49–65. doi: 10.1016/j.fct.2018.01.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Schweigert, N., Zehnder, A. J. B., and Eggen, R. I. L. (2001). Chemical properties of catechols and their molecular modes of toxic action in cells, from microorganisms to mammals. Environ. Microbiol. 3, 81–91. doi: 10.1046/j.1462-2920.2001.00176.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Seleim, M. M., Abu-Bakr, M. S., Hashem, E. Y., and El-Zohry, A. M. (2009). Simultaneous determination of aluminum (III) and iron (III) by first-derivative spectrophotometry in alloys. J. Appl. Spectrosc. 76, 554–563. doi: 10.1007/s10812-009-9224-9

CrossRef Full Text | Google Scholar

Seok, Y. J., Yang, K. S., and Kang, S. O. (1995). A simple spectrophotometric determination of dissociation constants of organic compounds. Anal. Chim. Acta 306, 351–356. doi: 10.1016/0003-2670(95)00011-N

CrossRef Full Text | Google Scholar

Sharma, I., and Kaminski, G. A. (2012). Calculating pKa values for substituted phenols and hydration energies for other compounds with the first-order fuzzy-border continuum solvation model. J. Comput. Chem. 33, 2388–2399. doi: 10.1002/jcc.23074

PubMed Abstract | CrossRef Full Text | Google Scholar

Slabbert, N. P. (1977). Ionisation of some flavanols and dihydroflavonols. Tetrahedron 33, 821–824. doi: 10.1016/0040-4020(77)80200-7

CrossRef Full Text | Google Scholar

Taulier, A., Levillain, P., and Lemonnier, A. (1987). Determining methemoglobin in blood by zero-crossing-point first-derivative spectrophotometry. Clin. Chem. 33, 1767–1770.

PubMed Abstract | Google Scholar

Timberlake, C. (1957). A potentimetric and polarographic study of coppercatechol complexes. J. Chem. Soc. 1957, 4987–4993. doi: 10.1039/JR9570004987

CrossRef Full Text | Google Scholar

Yang, H., Xue, X., Li, H., Apandi, S. N., Tay-Chan, S. C., Ong, S. P., et al. (2018). The relative antioxidant activity and steric structure of green tea catechins – a kinetic approach. Food Chem. 257, 399–405. doi: 10.1016/j.foodchem.2018.03.043

PubMed Abstract | CrossRef Full Text | Google Scholar

Zang, L. Y., Cosma, G., Gardner, H., Castranova, V., and Vallyathan, V. (2003). Effect of chlorogenic acid on hydroxyl radical. Mol. Cell. Biochem. 247, 205–210. doi: 10.1023/A:1024103428348

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, X. Q., Wang, C. H., and Liang, H. (2010). Scales of oxidation potentials, pKa, and BDE of various hydroquinones and catechols in DMSO. J. Org. Chem. 75, 7240–7257. doi: 10.1021/jo101455m

PubMed Abstract | CrossRef Full Text | Google Scholar