Novel sparging strategies to enhance dissolved carbon dioxide stripping in industrial scale stirred tank reactors

Aerated stirred tank reactors are widely used in bio-process engineering and pharmaceutical industries. To supply the organisms with oxygen and control the pH value, oxygen is transferred from air bubbles into the liquid phase, and, at the same time, carbon dioxide is stripped from the liquid phase with the same gas bubbles. The volumetric mass transfer coefficients for oxygen and carbon dioxide are, therefore, of crucial importance for the design and scale-up of aerated stirred tank reactors. In this experimental work, the volumetric mass transfer coefficients for oxygen and carbon dioxide are investigated simultaneously to study their mutual influence. The mass transfer performance for oxygen and carbon dioxide is conducted in stirred tank reactors on the 3 L laboratory scale, 30 L pilot scale, and 15,000 L production scale. First, the influence of dissolved carbon dioxide on the oxygen mass transfer performance is investigated in a 30 L pilot scale stirred tank reactor. The results show that the volumetric mass transfer coefficient of oxygen is not affected by the concentration of dissolved carbon dioxide, but the total mass flux of oxygen decreases with increasing carbon dioxide concentration due to the decreasing partial pressure difference. With rising gassing rate and volumetric power input, both mass transfer coefficients for oxygen and carbon dioxide show the same increasing trend. Although this trend can also be observed when scaling down to the 3 L laboratory scale reactor, a significantly different effect must be considered for the scale-up to the 15,000 L industrial scale reactor. The limited absorption capacity for carbon dioxide of the gas bubbles during the long residence time in the industrial scale reactor is noticeable here, which is why the specific interfacial area is of negligible importance. This effect is used to develop a method for independent control of oxygen and carbon dioxide mass transfer performance on an industrial scale and to increase the mass transfer performance for carbon dioxide by up to 25%.

1 Introduction

In bio-process engineering and pharmaceutical industries, the production of biologicals in high-density mammalian cell cultures is of great relevance (Matsunaga et al., 2009a). The cultivation of those cells is performed under aerobic conditions in aerated bioreactors. In order to sustain cellular metabolism and growth, an ideal supply of nutrients and dissolved oxygen must be ensured (Garcia-Ochoa and Gomez, 2009). Considering that most cells are able to retain nutrients, but only a small amount of dissolved oxygen is available at ambient pressure, oxygen is generally the limiting component (Eibl et al., 2009). Therefore, air or even pure oxygen is continuously supplied during the process to be transferred from the gaseous phase into the liquid phase. Simultaneously, carbon dioxide produced by cellular metabolism must be removed from the system by transfer from the liquid phase into the gaseous phase. If carbon dioxide stripping is insufficient, carbon dioxide accumulates in the culture medium. This can shift the pH value, which inhibits cell growth and productivity (Hu, 2018; Baehr, 2016; Matsunaga et al., 2009b; Sieblist et al., 2011b). In addition to the bio-processes, the carbon dioxide mass transfer is a crucial parameter in improving different techniques for carbon capture (Liu et al., 2018; Hu et al., 2020; Yu et al., 2024a; b).

Bubble columns or aerated stirred tank reactors are used to ensure a high mass transfer performance during biological processes (Matsunaga et al., 2009a). Aerated stirred tank reactors (STRs) provide high flexibility regarding their range of applications in combination with utilizing multiple different impeller types that create controlled and reproducible flow conditions. In addition, good mixing of two-phase flows with short mixing times and an efficient power input can be achieved (Fitschen et al., 2019). A crucial parameter for the design, characterization, and scale-up of stirred tank reactors, as well as for describing the mass transfer performance, is the volumetric mass transfer coefficient $k_{\text{L}}a$ (Paul et al., 2004; Benz, 2021; Zlokarnik, 2001).

For high- or even ultra-high seeding density cell culture processes, the scale-up of seed trains begins in laboratory scale STRs, proceeds to the pilot scale, and culminates on the industrial scale with thousands of liters (Catapano et al., 2009; Stepper et al., 2020). However, with an increased volume, the surface-to-volume ratio is decreased, and the carbon dioxide stripping through the liquid surface and the headspace of the reactor is reduced (Matsunaga et al., 2009b; Sieblist et al., 2011a).

The objective of this article is to compare the mass transfer performance of oxygen and carbon dioxide in laboratory- and industrial scale aerated stirred tank reactors. Moreover, a method for improving carbon dioxide stripping in a stirred tank reactor on an industrial scale is presented (Schulz and Wucherpfennig, 2021). For the investigations, an acrylic glass stirred tank reactor on an industrial scale with a total volume of $V_{\text{R}}=\mathrm{15,000}\mathrm{L}$ is used at the Hamburg University of Technology in cooperation with Boehringer Ingelheim Pharma GmbH & Co. KG.

2 Materials and methods

The experimental results presented in this paper are obtained in a 3 L, 30 L, or 15,000 L STR.

2.1 Theory

For stirred tank reactors, the specific power input (Equation 1) by the stirrers is defined as

$P/V=\frac{Po\cdot {\rho }_{\text{F}}\cdot n^3\cdot d^5}{V_{\text{F}}},(1)$

which includes the power number $Po$, fluid density ${\rho }_{\text{F}}$, stirrer frequency $n$, stirrer diameter $d$, and liquid volume $V_{\text{F}}$. The power number $Po$ $(Po=P/{\rho }_{\text{F}}\cdot n^3\cdot d^5)$ itself is dependent on the stirrer geometry and the stirrer frequency.

In a single-phase and fully baffled system, the turbulent flow regime is reached in the case at a stirrer Reynolds number of $\mathrm{R}\mathrm{e}>4\cdot 10^4$. Under these conditions, the power number $Po$ is constant (Kraume, 2020). For aerated conditions in two-phase systems, the power number can be influenced by the aeration rate. However, for low aeration rates as occur in mammalian cell cultivation processes, a constant power number $Po$ can be assumed (Zlokarnik, 2001; Gabelle et al., 2011).

In the case of an ideal gas and liquid phase, the concentration of dissolved gases can be determined with Henry’s law (Lohrengel, 2017; Baehr, 2016), and gas–liquid mass transfer can be described by the two-film theory (Whitman, 1923). Without the presence of mammalian cells, the mass transfer for dissolved oxygen from the gaseous into the liquid phase (Equation 2) can be calculated as

$\frac{\mathrm{d}{c}_{{\text{O}}_2}}{\mathrm{d}t}=k_{\text{L}}{a}_{{\text{O}}_2}\cdot \left(c_{{\text{O}}_2}^{*}-c_{{\text{O}}_2}\right),(2)$

with the concentration of dissolved oxygen $c_{{\text{O}}_2}$, the time $t$, the volumetric oxygen mass transfer coefficient $k_{\text{L}}{a}_{{\text{O}}_2}$, and the equilibrium concentration of dissolved oxygen $c_{{\text{O}}_2}^{*}$ (Garcia-Ochoa and Gomez, 2009). For oxygen mass transfer, the equilibrium concentration is the saturation concentration of dissolved oxygen for the respective system. The mass transfer for dissolved carbon dioxide (Equation 3) is defined as

$\frac{\mathrm{d}{c}_{{\text{CO}}_2}}{\mathrm{d}t}=k_{\text{L}}{a}_{{\text{CO}}_2}\cdot \left(c_{{\text{CO}}_2}-c_{{\text{CO}}_2}^{*}\right),(3)$

with $c_{{\text{CO}}_2}$ being the concentration of dissolved carbon dioxide, $k_{\text{L}}{a}_{{\text{CO}}_2}$ the volumetric carbon dioxide mass transfer coefficient, and $c_{{\text{CO}}_2}^{*}$ the equilibrium concentration of dissolved carbon dioxide. As the carbon dioxide mass transfer coefficient from the liquid into the gaseous phase is measured here, the driving potential is defined as $c_{{\text{CO}}_2}-c_{{\text{CO}}_2}^{*}$. For the carbon dioxide mass transfer, the equilibrium concentration of dissolved carbon dioxide in water against air is assumed as $c_{{\text{CO}}_2}^{*}\approx 0\mathrm{k}\mathrm{g}{\mathrm{m}}^{-\mathrm{3}}$ because the amount of carbon dioxide in air is negligible (Baehr, 2016; Matsunaga et al., 2009a; VDI, 2013).

The volumetric mass transfer coefficient $k_{\text{L}}a$ is influenced by different factors, such as the specific power input $P/V$, the gas volume flow rate ${\dot{V}}_{\text{G}}$, and the temperature $T$ (Boyd, 2020). The van’t Riet correlation for aerated stirred tank reactors can be used, in which the volumetric mass transfer coefficient can be modeled according to

$k_{\text{L}}a=K_1\cdot {\left(P/V\right)}^{K_2}\cdot u_{\text{G}}^{K_3},(4)$

with the superficial gas velocity $u_{\text{G}}$ and three constants $K_1$, $K_2$, and $K_3$. The constants are fitted to experimental data for each system and can then be applied to any operating conditions of this system. Therefore, the van’t Riet correlation is not limited to a defined field of application (Van’t Riet, 1979; Knoll et al., 2005; Bernemann et al., 2024).

2.2 Experimental setup and measurement procedure

The performed experiments can be divided into three parts. The first part, conducted in the 30 L STR (see Figure 1), is the determination of the influence of dissolved carbon dioxide on the oxygen mass transfer coefficient. Based on these results, the measuring method for the second part is defined. The second part of this work was performed in the laboratory and industrial-scale STR. During this work, the mass transfer coefficients of carbon dioxide and oxygen are determined in both systems for different power inputs and superficial gas velocities. The third part of the experiments was conducted in the industrial-size STR as an alternative sparging strategy to test the independent control of the oxygen and carbon dioxide concentration.

Figure 1

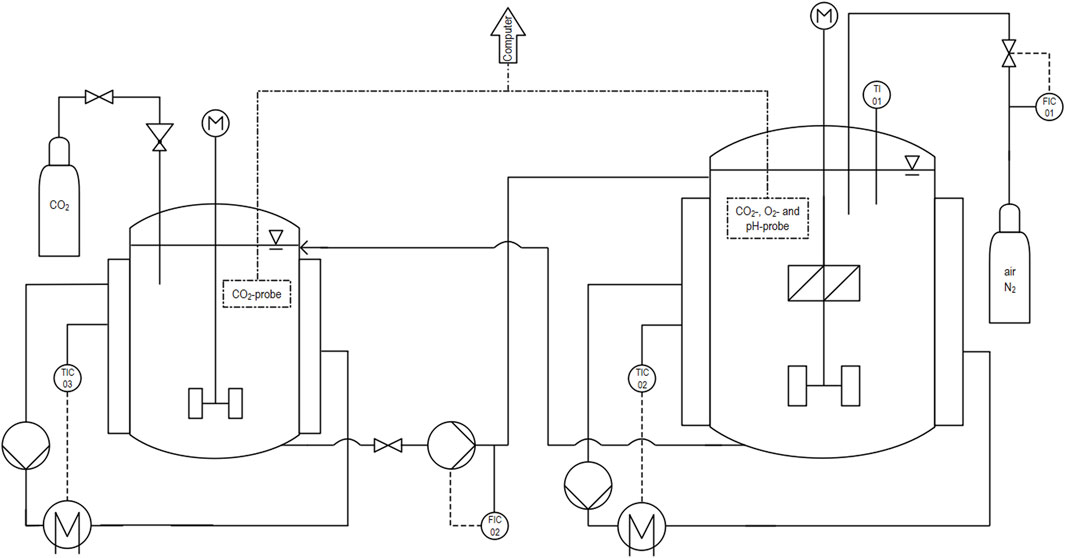
Figure 1. Process flow diagram of the experimental pilot scale setup with the connection of the 1.8-L (left) and the 30-L (right) stirred tank reactor.

The applied measuring methods are identical for all systems. To measure the concentration of dissolved oxygen $c_{{\text{O}}_2}$, an optical dissolved oxygen sensor (WTW SenTix HW-T 900) with an error of less than 5% was used, and for the concentration of dissolved carbon dioxide $c_{{\text{CO}}_2}$, a dissolved carbon dioxide sensor (Hamilton ${\mathrm{C}\mathrm{O}}_2$NTROL RS485) with an error of 3% was utilized. The carbon dioxide sensor measures the dissolved carbon dioxide and none of the dissociated products. To ensure that all dissolved carbon dioxide can be measured, a pH value of 3 is maintained to avoid dissociation.

An open tube sparger (submersed sparger) is used in each system for aeration. The sparger is mounted below the stirrer, as can be seen in Figure 2, which shows an example of the laboratory setup. Mass flow controllers (Bronkhorst EL-Flow) are used to control the gas flow rates. The stirrer geometry is given in Table 1. The different stirrer spacing for the elephant ears (EE) and the combination of Rushton turbine (RT) and pitched blade (PB) is shown in Figures 2, 3. The lowest stirrer has the distance $h=d$ from the reactor bottom, the distance between the RT and the PB stirrer is set to $s_1=1.65d$, and the spacing between the EE stirrer is set so $s_2=d$. The dynamic method is used to obtain the specific mass transfer coefficients for oxygen and carbon dioxide. For oxygen, this means the liquid is deoxygenated to 20% dissolved oxygen by stripping with pure nitrogen (99.9990%), and afterward, the mass transport coefficient is measured while aerating with air. To obtain the carbon dioxide mass transfer coefficient, the liquid is saturated with carbon dioxide (99.995%) to 15%, and then the stripping process with air is measured as the basis for the calculation. The air used is pressurized ambient air with an oxygen concentration of 21% and a carbon dioxide concentration of 0.04%. Both steps were combined for this work. First, the starting parameters are adjusted, and then, both specific mass transfer coefficients are measured simultaneously while gassing with a defined air flow rate and stirring with a given stirrer frequency. The measurement is stopped when reaching $c_{{\text{O}}_2}>80\%$ and $c_{{\text{CO}}_2}<5\%$ or after a measurement time of 45 min. The analysis of the measured data is done identically for the different reactor systems with a standardized procedure according to Fitschen et al. (2023).

Figure 2

Figure 2. Glass stirred tank reactor on the laboratory scale (3 L STR).

Table 1

Table 1. Specifications of the investigated systems.

Figure 3

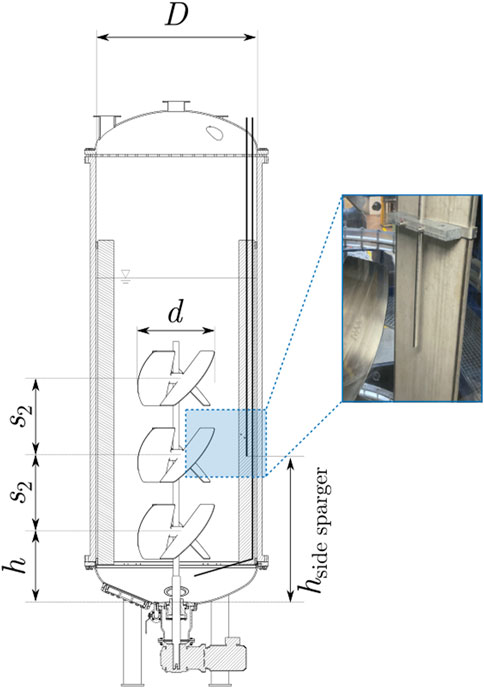
Figure 3. Schematic illustration of the stirred tank reactor on an industrial scale (15 kL STR) with the side sparger.

2.2.1 Pilot scale setup

The pilot scale reactor with a volume of 30 L is used to investigate the influence of a constant carbon dioxide concentration on the oxygen mass transfer performance. To ensure a constant carbon dioxide concentration inside of the pilot scale reactor, a 1.8 L stirred tank reactor is used to enrich the deionized water with carbon dioxide. The enriched water is subsequently pumped into the 30 L reactor by using a peristaltic pump (Ismatec ISM 405 A). A flow meter is used to control and adjust the pumping. The backflow from the 30 L reactor to the 1.8 L reactor is realized by a buoyancy-driven, siphon-like construction. The various dissolved carbon dioxide profiles between 5% and 15% of saturation concentration are simulated in the 30 L reactor by adjusting the volume flow of saturated carbon dioxide deionized water. The experiments are performed at a temperature of 20°C, which is controlled through an external heating and cooling circulator (IKA HRC 2). For the 30 L reactor, a stirrer setup consisting of an RT and a down-pumping PB is used. The 1.8 L reactor instead is only equipped with an RT as the only purpose is to enrich the deionized water with carbon dioxide. The stirrer frequency is controlled by a torque measurement instrument (HiTec Zang ViscoPakt-X7). The piping and instrumentation diagram (P&ID) of the setup is presented in Figure 1.

2.2.2 Laboratory scale setup

A glass STR with a volume of 3 L is used for the laboratory scale experiments. The geometry parameters and the stirrer combinations are displayed in Table 1. Further specifications of the stirrers and previously measured power numbers $Po$ according to the method by Fitschen et al. (2019) are also presented in Table 1. The stirrer shaft is connected to the motor above the reactor. The stirrer frequency is regulated and controlled with a torque measuring instrument (HiTec Zang ViscoPakt-X7). In the laboratory scale, both the RT and PB combination and three EE stirrers are used. To ensure a constant temperature of 37°C, the reactor is placed in a water bath that is heated through an external cooling and heating circulator (IKA HRC 2). The experiments are performed in 0.9% sodium chloride solution.

2.2.3 Industrial scale setup

The industrial scale reactor uses an operating volume of 12.5 kL. The geometric specifications, the stirrer combinations, and further specifications, such as the previously measured power numbers $Po$ according to the method by Fitschen et al. (2019), are displayed in Table 1. In contrast to the laboratory and pilot scale setups, the industrial scale reactor is equipped with a bottom-mounted magnetic agitator (Zeta BMRF-40000). The industrial scale reactor is operated with three EE stirrers and filled with 0.9% sodium chloride solution. The system has an external heating loop in which a pump and a heat exchanger are integrated. During the measurements at 37°C, the external loop is switched off so as not to influence the internal flow field. Due to the lid of the reactor and the good isolation characteristics of the acrylic glass, the temperature loss is about $△T\approx 0.1$°$\mathrm{C}{\mathrm{h}}^{-\mathrm{1}}$ only and therefore, adiabatic conditions for each experiment can be assumed. For the independent control of oxygen and carbon dioxide mass transfer performance, an additional open tube sparger (side sparger) for side aeration is attached to a baffle at middle reactor height (see Figure 3). The aeration of the side sparger can be controlled independently of the submersed sparger.

3 Experimental results

The following subsections provide the experimental results for the oxygen and carbon dioxide mass transfer performance in the stirred tank reactors on the laboratory (3 L STR), pilot (30 L STR), and industrial scales (15,000 L STR).

3.1 Influence of dissolved carbon dioxide concentration on oxygen mass transfer performance in a 30L stirred tank reactor

In Figure 4 the saturation concentration of dissolved oxygen $c_{{\text{O}}_2}^{*}$ is shown as a function of the dissolved carbon dioxide concentration $c_{{\text{CO}}_2}$. For a carbon dioxide concentration of $c_{{\text{CO}}_2}\approx 0$ kg m⁻³ and with a molar oxygen Henry coefficient of $H_{{\mathrm{O}}_2,\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}=72905\mathrm{P}\mathrm{a}{\mathrm{m}}^3{\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$ (Royce and Thornhill, 1991), the saturation concentration of dissolved oxygen calculated with the measured partial pressure is $c_{{\text{O}}_2}^{*}=9.34\cdot 10^{-3}$ kg m⁻³. This saturation concentration is measured under the condition that compressed ambient air is used for the aeration. Compared with the saturation concentration of dissolved oxygen, which is $c_{{\text{O}}_2}^{*}=9.08\cdot 10^{-3}$ kg m⁻³ in deionized water under atmospheric conditions noted in literature for a temperature of $T=20$°C (Montgomery et al., 1964), the determined and literature data are comparable. With increasing carbon dioxide concentration, the saturation concentration of dissolved oxygen decreases. This can be described with the linear function shown in Equation 5.

$c_{{\text{O}}_2}^{*}=\left(-6.0\cdot c_{{\text{CO}}_2}+9.3\right)\cdot 10^{-3}(5)$

Figure 4

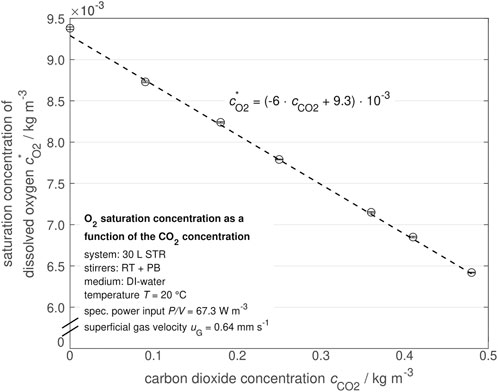
Figure 4. Saturation concentration of dissolved oxygen in dependency of the carbon dioxide concentration.

This linear dependency is determined empirically but can be explained physically. As the experiments are performed in an open system, the total pressure $p$ remains constant. Following Dalton’s law, the total pressure is the sum of all partial pressures $p_{\text{i}}$ in the system. With increasing carbon dioxide concentration, the partial pressure of carbon dioxide increases. Therefore, the partial pressure of oxygen must decrease at the same time. Following Henry’s law, the saturation concentration of oxygen must decrease as well, as it is directly dependent on the maximum partial pressure of dissolved oxygen. The molar Henry coefficients of oxygen $H_{{\text{O}}_2\text{,}\text{water}}$ and carbon dioxide $H_{{\text{CO}}_2\text{,}\text{water}}$ are assumed to be constant with increasing dissolved carbon dioxide concentration (Klamt, 1995).

For a defined saturation concentration of dissolved oxygen, the volumetric oxygen mass transfer coefficient $k_{\text{L}}{a}_{{\text{O}}_2}$ can be determined as a function of the carbon dioxide concentration. Figure 5 shows that the volumetric oxygen mass transfer coefficient increases with increasing specific power input $P/V$ and superficial gas velocity $u_{\text{G}}$. A higher specific power input causes higher shear forces and results in better gas dispersion, smaller gas bubbles, and a higher interfacial area for mass transfer with a more homogeneous gas bubble distribution (Garcia-Ochoa and Gomez, 2009; Matsunaga et al., 2009a). Increasing superficial gas velocity leads to a higher gas hold-up and thus to a higher specific interfacial area $a$ (Garcia-Ochoa and Gomez, 2009; Matsunaga et al., 2009b; Bouaifi et al., 2001).

Figure 5

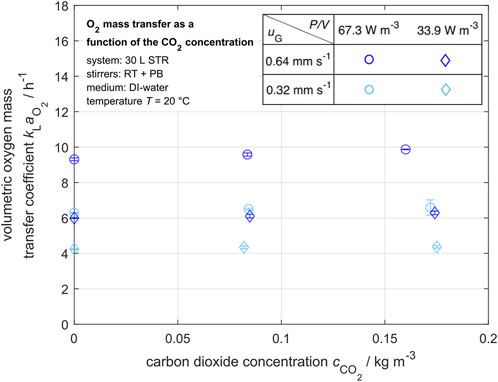
Figure 5. Volumetric oxygen mass transfer coefficient in dependency of the carbon dioxide concentration for various specific power inputs $P/V$ and superficial gas velocities $u_{\text{G}}$.

In contrast, the volumetric oxygen mass transfer coefficient $k_{\text{L}}{a}_{{\text{O}}_2}$ stays constant for increasing carbon dioxide concentrations, as shown in Figure 5. The carbon dioxide concentration $c_{{\text{CO}}_2}$ decreases the saturation concentration of dissolved oxygen $c_{{\text{O}}_2}^{*}$ but has no influence on the volumetric oxygen mass transfer coefficient in the investigated range because the flux of oxygen decreases as well due to the decreasing difference in partial pressure (see Equation 2).

3.2 Comparison of mass transfer performance on laboratory and industrial scales

For the stirred tank reactor on the laboratory scale (3 L STR), the determined volumetric oxygen mass transfer coefficient $k_{\text{L}}{a}_{{\text{O}}_2}$ and the volumetric carbon dioxide mass transfer coefficient $k_{\text{L}}{a}_{{\text{CO}}_2}$ are displayed as a function of the specific power input $P/V$ in Figures 6, 7. The van’t Riet correlation (Equation 4) for the corresponding systems is shown in addition to the values determined for the mass transfer coefficients. The obtained constants of the correlation and the accuracy $R^2$ are listed in Table 2. The coefficients $K_1$, $K_2$, and $K_3$ are constant for each system and independent of the stirrer frequency and the aeration rate. The constants must be adapted for different geometries and gaseous components.

Figure 6

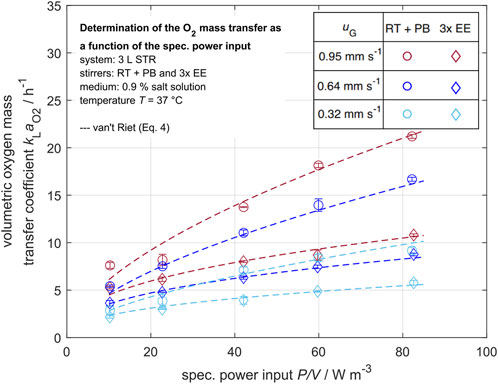
Figure 6. Volumetric oxygen mass transfer coefficient in dependency of the specific power input for various superficial gas velocities $u_{\text{G}}$ in the stirred tank reactor on laboratory scale (3 L STR).

Figure 7

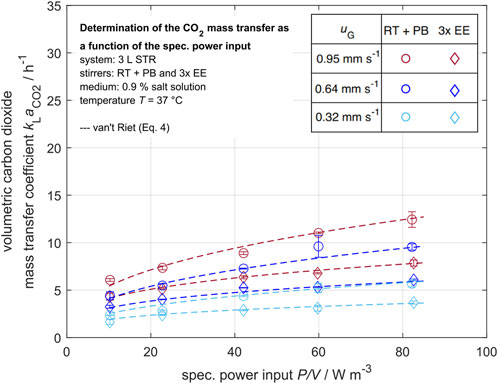
Figure 7. Volumetric carbon dioxide mass transfer coefficient in dependency of the specific power input for various superficial gas velocities $u_{\text{G}}$ in the stirred tank reactor on laboratory scale (3 L STR).

Table 2

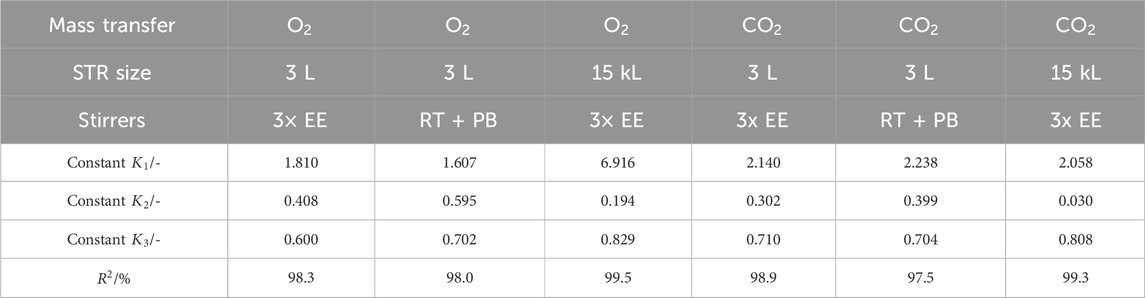
Table 2. Determined constants $K$ of the van’t Riet correlation with an accuracy $R^2$ for the respective system of the stirred tank reactor on a laboratory scale (3 L STR) and an industrial scale (15 kL STR).

As first shown in Figure 5, the volumetric mass transfer coefficients increase with rising specific power input and superficial gas velocity. This trend is observed to be stronger for oxygen than for carbon dioxide. For the superficial gas velocity of $u_G=$ 0.64 mm s⁻¹, the volumetric oxygen mass transfer coefficient increases from 5.4 h⁻¹ at 10.3 W m⁻³ to 16.7 h⁻¹ at 82.2 W m⁻³, while the carbon dioxide mass transfer coefficient only increases from 4.4 h⁻¹ at 10.3 W m⁻³ to 9.5 h⁻¹ at 82.2 W m⁻³. A similar trend is observed for the other superficial gas velocities. Although the volumetric oxygen transfer coefficient triples, the volumetric carbon dioxide transfer coefficient only doubles. Furthermore, the volumetric mass transfer coefficients for the stirrer configuration of the RT and PB are larger than for the three EE stirrers. This might be caused by higher tip speeds, which result in smaller gas bubbles obtained with the RT. Therefore, the specific interfacial area $a$ would be higher, and the gas bubbles would stay in the system longer. The shear force for both stirrer configurations determined in the literature does not vary significantly (Simmons et al., 2007).

For the stirred tank reactor on the industrial scale (15 kL STR) with three EE stirrers, the determined volumetric mass transfer coefficient of oxygen $k_{\text{L}}{a}_{{\text{O}}_2}$ and carbon dioxide $k_{\text{L}}{a}_{{\text{CO}}_2}$ are presented as a function of the specific power input $P/V$ and shown in Figure 8. Additionally, Figure 8 shows the van’t Riet correlation (Equation 4) with the respective constants $K_{\text{i}}$ (listed in Table 2) for oxygen and carbon dioxide mass transfer in the 15 kL stirred tank reactor.

Figure 8

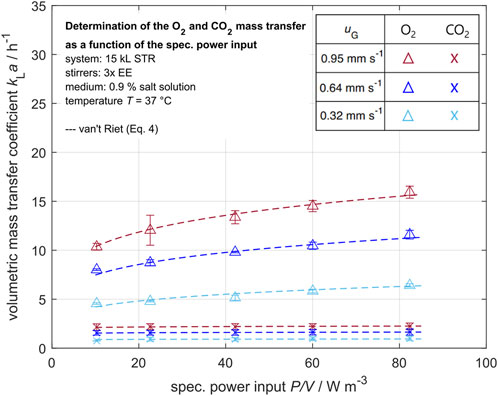
Figure 8. Volumetric mass transfer coefficients of oxygen and carbon dioxide in dependency of the specific power input for various superficial gas velocities $u_{\text{G}}$ in the stirred tank reactor on industrial scale (15 kL STR).

The determined volumetric oxygen mass transfer coefficients $k_{\text{L}}{a}_{{\text{O}}_2}$ for the industrial scale stirred tank reactor increase by approximately 50% with increasing specific power input in the investigated region. In addition, an increase nearly proportional to the increase in superficial gas velocity can be observed. These results are comparable to the volumetric oxygen mass transfer coefficients obtained in the laboratory scale STR (Figure 6). In comparison, the volumetric carbon dioxide mass transfer coefficients $k_{\text{L}}{a}_{{\text{CO}}_2}$ determined in the industrial scale STR do not show any influence of the specific power input in the investigated range. Although the volumetric carbon dioxide mass transfer coefficients increase with increasing superficial gas velocity, they do not exceed values of 2.5 h⁻¹.

The oxygen mass transfer coefficient outliers that can be seen in the data may be caused by changing ambient pressure, as the solubility of oxygen in water is highly pressure dependent. As the probes measure only locally, a certain error due to nonstationary effects is possible. Overall, the results are in good accordance with the van’t Riet correlation (van’t Riet, 1979).

To compare the carbon dioxide mass transfer performance of the laboratory and the industrial scale STR, the normalized volumetric carbon dioxide mass transfer coefficients $k_{\text{L}}{a}_{{\text{CO}}_2}$ $k_{\text{L}}{a}_{{\text{CO}}_{\mathrm{2,0}}}^{-1}$ are shown as a function of the specific power input $P/V$ in Figure 9. The reference volumetric carbon dioxide mass transfer coefficient $k_{\text{L}}{a}_{{\text{CO}}_{\mathrm{2,0}}}$ is defined as the volumetric carbon dioxide mass transfer coefficient for a specific power input of $P/V=10.3\mathrm{W}{\mathrm{m}}^{-\mathrm{3}}$ for each system, as it is the lowest specific power input measured.

Figure 9

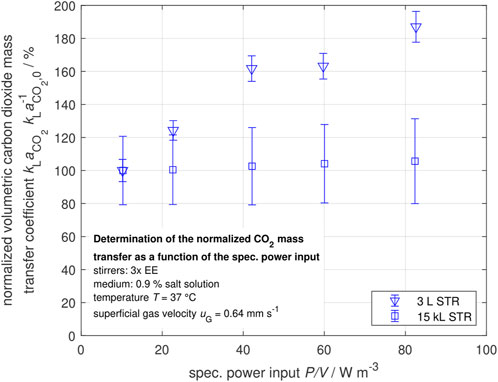
Figure 9. Normalized volumetric carbon dioxide mass transfer coefficient in dependency of the specific power input for a constant superficial gas velocity $u_{\text{G}}$ in the stirred tank reactor on laboratory (3 L STR) and industrial scale (15 kL STR).

Figure 9 indicates that the carbon dioxide mass transfer performance in the laboratory scale STR can be improved up to 80% in the investigated operation parameter range by increasing the specific power input $P/V$. In contrast, the carbon dioxide mass transfer performance in the industrial-scale STR can only be enhanced by about 5% by increasing specific power input.

The carbon dioxide mass transfer performance seems to be independent of the power input. It can be seen that the gas bubbles are rapidly saturated by carbon dioxide. In this case, an increased specific surface area due to an increased power input would have no influence on the carbon dioxide stripping (Sieblist et al., 2011b; Xing et al., 2017; Xu et al., 2017). This highlights the difficulties in scaling up from the laboratory to the industrial scale while accounting for mass transfer due to the saturation of rising gas bubbles through carbon dioxide. This is in good accordance with the effects observed by Mostafa and Gu (2003) and Garnier et al. (1996) in industrial-size STRs, who found a strong impact of the aeration rate on the carbon dioxide mass transfer. Therefore, a different approach is needed to improve the carbon dioxide mass transfer performance. In the following section, the influence of higher superficial gas velocities, injected as side aeration, on the carbon dioxide mass transfer performance is discussed.

3.3 Independent control of mass transfer performance for oxygen and carbon dioxide by using side aeration on an industrial scale

Additional side aeration is used on an industrial scale to enhance the mass transfer performance of carbon dioxide with a reduced influence on the oxygen mass transfer performance (Schulz and Wucherpfennig, 2021). The sparger for the side aeration and its arrangement can be seen in Figure 3.

In Figure 10, the normalized volumetric mass transfer coefficients $k_{\text{L}}a{k}_{\text{L}}{a}_0^{-1}$ for oxygen and carbon dioxide are shown as a function of the side aeration superficial gas velocity $u_{\text{G,\hspace{0.17em}side}}$ for a constant submersed aeration superficial gas velocity of $u_{\text{G}}=$ 0.64 mm s⁻¹. The volumetric mass transfer coefficient for a side aeration superficial gas velocity of $u_{\text{G,\hspace{0.17em}side}}$ = 0 mm s⁻¹ is defined as reference value $k_{\text{L}}{a}_0$ for the normalization.

Figure 10

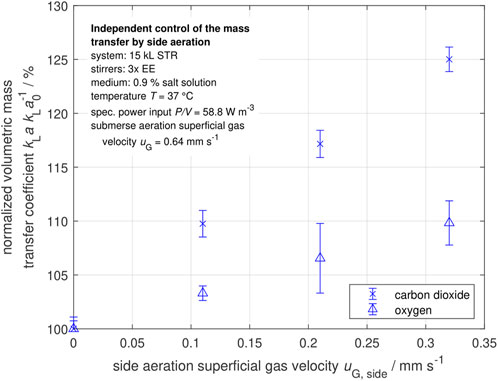
Figure 10. Normalized volumetric mass transfer coefficients of oxygen and carbon dioxide in dependency of the side aeration superficial gas velocity for a constant specific power input $P/V$ and submersed aeration superficial gas velocity $u_{\text{G}}$.

With increased side aeration superficial gas velocity, the volumetric oxygen mass transfer coefficient has a slight increase of +9.8% in the investigated range. At the same time, the volumetric carbon dioxide mass transfer coefficient increases up to 25.0%. With the side aeration, large gas bubbles enter the system with a smaller specific surface area and a larger volume than the small gas bubbles from the submersed aeration. As carbon dioxide is well-soluble in water (molar Henry coefficient of $H_{{\text{CO}}_2\text{,}\text{water}}=$ 4.028 Pa m³ mol⁻¹) at a temperature of $T=$37°C and oxygen (molar Henry coefficient of $H_{{\mathrm{O}}_2,\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}=93.947\mathrm{P}\mathrm{a}{\mathrm{m}}^3{\mathrm{m}\mathrm{o}\mathrm{l}}^{-1}$) (Royce and Thornhill, 1991) is not, the smaller specific surface area is not as critical for carbon dioxide as for oxygen. The larger gas bubble volume enables more carbon dioxide diffusion into the gas bubble until the saturation concentration is reached, which results in a higher rise velocity, which enables better carbon dioxide stripping. As a result, the carbon dioxide mass transfer performance is significantly improved, whereas the oxygen mass transfer performance is only slightly affected.

4 Conclusion

In this work, the mass transfer performance of oxygen and carbon dioxide are experimentally investigated in an aqueous salt solution by analyzing the volumetric mass transfer coefficients in STRs on various scales. For the simultaneous analysis, the volumetric oxygen mass transfer coefficient is investigated from the gaseous phase into the liquid phase, and the volumetric carbon dioxide mass transfer coefficient is investigated from the liquid phase into the gaseous phase for varying power inputs and superficial gas velocities. In the pilot-scale STR, the volumetric oxygen mass transfer coefficient remains constant and is not dependent on the dissolved carbon dioxide concentration for the investigated range.

The determined mass transfer performance of oxygen and carbon dioxide on the laboratory scale STR shows that the volumetric mass transfer coefficient has a comparable trend within the operating parameters. This is not transferable to the industrial scale STR. In this case, the volumetric carbon dioxide mass transfer coefficient cannot be significantly improved by an increased power input because carbon dioxide accumulates within the gas bubbles. Therefore, an easy scale-up of the carbon dioxide mass transfer performance is an open challenge for future research. This effect is utilized to develop and test a method for the industrial scale stirred tank reactor to enhance the mass transfer performance of carbon dioxide independently from the oxygen mass transfer by using additional side aeration. Due to the side aeration, the volumetric oxygen mass transfer coefficient increases only slightly, while the volumetric carbon dioxide mass transfer coefficient shows a more significant increase with a maximum of +25.0%. This method enables more independent control of the oxygen and carbon dioxide concentrations in industrial scale STR and, thus, more reliable scaling and processes.

The insights gathered for aerated STRs can be transferred to other fields like the chemical industry or carbon capture technologies. To improve the knowledge of the carbon dioxide mass transfer in aerated STRs, further experiments, such as the measurement of concentration profiles within the gaseous phase over the reactor height, will be performed to enable more detailed modeling.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

NN: visualization, writing–original draft, writing–review and editing, formal analysis, and investigation. JF: conceptualization, methodology, writing–review and editing, formal analysis, and project administration. IH: conceptualization, data curation, formal analysis, investigation, methodology, visualization, and writing–original draft. MK: project administration and writing–review and editing. TS: conceptualization, methodology, and writing–review and editing. TW: conceptualization, funding acquisition, methodology, project administration, and writing–review and editing. MS: conceptualization, funding acquisition, project administration, supervision, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors gratefully acknowledge the company Boehringer Ingelheim Pharma GmbH & Co. KG for its financial support in conducting the presented research work.

Acknowledgments

In particular, the authors would like to thank their students Helena Ostrinksy and Jakob Schulze. Publishing fees were supported by the Funding Programme Open Access Publishing of Hamburg University of Technology (TUHH).

Conflict of interest

Authors JF, MK, TS, and TW were employed by Boehringer Ingelheim Pharma GmbH & Co., KG.

The authors declare that this study received funding from Boehringer Ingelheim Pharma GmbH & Co. KG. The funder had the following involvement in the study: Dr. Jürgen Fitschen was a former PhD student at the TUHH and was involved in the planning and measuring phase of the study. Experiments were discussed upfront with the funder.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Baehr, H. D. (2016). Thermodynamik: Grundlagen und technische Anwendungen. Berlin Heidelberg: Springer Vieweg, 16. aktualiiserte auflage edn.

Google Scholar

Benz, G. T. (2021). Agitator design for gas–liquid fermenters and bioreactors. first edn. Wiley. doi:10.1002/9781119650546

CrossRef Full Text | Google Scholar

Bernemann, V., Fitschen, J., Leupold, M., Scheibenbogen, K.-H., Maly, M., Hoffmann, M., et al. (2024). Characterization data for the establishment of scale-up and process transfer strategies between stainless steel and single-use bioreactors. MDPI Fluids 9, 115. doi:10.3390/fluids9050115

CrossRef Full Text | Google Scholar

Bouaifi, M., Hebrard, G., Bastoul, D., and Roustan, M. (2001). A comparative study of gas hold-up, bubble size, interfacial area and mass transfer coefficients in stirred gas-liquid reactors and bubble columns. Chem. Eng. Process. 40, 97–111. doi:10.1016/s0255-2701(00)00129-x

CrossRef Full Text | Google Scholar

Boyd, C. E. (2020). “Water quality: an introduction,” in Springer eBooks earth and environmental science. 3rd ed. Cham: Springer.

Google Scholar

Catapano, G., Czermak, P., Eibl, R., Eibl, D., and Pörtner, R. (2009). “Bioreactor design and scale-up,” in Cell and tissue reaction engineering (Springer), 173–259.

CrossRef Full Text | Google Scholar

Eibl, R., Eibl, D., Pörtner, R., Catapano, G., and Czermak, P. (2009). “Cell and tissue reaction engineering: with a contribution by martin fussenegger and wilfried weber,” in Principles and practice. Springer. doi:10.1007/978-3-540-68182-3

CrossRef Full Text | Google Scholar

Fitschen, J., Bernemann, V., Haase, I., and Hofmann, S. (2023). Gitlab Repository: determintation of volumetric mass transfer coefficient in STR.

Google Scholar

Fitschen, J., Maly, M., Rosseburg, A., Wutz, J., Wucherpfennig, T., and Schlüter, M. (2019). Influence of spacing of multiple impellers on power input in an industrial-scale aerated stirred tank reactor. Chem. Ing. Tech. 91, 1794–1801. doi:10.1002/cite.201900121

CrossRef Full Text | Google Scholar

Gabelle, J.-C., Augier, F., Carvalho, A., Rousset, R., and Morchain, J. (2011). Effect of tank size on kla and mixing time in aerated stirred reactors with non-Newtonian fluids. Can. J. Chem. Eng. 89, 1139–1153. doi:10.1002/cjce.20571

CrossRef Full Text | Google Scholar

Garcia-Ochoa, F., and Gomez, E. (2009). Bioreactor scale-up and oxygen transfer rate in microbial processes: an overview. Biotechnol. Adv. 27, 153–176. Citation Status MEDLINE. doi:10.1016/j.biotechadv.2008.10.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Garnier, A., Voyer, R., Tom, R., Perret, S., Jardin, B., and Kamen, A. (1996). Dissolved carbon dioxide accumulation in a large scale and high density production of TGF receptor with baculovirus infected Sf-9 cells 22. Cytotechnology 22, 53–63. doi:10.1007/BF00353924

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, W.-S. (2018). “Includes bibliographical references and index,” in Engineering principles in biotechnology. Hoboken, NJ, USA Chichester, West Sussex: Wiley.

Google Scholar

Hu, X. E., Liu, L., Luo, X., Xiao, G., Shiko, E., Zhang, R., et al. (2020). A review of N-functionalized solid adsorbents for post-combustion CO2 capture. Appl. Energy 260, 114244. doi:10.1016/j.apenergy.2019.114244

CrossRef Full Text | Google Scholar

Klamt, A. (1995). Conductor-like screening model for real solvents: a new approach to the quantitative calculation of solvation phenomena. J. Phys. Chem. 99, 2224–2235. doi:10.1021/j100007a062

CrossRef Full Text | Google Scholar

Knoll, A., Maier, B., Tscherrig, H., and Büchs, J. (2005). The oxygen mass transfer, carbon dioxide inhibition, heat removal, and the energy and cost efficiencies of high pressure fermentation. Adv. Biochem. Engineering/Biotechnology 92, 77–99. doi:10.1007/b98918

PubMed Abstract | CrossRef Full Text | Google Scholar

Kraume, M. (2020). Transportvorgänge in der Verfahrenstechnik: Grundlagen und apparative Umsetzungen. auflage edn. Berlin Heidelberg: Springer Lehrbuch, 3.

CrossRef Full Text | Google Scholar

Liu, L., Chen, H., Shiko, E., Fan, X., Zhou, Y., Zhang, G., et al. (2018). Low-cost DETA impregnation of acid-activated sepiolite for CO2 capture. Chem. Eng. J. 353, 940–948. doi:10.1016/j.cej.2018.07.086

CrossRef Full Text | Google Scholar

Lohrengel, B. (2017). “Thermische Trennverfahren: Trennung von Gas-Dampf- und Flüssigkeitsgemischen,”, 3. Berlin Boston: De Gruyter Oldenbourg. , durchgesehene und bibliografisch ergänzte ausgabe edn. doi:10.1515/9783110473223

CrossRef Full Text | Google Scholar

Matsunaga, N., Kano, K., Maki, Y., and Dobashi, T. (2009a). Estimation of dissolved carbon dioxide stripping in a large bioreactor using model medium. J. Biosci. Bioeng. 107, 419–424. doi:10.1016/j.jbiosc.2008.11.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Matsunaga, N., Kano, K., Maki, Y., and Dobashi, T. (2009b). Culture scale-up studies as seen from the viewpoint of oxygen supply and dissolved carbon dioxide stripping. J. Biosci. Bioeng. 107, 412–418. doi:10.1016/j.jbiosc.2008.12.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Montgomery, H. A. C., Thom, N. S., and Cockburn, A. (1964). Determination of dissolved oxygen by the winkler method and the solubility of oxygen in pure water and sea water. J. Appl. Chem. 14, 280–296. doi:10.1002/jctb.5010140704

CrossRef Full Text | Google Scholar

Mostafa, S. S., and Gu, X. S. (2003). Strategies for improved dCO2 removal in large-scale fed-batch cultures. Biotechnol. Prog. 19, 45–51. doi:10.1021/bp0256263

PubMed Abstract | CrossRef Full Text | Google Scholar

Paul, E. L., Atiemo-Obeng, V. A., and Kresta, S. M. (2004). in Handbook of industrial mixing: science and practice (Hoboken, NJ, USA: Wiley-Interscience).

Google Scholar

Royce, P. N. C., and Thornhill, N. F. (1991). Estimation of dissolved carbon dioxide concentrations in aerobic fermentations. AIChE J. 37, 1680–1686. doi:10.1002/aic.690371111

CrossRef Full Text | Google Scholar

Schulz, T. W., and Wucherpfennig, T. (2021). Bioreactor or fermenter for the culturing of cells or microorganisms in suspension in industrial scale.

Google Scholar

Sieblist, C., Hägeholz, O., Aehle, M., Jenzsch, M., Pohlscheidt, M., and Lübbert, A. (2011a). Insights into large-scale cell-culture reactors: II. Gas-phase mixing and CO2 stripping. Biotechnol. J. 6, 1547–1556. doi:10.1002/biot.201100153

PubMed Abstract | CrossRef Full Text | Google Scholar

Sieblist, C., Jenzsch, M., Pohlscheidt, M., and Lübbert, A. (2011b). Insights into large-scale cell-culture reactors: I. Liquid mixing and oxygen supply. Biotechnol. J. 6, 1532–1546. doi:10.1002/biot.201000408

PubMed Abstract | CrossRef Full Text | Google Scholar

Simmons, M., Zhu, H., Bujalski, W., Hewitt, C., and Nienow, A. (2007). Mixing in a model bioreactor using agitators with a high solidity ratio and deep blades. Chem. Eng. Res. Des. 85, 551–559. doi:10.1205/cherd06157

CrossRef Full Text | Google Scholar

Stepper, L., Filser, F. A., Fischer, S., Schaub, J., Gorr, I., and Voges, R. (2020). Pre-stage perfusion and ultra-high seeding cell density in CHO fed-batch culture: a case study for process intensification guided by systems biotechnology. Bioprocess Biosyst. Eng. 43, 1431–1443. doi:10.1007/s00449-020-02337-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Van’t Riet, K. (1979). Review of measuring methods and results in nonviscous gas-liquid mass transfer in stirred vessels. Industrial & Eng. Chem. Process Des. Dev. 18, 357–364. doi:10.1021/i260071a001

CrossRef Full Text | Google Scholar

VDI (2013). Wärmeatlas: mit 320 Tabellen. VDI-Buch Berlin u.a., 11. Springer Vieweg.bearb. und erw. aufl. edn.

Google Scholar

Whitman, W. G. (1923). The two-film theory of gas absorption. Chem. Metall. Eng. 29, 146–148. doi:10.1016/0017-9310(62)90032-7

CrossRef Full Text | Google Scholar

Xing, Z., Lewis, A. M., Borys, M. C., and Li, Z. J. (2017). A carbon dioxide stripping model for mammalian cell culture in manufacturing scale bioreactors. Biotechnol. Bioeng. 114, 1184–1194. doi:10.1002/bit.26232

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, S., Hoshan, L., Jiang, R., Gupta, B., Brodean, E., O’Neill, K., et al. (2017). A practical approach in bioreactor scale-up and process transfer using a combination of constant P/V and vvm as the criterion. Biotechnol. Prog. 33, 1146–1159. doi:10.1002/btpr.2489

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, C., Ling, H., Cao, W., Deng, F., Zhao, Y., Cao, D., et al. (2024a). Revealing the potential of cyclic amine morpholine (MOR) for CO2 capture through a comprehensive evaluation framework and rapid screening experiments. Chem. Eng. J. 495, 153402. doi:10.1016/j.cej.2024.153402

CrossRef Full Text | Google Scholar

Yu, C., Ling, H., Shen, Z., Yang, H., Cao, D., and Hu, X. (2024b). A general model for prediction of the 2 equilibrium solubility in aqueous tertiary amine systems. Syst. n/a 70, e18551. doi:10.1002/aic.18551

CrossRef Full Text | Google Scholar

Zlokarnik, M. (2001). Stirring: theory and practice. Weinheim, Germany: Wiley-VCH Verlag GmbH.

Google Scholar