Predicting xylose yield from prehydrolysis of hardwoods: A machine learning approach

Hemicelluloses are amorphous polymers of sugar molecules that make up a major fraction of lignocellulosic biomasses. They have applications in the bioenergy, textile, mining, cosmetic, and pharmaceutical industries. Industrial use of hemicellulose often requires that the polymer be hydrolyzed into constituent oligomers and monomers. Traditional models of hemicellulose degradation are kinetic, and usually only appropriate for limited operating regimes and specific species. The study of hemicellulose hydrolysis has yielded substantial data in the literature, enabling a diverse data set to be collected for general and widely applicable machine learning models. In this paper, a dataset containing 1955 experimental data points on batch hemicellulose hydrolysis of hardwood was collected from 71 published papers dated from 1985 to 2019. Three machine learning models (ridge regression, support vector regression and artificial neural networks) are assessed on their ability to predict xylose yield and compared to a kinetic model. Although the performance of ridge regression was unsatisfactory, both support vector regression and artificial neural networks outperformed the simple kinetic model. The artificial neural network outperformed support vector regression, reducing the mean absolute error in predicting soluble xylose yield of test data to 6.18%. The results suggest that machine learning models trained on historical data may be used to supplement experimental data, reducing the number of experiments needed.

1 Introduction

Hemicellulose is the second most common component in lignocellulosic biomass, after cellulose, and its content ranges from 25 to 35 wt% (Isikgor and Becer, 2015). Hemicellulosic polymers are comprised of xyloses, arabinoses, mannoses, glucoses, and galactoses (Scheller and Ulvskov, 2010). Hemicellulose products, such as derived monomers and oligomers, have diverse applications in manufacturing (Sella Kapu and Trajano, 2014), energy (Spiridon and Popa, 2008; Sella Kapu and Trajano, 2014), and the pharmaceutical industry (Spiridon and Popa, 2008; Sella Kapu and Trajano, 2014). When hydrolyzed, hemicellulose degrades into its constituents through the breaking of glycosidic bonds to produce a mixture of oligomers and monomers. Hydrolysis is catalyzed by protons during autohydrolysis or dilute acid hydrolysis (Carvalheiro et al., 2008; Sella Kapu and Trajano, 2014). In addition to acids, other types of catalysts can be used, including metal salts and ionic liquids (Delbecq et al., 2018). Industrially, dilute acid hydrolysis and autohydrolysis processes are preferred owing to reduced chemical and capital cost (Carvalheiro et al., 2008; Sella Kapu and Trajano, 2014).

During both dilute acid hydrolysis and autohydrolysis, a proton catalyzes the breaking of glycosidic bonds. In dilute acid hydrolysis, these protons are provided by an external source of acid. During autohydrolysis, protons are provided by the autodissociation of water at high temperature and the acetic acid formed by deacetylation of hemicellulose. However, both phenomena also occur during dilute acid hydrolysis. Classically, kinetic models of dilute acid hydrolysis and autohydrolysis have been developed independently but use similar forms. For both systems, the hydrolysis reaction is typically described by either monophasic or biphasic kinetic models (Sella Kapu and Trajano, 2014) derived from Saeman’s model of cellulose decomposition (Saeman, 1945). Both models assume first order kinetics with Arrhenius rate constants (Sella Kapu and Trajano, 2014), and account for operating time, temperature, and proton concentration. Proton concentration will depend on: moles of external acid added, moles of acetic acid formed, amount of neutralization by biomass ash, and three equilibria (external acid, water dissociation, and acetic acid). Sella Kapu et al. (2016) demonstrated that when these phenomena are all accounted for in the chemical reaction pathway, the experimentally determined proton concentration under both autohydrolysis and dilute acid hydrolysis conditions can be described by a single model.

A persistent limitation of existing kinetic models is that the value of the experimentally determined parameters vary widely depending on feed and reaction conditions (Maloney et al., 1985; Kim and Lee, 1987; Esteghlalian et al., 1997; Jensen et al., 2008; Yat et al., 2008). Model structure rarely accounts for all relevant chemical phenomena such as feedstock composition (e.g., acetyl content, degree of carbohydrate cross-linking) or mass transfer effects. This is in part due to the difficulty of quantifying such phenomena in a substrate as chemically and structurally complex as woody biomass. Although a simple model structure gives good fit for individual cases, such as a single feedstock over a small range of temperature and time, it cannot give reliable predictions for a wide range of conditions (Fearon et al., 2020). Consequently, a unique model is needed for every feedstock; this approach is expensive and slow due to the resource and labour intensity of biomass experiments.

One alternative to kinetic models is to develop statistical models. Machine learning (ML) provides a powerful set of techniques to extract knowledge from datasets and develop statistical models. Popular methods include ridge regression, support vector regression, and artificial neural networks. Within the field of chemical engineering, ML has been successfully applied to various applications including molecular recognition (Cao et al., 2018), thermal decompositions of polymeric materials (Conesa et al., 2004), prediction of mass transfer coefficients (Kojić and Omorjan, 2017), and heat transfer coefficients (Gandhi and Joshi, 2010). Specifically in the field of reaction engineering and catalysis, ML techniques have been used to predict catalytic activity of water-gas shift reaction (Odabaş1 et al., 2014; Smith et al., 2020), study the kinetics of three-way catalytic converters (Glielmo et al., 1999), and model the conversion rates of complex heterogeneous reactions (Molga et al., 2000). In the field of biomass pretreatment, ML has been used to predict enzyme catalyzed bioethanol production from lignocellulosic biomass (Smuga-Kogut et al., 2021). However, the use of ML techniques in hemicellulose hydrolysis is quite new.

Hemicellulose hydrolysis has been studied in diverse biomass agricultural residues, grasses, hardwoods, and softwoods. It is well-known that the anatomical features of these classes differ; for example, softwood tissue is composed almost entirely of long, tapering tracheids while hardwood tissue is composed of long, narrow libriform fibers and shorter, wider vessels (Chen et al., 2017). The chemical composition, structure (e.g., molecular weight, degree of branching) and thus reactivity of hemicellulose also varies considerably between classes. In hardwoods, hemicellulose is predominantly in the form of acetyl-4-O-methylglucuronoxylan, and in softwoods, hemicellulose is predominantly galactoglucomannan (Scheller and Ulvskov, 2010). Within hardwood hemicellulose, differences in reactivity of the xylan backbone and side residues of arabinose and acetyl groups have been reported (Garrote et al., 1999). Given the inherent differences between biomass classes, we chose to limit our modeling efforts to hemicellulose hydrolysis in hardwoods. While differences in chemical composition and structure can be observed even tree to tree within a single species, (Porth et al., 2013), such detailed data is rarely reported or modeled in hydrolysis studies. As a statistical method, machine learning cannot explicitly capture the structural and chemical diversity of species, especially when this data is not widely available in the literature. We encode the wood species as an input variable to allow the models to differentiate the impact of species.

In this study, we use machine learning models to predict the xylose yield from hardwood hemicellulose hydrolysis in batch reactors. Specifically, 1955 data points were mined from the literature (Jensen et al., 2008; Shi et al., 2019; Mittal et al., 2009b; Morinelly et al., 2009; Jensen et al., 2010; Chen et al., 2015; Yan and Liu, 2015; Nitsos et al., 2016; Borrega et al., 2011; Gladyshko, 2011; Ahmad et al., 2016; Dagnino et al., 2013; Parajó et al., 1994, 1993; Vázquez et al., 1995; Garrote et al., 1999, 2001; Canettieri et al., 2007a,b; Garrote et al., 2007; Yu et al., 2009; Romaní et al., 2010; Chirat et al., 2012; Gutsch et al., 2012; McIntosh et al., 2012; Wei et al., 2012; Castro et al., 2014; López et al., 2014; Tunc, 2014; Rangel et al., 2016; Inalbon et al., 2017; Mateo et al., 2014; Cebreiros et al., 2018; Peleteiro et al., 2018; Mittal et al., 2009a; Zhang et al., 2013; Rafiqul and Sakinah, 2012b,a; Rafiqul et al., 2014; Tunc and van Heiningen, 2008; Kundu et al., 2015; Jeong and Lee, 2016; Springer, 1985; Fernández et al., 2018; Puentes et al., 2013; Mateo et al., 2014; Martínez-Patiño et al., 2017; Yan et al., 2013; Yan, 2015; Yan et al., 2016; Negro et al., 2003; Dai and McDonald, 2014; Hou et al., 2014; Li et al., 2014; Kundu and Lee, 2015; Liu et al., 2015; Lee et al., 2017; Liu et al., 2017; Wen et al., 2019; Jesus et al., 2017; Eklund et al., 1995; Sassner et al., 2008; Pu et al., 2011; Lim and Lee, 2012; Liu et al., 2018; Huang et al., 2018; Li et al., 2010; Tunc et al., 2014; Ma et al., 2017; Kim et al., 2011, 2014; Nitsos et al., 2013) and used to create the models. We establish baseline model prediction accuracy by preparing pretreatment and wood species-specific kinetic models. We then investigate three machine learning models of differing complexity (ridge regression, support vector regression, and artificial neural networks). We train and test the models using the collected dataset, and compare their performance to the pretreatment and wood species-specific kinetic models. We find that both support vector regression and artificial neural networks outperformed the simple kinetic model, with the artificial neural network reducing the mean absolute error in predicting soluble xylose yield of test data to 6.18%. The results suggest that machine learning models trained on historical data may be used to supplement experimental data, reducing the number of experiments needed.

2 Materials and methods

2.1 Data collection and processing

We performed a detailed search on published works dated from 1985 to 2019, related to batch isothermal dilute acid hydrolysis and batch isothermal autohydrolysis of hardwood. Alternate reactor configurations such as flow-through systems (Mok and Antal, 1992; Trajano et al., 2015) and the Dionex Accelerated Solvent Extractor (Song et al., 2011) were deliberately excluded as these systems result in relatively short residence times of solubilized products and different reaction regimes compared to classic batch reactors. Out of numerous articles we inspected, we considered 71 papers, which reported values for all variables in Table 1 (the remaining articles omitted some variables), and collected a dataset consisting of 1955 experimental data points. Data was only included if the source provided all of the variables listed in Table 1, as the machine learning techniques used require that there are no missing features in the inputs to the model. All reported values were converted to the units shown in Table 1. The dataset contains experiments on 15 different wood species with an additional mixed wood combination, and 6 acid species.

TABLE 1

TABLE 1. Collected variables and their ranges for each experimental data point.

Out of the variables in Table 1, the predicted variable was chosen to be xylose yield as a percentage of the initial hemicellulosic xylose contained in the raw material. Most of the papers did not directly report the initial proton concentration, and we compute its value based on the initial acid concentration, acid species, and the corresponding pKa values. A number of papers only reported xylose concentration at the end of the reaction, and we computed xylose yield using Eq. 1, in which ρ_W denotes the density of water and is approximated to be 1000 g/L, C denotes xylose concentration, and X₀ represents the initial hemicellulosic xylose concentration in the raw material. Several papers report raw material concentration in xylan basis, and which is converted to a xylose basis using the anhydrous correction shown in Eq. 2. Total soluble xylose yield (oligomers + monomers) can be computed from all 71 papers, however, only 30 of the 71 articles separately reported monomeric xylose. Of the 1955 experimental data points collected, only 882 data points contained information on monomeric xylose. Only 26 data points reported independent oligomer and monomer yields; this is too few data points for machine learning models. Therefore, we run two independent computational experiments. The first experiment is run on the whole dataset consisting of 1955 data points to build a model for predicting total soluble xylose yield, while the second experiment is run on the subset consisting of 882 data points to predict monomeric xylose yield.

$Y=100\% \ast \frac{C\times LSR}{{\rho }_w\times \frac{X_{\mathrm{o}}}{100}}(1)$

$X_{\mathrm{o}}=\frac{X_{xylan}}{0.88}(2)$

The remaining variables in Table 1 are used as feature variables for predicting xylose yield. Total reaction time is the sum of the isothermal reaction time and the time it takes the reactor to ramp to the desired temperature. For 413 data points across 26 sources, information about ramp rate was not available. In these data, the isothermal reaction time is taken to be the total reaction time. Each wood and acid species is represented as a binary feature, also known as one-hot encoding. The dataset covers a wide range of wood species including acacia (Shi et al., 2019), aspen (Jensen et al., 2008; Mittal et al., 2009b; Morinelly et al., 2009; Jensen et al., 2010; Li et al., 2010; Chen et al., 2015; Yan and Liu, 2015), basswood (Jensen et al., 2008), beech (Nitsos et al., 2016, 2013), birch (Li et al., 2010; Borrega et al., 2011; Gladyshko, 2011; Ahmad et al., 2016), carob (Dagnino et al., 2013), eucalyptus (Parajó et al., 1994, 1993; Vázquez et al., 1995; Garrote et al., 1999, 2001; Canettieri et al., 2007a,b; Garrote et al., 2007; Yu et al., 2009; Romaní et al., 2010; Chirat et al., 2012; Gutsch et al., 2012; McIntosh et al., 2012; Wei et al., 2012; Castro et al., 2014; López et al., 2014; Tunc, 2014; Rangel et al., 2016; Inalbon et al., 2017; Mateo et al., 2014; Cebreiros et al., 2018; Peleteiro et al., 2018; Ma et al., 2017), maple (Jensen et al., 2008; Mittal et al., 2009a; Li et al., 2010; Zhang et al., 2013), meranti (Rafiqul and Sakinah, 2012b,a; Rafiqul et al., 2014), oak (Springer, 1985; Fernández et al., 2018), olive (Puentes et al., 2013; Mateo et al., 2014; Martínez-Patiño et al., 2017), paulownia (Yan et al., 2013; Yan, 2015; Yan et al., 2016), poplar (Negro et al., 2003; Kim et al., 2011; Dai and McDonald, 2014; Hou et al., 2014; Li et al., 2014; Kundu and Lee, 2015; Liu et al., 2015; Lee et al., 2017; Liu et al., 2017; Huang et al., 2018; Liu et al., 2018; Wen et al., 2019), vine (Jesus et al., 2017), and willow (Eklund et al., 1995; Sassner et al., 2008). Mixed species were either combinations of sweet and black gum, oak, maple, and southern magnolia, (Tunc and van Heiningen, 2008; Tunc et al., 2014), oak, black locust, and Japanese chestnut, (Lim and Lee, 2012; Kundu et al., 2015; Jeong and Lee, 2016), maple, birch, and oak, (Pu et al., 2011), or not specified (Kim et al., 2014). Acid species in the collected data include acetic, formic, malic, oxalic, phosphoric, and sulfuric.

In addition to the basic descriptors of reaction conditions, combination features including Severity Factor (R_o), P-Factor, H-Factor, and their log values are added to features; calculated using Eq. 3a (Overend et al., 1987), Eq. 3b (Sixta et al., 2006), and Eq. 3c (Vroom, 1957), respectively. These combination features are widely used to reflect the trade-offs of temperature and time on the severity of hydrolysis. Temperature and time in Eq. 3a take units Celsius and minutes respectively, while temperature and time in Eqs 3b, 3c take units Kelvin and hours, respectively. In the event that the combination factors are equal to 0, the log of the factors are also set to 0.

$R_o=t_I*e^{\frac{T_R-100}{14.75}}(\mathrm{3a})$

$P_f=\underset{o}{\overset{t_I}{{\displaystyle \int }}}{e}^{40.48-\frac{15106}{T_R}}dt(\mathrm{3b})$

$H_f=\underset{o}{\overset{t_I}{{\displaystyle \int }}}{e}^{43.2-\frac{16117}{T_R}}dt(\mathrm{3c})$

For machine learning methods, we need to perform data preprocessing, since continuous feature variables can range over orders of magnitude, as in the case of reaction time and particle size. In this study, feature variables are standardized using a z-score transformation to ensure that each variable has zero mean and comparable variance values.

2.2 Computational methods

In this section, we describe several approaches we applied to predict xylose yield, including kinetic models and three machine learning approaches, namely ridge regression, support vector regression, and artificial neural networks. All of the features listed in Table 1, with the exception of xylose yield, are used as input features to the machine learning models, corresponding to 9 input features.

2.2.1 Kinetic models

We adopted the simplified Saemen-type kinetic model used by many, which models hemicellulose decomposition as a sequence of two first order reactions. In the first reaction, hemicellulose is hydrolyzed to xylose, and in the second reaction the xylose is further decomposed to degradation products. Equations 4a, 4b represent the mass balance equations that describe the decomposition of hemicellulose, and Eq. 4c is the analytical solution, where X represents the hemicellulosic xylose in feedstock with its initial value denoted as X₀, C is the concentration of xylose, k₁ and k₂ are kinetic constants for xylose formulation and xylose degradation.

$\frac{dX}{dt}={-k}_{1}X(\mathrm{4a})$

$\frac{dC}{dt}=k_{1}X-k_{2}C(\mathrm{4b})$

$C=\frac{-k_1{X}_0*(e^{-k_{1}t}-e^{-k_{2}t})}{k_1-k_2}(\mathrm{4c})$

For both dilute acid hydrolysis and autohydrolysis, The kinetic constants k₁ and k₂ are described by an Arrhenius model that accounts for proton concentration as shown in Eq. 5,

$k=A{e}^{\frac{-E}{RT}}f\left(\left[H^{+}\right]\right)(5)$

Note this formulation is very general in the sense that it covers both dilute acid hydrolysis and autohy-drolysis. For autohydrolysis, in which no acid is added, the proton dependence function f ([H⁺]) is set to be one. For dilute acid hydrolysis, the most common proton dependence function is:

$f\left(\left[H^{+}\right]\right)=\left[H^{+}\right]\begin{array}{l}M\\ 0\end{array}(6)$

where [H⁺]₀ is the initial proton concentration. For each of the two kinetic constants, the activation energy (E), prexponential factor (A) and proton dependent coefficient (M) need to be fitted, representing six total kinetic parameters in the system.

For the kinetic models, we performed two experiments. In the first experiment, we divide the whole dataset into two subsets, one for the dilute acid hydrolysis and another one for autohydrolysis, and then train two models. For each model, we optimized the six kinetic parameters by minimizing the mean absolute error between predicted and reported xylose yield on the training data. In the second experiment, we partitioned the whole datset based on both the type of pretreatment and wood species, and then obtained 32 models. For all experiments, accuracy was evaluated independently using the remaining test data set. In the evaluation step, we predict xylose yield based on the corresponding kinetic model with fitted parameters, and compare the predicted xylose yield with the reported xylose yield. The fmin function in the SciPy package in Python was used for parameter estimation.

2.3 Machine learning methods

Predicting xylose yield can be cast as a regression problem. Here, we aim to find a model or hypothesis f: ℝⁿ→ℝ that maps an input vector x_i ∈ ℝⁿ to predict output variables y_i ∈ ℝ. The input vector x_i is also called a feature vector (all the variables in Table 1 except xylose yield) while the output y_i is the target we aim to predict (xylose yield in our paper). A pair (x_i, y_i) is called a sample. We will use a database of m samples [(x₁, y₁),..., (x_m, y_m)] that we call a training set to learn the machine learning model. Diverse regression models have been explored in the literature. We now describe three popular methods: ridge regression, support vector regression (SVR), and deep neural networks. These models are chosen because they differ in complexity and hypothesis space. Less complex models are more prone to underfitting, in which the relationships between input and output do not fit the training data well. In contrast, more complex models are more prone overfitting, where the model learns spurious relationships from the training data that do not generalize well to unseen data (e.g., test data). Ridge regression is simpler than the other two models, and is less prone to overfitting, though the simplicity limits the model to purely linear relationships. Therefore, it is necessary to make use of the combination features to account for non-linearity. In contrast, artificial neural networks can fit more complex relationships between features, at the expense of overfitting risk. Since a model is evaluated by its accuracy on unseen test data, not training data, a more complex model is not guaranteed to perform better than a less complex one. By using these three models, we are able to assess the trade off between model complexity and overfitting. For machine learning methods, we use the Scikit-learn package in Python for ridge regression and support vector regression, and Keras package to create ANN models. Other important packages are numpy, scipy, and pandas. All scripts needed to reproduce the results are available at https://github.com/edwardwang1/BiorefiningAndMachineLearning.

2.3.1 Ridge regression

Ridge regression, is a type of linear regression, which uses a hypothesis function of the following form:

$f\left({\mathbf{x}}_{\mathrm{i}}\right)={\mathbf{w}}^T{\mathbf{x}}_{\mathrm{i}}+b(7)$

The model parameters to be learned from the training set are the weights w ∈ ℝⁿ and b ∈ ℝ. The learning process consists of solving an optimization problem to find the optimal feature weights:

$\begin{array}{l}\min \\ \mathbf{w},b\end{array}\frac{1}{m}{\displaystyle \sum }_{i=1}^m{\left(y_i-{\mathbf{w}}^T{\mathrm{x}}_{\mathrm{i}}-b\right)}^2+\alpha {\Vert \mathbf{w}\Vert }^2(8)$

The first term of the objective function measures the accuracy of the hypothesis on the training set and the second term is a regularization term that prevents over-fitting. The hyperparameter α ∈ ℝ₊ is a regularization parameter that determines the balance between how well the hypothesis fits the training set and how well the hypothesis generalizes to other data. Large values of α might cause under-fitting while a small value of α might cause overfitting. This hyperparameter is determined by a procedure called model selection.

2.3.2 Support vector regression

Support Vector Regression (SVR) is an adaptation of the popular support vector machine (SVM) classifier for continuous variables. It uses the same hypothesis function as ridge regression. However, it solves a different optimization problem to learn w and b, as shown below.

$\begin{array}{l}\min \\ \mathbf{w},b,\zeta \end{array}C{\displaystyle \sum }_{i=1}^m{\zeta }_i+{\Vert \mathbf{w}\Vert }^2(\mathrm{9a})$

$\mathrm{s}.\mathrm{t}.\left|y_i-{\mathbf{w}}^T{\mathbf{x}}_{\mathrm{i}}-b\right|\le ϵ+{\zeta }_{i,}(\mathrm{9b})$

${\zeta }_i\ge 0,i=1,...,m(\mathrm{9c})$

The objective of SVR is to penalize the samples falling above and below the residual threshold ϵ while ignore samples falling within the residual threshold. Similar to ridge regression, it also has a regularization term. Here C ∈ ℝ₊ is a hyperparameter that is used to prevent over- or under-fitting (as with α). Prior to optimization, a non-linear kernel is usually applied to introduce non-linear relations that map the original feature vector x_i ∈ ℝⁿ to a new vector of features [K (x_i, x₁),..., K (x_i, x_m)] ∈ ℝ^m, where K (·) is called a kernel function. One common choice of a kernel function is the Gaussian kernel K(x₁, x_i) = exp(−γ||x₁ − x_i||²), which can be viewed as the similarity between features x₁ and x_i. The resulting new transformed features are then feed into linear SVR to generate the hypothesis model. For non-linear SVR, we also need to decide the value of C, ϵ, kernel type, and the kernel function parameters (e.g., γ) in the model selection phase.

2.3.3 Artificial neural networks

An artificial neural network (ANN) is composed of an input layer, hidden layers, and an output layer. Each layer consists of several basic unit functions called neurons. The input layer are the features x_i and the output layer has only one neuron representing the predicted value of y_i. We denote the total number of layers as L, the number of neurons in layer ℓ as s_ℓ, and the value of j-th neuron at ℓ-th layer as a_ℓ,j. We denote a_ℓ: = [a_ℓ,1, ..., a_ℓ,sℓ]. The information of layer ℓ − 1 is fed to j-th neuron in layer ℓ using the mapping a_ℓ,j = g^ℓ(w_ℓ,j^T a_ℓ−1 + b_ℓ,j), here g_ℓ is an activation function of layer ℓ. One popular choice of the activation function is the logistic function. We denote w_ℓ: = [w_ℓ,1, ..., w_ℓ,sℓ], b_ℓ: = [b_ℓ,1, ..., b_ℓ,sℓ] and a_ℓ = g_ℓ(w_ℓ^T a_ℓ−1 + b_ℓ). The parameters learned in the training process are w_ℓ and b_ℓ for all ℓ = 1,..., L. The training process solves the following optimization problem:

$\begin{array}{l}\min \\ {\mathbf{w}}_{\mathcal{\ell }},{\mathbf{b}}_{\mathcal{\ell }}\end{array}\frac{1}{m}{\displaystyle \sum }_{i=1}^m{\left(y_i-{\alpha }_{L,i}\right)}^2(10)$

After the w_ℓ, b_ℓ are learned, we can predict y_i given any new input x_i by using forward propagation. Similar to ridge regression and SVR, we can also add regularization terms to prevent overfitting. In this study, we employed a technique called dropout to combat overfitting. In the dropout layer, a fraction of weights are forced to be zeros, reducing network complexity. Choosing the architecture of a neural network is an art and is commonly based on cross-validation, as discussed in more detail in the next section. In general, a more complex neural network with more hidden layers is able to better fit training data, but is more prone to overfitting.

2.4 Model selection and evaluation

For both kinetic model and machine learning methods, we partition the entire data set randomly into a training set and a test set. The training set is used to learn the kinetic and machine learning models and the test set (also known as hold-out set) is used to assess the generalization of the learned model. For a sample (x_i, y_i) in the test set, the predicted output yˆ_i = f (x_i) is computed and compared with the true output y_i.

For machine learning methods, during the training process, we need to decide some hyperparameters (e.g., α for ridge classification, C for SVR, and network layout for ANN). This procedure is called model selection. We use the popular model selection method, k-fold cross validation, in which the whole training set is split into k equal folders. For each specific choice of hyperparameters, we train the model with k-1 folders and evaluate this model with the left-out folder as validation set. This procedure is repeated by cycling through the training set. Therefore, for each specific choice of hyperparameters, k models are built and evaluated. The performance of a specific choice of the hyperparameters is evaluated by averaging the accuracy of these k models. We decide the optimal hyperparameters by looping over different hyperparameter choices.

3 Results

For both kinetic models and machine learning methods, we randomly split the entire data set into a training set and a test set (80% of the samples for training and 20% for test). In this paper, mean absolute error (MAE) between predicted and reported yields for all data points in the test set was used to quantify the performance of the model. The unit of MAE is percentage points of yield. Note that the accuracy of the test set depends on the initial partition of the training set and test set and thus this procedure is often repeated several times to enhance predictability. In our study, we repeat each computational experiment 5 times and then compute the mean and confidence interval of MAE. We also duplicated each experiment between the total soluble xylose dataset (1955 samples) and the monomer only dataset (882 samples). For the total soluble xylose dataset, the model was trained and evaluated for its ability to predict total soluble xylose yield, whereas monomeric xylose yield was investigated for the monomer-only sub-dataset.

3.1 Performance of kinetic models

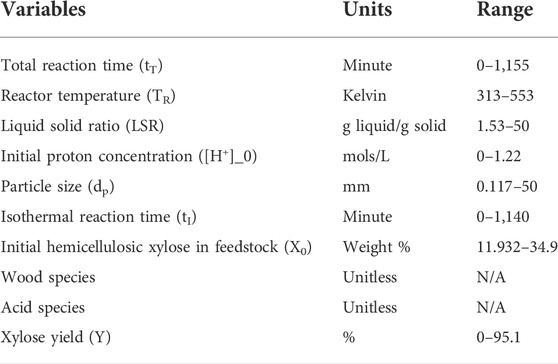
In the first kinetic model experiment, we determined model parameters for two data subsets: the dilute acid hydrolysis data subset and the autohydrolysis data subset. The mean absolute errors of predicting the value of total soluble xylose yield and monomeric xylose yield of the test data are 17.75 ± 0.894 and 9.32 ± 0.73 respectively. In the second kinetic model experiment, we determined parameters for 32 models, each describing a type of pretreatment applied to a single wood species. A comparison of the estimated Arrhenius parameters to values reported in literature can be found in the Supplementary Material. The mean absolute errors of predicting the value of total soluble xylose yield and monomeric xylose yield on test data are 15.49 ± 0.53 and 8.33 ± 0.56 respectively. Comparing the two experiments shows that wood species play a moderate role in hemicellulose hydrolysis. Figures 1, 2 shows the predicted value of total soluble xylose yield and monomeric xylose yield compared with the yield reported in the literature.

FIGURE 1

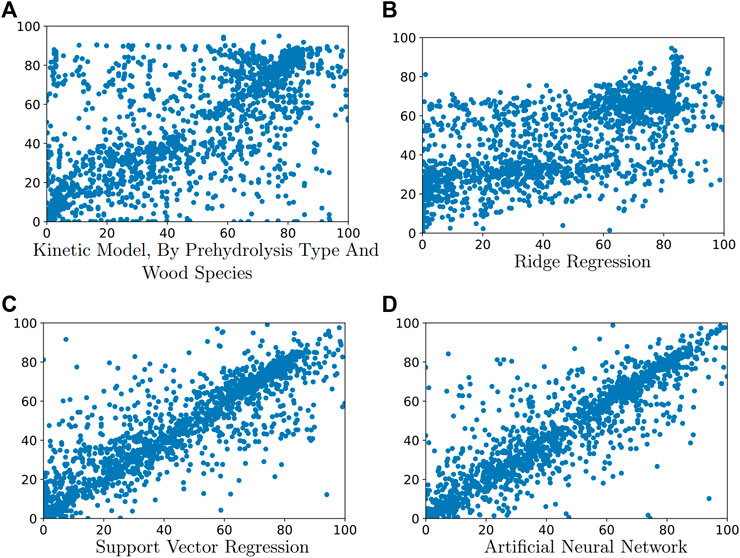
FIGURE 1. Predicted versus actual yield of total soluble xylose for test data for: (A) kinetic model fit by prehydrolysis type and wood species, (B) ridge regression, (C) support vector regression, and (D) artificial neural network.

FIGURE 2

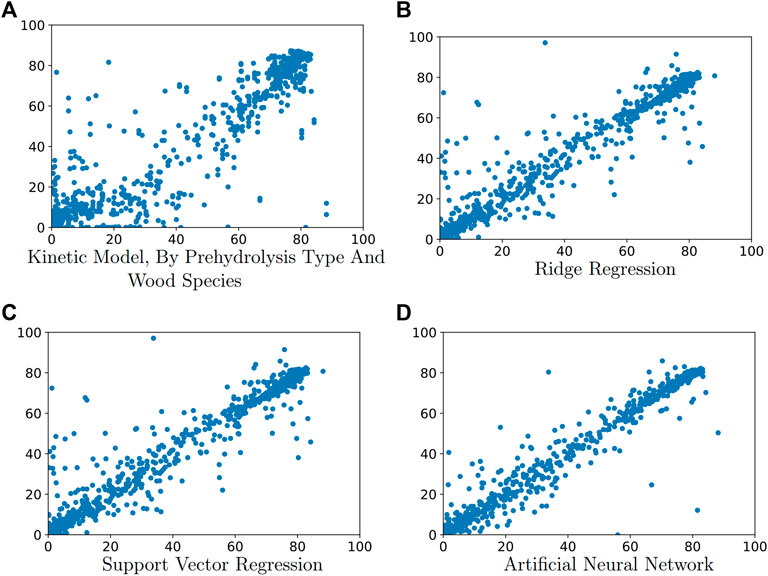
FIGURE 2. Predicted versus actual yield of monomeric xylose for test data for: (A) kinetic model fit by prehydrolysis type and wood species, (B) ridge regression, (C) support vector regression, and (D) artificial neural network.

These results demonstrate that a simple kinetic model is ineffective at predicting yield between experiments. The kinetic model takes into consideration only five variables: isothermal reaction time, initial proton concentration, hemicellulosic xylose in the feedstock, reaction temperature, and wood species (only for the second experiment). These models are adequate for scenarios where Liquid Solid Ratio (LSR) and particle size are constant. In cases where these change, however, a more comprehensive model is required. Efforts to advance kinetic modeling are on-going. The biphasic model, which divides hemicellulose into fast-reacting and slow-reacting fractions, is commonly used but the rationale for this division is not well-justified (Negahdar et al., 2016). There is growing recognition and effort to include additional phenomena such as mass transfer (Cahela et al., 1983; Krogell et al., 2013), depolymerization, (Kumar and Wyman, 2008; Hosseini and Shah, 2009; Chen et al., 2020), and the chemical and structural effects of biomass (Trajano et al., 2015; Mittal et al., 2019). These efforts are essential and also provide guidance for the development of more interpretable machine learning models (discussed in Future Work).

3.2 Performance of machine learning methods

In our study, we first decide hyperparameters based on k-fold cross validation (k = 5). For ridge regression the best value of α is found to be zero. For SVR, the hyperparameters includes the kernel type, kernel coefficient γ, regularization parameter C and residual threshold ε. The best combination of hyperparameters was chosen to be: kernel = “rbf”; ε = 1; C = 20,000; γ = “auto”. For ANNs, the structure of the neural network was chosen to be 6 layers, with 96, 96, 48, 48, and 1 neuron in layers 1 to 6 respectively. There was a dropout layer inserted between the first and second layer with a dropout value of 0.001. The batch size, learning rate, and maximum epoch were chosen to be 64, 0.005 and 3,000 respectively.

Figures 1, 2 shows the predicted value of total soluble xylose yield and monomeric xylose yield versus reported yield of the test data for machine learning methods and kinetic models. On these figures, the diagonal line represents theoretical perfect prediction with yˆ_i = y_i. Therefore points closer to the diagonal line have smaller prediction errors. These figures visually illustrates that the kinetic model was outperformed by all three machine learning models.

Figure 3 summarizes the performance of all computational methods in terms of mean absolute error of the test data. The mean absolute errors of predicting total soluble xylose yield of test data using ridge regression, SVR regression and ANN are 16.54 ± 0.46, 7.86 ± 0.49, and 6.18 ± 0.53 respectively. The mean absolute errors of predicting monomeric xylose yield of test data using ridge regression, SVR regression and ANN are 11.05 ± 0.66, 5.20 ± 1.26, and 2.90 ± 0.44 respectively.

FIGURE 3

FIGURE 3. Comparison of different computational methods in terms of mean absolute error of test data for: (A) total soluble xylose yield and (B) monomeric xylose yield. Mean absolute error was determined from five replicates of the computational experiment. Its units are percentage points of yield.

4 Discussion

Although the performance of ridge regression is unsatisfactory, both support vector regression and artificial neural networks outperform the simple kinetic model. All the models performed significantly different from each other (p < 0.05) as determined by a Student’s T-test. The results show that predictive power increases with increasing model complexity. The limitation of the kinetic model is that it only considers few features and suffers from non-generalizability. Although the ridge regression model has access to all features, its limitation is that it only uses linear relationships between features and thus suffers from underfitting. Both the SVR and ANN models are not constrained to linear relationships, and the difference in performance between the ANN and SVR models is lower than the difference in performance between the SVR and ridge models, illustrating the importance of capturing non-linear relationships. Overfitting does not become a serious problem for ANN models, partially because a relatively simple neural network structure was used. The MAE of the best model (ANN model) at predicting total soluble xylose yield is 6.18 ± 0.53, while the MAE at predicting monomeric xylose yield is only 2.90 ± 0.44. This level of error is acceptable, since the model is evaluated based on the data in the test set that the model has not seen before, and the reported data is also subjected to measurement noise.

Comparing Figures 3A,B shows that the performance of the models are better when predicting monomeric yield rather than total soluble xylose yield. One reason is that the value of total soluble xylose yield is usually larger than that of monomeric xylose yield.

4.1 Impact of feature information

In addition to determining the performance of the models, we also evaluated the importance of specific input features on ANN models. Since ANN models use non-linear functions, we cannot infer the importance of features from weights, and therefore they act as black boxes. Therefore we conducted a leave-one-out analysis. That is, a feature or group of features were iteratively hidden from the model during the training and testing process. When specific features are omitted (the remaining dataset has less information than the full dataset), the corresponding MAE will increase and the MAE increase is used to assess the impact of the features. Total and isothermal reaction time are linearly correlated, so the two features were removed together. All acid species and wood species were removed in their respective groups. The combination factors and their logs were removed together. As the combination factors contain information about both time and temperature, when those two features are removed, the combination factors must also be removed.

Figure 4 shows the results of such an analysis. The “No features removed” column represents the baseline accuracy of the model with all features available. The figure reveals that the three most important features with respect to yield for both total soluble xylose and monomeric xylose are: reaction time, temperature, and initial proton concentration. Specifically, in the total soluble xylose dataset, removing operating time, temperature, and initial proton concentration increases MAE from 6.18 ± 0.53 to 12.19 ± 0.52, 10.65 ± 0.73, and 7.89 ± 0.54, respectively. In the monomeric xylose dataset, removing operating time, temperature, and initial proton concentration increases MAE from 2.90 ± 0.44 to 10.06 ± 0.53, 7.26 ± 0.76, and 6.08 ± 0.95, respectively. These three variables are all considered in the classic kinetic models. The results of the leave one out analysis reinforces the importance of these variables and suggests that we should focus on optimizing these three variables for maximum yield. One interesting finding is that, despite having no information about operating time, the ANN model can still make a reasonable prediction (more accurate than ridge regression with full feature variables), likely due to the distribution of reaction times in the dataset.

FIGURE 4

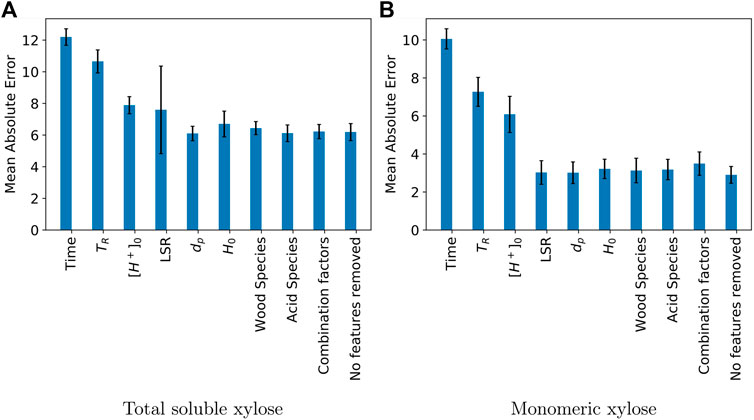
FIGURE 4. Effect of dropping features from the artificial neural network on mean absolute error of test data for: (A) total soluble xylose yield and (B) monomeric xylose yield. Mean absolute error was determined from five replicates of the computational experiment. Its units are percentage points of yield.

Removal of LSR has a moderate influence on model accuracy, especially for the prediction of total soluble xylose. This result is somewhat unexpected as this variable has typically received less attention than the others considered; 85% of the collected data has a LSR less than or equal to 10. The detailed review by Mäki-Arvela et al. (2011) highlights a mere six studies on the topic. Jaramillo et al. (2013) identify contradictory conclusions on the influence of liquid-solid ratio on sugar yield and concentration. Increasing solid concentration seems to decrease selectivity to hemicellulose dissolution but some authors report that solid concentration has no effect. Jaramillo et al. (2013) developed a model which uses suspension volume, not liquid phase volume, and a void fraction for biomass packing in the reactor. Consideration of these parameters enabled good prediction of glucose concentration from acid hydrolysis of sugar cane bagasse for initial liquid to solid ratios varying from 10 to 30. This approach also highlighted the importance of solid particle wetting and biomass neutralization capacity to the outcomes of acid hydrolysis. Liquid-solid ratio is important to industrial biorefining implementation as it will impact equipment sizing and separation requirements. From the results of past experimental studies and our leave-one-out analysis, it is clear that liquid-solid ratio deserves more nuanced modeling efforts. We highlight that if MAE is insensitive to the omission of a feature, it does not imply that the feature has low impact. For example, removal of wood species and acid species does not significantly change MAE, but this does not suggest that yield is independent of these features (wood species was shown to play a moderate role in the kinetic models). Predictability is not affected by dropping the wood species mainly because this information is also captured by other features that are not removed, such as initial hemicellulose content. Similarly, one possible explanation for why dropping acid species does not affect MAE is that its information is already used in the calculation of initial proton concentration.

4.2 Impact of data size

Finally, we also evaluate the effect of training data size on the performance of ANN. The number of samples in the dataset was randomly reduced to 10%, 25%, 50%, and 75% of the original sample size, and an ANN was trained and evaluated on each data subset. As shown in Figure 5, the effect of increasing data sample size is to decrease mean and variance of mean absolute error. However, the results also suggest that the decrease in prediction error is asymptotic, suggesting that increasing the number of samples further will not significantly improve performance.

FIGURE 5

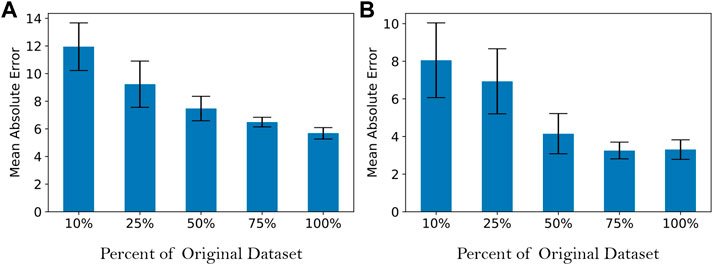
FIGURE 5. Effect of data size on mean absolute error of test data for the artificial neural network model for: (A) total soluble xylose yield and (B) monomeric xylose yield. Mean absolute error was determined from five replicates of the computational experiment. Its units are percentage points of yield.

4.3 Future work

One limitation of the ANN is its black box nature and lack of interpretability. The components within the ANN are related to each other through non-linear equations in a complex fashion. Though it achieves good performance, it is difficult to draw insights about the underlying mechanisms. Unlike simple models such as linear regression, the weights of the ANN that are determined during training are not directly applicable to physical relationships. Further work is needed to increase interpretability. One strategy is to develop a hybrid model which combines mechanistic insights with machine learning in order to gain the benefits of both. One way to construct a hybrid model is to use machine learning to analyze the residual mean absolute error of kinetics models. Another way is to use machine learning to predict the dependence of the kinetic parameters on an array of feature variables (e.g., particle size, wood species). These models provide predictions of how to achieve process outcomes such as maximum sugar yield and maximum oligomer mass. Development of such a model should be paired with experimental verification. Alternatively, models based on decision trees could be used to increase interpretability. An additional avenue of future work is to validate the ANN on data published after the data collection phase of this study was completed.

5 Conclusion

Significant research has been conducted in the field of hemicellulose hydrolysis, leading to a collection of data that can be mined and used in machine learning applications. We collected 1955 experimental data points from the literature, going as far back as 1985, and made the dataset, which to our knowledge, is the largest and most diverse of its type, publicly available. In this study, we train three machine learning models (ridge regression, support vector regression, and an artificial neural network) on the data to predict xylose yield, and evaluate them against a monophasic kinetic model. Both support vector regression and artificial neural network models outperformed the kinetic model, with the artificial neural network performing best, achieving a mean absolute error of 6.18 ± 0.53 percentage points (corresponding to 94% accuracy). This degree of accuracy is surprising given the diversity of feedstocks and conditions. A more “universal” model of hemicellulose hydrolysis can be used to reduce experimental demands. ANN model performance depends strongly on classic kinetic parameters: temperature, time and proton concentration. The machine learning models build on historical data can be used to supplement experimental data and reduce the amount of experiments needed.

Data availability statement

The dataset analyzed for this study can be found in the GitHub repository https://github.com/edwardwang1/BiorefiningAndMachineLearning. Further inquiries can be directed to the corresponding authors.

Author contributions

EW, RB, and GC collected data from the literature and prepared the database. EW prepared the code for the kinetic and machine learning models and wrote the manuscript. YC and HLT conceived the study, advised on model design, and interpretation. All authors reviewed and approved the manuscript.

Funding

RB and YC acknowledge financial support by the Natural Sciences and Engineering Research Council of Canada under grant RGPIN-2019-05499. HLT acknowledges financial support by the Natural Sciences and Engineering Research Council of Canada under grant RGPIN-2020-06003.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fceng.2022.994428/full#supplementary-material

References

Ahmad, W., Kuitunen, S., Borrega, M., and Alopaeus, V. (2016). Physicochemical modeling for hot water extraction of birch wood. Ind. Eng. Chem. Res. 55, 11062–11073. doi:10.1021/acs.iecr.6b02987

CrossRef Full Text | Google Scholar

Borrega, M., Nieminen, K., and Sixta, H. (2011). Degradation kinetics of the main carbohydrates in birch wood during hot water extraction in a batch reactor at elevated temperatures. Bioresour. Technol. 102, 10724–10732. doi:10.1016/j.biortech.2011.09.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Cahela, D. R., Lee, Y., and Chambers, R. (1983). Modeling of percolation process in hemicellulose hydrolysis. Biotechnol. Bioeng. 25, 3–17. doi:10.1002/bit.260250103

PubMed Abstract | CrossRef Full Text | Google Scholar

Canettieri, E. V., Rocha, G. J. d. M., de Carvalho, J. A., and de Almeida e Silva, J. B. (2007a). Optimization of acid hydrolysis from the hemicellulosic fraction of eucalyptus grandis residue using response surface methodology. Bioresour. Technol. 98, 422–428. doi:10.1016/j.biortech.2005.12.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Canettieri, E. V., Rocha, G. J. M., Carvalho, J. A., and Silva, J. B. A. (2007b). Evaluation of the kinetics of xylose formation from dilute sulfuric acid hydrolysis of forest residues of eucalyptus grandis. Ind. Eng. Chem. Res. 46, 1938–1944. doi:10.1021/ie0607494

CrossRef Full Text | Google Scholar

Cao, Y., Yu, H., Abbott, N. L., and Zavala, V. M. (2018). Machine learning algorithms for liquid crystal-based sensors. ACS Sens. 3, 2237–2245. doi:10.1021/acssensors.8b00100

PubMed Abstract | CrossRef Full Text | Google Scholar

Carvalheiro, F., Duarte, L., and Girio, F. (2008). Hemicellulose biorefineries: A review on biomass pretreatments. J. Sci. Ind. Res. 67, 849–864.

Google Scholar

Castro, E., Nieves, I. U., Mullinnix, M. T., Sagues, W. J., Hoffman, R. W., Fernández-Sandoval, M. T., et al. (2014). Optimization of dilute-phosphoric-acid steam pretreatment of eucalyptus benthamii for biofuel production. Appl. Energy 125, 76–83. doi:10.1016/j.apenergy.2014.03.047

CrossRef Full Text | Google Scholar

Cebreiros, F., Ferrari, M., and Lareo, C. (2018). Combined autohydrolysis and alkali pretreatments for cellulose enzymatic hydrolysis of eucalyptus grandis wood. Biomass Convers. biorefin. 8, 33–42. doi:10.1007/s13399-016-0236-4

CrossRef Full Text | Google Scholar

Chen, H., Fu, Y., Wang, Z., and Qin, M. (2015). Degradation and redeposition of the chemical components of aspen wood during hot water extraction. BioResources 10, 3005–3016. doi:10.15376/biores.10.2.3005-3016

CrossRef Full Text | Google Scholar

Chen, J., Martinez, D., Chang, X. F., Beatson, R. P., and Trajano, H. L. (2020). Evolution of hemicellulose molar mass during softwood hydrolysis. ACS Sustain. Chem. Eng. 8, 10345–10356. doi:10.1021/acssuschemeng.0c00814

CrossRef Full Text | Google Scholar

Chen, J., Yuan, Z., Zanuso, E., and Trajano, H. (2017). Response of biomass Species to hydrothermal pretreatment. 95–140. doi:10.1007/978-3-319-56457-94

CrossRef Full Text | Google Scholar

Chirat, C., Lachenal, D., and Sanglard, M. (2012). Extraction of xylans from hardwood chips prior to kraft cooking. Process Biochem. 47, 381–385. doi:10.1016/j.procbio.2011.12.024

CrossRef Full Text | Google Scholar

Conesa, J. A., Caballero, J. A., and Reyes-Labarta, J. A. (2004). Artificial neural network for modelling thermal decompositions. J. Anal. Appl. Pyrolysis 71, 343–352. doi:10.1016/s0165-2370(03)00093-7

CrossRef Full Text | Google Scholar

Dagnino, E., Chamorro, E., Romano, S., Felissia, F., and Area, M. (2013). Optimization of the pretreatment of prosopis nigra sawdust for the production of fermentable sugars. Bioresources 8, 499–514. doi:10.15376/biores.8.1.499-514

CrossRef Full Text | Google Scholar

Dai, J., and McDonald, A. G. (2014). Production of fermentable sugars and polyhydroxybutyrate from hybrid poplar: Response surface model optimization of a hot-water pretreatment and subsequent enzymatic hydrolysis. Biomass Bioenergy 71, 275–284. doi:10.1016/j.biombioe.2014.09.030

CrossRef Full Text | Google Scholar

Delbecq, F., Wang, Y., Muralidhara, A., El Ouardi, K., Marlair, G., and Len, C. (2018). Hydrolysis of hemicellulose and derivatives-a review of recent advances in the production of furfural. Front. Chem. 6, 146. doi:10.3389/fchem.2018.00146

PubMed Abstract | CrossRef Full Text | Google Scholar

Eklund, R., Galbe, M., and Zacchi, G. (1995). The influence of SO₂ and H₂SO₄ impregnation of willow prior to steam pretreatment. Bioresour. Technol. 52, 225–229. doi:10.1016/0960-8524(95)00042-D

CrossRef Full Text | Google Scholar

Esteghlalian, A., Hashimoto, A. G., Fenske, J. J., and Penner, M. H. (1997). Modeling and optimization of the dilute-sulfuric-acid pretreatment of corn stover, poplar and switchgrass. Bioresour. Technol. 59, 129–136. doi:10.1016/s0960-8524(97)81606-9

CrossRef Full Text | Google Scholar

Fearon, O., Nykänen, V., Kuitunen, S., Ruuttunen, K., Alén, R., Alopaeus, V., et al. (2020). Detailed modeling of the kraft pulping chemistry: Carbohydrate reactions. AIChE J. 66, e16252. doi:10.1002/aic.16252

CrossRef Full Text | Google Scholar

Fernández, M. A., Rissanen, J., Nebreda, A. P., Xu, C., Willför, S., Serna, J. G., et al. (2018). Hemicelluloses from stone pine, holm oak, and Norway spruce with subcritical water extraction comparative study with characterization and kinetics. J. Supercrit. Fluids 133, 647–657. doi:10.1016/j.supflu.2017.07.001

CrossRef Full Text | Google Scholar

Gandhi, A. B., and Joshi, J. B. (2010). Estimation of heat transfer coefficient in bubble column reactors using support vector regression. Chem. Eng. J. 160, 302–310. doi:10.1016/j.cej.2010.03.026

CrossRef Full Text | Google Scholar

Garrote, G., Domínguez, H., and Parajó, J. C. (2001). Generation of xylose solutions from Eucalyptus globulus wood by autohydrolysis-posthydrolysis processes: Posthydrolysis kinetics. Bioresour. Technol. 79, 155–164. S096085240100044X[pii]. doi:10.1016/s0960-8524(01)00044-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Garrote, G., Domínguez, H., and Parajó, J. C. (1999). Mild autohydrolysis: An environmentally friendly technology for xylooligosaccharide production from wood. J. Chem. Technol. Biotechnol. 74, 1101–1109. doi:10.1002/(sici)1097-4660(199911)74:11<1101::aid-jctb146>3.0.co;2-m.74:1

CrossRef Full Text | Google Scholar

Garrote, G., Kabel, M. A., Schols, H. A., Falqué, E., Domínguez, H., and Parajó, J. C. (2007). Effects of Eucalyptus globulus wood autohydrolysis conditions on the reaction products. J. Agric. Food Chem. 55, 9006–9013. doi:10.1021/jf0719510

PubMed Abstract | CrossRef Full Text | Google Scholar

Gladyshko, Y. (2011). Extraction of hemicelluloses by acid catalyzed hydrolysis. Ph.D. thesis. Imatra: Saimaa University of Applied Sciences.

Google Scholar

Glielmo, L., Santini, S., Milano, M., and Serra, G. (1999). Three-way catalytic converter modelling: A machine learning approach for the reaction kinetics. IEEE, 239–244.

Google Scholar

Gutsch, J. S., Nousiainen, T., and Sixta, H. (2012). Comparative evaluation of autohydrolysis and acid-catalyzed hydrolysis of Eucalyptus globulus wood. Bioresour. Technol. 109, 77–85. doi:10.1016/j.biortech.2012.01.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Hosseini, S. A., and Shah, N. (2009). Multiscale modelling of biomass pretreatment for biofuels production. Chem. Eng. Res. Des. 87, 1251–1260. doi:10.1016/j.cherd.2009.04.018

CrossRef Full Text | Google Scholar

Hou, Q., Wang, Y., Liu, W., Liu, L., Xu, N., and Li, Y. (2014). An application study of autohydrolysis pretreatment prior to poplar chemi-thermomechanical pulping. Bioresour. Technol. 169, 155–161. doi:10.1016/j.biortech.2014.06.091

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, K., Luo, J., Cao, R., Su, Y., and Xu, Y. (2018). Enhanced xylooligosaccharides yields and enzymatic hydrolyzability of cellulose using acetic acid catalysis of poplar sawdust. J. Wood Chem. Technol. 38, 371–384. doi:10.1080/02773813.2018.1500608

CrossRef Full Text | Google Scholar

Inalbon, M. C., Solier, Y. N., and Angel Zanuttini, M. (2017). Hydrothermal treatment of eucalyptus wood: Effects on ion permeability and material removing. Ind. Crops Prod. 104, 195–200. doi:10.1016/j.indcrop.2017.04.042

CrossRef Full Text | Google Scholar

Isikgor, F., and Becer, R. (2015). Lignocellulosic biomass: A sustainable platform for the production of bio-based chemicals and polymers. Polym. Chem. 6, 4497–4559. doi:10.1039/C5PY00263J

CrossRef Full Text | Google Scholar

Jaramillo, O. J., Gómez-García, M. Á., and Fontalvo, J. (2013). Prediction of acid hydrolysis of lignocellulosic materials in batch and plug flow reactors. Bioresour. Technol. 142, 570–578. doi:10.1016/j.biortech.2013.05.064

PubMed Abstract | CrossRef Full Text | Google Scholar

Jensen, J., Morinelly, J., Aglan, A., Mix, A., and Shonnard, D. R. (2008). Kinetic characterization of biomass dilute sulfuric acid hydrolysis: Mixtures of hardwoods, softwood, and switchgrass. AIChE J. 54, 1637–1645. doi:10.1002/aic.11467

CrossRef Full Text | Google Scholar

Jensen, J. R., Morinelly, J. E., Gossen, K. R., Brodeur-Campbell, M. J., and Shonnard, D. R. (2010). Effects of dilute acid pretreatment conditions on enzymatic hydrolysis monomer and oligomer sugar yields for aspen, balsam, and switchgrass. Bioresour. Technol. 101, 2317–2325. doi:10.1016/j.biortech.2009.11.038

PubMed Abstract | CrossRef Full Text | Google Scholar

Jeong, S. Y., and Lee, J. W. (2016). Sequential fenton oxidation and hydrothermal treatment to improve the effect of pretreatment and enzymatic hydrolysis on mixed hardwood. Bioresour. Technol. 200, 121–127. doi:10.1016/j.biortech.2015.10.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Jesus, M. S., Romaní, A., Genisheva, Z., Teixeira, J. A., and Domingues, L. (2017). Integral valorization of vine pruning residue by sequential autohydrolysis stages. J. Clean. Prod. 168, 74–86. doi:10.1016/j.jclepro.2017.08.230

CrossRef Full Text | Google Scholar

Kapu, N. S., Yuan, Z., Chang, X. F., Beatson, R., Martinez, D. M., and Trajano, H. L. (2016). Insight into the evolution of the proton concentration during autohydrolysis and dilute-acid hydrolysis of hemicellulose. Biotechnol. Biofuels 9, 224–304. doi:10.1186/s13068-016-0619-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, H.-Y., Lee, J.-W., Jeffries, T. W., and Choi, I.-G. (2011). Response surface optimization of oxalic acid pretreatment of yellow poplar (liriodendron tulipifera) for production of glucose and xylose monosaccarides. Bioresour. Technol. 102, 1440–1446. doi:10.1016/j.biortech.2010.09.075

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, S., and Lee, Y. (1987). Kinetics in acid-catalyzed hydrolysis of hardwood hemicellulose. Biotechnol. Bioeng. Symp. 17, 71–84.

Google Scholar

Kim, Y., Kreke, T., Mosier, N. S., and Ladisch, M. R. (2014). Severity factor coefficients for subcritical liquid hot water pretreatment of hardwood chips. Biotechnol. Bioeng. 111, 254–263. doi:10.1002/bit.25009

PubMed Abstract | CrossRef Full Text | Google Scholar

Kojić, P., and Omorjan, R. (2017). Predicting hydrodynamic parameters and volumetric gas–liquid mass transfer coefficient in an external-loop airlift reactor by support vector regression. Chem. Eng. Res. Des. 125, 398–407. doi:10.1016/j.cherd.2017.07.029

CrossRef Full Text | Google Scholar

Krogell, J., Korotkova, E., Eränen, K., Pranovich, A., Salmi, T., Murzin, D., et al. (2013). Intensification of hemicellulose hot-water extraction from spruce wood in a batch extractor – effects of wood particle size. Bioresour. Technol. 143, 212–220. doi:10.1016/j.biortech.2013.05.110

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, R., and Wyman, C. E. (2008). The impact of dilute sulfuric acid on the selectivity of xylooligomer depolymerization to monomers. Carbohydr. Res. 343, 290–300. doi:10.1016/j.carres.2007.10.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Kundu, C., and Lee, J.-W. (2015). Optimization conditions for oxalic acid pretreatment of deacetylated yellow poplar for ethanol production. J. Ind. Eng. Chem. 32, 298–304. doi:10.1016/j.jiec.2015.09.001

CrossRef Full Text | Google Scholar

Kundu, C., Trinh, L. T. P., Lee, J.-W., and Lee, H.-J. (2015). Bioethanol production from oxalic acid-pretreated biomass and hemicellulose-rich hydrolysates via a combined detoxification process. Fuel 161, 129–136. doi:10.1016/j.fuel.2015.08.045

CrossRef Full Text | Google Scholar

Lee, H., Kazlauskas, R., and Park, T. (2017). Mild pretreatment of yellow poplar biomass using sequential dilute acid and enzymatically-generated peracetic acid to enhance cellulase accessibility. Biotechnol. Bioprocess Eng. 22, 405–412. doi:10.1007/s12257-017-0139-7

CrossRef Full Text | Google Scholar

Li, H., Saeed, A., Jahan, M. S., Ni, Y., and van Heiningen, A. (2010). Hemicellulose removal from hardwood chips in the pre-hydrolysis step of the kraft-based dissolving pulp production process. J. Wood Chem. Technol. 30, 48–60. doi:10.1080/02773810903419227

CrossRef Full Text | Google Scholar

Li, Y., Liu, W., Hou, Q., Han, S., Wang, Y., and Zhou, D. (2014). Release of acetic acid and its effect on the dissolution of carbohydrates in the autohydrolysis pretreatment of poplar prior to chemi-thermomechanical pulping. Ind. Eng. Chem. Res. 53, 8366–8371. doi:10.1021/ie500637a

CrossRef Full Text | Google Scholar

Lim, W.-S., and Lee, J.-W. (2012). Effects of pretreatment factors on fermentable sugar production and enzymatic hydrolysis of mixed hardwood. Bioresour. Technol. 130C, 97–101. doi:10.1016/j.biortech.2012.11.122

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W., Chen, W., Hou, Q., Wang, S., and Liu, F. (2018). Effects of combined pretreatment of dilute acid pre-extraction and chemical-assisted mechanical refining on enzymatic hydrolysis of lignocellulosic biomass. RSC Adv. 8, 10207–10214. doi:10.1039/C7RA12732D

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W., Chen, W., Hou, Q., Zhang, J., and Wang, B. (2017). Surface lignin change pertaining to the integrated process of dilute acid pre-extraction and mechanical refining of poplar wood chips and its impact on enzymatic hydrolysis. Bioresour. Technol. 228, 125–132. doi:10.1016/j.biortech.2016.12.063

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W., Liu, L., Hou, Q., Chen, J., and Xu, N. (2015). Understanding of pH value and its effect on autohydrolysis pretreatment prior to poplar chemi-thermomechanical pulping. Bioresour. Technol. 196, 662–667. doi:10.1016/j.biortech.2015.08.034

PubMed Abstract | CrossRef Full Text | Google Scholar

López, F., García, M. T., Feria, M. J., García, J. C., de Diego, C. M., Zamudio, M. A. M., et al. (2014). Optimization of furfural production by acid hydrolysis of eucalyptus globulus in two stages. Chem. Eng. J. 240, 195–201. doi:10.1016/j.cej.2013.11.073

CrossRef Full Text | Google Scholar

Ma, M., Liu, R., Guo, Y., Li, H., Zhou, J., Wang, H., et al. (2017). Research on the dissolution of pentosans during eucalyptus hydrolysate pretreatment. BioResources 12, 3677–3694. doi:10.15376/biores.12.2.3677-3694

CrossRef Full Text | Google Scholar

Mäki-Arvela, P., Salmi, T., Holmbom, B., Willför, S., and Murzin, D. Y. (2011). Synthesis of sugars by hydrolysis of hemicelluloses-a review. Chem. Rev. 111, 5638–5666. doi:10.1021/cr2000042

PubMed Abstract | CrossRef Full Text | Google Scholar

Maloney, M. T., Chapman, T. W., and Baker, A. J. (1985). Dilute acid hydrolysis of paper birch: Kinetics studies of xylan and acetyl-group hydrolysis. Biotechnol. Bioeng. 27, 355–361. doi:10.1002/bit.260270321

PubMed Abstract | CrossRef Full Text | Google Scholar

Martínez-Patiño, J. C., Ruiz, E., Romero, I., Cara, C., López-Linares, J. C., and Castro, E. (2017). Combined acid/alkaline-peroxide pretreatment of olive tree biomass for bioethanol production. Bioresour. Technol. 239, 326–335. doi:10.1016/j.biortech.2017.04.102

PubMed Abstract | CrossRef Full Text | Google Scholar

Mateo, S., Puentes, J. G., Roberto, I. C., Sánchez, S., and Moya, A. J. (2014). Optimization of acid hydrolysis of olive tree pruning residue. fermentation with candida guilliermondii. Biomass Bioenergy 69, 39–46. doi:10.1016/j.biombioe.2014.07.007

CrossRef Full Text | Google Scholar

McIntosh, S., Vancov, T., Palmer, J., and Spain, M. (2012). Ethanol production from eucalyptus plantation thinnings. Bioresour. Technol. 110, 264–272. doi:10.1016/j.biortech.2012.01.114

PubMed Abstract | CrossRef Full Text | Google Scholar

Mittal, A., Chatterjee, S., Scott, G., and Amidon, T. (2009a). Modeling xylan solubilization during autohydrolysis of sugar maple and aspen wood chips: Reaction kinetics and mass transfer. Chem. Eng. Sci. 64, 3031–3041. doi:10.1016/j.ces.2009.03.011

CrossRef Full Text | Google Scholar

Mittal, A., Pilath, H. M., Parent, Y., Chatterjee, S. G., Donohoe, B. S., Yarbrough, J. M., et al. (2019). Chemical and structural effects on the rate of xylan hydrolysis during dilute acid pretreatment of poplar wood. ACS Sustain. Chem. Eng. 7, 4842–4850. doi:10.1021/acssuschemeng.8b05248

CrossRef Full Text | Google Scholar

Mittal, A., Scott, G. M., Amidon, T. E., Kiemle, D. J., and Stipanovic, A. J. (2009b). Quantitative analysis of sugars in wood hydrolyzates with 1h nmr during the autohydrolysis of hardwoods. Bioresour. Technol. 100, 6398–6406. doi:10.1016/j.biortech.2009.06.107

PubMed Abstract | CrossRef Full Text | Google Scholar

Mok, W. S. L., and Antal, M. J. (1992). Uncatalyzed solvolysis of whole biomass hemicellulose by hot compressed liquid water. Ind. Eng. Chem. Res. 31, 1157–1161. doi:10.1021/ie00004a026

CrossRef Full Text | Google Scholar

Molga, E. J., van Woezik, B. A. A., and Westerterp, K. R. (2000). Neural networks for modelling of chemical reaction systems with complex kinetics: Oxidation of 2-octanol with nitric acid. Chem. Eng. Process. Process Intensif. 39, 323–334. doi:10.1016/s0255-2701(99)00093-8

CrossRef Full Text | Google Scholar

Morinelly, J. E., Jensen, J. R., Browne, M., Co, T. B., and Shonnard, D. R. (2009). Kinetic characterization of xylose monomer and oligomer concentrations during dilute acid pretreatment of lignocellulosic biomass from forests and switchgrass. Ind. Eng. Chem. Res. 48, 9877–9884. doi:10.1021/ie900793p

CrossRef Full Text | Google Scholar

Negahdar, L., Delidovich, I., and Palkovits, R. (2016). Aqueous-phase hydrolysis of cellulose and hemicelluloses over molecular acidic catalysts: Insights into the kinetics and reaction mechanism. Appl. Catal. B Environ. 184, 285–298. doi:10.1016/j.apcatb.2015.11.039

CrossRef Full Text | Google Scholar

Negro, M., Manzanares, P., Ballesteros, I., Oliva, J., Caban˜as, A., and Ballesteros, M. (2003). Hydrothermal pretreatment conditions to enhance ethanol production from poplar biomass. Appl. Biochem. Biotechnol. 105, 87–100. doi:10.1385/ABAB:105:1-3:87

PubMed Abstract | CrossRef Full Text | Google Scholar

Nitsos, C. K., Choli-Papadopoulou, T., Matis, K. A., and Triantafyllidis, K. S. (2016). Optimization of hydrothermal pretreatment of hardwood and softwood lignocellulosic residues for selective hemicellulose recovery and improved cellulose enzymatic hydrolysis. ACS Sustain. Chem. Eng. 4, 4529–4544. doi:10.1021/acssuschemeng.6b00535

CrossRef Full Text | Google Scholar

Nitsos, C. K., Matis, K. A., and Triantafyllidis, K. S. (2013). Optimization of hydrothermal pretreatment of lignocellulosic biomass in the bioethanol production process. ChemSusChem 6, 110–122. doi:10.1002/cssc.201200546

PubMed Abstract | CrossRef Full Text | Google Scholar

Odabaş1, Ç., Günay, M. E., and Yıldırım, R. (2014). Knowledge extraction for water gas shift reaction over noble metal catalysts from publications in the literature between 2002 and 2012. Int. J. Hydrogen Energy 39, 5733–5746. doi:10.1016/j.ijhydene.2014.01.160

CrossRef Full Text | Google Scholar

Overend, R. P., Chornet, E., and Gascoigne, J. A. (1987). Fractionation of lignocellulosics by steam-aqueous pretreatments [and discussion]. Philos. Trans. R. Soc. A 321, 523–536.

Google Scholar

Parajó, J. C., Vázquez, D., Alonso, J. L., Santos, V., and Dominguez, H. (1994). Prehydrolysis of eucalyptus wood with dilute sulphuric acid: Operation in autoclave. Holz als Roh-und. Werkst. 52, 102–108. doi:10.1007/BF02615474

CrossRef Full Text | Google Scholar

Parajó, J., Vázquez, D., Alonso, J., Santos, V., and Dominguez, H. (1993). Prehydrolysis of eucalyptus wood with dilute sulphuric acid: Operation at atmospheric pressure. Holz als Roh-und. Werkst. 51, 357–363. doi:10.1007/BF02663809

CrossRef Full Text | Google Scholar

Peleteiro, S., Galletti, A. M. R., Antonetti, C., Santos, V., and Parajó, J. C. (2018). Manufacture of furfural from xylan-containing biomass by acidic processing of hemicellulose-derived saccharides in biphasic media using microwave heating. J. Wood Chem. Technol. 38, 198–213. doi:10.1080/02773813.2017.1418891

CrossRef Full Text | Google Scholar

Porth, I., Klápště, J., Skyba, O., Lai, B. S. K., Geraldes, A., Muchero, W., et al. (2013). Populus trichocarpa cell wall chemistry and ultrastructure trait variation, genetic control and genetic correlations. New Phytol. 197, 777–790. doi:10.1111/nph.12014

PubMed Abstract | CrossRef Full Text | Google Scholar

Pu, Y., Treasure, T., Gonzalez, R., Venditti, R., and Jameel, H. (2011). Autohydrolysis pretreatment of mixed hardwoods to extract value prior to combustion. Bioresources 6, 4856–4870. doi:10.15376/biores.6.4.4856-4870

CrossRef Full Text | Google Scholar

Puentes, J. G., Mateo, S., Fonseca, B. G., Roberto, I. C., Sánchez, S., and Moya, A. J. (2013). Monomeric carbohydrates production from olive tree pruning biomass: Modeling of dilute acid hydrolysis. Bioresour. Technol. 149, 149–154. doi:10.1016/j.biortech.2013.09.046

PubMed Abstract | CrossRef Full Text | Google Scholar

Rafiqul, I., Sakinah, A., and Karim, M. (2014). Production of xylose from meranti wood sawdust by dilute acid hydrolysis. Appl. Biochem. Biotechnol. 174, 542–555. doi:10.1007/s12010-014-1059-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Rafiqul, I. S. M., and Sakinah, A. M. M. (2012a). Design of process parameters for the production of xylose from wood sawdust. Chem. Eng. Res. Des. 90, 1307–1312. doi:10.1016/j.cherd.2011.12.009

CrossRef Full Text | Google Scholar

Rafiqul, I. S. M., and Sakinah, A. M. M. (2012b). Kinetic studies on acid hydrolysis of meranti wood sawdust for xylose production. Chem. Eng. Sci. 71, 431–437. doi:10.1016/j.ces.2011.11.007

CrossRef Full Text | Google Scholar

Rangel, J., Hornus, M., Felissia, F., and Area, M. (2016). Hydrothermal treatment of eucalyptus sawdust for a forest biorefinery. Cellul. Chem. Technol. 50, 5–6.

Google Scholar

Romaní, A., Garrote, G., Alonso, J. L., and Parajó, J. C. (2010). Bioethanol production from hydrothermally pretreated Eucalyptus globulus wood. Bioresour. Technol. 101, 8706–8712. doi:10.1016/j.biortech.2010.06.093

PubMed Abstract | CrossRef Full Text | Google Scholar

Saeman, J. F. (1945). Kinetics of wood saccharification - hydrolysis of cellulose and decomposition of sugars in dilute acid at high temperature. Ind. Eng. Chem. 37, 43–52. doi:10.1021/ie50421a009

CrossRef Full Text | Google Scholar

Sassner, P., Mårtensson, C.-G., Galbe, M., and Zacchi, G. (2008). Steam pretreatment of H₂SO₄ impregnatedsalix for the production of bioethanol. Bioresour. Technol. 99, 137–145. doi:10.1016/j.biortech.2006.11.039

CrossRef Full Text | Google Scholar

Scheller, H. V., and Ulvskov, P. (2010). Hemicelluloses. Annu. Rev. Plant Biol. 61, 263–289. doi:10.1146/annurev-arplant-042809-112315

PubMed Abstract | CrossRef Full Text | Google Scholar

Sella Kapu, N., and Trajano, H. L. (2014). Review of hemicellulose hydrolysis in softwoods and bamboo. Biofuel. Bioprod. Biorefin. 8, 857–870. doi:10.1002/bbb.1517

CrossRef Full Text | Google Scholar

Shi, H., Zhou, M., Jia, W., Li, N., and Niu, M. (2019). Balancing the effect of pretreatment severity on hemicellulose extraction and pulping performance during auto-hydrolysis prior to kraft pulping of acacia wood. Biotechnol. Prog. 35, e2784. doi:10.1002/btpr.2784/btpr.2784

PubMed Abstract | CrossRef Full Text | Google Scholar

Sixta, H., Potthast, A., and Krotschek, A. W. (2006). Chemical pulping processes:Sections 4.1–4.2.5. John Wiley & Sons. chap. 4. 109–229. doi:10.1002/9783527619887.ch4a

CrossRef Full Text | Google Scholar

Smith, A., Keane, A., Dumesic, J. A., Huber, G. W., and Zavala, V. M. (2020). A machine learning framework for the analysis and prediction of catalytic activity from experimental data. Appl. Catal. B Environ. 263, 118257. doi:10.1016/j.apcatb.2019.118257

CrossRef Full Text | Google Scholar

Smuga-Kogut, M., Kogut, T., Markiewicz, R., and Słowik, A. (2021). Use of machine learning methods for predicting amount of bioethanol obtained from lignocellulosic biomass with the use of ionic liquids for pretreatment. Energies 14, 243. doi:10.3390/en14010243

CrossRef Full Text | Google Scholar

Song, T., Pranovich, A., and Holmbom, B. (2011). Effects of ph control with phthalate buffers on hot-water extraction of hemicelluloses from spruce wood. Bioresour. Technol. 102, 10518–10523. doi:10.1016/j.biortech.2011.08.093

PubMed Abstract | CrossRef Full Text | Google Scholar

Spiridon, I., and Popa, V. (2008). Hemicelluloses: Major sources, properties and applications, 289–304. doi:10.1016/B978-0-08-045316-3.00013-2

CrossRef Full Text | Google Scholar

Springer, E. (1985). Prehydrolysis of hardwoods with dilute sulfuric acid. Ind. Eng. Chem. Prod. Res. Dev. 24, 614–623. doi:10.1021/i300020a023

CrossRef Full Text | Google Scholar

Trajano, H. L., Pattathil, S., Tomkins, B. A., Tschaplinski, T. J., Hahn, M. G., Berkel, G. J. V., et al. (2015). Xylan hydrolysis in Populus trichocarpa × P. deltoides and model substrates during hydrothermal pretreatment. Bioresour. Technol. 179, 202–210. doi:10.1016/j.biortech.2014.11.090

PubMed Abstract | CrossRef Full Text | Google Scholar

Tunc, M. (2014). Effect of liquid to solid ratio on autohydrolysis of eucalyptus globulus wood meal. BioResources 9, 3014–3024. doi:10.15376/biores.9.2.3014-3024

CrossRef Full Text | Google Scholar

Tunc, M. S., Chheda, J., van der Heide, E., Morris, J., and van Heiningen, A. (2014). Pretreatment of hardwood chips via autohydrolysis supported by acetic and formic acid. Holzforschung 68, 401–409. doi:10.1515/hf-2013-0102

CrossRef Full Text | Google Scholar

Tunc, M. S., and van Heiningen, A. R. P. (2008). Hemicellulose extraction of mixed southern hardwood with water at 150 ^◦c: Effect of time. Ind. Eng. Chem. Res. 47, 7031–7037. doi:10.1021/ie8007105

CrossRef Full Text | Google Scholar

Vázquez, G., Antorrena, G., and González, J. (1995). Kinetics of polysaccharide hydrolysis in the acid-catalysed delignification of eucalyptus globulus wood by acetic acid. Wood Sci. Technol. 30, 31–38. doi:10.1007/BF00195266

CrossRef Full Text | Google Scholar

Vroom, K. (1957). The H factor: A means of expressing cooking times and temperatures as a single variable. PPMC 58, 228–231.

Google Scholar

Wei, W., Wu, S., and Liu, L. (2012). Enzymatic saccharification of dilute acid pretreated eucalyptus chips for fermentable sugar production. Bioresour. Technol. 110, 302–307. doi:10.1016/j.biortech.2012.01.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Wen, P., Zhang, T., Wang, J., Lian, Z., and Zhang, J. (2019). Production of xylooligosaccharides and monosaccharides from poplar by a two-step acetic acid and peroxide/acetic acid pretreatment. Biotechnol. Biofuels 12, 87–13. doi:10.1186/s13068-019-1423-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, J., Joshee, N., and Liu, S. (2013). Kinetics of the hot-water extraction of paulownia elongata woodchips. J. bioprocess Engng. Biorefin. 2, 1–10. doi:10.1166/jbeb.2013.1041

CrossRef Full Text | Google Scholar

Yan, J., Joshee, N., and Liu, S. (2016). Utilization of hardwood in biorefinery: A kinetic interpretation of pilot-scale hot-water pretreatment of paulownia elongata woodchips. J. Biobased Mat. Bioenergy 10, 339–348. doi:10.1166/jbmb.2016.1609

CrossRef Full Text | Google Scholar

Yan, J. (2015). Kinetic interpretation of hot-water pretreatment of hardwood. New York: Ph.D. thesis, State University of.

Google Scholar

Yan, J., and Liu, S. (2015). Hot water pretreatment of boreal aspen woodchips in a pilot scale digester. Energies 8, 1166–1180. doi:10.3390/en8021166

CrossRef Full Text | Google Scholar

Yat, S. C., Berger, A., and Shonnard, D. R. (2008). Kinetic characterization for dilute sulfuric acid hydrolysis of timber varieties and switchgrass. Bioresour. Technol. 99, 3855–3863. doi:10.1016/j.biortech.2007.06.046

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, Q., Zhuang, X., Yuan, Z., Wang, Q., Qi, W., Wang, W., et al. (2009). Two-step liquid hot water pretreatment of Eucalyptus grandis to enhance sugar recovery and enzymatic digestibility of cellulose. Bioresour. Technol. 101, 4895–4899. doi:10.1016/j.biortech.2009.11.051

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, T., Kumar, R., and Wyman, C. E. (2013). Sugar yields from dilute oxalic acid pretreatment of maple wood compared to those with other dilute acids and hot water. Carbohydr. Polym. 92, 334–344. doi:10.1016/j.carbpol.2012.09.070

PubMed Abstract | CrossRef Full Text | Google Scholar