A Theoretical Model for the Charging Dynamics of Associating Ionic Liquids

Association between cations and anions plays an important role in the interfacial structure of room-temperature ionic liquids (ILs) and their electrochemical performance. Whereas great efforts have been devoted to investigating the association effect on the equilibrium properties of ILs, a molecular-level understanding of the charging dynamics is yet to be established. Here, we propose a theoretical procedure combining reaction kinetics and the modified Poisson-Nernst-Planck (MPNP) equations to study the influences of ionic association on the dynamics of electrical double layer (EDL) in response to an applied voltage. The ionic association introduces a new decay length λ_S and relaxation time scale ${\tau }_{RC}={\lambda }_{S}L/D$, where L is the system size and D is ion diffusivity, that are distinctively different those corresponding to non-associative systems. Analytical expressions have been obtained to reveal the quantitative relations between the dynamic timescales and the association strength.

Introduction

Room-temperature ionic liquids (ILs) have been broadly explored as promising electrolytes in various fields of electrochemistry (Xiao and Johnson, 2003; Sato et al., 2004; Wang, 2020) including both batteries (Lee et al., 2006; Rupp et al., 2008) and supercapacitors (Ue et al., 2003; Zhou et al., 2004; Arunachalam et al., 2020; Tao et al., 2020). Understanding their charging dynamics, i.e., the polarization of ionic distributions in response to a biased electrical potential, is desirable for many electrochemical applications (Zhang et al., 2020; Tao et al., 2021; Tao et al., 2022). Although the structure and thermodynamic properties of ILs in the electric double layer (EDL) have been widely studied (Chen et al., 2021a; Chen et al., 2021b; Gan et al., 2021; Wang et al., 2021), the dynamic behavior remains poorly understood in particular on how association between cations and anions influences charge relaxation and ion transport under confinement.

In comparison to that of an aqueous electrolyte solution, the relative permittivity of ILs is extremely small (∼2), implying the prevalence of ion pairing due to the strong electrostatic attraction between cations and anions (Wang and Voth, 2005; Canongia Lopes and Pádua, 2006; Fraser et al., 2007; Niedermeyer et al., 2012). From a thermodynamic perspective, the ionic association may be described in terms of a chemical reaction (Figure 1A):

$A^{+}+B^{-}\underset{k_d}{\overset{k_a}{\rightleftharpoons }}C(1)$

where the association constant is related to the kinetic parameters for the forward and backward reactions, $K=k_a/k_d$. Intuitively, the association constant K provides a direct measure of the strength of binding energy: A large association constant means strong binding thus a large number of neutral species formed by the reaction, giving rise to more deviations from a conventional electrolyte of monomeric ionic species in terms of the electrical conductivity, capacitance, charge distribution and other characteristics of an ionic system. A good understanding of the effects of ionic association is thus imperative for the design and optimization of IL-based electrochemical systems.

FIGURE 1

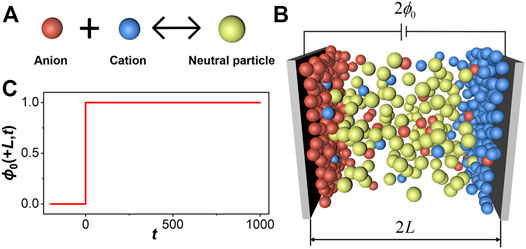
FIGURE 1. (A) Formation of a neutral particle by cation-anion association. (B) A cartoon sketch for the distribution of ionic species between two parallel electrodes. (C) An instantaneous increase of the electrical potential on the electrode surface located at position L.

In previous work (Jiang et al., 2014; Lian et al., 2016; Ma et al., 2022), we studied the dynamic behavior of room-temperature ionic liquids using a time-dependent density functional theory (TDDFT) that accounts for the ionic excluded volume effects, electrostatic correlations, and short-range attractions. We found that the electrokinetic behavior of ionic liquids is distinctively different from that predicted by the conventional equivalent-circuit (EC) models or theoretical methods based on the Poisson-Nernst-Planck (PNP) equations. While the EC model predicts a monotonic increase of the surface charge density upon the application of a biased voltage, TDDFT calculations indicate that there exist three types of charging behavior depending on the degree of confinement and the magnitude of the biased potential. A monotonic increase of the surface charge density occurs only when its equilibrium value has a sign the same as that of the applied voltage; kinetic charging inversion takes place when the equilibrium charge is below or opposite of the asymptotic charge density. The non-monotonic charging behavior was also reported for the response of a monomeric layer of ionic liquids in slit pores (Kondrat and Kornyshev, 2013). In addition to theoretical studies, the dynamics of EDL charging has been examined by a number of theoretical studies based on molecular dynamics (MD) simulations (Mceldrew et al., 2020; Mceldrew et al., 2021a; Mceldrew et al., 2021b). To our knowledge, the effects of ionic association have not been explicitly examined in spite of its apparent importance in determining the properties of ILs.

In this work, we proposed a set of reaction-coupled modified PNP (RC-MPNP) equations to describe the charging behavior of ILs near electrodes. Similar to TDDFT, RC-MPNP employs a local electrochemical potential as the driving force for the evolution of the density profiles of ionic species in response to an applied voltage. In comparison to alternative methods, its main advantage is that the dynamic equations for electric migration, diffusion, and chemical reaction can be solved self-consistently at time and length scales beyond those that could be achieved with TDDFT or MD simulation. Importantly, RC-MPNP allows us to study the ionic pairing effects on the dynamic structure and local physicochemical properties of ILs under an electrical field, including the density distributions of all ionic species (cations, anions and ion pairs), charge relaxation, as well as the relationship between various characteristic timescales, decay length and association strength. The theoretical results also reveal how ionic association affects the capacitance and resistance of ILs during the charging process.

Molecular Model and Theory

Model Description

As shown schematically in Figure 1A, association between cations and anions can be written in terms of a reversible reaction, i.e., one anion reacts with one cation to form a neutral particle labeled as m. At equilibrium, the fraction of neutral particles is determined by association constant K through the law of mass action. In the presence of an electric field, the equilibrium distribution of ionic species depends on the local electrical potential, various forms of non-electrostatic interactions as well as the equilibrium constant.

Figure 1B sketches a cartoon representation of the ionic system considered in this work. For simplicity, we assume that all ionic species, including the neutral ion pairs, can be represented by hard spheres of equal size. While ILs confined between two parallel plates of opposite charge do not reflect the configuration of any specific electrochemical device, the symmetric one-dimensional setup allows us to capture the essential features of charging dynamics for electrolytes near an electrode surface, in particular in terms of the evolutions of the local charge density and ionic density profiles in response to an applied voltage. The relaxation process is coupled with an evolving electric field, particle transport, and association between cations and anions. A realistic model for IL charging should capture all such effects in addition to thermodynamic non-ideality arising from other forms of inter-particle interactions.

Governing Equations and Chemical Potential

Our reaction-coupled modified PNP (RC-MPNP) equations are similar to those proposed by Suzuki who studied charge transport in weak electrolytes (Suzuki and Seki, 2018). The model ionic liquid consists of three kinds of ionic species: cations, anions, and neutral particles generated by cation-anion association. For simplicity, all these ionic species are represented by spherical particles of the same size. To describe the charging dynamics, we start with the continuity and diffusion-reaction equations

$\frac{\partial {\rho }_i}{\partial t}=-\nabla \cdot J_i+R_i,(2)$

$J_i=-\frac{D_i}{k_{B}T}{\rho }_i\nabla {\mu }_i,(3)$

where ${\rho }_i$ stands for the local number density of specie i, J_i is the mass flux, μ_i is the local electrochemical potential, k_B is the Boltzmann constant, T is the absolute temperature, D_i is the diffusion constant of specie i. The source term, R_i arises from ionic association

$R_{\pm }=k_d{\rho }_m-k_a{\rho }_{+}{\rho }_{-},(4)$

and

$R_m=-k_d{\rho }_m+k_a{\rho }_{+}{\rho }_{-},(5)$

Equations 4, 5 follow the kinetics of ion association, i.e., the change in the local ion concentration reflects a balance of the forward and backward reactions. As mentioned above, the equilibrium constant is related to the rate coefficients

$K=k_a/k_d={\rho }_m/\left({\rho }_{+}{\rho }_{-}\right),(6)$

We assume that the intrinsic chemical potential can be obtained by minimizing the grand potential (Detail derivations are given in Supplementary Material). Accordingly, the electrochemical potentials of the ionic species are

${\mu }_{\pm }=\pm e\psi +k_{B}T\left[\ln \left(a^3{\rho }_{\pm }\right)-\ln \left(1-a^3{\rho }_{+}-a^3{\rho }_{-}-a^3{\rho }_m\right)\right](7)$

${\mu }_m=k_{B}T\left[\ln \left(a^3{\rho }_m\right)-\ln \left(1-a^3{\rho }_{+}-a^3{\rho }_{-}-a^3{\rho }_m\right)\right](8)$

where e is the unit charge, a is the diameter of hard spheres, and $\psi$ is the local electrical potential. The latter is solved from the Poisson equation:

${\nabla }^2\psi =-\frac{e}{{\epsilon }_0{\epsilon }_r}{\displaystyle \sum _i{z}_i}{\rho }_i(9)$

where ${\epsilon }_r$ the relative permittivity, ε₀ = 8.854 × 10^–12 F/m is the absolute permittivity, z_i the valence of specie i. Substituting Eqs 7, 8 into Eqs. 3 leads to

$J_{\pm }=-D\left[\pm {\rho }_{\pm }\frac{e}{k_{B}T}\nabla \psi +\nabla {\rho }_{\pm }+\frac{a^3{\rho }_{\pm }}{1-a^3{\rho }_{+}-a^3{\rho }_{-}-a^3{\rho }_m}\nabla \left({\rho }_{+}+{\rho }_{-}+{\rho }_m\right)\right](10)$

$J_m=-D\left[\nabla {\rho }_m+\frac{a^3{\rho }_m}{1-a^3{\rho }_{+}-a^3{\rho }_{-}-a^3{\rho }_m}\nabla \left({\rho }_{+}+{\rho }_{-}+{\rho }_m\right)\right].(11)$

For simplicity, we assume that the diffusion coefficient and the particle size for ion pairs the same as those for ionic species.

In integration of the continuity equations, we need to solve the following equations simultaneously:

$\begin{array}{c}\frac{{\partial }^2\varphi }{\partial x^{\ast 2}}=-\frac{1}{2{\varsigma }^2}\left({\rho }_{+}^{\ast }-{\rho }_{-}^{\ast }\right)\\ \frac{\partial {\rho }_{\pm }^{\ast }}{\partial t^{\ast }}=\varsigma \left(\begin{array}{l}\frac{{\partial }^2{\rho }_{\pm }^{\ast }}{\partial x^{\ast 2}}\pm \frac{\partial }{\partial x^{\ast }}\left({\rho }_{\pm }^{\ast }\frac{\partial \varphi }{\partial x^{\ast }}\right)\\ +\frac{\partial }{\partial x^{\ast }}\left[\frac{\eta {\rho }_{\pm }^{\ast }}{1-\eta \left({\rho }_{+}^{\ast }+{\rho }_{-}^{\ast }+{\rho }_m^{\ast }\right)}\frac{\partial }{\partial x^{\ast }}\left({\rho }_{+}^{\ast }+{\rho }_{-}^{\ast }+{\rho }_m^{\ast }\right)\right]\end{array}\right)+k_d^{\ast }{\rho }_m^{\ast }-k_a^{\ast }{\rho }_{+}^{\ast }{\rho }_{-}^{\ast }\\ \frac{\partial {\rho }_m^{\ast }}{\partial t^{\ast }}=\varsigma \left(\frac{{\partial }^2{\rho }_m^{\ast }}{\partial x^{\ast 2}}+\frac{\partial }{\partial x^{\ast }}\left[\frac{\eta {\rho }_m^{\ast }}{1-\eta \left({\rho }_{+}^{\ast }+{\rho }_{-}^{\ast }+{\rho }_m^{\ast }\right)}\frac{\partial }{\partial x^{\ast }}\left({\rho }_{+}^{\ast }+{\rho }_{-}^{\ast }+{\rho }_m^{\ast }\right)\right]\right)-k_d^{\ast }{\rho }_m^{\ast }+k_a^{\ast }{\rho }_{+}^{\ast }{\rho }_{-}^{\ast }\end{array}.(12)$

where $x\ast =x/L$, $\varphi =\left(e\psi \right)/\left(k_{B}T\right)$, ${\rho }_i^{\ast }\left(i=+,-,m\right)={\rho }_i/{\rho }_s$ with ${\rho }_s$ being the number density of cations or anions in the bulk, $t^{\ast }=t/{\tau }_{RC}$ with ${\tau }_{RC}={\lambda }_{D}L/D$, ${\lambda }_D=\sqrt{{\epsilon }_0{\epsilon }_r{k}_{B}T/2e^2{\rho }_s}$ is the Debye screening length, $\eta =a^3{\rho }_s$, $K^{\ast }={\rho }_{s}K$, $k_d^{\ast }={\tau }_{RC}{k}_d$ and $k_a^{\ast }={\tau }_{RC}{\rho }_s{k}_a$. For later discussions, we also introduced a dimensionless scale factor, $\varsigma ={\lambda }_D/L$, and set $k_d^{\ast }=1$ as a unit time. With these dimensionless variables, the numerical results depend on only three basic parameters, i.e., $\eta$, $\varsigma$ and $k_a^{\ast }$. Physically, controlling these parameters amounts to adjusting ionic density ${\rho }_s$, the system size L, and association strength K.

Parameter Setting and Boundary Conditions

In describing the charging dynamics, the RC-MPNP equations entail three types of parameters that are affiliated with the system characteristics, boundary conditions and initial values. In this work, we assume that cations, anions and ion pairs have the same size of a = 0.5 nm, i.e., they all occupy a single lattice site. Both cations and anions are monovalent, $\left|z_i\right|=1$, and a single diffusivity is used for all particles D = 4.3 × 10^–11 m²/s. Similar parameters were used in previous studies on ILs and are in reasonable agreement with experimental results (Largeot et al., 2008; Lian et al., 2016; Yang et al., 2020a; Yang et al., 2020b; Ma et al., 2020). As ionic species are explicitly considered in this work, a fictitious dielectric constant ε_r = 2 was adopted to account for dispersion interactions and ionic polarizability of ILs not included in the coarse-grained model (Lian et al., 2018a; Lian et al., 2018b; Yang et al., 2020b). Temperature T = 293.15 K, and cell width L = 100 λ_D. Assuming that an ionic liquid has a typical bulk concentration of 3.3 mol/L, we have ${\lambda }_D\approx 0.025\text{nm}$, $L\approx 2.5\text{nm}$. To investigate the ionic association effects, we consider four association constants, K* = 0.1, 1, 10, 148, representing the cases of weak, moderate, strong, and extreme association strength, respectively.

In studying the charging dynamics, we assume that a biased potential of $2{\varphi }_0$ is initially applied to the cathode and anode (at t = 0). Based on the one-dimensional model illustrated in Figure 1, we have the following boundary conditions:

$\begin{array}{l}\varphi \left(\pm L,t>0\right)=\pm {\varphi }_0\\ \frac{\partial {\rho }_i\left(i=+,-,m\right)}{\partial x}\left(\pm L,t\right)=0\end{array}(13)$

where the initial particle densities are assumed identical to the corresponding bulk values, ${\rho }_{+,b}$, ${\rho }_{-,b}$, ${\rho }_{m,b}$. With the assumption that the bulk ionic liquid can be represented by an ideal solution, these densities can be determined from the association constant K

$\begin{array}{l}\frac{{\rho }_{m,b}}{{\rho }_{+,b}{\rho }_{-,b}}=K\\ \frac{{\rho }_{+,b}+{\rho }_{-,b}+2{\rho }_{m,b}}{2}={\rho }_s.\end{array}(14)$

Because the bulk concentrations are fixed during the charging process, an explicit consideration of the thermodynamic non-ideality is equivalent to changing the bulk concentration. In the presence of an electric field, the RC-MPNP equations allow us to describe the relaxation of the ionic density profiles until a new equilibrium is established. The time range used in the calculation is from 10^–3 τ_RC to 10³ τ_RC with ${\tau }_{RC}={\lambda }_{D}L/D$.

Results and Discussion

Time-dependent Density Distributions

The application of a biased potential introduces a local electric field driving ionic motions thereby breaking down the local ionic association equilibrium. Therefore, we expect that the evolution of the ionic density profiles is different from that corresponding to a non-reactive system. Figure 2 shows the variations of the total ionic density (${\rho }_{+}^{\ast }+{\rho }_{-}^{\ast }$), the local charge density (${\rho }_{+}^{\ast }-{\rho }_{-}^{\ast }$), and the density of neutral particles (${\rho }_m^{\ast }$) near the surface of the negative electrode. At the initial state, the whole system is assumed homogeneous as shown in uniform particle and charge distributions. Upon the application of an electrical potential, the counterions (cations) gradually accumulate at the electrode surface, concomitant with the receding of cations (anions). Interestingly, the total ionic density ${\rho }_{\pm }^{\ast }$ first falls slightly and rises monotonically to the equilibrium value. Both the total ion density (${\rho }_{+}^{\ast }+{\rho }_{-}^{\ast }$) and the local charge (${\rho }_{+}^{\ast }-{\rho }_{-}^{\ast }$) exhibit a U-shaped charging dynamic as indicated in Figures 2J,K. Due to the volume effect caused by the accumulation of anions and anions near the electrode, the neutral particles are enriched in the middle region of the cell (Figure 2L), leading to a density profile with a convex shape across the slit as the charging continues.

FIGURE 2

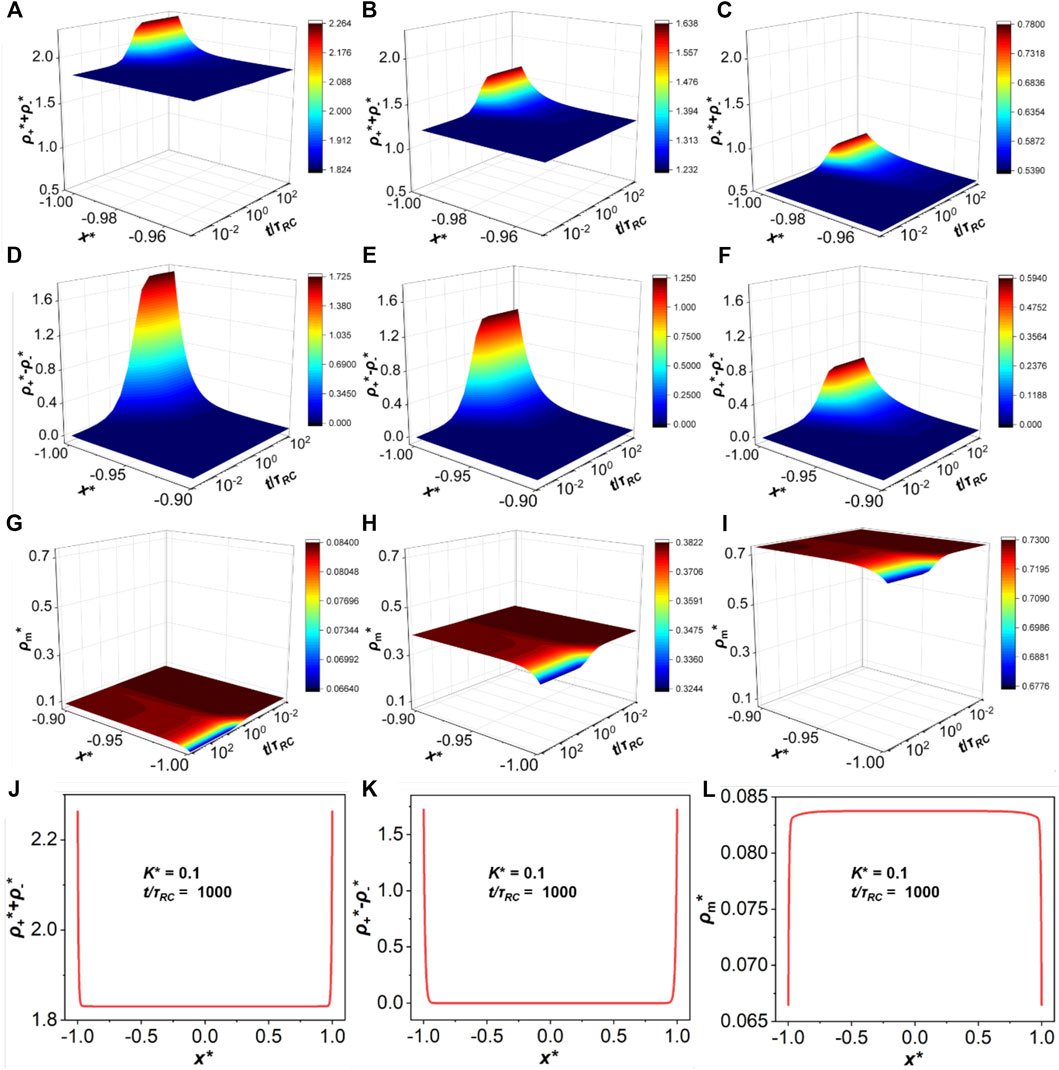
FIGURE 2. The evolutions of the total ion density (${\rho }_{+}^{\ast }+{\rho }_{-}^{\ast }$), local charge density (${\rho }_{+}^{\ast }-{\rho }_{-}^{\ast }$), and the number density of neutral particles (${\rho }_m^{\ast }$) for ionic liquids with three different association constants, K* = 0.1 (A,D,G), 1 (B,E,H), and 10 (C,F,I). (J) The total ion density (${\rho }_{+}^{\ast }+{\rho }_{-}^{\ast }$), (K) local charge density (${\rho }_{+}^{\ast }-{\rho }_{-}^{\ast }$), and (L) the number density of neutral particles (${\rho }_m^{\ast }$) at K* = 0.1, $t/{\tau }_{RC}=1$.

Furthermore, Figure 2 shows the influence of ionic association on density distribution. It can be found that with the increase of association strength (i.e., a larger K^*), the number densities of cations and anions are dramatically reduced while the number density of neutral particles increases. The ionic association affects the local concentrations of the three types of ionic species (cations, anions and ion pairs) hence the kinetic behavior and other physicochemical properties, such as timescales, capacitance and resistance.

Charge Decay Length

In order to understand the structural relaxation under the influence of ionic association, we need to identify the decay length from the density distributions. The decay length, λ_S, may be extracted by taking the logarithm of the charge distribution (log|q*|), which yields approximately a straight line at each position as shown in Figure 3. A decay length can be obtained by averaging over the slopes of the straight lines at different positions.

FIGURE 3

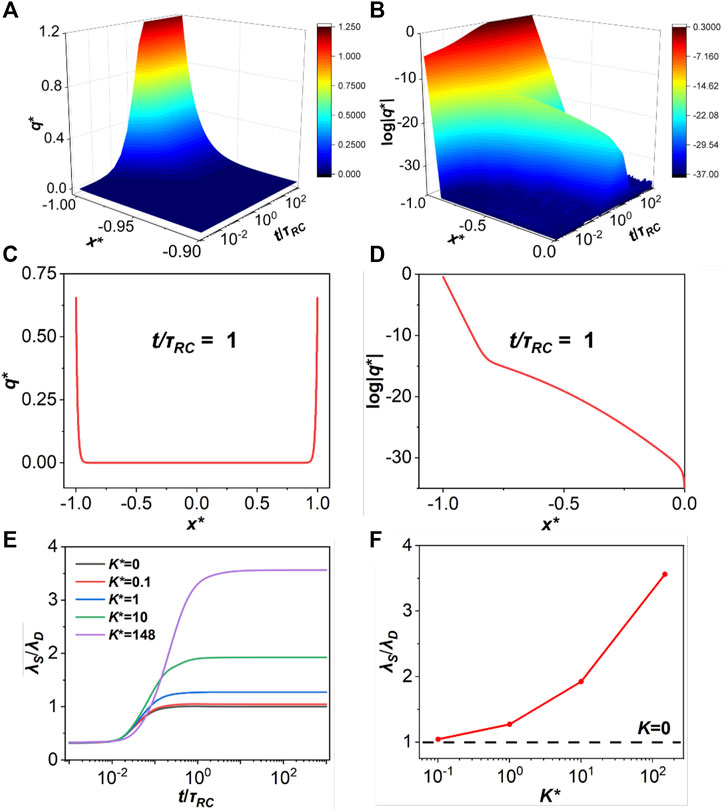
FIGURE 3. (A) Charge distribution at K* = 1, $\varphi \left(\pm L,t\right)=\pm 1$ for several successive times and (C) $t/{\tau }_{RC}=1$. (B) The relation between logarithm of charge (log|q*|) and distance x, and (D) $t/{\tau }_{RC}=1$ (E) The dependence of charge decay length λ_S on the time under different association strength. (F) The steady-state charge decay length λ_S as a function of the association strength K*.

Figure 3E presents the evolutions of the decay length λ_S for ionic liquids with different association constants. The decay length reaches a stable state at τ_RC approximately independent of K. Note that the dimensionless association constant is defined as $K^{\ast }={\rho }_{s}K$. The invariance of the relaxation time with the association strength conforms to the prediction of the RC transmission line theory (Lian et al., 2020). In Figure 3F, we show the decay length λ_S as a function of the association strength K* after the equilibrium is established. A larger association strength leads to a larger decay length, which can be intuitively understood in terms of the concentrations of free ions. According to Figure 3E, when K* = 0, λ_S = λ_D, the decay length λ_S in the figure is the Debye length λ_D, which characterizes the charge shielding effect. However, the decay length λ_S gradually deviates from the Debye length λ_D when K* > 0 due to the influence of association.

Alternatively, the decay length can be defined in terms of the density profiles of ionic species or neutral particles. Qualitatively, the conclusions are similar. As shown in Supplementary Figure S1, the stronger association that takes place between cations and anions, the longer decay length that we extract according to the evolution of the particle concentrations. While there is only one decay length if K = 0, The two slopes of the density profile allow us to identify two decay lengths at low association strength.

Charge Relaxation Timescale

It has been well established that the PNP equations yield a quantitative relation between the dynamic timescale and the Debye length, ${\tau }_{RC}={\lambda }_{D}L/D$. In the presence of ionic association, the Debye length does not reflect the association effect thus the relation is no longer valid. To explore the relation between timescale τ_RC and decay length λ_S, we assume that the RC time corresponds to the charging constant of a capacitor, which describes the speed of charging process. As the local charge profile relaxes, counterions are adsorbed on the electrode surface while the coions are depleted. The Gauss law, $\sigma \left(t\right)=-2{\rho }_s{\lambda }_D^2\left({\partial }_x\varphi \right)$, can be used to calculate the surface charge density of the electrode. Figure 4A shows the normalized surface charge density on the electrode surface, $\sigma \left(t\right)/{\sigma }_{eq}({\sigma }_{eq}\equiv \sigma \left(t/{\tau }_{RC}\to \infty \right))$. As expected, the increase of the association strength expands the relaxation time. The charge relaxation $1-\sigma \left(t\right)/{\sigma }_{eq}$ (shown in Supplementary Figure S1) shows two slopes, suggesting that the relaxation process can be divided into two stages: a faster initial response followed by a slower relaxation. A time-dependent function τ(t) can be used to characterize the timescales of early and late stages of the dynamic process:

$\tau \left(t\right)=-{\left[\frac{d\ln \left(1-\sigma \left(t\right)/{\sigma }_{eq}\right)}{dt}\right]}^{-1}.(15)$

FIGURE 4

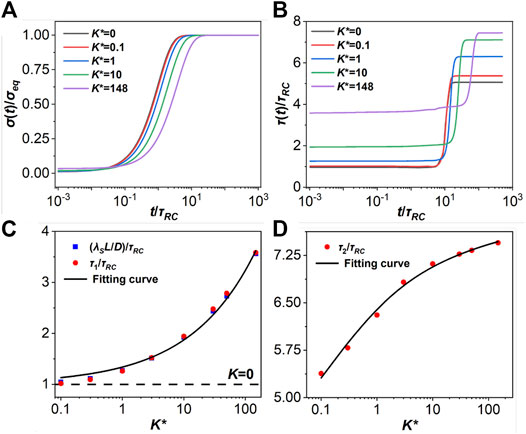
FIGURE 4. (A) The normalized surface charge density on the electrode plate $\sigma \left(t\right)/{\sigma }_{eq}$ as a function of the time. (B) Timescale τ(t) under different association strengths. (C) Comparison of ${\lambda }_{S}L/D$ and τ₁ under different values of K*. The fitting curve coincides well with the data points. (D) The fitting curve reveals a quantitative relation between τ₂ and the reduced association constant K*.

Figure 4B plots τ(t) for different association strengths. In the early stage (t/τ_RC < 1), τ(t) is controlled by the EDL formation, and the characteristic time is represented by τ₁. In the case of no association, the RC time is given by ${\tau }_1={\tau }_{RC}={\lambda }_{D}L/D$. The timescale for the early stage of charging grows with the increase of the association strength because the ionic association leads to the reduction of the concentrations of anions and cations. As a result, association slows down the formation of EDL. Due to the ionic association, the decay length λ_S, not the Debye length λ_D, should be used in the RC model, i.e., ${\tau }_1={\lambda }_{S}L/D$.

Figure 4C shows a quantitative relation between the decay length λ_S and the Debye length at a fixed association strength. Empirically, the relation can be fitted by using the following analytical form (R² > 0.99):

${\lambda }_S=\left[0.341{\left(K^{\ast }\right)}^{0.408}+1\right]{\lambda }_D.(16)$

Substituting the above formula into ${\tau }_1={\lambda }_{S}L/D$ gives:

${\tau }_1=\frac{{\lambda }_{S}L}{D}=\left[a{\left(K^{\ast }\right)}^b+1\right]\frac{{\lambda }_{D}L}{D}(17)$

where a = 0.341 and b = 0.408 are obtained by fitting the numerical results. By comparing ${\lambda }_{S}L/D$ and τ₁ for different values of K*, we assert that ${\tau }_1={\lambda }_{S}L/D$ reveals the quantitative relation between the RC time, the decay length and association strength.

In the later stage of charging (t/τ_RC > 1), τ(t) shows a step-like behavior with different plateaus τ_ad for different values of K*. In this case, τ(t) is controlled by the particle diffusion, and the dynamics is much slower than electrical motion in the early stage. The ion diffusion can be characterized by the timescale, ${\tau }_2={\tau }_{ad}=\alpha L^2/D$. If there is no association, the coefficient is $\alpha =0.05$. A different value should be used due to association. As shown in Figure 4D, we may derive a quantitative relation between τ₂ and association constant K* (R² > 0.99):

${\tau }_2=\left\{c\ln \left[\ln \left(K^{\ast }+1\right)\right]+d\right\}\alpha \frac{L^2}{D}.(18)$

where c = 0.109 and d = 1.318. Eqs 16–18 provide convenient estimations of the timescales for different stages of charging under the influence of ionic association.

Qualitatively, the equilibrium and dynamic properties of ionic liquids discussed above are relatively insensitive to the bulk concentration of ionic species (Supplementary Figures S3, S4). While both the bulk concentration and association strength affect the timescales of charging and particle relaxation, it is important to recognize that ionic association is mainly responsible for the increase of decay length and relaxation time.

Conclusion

In summary, we have integrated the modified Poisson-Nernst-Planck (MPNP) equations with the kinetics of inhomogeneous reaction to account for ionic association during electric double layer (EDL) charging. The reaction-coupled MPNP (RC-MPNP) equations were applied to study the charging dynamics of model EDL systems containing in room-temperature ionic liquids (ILs). By extracting the decay lengths and time scales from the evolution of the total local ion density and charge distribution, we found that ionic association has significant effects on the dynamics of EDL charging as characterized by a fast electrical motion at the early stage and a slower ion diffusion in the later stage. Quantitative relations have been established between the two timescales affiliated with the two stages of charging, τ₁ and τ₂, and the charging decay length λ_S and association constant K. The generic theoretical framework can be applied to other ionic systems that involve similar association reactions.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

JC, CL, and JW analyzed the results and wrote the manuscript. All coauthors contribute to the research. CL initiate the original ideas. All authors contributed to the article and approved the submitted version.

Funding

This work was sponsored by the National Natural Science Foundation of China (No. 91834301, 22078088, 21703153, 21808055), the Open Project of State Key Laboratory of Chemical Engineering and the Shanghai Rising-Star Program (No. 21QA1401900). JW thanks the financial support from the Fluid Interface Reactions, Structures and Transport (FIRST) Center, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Basic Energy Sciences.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

JC thanks Ms. Zhang Man for her helpful discussion.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fceng.2022.852070/full#supplementary-material

References

Arunachalam, S., Kirubasankar, B., Pan, D., Liu, H., Yan, C., Guo, Z., et al. (2020). Research Progress in Rare Earths and Their Composites Based Electrode Materials for Supercapacitors. Green. Energ. Environ. 5 (3), 259–273. doi:10.1016/j.gee.2020.07.021

CrossRef Full Text | Google Scholar

Canongia Lopes, J. N. A., and Pádua, A. A. H. (2006). Nanostructural Organization in Ionic Liquids. J. Phys. Chem. B 110 (7), 3330–3335. doi:10.1021/jp056006y

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, G., Song, Z., Qi, Z., and Sundmacher, K. (2021). Neural Recommender System for the Activity Coefficient Prediction and UNIFAC Model Extension of Ionic Liquid-Solute Systems[J]. AIChE J. 67 (4), e17171. doi:10.1002/aic.17171

CrossRef Full Text | Google Scholar

Chen, G., Song, Z., and Qi, Z. (2021). Transformer-convolutional Neural Network for Surface Charge Density Profile Prediction: Enabling High-Throughput Solvent Screening with COSMO-SAC. Chem. Eng. Sci. 246, 117002. doi:10.1016/j.ces.2021.117002

CrossRef Full Text | Google Scholar

Fraser, K. J., Izgorodina, E. I., Forsyth, M., Scott, J. L., and MacFarlane, D. R. (2007). Liquids Intermediate between "molecular" and "ionic" Liquids: Liquid Ion Pairs? Chem. Commun. 2007 (37), 3817–3819. doi:10.1039/b710014k

PubMed Abstract | CrossRef Full Text | Google Scholar

Gan, Z., Wang, Y., Wang, M., Gao, E., Huo, F., Ding, W., et al. (2021). Ionophobic Nanopores Enhancing the Capacitance and Charging Dynamics in Supercapacitors with Ionic Liquids. J. Mater. Chem. A. 9 (29), 15985–15992. doi:10.1039/d1ta01818c

CrossRef Full Text | Google Scholar

Jiang, J., Cao, D., Jiang, D.-e., and Wu, J. (2014). Kinetic Charging Inversion in Ionic Liquid Electric Double Layers. J. Phys. Chem. Lett. 5 (13), 2195–2200. doi:10.1021/jz5009533

PubMed Abstract | CrossRef Full Text | Google Scholar

Kondrat, S., and Kornyshev, A. (2013). Charging Dynamics and Optimization of Nanoporous Supercapacitors. J. Phys. Chem. C 117 (24), 12399–12406. doi:10.1021/jp400558y

CrossRef Full Text | Google Scholar

Largeot, C., Portet, C., Chmiola, J., Taberna, P.-L., Gogotsi, Y., and Simon, P. (2008). Relation between the Ion Size and Pore Size for an Electric Double-Layer Capacitor. J. Am. Chem. Soc. 130 (9), 2730–2731. doi:10.1021/ja7106178

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J. S., Quan, N. D., Hwang, J. M., Bae, J. Y., Kim, H., Cho, B. W., et al. (2006). Ionic Liquids Containing an Ester Group as Potential Electrolytes. Electrochemistry Commun. 8 (3), 460–464. doi:10.1016/j.elecom.2006.01.009

CrossRef Full Text | Google Scholar

Lian, C., Janssen, M., Liu, H., and van Roij, R. (2020). Blessing and Curse: How a Supercapacitor's Large Capacitance Causes its Slow Charging. Phys. Rev. Lett. 124 (7), 076001. doi:10.1103/PhysRevLett.124.076001

PubMed Abstract | CrossRef Full Text | Google Scholar

Lian, C., Liu, H., and Wu, J. (2018). Ionic Liquid Mixture Expands the Potential Window and Capacitance of a Supercapacitor in Tandem. J. Phys. Chem. C 122 (32), 18304–18310. doi:10.1021/acs.jpcc.8b05148

CrossRef Full Text | Google Scholar

Lian, C., Su, H., Liu, H., and Wu, J. (2018). Electrochemical Behavior of Nanoporous Supercapacitors with Oligomeric Ionic Liquids. J. Phys. Chem. C 122 (26), 14402–14407. doi:10.1021/acs.jpcc.8b04464

CrossRef Full Text | Google Scholar

Lian, C., Zhao, S., Liu, H., and Wu, J. (2016). Time-dependent Density Functional Theory for the Charging Kinetics of Electric Double Layer Containing Room-Temperature Ionic Liquids. J. Chem. Phys. 145 (20), 204707. doi:10.1063/1.4968037

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, K., Janssen, M., Lian, C., and van Roij, R. (2022). Dynamic Density Functional Theory for the Charging of Electric Double Layer Capacitors[J]. J. Chem. Phys. doi:10.1063/5.0081827

CrossRef Full Text | Google Scholar

Ma, K., Lian, C., Woodward, C. E., and Qin, B. (2020). Classical Density Functional Theory Reveals Coexisting Short-Range Structural Decay and Long-Range Force Decay in Ionic Liquids. Chem. Phys. Lett. 739, 137001. doi:10.1016/j.cplett.2019.137001

CrossRef Full Text | Google Scholar

Mceldrew, M., Goodwin, Z. A. H., Bi, S., Bazant, M. Z., and Kornyshev, A. A. (2020). Theory of Ion Aggregation and Gelation in Super-concentrated Electrolytes. J. Chem. Phys. 152 (23), 234506. doi:10.1063/5.0006197

PubMed Abstract | CrossRef Full Text | Google Scholar

Mceldrew, M., Goodwin, Z. A. H., Bi, S., Kornyshev, A. A., and Bazant, M. Z. (2021). Ion Clusters and Networks in Water-In-Salt Electrolytes. J. Electrochem. Soc. 168 (5), 050514. doi:10.1149/1945-7111/abf975

CrossRef Full Text | Google Scholar

Mceldrew, M., Goodwin, Z. A. H., Zhao, H., Bazant, M. Z., and Kornyshev, A. A. (2021). Correlated Ion Transport and the Gel Phase in Room Temperature Ionic Liquids. J. Phys. Chem. B 125 (10), 2677–2689. doi:10.1021/acs.jpcb.0c09050

PubMed Abstract | CrossRef Full Text | Google Scholar

Niedermeyer, H., Hallett, J. P., Villar-Garcia, I. J., Hunt, P. A., and Welton, T. (2012). Mixtures of Ionic Liquids. Chem. Soc. Rev. 41 (23), 7780–7802. doi:10.1039/c2cs35177c

PubMed Abstract | CrossRef Full Text | Google Scholar

Rupp, B., Schmuck, M., Balducci, A., Winter, M., and Kern, W. (2008). Polymer Electrolyte for Lithium Batteries Based on Photochemically Crosslinked Poly(ethylene Oxide) and Ionic Liquid. Eur. Polym. J. 44 (9), 2986–2990. doi:10.1016/j.eurpolymj.2008.06.022

CrossRef Full Text | Google Scholar

Sato, T., Masuda, G., and Takagi, K. (2004). Electrochemical Properties of Novel Ionic Liquids for Electric Double Layer Capacitor Applications. Electrochimica Acta 49 (21), 3603–3611. doi:10.1016/j.electacta.2004.03.030

CrossRef Full Text | Google Scholar

Suzuki, Y., and Seki, K. (2018). Possible Influence of the Kuramoto Length in a Photo-Catalytic Water Splitting Reaction Revealed by Poisson-Nernst-Planck Equations Involving Ionization in a Weak Electrolyte. Chem. Phys. 502, 39–49. doi:10.1016/j.chemphys.2018.01.006

CrossRef Full Text | Google Scholar

Tao, H., Chen, G., Lian, C., Liu, H., and Coppens, M. O. (2022). Multiscale Modelling of Ion Transport in Porous Electrodes[J]. AIChE J. n/a (n/a), e17571. doi:10.1002/aic.17571

CrossRef Full Text | Google Scholar

Tao, H., Lian, C., Jiang, H., Li, C., Liu, H., and van Roij, R. (2021). Enhancing Electrocatalytic N2 Reduction via Tailoring the Electric Double Layers[J]. AIChE J. 68 (3), e17549. doi:10.1002/aic.17549

CrossRef Full Text | Google Scholar

Tao, H., Lian, C., and Liu, H. (2020). Multiscale Modeling of Electrolytes in Porous Electrode: From Equilibrium Structure to Non-equilibrium Transport. Green. Energ. Environ. 5 (3), 303–321. doi:10.1016/j.gee.2020.06.020

CrossRef Full Text | Google Scholar

Ue, M., Takeda, M., Toriumi, A., Kominato, A., Hagiwara, R., and Ito, Y. (2003). Application of Low-Viscosity Ionic Liquid to the Electrolyte of Double-Layer Capacitors. J. Electrochem. Soc. 150 (4), A499. doi:10.1149/1.1559069

CrossRef Full Text | Google Scholar

Wang, J., Song, Z., Chen, L., Xu, T., Deng, L., Qi, Z., et al. (2021). Prediction of CO2 Solubility in Deep Eutectic Solvents Using Random forest Model Based on COSMO-RS-Derived Descriptors[J]. Green. Chem. Eng.

Google Scholar

Wang, J. (2020). Innovating Ionic Liquids as Repairable Electronics for Liquid Robots. Green. Energ. Environ. 5 (2), 122–123. doi:10.1016/j.gee.2020.04.005

CrossRef Full Text | Google Scholar

Wang, Y., and Voth, G. A. (2005). Unique Spatial Heterogeneity in Ionic Liquids. J. Am. Chem. Soc. 127 (35), 12192–12193. doi:10.1021/ja053796g

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, L., and Johnson, K. E. (2003). Electrochemistry of 1-Butyl-3-Methyl-1h-Imidazolium Tetrafluoroborate Ionic Liquid. J. Electrochem. Soc. 150 (6), E307. doi:10.1149/1.1568740

CrossRef Full Text | Google Scholar

Yang, J., Ding, Y., Lian, C., Ying, S., and Liu, H. (2020). Theoretical Insights into the Structures and Capacitive Performances of Confined Ionic Liquids. Polymers (Basel) 12 (3). doi:10.3390/polym12030722

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, J., Lian, C., and Liu, H. (2020). Chain Length Matters: Structural Transition and Capacitance of Room Temperature Ionic Liquids in Nanoporous Electrodes. Chem. Eng. Sci. 227, 115927. doi:10.1016/j.ces.2020.115927

CrossRef Full Text | Google Scholar

Zhang, S., Wang, X., Yao, J., and Li, H. (2020). Electron Paramagnetic Resonance Studies of the Chelate-Based Ionic Liquid in Different Solvents. Green. Energ. Environ. 5 (3), 341–346. doi:10.1016/j.gee.2020.06.018

CrossRef Full Text | Google Scholar

Zhou, Z.-B., Takeda, M., and Ue, M. (2004). New Hydrophobic Ionic Liquids Based on Perfluoroalkyltrifluoroborate Anions. J. Fluorine Chem. 125 (3), 471–476. doi:10.1016/j.jfluchem.2003.12.003

CrossRef Full Text | Google Scholar