Modeling of a Continuous Carbonation Reactor for CaCO3 Precipitation

To stop global warming well below 2°C, a rapid decarbonization of our economy, including the industrial sector is required—reaching net-zero GHG emissions in 2050. CO₂ mineralization processes, capturing CO₂ from industrial point sources and trapping it as carbonate minerals, have the potential to store climate-relevant amounts of CO₂. To get there, the potential processes have to be designed and developed, with the help of a process model that can support the process scale-up and optimization. In this work, a process model describing a gas-liquid-solid continuous cristallizer for CO₂ absorption into an aqueous ammonium nitrate solution and CaCO₃ precipitation has been developed. It consists of the relevant material balances, of a speciation model, and a population balance equation. While several of the model parameters can be obtained from the literature, a few have been estimated by fitting a comprehensive set of experimental data presented earlier. In particular, the process quantities used for parameter estimation are the CO₂ mass transfer rate, the calcium carbonate crystallization rate, and the average particle size of the CaCO₃ product crystals. The accuracy of the model, particularly in reproducing mass transfer rates and average particle sizes, has been assessed. Interestingly, it has been shown that the dominating mechanism for crystal formation is primary rather than secondary nucleation. The validated model has been used to explore the effect of the different operating conditions on various key performance indicators so as to gain a deeper insight into the process performance and potential. It has been shown that the CO₂ absorption efficiency is mainly affected by the feed stoichiometry and the gas feed rate, whereas the CO₂ capture and precipitation efficiency are controlled by the liquid phase composition and the residence time; increasing the calcium concentration in the feed is obviously one way to improve the efficiency. Moreover, we could show that the particle size tends to increase with calcium concentration and to decrease with liquid feed rate and supersaturation of the solution.

1 Introduction

Climate change is a major threat since it sets at risk both ecosystems directly (through global warming, sea level rise, loss of biodiversity…) and human society indirectly (through health effects, socio-economic impact, geo-political instability…) (IPCC, 2019). There is scientific evidence (IPCC, 2014) and political agreement (Nations, 2015) that climate change is caused by the accumulation of green house gases (GHG) in the atmosphere, caused by the human activities that involve the use of fossil carbon for energy generation and the release of geogenic carbon for construction materials. Hence, GHG emissions are generated across all sectors, and the related activities have been increasing the level of GHG present in the atmosphere, biosphere and oceans continuously since the industrial revolution.

Climate action requires a collaborative effort of all entities, both individuals and collectives, that cause CO₂ emissions, since local emissions have global impacts. In Paris, this collaborative strategy was framed into an agreement (Nations, 2015), with the aim to stop global warming well below 2°C. This aim implies the reduction of GHG emissions to net-zero; the economy has to undergo a rapid and complete decarbonisation in the years until 2050 (IPCC, 2018).

CO₂ is the GHG responsible for 80% of global warming (Janssens-Maenhout et al., 2017) and 20% of its total emissions are caused by the industry (IPCC, 2018). Such CO₂ emissions are often inherent to the manufacturing process—and therefore hard to avoid with conventional technologies. Moreover, they produce indispensable goods like cement, steel and chemicals. CO₂ capture, transportation, and storage (CCS) is a system of technologies, or in others words a value chain, that is designed to decarbonize industrial processes that represent large CO₂ point sources (IPCC, 2005). For the three main steps of the value chain, i.e., CO₂ capture, transportation and storage, solutions proven over many years are commercially available. The first full scale CCS chain started its operation in 1996 in Sleipner, Norway, where about 1 Mt of CO₂ per year have been captured and stored in deep saline aquifers ever since (Furre et al., 2017).

Despite the technology has been proven to operate in a robust and safe manner and the urgent need to decarbonize emission intensive industrial processes such as cement and steel manufacturing, progress in implementing CCS has been less than expected (Institute, 2019).

Implementing CCS value chains is complex, since it requires the development of policies, business models, CO₂ capture and transport infrastructure, as well as storage hubs, social acceptance, and all these elements in parallel. Thus, many stakeholders need to take a significant share of the risk—while their success is endangered if only a single element in the chain faces problems. At the same time, one element not being ready makes the chain incomplete and impossible to operate. This risk, coupled with political and business-related uncertainties delays investment decisions, which would affect the companies business model for twenty and more years to come.

As a result, the main hindering aspect of CCS is a missing business case for most locations. Unlike other technologies, CCS only avoids CO₂ emissions and does not generate any other associated value in today’s market, with the exception of enhanced oil recovery, which is however in contrast not climate positive; in fact after oil is produced and utilized a larger amount of CO₂ is emitted than it is ultimately stored in the depleted reservoir. Therefore, the emission avoidance approach based on CCS does not translate into economic value as long as there is no credible carbon policy in place (Durmaz, 2018; Gardarsdottir et al., 2019).

Utilizing CO₂ to manufacture added value products can generate this required economic value. To qualify as a climate change mitigation technology, the CO₂ has to be stored for a long period of time, unless it comes either directly or indirectly (e.g. via biomass growth followed by combustion) from the atmosphere. Thus, long lived products can offer the benefit of permanent storage. However, critics argue, that the scale at which CCS deployment is required is orders of magnitudes larger than the storage potential in such products. Therefore, CO₂ capture, and utilization (CCU) might be more of a distraction rather than a viable option to mitigate climate change (Mac Dowell et al., 2017). This holds especially true for energy intensive CCU processes, e.g., the production of synthetic fuels, which require large amounts of carbon-free electricity (Abanades et al., 2017; Sutter et al., 2019; Becattini et al., 2021).

In the construction sector, CCU is especially promising, because climate relevant amounts of CO₂ can be stored permanently as carbonate minerals (Initiative, 2016). Furthermore, carbonate minerals are the thermodynamically most stable form of CO₂, hence the reaction of CO₂ to carbonate minerals is exothermic and thus generates energy instead of consuming it. Scientists have identified significant potential for CCU in the cement sector; the resulting minerals do not only store CO₂, but they can partially replace an energy and emission intensive material, i.e., clinker (Ostovari et al., 2020; Tiefenthaler, 2021).

Among the most abundant minerals used in industrial applications is calcium carbonate. Clinker and cement (Anantharaman and David, 2017), concrete (IEA, 2018), iron and steel making, pulp and paper and fillers for daily home care products require large amounts of it.

Conventionally, calcium carbonate is extracted in quarries, ground, used and incinerated or recycled (e.g., concrete recycling). Applications, which require specific properties with respect to purity, particle size and morphology use precipitated calcium carbonate (PCC), which is manufactured by calcining limestone and then re-carbonating it and precipitating it again (Mattila et al., 2014).

We envision, that PCC will in the future be produced in a GHG neutral manner. One pathway is the substitution of the calcium source limestone with industrial mineral wastes, such as slags, ashes and demolition concrete. This can mitigate feedstock related emissions. If used for construction materials, PCC can become a carbon sink. Else, if used in products, it is usually incinerated and thus can become in the best case carbon neutral. Plenty of research has been conducted in this space to develop viable processes (Sanna et al., 2014). Most promising are pH swing technologies operating with an aqueous solvent containing an ammonia salt (Mattila and Zevenhoven, 2014a). In step one, calcium is extracted from the mineral waste stream, the solid residue material is removed by filtration. In step two, the calcium rich aqueous solution is carbonated with gaseous CO₂, and PCC precipitates.

Plenty of experimental work in batch and continuous mode (Mattila and Zevenhoven, 2014b; Tiefenthaler and Mazzotti, 2021) has been conducted. To the best knowledge of the authors, comprehensive models for mineral carbonation processes, which consider the kinetics of CO₂ absorption and of PCC precipitation are rare. Vučak (2002) provides a detailed model; however, their solvent system is considerably different than the one used here (monoethanolamine instead of an ammonium salt).

This work presents for the first time a kinetic model for CO₂ absorption into an aqueous ammonium nitrate solution, where calcium ions are present, and the ensuing precipitation of calcium carbonate, in a continuous reactive crystallization configuration. In practical applications of this process, the aforementioned solution would be prepared by contacting an ammonium nitrate solution (prepared ad hoc) with industrial mineral wastes, such as slags, ashes, and demolition concrete. The acid character of the ammonium nitrate solution enables the leaching of calcium ions from the mineral wastes. In the context of the overall process (not discussed here), the ammonium nitrate solution is recycled in a closed loop within the process itself. The relevant kinetic parameters of the system are estimated making use of experimental results obtained in a previous study (Tiefenthaler and Mazzotti, 2021).

This type of models are necessary to understand the system and to design, optimize and scale-up a process for the precipitation of PCC from waste materials. First, the thermodynamics of the system is described, upon which the kinetic model of the process is built. Afterwards, a number of empirical kinetic parameters are estimated based on experimental results, and the accuracy of the model is assessed. Finally, the model is used to gain new insights, going beyond the experimental learnings, which are presented and discussed in the Section 4.

2 Thermodynamic Modeling

The system investigated is a crystallizer that acts as carbonation reactor and consists of a gas, a liquid and a solid phase. The gas phase contains N₂, CO₂ and moisture [NH₃ volatility at such temperatures and pH conditions can be neglected (Said et al., 2016)]; the liquid phase is an aqueous ammonium nitrate solution rich in calcium, in which CO₂ absorbs and speciates; finally the solid phase consists of the mineral CaCO₃ only under the conditions explored here.

A CO₂ molecule enters the system through the inlet gas stream; it is first absorbed by the aqueous solution, then it undergoes speciation reactions to form amongst others the CO₃²⁻ ion, which either precipitates with a Ca²⁺ ion to form the solid CaCO₃ or exits from the reactor as ion dissolved i within the mother liquor. The physical and chemical equilibria relevant for this system are as follows (Thomsen and Rasmussen, 1999; Vu č ak, 2002; Wolery, 2002; Puxty et al., 2010):

2.1 Vapor-Liquid Equilibrium

$C{O}_{2,g}\stackrel{K_1}{\leftrightarrow }C{O}_{2,aq}$(2-1)

$H_2{O}_g\stackrel{K_2}{\leftrightarrow }{H}_2{O}_{aq}$(2-2)

2.2 Liquid Speciation

$C{O}_{2,aq}+2N{H}_{3,aq}\stackrel{K_3}{\leftrightarrow } N{H}_{2}CO{O}^{-}+N{H}_4^{+}$(2-3)

$C{O}_{2,aq}+O{H}^{-}\stackrel{K_4}{\leftrightarrow }HC{O}_3^{-}$(2-4)

$O{H}^{-}+H^{+}\stackrel{K_5}{\leftrightarrow }{H}_{2}O$(2-5)

$N{H}_4^{+}\stackrel{K_6}{\leftrightarrow }N{H}_3+H^{+}$(2-6)

$C{O}_3^{2-}+H^{+}\stackrel{K_7}{\leftrightarrow }HC{O}_3^{-}$(2-7)

$CaN{O}_3^{+}\stackrel{K_8}{\leftrightarrow }C{a}^{2+}+N{O}_3^{-}$(2-8)

$CaC{O}_{3,aq}+H^{+}\stackrel{K_9}{\leftrightarrow }C{a}^{2+}+HC{O}_3^{-}$(2-9)

$CaHC{O}_3^{+}\stackrel{K_{10}}{\leftrightarrow }C{a}^{2+}+HC{O}_3^{-}$(2-10)

$CaO{H}^{+}+H^{+}\stackrel{K_{11}}{\leftrightarrow }C{a}^{2+}+H_{2}O$(2-11)

2.3 Solid-Liquid Equilibrium

$C{a}^{2+}+C{O}_3^{2-}\stackrel{K_{12}}{\leftrightarrow }CaC{O}_{3,s}$(2-12)

The geochemical equilibrium package EQ3/6 was used to identify the relevant speciation reactions; reactions which result in ionic species at very low concentrations have been neglected.

The following assumptions have been made:

• N₂ is assumed to be insoluble, and thus it does not absorb in the aqueous solution.

• The liquid water is in equilibrium with the water vapor in the gas phase.

• NH₃ is assumed to be non-volatile, since the absorption of CO₂ shifts the equilibrium towards NH₄₊. This assumption has been tested in independent experiments which confirmed that ammonia is below the detection limit, which is in line with literature (Said et al., 2016).

• The gas and liquid phase are well mixed, i.e., both phases and its relevant intensive properties, i.e., temperature, pressure, and composition, are homogeneous in the reactor.

• CO₂ is not at equilibrium between gas and solution hence its absorption is mass transfer limited and can be described by the two film theory.

• The reaction of CO_2,aq with NH₃ in the liquid film is considered as the rate determining step of CO₂ uptake. Consequently, all reactions in the aqueous solution can be considered to be instantaneous hence at equilibrium (Puxty et al., 2010). Moreover, evaluating the Hatta number for various operating conditions confirmed, that the reaction of CO_2,aq with NH₃ is in the pseudo-first-order and fast reaction regime while the reaction of CO_2,aq with OH⁻ lies in the very-slow to slow reaction regime. Since both occur in parallel, the reaction with NH₃ is rate determining.

• The precipitation of CaCO₃ is not instantaneous hence it is governed by the principles of crystallization, whereby the amount of solid mass and the crystal size distribution are controlled by the interplay between nucleation and growth, whose rates depend on the relevant driving force (agglomeration of primary particles and crystal breakage are neglected for the sake of simplicity) (Davey, 2000; Wolthers et al., 2012).

• In this work we assume representative product removal, namely that the particle size distribution of the suspension withdrawn is the same as that of the suspension in the crystallizer. We believe that this is a reasonable assumption considering that the experiments on which this modeling work is based (Tiefenthaler and Mazzotti, 2021) yielded very small particles that should yield a homogeneous suspension. A study of this particular aspect should be considered in follow up studies.

2.4 Modelling of the Liquid Speciation

The reactions in the bulk liquid (Eqs 2-3–2-11) are considered to be instantaneous hence they can be assumed to be at equilibrium. The corresponding chemical equilibrium conditions must be fulfilled, which can be written as:

$K_i=\frac{{\displaystyle {\prod }_j{a}_{j,product}}}{{\displaystyle {\prod }_k{a}_{k,educt}}}$(2-13)

$a_j= {\gamma }_j{c}_j$(2-14)

$a_j$ and $c_j$ are the activity and the concentration of the ion or molecule $i$; $K_i$ is the equilibrium constant associated to the corresponding equilibrium (the equilibrium constants are reported in the Supplementary Appendix SA); ${\gamma }_i$ is the activity coefficient of the ion or molecule $i$. Literature correlations were used to calculate the activity coefficient for NH₃ (Maeda and Kato, 1995). The activity of water and the activity coefficient of CO_2,aq were calculated according to Wolery (2002). The activity coefficient of CaCO_3,aq was assumed to be equal to one. The B-dot equations, which consider the dominat long-range interactions between the ions and molecules, were used to calculate the activity coefficient of charged species. A complete description and discussion of these equations can be found elsewhere (Wolery, 2002).

In addition, the electro neutrality condition has to be met:

${\displaystyle \sum _i{c}_i{z}_i=0}$(2-15)

where the sum extends on all the ionic (charged) species and $z_i$ corresponds to the charge of ion $i$. The concentration of the ionic species and molecules in solution can be used to define the following four overall concentrations in solution, which in turn will have to satisfy the overall material balances (see below):

$c_C=c_{C{O}_2,aq}+c_{HC{O}_3^{-}}+c_{C{O}_3^{2-}}+c_{CaHC{O}_3^{+}}+c_{CaC{O}_{3,aq}}+c_{N{H}_{2}CO{O}^{-}}$(2-16)

$c_{Ca}=c_{C{a}^{2+}}+c_{CaO{H}^{+}}+c_{CaN{O}_3^{+}}+c_{CaHC{O}_3^{+}}+c_{CaC{O}_{3,aq}}$(2-17)

$c_{N{O}_3}=c_{N{O}_3^{-}}+c_{CaN{O}_3^{+}}$(2-18)

$c_{N{H}_3}=c_{N{H}_4^{+}}+c_{N{H}_3}+c_{N{H}_{2}CO{O}^{-}}$(2-19)

The system of equilibrium reactions is solved by making use of the geochemical equilibrium software package EQ3/6, v8.0a (Wolery, 2002). EQ3/6 is a software package for modeling geochemical interactions between aqueous solutions, solids, and gases, following principles of chemical thermodynamics and chemical kinetics, which is maintained and kept updated at the Lawrence Livermore National Laboratory¹, and has been used in earlier mineral carbonation studies (Hariharan and Mazzotti, 2017a; Hariharan and Mazzotti, 2017b; Hariharan et al., 2016; Hariharan, 2017; Werner et al., 2014a; Werner et al., 2014b). The equilibrium constant for Eq. 2-3 is provided by Thomsen and Rasmussen (1999).

The equations above involve the concentrations of the 14 molecules and ionic species in solution: $c_{C{O}_2,aq}, c_{HC{O}_3^{-}}, c_{C{O}_3^{2-}}, c_{CaHC{O}_3^{+}}, c_{CaC{O}_{3,aq}}, c_{N{H}_{2}CO{O}^{-}}, c_{C{a}^{2+}}, c_{CaO{H}^{+}}, c_{CaN{O}_3^{+}}, c_{N{O}_3^{-}}, c_{N{H}_4^{+}}, c_{N{H}_3}, c_{H^{+}} \text{and} c_{O{H}^{-}}$. If the total concentrations of carbon $c_C$, of calcium $c_{Ca}$, of ammonium $c_{N{H}_3}$, and of nitrate $c_{N{O}_3}$ are known, for instance because they are determined through the material balances for the whole system (see below) the liquid speciation equations (the nine Eqs 2-3–2-11) together with the definitions of the overall concentrations (Eqs 2-16–2-19) and the electro neutrality condition (Eq. 2-15) can be solved numerically to obtain the 14 unknown concentrations in solution.

3 Reactor Modelling

The reactor, as shown in Figure 1, is a continuous crystallizer, that has certain similarities to a classical MSMPR, of a total volume, $V_R$; it is filled with an aqueous solution of volume $V_s$. It is assumed that the gas, liquid and solid phases are well mixed and that the temperature is well controlled. The aqueous solution is fed at a rate $Q_{in}$ and a liquid phase composition $c_{i,in}$. The liquid outlet flow is specified at steady state by the composition $c_i$, obviously the same as within the crystallizer, and the outlet flow rate $Q_{out}$. Gas is bubbled through the reactor’s suspension at an inlet flow rate $F_{in}$ and an inlet composition $y_{i,in}$. The gas is exiting the reactor at a flow rate $F_{out}$ and a composition $y_{i,out}$. The CO₂ mass transfer is described by the two film theory, whereas water and water vapour are assumed to be at equilibrium. However, since the outlet gas passes through a condenser, it is assumed that the gas leaving the reactor is dry. The only solid precipitating from the solution is calcium carbonate, present either as calcite or vaterite. These solid particles are described as a population of spheres with particle size distribution (PSD) given by $f\left(L\right),$ where $L$ is the characteristic length. The primary particles are cuboidal and spherical depending on the polymorph (calcite or vaterite, respectively), and form spherical agglomerates (Tiefenthaler and Mazzotti, 2021). Calcium carbonate precipitation is controlled by the mechanisms of nucleation and growth, and occurs at a rate that depends on their corresponding rates.

FIGURE 1

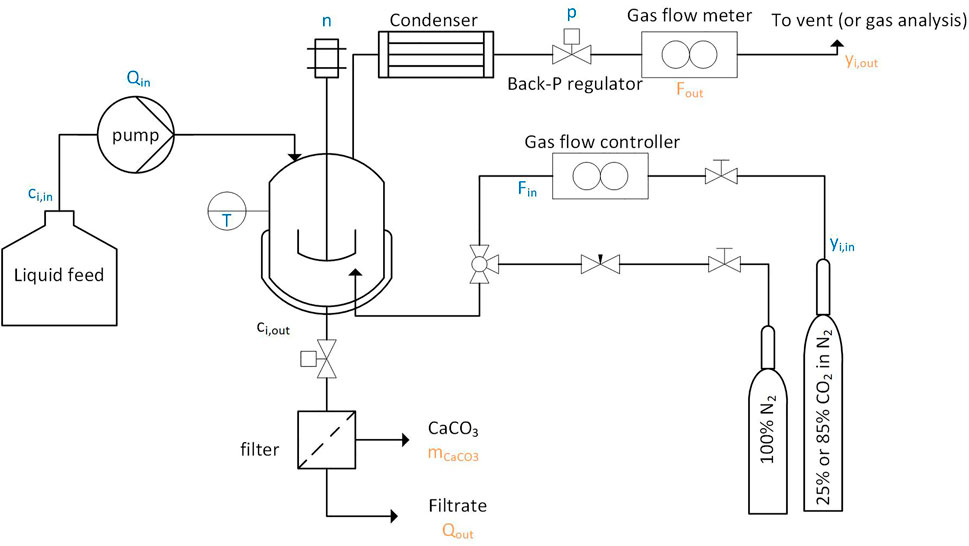
FIGURE 1. A schematic drawing of the crystallizer modeled in the scope of this project is shown. The experimental setup is described to a greater detail in a previous publication (Tiefenthaler and Mazzotti, 2021).

3.1 Aqueous Solution

The material balance for water in the reactor can be written as:

$\frac{d{V}_s\rho }{dt}=Q_{in}-Q_{out}$(3-1)

The product of the liquid phase volume $V_s$ and the liquid phase density $\rho$ corresponds to the amount of liquid present in the reactor. The system is operated at steady state, thus $Q_{in}$ is equal to $Q_{out}$, which from now are called simply Q. The mass balances for Ca, C, NH₃ and $N{O}_3^{-}$ in the aqueous solution are:

$V_s\rho \frac{d\left(c_{Ca}\right)}{dt}=Q\left(c_{Ca,in}-c_{Ca}\right)-r_c{V}_s$(3-2)

$V_s\rho \frac{d\left(c_C\right)}{dt}=Q\left(c_{C,in}-c_C\right)+V_s\left(f_{MT}-r_c\right)$(3-3)

$V_s\rho \frac{d\left(c_{N{H}_3}\right)}{dt}=Q\left(c_{N{H}_3,in}-c_{N{H}_3}\right)$(3-4)

$V_s\rho \frac{d\left(c_{N{O}_3}\right)}{dt}=Q\left(c_{N{O}_3,in}-c_{N{O}_3}\right)$(3-5)

The initial conditions for the system have to be assigned accordingly in case the calculation of the transient between start up and steady state is needed; they are not necessary for steady state simulations. The quantity $c_i$ represents the overall concentration of component $i$ in the aqueous solution, i.e., corresponding to the left hand side of Eqs 2.15–2.18.

3.2 Gas Phase

The gas phase mass balance is

$\frac{d{n}_{tot}}{dt}=F_{in}-F_{out}-f_{MT}{V}_s$(3-6)

The total number of moles of gas in the reactor’s overhead space, $n_{tot}$, is calculated by the ideal gas law

$n_{tot}=\frac{P}{RT}(V_R-V_s)$(3-7)

$P$ corresponds to the system pressure, $R$ to the ideal gas constant and $T$ to the reactor temperature. The CO₂ mass balance in the gas phase is

$\frac{d\left(n_{tot}{y}_{C{O}_2}\right)}{dt}=F_{in}{y}_{C{O}_2,in}-F_{out}{y}_{C{O}_2,out}-f_{MT}{V}_s$(3-8)

$y_{C{O}_2}$ corresponds to the CO₂ mole fraction in the overhead space. The outlet gas stream is assumed to be dry, thus the CO₂ outlet concentration is calculated as follows:

$y_{C{O}_2,out}=\frac{y_{C{O}_2}}{y_{C{O}_2}+y_{N_2}}$(3-9)

$y_{N_2}$ corresponds to the N₂ mole fraction in the overhead space of the reactor, whereby the sum of the molar gas fractions for CO₂, N₂ and H₂O in the overhead space must be equal to one.

${\displaystyle \sum _i{y}_i=1}$(3-10)

The quantity $f_{MT}$ that appears in Eqs 3-3, 3-7, 3-9 couples the equations for the gas phase and for the solution and needs to be defined based on an underlying mass transfer model; this is discussed in detail in Section 3.4.

3.3 Solid Phase

The solid phase mass balance is

$\frac{d{n}_{CaC{O}_3}}{dt}=r_c{V}_s-\frac{k_{V}Q{\rho }_c}{\rho M_{CaC{O}_3}}{\mu }_3$(3-11)

where $n_{CaC{O}_3}$ is the number of moles of CaCO₃ in the reactor, $k_V$ the volume shape factor of the crystals, equal to π/6 for spheres, ${\rho }_c$ the mass density and $M_{CaC{O}_3}$ the molar mass of CaCO₃, and ${\mu }_3$ is the 3^rd moment of the crystal size distribution, which must be calculated from the solution of the population balance equation, as discussed in Section 3.5 below. The quantity $r_c$ represents the number of moles of CaCO₃ that are transferred to the solid phase from solution per unit time and unit volume of the solution.

3.4 CO₂ Mass Transfer Model

A model for the gas-liquid mass transfer rate of CO₂ is adopted, which is based on the two-film theory. The rate of gaseous CO₂ absorbed by the liquid phase can be written as Levenspiel (1999a):

$f_{MT}= k_{L }{a}_{eff} E \rho \left(c_{C{O}_2,aq}^{\ast } -c_{C{O}_2,aq}\right)$(3-12)

$c_{C{O}_2,aq}^{\ast }=\frac{f_{C{O}_2}}{H_{C{O}_2}}$(3-13)

$k_{\text{L }}$ is the liquid phase mass transfer coefficient, $a_{\text{eff}}$ corresponds to the effective mass transfer area per unit volume of the suspension, $E$ the enhancement factor, $f_{{\text{CO}}_2 }$ is the arithmetic mean bulk gas phase fugacity of CO₂ of the incoming and exiting gas stream, $H_{C{O}_2}$ is the Henry constant of CO_2, $c_{{\text{CO}}_2,aq}$ is the molecular CO₂ concentration in the bulk liquid and $c_{C{O}_2,aq}^{\ast }$ is the concentration of molecular CO₂ at the gas—liquid interface, which is in equilibrium with the gas phase. Note that Eq. 3.14 is the isofugacity for the CO₂ gas-liquid equilibrium referred to by Eq. 2-1. As a consequence of its definition, $f_{\text{MT}}$ is given in moles of CO₂ per unit time per unit volume of the solution.

3.4.1 Enhancement Factor

The reaction of carbon dioxide with ammonia and hydroxyl ions in the liquid film enhances the CO₂ absorption. The liquid phase mass transfer coefficient has to account for this effect, hence the physical mass transfer coefficient $k_{\text{L }}$ (CO₂ absorption without reaction) is multiplied by E, accounting for the reactions of Eqs 2-3, 2-4 (Levenspiel, 1999b; Darde et al., 2011):

$C{O}_{2,aq}+2N{H}_3\stackrel{k_{N{H}_3}}{\leftrightarrow } N{H}_{2}CO{O}^{-}+N{H}_4^{+}$

$C{O}_{2,aq}+O{H}^{-}\stackrel{k_{O{H}^{-}}}{\leftrightarrow } HC{O}_3^{-}$

The functional form of the enhancement factor depends on the reaction regime. The reaction regime is specified by the value of the Hatta number $M_H$ and the enhancement factor for infinitely fast reactions $E_i$ (Darde et al., 2011).

$M_H=\frac{\sqrt{D_{C{O}_2}{k}_A{c}_A}}{k_L}$(3-14)

$E_i=1+\frac{D_A{c}_A}{2D_{C{O}_2}{c}_{C{O}_2,aq}^{\ast }}$(3-15)

The Hatta number compares the rate of reaction of Eqs 2-3, 2-4 within the liquid film with the rate of CO₂ mass transfer through the liquid film, whereby $D_{C{O}_2}$ is the diffusivity of CO₂ in the liquid phase and is calculated as follows (Versteeg and Van Swaaij, 1988)

$D_{C{O}_2}=2.35\ast {10}^{-6}{e}^{-\frac{2119}{T}}$(3-16)

$D_A$ is the diffusivity of NH₃ molecules respectively OH⁻ ions in the liquid film, which can be assumed to be equal to the diffusivity of CO₂ in the liquid phase (Zeng et al., 2011). $k_A$ is the reaction rate constant of NH₃ respectively OH⁻ ions with CO₂. $k_{O{H}^{-}}$ can be determined according to the following equation (Pohorecki and Moniuk, 1988):

$log\left(\frac{k_{O{H}^{-}}}{k_{O{H}^{-}}^{inf}}\right)=0.221I-0.016I^2$(3-17)

$k_{O{H}^{-}}^{inf}=11.916-\frac{2382}{T}$(3-18)

$I$ is the ionic strength of the aqueous solution. There are a number of correlations available for $k_{N{H}_3}$. The lower bound can be calculated as follows (Pinsent et al., 1956)

$k_{N{H}_3}=k_{REF}{e}^{-\frac{E_a}{RT}}$(3-19)

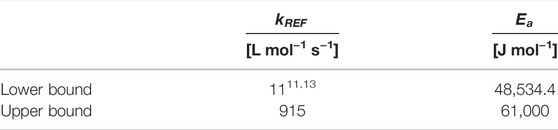
And the upper bound of the rate constant was determined as follows (Puxty et al., 2010).

$k_{N{H}_3}=k_{REF} e^{-\frac{E_a}{R}\left(\frac{1}{T}-\frac{1}{283}\right)}$(3-20)

The average between the maximum and the minimum values of $k_{N{H}_3}$ proposed in the literature (see Table 1) will be used for further calculations. The concentration $c_A$ corresponds to that of the relevant reactant. For the corresponding regimes, the functional form of $E$ is taken from a look-up table reported by Last and Stichlmair (2002). $k_{\text{L}}$ and $a_{\text{eff}}$ are system specific parameters, which have to be estimated from experimental data.

TABLE 1

TABLE 1. Parameters for the upper and lower bound of $k_{N{H}_3}$. At 25°C, $k_{N{H}_3}$ corresponds to 1,920 L mol⁻¹ s⁻¹.

One way to identify, which of the two reactions considered enhances CO₂ mass transfer, is to compute the Hatta number and the enhancement factor for a range of operating conditions. At a CO₂ partial pressure of 0.25 bars, 25°C, k_L of 2 * 10⁻⁴ m s⁻¹ (Last and Stichlmair, 2002) and a NH₃ concentration of 0.02–1 mol per kg water, the reaction regimes for both reactions were determined (not shown here). While the reaction of CO_2,aq with OH⁻ ions can be found to be between the very slow and the slow reaction regime, the reaction of CO_2,aq with NH₃ is between the fast reaction of pseudo first order and the fast reaction regime. As a result, only the presence of NH₃ enhances the CO₂ mass transfer through the gas-liquid interface. Thus, the effect of the OH⁻ ions on the mass transfer enhancement is neglected.

3.5 CaCO₃ Precipitation Model

A kinetic expression for the precipitation of CaCO₃ is developed. Calcium carbonate can precipitate in three main anhydrous forms: calcite, aragonite and vaterite, listed here by decreasing stability (Flaten et al., 2009). The two dominant mechanisms during precipitation are nucleation and crystal growth. In the case of the continuous process modeled here, nucleation is described according to the classic nucleation theory. To model the precipitation process of CaCO₃, we assume that the suspension is well mixed and that nucleation and growth are the dominant precipitation mechanisms, i.e., we have decided for the sake of simplicity to neglect the effect of agglomeration and breakage. The corresponding population balance equation can be written as (Davey, 2000; Ramkrishna, 2000; Alvarez et al., 2011):

$\frac{\partial f}{\partial t}+G\frac{\partial f}{\partial L}+\frac{1}{\tau }\left(f-f_{in}\right)=0$(3-21)

where $f$ corresponds to the number based particle size distribution in the reactor, $G$ to the size independent growth rate, $L$ to the characteristic length of a particle, $\tau$ to the residence time of the suspension in the reactor, i.e., $\tau =\frac{V_s{\rho }_s}{Q}$, and $f_{in}\left(L\right)$ is the number based particle size distribution of the population of particles entering the reactor with the feed stream.

Since the system operates at steady state, and the feed is free of particles, Eq. 3-21 can be simplified to:

$G\frac{df}{dL}+\frac{1}{\tau }f=0$(3-22)

With the boundary condition:

$f(L=0)=\frac{J}{G}$(3-23)

where $J$ is the rate of particle nucleation and G is the rate of crystal growth. It is worth noting that for the sake of simplicity but without loss of generality we have decided not to distinguish between different polymorphs precipitating; as a consequence the driving force for nucleation and growth is expressed with respect to the crystallization of the stable polymorph, i.e., calcite.

The nucleation rate is given by the classical nucleation theory relationship (Jun et al., 2016; Reis et al., 2018):

$J=A\exp \left(-\frac{16\pi {\sigma }^3{v}_m^2}{3k_B^3{T}^3{\left(\log \left(S\right)\right)}^2}\right)$(3-24)

where $S$ corresponds to the supersaturation with respect to calcite, $\sigma$ is the surface energy, $v_m$ represents the molecular volume of $CaC{O}_3$, both listed in the Supplementary Appendix SB. $k_B$ is the Boltzmann. Considering the boundary conditions, the population balance, Eq. 3-22, can be integrated to obtain the particle size distribution:

$f\left(L\right)=\frac{J}{G}\exp \left(-\frac{L}{G\tau }\right)$(3-25)

One can see, that as the characteristic length of the particle approaches the size of the smallest particle (L = 0), the corresponding boundary condition is fulfilled. Moreover, the regularity condition is fulfilled, since the value of f(L) becomes zero as the characteristic length approaches infinity (Ramkrishna, 2000).

The growth rate was assumed to be continuous in the entire range of calcite saturation values, meaning that the energy required to integrate a molecule to the solid lattice is low and that every growth unit arriving finds a site in the lattice (Davey, 2000). Thus, the growth rate can be expressed as:

$G=k_c{\left(S-1\right)}^{\alpha }$(3-26)

where $k_{\text{c}}$ is the rate constant for growth, $\alpha$ corresponds to an empirical exponent, and $S$ is the supersaturation with respect to calcite, which is defined as:

$S= \sqrt{\frac{a_{C{O}_3^{2-}}{a}_{C{a}^{2+}}}{K_{SP}}}$(3-27)

where $K_{SP}$ is the solubility product of calcite. Different growth rate models can be found in the literature, some of them are more of a theoretical nature while others more of an empirical one. Brečević (2007) developed a correlation for $k_c$ at 25°C and for $S$ ranging from 1 to 3 as a function of the ionic strength assuming $\alpha$ equal to 2. However, the discussed system operates at much higher values of supersaturation. Chen et al. (1997) claims that for gas—liquid systems, $\alpha$ is equal to 2.9. In addition, the surface integration is supposed to be rate limiting (also supported by others, see Nancollas and Reddy, 1971; Kazmierczak et al., 1982). Wolthers et al. (2012) develop an empirical model for ${\text{k}}_{\text{c}}$ valid for ionic strengths ranging from 0.001–0.7 M:

${\text{k}}_{\text{c}}=I^{-\beta }p{H}^{-\gamma }{\left(\frac{a_{C{a}^{2+}}}{a_{C{O}_3^{2-}}}\right)}^{-\Delta }$(3-28)

They estimated $\beta$ to be equal to 0.004, $\gamma$ to be equal to 10.71 and $\Delta$ to be equal to 0.35. Furthermore, they assume $\alpha$ equal to 2. Nehrke et al. (2007) identified experimentally that the growth rate of calcite has a maximum at a ratio of the $a_{C{a}^{2+}}$ to $a_{C{O}_3^{2-}}$ equal to one.

Finally, the jth moment of the crystal size distribution ${\mu }_j$ is defined as:

${\mu }_j=\underset{0}{\overset{\infty }{{\displaystyle \int }}}{L}^{j}f\left(L\right)\text{d}L$(3-29)

Using Eq. 3-26 the integral can explicitly be calculated in the case of interest as:

${\mu }_2=2J{\tau }^3{G}^2$(3-30)

${\mu }_3=6J{\tau }^4{G}^3$(3-31)

Thus, the moments of the crystal size distribution are function of the residence time and of the composition of the solution, through the values of J and G that depend in turn on the supersaturation $S$. Moreover, Eq. 3-11 can be solved at steady state, thus yielding the following expression for $r_c$:

$r_c=\frac{6k_V{\rho }_c}{M_{CaC{O}_3}}J{\tau }^3{G}^3$(3-32)

It is worth noting that the quantity $r_c$ can be calculated independently of Eq. 3-12 by considering that CaCO₃ uptake by the solid phase occurs through crystal growth only, since new nuclei are assumed to have L = 0 hence zero mass. To this aim, one must calculate the product of the growth rate and the total crystal surface, which is proportional to the second moment of the particle size distribution, ${\mu }_2$: the proper expression is $r_c=\frac{0.5k_A{\rho }_c}{M_{CaC{O}_3}}G{\mu }_2$, which yields Eq. 3-32 when substituting Eq. 3-31 and considering that $\frac{k_A}{k_V}=6$ for particles that do not change shape as they grow.

3.6 Key Operating Parameters and Key Performance Indicators

In the following, the KOPs and the KPIs, which have been developed in the scope of a previous experimental study (Tiefenthaler and Mazzotti, 2021) will be introduced as they are used in the Section 4 of the manuscript, particularly for the comparison between simulations and experiments. The stoichiometric ratio in the feed to the reactor, ${\psi }_F$, is defined as:

${\psi }_F=\frac{F_{in}{y}_{C{O}_2,in}}{Q_{in}{c}_{Ca,in}}$(3-33)

The CO₂ absorption efficiency ${\eta }_{C{O}_2,abs.}$ is defined and calculated as:

${\eta }_{C{O}_2,abs.}= \frac{f_{MT}{V}_s}{F_{in}{y}_{C{O}_2,in}}$(3-34)

The product of the feed stoichiometry ${\psi }_F$ and the CO₂ absorption efficiency ${\eta }_{C{O}_2,abs.}$ determines the actual ratio of the two reactants that enters the aqueous solution, $\psi$, which is thus:

$\psi =\frac{f_{MT}{V}_s }{Q_{in} c_{Ca,in}}={\eta }_{C{O}_2,abs.} {\psi }_F$(3-35)

The efficiency of the precipitation of CO₂ from the aqueous solution, ${\eta }_{C{O}_2,prec.}$, is defined as:

${\eta }_{C{O}_2,prec.}=\frac{r_c }{f_{MT}}$(3-36)

Finally, the CO₂ mineralization efficiency of the process with respect to CO₂, ${\eta }_{C{O}_2}$, is defined as:

${\eta }_{C{O}_2}={\eta }_{C{O}_2,abs.} {\eta }_{C{O}_2,prec. }=\frac{r_c V_s}{F_{in} y_{C{O}_2,in}}$(3-37)

whilst the overall efficiency of the process with respect to calcium, ${\eta }_{Ca}$, is calculated as:

${\eta }_{Ca}=\frac{r_c{V}_s}{Q_{in} c_{Ca,in}}$(3-38)

Note that

${\eta }_{Ca}= {\eta }_{C{O}_2}{\psi }_F$(3-39)

4 Results and Discussion

The experimental campaign published previously (Tiefenthaler and Mazzotti, 2021) provided insights about the effect of feed conditions on process efficiencies, but also particle related properties such as particle size and polymorph. Only experimental points at steady state have been considered for the parameter estimation. We want to assess whether the model presented in the previous sections captures the experimental trends qualitatively and/or quantitatively. If this is the case, one can use the model to develop a deeper understanding of the process, which goes beyond what observed experimentally. For this reason, this section is structured as follows. First, the system specific, empirical parameters $k_L$, $a_{eff}$, $A$ and $\alpha$ are estimated based on the available experimental data set, and the quantitative performance of the model will be assessed making use of parity plots and statistic quantities such the relative mean deviation. Second, once the model accuracy is assessed, a parametric study will be conducted, exploiting the model to study the key trends in terms of process performance as function of the process operating parameters.

4.1 Estimation of Model Parameters

The process model consists of a thermodynamic model, for the speciation, of material balances and of a population balance equation, as well as of kinetics constitutive equations for mass transfer and for nucleation and growth in the crystallization process. By solving the model equations, the key quantities $f_{MT}$ , $r_c$ and $L_{50}$ are calculated as function of the operating conditions. It is worth noticing that all these quantities are coupled, i.e., they are interdependent. As these quantities have been measured in our recent experimental study, the empirical model parameters $k_{\text{L }}$ and $a_{\text{eff}}$ as well as $A$ and $\alpha$ have been estimated by minimizing the sum of the squares of the difference between the calculated and the measured values of these quantities, or in other terms the sum of the mean relative deviations (MRD), which are calculated for each measured quantity as follows:

$MRD=\frac{1}{N_{\mathit{exp}} }{\displaystyle \sum _{i=1}^{N_{\mathit{exp}}}\frac{\sqrt{{\left(x_i^{\mathit{mod}\mathit{e}\mathit{l}}-x_i^{\mathit{exp}eriment}\right)}^2}}{x_i^{\mathit{exp}eriment}}};x_i=f_{MT} ;r_C;L_{50};$(4-1)

where $N_{exp}$ represents the number of experiments which are considered for estimating the parameters (exp = 16 in this work). The set of parameters reported in Table 2 has been obtained.

TABLE 2

TABLE 2. The four estimated model parameters are listed below.

The two mass transfer related parameters, $k_{\text{L }}$ and $a_{\text{eff}}$, fall in the typical ranges observed in the literature. The estimated $k_{\text{L }}$ is in the range for absorption processes (Last and Stichlmair, 2002). Furthermore, the interfacial surface area $a_{\text{eff}}$ for stirred bubble tanks varies usually between 20 and 200 m²/m³ (Levenspiel, 1999b). The values of the two parameters in the nucleation and growth rate, A and $\alpha$, must be interpreted as empirical, while the corresponding values reported in the literature have a degree of uncertainty. Therefore, we consider the values reported in the table accurate enough and acceptable (Nehrke et al., 2007).

Parity plots, shown in Figure 2, are used to illustrate the quantitative agreement between modelling and experimental results. They illustrate the experimental values (x-axis) of $f_{MT}$ (Figure 2A), $r_C$ (Figure 2B) and the volume based average particle size $L_{50}$ (Figure 2C) against the output of the model (y-axis). In case the experimental results and the model were in perfect agreement, the points would lie on the solid line with an angle of 45°. The dashed and the dotted line enclose the area with a 10% and a 25% relative deviation. Note, that $f_{MT}$, $r_c$ and $L_{50}$ are obtained through three independent measurements. In case a point falls above the solid line, the model overestimates the corresponding quantity, while on the other hand, points falling below the solid line are underestimated by the model.

FIGURE 2

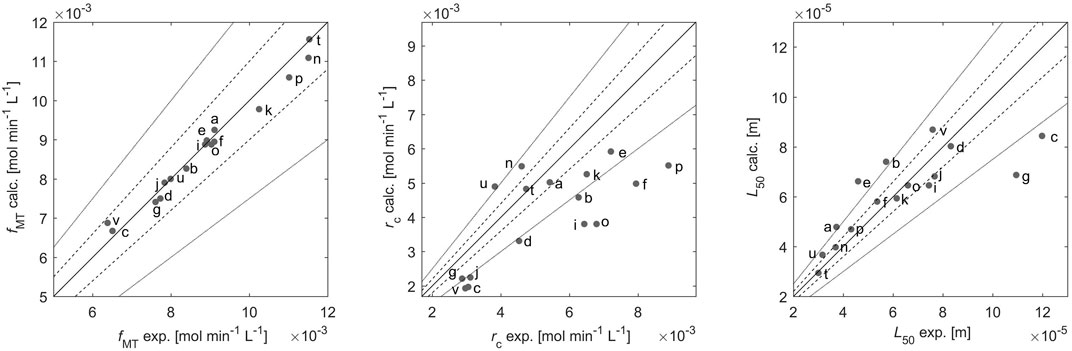
FIGURE 2. The experimental values und the modelling results of the CO₂ absorption rate $f_{MT}$, the CaCO₃ precipitation rate $r_C$ and the volume weighted average particle size $L_{50}$ are visualized in parity plots.

The experimental and modelling results for $f_{MT}$ show a very high quantitative agreement—as visualized by Figure 2A. Many points fall on the solid line, none of them exhibits a MRD exceeding 10%. This holds true for the whole range, from low (5.4 mmol min⁻¹ L⁻¹) to high (11.5 mmol min⁻¹ L⁻¹) absorption rates.

From an experimental viewpoint, the rate of CO₂ absorption is the quantity exhibiting the highest accuracy, since it is measured directly online with a previously calibrated mass spectrometer. The empirical parameters $k_{\text{L }}$ and $a_{\text{eff}}$ are usually a function of the properties of the aqueous solution, the reactor geometry and the mixing of the aqueous solution (Laakkonen, 2005). The effect of mixing is not considered by the modelling equations. The stirring speed was kept constant in the experimental campaign. Despite the variation of the inlet gas flowrate between 12.8 and 18.5 mmol min⁻¹, the effects on the mass transfer parameters seem to be small.

Moreover, Figure 2B shows that the model tends to underestimate the precipitation rate in many cases by 25% or more, possibly due to the fact that the model describes growth and nucleation in a rather empirical way, for instance without accounting for the effect of the solution composition on the growth rate; these effects might be important, as described in literature (Jung et al., 2000). Despite its relative simplicity the model manages to give a quantitative description of the precipitation rate, at least of the right order of magnitude.

The third quantity, which is measured independently, i.e., $L_{50}$, exhibits for experiments f, n, p, t, k, o, and d a very good quantitative agreement, while the other experimental points exhibit a deviation of mostly below 25% (Figure 2C). This good quantitative agreement is remarkable, since certain mechanisms, such as agglomeration, which affect the particle size in the experimental campaign (Tiefenthaler and Mazzotti, 2021), are not considered by the model.

The values of MRD obtained for each measured variable support the observations made based on Figure 2. The quantitative agreement between experimental and modelling results is the highest for $f_{MT}$, which exhibits a MRD of only 2.3%, followed by $L_{50}$ with a MRD of 16%, and finally by $r_c$ with a MRD of 27%.

It is worth noting that we have achieved a good accuracy between simulations and experiments using a primary nucleation rate expression. This might appear to be in contradiction with the fact that the model describes a continuous crystallization process, where new CaCO₃ crystals are formed in the presence of already existing CaCO₃ crystals, i.e., under conditions where secondary nucleation should be favored. We have tried to describe the experimental results using a secondary nucleation rate equation, with the specific feature that the nucleation rate is proportional to a moment of the crystal size distribution [the third moment, as in a recent paper (Chen et al., 1997)], but we have failed, i.e., always obtaining a worse fit than what shown in Figure 2 (results not presented here for brevity). We have rationalized this outcome by considering that primary particles are very small, thus making secondary nucleation by attrition, i.e., the dominant mechanism, unlikely, and that supersaturation is very high, thus favoring primary nucleation.

4.2 Model-Based Process Analysis

The model allows to compute process performance for any set of operating conditions, and thus helps to gain additional insights, far beyond the experimental evidence. For this reason the model was evaluated in hundreds of operating points (about 400), covering calcium concentrations from 0.2 to 0.35 molal, liquid feed rates from 9 to 36 g per minute and gas feed rates from 12.9 to 24 mmol per minute. The temperature, the CO₂ inlet concentration, and the NH₄NO₃ concentration in the feed solution were kept constant at 25 °C, 25% CO₂ and 0.7 molal, respectively.

4.2.1 Effect of Stoichiometric Feed Ratio ${\psi }_F$ on the CO₂ Absorption

The stoichiometric feed ratio ${\psi }_F$ determines how many moles of CO₂ per mole of calcium are fed to the reactor. Calcium carbonate precipitates to the reaction reported in Eq. 2-12, thus the reactants participate in the reaction with a stoichiometric ratio of one—to one. Figures 3A,C show the CO₂ absorption efficiency as a function of ${\psi }_F$. The variation of ${\psi }_F$ in Figure 3C was modelled by keeping $c_{Ca,in}$ constant at 0.3 molal while varying $Q_{in}$. An increase in gas feed rates reduces the CO₂ absorption efficiency—as shown by the model results (solid line) and by the experimental measurements (red and blue points). Moreover, Figure 3A shows ${\eta }_{C{O}_2,abs.}$ computed for various operating points. Dark blue corresponds to high values of $F_{in}$, while yellow corresponds to the lowest values investigated. The two trends observed previously—the linear reduction of ${\eta }_{C{O}_2,abs.}$ as soon as ${\psi }_F$ exceeds one, and the reduced ${\eta }_{C{O}_2,abs.}$ with increasing $F_{in}$, can be confirmed for a wide range of operating conditions (Figure 3A). The latter effect is an indication that in fact mass transfer is limiting the absorption rate, thus the process is not able to exploit the entire capacity of the solvent as more CO₂ is fed. Moreover, the results with respect to $\psi$ are obtained by multiplying ${\eta }_{C{O}_2,abs.}$ by ${\psi }_F$. As expected, the experimental points and the model first follow a straight line with an angle of 45°, thus indicating that CO₂ absorption is almost quantitative at ${\psi }_F$ values smaller than 1. At ${\psi }_F\sim 1$, the curve starts to saturate, and lower values of the effective stoichiometric ratios in solution, $\psi$ , are obtained as $F_{in}$ increases (Figure 3B).

FIGURE 3

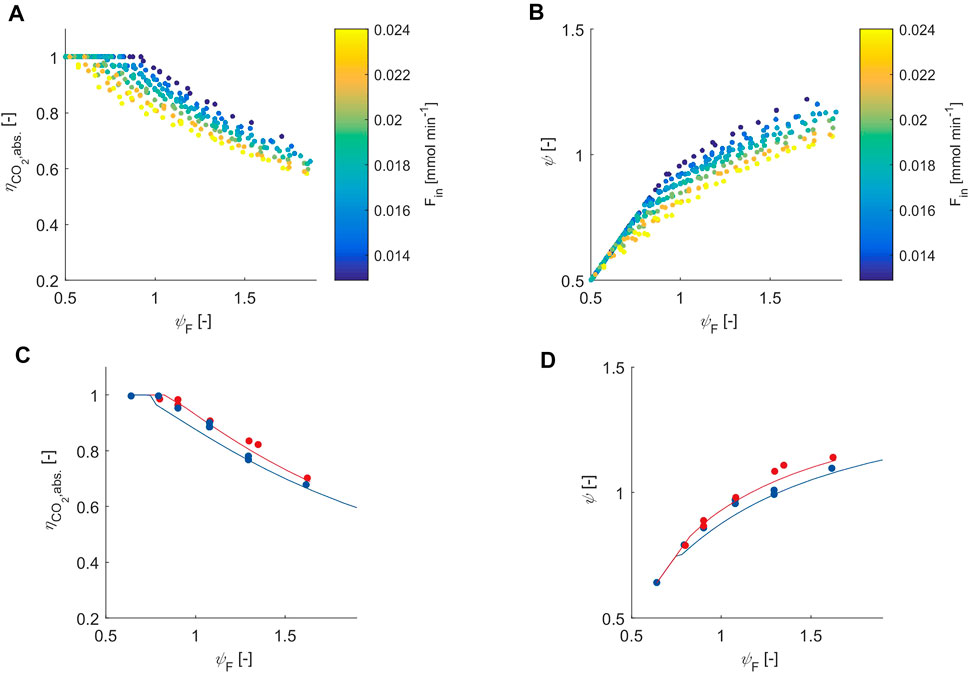
FIGURE 3. The ${\eta }_{C{O}_2,abs.}$ and $\psi$ are plotted as a function of ${\psi }_F.$ While subplot a and b visualize simulated operating points, subplot c and d combine experimental results (filled circles) with modelling results (solid lines). Red and blue data sets correspond to results obtained at 14.8 and 18.5 mmol min⁻¹. (A) CO₂ absorption efficiency. (B) $\psi$ vs. ψ_F. (C) CO₂ absorption efficiency. (D) $\psi$ vs. ${\psi }_F.$

4.2.2 Efficiency of CaCO₃ Precipitation Reaction

As CO₂ is absorbed, it speciates into bicarbonate and carbonate ions first, and either exits the reactor with the mother liquer or it reacts with calcium and precipitates as calcium carbonate. Figure 4 visualizes the calculated values of ${\eta }_{C{O}_2}$ and ${\eta }_{Ca}$ as a function of $\psi$. For a fixed calcium concentration, ${\eta }_{C{O}_2}$ exhibits a broad range of values. As $\psi$ increases, the capture efficiency tends to increase slightly, passes through a maximum and decreases again. If one fixes $\psi$, the capture efficiency increases with increasing $c_{Ca,in}$ (Figure 4A). Moreover, if one multiplies the ${\eta }_{C{O}_2}$ by ${\psi }_F$, one obtains the calcium precipitation efficiency, visualized in Figure 3B. As one increases $\psi$, while keeping the $c_{Ca,in}$ constant (e.g., following the yellow points), ${\eta }_{Ca}$ increases monotonically. At $\psi$ of about one, the calcium precipitation efficiency seems to reach a plateau. Interestingly, one can see that the capture efficiency peaks at a $\psi$ value smaller than one, while the ${\eta }_{Ca}$ exhibits its maximum at $\psi$ equal to one. Summarizing, both $\psi$ and $c_{Ca,in}$ constitute effective quantities, directly correlated to operating variables, to optimizing the process with respect to the CO₂ capture efficiency and to the Calcium precipitation efficiency.

FIGURE 4

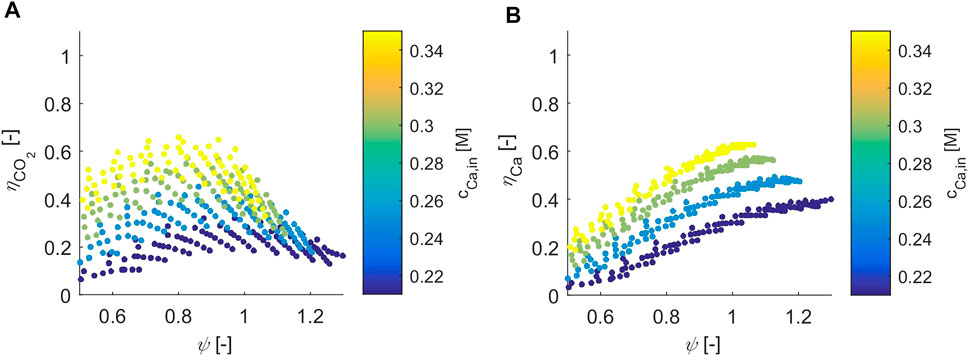
FIGURE 4. The CO₂ capture efficiency (subplot (A)) and the calcium precipitation efficiency (subplot (B)) are plotted as a function of $\psi$. The colors indicate the calcium concentration, read out at the color bar. (A) CO₂ capture efficiency. (B) Ca precipitation efficiency.

4.2.3 Liquid Speciation: Supersaturation and pH

So far, the effect of the gas flow rate and of the stoichiometry of the feed on the CO₂ absorption efficiency as well as the effect of the calcium concentration on the CO₂ capture and precipitation efficiency have been investigated. The model also allows to compute quantities that are not accessible experimentally, or at least not easily accessible, hence that have not been measured in the experimental campaign, e.g. the supersaturation of the solution, S, and the pH. In this scope, S is studied since it is the driving force for crystal nucleation and growth (it is worth reminding that S is calculated with respect to the solubility of calcite, and that the formation of different polymorphs is not described by the model for the sake of simplicity). Moreover, the pH is an important indicator of key features of the speciation, e.g., the alkalinity of the solution which gives an immediate indication whether the bicarbonate ion or the carbonate ion is dominating.

Figure 5A visualizes the supersaturation as a function of $\psi$. At low $\psi$, the supersaturation exhibits values between 70 and 105. As $\psi$ increases, this band of values becomes narrower. Moreover, at low $\psi$, the supersaturation increases with the calcium concentration, while exactly opposite results have been obtained for $\psi$ larger than one.

FIGURE 5

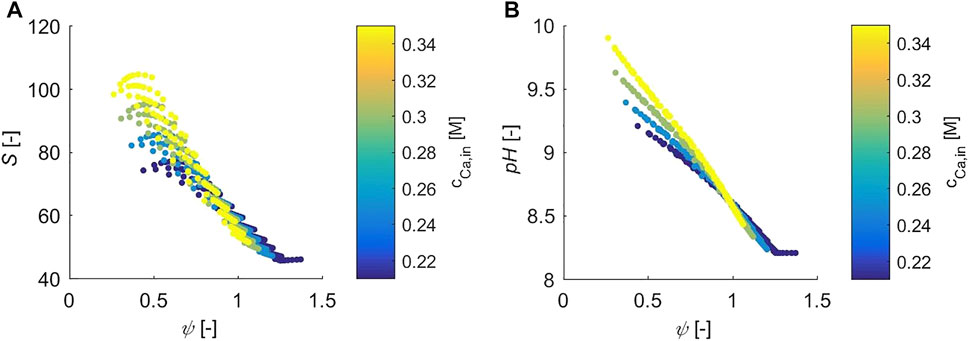
FIGURE 5. S and the pH are plotted as a function of $\psi$. The color indicates the calcium concentration. (A) S vs. $\psi$. (B) pH vs. $\psi$.

Figure 5B shows the pH of the aqueous solution as a function of $\psi$. The colors indicate the calcium concentration. As expected, the pH also shows a cross-over at a $\psi$ equal to one. It is remarkable that for a fixed calcium concentration, all operating points fall on a single line. As $\psi$ increases, the alkalinity of the solution is reduced, which results in a decreasing value of the pH. The pH values computed are typical for aqueous solutions supersaturated in calcite and vaterite (Chang et al., 2017).

4.2.4 Particle Size

Figures 6A,B visualize the average particle size $L_{50}$ as a function of $\psi$. As discussed previously (Figure 6D, grey points), experiments exhibit a general trend whereby the particle size increases monotonically with $\psi$. At a fixed $\psi$ value, smaller calcium concentration levels yield smaller particles (Figure 6A). Moreover, at a fixed $\psi$, low liquid feed rates generate larger particles (Figure 6B). This is expected, since the residence time is proportional to the reciprocal of $Q_{in}$. Long residence times usually lead to more particle growth and thus larger particles. Indeed, the solid line in Figure 6D was obtained by keeping all parameters constant, while decreasing $Q_{in}$. Under these circumstances, the model can reproduce the experimental increase of particle size with increasing residence time, also observed in Figure 6B.

FIGURE 6

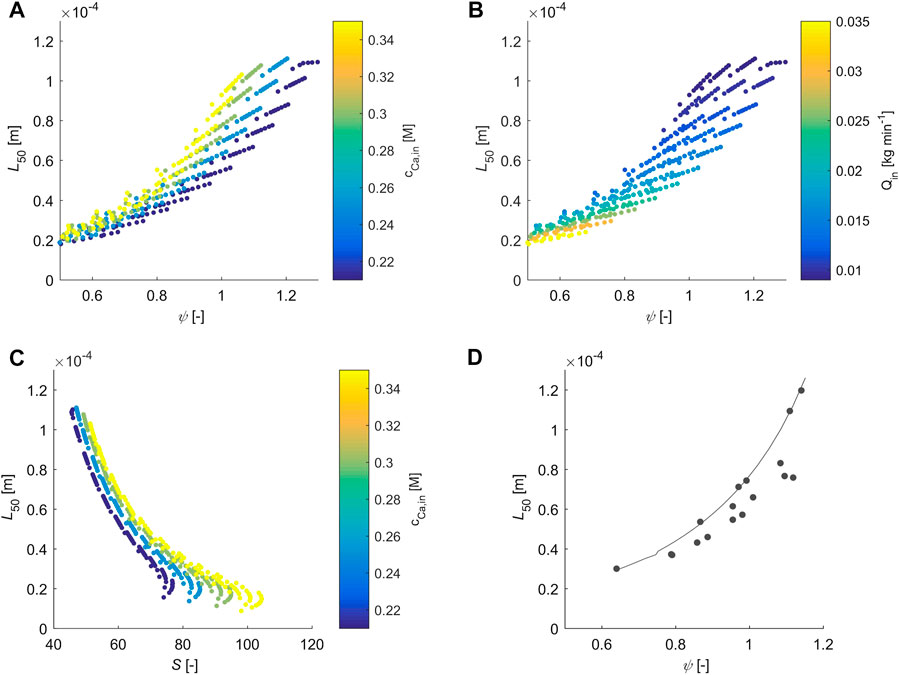
FIGURE 6. L₅₀ is plotted over Ψ and S. The filled cirles in subplot a-c correspond to simulated points, whereas the color represents the quantity specified in the with the color bar. Subplot d shows experimental results (grey circles) and modelling results (solid line), which was obtained by fixing the gas inlet flow rate to 18.5 mmol min^-1, the calcium concentration of the feed to 0.3 molal and by varying the liquid feed rate.

Finally, Figure 6C visualizes $L_{50}$ as a function of S. We observe, that for a fixed value of $c_{Ca,in}$, all points collapse on a line. Thus, at constant $c_{Ca,in}$, $L_{50}$ can be directly related to the supersaturation, S, only. Moreover, at a constant value of S, an increase in the calcium feed concentration yields larger particles. Summarizing, the particle size can be tuned by selecting the corresponding values of $Q_{in}$ and $c_{Ca,in}$.

5 Concluding Remarks

In this publication, we have developed a reactor model of a continuous crystallizer for the precipitation of calcium carbonate. The product, solid calcium carbonate, is the product of the reaction of a calcium ion with a carbonate ion followed by its transfer to the solid phase at supersaturated conditions. While the calcium is fed with the aqueous solution, CO₂ is fed as a gas to the reactor, absorbs to the solution, speciates into various ions and reacts with calcium. In order to obtain a precise description of this three-phase system, the model has to consider the thermodynamics of the system and the mechanisms of the kinetic steps of the process. The core of the model is represented by a thermodynamic description of the aqueous solution, considering the dominant reactions, as well as kinetic expressions for the rate of CO₂ mass transfer and the rate of solid formation. These expressions are embedded into material balances for the gas, liquid and solid phase—obtaining a system of equations which can be solved numerically.

In a next step, system specific empirical parameters, which are an integral part of the kinetic rate expressions, have been estimated making use of experimental data obtained in previously published experiments. In specific, the rate of CO₂ mass transfer, the rate of solid formation and the volume weighted average particle size have been used for the parameter estimation. The experimentally and simulated rate of CO₂ mass transfer show a very high quantitative agreement, while the simulated results of the rate of solid formation show a reasonal agreement with experimental results. Surprisingly, and despite its empirical nature and its relative simplicity, the model manages to describe the particle size rather well—although certain mechanism which conventionally affect the particle size, such as particle agglomeration, are not considered by the model. Furthermore, we identified with the help of the model that primary nucleation is dominant over secondary nucleation. This may sound counter intuitive, however the combined effect of the formation of small primary particles and of the occurrence of high supersaturation levels makes such conclusion plausible.

The model was used to compute many potential operating points in order to obtain an in-depth insight into the mechanisms of the process. Results show, that while the CO₂ absorption efficiency is mainly effected by the feed stoichiometry and the gas feed rate, the CO₂ capture and Ca precipitation efficiency exhibit the highest sensitivity towards the calcium concentration of the feed and the ratio of reactants in the aqueous solution. As expected, the liquid feed rate, indirectly proportional to the residence time of the suspension in the aqueous solution, is indirectly proportional to the particle size. Moreover, there is a strong dependency between the particle size and the supersaturation in solution, where a higher supersaturation yields smaller particles, and vice versa.

The obtained results—a good description of the rates as well as of the particle properties—is very encouraging, not the least because relatively simple empirical expressions manage to describe a highly complex process. Our work did not stop with the development of the presented model. At the time being, there is an Innosuisse supported and a Horizon 2020 project, which have the aim to advance the maturity of the technology towards TRL 7. In the scope of this projects, concrete fines as well as other alkaline industrial minerals will serve as a source for calcium. The use of such a model helps to design and conduct targeted experimental campaigns, which contribute to enhance the maturity and the potential of the process. Moreover, the reactor model will be an integral part of an overall process model—which is currently under development—describing a novel pH swing process circulating an aqueous solution between a dissolution and a precipitation reactor and accomplishing the so called indirect carbonation of a Ca-bearing precursor, e.g., powder obtained from recycled concrete. The model will be used to conduct a techno-economic and environmental assessment of the new technology.

Novelty—Contribution to Scientific Literature

- Advanced model of a continuous carbonation reactor with a gas-liquid and solid rate.

- Comparison of primary and secondary nucleation in the space of CO₂ mineralization.

- Combining both CO₂ absorption and crystal growth knowhow for developing a carbonation reactor model.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JT conducted the work presented and wrote the manuscript. MM was involve in many detailed discussions about the content of the manuscript, reviewing and editing it.

Funding

This research was partially funded by the Swiss Competence Centre for Energy Research—Efficiency Industrial Processes and partially by ETH Zurich.

Conflict of Interest

JT: PhD student in the Separation Processes Laboratory at ETH Zurich and Co-founder, member of the board and shareholder of the ETH-Spinoff neustark, which aims at scaling up and commercializing the presented technology. MM: Professor of the Separation Processes Laboratory at ETH Zurich and member of the advisory board of the ETH-Spinoff neustark.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to acknowledge the Swiss Competence Centre for Energy Research—efficiency industrial processes for founding the research activities on this topic. Besides that, we want to thank the ETH Zurich and thus the Swiss Federation for enabling such a research environment without limits. Beyond that, I want to thank Daniel Trottmann for his advice and hands-on support in constructing the setup, Sarah Kienast and Markus Huber for supporting me with the analytics and my predecessors Mischa Repmann and Subrahmaniam Hariharan for preparing the ground for these research activities. Furthermore, I want to thank Jose Francisco Perez Calvo giving me a hand in developing the CO₂ absorption model.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fceng.2022.849988/full#supplementary-material

Footnotes

¹https://www-gs.llnl.gov/energy-homeland-security/geochemistry

References

Abanades, J. C., Rubin, E. S., Mazzotti, M., and Herzog, H. J. (2017). On the Climate Change Mitigation Potential of CO₂ Conversion to Fuels. Energy Environ. Sci. 10 (12), 2491–2499. doi:10.1039/c7ee02819a

CrossRef Full Text | Google Scholar

Alvarez, A. J., Singh, A., and Myerson, A. S. (2011). Crystallization of Cyclosporine in a Multistage Continuous MSMPR Crystallizer. Cryst. growth & Des. 11 (10), 4392–4400. doi:10.1021/cg200546g

CrossRef Full Text | Google Scholar

Anantharaman, R. B., and David, B. (2017). CEMCAP Framework for Comparative Techno-Economic Analysis of CO₂ Capture from Cement Plants.

Google Scholar

Becattini, V., Gabrielli, P., and Mazzotti, M. (2021). Role of Carbon Capture, Storage, and Utilization to Enable a Net-Zero-CO₂-Emissions Aviation Sector. Ind. Eng. Chem. Res. 60 (18), 6848–6862. doi:10.1021/acs.iecr.0c05392

CrossRef Full Text | Google Scholar

Brečević, L. (2007). On Calcium Carbonates: From Fundamental Research to Application. Zagreb, Croatia: CROATICA CHEMICA ACTA.

Google Scholar

Chang, R., Choi, D., Kim, M. H., and Park, Y. (2017). Tuning Crystal Polymorphisms and Structural Investigation of Precipitated Calcium Carbonates for CO₂ Mineralization. ACS Sustain. Chem. Eng. 5 (2), 1659–1667. doi:10.1021/acssuschemeng.6b02411

CrossRef Full Text | Google Scholar

Chen, P.-C., Tai, C. Y., and Lee, K. (1997). Morphology and Growth Rate of Calcium Carbonate Crystals in a Gas-Liquid-Solid Reactive Crystallizer. Chem. Eng. Sci. 52 (21-22), 4171–4177. doi:10.1016/s0009-2509(97)00259-5

CrossRef Full Text | Google Scholar

Darde, V., van Well, W. J. M., Fosboel, P. L., Stenby, E. H., and Thomsen, K. (2011). Experimental Measurement and Modeling of the Rate of Absorption of Carbon Dioxide by Aqueous Ammonia. Int. J. Greenh. Gas Control 5 (5), 1149–1162. doi:10.1016/j.ijggc.2011.07.008

CrossRef Full Text | Google Scholar

Davey, R. G., J. (2000). From Molecules to Crystallizers. Manchester: Oxford Chemistry Primers.

Google Scholar

Durmaz, T. (2018). The Economics of CCS: Why Have CCS Technologies Not Had an International Breakthrough? Renew. Sustain. Energy Rev. 95, 328–340. doi:10.1016/j.rser.2018.07.007

CrossRef Full Text | Google Scholar

Flaten, E. M., Seiersten, M., and Andreassen, J.-P. (2009). Polymorphism and Morphology of Calcium Carbonate Precipitated in Mixed Solvents of Ethylene Glycol and Water. J. Cryst. Growth 311 (13), 3533–3538. doi:10.1016/j.jcrysgro.2009.04.014

CrossRef Full Text | Google Scholar

Furre, A.-K., Eiken, O., Alnes, H., Vevatne, J. N., and Kiær, A. F. (2017). 20 Years of Monitoring CO₂-injection at Sleipner. Energy procedia 114, 3916–3926. doi:10.1016/j.egypro.2017.03.1523

CrossRef Full Text | Google Scholar

Gardarsdottir, S., De Lena, E., Romano, M., Roussanaly, S., Voldsund, M., Pérez-Calvo, J.-F., et al. (2019). Comparison of Technologies for CO₂ Capture from Cement Production-Part 2: Cost Analysis. Energies 12 (3), 542. doi:10.3390/en12030542

CrossRef Full Text | Google Scholar

Hariharan, S. B. (2017). The Kinetics of CO₂ Mineralization Processes Using Thermally Activated Serpentine. Diss. ETH No. 24211.

Google Scholar

Hariharan, S., and Mazzotti, M. (2017). Growth Kinetics of Synthetic Hydromagnesite at 90 °C. Cryst. Growth & Des. 17 (1), 317–327. doi:10.1021/acs.cgd.6b01546

CrossRef Full Text | Google Scholar

Hariharan, S., and Mazzotti, M. (2017). Kinetics of Flue Gas CO₂ mineralization Processes Using Partially Dehydroxylated Lizardite. Chem. Eng. J. 324, 397–413. doi:10.1016/j.cej.2017.05.040

CrossRef Full Text | Google Scholar

Hariharan, S., Repmann-Werner, M., and Mazzotti, M. (2016). Dissolution of Dehydroxylated Lizardite at Flue Gas Conditions: III. Near-Equilibrium Kinetics. Chem. Eng. J. 298, 44–54. doi:10.1016/j.cej.2016.03.144

CrossRef Full Text | Google Scholar

IEA (2018). Low-Carbon Transition in the Cement Industry. Geneva: Technology Roadmap.

Google Scholar

Initiative, G. C. (2016). Global Roadmap for Implementing CO₂ Utilization. USA: University of Michigan.

Google Scholar

Institute, G. C. (2019). Global Status of CCS 2019.

Google Scholar

IPCC (2005). Carbon Dioxide Captuture and Storage.

Google Scholar

IPCC (2018). Global Warming of 1.5°C. Special report.

Google Scholar

IPCC (2019). Summary for Policymakers. in: Climate Change and Land: An IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes interrestrial Ecosystems.

Google Scholar

IPCC (2014). SynthesisReport: Summary for Policymakers. Geneva: Fifth Assessment Report.

Google Scholar

Janssens-Maenhout, G., Crippa, M., Guizzardi, D., Muntean, M., Schaaf, E., Dentener, F., et al. (2017). Global Atlas of the Three Major Greenhouse Gas Emissions for the Period 1970-2012. Earth System Science Data. essd-2017-79.

Google Scholar

Jun, Y.-S., Kim, D., and Neil, C. W. (2016). Heterogeneous Nucleation and Growth of Nanoparticles at Environmental Interfaces. Acc. Chem. Res. 49 (9), 1681–1690. doi:10.1021/acs.accounts.6b00208

PubMed Abstract | CrossRef Full Text | Google Scholar

Jung, W. M., Kang, S. H., Kim, W.-S., and Choi, C. K. (2000). Particle Morphology of Calcium Carbonate Precipitated by Gas-Liquid Reaction in a Couette-Taylor Reactor. Chem. Eng. Sci. 55 (4), 733–747. doi:10.1016/s0009-2509(99)00395-4

CrossRef Full Text | Google Scholar

Kazmierczak, T. F., Tomson, M. B., and Nancollas, G. H. (1982). Crystal Growth of Calcium Carbonate. A Controlled Composition Kinetic Study. J. Phys. Chem. 86 (1), 103–107. doi:10.1021/j100390a020

CrossRef Full Text | Google Scholar

Laakkonen, M. (2005). Local Bubble Size Distributions, Gas–Liquid Interfacial Areas and Gas Holdups in a Stirred Vessel with Particle Image Velocimetry. Chem. Eng. J. 109 (1-3), 37–47. doi:10.1016/j.cej.2005.03.002

CrossRef Full Text | Google Scholar

Last, W., and Stichlmair, J. (2002). Determination of Mass Transfer Parameters by Means of Chemical Absorption. Chem. Eng. Technol. 25 (4), 385–391. doi:10.1002/1521-4125(200204)25:4<385::aid-ceat385>3.0.co;2-l

CrossRef Full Text | Google Scholar

Levenspiel, O. (1999). Chem. React. Eng., 523–539.

Levenspiel, O. (1999). Chemical Reaction Engineering. Ind. Eng. Chem. Res. 38 (11), 4140–4143. doi:10.1021/ie990488g

CrossRef Full Text | Google Scholar

Mac Dowell, N., Fennell, P. S., Shah, N., and Maitland, G. C. (2017). The Role of CO₂ Capture and Utilization in Mitigating Climate Change. Nat. Clim. Change 7 (4), 243–249. doi:10.1038/nclimate3231

CrossRef Full Text | Google Scholar

Maeda, M., and Kato, K. (1995). Dissociation Constants of Ammonium Ion and Activity Coefficients of Ammonia in Ammonium Nitrate Solutions. J. Chem. Eng. Data 40 (1), 253–256. doi:10.1021/je00017a054

CrossRef Full Text | Google Scholar

Mattila, H.-P., Hudd, H., and Zevenhoven, R. (2014). Cradle-to-gate Life Cycle Assessment of Precipitated Calcium Carbonate Production from Steel Converter Slag. J. Clean. Prod. 84, 611–618. doi:10.1016/j.jclepro.2014.05.064

CrossRef Full Text | Google Scholar

Mattila, H.-P., and Zevenhoven, R. (2014). Design of a Continuous Process Setup for Precipitated Calcium Carbonate Production from Steel Converter Slag. ChemSusChem 7 (3), 903–913. doi:10.1002/cssc.201300516

PubMed Abstract | CrossRef Full Text | Google Scholar

Mattila, H.-P., and Zevenhoven, R. (2014). “Production of Precipitated Calcium Carbonate from Steel Converter Slag and Other Calcium-Containing Industrial Wastes and Residues,” in Advances in Inorganic Chemistry (Elsevier), 347–384. doi:10.1016/b978-0-12-420221-4.00010-x

CrossRef Full Text | Google Scholar

Nancollas, G. H., and Reddy, M. M. (1971). The Crystallization of Calcium Carbonate. II. Calcite Growth Mechanism. J. colloid interface Sci. 37 (4), 824–830. doi:10.1016/0021-9797(71)90363-8

CrossRef Full Text | Google Scholar

Nations, U. (2015). Paris Agreement.

Google Scholar

Nehrke, G., Reichart, G. J., Van Cappellen, P., Meile, C., and Bijma, J. (2007). Dependence of Calcite Growth Rate and Sr Partitioning on Solution Stoichiometry: Non-kossel Crystal Growth. Geochimica Cosmochimica Acta 71 (9), 2240–2249. doi:10.1016/j.gca.2007.02.002

CrossRef Full Text | Google Scholar

Ostovari, H., Sternberg, A., and Bardow, A. (2020). Rock ‘n’use of CO 2: Carbon Footprint of Carbon Capture and Utilization by Mineralization. Achen: Sustainable Energy & Fuels.

Google Scholar

Pinsent, B. R. W., Pearson, L., and Roughton, F. J. W. (1956). The Kinetics of Combination of Carbon Dioxide with Ammonia. Trans. Faraday Soc. 52, 1594–1598. doi:10.1039/tf9565201594

CrossRef Full Text | Google Scholar

Pohorecki, R., and Moniuk, W. (1988). Kinetics of Reaction between Carbon Dioxide and Hydroxyl Ions in Aqueous Electrolyte Solutions. Chem. Eng. Sci. 43 (7), 1677–1684. doi:10.1016/0009-2509(88)85159-5

CrossRef Full Text | Google Scholar

Puxty, G., Rowland, R., and Attalla, M. (2010). Comparison of the Rate of CO₂ Absorption into Aqueous Ammonia and Monoethanolamine. Chem. Eng. Sci. 65 (2), 915–922. doi:10.1016/j.ces.2009.09.042

CrossRef Full Text | Google Scholar

Ramkrishna, D. (2000). Population Balances: Theory and Applications to Particulate Systems in Engineering. Elsevier.

Google Scholar

Reis, M. C., Sousa, M. F. B., Alobaid, F., Bertran, C. A., and Wang, Y. (2018). A Two-Fluid Model for Calcium Carbonate Precipitation in Highly Supersaturated Solutions. Adv. Powder Technol. 29 (7), 1571–1581. doi:10.1016/j.apt.2018.03.022

CrossRef Full Text | Google Scholar

Said, A., Laukkanen, T., and Järvinen, M. (2016). Pilot-scale Experimental Work on Carbon Dioxide Sequestration Using Steelmaking Slag. Appl. energy 177, 602–611. doi:10.1016/j.apenergy.2016.05.136

CrossRef Full Text | Google Scholar

Sanna, A., Uibu, M., Caramanna, G., Kuusik, R., and Maroto-Valer, M. M. (2014). A Review of Mineral Carbonation Technologies to Sequester CO₂. Chem. Soc. Rev. 43 (23), 8049–8080. doi:10.1039/c4cs00035h

PubMed Abstract | CrossRef Full Text | Google Scholar

Sutter, D., Van der Spek, M., and Mazzotti, M. (2019). 110th Anniversary: Evaluation of CO₂-based and CO₂-free Synthetic Fuel Systems Using a net-zero-CO2-emission Framework. Ind. Eng. Chem. Res. 58 (43), 19958–19972. doi:10.1021/acs.iecr.9b00880

CrossRef Full Text | Google Scholar

Thomsen, K., and Rasmussen, P. (1999). Modeling of Vapor-Liquid-Solid Equilibrium in Gas-Aqueous Electrolyte Systems. Chem. Eng. Sci. 54 (12), 1787–1802. doi:10.1016/s0009-2509(99)00019-6

CrossRef Full Text | Google Scholar

Tiefenthaler, J., and Mazzotti, M. (2021). Frontiers in Chemical Engineering. submitted.Experimental Investigation of a Continuous Carbonation Reactor for CaCO₃ Precipitation

Google Scholar

Tiefenthaler, J. (2021). Technological Demonstration and Life Cycle Assessment of a Negative Emission Value Chain in the Swiss Concrete Sector. Front. Clim. 3 (128). doi:10.3389/fclim.2021.729259

CrossRef Full Text | Google Scholar

Versteeg, G. F., and Van Swaaij, W. P. M. (1988). Solubility and Diffusivity of Acid Gases (Carbon Dioxide, Nitrous Oxide) in Aqueous Alkanolamine Solutions. J. Chem. Eng. Data 33 (1), 29–34. doi:10.1021/je00051a011

CrossRef Full Text | Google Scholar

Vučak, M. (2002). A Study of Carbon Dioxide Absorption into Aqueous Monoethanolamine Solution Containing Calcium Nitrate in the Gas–Liquid Reactive Precipitation of Calcium Carbonate. Chem. Eng. J. 87 (2), 171–179.

Google Scholar

Werner, M., Hariharan, S., Zingaretti, D., Baciocchi, R., and Mazzotti, M. (2014). Dissolution of Dehydroxylated Lizardite at Flue Gas Conditions: I. Experimental Study. Chem. Eng. J. 241, 301–313. doi:10.1016/j.cej.2013.12.057

CrossRef Full Text | Google Scholar

Werner, M., Hariharan, S., and Mazzotti, M. (2014). Flue Gas CO₂ Mineralization Using Thermally Activated Serpentine: from Single- to Double-step Carbonation. Phys. Chem. Chem. Phys. 16 (45), 24978–24993. doi:10.1039/c4cp02786h

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolery, T. (2002). EQ3/6 - Software for Geochemical Modeling Version 8.0, UCRL-CODE-2003-009. Livermore, California: Lawrence Livermore National Laboratory.

Google Scholar

Wolthers, M., Nehrke, G., Gustafsson, J. P., and Van Cappellen, P. (2012). Calcite Growth Kinetics: Modeling the Effect of Solution Stoichiometry. Geochimica Cosmochimica Acta 77, 121–134. doi:10.1016/j.gca.2011.11.003

CrossRef Full Text | Google Scholar

Zeng, Q., Guo, Y., Niu, Z., and Lin, W. (2011). Mass Transfer Coefficients for CO₂ Absorption into Aqueous Ammonia Solution Using a Packed Column. Ind. Eng. Chem. Res. 50 (17), 10168–10175. doi:10.1021/ie101821b

CrossRef Full Text | Google Scholar

Nomenclature

$a_{eff}$ effective interfacial area (m²/m³)

$a_i$ activity of aqueous solute i (-)

A pre exponential factor of the nucleation rate (1/m³/s)

b number of experiments (-)

$c_{i,in}$ apparent (or total) concentration of aqueous solute i entering the reactor (mol/kg)

$c_i$ apparent (or total) concentration of aqueous solute i in the reactor (mol/kg)

$D_A$ diffusivity of component A (m²/s)

$E$ enhancement factor (-)

$E_i$ enhancement factor for infinitely fast reaction (-)

$f\left(L\right)$ particle size distribution (1/m⁴)

$f_{C{O}_2}$ fugacity of CO₂ (bar)

$F_{in}$ molar flow rate of the gas entering the reactor (mol/s)

$F_{out}$ molar flow rate of the gas exiting the reactor (mol/s)

$f_{MT}$ CO₂ capture rate (mol/s/m³)

$G$ growth rate (m/s)

$H_{C{O}_2}$ Henry constant (bar kg/mol)

$I$ ionic strength (mol/kg)

$J$ rate of particle nucleation (1/m³/s)

$k_A$ reaction rate constant of component A (m³/mol/s)

$k_B$ Boltzmann constant (m² kg/s²/K)

$k_c$ growth rate constant (m/s)

$K_i$ equilibrium constant (-)

$k_L$ liquid phase mass transfer coefficient (m/s)

$K_{SP}$ solubility product of calcite (-)

$k_V$ volume shape factor (-)

$L$ characteristic length of calcite particle (m)

${\psi }_F$ molar ratio of carbon to calcium feed rate (-)

$\psi$ effective ratio of reactants in liquid phase (-)

$M_{{\text{CaCO}}_3}$ molar mass of calcite (kg/mol)

$M_H$ Hatta number (-)

$m_w$ mass of water in the reactor (kg)

$n_{{\text{CaCO}}_3}$ total number of moles of CaCO₃ in the reactor suspension (mol)

n stirring rate

$n_{tot}$ total number of moles of gas in reactor overhead (mol)

$P$ total pressure (Pa)

$Q,Q_{in}$ flow rate of aqueous solution (kg/s)

$R$ ideal gas constant (J/mol/K)

$r_{min}$ rate of limiting reactant (mol/s/m³)

$r_c$ precipitation rate (mol/s/m³)

$S_c$ supersaturation with respect to calcite (-)

T temperature of the aqueous solution (K)

$t$ time (min)

$V_R$ volume of the reactor (m³)

$V_s$ volume of the liquid phase (m³)

$y_i$ mole fraction of component i in the reactor gas phase (-)

$y_{i,in}$ mole fraction of component i in the gas entering the reactor (-)

$y_{i,out}$ mole fraction of component i in the gas exiting the reactor (-)

$z_i$ charge of the ion i (-)

τ residence time of the aqueous solution (s)

${\eta }_{C{O}_2}$ CO₂ mineralization efficiency (-)

${\eta }_{C{O}_2, abs.}$ CO₂ absorption efficiency (-)

${\eta }_{Ca}$ precipitation efficiency of Ca (-)

$\alpha \beta \gamma \Delta$ parameter (-)

Ρ density of the solution (kg H₂O/m³)

ρ_c density of calcite (kg/m³)

$\sigma$ surface energy of CaCO₃ (N/m)

$\vartheta$ molecular volume of CaCO₃ (m³)

${\gamma }_i$ activity coefficient of ion or molecule i (1/M)

${\mu }_2$ 2nd moment (m² crystal/m³ aqueous solution)

${\mu }_3$ 3rd moment (m³ crystal/m³ aqueous solution)