- Laboratoire de Génie Chimique, Université de Toulouse, CNRS, INP, UPS, Toulouse, France
This work is part of the ongoing development of the attrition-leaching carbonation process, a single-step aqueous carbonation technology that integrates a stirred bead mill. The principle of the attrition-leaching carbonation process is to continuously refresh the surfaces of reactive particles so that leaching can proceed unimpeded, yielding enhanced carbonation kinetics and yield. Invariably, attrition-leaching carbonation experiments carried out under controlled temperature and CO2 partial pressure conditions with different silicate-rich carbonation feedstocks - natural ores and nickel slags - show a carbonation yield that tends towards a plateau 20–50% below the stoichiometric yield. This repeatable behaviour raises the question as to whether the carbonation limitation is due to specific equilibrium side reactions of the carbonation feedstock or to a kinetic limitation of the attrition-leaching carbonation process. To try to provide some answers to this puzzling question, this reflexive paper implements a “thermo-kinetic” modelling methodology based upon geochemical equilibrium simulations and particle reaction models. The results obtained indicate that the observed slowing down of the carbonation process can be explained either by the formation of Mg- and/or Fe-rich silicates that precipitate at the expense of carbonates, or by a decrease in the efficiency of the attrition process over time. Indeed, either one of these mechanisms could explain the observed behaviour of the attrition-leaching carbonation process. However, the cross comparison of different data sources pleads in favour of the attrition-leaching carbonation performance being limited by the attrition process. Pending further confirmation, this tentative conclusion suggests that further development of the attrition-leaching carbonation process requires new knowledge about its inner workings, and that there may be ways to optimize the performance of this process beyond that based on standard stirred bead mill operating rules.
Introduction
For several years now, aqueous mineral carbonation has stood out not only as a viable solution for CO2 sequestration in the form of stable carbonates, but also as a way of treating or recovering little-exploited minerals or mining industry wastes (Huijgen et al., 2005; Sipilä et al., 2008; Bodor et al., 2013; Sanna and Maroto-Valer, 2017; Veetil and Hitch, 2020). This process indeed allows the passivation or dilution of hazardous substances such as or asbestos or heavy metals (Gadikota et al., 2014), the feedstock beneficiation as aggregates or fillers (for road construction, concrete making, soil improvement, etc.) or, even better, for the synthesis of building materials with improved mechanical properties and reduced carbon footprint (National Academies of Sciences, Engineering, and Medicine, 2019). The Carboscories/Carboval projects (Bourgeois et al., 2020) aim to contribute to the latter by valorising slags from New Caledonias nickel industry as mineral additions and hydraulic binders. While their chemical composition is rather uniform from one industrial source to another, nickel slags exhibit different mineralogy depending on their cooling conditions. For instance, the air-dried carbonation feedstock considered in the present work is mainly crystallized magnesium silicates with iron and aluminium impurities, while other slags obtained from water quenching are mainly composed of vitreous phases. Not only does the mineralogy control the aqueous solubility of the slag, but it also affects the nature of the solid products that may form during carbonation at the expense of the desirable ones, namely carbonates and amorphous silica. Moreover, solid products (through dissolution/precipitation mechanisms) precipitate on the surface of the slag particles and form surface layers of variable thickness and permeability that limit the accessibility of the protons to the unreacted core and yield low conversion rates. The attrition-leaching carbonation process (Julcour et al., 2015; Bourgeois et al., 2020) has made it possible to remove all or part of these diffusion barriers, enabling the conversion of more than 50% of carbonatable species in about 10 h. This process uses the direct aqueous carbonation route, whose chemistry relies on two main features: 1) gaseous CO2 is the only reactant; 2) CO2 hydrolysis provides the proton source for the dissolution of the solid phase in water (see Figure 1). Attrition-leaching carbonation is operated inside a stirred bead mill, a proven industrial process for producing ultrafine particles (Jankovic, 2000). Optimization of the attrition-leaching carbonation process is related to matching surface layer formation and attrition rates. To this end, a better understanding of the process features is required. This is actually a complex system with several concomitant mechanisms (see Figure 1): attrition, but probably also particle breakage, chemical attack of the reactive feedstock phases, gas dissolution and precipitation of product phases.
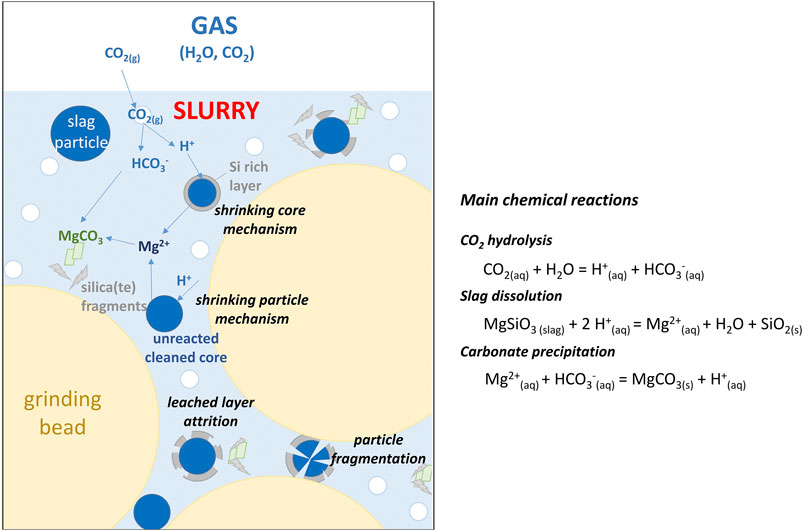
FIGURE 1. Schematics of concomitant mechanisms during attrition-leaching carbonation in a stirred bead mill.
Problem Statement
The authors have envisioned the attrition-leaching carbonation as a process that can be tuned to reach the thermodynamic carbonation limits of the carbonation feedstock, notwithstanding the kinetics involved with reaching this limit. As shown in Figure 2A for natural ores (which are all ferromagnesian silicates with various degrees of serpentinisation) and in Figure 2B for nickel slags, they have shown that attrition-leaching carbonation experiments yield largely material insensitive carbonation kinetics under nearly identical grinding conditions (same agitator and agitation speed, 180°C, 20 bar of CO2). This observation confirms the robustness of the attrition-leaching carbonation process, keeping in mind that carbonation yield would not exceed 10% with these materials should the attrition component not be coupled with the reaction.
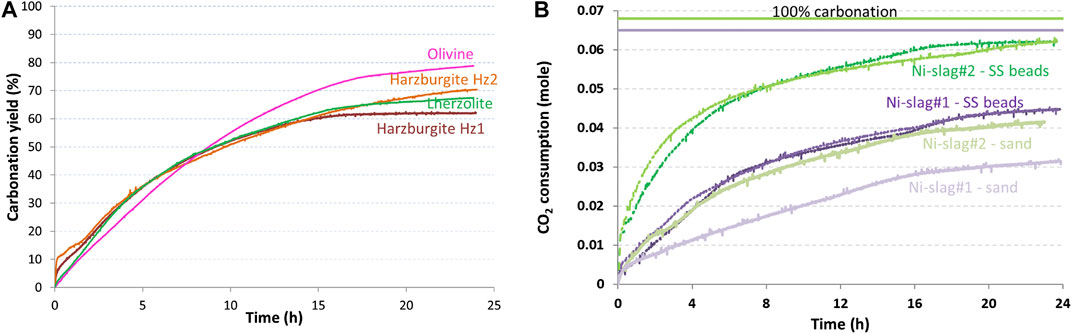
FIGURE 2. Extent of carbonation of different materials (at 180°C, 20 bar of CO2 and 90 g/Lwater) during the hybrid carbonation process: (A) ores (using 1–2 mm Al2O3 beads for attrition) and (B) nickel slags (using 1.25–1.6 mm quartz sand or 1.6 mm stainless steel (SS) beads for attrition).
However, invariably, the carbonation curves tend towards a plateau that is 20–50% below the stoichiometric carbonation yield. These observations lead to the main question that lies behind this paper: is this early slowing down in carbonation extent due to a thermodynamic limit linked with the carbonation feedstocks, or is it a intrinsic feature of the attrition-leaching carbonation process, or both?
Moreover, Figure 2B shows that grinding medium selection, all operating conditions being equal, yields different carbonation plateaus. Stirred mill operating conditions, and grinding medium selection in particular, are thus clearly part of the equation. Bringing elements of answer to this consistent behaviour of attrition-leaching carbonation in a stirred bead mill is the objective of this reflexive paper.
The paper uses a “thermo-kinetic” modelling methodology, under the assumption that both gas dissolution and precipitation of product phases are rapid phenomena compared to leaching and attrition processes. The thermodynamic component of the methodology uses geochemical equilibrium modelling to predict the phases that can form under given temperature and pressure conditions (Cassayre et al., 2016). The kinetic component uses traditional shrinking core and/or shrinking particle models for reacting particles. Predictions are assessed against experimental data obtained in a 300 ml laboratory stirred mill with a fully crystallized pyroxene-rich nickel slag whose leaching kinetics can be compared to published data (Oelkers and Schott, 2001).
Materials and Methods
Processed Material
The carbonation feedstock is a magnesium silicate slag from a nickel pyrometallurgical plant that operates in New-Caledonia (Koniambo Nickel SAS). As this slag cools down naturally under ambient conditions, its structure is fully crystallized. It is made of protoenstatite, clinoenstatite and forsterite. Its composition in wt.% of main metal oxides, measured by X-ray fluorescence, is SiO2: 52.1, MgO: 28.8 and Fe2O3: 14.4 (Augé and Touzé, 2015). It also exhibits traces of aluminium, manganese and calcium (Al2O3: 1.9%, CaO: 0.46%, MnO: 0.35%). This composition was found to be consistent with local analyses obtained from SEM-EDX elemental mapping of the particles (see Supplementary Table S1). As received samples were jaw crushed, then ground in a dry ball mill to minus 100 µm. The Particle Size Distribution (PSD) was measured by laser diffraction and yielded d10, d50, d90, and d32 values of 7.5, 39.0, 100.5, and 12.7 µm respectively (see Figure 3). Morphological analysis of 100,000 particles using an optical microscope (Morphologi G3, Malvern Instruments) gave an average HS (high sensitivity) circularity of 0.83 for their projected area (against 1.0 for a perfect circle). A closer look at the particles using both SEM and TEM images showed that particle surface exhibits some degree of roughness (see Supplementary Figure S1). This is in line with the fact that the specific surface area measured by nitrogen adsorption (1.25 m2 g−1) is about ten times higher than that calculated from the PSD assuming smooth spherical particles (0.13 m2 g−1).
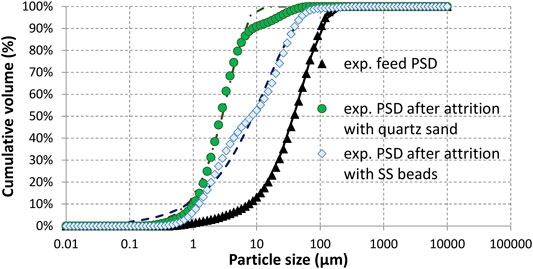
FIGURE 3. Cumulative particle size distributions measured by laser diffraction (symbols) and corresponding Rosin-Rammler fit (lines) for feed and product particles after 24 h of attrition-leaching using stainless steel beads and quartz sand.
A rotary sampler was used to produce equal mass (7.2 g) samples for carbonation testing. Based on Fe and Mg contents in the samples, the maximum amount of carbonate phases (FeCO3 and MgCO3) is 0.0645 mole (or 5.85 g), and up to 0.0655 mole when including Ca and Mn. The other elements (Si and Al) do not form carbonate compounds.
Experimental Set-Up and Protocol
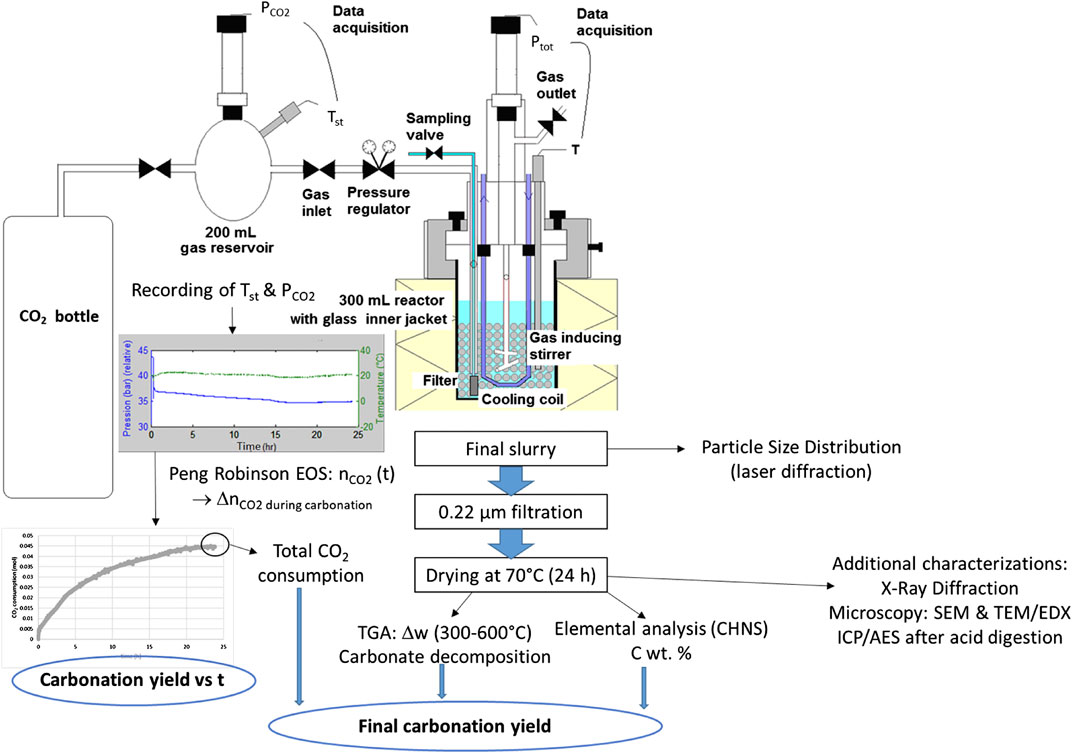
The carbonation experiments were performed in a 300 ml self-made stirred bead mill (Figure 4), built using an autoclave vessel suited to withstand pressure and temperature. Agitation was provided by a pin-type gas-inducing impeller. The mill tank was half-filled with millimetric grinding beads.
This investigation used either quartz sand (HN 0.6/1.6 from SIFRACO, 99% SiO2, 1.25–1.6 mm, 215 g) or AISI 420C stainless steel beads (1.6 mm in diameter, 675 g) as grinding media. Their density is 2.6 and 7.7 g cm−3, respectively, against 3.2 g cm−3 for the slag. Quartz sand exhibits hardness of 7 on the Mohs’ scale vs. 5–6 for enstatite.
The reactor was operated under controlled temperature and total pressure by means of a pressure regulator connected to a 200 ml CO2 supply tank. The latter was instrumented with temperature (Tst) and pressure (PCO2) gauges. The number of moles of CO2 inside the tank was deduced from PCO2 and Tst values using Peng-Robinson’s equation of state, which gave the instantaneous carbonation rate of the system. The duration of carbonation tests used in this work was 24 h. Once separated from grinding particles (on 800 µm sieve), filtered (on 0.22 µm filter) and oven dried at 70°C for 24 h, the carbonation products were analysed by two complementary techniques, namely thermogravimetry (TGA) and elemental carbon content analysis. In the former analysis, carried out under nitrogen atmosphere, bound water was released during a 30 min plateau applied at 120°C. The weight loss between 300 and 600°C was then used to determine the carbonate amount (Bonfils et al., 2012), since the slag exhibits a constant mass in this temperature range. All of these measures (mass loss from TGA, total carbon content determination, total CO2 consumption from storage tank) led to very consistent data regarding the final carbonation yield of the samples.
As part of a previous collaborative project (CNRT/Carboscories), the carbonated slags were also characterized by electron microscopy (SEM/EDX), X-Ray Diffraction (XRD), and elemental analysis (ICP/AES analysis after acid digestion) by IMPMC and BRGM partners (Touzé et al., 2015).
Reference conditions inside the reactor were set to 180°C and 20 bar of CO2 (leading to a total pressure of about 30 bar), a slurry concentration of 90 g of solid per liter of water and a stirring speed of 800 rpm.
In order to evaluate the benefit of the combined attrition-leaching mode of operation, benchmark tests were conducted using a two-step carbonation mode. This consists in 24 h of attrition under ambient temperature and inert (azote) atmosphere, followed by 24 h of carbonation under the reference conditions without grinding beads.
Thermodynamic and Kinetic Modelling of the Carbonation Process
This section lays the foundations for the thermodynamic and kinetic models used in this work to investigate the observed carbonation plateau observed in attrition-leaching carbonation experiments.
Initial System Description
The description of the system was as follows: 1) the temperature T was considered constant and homogeneous within the reactor; 2) the amount of water was 80 g; 3) the amount of solid was 7.2 g; 4) an excess of CO2 at temperature T and pressure PCO2 was available (accounting for the gas reservoir).
The slag was described as an assembly of oxides matching its elemental composition (see details in Processed Material):
• System 1included only the main three elements: Si, Mg and Fe, which accounts for 95.3 wt.% of the slag;
• System 2 accounted also for the minor elements: Al, Ca and Mn, as they can contribute to the formation of silicate and/or carbonate phases. For sake of illustration, Al is known, even as a trace element, to form a variety of species detrimental to carbonation, including alumino-silicates that can consume Mg at the expense of Mg-carbonates and Al-rich clay minerals instead of amorphous silica (Sissmann et al., 2014).
Under the conditions of the attrition-leaching carbonation process, the grinding beads themselves are potentially reactive and their chemical inertness was evaluated:
a. Quartz sand was considered as an inert grinding medium, due to its high chemical stability (log Ksp = −2.37 at 180°C) and low reactivity: its dissolution rate was reported to be 10–15.3 mol cm−2 s−1 at 70°C from the acid to neutral pH range (Knauss and Wolery, 1988) against 10–13.1 mol cm−2 s−1 for enstatite at 70°C and pH 5 (Oelkers and Schott, 2001).
b. Stainless steel beads on the other hand are potentially corroded under the test conditions. They were accounted for by including a certain amount of (Fe0.87Cr0.13) in the initial materials description (see Effect of the Nature of the Grinding Beads on the Carbonation Products).
Thermodynamic Model
Given the chemical constitution of the system, the thermodynamic model needs to account for multiphasic equilibria including a pressurized gaseous phase, an aqueous electrolytic phase and various solid compounds and their mixtures (i.e., solid solutions).
Equilibrium calculations were carried out using PHREEQC, a simulator designed to perform a wide variety of aqueous geochemical calculations, including high-pressure conditions (Parkhurst, 1995; Parkhurst and Appelo, 1999; Zhu and Anderson, 2002; Parkhurst and Appelo, 2013). In relation to the system constitution, this software implements the Peng-Robinson equation of state to describe gaseous mixtures at high pressure, three activity coefficient models to describe the aqueous phase (namely extended Debye-Hückel [the so-called B-dot equation, Helgeson (1969)], Specific Ion Theory (Biederman, 1986) and Pitzer (Pitzer, 1973), as well as solid solutions with binary interaction parameters (Glynn and Reardon, 1990).
In the present system, the very small ionic strength of the aqueous solutions (about 10–3–10–2 mol/kgwater) justified the use of the B-dot equation for activity coefficient calculations. Accordingly, this work used the Thermoddem 2017 database due to its ability to satisfactorily predict the solubility of possible slag carbonation species, including magnesium carbonates, iron carbonates (Fosbøl et al., 2010; Bénézeth et al., 2011) and a wide variety of alumino-silicate phases (Blanc et al., 2012; Blanc, 2017). This database selection is different from our previous work (Cassayre et al., 2016), which implemented the LLNL database. The decision of switching to the Thermoddem 2017 database is mostly motivated by an improved assessment of the SiO2(aq) specie properties, which takes into accounts more recent experimental data and evaluation from Rimstidt (1997) and Gunnarsson and Arnórsson (2000).
As for CO2-water vapour mixture, the simulations used Peng-Robinson equation of state to describe fugacities and thus to calculate the CO2 solubility in water according to Henry’s law.
Regarding solids, all mineral phases present in the database that include these elements were allowed to precipitate, with the exception of quartz due to the existence of a strong kinetic barrier that favours the formation of amorphous silica (Daval et al., 2011). Direct measurements confirmed this hypothesis. Indeed, with the exception of the experiments using sand as grinding media, XRD, and EDX analyses never detected quartz in the solid product, but an increased amount of Si-rich amorphous phase(s).
Precipitated carbonates have almost identical crystal structures (Effenberger et al., 1981) and can form substitutional solid solutions on a large composition range. Solid solutions are more stable than the separate phases and commonly exhibit deviations from ideal behaviour, hence the need to describe their thermodynamic properties accurately. However, PHREEQC only allows the definition of excess free energy for binary solid solutions. Therefore a (Mg,Fe)CO3 solid solution with a regular solution parameter of 4.44 kJ/mol (Chai and Navrostky, 1996) was considered for system 1 and an ideal (Mg, Fe, Ca, Mn) CO3 solid solution for system 2.
Kinetic Modelling of the Slag Dissolution
Slag dissolution (see Figure 1) is here considered as the rate-limiting step, owing to the low acidity provided by CO2 hydrolysis (the predicted pH of the system – including the basic slag – being about 5 at equilibrium). Consequently, both dissolved gas and formed solid products were supposed to be at thermodynamic equilibrium at each time step during the dissolution process.
To describe the slag leaching kinetics, three distinct scenarios (Figure 5) were envisaged in this paper. Although they do not account for the actual elementary comminution processes, they consider the main reaction mechanisms that govern carbonation yield under attrition conditions. These scenarios depend on the concomitance between attrition and carbonation and the presumed efficiency of attrition for surface layer removal:
(1) Scenario 1: A shrinking particle mechanism is assumed to represent the attrition-leaching process. In this case, attrition peels off completely (and only) the surface layers as they form on the reactive particles. Surface reaction is the rate-determining step in scenario 1 and the corresponding mass balance is represented by Eq. 1 for a given particle size class:
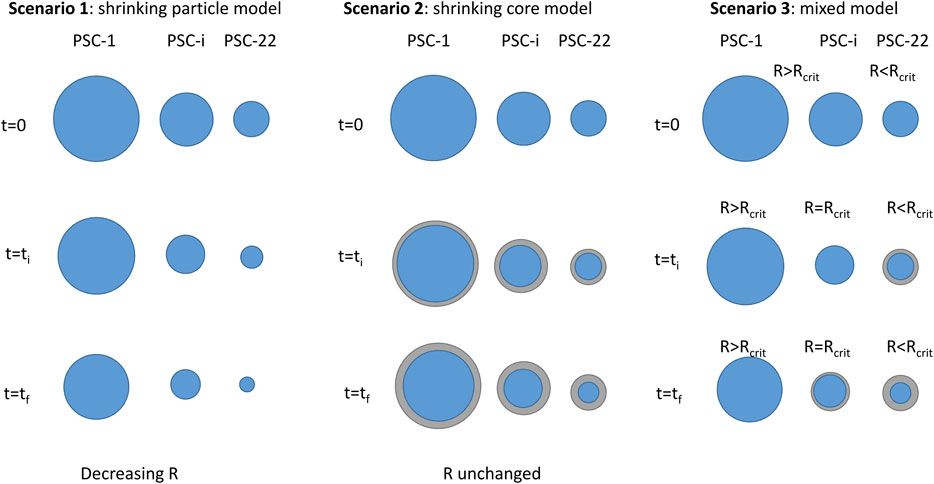
FIGURE 5. Schematics of the different scenarios considered for slag dissolution under the hybrid carbonation process (R refers to the radius of the particle, PSC is the particle size class).
The exponent 2/3 in Eq. 1 assumes an idealized spherical shape of the particles. For consistency, calculation of
The surface reaction rate, r, is expressed by:
Given the mineralogy of the slag, the saturation index SI and kinetic parameters (k0, EA, n, m) are those of enstatite, which are estimated from the work of Oelkers and Schott (2001): k0 = 2.4 mol m−2 s−1, EA = 48.5 kJ mol−1, n = 1/4 and m = −1/8 (
(2) Scenario 2: Slag dissolution mechanism obeys a shrinking core mechanism, while product layers form on the surface of the unreacted slag core. Diffusion within the solid layers is the rate-determining step for this scenario. This applies to the conventional aqueous carbonation process without attrition, for which the formation of surface layers has been already reported (Schott and Berner, 1983; Daval et al., 2011; Julcour et al., 2015). An illustration can be found in Supplementary Figure S2. Therefore, the two-step experiment, where attrition and carbonation are sequential (cf. Experimental Set-Up and Protocol), can be used to evaluate the corresponding diffusion parameter.
The associated mass balance is described by Eq. 3, derived from Levenspiel (1998), for a given particle size class:
where ni0 and ni are the initial and current number of moles of slag in particle size class i, mi0 the corresponding initial weight of slag (kg), SSAi0 the initial specific area (m2 kg−1) of the particles of mean radius Ri0 (equal to that of the sphere of the same radius),
Note that Eq. 3 is not defined at time zero of the dissolution when ni = ni0. Therefore a limitation by the surface chemical reaction (see Eq. 1) is first supposed until the conversion of slag
(3) Scenario 3: This scenario mixes scenarios 1 and 2. Indeed, it considers that attrition is no longer effective for surface layer removal below a critical slag particle diameter. In other words, scenario 3 means that slag particles larger than the critical diameter undergo scenario 1 while particles finer than the critical size are subject to scenario 2. It also means that particles with an initial diameter larger than the critical size might experience both scenarios during the attrition-leaching carbonation process.
Scenarios 1 to 3 are limiting cases. Several other scenarios, the likelihood of which cannot be denied will be considered in the future. One of them corresponds to attrition events peeling off more than the passivating surface layers, and producing fine unreacted slag particles at the same time. While this scenario is expected to yield an increased carbonation rate compared to scenario 1, it is also likely to be more energy intensive. Indeed, the least energy intensive attrition-leaching carbonation conditions are those that only use the energy necessary to exfoliate surface layers, hence the value of scenario 1. Fragmentation events, also likely to occur during attrition-leaching carbonation, are not considered either in the three selected scenarios.
All these models require the description of the particle size distribution (PSD) of the feed material. It was modelled using a Rosin-Rammler distribution, and then discretized into 22 size classes. Individual size classes were entered into the geochemical code as a distinct material, with the same thermodynamic properties but different specific surface area (
Figure 3 shows the corresponding cumulative PSDs and reveals that the d50 shifts from 39.0 to 8.1 and 2.8 µm after 24 h of attrition using stainless steel beads and quartz sand, respectively. The strongest reduction of the mean particle size observed in the latter case is explained by the self-attrition of the quartz sand particles, resulting into an increase in weight of the final solid product much higher than the CO2 uptake. Nevertheless, a different dominant comminution mechanism (breakage for steel beads vs. attrition for quartz sand) cannot be excluded to explain such a difference in the resulting PSDs, due to the high density difference between these grinding particles.
Results and Discussion
Thermodynamic considerations on the nature of the precipitated phases are discussed first. Then, the different mechanisms considered to describe the slag dissolution kinetics are assessed against the carbonation rates measured during the two-step and concomitant attrition-leaching processes.
Thermodynamic Predictions of Slag Dissolution Under Attrition-Leaching Carbonation Process Conditions
Product Speciation and Effect of Minor Elements on the Operating Window of Slag Carbonation
Figure 6 shows equilibrium calculations for the system SiO2-MgO-Fe2O3-CO2-H2O (system 1), which accounts for the major elements in the slag. Figure 6A gives the carbonation yield as a function of temperature and CO2 partial pressure, while Figure 6B shows the nature and amount of solid products at 20 bar of CO2.
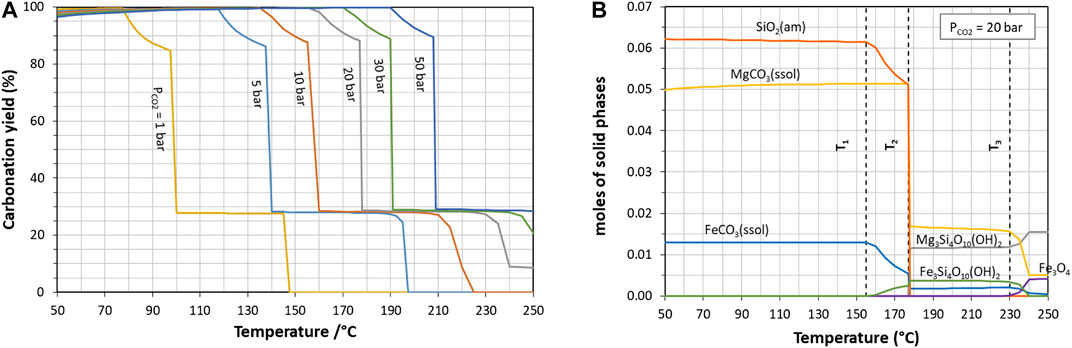
FIGURE 6. Effect of temperature on the carbonation of slag described as system 1 (major metal oxides only): (A) carbonation yield at different CO2 partial pressures and (B) solid carbonation products at 20 bar of CO2.
At a given CO2 partial pressure, mineral speciation varies with temperature in the range investigated (50–250°C), which results in a sharp decrease in carbonation extent beyond a certain temperature. In Figure 6B, T1 delineates the most suitable operating window for quantitative carbonate yield, in which leached silicon precipitates as amorphous silica, while leached iron and magnesium precipitate as a carbonate solid solution (ssol). At higher temperatures (T > T1), ferrous talc (minnesotaite), then magnesium talc (T > T2) and magnetite (T > T3) form at the expense of carbonates. Owing to the composition of the slag (with Mg >> Fe), the strongest reduction in carbonation extent coincides with T2. It should be noted that the reference conditions under investigation (180°C, 20 bar of CO2) stand beyond this second limit, while measured carbonation yield actually exceeded 50%.
The same pattern is found across the whole CO2 pressure range, with only a shift for the threshold temperatures, and the occurrence of antigorite for PCO2 less than 20 bar.
Our recent paper (Bourgeois et al., 2020) confirmed the existence of such pivot conditions for the carbonation of a water-quenched nickel slag, prompting a strong reduction of the extent of CO2 fixation (from 75% down to 25%) when further increasing temperature or reducing PCO2. The exact values of these thresholds are very sensitive to the equilibrium constants of the predicted phases, as shown below.
Including the minor elements of the slag (system 2), carbonation yield profiles (Figure 7A) exhibit not only one, but two successive steep drops (at T’1 and T’2), resulting for instance in a maximum yield of about 60% just below 180°C at 20 bar of CO2. This is due to the precipitation of various stable alumino-silicates that consume Mg and/or Fe (Figure 7B): montmorillonite (Mg0.3Mg0.6Al1.4Si4O10(OH)2) and saponite-like phases (Mg0.17Mg3Al0.34Si3.66O10(OH)2 and Mg0.17Mg2FeAl0.34Si3.66O10(OH)2).
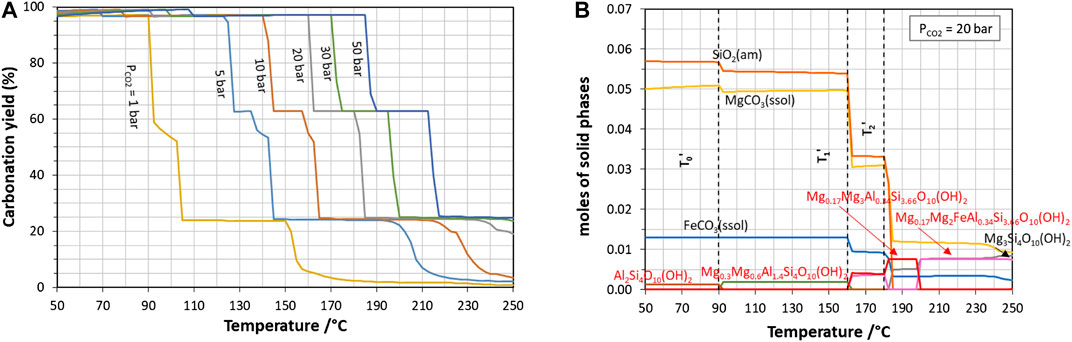
FIGURE 7. Effect of temperature on the carbonation of slag described as system 2 (major and minor metal oxides): (A) carbonation yield at different CO2 partial pressures and (B) solid carbonation products at 20 bar of CO2 (only precipitated phases containing Si, Mg and/or Fe are shown here).
Measured carbonation yield as high as 50% (corresponding to 0.032 mole of carbonates in the reactor) were obtained after 24 h of carbonation under the reference conditions, using quartz sand as grinding medium. X-ray diffraction analysis of the solid product showed initial mineral phases, quartz from sand grinding particles and mixed crystallized carbonates. Further examination with a transmission electron microscope pointed out that the solid product was made of an intimate mixture of nano-sized carbonates and silicate grains, the latter having different contents of magnesium, iron and aluminium and various structures (globules or fluffy aggregates) (see Figure 8A in Effect of the Nature of the Grinding Beads on the Carbonation Products). Although the exact nature of the remaining alumino-silicate phases has not been fully identified, these observations are consistent with the thermodynamic simulations, which predict the formation of a variety of alumino-silicate phases.
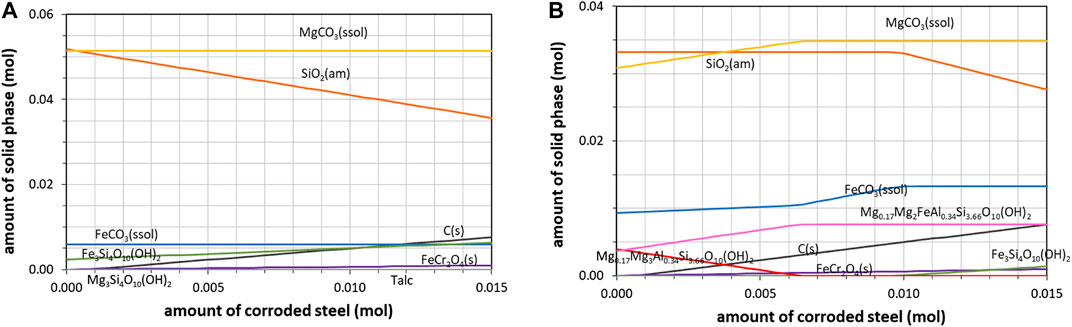
FIGURE 9. Predicted effect of the corrosion of stainless steel grinding beads on carbonation products (T = 175°C, PCO2 = 20 bar) for slag described as (A) system 1 (major metal oxides only) and (B) system 2 (major and minor metal oxides).
Effect of the Nature of the Grinding Beads on the Carbonation Products
To further test the reliability of the thermodynamic predictions, the case of stainless steel grinding beads was examined closely given their expected reactivity. Under the carbonation condition, a significant increase in CO2 consumption was measured, reaching up to 0.045 mole in 24 h. Such a value corresponds to a theoretical 70% carbonation yield. Carbonate amounts calculated from elemental C analysis were systematically higher - by as much as 15% - than those obtained from TGA analyses. This discrepancy, not observed in the previous experiments, raised the suspicion of a possible product contamination. Moreover, XRD revealed an enhanced formation of siderite (FeCO3) and mixed (Mg,Fe)CO3 carbonates, while ICP/AES analysis after acid digestion revealed that the iron to magnesium ratio jumped from 0.25 to 0.45 between the initial material and the final solid products.
In order to elucidate this chemical influence of stainless steel balls, the amount of iron-chromium solid solution was increased in the initial simulated system, up to the increment of iron measured in the product of about 0.01 mole (corresponding to 0.1% of the beads). This stainless steel corrosion behaviour under low solution acidity was reported in a previous contribution (Cassayre et al., 2016), which used a different thermodynamic database (see Thermodynamic Model) and led to somewhat different results for iron speciation since several (alumino)ferro-silicates were missing in the LLNL database.
Thermodynamic simulations performed at 175°C (just below T2 or T’2) predicted that the iron extracted from the steel beads could be converted to either minnesotaite or siderite and Fe-Mg saponite (with an increase of magnesite), depending on the system considered (Figure 9). These results prove that an accurate thermodynamic description of the various phyllosilicates formed is also of primary importance to evaluate the contribution of iron pollution to the carbonation yield. With the reference conditions, the simulation predicted that 0.048–0.057 mole of carbonates could be formed at the most when taking into account the iron dissolved from beads, but only the most complete system (system 2) could predict its transformation into siderite.
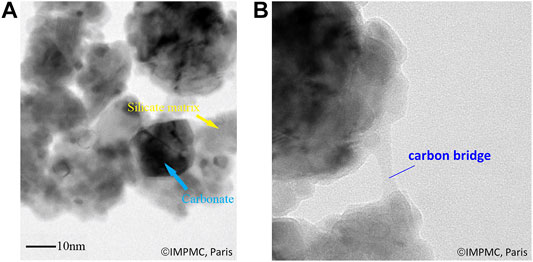
FIGURE 8. TEM micrographs of carbonated slag: (A) nano-sized carbonate particles and silicate matrix, (B) carbon bridge.
The simulation also predicts the formation of solid carbon as a by-product of iron oxidation, according to the following siderite forming reaction:
TEM micrographs confirmed the presence of carbon bridges between particles (Figure 8B), which supports the formation of solid carbon. Furthermore, the occurrence of this reaction is consistent with the higher carbon content measured by carbon analysis (carried out in oxidative conditions, and thus including elemental C) compared to the carbonates amounts determined by TGA (carried out in nitrogen atmosphere and thus not including elemental C). This observation also demonstrates the interest of combining both analytical techniques in carbonation products analysis.
Kinetic Modelling of Slag Dissolution During the Attrition-Leaching Carbonation Process
Operating particle leaching in a stirred bead mill leads to a change in PSD due to several concurrent processes: dissolution of the reactive slag, total or partial abrasion of surface product layers, the effectiveness of which may vary over time mainly due to its particle size dependency, and particle breakage. Instead of modelling these coupled phenomena, which is out of reach at this stage of our work, this section has no other objective than trying to identify the mechanisms that contribute the most to the carbonation extent. To this end, three limiting cases defined in Kinetic Modelling of the Slag Dissolution as scenarios 1 to 3 are used. They are briefly recalled hereafter:
• Scenario 1 is a purely surface-controlled (or reaction-controlled) process, which corresponds to an effective attrition process that peels off passivation layers as they form. It is described by the shrinking particle model;
• Scenario 2 is a purely diffusion-controlled process, which corresponds to a conventional aqueous carbonation process with surface passivation. It is described by the shrinking core model. It is also hypothesized that the change in particle size distribution by the grinding occurs much faster than the slag dissolution, so that the shrinking core model uses the PSD after attrition stage;
• Scenario 3 is a mixed process. It corresponds to a reaction-controlled process (scenario 1) for particles larger than a critical size, above which attrition is able to continuously remove surface layers. For particles finer than the critical size, this scenario switches to a diffusion-controlled process (scenario 2).
In the view of an efficient mineral carbonation, scenario 1 is considered the most favourable among the three, since it is not limited by any diffusion barrier. Furthermore, as aforementioned, attrition of the remaining reactive core (beyond the peeling off of the product surface layer) or particle fragmentation are not discussed here.
Scenario 1: Shrinking Particle Model
Figure 10 compares the carbonation rates measured with quartz sand to those calculated with this scenario, thus assuming that reaction on fresh surfaces is the rate-controlling step. For the sake of comparison with the experimental data, the simulations were performed at 175°C, that is thus below temperature T2 or T’2.
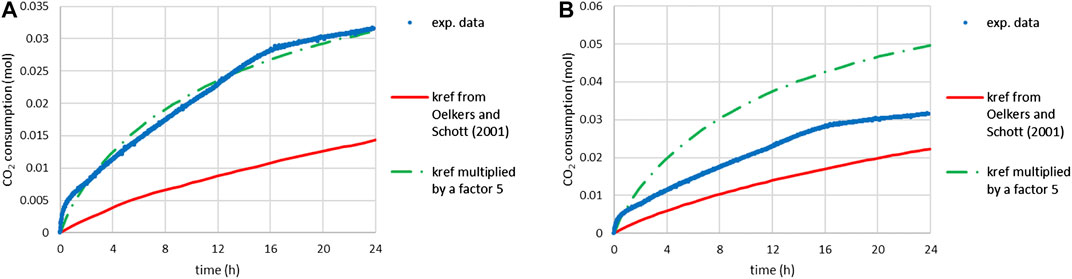
FIGURE 10. Time-CO2 consumption during slag carbonation (T = 180°C, PCO2 = 20 bar) under attrition with quartz sand: comparison of experimental data and predictions of scenario 1 (assuming a reaction-limiting process): (A) for system 2 (including main and secondary elements) and (B) for system 1 (limited to the main elements) with inhibition of minnesotaite precipitation.
Scenario 1 was first applied to system 2 (where the slag is described as its major and minor metal oxides), using the feed material PSD and the reaction rate law established by Oelkers and Schott (2001) for enstatite. Although the upper bound of the temperature range (28–168°C) over which Oelkers and Schott fitted their reaction rate is close to our experimental conditions (180°C), Figure 10A shows that scenario 1 largely underestimates the measured carbonation kinetics. It was necessary to increase the kinetic rate constant (kref) by a factor 5 to satisfactorily reproduce the experimental carbonation kinetics. This result is very likely influenced by the underestimation of the actual surface area of the particles from the measured PSD and the smooth spherical particle assumption. As mentioned in Processed Material, the ratio between the two surface areas was close to 10 for the initial slag particles.
After adjustment of the rate constant, the model predicts that conversion of the slag particles would have reached 77% in 24 h and the formation of alumino-silicate by-products containing Mg and/or Fe would explain the lower carbonation yield (of about 50%).
Scenario 1 was then applied to system 1 (where the slag is described as its major metal oxides only). Minnesotaite was excluded from the possible carbonation products as per the conclusions drawn in Effect of the Nature of the Grinding Beads on the Carbonation Products, and possible carbonation products were limited to the desired ones, namely siderite, magnesite and amorphous silica. It is noted that these phases were all that was observed to form by Bourgeois et al. (2020) during the attrition-leaching carbonation of another nickel slag. Figure 10B shows that scenario 1 predicted the very first moments of the reaction, but yielded too high a CO2 uptake, since in this case the carbonation yield always matches the conversion of slag particles (no Mg/Fe silicate by-product).
Thorough examination of XRD pattern of the product gave clues on the actual conversion of the slag: Rietveld refinement indicated that the remaining slag phases (forsterite, enstatite, augite, diopside) accounted for up to 50 wt.% of the crystalline Mg containing phases (and carbonates the rest) (Ploquin et al., 2016).
Therefore, the “fitted” shrinking particle model seems in fact to overestimate the slag conversion and the potential phyllosilicate by-products are most likely different from those predicted by the thermodynamic calculations, as mainly in the form of amorphous phases.
For the examination of scenarios 2 and 3, the simulated material was thus reduced to system 1, with inhibition of minnesotaite precipitation.
Scenario 2: Shrinking Core Model
This model (see Eq. 3) requires the value of the effective diffusion of the proton in the surface leach layer,
Estimation of the Effective Diffusivity
In the two-step mode, the slurry bearing the slag particles is first subjected to attrition under inert atmosphere and room temperature. The slurry and grinding beads are then separated by screening, after which the slurry undergoes a regular carbonation step, during which the surface of the slag particles is progressively covered by a product layer. Thus, knowing the PSD after attrition stage, the shrinking core model can be tuned on the corresponding experimental CO2 uptake.
To avoid any misevaluation of the product PSD after attrition due the presence of debris from the grinding medium, the model was applied to the case of stainless steel beads to estimate
Figure 11 shows that a satisfactory agreement between simulated and measured carbonation rates was found for a fitted value of
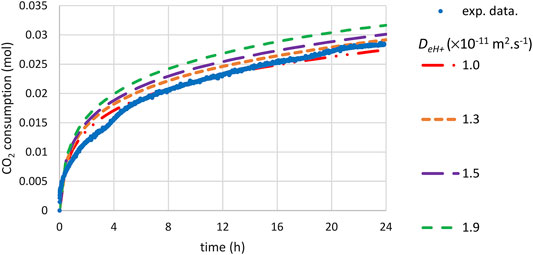
FIGURE 11. Time-CO2 consumption during slag carbonation (T = 180°C, PCO2 = 20 bar) following a preliminary attrition step under inert atmosphere and room temperature with stainless steel beads: comparison of experimental data and shrinking core model incorporating the PSD after grinding (see Figure 3).
The shrinking core model assumes that the fluid reactant migrates to the core surface through the porous structure of the surface layer. The effective diffusivity is then linked to the molecular diffusivity
where
The molecular diffusion coefficient of proton in water at 180°C can be estimated to 3.9 × 10–8 m2 s−1 according to the correlation of Lee and Rasaiah (2011). Considering a tortuosity value of about five for low-porous matrices (Ghanbarian et al., 2013), this yields a surface layer porosity of the order of 0.1%. This is not unrealistic according to the conclusions of Van Essendelft and Schobert, who accept up to 3 orders of magnitude difference between the two diffusivities.
Assessment of Scenario 2 for the Attrition-Leaching Carbonation Process
The shrinking core model using the estimated
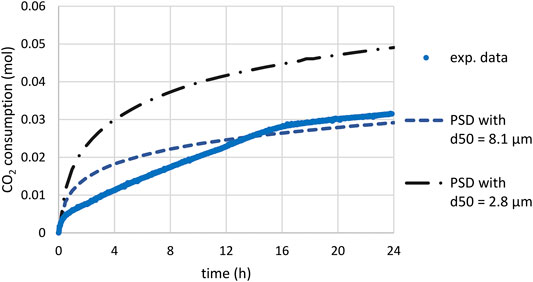
FIGURE 12. Time-CO2 consumption during slag carbonation (T = 180°C, PCO2 = 20 bar) under attrition with sand quartz: comparison of experimental data and predictions of models assuming a diffusion-limiting process (
Examination of scenarios 1 and 2 thus led to the conclusion that a mixed mechanism in between the two could have occurred to explain the experimental trend.
Scenario 3: Mixed Model
As discussed in Scenario 1: Shrinking Particle Model, the formation of undesirable silicate phases can lower the equilibrium carbonation yield. The slowing down of the attrition-leaching carbonation kinetics could also be ascribed to a gradual decrease in attrition efficiency related to the increasing fineness of the reactive particles. Several factors contribute to this statement. While attrition may increase the reactivity of reactive surfaces by amorphization, finer particles exhibit less surface defects and require more energy for their surface fragmentation (Kwade and Schwedes, 2007; Schilde et al., 2010). The finer the particles, the lesser the likelihood of particles to experience shear stress events inside the stirred bead mill. Although this may not apply here as tested slurries were dilute (∼3 vol.%), increased slurry fineness may yield a rise in slurry viscosity that reduces attrition efficiency. Scenario 3 proposes a mixed regime that could possibly approximate the drop in efficiency of attrition with increased fineness. This scenario subjects particles larger than a critical size to a reaction-controlled process (scenario 1), and finer particles to a surface-controlled process (scenario 2). Figure 13 shows the simulated prediction for scenario 3, for three critical particle sizes, using the modified kinetic rate constant (multiplied by a factor 5) and the value of
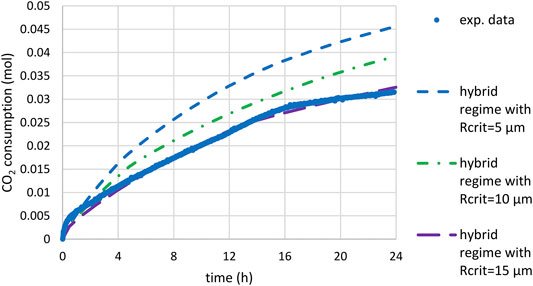
FIGURE 13. Time-CO2 consumption during slag carbonation (T = 180°C, PCO2 = 20 bar) under attrition with sand quartz: comparison of experimental data and prediction of the mixed model (starting under kinetic control and ending under diffusion control below a given critical radius Rcrit): calculations using the PSD of feed material, kref multiplied by a factor 5 and
The third limiting scenario matches the experimental trend for a critical radius Rcrit of 15 µm. This would mean that feed particles initially smaller than 30 µm in diameter would not change in size (owing to the shrinking core mechanism) while coarser particles would be reduced down to this diameter value. Attrition fragment would be much finer though (in the micrometer size range).
Based on the calculated conversion of the different size classes and assuming a similar molar volume of the reactant and the product mixture, this would yield 38% of the initial volume transformed into small fragments. The rest would correspond to a volume percentage of 13% for particles above 100 µm in diameter, 16% in between 30 and 50 µm, and 33% for those unchanged in size (below 30 µm in diameter in the initial PSD). As abovementioned, the particle size measured after attrition with quartz sand was affected by the autogenous attrition of quartz sand particles themselves, quartz contributing up to 60 wt.% of the crystalline phases for the hybrid process (Ploquin et al., 2016). With stainless steel beads, part of the product came from the dissolution of iron from the beads. Therefore, the PSD measured after attrition alone with stainless steel beads could be viewed as a better approximation of the final product’s PSD. As illustrated in Figure 14, the mixed scenario may be plausible when compared to this experimental size distribution (the smallest fragments being distributed equally over the 1–5 µm size classes in the modelled PSD). It should be noted, however, that the maximum fineness (d50) achievable in industrial stirred bead mills is down to 1/1,000 of the grinding medium size, but in practice it could be in the order of 200–500 times smaller than the bead size used (Hassal, 2008). This would correspond here to 2–10 µm particles, since the experiments used 1.6 mm grinding medium.
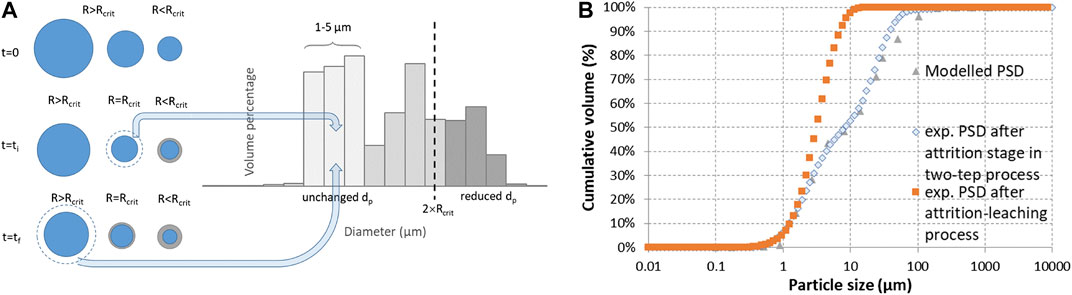
FIGURE 14. Modelled PSD issued from the mixed model: (A) schematic description and (B) comparison with measured cumulative size distributions of slag particles after 24 h of attrition grinding using stainless steel beads (in two-step and attrition-leaching processes) (conditions of Figure 13).
Finally, in Figure 15, the predictions of scenario 3 (with kref multiplied by 5, Rcrit = 15 µm and
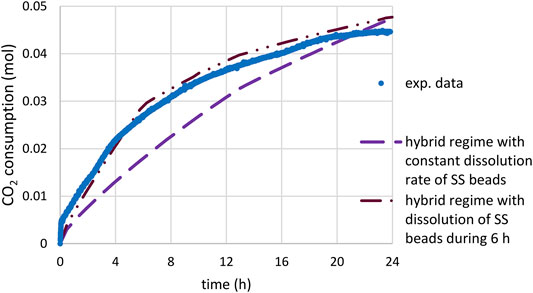
FIGURE 15. Time-CO2 consumption during slag carbonation (T = 180°C, PCO2 = 20 bar) under attrition with stainless steel beads: comparison of experimental data and prediction of the mixed model starting under kinetic control and ending under diffusion control below a given critical radius Rcrit (15 µm); calculations using the PSD of feed material, kref multiplied by a factor 5 and
Although based on a simplified mechanism, explaining the evolution of the material PSD through the attrition of product layer in small fragments as long as the slag particles remain large enough, scenario 3 could conciliate the measured carbonation rate, the final slag conversion and the final particle size.
Conclusions and Perspectives
Owing to the continuous renewal of reactive surfaces that goes beyond a simple particle size reduction effect, the attrition-leaching carbonation process has been shown to strongly improve the carbonation yield of natural minerals and industrial residues alike. Invariably, the attrition-leaching carbonation yield levels off 20–50% below the yield expected from stoichiometry with all feedstocks tested to date, including the nickel slags used in this study. Using an original thermo-kinetic modelling methodology that combines equilibrium thermodynamic and particle reaction kinetic models, this paper attempts to shed light on the mechanisms that govern this behaviour. Indeed, it is thought that this repeatable behaviour can originate either from the precipitation of undesirable silicate by-products whose formation competes with that of carbonates under single-step aqueous mineral carbonation conditions, or from a kinetic limitation specific to the attrition-leaching carbonation process itself.
Thermodynamic modelling is a powerful tool that can predict the likelihood of the formation of precipitated species, accounting for all the inputs to the process. In particular, this work has shown that it is invaluable for anticipating the possible effects of slag impurities and grinding medium on the aqueous carbonation system. The work also confirms that thermodynamic modelling cannot be used in isolation, as it must be accompanied by thorough analysis of the products by various complementary physico-chemical techniques for quantitative validation and use. The results obtained by thermodynamic modelling for the systems selected in this study, namely nickel slag with either stainless steel or quartz sand grinding media, show that the observed slowing down of the carbonation process could be explained by the formation of Mg- and/or Fe-rich silicates that precipitate at the expense of carbonates.
While the conclusion is not yet clear-cut, this work shows that a more likely explanation is of a kinetic nature. The kinetic limitation in question corresponds to a gradual reduction in attrition effectiveness as reactive feed particles leach out. Indeed, while neither the shrinking particle nor the shrinking core model could match the slowing down of the carbonation process, a mixed model that combines the two reproduced the complex course of the process satisfactorily. This model was built using a separate evaluation of the underlying parameters, in particular the surface reaction rate constant and diffusivity of the leached layer, as well as the measured evolution of the particle size distribution.
Pending additional confirmation, this finding is positive for the improvement of the attrition-leaching carbonation process. Indeed, if the carbonation limitation were of a thermodynamic nature, nothing simple could be done to improve carbonation yield of the attrition-leaching carbonation process. However, the likelihood of the limitation being of a kinetic nature opens the possibility to increase the carbonation yield by improving the performance of the attrition process itself. This requires however that the workings of the attrition process be understood at a local (particle) level in the context of the attrition-leaching carbonation process. As suggested by the good results obtained with the mixed model, the intrinsic limit of the attrition process to grind fine particles beyond a critical size is probably an important feature of the problem, along with the size-dependent efficiency of the attrition process. Notwithstanding their size, the choice of grinding media is also a critical component of the problem, as Ni slag for instance is a particularly abrasive carbonatable feedstock. Another parameter of importance is the rheology of the system, which was uncontrolled in the batch experiments used in this study. Other complex factors may be at work here also, considering that the attrition operates on particle surfaces whose mineralogical, mechanical and reactive properties are affected locally by mechanical stresses. Understanding these factors is inseparable from conducting extensive characterisation of the phases present - composition, nature and quantity - at different reaction times, which is most challenging.
While it is believed that the optimization of the attrition-leaching carbonation process lies in finding the right equilibrium between attrition and leaching rates, a comprehensive investigation of the attrition mechanisms at the particle level is now mandatory to elucidate and optimize the inner workings of the attrition-leaching carbonation process.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
CJ and FB wrote the manuscript. The attrition-leaching carbonation process is an original process proposed by FB. LC developed the theoretical framework of the thermodynamic modelling and provided input and critical feedback to the manuscript. CJ devised the main conceptual ideas of the kinetic modelling and performed the numerical calculations. IB carried out the experiments and JD contributed to the modelling work, under the supervision of FB, CJ, and LC. All authors analysed the data and discussed the results.
Funding
The CARBOSCORIES project (https://cnrt.nc/carboscories/) was funded by the National Centre for Technology Research – CNRT “Nickel and its environment” (cnrt.nc). This research work is currently ongoing within the framework of the CARBOSCORIES II and CARBOVAL projects co-funded by the New Caledonian Energy Agency ACE (grant #CS17‐3160‐00) and the French Environment and Energy Management Agency ADEME (grant #1894C0021).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was part of a multi-disciplinary project co-funded by the National Centre for Technology Research, CNRT “Nickel et son environnement” (New-Caledonia): Carboscories (2015–2016). It brought together different research institutes with expertise in geochemistry, mineralogy, crystallography (Institut de Minéralogie, de Physique des Matériaux et de Cosmochimie, Paris and Bureau de Recherches Géologiques et Minières, Orléans), chemical engineering (Laboratoire de Génie Chimique, Toulouse) and industrial integration (BRGM). The authors wish to thank Solène Touzé (BRGM) for the coordination of the project and ICP/AES analyses of the products, Thierry Augé (BRGM) for the characterization of the KNS slag, Florian Ploquin and Farid Juillot (IMPMC) for the DRX/Rietveld analyses and François Guyot (IMPMC) for the TEM images of the products. They also acknowledge the technical team of LGC, Jean-Louis Labat and Lahcen Farhi for their support on the experimental set-up and Christine Rey-Rouch for her help on thermogravimetry, particle morphology and size analyses, as well as Isabelle Borget (LCC Toulouse) for CHN measurements.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fceng.2020.588579/full#supplementary-material
References
Augé, T., and Touzé, S. (2015). Caractérisation des résidus de pyrométallurgie de l’usine de Koniambo. Rapport BRGM/RC-64842-FR.
Bénézeth, P., Saldi, G. D., Dandurand, J.-L., and Schott, J. (2011). Experimental determination of the solubility product of magnesite at 50 to 200°C. Chem. Geol. 286, 21–31. doi:10.1016/j.chemgeo.2011.04.016
Biederman, G. (1986). “Introduction to the specific interaction theory with emphasis on chemical equilibria,” in Metal complexes in solution. Editors Jenne, E. A., Rizzarelli, E., Romano, V., and Sammartano, S. (Padua, Italy: Piccin), 303–314.
Blanc, P. (2017). Thermoddem: update for the 2017 version. Report BRGM/RP-66811-FR. Available at: https://thermoddem.brgm.fr/sites/default/files/upload/documents/brgmrp-66811-fr_final_report.pdf (Accessed November 3, 2020).
Blanc, P., Lassin, A., Piantone, P., Azaroual, M., Jacquemet, N., Fabbri, A., et al. (2012). Thermoddem: a geochemical database focused on low temperature water/rock interactions and waste materials. Appl. Geochem. 27 (10), 2107–2116. doi:10.1016/j.apgeochem.2012.06.002
Bodor, M., Santos, R. M., Van Gerven, T., and Vlad, M. (2013). Recent developments and perspectives on the treatment of industrial wastes by mineral carbonation - a review. Cent. Eur. J. Eng. 3 (4), 566–584. doi:10.2478/s13531-013-0115-8
Bonfils, B. (2012). Mécanismes et verrous de la carbonatation minérale du CO2 en voie aqueuse. PhD thesis. Toulouse (France): Institut National Polytechnique de ToulouseAvailable at: https://oatao.univ-toulouse.fr/7920/1/bonfils_partie_1_sur_2.pdf.
Bonfils, B., Julcour-Lebigue, C., Guyot, F., and Bodénan, F., Chiquet, P., and Bourgeois, F. 2012). Comprehensive analysis of direct aqueous mineral carbonation using dissolution enhancing organic additives. Int. J. Greenh. Gas Control. 9, 334–346. doi:10.1016/j.ijggc.2012.05.009
Bourgeois, F., Laniesse, P., Cyr, M., and Julcour, C. (2020). Definition and exploration of the integrated CO2 mineralization technological cycle. Front. Energy Res. 8, 1-17. doi:10.3389/fenrg.2020.00113
Cassayre, L., Bourgeois, F., Julcour-Lebigue, C., Benhamed, I., Diouani, J., and Nahdi, K. (2016). “Defining the operating conditions of the attrition-leaching process using thermodynamic process modelling,” in IMPC 2016: XXVIII international mineral processing congress proceedings, Québec, Canada, September 2016, 2490–2501.
Chai, L., and Navrotsky, A. (1996). Synthesis, characterization, and enthalpy of mixing of the (Fe,Mg)CO3 solid solution. Geochem. Cosmochim. Acta. 60, 4377–4383. doi:10.1016/s0016-7037(96)00261-x
Daval, D., Martinez, I., Guigner, J.-M., Hellmann, R., Corvisier, J., Findling, N., et al. (2009). Mechanism of wollastonite carbonation deduced from micro- to nanometer length scale observations. Am. Mineral. 94, 1707–1726. doi:10.2138/am.2009.3294
Daval, D., Sissmann, O., Menguy, N., Saldi, G. D., Guyot, F., Martinez, I., et al. (2011). Influence of amorphous silica layer formation on the dissolution rate of olivine at 90°C and elevated pCO2. Chem. Geol. 284, 193–209. doi:10.1016/j.chemgeo.2011.02.021
Effenberger, H., Mereiter, K., and Zemann, J. (1981). Crystal structure refinements of magnesite, calcite, rhodochrosite, siderite, smithonite, and dolomite, with discussion of some aspects of the stereochemistry of calcite type carbonates. Z. Kristallogr. 156 (1–4), 233–243. doi:10.1524/zkri.1981.156.14.233
Fosbøl, P. L., Thomsen, K., and Stenby, E. H. (2010). Review and recommended thermodynamic properties of FeCO3. Corrosion Eng. Sci. Technol. 45, 115–135. doi:10.1179/174327808X286437
Gadikota, G., Natali, C., Boschi, C., and Park, A.-H. A. (2014). Morphological changes during enhanced carbonation of asbestos containing material and its comparison to magnesium silicate minerals. J. Hazard Mater. 264, 42–52. doi:10.1016/j.jhazmat.2013.09.068
Ghanbarian, B., Hunt, A. G., Ewing, R. P., and Sahimi, M. (2013). Tortuosity in porous media: a critical review. Soil Sci. Soc. Am. J. 77, 1461–1477. doi:10.2136/sssaj2012.0435
Glynn, P. D., and Reardon, E. J. (1990). Solid-solution aqueous-solution equilibria; thermodynamic theory and representation. Am. J. Sci. 290, 164–201. doi:10.2475/ajs.290.2.164
Gunnarsson, I., and Arnórsson, S. (2000). Amorphous silica solubility and the thermodynamic properties of H4SiO°4 in the range of 0° to 350°C at Psat. Geochem. Cosmochim. Acta. 64, 2295–2307. doi:10.1016/s0016-7037(99)00426-3
Hassal, P. (2008). Milling media review - Part 2: bead density effect, Paint and coatings industry. Available at https://www.pcimag.com/articles/87925-milling-media-review-part-2-bead-density-effect (Accessed June 27, 2020).
Helgeson, H. C. (1969). Thermodynamics of hydrothermal systems at elevated temperatures and pressures. Am. J. Sci. 267, 729–804. doi:10.2475/ajs.267.7.729
Huijgen, W. J. J., Comans, R. N. J., and Comans, R. N. J. (2005). Mineral CO2 Sequestration by steel slag carbonation. Environ. Sci. Technol. 39 (24), 9676–9682. doi:10.1021/es050795f
Jankovic, A. (2000). Fine grinding in the Australian minerals industry. J. Min. Metall. 36 (1–2), 51–61.
Julcour, C., Bourgeois, F., Bonfils, B., Benhamed, I., Guyot, F., Bodénan, F., et al. (2015). Development of an attrition-leaching hybrid process for direct aqueous mineral carbonation. Chem. Eng. J. 262, 716–726. doi:10.1016/j.cej.2014.10.031
Knauss, K. G., and Wolery, T. J. (1988). The dissolution kinetics of quartz as a function of pH and time at 70°C. Geochem. Cosmochim. Acta. 52 (1), 43–53. doi:10.1016/0016-7037(88)90055-5
Kwade, A., and Schwedes, J. (2007). Chapter 6: wet grinding in stirred media mills. Handbook of Powder Technology. 12, 251–382. doi:10.1016/s0167-3785(07)12009-1
Lee, S. H., and Rasaiah, J. C. (2011). Proton transfer and the mobilities of the H+ and OH− ions from studies of a dissociating model for water. J. Chem. Phys. 135 (12), 124505. doi:10.1063/1.3632990
National Academies of Sciences Engineering, and medicine (2019). “Chapter 3: mineral carbonation to produce construction materials,” in Gaseous carbon waste streams utilization: status and research needs. Washington DC: The National Academies Press. doi:10.17226/25232
Oelkers, E. H., and Schott, J. (2001). An experimental study of enstatite dissolution rates as a function of pH, temperature, and aqueous Mg and Si concentration, and the mechanism of pyroxene/pyroxenoid dissolution. Geochem. Cosmochim. Acta. 65 (8), 1219–1231. doi:10.1016/s0016-7037(00)00564-0
Parkhurst, D. L., and Appelo, C. A. J. (1999). “User’s guide to PHREEQC version 2—a computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations,” in Water-resources investigations report 99-4259. Reston, VA: U.S. Geological Survey, 312. doi:10.3133/wri994259
Parkhurst, D. L., and Appelo, C. A. J. (2013). Description of input and examples for PHREEQC version 3—a computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations. Reston, VA: U.S. Department of the Interior, U.S. Geological Survey. doi:10.3133/tm6a43
Parkhurst, D. L. (1995). User’s guide to PHREEQC A computer program for speciation, reaction-path, advective-transport, and inverse geochemical calculations, Issues 95-4227. Reston, VA: U.S. Department of the Interior, U.S. Geological Survey, 143. doi:10.3133/WRI954227
Pitzer, K. S. (1973). Thermodynamics of electrolytes. I. Theoretical basis and general equations. J. Phys. Chem. 77(2), 268–277. doi:10.1021/j100621a026
Ploquin, F., Juillot, F., and Guyot, F. (2016). Caractérisation minéralogique et cristallochimique des produits de carbonatation des scories SLN et KNS. Programme « Carboscories », CNRT « Nickel & son environnement », internal report IMPMC. 50.
Rimstidt, J. D. (1997). Quartz solubility at low temperatures. Geochem. Cosmochim. Acta. 61, 2553–2558. doi:10.1016/s0016-7037(97)00103-8
Sanna, A., and Maroto-Valer, M. (2017). CO2 sequestration by ex situ mineral carbonation. Singapore: World Scientific publishing. doi:10.1142/q0046
Schilde, C., Kampen, I., and Kwade, A. (2010). Dispersion kinetics of nano-sized particles for different dispersing machines. Chem. Eng. Sci. 65, 3518–3527. doi:10.1016/j.ces.2010.02.043
Schott, J., and Berner, R. A. (1983). X-ray photoelectron studies of the mechanism of iron silicate dissolution during weathering. Geochem. Cosmochim. Acta. 47, 2233–2240. doi:10.1016/0016-7037(83)90046-7
Sipilä, J., Teir, S., and Zevenhoven, R. (2008). Carbon dioxide sequestration by mineral carbonation. Literature review update 2005-2007. Report from Åbo Akademi University, Faculty of Technology, Heat Engineering Laboratory. Available at: http://innovationconcepts.nl/res/literatuurGPV/mineralcarbonationliteraturereview0507.pdf (Accessed November 3, 2020).
Sissmann, O., Brunet, F., Martinez, I., Guyot, F., Verlaguet, A., Pinquier, Y., et al. (2014). Enhanced olivine carbonation within a basalt as compared to single-phase experiments: reevaluating the potential of CO2 mineral sequestration. Environ. Sci. Technol. 48 (10), 5512–5519. doi:10.1021/es405508a
Touzé, S., Augé, T., Bodénan, F., Benhamed, I., Julcour, C., Bourgeois, F., et al. (2015). Carbonatation minérale en Nouvelle-Calédonie. Rapport de synthèse, Programme « Carboscories », CNRT Nickel & son environnement.
Van Essendelft, D. T., and Schobert, H. H. (2009). Kinetics of the acid digestion of serpentine with concurrent grinding. 1. Initial investigations. Ind. Eng. Chem. Res. 48 (5), 2556–2565. doi:10.1021/ie801085x
Veetil, S. P., and Hitch, M. (2020). Recent developments and challenges of aqueous mineral carbonation: a review. Int. J. Environ. Sci. Technol. 17, 4359–4380. doi:10.1007/s13762-020-02776-z
Keywords: aqueous mineral carbonation, slag valorization, attrition-leaching carbonation process, thermo-kinetic modelling, shrinking particle model, shrinking core model
Citation: Julcour C, Cassayre L, Benhamed I, Diouani J and Bourgeois F (2020) Insights Into Nickel Slag Carbonation in a Stirred Bead Mill. Front. Chem. Eng. 2:588579. doi: 10.3389/fceng.2020.588579
Received: 29 July 2020; Accepted: 19 October 2020;
Published: 19 November 2020.
Edited by:
Pasi Tolvanen, Åbo Akademi University, FinlandReviewed by:
Tapio Salmi, Åbo Akademi University, FinlandNarendra Kumar, Åbo Akademi University, Finland
Copyright © 2020 Julcour, Cassayre, Benhamed, Diouani and Bourgeois. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Carine Julcour, Y2FyaW5lLmp1bGNvdXJAZW5zaWFjZXQuZnI=
 Carine Julcour
Carine Julcour Laurent Cassayre
Laurent Cassayre Imane Benhamed
Imane Benhamed Florent Bourgeois
Florent Bourgeois