Object-Oriented Modeling of a Capacitive Deionization Process

The process of capacitive deionization (CDI) is a cost effective and energy efficient method that offers many opportunities in terms of desalination of brackish water and the removal of ionic contaminants. Current research focusses on evaluating different influence parameters to make the CDI process more competitive to other commercially available methods like reverse osmosis, direct distillation or ion exchange. CDI is based on the adsorption of ions to highly porous electrodes by applying an external voltage difference. Although, remarkable progress in CDI modeling has been achieved during the past decade, so far, only few models exist which fully describe the CDI process and which predict the cell behavior in all its aspects, including e.g., performance under constant voltage and/or constant current control or pH effects including water dissociation. However, in this paper a new approach to CDI modeling is presented, which opens a path to fast and easy implementation of a digital depiction of complex CDI setups having e.g., multiple cells. The model is based on the object-oriented modeling language Modelica that enables the simulation and prediction of the behavior of complete CDI cells by combining chemical, electrochemical and electrical components. Furthermore, there is the possibility to predict complex setups with e.g., complex electrolytes, concentration or voltage fluctuations as they appear due to environmental influences outside laboratory experiments. Besides detailed time courses of species concentrations in the bulk and the electrodes or local electrical potentials, the model enables the prediction of important sum parameters such as the salt adsorption capacity, current efficiency and power consumption. The results of the developed CDI model are validated by using parameter settings from literature and comparing the resulting predictions of equilibrium and kinetics. In addition, the agreement between our own experimental results and the respective model predictions is discussed.

Introduction

In recent years Capacitive Deionization (CDI) has become a commonly known technique for deionization of brackish water, as it is an energy efficient and cost effective technology (Oren, 2008; Zou et al., 2008; Anderson et al., 2010; Cohen et al., 2013; Porada et al., 2013; Han et al., 2014; Biesheuvel et al., 2015; Suss et al., 2015; Gude, 2016; Dykstra et al., 2018; Ma et al., 2018). In general, a CDI cell mainly consists of two porous electrodes oppositely placed to each other and separated by a permeable, non-conducting spacer through which the feed water is pumped. If an electrical potential of around 1.2 V (Han et al., 2014) is applied between the electrodes, ions dissolved in the feed solution migrate into the pores of the electrodes depending on their charge. A variety of electrode materials are available ranging from activated carbon materials to carbon nanotubes, graphene materials (Porada et al., 2013) and recently studied highly-ordered mesoporous carbon nanopolyhedra (Xu et al., 2019b, 2020), metal-organic frameworks (Wang et al., 2019; Xu et al., 2020) or nitrogen-doped polymers (Xu et al., 2019a). Charge can either be applied by a constant voltage (CV) or a constant current (CC) source. By discharging the electrodes, ions are released to the solution and the electrodes can be regenerated (Zou et al., 2008; Biesheuvel et al., 2015). As the CDI process has gained more importance in recent years, research into experimental optimization and modeling approaches have become more important (Biesheuvel et al., 2011b; Hemmatifar et al., 2015; Suss et al., 2015; Andres et al., 2017). Initial CDI-simulations were done by Johnson and Newman in 1971. It was assumed that the adsorption of ions to porous electrodes could be described by a distributed network of resistances and capacitors resulting in an equivalent circuit model of the porous electrode (Johnson and Newman, 1971). Later on, Biesheuvel et al. (2009) set up a dynamic process model based on the Gouy-Chapman-Stern (GCS) theory to simulate the influence of several parameters such as the flow rate or the applied voltage on the CDI performance. An important element was the definition of the charge efficiency which was developed by Zhao et al. (2010) to introduce an analytical expression for the effectiveness of a CDI system. In 2010, Ryu et al. (2010) implemented a mathematical model of several CDI unit cells by using Matlab Simulink to describe the basic CDI behavior and associated parameters. Also in 2010 Biesheuvel and Bazant (2010) presented a mean-field theory to predict ion transport and storage of ions in porous electrodes which is based on a linear “RC” transmission line. The so-called modified Donnan model for the prediction of ion storage in charged pores was published by Biesheuvel et al. (2011b). The modified Donnan model assumed a constant electrical potential inside the pores due to overlapping electrical double layers. Furthermore two modifications were implemented (Biesheuvel et al., 2011a,b). The first one includes a charge-free Stern layer which symbolizes an atomic “roughness” at the interface between electrode and electrolyte. Secondly, a non-electrostatic attraction term was implemented representing the attraction of ions into the micropores without an applied potential. Using these modifications Biesheuvel et al. (2012) were able to set up a model including ion transport and electrochemical reactions in porous electrodes in 2012. While most publications using the modified Donnan model show and discuss results obtained by the boundary condition of constant voltage operation, Jande and Kim (2013) use the model to investigate CDI performance under constant current operation. Attractive forces in microporous carbon electrodes were further studied by Biesheuvel et al. (2014). Experimental observations and a dynamic model about “enhanced CDI” were presented by Biesheuvel and Biesheuvel et al. (2015), showing the effect of immobile chemical charges on the salt adsorption capacity. In 2015 Hemmatifar et al. (Hemmatifar et al., 2015) presented a COMSOL Multiphysics model of a two-dimensional porous electrode to analyze the coupling of flow and charge transport in a capacitive deionization cell. Considering the importance of acid-base equilibria which are taking place at the electrodes surface, Hemmatifar et al. (2017) further adapted the modified Donnan model. A physics-based model was presented by Dykstra et al. (2017) showing the effect of pH changes in Membrane Capacitive Deionization (MCDI). A dynamic model was set up showing the influences of different ion mobilities in combination with acid-base equilibrium reactions and the effect of charged surface groups of the electrodes. By using a dynamic transport model, Wang and Lin (2018) quantified recently the intrinsic trade-off between the energetic and kinetic efficiencies which is caused by the different charging methods CC or CV. The effect of different charging methods in terms of energy recovery was also described by Dykstra et al. (2018), who presented a methodology to assess the energy consumption under different operation modes. All the above-mentioned models are based on self-programmed algorithms in programming languages such as C++ or MATLAB or commercially available software like COMSOL Multiphysics. On the one hand, they allow full control of the applied equations, but on the other hand subsequent modifications and extensions are not easily done. Therefore, in our new approach to CDI modeling, an object-oriented code generation was chosen using the software OpenModelica which is available as freeware. In addition to relatively easy visual programming, this offers the interesting possibility to combine (electro-) chemical elements such as thermodynamically controlled reactions with electronic components such as resistors, current sources, etc., thus allowing a realistic image of a full CDI system. In our eyes this opens a path to the implementation of a digital depiction of complex CDI cells. In a broader context the object-oriented modeling with Modelica offers the chance of fast and easy simulations of electrochemical processes where the combination of different physics is highly important. In order to follow the idea of open access we uploaded our CDI models into a public repository available at https://github.com/mfkage/Modelica-Simulation-Ragone-Plot.

Theory

Capacitive Deionization and Ion Storage in Electrical Double Layers

In a CDI cell, charge storage in the pores of the electrodes can be explained with the theory of the electrostatic double layer (EDL). A well-known model describing the EDL was proposed by Gouy-Chapman-Stern (GCS). Here, the EDL is formed by an inner compact layer and an adjoining diffuse layer. The main part of the potential difference between the electrode surface and the bulk decays linearly in the so-called Stern layer formed by fixed ions having immediate contact with the surface. The rest of the potential difference decays exponentially in the diffuse layer formed by a progressively decreasing ion concentration with increasing distance from the electrode surface. A characteristic extension of the EDL is the Debye length in which the potential has decreased by a factor of e (Porada et al., 2013; Biesheuvel et al., 2015). In the activated carbon particles which are typically used in electrodes of a CDI cell, the average pore size is around 2 nm (Hemmatifar et al., 2017; Dykstra et al., 2018). As this is generally smaller than the Debye length, it is assumed that the diffuse layers of the EDLs are overlapping. In this case, the GCS theory is not valid. This problem was solved by introducing the so-called modified Donnan model by Biesheuvel et al. (2011a,b, 2012); Porada et al. (2012). According to the theory of the modified Donnan model, it is assumed that strongly overlapping EDLs lead to a constant electrical potential in the so-called micropores (<2 nm diameter). It is assumed that charge accumulation and ion storage takes place in the micropores, whereas macropores (>50 nm) are used for ion transportation only. By using this theory, the relationship between the concentration of an ion “i" in the micropore and the adjacent macropore can be described as follows (Biesheuvel et al., 2011a,b; Zhao et al., 2012).

$\begin{array}{ll}{\text{c}}_{{\text{X}}_{\text{i}},\text{mi}}={\text{c}}_{{\text{X}}_{\text{i}},\text{ma}}·\text{ exp}(-{\text{z}}_{{\text{X}}_{\text{i}}}·{\text{Φ}}_{\text{D}}+{\text{μ}}_{\text{att}})& (1)\end{array}$

Here, c_{Xi, mi} is the concentration of ions i in the micropores, c_{Xi, ma} the salt concentration, z_Xi the ionic charge number and ϕ_D the Donnan potential which describes the effective electrical potential difference between micro- and macropores. The term μ_att is used to include a chemical attraction energy which is non-electrostatic and represents the affinity of the ions to adsorb on the electrodes without an applied voltage (Biesheuvel et al., 2014). Typical values calculated to define the performance of a CDI process are the salt adsorption capacity (SAC) and the charge efficiency Λ. The SAC is defined with c_i as the concentration of ions adsorbed from the bulk during charging, c₀ as the concentration of ions released into the bulk during discharging, m_e as the mass of electrodes and the flow rate Φ (see Equation 2). The charge efficiency is defined as the SAC value times the Faraday constant F and divided by the total charge Q as presented in Equation 3 (Avraham et al., 2009; Kang et al., 2014; Kim et al., 2015).

$\begin{array}{ll}\text{SAC }=\frac{\int ({\text{c}}_{\text{i}}-{\text{c}}_0)\text{ dt}}{{\text{m}}_{\text{e}}}·\Phi & (2)\end{array}$

$\begin{array}{ll}\Lambda =\frac{\text{SAC}·{\text{F}·\text{m}}_{\text{e}}}{Q}& (3)\end{array}$

Object-Oriented Modeling With the Modelica Language

Modelica is an equation-based object-oriented modeling language (Fritzson, 2011). The software which was used to set up the model was the open-source distribution “OpenModelica” of the Modelica language (Fritzson, 2015). Via drag and drop of various objects different models can be set up and easily changed. Thereby, it is possible to combine chemical objects together with electronic, mechanical or hydraulic objects. In the background, each object is described by equations. For example, an electrical resistor is described as U = R^*I, where U is the electrical voltage, R the electrical resistance and I the electric current which is applied. In addition, the object representing a resistor has an optional interface representing the heat flux generated by the current in the resistor. In this way, a multi-physics representation of technical or environmental systems is possible with this software (Elmqvist et al., 1998; Fritzson, 2011, 2015). Modelica models can be set up by connecting different objects with connecting lines. These connectors represent the physical or chemical coupling of the components. All connectors have a non-flow as well as a flow variable. The non-flow variable can be a potential, e.g., the electrical potential or the electrochemical potential of a substance, and the flow variables can be the electrical current I or the molar flow dn/dt. The two types of connectors used in our model are presented in Table 1 (Fritzson, 2015; Matejak et al., 2015). According to Kirchoff's law, the sum of all flow variables in one junction has to be zero. A junction can be a phase boundary in the case of chemical elements, or where wires are connected in the case of electrical elements. In all cases, the non-flow variables of the connected objects must have the same value in the junctions. For example, the equilibrium state of a chemical system is characterized by concordance of the (electro-) chemical potentials of the involved substances in the respective compartments (Fritzson, 2015; Matejak et al., 2015).

TABLE 1

Table 1. Overview of the chemical and electrical connectors used in the CDI model.

Definitions and Fundamentals of the Chemical Library

Available objects like electronic or chemical components, voltage sensors or sources and are stored in libraries. The electrical library is part of the “Modelica Standard Library” while the chemical library (“Modelica Library of Chemical and Electrochemical Processes,” Chemical 1.1.0) is an external library developed by Matejak (2015). In the models described in sections Implementation of a simple CDI model and Enhanced model including water dissociation, the chemical objects solution, substance, reaction and electron transfer are used. By multiple use of the object “solution,” different compartments can be defined e.g., the bulk solution in the CDI cell as well as the anode and the cathode. Inside one compartment, properties such as the temperature and pressure of the solution can be set. For every compartment, the included substances have to be defined and connected to the solution port. Substances are defined by selection from a predefined list in the chemical library or are created individually. Parameters defining the substances are the standard molar Gibbs free energy of formation and the electrical charge. To set up chemical reactions, all substrates and products taking part have to be connected to the reaction by considering their reaction coefficients. All chemical reactions are based on equilibrating the chemical- or electrochemical potential which will be further described in section Implementation of a simple CDI model. To model electrochemical systems, the object “Electron.Transfer” is used to realize the connection between chemical and electrical parts, as it has a chemical as well as an electrical connection port.

Implementation of a Simple CDI Model

In Figure 1 a sketch showing the basic principle of a CDI cell can be seen and how this was transferred into a computational model by using the graphical user interface of OpenModelica. It should be emphasized that the displayed model does not show a general sketch but a screenshot of the actual model as it was generated by drag and drop. Figure 1 represents the simplest case of a CDI model describing the reversible uptake of NaCl. To represent the main components of an experimental CDI setup, five compartments (defined by dashed pink lines) were included: the bulk solution in the spacer between the electrodes, feed and effluent solutions, as well as cathode and anode. The electrodes can be regarded as a black box that includes the micropores as well as the electrodes surface. All solutions contain mainly water and varying concentrations of Na⁺ and Cl⁻. The compartments feed, bulk, and effluent have connectors carrying the respective molar fluxes of all substances (green lines). In case of a convective connection caused by e.g., pumping the solution through the CDI cell, the extent of the molar fluxes is given by the stream of the solution multiplied by the respective molar concentration. Thereby the object “stream” was used which connects the respective solutions as well as the respective substances (e.g., effluent solution with bulk solution and Na⁺ in effluent and bulk solution). The compartments representing the electrodes include the substances Na_mi and Cl_mi accumulated in the micropores, as well as the substance water H₂O_mi. In addition, the electrodes have an object called “Electron.Transfer” describing the connection between chemical (marked in pink) and electrical (marked in blue) objects. The parameters of all substances which were used are defined and explained in Section 1 of the Supplementary Material. For the electrical components, an electrical voltage or current source is introduced to charge and discharge the cell, and an optional current sensor is used to measure the current in the cell. In front of each electrode, a capacitor and a variable resistor is placed. The functions of these components will be explained later in this section. The object “reaction” of the chemical library of Modelica defines a strict thermodynamic relationship of the involved substances, representing the equilibrium state by the condition that the sum of the Gibbs free energies of the educts and products is zero (see Equations 4–6). These equations are implemented automatically into the model by graphically adding a “reaction” object by drag and drop. The same holds for the equations defining mass balances or flows, which are also implemented automatically when adding the respective graphical objects into the model scheme. Therefore, the complete model can be generated without typing equations in form of programming code.

$\begin{array}{ll}\sum {\nu }_i·\overline{{\mu }_{X_i}}=0& (4)\end{array}$

Here, ν_i is the stoichiometric coefficient and $\overline{{\mu }_{X_i}}$ is the electrochemical potential of substance X_i:

$\begin{array}{ll}\overline{{\mu }_{X_i}}={\mu }_{X_i}^{°}+RTln(a_{X_i})+z_{X_i}·F·\varphi & (5)\end{array}$

The term ${\mu }_{X_i}^{°}$ is the standard chemical potential, and a_Xi is the activity of the substance X_i. In bulk solutions having a constant electrical potential, Equation 5 reduces to the thermodynamic derivation of the law of mass action. If the Equation 5 is applied to a reaction describing the transfer of a single substance X_i between the bulk (or a macropore) and a micropore having a potential difference ϕ_D the relationship reduces to:

$\begin{array}{ll}\overline{{\mu }_{X_{i,mi}}}=\overline{{\mu }_{X_{i,ma}}}& (6)\end{array}$

This states simply that the equilibrium is defined by the condition that the electrochemical potential of substance X_i in the micropore is the same as the one in the macropore, which is the same than the one in the bulk. Inserting Equation 6 into Equation 5 and using the definition that in case of infinite dilution the activity can be replaced by the molar concentration one gets:

$\begin{array}{ll}{c}_{Xi,mi}=c_{Xi,ma}·exp(-z_{Xi}·{\Delta \varphi }_D+{\Delta \mu }_{X_i}^{°})& (7)\end{array}$

here, ${\mu }_{X_i}^{°}$ is the difference between the standard chemical potential of substance X_i in the micropore and in the macropore, which is the same as μ_i,att in Equation 1. This shows that the Modelica model includes exactly the same relationship of the potential-dependent ratio between the ion concentration in the micro- and macropores as the modified Donnan model introduced previously (Biesheuvel et al., 2011a,b; Zhao et al., 2012).

FIGURE 1

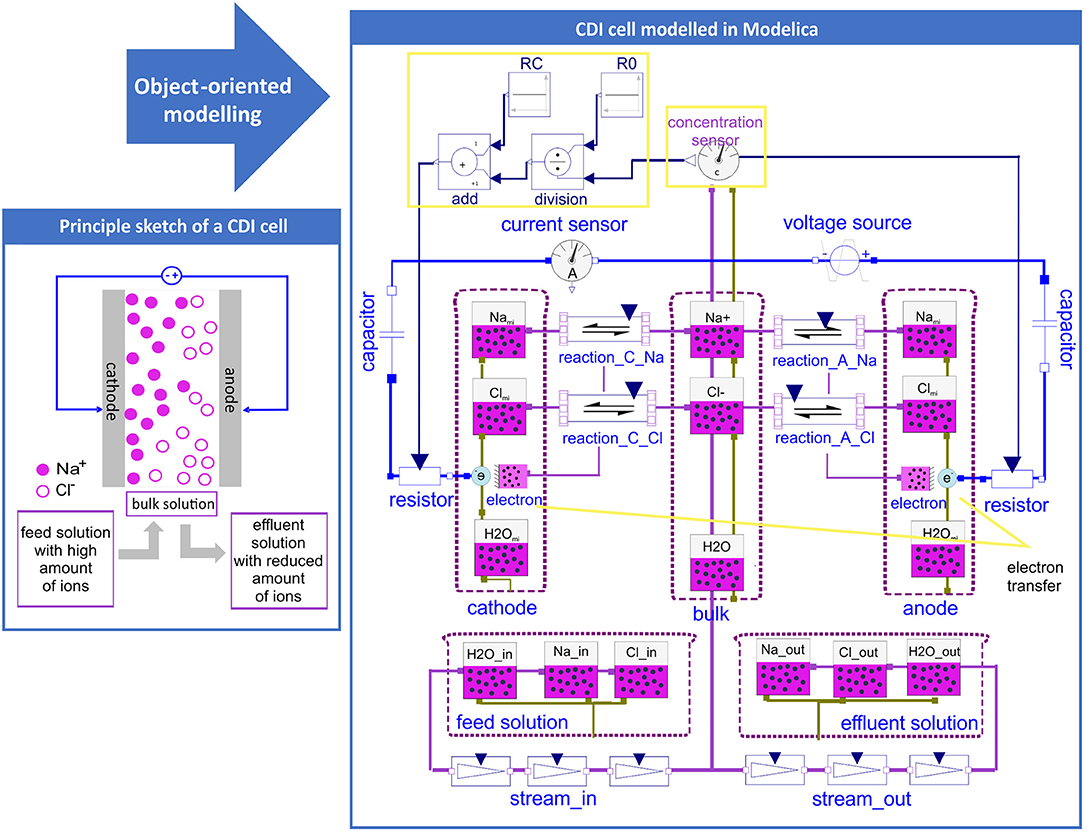
Figure 1. Principle sketch of the CDI setup and the corresponding basic CDI model setup generated by using the Modelica modeling language. In pink all chemical substances in the specific compartments (electrodes, bulk, feed or effluent solution) are shown in addition to the electrical circuit elements which are shown in blue (voltage source, capacitor and resistor).

Next we will see how this potential-driven accumulation of ions in the micropores is connected to current in the CDI system. With a closer look at the electrosorption reaction symbols of the CDI model shown in Figure 1, it can be seen that electrons are also involved. Actually, the accumulation of positively charged ions, e.g., Na⁺, requires the transport of a corresponding number of electrons from the electrical circuit into the electrode (Equation 8). Vice versa, the electrosorption of negatively charged ions such as Cl⁻ requires the transport of a corresponding number of electrons out of the electrode into the circuit (Equation 9).

$\begin{array}{ll}{X}_{i,ma}^{z_{X_i}+}+z_{X_i}\cdot e^{-}\stackrel{k_c}{\iff }{X}_{i,mi}& (8)\end{array}$

$\begin{array}{ll}{X}_{i,ma}^{z_{X_i}-}\stackrel{k_c}{\iff }{X}_{i,mi}+z_{X_i}\cdot e^{-}& (9)\end{array}$

In Equations 8, 9 the electrosorption of the substances X_i to the electrode looks like a redox reaction, which seems to be in contrast to the principle of CDI where there is no charge transfer between the electrode and the ions accumulated in the micropores (Biesheuvel and Bazant, 2010; Porada et al., 2013; Suss et al., 2015). However, the electrode must be viewed in its entirety. This means that on the macroscopic level, the electrosorption of a charged ion must be accompanied by a corresponding transport of electrons into or out of the electrode. From Equations 8, 9 it can also be seen that Modelica does not assume a spontaneous achievement of the equilibrium but rather that the calculation uses an adjustable kinetic coefficient k_c. As is explained in more detail in the Section 2 of the Supplementary Material, Modelica applies a kinetic expression using the difference of the electrochemical potentials of products and educts as a driving force. In order to get the unit $\frac{mol}{s}$ of the molar flux this requires that the kinetic coefficient be given in the somewhat unusual unit of $\frac{{mol}^2}{(J·s)}$. If the condition of the modified Donnan model is assuming spontaneous equilibrium between the concentrations in the micro- and macropores, we used a high value of$k_c=10^{-6}\frac{mo{l}^2}{(J·s)}$.

However, even if more realistic values of $k_c=10^{-10}\frac{mo{l}^2}{(J·s)}$ are estimated for the diffusivity of the substances in the electrodes (see Section 2 of the Supplementary Material), the influence of the kinetics of electrosorption between micro- and macropores stayed small. This confirms the assumption of conventional CDI models that this is not a rate-determining step (Biesheuvel et al., 2012). Nevertheless, it should be mentioned that the Modelica model offers the possibility to consider the kinetics of this step, if required. What is missing up to this point in the model is a mechanism describing that the buildup of the electric double layer is limited by the electrical capacity of the capacitor formed by the electrode surface and the adjacent Stern layer. In the same way the Stern layer is in series with the diffuse layer from an electrical point of view, this capacity limitation can be introduced into the model by putting an electrical capacitor in series to each electrode. The capacitors limit the uptake of ions and thus enable the control of the salt adsorption capacity of the CDI cell. Furthermore, they correctly display the increase of the potential drop in the Stern layer during charging. For example, the amount of charge stored in the capacitor added in series to the cathode is given by:

$\begin{array}{ll}{Q}_{cath}=C_{cath}·\Delta {\varphi }_{St,cath}& (10)\end{array}$

Here, Q_cath is the charge of the cathode, C_cath the electrical capacity of the cathode, and ϕ_St,cath the Stern potential. The amount of charge stored is connected to the amount of ionic species c_Xi stored in the cathode by Faraday's law:

$\begin{array}{ll}{Q}_{cath}=F·\sum z_{X_i}·c_{X_{i,cath}}& (11)\end{array}$

Finally, we consider the voltage across the cell that equals the sum of voltage drops along the complete circuit (compare Equation 12). Here Δϕ_St,cath, Δϕ_St,an are the respective Stern potentials in the cathode and anode, Δϕ_D,cath, Δϕ_D,an the potential difference between bulk solution (or macropore) and the respective electrode and Δϕ_{current lead+electrolyte} the potential drop caused by the electrical resistivity of the current leads, current collectors as well as the electrolyte solution. The electrical resistivity of the current collectors and the electrolyte were considered by adding variable electrical resistors to the CDI cell which picture the specific voltage drops in the wiring and the electrolyte across the flow channel of CDI cell. The applied relationship for the resistivity R = R₀ + R_c/c contains a constant term R₀, representing the resistivity of the current leads and collectors. The second term symbolizes an electrode specific term R_c varying with ionic strength of the electrolyte (Biesheuvel et al., 2011b). For this, the concentrations in the bulk can be determined by a sensor object of Modelica, modified by mathematical expressions and used as an input for the resistivity of the variable resistor (see yellow boxes in Figure 1).

$\begin{array}{l}{V}_{cell}=\Delta {\varphi }_{St,cath}+{\Delta \varphi }_{D,cath}+{\Delta \varphi }_{St,an}+{\Delta \varphi }_{D,an}\\ +{\Delta \varphi }_{currentlead+electrolyte}& (12)\end{array}$

What is important to mention is the fact that the introduced equations only have the purpose to illustrate the mathematical background of the CDI cell model implemented by Modelica objects and how these interrelationships are compared to conventional CDI models. However, none of these equations has to be implemented manually; the model is simply created by drag and drop of the respective Modelica objects, wiring the respective connectors and entering the required parameters describing the CDI cell.

Enhanced Model Including Water Dissociation

To picture a more general model of the processes in a CDI cell and to be able to show pH effects, water dissociation was implemented into the model (compare Figure 2). The species H+ und OH- were added (see green boxes in Figure 2), including the possibility that these ions could accumulate or deplete in the micropores of the electrodes (see gray boxes in Figure 2). In the compartments feed, bulk, and effluent, the dissociation equilibrium of water was included by applying the Modelica object “chemical reaction” (see green boxes Figure 2). In this manner, other dissociation reactions, e.g., of weak acids, could also be easily implemented in the Modelica CDI model.

FIGURE 2

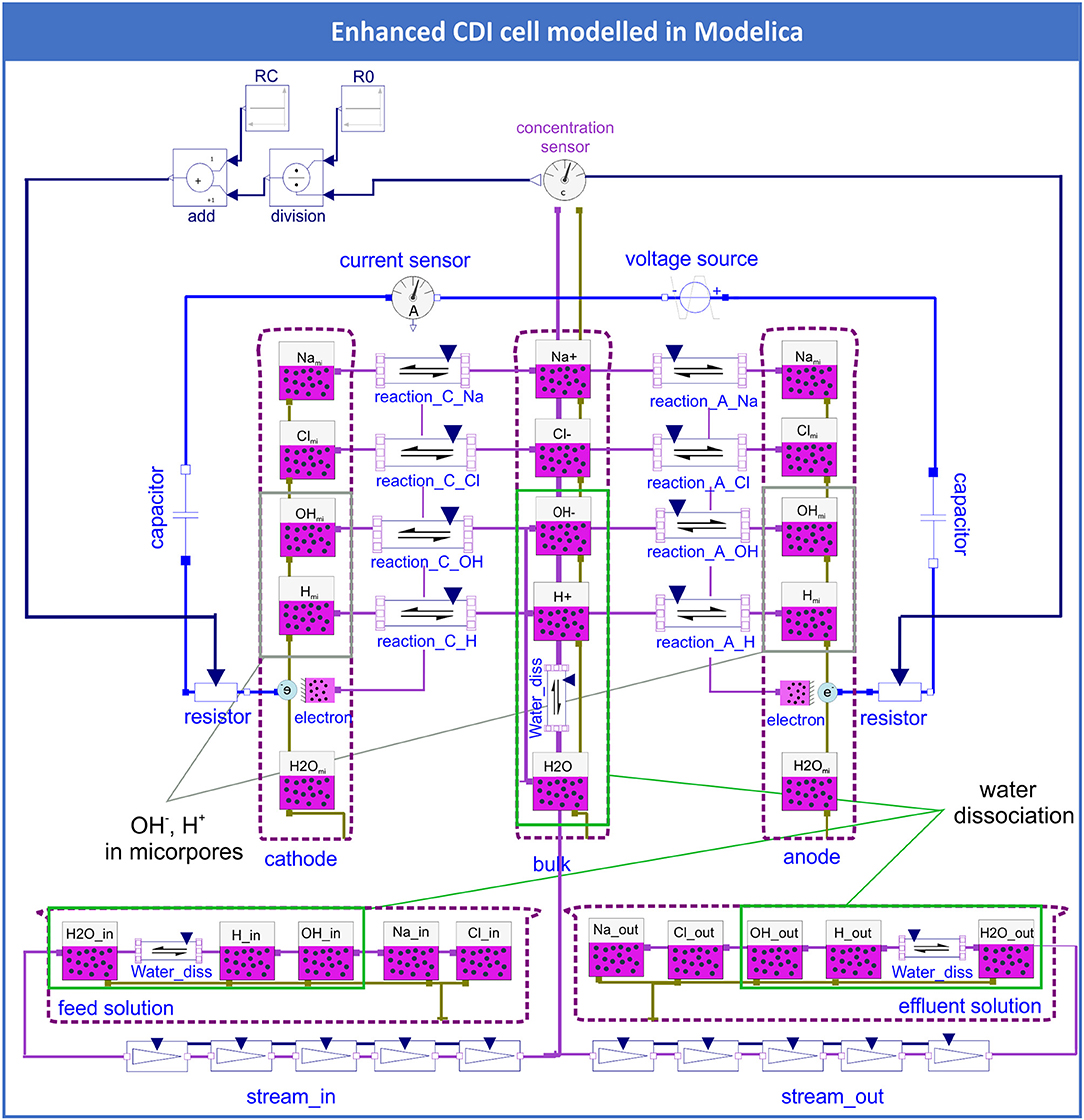
Figure 2. Enhanced CDI model that includes the species OH⁻ and H⁺ in the bulk, feed and effluent solutions (green frames) in addition to the adsorbed species OH_mi and H_mi on the electrodes (gray frames).

Results and Discussion

To validate the model presented here, simulation results are first compared to published simulation results of different versions of the modified Donnan model (Zhao et al., 2010; Biesheuvel et al., 2011b; Zhao, 2013). In a second step, the model predictions are compared to experimental results. For the analysis of simulated data, OpenModelica offers the possibility to study the time dependency of all parameters without the declaration of output variables. Furthermore, data can be transferred to other software such as MATLAB for analysis or further calculations, enabling easy and automated data analysis.

Simulation of Equilibrium Data

In Figure 3 simulation results of equilibrium data are plotted and compared to literature results of Biesheuvel et al. (2011b). The dependences of the calculated ion concentration in the micropores on the applied voltage can be seen. Thereby the co-ion concentration as well as the counter-ion concentration is plotted vs. the applied voltage for two different bulk concentrations. In Figure 3A, literature results taken from Biesheuvel et al. (2011b) are plotted which were predicted following calculations according to Equation 1. Biesheuvel et al. (2011b) calculated the ion concentration in the micropores by using a modified Donnan model which includes a chemical attraction term ${\mu }_{X_i}^{°}$ of 2 kT to consider non-electrostatic adsorption. Further calculation parameters were an electrode mass density of 0.58 g/ml and a microporosity of 0.37. Biesheuvel et al. also included a voltage depending Stern capacity following the empirical expression ${\text{C}}_{\text{st}}={\text{C}}_{\text{st},0}+\alpha ·\Delta {\varphi }^2$, where C_st,0 is the Stern capacity at 0 V and α represents the non-linear part of the Stern capacity (Zhao et al., 2010; Biesheuvel et al., 2011b; Zhao, 2013). In Figure 3B, simulated data using our Modelica model is shown. For this, all parameters (${\mu }_{X_i}^{°},$electrode mass density, microporosity etc.) were chosen accordingly to values used by Biesheuvel et al. (2011b) to derive a comparable model setup. In Modelica Stern capacity is represented by the capacitors used in the model. To fit the model to the literature results a voltage depending capacitor was chosen. It can be seen that both models predict consistent results showing that with increasing cell voltage the concentration of the counterions in the micropores increases, while the concentration of the co-ions is decreased. By assuming a chemical attraction ${\mu }_{X_i}^{°}$, an adsorption affinity is defined which permits adsorption even in the absence of an applied potential. By applying a cell voltage, co-ions are repelled from the electrodes, which leads to a negative micropore concentration relatively to the amount adsorbed at zero cell voltage. In Figure 4, the corresponding SAC values and charge efficiencies are plotted against the applied cell voltage. The literature results (solid line) as well as the simulated data (squares) are shown. Both models were calculated by adding a chemical attraction term of $\Delta {\mu }_{X_i}^{°}=2kT$ and again the results are highly consistent. Looking at the predicted charge efficiency in Figure 4, it can be seen that the charge efficiency increases with increasing voltage and is higher for lower bulk concentrations. This is reasonable, considering the effect of co-ion expulsion from the electrode. This effect gets more important for lower potentials or higher concentrations, where the ratio between non-electrostatically adsorbed and electrostatically adsorbed ions is high. The predicted SAC also increases for higher voltages and is higher for lower bulk concentrations. Again, the importance of co-ion repulsion when compared to capacitive ion adsorption is the reason for this trend.

FIGURE 3

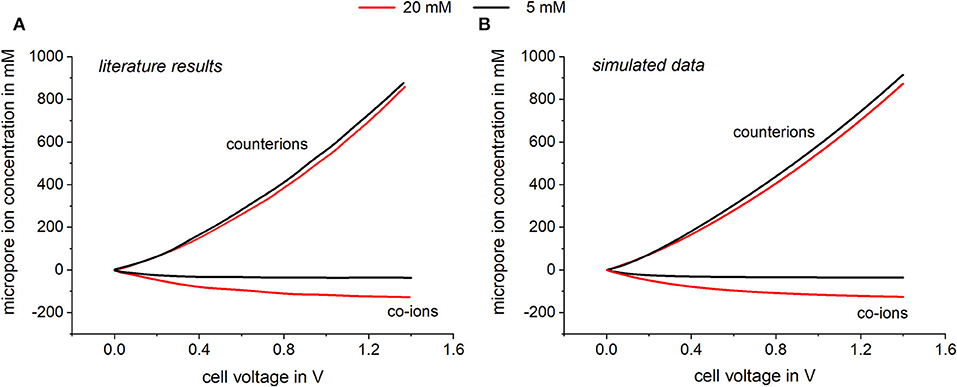
Figure 3. Comparison of the calculated micropore concentration relative to the adsorption at zero cell voltage of (A) the modified Donnan model and (B) with values calculated by Modelica. For the simulation, a variable capacitor was chosen represented by the empirical expression $C_{st}=C_{st,0}+\alpha ·\Delta {\varphi }^2$ with C_st,0 = 75 F and α = 10 F.

FIGURE 4

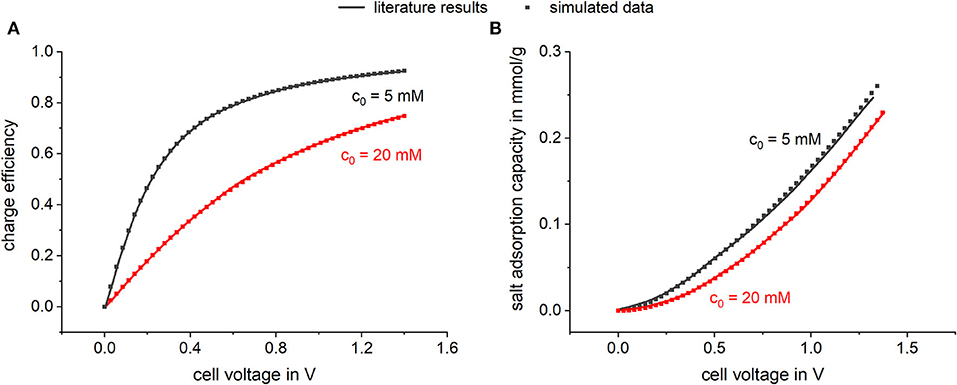
Figure 4. Simulated (A) charge efficiency and (B) salt adsorption capacity vs. cell voltage in comparison to literature results. For the simulation, a variable capacitor was chosen represented by the empirical expression $C_{st}=C_{st,0}+{\alpha }^{*}\Delta {\varphi }^2$ with C_st,0 = 75 F and α = 10 F.

Simulation of Kinetic Data

Kinetic aspects of a complete CDI-cell were calculated and compared to literature results by Zhao et al. (2010). Again literature results are derived by calculations based on the modified Donnan model. To fit Modelica data to the literature results an electrode specific resistor was chosen and adapted. This was done by a variable resistor depending on the concentration in the macropores as described in section Implementation of a simple CDI model and in analogy to the kinetic terms of the models of Biesheuvel et al. (2011b) and Zhao et al. (2010). For the simulation of the CDI process a flow rate of 60 ml/min for cyclic constant voltage operation with desorption at 0 V was chosen for both models. The results can be seen in Figure 5 where the bulk concentration over time is shown for different applied voltages and initial bulk concentrations. By comparing both models again a good agreement between literature and simulated data can be seen, validating the suitability of our model also in case of the prediction of kinetic data. Small differences in the kinetic behavior can be recognized between the models. These differences can be explained by the additional kinetic reaction coefficient which comes with the “reaction” model defined in the Modelica language and which we used to simulate the electrosorption of charged substances in the micropores of the electrodes. In contrast to the conventional formulation of the modified Donnan model, our model does not assume this as a spontaneous process which reaches local equilibrium instantaneously, but as a kinetic process having a fast but defined reaction rate.

FIGURE 5

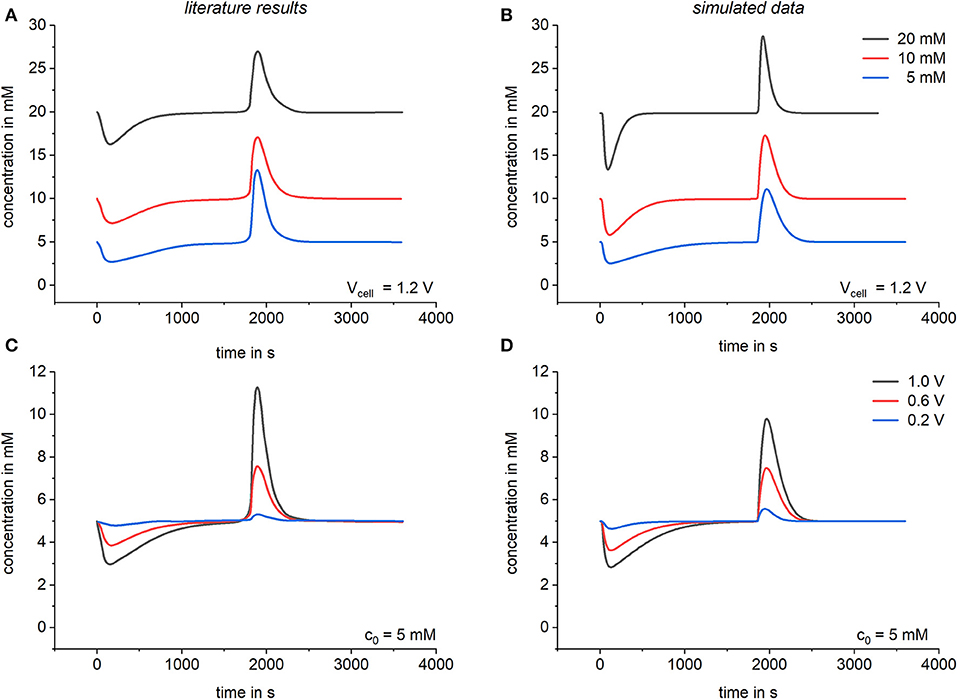
Figure 5. Comparison of the kinetic behavior. Literature results based on the modified Donnan model by Zhao et al. (2010) are shown in (A,C) and are compared to results simulated by Modelica in (B,D). Calculations were done by using a variable resistor R = R₀ + R_c/c with R₀ = 1 Ω and$R_c=22\Omega ·m^3/mol$.

Prediction of pH Effects

In terms of CDI, another important point is the effect of pH changes in between feed and effluent solution, as this can have a significant effect on the long-term stability of the electrodes (Cohen et al., 2013; Dykstra et al., 2017). To study those effects, water dissociation and the electrosorption of H⁺ and OH⁻ were implemented in the CDI model and the pH values resulting from different cell voltages were calculated for the bulk and the micropores (compare section Enhanced model including water dissociation). This enhanced model was compared to results available from literature (Dykstra et al., 2017) which is shown in Figure 6A. In the model of Dykstra et al. the general chemical attraction term μ_att is replaced by acidic and basic surface groups having a specific surface charge in the electrode. Nevertheless, results simulated with Modelica show that at least in the case of equal surface charges of the acidic and basic groups, the assumption of a chemical attraction delivers the same results, if the different regions of the electrode are averaged. To adjust simulated data to the literature results, again a chemical attraction term of ${\mu }_{X_i}^{°}=2kT$ proved to be suitable (see Figure 6B). If equilibrium calculations are conducted with a small stagnant bulk volume representing the flow channel, the two models predict the same pH behavior with respect to dependency on the applied voltage. Because of the balanced attraction of H⁺ and OH⁻ ions, the pH value in the bulk solution does not vary with the voltage, whereas the pH value in the cathode decreases with increasing cell voltage, a situation that is reversed at the anode. This is reasonable as it has to be considered that Equation 1 describing the ratio between the ion concentration in the micro- and macropores also holds for protons and hydroxyl ions. Therefore, the accumulation of protons on the anode and hydroxyl ions in the cathode is strictly coupled to the electrosorption of Na⁺ and Cl⁻ associated with the Donnan potential.

FIGURE 6

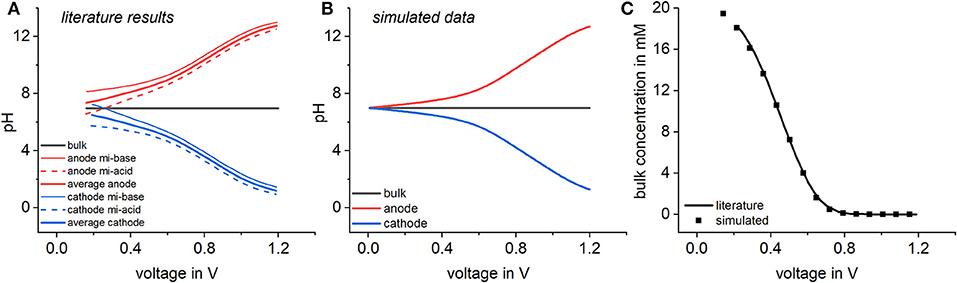
Figure 6. pH variations on the electrodes and in the bulk solution. Literature results by Dykstra et al. (2017) are plotted in (A) and calculated results with the enhanced model in (B). The dependency of the bulk Na+ concentration on the applied voltage is compared to the model (C).

Even in the case of electrodes with high capacity, the ion concentration in the cathode hardly exceeds 500 mM. Given an ion concentration of 5 mM in the bulk, this results in a ratio between the ion concentration in the micro- and macropores of 100. If the Donnan potential drives the same ratio for protons, this means that the pH in the cathode is only moderately decreased by two pH units compared to the pH in the bulk. Therefore extreme pH differences between the bulk and the electrodes, as shown in Figure 6A, are only possible if the amount of Na ions in the bulk solution is highly depleted in the course of the CDI process. For illustration, the equilibrium concentration of Na+ in the bulk as a function of the cell voltage is plotted in Figure 6C. A comparison shows that after the introduction of protons, hydroxyl ions, and the water dissociation reaction, the enhanced model is able to reproduce the recently published pH effects in CDI electrodes. The simplicity of how this could be achieved paves the way for the future introduction of further chemical equilibria such as the dissociation of weak electrolytes, in order to the study how this effects CDI processes.

Comparison With Experimental Data

In order to validate the model, simulated data were compared to experimental results. The experimental results were obtained by using a commercially available CDI cell (Ecomite U, PureChem CO., LTD). The dimensions of the electrodes were 10 × 10 cm² with a total weight of 3.32 g and a micropore volume of 0.62 ml/g which was measured using a BET analysis (Quantachrome Instruments). The experiments were done with a NaCl concentration of 10 mmol/l at a cell potential of 1.2 V and a flow rate of 2 ml/min. The voltage was applied with a potentiostat (Reference 600, Gamry Instruments) and the current was detected throughout the experiment. The pH value was measured with a pH meter (pH Meter 766 Calimatic, Knick) and the ion conductivity was determined online using a conductivity meter (Konduktometer 703, Knick) from which the ion concentration was calculated. For the simulation, all parameters (flow rate, bulk concentration etc.) were chosen in accordance to experimental data and a chemical attraction term of 2 kT was added. Again, a variable resistor was used, as explained in section Simulation of kinetic data, and a capacitance of 70 F was chosen. In Figure 7, the experimentally determined results as well as the simulated data are shown together. It can be seen that by using the enhanced model it is possible to predict the behavior of a complete CDI cell including a qualitative description of pH effects occurring in the bulk solution. While SAC and charge efficiency show a very good quantitative agreement between experimental and simulated data, the predicted pH effects are two small and the mean pH value of the experimental data is shifted toward slightly acidic values. The reasons for these discrepancies can be found, on the one hand in the neglection of functional groups, such as e.g., carboxy, at the carbon surface. On the other hand, the shift of the whole pH curve is probably caused by dissolved atmospheric CO₂. While the implementation of functional surface groups and dissolved carbon dioxide species would also be possible in the Modelica programming environment, for the sake of simplicity we did not add this feature in the current version of our model.

FIGURE 7

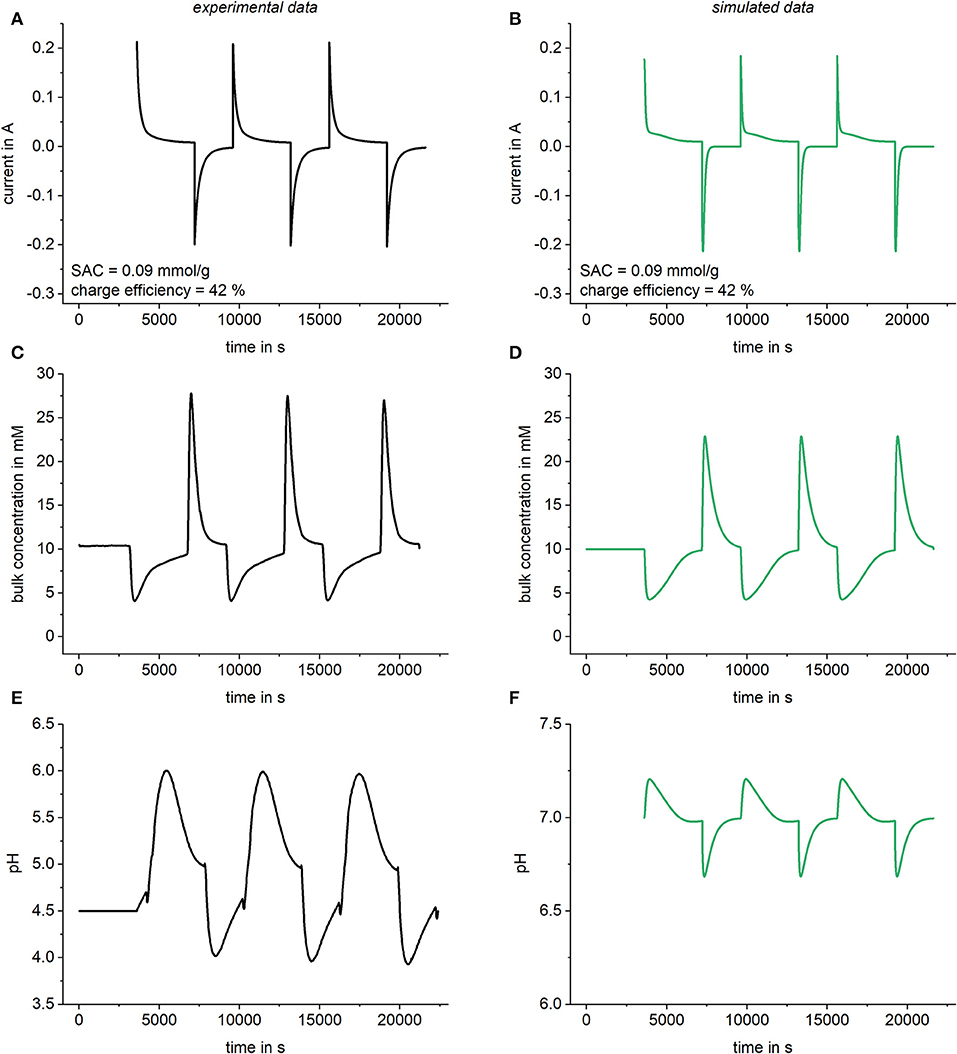
Figure 7. Comparison of experimentally determined data and simulated data. Results for the current in the cell (A,B), the bulk concentration (C,D) as well as the pH value (E,F) were compared. For the simulations, a variable resistor R = R₀ + R_c/c was used with R₀ = 1 Ω and$R_c=250\Omega ·m^3/mol$.

As explained in section Simulation of kinetic data, Modelica components can be easily changed by drag and drop. With this procedure, the same model can be used to simulate constant current experiments by changing the voltage source into a current source. Figure 8 shows a comparison of results and experimental data for such a constant current case. In accordance with the experimental setup, a flow rate of 1 ml/min, a concentration of 20 mM of NaCl, and a current source of 0.016 A were chosen for the simulation parameters. Furthermore, a variable resistor, a capacitor of 70 F and a chemical attraction term of 1.5 kT were used for the simulation. Looking at Figure 8, it is obvious that prediction of values for constant current experiments is possible and matches well with experimental results.

FIGURE 8

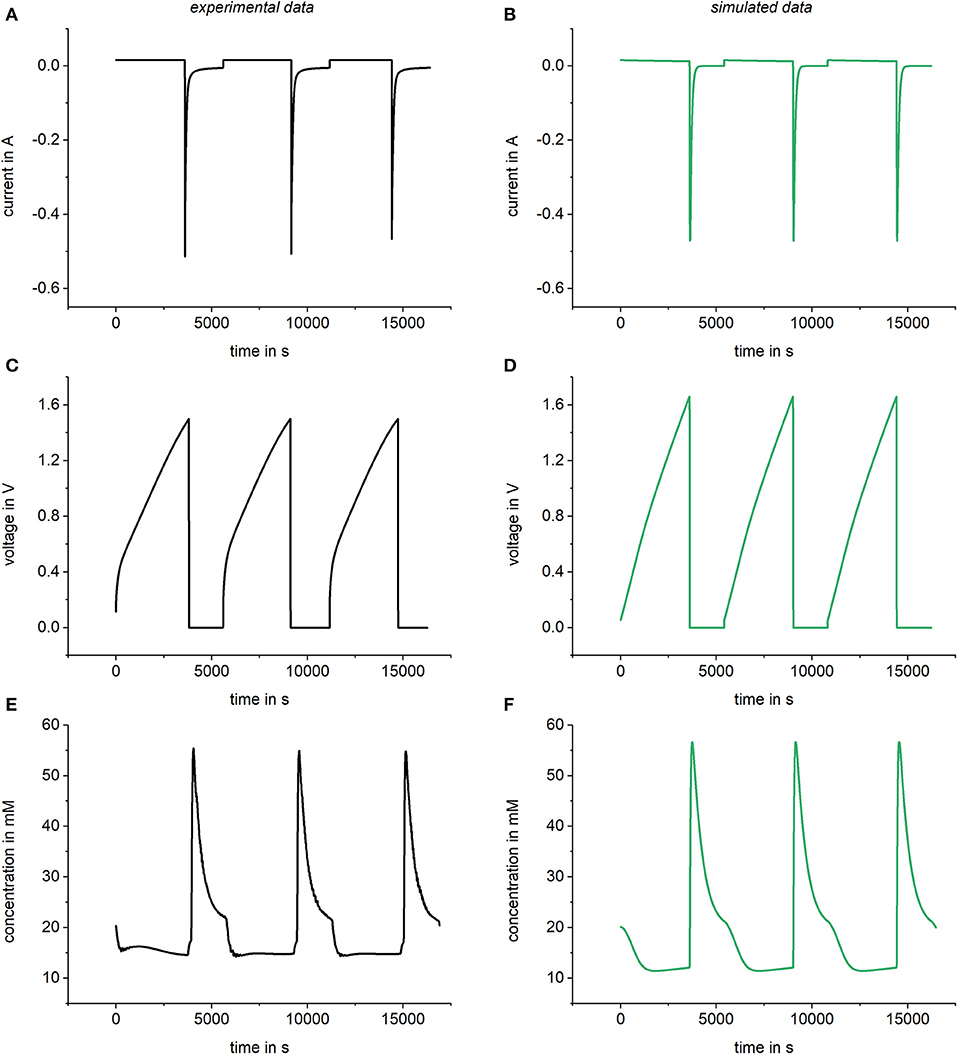
Figure 8. Comparison of experimental data and simulated data (right) using a constant current source of 0.016 A. Results for the current in the cell (A,B), the voltage (C,D), and the bulk concentration (E,F) were compared. For the simulations, a variable resistor R = R₀ + R_c/c was used with R₀ = 1 Ω and$R_c=250\Omega ·m^3/mol$.

Conclusion

In this work, a new modeling technique for CDI processes was demonstrated using the software OpenModelica, which is based on the object-oriented modeling language Modelica. Two models with different complexity were presented and were shown to be able to describe the main aspects of a CDI process, including time courses of the concentrations within the effluent and the electrodes and the current and potential drops at different locations in the cell. In addition, the model delivers performance parameters such as SAC, current and charge efficiency. Predicted results were compared to different literature results calculated by using state of the art modified Donnan models. The predictions show a very good agreement to literature results in terms of equilibrium as well as kinetics. Specific effects such as pH variations on the electrodes and in the bulk solution can be simulated by using the enhanced model; it was shown again that predicted results are comparable to results found in literature. The flexibility of the modeling approach was illustrated by a very simple switch to a variant simulating constant current charging and short-circuited discharge. Other adaptations like simulating e.g., voltage fluctuations during the CDI process are conceivable. Furthermore, we see the legitimation of our model not only in its graphical interface and the easy and straightforward usage, but in the possibility of the fast and easy adaption to new process setups, complex environmental conditions in real operation set-ups all the way to the possibility of building a digital twin of complete CDI process plants.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

ML executed the simulations and wrote the manuscript together with MF, who developed the concept of the paper. RW and EH conducted experimental studies.

Funding

The authors would like to thank the German Federal Ministry of Education and Research for the funding (FKZ: 13XP5038B) as well as the KIT-Publication Fund of the Karlsruhe Institute of Technology.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fceng.2020.00003/full#supplementary-material

References

Anderson, M. A., Cudero, A. L., and Palma, J. (2010). Capacitive deionization as an electrochemical means of saving energy and delivering clean water. Comparison to present desalination practices: will it compete? Electrochim. Acta 55, 3845–3856. doi: 10.1016/j.electacta.2010.02.012

CrossRef Full Text | Google Scholar

Andres, G. L., Mizugami, T., and Yoshihara, Y. (2017). Simulation of an electric behavior of the CDI system. Desalination 419, 211–218. doi: 10.1016/j.desal.2017.06.011

CrossRef Full Text | Google Scholar

Avraham, E., Noked, M., Bouhadana, Y., Soffer, A., and Aurbach, D. (2009). Limitations of charge efficiency in capacitive deionization II. on the behavior of CDI cells comprising two activatedcarbon electrodes. J. Electrochem. Soc. 156, P157–62. doi: 10.1149/1.3193709

CrossRef Full Text

Biesheuvel, P. M., and Bazant, M. Z. (2010). Nonlinear dynamics of capacitive charging and desalination by porous electrodes. Phys. Rev. E 81:031502. doi: 10.1103/PhysRevE.81.031502

PubMed Abstract | CrossRef Full Text | Google Scholar

Biesheuvel, P. M., Fu, Y., and Bazant, M. Z. (2011a). Diffuse charge and faradaic reactions in porous electrodes. Phys. Rev. E Stat. Nonlin. Soft. Matter Phys. 83:061507. doi: 10.1103/PhysRevE.83.061507

PubMed Abstract | CrossRef Full Text | Google Scholar

Biesheuvel, P. M., Fu, Y., and Bazant, M. Z. (2012). Electrochemistry and capacitive charging of porous electrodes in asymmetric multicomponent electrolytes. Russ. J. Electrochem. 48, 580–592. doi: 10.1134/S1023193512060031

CrossRef Full Text | Google Scholar

Biesheuvel, P. M., Porada, S., Levi, M., and Bazant, M. Z. (2014). Attractive forces in microporous carbon electrodes for capacitive deionization. J. Solid State Electrochem. 18, 1365–1376. doi: 10.1007/s10008-014-2383-5

CrossRef Full Text | Google Scholar

Biesheuvel, P. M., van Limpt, B., and van der Wal, A. (2009). Dynamic adsorption/desorption process model for capacitive deionization. J. Phys. Chem. C 113, 5636–5640. doi: 10.1021/jp809644s

CrossRef Full Text | Google Scholar

Biesheuvel, P. M., Zhao, R., Porada, S., and van der Wal, A. (2011b). Theory of membrane capacitive deionization including the effect of the electrode pore space. J. Colloid Interface Sci. 360, 239–248. doi: 10.1016/j.jcis.2011.04.049

PubMed Abstract | CrossRef Full Text | Google Scholar

Biesheuvel, P. M., Suss, M. E., and Hamelers, H. V. M. (2015). Theory of water desalination by porous electrodes with fixed chemical charge. Colloids Interface Sci. Commun. 9, 1–5. doi: 10.1016/j.colcom.2015.12.001

CrossRef Full Text | Google Scholar

Cohen, I., Avraham, E., Bouhadana, Y., Soffer, A., and Aurbach, D. (2013). Long term stability of capacitive de-ionization processes for water desalination: the challenge of positive electrodes corrosion. Electrochim. Acta 106, 91–100. doi: 10.1016/j.electacta.2013.05.029

CrossRef Full Text | Google Scholar

Dykstra, J. E., Keesman, K. J., Biesheuvel, P. M., and van der Wal, A. (2017). Theory of pH changes in water desalination by capacitive deionization. Water Res. 119, 178–186. doi: 10.1016/j.watres.2017.04.039

PubMed Abstract | CrossRef Full Text | Google Scholar

Dykstra, J. E., Porada, S., van der Wal, A., and Biesheuvel, P. M. (2018). Energy consumption in capacitive deionization - constant current versus constant voltage operation. Water Res. 143, 367–375. doi: 10.1016/j.watres.2018.06.034

PubMed Abstract | CrossRef Full Text | Google Scholar

Elmqvist, H., Mattsson, S. E., and Otter, M. (1998). Modelica — The new object-oriented modeling language. The 12th European Simulation Multiconference, ESM'98 (Manchester).

Google Scholar

Fritzson, P. (2015). Principles of Object Oriented Modeling and Simulation With Modelica 3.3: A Cyber-physical Approach. Hoboken NJ: IEEE Press; Wiley. doi: 10.1002/9781118989166

CrossRef Full Text | Google Scholar

Fritzson, P. A. (2011). Introduction to Modeling and Simulation of Technical and Physical Systems With Modelica. Hoboken NJ: Wiley; IEEE Press. doi: 10.1002/9781118094259

CrossRef Full Text | Google Scholar

Gude, V. G. (2016). Desalination and sustainability - an appraisal and current perspective. Water Res. 89, 87–106. doi: 10.1016/j.watres.2015.11.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, L., Karthikeyan, K. G., Anderson, M. A., and Gregory, K. B. (2014). Exploring the impact of pore size distribution on the performance of carbon electrodes for capacitive deionization. J. Colloid Interface Sci. 430, 93–99. doi: 10.1016/j.jcis.2014.05.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Hemmatifar, A., Oyarzun, D. I., Palko, J. W., Hawks, S. A., Stadermann, M., and Santiago, J. G. (2017). Equilibria model for pH variations and ion adsorption in capacitive deionization electrodes. Water Res. 122, 387–397. doi: 10.1016/j.watres.2017.05.036

PubMed Abstract | CrossRef Full Text | Google Scholar

Hemmatifar, A., Stadermann, M., and Santiago, J. G. (2015). Two-dimensional porous electrode model for capacitive deionization. J. Phys. Chem. C 119, 24681–24694. doi: 10.1021/acs.jpcc.5b05847

CrossRef Full Text | Google Scholar

Jande, Y. A. C., and Kim, W. S. (2013). Desalination using capacitive deionization at constant current. Desalination 329, 29–34. doi: 10.1016/j.desal.2013.08.023

CrossRef Full Text | Google Scholar

Johnson, A. M., and Newman, J. (1971). Desalting by means of porous carbon electrodes. J. Electrochem. Soc. 118, 510–517. doi: 10.1149/1.2408094

CrossRef Full Text | Google Scholar

Kang, J., Kim, T., Jo, K., and Yoon, J. (2014). Comparison of salt adsorption capacity and energy consumption between constant current and constant voltage operation in capacitive deionization. Desalination 352, 52–57. doi: 10.1016/j.desal.2014.08.009

CrossRef Full Text | Google Scholar

Kim, T., Dykstra, J. E., Porada, S., van der Wal, A., Yoon, J., and Biesheuvel, P. M. (2015). Enhanced charge efficiency and reduced energy use in capacitive deionization by increasing the discharge voltage. J Colloid Interface Sci. 446, 317–326. doi: 10.1016/j.jcis.2014.08.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, J., He, C., Di He, Zhang, C., and Waite, T. D. (2018). Analysis of capacitive and electrodialytic contributions to water desalination by flow-electrode CDI. Water Res. 144, 296–303. doi: 10.1016/j.watres.2018.07.049

PubMed Abstract | CrossRef Full Text | Google Scholar

Matejak, M. (2015). Formalization of Integrative Physiology. dissertation thesis. Prague: Charles University in Prague, First Faculty of Medicine.

Matejak, M., Tribula, M., JeŽek, F., and Kofranek, J. (2015). “Free modelica library for chemical and electrochemical processes,” in Proceedings of the 11th International Modelica Conference (Versailles: Linköping University Electronic Press), 359–366. doi: 10.3384/ecp15118359

CrossRef Full Text | Google Scholar

Oren, Y. (2008). Capacitive deionization (CDI) for desalination and water treatment — past, present and future (a review). Desalination 228, 10–29. doi: 10.1016/j.desal.2007.08.005

CrossRef Full Text | Google Scholar

Porada, S., Weinstein, L., Dash, R., van der Wal, A., Bryjak, M., Gogotsi, Y., et al. (2012). Water desalination using capacitive deionization with microporous carbon electrodes. ACS Appl. Mater. Interfaces 4, 1194–1199. doi: 10.1021/am201683j

PubMed Abstract | CrossRef Full Text | Google Scholar

Porada, S., Zhao, R., van der Wal, A., Presser, V., and Biesheuvel, P. M. (2013). Review on the science and technology of water desalination by capacitive deionization. Prog. Mater. Sci. 58, 1388–1442. doi: 10.1016/j.pmatsci.2013.03.005

CrossRef Full Text | Google Scholar

Ryu, J.-H., Kim, T.-J., Lee, T.-Y., and Lee, I.-B. (2010). A study on modeling and simulation of capacitive deionization process for wastewater treatment. J. Taiwan Inst.Chem. Eng. 41, 506–511. doi: 10.1016/j.jtice.2010.04.003

CrossRef Full Text | Google Scholar

Suss, M. E., Porada, S., Sun, X., Biesheuvel, P. M., Yoon, J., and Presser, V. (2015). Water desalination via capacitive deionization: what is it and what can we expect from it? Energy Environ. Sci. 8, 2296–2319. doi: 10.1039/C5EE00519A

CrossRef Full Text | Google Scholar

Wang, L., and Lin, S. (2018). Membrane capacitive deionization with constant current vs constant voltage charging: which is better? Environ. Sci. Technol. 52, 4051–4060. doi: 10.1021/acs.est.7b06064

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Xu, X., Kim, J., Malgras, V., Mo, R., Li, C., et al. (2019). Nanoarchitectured metal–organic framework/polypyrrole hybrids for brackish water desalination using capacitive deionization. Mater. Horiz. 6, 1433–1437. doi: 10.1039/C9MH00306A

CrossRef Full Text | Google Scholar

Xu, X., Allah, A. E., Wang, C., Tan, H., Farghali, A. A., Khedr, M. H., et al. (2019a). Capacitive deionization using nitrogen-doped mesostructured carbons for highly efficient brackish water desalination. Chem. Eng. J. 362, 887–896. doi: 10.1016/j.cej.2019.01.098

CrossRef Full Text | Google Scholar

Xu, X., Tan, H., Wang, Z., Wang, C., Pan, L., Kaneti, Y. V., et al. (2019b). Extraordinary capacitive deionization performance of highly-ordered mesoporous carbon nano-polyhedra for brackish water desalination. Environ. Sci. Nano 6, 981–989. doi: 10.1039/C9EN00017H

CrossRef Full Text | Google Scholar

Xu, X., Tang, J., Kaneti, Y. V., Tan, H., Chen, T., Pan, L., et al. (2020). Unprecedented capacitive deionization performance of interconnected iron–nitrogen-doped carbon tubes in oxygenated saline water. Mater. Horiz. 132:282. doi: 10.1039/C9MH01829H

CrossRef Full Text | Google Scholar

Zhao, R. (2013). Theory and Operation of Capacitive Deionization Systems. Wageningen: Wageningen University.

Google Scholar

Zhao, R., Biesheuvel, P. M., Miedema, H., Bruning, H., and van der Wal, A. (2010). Charge efficiency: a functional tool to probe the double-layer structure inside of porous electrodes and application in the modeling of capacitive deionization. J. Phys. Chem. Lett. 1, 205–210. doi: 10.1021/jz900154h

CrossRef Full Text | Google Scholar

Zhao, R., Biesheuvel, P. M., and van der Wal, A. (2012). Energy consumption and constant current operation in membrane capacitive deionization. Energy Environ. Sci. 5:9520–7. doi: 10.1039/C2EE21737F

CrossRef Full Text | Google Scholar

Zou, L., Li, L., Song, H., and Morris, G. (2008). Using mesoporous carbon electrodes for brackish water desalination. Water Res. 42, 2340–2348. doi: 10.1016/j.watres.2007.12.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Nomenclature