
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Cell Dev. Biol., 03 May 2022
Sec. Morphogenesis and Patterning
Volume 10 - 2022 | https://doi.org/10.3389/fcell.2022.871950
This article is part of the Research TopicPattern Formation in BiologyView all 13 articles
This is a brief account of Turing’s ideas on biological pattern and the events that led to their wider acceptance by biologists as a valid way to investigate developmental pattern, and of the value of theory more generally in biology. Periodic patterns have played a key role in this process, especially 2D arrays of oriented stripes, which proved a disappointment in theoretical terms in the case of Drosophila segmentation, but a boost to theory as applied to skin patterns in fish and model chemical reactions. The concept of “order from fluctuations” is a key component of Turing’s theory, wherein pattern arises by selective amplification of spatial components concealed in the random disorder of molecular and/or cellular processes. For biological examples, a crucial point from an analytical standpoint is knowing the nature of the fluctuations, where the amplifier resides, and the timescale over which selective amplification occurs. The answer clarifies the difference between “inelegant” examples such as Drosophila segmentation, which is perhaps better understood as a programmatic assembly process, and “elegant” ones expressible in equations like Turing’s: that the fluctuations and selection process occur predominantly in evolutionary time for the former, but in real time for the latter, and likewise for error suppression, which for Drosophila is historical, in being lodged firmly in past evolutionary events. The prospects for a further extension of Turing’s ideas to the complexities of brain development and consciousness is discussed, where a case can be made that it could well be in neuroscience that his ideas find their most important application.
As graduate students in the early 1970s, we were aware of Turing’s reaction-diffusion theory of pattern formation, but it was at that time more a curiosity than a part of mainstream developmental thinking. Fifty years on, Turing’s ideas have been successfully applied to a number of developmental systems (Maini et al., 2006; 2012; Othmer et al., 2009; Kondo and Miura, 2010; Davidson and Baum, 2012; Chatterjee et al., 2020; Green, 2021), though the mechanistic details often differ from his original proposal, with chemical autocatalysis being replaced by other self-enhancing molecular or cellular processes, and distance effects by other means of material transport, or by mechanochemical effects (for the latter, see Murray and Oster, 1984; Howard et al., 2011; Brinkmann et al., 2018; Veerman et al., 2021). For theorists, there have been disappointments along the way, in that patterns that appeared to match theoretical prediction were shown to arise by other mechanisms. But despite this, the theoretical enterprise has now reached a healthy middle age, with expectations of a vigorous and productive future. This review is designed as a broad survey with a focus less on mechanistic details than on what I consider the main turning points in the acceptance of Turing’s insight regarding the kinetic basis of pattern selection, whether specifically by reaction and diffusion, or via other means of self-enhancement and action over distance. While my account of the subject is retrospective, the intent is not, as my interest is in part to consider how Turing’s ideas might be extended in future, notably to neuroscience, as a way of accounting for the precise construction of the neurocircuitry required to support consciousness in the brain (Lacalli, 2020; Lacalli, 2021). Among scientific problems in search of a solution, this must surely be among the most daunting, and it remains a distinct possibility that the acknowledged importance of Turing to computer science (De Mol, 2021) will be equaled or surpassed in biology should his ideas on patterning prove applicable to the problem of biological consciousness.
The publication of Turing’s paper on morphogenesis (Turing, 1952) resulted in a brief period of interest among biologists, due in part to the efforts of C. W. Wardlaw, then Professor of Cryptogamic Botany at Manchester University (Wardlaw, 1953). Wardlaw would have been familiar with diverse examples of whorl formation and dichotomous branching in algae, ferns and the like, and that comparable patterns occur at both the unicellular and multicellular level (Figure 1). This latter feature probably accounts, at least in part, for the greater willingness of developmental botanists, in contrast to their zoological counterparts, to consider pattern as an entity in its own right irrespective of mechanistic details. So, for example, one can study whorl formation in a single cell, like the dasyclad alga Acetabularia, where distance effects are likely due to diffusion (Dumais et al., 2000), or in the apical meristem of conifers (Harrison and von Aderkas, 2004), where distance effects arise through polar transport of auxin between cells (Reinhardt et al., 2003; Shi and Vernoux, 2019). Auxin transport can also produce patterns suitable for explaining both phyllotaxis (Jönsson et al., 2006) and leaf veins (Mitchison, 1981; Scarpella et al., 2006; Biedroń and Banasiak, 2018) where, for the latter, regularity of spacing along the leaf margin appears to play an important role (Holloway and Wenzel, 2021; Lavania et al., 2021). Yet for all these examples, the mathematical and computational problems of dealing with material flow, growth and mechanistic redundancy will be much the same.
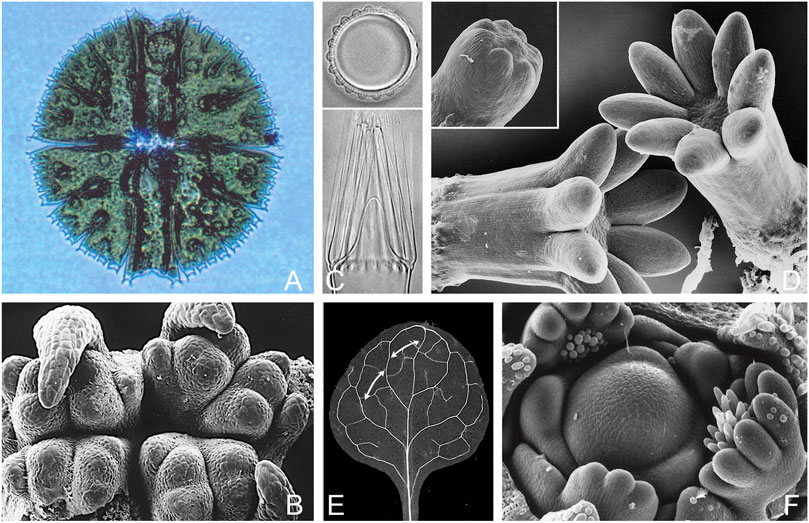
FIGURE 1. Turing-type patterns in plants: branching and whorl formation in uni- and multicellular examples, and leaf venation. (A). Dichotomous branching in one dimension: the freshwater desmid Micrasterias rotata, (cell diameter 230 μm) where form is generated following cell division by branching tip growth along the edge of the expanding semicell. The effective pattern scale (wavelength) declines during this process from ca. 30 μm at the beginning to 5 μm for the distal branches; see Lacalli & Harrison (1987) for quantitative details. (B). Alternating dichotomous branching in two dimensions: the shoot apex of Psilotum nudum, a basal fern whose simple aerial shoots originate through repeated dichotomous branching and only elongate, together, secondarily. Distance between adjacent primordia at this stage is in the 150–200 μm range (Takiguchi et al., 1997), but the pattern wavelength has not been measured through the branching sequence, and could well vary; specimen supplied by T. A. Steeves. (C). Whorl formation in a single cell: the pattern of hair initials (top) and their outgrowth (bottom) in the dasyclad alga Acetabularia. The distance between initials, typically 20 μm in culture, can range between 16 and 28 μm in a predictable way depending on temperature and calcium concentration, and from this one can make useful inferences about the mechanism; see Harrison & Hillier (1985), Dumais & Harrison (2000) for details. (D). Whorl formation in conifers: the cotyledons (primary needles) of cultured white spruce embryos; stem diameter is ca. 750 μm compared with 400 μm when the initials are first evident (inset), with a spacing of ca. 95 μm (Fowke et al., 1994). The most detailed statistical information available on cotyledon spacing is for larch, where the pattern wavelength has been measured precisely, at 98 ± 4 μm (Harrison & von Aderkas, 2004; Holloway et al., 2018). (E). Leaf venation in a young Arabidopsis leaf, where distance between secondary veins (arrows) in part reflects a spacing mechanism that acts along the leaf margin as the primordium develops. The leaf blade is ca. 2 mm long at the stage shown, but the first secondary veins appear when it is 20-fold smaller (100–120 μm long) with an effective wavelength between secondaries as they develop in the 20 μm range, down to a few cell diameters (10–15 μm) in some instances (Scarpella et al., 2006, Wenzel et al., 2007, Verna et al., 2019; see Holloway & Wenzel, 2021 for relevant modeling). The mechanistic basis of the discrepancy between vascular patterning at this scale and that of primordia across the apical meristem is as yet unresolved. (F). The shoot apical meristem of lupin (Lupinus polyphyllus), one of the largest among the angiosperms, with a central dome ca. 250 μm across at its base. The overall pattern of primordia, typical of angiosperms (with some exceptions, e.g., of decussate pattern), is one of spiral phyllotaxy, but the leaves are palmate, developing as partial whorls as can be seen here in three examples, where spacing would appear to be on a scale somewhere below 30 μm; see Runions et al. (2017) for a further discussion of leaf shape in relation to spacing mechanisms acting along the leaf margin. Photo credits: (A, B) T. C. Lacalli, (C) Jacques Dumais, (D) L. C. Fowke, (E) Enrico Scarpella, (F) V. K. Sawhney.
Developmental zoologists, faced with a more diverse range of patterning situations, have tended to focus more on identifying the proximate causal agents in each case than on the general features of broadly based theories like Turing’s. And in any case, the conventional wisdom in the early days, expressed by C. H. Waddington (see Waddington, 1956; page 423), was that a reaction-diffusion mechanism, being “inherently chancy” could at most account for the dapplings and mottlings filling otherwise unimportant spaces. It did not help that the specific equations Turing devised did not always produce regular patterns (Bard and Lauder, 1974), or that the one 2D pattern Turing included in his 1952 paper (his Figure 2) was itself rather irregular. But that example was computed for what Turing himself considered the least interesting case [his case (a), stationary waves of moderate wavelength being case (d)], and his preliminary attempts to document the formation of regular 2D patterns were unpublished at his death (Dawes, 2016). Hence, by default, it was left largely to physical chemists to explore Turing’s ideas more fully, and the energy-dissipative, far-from-equilibrium thermodynamics they embody. This was carried forward initially by Illya Prigogine and his Brussels research group (Prigogine and Lefever, 1968; Nicolis and Prigogine, 1977), using a hypothetical reaction system, the Brusselator, that was subsequently widely used and adapted by others (Tyson and Light, 1973; Harrison, 1987; Subramanian and Murray, 2021). On the experimental side, there was increasing interest in the Belousov-Zhabotinsky reaction, renowned for the production of oscillations and moving waves (Field and Burger, 1985; Zhabotinsky, 2007), a phenomenon so striking at the time as to be met frequently by disbelief among chemists when first encountered. This led, on the theoretical side, to an interest in model reaction systems that produced periodic oscillations that could be used to model biological processes, notably circadian rhythms (Winfree, 1980), segmentation (Cooke and Zeeman, 1976; Newman, 1993; Pourquié, 2003), and the mitotic oscillator, where Tyson has continued to make important contributions (e.g., see Tyson and Novák, 2015).
Interest in Turing’s ideas was reignited among developmental zoologists by two developments, first the work of Gierer and Meinhardt (1972) modeling pattern formation and regeneration in hydra, and second, by Murray’s comparatively well-received (for theory) account of animal coat patterns (Murray, 1981; Murray, 1988). Neither of these efforts, however, led immediately to a reassessment of the relevance of Turing’s theory to a wider range of developmental examples. This was perhaps in part because a role in specifying coat patterns reinforced the existing notion that the theory was applicable only to irregular surface patterns, but also because the Gierer-Meinhardt model, designed to amplify an existing prepattern rather than generating well-controlled patterns ab initio, was not at first widely recognized for being a Turing model in disguise. There was also, for a time, a degree of suspicion verging on hostility towards Turing’s theory on the part of some proponents of other mechanisms, where it should have been obvious from the start that Turing-type mechanisms could well be acting in concert with, for example, position-specific signaling, but at a different stage in the patterning process, as has proved to be the case (Miura, 2013; Green and Sharpe, 2015; Newman et al., 2018).
Even so, the main impediment to wider acceptance of Turing’s ideas among biologists has always been, and remains, a matter of expectations: that theory was to be judged in strictly reductionist terms, as to whether it either does, or does not provide a route towards identifying the proximate entity responsible for the pattern in question, be this a gene, a diffusible morphogen, or something else. This is different from the biomathematical focus, towards anything in biology that yields interesting mathematics, and from preconception of the physical chemistry community, that progress is first and foremost a matter of understanding principles and process, a point of view well represented in Harrison’s account of the subject (Harrison, 1987; Harrison, 1993). Here the details matter less than identifying the range of possible classes of explanation and establishing ground rules for distinguishing between them. Harrison identifies three such classes, of kinetics, self-assembly, and equilibrium, where Turing’s model belongs to the first. But among the broad class of kinetic processes, the subset of importance to patterning are those able to act as selective amplifiers, extracting a signal from the statistical noise of real-time molecular behavior. This is in fact the essence of Turing’s conception, explicit in the form of the solutions, and it precisely on this point, the form of the solutions, that he begins his mathematical account (Turing, 1952, pg. 39). The issue of the sensitivity (i.e., instability) of the un-patterned, homogeneous situation to fluctuations is then raised at various points in the text (e.g., pp. 56–57), using oscillatory electrical circuits as a point of reference. It is this feature I want specifically to highlight as distinguishing Turing’s theory (here Turing-type models or, in Harrison’s usage, kinetic theory and the kinetic preconception more broadly, or the “Turing problem” referred to by Kang et al., 2012), from other ways of accounting for biological pattern. And, for macro-scale biological pattern, kinetic mechanisms with the properties described by Turing would seem to have a distinct edge: “but what else could do it?” Harrison quotes a colleague as saying. The question here is rhetorical, and I return to it below (see section Inelegance and Ratchets, Error Suppression and Time) because, when it is indeed something else that “does it”, that something else needs to be characterized and understood. Applying the order-from-fluctuations principle more generally, there are three things to consider when distinguishing classes of patterning models in terms of what they do and how they do it: the nature of the fluctuations, the identity of the amplifier, and the time scale on which these both operate, where more than one notion of what we mean by “time” may be required.
Of various inaccurate notions about Turing’s theory, the first that needs addressing is Waddington’s objection, that it accounts only for irregular dapplings and mottlings. To do more than this, what is needed is a mechanism that is sufficiently flexible in the patterns it produces that it can be adapted by evolution as required. So, for example, on a two-dimensional surface the Gierer-Meinhardt model produces an irregular array of peaks frozen in place, which is not particularly useful for producing regular patterns of spots or stripes, let alone anything more elaborate. But the Gierer-Meinhardt model is rather idiosyncratic in this respect, because other models, including the Brusselator, generate regular hexagonal arrays of spots with ease. Turing’s own notes show preliminary calculations approaching this result, where there were parallels with contemporary observations in fluid dynamics (Dawes, 2016), but the first fully developed computational examples using reaction-diffusion equations, so far as I am aware, came from my own work on pattern in unicellular algae (Lacalli, 1981). The ability to produce a modulated, well-controlled pattern in two and three dimensions means also the ability to respond to changing influences throughout the non-linear phase of pattern development, including boundary conditions, imposed gradients and the presence of neighboring pattern elements (Hiscock and Megason, 2015), as well as the ability to subdivide cell and tissue domains in an orderly way (Lacalli and Harrison, 1978; Hunding, 1984). In stark contrast to Waddington’s view, and depending on the mechanistic details, boundary conditions and the like, a Turing model can in principle produce almost any pattern one cares to choose, and will do so in a reliable and reproducible fashion: “bespoke” patterning to borrow a phrase from Woolley et al. (2021), with evolution as the customer.
The ability to generate orderly patterns of stripes, in particular, quickly became a focus of attention with the discovery of the pair-rule pattern that precedes the formation of morphologically distinct segments in Drosophila embryos (Hafen et al., 1984 for the fushi-tarazu gene; see also Pick, 2016). The precision of this pattern at the cellular level (Figure 2A), with multiple stripes appearing essentially simultaneously, was astonishing at the time, and was interpreted by some, including myself, as strong circumstantial evidence for the involvement of a kinetic mechanism. The link between Turing and Drosophila stripes proved to be a bridge too far, as position-specific molecular events involving complex assemblages of transcriptional modulators responsive to graded signals along the length of the embryo were soon thereafter shown to be the means by which pattern was specified (Štanojević et al., 1989; Struhl et al., 1989, Struhl et al., 1992; Rivera-Pomar and Jäckle, 1996). This has been characterized as an inelegant solution to the patterning problem (Akam, 1989), in contrast to simplicity of global control over pattern, with pattern landmarks being preset by the action of maternal and gap genes (Diaz-Cuadros et al., 2021). A greater degree of hierarchical control is thereby imposed over what was previously, in more basal arthropods, a self-organizing process of sequential segmentation relying, as in vertebrates, on molecular clocks and moving wavefronts (Salazar-Ciudad et al., 2001; Pourquié, 2003; Hunding and Baumgartner, 2017). A sequential mode of segmentation is characteristic of basal arthropods and short germ band insects like the beetle Tribolium, and there are plausible scenarios for linking this to the Drosophila condition through a complicated series of transitional steps (Clark et al., 2019; Clark, 2021). If there is elegance here, it is well hidden.

FIGURE 2. Selected animal and chemical patterns: stripes, spots, and digits. (A). The Drosophila pair-rule pattern. Left: an embryo at stage 5 (length 505 μm, anterior to the left), nearing the completion of cellularization; nuclei in blue, even-skipped (eve) protein in red, with an enhancer tag (green) showing specificity for some stripes rather than others, a clear demonstration of stripe-specific control over eve expression. Right: detail of the eve transcript pattern; stripe spacing (centre-to-centre distance) is ca. 40 μm. (B). Chemical patterns, showing arrays of spots (left) and labyrinthine stripes (right) produced by the TuIS (thiourea-iodate-sulfite) reaction in a gel medium, a variant of the better known CIMA reaction. Spacing between pattern elements is ca. 2 mm; see Horvath et al. (2009) for details. (C). The ornate boxfish, Aracana ornata, native to waters off South Australia; female (left) and male (right) showing mixed stripe and spotted patterns characteristic of boxfishes, which often vary between the sexes despite, presumably, a common underlying mechanism. (D). Digit development in mouse embryos, showing patterns of the marker Sox9 in wild type limb (top) and the expanded fan of digits produced by the homozygous Gli3 null mutant (bottom). The pattern here is realized as a series of cartilaginous elements, but is a result of a one-dimensional periodicity along the limb margin that lays down a two-dimensional pattern as the limb grows (Hiscock et al., 2017), a 1D to 2D transition comparable to that seen in Micrasterias. The number of digits increases further in Hox11/13 mutants, but the underlying pattern results from Turing-type interactions between the protein products of Bmp, Sox9 and Wnt genes; see Raspopovic et al. (2014) for details; Onimaru et al. (2016), Stewart et al. (2017), Newman et al. (2018) for evolutionary perspectives. Photo credits: (A, left) Thomas Gregor, (A, right) Erik Clark, (B) Istvan Szalai, (C) the Birch Aquarium at Scripps, (D) Rushikesh Sheth and Marian Ros.
Even though the Drosophila pair-rule pattern proved not to depend on a Turing-type mechanism, the striking regularity of the pattern was a significant spur to theorists to understand the conditions under which model systems would generate stripes as opposed to spots or other patterns, in other words, to define the rules for pattern selection. This was first addressed in two nearly simultaneous publications, by Lyons and Harrison (1991) and Ermentrout (1991), making it immediately clear why symmetry features of the non-linear phase of pattern development are important, in that matched positive and negative departures from the steady state favored stripes (Lyons and Harrison, 1992). Further fueled by interest among chemists in the CIMA reaction (Lengyel and Epstein, 1991; Abdelmalek and Bendoukhu, 2020), which forms regular arrays of spots, stripes, and intermediate reticulate or labyrinthine patterns (Figure 2B), a burgeoning experimental literature appeared on pattern in chemical reaction systems (e.g. Ouyang and Swinney, 1991; Boissonade et al., 1995; Konow et al., 2021), with parallel advances in the theory (e.g. Dufiet and Boissonade, 1992; De Wit, 1999; Cross and Greenside, 2009). On the biological side, striking observations on fish pattern by Kondo and Asai (1995) made the likely involvement of a Turing-type mechanism of some kind increasingly hard to deny. And, while fish patterns arise through dynamics operating at the cellular level rather than diffusing reactants (Kondo et al., 2021), this does not matter when the point of the exercise is to validate the theory for kinetic processes as a class. Zebrafish have proven a useful model system here as well (Singh and Nüsslein-Volhard, 2015; Kondo et al., 2021), and even more dramatic patterns, combining arrays of spots, stripes and reticulate intermediates, are seen in coral reef fishes, amongst which boxfishes are noteworthy examples (Figure 2C; see Pearson, 1993, and Othmer et al., 2009 to compare with a range of computed examples). Combining these observations with more recent work on digit patterns (Figure 2D; see Newman and Frisch, 1979; Sheth et al., 2012; Raspopovic et al., 2014; Newman et al., 2018; and Chatterjee et al., 2020 for the basic theoretical case), it appears that two of the main objections to Turing’s ideas as applied to animal systems have been answered, at least for vertebrates, that 1) kinetic theory is perfectly capable of explaining a range of surface patterns that are regular, highly controlled and flexible in their adaptive capabilities, and 2) not only surface pattern, but skeletal patterns lodged within the body depend at least in part on Turing-type mechanisms (see Painter et al., 2021 for other examples of internal patterning).
A final, perennial objection to Turing’s reaction-diffusion mechanism is a supposed lack of robustness, that pattern formation depends on the parameters being adjusted within a narrow range. While this is true to a degree of 2-component models, more recent work has shown that having more components, especially if some are non-diffusing (Marcon et al., 2016; Diego et al., 2018; Landge et al., 2020; Krause et al., 2021), and discrete rather than continuous systems (Leyshon et al., 2021), yields models far more robust than previously supposed possible, and there is now a better understanding of how pattern stability is maintained in the non-linear regime (Subramanian and Murray, 2021). The burden of past misconceptions concerning kinetic theories has thus now, in large part, been removed.
The idea of the inelegance of the mechanisms underlying developmental pattern captures both a superficial truth and a deeper one. On the one hand, inelegance in this context refers to the complexity of developmental phenomena at the molecular level, which verges on the illogical (Lewin, 1984). Elegance equates to simplicity, in that patterning by a Turing-type mechanism can be encapsulated in a few lines of mathematical symbols, whereas accounting for the pair-rule pattern requires a detailed inventory of molecular components and their myriad functional interactions. But while the Drosophila stripe issue was resolved largely in favor of inelegance, the failure of theory, as often in science, proved a more interesting and informative result than success. In this instance, it led to a new appreciation of the problem of achieving a reliable developmental result in the face of the random noise that characterizes molecular events in the real world (Rao et al., 2002; Balázsi et al., 2011). The question was first posed in theoretical terms (Holloway and Harrison, 1999; Kang et al., 2012), and then addressed experimentally in considerable detail using Drosophlia, initially in work carried out by Eric Wieschaus and collaborators (e.g., Houchmandzadeh et al., 2002). This was part an emerging trend that has since made biomolecular science more quantitative (Maddox, 1992; Davidson and Baum, 2012; Gregor et al., 2014), and there is now both a much increased appreciation of the importance of error suppression in developmental systems at the molecular level, with the production of the Drosophila pair-rule pattern as a key model (Petkova et al., 2019; Bauer et al., 2021), and a far better understanding of how this is achieved.
Conceptually, the questions that need addressing, of precision, reliability and robustness, are more general than any one example, or any one pattern. And, if a Turing-type mechanism is not involved, we return to the chemist’s question, above, but now applied to error suppression: “but what else could do it?” The answer from Drosophila is that we have left the realm of microscopically reversible kinetic processes, where Turing models reside, but neither is this structural self-assembly of a jigsaw-puzzle type, e.g., of a virus particle. Instead, the Drosophila pair-rule pattern depends on macromolecular complexes that decode and implement a set of genetic instructions, and are assembled in a series of steps that are, in effect, thermodynamically irreversible (Carey, 1998; Poss et al., 2013). At the level of transcriptional control, this involves multiple enhancer elements that act at the level of the gene in a combinatorial way to optimize the response to graded inputs that convey information on cell position (Chen et al., 2018; Furlong and Levine, 2018; Petkova et al., 2019; Bauer et al., 2021), but there are strategies at all levels of the process, from the shape of the gradients (Song and Hyeon, 2021) to mechanisms for sharpening the stripes (Munteanu et al., 2014), that have been likewise optimized by evolution to ensure that patterning proceeds in a way that minimizes errors. To emphasize the programmatic aspect of the molecular assembly part of the process, I suggest the term “programmatic assembly”, which is also ratchet-like, to use a mechanical analogy (Oster, 2002), while being both combinatorial and synergistic, and there is a graph-theoretical formulation, of micro-states linked by unidirectional edges representing the irreversible assembly steps (Ahsendorf et al., 2014; Martinez-Corral et al., 2021) that is especially promising as an analytical methodology going forward. Implicitly all such approaches face the same problem, that, to quote from Ahsendorf et al., “history cannot be ignored away from thermodynamic equilibrium”, where by history, we mean the sequence of steps by which the machinery in question is assembled and operates. But there is a second history, and a second time scale, of the evolutionary sequence by which the machinery itself was refined and perfected over many generations, with all the contingency that implies. Taking the molecular level equivalents of coding and decoding as an example (e.g., Jarzynski, 2008; 2011), fully accounting for the thermodynamic driving forces behind each step in such cases is a complex and sometimes counterintuitive exercise. The same is true at a more abstract level, for a concept like positional information, since a device able to read and interpret such information will necessarily, like a human reader, be an energy dissipative product of evolution operating irreversibly far from equilibrium.
To go yet further, to the level of physics, the issue becomes one of time, of whether, in the terminology of Cortês and Smolin (2014), one is dealing with passive time or generative time. Passive time in this context is the “t” that appears in a typical set of equations, whether for Turing’s mechanism or for calculating a ballistic trajectory, and solving such equations yields the same answer each time. Drosophila segments also form the same way each time, but there is a difference. To see this, consider error suppression yet again, and how a developmental outcome can be produced as precisely realized as a pair-rule stripe. For a Turing mechanism, error suppression depends on feedback steps in the mechanism that amplify fluctuations and, together with diffusion, select one pattern over all others, including over background noise, doing so in real time as the pattern develops. For the transcriptional machinery employed in Drosophila segmentation, in contrast, the feedback step is evolution itself, in its role as a generator of gene sequences for the enhancers and transcriptional regulators required to produce the pattern in question, and to suitably refine their interactions. So in this case error suppression is in large part historical, that is, it has already occurred. And, because it is then embedded in the codes and structures that implement the genetic program, it does not appear explicitly in equations that model change in real time. Similarly, if we think about the fluctuations on which the amplifier acts, for a programmatic assembly process these are not spatial in character, but arise from genetic variation at the population level, because different individuals will vary as to the precision with which they replicate pattern, and it is by eliminating the more error-prone individuals, generation by generation, that the genome evolves in ways that reduce developmental errors for the population as a whole. It is then this mix of time scales and of history-dependent and history-independent features, which in analytical terms must be dealt with separately, rather than complexity per se, that precludes an elegant solution. From an error-suppression standpoint, this means that the problem of statistical noise at the level of positional cues can be dealt with analytically in a straightforward way (as by Tkačik and Gregor, 2021), but reliability and accuracy at the level of the interpreter cannot, as the evolutionary steps by which that interpreter was conjured into existence are inescapably part of the story. This also means, for the experimentalist, that quantitative tests of reliability for examples of programmatic assembly are less a measure of the physical limits of a given class of mechanisms, than they are of the effectiveness of evolution in its choice of an error-suppression strategy for each step in the assembly process.
A further lesson from Drosophila is, or would seem to be, that where evolution has replaced one mechanism by another, the transition is more likely than not to be in the direction of increased reliance on programmatic control, so that development becomes more complex, and hence inelegant, over time. For Drosophila in particular, the proximate advantage of making this change can be measured in the developmental time saved, as segment specification is significantly faster in Drosophila than in basal arthropods and short germ-band insects. This is a distinct advantage for insects like fruit flies, whose larvae compete with fungi and nematodes for a rapidly depleting food resource. But there is a potential cost in the loss of one key feature of oscillatory, clock-based segmentation mechanisms, in that errors accumulated from past steps in the developmental program are no longer overwritten by the new pattern and reset to zero. That this cost is not paid in reduced developmental reliability in Drosophila shows that programmatic assembly solves the problem of error suppression by other means, namely through structural innovations and enhanced specificity in the molecular machinery that implements the developmental program. This then begs the question of whether this same solution has been employed in the past, perhaps repeatedly, in multiple development pathways as a means of speeding the overall process of embryogenesis. Germ layer specification, for example, depends on highly complex gene regulatory networks (Loose and Patient, 2004; Kiecker et al., 2016), and is hence a good candidate for having imposed a programatic overlay on simpler, more purely kinetic ancestral mechanisms in order to achieve the same result more rapidly. There are implications here also on the botanical side, in providing a rationale for why mechanisms for plant patterning are generally more conserved across taxa than is typical of animals: that growth and patterning are tightly integrated in plants (Dumais and Kwiatkowska, 2002; Harashima and Schnittge, 2010; Rebocho et al., 2017), and so long as it is growth rather than patterning that is rate-limiting, there is little to be gained by reducing the time required to specify pattern. Ancestral mechanisms are then more likely to be retained rather than being replaced.
It has been gratifying, over the last 2 decades, to see Turing’s ideas gaining acceptance and proving their worth in specific biological situations. But this is only part of a larger enterprise, in the past a concern mainly of the more physico-chemically minded, but now more widely recognized, which is to better understand the essential underlying features of kinetic mechanisms as a class. A key concept here, featured in Turing’s own account, is the idea of generating order from fluctuations, that is, of extracting a meaningful signal from the underlying noise of the system, which can be at a molecular, subcellular or cellular level. The issue has relevance across a range of examples: from purely chemical systems, such as the CIMA reaction, to hybrid ones, like Drosophila, relying more on programmatic assembly than simple kinetics. Examples of programmatic assembly are then inherently less elegant than purely kinetic mechanisms because real time events play a lesser role than evolutionary ones. So, for example, achieving a precise outcome reliably depends on processes unfolding largely in real time for a kinetic mechanism like Turing’s, but for programmatic assembly these are embedded in the past, in the evolutionary sequence that produced the machinery that executes the program. Programmatic assembly cannot therefore be fully understood except in the context of an extended sequence of evolutionary events, which begs an analytical question, of how to deal in practice with events unfolding in two mutually exclusive time scales.
A final point I want to address is whether we have been missing what is potentially the most important application of Turing’s ideas, to controlling the assembly of neural circuits in the developing brain. If we consider the various cellular level activities needed to correctly configure the neural circuitry underpinning complex brain functions, there are many opportunities for competitive dynamics of the kind envisioned by Turing, but played out at a structural level, of cells, synapses and dendrites, rather than diffusing molecules (Lacalli, 2020). Turing himself had considered this issue, as is evident from a letter to J. Z. Young in February of 1951 (see Hodges, 1983, pg. 436), and his ideas have potential application to the period of synaptic remodeling that occurs in the neonatal nervous system, including in the cortex, whereby excess neurons and synaptic connections are removed in an activity-dependent way in response to sensory feedback (Le Bé and Markram, 2006; Low and Cheng, 2006; Kano and Hashimoto, 2009). But this is also the period when the newborn begins to develop a conscious awareness of its surroundings (Lagercrantz and Changeux, 2010), and for the circuits responsible for the basic sensations of phenomenal consciousness, i.e. qualia in most formulations, there is a problem. To illustrate this, consider a newborn hearing a sound, or experiencing pain, for the first time. The problem here is the absence of feedback mechanisms to correct any errors that may occur in the quality and character of the sensation evoked by the neural circuitry to which this task has been assigned. In other words, if the circuits evoking a particular sensation, of pain for example, or sound or light, have been incorrectly assembled in the embryonic period, the resulting sensations, whether they are the correct sensations or not, simply become the nature of experience for that individual. The brain thus faces the same problem that an insect does in correctly forming its segments, that it has one chance to get it right. The developmental options for doing so should then also be the same: to develop in a programmatic way to yield what is essentially a deterministic result, as in Drosophila, or to instead employ a Turing-type process of dynamic competition, either during the initial phase of circuit development or later remodeling, to amplify some circuitry variants at the expense of others. There may in fact be no single answer, as mechanisms by which brain circuitry is assembled will undoubtedly vary across taxa, from being more programmatic in the brains of small rapidly-developing invertebrates, to less programmatic in the brains of larger animals showing more flexible modes of learning and behavior, most notably cephalopods and vertebrates. For the circuits responsible for consciousness more specifically, there could in fact be a sequence, similar to that in insect segmentation, with global kinetic mechanisms being the ancestral way of generating the circuits responsible for phenomenal sensations as these first emerged in evolution, with more streamlined, programmatic ways of achieving the same result evolving secondarily.
We have, in sum, three options as to how the neural circuitry responsible for conscious sensation is assembled: that 1) it originated and remains a product of a global Turing-type patterning system operating at a structural, neurocircuitry level, or 2) like insect segmentation, it began that way but has since been converted, as in Drosophila, to some form of programmatic assembly, or 3) that the efficiencies inherent in programmatic assembly were themselves an essential part of the ability to evolve consciousness in the first place. It may be a mammalian bias to suppose that flexibility in behavior depends on more flexible, non-programmatic modes of development than is typically encountered in small invertebrates like Drosophila, but the general point remains valid in any case: that there are multiple scenarios under which mechanisms like those devised by Turing would lie at the very root of consciousness, and hence of the abilities of members of our species to engage in such activities as meaningful speech, logical thought and, not least, formulating and solving equations like Turing’s.
The author confirms being the sole contributor of this work and has approved it for publication.
Funds to support this work were received from the Lionel G. Harrison Research Trust.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
I thank those acknowledged in the figure legends, along with Patrick von Aderkas and Carol Wenzel, for images and/or additional information on the examples illustrated, Stuart Newman and the two reviewers for helpful comments on the manuscript, and Riley Lacalli for preparing the figures. The botanical portion of this paper is dedicated in memory of Taylor Steeves, the most kindly and helpful colleague one could wish to have. His connection with Turing is at one remove, through his work in Wardlaw’s lab in the mid 1950s. Apologies also to authors whose reviews on specific examples of pattern formation are not included due to space limitations. Completeness here is less a problem than it once would have been, as the literature on developmental pattern formation, like embryonic development itself, has now achieved a degree of robustness through redundancy.
Abdelmalek, S., and Bendoukha, S. (2020). “The Lengyel-Epstein Reaction Diffusion System,” in Applied Mathematical Analysis: Theory, Models, and Applications. Editors H. Dutta, and J. F. Peters (New York: Springer), 311–351. doi:10.1007/978-3-319-99918-0_10
Ahsendorf, T., Wong, F., Eils, R., and Gunawardena, J. (2014). A Framework for Modelling Gene Regulation Which Accommodates Non-Equilibrium Mechanisms. BMC Biol. 12, 102. doi:10.1186/s12915-014-0102-4
Balázsi, G., van Oudenaarden, A., and Collins, J. J. (2011). Cellular Decision Making and Biological Noise: From Microbes to Mammals. Cell 144, 910–925. doi:10.1016/j.cell.2011.01.030
Bard, J., and Lauder, I. (1974). How Well Does Turing's Theory of Morphogenesis Work? J. Theor. Biol. 45, 501–531. doi:10.1016/0022-5193(74)90128-3
Bauer, M., Petkova, M. D., Gregor, T., Wieschaus, E. F., and Bialek, W. (2021). Trading Bits in the Readout from a Genetic Network. Proc. Natl. Acad. Sci. U.S.A. 118, e2109011118. doi:10.1073/pnas.2109011118
Biedroń, M., and Banasiak, A. (2018). Auxin-Mediated Regulation of Vascular Patterning in Arabidopsis thaliana Leaves. Plant Cel Rep 37, 1215–1229. doi:10.1007/s00299-018-2319-0
Boissonade, J., Dulos, E., and De Kepper, P. (1995). “Turing Patterns: From Myth to Reality,” in Chemical Waves and Patterns. Editors R. Kapral, and K. Showalter (Dordrecht, NL: Kluwer Academic), 221–268. doi:10.1007/978-94-011-1156-0_7
Brinkmann, F., Mercker, M., Richter, T., and Marciniak-Czochra, A. (2018). Post-Turing Tissue Pattern Formation: Advent of Mechanochemistry. PLoS Comput. Biol. 14, e1006259. doi:10.1371/journal.pcbi.1006259
Carey, M. (1998). The Enhanceosome and Transcriptional Synergy. Cell 92, 5–8. doi:10.1016/S0092-8674(00)80893-4
Chatterjee, P., Glimm, T., and Kaźmierczak, B. (2020). Mathematical Modeling of Chondrogenic Pattern Formation during Limb Development: Recent Advances in Continuous Models. Math. Biosci. 322, 108319. doi:10.1016/j.mbs.2020.108319
Chen, H., Levo, M., Barinov, L., Fujioka, M., Jaynes, J. B., and Gregor, T. (2018). Dynamic Interplay between Enhancer-Promoter Topology and Gene Activity. Nat. Genet. 50, 1296–1303. doi:10.1038/s41588-018-0175-z
Clark, E. (2021). Time and Space in Segmentation. Interf. Focus. 11, 20200049. doi:10.1098/rsfs.2020.0049
Clark, E., Peel, A. D., and Akam, M. (2019). Arthropod Segmentation. Development 146, dev170480. doi:10.1242/dev.170480
Cooke, J., and Zeeman, E. C. (1976). A Clock and Wavefront Model for Control of the Number of Repeated Structures during Animal Morphogenesis. J. Theor. Biol. 58, 455–476. doi:10.1016/S0022-5193(76)80131-2
Cortês, M., and Smolin, L. (2014). The Universe as a Process of Unique Events. Phys. Rev. D 90, 084007. doi:10.1103/PhysRevD.90.084007
Cross, M., and Greenside, H. (2009). Pattern Formation and Dynamics in Nonequilibrium Systems. Cambridge, UK: Cambridge University Press.
Davidson, L. A., and Baum, B. (2012). Making Waves: The Rise and Fall and Rise of Quantitative Developmental Biology. Development 139, 3065–3069. doi:10.1242/dev.080093
Dawes, J. H. P. (2016). After 1952: The Later Development of Alan Turing's Ideas on the Mathematics of Pattern Formation. Historia Mathematica 43, 49–64. doi:10.1016/j.hm.2015.03.003
De Mol, L. (2021). “Turing Machines,” in The Stanford Encyclopedia of Philosophy (Winter 2021 Edition). Editor E. N. Zalta. Available at: https://plato.stanford.edu/asrchives/win2021/entries/turing-machine/.
De Wit, A. (1999). Spatial Patterns and Spatiotemporal Dynamics in Chemical Systems. Adv. Chem. Phys. 109, 435–513. doi:10.1002/9780470141687.ch5
Diaz-Cuadros, M., Pourquié, O., and El-Sherif, E. (2021). Patterning with Clocks and Genetic Cascades: Segmentation and Regionalization of Vertebrate versus Insect Body Plans. PLoS Genet. 17, e1009812. doi:10.1371/journal.pgen.1009812
Diego, X., Marcon, L., Müller, P., and Sharpe, J. (2018). Key Features of Turing Systems Are Determined Purely by Network Topology. Phys. Rev. X 8, 021071. doi:10.1103/PhysRevX.8.021071
Dufiet, V., and Boissonade, J. (1992). Conventional and Unconventional Turing Patterns. J. Chem. Phys. 96, 664–673. doi:10.1063/1.462450
Dumais, J., and Harrison, L. G. (2000). Whorl Morphogenesis in the Dasycladalean Algae: The Pattern Formation Viewpoint. Phil. Trans. R. Soc. Lond. B 355, 281–305. doi:10.1098/rstb.2000.0565
Dumais, J., and Kwiatkowska, D. (2002). Analysis of Surface Growth in Shoot Apices. Plant J. 31, 229–241. doi:10.1046/j.1365-313X.2001.01350.x
Dumais, J., Serikawa, K., and Mandoli, D. F. (2000). Acetabularia: A Unicellular Model for Understanding Subcellular Localization and Morphogenesis during Development. J. Plant Growth Regul. 19, 253–264. doi:10.1007/S003440000035
Ermentrout, B. (1991). Stripes or Spots? Nonlinear Effects in Bifurcation of Reaction-Diffusion Equations on the Square. Proc. R. Soc. Lond. A. 434, 413–417. doi:10.1098/rspa.1991.0100
Field, R. J., and Burger, M. (1985). Oscillations and Traveling Waves in Chemical Systems. New York: John Wiley & Sons.
Fowke, L., Attree, S., and Rennie, P. (1994). Scanning Electron Microscopy of Hydrated and Desiccated Mature Somatic Embryos and Zygotic Embryos of White Spruce (Picea glauca [Moench] Voss.). Plant Cel Rep. 13, 612–618. doi:10.1007/BF00232931
Furlong, E. E. M., and Levine, M. (2018). Developmental Enhancers and Chromosome Topology. Science 361, 1341–1345. doi:10.1126/science.aau0320
Gierer, A., and Meinhardt, H. (1972). A Theory of Biological Pattern Formation. Kybernetik 12, 30–39. doi:10.1007/BF00289234
Green, J. B. A. (2021). Computational Biology: Turing's Lessons in Simplicity. Biophysical J. 120, 4139–4141. doi:10.1016/j.bpj.2021.08.041
Green, J. B. A., and Sharpe, J. (2015). Positional Information and Reaction-Diffusion: Two Big Ideas in Developmental Biology Combine. Development 142, 1203–1211. doi:10.1242/dev.114991
Gregor, T., Garcia, H. G., and Little, S. C. (2014). The Embryo as a Laboratory: Quantifying Transcription in Drosophila. Trends Genet. 30, 364–375. doi:10.1016/j.tig.2014.06.002
Hafen, E., Kuroiwa, A., and Gehring, W. J. (1984). Spatial Distribution of Transcripts from the Segmentation Gene fushi tarazu during Drosophila Embryonic Development. Cell 37, 833–841. doi:10.1016/0092-8674(84)90418-5
Harashima, H., and Schnittger, A. (2010). The Integration of Cell Division, Growth and Differentiation. Curr. Opin. Plant Biol. 13, 66–74. doi:10.1016/j.pbi.2009.11.001
Harrison, L. G. (1987). What is the Status of Reaction-Diffusion Theory Thirty-Four Years after Turing? J. Theor. Biol. 125, 369–384. doi:10.1016/s0022-5193(87)80208-4
Harrison, L. G. (1993). Kinetic Theory of Living Pattern. Cambridge, UK: Cambridge University Press.
Harrison, L. G., and Hillier, N. A. (1985). Quantitative Control of Acetabularia Morphogenesis by Extracellular Calcium: A Test of Kinetic Theory. J. Theor. Biol. 114, 177–192. doi:10.1016/S0022-5193(85)80261-7
Harrison, L. G., and von Aderkas, P. (2004). Spatially Quantitative Control of the Number of Cotyledons in a Clonal Population of Somatic Embryos of Hybrid Larch Larix x leptoeuropaea. Ann. Bot. 93, 423–434. doi:10.1093/aob/mch061
Hiscock, T. W., and Megason, S. G. (2015). Orientation of Turing-Like Patterns by Morphogen Gradients and Tissue Anisotropies. Cel Syst. 1, 408–416. doi:10.1016/j.cels.2015.12.001
Hiscock, T. W., Tschopp, P., and Tabin, C. J. (2017). On the Formation of Digits and Joints during Limb Development. Developmental Cel 41, 459–465. doi:10.1016/j.devcel.2017.04.021
Holloway, D. M., and Harrison, L. G. (1999). Suppression of Positional Errors in Biological Development. Math. Biosciences 156, 271–290. doi:10.1016/S0025-5564(98)10070-6
Holloway, D. M., Rozada, I., and Bray, J. J. H. (2018). Two-Stage Patterning Dynamics in Conifer Cotyledon Whorl Morphogenesis. Ann. Bot. 121, 525–534. doi:10.1093/aob/mcx185
Holloway, D. M., and Wenzel, C. L. (2021). Polar Auxin Transport Dynamics of Primary and Secondary Vein Patterning in Dicot Leaves. in silico Plants 3, diab030. doi:10.1093/insilicoplants/diab030
Horváth, J., Szalai, I., and De Kepper, P. (2009). An Experimental Design Method Leading to Chemical Turing Patterns. Science 324, 772–775. doi:10.1126/science.1169973
Houchmandzadeh, B., Wieschaus, E., and Leibler, S. (2002). Establishment of Developmental Precision and Proportions in the Early Drosophila Embryo. Nature 415, 798–802. doi:10.1038/415798a
Howard, J., Grill, S. W., and Bois, J. S. (2011). Turing's Next Steps: The Mechanochemical Basis of Morphogenesis. Nat. Rev. Mol. Cel. Biol. 12, 392–398. doi:10.1038/nrm3120
Hunding, A. (1984). Bifurcations of Nonlinear Reaction-Diffusion Systems in Oblate Spheroids. J. Math. Biol. 19, 249–263. doi:10.1007/BF00277098
Hunding, A., and Baumgartner, S. (2017). Ancient Role of ten-m/odz in Segmentation and the Transition from Sequential to Syncytial Segmentation. Hereditas 154, 8. doi:10.1186/s41065-017-0029-1
Jarzynski, C. (2008). The Thermodynamics of Writing a Random Polymer. Proc. Natl. Acad. Sci. U.S.A. 105, 9451–9452. doi:10.1073/pnas.0805209105
Jarzynski, C. (2011). Equalities and Inequalities: Irreversibility and the Second Law of Thermodynamics at the Nanoscale. Annu. Rev. Condens. Matter Phys. 2, 329–351. doi:10.1146/annurev-conmatphys-062910-140506
Jönsson, H., Heisler, M. G., Shapiro, B. E., Meyerowitz, E. M., and Mjolsness, E. (2006). An Auxin-Driven Polarized Transport Model for Phyllotaxis. Proc. Natl. Acad. Sci. U.S.A. 103, 1633–1638. doi:10.1073/pnas.0509839103
Kang, H.-W., Zheng, L., and Othmer, H. G. (2012). The Effect of the Signalling Scheme on the Robustness of Pattern Formation in Development. Interf. Focus. 2, 465–486. doi:10.1098/rsfs.2011.0116
Kano, M., and Hashimoto, K. (2009). Synapse Elimination in the Central Nervous System. Curr. Opin. Neurobiol. 19, 154–161. doi:10.1016/j.conb.2009.05.002
Kiecker, C., Bates, T., and Bell, E. (2016). Molecular Specification of Germ Layers in Vertebrate Embryos. Cell. Mol. Life Sci. 73, 923–947. doi:10.1007/s00018-015-2092-y
Kondo, S., and Asai, R. (1995). A Reaction-Diffusion Wave on the Skin of the Marine Angelfish Pomacanthus. Nature 376, 765–768. doi:10.1038/376765a0
Kondo, S., and Miura, T. (2010). Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation. Science 329, 1616–1620. doi:10.1126/science.1179047
Kondo, S., Watanabe, M., and Miyazawa, S. (2021). Studies of Turing Pattern Formation in Zebrafish Skin. Phil. Trans. R. Soc. A. 379, 20200274. doi:10.1098/rsta.2020.0274
Konow, C., Dolnik, M., and Epstein, I. R. (2021). Insights From Chemical Systems into Turing-Type Morphogenesis. Phil. Trans. R. Soc. A. 379, 20200269. doi:10.1098/rsta.2020.0269
Krause, A. L., Gaffney, E. A., Maini, P. K., and Klika, V. (2021). Modern Perspectives on Near-Equilibrium Analysis of Turing Systems. Phil. Trans. R. Soc. A. 379, 20200268. doi:10.1098/rsta.2020.0268
Lacalli, T. C. (1981). Dissipative Structures and Morphogenetic Pattern in Unicellular Algae. Phil. Trans. R. Soc. Lond. B 294, 547–588. doi:10.1098/rstb.1981.0118
Lacalli, T. (2020). Evolving Consciousness: Insights from Turing, and the Shaping of Experience. Front. Behav. Neurosci. 14, 598561. doi:10.3389/fnbeh.2020.598561
Lacalli, T. (2021). Consciousness as a Product of Evolution: Contents, Selector Circuits, and Trajectories in Experience Space. Front. Syst. Neurosci. 15, 697129. doi:10.3389/fnsys.2021.697129
Lacalli, T. C., and Harrison, L. G. (1978). The Regulatory Capacity of Turing's Model for Morphogenesis, with Application to Slime Moulds. J. Theor. Biol. 70, 273–295. doi:10.1016/0022-5193(78)90377-6
Lacalli, T. C., and Harrison, L. G. (1987). Turing's Model and Branching Tip Growth: Relation of Time and Spatial Scales in Morphogenesis, with Application to Micrasterias. Can. J. Bot. 65, 1308–1319. doi:10.1139/b87-184
Lagercrantz, H., and Changeux, J.-P. (2010). Basic Consciousness of the Newborn. Semin. Perinatology 34, 201–206. doi:10.1053/j.semperi.2010.02.004
Landge, A. N., Jordan, B. M., Diego, X., and Müller, P. (2020). Pattern Formation Mechanisms of Self-Organizing Reaction-Diffusion Systems. Developmental Biol. 460, 2–11. doi:10.1016/j.ydbio.2019.10.031
Lavania, D., Linh, N. M., and Scarpella, E. (2021). Of Cells, Strands, and Networks: Auxin and the Patterned Formation of the Vascular System. Cold Spring Harb Perspect. Biol. 13, a039958. doi:10.1101/cshperspect.a039958
Le Bé, J.-V., and Markram, H. (2006). Spontaneous and Evoked Synaptic Rewiring in the Neonatal Neocortex. Proc. Natl. Acad. Sci. U.S.A. 103, 13214–13219. doi:10.1073/pnas.0604691103
Lengyel, I., and Epstein, I. R. (1991). Modeling of Turing Structures in the Chlorite-Iodide-Malonic Acid-Starch Reaction System. Science 251, 650–652. doi:10.1126/science.251.4994.650
Lewin, R. (1984). Why is Development So Illogical? Science 224, 1327–1329. doi:10.1126/science.6374894
Leyshon, T., Tonello, E., Schnoerr, D., Siebert, H., and Stumpf, M. P. H. (2021). The Design Principles of Discrete Turing Patterning Systems. J. Theor. Biol. 531, 110901. doi:10.1016/j.jtbi.2021.110901
Loose, M., and Patient, R. (2004). A Genetic Regulatory Network for Xenopus Mesendoderm Formation. Developmental Biol. 271, 467–478. doi:10.1016/j.ydbio.2004.04.014
Low, L. K., and Cheng, H.-J. (2006). Axon Pruning: An Essential Step Underlying the Developmental Plasticity of Neuronal Connections. Phil. Trans. R. Soc. B 361, 1531–1544. doi:10.1098/rstb.2006.1883
Lyons, M. J., and Harrison, L. G. (1991). A Class of Reaction-Diffusion Mechanisms Which Preferentially Select Striped Patterns. Chem. Phys. Lett. 183, 158–164. doi:10.1016/0009-2614(91)85117-F
Lyons, M. J., and Harrison, L. G. (1992). Stripe Selection: An Intrinsic Property of Some Pattern-Forming Models with Nonlinear Dynamics. Dev. Dyn. 195, 201–215. doi:10.1002/aja.1001950306
Maini, P. K., Baker, R. E., and Chuong, C.-M. (2006). The Turing Model Comes of Molecular Age. Science 314, 1397–1398. doi:10.1126/science.1136396
Maini, P. K., Woolley, T. E., Baker, R. E., Gaffney, E. A., and Lee, S. S. (2012). Turing's Model for Biological Pattern Formation and the Robustness Problem. Interf. Focus. 2, 487–496. doi:10.1098/rsfs.2011.0113
Marcon, L., Diego, X., Sharpe, J., and Müller, P. (2016). High-Throughput Mathematical Analysis Identifies Turing Networks for Patterning with Equally Diffusing Signals. eLife 5, e14022. doi:10.7554/eLife.14022
Martinez-Corral, R., Park, M., Biette, K., Friedrich, D., Scholes, C., Khalil, A. S., et al. (2021). Transcriptional Kinetic Synergy: A Complex Landscape Revealed by Integrating Modelling and Synthetic Biology. bioRxiv preprint. doi:10.1101/2020.08.31.276261
Mitchison, G. J. (1981). The Polar Transport of Auxin and Vein Patterns in Plants. Phil. Trans. R. Soc. Lond. B 295, 461–471. doi:10.1098/rstb.1981.0154
Miura, T. (2013). Turing and Wolpert Work Together during Limb Development. Sci. Signal. 6, pe14. doi:10.1126/scisignal.2004038
Munteanu, A., Cotterell, J., Solé, R. V., and Sharpe, J. (2014). Design Principles of Stripe-Forming Motifs: The Role of Positive Feedback. Sci. Rep. 4, 5003. doi:10.1038/srep05003
Murray, J. D. (1981). A Pre-Pattern Formation Mechanism for Animal Coat Markings. J. Theor. Biol. 88, 161–199. doi:10.1016/0022-5193(81)90334-9
Murray, J. D. (1988). How the Leopard Gets its Spots. Sci. Am. 258, 80–87. doi:10.1038/scientificamerican0388-80
Murray, J. D., and Oster, G. F. (1984). Cell Traction Models for Generating Pattern and Form in Morphogenesis. J. Math. Biol. 19, 265–279. doi:10.1007/BF00277099
Newman, S. A. (1993). Problems and Paradigms: Is Segmentation Generic? BioEssays 15, 277–283. doi:10.1002/bies.950150409
Newman, S. A., and Frisch, H. L. (1979). Dynamics of Skeletal Pattern Formation in Developing Chick Limb. Science 205, 662–668. doi:10.1126/science.462174
Newman, S. A., Glimm, T., and Bhat, R. (2018). The Vertebrate Limb: An Evolving Complex of Self-Organizing Systems. Prog. Biophys. Mol. Biol. 137, 12–24. doi:10.1016/j.pbiomolbio.2018.01.002
Nicolis, G., and Prigogine, I. (1977). Self-Organization in Non-Equilibrium Systems: From Dissipative Structures to Order through Fluctuations (New York: John Wiley & Sons).
Onimaru, K., Marcon, L., Musy, M., Tanaka, M., and Sharpe, J. (2016). The Fin-To-Limb Transition as the Re-Organization of a Turing Pattern. Nat. Commun. 7, 11582. doi:10.1038/ncomms11582
Othmer, H. G., Painter, K., Umulis, D., and Xue, C. (2009). The Intersection of Theory and Application in Elucidating Pattern Formation in Developmental Biology. Math. Model. Nat. Phenom. 4, 3–82. doi:10.1051/mmnp/20094401
Ouyang, Q., and Swinney, H. L. (1991). Transition from a Uniform State to Hexagonal and Striped Turing Patterns. Nature 352, 610–612. doi:10.1038/352610a0
Painter, K. J., Ptashnyk, M., and Headon, D. J. (2021). Systems for Intricate Patterning of the Vertebrate Anatomy. Phil. Trans. R. Soc. A. 379, 20200270. doi:10.1098/rsta.2020.0270
Pearson, J. E. (1993). Complex Patterns in a Simple System. Science 261, 189–192. doi:10.1126/science.261.5118.189
Petkova, M. D., Tkačik, G., Bialek, W., Wieschaus, E. F., and Gregor, T. (2019). Optimal Decoding of Cellular Identities in a Genetic Network. Cell 176, 844–855. doi:10.1016/j.cell.2019.01.007
Pick, L. (2016). Hox Genes, Evo-Devo, and the Case of the ftz Gene. Chromosoma 125, 535–551. doi:10.1007/s00412-015-0553-6
Poss, Z. C., Ebmeier, C. C., and Taatjes, D. J. (2013). The Mediator Complex and Transcription Regulation. Crit. Rev. Biochem. Mol. Biol. 48, 575–608. doi:10.3109/10409238.2013.840259
Pourquié, O. (2003). The Segmentation Clock: Converting Embryonic Time into Spatial Pattern. Science 301, 328–330. doi:10.1126/science.1085887
Prigogine, I., and Lefever, R. (1968). Symmetry Breaking Instabilities in Dissipative Systems. II. J. Chem. Phys. 48, 1695–1700. doi:10.1063/1.1668896
Rao, C. V., Wolf, D. M., and Arkin, A. P. (2002). Control, Exploitation and Tolerance of Intracellular Noise. Nature 420, 231–237. doi:10.1038/nature01258
Raspopovic, J., Marcon, L., Russo, L., and Sharpe, J. (2014). Digit Patterning is Controlled by a Bmp-Sox9-Wnt Turing Network Modulated by Morphogen Gradients. Science 345, 566–570. doi:10.1126/science.1252960
Rebocho, A. B., Southam, P., Kennaway, J. R., Bangham, J. A., and Coen, E. (2017). Generation of Shape Complexity through Tissue Conflict Resolution. eLife 6, e20156. doi:10.7554/elife.20156
Reinhardt, D., Pesce, E.-R., Stieger, P., Mandel, T., Baltensperger, K., Bennett, M., et al. (2003). Regulation of Phyllotaxis by Polar Auxin Transport. Nature 426, 255–260. doi:10.1038/nature02081
Rivera-Pomar, R., and Jãckle, H. (1996). From Gradients to Stripes in Drosophila Embryogenesis: Filling in the Gaps. Trends Genet. 12, 478–483. doi:10.1016/0168-9525(96)10044-5
Runions, A., Tsiantis, M., and Prusinkiewicz, P. (2017). A Common Developmental Program Can Produce Diverse Leaf Shapes. New Phytol. 216, 401–418. doi:10.1111/nph.14449
Salazar-Ciudad, I., Sole, R. V., and Newman, S. A. (2001). Phenotypic and Dynamical Transitions in Model Genetic Networks II. Application to the Evolution of Segmentation Mechanisms. Evol. Dev. 3, 95–103. doi:10.1046/j.1525-142x.2001.003002095.x
Scarpella, E., Marcos, D., Friml, J., and Berleth, T. (2006). Control of Leaf Vascular Patterning by Polar Auxin Transport. Genes Dev. 20, 1015–1027. doi:10.1101/gad.1402406
Sheth, R., Marcon, L., Bastida, M. F., Junco, M., Quintana, L., Dahn, R., et al. (2012). Hox Genes Regulate Digit Patterning by Controlling the Wavelength of a Turing-Type Mechanism. Science 338, 1476–1480. doi:10.1126/science.1226804
Shi, B., and Vernoux, T. (2019). Patterning at the Shoot Apical Meristem and Phyllotaxis. Curr. Top. Dev. Biol. 131, 81–107. doi:10.1016/bs.ctdb.2018.10.003
Singh, A. P., and Nüsslein-Volhard, C. (2015). Zebrafish Stripes as a Model for Vertebrate Colour Pattern Formation. Curr. Biol. 25, R81–R92. doi:10.1016/j.cub.2014.11.013
Song, Y., and Hyeon, C. (2021). Cost-Precision Trade-Off Relation Determines the Optimal Morphogen Gradient for Accurate Biological Pattern Formation. eLife 10, e70034. doi:10.7554/eLife.70034
Štanojević, D., Hoey, T., and Levine, M. (1989). Sequence-Specific DNA-Binding Activities of the Gap Proteins Encoded by Hunchback and Krüppel in Drosophila. Nature 341, 331–335. doi:10.1038/341331a0
Stewart, T. A., Bhat, R., and Newman, S. A. (2017). The Evolutionary Origin of Digit Patterning. EvoDevo 8, 21. doi:10.1186/s13227-017-0084-8
Struhl, G., Johnston, P., and Lawrence, P. A. (1992). Control of Drosophila Body Pattern by the Hunchback Morphogen Gradient. Cell 69, 237–249. doi:10.1016/0092-8674(92)90405-2
Struhl, G., Struhl, K., and Macdonald, P. M. (1989). The Gradient Morphogen bicoid is a Concentration-Dependent Transcriptional Activator. Cell 57, 1259–1273. doi:10.1016/0092-8674(89)90062-7
Subramanian, S., and Murray, S. M. (2021). Pattern Selection in Reaction Diffusion Systems. Phys. Rev. E 103, 012215. doi:10.1103/PhysRevE.103.012215
Takiguchi, Y., Imaichi, R., and Kato, M. (1997). Cell Division Patterns in the Apices of Subterranean Axis and Aerial Shoot of Psilotum nudum (Psilotaceae): Morphological and Phylogenetic Implications for the Subterranean Axis. Am. J. Bot. 84, 588–596. doi:10.2307/2445894
Tkačik, G., and Gregor, T. (2021). The Many Bits of Positional Information. Development 148, dev176065. doi:10.1242/dev.176065
Turing, A. M. (1952). The Chemical Basis of Morphogenesis. Phil. Trans. R. Soc. Lond. B 237, 37–72. doi:10.1098/rstb.1952.0012
Tyson, J. J., and Light, J. C. (1973). Properties of Two‐component Bimolecular and Trimolecular Chemical Reaction Systems. J. Chem. Phys. 59, 4164–4173. doi:10.1063/1.1680609
Tyson, J. J., and Novák, B. (2015). Models in Biology: Lessons from Modeling Regulation of the Eukaryotic Cell Cycle. BMC Biol. 13, 46. doi:10.1186/s12915-015-0158-9
Veerman, F., Mercker, M., and Marciniak-Czochra, A. (2021). Beyond Turing: Far-From-Equilibrium Patterns and Mechano-Chemical Feedback. Phil. Trans. R. Soc. A. 379, 20200278. doi:10.1098/rsta.2020.0278
Verna, C., Ravichandran, S. J., Sawchuk, M. G., Linh, N. M., and Scarpella, E. (2019). Coordination of Tissue Cell Polarity by Auxin Transport and Signaling. eLife 8, e51061. doi:10.7554/eLife.51061
Wardlaw, C. W. (1953). A Commentary on Turing's Diffusion-Reaction Theory of Morphogenesis. New Phytol. 52, 40–47. doi:10.1111/j.1469-8137.1953.tb05203.x
Wenzel, C. L., Schuetz, M., Yu, Q., and Mattsson, J. (2007). Dynamics of MONOPTEROS and PIN-FORMED1 Expression during Leaf Vein Pattern Formation in Arabidopsis thaliana. Plant J. 49, 387–398. doi:10.1111/j.1365-313X.2006.02977.x
Woolley, T. E., Krause, A. L., and Gaffney, E. A. (2021). Bespoke Turing Systems. Bull. Math. Biol. 83, 41. doi:10.1007/s11538-021-00870-y
Keywords: pattern formation, reaction-diffusion theory, irreversible processes, neurocircuit assembly, error suppression in evolution and development
Citation: Lacalli TC (2022) Patterning, From Conifers to Consciousness: Turing’s Theory and Order From Fluctuations. Front. Cell Dev. Biol. 10:871950. doi: 10.3389/fcell.2022.871950
Received: 08 February 2022; Accepted: 11 March 2022;
Published: 03 May 2022.
Edited by:
David M Holloway, British Columbia Institute of Technology, CanadaReviewed by:
Luciano Marcon, Spanish National Research Council (CSIC), SpainCopyright © 2022 Lacalli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Thurston C. Lacalli, bGFjYWxsaUB1dmljLmNh
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.