- 1Institute of Medical Physics and Biophysics, Medical Faculty, University of Münster, Münster, Germany
- 2Cells in Motion Interfaculty Centre, University of Münster, Münster, Germany
- 3CIM-IMRPS Graduate Program, Münster, Germany
Migration of single adherent cells is frequently observed in the developing and adult organism and has been the subject of many studies. Yet, while elegant work has elucidated molecular and mechanical cues affecting motion dynamics on a flat surface, it remains less clear how cells migrate in a 3D setting. In this review, we explore the changing parameters encountered by cells navigating through a 3D microenvironment compared to cells crawling on top of a 2D surface, and how these differences alter subcellular structures required for propulsion. We further discuss how such changes at the micro-scale impact motion pattern at the macro-scale.
1 Introduction
How cell motion is accomplished in a 3D microenvironment, and to which degree observations acquired in a planar system can be translated into such a heterogenous environment, is object of intense ongoing research and the topic of this review. This essay is divided into two sections: a general introduction into the field, and a detailed analysis of how environmental factors affect a specific signaling circuit at the leading edge (LE) of mesenchymal cells. We begin the first section with a brief survey on the molecular mechanisms driving cell motion, and their emerging motion patterns in a planar system. Next, we review published work describing how changes in material properties impact force transmission and motion patterns. Following, we summarize which parameters differ when cells migrate on top of a 2D surface compared to cells embedded in a 3D environment, and how mechanical properties determine what mode of motion is employed by cells. The second section is focused on a self-organizing signaling circuit present at the LE of cells migrating in a mesenchymal mode. Considering the relevance of membrane geometry for the assembly of this signaling circuit, we begin the second part with an introduction on curvature-dependent protein activation, before exploring how mechanical properties may affect this signaling circuit and in consequence change the motion pattern employed by the cell. Along the whole review, we try to identify open questions and current limitations in the field.
2 Single cell migration in 2D vs. 3D
Migration of single cells on a 2D surface was first described more than half a century ago by pioneers of this field (Abercrombie, 1980; Ingram, 1969; Weiss, 1961; among others). Since then, many of the underlying mechanisms responsible for cell propulsion have been unveiled. We begin by summarizing the general properties of mesenchymal cell motion. Similarities and differences to other migration modes will be discussed later in the review.
2.1 Force transmission at the leading edge of migrating mesenchymal cells in 2D
The prerequisite of any form of directed force transmission is an initial symmetry breaking step, which determines the future front and rear end of the cell (Lauffenburger and Horwitz, 1996). Symmetry breaking is fueled by various internal and external signaling cues (Drubin and Nelson, 1996). One of the main sensors for polarized chemotactic signaling cues are G protein-coupled receptors (Rodríguez-Frade et al., 1999). At the molecular level, receptor activation converges into the polarization of commonly used secondary messengers. For instance, the LE displays increased phosphotyrosine kinase activity and elevated levels of PI (3,4,5) P3 and DAG, while cytosolic Ca2+ levels are lowered (Tsai et al., 2014). This polarized distribution of secondary messengers is associated with a non-isotropic distribution of small Rho GTPase activity that either promotes actin polymerization (e.g., Rac, Cdc42) or actomyosin contractility (e.g., RhoA). Importantly, as small GTPases transition between an active and inactive state, such a polarized activity does not necessarily rely on a redistribution of the GTPase itself, but may also be coordinated through relocation of actuators (i.e., GTPase exchange factors, GEFs) and inhibitors (i.e., Guanine nucleotide exchange factors, GEFs) of the respective Rho GTPase. Analysis of Rho GTPase activation presents an intriguing spatio-temporal pattern, with high levels of GTP-Rac and GTP-Cdc42 at protruding sites, while contractile regions show increased GTP-RhoA levels (Kraynov et al., 2000; Nalbant et al., 2004; Pertz et al., 2006; Machacek et al., 2009). Strikingly, as many receptor-based systems rely on secondary messengers that are mutually exclusive, initial symmetry breaking can also occur in the absence of external signaling inputs (Kirschner et al., 2000). One example, how this may be achieved, is the so-called local excitation global inhibition (LEGI) model (Xiong et al., 2010), an extension of the classical reaction-diffusion systems initially described by Alan Turing (Turing, 1952) and later by Meinhardt and Gierer (Gierer and Meinhardt, 1972), where two mutually exclusive states take advantage of minor fluctuations to stochastically induce stable polarized structures.
Cell polarization translates into directed cell motion. A result of polarized GTPase activity is a non-isotropic change in actin polymerization dynamics (Peskin et al., 1993) and actin branching (Small et al., 1995), causing cell-wide rearrangements of the cytoskeleton (Figure 1A). Of particular importance for cell motion are changes in actin dynamics at the LE. Considering that the LE has over the last decades been the subject of extensive research, we refer readers interested in this topic to reviews written elsewhere (Pollard and Borisy, 2003; Krause and Gautreau, 2014). Here, we only note that the polymerization rates of individual actin filaments at the LE can reach rates of up to 7 μm/min (Kiuchi et al., 2011), while the LE extends at a rate of only 1–2 μm/min (Begemann et al., 2019). The difference between the polymerization rate of actin and the net forward motion of the LE results in a retrograde actin flow (Lin et al., 1997). This continuous actin treadmilling, further augmented by inward directed actomyosin pulling (Gardel et al., 2008), provides the basic force used for cell propulsion.
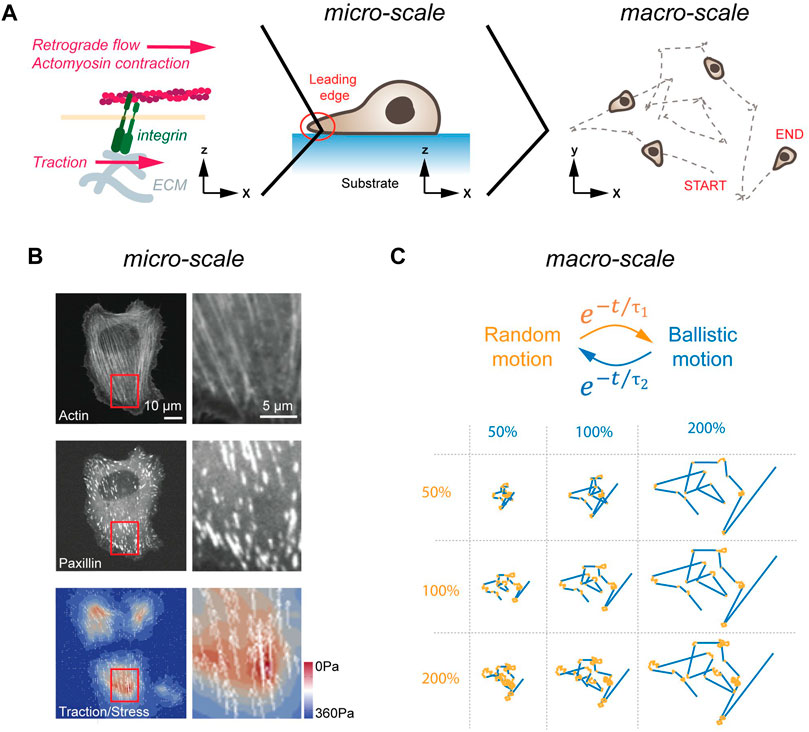
FIGURE 1. Cell migration in 2D. (A) LE dynamics in 2D. From left to right, the molecular clutch, the leading edge of a cell migrating, and a cross-section of a cell migrating on a flat, homogenous surface are shown. The molecular clutch allows to couple the ECM to the cytoskeleton in the presence of tensile forces. The resulting traction is used for cell migration. (B) Traction forces of cells plated on elastic substrates. Image of a cell plated on a soft substrate. Image (left) and magnification of a cell stained for actin (top), and the FA protein paxillin (middle), as well as traction forces are shown (bottom). Scale bars, 10 μm (left panels) and 5 μm (right panels). (C) Emerging motion pattern at the macro-scale. Cells transition between phases of random (orange) and ballistic (blue) motion. Single trace for different random (orange, duration in percent) and persistent (blue, duration in percent) lifetimes are shown below. Image in (B) adapted under CC-BY license from Soiné et al., 2015.
Transfer of tractile forces from the cell to the substrate is accomplished by Integrin molecules (Izzard and Lochner, 1976). Integrins are transmembrane receptors, consisting of non-covalently interacting α and ß subunits. To date, over 20 unique combinations of α (18 types) and ß (8 types) subunits have been described that differ in selectivity to extracellular matrix (ECM) components (Humphries et al., 2006). Common to all Integrins is the ability of participating in bidirectional signaling. Inside-out signaling describes the conformational change in the extracellular domain (i.e., activation) upon binding of Talin to the cytoplasmatic tail of Integrin (Tadokoro et al., 2003). In addition, Integrins also engage in outside-in signaling. Here, Integrins become activated upon force application from outside, which induces conformational changes in Integrin and increased ligand binding affinity (Friedland et al., 2009). In response to this external stimulation, Integrins trigger activation of FAK and other signaling pathways on its cytosolic site (reviewed in Hamidi and Ivaska, 2018). The two central elements for successful force-transduction through Integrins are on the extracellular site the binding of the heterodimer head to the ligand, and on the cytosolic site the unfolding of Talin (del Rio et al., 2009). As individual Integrins display ligand selectivity [e.g., αMβ2 binds ICAM1 (Rosetti et al., 2015); α3β1 binds VCAM1 (Chen et al., 2010)], the former element may give rise to selective cell-ECM interactions. The latter element refers to the fact that Talin only unfolds and binds to Vinculin and to actin in the presence of tensile forces. Hence, only under strain are mechanical forces transmitted from the cytoskeleton to the substrate, a mechanism called the ‘molecular clutch’ (Mitchison and Kirschner, 1988) (Figure 1B). Ultimately, the resulting force asymmetry along the planar cell axis yields forward propulsion, which is further augmented by de-adhesion of focal adhesions (FAs) and retraction at the rear of the cell (Abercrombie, 1980).
Importantly, the LE in most cells is not a stable structure but repeatedly transitions through cycles consisting of extension, adhesion and contraction (Lauffenburger and Horwitz, 1996; Ridley et al., 2003; Stock and Pauli, 2021). With each cycle, the cells crawl only a few micrometers forward. Hence, to efficiently migrate over a long distance in a persistent manner, the LE needs to be continuously reinitiated in the same direction. The need to repeatedly reinitiate the LE is not a design flaw, but a beneficial feature, as periodic extinguishing of activity permits a system to adapt more readily to changing external directional stimuli (Meinhardt and Gierer, 1974; Jilkine and Edelstein-Keshet, 2011). As will be discussed in more detail later, pairing these extension-retraction cycles with differential Integrin activation, caused by environmental factors, can gives rise to distinct changes in LE dynamics.
2.2 From force transmission to motion pattern in 2D
The literature presented to this point establishes a mechanism that allows cells to spontaneously polarize and migrate in an arbitrary direction, even in the absence of polarized signaling cues. To properly discuss the relevance of such cell motion, we first need to introduce the concept of self-organization. Following the physico-chemical definition, according to Ilya Prigogine (Nicolis and Prigogine, 1977), self-organization describes the ability of a system to create a spatial or temporal pattern at the macro-scale upon interactions of its components at the micro-scale. Importantly, to qualify for this definition, the emerging properties at the macro-scale need to be fundamentally different than the interactions that drive the pattern formation at the micro-scale, and the system needs to operate far off the thermodynamic equilibrium. Examples that meet these requirements are the animal swarm dynamics (Tunstrøm et al., 2013), and certain patterns arising from reaction-diffusion systems (Turing, 1952). Self-assembling structures, such as crystals, lipid bilayers or polypeptides, which operate near or at the thermodynamic equilibrium, however, do not qualify. Readers interested in learning more about the concept of self-organization, we refer to reviews written elsewhere (Kondo and Miura, 2010; Saha and Galic, 2018; Mancinelli and Galic, 2020).
As summarized above, cells initiate symmetry breaking spontaneously or in response to a polarized input. In the terminology of self-organization, cells employ at the micro-scale cytoskeletal forces at the LE to migrate for a certain amount of time in one direction. At the macro-scale, this causes cells to transition between phases of random and directed motion (Figure 1C). Strikingly, these emerging motion pattern strongly resembles the swimming pattern of E. coli, which also transitions stochastically between phases of random and ballistic propulsion (Berg, 1975). As proposed half a century ago, and revisited more recently theoretically, random transitions between phases of persistent and random motion present a search strategy to find sparsely distributed objects in a planar system (Bénichou et al., 2006; Harris et al., 2012). Notably, such a search strategy can also be found in foraging animals (Viswanathan et al., 1996). Here, depending on the distance between individual targets and the detection sensitivity of the searching agent, the lifetime of the persistent phase is adjusted to maximize the search efficiency (Bénichou et al., 2006). Hence, motion patterns arising at the micro-scale from stochastically formed LE can be interpreted at the macro-scale as a search strategy used by cells in pursuit of polarized signaling cues. Importantly, once a chemotactic signal is detected, cellular motion pattern become biased towards the source but maintain a random element (Arrieumerlou and Meyer, 2005), suggesting that stochastic search pattern act as a basic element that is fine-tuned by polarized signaling inputs.
2.2 1 Substrate-dependence of 2D cell dynamics
To this point, we assumed the substrate as uniform with no local or global inhomogeneities, which obviously is an oversimplification, as the environment varies in its adhesiveness, degradability, elasticity, and geometrical properties.
To determine how material properties affect cell dynamics at the micro-sale (Table 1, top left), we take a closer look at force transmission at the LE. As mentioned above, Integrin heads interact selectively with their ligands at the ECM. Importantly, this interaction displays catch-slip-bond dynamics, which means that the lifetime increases with higher tensile forces to an optimum, beyond which it again drops. For example, the maximum lifetime for α5β1 Integrins occurs at 20–30 pN (Kong et al., 2009). Since tensile forces of 5 pN are required to unfold Talin (Yao et al., 2016), the adhesion strength between receptor and ligand is sufficiently strong to trigger the molecular clutch on a rigid surface. On a soft surface, however, deformation of the substrate will preclude Talin unfolding and thus force transmission. Furthermore, assuming a constant pulling force, the absolute tensile force critically relies on the number of Integrin molecules involved in force transmission. Hence, the spatial distribution of ligands will also influence the threshold at which the molecular clutch is engaged. Finally, there are also indirect consequences to be considered. For instance, increased Integrin endocytosis has been observed in response to substrate elasticity, leading to increased rupture of Integrin-ligand complexes on soft substrates (Du et al., 2011).
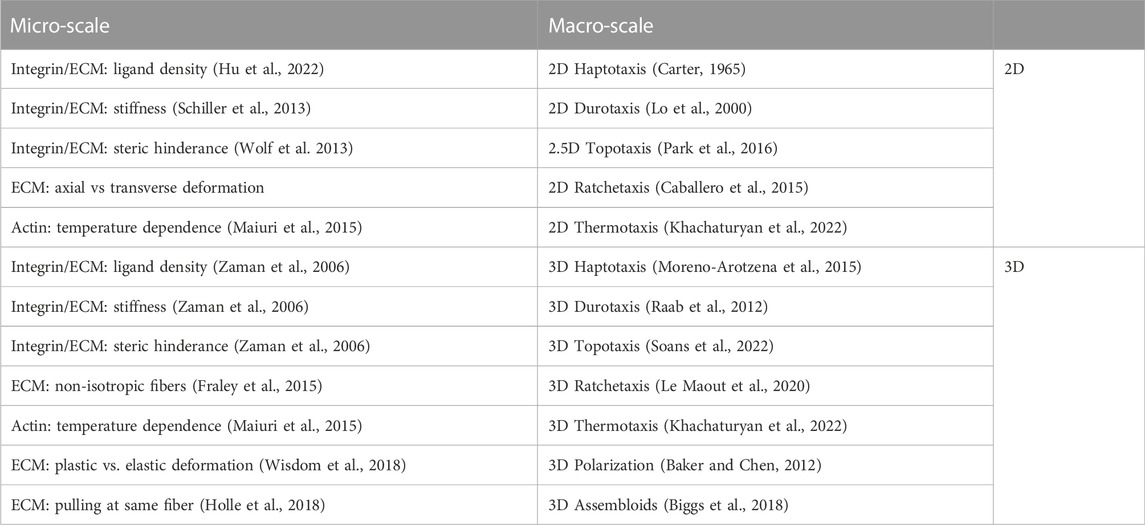
TABLE 1. Modulating cell dynamics at the micro-scale and at the macro-scale. Top panels depicting how changes in 2D substrate properties alter leading edge dynamics (left), as well as some of the corresponding changes in motion pattern (right). Below, changes in cell dynamics at the micro-scale (left) and emerging properties that may arise at the macro-scale (right) are indicated for cells cultured in 3D.
Differences in material properties alter emerging motion pattern at the macro-scale (Table 1, top right). For instance, depending on the ability of engaging the molecular clutch, cells will move towards areas of higher adhesiveness (haptotaxis; Carter, 1965). Haptotactic behavior may also be induced by changing the density of ligands. Considering that individual Integrins display some degree of selectivity (see above), cells may also respond to spatial changes in ligand-composition of the ECM, even if the global ligand and receptor levels remain constant. In its most extreme case, such changes in ligand levels may lead to 2D cell confinement. Notably, experimental systems that rely on such cell confinement (e.g., micropatterning) present an excellent platform to study systems-level decisions in single and collective cell motion (Segerer et al., 2015; Schreiber et al., 2016; Brückner et al., 2019). Yet, motion patterns are not only regulated through changes in adhesion strength. A second material property that influences the direction towards which cells migrate is the substrate rigidity, a phenomenon called durotaxis (Lo et al., 2000). Depending on the efficiency with which the molecular clutch is engaged, a consequence of ligand binding affinity and Integrin density, cells were reported to display positive (i.e., migration towards higher stiffness) and negative (i.e., migration towards lower stiffness) durotaxis. Importantly, as rigidity is a passive parameter that cannot be directly measured (Elosegui-Artola et al., 2018), cells need to probe the ECM to determine its mechanical properties. This is accomplished using both, lamellipodial as well as filopodia protrusions (Wong et al., 2014). Building on the same theme, cells were further shown to be sensitive to certain topologies (topotaxis; Park et al., 2016). Complementing these mechanisms that rely on variations of the molecular clutch, cells were also described to sense gradients in temperature (thermotaxis; Bahat et al., 2003). While the mechanism remains elusive, it is noteworthy that an increase in temperature yields augmented cell speed and persistence (Maiuri et al., 2015). It is thus plausible that thermotaxis relies on a biased random walk, as observed for chemotaxis.
2.2 2 Substrate-dependence of 3D cell dynamics
As we just elaborated, cells rapidly alter motion dynamics when presented with changing mechanical properties. The same is also true for cells embedded in a 3D environment. Prominent examples are the elevated speed mesenchymal cells display upon being squeezed under a glass slide (Liu et al., 2015) and the increased motility in the presence of a viscous extracellular medium (Bera et al., 2022). To understand the underlying mechanisms, again the material properties of the surrounding substrate need to be considered.
We begin with the similarities at the micro-scale (Table 1, bottom left). One variable that is likely to change is the substrate stiffness, which will drop from a GPa to KPa range when transitioning from rigid glass and plastic dishes to soft gels or tissues (Baker and Chen, 2012). As in a planar system, cells in a 3D environment were shown to move towards higher substrate stiffness (DuChez et al., 2019), and display haptotactic behavior (Moreno-Arotzena et al., 2015). As these parameters appear to be equally important, we will not further pursue them here. Readers interested in learning more on this topic, we refer to excellent reviews written elsewhere (Friedl and Wolf, 2010; Charras and Sahai, 2014; SenGupta et al., 2021; among others). While some parameters remain the same, others change, and a few new ones arise in cells navigating a complex 3-dimensional space. One parameter that changes is the ability of cells to engage with its surroundings on all sides, with potential consequences considering possible asymmetries in global protein distribution. Once cells begin moving through a 3D environment, new parameters need to be faced. For instance, the pore sizes of the ECM through which the cells will squeeze (Wolf et al., 2013) suddenly become relevant. Critical here is the size of the nucleus, as it is the largest organelle of the cell and fragile to mechanical damage. Squeezing the nucleus while moving through a narrow opening not only activates cellular signaling cascades (McGregor et al., 2016), but may in extreme cases yield nuclear rupture causing DNA damage and cell death (Chen et al., 2019). To prevent this, laminin levels that determine the nuclear stiffness were shown to correlate with ECM stiffness (Swift et al., 2013). Conversely, postmitotic and cancer cells that no longer need to protect the nucleus from damage display a soft nucleus (Cross et al., 2007). Where the mesh size is too narrow for cells to move through, secretion of proteases will locally digest the ECM to create space for migration (Gross and Lapiere, 1962). Strikingly, cleavage of collagen through metalloproteases leads to exposure of RGD-containing domains. This, in turn, allows binding to Integrins (Taubenberger et al., 2010) and other ECM molecules (Ortiz Franyuti et al., 2018). Hence, digestion of the environment may not only give space to crawl through, but also reveal adhesion sites needed to generate sufficient traction. Finally, it is noteworthy mentioning that the ECM will also be modified by cells traveling through it. For instance, pulling of cells via Integrins on ECM fibers leads to exposure of cryptic binding sites (in fibronectin), which is necessary for its polymerization into fibers (Lemmon et al., 2009). Furthermore, it was shown that aligned ECM fibers are secreted by cells migrating through a 3D environment (Ingman et al., 2006). Intriguingly, since a fiber will more readily give in when pulled perpendicularly, any deviations from a completely isotropic ECM will yield a directional bias, causing ratchetaxis (Caballero et al., 2015). Consequently, the ECM will be subject to modifications as cells travel through it, ultimately changing the trajectories of the cells that will follow, creating a possible memory effect.
Since many mechanisms identified in 2D were also observed in 3D, comparable motion patterns were reported for both systems (Table 1, bottom right). Unfortunately, no systematic analysis of 3D migration patterns exists to date. Considering that mechanical properties within a tissue are not homogenous (i.e., boundary conditions), and as the migrating cell population will inevitably come in contact with resident cell types (i.e., changing mechanical properties, signaling activity), an ex vivo approach with precise control of all parameters provides the best strategy to determine how individual constituents affect motion pattern. Yet even an ideal homogenous substrate will show varying pore sizes, obstacles, fiber lengths and stiffnesses, which argues that cell migration in 3D will by default display a larger variance in the motion pattern compared to a 2D system.
2.2 3 Modes of cell migration in 3D
To this point, we were exploring changes in motion from the perspective of a mesenchymal cell. Yet, from a physiological perspective, it is desirable to vary modes of propulsion depending on cell function. For instance, it would be beneficial for immune cells to display low selectivity to the substrate, as they frequently change their local environment on their pursuit of pathogens, while slow moving cells with a specific destination should be more selective. To account for these opposing needs, different types of motion have developed. The most frequent forms are mesenchymal and amoeboid. Mesenchymal cell migration (Figure 2, left), which is observed among others in neural crest cells (Ebendal, 1977) and fibroblasts (Abercrombie, 1980), locates the microtubule organizing center (MTOC) and most organelles in front of the nucleus (Etienne-Manneville and Hall, 2001), and relies as described above on force-transmission through Integrins to the ECM (Doyle et al., 2015).
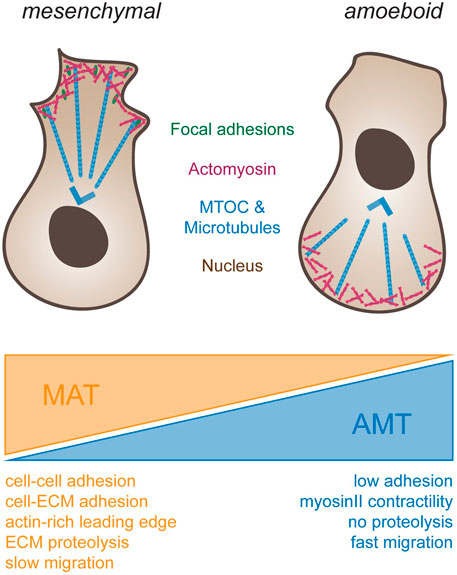
FIGURE 2. Different types of cell migration. To the left, schematic drawing of a cell using mesenchymal migration. Forces for propulsion are generated by connecting actomyosin-based forces (blue) through focal adhesions (green) to the substrate. Note that the MTOC (blue) is in front of the nucleus. To the right, amoeboid migration is depicted. Cells do not adhere to the substrate but rely on actomyosin-based compression of the cytosol at the back end of the cell for propulsion. Note that in immune cells, such as dendritic cells or macrophages, the MTOC is located behind the nucleus. Transitions from mesenchymal to ameboid migration (orange wedge, mesenchymal-amoeboid transition MAT) are promoted by low adhesion and Rho-ROCK driven Myosin-II activity (Friedl and Wolf, 2010; Graziani et al., 2022). Conversely, transition from amoeboid to mesenchymal migration (blue wedge, amoeboid-mesenchymal transition AMT) are induced by cell-cell and cell-ECM adhesions, actin-rich protrusions at the leading edge driven by Rac and Cdc42, ECM degradability and high Integrin-mediated adhesiveness (Panková et al., 2010; Graziani et al., 2022).
In contrast, amoeboid cell motion (Figure 2, right), as seen in leukocytes (Norberg et al., 1977) and primordial germ cells (Olguin-Olguin et al., 2021), frequently positions the MTOC and most organelles behind the nucleus (Chiplonkar et al., 1992). Amoeboid migration further relies on short lived adhesions, rather than on mature FA complexes. When inhibiting integrin adhesion to their surroundings, dendritic cells were shown to still migrate in a 3D environment without any change in speed (Lämmermann et al., 2008). However, such cells were impaired in their interaction with endothelial or epithelial surfaces, and displayed reduced resistance to blood flow shear forces, highlighting the importance of Integrins for additional leukocyte-associated functions besides cell migration. When trapped between two planar surfaces, immune cells were further shown to move without FAs by exerting forces on their surroundings, a migration mode termed “chimneying” (Pinner and Sahai, 2009). Here, by applying forces on the surrounding surfaces, sufficient friction is created for traction and locomotion of the cell. In contrast to the mesenchymal migration mode, traction force in this case was generated without the need to couple contraction within the cell to the substrate via adhesion complexes. These results point to the existence of subtypes within the amoeboid migration mode, depending on the extent of adhesive, contractile and protrusive forces (Lämmermann and Sixt, 2009). Amoeboid migrating cells make use of protrusive or contractile forces for cell locomotion with varying degrees of adhesiveness, leading to membrane protrusion governed by actin polymerization or by hydrostatic pressure caused by actomyosin contractility (actin-free membrane blebs). Hence, the combination of the degree of adhesion, contraction and protrusion appears to determine the amoeboid migration mode and is cell type specific (Lämmermann and Sixt, 2009).
Intriguingly, the environment does not only affect the mode of migration, but the mode of migration has also a reciprocal effect on the environment (Table 1). Mesenchymal cells are associated with long-lasting remodeling of the ECM. This is due to digestion, as well as due to pulling and rearrangement of the ECM. Amoeboid cells, in contrast, only leave a small imprint as proteolytic activity is minor, and no mechanical forces are exerted on the ECM. Notably, as the ECM is a viscoelastic material, a rapid migration mode may result in an elastic deformation that will close behind the cell, whereas slowly moving mesenchymal cells may yield plastic deformations, which may leave a tunnel, even in the absence of enzymatic modifications.
Importantly, mesenchymal and amoeboid modes should not be considered as mutually exclusive, but rather as two extremes on a continuum. Cells were reported to change between different modes depending on their environment. For instance, some cancer cells switch from mesenchymal to amoeboid upon protease inhibition (Wolf et al., 2003), while others switch from amoeboid to mesenchymal upon increase in the relative HIC5-to-paxillin ratio (Gulvady et al., 2018). Similarly, the viscoelastic properties were reported to change motion dynamics (Petrie et al., 2012; Bera et al., 2022). These findings argue that cells can readily transition between migration modes in response of the level of confinement and adhesion. Consistently, the underlying machinery used for propulsion remains the same. These considerations may also explain the presence of hybrid modes of propulsion such as lobopodial motion (Petrie et al., 2012). Here, similarly to amoeboid migration, cells use hydrostatic pressure to form a blunt spherical protrusion at the cell front, yet rely on pulling forces to the ECM for propulsion. Finally, it is noteworthy to mention the Reynolds number, and its effect on motion at the cellular level. The Reynolds number describes the ratio between the inertia and viscosity of a fluid. Objects at the length scale of cells have a negligible inertia, leaving them to be subject of large viscous forces. Consequently, many cell have adapted to the environment, using non-symmetric motion types to ensure forward movement (Purcell, 1977). Considering this aspect, a more continuous transition between “walking” and “swimming” should be considered, yielding additional forms of propulsion that rely on fluid-like streams (Stroka et al., 2014), or cytoskeletal waves (Barry and Bretscher, 2010). In this review, we only mention these additional modes of motion in passing. Again, we refer readers interested in this topic to excellent reviews written elsewhere (Purcell, 1977; Lauga and Powers, 2009; Caballero et al., 2020).
3 Mechanochemical feedback loop in 2D and 3D—A case study
As summarized above, several factors change when transitioning from migration on a planar surface to a three-dimensional environment. To explore how individual parameters may alter cell dynamics, we will take advantage of a curvature-dependent self-organizing circuit, which was previously described to control LE and motion pattern in single mesenchymal cells (Begemann et al., 2019). To properly assess this topic, we first revisit some basic concepts from actin and membrane mechanics.
3.1 Curvature-dependent regulation of actin polymerization dynamics
Cell migration in a planar system relies on mechanical forces exerted by the actomyosin network (Gardel et al., 2008). Within the LE, individual actin filaments are facing the cell periphery with their barbed ends (Urban et al., 2010), bringing this heavily regulated end of actin filaments in close proximity to the plasma membrane. This proximity to the site of action provides the system with an intriguing control unit. For one, it allows regulatory elements to be limited to the plasma membrane. More relevant for this review, however, it allows to couple actin dynamics directly to the shape of the membrane itself, thereby bypassing the need for receptor-based signaling cascades.
Cell migration is associated with outward (i.e., negative) and inward (i.e., positive) deformations of the plasma membrane. Such highly curved membrane sections per se are energetically not favorable and will rapidly return to their lowest energy state, unless additional circuits are in place to maintain these membrane deformations. Intriguingly, studies identified a protein family consisting of over 70 members that are capable of sensing inward (i.e., positive) and outward (i.e., negative) membrane curvature with the help of a BAR domain (Peter et al., 2004; Bhatia et al., 2009; Galic et al., 2012). Within this protein family, 17 members carry actin-regulatory domains, allowing changes in actin polymerization dynamics in a curvature-dependent manner. Examples regulating actin dynamics at positively curved membrane sites include Arhgap17 and Arhgap44 that accomplish this through its RhoGAP domains (Richnau and Aspenström, 2001; Galic et al., 2014). Complementing these proteins, several I-BAR domain proteins regulate actin polymerization at negatively curved membrane sections through binding of Rho GTPases to the CRIB domain (Zhang et al., 1997), or of actin monomers to the WH2 domain (Marchand et al., 2001). By coupling membrane curvature to actin polymerization dynamics, distinct emerging properties can be achieved. Prominent examples based on stochastic curvature-dependent feedback loops include the emergence of travelling waves (Wu et al., 2018), or the formation of exploratory filopodia in developing neurons (Mancinelli et al., 2021). Intriguingly, recent work established that actin polymerization may depend on the membrane geometry itself. From theoretical (Peskin et al., 1993) and experimental (Bieling et al., 2016) work, we know that individual actin filaments can exert a forced of up to 6 pN. Since forming a protrusion requires more force (Helfrich, 1973; Raucher and Sheetz, 1999), a single filament will only cause shallow membrane deformations. If, however, two (or more) such minor deformations occur in close proximity, membrane tension will cause bundling of individual actin filaments, which may cause the formation of protrusions with multiple actin filaments over time (Liu et al., 2008). In addition, experimental and numerical analysis showed that the shape of the plasma membrane changes the local polymerization rates of branched actin filaments, thus causing the outgrowth of finger-like protrusions (Simon et al., 2019). While limited in number, these experimental and theoretical considerations show the ability of membrane shape to influence actin dynamics and in consequence cell shape and function. Notably, similar self-organization circuits were also described for microtubules (Singh et al., 2018; Gavriljuk et al., 2021).
3.2 Curvature-dependent self-organization in 2D
Keeping in mind the ability of subcellular systems to self-organize in a curvature-dependent manner, we now focus on the LE of migrating cells. Outgrowth of the LE yields outward (i.e., negative) plasma membrane deformations with a curvature of 200–300 nm along the Z-axis (Urban et al., 2010). This local negative curvature was reported to trigger assembly of a self-organizing circuit at the tip of the LE (Begemann et al., 2019), which leads to increased actin polymerization and therefore to LE extension (Figure 3A). At the molecular level, this is accomplished through the recruitment of the curvature-sensitive I-BAR domain protein Baiap2 to negative membrane deformation sites. Baiap2 interacts through its CRIB and WH2 domain with actuators of actin polymerization dynamics. Hence, Baiap2 recruitment locally increases actin polymerization dynamics, leading to outgrowth of the LE. While this presents a mechanism for LE extension, it does not explain how the cell terminates this process. One factor, which likely limits the positive feedback loop, is a local increase in membrane tension at the LE (Shi et al., 2018). Published work demonstrates that an increase in membrane tension reduces actin polymerization (Raucher and Sheetz, 2000; Tsujita et al., 2015; Diz-Muñoz et al., 2016). At the same time, increase in membrane tension may also induce mechanically activated ion channels (Coste et al., 2010) to mediate transition from extension to collapsing the LE. Strikingly, the collapse of a retracting LE will cause to the formation of a highly curved membrane site adjacent to adhesion complexes, triggering the enrichment of the signaling machinery and re-initiation of the next LE protrusion. With this mechanochemical feedback loop, the maintenance of the polarization is ensured and therefore the longevity of the LE increased.
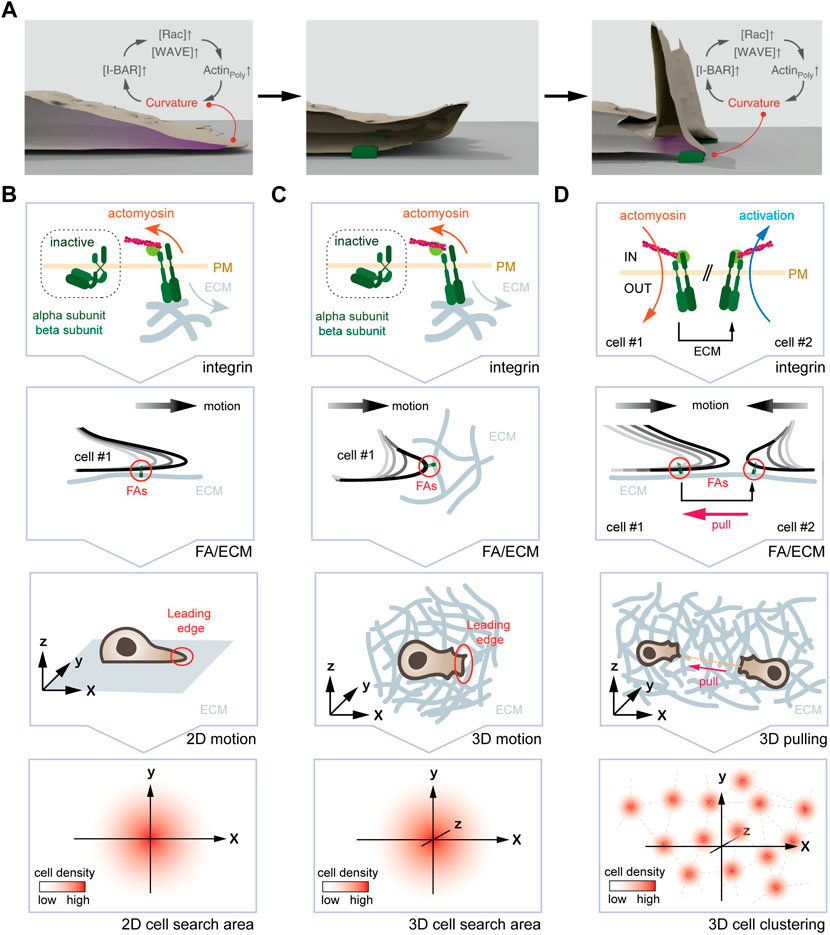
FIGURE 3. One curvature-dependent self-organizing circuit yields different emerging properties for mesenchymal cells plated in 2D and 3D. (A) Self-organizing LE re-initiation circuit in 2D. High local curvature triggers I-BAR domain protein enrichment, which further promotes actin polymerization and protrusion formation. Upon retraction, adhesion of FAs (green) to the ECM leads to a local high plasma membrane curvature, promoting I-BAR protein enrichment, increased actin polymerization, and LE re-initiation. (B) From the molecular clutch to motion pattern in 2D. From top to bottom, engagement of the molecular clutch leads to the activation of the curvature-dependent feedback-loop at the LE. The arising motion pattern displays an augmented persistence, which manifests in an increased search efficiency due to lower oversampling of the same areas. (C) From the molecular clutch to motion pattern in 3D. From top to bottom, engagement of the molecular clutch, the resulting deformation of the LE, and the arising motion pattern are shown. Again, an increase in persistence time augments the search efficiency. (D) Hypothetical mechanism for the formation of cell clusters in 3D. From top to bottom, engagement of the molecular clutch in two adjacent cells is shown. Here, one cell pulling at the ECM will cause inverse membrane deformations in an adjacent cell. This, in turn could activate the self-organizing feedback loop causing cell assembly. Image in (A) modified with permission from Begemann et al., 2019.
This curvature-dependent feedback loop is likely to interface with other regulatory circuits present at the LE. For instance, recent work showed that the retrograde flow of actin filaments at the LE maintains cell polarity, whereby increased polymerization speed (e.g., at higher temperatures) yields faster and more persistent migration (Maiuri et al., 2015). As just mentioned, increased membrane curvature augments recruitment of I-BAR domain proteins, likely resulting in higher actin polymerization rates that will further increase membrane curvature. At the same time, elevated temperatures will reduce membrane rigidity (Lamparter and Galic, 2020), which will lead to an increase in membrane curvature in response to a constant force. It is thus plausible to envision that a curvature-dependent feedback loop may contribute to previously described correlation of actin dynamics and motion persistence of the cell. Yet, published work demonstrates that the retrograde flow does not decrease but increases when Integrin binding is abolished due to actin slippage (Renkawitz and Sixt, 2010), arguing for the presence of additional (compensatory) circuits that work in parallel with the curvature-dependent signaling circuit at the LE.
At the macro-scale, increasing the longevity of LE through repeated re-initiation and other parameters leads to augmented motion persistence (Figure 3B). Augmented persistence, as discussed above, yields increased search efficiency, as it reduces oversampling of the very same position (Begemann et al., 2019).
3.3 Curvature-dependent self-organization in 3D
We next discuss how 3D material properties affect this particular self-organizing circuit at the micro- and macro-scale. The LE of mesenchymal cells in 3D resembles structurally the situation in 2D (Thievessen et al., 2015; Doyle et al., 2021). While it remains elusive whether contraction and coordination with subsequent LE extensions occurs in 3D, it is plausible to envision a similar mechanism (Figure 3C). Consistently, the LE of mesenchymal cells grown in a 3D system relies on extension-retraction cycles for forward movement (Doyle et al., 2021). However, LE outgrowth in 3D is not restricted to a plane, but stochastically distributed in all dimensions (Thievessen et al., 2015), thus allowing cells to sample its entire environment for optimal migration conditions (Doyle et al., 2021). Notably, contractile forces are independent of matrix properties (Feld et al., 2020), and single FAs were shown to act as rigidity sensors (Plotnikov et al., 2012). However, while the LE in 2D and 3D both grow out as planar sheets, reduced traction due to lower substrate stiffness is likely to delay and/or reduce membrane curvature at the tip of the LE. Changes in membrane curvature, in turn, may alter protein and isoform composition at the LE. Considering that individual curvature-sensitive proteins bind to distinct target proteins (Safari and Suetsugu, 2012), shape-dependent changes in protein stoichiometry may arise at the LE. Noteworthy, altered protrusion dynamics can be observed in some cell types when transitioning from a stiff 2D to a soft 3D environment (Santos et al., 2020). In the absence of mature FAs, for instance at sites where the ECM surrounding the cell is not suitable to build up sufficient tension, no mesenchymal migration is possible (Thievessen et al., 2015; Doyle et al., 2021). Here, Integrin-independent mechanisms, as shown for a number of cell types (Paluch et al., 2006; Lämmermann et al., 2008), promote cell locomotion. Strikingly, recent work showed that force-induced membrane deformations can lead to Talin-independent activation of integrins (Kim et al., 2020), raising the possibility that Integrins activate upon LE outgrowth to test the strength of the bond by actomyosin contractions. If true, this would leave only the connections that have the optimal conditions for further migration in this direction. For a full understanding of this process, the activation status of Integrins could be imaged during 3D cell migration with focus on the protrusion-adhesion-contraction cycle at the LE.
At the macro-scale, the self-organizing circuit is likely to influence motion pattern as described for the planar system (Begemann et al., 2019). In support of such a notion, published work showed that 3D mesenchymal migration depends on the relative LE adhesiveness (Caballero et al., 2015), whereby FAs will dictate the direction (Lo Vecchio et al., 2020) and the speed (Kim and Wirtz, 2013) of motion. Consistently, ablating collagen fibers 20 µm in front of the LE, which precludes among others re-initiation of the self-organizing circuit, was shown to avoid further migration in this direction (Doyle et al., 2021). How exactly FAs (size, number, maturity, stability, and density) and ECM (composition, density, rigidity, orientation) properties alter LE dynamics and in consequence cell migration, remains elusive. As that the self-organizing circuit is well suited to detect gradients in adhesion strength (haptotaxis), ECM stiffness (durotaxis), and fiber orientation (ratchetaxis), it raises the possibility that it may not only contribute to persistent cell migration but also bias stochastic 3D motion pattern in a particular direction (Figure 3C).
Finally, changing mechanical properties of a 3D system may not only influence motion pattern, but could also yield additional emerging features of the self-organizing circuit. As mentioned above, a cell pulling on the substrate will deform the adjacent matrix (Doyle et al., 2021). For two neighboring cells that adhere to the same fiber, this means that one cell will sense the other cell tugging the fiber (Figure 3D). As pulling the fiber away from a cell will form an outward membrane deformation, this may trigger activation of the self-organizing circuit and LE extension in that direction. Hence, it is plausible to envision that pulling on the same fiber may yield self-organization of cells into equidistant cell aggregates, which has been observed in vitro (Trappmann et al., 2017) and in vivo (Biggs et al., 2018; Trela et al., 2021). To determine this putative emerging property, the activation status of Integrins in neighboring cells could be imaged, and corresponding motion pattern determined.
4 Concluding remarks
In this review we surveyed the changing mechanical properties encountered by cells when transitioning from a 2D to a 3D environment and discussed its functional consequences. While incomplete, the presented data demonstrates that the ECM-cell interactions are by no means linear. For instance, increasing the concentration of an ECM component in a hydrogel will not only change the material properties (i.e., rigidity, mesh size), but also the ligand density, and may also induce receptor endocytosis. Furthermore, reducing the mesh size beyond a certain threshold may lead to increased protease secretion, which would not only soften the ECM but also expose new ligands for Integrin-binding. Considering this intricate interdependence of material and cellular parameters, the ECM-cell system should be considered a N-dimensional space with numerous distinct constellations that cells populate (and transition in-between) to efficiently navigate the 3D space.
How to untangle such an interdependent system? Considering its importance at the microscale, a promising first step towards a comprehensive understanding of 3D cell migration is a better grasp on Integrin-ligand dynamics. Towards this goal, microscopic studies and biophysical measurements of biomimetic hydrogels will be essential to clearly separate individual parameters influencing 3D cell migration, and to determine the hierarchy of these factors. Such quantitative measurements will further be crucial for developing future numerical models that recapitulate an idealized 3D environment–a critical prerequisite towards exploring optimal search strategies in three dimensions. Such a quantitative approach, however, hinges on the development of suitable 3D microscopy techniques, as well as an extensive description of the matrix properties. Only such a systematic analysis will provide us with a holistic view of motion patterns in 3D, and may on the long turn open up new inroads to study cell dynamics under physiological (e.g., immune system; Tabdanov et al., 2021) and pathological (e.g., cancer metastasis; Eddy et al., 2021) conditions.
Author contributions
AP and MG wrote the manuscript and prepared the figures.
Funding
This work was supported by funding from the Medical Faculty of the University of Münster (IZKF Ga3/016/21) and the DFG (GA2268/3-1, GA2268/4-1, and CRC1348/A06).
Acknowledgments
The authors thank the members of the Galic lab for critical discussion and feedback on the article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abercrombie, M. (1980). The Croonian Lecture, 1978 - the crawling movement of metazoan cells. Proc. R. Soc. Lond. B 207, 129–147. doi:10.1098/rspb.1980.0017
Arrieumerlou, C., and Meyer, T. (2005). A local coupling model and compass parameter for eukaryotic chemotaxis. Dev. Cell 8, 215–227. doi:10.1016/j.devcel.2004.12.007
Bahat, A., Tur-Kaspa, I., Gakamsky, A., Giojalas, L. C., Breitbart, H., and Eisenbach, M. (2003). Thermotaxis of mammalian sperm cells: A potential navigation mechanism in the female genital tract. Nat. Med. 9, 149–150. doi:10.1038/nm0203-149
Baker, B. M., and Chen, C. S. (2012). Deconstructing the third dimension: How 3D culture microenvironments alter cellular cues. J. Cell Sci. 125, 3015–3024. doi:10.1242/jcs.079509
Barry, N. P., and Bretscher, M. S. (2010). Dictyostelium amoebae and neutrophils can swim. Proc. Natl. Acad. Sci. U. S. A. 107, 11376–11380. doi:10.1073/pnas.1006327107
Begemann, I., Saha, T., Lamparter, L., Rathmann, I., Grill, D., Golbach, L., et al. (2019). Mechanochemical self-organization determines search pattern in migratory cells. Nat. Phys. 15, 848–857. doi:10.1038/s41567-019-0505-9
Bénichou, O., Loverdo, C., Moreau, M., and Voituriez, R. (2006). Two-dimensional intermittent search processes: An alternative to Lévy flight strategies. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 74, 020102. doi:10.1103/PhysRevE.74.020102
Bera, K., Kiepas, A., Godet, I., Li, Y., Mehta, P., Ifemembi, B., et al. (2022). Extracellular fluid viscosity enhances cell migration and cancer dissemination. Nature 611, 365–373. doi:10.1038/s41586-022-05394-6
Bhatia, V. K., Madsen, K. L., Bolinger, P.-Y., Kunding, A., Hedegård, P., Gether, U., et al. (2009). Amphipathic motifs in BAR domains are essential for membrane curvature sensing. EMBO J. 28, 3303–3314. doi:10.1038/emboj.2009.261
Bieling, P., Li, T.-D., Weichsel, J., McGorty, R., Jreij, P., Huang, B., et al. (2016). Force feedback controls motor activity and mechanical properties of self-assembling branched actin networks. Cell 164, 115–127. doi:10.1016/j.cell.2015.11.057
Biggs, L. C., Mäkelä, O. J., Myllymäki, S.-M., Das Roy, R., Närhi, K., Pispa, J., et al. (2018). Hair follicle dermal condensation forms via Fgf20 primed cell cycle exit, cell motility, and aggregation. Elife 7, e36468. doi:10.7554/eLife.36468
Brückner, D. B., Fink, A., Schreiber, C., Röttgermann, P. J. F., Rädler, J. O., and Broedersz, C. P. (2019). Stochastic nonlinear dynamics of confined cell migration in two-state systems. Nat. Phys. 15, 595–601. doi:10.1038/s41567-019-0445-4
Caballero, D., Comelles, J., Piel, M., Voituriez, R., and Riveline, D. (2015). Ratchetaxis: Long-Range directed cell migration by local cues. Trends Cell Biol. 25, 815–827. doi:10.1016/j.tcb.2015.10.009
Caballero, D., Kundu, S. C., and Reis, R. L. (2020). The biophysics of cell migration: Biasing cell motion with feynman ratchets. Biophys. (Rockv). 1. doi:10.35459/tbp.2020.000150
Carter, S. B. (1965). Principles of cell motility: The direction of cell movement and cancer invasion. Nature 208, 1183–1187. doi:10.1038/2081183a0
Charras, G., and Sahai, E. (2014). Physical influences of the extracellular environment on cell migration. Nat. Rev. Mol. Cell Biol. 15, 813–824. doi:10.1038/nrm3897
Chen, N. Y., Yang, Y., Weston, T. A., Belling, J. N., Heizer, P., Tu, Y., et al. (2019). An absence of lamin B1 in migrating neurons causes nuclear membrane ruptures and cell death. Proc. Natl. Acad. Sci. U. S. A. 116, 25870–25879. doi:10.1073/pnas.1917225116
Chen, W., Lou, J., and Zhu, C. (2010). Forcing switch from short- to intermediate- and long-lived states of the alphaA domain generates LFA-1/ICAM-1 catch bonds. J. Biol. Chem. 285, 35967–35978. doi:10.1074/jbc.M110.155770
Chiplonkar, J. M., Vandré, D. D., and Robinson, J. M. (1992). Stimulus-dependent relocation of the microtubule organizing center in human polymorphonuclear leukocytes. J. Cell Sci. 102 (4), 723–728. doi:10.1242/jcs.102.4.723
Coste, B., Mathur, J., Schmidt, M., Earley, T. J., Ranade, S., Petrus, M. J., et al. (2010). Piezo1 and Piezo2 are essential components of distinct mechanically activated cation channels. Science 330, 55–60. doi:10.1126/science.1193270
Cross, S. E., Jin, Y.-S., Rao, J., Gimzewski, J. K., Perez-Jimenez, R., Liu, R., et al. (2007). Nanomechanical analysis of cells from cancer patientsStretching single talin rod molecules activates vinculin binding. Nat. nanotechnologyScience 2323, 780638–783641. doi:10.1038/nnano.2007.388.del.Rio10.1126/science.1162912
del Rio, A., Perez-Jimenez, R., Liu, R., Roca-Cusachs, P., Fernandez, J. M., Sheetz, M. P., et al. (2009). Stretching single talin rod molecules activates vinculin binding. Science 323, 638–641. doi:10.1126/science.1162912
Diz-Muñoz, A., Thurley, K., Chintamen, S., Altschuler, S. J., Wu, L. F., Fletcher, D. A., et al. (2016). Membrane tension acts through PLD2 and mTORC2 to limit actin network assembly during neutrophil migration. PLoS Biol. 14, e1002474. doi:10.1371/journal.pbio.1002474
Doyle, A. D., Carvajal, N., Jin, A., Matsumoto, K., and Yamada, K. M. (2015). Local 3D matrix microenvironment regulates cell migration through spatiotemporal dynamics of contractility-dependent adhesions. Nat. Commun. 6, 8720. doi:10.1038/ncomms9720
Doyle, A. D., Sykora, D. J., Pacheco, G. G., Kutys, M. L., and Yamada, K. M. (2021). 3D mesenchymal cell migration is driven by anterior cellular contraction that generates an extracellular matrix prestrain. Dev. Cell 56, 826–841.e4. doi:10.1016/j.devcel.2021.02.017
Drubin, D. G., and Nelson, W. (1996). Origins of cell polarity. Cell 84, 335–344. doi:10.1016/S0092-8674(00)81278-7
Du, J., Chen, X., Liang, X., Zhang, G., Xu, J., He, L., et al. (2011). Integrin activation and internalization on soft ECM as a mechanism of induction of stem cell differentiation by ECM elasticity. Proc. Natl. Acad. Sci. U. S. A. 108, 9466–9471. doi:10.1073/pnas.1106467108
DuChez, B. J., Doyle, A. D., Dimitriadis, E. K., and Yamada, K. M. (2019). Durotaxis by human cancer cells. Biophys. J. 116, 670–683. doi:10.1016/j.bpj.2019.01.009
Ebendal, T. (1977). Extracellular matrix fibrils and cell contacts in the chick embryo. Possible roles in orientation of cell migration and axon extension. Cell Tissue Res. 175, 439–458. doi:10.1007/BF00222411
Eddy, C. Z., Raposo, H., Manchanda, A., Wong, R., Li, F., and Sun, B. (2021). Morphodynamics facilitate cancer cells to navigate 3D extracellular matrix. Sci. Rep. 11, 20434. doi:10.1038/s41598-021-99902-9
Elosegui-Artola, A., Trepat, X., and Roca-Cusachs, P. (2018). Control of mechanotransduction by molecular clutch dynamics. Trends Cell Biol. 28, 356–367. doi:10.1016/j.tcb.2018.01.008
Etienne-Manneville, S., and Hall, A. (2001). Integrin-mediated activation of Cdc42 controls cell polarity in migrating astrocytes through PKCzeta. Cell 106, 489–498. doi:10.1016/s0092-8674(01)00471-8
Feld, L., Kellerman, L., Mukherjee, A., Livne, A., Bouchbinder, E., and Wolfenson, H. (2020). Cellular contractile forces are nonmechanosensitive. Sci. Adv. 6, eaaz6997. doi:10.1126/sciadv.aaz6997
Fraley, S. I., Wu, P.-H., He, L., Feng, Y., Krisnamurthy, R., Longmore, G. D., et al. (2015). Three-dimensional matrix fiber alignment modulates cell migration and MT1-MMP utility by spatially and temporally directing protrusions. Sci. Rep. 5, 14580. doi:10.1038/srep14580
Friedl, P., and Wolf, K. (2010). Plasticity of cell migration: A multiscale tuning model. J. Cell Biol. 188, 11–19. doi:10.1083/jcb.200909003
Friedland, J. C., Lee, M. H., and Boettiger, D. (2009). Mechanically activated integrin switch controls alpha5beta1 function. Science 323, 642–644. doi:10.1126/science.1168441
Galic, M., Jeong, S., Tsai, F.-C., Joubert, L.-M., Wu, Y. I., Hahn, K. M., et al. (2012). External push and internal pull forces recruit curvature-sensing N-BAR domain proteins to the plasma membrane. Nat. Cell Biol. 14, 874–881. doi:10.1038/ncb2533
Galic, M., Tsai, F.-C., Collins, S. R., Matis, M., Bandara, S., and Meyer, T. (2014). Dynamic recruitment of the curvature-sensitive protein ArhGAP44 to nanoscale membrane deformations limits exploratory filopodia initiation in neurons. Elife 3, e03116. doi:10.7554/eLife.03116
Gardel, M. L., Sabass, B., Ji, L., Danuser, G., Schwarz, U. S., and Waterman, C. M. (2008). Traction stress in focal adhesions correlates biphasically with actin retrograde flow speed. J. Cell Biol. 183, 999–1005. doi:10.1083/jcb.200810060
Gavriljuk, K., Scocozza, B., Ghasemalizadeh, F., Seidel, H., Nandan, A. P., Campos-Medina, M., et al. (2021). A self-organized synthetic morphogenic liposome responds with shape changes to local light cues. Nat. Commun. 12, 1548. doi:10.1038/s41467-021-21679-2
Gierer, A., and Meinhardt, H. (1972). A theory of biological pattern formation. Kybernetik 12, 30–39. doi:10.1007/BF00289234
Graziani, V., Rodriguez-Hernandez, I., Maiques, O., and Sanz-Moreno, V. (2022). The amoeboid state as part of the epithelial-to-mesenchymal transition programme. Trends Cell Biol. 32, 228–242. doi:10.1016/j.tcb.2021.10.004
Gross, J., and Lapiere, C. M. (1962). Collagenolytic activity in amphibian tissues: A tissue culture assay. Proc. Natl. Acad. Sci. U. S. A. 48, 1014–1022. doi:10.1073/pnas.48.6.1014
Gulvady, A. C., Dubois, F., Deakin, N. O., Goreczny, G. J., and Turner, C. E. (2018). Hic-5 expression is a major indicator of cancer cell morphology, migration, and plasticity in three-dimensional matrices. Mol. Biol. Cell 29, 1704–1717. doi:10.1091/mbc.E18-02-0092
Hamidi, H., and Ivaska, J. (2018). Every step of the way: Integrins in cancer progression and metastasis. Nat. Rev. Cancer 18, 533–548. doi:10.1038/s41568-018-0038-z
Harris, T. H., Banigan, E. J., Christian, D. A., Konradt, C., Tait Wojno, E. D., Norose, K., et al. (2012). Generalized Lévy walks and the role of chemokines in migration of effector CD8+ T cells. Nature 486, 545–548. doi:10.1038/nature11098
Helfrich, W. (1973). Elastic properties of lipid bilayers: Theory and possible experiments. Z. Naturforsch. C 28, 693–703. doi:10.1515/znc-1973-11-1209
Holle, A. W., Young, J. L., van Vliet, K. J., Kamm, R. D., Discher, D., Janmey, P., et al. (2018). Cell-extracellular matrix mechanobiology: Forceful tools and emerging needs for basic and translational research. Nano Lett. 18, 1–8. doi:10.1021/acs.nanolett.7b04982
Hu, X., Roy, S. R., Jin, C., Li, G., Zhang, Q., Asano, N., et al. (2022). Control cell migration by engineering integrin ligand assembly. Nat. Commun. 13, 5002. doi:10.1038/s41467-022-32686-2
Humphries, J. D., Byron, A., and Humphries, M. J. (2006). Integrin ligands at a glance. J. Cell Sci. 119, 3901–3903. doi:10.1242/jcs.03098
Ingman, W. V., Wyckoff, J., Gouon-Evans, V., Condeelis, J., and Pollard, J. W. (2006). Macrophages promote collagen fibrillogenesis around terminal end buds of the developing mammary gland. Dev. Dyn. 235, 3222–3229. doi:10.1002/dvdy.20972
Izzard, C. S., and Lochner, L. R. (1976). Cell-to-substrate contacts in living fibroblasts: An interference reflexion study with an evaluation of the technique. J. Cell Sci. 21, 129–159. doi:10.1242/jcs.21.1.129
Jilkine, A., and Edelstein-Keshet, L. (2011). A comparison of mathematical models for polarization of single eukaryotic cells in response to guided cues. PLoS Comput. Biol. 7, e1001121. doi:10.1371/journal.pcbi.1001121
Khachaturyan, G., Holle, A. W., Ende, K., Frey, C., Schwederski, H. A., Eiseler, T., et al. (2022). Temperature-sensitive migration dynamics in neutrophil-differentiated HL-60 cells. Sci. Rep. 12, 7053. doi:10.1038/s41598-022-10858-w
Kim, D.-H., and Wirtz, D. (2013). Focal adhesion size uniquely predicts cell migration. FASEB J. 27, 1351–1361. doi:10.1096/fj.12-220160
Kim, J., Lee, J., Jang, J., Ye, F., Hong, S. J., Petrich, B. G., et al. (2020). Topological adaptation of transmembrane domains to the force-modulated lipid bilayer is a basis of sensing mechanical force. Curr. Biol. 30, 1614–1625. e5. doi:10.1016/j.cub.2020.02.028
Kirschner, M., Gerhart, J., and Mitchison, T. (2000). Molecular "vitalism". Cell 100, 79–88. doi:10.1016/S0092-8674(00)81685-2
Kiuchi, T., Nagai, T., Ohashi, K., and Mizuno, K. (2011). Measurements of spatiotemporal changes in G-actin concentration reveal its effect on stimulus-induced actin assembly and lamellipodium extension. J. Cell Biol. 193, 365–380. doi:10.1083/jcb.201101035
Kondo, S., and Miura, T. (2010). Reaction-diffusion model as a framework for understanding biological pattern formation. Science 329, 1616–1620. doi:10.1126/science.1179047
Kong, F., García, A. J., Mould, A. P., Humphries, M. J., and Zhu, C. (2009). Demonstration of catch bonds between an integrin and its ligand. J. Cell Biol. 185, 1275–1284. doi:10.1083/jcb.200810002
Krause, M., and Gautreau, A. (2014). Steering cell migration: Lamellipodium dynamics and the regulation of directional persistence. Nat. Rev. Mol. Cell Biol. 15, 577–590. doi:10.1038/nrm3861
Kraynov, V. S., Chamberlain, C., Bokoch, G. M., Schwartz, M. A., Slabaugh, S., and Hahn, K. M. (2000). Localized Rac activation dynamics visualized in living cells. Science 290, 333–337. doi:10.1126/science.290.5490.333
Lamparter, L., and Galic, M. (2000). Cellular membranes, a versatile adaptive composite material. Front. Cell Dev. Biol. 8. doi:10.3389/fcell.2020.00684
Lämmermann, T., Bader, B. L., Monkley, S. J., Worbs, T., Wedlich-Söldner, R., Hirsch, K., et al. (2008). Rapid leukocyte migration by integrin-independent flowing and squeezing. Nature 453, 51–55. doi:10.1038/nature06887
Lämmermann, T., and Sixt, M. (2009). Mechanical modes of 'amoeboid' cell migration. Curr. Opin. Cell Biol. 21, 636–644. doi:10.1016/j.ceb.2009.05.003
Lauffenburger, D. A., and Horwitz, A. F. (1996). Cell migration: A physically integrated molecular process. Cell 84, 359–369. doi:10.1016/S0092-8674(00)81280-5
Lauga, E., and Powers, T. R. (2009). The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72, 096601. doi:10.1088/0034-4885/72/9/096601
Le Maout, E., Lo Vecchio, S., Kumar Korla, P., Jinn-Chyuan Sheu, J., and Riveline, D. (2020). Ratchetaxis in channels: Entry point and local asymmetry set cell directions in confinement. Biophys. J. 119, 1301–1308. doi:10.1016/j.bpj.2020.08.028
Lemmon, C. A., Chen, C. S., and Romer, L. H. (2009). Cell traction forces direct fibronectin matrix assembly. Biophys. J. 96, 729–738. doi:10.1016/j.bpj.2008.10.009
Lin, C. H., Espreafico, E. M., Mooseker, M. S., and Forscher, P. (1997). Myosin drives retrograde F-actin flow in neuronal growth cones. Biol. Bull. 192, 183–185. doi:10.2307/1542600
Liu, A. P., Richmond, D. L., Maibaum, L., Pronk, S., Geissler, P. L., and Fletcher, D. A. (2008). Membrane-induced bundling of actin filaments. Nat. Phys. 4, 789–793. doi:10.1038/nphys1071
Liu, Y.-J., Le Berre, M., Lautenschlaeger, F., Maiuri, P., Callan-Jones, A., Heuzé, M., et al. (2015). Confinement and low adhesion induce fast amoeboid migration of slow mesenchymal cells. Cell 160, 659–672. doi:10.1016/j.cell.2015.01.007
Lo, C.-M., Wang, H.-B., Dembo, M., and Wang, Y. (2000). Cell movement is guided by the rigidity of the substrate. Biophys. J. 79, 144–152. doi:10.1016/S0006-3495(00)76279-5
Lo Vecchio, S., Thiagarajan, R., Caballero, D., Vigon, V., Navoret, L., Voituriez, R., et al. (2020). Collective dynamics of focal adhesions regulate direction of cell motion. Cell Syst. 10, 535–542. e4. doi:10.1016/j.cels.2020.05.005
Machacek, M., Hodgson, L., Welch, C., Elliott, H., Pertz, O., Nalbant, P., et al. (2009). Coordination of Rho GTPase activities during cell protrusion. Nature 461, 99–103. doi:10.1038/nature08242
Maiuri, P., Rupprecht, J.-F., Wieser, S., Ruprecht, V., Bénichou, O., Carpi, N., et al. (2015). Actin flows mediate a universal coupling between cell speed and cell persistence. Cell 161, 374–386. doi:10.1016/j.cell.2015.01.056
Mancinelli, G., and Galic, M. (2020). Exploring the interdependence between self-organization and functional morphology in cellular systems. J. Cell Sci. 133, jcs242479. doi:10.1242/jcs.242479
Mancinelli, G., Lamparter, L., Nosov, G., Saha, T., Pawluchin, A., Kurre, R., et al. (2021). Dendrite tapering actuates a self-organizing signaling circuit for stochastic filopodia initiation in neurons. Proc. Natl. Acad. Sci. U. S. A. 118, e2106921118. doi:10.1073/pnas.2106921118
Marchand, J. B., Kaiser, D. A., Pollard, T. D., and Higgs, H. N. (2001). Interaction of WASP/Scar proteins with actin and vertebrate Arp2/3 complex. Nat. Cell Biol. 3, 76–82. doi:10.1038/35050590
McGregor, A. L., Hsia, C.-R., and Lammerding, J. (2016). Squish and squeeze-the nucleus as a physical barrier during migration in confined environments. Curr. Opin. Cell Biol. 40, 32–40. doi:10.1016/j.ceb.2016.01.011
Meinhardt, H., and Gierer, A. (1974). Applications of a theory of biological pattern formation based on lateral inhibition. J. Cell Sci. 15, 321–346. doi:10.1242/jcs.15.2.321
Mitchison, T., and Kirschner, M. (1988). Cytoskeletal dynamics and nerve growth. Neuron 1, 761–772. doi:10.1016/0896-6273(88)90124-9
Moreno-Arotzena, O., Borau, C., Movilla, N., Vicente-Manzanares, M., and García-Aznar, J. M. (2015). Fibroblast migration in 3D is controlled by haptotaxis in a non-muscle myosin II-dependent manner. Ann. Biomed. Eng. 43, 3025–3039. doi:10.1007/s10439-015-1343-2
Nalbant, P., Hodgson, L., Kraynov, V., Toutchkine, A., and Hahn, K. M. (2004). Activation of endogenous Cdc42 visualized in living cells. Science 305, 1615–1619. doi:10.1126/science.1100367
Nicolis, G., and Prigogine, I. (1977). Self-organization in nonequilibrium systems: From dissipative structures to order through fluctuations/ G. Nicolis, I. Prigogine. New York, London: Wiley.
Norberg, B., Bandmann, U., and Rydgren, L. (1977). Amoeboid movement in human leucocytes: Basic mechanisms, cytobiological and clinical significance. J. Mechanochem. Cell Motil. 4, 37–53.
Olguin-Olguin, A., Aalto, A., Maugis, B., Boquet-Pujadas, A., Hoffmann, D., Ermlich, L., et al. (2021). Chemokine-biased robust self-organizing polarization of migrating cells in vivo. Proc. Natl. Acad. Sci. U. S. A. 118, e2018480118. doi:10.1073/pnas.2018480118
Ortiz Franyuti, D., Mitsi, M., and Vogel, V. (2018). Mechanical stretching of fibronectin fibers upregulates binding of interleukin-7. Nano Lett. 18, 15–25. doi:10.1021/acs.nanolett.7b01617
Paluch, E., Sykes, C., Prost, J., and Bornens, M. (2006). Dynamic modes of the cortical actomyosin gel during cell locomotion and division. Trends Cell Biol. 16, 5–10. doi:10.1016/j.tcb.2005.11.003
Panková, K., Rösel, D., Novotný, M., and Brábek, J. (2010). The molecular mechanisms of transition between mesenchymal and amoeboid invasiveness in tumor cells. Cell. Mol. Life Sci. 67, 63–71. doi:10.1007/s00018-009-0132-1
Park, J., Kim, D.-H., Kim, H.-N., Wang, C. J., Kwak, M. K., Hur, E., et al. (2016). Directed migration of cancer cells guided by the graded texture of the underlying matrix. Nat. Mat. 15, 792–801. doi:10.1038/nmat4586
Pertz, O., Hodgson, L., Klemke, R. L., and Hahn, K. M. (2006). Spatiotemporal dynamics of RhoA activity in migrating cells. Nature 440, 1069–1072. doi:10.1038/nature04665
Peskin, C. S., Odell, G. M., and Oster, G. F. (1993). Cellular motions and thermal fluctuations: The brownian ratchet. Biophys. J. 65, 316–324. doi:10.1016/S0006-3495(93)81035-X
Peter, B. J., Kent, H. M., Mills, I. G., Vallis, Y., Butler, P. J. G., Evans, P. R., et al. (2004). BAR domains as sensors of membrane curvature: The amphiphysin BAR structure. Science 303, 495–499. doi:10.1126/science.1092586
Petrie, R. J., Gavara, N., Chadwick, R. S., and Yamada, K. M. (2012). Nonpolarized signaling reveals two distinct modes of 3D cell migration. J. Cell Biol. 197, 439–455. doi:10.1083/jcb.201201124
Pinner, S., and Sahai, E. (2009). Integrin-independent movement of immune cells. F1000 Biol. Rep. 1, 67. doi:10.3410/B1-67
Plotnikov, S. V., Pasapera, A. M., Sabass, B., and Waterman, C. M. (2012). Force fluctuations within focal adhesions mediate ECM-rigidity sensing to guide directed cell migration. Cell 151, 1513–1527. doi:10.1016/j.cell.2012.11.034
Pollard, T. D., and Borisy, G. G. (2003). Cellular motility driven by assembly and disassembly of actin filaments. Cell 112, 453–465. doi:10.1016/S0092-8674(03)00120-X
Raab, M., Swift, J., Dingal, P. C. D. P., Shah, P., Shin, J.-W., and Discher, D. E. (2012). Crawling from soft to stiff matrix polarizes the cytoskeleton and phosphoregulates myosin-II heavy chain. J. Cell Biol. 199, 669–683. doi:10.1083/jcb.201205056
Raucher, D., and Sheetz, M. P. (2000). Cell spreading and lamellipodial extension rate is regulated by membrane tension. J. Cell Biol. 148, 127–136. doi:10.1083/jcb.148.1.127
Raucher, D., and Sheetz, M. P. (1999). Characteristics of a membrane reservoir buffering membrane tension. Biophys. J. 77, 1992–2002. doi:10.1016/S0006-3495(99)77040-2
Renkawitz, J., and Sixt, M. (2010). Mechanisms of force generation and force transmission during interstitial leukocyte migration. EMBO Rep. 11, 744–750. doi:10.1038/embor.2010.147
Richnau, N., and Aspenström, P. (2001). Rich, a rho GTPase-activating protein domain-containing protein involved in signaling by Cdc42 and Rac1. J. Biol. Chem. 276, 35060–35070. doi:10.1074/jbc.M103540200
Ridley, A. J., Schwartz, M. A., Burridge, K., Firtel, R. A., Ginsberg, M. H., Borisy, G., et al. (2003). Cell migration: Integrating signals from front to back. Science 302, 1704–1709. doi:10.1126/science.1092053
Rodríguez-Frade, J. M., Vila-Coro, A. J., Martín, A., Nieto, M., Sánchez-Madrid, F., Proudfoot, A. E., et al. (1999). Similarities and differences in RANTES- and (AOP)-RANTES-triggered signals: Implications for chemotaxis. J. Cell Biol. 144, 755–765. doi:10.1083/jcb.144.4.755
Rosetti, F., Chen, Y., Sen, M., Thayer, E., Azcutia, V., Herter, J. M., et al. (2015). A lupus-associated mac-1 variant has defects in integrin allostery and interaction with ligands under force. Cell Rep. 10, 1655–1664. doi:10.1016/j.celrep.2015.02.037
Safari, F., and Suetsugu, S. (2012). The BAR domain superfamily proteins from subcellular structures to human diseases. Membr. (Basel) 2, 91–117. doi:10.3390/membranes2010091
Saha, T., and Galic, M. (2018). Self-organization across scales: From molecules to organisms. Philos. Trans. R. Soc. Lond. B Biol. Sci. 373, 20170113. doi:10.1098/rstb.2017.0113
Santos, T. E., Schaffran, B., Broguière, N., Meyn, L., Zenobi-Wong, M., and Bradke, F. (2020). Axon growth of CNS neurons in three dimensions is amoeboid and independent of adhesions. Cell Rep. 32, 107907. doi:10.1016/j.celrep.2020.107907
Schiller, H. B., Hermann, M.-R., Polleux, J., Vignaud, T., Zanivan, S., Friedel, C. C., et al. (2013). β1- and αv-class integrins cooperate to regulate myosin II during rigidity sensing of fibronectin-based microenvironments. Nat. Cell Biol. 15, 625–636. doi:10.1038/ncb2747
Schreiber, C., Segerer, F. J., Wagner, E., Roidl, A., and Rädler, J. O. (2016). Ring-shaped microlanes and chemical barriers as a platform for probing single-cell migration. Sci. Rep. 6, 26858. doi:10.1038/srep26858
Segerer, F. J., Thüroff, F., Piera Alberola, A., Frey, E., and Rädler, J. O. (2015). Emergence and persistence of collective cell migration on small circular micropatterns. Phys. Rev. Lett. 114, 228102. doi:10.1103/PhysRevLett.114.228102
SenGupta, S., Parent, C. A., and Bear, J. E. (2021). The principles of directed cell migration. Nat. Rev. Mol. Cell Biol. 22, 529–547. doi:10.1038/s41580-021-00366-6
Shi, Z., Graber, Z. T., Baumgart, T., Stone, H. A., and Cohen, A. E. (2018). Cell membranes resist flow. Cell 175, 1769–1779. e13. doi:10.1016/j.cell.2018.09.054
Simon, C., Kusters, R., Caorsi, V., Allard, A., Abou-Ghali, M., Manzi, J., et al. (2019). Actin dynamics drive cell-like membrane deformation. Nat. Phys. 15, 602–609. doi:10.1038/s41567-019-0464-1
Singh, A., Saha, T., Begemann, I., Ricker, A., Nüsse, H., Thorn-Seshold, O., et al. (2018). Polarized microtubule dynamics directs cell mechanics and coordinates forces during epithelial morphogenesis. Nat. Cell Biol. 20, 1126–1133. doi:10.1038/s41556-018-0193-1
Small, J. V., Herzog, M., and Anderson, K. (1995). Actin filament organization in the fish keratocyte lamellipodium. J. Cell Biol. 129, 1275–1286. doi:10.1083/jcb.129.5.1275
Soans, K. G., Ramos, A. P., Sidhaye, J., Krishna, A., Solomatina, A., Hoffmann, K. B., et al. (2022). Matrix topology guides collective cell migration in vivo. bioRxiv, doi:10.1101/2022.01.31.478442
Soiné, J. R. D., Brand, C. A., Stricker, J., Oakes, P. W., Gardel, M. L., and Schwarz, U. S. (2015). Model-based traction force microscopy reveals differential tension in cellular actin bundles. PLoS Comput. Biol. 11, e1004076. doi:10.1371/journal.pcbi.1004076
Stock, J., and Pauli, A. (2021). Self-organized cell migration across scales - from single cell movement to tissue formation. Development 148, dev191767. doi:10.1242/dev.191767
Stroka, K. M., Jiang, H., Chen, S.-H., Tong, Z., Wirtz, D., Sun, S. X., et al. (2014). Water permeation drives tumor cell migration in confined microenvironments. Cell 157, 611–623. doi:10.1016/j.cell.2014.02.052
Swift, J., Ivanovska, I. L., Buxboim, A., Harada, T., Dingal, P. C. D. P., Pinter, J., et al. (2013). Nuclear lamin-A scales with tissue stiffness and enhances matrix-directed differentiation. Science 341, 1240104. doi:10.1126/science.1240104
Tabdanov, E. D., Rodríguez-Merced, N. J., Cartagena-Rivera, A. X., Puram, V. V., Callaway, M. K., Ensminger, E. A., et al. (2021). Engineering T cells to enhance 3D migration through structurally and mechanically complex tumor microenvironments. Nat. Commun. 12, 2815. doi:10.1038/s41467-021-22985-5
Tadokoro, S., Shattil, S. J., Eto, K., Tai, V., Liddington, R. C., Pereda, J. M. de, et al. (2003). Talin binding to integrin beta tails: A final common step in integrin activation. Science 302, 103–106. doi:10.1126/science.1086652
Taubenberger, A. V., Woodruff, M. A., Bai, H., Muller, D. J., and Hutmacher, D. W. (2010). The effect of unlocking RGD-motifs in collagen I on pre-osteoblast adhesion and differentiation. Biomaterials 31, 2827–2835. doi:10.1016/j.biomaterials.2009.12.051
Thievessen, I., Fakhri, N., Steinwachs, J., Kraus, V., McIsaac, R. S., Gao, L., et al. (2015). Vinculin is required for cell polarization, migration, and extracellular matrix remodeling in 3D collagen. FASEB J. 29, 4555–4567. doi:10.1096/fj.14-268235
Trappmann, B., Baker, B. M., Polacheck, W. J., Choi, C. K., Burdick, J. A., and Chen, C. S. (2017). Matrix degradability controls multicellularity of 3D cell migration. Nat. Commun. 8, 371. doi:10.1038/s41467-017-00418-6
Trela, E., Lan, Q., Myllymäki, S.-M., Villeneuve, C., Lindström, R., Kumar, V., et al. (2021). Cell influx and contractile actomyosin force drive mammary bud growth and invagination. J. Cell Biol. 220, e202008062. doi:10.1083/jcb.202008062
Tsai, F.-C., Seki, A., Yang, H. W., Hayer, A., Carrasco, S., Malmersjö, S., et al. (2014). A polarized Ca2+, diacylglycerol and STIM1 signalling system regulates directed cell migration. Nat. Cell Biol. 16, 133–144. doi:10.1038/ncb2906
Tsujita, K., Takenawa, T., and Itoh, T. (2015). Feedback regulation between plasma membrane tension and membrane-bending proteins organizes cell polarity during leading edge formation. Nat. Cell Biol. 17, 749–758. doi:10.1038/ncb3162
Tunstrøm, K., Katz, Y., Ioannou, C. C., Huepe, C., Lutz, M. J., and Couzin, I. D. (2013). Collective states, multistability and transitional behavior in schooling fish. PLoS Comput. Biol. 9, e1002915. doi:10.1371/journal.pcbi.1002915
Turing, A. (1952). The chemical basis of morphogenesis. Phil. Trans. R. Soc. Lond. B 237, 37–72. doi:10.1098/rstb.1952.0012
Urban, E., Jacob, S., Nemethova, M., Resch, G. P., and Small, J. V. (2010). Electron tomography reveals unbranched networks of actin filaments in lamellipodia. Nat. Cell Biol. 12, 429–435. doi:10.1038/ncb2044
Viswanathan, G. M., Afanasyev, V., Buldyrev, S. V., Murphy, E. J., Prince, P. A., and Stanley, H. E. (1996). Lévy flight search patterns of wandering albatrosses. Nature 381, 413–415. doi:10.1038/381413a0
Weiss, P. (1961). Guiding principles in cell locomotion and cell aggregation. Exp. Cell Res. 8, 260–281. doi:10.1016/0014-4827(61)90354-8
Wisdom, K. M., Adebowale, K., Chang, J., Lee, J. Y., Nam, S., Desai, R., et al. (2018). Matrix mechanical plasticity regulates cancer cell migration through confining microenvironments. Nat. Commun. 9, 4144. doi:10.1038/s41467-018-06641-z
Wolf, K., Mazo, I., Leung, H., Engelke, K., Andrian, U. H. von, Deryugina, E. I., et al. (2003). Compensation mechanism in tumor cell migration: Mesenchymal-amoeboid transition after blocking of pericellular proteolysis. J. Cell Biol. 160, 267–277. doi:10.1083/jcb.200209006
Wolf, K., te Lindert, M., Krause, M., Alexander, S., te Riet, J., Willis, A. L., et al. (2013). Physical limits of cell migration: Control by ECM space and nuclear deformation and tuning by proteolysis and traction force. J. Cell Biol. 201, 1069–1084. doi:10.1083/jcb.201210152
Wong, S., Guo, W.-H., and Wang, Y. (2014). Fibroblasts probe substrate rigidity with filopodia extensions before occupying an area. Proc. Natl. Acad. Sci. U. S. A. 111, 17176–17181. doi:10.1073/pnas.1412285111
Wu, Z., Su, M., Tong, C., Wu, M., and Liu, J. (2018). Membrane shape-mediated wave propagation of cortical protein dynamics. Nat. Commun. 9, 136. doi:10.1038/s41467-017-02469-1
Xiong, Y., Huang, C.-H., Iglesias, P. A., and Devreotes, P. N. (2010). Cells navigate with a local-excitation, global-inhibition-biased excitable network. Proc. Natl. Acad. Sci. U. S. A. 107, 17079–17086. doi:10.1073/pnas.1011271107
Yao, M., Goult, B. T., Klapholz, B., Hu, X., Toseland, C. P., Guo, Y., et al. (2016). The mechanical response of talin. Nat. Commun. 7, 11966. doi:10.1038/ncomms11966
Zaman, M. H., Trapani, L. M., Sieminski, A. L., Siemeski, A., MacKellar, D., Gong, H., et al. (2006). Migration of tumor cells in 3D matrices is governed by matrix stiffness along with cell-matrix adhesion and proteolysis. Proc. Natl. Acad. Sci. U. S. A. 103, 10889–10894. doi:10.1073/pnas.0604460103
Zhang, B., Wang, Z. X., and Zheng, Y. (1997). Characterization of the interactions between the small GTPase Cdc42 and its GTPase-activating proteins and putative effectors. Comparison of kinetic properties of Cdc42 binding to the Cdc42-interactive domains. J. Biol. Chem. 272, 21999–22007. doi:10.1074/jbc.272.35.21999
Keywords: cell migration, cytoskeletal forces, extracellular matrix, self-organization, membrane curvature
Citation: Pawluchin A and Galic M (2022) Moving through a changing world: Single cell migration in 2D vs. 3D. Front. Cell Dev. Biol. 10:1080995. doi: 10.3389/fcell.2022.1080995
Received: 26 October 2022; Accepted: 05 December 2022;
Published: 20 December 2022.
Edited by:
Yi Wu, UCONN Health, United StatesReviewed by:
Miguel Vicente-Manzanares, Spanish National Research Council (CSIC), SpainBenjamin Lin, New York University, United States
Copyright © 2022 Pawluchin and Galic. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Milos Galic, Z2FsaWNAdW5pLW11ZW5zdGVyLmRl
 Anna Pawluchin
Anna Pawluchin Milos Galic
Milos Galic