A Reverse-Osmosis Model of Apoptotic Shrinkage

Introduction

The remarkable and often the most noticeable feature of apoptosis is a decrease in cell size. While many other characteristics of apoptosis are often cell- and stimulus-dependent, shrinkage occurs very reliably. Numerous publications investigating various aspects of apoptotic volume decrease (AVD) have appeared in the 1990–2000s and resulted in a significant progress in our understanding of this phenomenon.

When apoptosis was first recognized as a distinct type of cell death, it was dubbed “shrinkage necrosis” (Kerr, 1971) because cells undergoing this type of death become smaller. This observation was surprising because, when exposed to an unfavorable environment, cells are expected to accumulate water, increase their volume and eventually lose membrane integrity. Water accumulation is a natural response to cessation of the Na⁺-K⁺ pump activity (Armstrong, 2003) and is a hallmark of unregulated necrotic death (Zong and Thompson, 2006). If the opposite occurs during apoptosis, one is tempted to conclude that cell shrinkage is a purposeful response.

AVD occurs early in apoptosis, often before caspase activation (Maeno et al., 2000). It can continue for several hours (Maeno et al., 2000; l’Hoste et al., 2010; Poulsen et al., 2010; Kasim et al., 2013), and cells often reduce their volume by 10–20% (Model, 2014). Sometimes, application of potassium or chloride channel inhibitors simultaneously with an apoptotic stimulus prevents caspase activation as well as all other signs of apoptosis (Maeno et al., 2000; Wei et al., 2004). These facts have been interpreted in the sense that either the loss of water or the loss of potassium is a necessary step in apoptosis development.

It is worth noting that a decrease in apoptotic cell size can be brought about by two mechanisms, dehydration and fragmentation. Because of the sensitivity of shrinkage to potassium and chloride, dehydration has received much more attention in the literature and in effect has become synonymous with AVD. But these two paths are not always easy to distinguish from one another, and not every instance of cell volume decrease should automatically be attributed to dehydration (Model, 2014; Model et al., 2018). Dehydration can often be surmized (though not definitively established) by prominent cell borders in bright-field transmission images (Figure 1). It can been more rigorously demonstrated by buoyant density centrifugation (Wyllie and Morris, 1982; Yamada and Ohyama, 1988; Cohen et al., 1992; Patterson et al., 1995; Yurinskaya et al., 2005) or by combined phase/volume measurements (Model and Schonbrun, 2013; Model et al., 2018). A loss of osmotically active ions in UV-irradiated U937 cells with preservation of the amount of phosphorus (Fernández-Segura et al., 1999) can be taken as another evidence of dehydration. Apoptotically-induced activation of outward Cl^– currents (Porcelli et al., 2004; Okada et al., 2006; Ernest et al., 2008) also indirectly supports the notion of water loss since chloride is, theoretically, the main correlate of intracellular water (Armstrong, 2003; Fraser and Huang, 2007).

FIGURE 1

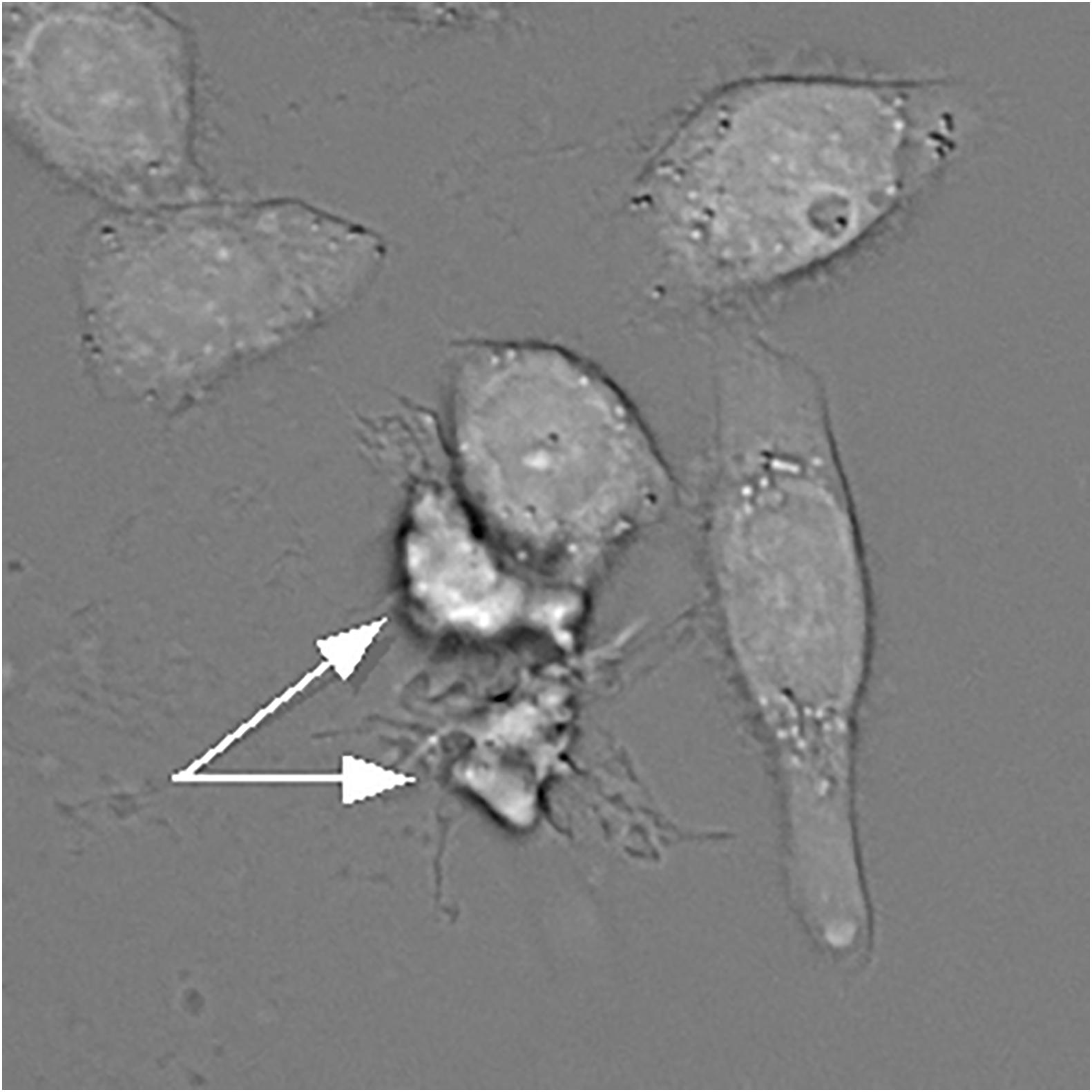
Figure 1. A bright-field transmission image of HeLa cells treated with actinomycin D. Two apoptotic and apparently dehydrated HeLa cells indicated by the arrows have much darker borders. However, this feature alone can only serve as a suggestion, but not as a definitive proof of dehydration. Water content can be accurately quantified under a transmission microscope as described by Mudrak et al. (2018).

But chloride cannot leave the cell alone, without being accompanied by a cation (potassium), and the outward electrochemical drive for potassium is usually stronger than that for chloride. Thus, the standard model of AVD presumes an early activation of potassium channels, which stimulate an efflux of chloride; the resulting loss of osmolytes leads to osmotic dehydration (Yu, 2003; Lang et al., 2005; Bortner and Cidlowski, 2007; Lang and Hoffmann, 2012; Kondratskyi et al., 2015). One general difficulty with this theory has already been pointed out by other authors. “Very different types of K⁺ channels have been implicated in activation of apoptosis, like voltage-gated K_v channels, ATP-regulated K_ATP channels, two-pore K⁺ channels, several types of Ca²⁺-dependent K⁺ channels and others. The variety of K⁺ channels that have been implicated in apoptosis suggests that in principle any type of K⁺ channel can support apoptosis, but it is not entirely clear how this can operate as a specific switch driving cells into regulated cell death” (Kunzelmann, 2016). Indeed, one would expect that such a universal phenomenon as apoptotic dehydration should have a more universal reason than relying on activation of specific channels present in each particular cell type.

Cytoskeleton-Driven, Ion-Dependent Dehydration

Here we wish to propose an alternative, or rather a complementary, mechanism of dehydration. It is not only ions that can drive water, but water can also drive ions through whatever channels happen to be available. One possible scenario would involve cytoskeleton-mediated intracellular pressure (IP).

IP in animal cells is conceptually similar to turgor in plant cells, although much smaller in magnitude—from tens to thousands Pa (Chengappa et al., 2018). The existence of intracellular pressure is evident from membrane blebs—the areas where membrane-cytoskeleton linkages mediated by numerous lipid-protein and protein-protein interactions (Doherty and McMahon, 2008) are weakened, and membrane forms protruding bubbles (Dai and Sheetz, 1999). Such blebs are frequently observed in apoptotic cells.

IP is believed to result from contraction of the actomyosin cytoskeleton. Since cell membranes are permeable to water, the existence of hydrostatic pressure implies that cells with stable water content must maintain a slight excess of intracellular osmolarity to keep water in balance. This is analogous to the balance of the Starling forces in blood capillaries.

We hypothesize that the balance of hydrostatic and osmotic forces becomes disrupted in apoptotic cells due to an increased cytoskeletal tension. Cytoskeleton has been long dismissed as a possible dehydration factor because the osmotic pressure that needs to be overcome to push water out of the cell is much stronger than any forces that can develop within the cytoskeleton; thus, researchers have come to believe that it is impossible for the cytoskeleton to produce any substantial water loss (Janmey, 1998). However, the situation would change radically if ion transport is taken into consideration. Suppose that a cell, initially at equilibrium, has developed a higher IP. This excess of pressure would result in a small water efflux, as in reverse osmosis, which, in turn, would create a slight increase in intracellular concentration of ions. If ion channels were blocked, water efflux would stop at this point because cytoskeleton would not be able to push against the ever-increasing concentration difference. But if ion channels were open, some ions would exit the cell down the concentration gradient (also aided by an excess of hydrostatic pressure inside). That would relieve the osmotic resistance and enable the cytoskeleton to push a little further, so that shrinkage would be able to continue.

As the following calculations show, the balance can be disrupted not only by an increase in hydrostatic pressure, but also by an increase in membrane permeability for ions (which makes the model equivalent to the standard one) or for water.

We will first describe the model in quantitative terms and then will discuss the experimental evidence for the cytoskeletal mechanism.

Theory

Shrinkage rate due to cytoskeletal compression can be estimated as follows.

Consider a cell with volume V immersed in a solution with osmolarity C₀; the internal concentration of osmolytes is C_i = C₀ + ΔC, where ΔC is a small positive number. Additional cytoskeletal pressure S (which can be expressed in equivalent concentration units by dividing physical pressure by RT, which equals to 2.5⋅10⁶ Pa⋅L⋅mol^–1 at 300K) causes an efflux of water and cell volume decrease, according to:

$$\frac{1}{\mathrm{\rho }}\frac{\text{dV}}{\text{dt}}=-\left[\mathrm{S}-\left({\text{C}}_{\text{i}}-{\text{C}}_{\text{o}}\right)\right]{\text{AP}}_{\text{w}}=-\left(\mathrm{S}-\mathrm{△}\text{C}\right){\text{AP}}_{\text{w}}(1)$$

where ρ is the molar volume of water (18 cm³/mol), A is the surface area of the cell (cm²), and P_w is membrane permeability for water (cm/s). We can assume for simplicity that S, A, and P_w remain constant and only ΔC changes with time. Time-dependent changes in ΔC result from two factors: a decrease in the cell volume V (cm³) and an efflux of the osmolyte. If the total molar amount of the osmolyte present in the cell is N (mol), then:

$$\frac{{\text{dC}}_{\text{i}}}{\text{dt}}=\frac{\text{d}}{\text{dt}}\left(\frac{\text{N}}{\text{V}}\right)=\frac{\text{d}}{\text{dt}}\frac{\mathrm{VdN}-\mathrm{NdV}}{{\text{V}}^2}=\frac{\text{dN}/\text{dt}}{\text{V}}-\text{N}\frac{\text{dV}/\text{dt}}{{\text{V}}^2}=\frac{\text{dN}/\text{dt}}{\text{V}}-{\text{C}}_{\text{i}}\frac{\text{dV}/\text{dt}}{\text{V}}(2)$$

Time derivative of the volume dV/dt is expressed by Eq. 1, and the change in the amount of osmolyte dN/dt is expressed through membrane permeability for the osmolyte:

$$\frac{\text{dN}}{\text{dt}}=-\left(\mathrm{S}+\mathrm{△}\text{C}\right){\text{AP}}_{\text{i}}(3)$$

Since

$$\frac{{\text{dC}}_{\text{i}}}{\text{dt}}=\frac{\text{d}\mathrm{△}\text{C}}{\text{dt}}$$

we obtain:

$$\frac{\text{d}\mathrm{△}\text{C}}{\text{dt}}=-\frac{\mathrm{S}+\mathrm{△}\text{C}}{\text{V}}{\text{AP}}_{\text{i}}+\frac{{\text{C}}_0+\mathrm{△}\text{C}}{\text{V}}\left(\mathrm{S}-\mathrm{△}\text{C}\right)\mathrm{\rho }{\text{AP}}_{\text{w}}(4)$$

We can further assume that the process has reached a quasi-steady state, when ΔC remains nearly constant; this allows us to estimate the rate of shrinkage by equating $\frac{\text{d}\mathrm{△}\text{C}}{\text{dt}}$to zero. By neglecting quadratic terms and taking into account that C₀ ≫ S, we find that, in a steady state:

$$\mathrm{△}\text{C}\approx \text{S}\frac{{\text{C}}_0\mathrm{\rho }{\text{P}}_{\text{w}}-{\text{P}}_{\text{i}}}{{\text{C}}_0\mathrm{\rho }{\text{P}}_{\text{w}}+{\text{P}}_{\text{i}}}(5)$$

For an impermeant membrane (P_i = 0), the concentration difference becomes equal to S.

To find the rate of volume change, we substitute Eq. 5 into Eq. 1 and obtain:

$$\frac{\text{dV}}{\text{dt}}=\frac{2\mathrm{\rho }{\text{AP}}_{\text{i}}{\text{P}}_{\text{w}}}{{\text{C}}_0\mathrm{\rho }{\text{P}}_{\text{w}}+{\text{P}}_{\text{i}}}\text{S}(6)$$

As expected, shrinkage depends both on water and osmolyte permeabilities. For a spherical cell with radius r (cm), the relative rate of shrinkage will be:

$$\frac{\text{dV}/{\text{V}}_0}{\text{dt}}=\frac{6\mathrm{\rho }{\text{P}}_{\text{i}}{\text{P}}_{\text{w}}}{\text{r}\left({\text{C}}_{\text{o}}\mathrm{\rho }{\text{P}}_{\text{w}}+{\text{P}}_{\text{i}}\right)}\text{S}(7)$$

To evaluate this expression, we assume r = 5⋅10^–4 cm and C₀ = 10^–4 mol/cm³ and use some literature values for the other parameters: P_i = 10^–5 cm/s (Strickholm, 1981), P_W = 2⋅10^–3 cm/s (Farinas et al., 1997), and S = 1,000 Pa (Chengappa et al., 2018), which correspond to 10³ Pa/(2.5⋅10⁶ Pa⋅L⋅mol^–1) = 4⋅10^–7 mol/cm³. That gives us the shrinkage rate of more than 40% per hour. Even though the parameters have been chosen rather arbitrarily, this estimate demonstrates that cytoskeleton-driven shrinkage is possible.

Discussion

The standard theory of the AVD postulates that some yet unidentified early apoptotic reactions alter membrane permeability in such a way that intracellular osmolytes begin to come out of the cell. Because potassium is the only major ion with electrochemical gradient strongly favoring its exit, it is best suited for the role. However, leakage of potassium alone would immediately cause hyperpolarization that would terminate the process. To keep electroneutrality, potassium can be replaced with sodium, but that would fail to produce any osmotic imbalance. The only way inorganic ions can cause shrinkage is when the exit of potassium exceeds the entry of sodium, and the charge difference is balanced by the loss of chloride.

The results with ionophores agree with this reasoning. Specific potassium ionophore valinomycin causes cell volume loss only when anion exchange is allowed (Dise and Goodman, 1985), but since cells are normally permeable for chloride to some extent, application of valinomycin to intact cells results in a volume decrease (Rana et al., unpublished). A detailed analysis of ion and water balance in the presence of various membrane channels and transporters (Vereninov et al., 2004, 2007) confirms that an increase in potassium permeability may cause AVD, especially if accompanied by a reduced activity of the Na⁺-K⁺ pump. To our knowledge, IP has not been included in any of the previous models.

At the same time, the idea that hydrostatic pressure may affect cell volume is not entirely new. Bereiter-Hahn and Strohmeier (1987) suggested that calcium-dependent intracellular pressure is strong enough to prevent osmotic fluxes. However, that effect was only observed in hypotonic media, and therefore the intracellular pressure in their case was rather a passive resistance to stretch, which is different from active compression that we are hypothesizing. Another model of cell volume regulation assumes that changes in cell volume affect membrane tension and mechanosensitive channels, providing a negative feedback for volume maintenance (Jiang and Sun, 2013).

We approached the problem from a different angle. Equation (6) does not aim to describe a specific molecular process; we omit the membrane potential from the picture, and the nature of the membrane-permeant osmolyte is not even specified. Thus, our model is different from the detailed descriptions of osmotic balance found in the works of other authors (Armstrong, 2003; Fraser and Huang, 2004; Vereninov et al., 2004, 2007). Nevertheless, our result proves that cytoskeletal compression is in principle capable of slowly expelling water if accompanied by an efflux of osmolytes. Equation (6) predicts that the rate of shrinkage should be proportional to IP; it should also be an increasing function of ion and water permeabilities and a decreasing function of external osmolarity. All these trends can be subject to experimental test.

Intracellular Pressure

The dependence of the AVD rate on IP is the critical feature of our model; moreover, we suggest that IP increases during apoptosis. The frequent occurrence of apoptotic blebs indicates that this indeed may be the case, with one qualification that blebs may result either from an increase in IP or from loosening of membrane attachment to the cytoskeleton. Most likely, both factors are in operation, but only the first one is relevant to our model.

The only known mechanism of IP generation is actomyosin contraction (Mills et al., 1998; Hagmann et al., 1999; Miñambres et al., 2006; Tinevez et al., 2009). The force is created by non-muscle myosin II, whose activity is regulated by phosphorylation by various kinases (Vicente-Manzanares et al., 2009), most importantly by myosin light chain kinase (MLCK) and by Rho-associated protein kinase (ROCK; Amano et al., 2010). MLCK is controlled by calcium and, indeed, persistent calcium elevation is a typical feature of apoptosis (Hajnóczky et al., 2003; Orrenius et al., 2003). Furthermore, MLCK activation during apoptosis has been demonstrated directly (Mills et al., 1998; Petrache et al., 2003; Nusbaum et al., 2004). On the other hand, buffering of intracellular calcium did not prevent a decrease in forward light scatter from apoptotic Jurkat cells (Scoltock et al., 2000), nor did it affect the loss of potassium and chloride in staurosporine-treated HeLa cells (Dezaki et al., 2012). The significance of these negative results is unclear because cell volume has not been measured in these works directly. Other authors did associate calcium with AVD, but only through its stimulatory effect on calcium-dependent chloride channels (Hoffmann et al., 2015).

The role of ROCK in apoptosis has also been a subject of investigation, mostly in connection to bleb formation. Under normal conditions, ROCK is activated by Rho GTPase but, during apoptosis, ROCK is cleaved by caspases 2 and 3 with release of a constitutively active fragment (Ndozangue-Touriguine et al., 2008; Street and Bryan, 2011). ROCK activation is responsible for apoptotic blebbing and detachment of apoptotic bodies (Street and Bryan, 2011).

Conceivably, not every type of cytoskeletal tension would translate into an increased IP; the cytoskeleton must form a continuous shell and be firmly attached to the membrane, so that it would be effectively pulling the membrane inside; such actin-myosin rings are in fact observed during apoptosis (Coleman and Olson, 2002; Miñambres et al., 2006; Ndozangue-Touriguine et al., 2008; Povea-Cabello et al., 2017). The shape of the membrane may also play a role: the membrane must be sufficiently convex, so that cortical tension would have a radial component (Figure 2). Alternatively, inward pulling may be mediated by non-cortical filaments.

FIGURE 2

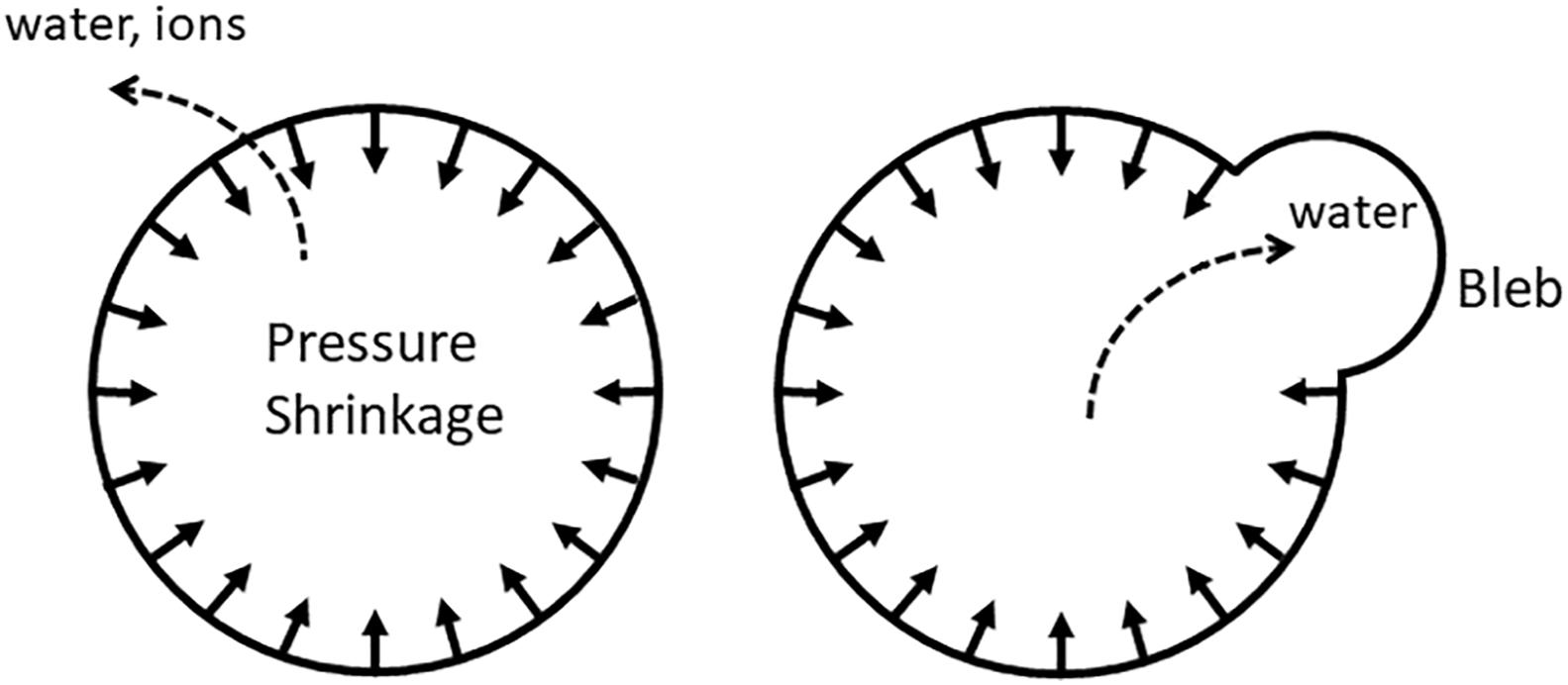
Figure 2. Uniform pulling on the membrane (either by the radial component of cortical tension or by non-cortical fibers oriented perpendicular to the membrane) produces IP that would slowly push water and ions out of the cell. When gaps in the cytoskeleton-membrane linkages are present, water is squeezed out into the bleb instead.

A more direct evidence in favor of the cytoskeletal hypothesis comes from two observations. Firstly, a myosin II inhibitor, blebbistatin, causes a slight but measurable increase in the volume of normal mitotic cells (Stewart et al., 2011). Our preliminary experiments on the effect of blebbistatin on apoptotic cells did show inhibition of water loss, but much more extensive studies would be needed for definitive conclusions. The problem with blebbistatin is that it inhibits apoptosis in general (Xiao et al., 2009; Street et al., 2010; Li et al., 2018; Chai et al., 2019). While such inhibition is compatible with the view that (1) cytoskeletal compression causes dehydration and that (2) dehydration is needed for apoptosis, one cannot claim that blebbistatin inhibits AVD if apoptosis is no longer present.

The second observation is that apoptotic water loss requires intact actin cytoskeleton. We subjected Madin-Darby Canine Kidney cells to a treatment with 2 mM staurosporine and measured intracellular water content, as described in Mudrak et al. (2018). After 3 h, cells lost 4.2% of their water (SEM 0.15 based on 45 cells analyzed in 3 separate experiments). However, the presence of 0.4 mM of the actin-depolymerizing drug cytochalasin D completely abrogated water loss (0.00 + 0.03, 31 cells in 3 experiments; P < 0.0001). A related finding has been reported by Bortner et al. (2008), who noticed that cytochalasin prevents potassium loss during apoptosis.

The other fact that agrees with the cytoskeletal model is that shrinkage does not occur in actively blebbing cells (Kasim et al., 2013; Gibbons et al., 2016), presumably because blebs provide an internal reservoir for water (Tinevez et al., 2009; Gibbons et al., 2016; Figure 2). Incidentally, blebbing in healthy cells also occurs with volume preservation (Langridge and Kay, 2006; Young and Mitran, 2010). On the other hand, application of blebbistatin or inhibition of ROCK by Y-27632 not prevent the development of cells with shrunken appearance (Kasim et al., 2013). However, neither water content nor IP have been determined in that study.

Unlike intracellular water, which can be quantified non-invasively under a regular transmission microscope (Mudrak et al., 2018), measuring IP in animal cells is a more challenging undertaking. The servo-null method that uses a microelectrode inserted into the cytoplasm (Kelly and Macklem, 1991; Petrie and Koo, 2014) may be the most direct and the least affected by the stiffness of the cytoskeleton because the needle penetrates past the cortical layer. A pressure-sensitive microinterferometer internalized by cells (Gómez-Martínez et al., 2013) is another interesting and apparently gentle technique for IP measurements.

Ion Permeability

Permeability for ions should be an integral part of any dehydration scheme and does not represent a unique feature of our hypothesis. The value of 1.3^∗10^–5 cm/s used in our calculations has been reported for K⁺ in the resting axon (Strickholm, 1981). Even though some other published numbers are smaller (Costa et al., 1989; Fraser and Huang, 2004), an increase in potassium permeability and the loss of potassium from apoptotic cells have been convincingly demonstrated (Yu et al., 1997; Dallaporta et al., 1998), and this observation is the main buttress for the ionic theory of the AVD. Clearly, if ion permeability during apoptosis is sufficient to allow potassium out by electrochemical gradient alone, it should be all the more sufficient when electrochemical gradient is assisted by pressure. Volume-regulated anion channels (VRAC) that pass chloride and organic osmolytes also become activated during apoptosis (Osei-Owusu et al., 2018). Multiple ion fluxes are always interconnected (Vereninov et al., 2007), and the single P_i and C₀ in Eq. 6 should be interpreted as cumulative parameters.

Water Permeability

If dehydration is the essence of the AVD, it is only natural that water permeability should be a factor. The assumed value for water permeability, P_W = 2⋅10^–3 cm/s, seems to be typical, although the numbers vary from 3 to 6 × 10^–4 cm/s in MDCK cells (Farinas and Verkman, 1996; Zelenina and Brismar, 2000) to 0.1 cm/s in the rat proximal tubule (Preisig and Berry, 1985). When water permeability is high, Eq. 7 turns into:

$$\frac{\text{dV}/{\text{V}}_0}{\text{dt}}=\frac{6\mathrm{\rho }{\text{P}}_{\text{i}}{\text{P}}_{\text{w}}}{\text{r}\left({\text{C}}_{\text{o}}\mathrm{\rho }{\text{P}}_{\text{w}}+{\text{P}}_{\text{i}}\right)}\text{S}\approx \frac{6{\text{P}}_{\text{i}}}{{\text{rC}}_{\text{o}}}\text{S}(8)$$

and ion permeability becomes the only limiting factor.

The dependence of apoptosis on water permeability has been demonstrated by several authors using either chemical inhibition of aquaporins or by comparing similar cell types with different aquaporin expression (Jablonski et al., 2004; Flamenco et al., 2009; Younts and Hughes, 2009; Lakner et al., 2011; Zhang et al., 2011). To explain the relationship between apoptosis and aquaporins, Jablonski et al. (2004) suggested that, when aquaporins are blocked, the loss of potassium exceeds the loss of water, and a drop in potassium concentration causes apoptosis. Whether this is so or not, our main focus here is on the loss of water rather than on caspase activation and other degradative processes. The published results do not provide enough information to test Eq. 6, and more pointed and quantitative experiments would be desirable.

Osmolarity

Cells adapt to a large range of osmolarities, and even the osmolarity of commercial DMEM media from different sources may vary from 230 to 360 mOsm. Although it is technically straightforward to manipulate osmolarity to test its effect on the AVD rate, varying levels of osmolarity may affect too many processes (Burg et al., 2007), and it would be difficult to guarantee that any changes in shrinkage rate are due to the described mechanism.

Conclusion

The main claim of our hypothesis is that cytoskeletal pressure plays an active role in apoptotic water loss. The attractiveness of this proposition is that cytoskeletal rearrangements appear to be a general feature of apoptosis and therefore, this mechanism would not have to rely on specific properties of ion channels. The effect of blebbistatin on cell volume (Stewart et al., 2011) and the dependence of AVD on actin show that the model is not in conflict with observations. Its more direct testing may proceed in two main directions.

(1) Demonstration of an increased IP during AVD. It is unclear whether the existing technology would be adequate for the task. For example, puncturing apoptotic cells with a needle may be difficult to perform, and the use of intracellular microinterferometer may not have been sufficiently developed.

(2) Manipulation of myosin activity by drugs. The previously mentioned difficulty with blebbistatin (namely, its interference with apoptosis) could possibly be circumvented by applying it at later stages, when apoptosis has become irreversible.

It is less clear if quantification of the dependence of the AVD rate on ion and water permeability to test Eq. 6 can be accurate enough to distinguish between this model and the model based on ion channel activation (Vereninov et al., 2004, 2007). Moreover, these mechanisms are not mutually exclusive, and both are likely to operate in parallel.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation, to any qualified researcher.

Author Contributions

PR performed the experiments and participated in writing the manuscript. MM conceived the model and wrote the manuscript. All authors contributed to the article and approved the submitted version.

Funding

The work was supported by the Research Council of the Kent State University.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We gratefully acknowledge the feedback and comments from Drs. M. Kurokawa, A. Vereninov, J. Bereiter-Hahn, and R. Petrie.

References

Amano, M., Nakayama, M., and Kaibuchi, K. (2010). Rho-kinase/ROCK: a key regulator of the cytoskeleton and cell polarity. Cytoskeleton 67, 545–554. doi: 10.1002/cm.20472

PubMed Abstract | CrossRef Full Text | Google Scholar

Armstrong, C. M. (2003). The Na/K pump, Cl ion, and osmotic stabilization of cells. Proc. Natl. Acad. Sci. U.S.A. 100, 6257–6262. doi: 10.1073/pnas.0931278100

PubMed Abstract | CrossRef Full Text | Google Scholar

Bereiter-Hahn, J., and Strohmeier, R. (1987). “Hydrostatic pressure in metazoan cells in culture: its involvement in locomotion and shape generation,” in Cytomechanics, eds W.-E. Reif, J. Bereiter-Hahn, and O. Roger Anderson (Berlin: Springer), 261–272. doi: 10.1007/978-3-642-72863-1_18

CrossRef Full Text | Google Scholar

Bortner, C. D., and Cidlowski, J. A. (2007). Cell shrinkage and monovalent cation fluxes: role in apoptosis. Arch. Biochem. Biophys. 462, 176–188. doi: 10.1016/j.abb.2007.01.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Bortner, C. D., Sifre, M. I., and Cidlowski, J. A. (2008). Cationic gradient reversal and cytoskeleton-independent volume regulatory pathways define an early stage of apoptosis. J. Biol. Chem. 283, 7219–7229. doi: 10.1074/jbc.M707809200

PubMed Abstract | CrossRef Full Text | Google Scholar

Burg, M. B., Ferraris, J. D., and Dmitrieva, N. I. (2007). Cellular response to hyperosmotic stresses. Physiology 87, 1441–1474. doi: 10.1152/physrev.00056

CrossRef Full Text | Google Scholar

Chai, R., Gao, S., Cheng, C., Wang, M., Jiang, P., Wang, Y., et al. (2019). Blebbistatin inhibits neomycin-induced apoptosis in hair cell-like HEI-OC-1 cells and in cochlear hair cells. Front. Cell. Neurosci. 13:590. doi: 10.3389/fncel.2019.00590

PubMed Abstract | CrossRef Full Text | Google Scholar

Chengappa, P., Sao, K., Jones, T. M., and Petrie, R. J. (2018). Intracellular pressure: a driver of cell morphology and movement. Int. Rev. Cell. Mol. Biol. 337, 185–211. doi: 10.1016/bs.ircmb.2017.12.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, G. M., Sun, X. M., Snowden, R. T., Dinsdale, D., and Skilleter, D. N. (1992). Key morphological features of apoptosis may occur in the absence of internucleosomal DNA fragmentation. Biochem. J. 286, 331–334. doi: 10.1042/bj2860331

PubMed Abstract | CrossRef Full Text | Google Scholar

Coleman, M. L., and Olson, M. F. (2002). Rho GTPase signalling pathways in the morphological changes associated with apoptosis. Cell Death Differ. 9, 493–504. doi: 10.1038/sj.cdd.4400987

PubMed Abstract | CrossRef Full Text | Google Scholar

Costa, P. F., Emilio, M. G., Fernandes, P. L., Gil Ferreira, H., and Gil Ferreira, K. (1989). Determination of ionic permeability coefficients of the plasma membrane of Xenopus laevis oocytes under voltage clamp. J. Physiol. 413, 199–211. doi: 10.1113/jphysiol.1989.sp017649

PubMed Abstract | CrossRef Full Text | Google Scholar

Dai, J., and Sheetz, M. P. (1999). Membrane tether formation from blebbing cells. Biophys. J. 77, 3363–3370. doi: 10.1016/S0006-3495(99)77168-7

CrossRef Full Text | Google Scholar

Dallaporta, B., Hirsch, T., Susin, S. A., Zamzami, N., Larochette, N., Brenner, C., et al. (1998). Potassium leakage during the apoptotic degradation phase. J. Immunol. 160, 5605–5615.

Google Scholar

Dezaki, K., Maeno, E., Sato, K., Akita, T., and Okada, Y. (2012). Early-phase occurrence of K+ and Cl− efflux in addition to Ca2+ mobilization is a prerequisite to apoptosis in HeLa cells. Apoptosis 17, 821–831. doi: 10.1007/s10495-012-0716-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Dise, C. A., and Goodman, D. B. (1985). The relationship between valinomycin-induced alterations in membrane phospholipid fatty acid turnover, membrane potential, and cell volume in the human erythrocyte. J. Biol. Chem. 260, 2869–2874.

Google Scholar

Doherty, G. J., and McMahon, H. T. (2008). Mediation, modulation, and consequences of membrane-cytoskeleton interactions. Annu. Rev. Biophys. 37, 65–95. doi: 10.1146/annurev.biophys.37.032807.125912

PubMed Abstract | CrossRef Full Text | Google Scholar

Ernest, N. J., Habela, C. W., and Sontheimer, H. (2008). Cytoplasmic condensation is both necessary and sufficient to induce apoptotic cell death. J. Cell Sci. 121, 290–297. doi: 10.1242/jcs.017343

PubMed Abstract | CrossRef Full Text | Google Scholar

Farinas, J., Kneen, M., Moore, M., and Verkman, A. S. (1997). Plasma membrane water permeability of cultured cells and epithelia measured by light microscopy with spatial filtering. J. Gen. Physiol. 110, 283–296. doi: 10.1085/jgp.110.3.283

PubMed Abstract | CrossRef Full Text | Google Scholar

Farinas, J., and Verkman, A. S. (1996). Cell volume and plasma membrane osmotic water permeability in epithelial cell layers measured by interferometry. Biophys. J. 71, 3511–3522. doi: 10.1016/s0006-3495(96)79546-2

CrossRef Full Text | Google Scholar

Fernández-Segura, E., Cañizares, F. J., Cubero, M. A., Warley, A., and Campos, A. (1999). Changes in elemental content during apoptotic cell death studied by electron probe X-ray microanalysis. Exp. Cell Res. 253, 454–462. doi: 10.1006/excr.1999.4657

PubMed Abstract | CrossRef Full Text | Google Scholar

Flamenco, P., Galizia, L., Rivarola, V., Fernandez, J., Ford, P., and Capurro, C. (2009). Role of AQP2 during apoptosis in cortical collecting duct cells. Biol. Cell. 101, 237–250. doi: 10.1042/BC20080050

PubMed Abstract | CrossRef Full Text | Google Scholar

Fraser, J. A., and Huang, C. L. (2007). Quantitative techniques for steady-state calculation and dynamic integrated modelling of membrane potential and intracellular ion concentrations. Prog. Biophys. Mol. Biol. 94, 336–372. doi: 10.1016/j.pbiomolbio.2006.10.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Fraser, J. A., and Huang, C. L. H. (2004). A quantitative analysis of cell volume and resting potential determination and regulation in excitable cells. J. Physiol. 559, 459–478. doi: 10.1113/jphysiol.2004.065706

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibbons, B. A., Kharel, P., Robinson, L. C., Synowicki, R. A., and Model, M. A. (2016). Volume measurements and fluorescent staining indicate an increase in permeability for organic cation transporter substrates during apoptosis. Exp. Cell Res. 344, 112–119. doi: 10.1016/j.yexcr.2016.03.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Gómez-Martínez, R., Hernández-Pinto, A. M., Duch, M., Vázquez, P., Zinoviev, K., de la Rosa, E. J., et al. (2013). Silicon chips detect intracellular pressure changes in living cells. Nat. Nanotechnol. 8, 517–521. doi: 10.1038/nnano.2013.118

PubMed Abstract | CrossRef Full Text | Google Scholar

Hagmann, J., Burger, M. M., and Dagan, D. (1999). Regulation of plasma membrane blebbing by the cytoskeleton. J. Cell. Biochem. 73, 488–499. doi: 10.1002/(SICI)1097-4644(19990615)73:4<488::AID-JCB7>3.0.CO;2-P

CrossRef Full Text | Google Scholar

Hajnóczky, G., Davies, E., and Madesh, M. (2003). Calcium signaling and apoptosis. Biochem. Biophys. Res. Commun. 304, 445–454. doi: 10.1016/S0006-291X(03)00616-8

CrossRef Full Text | Google Scholar

Hoffmann, E. K., Sørensen, B. H., Sauter, D. P., and Lambert, I. H. (2015). Role of volume-regulated and calcium-activated anion channels in cell volume homeostasis, cancer and drug resistance. Channels 9, 380–396. doi: 10.1080/19336950.2015.1089007

PubMed Abstract | CrossRef Full Text | Google Scholar

Jablonski, E. M., Webb, A. N., McConnell, N. A., Riley, M. C., and Hughes, F. M. Jr. (2004). Plasma membrane aquaporin activity can affect the rate of apoptosis but is inhibited after apoptotic volume decrease. Am. J. Physiol. Cell Physiol. 286, C975–C985. doi: 10.1152/ajpcell.00180.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

Janmey, P. A. (1998). The cytoskeleton and cell signaling: component localization and mechanical coupling. Physiol. Rev. 78, 763–781. doi: 10.1152/physrev.1998.78.3.763

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, H., and Sun, S. X. (2013). Cellular pressure and volume regulation and implications for cell mechanics. Biophys. J. 105, 609–619. doi: 10.1016/j.bpj.2013.06.021

PubMed Abstract | CrossRef Full Text | Google Scholar

Kasim, N. R., Kuželová, K., Holoubek, A., and Model, M. A. (2013). Live fluorescence and transmission-through-dye microscopic study of actinomycin D-induced apoptosis and apoptotic volume decrease. Apoptosis 18, 521–532. doi: 10.1007/s10495-013-0804-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Kelly, S. M., and Macklem, P. T. (1991). Direct measurement of intracellular pressure. Am. J. Physiol. 260, C652–C657. doi: 10.1152/ajpcell.1991.260.3.C652

PubMed Abstract | CrossRef Full Text | Google Scholar

Kerr, J. F. (1971). Shrinkage necrosis: a distinct mode of cellular death. J. Pathol. 105, 13–20. doi: 10.1002/path.1711050103

PubMed Abstract | CrossRef Full Text | Google Scholar

Kondratskyi, A., Kondratska, K., Skryma, R., and Prevarskaya, N. (2015). Ion channels in the regulation of apoptosis. Biochim. Biophys. Acta 1848, 2532–2546. doi: 10.1016/j.bbamem.2014.10.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Kunzelmann, K. (2016). Ion channels in regulated cell death. Cell. Mol. Life Sci. 73, 2387–2403. doi: 10.1007/s00018-016-2208-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Lakner, A. M., Walling, T. L., McKillop, I. H., and Schrum, L. W. (2011). Altered aquaporin expression and role in apoptosis during hepatic stellate cell activation. Liver Int. 31, 42–51. doi: 10.1111/j.1478-3231.2010.02356.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lang, F., Föller, M., Lang, K. S., Lang, P. A., Ritter, M., Gulbins, E., et al. (2005). Ion channels in cell proliferation and apoptotic cell death. J. Membr. Biol. 205, 147–157. doi: 10.1007/s00232-005-0780-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Lang, F., and Hoffmann, E. K. (2012). Role of ion transport in control of apoptotic cell death. Comprehensive Physiol. 2, 2037–2061. doi: 10.1002/cphy.c110046

PubMed Abstract | CrossRef Full Text | Google Scholar

Langridge, P. D., and Kay, R. R. (2006). Blebbing of Dictyostelium cells in response to chemoattractant. Exp. Cell Res. 312, 2009–2017. doi: 10.1016/j.yexcr.2006.03.007

PubMed Abstract | CrossRef Full Text | Google Scholar

l’Hoste, S., Chargui, A., Belfodil, R., Corcelle, E., Duranton, C., Rubera, I., et al. (2010). CFTR mediates apoptotic volume decrease and cell death by controlling glutathione efflux and ROS production in cultured mice proximal tubules. Am. J. Physiol. Renal Physiol. 298, F435–F453. doi: 10.1152/ajprenal.00286.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, F., Fan, X., Zhang, Y., Zhang, Y., Ma, X., Kou, J., et al. (2018). Inhibition of myosin IIA–actin interaction prevents ischemia/reperfusion induced cardiomyocytes apoptosis through modulating PINK1/Parkin pathway and mitochondrial fission. Int. J. Cardiol. 271, 211–218. doi: 10.1016/j.ijcard.2018.04.079

PubMed Abstract | CrossRef Full Text | Google Scholar

Maeno, E., Ishizaki, Y., Kanaseki, T., Hazama, A., and Okada, Y. (2000). Normotonic cell shrinkage because of disordered volume regulation is an early prerequisite to apoptosis. Proc. Natl. Acad. Sci. U.S.A. 97, 9487–9492. doi: 10.1073/pnas.140216197

PubMed Abstract | CrossRef Full Text | Google Scholar

Mills, J. C., Stone, N. L., Erhardt, J., and Pittman, R. N. (1998). Apoptotic membrane blebbing is regulated by myosin light chain phosphorylation. J. Cell Biol. 140, 627–636. doi: 10.1083/jcb.140.3.627

PubMed Abstract | CrossRef Full Text | Google Scholar

Miñambres, R., Guasch, R. M., Perez-Aragó, A., and Guerri, C. (2006). The RhoA/ROCK-I/MLC pathway is involved in the ethanol-induced apoptosis by anoikis in astrocytes. J. Cell Sci. 119, 271–282. doi: 10.1242/jcs.02723

PubMed Abstract | CrossRef Full Text | Google Scholar

Model, M. A. (2014). Possible causes of apoptotic volume decrease: an attempt at quantitative review. Am. J. Physiol. 306, C417–C424. doi: 10.1152/ajpcell.00328.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

Model, M. A., Mudrak, N. J., Rana, P. S., and Clements, R. J. (2018). Staurosporine-induced apoptotic water loss is cell- and attachment-specific. Apoptosis 23, 449–455. doi: 10.1007/s10495-018-1471-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Model, M. A., and Schonbrun, E. (2013). Optical determination of intracellular water in apoptotic cells. J. Physiol. 591, 5843–5849. doi: 10.1113/jphysiol.2013.263228

PubMed Abstract | CrossRef Full Text | Google Scholar

Mudrak, N. J., Rana, P. S., and Model, M. A. (2018). Calibrated brightfield-based imaging for measuring intracellular protein concentration. Cytometry Part A 93, 297–304. doi: 10.1002/cyto.a.23145

PubMed Abstract | CrossRef Full Text | Google Scholar

Ndozangue-Touriguine, O., Hamelin, J., and Bréard, J. (2008). Cytoskeleton and apoptosis. Biochem. Pharmacol. 76, 11–18. doi: 10.1016/j.bcp.2008.03.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Nusbaum, P., Laine, C., Seveau, S., Lesavre, P., and Halbwachs-Mecarelli, L. (2004). Early membrane events in polymorphonuclear cell (PMN) apoptosis: membrane blebbing and vesicle release, CD43 and CD16 down-regulation and phosphatidylserine externalization. Biochem. Soc. Trans. 32, 477–479. doi: 10.1042/bst0320477

PubMed Abstract | CrossRef Full Text | Google Scholar

Okada, Y., Shimizu, T., Maeno, E., Tanabe, S., Wang, X., and Takahashi, N. (2006). Volume-sensitive chloride channels involved in apoptotic volume decrease and cell death. J. Membr. Biol. 209, 21–29. doi: 10.1007/s00232-005-0836-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Orrenius, S., Zhivotovsky, B., and Nicotera, P. (2003). Regulation of cell death: the calcium-apoptosis link. Nat. Rev. Mol. Cell. Biol. 4, 552–565. doi: 10.1038/nrm1150

PubMed Abstract | CrossRef Full Text | Google Scholar

Osei-Owusu, J., Yang, J., del Carmen Vitery, M., and Qiu, Z. (2018). Molecular biology and physiology of volume-regulated anion channel (VRAC). Curr. Top. Membr. 81, 177–203. doi: 10.1016/bs.ctm.2018.07.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Patterson, S. D., Grossman, J. S., D’Andrea, P., and Latter, G. I. (1995). Reduced numatrin/B23/nucleophosmin labeling in apoptotic Jurkat T-lymphoblasts. J. Biol. Chem. 270, 9429–9436. doi: 10.1074/jbc.270.16.9429

PubMed Abstract | CrossRef Full Text | Google Scholar

Petrache, I., Birukov, K., Zaiman, A. L., Crow, M. T., Deng, H., Wadgaonkar, R., et al. (2003). Caspase-dependent cleavage of myosin light chain kinase (MLCK) is involved in TNF-α-mediated bovine pulmonary endothelial cell apoptosis. FASEB J. 17, 407–416. doi: 10.1096/fj.02-0672com

PubMed Abstract | CrossRef Full Text | Google Scholar

Petrie, R. J., and Koo, H. (2014). Direct measurement of intracellular pressure. Curr. Protoc. Cell Biol. 63, 12–19. doi: 10.1002/0471143030.cb1209s63

PubMed Abstract | CrossRef Full Text | Google Scholar

Porcelli, A. M., Ghelli, A., Zanna, C., Valente, P., Ferroni, S., and Rugolo, M. (2004). Apoptosis induced by staurosporine in ECV304 cells requires cell shrinkage and upregulation of Cl- conductance. Cell Death Differ. 11, 655–662. doi: 10.1038/sj.cdd.4401396

PubMed Abstract | CrossRef Full Text | Google Scholar

Poulsen, K. A., Andersen, E. C., Hansen, C. F., Klausen, T. K., Hougaard, C., Lambert, I. H., et al. (2010). Deregulation of apoptotic volume decrease and ionic movements in multidrug-resistant tumor cells: role of chloride channels. Am. J. Physiol. Cell Physiol. 298, C14–C25. doi: 10.1152/ajpcell.00654.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Povea-Cabello, S., Oropesa-Ávila, M., de la Cruz-Ojeda, P., Villanueva-Paz, M., de la Mata, M., Suárez-Rivero, J. M., et al. (2017). Dynamic reorganization of the cytoskeleton during apoptosis: the two coffins hypothesis. Int. J. Mol. Sci. 18:2393. doi: 10.3390/ijms18112393

PubMed Abstract | CrossRef Full Text | Google Scholar

Preisig, P. A., and Berry, C. A. (1985). Evidence for transcellular osmotic water flow in rat proximal tubules. Am. J. Physiol. Renal Physiol. 249, F124–F131. doi: 10.1152/ajprenal.1985.249.1.F124

PubMed Abstract | CrossRef Full Text | Google Scholar

Scoltock, A. B., Bortner, C. D., St, J., Bird, G., Putney, J. W. Jr., and Cidlowski, J. A. (2000). A selective requirement for elevated calcium in DNA degradation, but not early events in anti-Fas-induced apoptosis. J. Biol. Chem. 275, 30586–30596. doi: 10.1074/jbc.M004058200

PubMed Abstract | CrossRef Full Text | Google Scholar

Stewart, M. P., Helenius, J., Toyoda, Y., Ramanathan, S. P., Muller, D. J., and Hyman, A. A. (2011). Hydrostatic pressure and the actomyosin cortex drive mitotic cell rounding. Nature 469, 226–230. doi: 10.1038/nature09642

PubMed Abstract | CrossRef Full Text | Google Scholar

Street, C. A., and Bryan, B. A. (2011). Rho kinase proteins—pleiotropic modulators of cell survival and apoptosis. Anticancer. Res. 31, 3645–3657.

Google Scholar

Street, C. A., Routhier, A. A., Spencer, C., Perkins, A. L., Masterjohn, K., Hackathorn, A., et al. (2010). Pharmacological inhibition of Rho-kinase (ROCK) signaling enhances cisplatin resistance in neuroblastoma cells. Int. J. Oncol. 37, 1297–1305. doi: 10.3892/ijo_00000781

CrossRef Full Text | Google Scholar

Strickholm, A. (1981). Ionic permeability of K, Na, and Cl in potassium-depolarized nerve. Dependency on pH, cooperative effects, and action of tetrodotoxin. Biophys. J. 35, 677–697. doi: 10.1016/S0006-3495(81)84820-5

CrossRef Full Text | Google Scholar

Tinevez, J. Y., Schulze, U., Salbreux, G., Roensch, J., Joanny, J. F., and Paluch, E. (2009). Role of cortical tension in bleb growth. Proc. Natl. Acad. Sci. U.S.A. 106, 18581–18586. doi: 10.1073/pnas.0903353106

PubMed Abstract | CrossRef Full Text | Google Scholar

Vereninov, A. A., Goryachaya, T. S., Moshkov, A. V., Vassilieva, I. O., Yurinskaya, V. E., Lang, F., et al. (2007). Analysis of the monovalent ion fluxes in U937 cells under the balanced ion distribution: recognition of ion transporters responsible for changes in cell ion and water balance during apoptosis. Cell Biol. Int. 31, 382–393. doi: 10.1016/j.cellbi.2007.01.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Vereninov, A. A., Yurinskaya, V. E., and Rubashkin, A. A. (2004). The role of potassium, potassium channels, and symporters in the apoptotic cell volume decrease: experiment and theory. Doklady Biol. Sci. 398, 417–420. doi: 10.1023/B:DOBS.0000046672.99148.fb

CrossRef Full Text | Google Scholar

Vicente-Manzanares, M., Ma, X., Adelstein, R. S., and Horwitz, A. R. (2009). Non-muscle myosin II takes centre stage in cell adhesion and migration. Nat. Rev. Mol. Cell Biol. 10, 778–790. doi: 10.1038/nrm2786

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, L., Xiao, A. Y., Jin, C., Yang, A., Lu, Z. Y., and Yu, S. P. (2004). Effects of chloride and potassium channel blockers on apoptotic cell shrinkage and apoptosis in cortical neurons. Pflügers Arch. 448, 325–334. doi: 10.1007/s00424-004-1277-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Wyllie, A. H., and Morris, R. G. (1982). Hormone-induced cell death. Purification ad properties of thymocytes undergoing apoptosis after glucocorticoid treatment. Am. J. Pathol. 109, 78–87.

Google Scholar

Xiao, L., Eto, M., and Kazanietz, M. G. (2009). ROCK mediates phorbol ester-induced apoptosis in prostate cancer cells via p21Cip1 up-regulation and JNK. J. Biol. Chem. 284, 29365–29375. doi: 10.1074/jbc.M109.007971

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamada, T., and Ohyama, H. (1988). Radiation-induced interphase death of rat thymocytes is internally programmed (apoptosis). Int. J. Radiat. Biol. Relat. Stud. Phys. Chem. Med. 53, 65–75. doi: 10.1080/09553008814550431

PubMed Abstract | CrossRef Full Text | Google Scholar

Young, J., and Mitran, S. (2010). A numerical model of cellular blebbing: a volume-conserving, fluid-structure interaction model of the entire cell. J. Biomech. 43, 210–220. doi: 10.1016/j.jbiomech.2009.09.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Younts, T. J., and Hughes, J. (2009). “Emerging role of water channels in regulating cellular volume during oxygen deprivation and cell death,” in Brain Hypoxia and Ischemia with Special Emphasis on Development, eds G. G. Haddad and S. P. Yu (New York: Humana Press), 79–96. doi: 10.1007/978-1-60327-579-8_5

CrossRef Full Text | Google Scholar

Yu, S. P. (2003). Regulation and critical role of potassium homeostasis in apoptosis. Prog. Neurobiol. 70, 363–386. doi: 10.1016/S0301-0082(03)00090-X

CrossRef Full Text | Google Scholar

Yu, S. P., Yeh, C. H., Sensi, S. L., Gwag, B. J., Canzoniero, L. M., Farhangrazi, Z. S., et al. (1997). Mediation of neuronal apoptosis by enhancement of outward potassium current. Science 278, 114–117. doi: 10.1126/science.278.5335.114

PubMed Abstract | CrossRef Full Text | Google Scholar

Yurinskaya, V., Goryachaya, T., Guzhova, I., Moshkov, A., Rozanov, Y., Sakuta, G., et al. (2005). Potassium and sodium balance in U937 cells during apoptosis with and without cell shrinkage. Cell Physiol. Biochem. 16, 155–162. doi: 10.1159/000089841

PubMed Abstract | CrossRef Full Text | Google Scholar

Zelenina, M., and Brismar, H. (2000). Osmotic water permeability measurements using confocal laser scanning microscopy. Eur. Biophys. J. 29, 165–171. doi: 10.1007/PL00006645

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, L., Li, J., Jiang, Z., Sun, L., Mei, X., Yong, B., et al. (2011). Inhibition of aquaporin-1 expression by RNAi protects against aristolochic acid I-induced apoptosis in human proximal tubular epithelial (HK-2) cells. Biochem. Biophys. Res. Commun. 405, 68–73. doi: 10.1016/j.bbrc.2010.12.128

PubMed Abstract | CrossRef Full Text | Google Scholar

Zong, W. X., and Thompson, C. B. (2006). Necrotic death as a cell fate. Genes Dev. 20, 1–15. doi: 10.1101/gad.1376506

PubMed Abstract | CrossRef Full Text | Google Scholar