Three-dimensional tunnel face stability analysis with gate layout by discretization-based kinematic approach

Existing approaches for tunnel face stability analysis usually apply for circular cross-sections and solutions for tunnel face stability evaluation with city gate cross-sections by kinematic approach of limit analysis have not been reported. The present study developed a kinematic approach on tunnel face stability analysis for city gate sections by using spatial discretization technique. The proposed discretization-based kinematic approach applies to shallow tunnel stability analysis with cover depth ratio less than 5 by comparison with finite element limit analysis (FELA). The required support pressure increases with the increase of tunnel width, straight wall height and the central angle of the circular arch.

1 Introduction

Recent years have witnessed the rapid development of water conservancy and hydropower industry. Meanwhile, higher requirements have been put forward for the engineering quality and construction safety of water conveyance tunnel projects (Wang et al., 2024; He and Zhang, 2023; Li et al., 2024). The city gate shaped section, also known as the circular arch straight wall section, is a commonly used section form in water conveyance tunnels. Its top surface is in a circular arch shape, which can better bear the rock and soil pressure from the top of the tunnel. The two sides of the tunnel are straight walls, and the bottom of the tunnel is generally flat. The tunnel with the geometric configuration of the city gate not only facilitates early construction but also facilitates later maintenance work.

In the process of tunnel construction, determining the limit support pressure on the excavation face is a key content (Jia et al., 2024; Guo et al., 2024). Due to the significant three-dimensional boundary effect, the plane strain assumption should not be used for the stability evaluation of the tunnel excavation face. Instead, a three-dimensional analysis method should be used. Among the available stability analysis methods, the upper bound limit analysis method has become increasingly popular for its rigorous theoretical basis. It can also provide an upper bound to the ultimate failure load. In previous studies on upper bound stability analysis of three-dimensional tunnel faces, the failure modes based on rigid translational or rotational movements are commonly used. Among them, Mollon et al. (2009) derived the critical support pressure required to maintain the stability of the tunnel excavation face in a homogeneous stratum based on a rigid translational mechanism. Tang et al. (2014) further extended the multi-block translational mechanism to layered soils. In the above studies, truncated cones are generally used to simulate collapsed soil, but the truncated cone mechanism has the problem of not being able to fully fit the tunnel excavation face. In response to this issue, Mollon et al. (2010) proposed a kinematic approach based on spatial discretization techniques and successfully applied it to the stability study of tunnel excavation faces with circular sections (Ibrahim et al., 2015), and non-circular sections such as horseshoe sections (Pan and Dias, 2017; Ye and Ai, 2024; Hou et al., 2023). Zhong et al. (2023) proposed piecewise linear method (PLM) to consider the nonlinearity of rock strength, and generated two typical linearization methods: Generalized Tangential technique (GTT) and equivalent Mohr-Coulomb parameter method (EMM) are compared and analyzed. Finally, the confining pressure of rocks predicted by PLM is 9% higher than that predicted by GTT. Pan and Dias (2015) used the kinematic method of limit analysis, the advanced three-dimensional failure mechanism is extended to the stability analysis of the tunnel in anisotropic and heterogeneous soil. Chen et al. (2024) calculated the seepage field behind the inclined roadway working face based on FLAC3D, and proposed an improved rotating failure mechanism, which enabled the analytical method to study the stability of the inclined roadway working face. Tu et al. (2023) used discretization technology to improve the collapse mechanism of three-dimensional rotating rigid body based on limit analysis, and proves that the pressure and failure mechanism derived by this method are feasible by comparing with the experimental results. Bai et al. (2020) established the nonlinear coupled heat-moisture-pollution transport equation and analyzed it temperature of water in unsaturated soil drives movement and heavy metal Pb2+ migration. Bai et al. (2023) established a multi-phase constitutive model of water-bearing sediment under particle thermodynamics conditions, and verified the validity of the model through the experimental results of natural and synthetic samples with different hydrate saturation, sediment porosity and hydrate behavior. Sun et al. (2022) conducted 8 sets of model tests to study the failure behavior of roadway working face and describe the ground displacement and stress distribution.

In addition to rigid block mechanisms, some scholars have attempted to construct continuous mechanisms with compatible velocity fields to study the stability of tunnel excavation faces. The variation pattern of velocity fields can be derived from the elastic mechanics solutions (Klar et al., 2007), numerical simulation results (Mollon et al., 2013) or engineering experiences (Huang et al., 2019). The continuous mechanisms can significantly improve upper bound solutions on critical support pressure to the rigid block mechanisms when tunnel cover to depth ratio is greater than 3 (Zhang et al., 2018). However, the solutions produced by continuous mechanisms are still higher than rigid block mechanisms. In view of this, mechanisms consisting of both rigid blocks and shear zones (Li et al., 2022) are proposed and further improve the results of continuous mechanisms. Lai et al. studied the influence of tunnel excavation on adjacent foundation pits and the generalized analysis framework of active earth pressure in retaining walls (Lai et al., 2025; Lai et al., 2022; Lai et al., 2024).

In previous studies related to upper bound stability analysis of tunnel excavation face, the main focus is placed on circular cross-sections. This can be attributed to the difficulties in analyzing the stability of excavation faces of other types of tunnel cross-section using analytical methods. In engineering practice, the city gate shaped cross-section is commonly used in water conveyance tunnel projects, and its excavation face stability directly affects the quality and safety of engineering construction, which has important practical significance. However, there is still a lack of reliable stability analysis models for the excavation face of city gate tunnel, especially the influence of section geometries on the stability of tunnel excavation face is not clear, and further research is needed.

To solve the above problems, this paper proposes a method for upper bound stability analysis of the excavation face for a city gate tunnel based on spatial discretization technique. Firstly, the upper bound analysis theory based on spatial discretization technique was introduced. Then, a city gate tunnel excavation face instability and failure mechanism based on rigid rotational mode was constructed. Secondly, in the calculation of the work rate equations, by equating the internal energy dissipation rate to the work rate of external forces, the expression for the critical support pressure of the tunnel excavation face is derived. The most critical failure mode is obtained through optimization algorithms. Finally, the influence of soil strength parameters and tunnel section geometries on the stability of tunnel excavation face was discussed in depth.

2 Upper-bound theory

2.1 Instability mode of excavation face for city gate tunnel

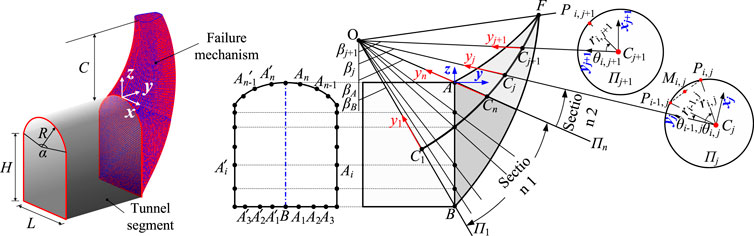
When analyzing the stability of the tunnel excavation face, it is assumed that the soil material follows the Mohr-Coulomb yield condition and associated flow rule. On this basis, based on the geometric characteristics of the excavation face of the city gate tunnel, a Cartesian coordinate system is established with the tunnel arch as the coordinate origin. The proposed three-dimensional failure mechanism follows a rigid rotational mode, as shown in Figure 1. In Figure 1, the depth of the tunnel is C, the transverse width of the tunnel is L, the height of the straight wall is H, the radius of the circular arch is R, and the center angle of the circular arch is α.

Figure 1

Figure 1. Instability and failure mechanism of city gate tunnel.

The formulated failure mechanism rotates rigidly at an angular velocity of $\omega$ around a rotation axis passing through point O, and the projection of the failure profile of the mechanism on the symmetry plane is two logarithmic spiral lines. Point A and point B are two points on the upper and lower logarithmic traces, respectively. The distances between the two logarithmic traces and point O are $r_1$ and $r_2$. In the polar coordinate system with point O as the origin, these two logarithmic traces can be written in Equation 1:

$\left\{\begin{array}{l}{r}_1\left(\beta \right)=r_A{e}^{\left(\beta -{\beta }_A\right)\tan \phi }\\ r_2\left(\beta \right)=r_B{e}^{\left({\beta }_B-\beta \right)\tan \phi }\end{array}\right.(1)$

where $r_A$ and $r_B$ are polar radius at angle ${\beta }_A$ and ${\beta }_B$, respectively; $\phi$ is soil frictional angle.

The position of the rotation axis can be determined by optimizing parameters ${\mathit{\beta }}_{\mathit{A}}$ and ${\mathit{\beta }}_{\mathit{B}}$. Velocity of any point within the rotating block can be determined by the relative position between that point and the rotation axis.

2.2 Discretization algorithm for failure surface generation

In the spatial discretization technique, the excavation face of the city gate tunnel is taken as the initial boundary surface to meet the geometrical restrictions, and it is discretized into 2n elementary nodes with the z-axis as the symmetry axis, as shown in Figure 1.

After determining the discrete points on the initial plane, the discrete points on the initial plane can be used as boundary conditions, and combined with the velocity field boundary conditions, the subsequent discrete nodes on the velocity discontinuity surfaces can be obtained.

When constructing the boundary surface of a discretization-based mechanism using spatial discretization techniques, a local coordinate system $\left(C_j,x_{c,j},y_{c,j}\right)$ is defined in each radial plane ${\mathrm{\Pi }}_j$ as shown in Figure 1. In a Cartesian coordinate system, the spatial coordinates of the centroid $C_j$ in plane ${\mathrm{\Pi }}_j$ can be represented in Equation 2:

$\left\{\begin{array}{l}{x}_{c,j}=0\\ y_{c,j}=y_o+r_m\sin {\beta }_j\\ z_{c,j}=z_o-r_m\cos {\beta }_j\end{array}\right.(2)$

where β_j is the polar angle for plane ${\mathrm{\Pi }}_j$; polar radius $r_m$ is the average polar radius to point O.

Vector ${\mathbf{C}}_{\mathbf{j}}{\mathbf{P}}_{\mathbf{i},\mathbf{j}}$ composed of discrete points $P_{i,j}$ and the centroid of the plane $C_j$ is defined in Equation 3:

${\mathbf{C}}_{\mathbf{j}}{\mathbf{P}}_{\mathbf{i},\mathbf{j}}=\left(x_{i,j}-x_{c,j},y_{i,j}-y_{c,j},z_{i,j}-z_{c,j}\right)(3)$

The vector composed of the centroid point of the plane $C_j$ and point O is defined in Equation 4:

${\mathbf{y}}_{\mathbf{j}}=\left(0,-\sin {\beta }_j,\cos {\beta }_j\right)(4)$

The angle between vectors ${\mathbf{C}}_{\mathbf{j}}{\mathbf{P}}_{\mathbf{i},\mathbf{j}}$ and ${\mathbf{y}}_{\mathbf{j}}$ is ${\theta }_{i,j}$, and the relative spatial position of discrete point $P_{i,j}$ in the plane can be determined based on angle ${\theta }_{i,j}$. Angle ${\theta }_{i,j}$ can be calculated using Equation 5:

$\cos {\theta }_{i,j}=\frac{\left(y_{i,j}-y_{c,j}\right)\left(-\sin {\beta }_j\right)+\left(z_{i,j}-z_{c,j}\right)\cos {\beta }_j}{\sqrt{{\left(x_{i,j}-x_{c,j}\right)}^2+{\left(y_{i,j}-y_{c,j}\right)}^2+{\left(z_{i,j}-z_{c,j}\right)}^2}}(5)$

In the discretization-based approach, the spatial position of a discrete point $P_{i,j+1}$ on the radial plane ${\mathrm{\Pi }}_{j+1}$ is determined by the two discrete points on the preceding radial plane $P_{i-1,j}$ and $P_{i,j}$ by the velocity compatibility condition, namely:

① The angle between the normal vector of the plane where the three points $P_{i-1,j}$, $P_{i,j}$ and $P_{i,j+1}$ are located and the velocity vector at the midpoint of the line connecting $P_{i-1,j}$ and $P_{i,j}$ is $\pi /2+\phi$;

② Discrete point $P_{i,j+1}$ is on plane ${\mathrm{\Pi }}_{j+1}$;

③ The polar angle ${\theta }_{i,j+1}$ of discrete point $P_{i,j+1}$ is half of the sum of ${\theta }_{i-1,j}$ and ${\theta }_{i,j}$.

Based on the above criterion, the specific spatial position of the discrete point $P_{i,j+1}$ can be determined by both of the discrete points $P_{i-1,j}$ and $P_{i,j}$. When solving the coordinates of discrete point $P_{i,j+1}$, it is necessary to firstly calculate the unit normal vector $\mathbf{N}\left(x_n,y_n,z_n\right)$ of the plane where the three points $P_{i-1,j}$, $P_{i,j}$ and $P_{i,j+1}$ are located. As mentioned earlier, it is stipulated here that the unit normal vector $\mathbf{N}$ points to the outside of the plane, and the unit normal vector must meet the following three conditions:

① The normal vector $\mathbf{N}$ is a unit vector (see Equation 6):

$\left|\mathbf{{\rm N}}\right|=1\Rightarrow x_n^2+y_n^2+z_n^2=1(6)$

② Normal vector $\mathbf{N}$ is perpendicular to vector ${\mathbf{P}}_{\mathbf{i}-\mathbf{1},\mathbf{j}}{\mathbf{P}}_{\mathbf{i},\mathbf{j}}$ (see Equation 7):

$\mathbf{{\rm N}}\cdot {\mathbf{P}}_{\mathbf{i}-\mathbf{1},\mathbf{j}}{\mathbf{P}}_{\mathbf{i},\mathbf{j}}=0\Rightarrow x_n\left(x_{i,j}-x_{i-1,j}\right)+y_n\left(y_{i,j}-y_{i-1,j}\right)+z_n\left(z_{i,j}-z_{i-1,j}\right)=0(7)$

③ The angle between the normal vector $\mathbf{N}$ and the unit velocity vector $\mathbf{v}$ at the midpoint $M_{i,j}$ of the line $P_{i-1,j}$ and $P_{i,j}$ is $\pi /2+\phi$ (i.e., the boundary conditions of the velocity field are strictly satisfied at this point) (see Equation 8):

$\mathbf{N}\cdot \mathbf{v}=\cos \left(\pi /2+\phi \right)(8)$

The unit velocity vector $\mathbf{v}$ at point $M_{i,j}$ is related to the polar angle of its plane and can be calculated using Equation 9:

$\mathbf{v}=\left(0,-\cos {\beta }_j,-\sin {\beta }_j\right)(9)$

Equation 9 reveals that the velocity vector is normal to the radius of the given point to the rotation axis. Therefore, the velocity field is continuous within the failure block.

Unit normal vector $\mathbf{N}$ can be derived by Equation 10:

$\left\{\begin{array}{l}{x}_n=C{y}_n+D\\ y_n=\frac{-F\pm \sqrt{\Delta }}{2E}\\ z_n=A{y}_n+B\end{array}\right.(10)$

where relevant parameters can be found in Equations 11–18,

$A=-\cot {\beta }_j(11)$

$B=\sin \phi /\sin {\beta }_j(12)$

$C=-\frac{\left(y_{i,j}-y_{i-1,j}\right)+A\left(z_{i,j}-z_{i-1,j}\right)}{x_{i,j}-x_{i-1,j}}(13)$

$D=-\frac{B\left(z_{i,j}-z_{i-1,j}\right)}{x_{i,j}-x_{i-1,j}}(14)$

$E=A^2+C^2+1(15)$

$F=2\left(AB+CD\right)(16)$

$G=B^2+D^2-1(17)$

$\Delta =F^2-4EG(18)$

Unit normal vector also follows Equation 19:

$\mathbf{N}\cdot \left({\mathbf{P}}_{\mathbf{i}-\mathbf{1},\mathbf{j}}{\mathbf{P}}_{\mathbf{i},\mathbf{j}}\times \mathbf{v}\right)>0(19)$

Discrete point $P_{i,j+1}$ is located on the plane ${\mathrm{\Pi }}_{j+1}$, this leads to Equation 20:

${\mathbf{C}}_{\mathbf{j}+\mathbf{1}}{\mathbf{P}}_{\mathbf{i},\mathbf{j}+\mathbf{1}}=r_{i,j+1}{\mathbf{\delta }}_{\mathbf{i},\mathbf{j}+\mathbf{1}}(20)$

where, $r_{i,j+1}$ is the distance between discrete points $P_{i,j+1}$ and $C_{j+1}$; ${\mathbf{\delta }}_{\mathbf{i},\mathbf{j}+\mathbf{1}}$ is a unit vector, it can be expressed in a Cartesian coordinate system as (see Equation 21):

${\mathbf{\delta }}_{\mathbf{i},\mathbf{j}+\mathbf{1}}\left\{\begin{array}{l}{\delta }_x=\sin {\theta }_{i,j+1}\\ {\delta }_y=-\cos {\theta }_{i,j+1}\sin {\beta }_{j+1}\\ {\delta }_z=\cos {\theta }_{i,j+1}\cos {\beta }_{j+1}\end{array}\right.(21)$

Considering Equation 22:

${\mathbf{M}}_{\mathbf{i},\mathbf{j}}{\mathbf{P}}_{\mathbf{i},\mathbf{j}+\mathbf{1}}={\mathbf{M}}_{\mathbf{i},\mathbf{j}}{\mathbf{C}}_{\mathbf{j}+\mathbf{1}}+{\mathbf{C}}_{\mathbf{j}+\mathbf{1}}{\mathbf{P}}_{\mathbf{i},\mathbf{j}+\mathbf{1}}={\mathbf{M}}_{\mathbf{i},\mathbf{j}}{\mathbf{C}}_{\mathbf{j}+\mathbf{1}}+r_{i,j+1}{\mathbf{\delta }}_{\mathbf{i},\mathbf{j}+\mathbf{1}}(22)$

As the unit normal vector $\mathbf{N}$ is perpendicular to the vector ${\mathbf{M}}_{\mathbf{i},\mathbf{j}}{\mathbf{P}}_{\mathbf{i},\mathbf{j}+\mathbf{1}}$, it yields Equation 23:

$r_{i,j+1}=-\frac{x_n\left(x_{c,j+1}-x_{i,j}^{\prime }\right)+y_n\left(y_{c,j+1}-y_{i,j}^{\prime }\right)+z_n\left(z_{c,j+1}-z_{i,j}^{\prime }\right)}{x_n{\delta }_x+y_n{\delta }_y+z_n{\delta }_z}(23)$

Thus Equation 24 can be obtained,

$\left\{\begin{array}{l}{x}_{i,j+1}=x_{c,j+1}+r_{i,j+1}{\delta }_x\\ y_{i,j+1}=y_{c,j+1}+r_{i,j+1}{\delta }_y\\ z_{i,j+1}=z_{c,j+1}+r_{i,j+1}{\delta }_z\end{array}\right.(24)$

Based on the above derivations, the spatial positions of each discrete point on the velocity cross-section can be calculated to obtain the velocity cross-section of the entire discrete rotating mechanism. When all discrete points in plane ${\mathrm{\Pi }}_j$ reach or exceed the ground surface, the calculation terminates and linear interpolation is used to adjust the discrete points above the ground surface to the ground surface. The calculation accuracy of a discrete rotating mechanism is controlled by the number of discrete points n on the initial plane and the angle increment $\Delta \beta$ between adjacent planes ${\mathrm{\Pi }}_j$ and ${\mathrm{\Pi }}_{j+1}$. Parameters n and $\Delta \beta$ are set as 160° and 0.01°, respectively.

2.3 Work rate equation

In the upper bound theorem, the rate of internal energy dissipation should be equal to the work rate of external forces. The rate of external forces includes soil gravity and the support pressure on the excavation face.

In a discretization-based mechanism, four adjacent discrete points, $P_{i,j}$, $P_{i+1,j}$, $P_{i,j+1}$ and $P_{i+1,j+1}$ are used as computing units and grouped together. By calculating and accumulating the work rates of the elementary blocks, the energy dissipation rate and the work rate of external forces of the entire mechanism can be obtained.

The work rate of soil gravity is given by Equation 25:

$W_g=\omega \gamma {\displaystyle \sum _{i,j}}\left(V_{i,j}{R}_{i,j}\sin {\beta }_{i,j}\right)(25)$

where $\gamma$ is soil unit weight; $V_{i,j}$ is the elementary volume; $R_{i,j}$ is the distance from the barycenter of the element to the rotation axis and ${\beta }_{i,j}$ is the corresponding angle in polar coordinates.

The work rate of support pressure acting on the tunnel face is calculated by Equation 26:

$W_p=\omega {\sigma }_T{\displaystyle \sum _j}{s}_j{r}_j\cos {\beta }_j(26)$

where ${\sigma }_T$ is uniform tunnel support pressure; $s_j$ is its elementary area of tunnel excavation face; $r_j$ and ${\beta }_j$ are polar radius and angle, respectively.

The internal work rate of energy dissipation can be expressed as Equation 27:

$E=\omega c{\displaystyle \sum _{i,j}}{S}_{i,j}{R}_{i,j}^{\prime }(27)$

where c is soil cohesion, $S_{i,j}$ is the elementary area of the failure surface, $R_{i,j}^{\prime }$ is the distance between the centroid of the calculated element and the center of rotation.

The upper bound theorem states that at the limit state, the ultimate failure load obtained by equating the work rate of external forces to the rate of energy dissipation is the upper limit of the exact failure load. By optimizing the position of the rotation axis through optimization algorithms, the optimal failure mode and the corresponding upper bound solutions for the critical support pressure at the tunnel excavation face can be obtained. The rotating mechanism based on spatial discretization technique contains two optimization parameters, β_A and β_B. The optimal upper bound solution can be obtained by optimizing the values of β_A and β_B in Equation 28 by using the genetic algorithm implemented in MATLAB. In addition, optimizing parameters β_A and β_B obey the following constraints (see Equation 29):

${\sigma }_T=\min f\left({\beta }_A,{\beta }_B|\gamma ,c,\phi ,\alpha ,C,L,H\right)(28)$

$\left\{\begin{array}{l}0<{\beta }_A<\pi /2\\ 0<{\beta }_B<\pi /2\\ {\beta }_B<{\beta }_A\end{array}\right.(29)$

3 Verification of the proposed mechanism

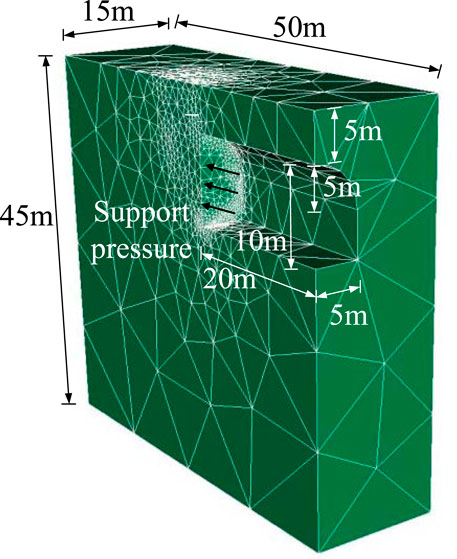
The reliability of the discretization-based kinematic approach proposed in this paper was verified using the three-dimensional limit analysis finite element software Optum G3. The numerical analysis model established is shown in Figure 2.

Figure 2

Figure 2. Finite element numerical model for limit analysis.

In the verification example, the tunnel depth is 5 m, the tunnel width is 10 m, the vertical wall height is 5 m, the circular arch radius is 5 m, and the central angle of the circular arch is 180°. The soil unit weight is 20 kN/m³, the internal friction angle is 15°, and the cohesion is 20 kPa. Considering the symmetry of the model, only a general geometric model is established to reduce computational complexity, where the bottom of the model is fully constrained and the vertical boundary constrains the normal displacement. When analyzing, it is assumed that the lining will not be damaged and only face failure is considered, so the displacement of the lining in all directions is constrained.

The spatial discretization-based upper bound limit analysis method proposed in this paper provides a critical support pressure of 9.98 kPa for the tunnel excavation face. Apply the calculated result as the force boundary condition in the numerical model to the excavation face of the tunnel, and combine the strength reduction technique to calculate the safety factor of the tunnel excavation face in the numerical model. The closer the calculated safety factor of the numerical model is to 1, the better the agreement between the two methods. After 3 iterations of calculation and the introduction of mesh adaptive technology, the safety factor calculation result in the limit analysis finite element method was 0.975 with 15,861 grids, which is very close to the method proposed in this paper and has an error of only 2.5%, verifying the reliability of the proposed discretization-based method.

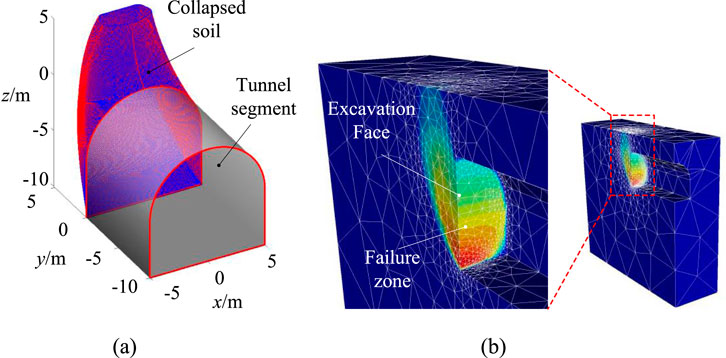
The instability diagram of the tunnel excavation face given in the discrete method and numerical model is shown in Figure 3. Finite element limit analysis adopts mesh refinement technique, and refinement zone can be regarded as possible failure surface. From Figure 3, it can be seen that the predicted failure surface of the discrete method is in good agreement with the numerical simulation results, further verifying the rationality of the constructed tunnel excavation surface failure mechanism.

Figure 3

Figure 3. Comparison on failure pattern. (A) Discretization approach (B) FELA.

4 Results and discussion

4.1 Effect of soil strength parameters

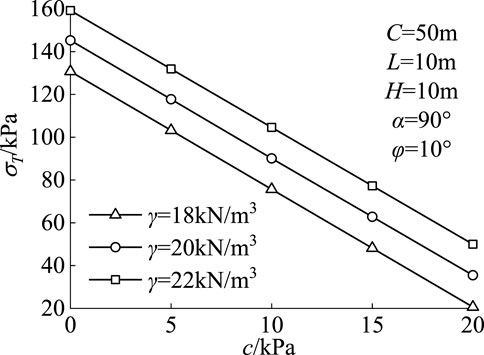
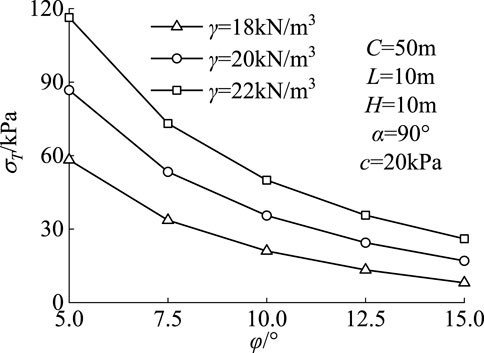
The critical support pressure required to maintain the stability of the tunnel excavation face decreases with the increase of soil strength parameters, as shown in Figures 4, 5. The support pressure decreases linearly with the increase of soil cohesion and nonlinearly with the increase of soil frictional angle. As the internal frictional angle of the soil increases, its impact on the critical support pressure weakens. Considering that soil gravity is the driving force for the failure of the tunnel excavation face, an increase in soil unit weight will lead to an increase in the required support pressure.

Figure 4

Figure 4. Critical support pressure with soil cohesion.

Figure 5

Figure 5. Critical support pressure with soil friction angle.

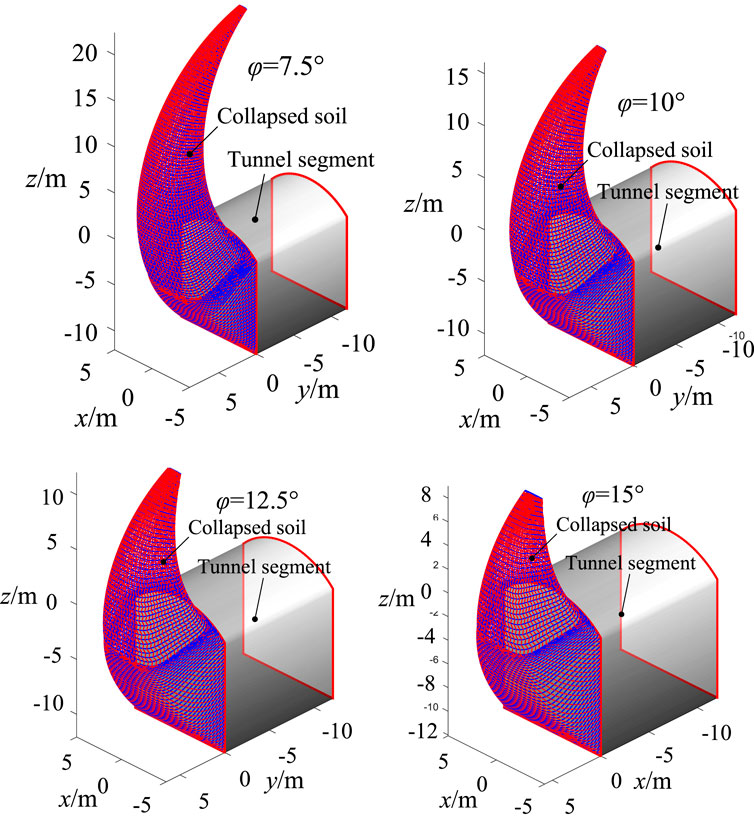
The effect of soil internal friction angle on the failure mode of tunnel excavation face is shown in Figure 6, where the tunnel depth is 50 m, the tunnel width is 10 m, the vertical wall height is 10 m, and the center angle of the circular arch is 90°. Soil unit weight is 20 kN/m³, and soil cohesion is 20 kPa. From Figure 6, it can be seen that the increase in internal friction angle can significantly constrain the expansion of the failure region. When soil internal friction angle increases from 7.5° to 15°, the height of the collapsed soil decreases by 59.4%.

Figure 6

Figure 6. Failure mode with soil friction angle.

4.2 Effect of excavation face dimensions

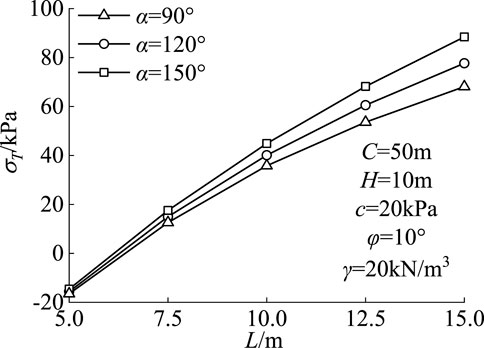
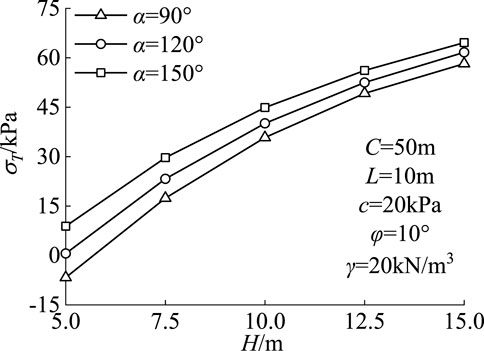
The variation of the critical support pressure of the tunnel with the geometric dimensions of the tunnel section is shown in Figures 7, 8. As the transverse width of the tunnel section and the height of the straight wall increase, the critical support pressure required to maintain the stability of the tunnel excavation face also increases. In addition, as the center angle of the tunnel arch increases, the curvature of the arch section at the top of the tunnel tends to be flatten, resulting in a weakening of the soil arch effect and an increase in the required critical support pressure. As the lateral width increases, the difference in required critical support pressure under different arch center angle conditions becomes more significant; As the height of the straight wall increases, the difference in support pressure required for different arch center angles gradually decreases.

Figure 7

Figure 7. Critical support pressure with tunnel width.

Figure 8

Figure 8. Critical support pressure with vertical wall height.

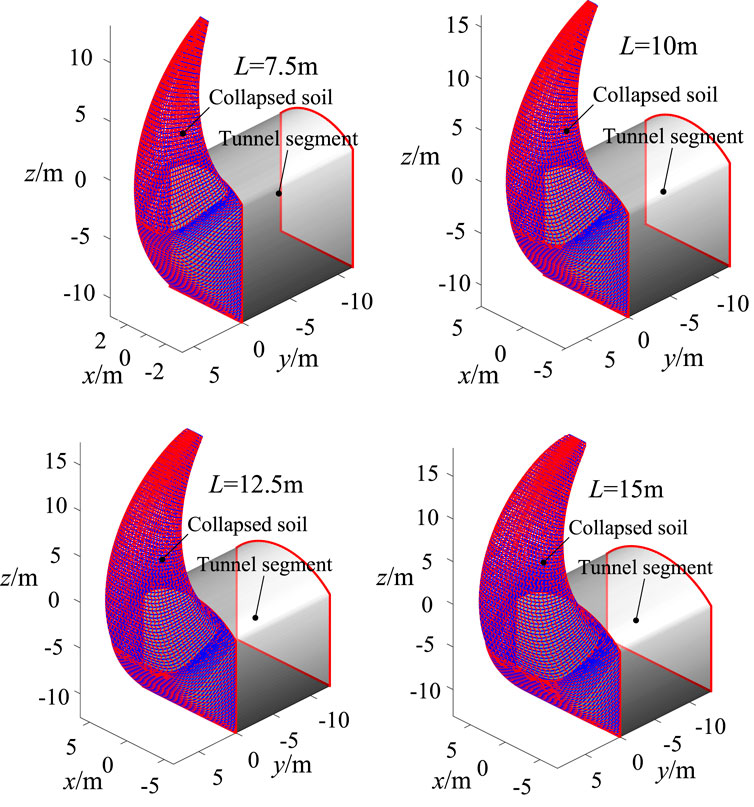
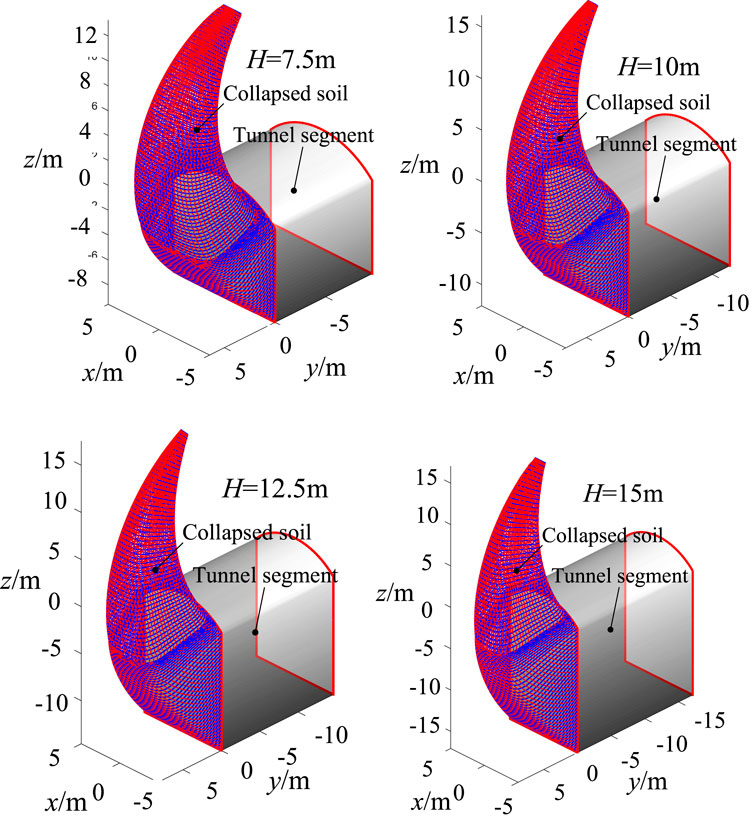
The influence of tunnel section dimensions on the failure mode of excavation face is shown in Figures 9, 10, where the tunnel depth is 50 m and the center angle of the circular arch is 90°. The soil unit weight is 20 kN/m³, soil cohesion is 20 kPa, and soil internal friction angle is 10°. As the lateral width of the tunnel increases, the unstable area of the tunnel also expands, especially at the longitudinal scale where the expansion is more significant. When the center angle of the circular arch is 90°, as the lateral dimension increases from 5 m to 15 m, the longitudinal height of the damaged soil increases by 137.1%. The increase in failure height can be attributed to the decrease of arching effect by increasing lateral dimension. As the height of the vertical wall increases from 5 m to 15 m, the longitudinal height of the damaged soil increases by 64.3%.

Figure 9

Figure 9. Failure mode of excavation face with tunnel width.

Figure 10

Figure 10. Failure mode of excavation face with the height of the straight wall.

5 Conclusion

This study proposes a discretization-based kinematic approach for the stability analysis of tunnel excavation face with a city gate layout. In-depth research was conducted on the influence of soil strength parameters and tunnel section dimensions on the stability of excavation surfaces. The main conclusions are summarized as follows:

(1) Support pressure required to maintain the stability of the tunnel excavation face decreases with the increase of soil strength parameters. The change in cohesion has a relatively small impact on the tunnel failure mode, while the increase in internal friction angle can significantly constrain the expansion of collapsed soil.

(2) The critical support pressure increases with the increase of tunnel width, straight wall height and the central angle of the circular arch. The influence of the transverse width of the tunnel on the failure mode is more significant compared to the height of the straight wall.

After comprehensive case studies, it is found that the proposed discretization-based rotational mechanism applies to shallow tunnels to ensure its accuracy when cover to depth less than 5. Future study is needed to further improve the current method and guide practical construction projects.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

BZ: Conceptualization, Investigation, Supervision, Validation, Writing–original draft. GC: Conceptualization, Validation, Writing–review and editing. ZX: Funding acquisition, Methodology, Visualization, Writing–review and editing. HL: Software, Supervision, Writing–review and editing. HW: Formal Analysis, Writing–review and editing. BX: Project administration, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. 2023 Major science and technology project of Henan Province, grant number 231100320100.

Conflict of interest

Author GC was employed by Henan Shuitou Xiaolangdi North Bank Irrigation District Engineering Co., Ltd. Author ZX was employed by Central Plains Regional headquarters of China South-to-North Water Transfer Group Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, B., Xu, T., Nie, Q. K., and Li, P. (2020). Temperature-driven migration of heavy metal Pb 2+ along with moisture movement in unsaturated soils. Int. J. Heat Mass Transf. 153, 119573. doi:10.1016/j.ijheatmasstransfer.2020.119573

CrossRef Full Text | Google Scholar

Bai, B., Zhou, R., Yang, G. C., Zou, W., and Yuan, W. (2023). The constitutive behavior and dissociation effect of hydrate-bearing sediment within a granular thermodynamic framework. Ocean. Eng. 268, 113408. doi:10.1016/j.oceaneng.2022.113408

CrossRef Full Text | Google Scholar

Chen, G. H., Zou, J. F., Guo, Y. C., Tan, Z., and Dan, S. (2024). Face stability assessment of a longitudinally inclined tunnel considering pore water pressure. Int. J. Numer. Anal. Methods Geomechanics 48 (15), 3725–3747. doi:10.1002/nag.3815

CrossRef Full Text | Google Scholar

Guo, F., Yu, X., Shi, Y., Shen, C., Zhu, B., Peng, H., et al. (2024). Evaluation of critical thresholds for surrounding rock stability in TBM tunnels utilizing limit state analysis. Buildings 14 (6), 1838. doi:10.3390/buildings14061838

CrossRef Full Text | Google Scholar

He, N., and Zhang, X. (2023). Excavation and construction technology of diversion tunnel under complex geological conditions. Appl. Sci. 13 (20), 11538. doi:10.3390/app132011538

CrossRef Full Text | Google Scholar

Hou, C., Yang, X., Liu, M., Chen, M., Wu, Z., and Long, G. (2023). Stability assessment of a non-circular tunnel face with tensile strength cut-off subject to seepage flows: a comparison analysis. Comput. Geotech. 163, 105764. doi:10.1016/j.compgeo.2023.105764

CrossRef Full Text | Google Scholar

Huang, M., Wang, H., Yu, J., and Tang, Z. (2019). Undrained stability analysis of a plane strain circular tunnel using streamline velocity fields. Int. J. Geomechanics 19 (5), 06019006. doi:10.1061/(asce)gm.1943-5622.0001395

CrossRef Full Text | Google Scholar

Ibrahim, E., Soubra, A., Mollon, G., Raphael, W., Dias, D., and Reda, A. (2015). Three-dimensional face stability analysis of pressurized tunnels driven in a multilayered purely frictional medium. Tunn. Undergr. Space Technol. 49, 18–34. doi:10.1016/j.tust.2015.04.001

CrossRef Full Text | Google Scholar

Jia, Y., Pei, C., Liang, F., and Li, T. (2024). Critical face pressure of a tunnel driven by a shield machine considering seismic forces and tunnel shape influence. Buildings 14 (6), 1760. doi:10.3390/buildings14061760

CrossRef Full Text | Google Scholar

Klar, A., Osman, A. S., and Bolton, M. (2007). 2D and 3D upper bound solutions for tunnel excavation using “elastic” flow fields. Int. J. Numer. Anal. Methods Geomechanics 31 (12), 1367–1374. doi:10.1002/nag.597

CrossRef Full Text | Google Scholar

Lai, F., Yang, D., Liu, S., Zhang, H., and Cheng, Y. (2022). Towards an improved analytical framework to estimate active earth pressure in narrow c–ϕ soils behind rotating walls about the base. Comput. Geotechnics 141, 104544. doi:10.1016/j.compgeo.2021.104544

CrossRef Full Text | Google Scholar

Lai, F., Zhang, N., Liu, S., and Yang, D. (2024). A generalised analytical framework for active earth pressure on retaining walls with narrow soil. Géotechnique 74 (11), 1127–1142. doi:10.1680/jgeot.21.00305

CrossRef Full Text | Google Scholar

Lai, F. W., Tschuchnigg, F., Schweiger, H., Liu, S., Shiau, J., and Cai, G. (2025). A numerical study of deep excavations adjacent to existing tunnels: integrating CPTU and SDMT to calibrate soil constitutive model. Can. Geotechnical J., 1–23. doi:10.1139/cgj-2024-0203

CrossRef Full Text | Google Scholar

Li, W., Zhang, C., Zhang, D., Ye, Z., and Tan, Z. (2022). Face stability of shield tunnels considering a kinematically admissible velocity field of soil arching. J. Rock Mech. Geotechnical Eng. 14 (2), 505–526. doi:10.1016/j.jrmge.2021.10.006

CrossRef Full Text | Google Scholar

Li, X., Sun, W., Fu, H., Bu, Q., Zhang, Z., Huang, J., et al. (2024). Schedule risk model of water intake tunnel construction considering mood factors and its application. Sci. Rep. 14 (1), 3857. doi:10.1038/s41598-024-54261-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Mollon, G., Dias, D., and Soubra, A. (2009). Probabilistic analysis and design of circular tunnels against face stability. Int. J. Geomechanics 9 (6), 237–249. doi:10.1061/(asce)1532-3641(2009)9:6(237)

CrossRef Full Text | Google Scholar

Mollon, G., Dias, D., and Soubra, A. (2010). Face stability analysis of circular tunnels driven by a pressurized shield. J. Geotechnical Geoenvironmental Eng. 136 (1), 215–229. doi:10.1061/(asce)gt.1943-5606.0000194

CrossRef Full Text | Google Scholar

Mollon, G., Dias, D., and Soubra, A. (2013). Continuous velocity fields for collapse and blowout of a pressurized tunnel face in purely cohesive soil. Int. J. Numer. Anal. Methods Geomechanics 37 (13), 2061–2083. doi:10.1002/nag.2121

CrossRef Full Text | Google Scholar

Pan, Q., and Dias, D. (2015). Face stability analysis for a shield-driven tunnel in anisotropic and nonhomogeneous soils by the kinematical approach. Int. J. Geomechanics 16 (3), 04015076. doi:10.1061/(asce)gm.1943-5622.0000569

CrossRef Full Text | Google Scholar

Pan, Q., and Dias, D. (2017). Upper-bound analysis on the face stability of a non-circular tunnel. Tunn. Undergr. Space Technol. 62, 96–102. doi:10.1016/j.tust.2016.11.010

CrossRef Full Text | Google Scholar

Sun, Z. Y., Zhang, D. L., Li, A., Lu, S., Tai, Q., and Chu, Z. (2022). Model test and numerical analysis for the face failure mechanism of large cross-section tunnels under different ground conditions. Tunn. Undergr. Space Technol. Incorporating Trenchless Technol. Res. 130, 104735. doi:10.1016/j.tust.2022.104735

CrossRef Full Text | Google Scholar

Tang, X., Liu, W., Albers, B., and Savidis, S. (2014). Upper bound analysis of tunnel face stability in layered soils. Acta Geotech. 9, 661–671. doi:10.1007/s11440-013-0256-1

CrossRef Full Text | Google Scholar

Tu, S., Li, W., Zhang, C. P., and Chen, W. (2023). Effect of inclined layered soils on face stability in shield tunneling based on limit analysis. Tunn. Undergr. Space Technol. 131, 104773. doi:10.1016/j.tust.2022.104773

CrossRef Full Text | Google Scholar

Wang, T., Liu, H., Kang, M., Zhao, B., Shen, J., Li, Y., et al. (2024). Study on the synergistic effect of primary support and surrounding rock of large buried depth tunnel in soft and fractured strata. Appl. Sci. 14 (5), 2028. doi:10.3390/app14052028

CrossRef Full Text | Google Scholar

Ye, Z. K., and Ai, Z. Y. (2024). A matrix-form complex variable method for multiple non-circular tunnels in layered media. Appl. Math. Model. 131, 570–595. doi:10.1016/j.apm.2024.04.033

CrossRef Full Text | Google Scholar

Zhang, F., Gao, Y. F., Wu, Y., and Zhang, N. (2018). Upper-bound solutions for face stability of circular tunnels in undrained clays. Géotechnique 68 (1), 76–85. doi:10.1680/jgeot.16.t.028

CrossRef Full Text | Google Scholar

Zhong, J. H., H, C. T., and Yang, X. L. (2023). Three-dimensional face stability analysis of rock tunnels excavated in Hoek-Brown media with a novel multi-cone mechanism. Comput. Geotechnics 154, 105158. doi:10.1016/j.compgeo.2022.105158

CrossRef Full Text | Google Scholar