- 1Faculty of Mining and Petroleum Engineering, Institut Teknologi Bandung, Bandung, Indonesia
- 2Research Center for Hydrodynamic Technology, Badan Riset dan Inovasi Nasional, Surabaya, Indonesia
- 3Ikatan Ahli Tsunami Indonesia (IATSI), Jakarta, Indonesia
This study re-examines a broad region of the Sumatran subduction zone and off-coast southern West Java, building on findings of relative quiescence and utilizing the modified probability gain (mG) concept. By comparing pre- and post-quiescence seismicity, we identify potential earthquake sources and assess associated tsunami hazards. We propose a novel combined model integrating normalized seismicity smoothing, geodetic moment rate, and mG to characterize earthquake likelihood better. This model, coupled with a robust seismicity rate model, enables a spatiotemporal earthquake potential hierarchy for refined seismic hazard assessment. Our results confirm prior quiescence findings in specific zones and identify novel potential source regions for significant future earthquakes. We estimate tsunami height, emphasizing the importance of multiple source areas and static stress loading. By examining pre- and post-event expectations, we aim to improve understanding of major earthquakes in the Sumatran Subduction Zone and inform disaster mitigation strategies. This study provides crucial insights for enhanced regional earthquake and tsunami preparedness.
1 Introduction
The Sumatra subduction zone is a highly active seismic region prone to large and destructive earthquakes. Understanding the earthquake potential along this zone is crucial for preparedness and mitigation efforts. The key factors contributing to high earthquake potential can be described as follows:
The subduction Zone Activity, in which the Indian-Australian Plate is subducted beneath the Sunda Plate along the Sumatra coast, causes significant stress build-up. This tectonic activity releases energy in the form of earthquakes. Sumatra has a history of major earthquakes, including the devastating 2004 Indian Ocean earthquake and tsunami, highlighting the region’s vulnerability. The subduction zone can generate megathrust earthquakes, which can have magnitudes exceeding 8.0 and cause widespread destruction and tsunamis. While it is impossible to predict future earthquakes’ exact timing and location, scientists and seismologists continuously monitor the region for signs of increased seismic activity. Some areas along the Sumatra subduction zone are considered at higher risk due to their specific tectonic characteristics and historical earthquake patterns. Thus, by understanding the earthquake potential along the Sumatra subduction zone and taking proactive measures, it is possible to mitigate the impact of future earthquakes and safeguard lives and property. Shearer and Burgmann’s (2010) analysis of the 2004 Sumatra-Andaman earthquake provides crucial insights into the complexities of large-scale seismic events. While the earthquake exhibited many characteristics of other major earthquakes, it also revealed significant uncertainties and long-term consequences. Following the suggestion of Shearer and Burgmann (2010), the implications and future research directions to reduce the uncertainties in estimating the potential of slip distribution for seismic hazard assessment could be done by combining seismic and geodetic data, which can provide a more comprehensive understanding of earthquake rupture processes and improve seismic hazard assessments and advanced seismic imaging techniques to constrain slip distribution better and assess the potential for future large earthquakes. Numerous regional hazard models have been developed to characterize slip along the Sumatran megathrust. Early models, such as the Global Seismic Hazard Assessment Program, highlighted the Sumatra Subduction Zone and the Sumatran Fault as major sources. Subsequent studies expanded assessments and refined hazard maps using updated earthquake catalogs (Petersen et al., 2004; Petersen et al., 2007; Megawati and Pan, 2009); these early studies lacked integrated geologic, seismic, and geodetic data.
Triyoso et al. (2020) addressed a significant gap in seismic hazard assessment along Sumatra’s Padang and Bengkulu coasts by incorporating GPS-derived surface strain rates to estimate seismic moment rates, a crucial factor in determining earthquake magnitude. Their approach combined a smoothed seismicity rate with a model of pre-earthquake surface strain derived primarily from GPS data from several previous studies (Prawirodirdjo et al., 2010; Bradley et al., 2017). For the Andaman and Nicobar Islands, a pre-earthquake crustal motion model was developed using forward modeling methods, incorporating existing seismic data and assuming a plate convergence rate of 14 mm/yr (Triyoso et al., 2020). Finally, they constructed a model to characterize fault parameters in the Sumatran subduction zone, utilizing forward modeling and GPS data from the coastal region as a reference.
Triyoso and Sahara (2021) studied the seismic hazard function mapping using estimated horizontal crustal strain off the west coast of northern Sumatra. Their study aims to understand and assess the seismic hazard potential in the region off the west coast of Northern Sumatra by utilizing estimated horizontal crustal strain data. This approach provides a valuable tool for evaluating the likelihood of future large earthquakes and their potential impacts. In their study, the horizontal crustal strain quantifies the deformation of the Earth’s crust, providing insights into the accumulation of stress along fault lines. The Seismic Hazard Function (SHF) represents the probability of exceeding a specific level of ground motion within a given time frame. Pre-seismic and co-seismic GPS data are crucial for estimating crustal strain and understanding tectonic processes. Historical earthquake data provide valuable information about past seismic activity and recurrence intervals. Various modeling techniques, such as the deterministic and probabilistic approaches, are employed to assess seismic hazard. Their study suggests that by understanding the seismic hazard potential in the region, policymakers, engineers, and communities can take proactive measures to mitigate the risks associated with future earthquakes.
Taroni and Akinci (2021) emphasize the importance of accurate spatial earthquake forecasting for hazard analysis. While historical earthquake records, analyzed through zone division or seismicity smoothing methods (Frankel, 1995; Helmstetter et al., 2007), are commonly used for predicting future earthquake locations, they propose that incorporating foreshocks and aftershocks utilizing the methodology developed by Marzocchi and Taroni (2014) can enhance forecasting accuracy.
Nishimura (2022) emphasizes that geodetic data is valuable because it captures the permanent deformation caused by earthquakes, as explained by Reid’s (1910) elastic rebound theory (Rhoades et al., 2011). Ward (1994); Ward (1998) highlighted the importance of geodetic data in understanding the earthquake potential of poorly understood faults, especially in regions like southern California. The success of earthquake forecasting models utilizing GNSS data at global and regional scales further underscores this point (e.g., Bird and Kreemer, 2015). Building upon the need to reassess earthquake risk and enhance early warning systems, Regional Earthquake Likelihood Models (RELMs) play a crucial role in understanding and mitigating earthquake hazards (Nishimura, 2022). While many RELMs traditionally rely on active fault data or historical seismicity records to estimate long-term earthquake rates (e.g., Zechar et al., 2010), incorporating geodetic data, particularly from GNSS networks, can significantly improve their accuracy (Nishimura, 2022). This approach aligns with the need for more robust and comprehensive earthquake hazard assessment strategies.
Anderson and Zaliapin (2023) recently refined the seismicity model framework that Petersen et al. (2020) developed by incorporating spatial and temporal declustering. Their goal was to compare their method’s results with those obtained using the Gardner and Knopoff window method (Gardner and Knopoff, 1974) and a modified version of this method by Anderson et al. (2021) that prioritizes retaining significant events from an engineering perspective. Declustering earthquake catalogs, which involves retaining the most significant earthquakes while excluding smaller events with negligible impact on ground shaking, is a common practice in seismicity analysis. However, Marzocchi and Taroni (2014) caution that using complete seismic catalogs, particularly those derived from instrumental recordings, without declustering can lead to a distorted perception of the future spatial distribution of seismicity rates. Despite the focus on major earthquakes, monitoring minor seismic events, including earthquake swarms that lack an apparent main shock, is crucial for identifying areas with an elevated potential for larger seismic events. Research has demonstrated the value of information on small-scale seismic events and inter-seismic strain accumulation as predictors of major earthquake locations (Strader et al., 2018; Zeng et al., 2018). Triyoso and colleagues have developed a novel approach for estimating the likelihood of earthquakes exceeding a specified magnitude threshold (Triyoso, 2023; Triyoso et al., 2023). This method weights the uniform background seismicity rate, derived from declustered earthquake catalogs, based on the normalized maximum shear strain rate or seismic moment rate inferred from pre-seismic surface strain data using a data model based on GPS. Building upon this, Triyoso (2023) developed a robust model for forecasting seismogenic earthquake potential by integrating methodologies from previous studies and analyzing earthquake catalogs spanning various timeframes.
Further research by Triyoso (2024a) proved that by building upon a foundation of research in probabilistic seismic hazard analysis (Marzocchi and Taroni, 2014; Strader et al., 2018; Zeng et al., 2018; Taroni and Akinci, 2021; Triyoso 2023; Triyoso et al., 2023), conducted a study focused on earthquake spatial forecasting in the Sumatran subduction zone. The study involved creating and comparing models based on an extensive catalog of shallow earthquakes over different observation periods. Model fit regarding the reference event was evaluated using the Akaike Information Criterion (Akaike, 1974). The study identified a smoothed seismicity approach as the most reliable for model construction. This approach incorporated data from a complete catalog of small to moderate earthquakes with seismicity smoothing applied and normalized (Triyoso, 2024a; Triyoso et al., 2024). This data was combined with the normalized seismic moment rate from the surface strain rate to produce a spatial seismicity pattern model. Seismicity rate estimation combines the spatial seismicity model with a uniform background seismicity rate model. This background model was calculated from declustered earthquake data (Mw ≥ 5.0 and depth ≤50 km from 1963 to 2016) using the Gardner and Knopoff algorithm (Gardner and Knopoff, 1974) implemented in ZMAP software (Wiemer, 2001). The study suggests that using a complete earthquake catalog, encompassing smaller magnitudes and spanning an extended observation period, contributes to developing more reliable models.
Helmstetter et al. (2007) assessed the effectiveness of earthquake forecasting models by comparing their probability gain per earthquake to a uniform density model. Their study focused on a time-independent forecast derived from smoothed seismicity data. A key finding was the significant improvement in model performance when incorporating small earthquakes (M ≥ 2) to predict larger events (M ≥ 5). It suggests a relationship between the spatial distributions of smaller and larger earthquakes. Interestingly, the model’s performance remained consistent regardless of the minimum magnitude set for target events. The model effectively predicted events with magnitudes M ≥ 3 and M ≥ 5.5, further supporting that large earthquakes share spatial patterns with smaller ones. This research highlights the value of utilizing data from smaller earthquakes to estimate the probability of larger seismic events, contributing to advancements in earthquake forecasting and hazard assessment.
Rundle et al. (2011), Rundle et al. (2021) explored two contrasting earthquake forecasting models: activation and quiescence models. Both models leverage the frequency of small earthquakes as a predictor of larger events, but their core assumptions differ. Activation models, such as The Epidemic Type Aftershocl-Sequence (ETAS; Ogata, 2005), the Branching Aftershock Sequence (BASS; Holliday et al., 2007), and Short-Term Earthquake Probability (STEP; Gerstenberger et al., 2005), propose that a surge in small earthquakes signals a heightened risk of a large earthquake. Conversely, quiescence models suggest that a lull in small earthquake activity indicates a greater likelihood of a large earthquake.
Using the Z-value method, Sukrungsri and Pailoplee (2016) analyzed seismicity rate changes preceding eight significant earthquakes in the Sunda Arc from 2004 to 2012. The analysis was conducted on a comprehensive earthquake catalog (Mw ≥ 4.4) spanning 1980 to 2015. Optimal parameters, N = 50 events and T = 2 years, were determined to effectively identify anomalous Z-values associated with these major earthquakes. Spatial analysis revealed a strong correlation between seismic quiescence and subsequent large earthquakes. Three significant seismic quiescence zones were identified by applying these parameters to recent seismicity data (2008–2013): Nicobar Islands, Western offshore Sumatra, and Western Myanmar. These findings align with previous studies using the FMD b-value and RTL score methods, suggesting a high probability of future large earthquakes in these regions. While these methods provide valuable intermediate-term forecasting, short-term prediction remains a significant challenge. To enhance short-term forecasting capabilities, exploring alternative physical precursors, such as seismic electric signals or natural time analysis, may offer promising avenues.
Several studies have shown a correlation between decreasing b-values and the occurrence of large earthquakes. A lower b-value indicates higher regional stress accumulation, making it more susceptible to seismic events. De Santis et al. (2022) observed a significant decrease in b-value preceding the Mw 7.2 Kermadec Islands earthquake in 2019. Similarly, Wang et al. (2022) found that low b-value regions in Yunnan Province, China, had a higher probability of experiencing moderate to large earthquakes. Their analysis demonstrated the potential of b-value as a precursor for mid-to-long-term earthquake forecasting. Nuannin et al. (2012) highlighted the strong association between low b-values and large earthquakes in the Andaman-Sumatra region. All 15 significant earthquakes (Mw ≥ 7) between 2000 and 2010 occurred within low b-value zones, preceded by notable b-value decreases. This finding underscores the potential of b-value analysis for probabilistic seismic hazard assessment and mitigation. In the case of the 2002 and 2004 Sumatra earthquakes, the temporal b-value exhibited significant drops before the events, and spatial analysis revealed low b-values around the epicenters. While these studies suggest a promising link between b-value and earthquake occurrence, it is crucial to approach such analyses with caution. Retrospective studies can be prone to bias, and it is essential to conduct prospective tests to validate the predictive capabilities of b-value variations.
Triyoso (2023) assessed the reliability of using the b-value as a precursor for large earthquakes by evaluating the Probabilistic Seismic Hazard Function (PSHF) before these events. The study employed the Akaike Information Criterion (AIC) to assess the model’s reliability in constructing the PSHF. A key finding is identifying a critical δAIC value, which signifies a significant change in the PSHF. It suggests that a drastic change in the PSHF is associated with large δAIC values. As the earthquake potency and PSHF are linked to b-value variations, this method enables us to gauge the reliability of b-value as a precursor from a PSHA perspective. This insight can be valuable for improving PSHA and seismic mitigation strategies.
Triyoso (2024a) proposed an innovative approach to enhance the spatial forecasting of earthquakes (Mw ≥ 5.0) by addressing the limitations associated with using complete seismic catalogs, which can introduce bias in predicting future seismicity rates. Building upon established research in probabilistic seismic hazard analysis (Marzocchi and Taroni, 2014; Strader et al., 2018; Zeng et al., 2018; Taroni and Akinci, 2021; Triyoso 2023; Triyoso et al., 2023; Triyoso, 2024b), Triyoso et al. (2024) conducted a study on earthquake spatial forecasting in the Sumatran subduction zone. This study focused on developing and comparing models using a comprehensive catalog of shallow earthquakes recorded over various periods. The study highlighted two key improvements (Triyoso 2024a; Triyoso, et al., 2024).
1. Incorporating Foreshocks and Aftershocks: Recognizing the significance of small-scale seismic events, the study incorporated foreshocks and aftershocks into the model.
2. Considering Strain Accumulation: The study acknowledged that areas with rapid strain build-up are more susceptible to earthquakes. By combining normalized spatial seismicity patterns with strain accumulation data, the study aimed to develop a more accurate spatial forecasting model, ultimately improving the prediction of future seismic events.
Foreshocks appear closely linked to the activation model. At the same time, strain accumulation, particularly in areas with rapid build-up, seems closely associated with the quiescence model, as Rundle et al. (2011) suggested.
Triyoso (2024b) emphasized the need for rigorous reference data selection and model development to effectively incorporate seismicity patterns, including quiescence periods, into seismic hazard analysis. Precisely capturing the evolution of seismic rates is paramount. As Yavas et al. (2024) underscored, identifying patterns within seismicity data, particularly clustering, is crucial for accurate forecasting and hazard assessment. Spatial smoothing of historical seismicity, a standard technique for extracting these clustering patterns, offers valuable insights for future seismic hazard assessment and mitigation strategies. Several studies, including Triyoso et al. (2020); Triyoso et al. (2024); Triyoso et al. (2023), have successfully applied Gaussian function-based seismicity smoothing techniques. This study delves into seismicity rate changes off the coast of Southern Sumatra-West Java using declustered data from a shallow crustal earthquake catalog. The analysis identified a period of relative seismic quiescence from 1993 to 2005 (P2) compared to 1978 to 1992 (P1). The result was interpreted that quiescence is closely correlated with periods of seismic strain accumulation.
Consequently, the potential for future large earthquakes is likely inversely proportional to activation probability. The study utilizes probability gain, an adapted concept presented by Helmstetter et al. (2007), to re-examine these findings. Instead of relying on a uniform density model, the study leverages the seismicity model from the period preceding the quiescence (1978–1992) as a benchmark for comparison. In alignment with the recommendations of Triyoso et al. (2024), strain accumulation is considered a crucial factor in identifying areas prone to earthquakes. By calculating the modified probability gain (mG) relative to the pre-quiescence model, the study aims to quantify and assess the likelihood of the identified quiescent zone representing a potential source area for future large earthquakes. The mG can be used to evaluate the potential for large earthquakes, providing valuable insights for hazard assessment.
Moreover, the study integrates the modified probability gain with the most robust seismicity rate model, as Triyoso (2024b) recommended, to enhance the accuracy and reliability of earthquake hazard assessments in the region. The study estimates the seismic hazard curve, expressed as peak ground acceleration (PGA) versus exceedance probability over 50 years for various sites. The amplification factor, calculated based on previous studies, is used to refine the PGA estimates. To further enhance the precision of PGA estimations for seismic disaster mitigation, an amplification factor specific to different locations is calculated using the horizontal vertical Spectral Ratio (HVSR) method on the data used and applied to the PGA estimations.
This study investigates the potential for a broader area for future large earthquakes in the Sumatran subduction zone and off the southern coast of West Java. The study identifies regions with heightened earthquake likelihood by analyzing historical seismicity data, employing the mG approach, and comparing it with the previous study findings (Triyoso et al., 2023; 2024; Triyoso 2024a; Triyoso 2024b). The mG values, calculated relative to a pre-quiescence seismicity model, highlight areas with increased strain accumulation. These findings estimate seismic hazards, including peak ground acceleration and potential tsunami heights. By integrating the mG model with a reliable seismicity rate model, the study aims to improve the accuracy of regional earthquake hazard assessments. Ultimately, this research contributes to a better understanding of seismic hazards in the region, enabling more effective disaster mitigation strategies.
2 Data and method
2.1 Data
This study utilizes seismicity data from previous research, specifically “The 2017 PusGEN (Tim Pusat Studi Gempa Nasional, 2017)”. The initial dataset encompasses earthquakes with a moment magnitude (Mw) range of 4.7–9.2 and a maximum depth of 50 km within the Andaman-Sumatra-West Java region.
To ensure the analysis considers only independent seismic events, the earthquake catalog undergoes declustering using the Gardner and Knopoff algorithm (Gardner and Knopoff, 1974). This algorithm, implemented through the ZMAP software (Wiemer, 2001), helps to distinguish between foreshocks, aftershocks, and independent earthquakes. Figure 1A visually represents the comprehensive earthquake catalog, while Figure 1B illustrates the catalog after the declustering process. Figure 2A illustrates the pre-seismic GPS velocity field model employed in this study. This model is constructed by integrating data from two primary sources.
1. Triyoso et al. (2020): This dataset provides valuable GPS measurements for the region.
2. ITRF 2000 (Bock et al., 2003): Incorporating ITRF2000 data helps establish a stable reference frame.
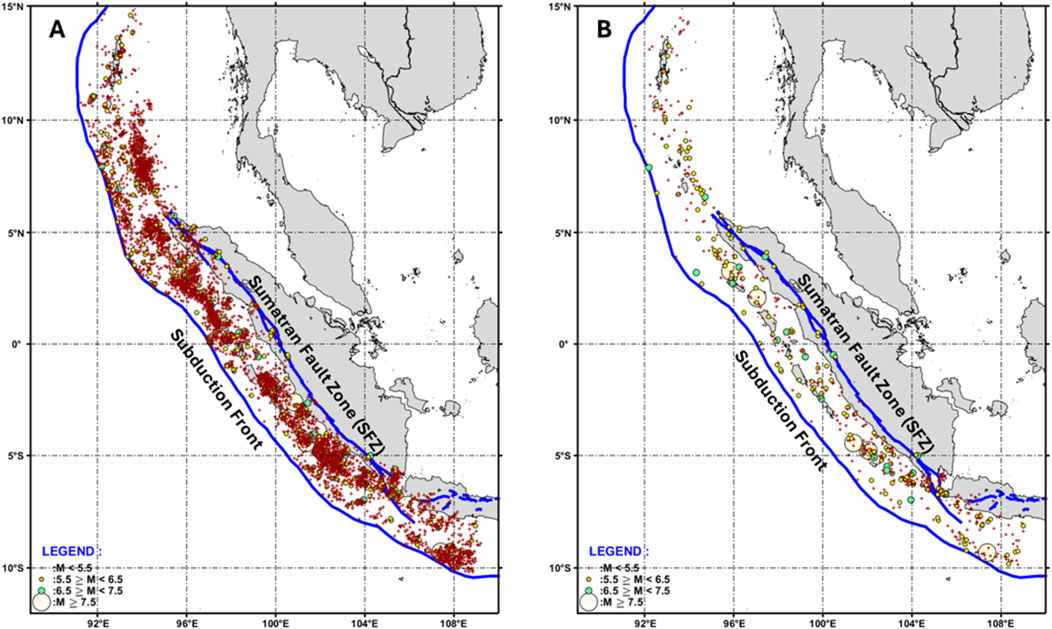
Figure 1. The distribution of shallow earthquakes with depths less than 50 km during 1963–2016 (Tim Pusat Studi Gempa Nasional, 2017) (A) and the catalog after the declustering process (B).
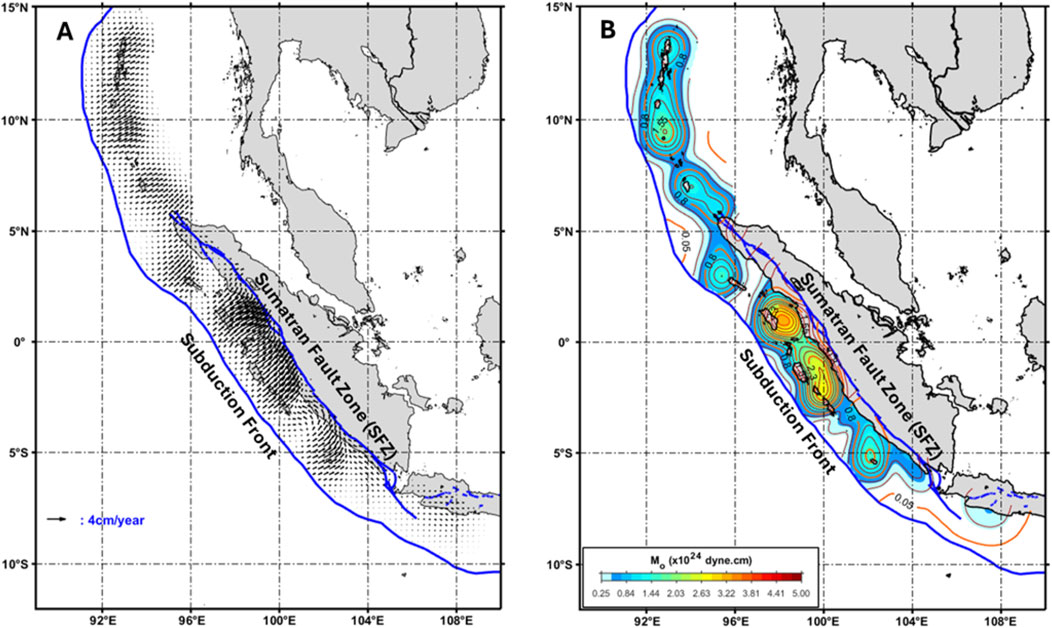
Figure 2. The pre-seismic GPS velocity field model was employed in this study (A). (B) presents this study’s visualizations of the seismic moment rate estimated using Equation 7.
The rationale behind combining these datasets is to exclude the influence of significant earthquakes after the year 2000. This approach ensures that the pre-seismic model reflects the tectonic setting prior to major seismic events, allowing for a more focused analysis of subsequent earthquake impacts. Further analysis focuses on relatively large earthquakes (Mw ≥ 6.5 and depth ≤50 km) from the declustered catalog. This subset, combining data from “The 2017 PusGEN (Tim Pusat Studi Gempa Nasional, 2017)” (1900–2016) and the GCMT catalog (2017–2020), is employed to establish a uniform background seismicity rate model for the study area. The bathymetry data used for the tsunami simulation was sourced from a combination of the General Bathymetric Charts of the Oceans (GEBCO, 2008) and a digitized nautical chart from the Centre for Hydrographic Office, an Indonesian Navy subsidiary. This data was initially arranged in a 1′arc grid (approximately 1,854 m) and resampled for more detailed analysis at a 30″ spatial resolution (roughly 927 m).
2.2 The b-value
The b-value, an essential parameter within the Gutenberg-Richter Equation (Gutenberg and Richter, 1944), provides crucial insights into the distribution of earthquake magnitudes within a region. According to Geffers et al. (2023), here’s a breakdown of its significance.
• Global vs Local: While the b-value tends to be approximately one on a global scale, it exhibits greater fluctuations at local levels, reflecting variations in regional seismicity patterns.
• Magnitude Distribution: The b-value quantifies the relative proportion of smaller to larger earthquakes. A higher b-value indicates a greater prevalence of smaller earthquakes than larger ones.
• Maximum Likelihood Estimation: The most robust method for determining the b-value is the maximum likelihood method. Utsu (1978) introduced a widely used equation for this estimation:
where
This equation provides a reliable means of calculating the b-value, which is crucial for understanding the potential earthquake hazard in a given area.
This study utilizes a robust approach to determine the b-value, a crucial parameter for understanding earthquake magnitude distribution. Here’s a breakdown of the methodology (Triyoso, 2023; Triyoso, 2024a; Geffer et al., 2023; Li and Luo, 2024).
• Magnitude Threshold: The calculation considers earthquakes with an average magnitude greater than or equal to Mc, representing the minimum magnitude of completeness. It ensures that the analysis includes only reliably recorded events.
• Correction Constant: A constant value of 0.05 is incorporated into the equation as a standard correction factor.
• Dataset: The b-value estimation relies on a comprehensive dataset of relatively shallow, large earthquakes (Mw ≥ 6.5 and depth ≤50 km) spanning from 1900 to 2020.
• Estimated b-value: The analysis yields an estimated b-value of approximately 1.0.
This calculated b-value provides valuable input for seismic hazard assessments, contributing to a more accurate understanding of the potential for future earthquakes in the study area.
2.3 Seismicity smoothing using a Gaussian kernel function
This study uses a seismicity smoothing technique based on the Gaussian function to represent earthquake occurrence visually. This approach builds upon established methods in seismic hazard assessment (Frankel, 1995; Petersen et al., 2017; Triyoso et al., 2020) and involves the following steps.
1. Grid Creation: The study area is divided into a grid system.
2. Earthquake Count: The number of earthquakes (ni) exceeding a predetermined reference magnitude within each grid cell is tallied. This count is an initial estimate of earthquake activity within that cell. This count, ni, represents the maximum likelihood estimate 10a for earthquakes above magnitude reference (Mref). Mref is equal to or larger than the magnitude of completeness in that specific cell (Bender, 1983).
3. Gaussian Smoothing: To generate a smoother seismicity model, the grid of ni values undergoes spatial smoothing using a Gaussian kernel function (Frankel, 1995; Petersen et al., 2017; Penarubia et al., 2020; Triyoso et al., 2020). This function incorporates a correlation distance (c) to determine the extent of smoothing.
4. Smoothed Value Calculation: The smoothed seismicity value for each grid cell (i) is computed using the following formula:
in which
• Normalization: The formula includes a normalization factor, ensuring that the total number of earthquake events within the study area is conserved throughout the smoothing process.
• Distance Weighting: ∆ij represents the distance between the central grid cell (i) and a neighboring cell (j). The Gaussian function uses this distance to weight the contribution of earthquakes in cell j to the smoothed value of cell i. Cells closer to the central cell have a more significant influence on the final smoothed value.
• Correlation Distance: The correlation distance (c) determines the spatial extent of the smoothing effect—a larger correlation distance results in a smoother seismicity model.
• Summation Range: The summation in the formula considers neighboring cells (j) located within a distance of 3c from the central cell (i). This range ensures that the smoothing effect is adequately captured while maintaining computational efficiency.
By incorporating these components, the Gaussian smoothing formula effectively generates a continuous and refined representation of seismicity, enhancing the accuracy and reliability of subsequent seismic hazard analyses.
2.4 Occurrence rate function and probability of occurrence
2.4.1 Occurrence rate function
We utilize an occurrence rate function to quantify the likelihood of earthquakes exceeding a given magnitude within a specific region. This function, denoted as vi (≥Mref), represents the theoretical rate of earthquake occurrence for a particular grid cell (i) and considers earthquakes with magnitudes greater than or equal to a reference magnitude. In essence, vi (≥Mref) measures how frequently we expect earthquakes of at least magnitude Mref to occur within the defined grid cell. This rate is essential for calculating probabilities and assessing seismic hazard levels in the study area, and it can be expressed as:
Where:
• Ni: Represents the total number of recorded earthquakes within a specific grid cell (i) with a magnitude equal to or greater than the reference magnitude.
• T: Represents the total period covered by the earthquake catalog used in the analysis.
This formula calculates the average earthquake rate exceeding the reference magnitude within the given grid cell over the observation period.
The choice of the reference magnitude, Mref, is crucial and is determined by the completeness of the earthquake catalog. It ensures that the analysis considers only reliably recorded events, leading to a more accurate representation of seismicity.
Applying the Gaussian function to smooth the seismicity distribution implies adopting the 10a value calculated using Equation 2. By substituting this 10a value from Equation 2 into Equation 3, we obtain the following equation:
In this case, vi (≥Mref) of Equation 4 is the smoothed value for cell i of the number of earthquakes above reference magnitude during the time interval T, and b is the uniform b-value. Mmax is the magnitude maximum used in this study. In this specific application of the occurrence rate function, we incorporate two key refinements.
1. Smoothed Seismicity: Instead of using raw earthquake counts, we employ the smoothed seismicity value (vi (≥Mref)) for each grid cell (i). This smoothed value, derived from the Gaussian kernel smoothing process, provides a more continuous and realistic representation of earthquake distribution.
2. Uniform b-value: A constant b-value is applied across the entire study area. The b-value, a crucial parameter in the Gutenberg-Richter law, governs the relationship between earthquake magnitude and frequency. Using a uniform b-value simplifies the analysis while capturing overall seismicity patterns.
Furthermore, a maximum magnitude (Mmax) of approximately 9.2 is assumed for this study. This value represents the upper limit of earthquake magnitudes considered in the analysis.
By incorporating smoothed seismicity, a uniform b-value, and a defined Mmax, the occurrence rate function provides a robust and refined estimate of earthquake probabilities for different magnitudes within each grid cell.
2.4.2 Probability of occurrence
The probability of occurrence of a given earthquake with a magnitude larger than or equal to m at a particular cell k during time interval T under the Poisson distribution is given by:
In the Equation 5, p(≥m) is the probability of the smoothed value for cell i of the number of earthquakes above the reference magnitude. The vi is estimated based on Equation 4.
2.5 Probability gain: likelihood potential source area for future large earthquakes
This study focuses on seismic quiescence, a period of reduced earthquake activity that can precede significant earthquakes. While the duration and extent of quiescence can vary depending on factors like tectonic conditions, monitoring these patterns provides valuable insights into potential future seismic hazards.
2.5.1 Background and motivation
Previous studies, including those in the Andaman-Northern Sumatra region (Sukrungsri and Pailoplee, 2016), have demonstrated the significance of incorporating seismicity patterns, particularly quiescence, into seismic hazard assessments. However, accurately representing and interpreting these patterns requires careful consideration of reference data and model selection. This study explicitly examines variations in seismicity rates in Andaman, off the coast of Sumatra Island, West Java, using a declustered catalog of shallow crustal earthquakes. The analysis reveals a distinct period of relative seismic quiescence between 1986 and 2004 (P2A) compared to the period from 1966 to 1985 (P1A) and 1993 to 2005 (P2B) compared to the preceding period from 1978 to 1992 (P1B).
2.5.2 Hypothesis and methodology
Building upon previous research (Philibosian and Meltzner, 2020), this quiescence is interpreted as a potential indicator of seismic strain accumulation, suggesting a correlation between quiescence and the likelihood of future large earthquakes. To further investigate this hypothesis, the study employs a modified probability gain approach inspired by the work of Helmstetter et al. (2007). Instead of relying on a uniform density model, this study utilizes the seismicity model from the pre-quiescence period from 1966 to 1985 in the case of Andaman-Off Coast Northern Sumatra and the period from (1978–1992) in the case of Offcoast of Central-Soutthern Sumatra–West Java as a baseline.
2.5.3 Introducing “future potency”
By calculating the normalized inverse probability gain (mG) relative to this pre-quiescence model, the study aims to characterize and assess the likelihood of the quiescence zone representing a potential source area for future large earthquakes. This likelihood is referred to as “future potency,” which could be expressed as,
Where:
• mG: Represents the modified probability gain.
• Lpq: Represents the likelihood derived from the pre-quiescence seismicity model.
• Lqs: Represents the likelihood derived from the seismicity model during the quiescent period.
• Nt: Represents the total number of earthquakes observed within the defined observation period.
In essence, mG compares the likelihood of observing the recorded seismicity under two scenarios: a model based on pre-quiescence activity and a model reflecting the observed quiescence. A higher mG value indicates a more pronounced decrease in seismicity during the quiescence period relative to the pre-quiescence baseline, suggesting a more significant potential for future large earthquakes. For this analysis, mG is calculated for each grid cell using a constant radius of 75 km. This approach ensures a consistent spatial scale for comparison across the study area.
In essence, “future potency” quantifies the potential of a quiescence region to generate significant earthquakes in the future based on the observed decrease in seismic activity relative to a pre-quiescence baseline. This concept provides a valuable framework for interpreting seismic quiescence and incorporating it into seismic hazard assessments.
2.6 Geodetic modeling: seismic moment rate estimation
A seismic moment rate model was developed following the methodologies Triyoso et al. (2020) and Triyoso and Sahara (2021) outlined. This model utilizes merged pre-seismic GPS data based on the work of Triyoso et al. (2020) and the ITRF2000 framework (Bock et al., 2003).
2.6.1 Model assumptions and setup
The model operates under the assumption of homogeneity and isotropy for each observation point across the entire seismogenic thickness within the geodetic data. Horizontal displacement components in the East-West (u) and North-South (v) directions are considered uncorrelated, as proposed by El-fiky et al. (1999). The study area was discretized into a grid with a cell size of 10 km × 10 km to facilitate strain rate estimation.
2.6.2 Calculation steps
1. Horizontal Crustal Strain Rate Calculation: The horizontal crustal strain rate for each cell was computed using the procedures established in previous studies (Triyoso et al. 2020; Triyoso and Sahara 2021; Triyoso, 2023).
2. Least-Squares Collocation (LSC) Application: The LSC method incorporated local covariance functions derived from horizontal surface displacement data. This step aimed to estimate the horizontal surface displacement for each grid cell (illustrated in Figure 3A) and the crustal strain within the study area.
3. Maximum Shear Strain Estimation: The calculated horizontal crustal strain was input to determine the maximum shear strain across the study area.
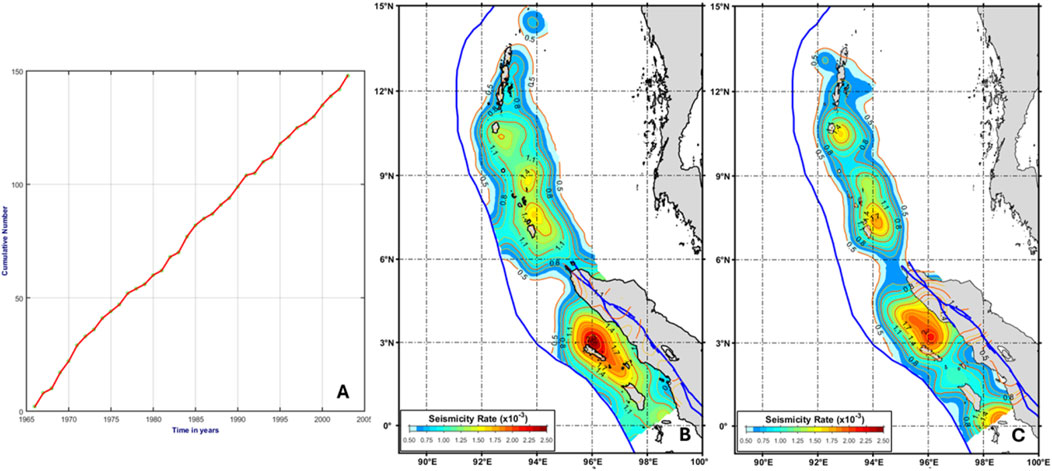
Figure 3. The periods of relative seismic quiescence: P2A (1986–2004) compared to P1A (1966–1985) around Andaman–Off coast Northern Sumatra (A). The seismicity smoothing models use the recommended correlation distance of 75 km (Frankel, 1995) of P1A (B)and P2A (C).
2.6.3 Seismic moment rate calculation
The LSC-derived surface strain rate model was employed to calculate the scalar moment rate. This approach builds upon the approximations established by Ward (1994) and is further refined by Savage and Simpson (1997), Field et al. (1999), and Triyoso et al. (2020). The following equation represents this calculation:
Where:
•
• µ denotes the rigidity, assigned a value of 3.4 × 1011 dyn cm⁻2 based on Triyoso et al. (2020) and Triyoso and Sahara (2021).
• H represents the seismogenic thickness, set at 20 km, consistent with Ito and Nakamura (1998) and others (Tim Pusat Studi Gempa Nasional, 2017; Viveros et al. 2019; Triyoso et al. 2020; Triyoso and Sahara 2021).
• A is the unit area in km2.
• e₁ and e₂ represent the principal strain rates.
Figure 2B presents this study’s visualizations of the seismic moment rate.
3 Seismic hazard function and deterministic seismic hazard estimation
3.1 Seismicity rate modelling: potential source area and rate formulation
Referring to Triyoso (2024a); Triyoso (2024b) and Triyoso et al. (2024), the potential future earthquake occurrence rate above or equal to magnitude completeness as a reference (Mc) in the particular grid i is modeled by using the uniform background seismicity rate (Abackground) estimated using Equation 7 weighted by the normalized maximum seismic moment rate (Mo-rate) and normalized mG estimated using Equation 6. The formulation could be written as:
Where Abackground is uniform background seismicity with magnitude ≥ Mc in grid i, the Mo-rate is the seismic rate estimated at the grid of i, and the maximum (Mo-rate) is the maximum value of the Mo-rate over the entire study area and normalized (mG) is the normalized modified probability gain. vi represents the likelihood estimation seismicity rate (annual of the 10a) with a magnitude greater than or equal to Mc.
Furthermore, by substituting 10a of Equation 8 in the Frequency-Magnitude of the Gutenberg and Richter equation (Gutenberg and Richter, 1944), we may write the following equation:
Afuture potency-rate is the estimated potential future seismicity rate above or equal to magnitude completeness (Mc). The b is the b-value.
3.2 Probabilistic seismic hazard function estimation: ground motion prediction equations (GMPE) and probability exceedance (PE)
This section outlines the estimation of the Probabilistic Seismic Hazard Function, a crucial aspect of seismic hazard assessment. The Seismic Hazard Function (SHF), represented as a plot of Probability of Exceedance versus Peak Ground Acceleration, helps quantify the likelihood of experiencing a specific level of ground shaking at a given location.
3.2.1 Ground motion prediction equation and probability exceedance
At the heart of SHF estimation lies the GMPE, which relates earthquake magnitude, distance, and other factors to PGA. Conversely, the PE represents the annual probability of exceeding a certain PGA threshold at a site.
3.2.2 Calculating probability of exceedance
The annual PE of exceeding a PGA threshold (ao) at an observation point due to an earthquake source in grid cell ‘l’ is given by:
Where:
•
•
• Rl is the distance between the site and grid cell ‘l’.
• vl is the seismicity rate for magnitudes greater than or equal to a given magnitude in grid cell ‘l’ based on Equation 9.
3.2.3 Seismogenic zone parameters
The starting depth of the seismogenic zone (locking depth) and thickness are crucial parameters. Based on Tim Pusat Studi Gempa Nasional (2017) and previous studies (Triyoso et al., 2020; Triyoso and Sahara, 2021), a locking depth of 3 km and a seismogenic thickness of 20 km (Viveros et al., 2019) was adopted for this study.
3.2.4 Total probability of exceedance
To estimate the total PE distribution based on Equation 10 of PGA at the site, contributions from all potential earthquake sources (grid cells) are considered:
Substituting the GMPE into the Equation 11 yields the annual PE for a specific PGA:
3.2.5 Probability of exceedance over time
For a given observation period T, the PE of Equation 12 can be calculated as:
Equation 13 and provide a framework for calculating the PE of exceeding a specified PGA at a site, considering contributions from all potential earthquake sources and a defined observation period. These calculations are fundamental for probabilistic seismic hazard assessment.
3.3 Deterministic seismic hazard estimation (DSHE)
This study utilizes a characterized source area and a deterministic approach to estimate peak ground acceleration. The rectangular fault model, including its geometry and parameters, is based on the work of Triyoso et al. (2024) and Triyoso (2024b), with adjustments made based on the findings of this study. Following the recommendations of Triyoso et al. (2024) and Triyoso (2024b), PGA estimation is conducted using the Maximum Possible Earthquake (MPE) magnitude and the recommended GMPE for megathrust sources refer to Triyoso et al. (2023); Triyoso et al. (2024). These are the names of several ground motion prediction equations (GMPEs) used in seismology to estimate the intensity of ground shaking from earthquakes.
✓Atkinson and Boore (2006): This GMPE is widely used in the United States and other regions. It is based on a large dataset of strong-motion recordings and incorporates various factors such as magnitude, distance, and site conditions.
✓Youngs et al. (1997): This GMPE is also commonly used in the United States and is based on a similar dataset as the Atkinson and Boore (2006) model. It is known for its simplicity and ease of use.
✓Zhao et al. (2006): This GMPE is designed explicitly for subduction zones and is based on strong-motion recordings from Japan. It is considered more accurate than other GMPEs for predicting ground motions in subduction zones.
These GMPEs are essential tools for seismic hazard assessment and risk analysis. They are used to estimate the potential ground shaking at a specific location from a future earthquake, which can help inform decisions about building codes, emergency response planning, and land use planning.
4 Tsunami modeling
This study utilizes the TUNAMI-N3 model, a Non-Linear Shallow Water Equation model developed by Tohoku University (Imamura et al., 2006), to simulate and predict tsunami behavior (Pakoksung et al., 2021). TUNAMI-N3, a modified version of TUNAMI-N2, incorporates linear theory in deep sea, shallow water theory in shallow sea, and runup on land with varying grids. Instead of directly using fault data, TUNAMI-N3 requires an initial wave model generated by the fault model. This initial wave is derived from the vertical deformation of the fault slip model using Okada’s method (Okada, 1985; 1992).
4.1 Tsunami source potential and scenarios
Tsunami source zone potential is characterized using a normalized mG and Mo-rate method. Based on (Triyoso et al., 2024), this study establishes several source scenarios for the off-coast of central Sumatra. A simple source model with uniform slip is assumed for the off-coast of southern Sumatra–West Java (Triyoso, 2024b). Fault geometry parameters are defined based on the subduction zone geometry from Hayes et al. (2012) and the identified tsunami source zone potential. Dip, width, and rake are derived based on Triyoso et al. (2024) and Triyoso (2024b), with a fault length of approximately 536.5 km, 365 km, and 335 km. Based on the empirical scaling law, the estimated Mw for the Oceanic/Subduction Zone Earthquake source model is about 8.9–9.0, 8.6–8.7, and 8.5–8.6 (Blaser et al., 2010). Following Hanks and Kanamori (1979), the seismic moment summation of the fault model is used to estimate Mw.
4.2 Tsunami height potential and scenarios
Two locking area scenarios are proposed to assess the potential tsunami height, represented by two different source depths with epicenters located at the center of the source zone. Table 1 summarizes the potential source parameters around the off-coast of Southern Sumatra and West Java. This study incorporates the controlling factors of Megathrust Earthquake and Tsunami Dynamics: Stress, Rigidity, and Sediment Strength, as described by Bilek and Lay (1999), in which the rigidity used in the scenario is about 33.9 GPa and 24.3 GPa with the possible moment magnitude is about 8.6–8.7 for model A and 8.5–8.6 for model B.

Table 1. The source parameters used in this study for tsunami simulations. The potential source areas are located off the coast of Southern Sumatra (model A) and West Java (model B). Our simulations incorporate the controlling factors of megathrust earthquake and tsunami dynamics, as Bilek and Lay (1999) described. We considered rigidity values of 33.9 GPa and 24.3 GPa, respectively, for models A and B, with corresponding moment magnitudes of 8.6–8.7 and 8.5–8.6.
5 Results and discussion
This study seeks to identify potential future large earthquake zones in the Sumatran subduction zone and off West Java’s southern coast. By analyzing historical seismicity data and applying the mG approach, we aim to improve our understanding of seismic hazards in the region. Our findings estimate ground shaking and potential tsunami impacts, which can inform more effective disaster mitigation strategies. By combining the mG model with a reliable seismicity rate model, we seek to enhance the accuracy of regional earthquake hazard assessments. The accuracy of the mG calculations is significantly influenced by the precision with which the period of seismicity rate change can be identified and characterized. By enhancing the identification and characterization of this rate change, the uncertainties can be minimized, and improve the overall accuracy of the calculations. In this study, identifying rate change between two distinct periods could be achieved by considering the magnitude completeness as a function of time and duration of the rate change. Thus, by evaluating both magnitude completeness as a function of time, it can be expected that the uncertainties could be reduced and the accuracy can be improved. By carefully considering those factors and adopting a rigorous approach to seismicity rate change identification, the accuracy and reliability of the mG calculations can significantly improve. It, in turn, will contribute to a better understanding of seismic hazards and ultimately enhance this study’s ability to mitigate their impact.
This study investigates shallow crustal earthquakes in the Andaman and off-coast northern Sumatra regions to characterize seismic patterns. We identify distinct periods of relative seismic quiescence: P2A (1986–2004) compared to P1A (1966–1985). There is a similar pattern between 1993 and 2005 (P2B) compared to the prior period (P1B) for the study area around off-coast central Sumatra–West Java. Our analysis suggests that these quiescence periods indicate seismic strain accumulation. Figures 3, 4 show identifying rate change between two distinct periods around the Andaman and off-coast northern Sumatra regions and off-coast central Sumatra–West Java and the seismicity smoothing algorithm using the recommended correlation distance of 75 km as suggested by Frankel (1995) is applied to both datasets. The modified probability gain (mG) is then estimated for the period P1A and P2A for Andaman and off-coast northern Sumatra regions and period P1B and P2B for off-coast central Sumatra–West Java. The result can be found in Figures 5A, B. Figure 5C shows the estimation and merging result of mG based on the period P1A and P2A, P1B, and P2B along Andaman–Off-coast Sumatra and West Java.
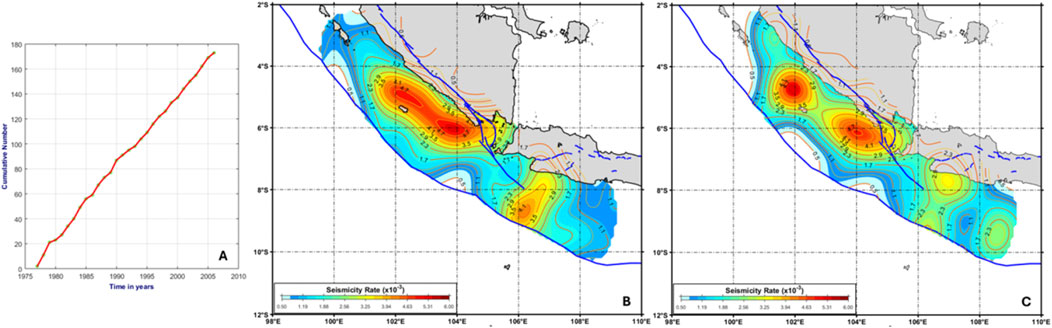
Figure 4. The periods of relative seismic quiescence: P2B between 1993 and 2005 compared to the prior period P1B between 1978 and 1992 for the study area around off-coast central Sumatra–West Java (A). The seismicity smoothing models use the recommended correlation distance of 75 km (Frankel, 1995) of P1B (B) and P2B (C).
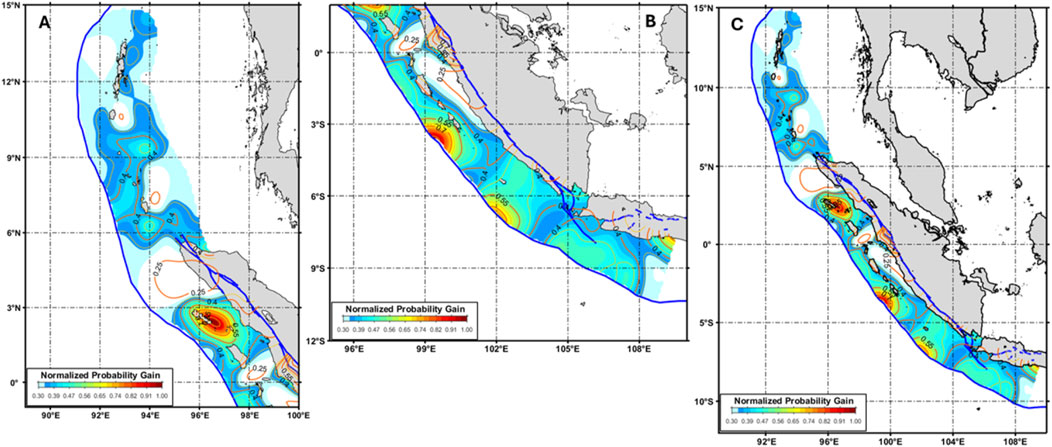
Figure 5. The modified probability gain (mG) as estimated using Equation 6 for the period P1A and P2A for Andaman and off-coast northern Sumatra regions (A) and period P1B and P2B for off-coast central Sumatra–West Java (B). The estimation and merging result of mG based on the period P1A and P2A, P1B, and P2B along Andaman–Off-coast Sumatra and West Java (C).
Comparing the result of Figures 5A, B, we may find the consistency between the consequence of Triyoso et al. (2023) and Triyoso et al. (2024), in which a significant strain build-up could be found around the off-coast of Northern Sumatra around Simelue, Nias, upto Batu Island (Figure 5A). A similar result is also found around Mentawai Island, in which the result of Figure 5B can be interpreted as a significant strain build-up consistent with the result of Triyoso et al. (2023) and Triyoso et al. (2024).
To compare the area that could be interpreted as the high potential area of strain build-up around Mentawai between the result of this study and Triyoso et al. (2024), it appears that the fault model of Triyoso et al. (2024) supports the finding of this study and the result of this study is consistent with Triyoso et al. (2024), which is related to the possible source around the Mentawai Islands. Thus, in terms of the PGA and Tsunami Height simulation estimated using the maximum potential earthquake magnitude, the result of Triyoso et al. (2024) will not change. However, compared to Triyoso et al. (2023), the result of this study appears to be more significant in terms of PGA and Tsunami Height estimated. This is because the fault parameter is larger than the result of Triyoso et al. (2023).
To assess the potential for future large earthquakes, we propose incorporating seismicity patterns, especially periods of quiescence, into seismic hazard assessments. Following Triyoso’s (2024a) approach, we utilize a combined model that integrates normalized seismicity smoothing, normalized geodetic moment rate (Mo-rate), and normalized mG values (mG-model) to characterize the likelihood of earthquake occurrence within specific source areas. The seismicity smoothing is based on the shallow catalog of relatively small to moderate earthquakes (Eq-model). Then, the seismicity rate is produced by multiplying the combined model with the uniform background rate (Abackground) of the declustered shallow earthquake data used to develop the seismicity rate model. The Eq-model is constructed based on the shallow earthquake data of 1963–1999 and the Abackground. It is proposed that the spatial correlation between the sizeable shallow earthquake events after 1999 and before 1963 be evaluated to better understand the future potency by overlapping with the historical shallow large earthquakes from 1900 to 1962 and 2000 to 2020. Through this analysis, we intend to understand the potential of earthquakes better to anticipate and prepare for possible significant earthquakes and tsunami hazard analysis, as shown in Figure 6A. Figure 6B shows the result of the sources for possible future significant earthquakes and tsunami overlay with the shallow large earthquake of 2000–2020. Figure 6C shows the result of the overlay with the shallow large earthquake of 1900–1962. Based on Figure 6A, the result of this study supports the study of Martin et al. (2019) and others (Bilek and Engdahl, 2007; Chlieh et al., 2007; Konca et al., 2008; Hill et al., 2012), especially in characterizing the possible source of significant earthquake events of 2004, 2005, as well as 1797 and 1833. An important lesson learned could be noted from the result of Figure 6A, which is primarily related to the 2004 source event. There is a high possibility of simultaneously breaking several source areas along the Sumatran subduction zone closely associated with the existence of sliver force, as pointed out by McCaffrey (2009). The rapid generation of the 2005 M8.6 earthquake suggests a strong connection between static stress loading from large earthquakes and the triggering of subsequent significant events. As highlighted by Pollitz et al. (2006) and Triyoso and Sahara (2021), this mechanism likely played an essential role in the occurrence of this particular earthquake. In our interpretation, it can happen when a relatively high rate’s closure closes and is connected, as shown in Figure 6.
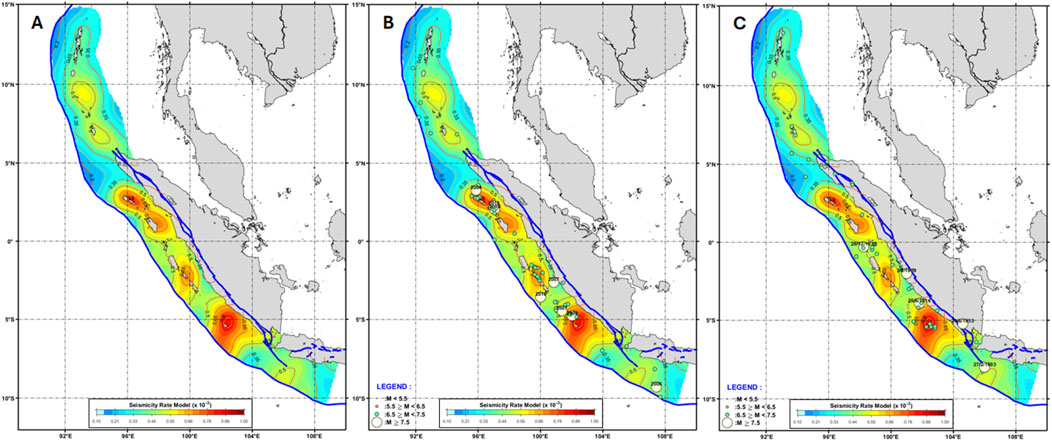
Figure 6. The potential of earthquakes model to anticipate and prepare for possible significant earthquakes and tsunami hazard analysis (A). The combined model integrates normalized seismicity smoothing, normalized geodetic moment rate (Mo-rate), and normalized mG values (mG-model) to characterize the likelihood of earthquake occurrence within specific source areas. The seismicity smoothing is based on the shallow catalog of relatively small to moderate earthquakes (Eq-model). Then, the seismicity rate is produced by multiplying the combined model with the uniform background rate (Abackground) of the declustered shallow earthquake data used to develop the seismicity rate model. The Eq-model is constructed based on the shallow earthquake data of 1963–1999 and the Abackground. It is proposed that the spatial correlation between the large shallow earthquake event after 1999 (B) and before 1963 (C) be evaluated to better understand the future potency by overlapping with the historical shallow large earthquake from 1900 to 1962 and 2000 to 2020.
A more detailed analysis of the result in this study, especially around off-coast Southern Sumatra–West Java, overlaps it with the historical large earthquake data from 1900 to 1962 to characterize the possible future earthquake or tsunami potential. It coincides with the area of the 1903 subduction earthquake event (Newcomb and McCann, 1987), especially around the off coast of West Java. By following the suggestion of Shearer and Burgmann (2010), in which every active subduction zone should be considered a potential source of great earthquakes, then referring to Huchon and LePichon (1984), Triyoso et al. (2024) and Triyoso (2024b), we characterize the fault parameter model to estimate the possible future earthquake or tsunami potential around the off-coast of central Sumatra. For the off-coast of southern Sumatra–West Java, as shown in Figure 7, based on Figure 7, we could identify the possible seismic gap area of the seismic and tsunami hazard in the future. The potential source area around the Mentawai zone shows a consistent result compared to Triyoso et al. (2024), and even the possible source zone of the 1935 event could be identified (Rivera et al., 2002). Our segmentation model around the off-coast of southern Sumatra-West Java is a bit different compared to Supendi et al. (2023), especially around the front of Sunda Strait since we found the consistency based on the mG model and suggestion result of Huchon and LePichon (1984) also coinciding the mG area with the area of the 1903 subduction earthquake event as pointed out by Newcomb and McCann (1987), especially around the off-coast of West Java.
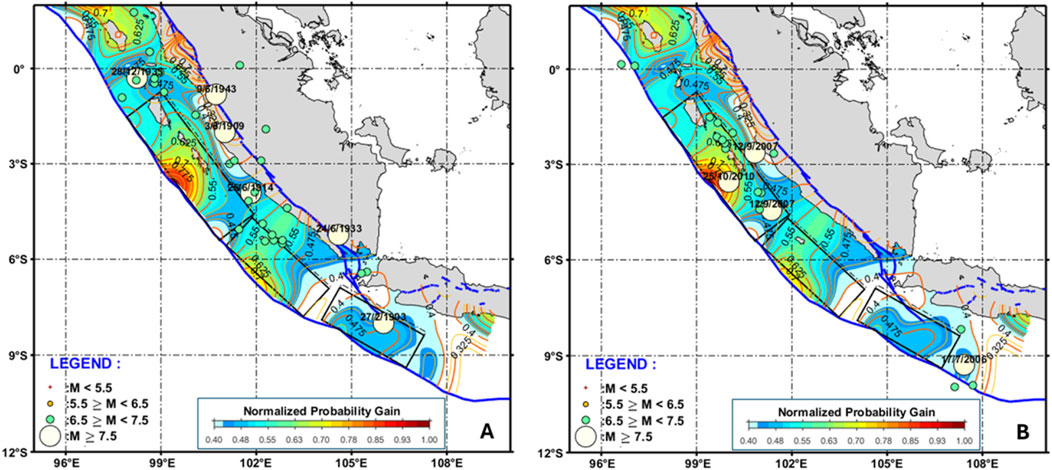
Figure 7. The modified probability gain (mG) map identifies potential seismic gap areas susceptible to future large earthquakes and tsunamis. This map overlaps with historical records of shallow, large earthquakes between 1900 and 1962 (A) and 2000 and 2020 (B). The fault segmentation model, informed by the work of Huchon and LePichon (1984), aligns the mG areas with the 1903 subduction earthquake region, particularly near the coast of West Java, as suggested by Newcomb and McCann (1987).
Figure 8 shows the estimated seismic hazard expressed as the MPE Peak Ground Acceleration (g) at the base rock based on the defined fault parameter around the off-coast of southern Sumatra (A) and the off coast of West Java (B). It can be found that at the site of S1-S19, the PGAs estimate are around ∼0.05g.
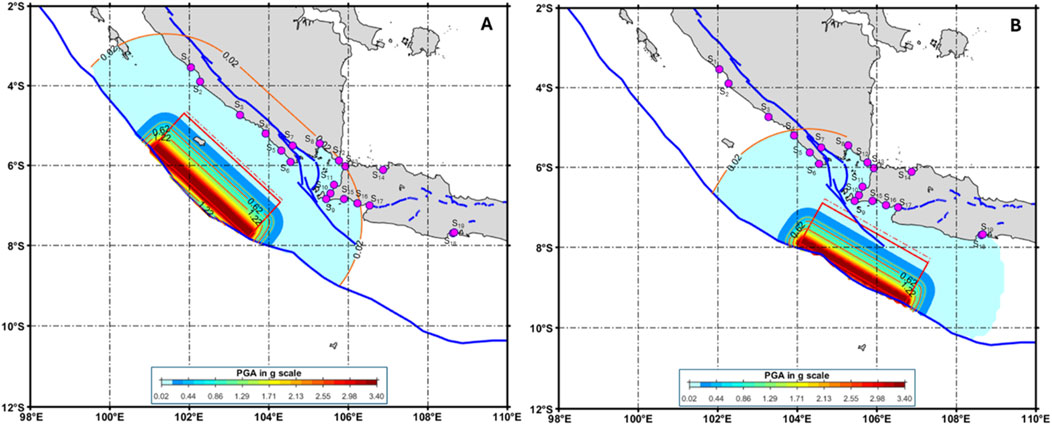
Figure 8. The estimated seismic hazard expressed as the MPE Peak Ground Acceleration (g) at the base rock is based on the defined fault parameter around the off-coast of southern Sumatra (A) and the off-coast of West Java (B). It can be found that at the site of S1-S19, the PGAs estimate are around ∼0.05g.
Figure 9A illustrates the seven selected sites (S1, S2, S3, S4, S5, S6, and S9) used to estimate the Probabilistic Seismic Hazard Function (PSHF). Aligned with Triyoso et al. (2020) and Triyoso and Sahara (2021), our probabilistic seismic hazard calculations considered a maximum radius distance of approximately 100 km and a magnitude range of 6.0–9.0. As depicted in Figure 9B, the resulting PSHF curve, representing the 10% probability of exceeding earthquake events within 50 years, indicates estimated peak ground acceleration (PGA) values in the 150 to 200 gals range.
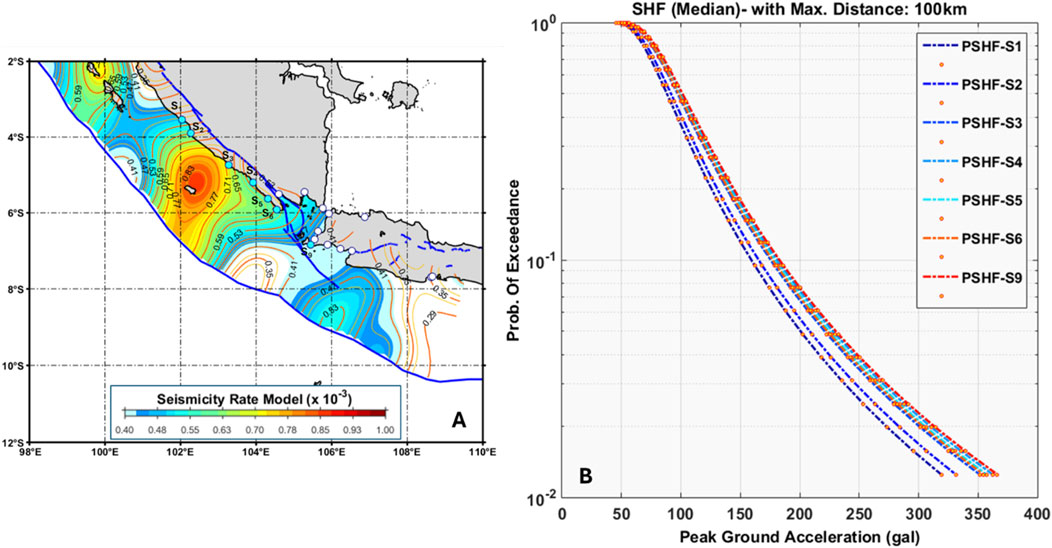
Figure 9. The selected sites (S1, S2, S3, S4, S5, S6, and S9) were used to estimate the Probabilistic Seismic Hazard Function (PSHF) (A). The PSHF curve represents the PGA versus the Probability of Exceedance in 50 years (B). In this study, we follow Triyoso et al. (2020) and Triyoso and Sahara (2021) in estimating the probabilistic seismic hazard calculations considering a maximum radius distance of approximately 100 km and a magnitude range of 6.0–9.0.
The tsunami modeling results from the proposed tsunamigenic area show that the maximum tsunami height of about ∼8m along the coastline occurred perpendicular to the source region along the coast of Southern Sumatra and West Java based on the scenario A by referring to Bilek and Lay (1999) with the maximum uniform slip of 9 and 8 m with rigidity used about 33.9 GPa as is shown by Figure 10A. Based on the result of scenario B with the maximum uniform slip of 15 and 14 m with rigidity used of about 24.3 GPa, as is shown in Figure 10B, the tsunami height reaches up to 15m with a tsunami arrival time between 20–30 min. Along the coast of Southern Sumatra–West Java, the height ranges between 4 m, and the maximum tsunami height reaches 11m–15m. Offshore Enggano Island shows a high risk of tsunami attack based on both scenarios A and B of both tsunami sources model.
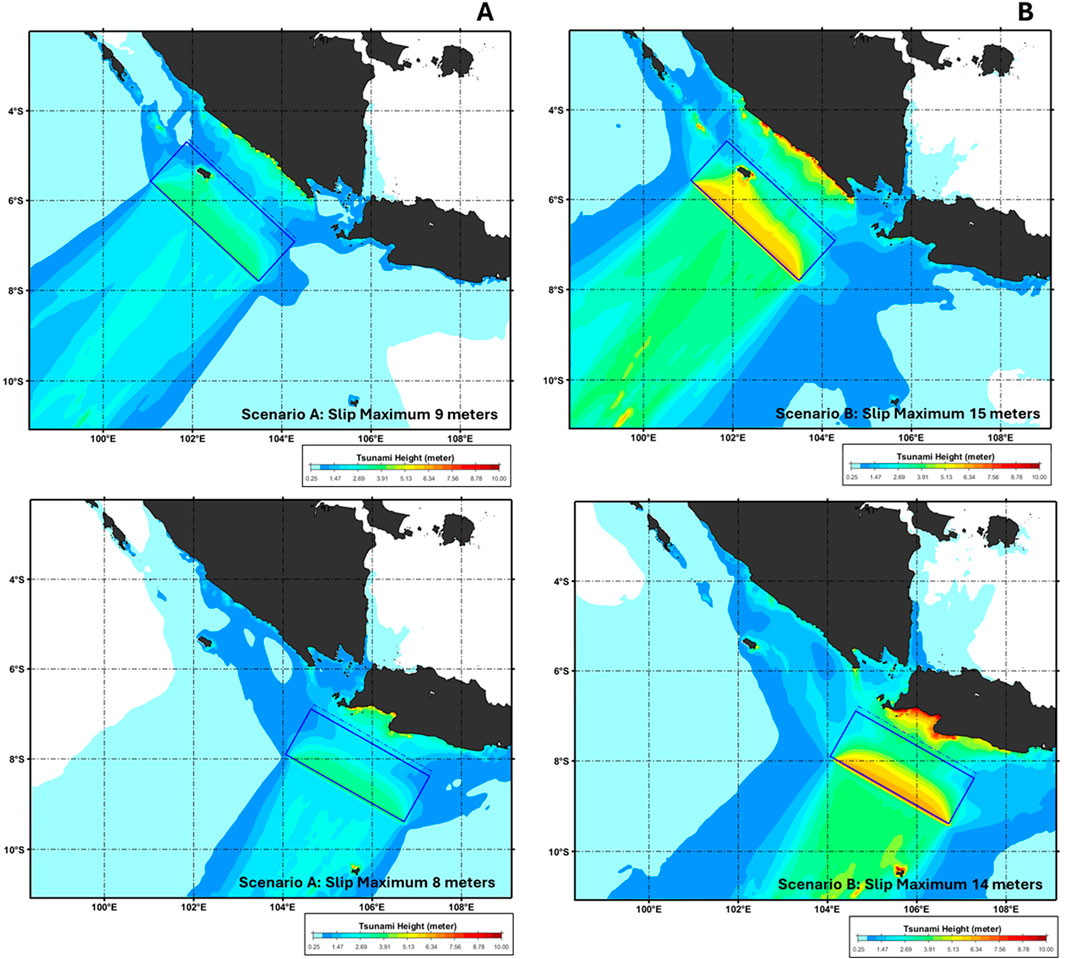
Figure 10. The tsunami modeling results from the proposed tsunamigenic area show that the maximum tsunami height of about ∼8m along the coastline occurred perpendicular to the source region along the coast of Southern Sumatra and West Java based on scenario (A) with the maximum uniform slip of 9 and 8 m. Based on the result of scenario (B), with the maximum uniform slip of 15 and 14 m, the maximum tsunami height reaches up to 11m–15m, with a tsunami arrival time of 20–30 min.
This research provides valuable insights into seismic hazards in the Sumatran subduction zone and off-coast southern West Java. The result of this study suggested to be used to enhance the impact for urban studies and policymakers by considering the following findings and implications that can be used for some recommendations for urban studies and policymakers as follow (Aldea et al., 2018; Matari et al., 2023; Sabeur et al., 2023).
5.1 Key findings and implications
•Identification of Relative Quiescence and Potential Source Areas:
○ Pinpointing areas with decreased seismic activity can help prioritize monitoring and preparedness efforts.
○ Identifying potential earthquake source areas allows for targeted risk assessments and mitigation strategies.
•Tsunami Height Estimation:
○ Estimating tsunami heights helps develop evacuation plans and design resilient infrastructure.
○ Understanding the impact of multiple source areas and static stress loading improves the accuracy of tsunami predictions.
•Pre- and Post-Event Expectations:
○ Analyzing pre- and post-event expectations helps understand the public’s risk perception and develop effective communication strategies.
○ Identifying knowledge gaps and misconceptions can inform public education and awareness campaigns.
5.2 Recommendations for urban studies and policymakers
•Incorporate Findings into Urban Planning:
○ Consider seismic hazards in land use planning, building codes, and infrastructure development.
○ Identify areas with higher risk and implement appropriate zoning regulations.
• Enhance Disaster Preparedness and Response:
○ Develop comprehensive emergency response plans that account for multiple scenarios.
○ Invest in early warning systems and public education campaigns.
○ Strengthen building codes and enforce strict construction standards.
• Support Scientific Research:
○ Continue research on seismic hazards and tsunami modeling to improve understanding and prediction capabilities.
○ Collaborate with international researchers to share knowledge and best practices.
5.3 Communication and engagement
• Communicate Findings Effectively:
○ The present study’s findings are clear and accessible to policymakers, scientists, and the public.
○ Use visual aids like maps and infographics to illustrate key points.
• Engage with Stakeholders:
○ Collaborate with local governments, communities, and businesses to develop tailored mitigation strategies.
○ Seek input from stakeholders to ensure that plans are practical and feasible.
By incorporating these findings and recommendations, urban studies and policymakers can make informed decisions to reduce the impact of future seismic events and build more resilient communities.
6 Conclusion
This study investigates the potential for future large earthquakes in the Sumatran subduction zone and off the coast of West Java. By analyzing historical seismicity data and applying the mG approach, the researchers identified areas with significant strain accumulation and potential for large earthquakes. The key findings are as follows: Relative Quiescence: The study identified periods of relative seismic quiescence in the Andaman and off-coast northern Sumatra regions as well as off-coast central Sumatra and West Java. These periods suggest potential strain accumulation and increased risk of future large earthquakes. Potential Source Areas: The researchers identified potential areas for future large earthquakes, including the Mentawai Islands, the off-coast of northern Sumatra, and the off-coast of southern Sumatra-West Java. Tsunami Height Estimation: The study estimated potential tsunami heights based on different earthquake scenarios. The results indicate significant tsunami hazards, particularly along the coasts of southern Sumatra and West Java. Based on this study, some recommendations related to urban planning and policymakers could be described as follows: Incorporate Findings into Urban Planning: Consider seismic hazards in land use planning, building codes, and infrastructure development. Enhance Disaster Preparedness and Response: Develop comprehensive emergency response plans, invest in early warning systems, and strengthen building codes. Support Scientific Research: Continue research on seismic hazards and tsunami modeling to improve understanding and prediction capabilities. Effective Communication and Engagement: Communicate findings clearly and engage with stakeholders to develop tailored mitigation strategies. By implementing these recommendations, urban planners and policymakers can make informed decisions to reduce the impact of future seismic events and build more resilient communities.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
WT: Conceptualization, Formal Analysis, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing. WK: Validation, Writing–review and editing. GP: Supervision, Visualization, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was partly supported by the Research, Community Service, and Innovation (PPMI) ITB 2024 grant funded by the Research and Community Services program (LPPM), Institute of Technology, Bandung (ITB), Indonesia.
Acknowledgments
The authors gratefully acknowledge the support of the Global Geophysics Group, Faculty of Mining and Petroleum Engineering, Bandung Institute of Technology, in the production of this paper. They also extend their sincere thanks to the reviewers for their invaluable comments, critiques, and suggestions, which significantly improved the clarity and logical flow of the manuscript. Finally, the authors wish to thank Grammarly Premium and Google Gemini 1.5 for their assistance with grammar correction and enhancing the writing style.
Conflict of interest
The authors declare that the research was conducted without commercial or financial relationships construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akaike, H. (1974). A new look at the statistical model identification. IEEE Trans. Autom. Contr 19 (6), 716–723. doi:10.1109/TAC.1974.1100705
Aldea, A., Neagu, C., Lozinca, E., Demetriu, S., El-Amine Bourdim, S. M., and Turano, F. (2018). “Toward the seismic evaluation of “carol I” royal mosque in constanța,” in Seismic hazard and risk assessment. Editors R. Vacareanu, and C. Ionescu (Cham: Springer Natural Hazards. Springer). doi:10.1007/978-3-319-74724-8_23
Anderson, J. G., Cotton, F., and Bindi, D. (2021). A ground motion based procedure to identify the earthquakes that are the most relevant for probabilistic seismic hazard analysis. Earthq. Spectra 37 (2), 762–788. doi:10.1177/8755293020981987
Anderson, J. G., and Zaliapin, I. (2023). Effects on probabilistic seismic hazard estimates that result from nonuniqueness in declustering an earthquake catalog. Bull. Seismol. Soc. Am. 113 (6), 2615–2630. doi:10.1785/0120220239
Atkinson, G. M., and Boore, D. M. (2006). Earthquake ground-motion prediction equations for Eastern North America. Bull. Seismol. Soc. Am. 96 (6), 2181–2205. doi:10.1785/0120050245
Bender, B. (1983). Maximum likelihood estimation of b values for magnitude grouped data. Bull. Seismol. Soc. Am. 73, 831–851. doi:10.1785/bssa0730030831
Bilek, S. L., and Engdahl, E. R. (2007). Rupture characterization and aftershock relocations for the 1994 and 2006 tsunami earthquakes in the Java subduction zone. Geophys. Res. Lett. 34, L20311. doi:10.1029/2007gl031357
Bilek, S. L., and Lay, T. (1999). Rigidity variations with depth along interplate megathrust faults in subduction zones. Nature 400, 443–446. doi:10.1038/22739
Bird, P., and Kreemer, C. (2015). Revised tectonic forecast of global shallow seismicity based on version 2.1 of the Global Strain Rate Map. Bull. Seismol. Soc. Am. 105 (1), 152–166. doi:10.1785/0120140129
Blaser, L. F., Kru¨ger, M. O., and Scherbaum, F. (2010). Scaling relations of earthquake source parameter estimates with special focus on subduction environment. Bull. Seismol. Soc. Am. 100, 2914–2926. doi:10.1785/0120100111
Bock, Y., Prawirodirdjo, L., Genrich, J. F., Stevens, C. W., McCaffrey, R., Subarya, C., et al. (2003). Crustal motion in Indonesia from global positioning system measurements. J. Geophys. Res. 108 (B8), 2367. doi:10.1029/2001JB000324
Bradley, K. E., Feng, L., Hill, E. M., Natawidjaja, D. H., and Sieh, K. (2017). Implications of the diffuse deformation of the Indian Ocean lithosphere for slip partitioning of oblique plate convergence in Sumatra. J. Geophys Res. Solid Earth 122, 572–591. doi:10.1002/2016jb013549
Chlieh, M., Avouac, J., Hjorleifsdottir, V., Song, T. A., Ji, C., Sieh, K., et al. (2007). Coseismic slip and afterslip of the great Mw 91.5 sumatra-andaman earthquake of 2004. Bull. Seismol. Soc. Am. 97 (1A), S152–S173. doi:10.1785/0120050631
De Santis, A., Perrone, L., Calcara, M., Campuzano, S. A., Cianchini, G., D’Arcangelo, S., et al. (2022). A comprehensive multiparametric and multilayer approach to study the preparation phase of large earthquakes from ground to space: the case study of the June 15 2019, M7.2 Kermadec Islands (New Zealand) earthquake. Remote Sens. Environ. 283 (1), 1386–1395. doi:10.1016/j.rse.2022.113325
El-fiky, G. S. A., Kato, T., and Oware, E. N. (1999). Crustal deformation and interplate coupling in the Shikoku district, Japan, as seen from continuous GPS observation. Tectonophysics 314, 387–399. doi:10.1016/s0040-1951(99)00226-7
Field, E. H., Jackson, D. D., and Dolan, J. F. (1999). A mutually consistent seismic-hazard source model for Southern California. Bull. Seismol. Soc. Am. 89 (3), 559–578. doi:10.1785/bssa0890030559
Frankel, A. (1995). Mapping seismic hazard in the central and eastern United States. Seismol. Res. Lett. 66 (4), 8–21. doi:10.1785/gssrl.66.4.8
Gardner, J. K., and Knopoff, L. (1974). Is the sequence of earthquakes in southern California, with aftershocks removed, Poissonian? Bull. Seismol. Soc. Am. 64, 1363–1367. doi:10.1785/bssa0640051363
GEBCO (2008). The general bathymetric charts of the Oceans: the GEBCO version 11.1, september 2008 (2008) - GEBCO website. Available at: https://www.gebco.net/.
Geffers, G. M., Main, I. G., and Naylor, M. (2023). Accuracy and precision of frequency-size distribution scaling parameters as a function of dynamic range of observations: example of the Gutenberg-Richter law b-value for earthquakes. Geophys. J. Int. 232, 2080–2086. doi:10.1093/gji/ggac436
Gerstenberger, M. C., Wiemer, S., Jones, L. M., and Reasenberg, P. A. (2005). Real-time forecasts of tomorrow's earthquakes in California. Nature 435, 328–331. doi:10.1038/nature03622
Gutenberg, B., and Richter, C. F. (1944). Frequency of earthquakes in California*. Bull. Seismol. Soc. Am. 34, 185–188. doi:10.1785/bssa0340040185
Hanks, T. C., and Kanamori, H. (1979). A moment magnitude scale. J. Geophys. Res. 84 (5), 2348–2350. doi:10.1029/JB084iB05p02348
Hayes, G. P., Wald, D. J., and Johnson, R. L. (2012). Slab1.0: a three-dimensional model of global subduction zone geometries. J. Geophys. Res. 117, B01302. doi:10.1029/2011jb008524
Helmstetter, A., Kagan, Y. Y., and Jackson, D. D. (2007). High-resolution time-independent grid-based forecast for M >= 5 earthquakes in California. Seismol. Res. Lett. 78, 78–86. doi:10.1785/gssrl.78.1.78
Hill, E. M., Borrero, J. C., Huang, Z., Qiu, Q., Banerjee, P., Natawidjaja, D. H., et al. (2012). The 2010 MW 7.8 Mentawai earthquake: very shallow source of a rare tsunami earthquake determined from tsunami field survey and near-field GPS data. J. Geophys. Res. 117, B06402. doi:10.1029/2012jb009159
Holliday, J. R., Chen, C.-c., Tiampo, K. F., Rundle, J. B., Turcotte, D. L., and Donnellan, A. (2007). A relm earthquake forecast based on pattern informatics. Seismol. Res. Lett. 78 (1), 87–93. doi:10.1785/gssrl.78.1.87
Huchon, P., and LePichon, X. (1984). Sunda Strait and central Sumatra fault. Geology 12, 668–672. doi:10.1130/0091-7613(1984)12<668:ssacsf>2.0.co;2
Imamura, F., Yalciner, A. C., and Ozyurt, G. (2006). TSUNAMI MODELLING MANUAL (TUNAMI model), disaster control research center. Japan: Sendai.
Ito, K., and Nakamura, S. (1998). Variation in thickness of the seismogenic layer in southwestern Japan and their relation to large inland earthquake. Annu. Disas Prev Res Inst 41 (B-1), 27–35.
Konca, A. O., Avouac, J. P., Sladen, A., Meltzner, A. J., Sieh, K., Fang, P., et al. (2008). Partial rupture of a locked patch of the Sumatra megathrust during the 2007 earthquake sequence. Nature 456 (7222), 631–635. doi:10.1038/nature07572
Li, L., and Luo, G. (2024). Can we obtain reliable seismic b-values for real-time catalogues? Geophys. J. Int. 237 (3), 1554–1566. doi:10.1093/gji/ggae124
Martin, S. S., Li, L., Okal, E. A., Morin, J., Tetteroo, A. E. G., Switzer, A. D., et al. (2019). Reassessment of the 1907 Sumatra “tsunami earthquake” based on macroseismic, seismological, and tsunami observations, and modeling. Pure Appl. Geophys. 176, 2831–2868. doi:10.1007/s00024-019-02134-2
Marzocchi, W., and Taroni, M. (2014). Some thoughts on declustering in probabilistic seismic-hazard analysis. Bull. Seismol. Soc. Am. 104, 1838–1845. doi:10.1785/0120130300
Matari, Z., El-Amine Bourdim, S. M., Rodrigues, H., and Kadri, T. (2023). Earthquake analysis of an old RC minaret retrofitting with shape memory alloy. Buildings 13 (5), 1121. doi:10.3390/buildings13051121
McCaffrey, R. (2009). The tectonic framework of the Sumatran subduction zone. Annu. Rev. Earth Planet Sci. 3737, 345–366. doi:10.1146/annurev.earth.031208.100212
Megawati, K., and Pan, T. (2009). Regional seismic hazard posed by the mentawai segment of the sumatran megathrust. Bull. Seismol. Soc. Am. 99, 566–584. doi:10.1785/0120080109
Newcomb, K. R., and McCann, W. R. (1987). Seismic history and seismotectonics of the Sunda Arc. J. Geophys Res. 92, 421–439. doi:10.1029/JB092iB01p00421
Nishimura, T. (2022). Time-independent forecast model for large crustal earthquakes in southwest Japan using GNSS data. Earth Planets Space 74, 58. doi:10.1186/s40623-022-01622-5
Nuannin, P., Kulhánek, O., and Persson, L. (2012). Variations of b-values preceding large earthquakes in the Andaman–Sumatra subduction zone. J. Asian Earth Sci. 61, 237–242. doi:10.1016/j.jseaes.2012.10.013
Ogata, Y. (2005). Synchronous seismicity changes in and around the northern Japan preceding the 2003 Tokachi-oki earthquake of M8.0. J. Geophys Res. 110, B08305. doi:10.1029/2004JB003323
Okada, Y. (1985). Surface deformation due to shear and tensile faults in a halfspace. Bull. Seismol. Soc. Am. 75 (4), 1135–1154. doi:10.1785/bssa0750041135
Okada, Y. (1992). Internal deformation due to shear and tensile faults in a halfspace. Bull. Seismol. Soc. Am. 82 (2), 1018–1040. doi:10.1785/bssa0820021018
Pakoksung, K., Suppasri, A., and Imamura, F. (2021). Probabilistic tsunami hazard analysis of inundated buildings following a subaqueous volcanic explosion based on the 1716 tsunami scenario in taal lake. Available at: https://scite.ai/reports/10.3390/geosciences11020092.
Penarubia, H. C., Johnson, K. L., Styron, R. H., Bacolcol, T. C., Sevilla, W. I. G., Perez, J. S., et al. (2020). Probabilistic seismic hazard analysis model for the Philippines. Earthq. Spectra 36 (S1), 44–68. doi:10.1177/8755293019900521
Petersen, M. D., Harmsen, S., Mueller, C., Haller, K., Dewey, K., Luco, N., et al. (2007). Documentation for the Southeast Asia Seismic Hazard Maps, Administrative Report September 30, 2007, U.S. Department of the Interior. Reston, Virginia: U.S. Geological Survey.
Petersen, M. D., Mueller, C. S., Moschetti, M. P., Hoover, S. H., Shumway, A. M., McNamara, D. E., et al. (2017). One-year seismic-hazard forecast for the central and eastern United States from induced and natural earthquakes. Seismol. Res. Lett.; 88 (3): 772–783. doi:10.1785/0220170005
Petersen, M. D., Shumway, A. M., Powers, P. M., Mueller, C. S., Moschetti, 750 M. P., Frankel, A. D., et al. (2020). The 2018 update of the U.S. National seismic hazard model: overview of model and implications. Earthq. Spectra 36 (1), 5–41. doi:10.1177/8755293019878199
Philibosian, B., and Meltzner, A. J. (2020). Segmentation and supercycles: a catalog of earthquake rupture patterns from the Sumatran Sunda Megathrust and other well-studied faults worldwide. Quat. Sci. Rev. 241, 106390. doi:10.1016/j.quascirev.2020.106390
Pollitz, F. F., Banerjee, P., Burgmann, R., Hashimoto, M., and Choosakul, N. (2006). Stress changes along the Sunda trench following the 26 december 2004 sumatra-andaman and 28 march 2005 Nias earthquakes. Geophy. Res. Lett. 33, L06309. doi:10.1029/2005GL024558
Prawirodirdjo, L., McCaffrey, R., Chadwell, C. D., Bock, Y., and Subarya, C. (2010). Geodetic observations of an earthquake cycle at the Sumatra subduction zone: role of interseismic strain segmentation. J. Geophys Res. Sol. Earth 115, B03414. doi:10.1029/2008JB006139
Reid, H. F. (1910). “The mechanics of the earthquake, the California earthquake of april 18, 1906; report of the state investigation commission,”, 2. Washington, Washington, D.C: Carnegie Institution of.
Rhoades, D. A., Christophersen, A., and Gerstenberger, M. C. (2017). Multiplicative earthquake likelihood models incorporating strain rates. Geophys J. Int., ggw486. doi:10.1093/gji/ggw486
Rhoades, D. A., Schorlemmer, D., Gerstenberger, M. C., Christophersen, A., Zechar, J. D., and Imoto, M. (2011). Efficient testing of earthquake forecasting models. Acta Geophys. 59, 728–747. doi:10.2478/s11600-011-0013-5
Rivera, L., Sieh, K., Helmberger, D., and Natawidjaja, D. H. (2002). A comparative study of the sumatran subduction-zone earthquakes of 1935 and 1984. BSSA 92, 1721–1736.
Rundle, J. B., Holliday, J. R., Yoder, M., Sachs, M. K., Donnellan, A., Turcotte, D. L., et al. (2011). Earthquake precursors: activation or quiescence? Geophys. J. Int. 187, 225–236. doi:10.1111/j.1365-246X.2011.05134.x
Rundle, J. B., Donnellan, A., Fox, G., Crutchfield, J. P., and Granat, R. (2021). Nowcasting earthquakes: Imaging the earthquake cycle in California with machine learning. Earth and Space Science 8, e2021EA001757. doi:10.1029/2021EA001757
Sabeur, B., Bourdim, S. M. E. A., and Rodrigues, H. (2023). Seismic damage scenarios for existing masonry buildings for educational use in the mostaganem city. KSCE J. Civ. Eng. 27, 2148–2162. doi:10.1007/s12205-023-1592-9
Savage, J. C., and Simpson, R. W. (1997). Surface strain accumulation and the seismic moment tensor. Bull. Seismol. Soc. Am. 87 (5), 1345–1353. doi:10.1785/bssa0870051345
Shearer, P., and Burgmann, R. (2010). Lessons learned from the 2004 sumatra-andaman megathrust rupture. Annu. Rev. Earth Planet Sci. 38, 103–131. doi:10.1146/annurev-earth-040809-152537
Strader, A., Maximilian, W., Bayona, J., Maechling, P., Silva, F., Liukis, M., et al. (2018). Prospective evaluation of global earthquake forecast models: 2 yrs of observations provide preliminary support for merging smoothed seismicity with geodetic strain rates. Seismol. Res. Lett. 89 (4), 1262–1271. doi:10.1785/0220180051
Sukrungsri and Pailoplee (2016). Seismicity change prior to major earthquakes of the sumatra-andaman subduction zone; implication for tectonic regime. Bull. Earth Sci. Thail. 7 (1), 16–24.
Supendi, P., Widiyantoro, S., Rawlinson, N., Yatimantoro, T., Muhari, A., Hanifa, N. R., et al. (2023). On the potential for megathrust earthquakes and tsunamis off the southern coast of West Java and southeast Sumatra, Indonesia. Nat. Hazards 116, 1315–1328. doi:10.1007/s11069-022-05696-y
Taroni, M., and Akinci, A. (2021). A new smoothed seismicity approach to include aftershocks and foreshocks in spatial earthquake forecasting: application to the global Mw ≥ 5.5 seismicity. Appl. Sci. 11, 10899. doi:10.3390/app112210899
Tim Pusat Studi Gempa Nasional (The PuSGen) (2017). Peta sumber dan bahaya Gempa Indonesia tahun 2017. Jakarta: Kementrian Pekerjaan Umum dan Perumahan Rakyat. (In Indonesian).
Triyoso, W. (2023). Probabilistic seismic hazard function based on spatiotemporal earthquake likelihood simulation and Akaike information criterion: the PSHF study around off the west coast of Sumatra Island before large earthquake events. Front. Earth Sci. 11, 1104717. doi:10.3389/feart.2023.1104717
Triyoso, W. (2024a). Applying the Akaike Information Criterion (AIC) in earthquake spatial forecasting: a case study on probabilistic seismic hazard function (PSHF) estimation in the Sumatra subduction zone. Geomatics, Nat. Hazards Risk 15 (1), 2319187. doi:10.1080/19475705.2024.2319187
Triyoso, W. (2024b). Regional earthquake likelihood models (RELMs) for probabilistic seismic hazard analysis (PSHA) around the southern off-coast of Sumatra - west Java. Submitt. Nat. Hazards Accept.
Triyoso, W., Kongko, W., Prasetya, G. S., and Sarsito, D. A. (2023). Spatial correlation of the maximum shear strain loading rate and the correlation dimension along the Sumatra subduction margin for potential earthquake and tsunami hazard study and analysis. All Earth 35 (1), 287–301. doi:10.1080/27669645.2023.2249669
Triyoso, W., Kongko, W., Prasetya, G. S., and Suwondo, A. (2024). Study on earthquake and tsunami hazard: evaluating probabilistic seismic hazard function (PSHF) and potential tsunami height simulation in the coastal cities of Sumatra Island. Front. Built Environ. 10, 1310251. doi:10.3389/fbuil.2024.1310251
Triyoso, W., and Sahara, D. P. (2021). Seismic hazard function mapping using estimated horizontal crustal strain off West Coast Northern Sumatra, Front. Earth Sci. 9, doi:10.3389/feart.2021.558923
Triyoso, W., Suwondo, A., Yudistira, T., and Sahara, D. P. (2020). Seismic hazardfunction (SHF) study of coastal sources of Sumatra Island: SHF evaluation of Padang and Bengkulu cities. Geosci. Lett. 7, 2. doi:10.1186/s40562-020-00151-x
Utsu, T. (1978). Estimation of parameters in formulas for frequency-magnitude relation of earthquake occurrence. Zisin 31, 367–382. doi:10.4294/zisin1948.31.4_367
Viveros, J. A. B., von Specht, S., Strader, A., Hainzl, S., Cotton, F., and Schorlemmer, D. (2019). A regionalized seismicity model for subduction zones based on geodetic strain rates, geomechanical parameters, and earthquake-catalog data. Bull. Seismol. Soc. Am. 109 (5), 2036–2049. doi:10.1785/0120190034
Wang, S., Werner, M. J., and Yu, R. (2022). How well does Poissonian probabilistic seismic hazard assessment (PSHA) approximate the simulated hazard of epidemic-type earthquake sequences? Bull. Seismol. Soc. Am. 112 (5), 2762–2769. doi:10.1785/0120220081
Ward, S. N. (1994). A multidisciplinary approach to seismic hazard in Southern California. Bull. Seismol. Soc. Am. 84 (5), 1293–1309. doi:10.1785/bssa0840051293
Ward, S. N. (1998). On the consistency of earthquake moment rates, geological fault data, and space geodetic strain: the United States. Geophys. J. Int. 134, 172–186. doi:10.1046/j.1365-246x.1998.00556.x
Wiemer, S. (2001). A software package to analyze seismicity: ZMAP. Seismol. Res. Lett. 72 (2), 373–382. doi:10.1785/gssrl.72.3.373
Yavas, C. E., Chen, L., Kadlec, C., and Ji, Y. (2024). Improving earthquake prediction accuracy in Los Angeles with machine learning. Sci. Rep. 14 (1), 24440. doi:10.1038/s41598-024-76483-x
Youngs, R. R., Chiou, S. J., Silva, W. J., and Humphrey, J. R. (1997). Strong ground motion attenuation relationships for subduction zone earthquakes. Seismol. Res. Lett. 68 (1), 58–73. doi:10.1785/gssrl.68.1.58
Zechar, J. D., Schorlemmer, D., Liukis, M., Yu, J., Euchner, F., Maechling, P. J., et al. (2010). The Collaboratory for the Study of Earthquake Predictability perspective on computational earthquake science. Pract. Ex. 22, 1836–1847. doi:10.1002/cpe.1519
Zeng, Y., Petersen, M. D., and Shen, Z. K. (2018). Earthquake potential in California-Nevada implied by correlation of strain rate and seismicity. Geophys. Res. Lett. 45, 1778–1785. doi:10.1002/2017GL07596
Keywords: subduction zone, quiescence, probability gain, potential earthquake and tsunami source, seismic mitigation
Citation: Triyoso W, Kongko W and Prasetya GS (2025) Understanding earthquake potential for future hazard mitigation. Front. Built Environ. 10:1499848. doi: 10.3389/fbuil.2024.1499848
Received: 21 September 2024; Accepted: 02 December 2024;
Published: 07 January 2025.
Edited by:
Pengfei Dang, Ningbo University, ChinaReviewed by:
Sidi Mohammed El-Amine Bourdim, University Center of Maghnia, AlgeriaSuli Yao, The Chinese University of Hong Kong, China
Copyright © 2025 Triyoso, Kongko and Prasetya. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wahyu Triyoso, d3RyaXlvc29AZ21haWwuY29t
 Wahyu Triyoso
Wahyu Triyoso Widjo Kongko2
Widjo Kongko2