Seismic capacity evaluation of reinforced concrete moment-resisting frames with steel damper columns using incremental critical pseudo-multi impulse analysis

Steel damper columns (SDCs) are energy-dissipating members that are suitable for reinforced concrete (RC) moment-resisting frames (MRFs) and those often used for multistory housing. In a previous study, the authors proposed an energy-based prediction procedure for the peak and cumulative response of an RC frame building with SDCs. In this procedure, the accuracy of the equivalent velocity of the maximum momentary input energy (V_ΔE1^*)–peak equivalent displacement (D₁^*_max) relationship is essential for improved prediction. In this article, the seismic capacity curve (V_ΔE1^*–D₁^*_max relationship) of RC MRFs with and without SDCs is evaluated using incremental critical pseudo-multi impulse analysis (ICPMIA). In the ICPMIA, which is based on a study by Takewaki and coauthors, the structure is subjected to various intensities of critical pseudo-multi impulsive lateral force. An ICPMIA of planer four 8- and 16-story RC MRFs with and without SDCs is performed to obtain their structural behaviors under various intensities of pulsive input. Then, the seismic capacity curve obtained from the ICMPIA results are compared with the predicted results based on the simplified equations. The main findings of this article are as follows. (i) The seismic capacity curve of RC MRFs without SDCs strongly depends on the number of impulsive lateral forces (N_p). As N_p increases, the seismic capacity decreases. The predicted seismic capacity curve severely underestimates that obtained from the ICMPIA in the case of large N_p. This trend is notable when the level of pinching behavior in the RC members is severe. (ii) In the case of an RC MRF with SDCs, however, the influence of N_p on its seismic capacity curve is small. The predicted seismic capacity curve agrees very well with that obtained from the ICMPIA. The influence of the level of pinching behavior in RC members on the seismic capacity curve is small.

1 Introduction

1.1 Background and motivation

The peak deformation, cumulative strain energy, and residual deformation are essential parameters in assessing the seismic performance of structural members. Two energy-based seismic intensity parameters—the maximum momentary input energy (Hori et al., 2000; Inoue et al., 2000; Hori and Inoue, 2002) and the total input energy (Akiyama, 1985; Akiyama, 1999)—are related to the peak and cumulative responses, respectively. According to a study by Hori and Inoue (2002), the peak displacement of a structure can be evaluated by considering the energy balance during a half cycle of the structural response using the maximum momentary input energy. Meanwhile, the cumulative strain energy of structural members can be evaluated by considering the energy balance during an entire seismic event using the total input energy.

The motivation for using energy dissipation devices (dampers) is to mitigate damage to beams and columns during strong seismic events. A dual system which consists of an elastic flexible main frame with stiff hysteresis dampers, e.g., a damage-tolerant structure (Wada et al., 2000), is one solution for creating structures with superior seismic performance. In such a dual system, dampers play important roles (a) to reduce the peak displacement of the system and (b) to reduce the cumulative damage to beams and columns by absorbing seismic energy before it reaches the beams and columns. Accordingly, a building with such a dual system is more resilient than one with a traditional earthquake-resistant system. e.g., a traditional moment-resisting frames (MRFs): in the case of traditional MRFs, most of the seismic energy is absorbed by the plastic hinges at the beam ends. Conversely, in the case of a dual system, most of the seismic energy is absorbed by the dampers; therefore, the seismic energy absorbed by the beams and columns is much smaller than in the case of traditional MRFs. Steel damper columns (SDCs; Katayama et al., 2000) are dampers suitable for reinforced concrete (RC) multistory housing. A SDC consists of a damper panel made of low-yield-strength steel plate, which absorbs the hysteresis energy, and a roll-formed H-section column, which behaves elastically. Numerous studies have been conducted on the seismic rehabilitation of existing RC buildings using SDCs (Fujii and Miyagawa, 2018; Fujii et al., 2019) and the seismic design of new RC MRFs with SDCs (Fujii and Kato, 2021; Mukoyama et al., 2021).

For evaluating the relationship between the seismic intensity and response parameters discussed above, the incremental dynamic analysis (IDA) (Vamvatsikos and Cornell, 2002) is the most rigorous method. In IDA, an nonlinear time-history analysis (NTHA) of the model is performed using the time-history of the ground accelerations. It is no doubt that the IDA is the most rigorous method for evaluating the response parameters. However, the IDA result is complex to understand with respect to the nonlinear structural characteristics because the IDA result is intricately intertwined with the nonlinear structural characteristics and the ground motion characteristics. As an alternative of IDA method, the incremental N2 (IN2) method has been proposed by Dolšek and Fajfar (2004). In IN2, a nonlinear static (pushover) analysis of the model is performed to obtain the nonlinear structural characteristics. Then, the seismic response (the seismic intensity corresponds to a certain peak displacement) is evaluated based on the inelastic spectra. The IN2 result is simpler and easier to understand than IDA result. However, only the peak deformation can be obtained from the IN2 results: the IN2 cannot predict the cumulative strain energy and residual deformation. In addition, its accuracy strongly depends on several assumptions, that the structure oscillates predominantly in a fundamental mode and that the spectra are inelastic. Therefore, another method which can predict the peak deformation, cumulative strain energy and residual deformation would be useful: this method would be better if its result is not too complicated to understand as IDA. Specifically, for the damage evaluation of damper panel in SDC, its peak shear strain and cumulative strain energy are needed. In addition, the problem of residual deformation would be more important for RC MRFs with SDCs, because the larger residual deformation may occur due to the presence of hysteresis dampers. Therefore, the evaluation of three parameters described above is important for RC MRFs with SDCs.

The concept of energy balance is quite useful to understand how such dampers work to improve the seismic performance of buildings. Recent advances in energy-based earthquake engineering can be found in Benavent-Climent and Mollaioli (2021) and Varum et al. (2023). Following Akiyama (1985), Benavent-Climent and his research group proposed a simplified seismic retrofitting design method for RC frames using dampers (Benavent-Climent, 2011; Benavent-Climent and Mota-Páez, 2017; Mota-Páez, et al., 2021; Benavent-Climent et al., 2024).

Takewaki and his research group (Kojima and Takewaki, 2015a; Kojima and Takewaki, 2015b; Kojima and Takewaki, 2015c; Kojima et al., 2015; Akehashi and Takewaki, 2021; Akehashi and Takewaki, 2022) have introduced the concepts of critical double impulse (DI) and critical multi impulse (MI) as substitutes for near-fault and long-duration earthquake ground motions. First, the concept of the critical DI was introduced to derive the upper bound of the earthquake input energy to a building structure (Kojima et al., 2015). Following this study, the critical response of an undamped elastoplastic single-degree-of-freedom (SDOF) model subjected to near-fault and long-duration earthquake ground motions was examined (Kojima and Takewaki, 2015a; Kojima and Takewaki, 2015b; Kojima and Takewaki, 2015c). Then, Akehashi and Takewaki introduced pseudo-double impulse (PDI) (Akehashi and Takewaki, 2021) and pseudo-multi impulse (PMI) (Akehashi and Takewaki, 2022) to form a multi-degree-of-freedom (MDOF) model. In PDI and PMI analyses, the MDOF model oscillates predominantly in a single mode, considering the impulsive lateral force corresponding to a certain mode vector. When the impulsive lateral force corresponding to the first mode vector is considered, the MDOF model oscillates predominantly in the first mode.

An energy-based prediction procedure for the peak and cumulative response of RC MRFs with SDCs has been proposed (Fujii and Shioda, 2023). In the presented procedure, the building model is converted to an equivalent SDOF model that represents the first modal response based on a monotonic pushover analysis result. Then, the peak displacement is predicted using the maximum momentary input energy (Hori and Inoue, 2002), while the cumulative energy dissipation demand is predicted using the total input energy (Akiyama, 1985). In this procedure, the accuracy of the equivalent velocity of the maximum momentary input energy of the first modal response (${V_{\Delta E1}}^{*}$)–peak equivalent displacement of the first modal response (${{D_1}^{*}}_{\max }$) relationship is essential for high quality prediction of the peak displacement. This procedure has been verified by comparing NTHA results using non-pulse-like ground motions (Fujii and Shioda, 2023) and 30 recorded pulse-like ground motions (Fujii, 2023). The accuracy of the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ relationship (seismic capacity curve) has also been verified by comparing the critical PDI analysis results (Fujii, 2024). However, the following issues remain.

• The verification in the previous study (Fujii, 2024) was limited because the number of impulsive inputs is fixed to two in a critical PDI analysis. The accuracy of the predicted ${V_{\Delta E1}}^{*}$ corresponding to ${{D_1}^{*}}_{\max }$ depends on the shape of the assumed half cycle of the structural response. In the case of the critical pseudo-multi impulse (PMI) input, the shape of the half cycle of the structural response depends on the number of impulsive inputs ($N_p$). Therefore, further numerical investigation considering $N_p$ as a parameter is indispensable.

• In the simplified equation using ${V_{\Delta E1}}^{*}$, the influence of the pinching behavior of the RC members on the energy dissipation is not considered. The severe pinching behavior of RC beam-column connections has been reported in experimental studies (e.g., Gentry and Wight, 1994; Kusuhara et al., 2004; Kusuhara and Shiohara, 2008; Benavent-Climent et al., 2009; Benavent-Climent et al., 2010). Toyoda et al. (2014) compared the shaking table test results of a 1/4-scaled 20-story RC building model conducted at E-defense with NTHA results. They found that, for a better prediction of the peak response, the influence of the pinching behavior of RC beams should be considered. Following their study, Shirai et al. (2024) demonstrated that the pinching behavior of RC members affects the peak responses of 40-story RC super-high-rise buildings. Therefore, the influence of the pinching behavior of RC members on the seismic capacity curve should be investigated.

The residual displacement (Farrow and Kurama, 2003) is another essential parameter that is important to discuss in the repair of structures after earthquakes. The residual displacement is also important when the seismic sequence is considered (Ruiz-García and Negrete-Manriquez, 2011; Ruiz-García, 2012a; Ruiz-García, 2012b; Tesfamariam and Goda, 2015; Hoveidae and Radpour, 2021; Fujii, 2022). Specifically, Ruiz-García (2012b) pointed out that the residual displacement of a stiffness-degrading SDOF model is smaller than that of an elastoplastic SDOF model, even though the peak displacement of a stiffness-degrading SDOF model is larger than that of an elastoplastic SDOF model. In addition, Hoveidae and Radpour (2021) found that the large residual displacement after a mainshock can significantly increase the peak response under an aftershock. In Fujii (2024), the residual displacement obtained from the critical PDI analysis of RC MRFs with SDCs is larger than that of RC MRFs without SDCs: the residual equivalent displacement reaches close to 30% of the peak equivalent displacement in the case of RC MRFs with SDCs. This is larger than that obtained in the NTHA considering the ground motion records (Fujii, 2022). Therefore, the residual displacement obtained from the critical PDI analysis may be the upper bound. Accordingly, the influence of the number of impulsive inputs ($N_p$) on the residual displacement should be investigated.

1.2 Objectives

Given the above-outlined background, this study addresses the following questions.

(i) Considering the critical response of an RC MRF with SDCs subjected to critical PMI input, what is the dependence of the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ relationship on the number of impulsive inputs ($N_p$)?

(ii) How does the pinching behavior of RC members affect the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ relationship of RC MRFs? Can the negative influence of the pinching behavior of the RC members on the ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ relationship be improved by installing SDCs?

(iii) How do $N_p$ and the pinching behavior of RC members affect the ratios of the cumulative energies (cumulative strain energies of the RC MRFs and SDCs) at the end of simulation?

(iv) How does $N_p$ affect the residual equivalent displacement of RC MRFs?

In this article, the seismic capacities of RC MRFs with and without SDCs are evaluated using incremental critical pseudo-multi impulse analysis (ICPMIA). Then, the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ relationships (seismic capacity curves) obtained from the ICPMIA results are compared with the predicted results based on the simplified equations.

The rest of this paper is organized as follows. Section 2 outlines the critical PMI analysis and ICPMIA. Section 3 presents four RC MRFs with and without SDCs and the analysis methods. Section 4 describes the responses of the RC MRFs obtained from the critical PDI and PMI analysis results, focusing in particular on (i) the pulse velocity ($V_p$)–peak equivalent displacement (${{D_1}^{*}}_{\max }$) relationship, (ii) the hysteresis loop and residual displacement of the first modal response, and (iii) the cumulative strain energies of the RC MRFs and SDCs. Section 5 focuses on comparisons with the predicted results based on the study of Fujii and Shioda (2023) and the ICPMIA results. First, the simplified equations for calculating the energy dissipation capacity during a half cycle of the structural response are formulated. Next, the seismic capacity curve is predicted using the pushover analysis results. Then, the predicted seismic capacity curve is compared with the ${V_{\Delta E1}}^{*}$ − ${{D_1}^{*}}_{\max }$ plot obtained from the ICPMIA results. The conclusions drawn from this study and the directions of future research are discussed in Section 6.

2 Incremental critical pseudo-multi impulse analysis

2.1 Outline of the critical pseudo-multi impulse analysis

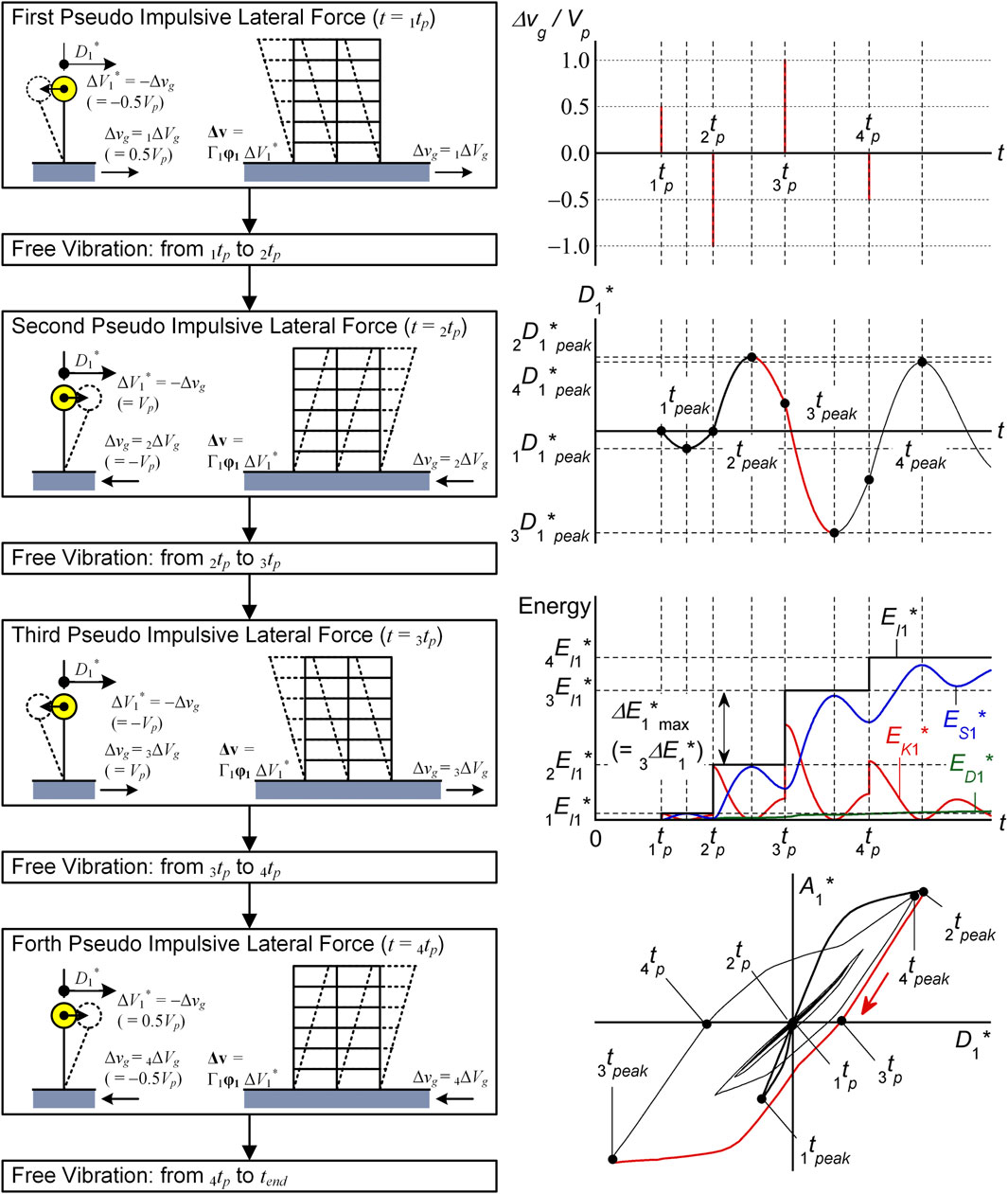
First, an outline of the critical PMI analysis is described as follows. Note that this analysis is based on the critical PDI analysis presented in Fujii (2024). Figure 1 outlines the critical PMI analysis.

Figure 1

Figure 1. Outline of the critical PMI analysis.

Following a study by Kojima and Takewaki (2015c), the ground acceleration ($a_g\left(t\right)$) in the case of the critical PDI and PMI analysis can be written as

$a_g\left(t\right)=-{\displaystyle \sum _{k=1}^{N_p}}{}_k\Delta V_g\delta \left(t-{}_k{t}_p\right),(1)$

$\left.\begin{array}{r}\delta \left(t\right)=\underset{\epsilon \to +0}{\lim }\left\{\begin{array}{cc}0& \left|t\right|>\epsilon \\ \frac{1}{2\epsilon }& \left|t\right|\le \epsilon \end{array}\right.\\ \hfill {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\delta \left(t\right)dt=1\\ \hfill {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\delta \left(t\right)f\left(t\right)dt=f\left(0\right)\end{array}\right\}.(2)$

In Eq. 1, $N_p$ (≥2) is the number of pseudo impulsive lateral forces, ${}_k\Delta V_g$ is the ground motion velocity increment of the $k$-th pulse, ${}_k{t}_p$ is the time when the pseudo impulsive lateral force acts, and $\delta \left(·\right)$ is the Dirac delta function that satisfies Eq. 2. In the case of the PDI analysis ($N_p$ = 2), ${}_k\Delta V_g$ is defined as in Eq. 3:

${}_k\Delta V_g={\left(-1\right)}^k{V}_p,(3)$

where $V_p$ is the pulse velocity. Similarly in the case of the PMI analysis ($N_p$ ≥ 3), ${}_k\Delta V_g$ is defined as in Eq. 4:

${}_k\Delta V_g=\left\{\begin{array}{ll}0.5{\left(-1\right)}^k{V}_p\hfill & :k=1,N_p\\ {\left(-1\right)}^k{V}_p\hfill & :2\le k\le N_p-1\end{array}\right..(4)$

Next, consider a planer frame building model (number of stories, $N$) subjected to a pseudo impulsive lateral force proportional to the first mode vector (${\mathrm{\Gamma }}_1{\mathbf{\phi }}_{\mathbf{1}}$). Here, $\mathbf{M}$ is the mass matrix of the building model; $\mathbf{d}\left(t\right)$, $\mathbf{v}\left(t\right)$, and $\mathbf{a}\left(t\right)$ are the relative displacement, velocity, and acceleration vector, respectively; and ${\mathbf{f}}_{\mathbf{R}}\left(t\right)$ and ${\mathbf{f}}_{\mathbf{D}}\left(t\right)$ are the restoring and damping force vectors, respectively. The equivalent displacement (${D_1}^{*}\left(t\right)$), equivalent velocity (${V_1}^{*}\left(t\right)$), and equivalent relative acceleration (${A_{r1}}^{*}\left(t\right)$) of the first modal response are defined in Eqs 5–8:

${D_1}^{*}\left(t\right)=\frac{{\mathrm{\Gamma }}_1{{\mathbf{\phi }}_{\mathbf{1}}}^{\mathbf{T}}\mathbf{\text{Md}}\left(t\right)}{{M_1}^{*}},(5)$

${V_1}^{*}\left(t\right)=\frac{d}{dt}\left\{{D_1}^{*}\left(t\right)\right\}=\frac{{\mathrm{\Gamma }}_1{{\mathbf{\phi }}_{\mathbf{1}}}^{\mathbf{T}}\mathbf{\text{Mv}}\left(t\right)}{{M_1}^{*}},(6)$

${A_{r1}}^{*}\left(t\right)=\frac{d}{dt}\left\{{V_1}^{*}\left(t\right)\right\}=\frac{{\mathrm{\Gamma }}_1{{\mathbf{\phi }}_{\mathbf{1}}}^{\mathbf{T}}\mathbf{\text{Ma}}\left(t\right)}{{M_1}^{*}},(7)$

${M_1}^{*}={{\mathrm{\Gamma }}_1}^2{{\mathbf{\phi }}_{\mathbf{1}}}^{\mathbf{T}}\mathbf{M}{\mathbf{\phi }}_{\mathbf{1}},(8)$

where ${M_1}^{*}$ is the effective first modal mass. Note that ${\mathrm{\Gamma }}_1{\mathbf{\phi }}_{\mathbf{1}}$ and ${M_1}^{*}$ depend on the local maximum equivalent displacement within the range $\left(0,t\right)$. In this study, the first mode vector at time $t$ is updated assuming that ${\mathrm{\Gamma }}_1{\mathbf{\phi }}_{\mathbf{1}}$ is proportional to the displacement vector at the time when the maximum equivalent displacement occurs ($t_{\max }$). The first mode vector at time $t$ is updated via Eq. 9:

${\mathrm{\Gamma }}_1{\mathbf{\phi }}_{\mathbf{1}}\leftarrow \frac{1}{{D_1}^{*}\left(t_{\max }\right)}\mathbf{d}\left(t_{\max }\right).(9)$

The equivalent acceleration ${A_1}^{*}\left(t\right)$ is defined as in Eq. 10:

${A_1}^{*}\left(t\right)=\frac{{\mathrm{\Gamma }}_1{{\mathbf{\phi }}_{\mathbf{1}}}^{\mathbf{T}}{\mathbf{f}}_{\mathbf{R}}\left(t\right)}{{M_1}^{*}}.(10)$

Note that the relative equivalent acceleration ${A_{r1}}^{*}\left(t\right)$ and the equivalent acceleration ${A_1}^{*}\left(t\right)$ is different. The relative equivalent acceleration (${A_{r1}}^{*}\left(t\right)$) is the second differentiation of the equivalent displacement (${D_1}^{*}\left(t\right)$), which is used in the critical PMI analysis for determining the timing of the action of the pseudo impulsive lateral force. While the equivalent acceleration (${A_1}^{*}\left(t\right)$) is the equivalent restoring force of the first modal response per unit mass, which is used for the capacity diagram of an equivalent SDOF model in acceleration–displacement (AD) format in well-known N2 method (Fajfar, 2000).

Details of the critical PMI analysis is shown in the in the Supplementary Appendix S1 of this article.

The peak equivalent displacement of the first modal response over the course of the entire seismic event (${{D_1}^{*}}_{\max }$) is obtained using Eq. 11:

${{D_1}^{*}}_{\max }=\max \left(\left|{}_1{{D_1}^{*}}_{peak}\right|,\left|{}_2{{D_1}^{*}}_{peak}\right|,\cdots ,\left|{}_{N_p}{{D_1}^{*}}_{peak}\right|\right).(11)$

In Eq. 11, ${}_k{{D_1}^{*}}_{peak}$ is the $k$-th local peak of ${D_1}^{*}\left(t\right)$ shown in Figure 1. The maximum momentary input energy of the first modal response per unit mass ($\Delta {{E_1}^{*}}_{\max }/{M_1}^{*}$) is obtained via Eq. 12:

$\frac{\Delta {{E_1}^{*}}_{\max }}{{M_1}^{*}}=\max \left\{{}_1\left(\frac{\Delta {E_1}^{*}}{{M_1}^{*}}\right),{}_2\left(\frac{\Delta {E_1}^{*}}{{M_1}^{*}}\right),\cdots ,{}_{N_p}\left(\frac{\Delta {E_1}^{*}}{{M_1}^{*}}\right)\right\}.(12)$

In Eq. 12, ${}_k\left(\Delta {E_1}^{*}/{M_1}^{*}\right)$ is the input energy increment of the first modal response per unit mass at time $t={}_k{t}_p$. The cumulative input energy of the first modal response per unit mass (${E_{I1}}^{*}/{M_1}^{*}$) is calculated using Eq. 13:

$\frac{{E_{I1}}^{*}}{{M_1}^{*}}={\displaystyle \sum _{k=1}^{N_p}}{}_k\left(\frac{\Delta {E_1}^{*}}{{M_1}^{*}}\right).(13)$

The equivalent velocity of the maximum momentary input energy of the first modal response (${V_{\Delta E1}}^{*}$) is calculated using Eq. 14:

${V_{\Delta E1}}^{*}=\sqrt{2\Delta {{E_1}^{*}}_{\max }/{M_1}^{*}}.(14)$

In addition, the equivalent velocity of the cumulative input energy of the first modal response (${V_{I1}}^{*}$) is calculated using Eq. 15:

${V_{I1}}^{*}=\sqrt{2{E_{I1}}^{*}/{M_1}^{*}}.(15)$

2.2 Calculation of the seismic capacity curve from the incremental critical pseudo-multi impulse analysis (ICPMIA) results

Incremental critical pseudo-multi impulse analysis (ICPMIA) is a parametric analysis method used to evaluate the nonlinear response of a structure by performing a critical PMI analysis considering various pulse velocities ($V_p$). In the ICPMIA analysis, $V_p$ varies from small to large levels until the structural response reaches a predetermined damage level (e.g., Life Safety of Collapse Prevention). In ICPMIA, a critical PMI analysis is performed to obtain the nonlinear structural characteristics. The peak deformation, cumulative strain energy and residual deformation can be directly obtained from the ICPMIA results, as IDA. Because ICPMIA can directly include the influence of cyclic loading, the influence of the duration of ground motions can be considered in ICPMIA by adjusting the number of pulsive inputs ($N_p$). In addition, because the ground motion in ICPMIA is simplified as the critical pulses determined automatically from the structural response, the ICPMIA result is still simple to understand with respect to the nonlinear structural characteristics.

The ${V_{\Delta E1}}^{*}$ − ${{D_1}^{*}}_{\max }$ plot is obtained from the ICPMIA result. In this study, the ${V_{\Delta E1}}^{*}$ − ${{D_1}^{*}}_{\max }$ curve is referred to as the “seismic capacity curve.” Note that the peak equivalent displacement (${{D_1}^{*}}_{\max }$) may not occur at the end of the half cycle of the structural response corresponding to the maximum momentary input energy per unit mass ($\Delta {{E_1}^{*}}_{\max }/{M_1}^{*}$). However, because ${{D_1}^{*}}_{\max }$ occurs at the end of a half cycle of the structural response, corresponding to $\Delta {{E_1}^{*}}_{\max }/{M_1}^{*}$ in most cases analyzed herein, the relationship between the as-obtained ${V_{\Delta E1}}^{*}$ and the as-obtained ${{D_1}^{*}}_{\max }$ is simply plotted in this study.

3 Analysis data and methods

3.1 Building data

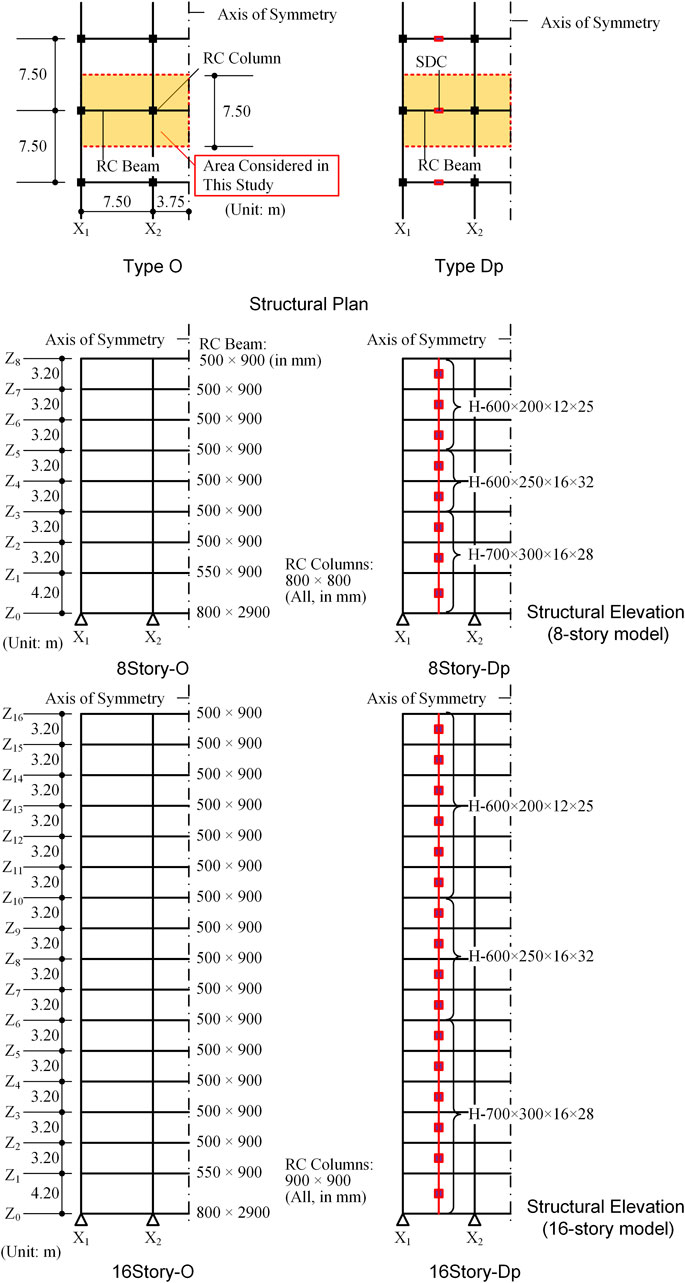
The four planar building models analyzed in this study are 8- and 16-story RC MRFs with and without SDCs. Figure 2 shows the simplified plan and elevation of the RC MRF building models. The two models labeled Type Dp (8Story-Dp and 16Story-Dp) are the same as those used in Fujii and Shioda (2023). The two models made from Type Dp by removing all SDCs are referred to as Type O (8Story-O and 16Story-O). All RC MRFs analyzed herein were designed according to the strong-column/weak-beam concept, except at the foundation level beam and in the case of steel damper columns installed in an RC frame. In the latter case, at the joints between an RC beam and a steel damper column, the RC beam was designed to be sufficiently stronger than the yield strength of the steel damper column considering strain hardening. Sufficient shear reinforcement of all RC members was provided to prevent premature shear failure. The failure of beam–column joints is not considered because it is assumed that sufficient reinforcement is provided. The natural periods of the first modal response in the elastic range ($T_{1e}$) of the 8-story models are 0.740 s and 0.561 s for Types O and Dp, respectively. Similarly, the $T_{1e}$ values of the 16-story models are 1.41 s and 1.12 s for Types O and Dp, respectively.

Figure 2

Figure 2. Simplified structural plan and elevation of RC MRF building model.

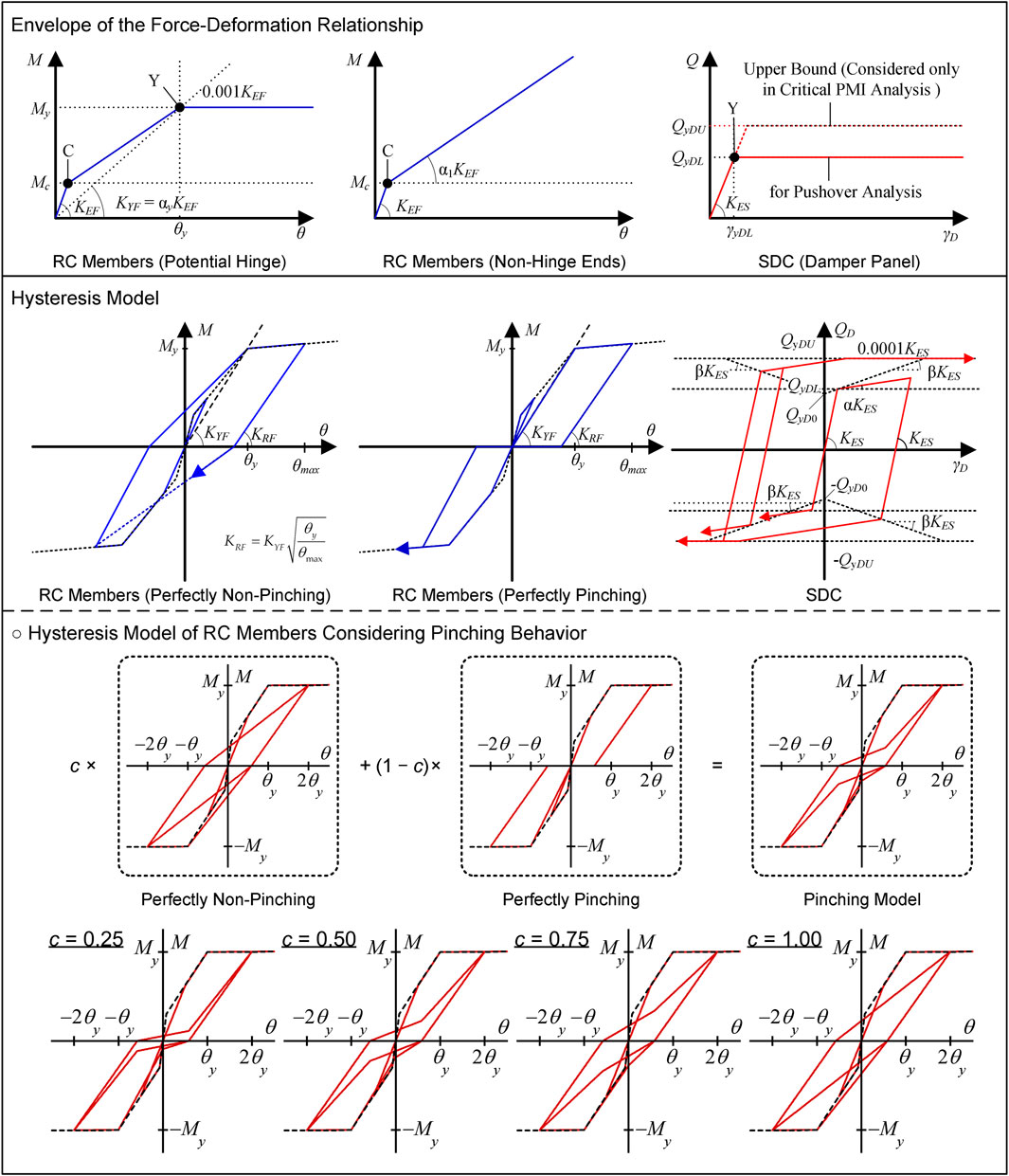
The nonlinear behavior of the RC members and SDCs is modeled as in previous studies (Mukoyama et al., 2021; Fujii, 2022; Fujii and Shioda, 2023), except the hysteresis rule used for the RC members. Figure 3 shows the nonlinear force–deformation relationship. In this study, the pinching behavior of the RC members is considered. The pinching model is assumed to be a linear combination of perfectly non-pinching and perfectly pinching models. The perfectly non-pinching model is identical to the stiffness degradation model used for RC members in previous studies (Mukoyama et al., 2021; Fujii, 2022; Fujii and Shioda, 2023). Meanwhile, the perfectly pinching model is a model that has no energy hysteresis energy dissipation in symmetric loading. A parameter $c$ (0 ≤ $c$ ≤ 1) is introduced to control the pinching behavior. When $c$ is 0, its behavior is that of a perfectly pinching model; when $c$ is 1, its behavior is that of a perfectly non-pinching model. In this study, four different pinching behaviors are considered: the parameter $c$ was set to 0.25, 0.50, 0.75, and 1.00, as shown in the bottom of Figure 3. For the damper panel in the SDCs, the same hysteresis model (trilinear model) is used. Other details concerning the four structural models can be found in previous studies (Fujii, 2022; Fujii and Shioda, 2023). In this study, the viscous damping ratio of the first modal response of the RC MRFs in the elastic range ($h_{1f}$) was set to 0.03.

Figure 3

Figure 3. Nonlinear force-deformation relationship of members.

3.2 Analysis method

In this study, the pulse velocity ($V_p$) was set from 0.10 m/s, with an interval of 0.05 m/s, until ${{D_1}^{*}}_{\max }$ was close to the target value: it is assumed as 1/75 of the assumed equivalent height (${H_1}^{*}$): in Fujii and Shioda (2023), the two models (8Story-Dp and 16Story-Dp) were designed so that the peak equivalent displacement ${{D_1}^{*}}_{\max }$ is close to $\left(1/75\right){H_1}^{*}$ when the design ground motion spectrum is taken from the Building Standard Law of Japan with consideration of the type-2 soil condition. Therefore, the target ${{D_1}^{*}}_{\max }$ was set to 0.252 m for the 8-story models, while for the 16-story models the target ${{D_1}^{*}}_{\max }$ was set to 0.479 m. The total number of pseudo impulsive lateral forces ($N_p$) was set to 4, 6, and 8. A critical PDI analysis ($N_p$ = 2) of each model was performed for the comparisons. In each analysis, the ending time of the analysis ($t_{end}$) was determined as the ending of the 32nd half cycle of free vibration after the action of the second pseudo impulsive lateral force.

The range of $V_p$ depends on the models and $N_p$. For 8story-O and $c$ = 0.25 (significant pinching), the range of $V_p$ is from 0.10 m/s to 0.55 m/s in case of $N_p$ = 2, while the range of $V_p$ is from 0.10 m/s to 0.25 m/s in case of $N_p$ = 8. In addition, for 8story-Dp and $c$ = 0.25 (significant pinching), the range of $V_p$ is from 0.10 m/s to 0.80 m/s in case of $N_p$ = 2, while the range of $V_p$ is from 0.10 m/s to 0.65 m/s in case of $N_p$ = 8. In Kojima and Takewaki (2015a), the double impulse input is introduced as a substitute of the fling-step near-fault ground motions. While in Kojima and Takewaki (2015c), the multi impulse input is introduced as a substitute of the long-duration ground motion which may cause the resonant. In this study, the author chose the range of $N_p$ as two to 8, as a substitute of ground motions with various durations. However, at the moment, it is difficult to relate the duration of recorded ground motions and $N_p$. This issue of out of the scope of this study.

4 Analysis results

This section describes the responses of the RC MRFs obtained from the critical PDI and PMI analysis results, focusing in particular on (i) the pulse velocity ($V_p$)–peak equivalent displacement (${{D_1}^{*}}_{\max }$) relationship, (ii) the hysteresis loop and residual displacement of the first modal response, and (iii) the cumulative strain energies of the RC MRFs and SDCs.

4.1 Peak response

Figure 4 compares the relationship between the pulse velocity ($V_p$) and the peak equivalent displacement (${{D_1}^{*}}_{\max }$). The following conclusions can be drawn.

• The peak equivalent displacement (${{D_1}^{*}}_{\max }$) increases as the pulse velocity ($V_p$) increases. For the same value of $V_p$, the ${{D_1}^{*}}_{\max }$ obtained by PDI is smaller than that obtained by PMI ($N_p$ = 4, 6, and 8).

• For Type O, the increase in ${{D_1}^{*}}_{\max }$ because of the increase in $N_p$ is significant. This trend is more pronounced when the pinching behavior of the RC members is significant. Comparing ${{D_1}^{*}}_{\max }$ of 8story-O with $V_p$ = 0.25 m/s and $c$ = 0.25 (significant pinching), ${{D_1}^{*}}_{\max }$ is 0.082 m when $N_p$ = 2 (PDI) and 0.247 m when $N_p$ = 8. Similar observations can be made for 16story-O.

• For Type Dp, however, the increase in ${{D_1}^{*}}_{\max }$ as a result of the increase in $N_p$ is less significant than for Type O. Comparing ${{D_1}^{*}}_{\max }$ of 8story-Dp, considering $V_p$ = 0.65 m/s and $c$ = 0.25 (significant pinching), ${{D_1}^{*}}_{\max }$ is 0.196 m when $N_p$ = 2 (PDI) and 0.258 m when $N_p$ = 8. Similar observations can be made for 16story-Dp.

Figure 4

Figure 4. Relationship between pulse velocity (V_p) and peak equivalent displacement (D₁^*_max).

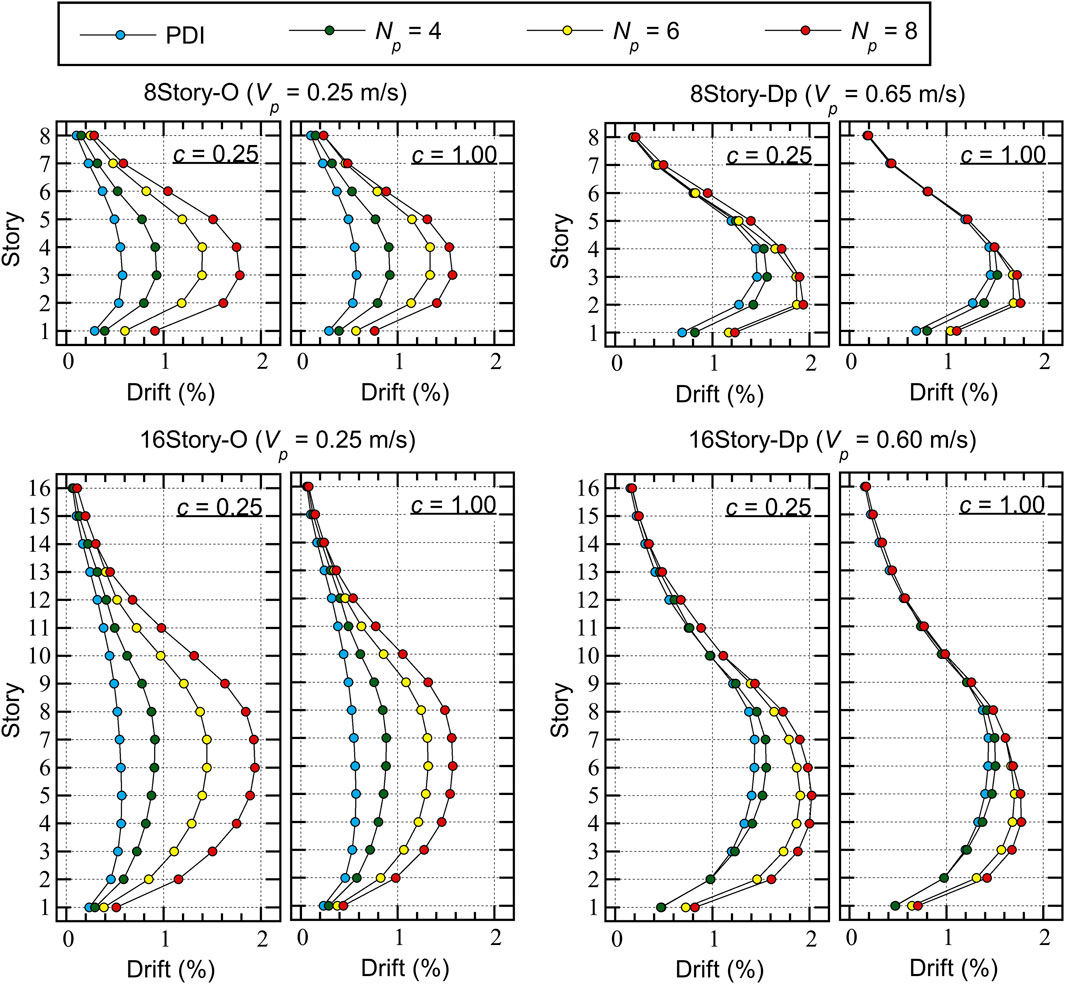
Figure 5 compares the peak story drift. Here, the cases $c$ = 0.25 (significant pinching) and $c$ = 1.00 (perfectly non-pinching) are selected.

Figure 5

Figure 5. Comparisons of the peak story drift.

The following conclusions can be drawn from Figure 5.

• For Type O, the increase in the peak story resulting from the increase in $N_p$ is significant, as observed in the trend of ${{D_1}^{*}}_{\max }$. This trend is more pronounced when the pinching behavior of the RC members is significant. Comparing the largest peak story drift of 8story-O, considering $V_p$ = 0.25 m/s and $c$ = 0.25 (significant pinching), the largest peak story drift is 0.577% (third story) when $N_p$ = 2 (PDI) and 1.78% (third story) when $N_p$ = 8. Meanwhile, considering $V_p$ = 0.25 m/s and $c$ = 1.00 (perfectly non-pinching), the largest peak story drift is 0.577% (third story) when $N_p$ = 2 (PDI) and 1.57% (third story) when $N_p$ = 8.

• For Type Dp, however, the increase in the peak story drift as a result of the increase in $N_p$ is less significant than for Type O. Comparing the largest peak story drift of 8story-Dp, considering $V_p$ = 0.65 m/s and $c$ = 0.25 (significant pinching), the largest peak story drift is 1.46% (third story) when $N_p$ = 2 (PDI) and 1.94% (second story) when $N_p$ = 8. Meanwhile, considering $V_p$ = 0.65 m/s and $c$ = 1.00 (perfectly non-pinching), the largest peak story drift is 1.46% (third story) when $N_p$ = 2 (PDI) and 1.77% (second story) when $N_p$ = 8. Similar observations can be made for 16story-Dp.

4.2 Hysteresis loop and residual displacement

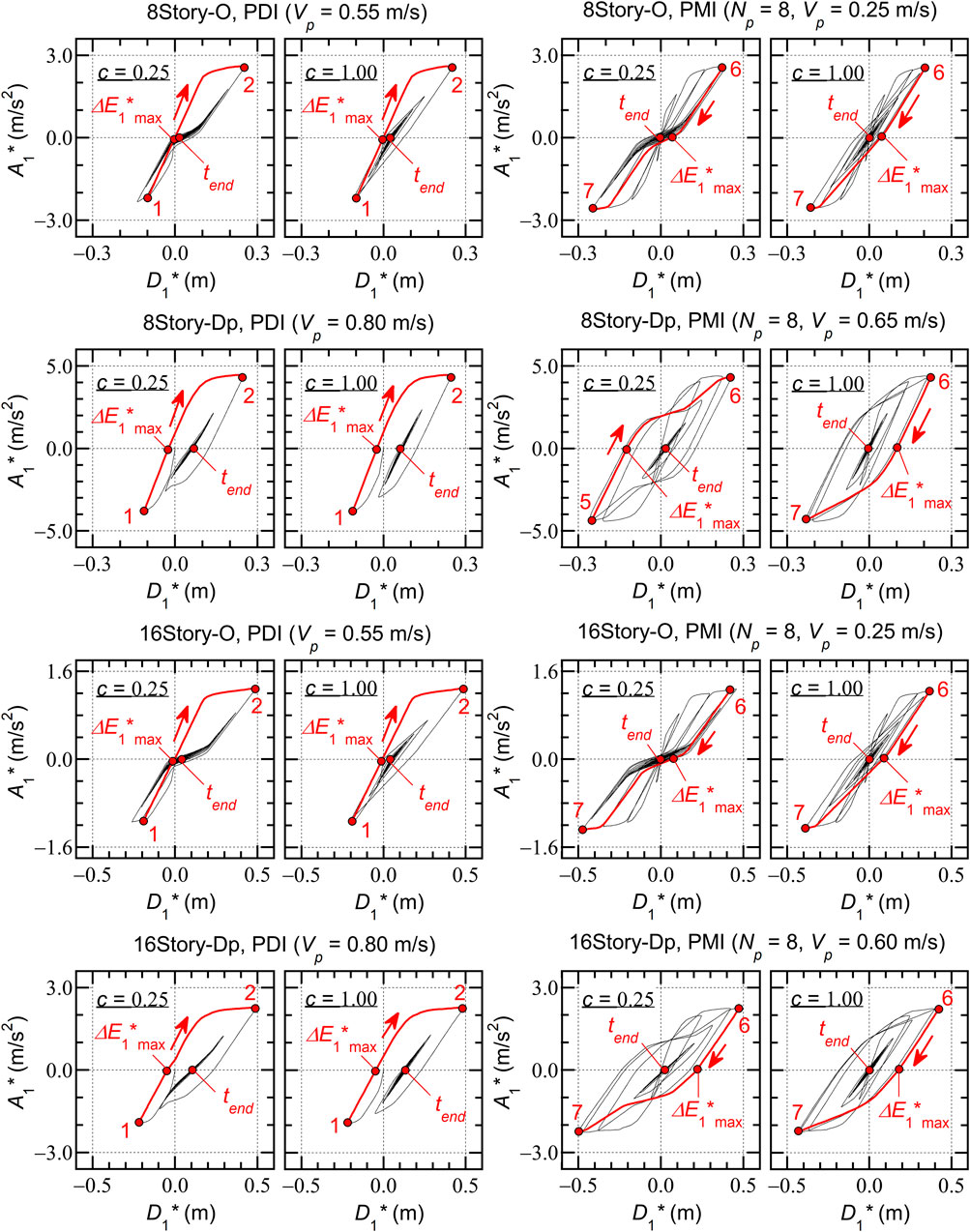
Figure 6 shows the hysteresis loops of the first modal response (${A_1}^{*}\left(t\right)$ − ${D_1}^{*}\left(t\right)$ relationship) for each model. The hysteresis loops obtained from the critical PDI analysis ($N_p$ = 2) and critical PMI analysis ($N_p$ = 8) are shown in this figure; the hysteresis loops for $c$ = 0.25 (significant pinching) and $c$ = 1.00 (perfectly non-pinching) are compared. In Figure 6, the beginning and ending points of the half cycle of the structural response when the maximum momentary input energy per unit mass ($\Delta {{E_1}^{*}}_{\max }/{M_1}^{*}$) occurs is shown by the red curve. The numbers in the figure indicate the number of the local peak. The points at which the pseudo impulsive lateral force acts ($\Delta {{E_1}^{*}}_{\max }$) and the point at the end of the simulation ($t_{end}$) are also shown.

Figure 6

Figure 6. Hysteresis loop and residual displacement.

The following conclusions can be drawn from Figure 6.

• In the critical PDI analysis results ($N_p$ = 2), the difference in the half cycle of the structural response resulting from the pinching behavior is negligibly small. The displacement response is larger in positive directions than in negative directions. A notable residual equivalent displacement at $t$ = $t_{end}$ is observed, especially for Type Dp.

• In the critical PMI analysis results ($N_p$ = 8), the difference in the half cycle of the structural response resulting from the pinching behavior is noticeable. In the case of $c$ = 0.25 (significant pinching), the pinching behavior in the half cycle of the structural response is clearly observed for both Types O and Dp. The displacement response is almost symmetric in the positive and negative directions. The residual equivalent displacement is negligibly small for both Types O and Dp.

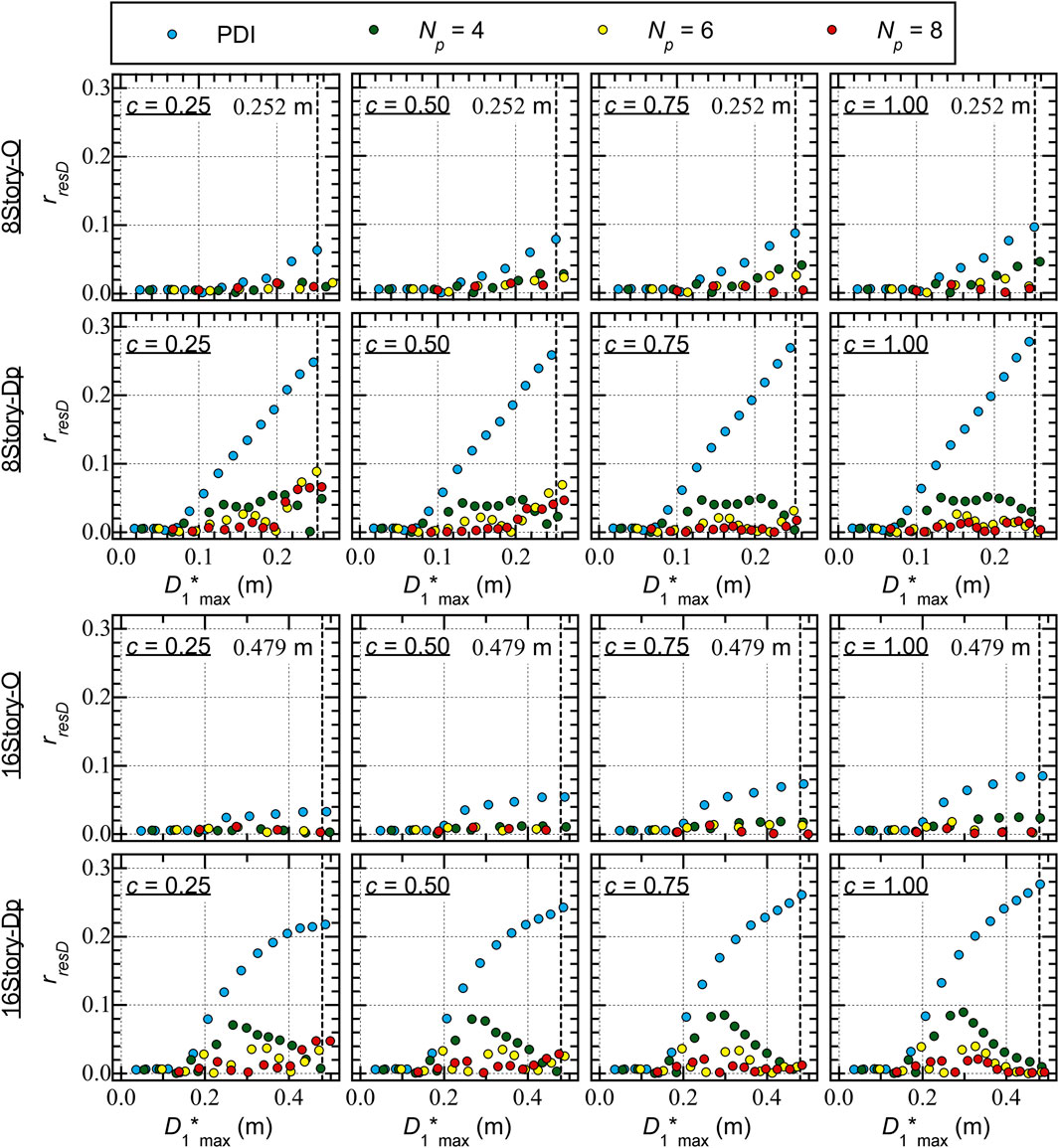
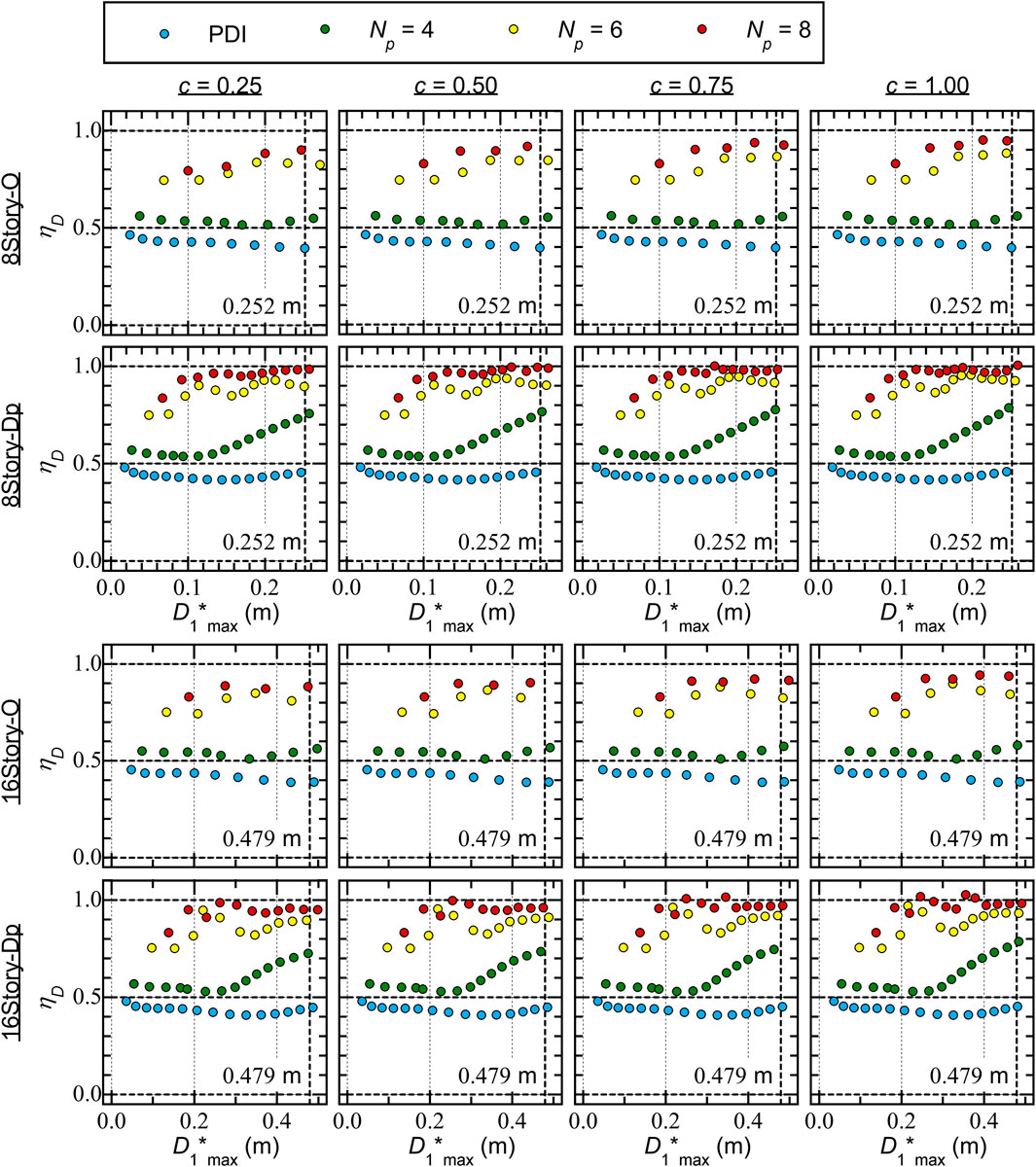
Figure 7 shows the residual equivalent displacement ratio ($r_{resD}$). Here, the $r_{resD}$ ratio is defined as shown in Eq. 16:

$r_{resD}=\left|{D_1}^{*}\left(t_{end}\right)/{{D_1}^{*}}_{\max }\right|.(16)$

Figure 7

Figure 7. Residual equivalent displacement ratio.

The following conclusions can be drawn from Figure 7.

• For Type O, $r_{resD}$ is smaller than 0.1. The $r_{resD}$ ratio is largest in the critical PDI analysis ($N_p$ = 2), and $r_{resD}$ increases as ${{D_1}^{*}}_{\max }$ increases. However in the critical PMI analysis, $r_{resD}$ is small and no regular trend is observed between $r_{resD}$ and ${{D_1}^{*}}_{\max }$: the $r_{resD}$ ratio may decrease when ${{D_1}^{*}}_{\max }$ increases.

• For Type Dp, the $r_{resD}$ ratio increases as ${{D_1}^{*}}_{\max }$ increases in the critical PDI analysis ($N_p$ = 2) and the $r_{resD}$ ratio may be larger than 0.2. The $r_{resD}$ ratio is larger when the parameter $c$ is larger (pinching behavior is not significant). However, in the critical PMI analysis, the $r_{resD}$ ratio is smaller than 0.1. In addition, no regular trend is observed between $r_{resD}$ and ${{D_1}^{*}}_{\max }$: the $r_{resD}$ ratio may decrease when ${{D_1}^{*}}_{\max }$ increases.

4.3 Cumulative strain energy

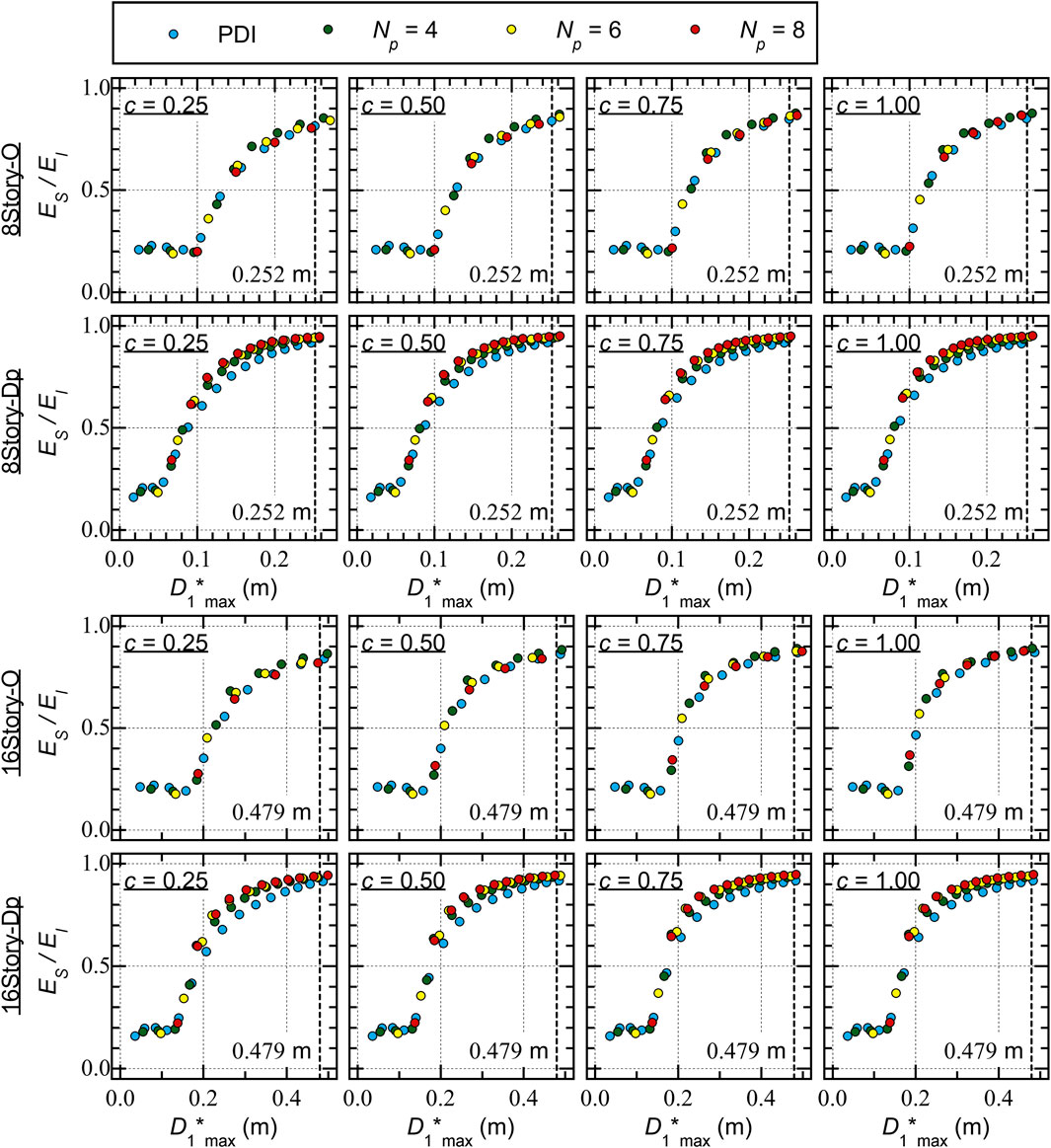
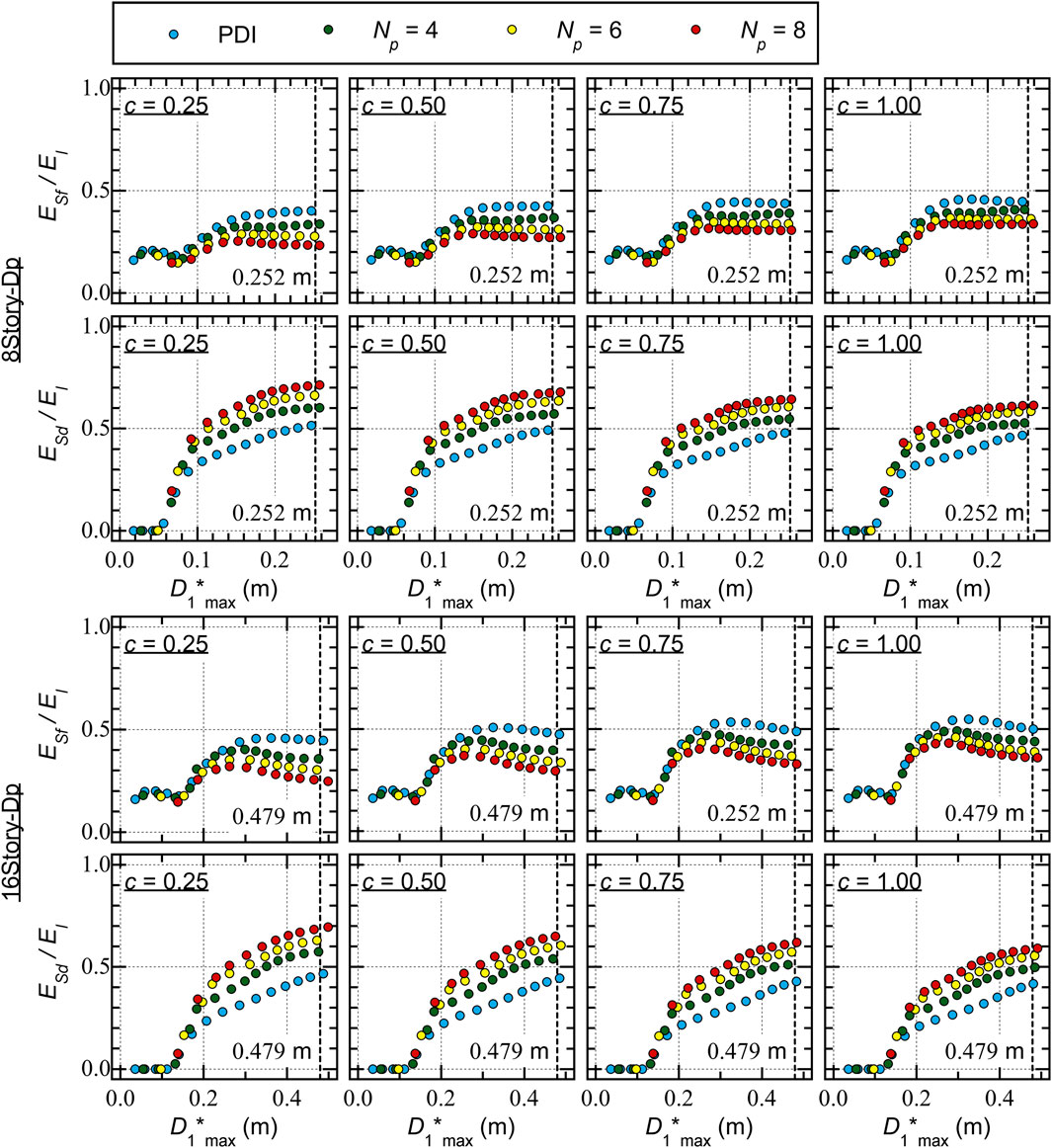
Figure 8 compares the ratios of the cumulative strain energy of the entire frame model ($E_S/E_I$) at the end of the simulation.

Figure 8

Figure 8. Ratio of the cumulative strain energy at the end of the simulation.

For Type O, the following conclusions can be drawn from Figure 8.

• For 8story-O, the $E_S/E_I$ ratio is close to 0.2 when ${{D_1}^{*}}_{\max }$ is less than 0.1 m. The $E_S/E_I$ ratio increases as ${{D_1}^{*}}_{\max }$ increases when ${{D_1}^{*}}_{\max }$ is larger than 0.1 m. When ${{D_1}^{*}}_{\max }$ is close to 0.25 m, $E_S/E_I$ is between 0.8 and 0.9.

• For 16story-O, the $E_S/E_I$ ratio increases as ${{D_1}^{*}}_{\max }$ increases when ${{D_1}^{*}}_{\max }$ is larger than 0.2 m. When ${{D_1}^{*}}_{\max }$ is larger than 0.4 m, $E_S/E_I$ is between 0.8 and 0.9.

• The difference in the $E_S/E_I$ ratio resulting from the difference in $N_p$ is negligible.

In addition, the following conclusions can be drawn from Figure 8 for Type Dp.

• The $E_S/E_I$ ratio increases rapidly as ${{D_1}^{*}}_{\max }$ increases. For 8story-Dp, the $E_S/E_I$ ratio reaches 0.9 when ${{D_1}^{*}}_{\max }$ is larger than 0.2 m. Meanwhile, for 16story-Dp, the $E_S/E_I$ ratio reaches 0.9 when ${{D_1}^{*}}_{\max }$ is larger than 0.4 m.

• In the PMI analysis results ($N_p$ ≥ 4), the $E_S/E_I$ ratio is larger than that obtained from the PDI analysis results ($N_p$ = 2).

Next, the discussion focuses on the cumulative strain energy ratio of the RC MRF ($E_{Sf}/E_I$) and the cumulative strain energy ratio of the SDCs ($E_{Sd}/E_I$) for Type Dp models. Figure 9 compares the ratios $E_{Sf}/E_I$ and $E_{Sd}/E_I$.

Figure 9

Figure 9. Ratio of the cumulative strain energy of RC MRF and SDCs at the end of the simulation.

For 8story-Dp, the following conclusions can be drawn from Figure 9.

• The $E_{Sf}/E_I$ ratio is close to 0.2 when ${{D_1}^{*}}_{\max }$ is less than 0.1 m. When ${{D_1}^{*}}_{\max }$ is larger than 0.1 m, $E_{Sf}/E_I$ increases as ${{D_1}^{*}}_{\max }$ increases. However, $E_{Sf}/E_I$ decreases as $N_p$ increases. This trend is pronounced when the parameter $c$ is small (the pinching behavior is significant).

• The $E_{Sd}/E_I$ ratio is negligibly small when ${{D_1}^{*}}_{\max }$ is less than 0.06 m. The $E_{Sd}/E_I$ ratio increases rapidly as ${{D_1}^{*}}_{\max }$ increases. The $E_{Sd}/E_I$ ratio increases as $N_p$ increases. This trend is pronounced when the parameter $c$ is small.

In addition, the following conclusions can be drawn from Figure 9 for 16story-Dp.

• The $E_{Sf}/E_I$ ratio is close to 0.2 when ${{D_1}^{*}}_{\max }$ is less than 0.15 m. When ${{D_1}^{*}}_{\max }$ is larger than 0.15 m, $E_{Sf}/E_I$ increases as ${{D_1}^{*}}_{\max }$ increases. However, $E_{Sf}/E_I$ decreases as $N_p$ increases. Considering $c$ = 0.25, the $E_{Sf}/E_I$ ratio is 0.447 when ${{D_1}^{*}}_{\max }$ is 0.487 m in the PDI analysis results ($N_p$ = 2). Conversely, the $E_{Sf}/E_I$ ratio is 0.248 when ${{D_1}^{*}}_{\max }$ is 0.498 m in the PMI analysis results ($N_p$ = 8).

• The $E_{Sd}/E_I$ ratio is negligibly small when ${{D_1}^{*}}_{\max }$ is less than 0.1 m. The $E_{Sd}/E_I$ ratio increases rapidly as ${{D_1}^{*}}_{\max }$ increases. The $E_{Sd}/E_I$ ratio increases as $N_p$ increases. Considering $c$ = 0.25, the $E_{Sd}/E_I$ ratio is 0.466 when ${{D_1}^{*}}_{\max }$ is 0.487 m in the PDI analysis results ($N_p$ = 2). Conversely, the $E_{Sd}/E_I$ ratio is 0.695 when ${{D_1}^{*}}_{\max }$ is 0.498 m in the PMI analysis results ($N_p$ = 8).

It should be emphasized that the increase of the $E_{Sd}/E_I$ ratio is not only the positive aspect. In general, the increase of the $E_{Sd}/E_I$ ratio may be considered as the superior performance of dampers as the reduction of cumulative strain energy of RC MRF. However, for SDC itself, the increase of cumulative strain energy demand would be critical. Therefore, the conclusions shown above should be considered as the alert that the cumulative strain energy demand of SDCs may increase when the pinching behavior of RC members is significant.

4.4 Summary of the analysis results

This section summarizes the responses of the RC MRF models with and without SDCs as obtained from the critical PMI analysis results.

A) The influence of the number of pseudo impulsive lateral forces ($N_p$) on the $V_p$–${{D_1}^{*}}_{\max }$ relationship is significant in the case of RC MRFs without SDCs (Type O). For the same value of $V_p$, the ${{D_1}^{*}}_{\max }$ increases as $N_p$ increases. This trend is pronounced when the pinching behavior is significant. In cases of RC MRFs with SDCs (Type Dp), ${{D_1}^{*}}_{\max }$ increases as $N_p$ increases; however, this trend is less pronounced than that observed in the RC MRFs without SDCs. The influence of the pinching behavior of the RC MRFs on the $V_p$–${{D_1}^{*}}_{\max }$ relationship in the RC MRFs with SDCs is smaller than that in the RC MRFs without SDCs.

B) In the PMI analysis results ($N_p$ ≥ 4), the difference in the half cycle of the structural response resulting from the pinching behavior is more pronounced than that in the PDI analysis results ($N_p$ = 2). Therefore, the influence of the pinching behavior of the RC members on the peak equivalent displacement (${{D_1}^{*}}_{\max }$) is more notable in PMI than in PDI.

C) The residual displacement obtained from the PMI analysis results is smaller than that obtained from the PDI analysis results ($N_p$ = 2). This difference is significant in the case of RC MRFs with SDCs.

D) The ratio of the cumulative strain energy of the entire frame model ($E_S/E_I$) at the end of the simulation is nearly independent of the number of pseudo impulsive lateral forces ($N_p$), regardless of the presence or absence of SDCs. Meanwhile, the ratio of the cumulative strain energy of the RC MRFs ($E_{Sf}/E_I$) decreases and that of the SDCs ($E_{Sd}/E_I$) increases as $N_p$ increases in the RC MRFs with SDCs (Type Dp). This trend is pronounced when the pinching behavior of the RC members is significant.

5 Prediction of the maximum momentary input energy of RC MRFs

This section focuses on comparisons with the predicted results based on the study of Fujii and Shioda (2023) and the ICPMIA results. First, simplified equations for calculating the energy dissipation capacity during a half cycle of the structural response are formulated. Next, the seismic capacity curve (the ${V_{\Delta E1}}^{*}$ − ${{D_1}^{*}}_{\max }$ curve) is predicted using the pushover analysis results. Then, the predicted seismic capacity curve is compared with the ${V_{\Delta E1}}^{*}$ − ${{D_1}^{*}}_{\max }$ plot obtained from the ICPMIA results.

5.1 Prediction of the seismic capacity curve based on the pushover analysis

First, a pushover analysis of the $N$-story MRF model is performed. Then, the equivalent displacement at loading step $n$ (${}_n{D_1}^{*}$) and the equivalent acceleration at step $n$ (${}_n{A_1}^{*}$) are calculated as in Eqs 17, 18, assuming that the displacement vector at the loading step $n$ (${}_{\mathbf{n}}\mathbf{d}$) is proportional to the first mode vector at step $n$ (${}_n{\mathrm{\Gamma }}_1{}_{\mathbf{n}}{\mathbf{\phi }}_{\mathbf{1}}$):

${}_n{D_1}^{*}=\frac{{}_n{\mathrm{\Gamma }}_1{}_{\mathbf{n}}{{\mathbf{\phi }}_{\mathbf{1}}}^{\mathbf{T}}\mathbf{M}{}_{\mathbf{n}}\mathbf{d}}{{}_n{M_1}^{*}}=\frac{{}_{\mathbf{n}}{\mathbf{d}}^{\mathbf{T}}\mathbf{M}{}_{\mathbf{n}}\mathbf{d}}{{}_{\mathbf{n}}{\mathbf{d}}^{\mathbf{T}}\mathbf{M}\mathbf{1}},(17)$

${}_n{A_1}^{*}=\frac{{}_n{\mathrm{\Gamma }}_1{}_{\mathbf{n}}{{\mathbf{\phi }}_{\mathbf{1}}}^{\mathbf{T}}\mathbf{M}{}_{\mathbf{n}}{\mathbf{f}}_{\mathbf{R}}}{{}_n{M_1}^{*}}=\frac{{}_{\mathbf{n}}{\mathbf{d}}^{\mathbf{T}}{}_{\mathbf{n}}{\mathbf{f}}_{\mathbf{R}}}{{}_{\mathbf{n}}{\mathbf{d}}^{\mathbf{T}}\mathbf{M}\mathbf{1}}.(18)$

In Eqs 17, 18, $\mathbf{1}$ is the vector defined as Eq. 19:

$\mathbf{1}={\left\{\begin{array}{ccc}1& \cdots & 1\end{array}\right\}}^{\mathbf{T}}.(19)$

In Eq. 18, ${}_{\mathbf{n}}{\mathbf{f}}_{\mathbf{R}}$ denotes the restoring force of the entire MRF model. The contributions of the equivalent accelerations of the RC MRFs and SDCs (${}_n{A_{1f}}^{*}$ and ${}_n{A_{1d}}^{*}$, respectively) are calculated using Eqs 20, 21:

${}_n{A_{1f}}^{*}=\frac{{}_n{\mathrm{\Gamma }}_1{}_{\mathbf{n}}{{\mathbf{\phi }}_{\mathbf{1}}}^{\mathbf{T}}\mathbf{M}{}_{\mathbf{n}}{\mathbf{f}}_{\mathbf{\text{Rf}}}}{{}_n{M_1}^{*}}=\frac{{}_{\mathbf{n}}{\mathbf{d}}^{\mathbf{T}}{}_{\mathbf{n}}{\mathbf{f}}_{\mathbf{\text{Rf}}}}{{}_{\mathbf{n}}{\mathbf{d}}^{\mathbf{T}}\mathbf{M}\mathbf{1}},(20)$

${}_n{A_{1d}}^{*}=\frac{{}_n{\mathrm{\Gamma }}_1{}_{\mathbf{n}}{{\mathbf{\phi }}_{\mathbf{1}}}^{\mathbf{T}}\mathbf{M}{}_{\mathbf{n}}{\mathbf{f}}_{\mathbf{\text{Rd}}}}{{}_n{M_1}^{*}}=\frac{{}_{\mathbf{n}}{\mathbf{d}}^{\mathbf{T}}{}_{\mathbf{n}}{\mathbf{f}}_{\mathbf{\text{Rd}}}}{{}_{\mathbf{n}}{\mathbf{d}}^{\mathbf{T}}\mathbf{M}\mathbf{1}}.(21)$

Here, ${}_{\mathbf{n}}{\mathbf{f}}_{\mathbf{\text{Rf}}}$ and ${}_{\mathbf{n}}{\mathbf{f}}_{\mathbf{\text{Rd}}}$ denote the restoring forces of the RC MRFs and SDCs, respectively. The restoring force vector ${}_{\mathbf{n}}{\mathbf{f}}_{\mathbf{R}}$ is equal to the sum of ${}_{\mathbf{n}}{\mathbf{f}}_{\mathbf{\text{Rf}}}$ and ${}_{\mathbf{n}}{\mathbf{f}}_{\mathbf{\text{Rd}}}$, which are calculated from the shear forces of the RC columns and SDCs, respectively. Then, the ${}_n{A_{1f}}^{*}$ − ${D_1}^{*}$ and ${}_n{A_{1d}}^{*}$ − ${D_1}^{*}$ relationships are idealized by bilinear curves. Here, the ${A_{1f}}^{*}$ − ${D_1}^{*}$ and ${A_{1d}}^{*}$ − ${D_1}^{*}$ relationships are idealized by bilinear curves, where the “yield” point of the idealized ${A_{1f}}^{*}$ − ${D_1}^{*}$ relationship is Y_F(${D_{1yf}}^{*}$; ${A_{1yf}}^{*}$) and that of the idealized ${A_{1d}}^{*}$ − ${D_1}^{*}$ relationship is Y_D (${D_{1yd}}^{*}$; ${A_{1yd}}^{*}$).

Then, the energy dissipation capacity during a half cycle of the structural response of the equivalent SDOF model (${}_n\Delta {{E_1}^{*}}_{\max }/{}_n{M_1}^{*}$) is calculated using Eq. 22:

$\frac{{}_n\Delta {{E_1}^{*}}_{\max }}{{}_n{M_1}^{*}}=\frac{{}_n\Delta {E_{\mu 1f}}^{*}}{{}_n{M_1}^{*}}+\frac{{}_n\Delta {E_{\mu 1d}}^{*}}{{}_n{M_1}^{*}}+\frac{{}_n\Delta {E_{D1}}^{*}}{{}_n{M_1}^{*}}.(22)$

The contributions of the hysteretic dissipated energy of the RC MRFs and SDCs are calculated using Eqs 23, 24:

$\frac{{}_n\Delta {E_{\mu 1f}}^{*}}{{}_n{M_1}^{*}}={A_{1yf}}^{*}{D_{1yf}}^{*}\stackrel{\sim }{f_F}\left({}_n{\mu }_f\right),(23)$

$\frac{{}_n\Delta {E_{\mu 1d}}^{*}}{{}_n{M_1}^{*}}={A_{1yd}}^{*}{D_{1yd}}^{*}\stackrel{\sim }{f_D}\left({}_n{\mu }_d\right).(24)$

In Eqs 23, 24, the functions $\stackrel{\sim }{f_F}\left({}_n{\mu }_f\right)$ and $\stackrel{\sim }{f_D}\left({}_n{\mu }_d\right)$ are calculated as

$\stackrel{\sim }{f_F}\left({\mu }_f\right)=\left\{\begin{array}{ll}\frac{1}{3}{{\mu }_f}^2& 0\le {\mu }_f\le 1\\ \frac{1}{2}\left(1+c\right){\mu }_f-\frac{2}{3}c\sqrt{{\mu }_f}-\frac{1}{6{\mu }_f}\left(1-c\right)& {\mu }_f\ge 1\end{array}\right.,(25)$

$\stackrel{\sim }{f_D}\left({\mu }_d\right)=\left\{\begin{array}{cc}\frac{1}{3}{{\mu }_d}^2& 0\le {\mu }_d\le 1\\ \frac{1}{6}\left(9{\mu }_d-12+\frac{5}{{\mu }_d}\right)& {\mu }_d\ge 1\end{array}\right..(26)$

The values of ${}_n{\mu }_f$ and ${}_n{\mu }_d$ are calculated via Eq. 27:

${}_n{\mu }_f={}_n{D_1}^{*}/{D_{1yf}}^{*},{}_n{\mu }_d={}_n{D_1}^{*}/{D_{1yd}}^{*}.(27)$

The derivations of Eqs 25, 26 can be found in Supplementary Appendix S2 of this article.

The contributions of the viscous damping are calculated such that

$\frac{{}_n\Delta {E_{D1}}^{*}}{{}_n{M_1}^{*}}=\frac{7\pi h_{1f}}{12}\frac{{}_n{\omega }_{1f}}{{}_1{\omega }_{1f}}{}_n{A_{1f}}^{*}{}_n{D_1}^{*},(28)$

${}_n{\omega }_{1f}=\sqrt{{}_n{A_{1f}}^{*}/{}_n{D_1}^{*}}.(29)$

In Eq. 28, $h_{1f}$ is the viscous damping ratio of the RC MRFs for the first modal response in the elastic range, while ${}_n{\omega }_{1f}$ defined in Eq. 29 is the secant circular frequency of the first mode of the RC MRFs.

The equivalent velocity of the energy dissipation capacity during a half cycle of the structural response of the equivalent SDOF model corresponding to ${}_n{D_1}^{*}$ (${}_n{V_{\Delta E1}}^{*}$) is calculated via Eq. 30:

${}_n{V_{\Delta E1}}^{*}=\sqrt{2{}_n\Delta {{E_1}^{*}}_{\max }/{}_n{M_1}^{*}}.(30)$

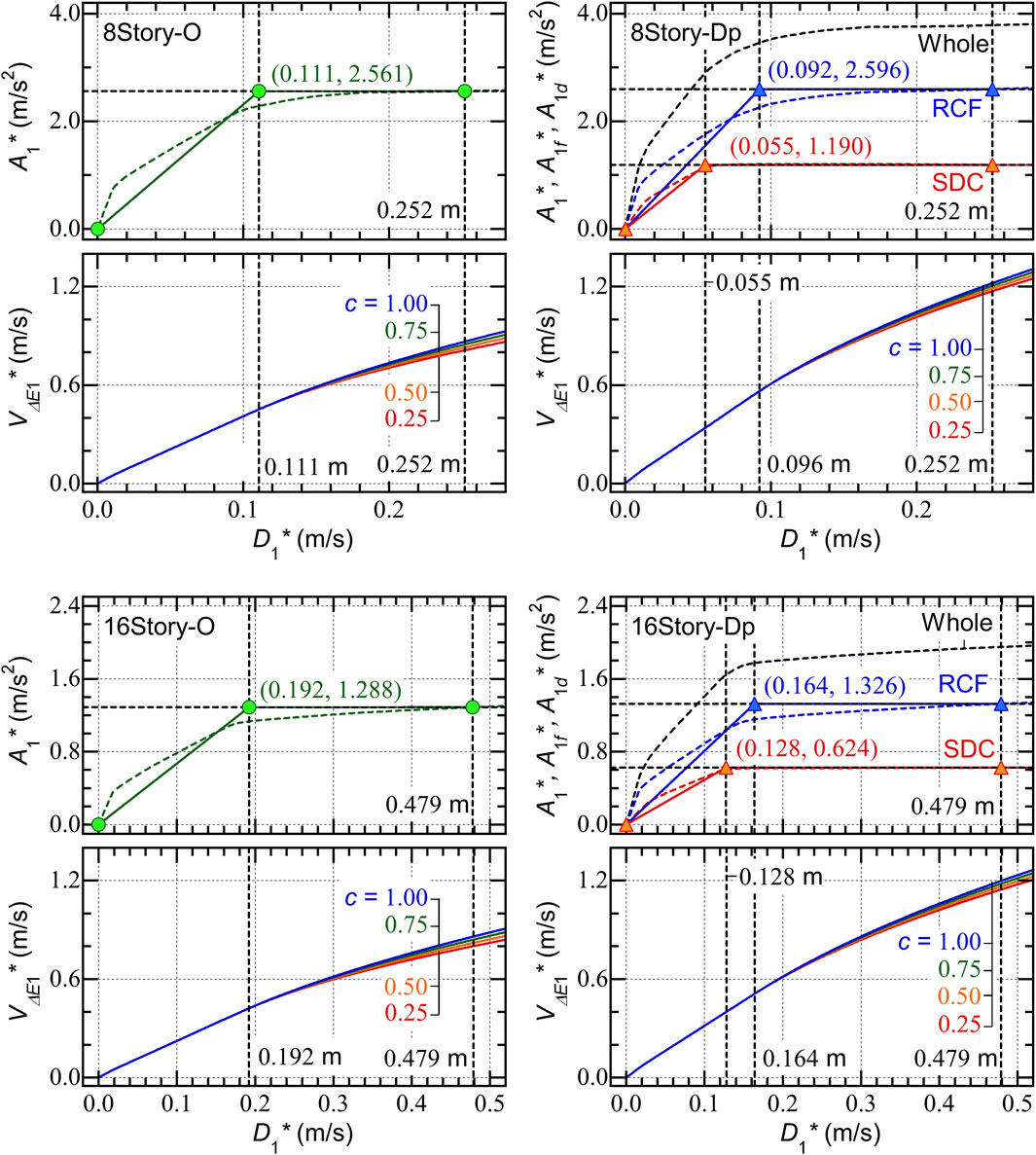
Figure 10 shows the calculated seismic capacity curves (the ${}_n{V_{\Delta E1}}^{*}$ − ${}_n{D_1}^{*}$ relationships) of the four models calculated from the pushover analysis results. The calculated curves for $c$ = 0.25, 0.50, 0.75, and 1.00 are compared in the figure. As shown here, the differences in the calculated curves resulting from the parameter $c$ are limited.

Figure 10

Figure 10. Capacity curves of MRF models calculated from the pushover analysis results.

5.2 Comparisons with ICPMIA results

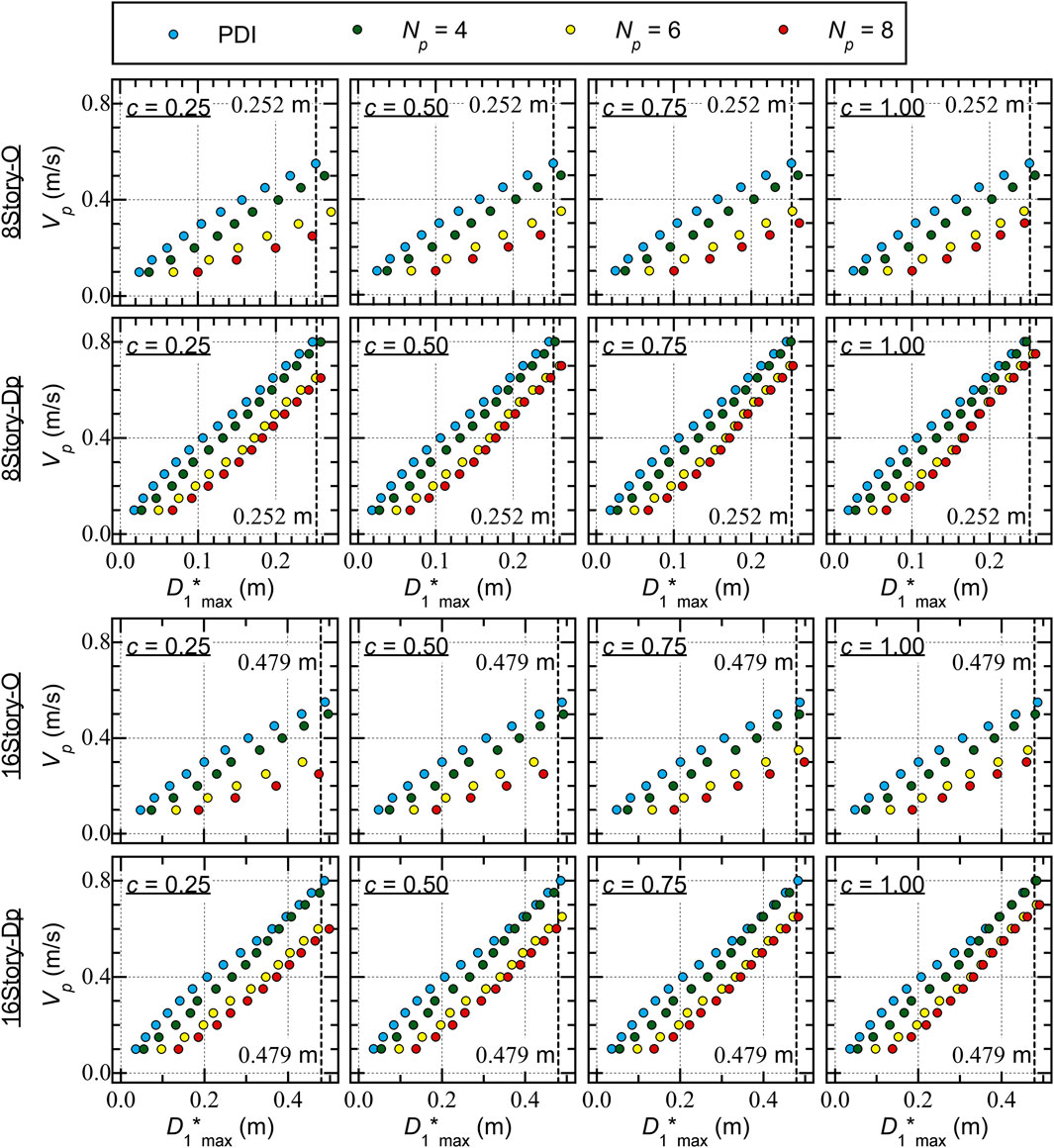
Figure 11 shows comparisons between the predicted seismic capacity curves and the ICPMIA analysis results. The following conclusions can be drawn.

• For Type O, the plots obtained from the PDI and PMI analysis ($N_p$ = 4) results are above the predicted seismic capacity curve. However, the plots obtained from the PMI analysis ($N_p$ = 6 and 8) results are below the predicted curve. Specifically, for 8story-O, with $c$ = 0.25 (significant pinching) and $N_p$ = 8, the ${V_{\Delta E1}}^{*}$ value corresponding to ${{D_1}^{*}}_{\max }$ = 0.247 m is 0.616 m/s, while the predicted ${}_n{V_{\Delta E1}}^{*}$ value corresponding to ${}_n{D_1}^{*}$ = 0.247 m is 0.802 m/s; this is a 23.1% underestimation of ${V_{\Delta E1}}^{*}$.

• For Type Dp, the plots obtained from the PDI and PMI analysis ($N_p$ = 4) results agree very well with the predicted seismic capacity curve. In addition, the plots obtained from the PMI analysis ($N_p$ = 6 and 8) results are slightly below the predicted curve. The dependence of the Type Dp ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots on $N_p$ is limited.

Figure 11

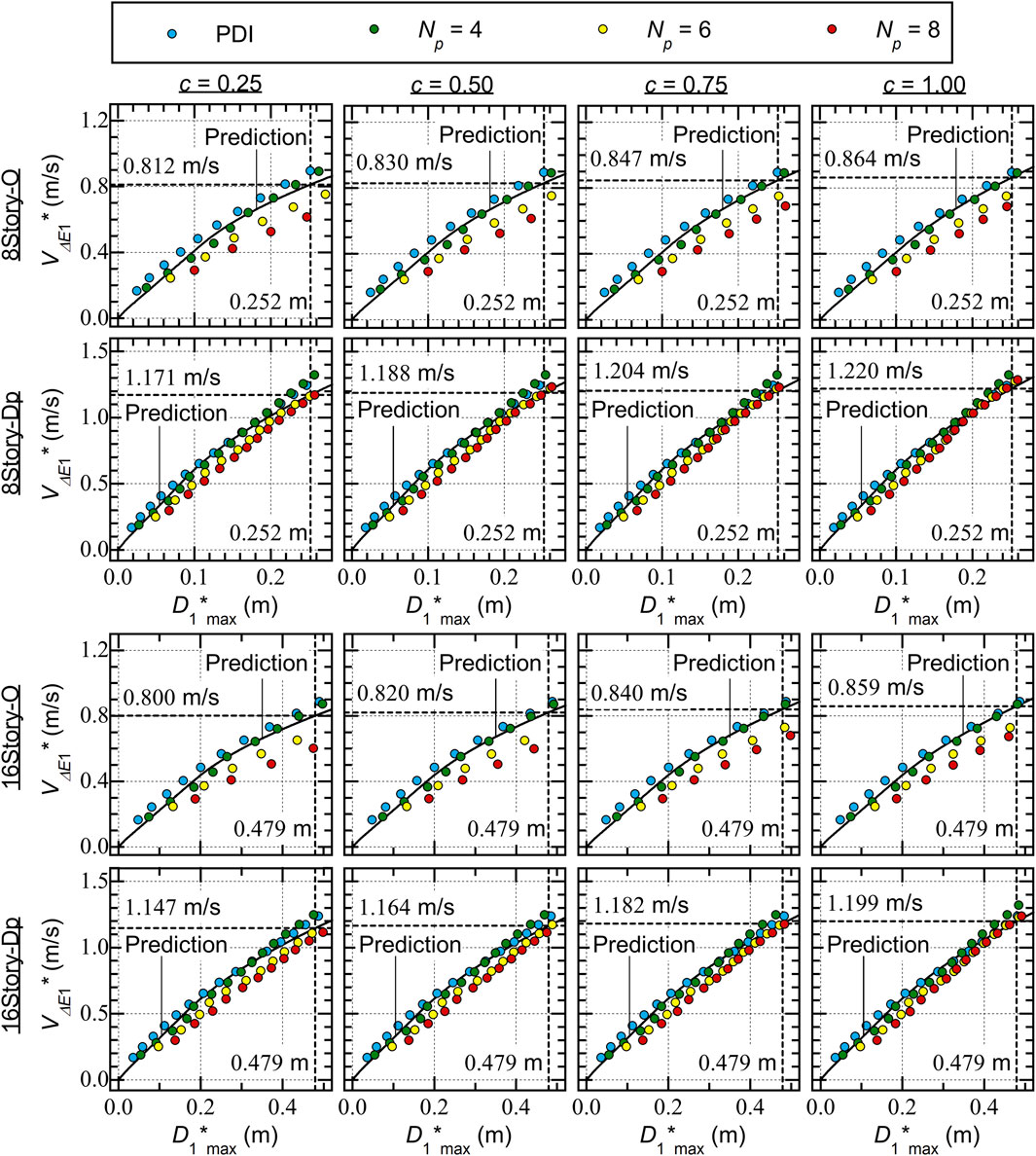
Figure 11. Comparisons with the predicted capacity curves and the V_ΔE1^*-D₁^*_max relationship obtained from ICPMIA results.

The results shown in Figure 11 indicate that the accuracy of the predicted capacity curve is acceptable for Type Dp, while the predicted capacity curve is unacceptably underestimated for Type O for larger $N_p$. The equation for calculating the energy dissipation capacity during a half cycle of the structural response (Eqs. 25 and (26)) is simplified by calculating the average in the range of $0\le {\eta }_D\le 1$ (detailed explanation of these two equations can be found in Supplementary Appendix S2). Accordingly, the following discussion focuses on the ${\eta }_D$ ratio. First, Figure 12 shows the ${\eta }_D$ ratio obtained from the PDI and PMI analysis results. Here, ${\eta }_D$ is calculated using Eq. 31:

${\eta }_D=\left|{}_{k-1}{{D_1}^{*}}_{peak}/{}_k{{D_1}^{*}}_{peak}\right|,(31)$

where $k$ is the counting number when the maximum momentary energy input occurs. The following conclusions can be drawn from Figure 12.

• For Type O, the ${\eta }_D$ ratio is between 0.4 and 0.5 in the PDI analysis results. Similarly, in the PMI analysis ($N_p$ = 4) results, ${\eta }_D$ is between 0.5 and 0.6. Meanwhile, in the PMI analysis ($N_p$ = 6 and 8) results, ${\eta }_D$ increases as ${{D_1}^{*}}_{\max }$ increases: ${\eta }_D$ is between 0.7 and 0.9 when $N_p$ is 6, while ${\eta }_D$ is larger than 0.8 when $N_p$ is 8.

• For Type Dp, the ${\eta }_D$ ratio is between 0.4 and 0.5 in the PDI analysis results. However, in the PMI analysis ($N_p$ = 4) results, ${\eta }_D$ increases as ${{D_1}^{*}}_{\max }$ increases. For 8story-Dp, ${\eta }_D$ is close to 0.5 when ${{D_1}^{*}}_{\max }$ is close to 0.1 m and ${\eta }_D$ reaches 0.7 when ${{D_1}^{*}}_{\max }$ is close to 0.25 m. In the PMI analysis ($N_p$ = 6 and 8) results, ${\eta }_D$ is larger than 0.7 and increases as ${{D_1}^{*}}_{\max }$ increases; then, ${\eta }_D$ approaches 1.

Figure 12

Figure 12. Ratio of the displacements in the positive and negative directions (η_D).

The results shown in Figure 12 indicate that the ${\eta }_D$ ratio increases as $N_p$ increases for both Types O and Dp.

Next, the relationship between the energy dissipation capacity during a half cycle of the structural response and ${\eta }_D$ is investigated. Here, ${{D_1}^{*}}_{\max }$ is assumed to be 1/75 of the assumed equivalent height (${H_1}^{*}$): ${{D_1}^{*}}_{\max }$ is set to 0.252 m for the 8-story models and to 0.479 m for the 16-story models. The contributions from the hysteretic dissipated energies of the RC MRFs and SDCs ($\Delta {E_{\mu 1f}}^{*}/{M_1}^{*}$ and $\Delta {E_{\mu 1d}}^{*}/{M_1}^{*}$, respectively) can be expressed as shown in Eqs 32, 33:

$\frac{\Delta {E_{\mu 1f}}^{*}}{{M_1}^{*}}\left({\mu }_f,{\eta }_D\right)={A_{1yf}}^{*}{D_{1yf}}^{*}{f}_F\left({\mu }_f,{\eta }_D\right),(32)$

$\frac{\Delta {E_{\mu 1d}}^{*}}{{M_1}^{*}}\left({\mu }_d,{\eta }_D\right)={A_{1yd}}^{*}{D_{1yd}}^{*}{f}_D\left({\mu }_d,{\eta }_D\right).(33)$

In Eqs 32, 33, the functions $f_F\left({\mu }_f,{\eta }_D\right)$ and $f_D\left({\mu }_d,{\eta }_D\right)$ are calculated via Eqs 34, 35.

$f_F\left({\mu }_f,\eta \right)=\left\{\begin{array}{ll}\frac{1}{2}{{\mu }_f}^2\left(1-{{\eta }_D}^2\right)& 0\le {\mu }_f\le 1\\ {\mu }_f-\frac{1}{2}\left\{1+{\left({\eta }_D{\mu }_f\right)}^2\right\}& {\mu }_f\ge 1\text{ and }0\le {\eta }_D\le \frac{1}{{\mu }_f}\\ {\mu }_f\left(1-{\eta }_D\right)+c\left({\eta }_D{\mu }_f-\sqrt{{\eta }_D{\mu }_f}\right)& {\mu }_f\ge 1\text{ and }\frac{1}{{\mu }_f}\le {\eta }_D\le 1\end{array}\right.,(34)$

$f_D\left({\mu }_d,{\eta }_D\right)=\left\{\begin{array}{cc}\frac{1}{2}{{\mu }_d}^2\left(1-{{\eta }_D}^2\right)& 0\le {\mu }_d\le 1\\ {\mu }_d-\frac{1}{2}\left\{1+{\left({\eta }_D{\mu }_d\right)}^2\right\}& {\mu }_d\ge 1\text{ and }0\le {\eta }_D\le \frac{1}{{\mu }_d}\\ \left(1+{\eta }_D\right){\mu }_d-2& {\mu }_d\ge 1\text{ and }\frac{1}{{\mu }_d}\le {\eta }_D\le 1\end{array}\right..(35)$

In addition, the contribution from the viscous damping ($\Delta {E_{D1}}^{*}/{M_1}^{*}$) can be expressed as

$\frac{\Delta {E_{D1}}^{*}}{{M_1}^{*}}\left({{D_1}^{*}}_{\max },{\eta }_D\right)=\frac{\pi {\left(1+{\eta }_D\right)}^2}{4}\frac{{\omega }_{1f\max }}{{}_1{\omega }_{1f}}{h}_{1f}{{A_{1f}}^{*}}_{\max }{{D_1}^{*}}_{\max }.(36)$

In Eq. 36, ${\omega }_{1f\max }$, the secant circular frequency of the first mode of the RC MRFs, corresponds to ${{D_1}^{*}}_{\max }$ and is calculated from Eq. 29.

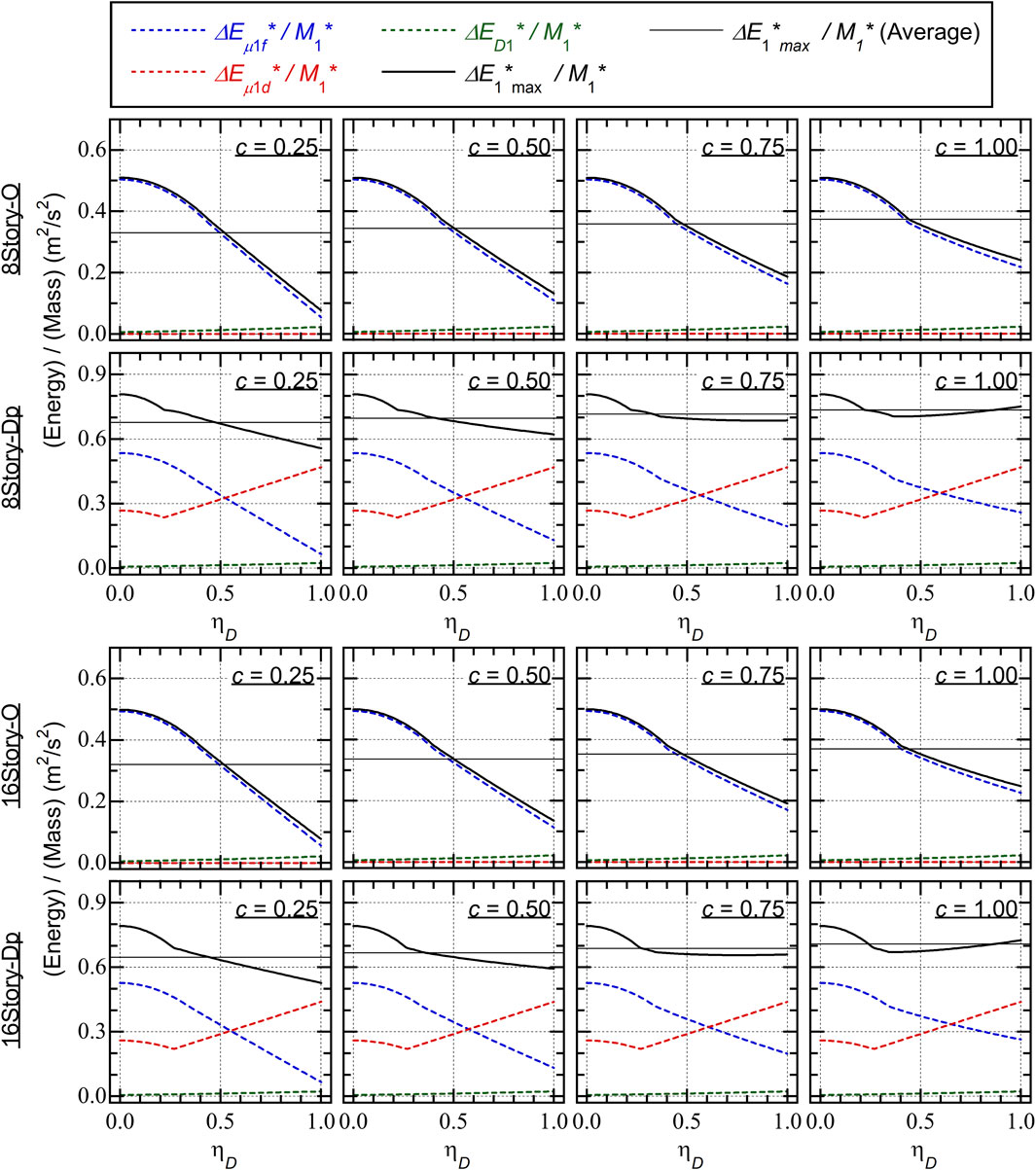
Figure 13 shows the relationships between the energy dissipation capacity calculated from Eqs 32–36 and the ${\eta }_D$ ratio. The following conclusions can be drawn for Type O from Figure 13.

• The contribution from the hysteretic dissipated energy of the RC MRFs ($\Delta {E_{\mu 1f}}^{*}/{M_1}^{*}$) decreases rapidly as ${\eta }_D$ increases. Conversely, the contribution from the viscous damping ($\Delta {E_{D1}}^{*}/{M_1}^{*}$) increases as ${\eta }_D$ increases. However, because $\Delta {E_{D1}}^{*}/{M_1}^{*}$ is much smaller than $\Delta {E_{\mu 1f}}^{*}/{M_1}^{*}$, the calculated $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ decreases rapidly as ${\eta }_D$ increases: $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ is largest when ${\eta }_D$ is zero and smallest when ${\eta }_D$ is unity.

• The variation in the calculated $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ as a result of the ${\eta }_D$ ratio is predominant when the parameter $c$ is 0.25 (significant pinching). For 8story-O and $c$ = 0.25, the calculated $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ corresponding to ${\eta }_D$ = 0 is 0.509 m²/s², while the calculated $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ corresponding to ${\eta }_D$ = 1 is 0.077 m²/s² (only 15.2% of the value when ${\eta }_D$ = 0). Meanwhile, for 8story-O and $c$ = 1.00 (perfectly non-pinching), the calculated $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ corresponding to ${\eta }_D$ = 0 is 0.509 m²/s² (the same value as for $c$ = 0.25) and the calculated $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ corresponding to ${\eta }_D$ = 1 is 0.241 m²/s² (47.3% of the value when ${\eta }_D$ = 0).

Figure 13

Figure 13. Relations between the calculated dissipated energy per unit mass and η_D.

The following conclusions can be drawn for Type Dp from Figure 13.

• The contribution from the hysteretic dissipated energy of the SDCs ($\Delta {E_{\mu 1d}}^{*}/{M_1}^{*}$) increases as ${\eta }_D$ increases. Therefore, the variation in the calculated $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ of Type Dp resulting from the ${\eta }_D$ ratio is less significant than that of Type O.

• The variation in the calculated $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ of Type Dp resulting from the ${\eta }_D$ ratio is much less significant than that of Type O, even for $c$ = 0.25 (significant pinching). For 8story-Dp and $c$ = 0.25, the calculated $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ corresponding to ${\eta }_D$ = 0 is 0.808 m²/s², while the calculated $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ corresponding to ${\eta }_D$ = 1 is 0.557 m²/s² (68.9% of the value when ${\eta }_D$ = 0). Meanwhile, for 8story-Dp and $c$ = 1.00, the calculated $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ corresponding to ${\eta }_D$ = 0 is 0.808 m²/s² (the same value as for $c$ = 0.25) and the calculated $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ corresponding to ${\eta }_D$ = 1 is 0.751 m²/s² (92.9% of the value when ${\eta }_D$ = 0).

The results shown in Figures 12, 13 can explain why the Type O ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots are influenced significantly by $N_p$ while the dependence of the Type Dp ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots on $N_p$ is limited. As shown in Figure 12, in general, ${\eta }_D$ increases as $N_p$ increases for both Types O and Dp. In addition, $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ decreases significantly as ${\eta }_D$ increases in the case of Type O, as shown in Figure 13. Therefore, in the case of Type O, ${V_{\Delta E1}}^{*}$ decreases as $N_p$ increases because the increase in $N_p$ leads to an increase in ${\eta }_D$. Conversely, in the case of Type Dp, the variation in $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ resulting from ${\eta }_D$ is less significant, as shown in Figure 13. Therefore, in the case of Type Dp, the variation in ${V_{\Delta E1}}^{*}$ because of the increase in $N_p$ is less significant.

Note that the contribution of the hysteresis energy of the RC MRFs ($\Delta {E_{\mu 1f}}^{*}/{M_1}^{*}$) decreases drastically as ${\eta }_D$ increases, especially when the pinching behavior of the RC members is significant. Therefore, the variation in $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ of RC MRFs without SDCs because of ${\eta }_D$ becomes larger. This implies that the variation in the peak displacement (${{D_1}^{*}}_{\max }$) of RC MRFs without SDCs corresponds to the given ${V_{\Delta E1}}^{*}$ becoming larger. Conversely, the contribution of the hysteresis energy of the SDCs ($\Delta {E_{\mu 1d}}^{*}/{M_1}^{*}$) increases as ${\eta }_D$ increases. Therefore, the variation in $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ of RC MRFs resulting from ${\eta }_D$ can be reduced by installing SDCs within the MRFs. Consequently, the use of SDCs as supplemental energy dissipating devices in RC MRFs is effective in reducing: (i) the peak displacement; (ii) the cumulative strain energy of RC members; and (iii) the variation in the peak displacement.

5.3 Summary of the discussion

This section focuses on comparisons with the predicted results based on Fujii and Shioda (2023) and the ICPMIA results. Based on these comparisons, the following conclusions can be drawn.

A) In the case of RC MRFs without SDCs, the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots obtained from the PDI and PMI analysis ($N_p$ = 4) results are above the predicted seismic capacity curve. However, the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots obtained from the PMI analysis ($N_p$ = 6 and 8) results are below the predicted curve. The dependence of the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots of RC MRFs without SDCs on $N_p$ is significant.

B) In the case of RC MRFs with SDCs, the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots obtained from the PDI and PMI analysis ($N_p$ = 4) results agree very well with the predicted seismic capacity curve. In addition, the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots obtained from the PMI analysis ($N_p$ = 6 and 8) results are slightly below the predicted curve. The dependence of the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots of the RC MRFs with SDCs on $N_p$ is limited.

C) The ratio of the displacements in the positive and negative directions (${\eta }_D$) increases as $N_p$ increases. In the case of RC MRFs without SDCs, $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ decreases drastically as ${\eta }_D$ increases, especially when the pinching behavior of the RC members is significant. Meanwhile, in the case of RC MRFs with SDCs, the variation in $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ resulting from ${\eta }_D$ is less significant.

6 Conclusion

In this article, the seismic capacities of RC MRFs with and without SDCs were evaluated using incremental critical pseudo-multi impulse analysis (ICPMIA). The main results and conclusions can be summarized as follows.

(i) In the case of RC MRFs without SDCs, the influence of $N_p$ on the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ relationship is notable: ${V_{\Delta E1}}^{*}$ decreases as $N_p$ increases. Meanwhile, in the case of RC MRFs with SDCs, the influence of $N_p$ on the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ relationship is limited.

(ii) In the case of RC MRFs without SDCs, the influence of the pinching behavior of RC members on the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ relationship is notable when $N_p$ is large. Conversely, the influence of the pinching behavior of RC members on the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ relationship is limited in the case of RC MRFs with SDCs, regardless of $N_p$.

(iii) For RC MRFs with SDCs, the ratio of the cumulative strain energy of the RC MRFs ($E_{Sf}/E_I$) decreases and that of the SDCs ($E_{Sd}/E_I$) increases as $N_p$ increases. This trend is pronounced when the pinching behavior of the RC members is significant.

(iv) The residual equivalent displacement ratio ($r_{resD}$), defined as the ratio of the residual equivalent displacement to the peak equivalent displacement (${{D_1}^{*}}_{\max }$), obtained from the critical PMI analysis results is smaller than that obtained from the critical PDI analysis results. No regular trend was observed between the $r_{resD}$ ratio and ${{D_1}^{*}}_{\max }$.

Conclusion (i) supports the accuracy of the prediction procedure (Fujii and Shioda, 2023). Specifically, the predicted ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ curve is sufficiently accurate for RC MRFs with SDCs, regardless of the number of impulsive lateral forces $N_p$. For RC MRFs without SDCs, however, the predicted ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ curve may not be conservative in the case of long-duration earthquake ground motion and resonance. Conclusion (ii) indicates that the installation of SDCs within RC MRFs can effectively reduce the peak displacement, especially when long-duration earthquake ground motion is considered. This conclusion is consistent with the study by Shirai et al. (2024). Conclusion (iii) indicates that the contribution of SDCs in terms of the cumulative strain energy depends on the duration of the input ground motion. Therefore, to better predict the cumulative strain energy of RC members and SDCs, such phenomena should be properly considered. Conclusion (iv) indicates that the residual deformation obtained from the critical PDI analysis results may be the upper bound for RC MRFs with and without SDCs. It is important to consider the extension of the critical PMI analysis as a substitute for seismic sequences because, as shown by Hoveidae and Radpour (2021), the residual displacement after the first earthquake affects the peak response under the second earthquake.

As described in conclusion (ii), the pinching behavior of RC members affects notably the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ relationship of RC MRFs without SDCs when $N_p$ is large. Therefore, a question such that “how to determine the number $N_p$?” may arise. Unfortunately, to the author’s best knowledge, there is no guideline for this issue.

Another finding of interest is the dependence of the calculated energy dissipation capacity ($\Delta {E_{1\max }}^{*}/{M_1}^{*}$) on the ratio of the displacement in the positive and negative directions (${\eta }_D$). Based on the discussions in Section 5.3, if $\Delta {E_{1\max }}^{*}/{M_1}^{*}$ were constant in the range of $0\le {\eta }_D\le 1$, the variation in the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plot would be minimized. The author thinks, this information is useful to minimize the influence of duration of ground motion on the peak response of structure. Such a structural system can be constructed by considering the proper combination of RC MRFs and SDCs or by developing a new energy dissipating system with the proper $\Delta {E_{1\max }}^{*}/{M_1}^{*}$–${\eta }_D$ relationship.

Note that the results shown in this study are, so far, valid only for RC MRF models with and without SDCs. Therefore, apart from further verifications using additional building models, the following questions remain unanswered, although the list below is not comprehensive.

• How can the number of impulsive inputs $N_p$ as a substitute of recorded ground motions be determined? To the author’s best knowledge, the ratio of the equivalent velocities of the total input energy to the maximum momentary input energy ($V_I/V_{\Delta E}$) would be the best parameter for this purpose. If the number $N_p$ were chosen to obtain the $V_I/V_{\Delta E}$ ratio of the considered ground motion, the response obtained from the critical PMI analysis results could represent the peak and cumulative response of the structure subjected to the considered ground motion.

• Can the prediction procedure (Fujii and Shioda, 2023) properly predict the cumulative strain energies of RC MRFs and SDCs obtained by the critical PMI analysis results? As far as the peak response is concerned, the prediction procedure has been validated. However, the prediction procedure has not been validated for the cumulative response. In such a validation, the pinching behavior of the RC members and the number of impulsive inputs $N_p$ would be key parameters.

• Can the ICPMIA be extended for the case of seismic sequences? To the author’s best knowledge, the NTHA is the only method that analyzes the responses of structures subjected to seismic sequences. However, the results obtained from NTHA are too complex to derive general conclusions. This is because the NTHA results are intricately intertwined with the nonlinear structural characteristics and the ground motion characteristics. In the case of a seismic sequence, the complexity increases because of the mainshock-aftershock (or foreshock-mainshock) combined ground motions. The nonlinear characteristics of the damaged structure would likely be easier to understand using ICPMIA.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

KF: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Software, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study received financial support from JSPS KAKENHI Grant Number JP23K04106.

Acknowledgments

We thank Martha Evonuk, PhD, from Edanz (https://jp.edanz.com/ac), for editing a draft of this manuscript.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2024.1431000/full#supplementary-material

Abbreviations

ICPMIA = incremental critical pseudo-multi impulse analysis. MDOF = multi-degree-of-freedom. MRF = moment-resisting frame. NTHA = nonlinear time-history analysis. PDI = pseudo-double impulse. PMI = pseudo-multi impulse. RC = reinforced concrete. SDC = steel damper column. SDOF = single-degree-of-freedom.

References

Akehashi, H., and Takewaki, I. (2021). Pseudo-double impulse for simulating critical response of elastic-plastic MDOF model under near-fault earthquake ground motion. Soil Dyn. Earthq. Eng. 150, 106887. doi:10.1016/j.soildyn.2021.106887

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2022). Pseudo-multi impulse for simulating critical response of elastic-plastic high-rise buildings under long-duration, long-period ground motion. Struct. Des. Tall Special Build. 31 (14), e1969. doi:10.1002/tal.1969

CrossRef Full Text | Google Scholar

Akiyama, H. (1985). Earthquake resistant limit-state design for buildings. Tokyo: University of Tokyo Press.

Google Scholar

Akiyama, H. (1999). Earthquake-resistant design method for buildings based on energy balance. Tokyo: Gihodo Shuppan.

Google Scholar

Benavent-Climent, A. (2011). An energy-based method for seismic retrofit of existing frames using hysteretic dampers. Soil Dyn. Earthq. Eng. 31, 1385–1396. doi:10.1016/j.soildyn.2011.05.015

CrossRef Full Text | Google Scholar

Benavent-Climent, A., Cahís, X., and Vico, J. M. (2010). Interior wide beam-column connections in existing RC frames subjected to lateral earthquake loading. Bull. Earthq. Eng. 8, 401–420. doi:10.1007/s10518-009-9144-3

CrossRef Full Text | Google Scholar

Benavent-Climent, A., Cahís, X., and Zahran, R. (2009). Exterior wide beam-column connections in existing RC frames subjected to lateral earthquake loads. Eng. Struct. 31, 1414–1424. doi:10.1016/j.engstruct.2009.02.008

CrossRef Full Text | Google Scholar

A. Benavent-Climent, and F. Mollaioli (2021). Energy-based seismic engineering, proceedings of IWEBSE 2021 (Cham, Switzerland: Springer Nature).

Google Scholar

Benavent-Climent, A., and Mota-Páez, S. (2017). Earthquake retrofitting of R/C frames with soft first story using hysteretic dampers: energy-based design method and evaluation. Eng. Struct. 137, 19–32. doi:10.1016/j.engstruct.2017.01.053

CrossRef Full Text | Google Scholar

Benavent-Climent, A., Oliver-Saiz, E., and Donaire-Ávila, J. (2024). Seismic retrofitting of RC frames combining metallic dampers and limited strengthening with FRP/SRP applying energy-based methods. Soil Dyn. Earthq. Eng. 177, 108432. doi:10.1016/j.soildyn.2023.108432

CrossRef Full Text | Google Scholar

Dolšek, M., and Fajfar, P. (2004). “IN2 – a simple alternative for IDA,” in Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, Canada, August, 2004.

Google Scholar

Fajfar, P. (2000). A nonlinear analysis method for performance-based seismic design. Earthq. Spectra 16 (3), 573–592. doi:10.1193/1.1586128

CrossRef Full Text | Google Scholar

Farrow, K. T., and Kurama, Y. C. (2003). SDOF demand index relationships for performance-based seismic design. Earthq. Spectra 19 (4), 799–838. doi:10.1193/1.1622955

CrossRef Full Text | Google Scholar

Fujii, K. (2022). Peak and cumulative response of reinforced concrete frames with steel damper columns under seismic sequences. Buildings 12, 275. doi:10.3390/buildings12030275

CrossRef Full Text | Google Scholar

Fujii, K. (2023). Energy-based response prediction of reinforced concrete buildings with steel damper columns under pulse-like ground motions. Front. Built Environ. 9, 1219740. doi:10.3389/fbuil.2023.1219740

CrossRef Full Text | Google Scholar

Fujii, K. (2024). Critical pseudo-double impulse analysis evaluating seismic energy input to reinforced concrete buildings with steel damper columns. Front. Built Environ. 10, 1369589. doi:10.3389/fbuil.2024.1369589

CrossRef Full Text | Google Scholar

Fujii, K., and Kato, M. (2021). Strength balance of steel damper columns and surrounding beams in reinforced concrete frames. Earthquake Resistant Engineering Structures XIII. WIT Trans. Built Environ. 202, PII25–36. doi:10.2495/ERES210031

CrossRef Full Text | Google Scholar

Fujii, K., and Miyagawa, K. (2018). “Nonlinear seismic response of a seven-story steel reinforced concrete condominium retrofitted with low-yield-strength-steel damper columns,” in Proceedings of the 16th European Conference on Earthquake Engineering (Thessaloniki), Greece, June, 2018.

Google Scholar

Fujii, K., and Shioda, M. (2023). Energy-based prediction of the peak and cumulative response of a reinforced concrete building with steel damper columns. Buildings 13, 401. doi:10.3390/buildings13020401

CrossRef Full Text | Google Scholar

Fujii, K., Sugiyama, H., and Miyagawa, K. (2019). Predicting the peak seismic response of a retrofitted nine-storey steel reinforced concrete building with steel damper columns. Earthquake Resistant Engineering Structures XII. WIT Trans. Built Environ. 185, PII75–85. doi:10.2495/ERES190061

CrossRef Full Text | Google Scholar

Gentry, T. R., and Wight, J. K. (1994). Wide beam-column connections under earthquake-type loading. Earthq. Spectra 10 (4), 675–703. doi:10.1193/1.1585793

CrossRef Full Text | Google Scholar

Hori, N., and Inoue, N. (2002). Damaging properties of ground motions and prediction of maximum response of structures based on momentary energy response. Earthq. Eng. Struct. Dyn. 31, 1657–1679. doi:10.1002/eqe.183

CrossRef Full Text | Google Scholar

Hori, N., Iwasaki, T., and Inoue, N. (2000). “Damaging properties of ground motions and response behavior of structures based on momentary energy response,” in Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, January, 2000.

Google Scholar

Hoveidae, N., and Radpour, S. (2021). Performance evaluation of buckling-restrained braced frames under repeated earthquakes. Bull. Earthq. Eng. 19, 241–262. doi:10.1007/s10518-020-00983-0

CrossRef Full Text | Google Scholar

Inoue, N., Wenliuhan, H., Kanno, H., Hori, N., and Ogawa, J. (2000). “Shaking table tests of reinforced concrete columns subjected to simulated input motions with different time durations,” in Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 4 February 2000.

Google Scholar

Katayama, T., Ito, S., Kamura, H., Ueki, T., and Okamoto, H. (2000). “Experimental study on hysteretic damper with low yield strength steel under dynamic loading,” in Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, January 2000.

Google Scholar

Kojima, K., Fujita, K., and Takewaki, I. (2015). Critical double impulse input and bound of earthquake input energy to building structure. Front. Built Environ. 1, 5. doi:10.3389/fbuil.2015.00005

CrossRef Full Text | Google Scholar

Kojima, K., and Takewaki, I. (2015a). Critical earthquake response of elastic–plastic structures under near-fault ground motions (Part 1: fling-step input). Front. Built Environ. 1, 12. doi:10.3389/fbuil.2015.00012

CrossRef Full Text | Google Scholar

Kojima, K., and Takewaki, I. (2015b). Critical earthquake response of elastic–plastic structures under near-fault ground motions (Part 2: forward-directivity input). Front. Built Environ. 1, 13. doi:10.3389/fbuil.2015.00013

CrossRef Full Text | Google Scholar

Kojima, K., and Takewaki, I. (2015c). Critical input and response of elastic–plastic structures under long-duration earthquake ground motions. Front. Built Environ. 1, 15. doi:10.3389/fbuil.2015.00015

CrossRef Full Text | Google Scholar

Kusuhara, F., Azukawa, K., Shiohara, H., and Otani, S. (2004). “Tests of reinforced concrete Interior beam-column joint subassemblage with eccentric beams,” in Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, Canada, August 2004.

Google Scholar

Kusuhara, F., and Shiohara, H. (2008). “Tests of R/C beam-column joint with variant boundary conditions and irregular details on anchorage of beam bars,” in Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, October 2008.

Google Scholar

Mota-Páez, S., Escolano-Margarit, D., and Benavent-Climent, A. (2021). Seismic response of RC frames with a soft first story retrofitted with hysteretic dampers under near-fault earthquakes, Appl. Sci., 11, 1290, doi:10.3390/app11031290

CrossRef Full Text | Google Scholar

Mukoyama, R. K., Fujii, K., Irie, C., Tobari, R., Yoshinaga, M., and Miyagawa, K. (2021). “Displacement-controlled seismic design method of reinforced concrete frame with steel damper column,” in Proceedings of the 17th world conference on earthquake engineering, Sendai, Japan, September, 2021.

Google Scholar

Ruiz-García, J. (2012a). Mainshock-aftershock ground motion features and their influence in building's seismic response. J. Earthq. Eng. 16 (5), 719–737. doi:10.1080/13632469.2012.663154

CrossRef Full Text | Google Scholar

Ruiz-García, J. (2012b). “Issues on the response of existing buildings under mainshock-aftershock seismic sequences,” in Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24-28 September 2012.

Google Scholar

Ruiz-García, J., and Negrete-Manriquez, J. C. (2011). Evaluation of drift demands in existing steel frames under as-recorded far-field and near-fault mainshock–aftershock seismic sequences. Eng. Struct. 33, 621–634. doi:10.1016/j.engstruct.2010.11.021

CrossRef Full Text | Google Scholar

Shirai, K., Okano, H., Nakanishi, Y., Takeuchi, T., Sasamoto, K., Sadamoto, M., et al. (2024). Evaluation of response, damage, and repair cost of reinforced concrete super high-rise buildings subjected to large-amplitude earthquakes. Jpn. Archit. Rev. 7, e12418. doi:10.1002/2475-8876.12418

CrossRef Full Text | Google Scholar

Tesfamariam, S., and Goda, K. (2015). Seismic performance evaluation framework considering maximum and residual inter-story drift ratios: application to non-code conforming reinforced concrete buildings in Victoria, BC, Canada. Front. Built Environ. 1, 18. doi:10.3389/fbuil.2015.00018

CrossRef Full Text | Google Scholar

Toyoda, S., Kuramoto, H., Katsumata, H., and Fukuyama, H. (2014). Earthquake response analysis of a 20-story RC building under long period seismic ground motion. J. Struct. Constr. Eng. Trans. AIJ. 79 (702), 1167–1174. (in Japanese). doi:10.3130/aijs.79.1167

CrossRef Full Text | Google Scholar

Vamvatsikos, D., and Cornell, C. A. (2002). Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 31, 491–514. doi:10.1002/eqe.141

CrossRef Full Text | Google Scholar

H. Varum, A. Benavent-Climent, and F. Fabrizio Mollaioli (2023). Energy-based seismic engineering, proceedings of IWEBSE 2023 (Cham, Switzerland: Springer Nature).

Google Scholar

Wada, A., Huang, Y. H., and Iwata, M. (2000). Passive damping technology for buildings in Japan. Prog. Struct. Eng. Mater. 2 (3), 335–350. doi:10.1002/1528-2716(200007/09)2:3<335::aid-pse40>3.0.co;2-a

CrossRef Full Text | Google Scholar