Limit analysis of multi-ring masonry arches: a parametric study on the effects of friction angle, geometry, interlocking, and ring number

The majority of built heritage covering large spans are built with curved masonry components, such as multi-ring arches, to attain greater overall thickness. Their ultimate structural capacity when subjected to external loads is significantly influenced by the various construction techniques utilized. Such structures are made up of independent rings that communicate with one another through interface contacts, and the geometrical features, like size, orientation, and the arrangement of units, play a significant role, as do the mechanical characteristics, like friction. Multi-ring arches subjected to a vertical load at quarter span are assessed utilizing an in-house code implementing the upper bound approach of the limit analysis for masonry structures. The formulation of a script for geometry generation has been given and used for the input to the code. A discrete model has been adopted accounting for a combination of size and disposition of blocks, friction angle, number of rings and the span length are taken into account. Following their combination of impacts in terms of collapse multipliers, which are classified as per respective influencing parameters, each one’s importance was demonstrated by classifying them into two major groups as per unit size. The outcomes showed that all the parameters were key influencing factors in the performance of such structures. Using relatively larger units enhanced the impact of interlocking and provided larger collapse multipliers. While interlocking played a more significant role when span was considered, it together with friction had a larger impact when ring number was varied, such that better interlocking and larger friction values provided higher collapse multipliers.

1 Introduction

Masonry as a building material has significant geometrical and mechanical variety in its components. Approximately 70% of the world’s building inventory is made of masonry (Matthys and Noland, 1989), which is typically represented by assemblies of blocks (stone, bricks, or adobes) with or without the use of mortar made of cement, lime, or clay-based (Lourenço, 1998). This material has been used extensively all over the world, including in earthquake-prone areas, to build both new and historic buildings. Small adjustments to these factors result in significant variations in their structural behavior. It is one of the reasons why historical existent masonry constructions cannot be standardized.

Unreinforced masonry (URM), which is mostly found in ancient masonry buildings and heritage sites, encompasses quite poor structural responses to seismic actions (Choudhury et al., 2020; Tabrizikahou et al., 2021) and shows a non-linear response at very low stress levels, making numerical simulation of this material difficult and far from a standard resolution. A substantial part of the scientific community in this area is always in search of appropriate modeling methods (D’Altri et al., 2020) for the numerical simulation of the intricate structural response of masonry. These simulations have taken into account a broad spectrum of approaches and methods for masonry modeling, from simplified ones (Block et al., 2006; Pantò et al., 2016; Bruggi et al., 2021) to homogenous (Masiani and Trovalusci, 1996; Lourenço and Rots, 1997; Bruggi, 2014) and discrete ones (Orduña and Lourenço, 2005; Gilbert et al., 2006; Sarhosis and Lemos, 2018).

A major part of the built heritage in masonry consisting of curved structures is built using multiple rings of masonry arches to reach larger thickness. There are many examples of masonry structures constructed using multi-ring arches, such as those shown in Figure 1. Although this type of construction is mainly related to masonry bridges (Figures 1C,D), a lot of masonry buildings include multi-ring arches as well (Figures 1A,B). A modern challenge remains the assessment of such structures that withstood time for many years. Multi-ring arches have a different structural behavior compared to the standard one-ring arches due to the inter-ring planes present. In most of the cases, the joints between the blocks are with very weak mortar, damaged one or non-existent. As such, they represent potential planes of weakness for the structure, leading to premature collapse due to ring separation.

FIGURE 1

FIGURE 1. Examples of multi-ring arched structures: (A) Basilica in Albania, (B) Vaults of Matera in Italy, (C) Masonry bridge in France and (D) Masonry bridge in Slovenia.

The discussion on the assessment of multi-ring arches is not a recent topic but dates back to the late 19th century. On the recorded Minutes of the Institution of Civil Engineers 1846, Barlow (1846), a disagreement between two ingenious engineering minds, Robert Stephenson and Isambard Kingdom Brunei, follows over the treatment of rings as separate or homogeneous for the representation and assessment of multi-ring arches. The former suggested a discrete approach while the latter continued on the idea of a homogenized media without accounting for the separate rings. Despite the advancement of knowledge and the improvement of computational tools and skills, in many structural analyses, such structures are still simplified as homogeneous media and the separate rings are not taken into consideration. This approach completely neglects the fundamental behavior of masonry where the contact surfaces between each ring present planes of weakness and, as is common especially in historical structures, mortar layers are weaker in respect to the units and as such form the planes of damage.

Gilbert and Melbourne (1995) performed a series of tests on 3 m and 5 m span multi-ring bridges and then compared the results with a discrete rigid-block mechanism method. The formulated method (Gilbert and Melbourne, 1994) assumes the non-Heyman approach, thus taking into account the ring separation for the study of such structural systems made of multiple rings. Later, the addition of crushing failure was introduced (Gilbert, 1998), which does not prove to be affecting majorly in the case of multi-ring arches. Friction between the rings is included in the form of a separation coefficient. As for the tests, seven 3 m and 5 m span masonry arch bridges were evaluated, each having been constructed with or without known flaws, together with four model arch ribs, each with a 3 m span. Nevertheless, the ring separation was introduced as a flaw in construction. Load was applied at quarter span by considering the infill of the bridge as well. The study shows the efficiency of discrete approaches compared to the more complex ones due to the involvement of many parameters that are not justifiable, and the analysis becomes sensitive. Moreover, they stress that multi-ring arches should not be assessed using methods that are not able to consider ring separation as it proves to be crucial to the outcome.

Similar experiments were conducted on several other multi-ring masonry arches (Sarhosis et al., 2016), such as the ones by Melbourne et al. (1995b), Melbourne et al. (1995a) and Melbourne and Tao (1995). All the tests show the importance of ring separation which causes failure in the majority of the cases. Furthermore, Melbourne et al. (2007), in a research report containing an exhaustive number of tested multi-ring arches, provide empirical insight into the behavior of such structures. It is further highlighted that the main failure mechanisms obtained are ring separation, four-hinged mechanisms, and sliding, with ring separation being the most common. This further emphasized that multi-ring arches, in this case for bridges, present a very sensitive case to the phenomena of ring separation. In particular, Melbourne et al. (1995b) point out the importance of the bond patterns of the units as a key factor for the prevention of ring separation. In a recent parametric study, Rios et al. (2023) show the importance of texture on the behavior of masonry arches. They highlight the significance of the interlocking effect provided by a proper arrangement of masonry units.

A discrete approach using the discrete element method (DEM) was used by Kassotakis et al. (2017) to perform a parametric study of multi-ring arches. They investigated the impact of the number of rings (2–5) using different span lengths (3, 5, 7, and 9 m) on the structural capacity of the arches. Tensile resistance and cohesion was introduced on all of the joints. During their study, they achieved only four-hinged mechanism and no ring separation. They further found out that for fewer rings, the hinges were more concentrated while for more rings the hinges were more diffused with more radial cracks. On the contrary, Pantò et al. (2022) propose a hybrid continuum and discrete strategy following macro-modeling and the simulation of internal structure by multiscale calibration. They model ring separation using zero thickness interfaces between the rings and also between the arch and backfill as they take the latter into consideration. From the comparative studies performed, they stress the sensitivity of continuum finite element models to the calibration of parameters. Even then, these models can lead to inaccurate results especially when dealing with ring separation which were obtained using the strategy proposed.

Additionally, Cangi (2023) demonstrates how the construction method of multi-ring arches has an impact on the stress distribution of each ring where clear distinguishment is observed. Construction of such arches can be done by following a consecutive order of ring construction, where the first one serves as a formwork for the rest. The other construction technique is by arranging the units up to the intended thickness of the arch, all rings at once. Using the former technique, it is not possible to achieve different internal texture of units other than the running bond while, using the latter, any type of texture can be introduced. Nonetheless, the interlocking of units between the rings can be achieved in both. On top of this, Cangi (2023) shows how, at the key arch, the first construction technique yields in a maximum compressive stress at the intrados while for the second on the extrados. This intensifies how the discrete treatment of each ring has an influence on the overall behavior and the capacity of multi-ring arches.

Furthermore, discrete models are computationally expensive, thus making it very difficult to perform parametric studies. Nevertheless, this study intends to use an upper bound limit analysis approach that is able to account for the finite friction of the joints implemented in an in-house code. Taking advantage of the full description of the internal structure, the code enables the detection of the collapse mechanisms exploiting the interlocking effect within the units. With the help of rapid tools for the input and the efficiency of the in-house code for the processing of such complex structures, a large number of simulations is performed under the influence of the most influencing parameters. The set of parameters for this study involve.

• The size of the blocks grouped into two general categories of big and small;

• the variation of the span to consider small, medium, and large spans;

• The number of rings composing the arch;

• The interlocking of the units between the rings;

• The friction angle levels.

Even though cohesion is also possible to be input for mortared joints, here it is omitted to avoid factorial designs of high orders that create difficulties in result presentation.

The article is organized as follows; in Section 2, the above-mentioned approach for the study of the multi-ring arches is described. Section 3 illustrates the parametric study performed on such structures to analyze the most influencing parameters and, further, a script that automatically generates the geometry of multi-ring arches is given for a more rapid parametric assessment. In Section 5, the results achieved are provided, and a discussion on the collapse mechanisms and multipliers is given with the conclusive remarks of this study in Section 6.

2 Methodology: Limit analysis with the in-house ALMA code

An in-house code entitled ALMA (Analisi Limite Murature Attritive) (Baggio and Trovalusci, 1998) has been implemented in order to study masonry structures accounting for frictional joints. The code is implemented entirely in a Python^TM environment that uses a CAD interface for the geometry input of the structure while numerical parameters are given and processed separately from a xml file. The results are achieved after processing within Python^TM and solving of the linear programming problem using the optimization library MOSEK^® (ApS, 2022). The obtained output is the collapse multiplier and the corresponding collapse mechanism that is visually plotted using the open source software Paraview (Ahrens et al., 2005). The core of the ALMA code is based on the works of Baggio and Trovalusci, (1998), Baggio and Trovalusci, (2000) and recently improved to account for more parameters and for increased efficiency (Pepe et al., 2020). As stated above, the implementation of the new version of the code in a Python^TM environment and utilizing fast optimization tools such as MOSEK^® enables the study of much more complex structures, including large numbers of joints, with a very detailed discretization without compromising the computational cost. Additionally, in the new version, among others, it is able to study settlements (Pepe et al., 2020) and joint reinforcements (Nela et al., 2022; Nela et al., 2023a), and with the improved pre-processor, the user can easily generate various shapes and complex geometries that can be also scripted (shown in the upcoming sections) for easiness, especially when dealing with parametric studies.

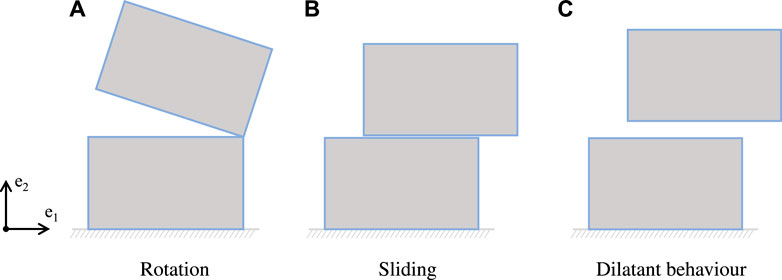
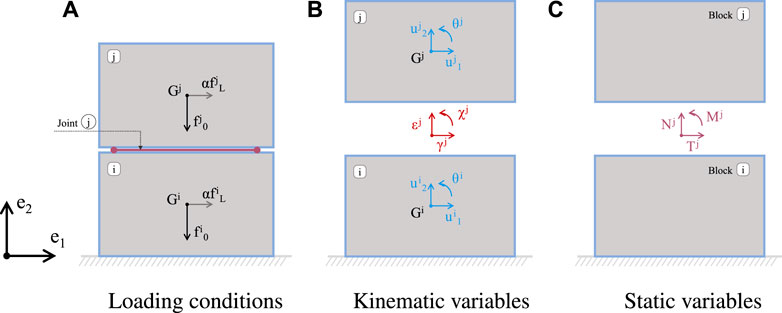
Within the framework of limit analysis, the masonry structures are described as a system of n rigid blocks and m joints unable to carry tension and resistant to sliding by a friction coefficient, tan(ϕ), where ϕ is the friction angle. Considering the in-plane problem, the blocks can translate and rotate about the edges of the contact blocks (hinging) as well as slide along the joints as shown in Figures 2A,B, respectively, in which a two-block mechanism is depicted. It is important to state that, for the case of sliding, a dilatant behavior (Figure 2C) is assumed, such that the block slides with an uplift due to dilatancy as the equivalent of the friction angle, ϕ.Considering a system of n parallelepiped blocks in two-dimensional space, the orthonormal basis is $\mathit{e}={\left\{e_1,e_2\right\}}^T$. Loads are applied in the respective centroid of mass of each ith rigid block:

${\mathit{f}}^i={\mathit{f}}_0^i+\alpha {\mathit{f}}_L^i,\text{with\hspace{0.17em}}i=1,\dots ,n,(1)$

where ${\mathit{f}}_0^i={\left\{f_{01}^i,f_{02}^i,m_0^i\right\}}^T$ and ${\mathit{f}}_L^i={\left\{f_{L1}^i,f_{L2}^i,m_L^i\right\}}^T$ are the constant ‘dead’ and ‘live’ generalized loads vectors, respectively. As usual in limit analysis, the load vector in Eq. (1) is split into two parts in which live loads are proportional to the dead loads through a non-negative coefficient α, called the load multiplier, as shown in Figure 3A. The global load vector f is obtained by collecting the single load vectors fⁱ.

FIGURE 2

FIGURE 2. Schematic representation of possible failure modes for a two-block structure.

FIGURE 3

FIGURE 3. Schematic representation of a joint for a two-block structure.

The vector ${\mathit{u}}^i={\left\{u_1^i,u_2^i,{\theta }^i\right\}}^T$, that contains the displacement components u₁, u₂, and the rotation θ (Figure 3C), represents the generalized displacement of the center of the block. Similarly, all the single vectors of generalized displacements are collected in a global vector u, that in a virtual work sense corresponds to the global load vector f.

Additionally, over each jth joint, which is the contact surface between the blocks, generalized stress σ^j and strain measures (relative displacements) ϵ^j are introduced (Figures 3B,C). The collection of the local generalized stress vector containing the static variables ${\mathit{\sigma }}^j={\left\{N^j,T^j,M^j\right\}}^T$ forms the global generalized stress vector σ. N^j, T^j, and M^j are the components of the normal force, shear force, and moment, respectively, acting at each jth joint. The kinematic variables, or generalized strain, are the relative displacement rates at joints, that is, normal displacement ξ^j, tangential displacement γ^j, and rotation χ^j, and are collected in the vector ${\mathit{ϵ}}^j={\left\{{\xi }^j,{\gamma }^j,{\chi }^j\right\}}^T$. In a similar manner, these vectors are collected in a global vector of the generalized strains ϵ and correspond in a virtual work sense to the vector of static variables σ.

Herein, the relations that govern the problem of a non-standard rigid–plastic discrete material as framework of the holonomic perfect plasticity. The kinematic compatibility for the whole system is expressed as follows:

$\mathit{ϵ}=\mathit{B}\mathit{u},(2)$

where B represents the compatibility matrix. The equilibrium equation of the system is formulated as:

${\mathit{B}}^T\mathit{\sigma }+\mathit{f}=\mathbf{0}.(3)$

The generalized yield domain of the system can be written as:

$\mathit{y}={\mathit{N}}^T\mathit{\sigma }\le \mathbf{0},(4)$

where N is the block-diagonal gradient matrix referred to the adopted failure surface. The flow rule for the non-associative case expresses the vector ϵ as a linear combination of non-negative coefficients ordered in the vector λ, called plastic multiplier vector, and it can be written as:

$\mathit{ϵ}=\mathit{M}\mathit{\lambda },(5)$

where M is the block-diagonal matrix of the modes of failures that for a two-dimensional framework consist of two rotations and two slidings of the ith block in both positive and negative directions. For systems with non-associated flow rules, the solution is not unique as the Drucker stability postulate no longer holds. In this case, only the lower/upper bounds of the collapse multipliers can be found (Drucker, 1953; Radenkovic, 1961). The solution, if found, of a non-linear and non-convex programming (NLNCP), that in this case constitutes the mathematical problem, usually converges to a local minimum rather than the global one (Kirsch, 1993; Baggio and Trovalusci, 2000) replaced the friction angle with dilatancy and in this manner the direction of the flow is associated with the yield surface and the problem is linearized. As such, the normality rule holds and the static and kinematic theorems of limit analysis provide a unique solution for the collapse multiplier. The approach followed within the code is the upper bound kinematic theorem and can be solved using the linear programming for the optimization problem. After considering the complementarity condition and the condition of non-negative work of the live loads, herein normalized, as expressed in the following Eqs 6, 7.

${\mathit{\lambda }}^T\mathit{y}=0,(6)$

${\mathit{f}}_L^T\mathit{u}=1,(7)$

and after some algebraic operations, the minimization problem is formulated in Eq. (8) as:

$\begin{array}{cc}\hfill {\alpha }_c=& \text{min}\left\{{\mathit{\lambda }}^T\left[\mathit{c}-{\left({\mathit{A}}_0{\mathit{N}}_1\right)}^T\right]{\mathit{f}}_0\right\}\text{\hspace{0.17em}subjected\hspace{0.17em}to:}\hfill \\ \hfill & \left(\mathit{A}{\mathit{N}}_1-{\mathit{N}}_2\right)\mathit{\lambda }=\mathbf{0},\left(\text{compatibility\hspace{0.17em}condition}\right)\hfill \\ \hfill & {\mathit{\lambda }}^T{\left({\mathit{A}}_0{\mathit{N}}_1\right)}^T{\mathit{f}}_L-1=0,\left(\text{positive\hspace{0.17em}live\hspace{0.17em}loads}\right)\hfill \end{array}(8)$

with the bounds on the unknowns λ ≥0. In the objective function, α_C is the collapse multiplier, while the compatibility matrix B is decomposed into B₁ as the kinematical submatrix of maximum rank and the remainder of it as B₂. Inverting matrix B₁ gives A₀, while matrix A is obtained as $\mathit{A}={\mathit{B}}_2{\mathit{B}}_1^{-1}$. Similarly, N₁ and N₂ are two submatrices of N. On the other hand, due to the associative flow rule, matrices N and M are identical and M vanishes in Eq. (8). Vector c is the joint cohesion which is formulated in Nela et al. (2023a) and can be applied to account for mortared joints or joint reinforcement.

3 Description of the parametric study

This study intends to perform a parametric analysis on a large domain of data set with the most influential parameters that characterize multi-ring arches. It must be noted that the backfill is not considered in this research since the influence of arch parameters are solely the focus. Nonetheless, backfill is able to be considered and such analysis using the ALMA code has been done by Nela et al. (2022). The main structural layout of the arch under consideration is shown in Figure 4. Arches are subjected to their own self-weight and to an additional live load applied at the quarter span. The live load is proportional to the self-weight of the block where the load is applied onto and factorized with the collapse multiplier α_c. A rigidly connected support has been placed under the arch springing (shown in the collapse mechanism figures) to ensure the mechanism development within the arch.

FIGURE 4

FIGURE 4. General parametric scheme of the multi-ring arch under study.

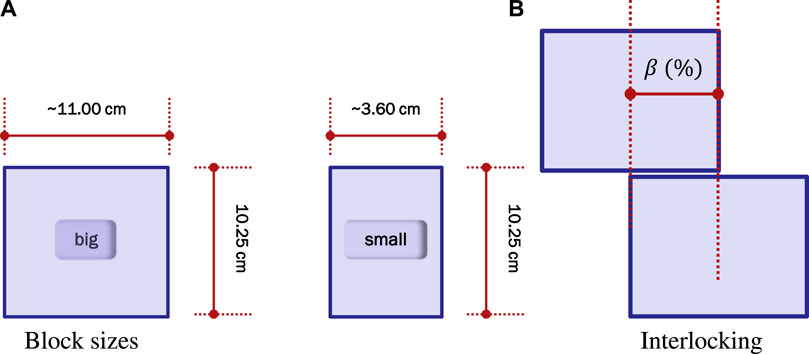
The parametric study is divided between two main categories that are split as per consideration of unit size. Small and big sizes of units are idealized into dimensions of 3.6 by 10.25 cm and 11.0 by 10.25 cm, respectively, as given in Figure 5A. The dimension of 10.25 cm is kept constant to ensure the same ring thickness for the arches. Springing angle is also the kept same for all the arches at an angle of 30^o. Both the thickness of rings and the springing angle are taken as reference from Kassotakis et al. (2017) that also resulted in the size of the small blocks. On the other hand, the size of the big blocks is taken as reference from the Matera vaults as shown in Figure 1B, where the blocks appear almost square sized with the radial dimension restricted to 10.25 cm for consistency in ring thickness. Regarding the third dimension, as it is strictly confined to a two-dimensional planar problem, it does not influence the solution in this case. Different sizes of units were chosen to understand which one performs better and especially where interlocking plays a more significant role as, for the small blocks, the interlocking percentage may be the same but the physical surface of contact differs.

FIGURE 5

FIGURE 5. Parameter descriptions.

For dry-joint masonry, considering different bond textures which incorporate different levels of interlocking, various crosswise tensile resistances are achieved (Chen and Bagi, 2020). In this aspect, although interlocking is a geometrical parameter, it provides mechanical resistance to the assemblage due to the contact surface friction. The general texture for the disposition of voussoirs consists of stack and running bonds with a parametrization of the interlocking between blocks. Interlocking is represented with a coefficient of interlock (β - in percentage) relative to the thickness of the block (b) that varies from 0% (no interlock; stack), 15% and 35% (medium interlock; running), up to a maximum of 50% (complete interlock; running), as schematically shown in Figure 5B.

Another mechanical parameter is friction, which is related to the surface contact of the units and, as stated before, in combination with interlock, it provides a tensile strength, while alone, it gives shear strength and resistance to sliding. In the case of multi-ring arches, it is also important for ring separation and it highly influences the response of the assembly. Friction between the surfaces is described by the angle of friction (ϕ) with practical values ranging between 15^o and 63^o (Rahman and Ueda, 2014). However, more closely spaced values are taken into account that are more realistic for multi-ring arches. In this study, three different levels of friction such as 25^o, 30^o, and 35^o are adopted.

As for geometrical parameters, three spans (S) are considered, that is, the short, middle, and large spans in relative terms that vary from 3.0 m, 5.0 m, and 7.0 m, respectively. For the constitution of multi-ring arches, a minimum number of two rings is necessary and then three additional rings are added to account for a total of five rings. Therefore, four different types of rings are generated, namely, two-, three-, four-, and five-ringed arches. As mentioned above, the thickness (t) of each ring is kept constant, constructing in this way different overall arch thicknesses (T) that are based on the considered number of rings. For each type of arch in terms of rings, an equivalent (EQ) thickness of a one-ringed arch is analyzed as well. The equivalent arches differ in span and overall thickness (T), but not in interlock coefficient.

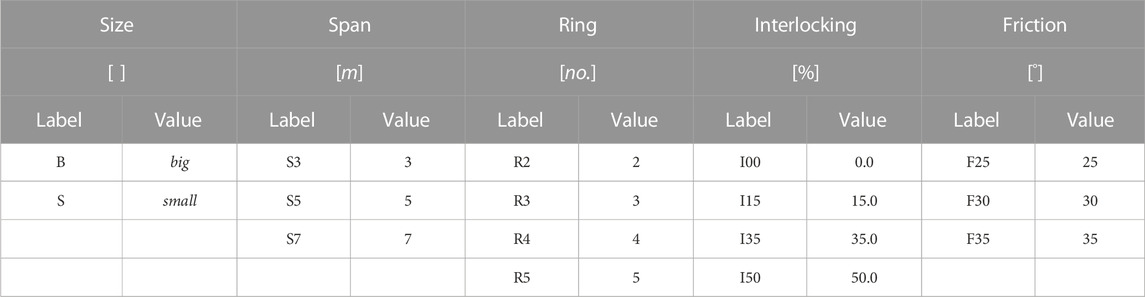
A full composite factorial design has been carried out where all parameter levels have been combined among each other resulting in a large number of simulations to be performed. Considering the main parameter of Size with two levels, Span with three levels, Ring number with four levels (excluding the equivalent ring arches), Interlocking effect with four levels, and Friction angle with three levels, a total of 288 runs were yielded from the full combination. An additional 72 runs resulted from considering the one-ring equivalent arches. Exploiting the advantage of the in-house code of being able to run the simulations in a very rapid manner, accounting for the fact that this is a discrete approach, it was possible to have all the results efficiently for further processing. The simulations were run on the same personal computer with Intel^® Core™ i7-10750H CPU 2.60 GHz and 32 GB of RAM. The average time necessary for running all the simulations was 24 min with a minimum of 1.65 s for fewer joints considered (i.e., the equivalent arches) and a maximum of 355 min for the structures with larger numbers of joints (i.e., the largest span with the biggest ring number).

In order to simplify references to figures, an acronym system is used and it follows a sequence of “size_span_ring_interlock_ friction”. Size takes the attributes S-small and B-big while span takes the number attributes based on the span, such as S3, S5, and S7 for spans of 3, 5, and 7 m, respectively. Ring number similarly is based on the number of rings as R2, R3, R4, and R5, and interlock takes the following attributes, I00, I15, I35, and I50 for the interlocking percentage considered such that 00-stacked, 15%, 35%, and 50%, respectively. Finally, friction takes the attributes following the angle of friction such as F25—low level, F30—medium level, and F35—high level. The acronym used for the equivalent one-ring arches used is simply EQ. For example, the acronym “S_S7_R4_I35_F30” refers to the arch with small blocks, a span of 7 m, consisting of 4 rings, and with blocks interlocked at 35% with a joint friction of 30^o. All the parameters studied and corresponding labels are summarized in the following Table 1.

TABLE 1

TABLE 1. Description and labeling of the parameters used in the study.

4 AutoGeom script for geometry generation

The processing speed of the code has been proven to be convenient for such studies. Nevertheless, the input file requires a drawing of the discrete structure in a CAD environment where each joint and block are specified accordingly. Taking into account also the differences of the considered parameters that have to be placed accurately in each ring and on curved structures, it provides a challenge for the user. For this reason, a script that generates the input file for any type of circular arch has been developed that is also able to account for different internal structures (texture) of the masonry and also the above mentioned factors intended for the parametric study. Herein, the mathematical formulations for the implementation of this script are given and they can be used in any programming language or CAD software.

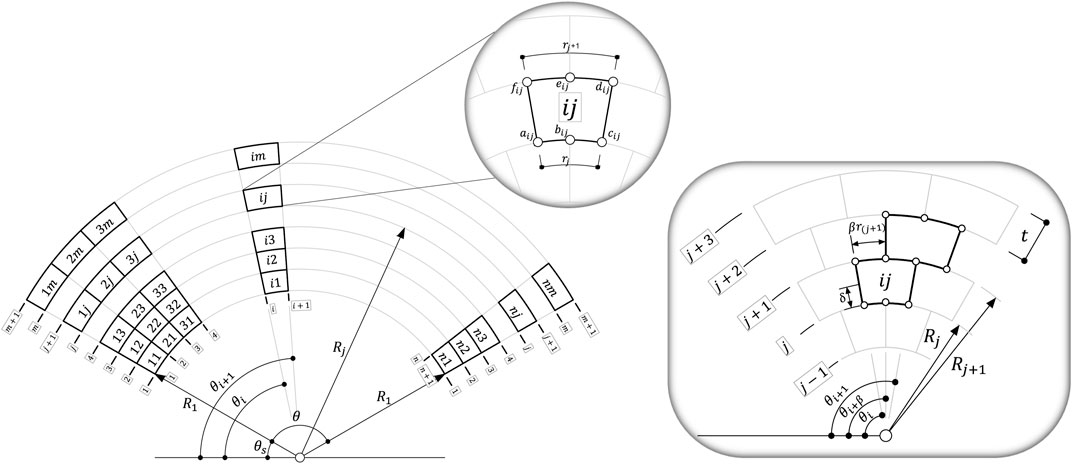
A general schematic drawing of the arch is provided in Figure 6 (left), which is a reference regarding any internal texture that the arch may have. The arch consists of n blocks and m rings and, based on the given springing angle θ_s, it can be a segmental one (for θ_s > 0) or a complete semi-circular one (for θ_s = 0). Based on this generalized scheme, each block ij represents a possible placement of a periodic texture inside, and each of these blocks can be shifted at a certain percentage radially to create an interlock. Given a number of radial blocks n, the angle θ that runs tangentially across the arch is achieved and, given the number of rings m, the overall thickness of the arch T is divided tangentially into small ring thickness t.Concerning each block (see Figure 6 on the right), the radial distance (arc length) between two consecutive coordinates is given as the general arc length of the specific ring S_j divided by the number of blocks n. The general arc length of each ring S_j can be found as the multiplication of each ring radius R_j and the total segmental angle of the arch θ, whereas each ring radius R_j is obtained by adding the thickness of each ring to it in a sequential way. A summary of these formulations are reported below in Eq. 9:

$\begin{array}{cccccc}\hfill r_j& =S_j/n;\hfill & \hfill r_{j+\delta }& =S_{j+\delta }/n;\hfill & \hfill r_{j+1}& =S_{j+1}/n,\hfill \\ \hfill S_j& =R_j\theta ;\hfill & \hfill S_{j+\delta }& =R_{j+\delta }\theta ;\hfill & \hfill S_{j+1}& =R_{j+1}\theta ,\hfill \\ \hfill R_j& =R+\left(j-1\right)t;\hfill & \hfill R_{j+\delta }& =R+\left(j+\delta -1\right)t;\hfill & \hfill R_{j+1}& =R+jt,\hfill \\ \hfill {\theta }_i& =\theta \left(i-1\right)/n+{\theta }_s;\hfill & \hfill {\theta }_{i+\beta }& =\theta \left(i+\beta -1\right)/n+{\theta }_s;\hfill & \hfill {\theta }_{i+1}& =\theta i/n+{\theta }_s,\hfill \end{array}(9)$

where β ∈ (0, 0.5) and δ ∈ (0, 1) are coefficients of interlock and texture, respectively, and they determine in percentage the location of an intermediate node. For β = 0 and δ = 0, are obtained exactly the coordinates (x_i,j, y_i,j) of the block i, j, and for β = 0.5 and δ = 1, the intersection point between blocks i, j and i, j + 1 for full interlock of 50% is obtained. For the former case, i.e., β = 0 and δ = 0, all the blocks are stacked radially due to β and no internal texture has been considered due to δ.Among many types of bonds (textures) that can be formed for the arch, the bond of “Type_1” has been chosen in this case. Here, each block ij stands as one, and only the staggering effect, i.e., the interlock, can be considered with the help of the β coefficient and that is why the nodes are only located tangentially at each ring with corresponding coordinates as shown in Figure 6.In this case, a convention is adopted that assumes the global origin of the coordinate system on the bottom left-side of the geometry. Furthermore, to be in line with our code for limit analysis, the nodes are drawn counterclockwise. Therefore, in this order, the node coordinates are obtained using the following equations:

$\begin{array}{cc}\hfill {\left[a_x,a_y\right]}_{ij}^O& =\left[\left(-R_j\cos {\theta }_i\right),\left(R_j\sin {\theta }_i\right)\right],\hfill \\ \hfill {\left[b_x,b_y\right]}_{ij}^O& =\left[\left(-R_j\cos {\theta }_{i+\beta }\right),\left(R_j\sin {\theta }_{i+\beta }\right)\right],\hfill \\ \hfill {\left[c_x,c_y\right]}_{ij}^O& =\left[\left(-R_j\cos {\theta }_{i+1}\right),\left(R_j\sin {\theta }_{i+1}\right)\right],\hfill \\ \hfill {\left[d_x,d_y\right]}_{ij}^O& =\left[\left(-R_{j+1}\cos {\theta }_{i+1}\right),\left(R_{j+1}\sin {\theta }_{i+1}\right)\right],\hfill \\ \hfill {\left[e_x,e_y\right]}_{ij}^O& =\left[\left(-R_{j+1}\cos {\theta }_{i+\beta }\right),\left(R_{j+1}\sin {\theta }_{i+\beta }\right)\right],\hfill \\ \hfill {\left[f_x,f_y\right]}_{ij}^O& =\left[\left(-R_{j+1}\cos {\theta }_i\right),\left(R_{j+1}\sin {\theta }_i\right)\right],\hfill \\ \hfill {\left[a_x,a_y\right]}_{ij}^E& =\left[\left(-R_j\cos {\theta }_{i+\beta }\right),\left(R_j\sin {\theta }_{i+\beta }\right)\right],\hfill \\ \hfill {\left[b_x,b_y\right]}_{ij}^E& =\left[\left(-R_j\cos {\theta }_{i+1}\right),\left(R_j\sin {\theta }_{i+1}\right)\right],\hfill \\ \hfill {\left[c_x,c_y\right]}_{ij}^E& =\left[\left(-R_j\cos {\theta }_{i+1+\beta }\right),\left(R_j\sin {\theta }_{i+1+\beta }\right)\right],\hfill \\ \hfill {\left[d_x,d_y\right]}_{ij}^E& =\left[\left(-R_{j+1}\cos {\theta }_{i+1+\beta }\right),\left(R_{j+1}\sin {\theta }_{i+1\beta }\right)\right],\hfill \\ \hfill {\left[e_x,e_y\right]}_{ij}^E& =\left[\left(-R_{j+1}\cos {\theta }_{i+1}\right),\left(R_{j+1}\sin {\theta }_{i+1}\right)\right],\hfill \\ \hfill {\left[f_x,f_y\right]}_{ij}^E& =\left[\left(-R_{j+1}\cos {\theta }_{i+\beta }\right),\left(R_{j+1}\sin {\theta }_{i+\beta }\right)\right],\hfill \end{array}(10)$

where the superscript O and E denote an odd ring or an even ring, respectively. In the case of large geometries, in terms of blocks number, to decrease the computational cost, a switch can be added to skip the nodes b_ij and e_ij when a stack bond is intended.

FIGURE 6

FIGURE 6. Generalized parametric scheme of the arch and Type_1 bond.

5 Results and discussion

A total of 360 simulations have been run, where 72 are regarding the equivalent one-ring arches and 288 are the multi-ring ones. The outcomes from these results are grouped into the collapse mechanisms as qualitative results and then the collapse multipliers as quantitative. Finally, a statistical assessment is carried out to better understand the impact of the factors in a mathematical aspect and relate them to the physical meaning. Raw results extracted from all the simulations can be found in Nela et al. (2023b); Nela et al. (2023c); Nela et al. (2023d).

5.1 Collapse mechanisms

Collapse mechanisms provide an insight into the structural condition at the instant of collapse. The plots show in a light gray color the undeformed state and in a bold color the collapse mechanism; the hinges are zoomed for an increased readability. Due to the large amount of results yielded from this research, it is not possible to plot all the mechanisms achieved. Consequently, only some of the them are herein shown while the reader is referred to the above-mentioned repository for the rest of the results.

5.1.1 Collapse mechanisms considering big-sized blocks

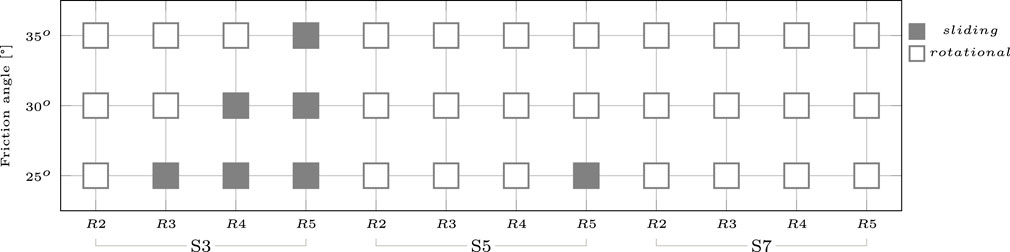
Evaluating the collapse mechanisms for the equivalent (EQ) one ring arches, it is possible to extract how different thicknesses of arches produce different types of failure. Due to the multi-factorial dataset of parameters involved in the study, a matrix plot of the type of collapse mechanisms only for the equivalent arches is given in Figure 7. This plot provides the change of collapse mechanisms from sliding (marked with solid squares) to a rotational (marked with hollow squares) one given three levels of friction, four levels of rings, and three levels of span. Considering big blocks, for the case of R2-EQ, a four-hinge rotational mechanism occurs at any level of friction and any span length. On the contrary, for the span of 3 m and for the R3-EQ, sliding occurs for a friction angle of 25^o but for higher values, it is restricted. Nevertheless, this is not the same for spans of 5 and 7 m. Assessing greater thicknesses while remaining on the span of 3 m, for R4-EQ, sliding occurs for friction angles of 25^o and 30^o, whereas for R5-EQ, it happens for all levels of friction. Different results are achieved for the span of 5 m where sliding is present only for the R5-EQ at a friction level of 25^o. On the contrary, for the span of 7 m, there is no sliding present for any level of friction.

FIGURE 7

FIGURE 7. Matrix plot of the differences in collapse mechanisms for the big-sized blocks.

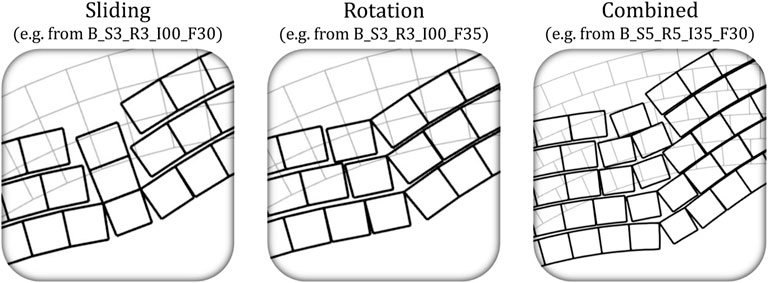
While for the equivalent arches, the collapse mechanisms are evident and straightforward, for the multi-ringed ones, they are not. In Figure 8, a categorization is given of the collapse mechanisms involved in the assessment of multi-ringed arches. The arches with two rings, R2, follow the same mechanisms of no sliding as fewer rings are involved and this is the same for all spans. Nevertheless, different outcomes are achieved for the other ring numbers, where for the span of 3 m, R3 shows sliding at friction angles of 25^o and 30^o, while for 35^o, it slides at a different location from the one seen in the equivalent arch. This occurs only for the stack bond which in fact is closely related to the equivalent arch, while for I-15, I-35, and I-50, there is no sliding mechanism present. R4 and R5 exhibit sliding for all levels of friction when the units are in a stack bond, while a combined rotation/sliding mechanism is observed for the I-15 and rotational ones for I-35 and I-50 (see Figure 8). At larger spans of 5 and 7 m, the sliding effect diminishes and is less evident as observed for the equivalent arches, and also the unit interlocking restricts it more. In every instance, it was observed that higher levels of friction make ring separation more evident.

FIGURE 8

FIGURE 8. Collapse mechanism categories for multi-ring arches.

An example of a four-ring arch with big-sized blocks and the span of 3 m is given in Figure 9. The case of equivalent arches are shown on top, where the mechanism differs from sliding to rotational for a slight change of 5^o in friction. On the bottom, the mechanisms for friction angles of 35^o are given but with a slight variation in interlocking, namely, I-00 and I-15. For I-00, the sliding continues also for a higher angle of friction, while for I-15, it is a combined sliding and rotational. Furthermore, between these two mechanisms, a shift of hinges is observed as well as different local modes. Similar results are found also for other slight variations in parameter levels that yield different mechanisms and this holds for all spans. Certain examples show similar collapse but almost all cases are non-identical.

FIGURE 9

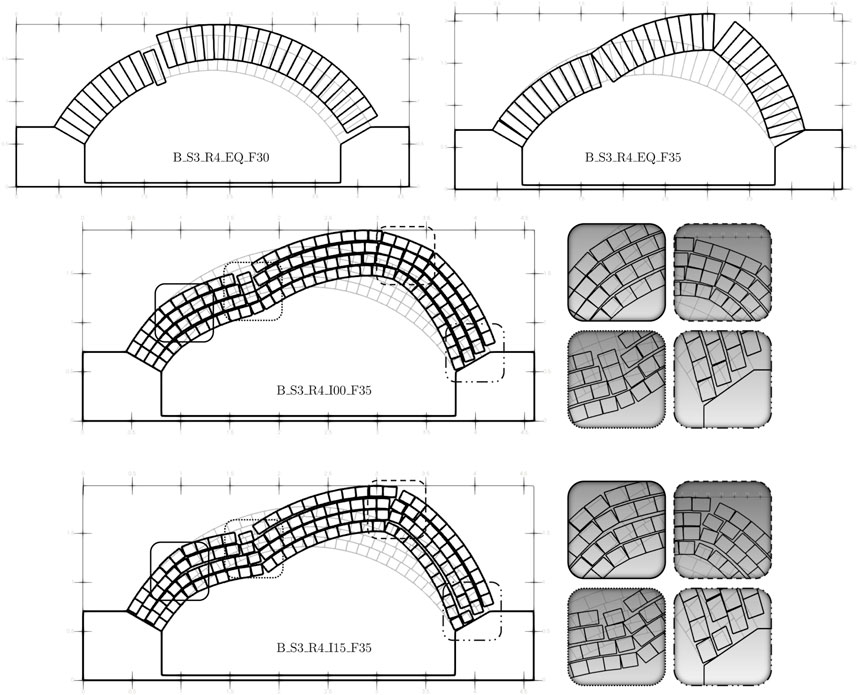
FIGURE 9. Examples of collapse mechanisms for the big-sized blocks (B) with a span of 3 m (S3) and four-ringed (R4) arches varying in equivalent thickness (EQ), stacked texture with no interlocking (I00), interlocking of 15% (I15), and two different levels of friction, 30^o (F30) and 35^o (F35).

5.1.2 Collapse mechanisms considering small-sized blocks

The assessment of equivalent one-ring arches of small blocks likewise offers insight into the various modes of failure. Similar to the case of big blocks, a matrix plot of the collapse mechanism types only for the equivalent arches is given in Figure 10. Analogous mechanisms are obtained as for the case of big blocks and equivalent arches. Considering the small span of 3 m, for the R3, sliding occurs at a friction angle of 25^o, for R4, at angles of 25^o and 30^o, while for R5, it occurs at all levels of friction. At larger spans such as 5 m, it occurs for the R5 at a friction level of 25^o, whereas for the largest span of 7 m, there is no sliding present.

FIGURE 10

FIGURE 10. Matrix plot of the differences in collapse mechanisms for the small-sized blocks.

Since fewer rings are involved in R2 arches, the mechanisms obtained are rotational for all spans. For the other ring numbers, however, different results are obtained, such as for the span of 3 m, R3 exhibits sliding at friction angles of 25^o and 30^o. Only the stack bond exhibits this, which is very closely connected to the equivalent arch; there is no sliding mechanism in place for the I-15, I-35, and I-50. When the units are in a stack bond, R4 and R5 show sliding for all degrees of friction, but I-15 exhibits a combination rotation/sliding mechanism and I-35 and I-50 demonstrate rotational ones. The sliding effect hinders and becomes less noticeable as shown for equivalent arches at higher spans of 5 and 7 m, and the unit interlocking further inhibits it.

In a similar manner, the example of a four-ring arch but with small-sized blocks for the span of 3 m is shown in Figure 11. The case of equivalent arches depicted on top shows again the difference in mechanism, sliding to rotational, for the slight change of 5^o in friction. The same set of mechanisms corresponding to the case of big blocks in Figure 9 are given on the bottom. Interlocking of I-00 exhibits sliding also for the higher level of friction while the variation of the interlocking parameter to I-15 converts the hinge to a combined sliding and rotational. It was further noted that one of the two mechanisms had its hinges shift, along with other local modes. Minor adjustments in parameter levels trigger various mechanisms resulting in different outcomes. Despite some examples exhibiting comparable results, almost no equal scenarios are found. It is shown that with higher levels of friction, ring separation is more obvious, much like in the case of big blocks.

FIGURE 11

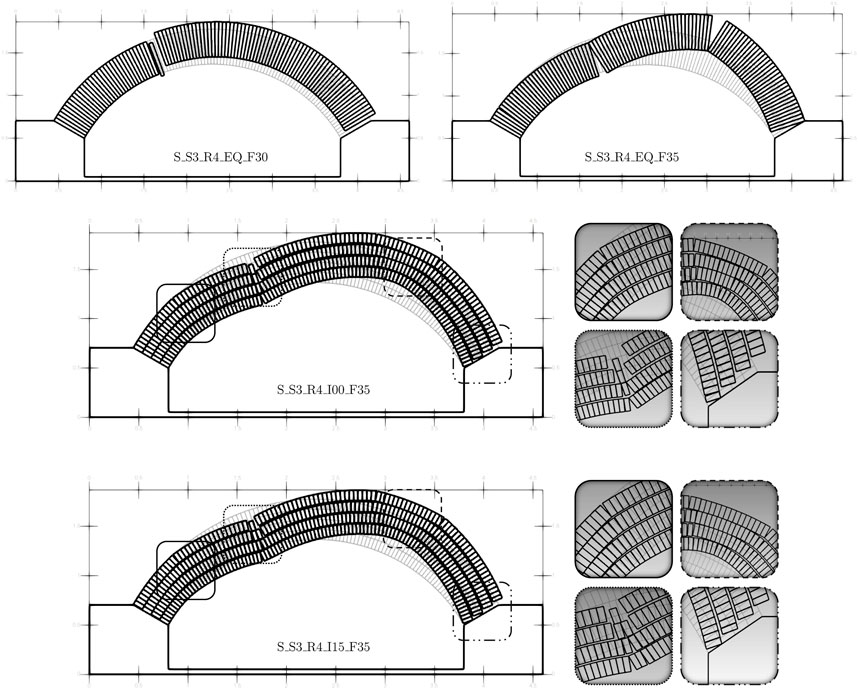
FIGURE 11. Examples of collapse mechanisms for the small-sized blocks (S) with span of 3 m (S3) and four-ringed (R4) arches varying in equivalent thickness (EQ), stacked texture with no interlocking (I00), interlocking of 15% (I15), and two different levels of friction, 30^o (F30) and 35^o (F35).

The discretizing nature of the approach and consideration of sliding by the in-house code has enabled the capture of a larger range of mechanisms that are involved in the failure behavior of multi-ring arches. Rotational and sliding mechanisms are achieved in almost all of the cases to be combined also with ring separation. Additionally, the combination of sliding and rotational mechanisms at the same location are observed. It is crucial to highlight that, in the cases where masonry is modeled as a homogenous continua, these failure modes are not able to be captured. On top of that, simplifications of the internal structure of the arch provide different quantitative and qualitative results. The importance of such mechanisms is reflected in the different failure loads that follow according to the mechanism they correspond to. More importantly, if the proper failure mode is not captured, this may lead to inaccurate strengthening strategies.

Moreover, Figures 9, 11 depict an uplift of the blocks, which is evident for both block sizes. Considering a dilatant behavior for the joints simplifies the problem to an associative one, but at a cost of an uplift instead of perfect sliding when the mechanisms involve sliding. The question of substituting friction with dilatancy has been widely discussed, originally by Baggio and Trovalusci (2000). This implies a linearization of programming problems adopted for the limit analysis and provides an upper bound for the collapse loads. Furthermore, this has a specific mechanical justification related to the roughness of interfaces. While choosing non-associative flow rules can potentially lead to more accurate results, it introduces a non-linear and non-convex mathematical programming problem. In such cases, the solution may not be unique, and there is even a possibility that a solution may not exist at all. Delimitations of the collapse load can be addressed within the framework of Drucker’s theory (Drucker, 1953), refined by Radenkovic (Radenkovic, 1961). This approach based on dilatancy instead of friction has proven to be valuable, especially in applications where computational costs are a concern.

5.2 Collapse multipliers

The live load is applied at one block on the quarter span of the structure and the collapse multiplier corresponds to the weight of that specific block. For this reason, collapse multipliers are normalized by the weight of the entire structure for intercomparable results.

5.2.1 Collapse multipliers considering big-sized blocks

Collapse multipliers for the big-sized blocks are grouped into plotted in graphs for various parameters and given in Figure 12. Horizontally, each graph represents a different span, while vertically, the graphs on the left vary in interlocking parameters and those on the right vary in friction parameters. In the case where interlocking varies, friction is averaged and analogously for the other. Additionally, the results are given with respect to ring number and all the equivalent arch results obtained are omitted from these plots as they result in very large multipliers as it will be shown after.

FIGURE 12

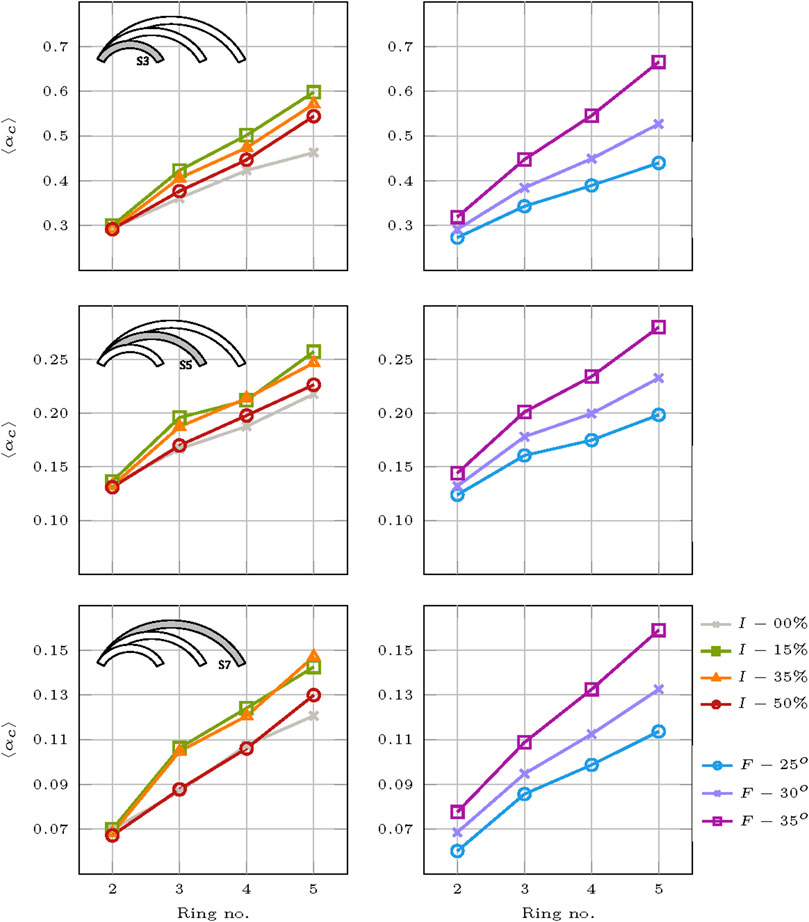
FIGURE 12. Parameter interaction of the collapse multipliers with respect to span and ring number for the big blocks.

From the plots, it is able to extract how the interlocking effect is more significant for the span of 3 m compared to the others, whereas its impact is more evident for the larger number of rings, as expected. Stacked bonds show the lowest multipliers in all the cases and the difference in results is achieved mostly for the span of 3 m.

Nevertheless, counter-intuitively, the arches with an interlocking coefficient of I-50% perform relatively worse than the two others. This can be due to the fact that as the structure is curved, the staggering of blocks forms an internal triangle, and its mechanism is activated faster compared to the other ones, and this can be also observed looking at the collapse mechanisms and also the close-up illustration given in Figure 13. For an interlocking of I-00% and I-50%, it is shown how the failure lines follow the same path from extrados to intrados, while in the case of I-15% and I-35%, it is interrupted as a combined sliding (given by the uplift) and rotation.

FIGURE 13

FIGURE 13. Change of failure mode at the load application point with variations of interlocking.

In spite of that, the multipliers for interlocking levels of I-15 and I-35 show a non-linear relationship with respect to spans of 5 and 7 m and for more than two rings. In general, I-15 produces larger multipliers but in the larger spans this outcome is shifted between I-15 and I-35. Friction parameters show a more linear influence and more equally distributed results which holds for all spans considered. Larger values of friction provide higher collapse multipliers. In general, the arches with a larger number of rings outperform the ones with fewer as the overall arch thickness increases.

A general overview of the results can be seen in Figure 14 following a similar layout of the graphs in Figure 12 but with reference to averaged spans. From this figure, a clearer relationship between the parameters can be seen for both interlocking and friction. As given in the previous graphs, a linear increase in the collapse multiplier is achieved when considering more rings. Both interlocking and friction play a more significant role when more rings are considered, while for the smaller number of rings, interlocking almost provides the same results for all levels and it starts to become influential with the consideration of three rings and above where also a better performance of I-15 and I-35 are obtained for the averaged results.

FIGURE 14

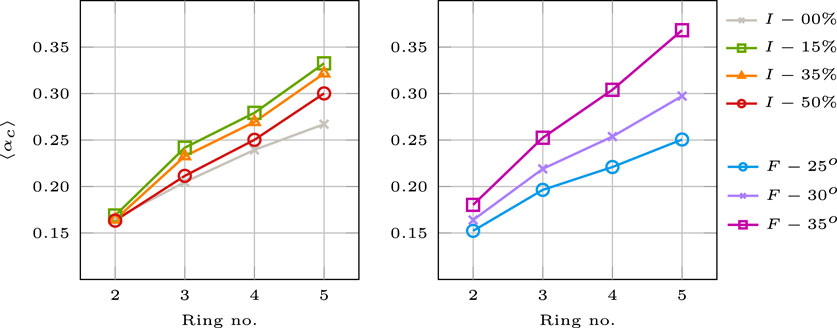
FIGURE 14. Parameter interaction of the collapse multipliers for the averaged span with respect to ring number for the big blocks.

5.2.2 Collapse multipliers considering small-sized blocks

Collapse multipliers for the small-sized blocks are grouped into plotted in graphs similar to the ones for big-sized blocks and shown in Figure 15. Differently from the big-sized blocks, for the small ones, interlocking plays an almost insignificant role for the collapse multiplier. This is attributed directly to the size of the blocks and the inability to achieve the tensile strength that masonry inherits from its texture. Smaller contact surfaces in this case result in a smaller grasp from unit to unit, thus yielding lower collapse multipliers in general, and they are not influenced by the interlock.

FIGURE 15

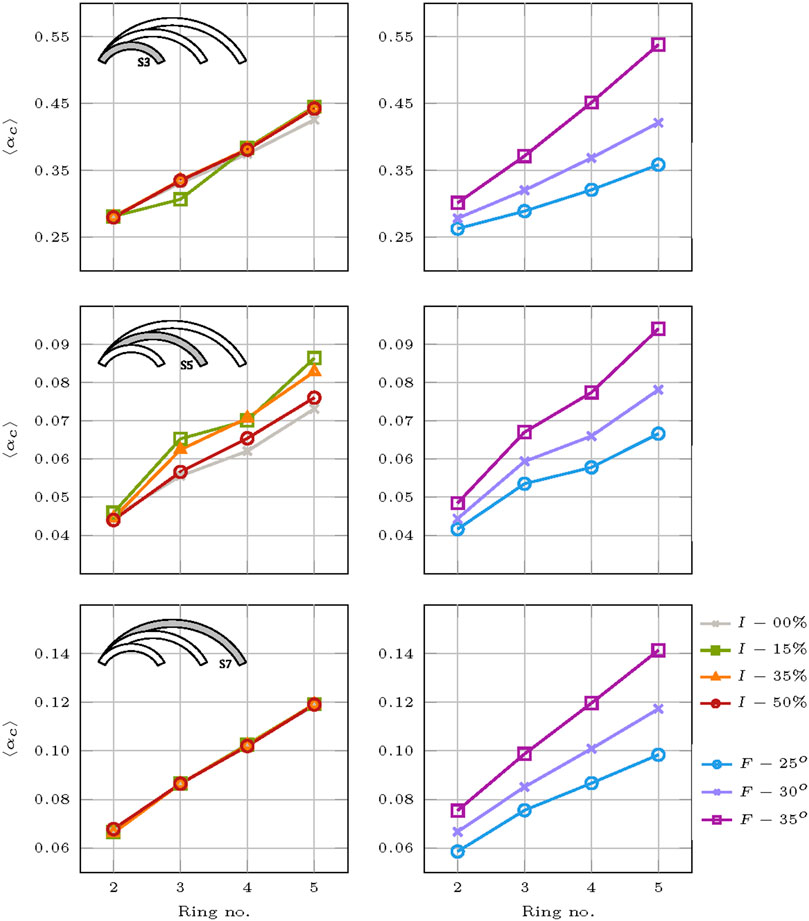
FIGURE 15. Parameter interaction of the collapse multipliers with respect to span and ring number for the small blocks.

Interestingly enough, beside the span of 3 and 7 m, for the mid-span of 5 m, interlocking shows a wider distribution of results and an increased significance. This is also more visible due to the very low results for this span compared to the others and a closer overview enlarges the differences. Nevertheless, the larger the number of rings, the more significant interlocking becomes, which was also shown for the big-sized blocks. Again, arches with an interlocking coefficient of I-50% perform relatively worse than the two others due to the same reasons explained for the big blocks, whereas the stacked ones behave the poorest in term of collapse multipliers in relative terms to the ones interlocked.

In contrast to the big blocks, the line plots are more linear and no interchange of results is seen when accounting for the various ring numbers. The size of blocks does not seem to impact the correlation of friction to the capacity of the arches. A linear influence is observed and the results are equally distributed, persisting for all spans considered. The increase in friction coefficient yields higher collapse multiplier values. Similarly, as the thickness of the arch rises, the ones with more rings perform better compared to those with fewer rings.

Figure 16 provides another summary of the findings for the small size of blocks in a layout similar to the previous graphs, but with the spans averaged as in Figure 14. This illustration highlights the relationship between the parameters for friction and interlocking apparent. As seen in the preceding figures, taking into account more rings results in a linear rise in the collapse multiplier. Also, for more rings, friction become more important, while for this case of small blocks, interlocking does not. Due to the use of different scales for collapse multipliers, in order to intensify the impact of friction and interlocking in Figures 12, 15, the overall influence is not visible for the different block sizes. In the case of averaged spans, this effect is more evident where influence of interlocking is easily seen as not prevailing in the case of small size and the opposite for the big size.

FIGURE 16

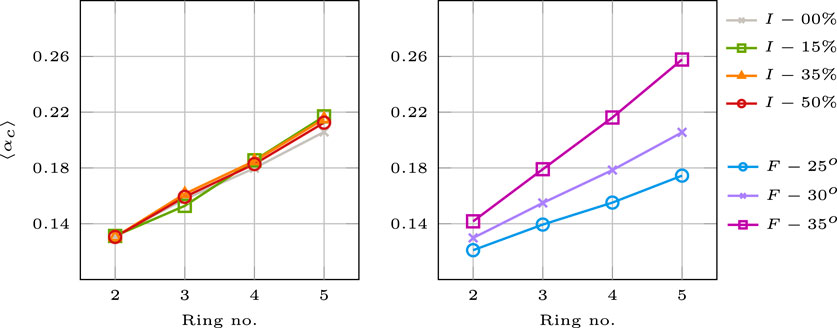
FIGURE 16. Parameter interaction of the collapse multipliers for the averaged span with respect to ring number for the small blocks.

5.2.3 Results comparison for both sizes

In all the above cases, the collapse multipliers are plotted without taking into consideration the results of equivalent arches. Figure 17 shows different plots of the collapse multipliers with respect to span by varying interlocking in the plot on the left and friction in the plot on the right. While considering equivalent arches, it is not possible to introduce the interlocking effect; thus, equivalent arches are given only for the varying friction parameters. Considering that the size of the blocks and thickness of the arches are kept the same for all the spans, a decrease in capacity is seen for the big blocks. In the case of small blocks, this does not properly occur because of a slight decrease obtained at the span of 5 m interrupting the linearity of results.

FIGURE 17

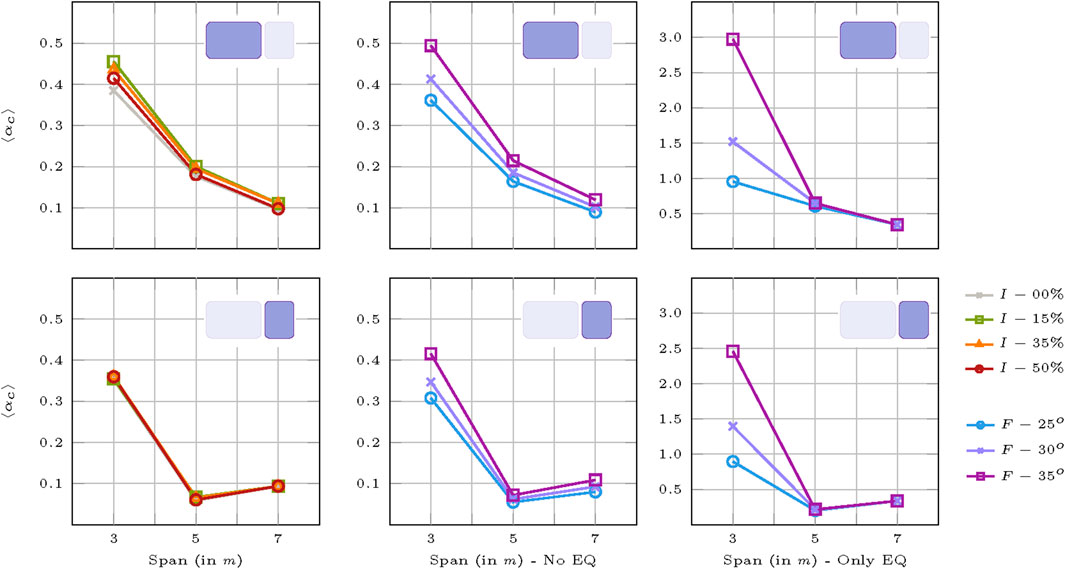
FIGURE 17. Parameter interaction of the collapse multipliers for averaged ring number with respect to span and block size; differences between equivalent arches and discretized ones.

From the interlocking effect on the graph, it is emphasized even more how it plays a role in the case of big blocks and is almost negligible for the small ones even with respect to span. On the other hand, when arches are discretized into multi-ring ones, friction is significant for both big and small blocks with a larger dispersion of results for the case of the former. The same cannot be said when equivalent arches are considered. A very significant dispersion of collapse multipliers is obtained for the case of the smallest 3 m span. Afterwards, the results do not differentiate among each other with respect to friction levels for the 5 and 7 m spans. This was also shown during the discussion of the collapse mechanisms. Carefully checking at the values of the collapse multipliers, the results for the discretized multi-ring arches and the equivalent ones vary by large amounts of about six times. More clearly, this discrepancy is highlighted in Figure 18.

FIGURE 18

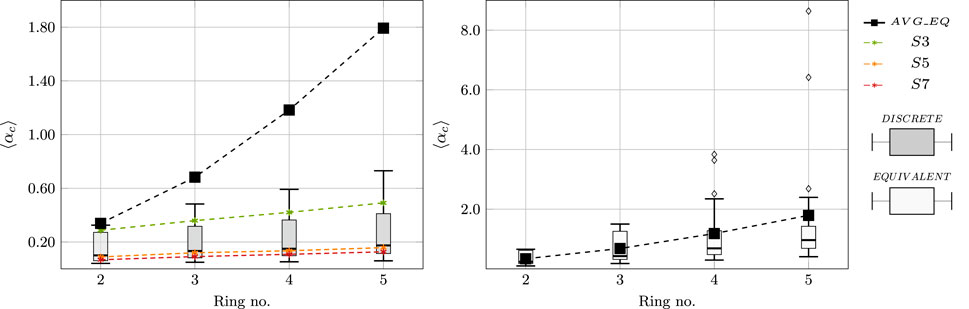
FIGURE 18. Boxplot of collapse multipliers with respect to ring size; differences between equivalent arches and discretized ones.

In Figure 18 (left), using a boxplot, the vertical distribution of results is illustrated, where both equivalent arches and discretized ones are shown. Boxplots are given with respect to ring number as a distribution of results without differentiation among other parameters. In other words, block size, span length, interlocking, and friction are averaged without considering the equivalent arches. Changes in the span length, however, are differentiated in the line plots by averaging block size, interlocking, and friction. Separately, the collapse multipliers for the equivalent arches are plotted in a line plot where all the considered parameters are averaged with the exception of ring number. Moreover, on the graph in Figure 18 (right), only the equivalent arches are shown as a boxplot and line plot to illustrate in more detail the distribution of the results for the case of equivalent arches. In this case, a distinct increase in strength is achieved for the equivalent arches. For this reason, it is crucial to highlight the importance of considering the internal structure of masonry during structural assessment, since even the slightest simplifications may lead to exaggerated overestimation.

6 Conclusive remarks

In this research, a parametric study of influential factors for the behavior of multi-ring arches was performed. Using an upper bound limit analysis aided by the in-house code, it was possible to achieve a large pool of simulations for this study. Factors considered included two levels for size (big and small), three levels for span (3, 5, and 7 m), four levels for ring number (2, 3, 4, and 5 rings) with also representative equivalent arches for all of the rings, four levels of interlocking coefficient (0, 15, 35, and 50%), and three levels of friction (25^o, 30^o, and 35^o). As such, 360 simulations were performed to detect the collapse multipliers and mechanisms. The main conclusions that have been deduced from the parametric study are as follows.

• Considering the size of the blocks, bigger ones perform better than the small ones in terms of the structural capacity of the multi-ring arch. Although for the big blocks there is a larger variety and range of distribution in the collapse multipliers, interlocking is better accomplished as a result of the larger areas of contact between the interconnected surfaces that provide a better grip.

• Regarding span, it was illustrated how there are different behaviors of such structures in correlation with other parameters. For small spans and large-sized blocks, the interlocking parameter has more influence, while for smaller spans in general, the friction parameter has an increased impact.

• Ring number, on the other hand, plays a crucial role in combination with interlocking and the friction coefficient. As more contact surfaces are involved in the collapse mechanism of multi-ring arches, interlocking and friction provide indirect tensile strength to masonry. Nevertheless, it was seen that interlocking is less influential when blocks of smaller size compose the rings.

• The friction coefficient, as a general overview, was better observed when using equivalent arches for the internal structure of the rings and comparing to the discretized ones. The correlation between sliding mechanisms of equivalent and ringed arches differed based on the internal structure, where friction proved to be crucial. Additionally, it was seen that larger values of the friction coefficient, even at smaller increments of 5^o, play an important role in the outcome.

Using the capabilities of the code for a discretized description of the texture, the importance of taking into account the internal structure of masonry has been emphasized. Equivalent arches, instead of the discretized multi-ring ones, produced an increase of about six times more for the collapse multipliers, resulting in an inflated overestimation of the structural capacity.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary material.

Author contributions

BN: Writing–original draft, Conceptualization, Methodology, Software, Data curation, Formal analysis, Investigation, Validation, Visualization; MPi: Writing–review and editing, Methodology, Funding acquisition, Software, Resources, Validation; PT: Writing–review and editing, Funding acquisition, Resources, Project administration, Supervision; MPa: Writing–review.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work is supported by the Sapienza University Research Grant “Progetti Grandi” 2021 (B85F21008380001) and the Sapienza Research Grant “Progetti Medi” 2022 (B83C22007020005).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahrens, J., Geveci, B., and Law, C. (2005). “36 - Paraview: an end-user tool for large-data visualization,” in Visualization handbook. Editors C. D. Hansen, and C. R. Johnson (Burlington: Butterworth-Heinemann), 717–731. doi:10.1016/B978-012387582-2/50038-1

CrossRef Full Text | Google Scholar

ApS, M. (2022). MOSEK optimizer API for Python 9, 3, 18.

Google Scholar

Baggio, C., and Trovalusci, P. (1998). Limit analysis for no-tension and frictional three-dimensional discrete systems. Mech. Struct. Mach. 26, 287–304. doi:10.1080/08905459708945496

CrossRef Full Text | Google Scholar

Baggio, C., and Trovalusci, P. (2000). Collapse behaviour of three-dimensional brick-block systems using non-linear programming. Struct. Eng. Mech. 10, 181–195. doi:10.12989/sem.2000.10.2.181

CrossRef Full Text | Google Scholar

Barlow, W. H. (1846). On the existence (practically) of the line of equal horizontal thrust in arches, and the mode of determining it by geometrical construction. (includes plate). Minutes Proc. Institution Civ. Eng. 5, 162–172. doi:10.1680/imotp.1846.24301

CrossRef Full Text | Google Scholar

Block, P., Ciblac, T., and Ochsendorf, J. (2006). Real-time limit analysis of vaulted masonry buildings. Comput. Struct. 84, 1841–1852. doi:10.1016/j.compstruc.2006.08.002

CrossRef Full Text | Google Scholar

Bruggi, M. (2014). Finite element analysis of no-tension structures as a topology optimization problem. Struct. Multidiscip. Optim. 50, 957–973. doi:10.1007/s00158-014-1093-z

CrossRef Full Text | Google Scholar

Bruggi, M., Lógó, B., and Deák, Z. (2021). Funicular analysis of ribbed masonry vaults: a case study. Int. J. Archit. Herit. 1, 1809–1823. doi:10.1080/15583058.2021.1910879

CrossRef Full Text | Google Scholar

Cangi, G. (2023). Manuale del consolidamento e restauro: archi e volte. Tecniche costruttive, dissesti e interventi (DEI Srl).

Google Scholar

Chen, S., and Bagi, K. (2020). Crosswise tensile resistance of masonry patterns due to contact friction. Proc. R. Soc. A Math. Phys. Eng. Sci. 476, 20200439. doi:10.1098/rspa.2020.0439

CrossRef Full Text | Google Scholar

Choudhury, T., Milani, G., and Kaushik, H. B. (2020). Experimental and numerical analyses of unreinforced masonry wall components and building. Constr. Build. Mater. 257, 119599. doi:10.1016/j.conbuildmat.2020.119599

CrossRef Full Text | Google Scholar

D’Altri, A. M., Sarhosis, V., Milani, G., Rots, J., Cattari, S., Lagomarsino, S., et al. (2020). Modeling strategies for the computational analysis of unreinforced masonry structures: review and classification. Archives Comput. Methods Eng. 27, 1153–1185. doi:10.1007/s11831-019-09351-x

CrossRef Full Text | Google Scholar

Drucker, D. C. (1953). Coulomb friction, plasticity, and limit loads. Tech. rep., Brown Univ Providence R. I. DIV Appl. Math. doi:10.21236/AD0002902

CrossRef Full Text | Google Scholar

Gilbert, M. (1998). On the analysis of multi-ring brickwork arch bridges. London: CRC Press, 109–118. doi:10.1201/9781003078494-16

CrossRef Full Text | Google Scholar

Gilbert, M., Casapulla, C., and Ahmed, H. (2006). Limit analysis of masonry block structures with non-associative frictional joints using linear programming. Comput. Struct. 84, 873–887. doi:10.1016/j.compstruc.2006.02.005

CrossRef Full Text | Google Scholar

Gilbert, M., and Melbourne, C. (1994). Rigid-block analysis of masonry structures. Struct. Eng. 72, 356–361.

Google Scholar

Gilbert, M., and Melbourne, C. (1995). Analysis of multi-ring brickwork arch bridges, 225–238. doi:10.1680/ab.20481.0023

CrossRef Full Text | Google Scholar

Giuffrè, A., and Carocci, C. (1997). Codice di Pratica per la sicurezza e la conservazione dei Sassi di Matera (La Bautta).

Google Scholar

Kassotakis, N., Sarhosis, V., Forgács, T., and Bagi, K. (2017). “Discrete element modelling of multi-ring brickwork masonry arches,” in 13th Canadian masonry symposium (halifax, Canada).

Google Scholar

Kirsch, U. (1993). Structural optimization: fundamentals and applications. Springer-Verlag Berlin Heidelberg. doi:10.1007/978-3-642-84845-2

CrossRef Full Text | Google Scholar

Lourenço, P. B. (1998). Experimental and numerical issues in the modelling of the mechanical behaviour of masonry.

Google Scholar

Lourenço, P. B., and Rots, J. G. (1997). Multisurface interface model for analysis of masonry structures. J. Eng. Mech. 123, 660–668. doi:10.1061/(asce)0733-9399(1997)123:7(660)

CrossRef Full Text | Google Scholar

Masiani, R., and Trovalusci, P. (1996). Cosserat and cauchy materials as continuum models of brick masonry. Meccanica 31, 421–432. doi:10.1007/bf00429930

CrossRef Full Text | Google Scholar

Matthys, J. H., and Noland, J. L. (1989). International seminar, evaluating, strengthening and retrofitting masonry buildings. Boulder, Colo: Masonry Society (U. S.) University of Texas at Arlington. Construction Research Center.

Google Scholar

Melbourne, C., Begimgil, M., and Gilbert, M. (1995a). The load test to collapse of a 5m span brickwork arch bridge with tied spandrel walls, 509–517. doi:10.1680/ab.20481.0051

CrossRef Full Text | Google Scholar

Melbourne, C., Begimgil, M., and Weekes, L. (1995b). The load test to collapse a 5m span brickwork flat arch barrel, 397–406. doi:10.1680/ab.20481.0040

CrossRef Full Text | Google Scholar

Melbourne, C., Holm, G., Bien, J., Casas, J. R., Tommor, A., Bengtsson, P. E., et al. (2007). Tech. Rep., USalford, manchester, UK. EC sixth framework ProgramSustainable bridges – assessment for future traffic demands and longer LivesTIP3-CT-2003-001653, Masonry arch bridges: sustainable bridges background document 4.7.

Google Scholar

Melbourne, C., and Tao, H. (1995). The behaviour of open spandrel masonry arch bridges, 239–244. doi:10.1680/ab.20481.0024

CrossRef Full Text | Google Scholar

Nela, B., Jiménez Rios, A., Pingaro, M., Reccia, E., and Trovalusci, P. (2022). Limit analysis of locally reinforced masonry arches. Eng. Struct. 271, 114921. doi:10.1016/j.engstruct.2022.114921

CrossRef Full Text | Google Scholar

Nela, B., Pingaro, M., Jiménez Rios, A., Reccia, E., and Trovalusci, P. (2023a). Masonry arches simulations using cohesion parameter as code enrichment for limit analysis approach. Int. J. Mason. Res. Innovation 1, 1. doi:10.1504/IJMRI.2023.10053576

CrossRef Full Text | Google Scholar

Nela, B., Pingaro, M., and Trovalusci, P. (2023b). Data from the parametric analysis of multi-ring masonry arches using a limit analysis approach for the span of 3m. doi:10.5281/zenodo.8369933

CrossRef Full Text | Google Scholar

Nela, B., Pingaro, M., and Trovalusci, P. (2023c). Data from the parametric analysis of multi-ring masonry arches using a limit analysis approach for the span of 5m. doi:10.5281/zenodo.8370031

CrossRef Full Text | Google Scholar

Nela, B., Pingaro, M., and Trovalusci, P. (2023d). Data from the parametric analysis of multi-ring masonry arches using a limit analysis approach for the span of 7m. doi:10.5281/zenodo.8370053

CrossRef Full Text | Google Scholar

Orduña, A., and Lourenço, P. B. (2005). Three-dimensional limit analysis of rigid blocks assemblages. part ii: load-path following solution procedure and validation. Int. J. Solids Struct. 42, 5161–5180. doi:10.1016/j.ijsolstr.2005.02.011

CrossRef Full Text | Google Scholar

Pantò, B., Cannizzaro, F., Caddemi, S., and Caliò, I. (2016). 3d macro-element modelling approach for seismic assessment of historical masonry churches. Adv. Eng. Softw. 97, 40–59. doi:10.1016/j.advengsoft.2016.02.009

CrossRef Full Text | Google Scholar

Pantò, B., Chisari, C., Macorini, L., and Izzuddin, B. A. (2022). A hybrid macro-modelling strategy with multi-objective calibration for accurate simulation of multi-ring masonry arches and bridges. Comput. Struct. 265, 106769. doi:10.1016/j.compstruc.2022.106769

CrossRef Full Text | Google Scholar

Pepe, M., Sangirardi, M., Reccia, E., Pingaro, M., Trovalusci, P., and de Felice, G. (2020). Discrete and continuous approaches for the failure analysis of masonry structures subjected to settlements. Front. Built Environ. 6. doi:10.3389/fbuil.2020.00043

CrossRef Full Text | Google Scholar

Radenkovic, D. (1961). Théorèmes limites pour un matériau de Coulomb á dilation non standardisée. Comptes rendus Hebd. séances l’Académie Sci. 252, 4103.

Google Scholar

Rahman, A., and Ueda, T. (2014). Experimental investigation and numerical modeling of peak shear stress of brick masonry mortar joint under compression. J. Mater. Civ. Eng. 26. doi:10.1061/(ASCE)MT.1943-5533.0000958

CrossRef Full Text | Google Scholar

Rios, A. J., Nela, B., Pingaro, M., Reccia, E., and Trovalusci, P. (2023). Parametric analysis of masonry arches following a limit analysis approach: influence of joint friction, pier texture, and arch shallowness. Math. Mech. Solids. doi:10.1177/10812865231175385

CrossRef Full Text | Google Scholar

Sarhosis, V., De Santis, S., and de Felice, G. (2016). A review of experimental investigations and assessment methods for masonry arch bridges. Struct. Infrastructure Eng. 12, 1439–1464. doi:10.1080/15732479.2015.1136655

CrossRef Full Text | Google Scholar

Sarhosis, V., and Lemos, J. (2018). A detailed micro-modelling approach for the structural analysis of masonry assemblages. Comput. Struct. 206, 66–81. doi:10.1016/j.compstruc.2018.06.003

CrossRef Full Text | Google Scholar

Tabrizikahou, A., Hadzima-Nyarko, M., Kuczma, M., and Lozančić, S. (2021). Application of shape memory alloys in retrofitting of masonry and heritage structures based on their vulnerability revealed in the bam 2003 earthquake. Materials 14, 4480. doi:10.3390/ma14164480

PubMed Abstract | CrossRef Full Text | Google Scholar