Ventilation and disease monitoring of indoor spaces and public transportation using an NDIR sensor network

With the COVID-19 pandemic still ongoing, there is a need to ensure that people are not subjected to the risk of getting infected with the disease. Since COVID-19 is airborne, engineering controls must be provided to monitor and mitigate the spread of the disease in the air. One of the measures is to ensure proper ventilation within indoor spaces where superspreader events were previously documented in poorly ventilated spaces. CO₂ levels reflect the rate at which the used air within is replaced and, therefore, can be used as a proxy for COVID-19 risk. This study developed economical CO₂ monitors which are deployed across indoor spaces and public transportation, such as air-conditioned jeepneys, to communicate the risk. Using the least squares method on the first-order ODE of mass balance, a multivariate method is devised for deriving the occupancy and the ventilation rate from the recorded CO₂ levels. Using the multivariate method, the ventilation rates of different indoor spaces are determined and used for the subsequent computations using the Wells–Riley model to derive the respective infection risk, particularly of COVID-19.

1 Introduction

At the onset of the ongoing COVID-19 pandemic, indoor spaces are identified to have higher infection rates than outdoor spaces (Qian, et al., 2021). Poor ventilation has been attributed to many of the superspreader events (Miller, et al., 2021). Because of the low air changes due to poor ventilation, SARS-CoV-2, the virus that causes COVID-19, is found to be deposited on ventilation ducts and other surfaces with greater distances which cannot be explained by droplet transmissions (Nissen, et al., 2020). A literature review on droplet transmission shows no direct evidence for ballistic droplets as the route of transmission of any diseases (Chen, et al., 2020). Inhalation of the suspended pathogenic aerosols is determined to have been causing COVID-19 infections (Greenhalgh, et al., 2021) as confirmation that SARS-CoV-2 is detected within particulate matter captured in the air (López, et al., 2021). As a result, medical insights on respiratory virus transmission and the subsequent infection control programs have been undergoing a paradigm shift in acknowledging airborne transmissions (Klopmas, et al., 2021) despite historical resistance (Jimenez, et al., 2022).

Initially for measles, which was then identified as an airborne disease (Wells, 1955), an epidemiological model was developed to estimate its infection risk in classrooms (Riley, et al., 1978). The application of the model has been extended to tuberculosis (Gammaitoni and Nucci, 1997) and then to COVID-19 (Buonnano, et al., 2020). This enables readily quantifying the practical infection risk by compiling all the previous superspreader events due to shared room air transmission (Peng, et al., 2022) and using CO₂ as the relative risk indicator (Bazant, et al., 2021; Peng and Jimenez, 2021).

However, the formulation of using CO₂ as a relative risk indicator mainly assumes that the recorded CO₂ level has been the steady-state level. When not in steady-state conditions, the ventilation rate must be derived from the prior knowledge of the occupancy. Such a condition is true for buildings with a low supply of outdoor air, provided that the rate does not vary in time (Rudnick and Milton, 2003). This study aims to develop a multivariate technique for deriving occupancy and ventilation rates simultaneously. In addition, this study also aims to create a low-cost CO₂ monitor which will cover the physical measurement of the CO₂ concentration. These will enable the study to determine the infection risk of COVID-19, the disease that is being closely monitored due to the ongoing pandemic, over indoor spaces such as classrooms and the common modes of transportation present in the Philippines.

2 Materials and methods

2.1 Multivariate technique on deriving occupancy and ventilation

This study assumes a well-mixed indoor room where the CO₂ emissions from the occupants are evenly distributed across the room while air is constantly replaced by outdoor air with a uniform outdoor CO₂ concentration. This results in a first-order ordinary differential equation:

$\frac{\mathit{d}\mathit{C}}{\mathit{d}\mathit{t}}=\frac{\mathit{E}}{\mathit{V}}-\left(\mathit{C}-{\mathit{C}}_{\mathit{o}\mathit{u}\mathit{t}\mathit{d}\mathit{o}\mathit{o}\mathit{r}}\right)\mathit{\lambda }(1)$

where $C$ is the CO₂ concentration, $E$ is the CO₂ emission rate, $V$ is the volume of the room, and $C_{outdoor}$ is the uniform outdoor CO₂ concentration.

This study will focus on the differential equation given in Eq. 1. The first-order ODE is discretized and restated as

$\frac{{\mathit{C}}_{\mathit{i}}-{\mathit{C}}_{\mathit{i}-\mathbf{1}}}{\Delta \mathit{t}}=\frac{\mathit{E}}{\mathit{V}}-\left({\mathit{C}}_{\mathit{i}}-{\mathit{C}}_{\mathit{o}\mathit{u}\mathit{t}\mathit{d}\mathit{o}\mathit{o}\mathit{r}}\right)\mathit{\lambda }(2)$

where $C_i$ is the CO₂ level measured at the present time, $C_{i-1}$ is the previously measured CO₂ level, and $\Delta t$ is the time between the CO₂ readings.

The emission rate $E$ can be expressed as a function of the number of occupants $n$. The breathing rate and exhaled CO₂ concentration are assumed as an average value of $0.65\raisebox{1ex}{$m^3$}\!\left/ \!\raisebox{-1ex}{$hr$}\right.$ (Buonnano, et al., 2020; $38000ppm$ Bazant, et al., 2021 $38000ppm$). The average value of both the breathing rate and the exhaled CO₂ concentration are considered because of the limitation of the computational power of the microcontroller unit used in the developed CO₂ monitor. The reader is pointed to the studies of Persily and de Jonge (2018) and Yang et al. (2020) for CO₂ generation that varies with age, gender, body mass, and the nature of physical activity.

The whole Eq. 2 is multiplied with $\Delta t$, which is expressed in terms of seconds, therefore needing conversion. This results in the Eq. 3 below:

$\mathbf{36}\mathit{V}\left({\mathit{C}}_{\mathit{i}}-{\mathit{C}}_{\mathit{i}-\mathbf{1}}\right)=\mathbf{24700}\Delta \mathit{t}\mathit{n}-\left({\mathit{C}}_{\mathit{i}}-{\mathit{C}}_{\mathit{o}\mathit{u}\mathit{t}\mathit{d}\mathit{o}\mathit{o}\mathit{r}}\right)\mathit{Q}\Delta \mathit{t}(3)$

This study assumes that CO₂ readings from the CO₂ sensors are measured at regular intervals, although it can also work for readings at irregular intervals. As this study maintained that only integers will be used to simplify computations for the target ESP32 microcontroller, $\Delta t$, which is also an integer, is kept at the right-hand side of Eq. 3.

Eq. 3 will then have two unknowns, namely, the estimated occupancy $n$ and ventilation rate $\mathit{\lambda }$. To determine the two unknowns from the given time history of CO₂ levels containing N number of datapoints, a multivariate regression analysis will be performed, resulting in Eqs 4, 5 with two unknowns:

$\mathit{n}\frac{\mathbf{10000}}{\mathbf{3600}\mathit{V}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}{\left(\mathbf{247}\right)}^{\mathbf{2}}+\mathit{\lambda }\frac{\mathbf{247}}{\mathbf{36}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}\left({\mathit{C}}_{\mathit{o}\mathit{u}\mathit{t}\mathit{d}\mathit{o}\mathit{o}\mathit{r}}-{\mathit{C}}_{\mathit{i}}\right)=\mathbf{24700}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}\frac{\left({\mathit{C}}_{\mathit{i}}-{\mathit{C}}_{\mathit{i}-\mathbf{1}}\right)}{\Delta \mathit{t}}(4)$

$\mathit{\lambda }\frac{\mathbf{1}}{\mathbf{3600}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}{\left({\mathit{C}}_{\mathit{o}\mathit{u}\mathit{t}\mathit{d}\mathit{o}\mathit{o}\mathit{r}}-{\mathit{C}}_{\mathit{i}}\right)}^{\mathbf{2}}+\mathit{n}\frac{\mathbf{247}}{\mathbf{36}\mathit{V}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}\left({\mathit{C}}_{\mathit{o}\mathit{u}\mathit{t}\mathit{d}\mathit{o}\mathit{o}\mathit{r}}-{\mathit{C}}_{\mathit{i}}\right)={\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}\frac{\left({\mathit{C}}_{\mathit{i}}-{\mathit{C}}_{\mathit{i}-\mathbf{1}}\right)\left({\mathit{C}}_{\mathit{o}\mathit{u}\mathit{t}\mathit{d}\mathit{o}\mathit{o}\mathit{r}}-{\mathit{C}}_{\mathit{i}}\right)}{\Delta \mathit{t}}(5)$

With a known volume $V$ in the room, the number of occupants $n$ can be estimated simultaneously with the ventilation rate $\lambda$.

To determine the stability of the solution, the analytical solution of the first-order ODE is derived:

$\mathit{C}\left(\mathit{t}\right)=\left[\frac{\mathit{E}}{\mathit{\lambda }\mathit{V}}+{\mathit{C}}_{\mathit{o}\mathit{u}\mathit{t}}\right]-\left[\frac{\mathit{E}}{\mathit{\lambda }\mathit{V}}+{\mathit{C}}_{\mathit{o}\mathit{u}\mathit{t}}-{\mathit{C}}_{\mathbf{0}}\right]{\mathit{e}}^{-\mathit{\lambda }\mathit{t}}(6)$

Substituting the analytical solution to the discrete first-order ODE and simplifying will result in the relationship between the time step and ventilation rate in a stable solution:

$\frac{{\mathit{e}}^{-\mathit{\lambda }\left(∆\mathit{t}\right)}-\mathbf{1}}{∆\mathit{t}}=-\mathit{\lambda }(7)$

$\left[\frac{\mathit{E}}{\mathit{\lambda }\mathit{V}}+{\mathit{C}}_{\mathit{o}\mathit{u}\mathit{t}}-{\mathit{C}}_{\mathbf{0}}\right]\left[{\mathit{e}}^{-\mathit{\lambda }\left(∆\mathit{t}\right)}+\mathit{\lambda }\left(∆\mathit{t}\right)-\mathbf{1}\right]\in \left(\mathbf{0,1.5}\right)(8)$

Given that the sensor transmits integer values for the CO₂ levels, for the solution to remain stable, the following relation must be satisfied as values less than zero reflect that the computed ventilation rates are negative, while values greater than 1.5 reflect that the time scale for the temporal averaging is reducing the resolution of the solution. Figure 1 shows a sample time history of ventilation rate estimates over different given time steps.

FIGURE 1

FIGURE 1. Solution stability on a sample case.

Alternatively, if the number of occupants $n$ is already known, the regression equation can be used to estimate the average ventilation rate.

$\mathit{\lambda }=\frac{\mathbf{24700}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}\frac{\left({\mathit{C}}_{\mathit{i}}-{\mathit{C}}_{\mathit{i}-\mathbf{1}}\right)}{\Delta \mathit{t}}-\mathit{n}\frac{\mathbf{10000}}{\mathbf{3600}\mathit{V}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}{\left(\mathbf{247}\right)}^{\mathbf{2}}}{\frac{\mathbf{247}}{\mathbf{36}}{\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}}\left({\mathit{C}}_{\mathit{o}\mathit{u}\mathit{t}\mathit{d}\mathit{o}\mathit{o}\mathit{r}}-{\mathit{C}}_{\mathit{i}}\right)}(9)$

2.2 Wells–Riley model

Using the derived ventilation rates and occupancy, the infection risk due to airborne diseases can be computed using the Wells–Riley model.

$P=1-\exp \left(-Q_i{B}_0{f}_{i}t\right)(10)$

where $P$ is the infection risk, $B_0$ is the breathing rate, t is the duration of exposure, $f_i$ is the inward filtration efficiency of the mask, and $Q_i$ is the quanta concentration. This study assumes that the room is a well-mixed environment where the quanta concentration is uniform and is determined by a first-order ODE in Eq. 11 below:

$\frac{d{Q}_i}{dt}=\frac{q_i{f}_o}{V}-Q_i\left[\lambda \right](11)$

where $q_i$ is the quantum generation rate and $f_o$ is the outward filtration efficiency of the mask. This study assumes an asymptomatic case with the upper-bound quantum generation rates of 165 quanta/hr for the Alpha variant, 935 quanta/hr for the Delta variant, and 2345 quanta/hr for the Omicron variant. The inward and outward efficiencies of masks are established as 50% for surgical masks and 90% for medical-grade N95 masks (Dai and Zhao, 2023).

Scenario the worst case, which is the exposure to the steady-state condition, by substituting the analytical solution for the mixing equation of quanta in Eq. 11 and substituting the Wells–Riley Model in Eq. 10 yield Eq. 12 for the infection risk as a function of time, volume, ventilation rate, room volume, and the reduction factors of the respiratory protection:

$\mathit{P}\left(\mathit{t},\mathit{V},\mathit{\lambda },{\mathit{q}}_{\mathit{i}},{\mathit{f}}_{\mathit{o}},{\mathit{f}}_{\mathit{i}},{\mathit{B}}_{\mathbf{0}}\right)=\mathbf{1}-\mathbf{exp}\left(-\frac{{\mathit{q}}_{\mathit{i}}{\mathit{f}}_{\mathit{o}}{\mathit{f}}_{\mathit{i}}{\mathit{B}}_{\mathbf{0}}}{\mathit{\lambda }\mathit{V}}\mathit{t}\right)(12)$

Three infection risk cases are then explored for each variant in each setting: 1) with the occupants not wearing masks, 2) two-way masking with surgical masks, and 3) two-way masking with N95 masks.

2.3 CO₂ monitoring

This study deployed these CO₂ monitors, shown in Figure 2, in classrooms of the UP Institute of Civil Engineering. This study has also tackled making a reliable yet economical CO₂ monitor for potential mass distribution. Winsen MH-Z19E NDIR sensors are used, which are connected to an ESP32 module which then transmits the CO₂ readings through the internet of things (IoT) using its built-in Bluetooth and WiFi module. The readings and the estimates on ventilation rates will be displayed through a connected LCD module.

FIGURE 2

FIGURE 2. Components of the CO₂ monitor device.

This study deployed these CO₂ monitors in classrooms of the UP Institute of Civil Engineering. Four scenarios were tested: when people are occupying the room while the room is enclosed for air-conditioning (stale air seeps out through leaks), when the room is occupied by the one conducting the measurement, when there is one-way ventilation, and when there is two-way ventilation. This study has also deployed these CO₂ monitors in public transportation during operation. The list and the details of the public transportation are shown in Figure 3.

FIGURE 3

FIGURE 3. Indoor spaces and public transportation subject in CO₂ monitoring.

3 Results and discussion

3.1 Classroom

The CO₂ levels in the first classroom (Volume: 154 m³) were monitored during class, as shown in Figure 4. The algorithm has estimated a lower occupancy rate of eight people while estimating a ventilation rate of 0.1 ACH. This is because of the lower breathing activity rate in the classroom due to the students listening only to the lecture, resulting in lower CO₂ levels. Artificially, plugging the actual number of occupants of 20 using Eq. 9 gives a ventilation rate of 3.2 ACH, which does not fit the ventilation rates of a typical fully enclosed room.

FIGURE 4

FIGURE 4. ICE Room 408 CO₂ readings.

On the other hand, the measurements in Room 409A were conducted right after the students had vacated the room at CO₂ levels of 1797 ppm. Eqs 4, 5 struggled to determine occupancy and ventilation rates on downward trends as the equations gave negative values, so Eq. 9 was used instead, as shown in Figure 5.

FIGURE 5

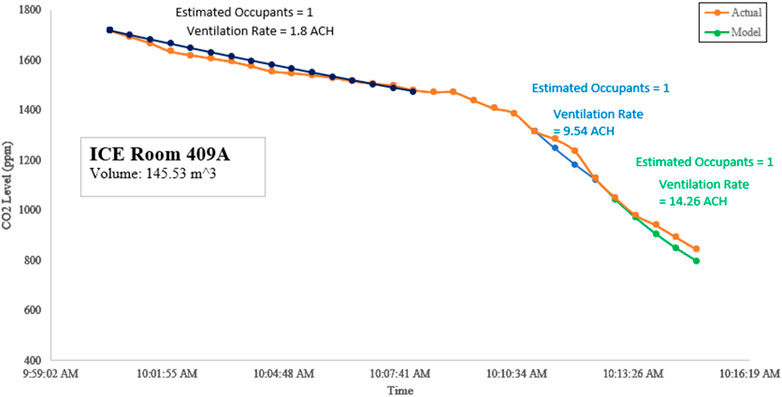
FIGURE 5. ICE Room 409A CO₂ readings when air only exits through the leaks (dark blue), when windows are opened (light blue), and when two-way ventilation is implemented (green).

Room 409A has an adjacent room that was separated by a removable barrier which can introduce more leaks for the stale air within to pass through. As a result, a ventilation rate of 1.8 ACH was determined. However, opening the windows on just one side of the room results in the ventilation rate increasing to 9.54 ACH. Moreover, opening the door on the other side of the room to facilitate two-way ventilation results in the ventilation rate increasing further to 14.26 ACH.

3.2 Traditional jeepney

CO₂ levels were also measured in a traditional jeepney. Traditional jeepneys are windowless public transport vehicles, with both sides open. Their typical seating capacity ranges from 12 to 18 for short type and up to 26–32 for long type. A short-type jeepney was considered in this study.

The jeepney initially was stationary as it waited for passengers to fully board. As shown in Figure 6A, the ventilation rate was determined to be 47.56 ACH. As the jeepney started to move, the ventilation rate further increased to 151.54 ACH, as shown in Figure 6B.

FIGURE 6

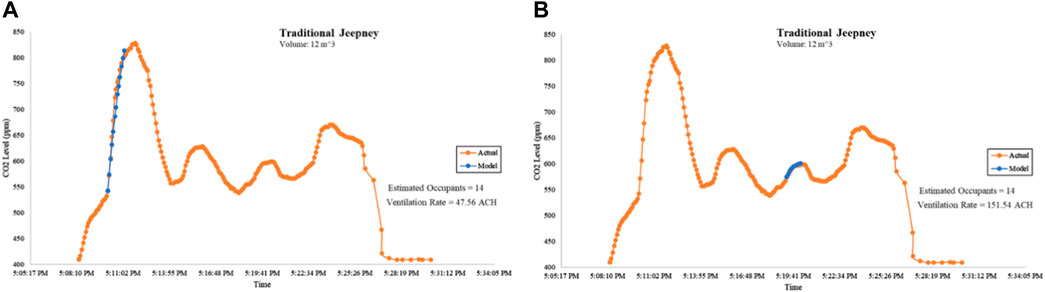
FIGURE 6. CO₂ levels at a traditional jeepney. (A) Derivation of the ventilation rate when the jeepney was stationary and (B) derivation of the ventilation rate when the jeepney was in motion.

The algorithm programmed to the microcontroller units resets its multivariate analysis once it detects an inflection point as this indicates a change in the occupancy and/or the ventilation rate. For example, at the time frame shown in Figure 6A, the jeepney was stationary. After that, the jeepney began moving, resulting in a change in ventilation rates.

3.3 Modern jeepney

Air-conditioned minibuses, also known as the “Modern Jeepneys,” were also subjected to CO₂ measurements. Unlike air-conditioned commuter vehicles such as buses or trains, these modern jeepneys follow the operation of traditional jeepneys, i.e., they stop and open the doors randomly whenever a passenger gets on or off. This scenario creates imperfect mixing. Their typical seating capacity is 23, with up to five people standing on the aisle.

As shown in Figure 7, due to the imperfect mixing within the modern jeepneys, Eqs 4, 5 estimated high emission rates and high ventilation rates. So, Eq. 9 was instead used, using the known occupant count of 26 people, resulting in a ventilation rate of 1.23 ACH.

FIGURE 7

FIGURE 7. CO₂ levels at the modern jeepney.

3.4 MRT-3

To capture a perfectly mixed environment for the derivation of the ventilation rates, the CO₂ measurements on the MRT 3000 trains of the MRT-3 lines are focused on the first leg of the trip before the doors reopened on the next station, as shown in Figure 8. MRT 3000 coaches are air-conditioned, and the windows on both sides are closed. The derived ventilation rate was 2.78 ACH.

FIGURE 8

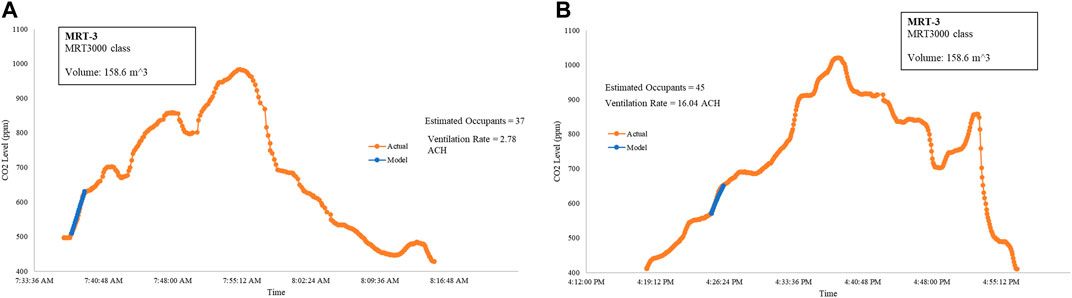
FIGURE 8. Derivation of the ventilation rate on MRT-3 trains at the first leg of the northbound trip (A) and mid-journey of the southbound trip (B).

Once the doors are opened, as shown in Figure 8B, the ventilation rate increases to 16.04 ACH. Both the ACH reports are done, given that the estimated number of occupants matched the actual number of occupants.

The train direction and the time presented in Figure 8 are at a moderately busy window of MRT-3 operations. Note that a sudden influx of passengers due to rush hour can plummet the ventilation rate. One way to increase the ventilation rate in commuter trains is by opening the windows (Shinohara, et al., 2021).

3.5 LRT-2

Unlike MRT-3, the trains on LRT-2 have a continuous air-conditioned train cabin extending from the front to the back. The windows on both sides are also closed. As the train accelerates, the air from the front rushes to the back of the train, resulting in internal compartmentalization of the inside air. As shown in Figure 9, despite Eqs 4, 5 having good estimates of the occupancy, the ventilation rate was estimated to be at 15.34 ACH.

FIGURE 9

FIGURE 9. Estimation of ventilation rates from CO₂ levels within LRT-2 trains.

3.6 LRT-1

This study has also covered the modern air-conditioned trains of the LRT-1 line. Within LRT-1, the train was divided into three separate train wagons. The windows on both sides were also closed. The passenger count within the train wagon was constant from the EDSA Station to Central Station. The CO₂ levels within that interval were used in Eqs 4, 5, as shown in Figure 10.

FIGURE 10

FIGURE 10. Estimation of the ventilation rates from CO₂ levels within LRT-1 trains.

Although doors were opening and closing during the train stops at train stations, the drop in CO₂ levels and the change in ventilation rates were not observed as the passengers were not moving within and passengers stood by the doors. Northbound LRT-1 trains are typically busy at this time of the evening as they ferry people who are working in Pasay city, Makati city, and Manila city to North Manila. The average ventilation rate measured from the EDSA Station to Central Station was determined to be at 3.62 ACH. Eqs 4, 5 returned the negative values for occupancy and ventilation rate when tested over the downward trend.

3.7 EDSA Carousel bus

The CO₂ measurements were done during the rush hour when the air-conditioned buses were queuing at the bus stops. The windows on both sides are closed. Figure 11A shows Eqs 4, 5 being tested at the time the bus was moving at a slow pace, while Figure 11B shows Eqs 4, 5 being tested at the time the bus was stationary as it queued for the bus stop.

FIGURE 11

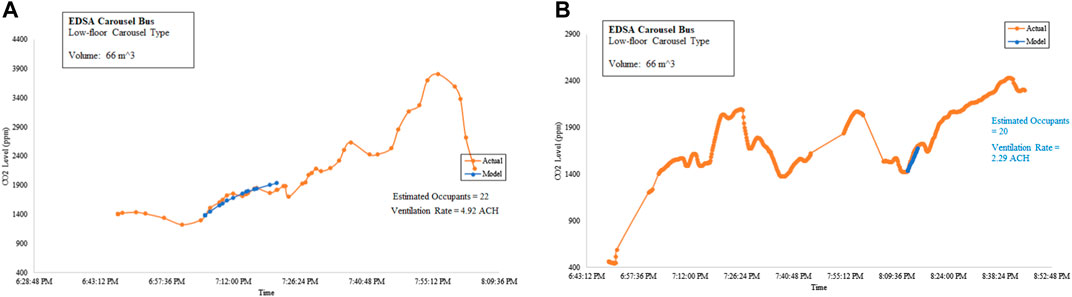
FIGURE 11. Estimation of ventilation rates from CO₂ levels within EDSA Carousel buses. (A) Northbound and (B) southbound.

Upon Eqs 4, 5 computing the same occupancy as the actual occupancy, the ventilation rates were determined. The ventilation rate of the EDSA Carousel bus when stationary was 2.29 ACH, while when in motion, the ventilation rate was 4.92 ACH.

3.8 Provincial bus

CO₂ levels were measured in the first continuous leg of the 12-h journey onboard an air-conditioned provincial bus without the doors opening. As shown in Figure 12, upon Eqs 4, 5 computing the same number of people as with the actual number of people, the ventilation rate was determined to be equal to 2.49 ACH.

FIGURE 12

FIGURE 12. Estimation of the ventilation rates from CO₂ levels within a provincial bus.

3.9 COVID-19 infection risk

With the ventilation rates derived, the infection risks are determined in Tables 1, 2, and 3 for the Alpha, Delta, and Omicron variants, respectively.

TABLE 1

TABLE 1. Summary of infection risk due to the Alpha variant.

TABLE 2

TABLE 2. Summary of infection risk due to the Delta variant.

TABLE 3

TABLE 3. Summary of infection risk due to the Omicron variant.

Due to the inverse relationship between ventilation rates and infection risks, infection risks are determined to be higher in indoor spaces with low ventilation rates. However, having high ventilation rates do not mean low infection risks as smaller spaces will also have higher infection risks. The computations also show that the better the quality of masks that were used, the lower the infection risk.

4 Conclusion and recommendations

The study developed an economical CO₂ monitoring device that was deployed in various indoor spaces. The CO₂ readings then undergo multivariate analysis using the least squares method to derive the ventilation rate and occupancy.

The method augments the limitation to the previous steady-state methods in deriving the ventilation rates; however, the method itself is incapable of deriving the ventilation rates and occupancy when the CO₂ levels presume a steady-state condition. The method is also limited to increasing CO₂ levels as it returns negative values when tested on decreasing CO₂ levels. The method could also underestimate the occupancy if the activity rate of the occupants is less than the average.

To handle the limitations, an alternate method was used to derive the CO₂ levels with the known number of occupants as an additional input. A camera-based people counter can be coupled to the CO₂ monitor to accurately derive the ventilation rates. As to the activity rate, noise meters can be used to gauge human activity within the indoor facility, which can be related to the activity rates to adjust the parameters of the method.

The derived ventilation rates were then used to estimate the infection risk of different indoor spaces and public transportation modes. For most of the indoor spaces, the higher ventilation rates indicate lower risks, apart from traditional jeepneys which may have medium risk, especially if the jeepneys were stationary. Masking was also determined to have attributed to most infection risk reduction.

The developed CO₂ monitors, which employ the multivariate method and the Wells–Riley formulations, can be a useful tool in informing occupants of the relative risk that they may be subjected to due to airborne diseases transmitted through shared room air transmission.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

JA: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, visualization, and writing–original draft. JL: editing and revisions. PM: software and writing–review and editing. JH: resources, supervision, and writing–review and editing. JR: resources, supervision, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The development of the CO₂ monitors and part of this study are funded by the UPD OVCRD Extension Grant under (Project No. 222201 UPD-EG). This study is also funded by the DOST through the UP Center for Air Research in Urban Environments (UP CARE) research program.

Acknowledgments

The main author also acknowledges Dr. Jose Regin F. Regidor, the Director of the UPD Institute of Civil Engineering, who has been supportive of this initiative. The main author also acknowledges Dr. Ma. Antonia N. Tanchuling, the Dean of the UPD College of Engineering, for the endorsement and support. The authors acknowledge the Department of Transportation for allowing them to conduct CO₂ measurements.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bazant, M., Kodio, O., Cohen, A., Khan, K., Gu, Z., Bush, J. W. M., et al. (2021). Monitoring carbon dioxide to quantify the risk of indoor airborne transmission of COVID-19. doi:10.1017/flo.2021.10

CrossRef Full Text | Google Scholar

Buonnano, G., Stabile, L., and Morawska, L. (2020). Estimation of airborne viral emission: quanta emission rate of SARS-CoV-2 for infection risk assessment. Environ. Int. 141, 105794. doi:10.1016/j.envint.2020.105794

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, W., Zhang, N., Wei, J., Yen, H. L., and Li, Y. (2020). Short-range airborne route dominates exposure of respiratory infection during close contact. Build. Environ. 176, 106859. doi:10.1016/j.buildenv.2020.106859

CrossRef Full Text | Google Scholar

Dai, H., and Zhao, B. (2023). Association between the infection probability of COVID-19 and ventilation rates: an update for SARS-CoV-2 variants. Build. Simul. 6, 3–12. doi:10.1007/s12273-022-0952-6

CrossRef Full Text | Google Scholar

Gammaitoni, L., and Nucci, M. C. (1997). Using a mathematical model to evaluate the efficacy of TB control measures. Emerg. Infect. Dis. 3, 335–342. doi:10.3201/eid0303.970310

PubMed Abstract | CrossRef Full Text | Google Scholar

Greenhalgh, T., Jimenez, J. L., Prather, K. A., Tufekci, Z., Fisman, D., and Schooley, R. (2021). Ten scientific reasons in support of airborne transmission of SARS-CoV-2. Lancet 397 (10285), 1603–1605. doi:10.1016/s0140-6736(21)00869-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Jimenez, J. L., Marr, L. C., Randall, K., Ewing, E. T., Tufekci, Z., Greenhalgh, T., et al. (2022). What were the historical reasons for the resistance to recognizing airborne transmission during the COVID-19 pandemic? Indoor Air 32 (8), e13070. doi:10.1111/ina.13070

PubMed Abstract | CrossRef Full Text | Google Scholar

Klopmas, M., Milton, D. K., Ree, C., Baker, M. A., and Leekha, S. (2021). Current insights into respiratory virus transmission and potential implications for infection control programs: a narrative review. Ann. Intern. Med. 172 (12), 1710–1718. doi:10.7326/m21-2780

CrossRef Full Text | Google Scholar

López, J. H., Romo, Á. S., Molina, D. C., Hernández, G. Á., Cureño, Á. B. G., Acosta, M. A., et al. (2021). Detection of Sars-Cov-2 in the air of two hospitals in Hermosillo, Sonora, México, utilizing a low-cost environmental monitoring system. Int. J. Infect. Dis. 102, 478–482. doi:10.1016/j.ijid.2020.10.089

PubMed Abstract | CrossRef Full Text | Google Scholar

Miller, S. L., Nazaroff, W. W., Jimenez, J. L., Boerstra, A., Buonanno, G., Dancer, S. J., et al. (2021). Transmission of SARS-CoV-2 by inhalation of respiratory aerosol in the Skagit Valley Chorale superspreading event. Indoor Air 31 (2), 314–323. doi:10.1111/ina.12751

PubMed Abstract | CrossRef Full Text | Google Scholar

Nissen, K., Krambrich, J., Akaberi, D., Hoffman, T., Ling, J., Lundkvist, Å., et al. (2020). Long-distance airborne dispersal of SARS-CoV-2 in COVID-19 wards. Sci. Rep. 10, 19589. doi:10.1038/s41598-020-76442-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, Z., and Jimenez, J. L. (2021). Exhaled CO2 as a COVID-19 infection risk proxy for different indoor environments and activities. Environ. Sci. Technol. 8 (5), 392–397. doi:10.1021/acs.estlett.1c00183

CrossRef Full Text | Google Scholar

Peng, Z., Rojas, A. P., Kropff, E., Bahnfleth, W., Buonanno, G., Dancer, S., et al. (2022). Practical indicators for risk of airborne transmission in shared indoor environments and their application to COVID-19 outbreaks. Environ. Sci. Technol. 56 (2), 1125–1137. doi:10.1021/acs.est.1c06531

PubMed Abstract | CrossRef Full Text | Google Scholar

Persily, A., and de Jonge, L. (2018). Carbon dioxide generation rates for building occupants. Indoor Air 27 (5), 868–879. doi:10.1111/ina.12383

PubMed Abstract | CrossRef Full Text | Google Scholar

Qian, H., Miao, T., Liu, L., Zheng, X., Luo, D., and Li, Y. (2021). Indoor transmission of SARS-CoV-2. Indoor Air 31 (3), 639–645. doi:10.1111/ina.12766

PubMed Abstract | CrossRef Full Text | Google Scholar

Riley, E. C., Murphy, G., and Riley, R. L. (1978). Airborne spread of measles in a suburban elementary school. Am. J. Epidemiol. 107 (5), 421–432. doi:10.1093/oxfordjournals.aje.a112560

PubMed Abstract | CrossRef Full Text | Google Scholar

Rudnick, S., and Milton, D. (2003). Risk of indoor airborne infection transmission estimated from carbon dioxide concentration. Indoor Air 13 (3), 237–245. doi:10.1034/j.1600-0668.2003.00189.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Shinohara, N., Sakaguchi, J., Kim, H., Kagi, N., Tatsu, K., Mano, H., et al. (2021). Survey of air exchange rates and evaluation of airborne infection risk of COVID-19 on commuter trains. Environ. Int. 157, 106774. doi:10.1016/j.envint.2021.106774

PubMed Abstract | CrossRef Full Text | Google Scholar

Wells, W. F. (1955). Airborne contagion and air hygiene. Cambridge, Massachussetts: Harvard University Press.

Google Scholar

Yang, L., Wang, X., Li, M., Zhou, X., Liu, S., Zhang, H., et al. (2020). Carbon dioxide generation rates of different age and gender under various activity levels. Build. Environ. 186, 107317. doi:10.1016/j.buildenv.2020.107317

CrossRef Full Text | Google Scholar