- 1Department of Structural and Geotechnical Engineering, Sapienza University of Rome, Rome, Italy
- 2Institute for Risk and Disaster Reduction, University College London, London, United Kingdom
- 3Department of Civil, Environmental and Geomatic Engineering, University College London, London, United Kingdom
In recent decades, significant research efforts have been devoted to developing fragility and vulnerability models for mainshock-damaged buildings, i.e., depending on the attained damage state after a mainshock ground motion (state-dependent fragility/vulnerability relationships). Displacement-based peak quantities, such as the maximum interstory drift ratio, are widely adopted in fragility analysis to define both engineering demands and structural capacities at the global and/or local levels. However, when considering ground-motion sequences, the use of peak quantities may lead to statistical inconsistencies (e.g., fragility curves’ crossings) due to inadequate consideration of damage accumulation. In this context, energy-based engineering demand parameters (EDPs), explicitly accounting for cumulative damage, can help address this issue. This paper provides an overview of recent findings on the development of aftershock-fragility models of mainshock-damaged buildings. Particular focus is given to state-of-the-art frameworks for fragility analyses based on cumulative damage parameters. Moreover, a literature review on damage indices and energy-based concepts and approaches in earthquake engineering is reported to better understand the main advantages of the mostly adopted energy-based parameters, as well as their limitations. Different refinement levels of seismic response analyses to derive fragility relationships of mainshock-damaged buildings are also discussed. Finally, the benefits of adopting energy-based EDPs rather than, or in addition to, peak quantities in state-dependent fragility analyses are demonstrated on a reinforced concrete frame building. Specifically, a refined lumped plasticity modeling approach is adopted, and sequential cloud-based time-history analyses of a Multi-Degree-of-Freedom (MDoF) model are carried out. The results highlight that energy-based approaches for fragility analysis effectively capture damage accumulation during earthquake sequences without inconsistencies in the obtained statistical models. On the other hand, estimating global or local structural capacity in terms of cumulative EDPs is still challenging. Further experimental data are needed to better calibrate the quantification of energy-based damaged states.
1 Introduction and motivations
After an earthquake, buildings can be affected by substantial structural and non-structural damage, leading to loss of their lateral-force resisting capacity and functionality. Recent worldwide earthquake sequences have further highlighted that mainshock-damaged buildings are more vulnerable to severe damage and potentially catastrophic consequences in subsequent seismic events. This issue is critically emphasized by triggered earthquakes (e.g., Aljawhari et al., 2020), i.e., subsequent seismic events generated by different rupture zones due to the energy/stress released by a mainshock and transferred to nearby faults, such as the 2010–2011 Canterbury earthquake sequence (e.g., Bradley et al., 2014) and the 2016–2017 Central Italy earthquake sequence (e.g., Chiaraluce et al., 2017). As an example, to better understand the observed consequences related to earthquake sequences, Figure 1 shows the evolution of the Building Safety Evaluation procedure (i.e., tagging) for Reinforced Concrete (RC) frame structures in the Christchurch Central Business District (CBD) area after both the 4/9/2010 Darfield (Canterbury) earthquake (Kam et al., 2010) and the 22/2/2011 Christchurch (Lyttelton) earthquake (Kam et al., 2011). After the September mainshock, almost 90% of the RC frame structures in the CBD area were classified as safe to re-occupy (i.e., green tag), while 0.7% of them were classified as unsafe (i.e., red tag) (Kam et al., 2010). However, after the 2011 Christchurch (Lyttelton) earthquake, the number of RC frame structures classified as safe to re-occupy decreased to 50.1%, with a consequent increase of structures with yellow tag (i.e., restricted use) and red tag, 28.6% and 21.3%, respectively (Kam et al., 2011).
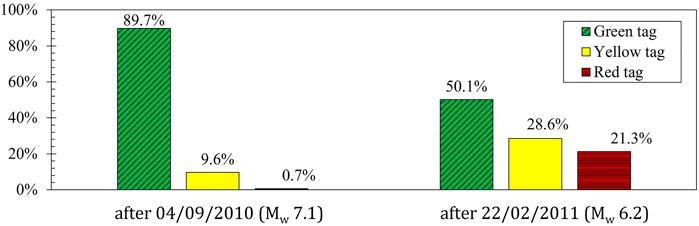
FIGURE 1. Building Safety Evaluation tagging in the Christchurch Central Business District after the 4/9/2010 Darfield (Canterbury) earthquake and the 22/2/2011 Christchurch (Lyttelton) earthquake (data from Kam et al., 2010; Kam et al., 2011). Mw is the moment magnitude of those events.
However, current seismic-risk assessment studies typically neglect the effects of seismic damage accumulation (as well as those due to time dependencies in seismic hazard; e.g., Iacoletti et al., 2022), considering that immediate repair takes place after every earthquake. Neglecting the impact of prior earthquake damage may lead to an underestimation of structural vulnerability and loss metrics, thus affecting decision-making for defining emergency planning strategies and insurance policies (e.g., de Quevedo Iñarritu et al., 2021). Moreover, a detailed assessment of the residual capacity of earthquake-damaged buildings to sustain subsequent seismic events is critical to support decision-making on both re-occupancy and repair vs. demolition, as well as for the selection, design, and implementation of suitable techniques to ‘restore’ the building to its undamaged conditions (e.g., Cuevas and Pampanin, 2017; Pampanin, 2021).
In line with the current practice for probabilistic seismic-risk assessment of building portfolios, building-level damage is typically expressed through fragility relationships (e.g., D’Ayala et al., 2014; Silva et al., 2019; Martins and Silva, 2021). They represent the probability of reaching or exceeding a specific damage state (DS) given the earthquake-induced ground-motion intensity. Fragility relationships are often modelled as lognormal cumulative distribution functions. On the other hand, when dealing with seismic-risk studies explicitly accounting for seismicity clustering and damage accumulation, the concept of state-dependent fragility relationships (i.e., fragility relationships depending on the attained damage state after a mainshock) should be adopted (e.g., Luco et al., 2004; Gentile et al., 2022). Displacement-based peak quantities, such as the maximum interstory drift ratio (MIDR), are typically considered in fragility analysis as engineering demand parameters (EDPs) and used to define DS thresholds. The main advantage of such quantities is that they are currently used in seismic codes worldwide to estimate both member and global structural capacity, resulting in a more “understandable” and direct definition of damage and, consequently, DS thresholds. However, using displacement-based peak quantities, as opposed to cumulative EDPs, may result in improper consideration of damage accumulation effects. In turn, this may lead to statistical inconsistencies in the state-dependent fragility results (e.g., fragility curves crossing among various damage states). To overcome this issue, some recent studies in the literature (e.g., Gentile and Galasso, 2021a; de Quevedo Iñarritu et al., 2021; Kalateh-Ahani and Amiri, 2021; Yu et al., 2021; Zhou et al., 2021) suggested performing state-dependent fragility analyses considering energy-based EDPs. One of the main advantages of energy-based approaches is that they rely on scalar measures (e.g., dynamic hysteretic energy) that monotonically increase with the length of the ground-motion excitation (or the number of subsequent excitations). Moreover, energy-based quantities reflect more damage-related information than displacements (e.g., the number of equivalent cycles; e.g., Fardis, 2018). Yet, assessing the capacity of structural members and defining reliable DS thresholds in terms of energy is still challenging (e.g., Fardis, 2018; Gentile and Galasso, 2021a; Benavent-Climent et al., 2021). However, the stable relationship between peak deformation and hysteretic energy observed in past studies (e.g., Decanini et al., 2000; Mollaioli et al., 2011; Gentile and Galasso, 2021a; Benavent-Climent et al., 2021) could provide an effective and direct tool to convert displacement-based DS thresholds into energy-based ones. Therefore, the promising idea of energy-based seismic design/assessment, extensively investigated a few decades ago (e.g., Akiyama, 1988), has reemerged in the recent past, intending to better capture the damage accumulation consistently with the physics of ground-motion sequences.
This paper aims to provide an overview of the recent findings and development on state-dependent fragility analyses for ground-motion sequences. First, a review of the energy-based approaches in earthquake engineering and the related damage indices mostly adopted in literature is reported to better understand their main advantages and limitations. Then, an overview of available procedures for state-dependent fragility analyses is given, considering frameworks based on either displacement-based or cumulative EDPs. The possible implementation of alternative frameworks based on different levels of seismic response analyses (i.e., from simplified methods, suitable for building portfolios, to higher-refinement methods, suitable for individual buildings; e.g., Gentile and Galasso, 2021b) is also discussed. Finally, an illustrative application to an RC frame building is presented to demonstrate the benefits of adopting energy-based EDPs rather than, or in addition to, displacement-based peak quantities in state-dependent fragility analyses. The paper is structured as follows: Section 2 presents an overview of the damage indices and energy-based approaches in earthquake engineering; Section 3 discusses the state-of-the-art procedures for state-dependent fragility analysis, while Section 4 introduces the illustrative application; finally, Section 5 offers some concluding remarks for the study.
2 Energy-based concepts and approaches in seismic engineering
2.1 Energy-based seismic response of dynamic systems
Energy-based approaches rely on the energy-balance equation of a dynamic system subjected to a ground-motion excitation. Considering for the sake of simplicity a Single-Degree-of-Freedom (SDoF) inelastic system, characterized by a mass
where
The first term of Eq. 2 represents the “relative” (i.e., calculated with respect to the ground) kinetic energy of the system,
The energy-balance equation can be also written in terms of “absolute” values (i.e., considering both the relative deformation of the system and the rigid body translation due to the ground displacement). However, past research studies (e.g., Uang and Bertero, 1990) have demonstrated that relative and absolute input energies are very similar in the range of interest for engineering application, i.e., 0.3–5.0 s, making that distinction mostly academic than actual (e.g., Kazantzi and Vamvatsikos, 2018). Nevertheless, Kalkan and Kunnath (2008) showed that the difference between absolute and relative input energy is more significant for near-fault than far-fault ground motions. Therefore, the above authors concluded that relative input energy is a more meaningful measure than absolute input energy in the case of forward directivity near-fault records.
It is worth highlighting that, for a given ground motion record, the amount of input energy and, as a result, of hysteretic energy is not constant. The input energy depends on the period and damping of the system, as well as on the force-deformation backbone curve and the cyclic hysteretic rule. Thus, maximizing the area of the cyclic hysteresis loops does not necessarily lead to better seismic behavior of the structure since also the input energy can be affected by this modification–Priestley (1993) defined it as one of the “myths in earthquake engineering”. Yet, by increasing the damping capacity of the system, a higher dissipating action can be obtained, reducing the seismic demand.
The total input energy that contributes to damage,
Moreover, for a fixed value of
As an example, Figure 2 shows the results of non-linear dynamic time history analyses (NLTHAs) of an SDoF system subjected to “artificial” ground-motion sequences (i.e., ground-motion sequences defined by coupling two different random records). The selected SDoF system is characterized by a simple elastic-perfectly plastic hysteresis behavior with yielding acceleration
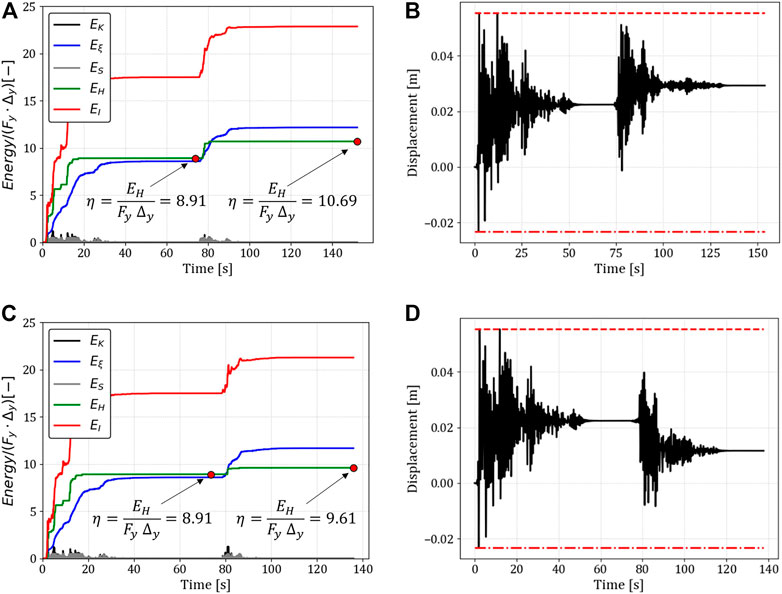
FIGURE 2. Example of non-linear dynamic behavior in terms of (A,C) hysteretic energy; and (B,D) displacement over time of an SDoF system subjected to two different ground motion sequences.
Figures 2A, C show that the hysteretic energy monotonically increases with the length of the ground motion excitation. In comparison, the peak displacement is not monotonic for these specific sequences (Figures 2B, D). Figure 2B would suggest that the residual displacement could be adopted as an effective complementary metric to assess structural damage, as already investigated in past studies (e.g., Pampanin et al., 2002b; Christopoulos et al., 2003; Nuzzo et al., 2020). However, such a quantity (i.e., residual displacement) strongly depends on the adopted hysteretic rules and on the characteristics of the “small cycles” (e.g., Dazio, 2004; Kazantzi and Vamvatsikos, 2018). In addition, in the case of earthquake sequences, it can be affected by the polarity of both ground-motion excitations, potentially leading to a “recentering” effect, as observed in Figure 2D. However and overall, it is not straightforward to quantify structural damage and estimate the maximum displacement values by just looking at the energy-based results.
2.2 Damage indices
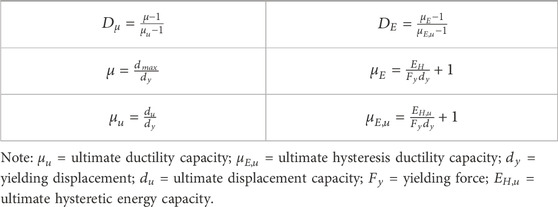
The concepts discussed above led a few decades ago to extensive investigations to provide damage parameters able to quantify and generally define the evolution of damage at both local and global structural levels. Currently, the most commonly adopted EDP is still ductility demand
By assessing the acceleration spectra of an SDoF system using the damage criteria listed in Table 1, Cosenza et al. (1993) showed that these two extreme hypotheses of seismic failure may lead to unacceptable uncertainty in the design accelerations, higher than 100%. Therefore, the authors noted the need to introduce more realistic damage functionals/indices. To overcome these issues, damage models based on the combination of maximum deformation and hysteretic energy have also been proposed (e.g., Banon and Veneziano, 1982; Park and Ang, 1985; Kunnath et al., 1992; Cosenza et al., 1993). These approaches are based on a low-cycle fatigue type of failure, considering that the number of cycles before failure decreases as the amplitude increases (Christopoulos et al., 2003). Another relevant parameter in energy-based approaches is represented by the ratio
Among other damage models, the one proposed by Park and Ang (1985) is the most widely adopted in the literature. Therefore, particular focus is given to this approach in this section.
The Park and Ang damaged index,
In Eq. 4,
Substantial differences were observed by the authors when comparing the experimental data and the calculated values of
An alternative modified expression of this index
where
Park et al. (1985) suggested that the overall performance of the building (i.e., global Park and Ang DI,
However, providing an adequate definition of global damage indices for the structure is an obvious difficulty. In many cases, it should not be addressed by simply adopting a weighted average of member indices (Kappos, 1997). Moreover, one of the significant issues related to using DIs is the definition of DS thresholds for engineering applications. In that direction, an interesting investigation was presented by Park et al. (1985) and Park et al. (1987), where the DIs were calculated for nine RC buildings that were damaged during the 1971 San Fernando earthquake in the US and the 1978 Miyagiken-Oki earthquake in Japan; DS thresholds were thus calibrated based on the observed damage. The authors concluded that
Finally, the relationship between peak deformation and energy-based parameters has been widely investigated in the past (e.g., Decanini et al., 2000; Mollaioli et al., 2011; Gentile and Galasso, 2021a; Benavent-Climent et al., 2021). Specifically, a stable pseudo-parabolic relationship between peak deformation and hysteretic energy has been observed (e.g., Decanini et al., 2000; Gentile and Galasso, 2021a). Gentile and Galasso (2021a) pointed out that hysteretic energy depends on the force-deformation backbone curve of the system and the adopted hysteretic rules. Therefore, the hysteretic energy vs. deformation relationship cannot be easily generalized. However, they point out that the above parameters are not variable for a given archetype structure. Hence, the hysteretic energy vs. deformation relationship can be successfully characterized, provided that record-to-record variability is considered. Gentile and Galasso (2021a) suggested using the median of such a relationship to rationally convert drift-based DS thresholds into hysteretic energy-based ones to be used in state-dependent fragility analysis. The authors finally highlighted that experimental/field data should be used to further validate such DS conversion method.
3 Seismic residual capacity and state-dependent fragility analysis
Post-earthquake seismic residual capacity of earthquake-damaged buildings has been widely investigated in the last decades. In the late 1990s, the Federal Emergency Management Agency (FEMA) 306 report (FEMA, 1998) introduced a simplified pushover-based methodology to assess the seismic performance of earthquake-damaged RC walls and masonry buildings. The proposed approach is based on capacity reduction factors for plastic hinges’ response of damaged components in terms of stiffness
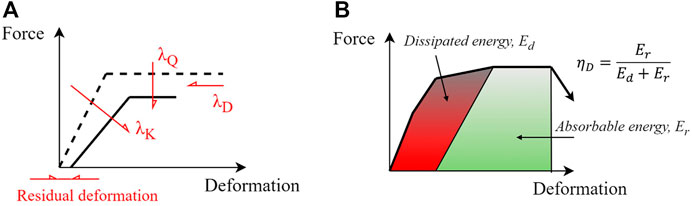
FIGURE 3. (A) Stiffness, strength, and displacement reduction coefficients in FEMA 306; and (B) capacity reduction factor for structural members in JBDPA Guideline (modified after FEMA, 1998,; Nakano et al., 2004).
In line with these approaches, past research focused on deriving plastic hinges’ modification factors for damaged RC components. Di Ludovico et al. (2013) proposed suitable expressions for
3.1 State-dependent fragility analysis
State-dependent fragility relationships are needed when dealing with probabilistic seismic-risk assessments explicitly accounting for mainshock-aftershock sequences or initial structural damage due to prior earthquakes. It is worth highlighting that the term “mainshock-aftershock” is herein adopted to refer to earthquake sequences in which a first ground motion (i.e., mainshock, MS) is followed by a second one (called aftershock, AS, for simplicity) which can refer to either an actual aftershock, a triggered seismic event, or another MS (i.e., MS-MS sequence) happening in a short time window, in line with the previous discussion in Section 1 (the same considerations are thus valid for the expression “aftershock-fragility analysis”). Typically, aftershock fragilities express the probability of being in or exceeding an EDP threshold given an Intensity Measure (IM) of the aftershock and an initial DS due to the mainshock. Clearly, an initial earthquake-related structural damage is expected to cause a reduction of the median of the fragility relationships of any given DS if compared to the undamaged configuration (i.e., a left shift of the fragility must be observed). Moreover, no state-dependent fragility curves’ crossing must occur to avoid inconsistencies in the resulting statistical models. For example, the intersection between different state-dependent fragility curves (i.e., related to different initial DSs) would indicate that, for some values of the IM, the intact structure has a higher probability of reaching or exceeding a DS than the same structure when affected by initial earthquake-related damage, which is an apparent inconsistency.
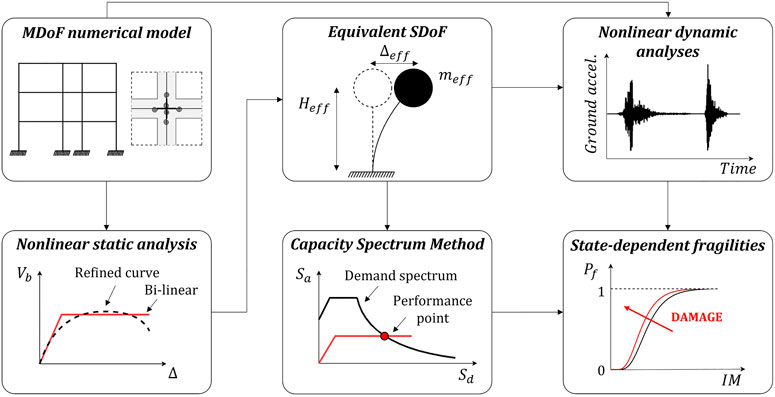
Conceptually, fragility relationships for earthquake-damaged buildings can be evaluated through different seismic response analysis methods, as shown in Figure 4. This aspect is deemed crucial since, as pointed out by Gentile and Galasso (2021b), various end-users and stakeholders may have different analysis requirements. For instance, government agencies or (re)insurance companies – that typically deal with large building portfolios – could be interested in a time-saving lower refinement level of analysis, accepting higher uncertainties in the results. It can be noted that the methods reported in Figure 4 can be grouped into different categories, based on the refinement of the analysis (e.g., non-linear dynamic vs. non-linear static analyses) and the complexity of the model (e.g., non-linear MDoF vs. SDoF models; numerical software-based vs. analytical mechanically-based models). Each approach shown in Figure 4 is discussed in more detail in the following paragraphs.
3.1.1 Non-linear dynamic analyses on MDoF numerical models
When different refinement levels of analyses are considered, the benchmark should be NLTHAs on an MDoF non-linear numerical model since they currently represent the most advanced seismic response analysis method. In this context, an extended version of Incremental Dynamic Analysis (IDA, Vamvatsikos and Cornell, 2002), i.e., the so-called back-to-back IDA, has been widely adopted in past studies (e.g., Ruiz-García and Aguilar, 2015; Raghunandan et al., 2015; Di Trapani and Malavisi, 2019; Gaetani d’Aragona et al., 2017). In this approach, fragility analysis of the intact (i.e., as built) structure is performed through the traditional IDA method. Initial earthquake-related damage is simulated by scaling each ground-motion record to achieve a prescribed DS. Then, for each mainshock-damaged configuration, a subsequent IDA is performed for each selected record; the same analysis is carried out for each considered initial DS. The main advantage of this approach is that it directly considers a specific initial DS of a structure after a mainshock; on the other hand, carrying out aftershock fragility analysis of mainshock-damaged buildings following this approach typically requires a costly computational effort. Moreover, the IDA procedure generally uses the same record set to analyze all IM ranges of values, potentially leading to excessive scaling and unrealistically large ground motions (e.g., Baker and Cornell, 2006). Alternatively, methods employing unscaled ground motions can be adopted, such as the so-called cloud analysis (e.g., Cornell et al., 2002; Jalayer et al., 2015; Jalayer et al., 2017). Cloud analysis allows one to perform fragility analysis by fitting a power-law model (
Recently, an innovative hysteretic energy-based framework to derive fragility relationships of structures subjected to ground-motion sequences has been proposed by Gentile and Galasso (2021a), which embeds a methodology to calibrate energy-based DS thresholds. Starting from the observation that the relationship between peak deformation and hysteretic energy is pseudo-parabolic and that, for the same peak displacement demand, lower energy dissipation in the aftershock is expected considering a higher damage level in the mainshock (i.e., initial DS), the authors proposed the five-parameter PSDM shown in Eq. 8:
where
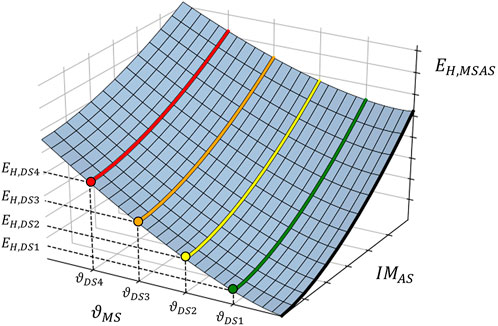
FIGURE 5. Conceptual illustration of the PSDM proposed by Gentile and Galasso (2021a).
This PSDM allows one to perform state-dependent fragility analysis using Eqs 9–11.
where
In this methodology, energy-based DS thresholds are defined starting from structure-specific drift-based ones (assessed by a pushover analysis) and using the fitted energy-vs-displacement relationship (i.e.,
The same PSDM has recently been adopted and extended by Otárola et al. (2022) to derive state-dependent fragility and vulnerability relationships for bridge structures subjected to corrosion deterioration and ground-motion sequences. The authors adopted a modified regression model for fitting the relationship between
Finally, it is worth mentioning that, when dealing with non-linear dynamic analyses for ground-motion sequences, also the earthquake data type and the record selection process may affect the complexity of the methodology. Some studies in the literature investigated the seismic performance of structures subjected to “real” (i.e., recorder) MS-AS sequences (e.g., Ruiz-García, 2012). However, using real sequences may be deemed not suitable for fragility estimation since typically only few ASs characterized by high IMs are available. For these reasons, “artificial” MS-AS sequences have been widely adopted in the literature. Artificial MS-AS sequences can be derived by randomly combining two MSs (e.g., Aljawhari et al., 2020; Gentile and Galasso, 2021a) or by adopting more advanced approaches involving the combination of ground-motion records by using an MS-AS correlation model (e.g., Papadopoulos et al., 2020). Finally, artificial MS-AS sequences can be used in addition to real ones to improve the ground-motion sequence set and cover a wider range of MS-AS IMs (e.g., de Quevedo Iñarritu et al., 2021).
3.1.2 Non-linear dynamic analyses on equivalent SDoF systems
Conceptually, all the methodologies discussed above for MDoF models can also be used considering NLTHAs on equivalent SDoF systems to reduce the computational effort. Typically, the backbone curve of an equivalent SDoF is defined using the results of a pushover analysis on an MDoF numerical model of the structure, thus assessing the equivalent mass
Several past research works investigated the mainshock-damaged fragility relationships using equivalent SDoF systems (e.g., Luco et al., 2004; Papadopoulos and Bazzurro, 2021), generally adopting a back-to-back IDA approach. Orlacchio et al. (2020) proposed a simplified procedure based on a semi-empirical predictive model to assess the MS-damaged backbone curve of an equivalent SDoF system to further reduce the computational effort. Monte-Carlo sampling is thus adopted to obtain damaged structural configurations, and subsequent IDAs on those models are carried out to perform state-dependent fragility analysis.
3.1.3 Non-linear static approaches
Moving to a low-refinement level of analysis, the state-dependent fragility estimation can also be performed using non-linear static analyses (capacity) and spectrum-based domain (demand) or other simplified approaches (Figure 4). In this context, Bazzurro et al. (2004) proposed a simplified procedure to derive pushover capacity curves of the structure in its both intact and damaged configurations. Structural damage is simulated by loading the intact structure until reaching a fixed damage level (expressed in terms of roof drift), then unloading it to zero and finally reloading until a plastic mechanism develops (Figure 6). Then, the SPO2IDA tool (Vamvatsikos and Cornell, 2005) is used to assess the median values of fragility relationships for the intact and earthquake-damaged configuration. The results have also been used to propose a building tagging procedure based on the increase in Mean Annual Frequency (MAF) of exceeding the life-safety limit state in post-earthquake conditions. Later, following the FEMA 306 approach, Polese et al. (2012) proposed a simplified pushover-based procedure to develop damage-dependent fragility curves. The median values of the fragility relationships are estimated through the incremental N2 method (IN2, Dolšek and Fajfar, 2004), considering the capacity curve of the structure in its as-built and damaged configuration, while default dispersion values are selected. The study was limited to collapse fragility estimation. The main issue in adopting pushover analyses and demand spectrum-based procedures (e.g., N2 method, Fajfar, 2000, and the Capacity Spectrum Method CSM, ATC, 1996) for fragility estimation is the evaluation of the dispersion values. In fact, these approaches typically do not account for record-to-record variability since the seismic demand is represented by smooth code-compliant design spectra (Silva et al., 2019); therefore, only the median value of fragilities can be estimated, while default dispersion values of fragility (e.g., the ones proposed in the FEMA P-58 report, FEMA, 2012) are generally adopted. To overcome this issue, an extended version of the CSM, namely, the Cloud-CSM, has been recently proposed by Nettis et al. (2021). The method involves calculating the performance displacement for “real” (i.e., as recorded) ground-motion spectra to account for record-to-record variability in a cloud-based approach explicitly. This approach was recently adopted by Pedone et al. (2021) to propose a simplified pushover-based framework to develop state-dependent fragility relationships. Specifically, similarly to Polese et al. (2012) (i.e., following the FEMA 306 approach), achieving a specific DS after the MS is simulated by using capacity reduction factors for stiffness, strength, and ductility of damaged structural members. Then, seismic response analysis is performed using the Cloud-CSM, considering the pushover curve of the structure in its undamaged and damaged configurations. Finally, state-dependent fragility relationships are evaluated for each DS via cloud analysis (Jalayer et al., 2017). Based on this discussion, Figure 6 shows different conceptual frameworks for state-dependent fragility analysis based on non-linear static procedures and spectrum-based approaches.
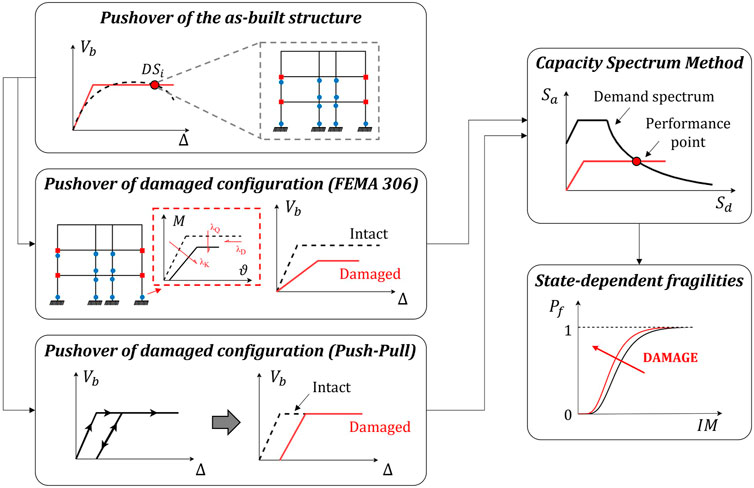
FIGURE 6. Conceptual illustration of frameworks for state-dependent fragility analysis based on non-linear static procedures.
Non-linear static analyses coupled with demand spectrum-based approaches do not yet explicitly allow to evaluate energy-based EDPs, if not through drift vs. dissipated energy empirical relationships. Nevertheless, the pushover force-displacement capacity curve of a damaged structure is characterized by a reduction in terms of ductility capacity. In the CSM approach, the equivalent viscous damping factor
Finally, simplified analytical/mechanical procedures, able to provide the force-displacement capacity curve of a structure, can be involved in the framework as an alternative to numerical pushover analyses. These procedures do not need the implementation of a numerical model and can support the development of seismic risk studies at a large (regional) scale involving large building portfolios. For example, Polese et al., 2013, Polese et al., 2015 investigated a mechanism-based approach for assessing damage-dependent fragility curves of buildings. The proposed assessment methodology requires an “a-priori” definition of the expected inelastic mechanism of the structure, which is limited to a soft-story mechanism type or global beam-sway mechanism. The force-displacement capacity curves of the structure in its intact and damaged configuration, obtained through the simplified mechanism-based methods, are thus used in the same framework of Polese et al. (2012) to assess the seismic residual capacity of earthquake-damaged buildings. More recently, Pampanin (2021) discussed the development of a refined version of the SLaMA (Simple Lateral Mechanism Analysis, NZSEE, 2017) method for safety evaluation and loss assessment of buildings in either pre- or post-earthquake configuration. The SLaMA method is a simplified analytical mechanical procedure, widely adopted and validated in past studies in the literature (e.g., Pampanin, 2017; Del Vecchio et al., 2018; Gentile et al., 2019a,b,c,d; Bianchi et al., 2019; Pedone et al., 2022, 2023; Sansoni et al., 2022). It evaluates the capacities of the structure at both local and global levels, as well as the hierarchy of strength, and sequence of events, within each subassembly and, thus, the expected global inelastic mechanism. Therefore, the seismic assessment results at the local level can be conceptually used to assess the seismic residual capacity of damaged components in line with the FEMA 306 or the JBDPA approach. Thus, the SLaMA result can be updated, providing the global force-displacement capacity curve of the structure in its damaged configuration.
The observed error between simplified and more refined analyses to carry out fragility relationships has been investigated by Gentile and Galasso (2021b) for RC frame structures. Specifically, alternative seismic response analysis methods were analyzed, involving i) non-linear static analyses (either SLaMA or pushover analysis) coupled with the CSM; ii) NLTHA of equivalent SDoF systems (defined using the force-displacement capacity curve assessed by either SLaMA or numerical pushover analyses); and iii) NLTHA of MDoF numerical models. 14 RC frames were selected to implement the study. The authors concluded that all the simplified methods generally allow assessing the median and dispersion values of fragility relationships with an error in the range of ±20% compared to the more advanced analysis method (i.e., NLTHA of MDoF numerical model). Moreover, using NLTHAs of equivalent SDoF systems seems not substantially superior to non-linear static approaches coupled with the CSM. Conceptually, a similar investigation can be performed for simplified-to-refined frameworks for state-dependent fragility analysis.
4 Illustrative application
4.1 Description of the case-study building
An illustrative application is herein presented to show and discuss the advantages of adopting energy-based EDPs rather than displacement-based peak quantities in state-dependent fragility analyses. An RC frame structure, representative of a pre-seismic-code building in Italy, is selected to implement the proposed procedures. The case-study structure is a 4-story RC frame with global dimensions shown in Figure 7. The structural skeleton consists of moment-resistant three-bay frames in one direction and moment-resistant two-bay frames in the orthogonal direction. Story masses are approximately 101.5 tons and 93.6 tons for a typical story and the roof, respectively. As mentioned before, the structure represents an archetype pre-1970s building in Italy. Therefore, according to old code provisions, it is designed for gravity-loads-only, and no capacity design principles are provided; i.e., a no-ductile global behavior is expected. In this study, the 3-bay frame in the longitudinal direction is analyzed. The geometrical details of RC members are shown in Figure 7. Transversal reinforcement is φ6/15 (i.e., 6-mm-diameter stirrups at 15 cm) and φ8/15 for columns and beams, respectively. The mean concrete cylindrical strength, f’c, equals 14.4 MPa, while the mean steel yield stress, fy, equals 340.5 MPa.
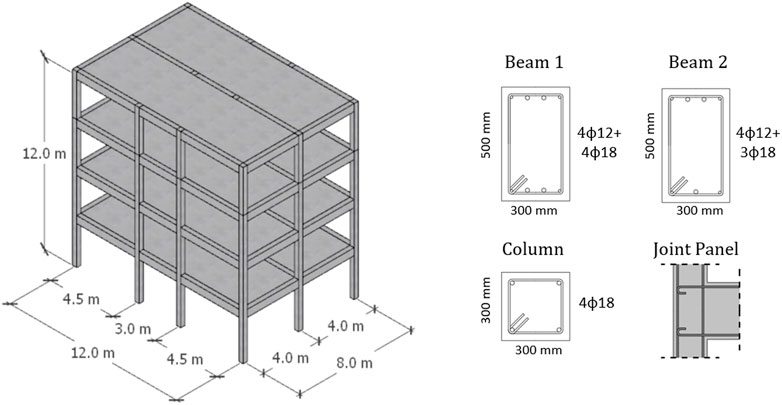
FIGURE 7. Global dimensions of the case-study building and geometrical details of RC members (φ = diameter of reinforcement bar).
4.2 Modeling approach
The seismic performance of the structure is analyzed by implementing a two-dimensional lumped plasticity model in the structural software Ruaumoko (Carr, 2016). The adopted modeling strategy is conceptually shown in Figure 8. For the sake of simplicity, the soil-structure interaction contribution is herein neglected, and fixed base joints are considered. Moreover, floor diaphragms are assumed rigid in their plane. Frame structural members are modelled as mono-dimensional elastic elements with plastic hinges at the ends (Giberson elements). The plastic hinges’ flexural capacity is defined through bi-linear moment-curvature relationships, considering a plastic hinge length, according to Priestley et al. (2007). An axial load-moment interaction diagram is implemented for column plastic hinges. The shear failure mechanism is also evaluated. Additional non-linear rotational springs are implemented to model the panel zones, characterized by equivalent column moment vs. shear deformation relationships. Additionally, an axial load-moment interaction diagram is implemented to account for the influence of the axial load on the beam-column joint capacity. Accounting for beam-column joints’ capacity in the model is deemed critical for existing RC buildings since they can exhibit a brittle failure, potentially limiting the overall seismic performance of the structure (Pampanin et al., 2002a). Finally, a linear strength degradation is defined for all RC structural members; the moment capacity is set equal to zero when a deformation equal to twice the near-collapse capacity of the member is achieved (as suggested in Gentile and Galasso, 2021b). Concerning the hysteresis behavior, the Takeda hysteretic model is used for beams and columns, setting the unloading and reloading-stiffness factors as αTak = 0.3 and βTak = 0.5 for beams and αTak = 0.5 and βTak = 0.0 for columns (a thinner hysteresis loop for columns is considered, Priestley et al., 2007). The hysteretic behavior of beam-column joints is modelled using the modified Sina model (Saiidi and Sozen, 1979), including the “pinching” effect. A load distribution proportional to the story masses is adopted for the pushover analysis. For NLTHAs, a tangent stiffness-proportional damping of 5% of the critical one is adopted for all the vibration modes.
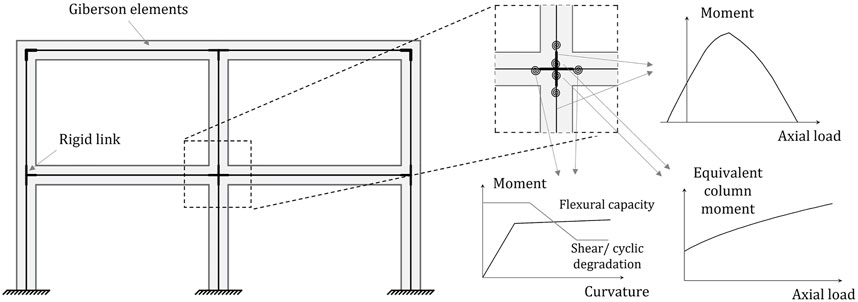
FIGURE 8. Adopted modeling strategy (modified after Gentile et al., 2019a).
4.3 Record selection
To perform state-dependent fragility analysis through a cloud-based approach, a set of 621 ground motion sequences is selected to implement the study. Cloud analysis does not need a site-specific, hazard-consistent record selection or excessive scaling records for its implementation (Jalayer et al., 2017). The ground motion records are selected from three different databases (as in Aljawhari et al., 2020; Gentile and Galasso, 2021a): 1) the 2012 KKiKSK ground-motion database (Goda, 2015); 2) the database developed by Goda and Taylor, 2012; and 3) the first 100 records in the SIMBAD Database (which includes 3-component 467 records, Smerzini et al., 2014), ranked according to their peak ground acceleration (PGA) values considering the geometric mean of the two horizontal (X-Y) components, and then keeping the component with the largest PGA value (as in Gentile and Galasso, 2021b). Specifically, from the previous two databases, only the mainshocks are selected. Information about the magnitude and source-to-distance values, soil types, and PGA values for the considered records can be found in Aljawhari et al. (2020). In this work, the same earthquake sequences used in Gentile and Galasso (2021a) are adopted. These sequences were assembled by randomly combining two records through a Latin hypercube sampling approach. More details about this procedure can be found in Gentile and Galasso (2021a). The 621 ground motion sequences were selected from the 1,000 ones used in Gentile and Galasso (2021a) by choosing only the sequences with a different record for the AS. Figure 9A shows the values of the IM for MS and AS in each ground motion sequence; avgSA, i.e., the geometric mean of the 5%-damped pseudo-spectral acceleration in a range of periods, is selected as IM in this study. This IM is deemed suitable for state-dependent fragility analysis since it accounts for both higher mode effects and period elongation. Moreover, avgSA has been showed to provide better accuracy and higher (relative) sufficiency when compared to other IMs widely adopted in the literature (e.g., spectral pseudo-acceleration at the fundamental period of the structure, Sa (T1)) (Minas and Galasso, 2019; O’Reilly, 2021). For each sequence, 20 s of free vibration between MS and AS and at the end of the sequence are provided. An example of a ground-motion sequence is shown in Figure 9B.
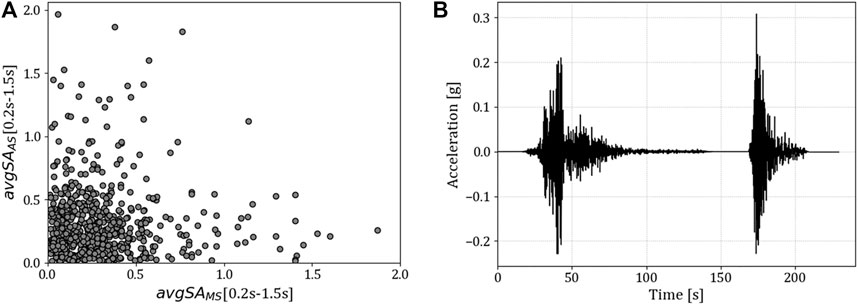
FIGURE 9. (A) IM values for MS and AS for the selected sequences; (B) example of a ground-motion sequence.
4.4 Pushover analysis and damage states definition
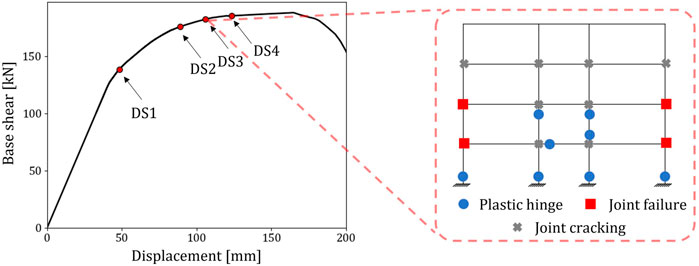
In the first step, a non-linear static (pushover) analysis is carried out to investigate the structural behavior of the case-study building. The results in terms of the global force-displacement pushover curve are shown in Figure 10, together with the observed plastic mechanism.
As expected, due to the lack of capacity-design principles, a mixed-sway mechanism involving external beam-columns joint failures coupled with beam and column failures characterizes the seismic behavior of the structure. The pushover analysis results are used to define the DS thresholds adopted for the fragility analysis. Specifically, four different structure-specific DSs are considered in this study, namely: DS1 (slight damage), DS2 (moderate damage), DS3 (extensive damage), and DS4 (complete damage). The DS1 threshold corresponds to the yield displacement of the idealized pushover curve. The DS3 threshold is identified considering the first attainment of the Life-Safety (LS) deformation capacity for any structural element. In contrast, the DS2 threshold corresponds to the first attainment of 50% of the same LS deformation capacity. Finally, the DS4 threshold refers to the first attainment of the collapse prevention limit state for any structural element. The applied methodology for fragility estimation is independent of the definition of the DS thresholds, thus different criteria can also be adopted (Gentile and Galasso, 2021a). The defined DS thresholds are shown on the global force-displacement capacity curve in Figure 10. A no-ductile global seismic behavior is observed due to the failure of external beam-column joints.
4.5 State-dependent fragility analyses
Seismic response analyses are preliminarily performed by adopting a sequential cloud-based approach and considering the MIDR as EDP. The DS thresholds shown in Figure 10 are converted to MIDR thresholds using the displacement profile observed in the numerical pushover analysis. Figure 11A shows the results of NLTHA for MS only and the observed trend between IM (i.e., avgSA) and EDP (i.e., MIDR) in the log-log space, as well as the fitted PSDM (through linear regression). Moreover, the observed DSs, based on the MIDR thresholds, are also reported.
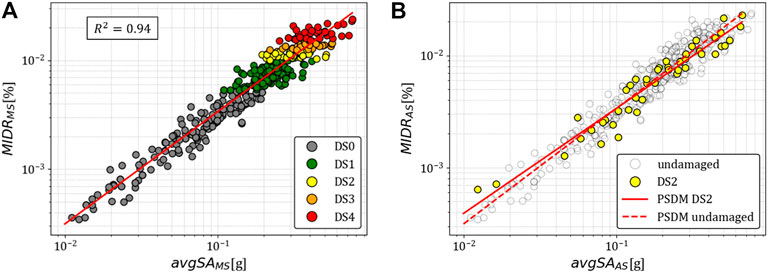
FIGURE 11. Cloud analysis results and PSDM for: (A) undamaged configuration and MS only; and (B) initial DS2 configuration and AS records.
For the undamaged configuration and MS only, a linear relationship between avgSA and MIDR in the log-log space is observed, and the linear regression model provides good accuracy in estimating the seismic behavior of the structure
These issues can be addressed by using cumulative EDPs, in this case, using hysteretic energy
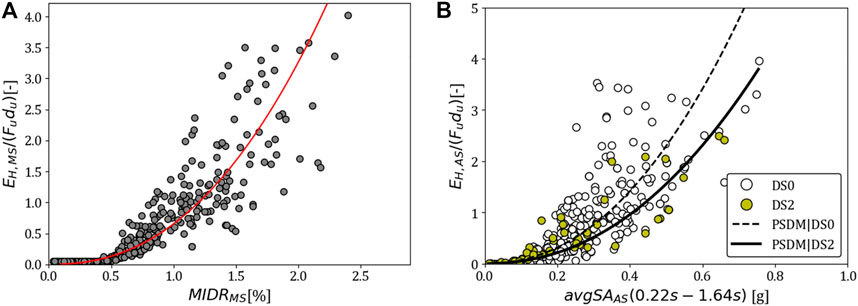
FIGURE 12. (A)
Results in Figure 12B highlight that less hysteretic energy is dissipated in the AS if the structure has experienced a DS in the MS (initial DS2 in Figure 12B, as an example), in line with the observations of Gentile and Galasso (2021a).
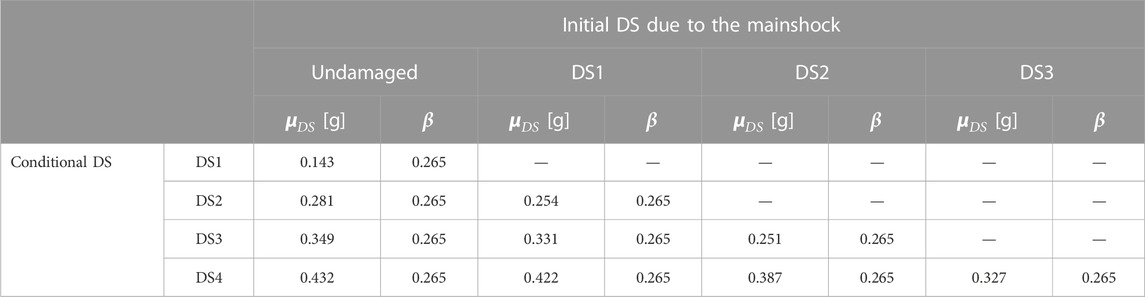
The fitted PSDM for each initial DS is shown in Figure13A, together with the energy-based DS thresholds. The PSDM allows properly considering the effect of damage accumulation, as discussed in Section 3. Specifically, in the case of an initial DS due to an MS, part of the hysteretic energy capacity of the structure has already been dissipated. Since energy is a cumulative EDP, the hysteretic energy dissipated in the AS is summed to the one dissipated in the MS, consistently with the physics of ground-motion sequence effects. Looking at the DS thresholds, a left shifting of the point is observed for state-dependent results when compared to the undamaged configuration, i.e., lower values of IM would cause the attainment of a specific DS for such cases. Finally, state-dependent fragility analysis is performed using the fitted PSDM. Figure 13B shows the state-dependent fragilities curves. Median and standard deviation values of both undamaged and state-dependent fragility curves are listed in Table 2.
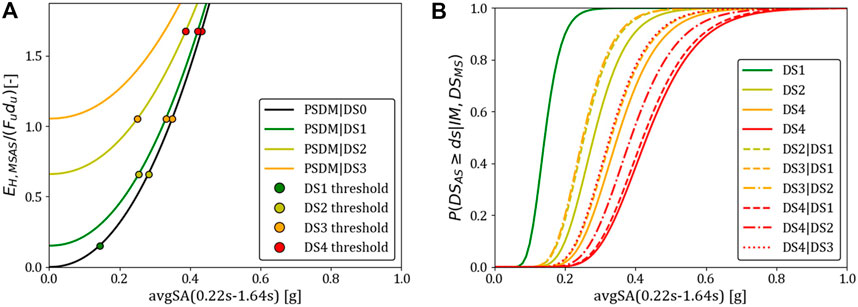
FIGURE 13. (A) PSDMs and DS thresholds for both undamaged and damage-state-dependent configurations; (B) state-dependent fragility curves.
The results show that cumulative EDPs can enable to derive state-dependent fragility relationships without any statistical inconsistency. Indeed, no fragility-curve crossings are observed. Considering a low level of damage (i.e., DS1), a reduction in fragility median (left shifting of fragility curves) approximately equal to 10%, 5%, and 2% are observed for DS2|DS1, DS3|DS1, and DS4|DS1, respectively. Although this reduction leads to slight modifications of the structural behavior of the building, with limited impact on the safety level evaluation, they can potentially lead to significant variations in terms of seismic economic losses (both direct and indirect) and/or other seismic-risk metrics due to a lower seismic performance of the structure in the operational and damage limit states. Concerning more severe initial DSs, initial DS2 damage leads to a reduction in the median of the fragility relationships, approximately equal to 28% and 10% for DS3|DS2 and DS4|DS2. In comparison, DS4|DS3 shows a reduction of 24% compared to DS4 fragility. In these cases, assessing the increased fragility due to initial earthquake-related damage is critical to support the decision-making process for retrofit/repair vs. demolition in a post-earthquake scenario.
It is worth noting that, for the sake of simplicity, “collapse cases” - i.e., results of NLTHAs characterized by global dynamic instability or unrealistically high MIDR value exceeding a conventionally-adopted 10% drift threshold (e.g., Vamvatsikos and Cornell, 2002; Jalayer et al., 2017, among many others) - are not included in this investigation. However, the influences of such cases in the state-dependent fragility results can be considered by grouping the results in “no collapse” and “collapse” cases and fitting a logistic regression, as implemented in Iacoletti et al. (2023). Moreover, Gentile and Galasso (2021a) highlighted that the proposed procedure to convert deformation DS thresholds into energy-based ones should be better supported by experimental data.
5 Conclusions
This paper investigated and discussed the recent findings on the development of damage-state-dependent fragility relationships of buildings (i.e., fragility relationships depending on the attained damage state after a first ground motion). State-dependent fragilities are deemed necessary when dealing with time-dependent probabilistic seismic-risk assessments considering mainshock-aftershock sequences or initial structural damage due to prior earthquakes. In this context, particular focus has been given to the use of cumulative energy-based damage parameters rather than, or in addition to, the more traditional displacement-based ones.
Firstly, to better understand the main advantages of adopting energy-based parameters, as well as their limitations, an overview of the energy-based seismic design/assessment procedures and damage indices has been provided. Specifically, it has been highlighted that, in the case of ground-motion sequences, displacement-based peak quantities such as the maximum interstory drift ratio or the residual drift may lead to improper consideration of cumulative damage. In fact, these quantities do not monotonically increase with either the number of ground motions or the length of ground-motion excitation, differently from energy-based quantities (e.g., hysteretic energy). Yet, displacement-based peak quantities still provide a more “understandable” definition of damage, while defining the structural capacity in terms of energy-based quantities is a more complex task. In that direction, the development of damage indices based on the combination of maximum deformation and hysteretic energy has also been discussed, with a particular focus on the model proposed by Park and Ang (1985), which is the most widely adopted in the literature. Although this model relies on the concept of low-cycle fatigue failure, suitable for ground-motion sequences, some limitation has been highlighted that can be summarized as i) the evaluation of the β-coefficient, representing the strength deterioration as a function of the amount of dissipated energy; ii) the definition of a global damage index based on the local ones; iii) the definition of reliable DS thresholds for lower damage limit state (i.e., occupancy and damage control).
Then, a literature review on the state-of-the-art methodologies for state-dependent fragility analyses has been carried out. Specifically, available procedures based on either displacement-based peak quantities or energy-based EDPs were reported. A particular focus has been given to the hysteretic energy-based framework recently proposed by Gentile and Galasso (2021a). Starting from the observation that a stable pseudo-parabolic relationship between peak deformation and hysteretic energy can be defined, this methodology suggests calibrating energy-based DS thresholds using displacement-based ones. Then, a five-parameter PSDM is fitted, consisting of a surface relating the hysteretic energy dissipated in the sequence to the peak deformation in the first ground motion (i.e., mainshock) and the IM of the second ground motion (called for simplicity aftershock). This PSDM is consistent with the relevant physics of ground-motion sequences, specifically: i) the dissipated hysteretic energy monotonically increases considering the maximum response in the mainshock and the IM of the aftershock; and ii) lower hysteretic energy dissipated in the aftershock is obtained if higher peak deformation in the mainshock is considered. Moreover, different possible refinement levels of seismic response analysis methods were also discussed, as well as the possible implementation of simplified-to-refined frameworks for developing fragility relationships of mainshock-damaged buildings. The discussed frameworks involve the use of i) sequential cloud-based NLTHA of MDoF numerical models (deemed as the benchmark methodology); ii) sequential cloud-based NLTHA of equivalent SDoF systems; and iii) non-linear static analyses coupled with the CSM, using simplified pushover-based methodologies for accounting for initial earthquake-related damage (e.g., FEMA, 1998). Concerning the latter, the possible use of simplified analytical/mechanical procedures providing the force-displacement pushover curve of structure (such as the SLaMA method) has also been reported.
Finally, an illustrative application has been developed to show the limits of adopting traditional displacement-based EDPs (e.g., the maximum interstory drift ratio) in aftershock-fragility analyses and demonstrate the benefit of adopting energy-based ones. Specifically, an RC frame structure, representative of a pre-seismic-code building in the Italian region, has been selected to implement the study. The state-dependent fragility analysis has been carried out through sequential cloud-based time-history analyses on a MDoF numerical model of the structure. The results highlighted that energy-based approaches for fragility analysis allow one to capture damage accumulation during the earthquake sequences without statistical inconsistencies (i.e., no fragility curves crossing between the various DSs were observed). However, some limitations have been observed when adopting displacement-based (no cumulative) EDPs, leading to inappropriate consideration of the effect of damage accumulation.
The promising idea of energy-based seismic assessment should represent an effective tool for developing statistical models consistent with the earthquake sequences problem. However, defining the global or local structural capacity in energy-based EDPs is still challenging, and further experimental investigations are deemed necessary to calibrate energy-based damage state thresholds better. Moreover, as the energy-based EDPs are more sensitive to the selected hysteresis rules than displacement-based peak ones, the implementation of a proper numerical model is deemed critical to ensure the reliability of the fragility evaluation (although the same consideration is still valid for more traditional fragility estimation methods as well). Future developments in this field could involve a sensitivity analysis to investigate the impact of the selected hysteresis rules (e.g., typology and relevant parameters) to further validate the reliability of the method.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
LP: conceptualization, methodology, formal analysis, writing—original draft, review and editing, visualization. RG, CG, and SP: conceptualization, project administration, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
The authors acknowledge the financial support of the Italian Ministry of University and Research (MUR) for funding the Doctoral Scholarship of LP. The authors gratefully acknowledge the UCL’ Department of Civil, Environmental and Geomatic Engineering (CEGE) for hosting LP as “visiting researcher” and the financial support of the Joint Research Project Program of Sapienza University of Rome (DR 1625/2020) for travelling and living allowances during the visiting research period.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akiyama, H. (1985). Earthquake resistant limit-state design for buildings (English version). Tokyo, Japan: University of Tokyo Press.
Akiyama, H. (1988). “Earthquake-resistant design based on the energy concept,” in Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo-Kyoto, Japan, 2-9-1988.
Akiyama, H. (1999). Earthquake-resistant design method for buildings based on energy balance. Tokyo: Gihodo Shuppan.
Aljawhari, K., Gentile, R., Freddi, F., and Galasso, C. (2020). Effects of ground-motion sequences on fragility and vulnerability of case-study reinforced concrete frames. Bull. Earthq. Eng. 19, 6329–6359. doi:10.1007/s10518-020-01006-8
Ancheta, T. D., Darragh, R. B., Stewart, J. P., Seyhan, E., Silva, W. J., Chiou, B. S. J., et al. (2014). NGA-West2 database. Earthq. Spectra 30 (3), 989–1005. doi:10.1193/070913eqs197m
Ang, A. H., Kim, W. J., and Kim, S. B. (1993). “Damage estimation of existing bridge structures,” in Structural engineering in natural hazards mitigation (Virginia: ASCE).
ATC (1996). Seismic evaluation and retrofit of concrete buildings. Redwood City, CA, USA: Applied Technology Council. ATC-40.
Baker, J. W., and Cornell, C. A. (2006). “Vector-valued ground motion intensity measures for probabilistic seismic demand analysis,” in PEER report 2006/08, pacific earthquake engineering research center-college of engineering (Berkeley: University of California).
Banon, H., and Veneziano, D. (1982). Seismic safety of reinforced concrete members and structures. Earthq. Eng. Struct. Dyn. 10 (2), 179–193. doi:10.1002/eqe.4290100202
Bazzurro, P., Cornell, C. A., Menun, C., and Motahari, M. (2004). “Guidelines for seismic assessment of damaged buildings,” in Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, B.C., Canada, August 1-6, 2004.
Benavent-Climent, A., Donaire-Ávila, J., and Mollaioli, F. (2021). “Key points and pending issues in the energy-based seismic design approach,” in Energy-based seismic engineering: Proceedings of IWEBSE 2021 (Cham: Springer International Publishing).
Bianchi, S., Ciurlanti, J., and Pampanin, S. (2019). “A SLaMA-based analytical procedure for the cost/performance-based evaluation of buildings,” in Proceedings of the 8th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete, Greece, 24-26 June 2019.
Bradley, B. A., Quigley, M. C., Van Dissen, R. J., and Litchfield, N. J. (2014). Ground motion and seismic source aspects of the canterbury earthquake sequence. Earthq. Spectra 30, 1–15. doi:10.1193/030113EQS060M
Carr, A. J. (2016). RUAUMOKO2D - the maori god of volcanoes and earthquakes. Inelastic analysis finite element program. Christchurch, New Zealand.
Ceccarelli, C., Bianchi, S., Pedone, L., and Pampanin, S. (2021). “Numerical investigations on the residual capacity and economic losses of earthquake-damaged reinforced concrete wall structures,” in Proceedings of the 8th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Athens, Greece, 27-30 June 2021.
Cheng, Y., Mollaioli, F., and Donaire-Ávila, J. (2021). Characterization of dissipated energy demand. Soil Dyn. Earthq. Eng. 147, 106725. doi:10.1016/J.SOILDYN.2021.106725
Chiaraluce, L., Di Stefano, R., Tinti, E., Scognamiglio, L., Michele, M., Casarotti, E., et al. (2017). The 2016 central Italy seismic sequence: A first look at the mainshocks, aftershocks, and source models. Seismol. Res. Lett. 88, 757–771. doi:10.1785/0220160221
Chiu, C. K., Sung, H. F., and Chiou, T. C. (2021). Quantification of the reduction factors of seismic capacity for damaged RC column members using the experiment database. Earthq. Eng. Struct. Dyn. 50 (3), 756–776. doi:10.1002/eqe.3355
Christopoulos, C., Pampanin, S., and Priestley, M. J. N. (2003). Performance-based seismic response of frame structures including residual deformations. Part I: Single-degree of freedom systems. J. Earthq. Eng. 7, 97–118. doi:10.1080/13632460309350443
Cornell, C. A., Jalayer, F., Hamburger, R. O., and Foutch, D. A. (2002). Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines. J. Struct. Eng. 128, 526–533. doi:10.1061/(asce)0733-9445(2002)128:4(526)
Cosenza, E., Manfredi, G., and Ramasco, R. (1993). The use of damage functionals in earthquake engineering: A comparison between different methods. Earthq. Eng. Struct. Dyn. 22, 855–868. doi:10.1002/eqe.4290221003
Cuevas, A., and Pampanin, S. (2014). “Accounting for residual capacity of reinforced concrete plastic hinges: Current practice and proposed framework,” in Proceedings of the New Zealand Society of Earthquake Engineering Conference, Auckland, New Zealand, 21-23 March 2014.
Cuevas, A., and Pampanin, S. (2017). “Post-seismic capacity of damaged and repaired reinforced concrete plastic hinges extracted from a real building,” in Proceedings of 16th World Conference on Earthquake Engineering, Santiago Chile, 9-13 January 2017.
D’Ayala, D., Meslem, A., Vamvatsikos, D., Porter, K., Rossetto, T., Crowley, H., et al. (2014). “Guidelines for analytical vulnerability assessment - low/mid-rise,”. GEM Technical Report.
Dazio, A. (2004). “Residual displacements in capacity designed reinforced concrete structures,” in Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, August 1-6, 2004.
de Quevedo Iñarritu, P. G., Šipčić, N., Kohrangi, M., and Bazzurro, P. (2021). “Effects of pre-existing damage on fragility of URM and RC frame buildings,” in Energy-based seismic engineering. IWEBSE. Lecture Notes in Civil Engineering (Cham: Springer). Vol. 155. doi:10.1007/978-3-030-73932-4_2
Decanini, L. D., Bruno, S., and Mollaioli, F. (2004). Role of damage functions in evaluation of response modification factors. J. Struct. Eng. 130, 1298–1308. doi:10.1061/(asce)0733-9445(2004)130:9(1298)
Decanini, L. D., and Mollaioli, F. (2001). An energy-based methodology for the assessment of seismic demand. Soil Dyn. Earthq. Eng. 21, 113–137. doi:10.1016/s0267-7261(00)00102-0
Decanini, L. D., and Mollaioli, F. (1998). Formulation of elastic earthquake input energy spectra. Earthq. Eng. Struct. Dyn. 27, 1503–1522. doi:10.1002/(sici)1096-9845(199812)27:12<1503::aid-eqe797>3.0.co;2-a
Decanini, L. D., Mollaioli, F., and Saragoni, R. (2000). Energy and displacement demands imposed by near-source ground motions. Auckland, New Zealand: Proceedings of the 12th World Conference on Earthquake Engineering.
Del Vecchio, C., Gentile, R., Di Ludovico, M., Uva, G., and Pampanin, S. (2018). Implementation and validation of the simple lateral mechanism analysis (SLaMA) for the seismic performance assessment of a damaged case study building. J. Earthq. Eng. 24, 1771–1802. doi:10.1080/13632469.2018.1483278
Di Ludovico, M., Polese, M., Gaetani d’Aragona, M., Prota, A., and Manfredi, G. (2013). A proposal for plastic hinges modification factors for damaged RC columns. Eng. Struct. 51, 99–112. doi:10.1016/j.engstruct.2013.01.009
Di Trapani, F., and Malavisi, M. (2019). Seismic fragility assessment of infilled frames subject to mainshock/aftershock sequences using a double incremental dynamic analysis approach. Bull. Earthq. Eng. 17, 211–235. doi:10.1007/s10518-018-0445-2
Dolšek, M., and Fajfar, P. (2004). “IN2 - a simple alternative for IDA,” in Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, B.C., Canada, 1-6 August 2004.
Donaire-Ávila, J., and Benavent-Climent, A. (2020). Optimum strength distribution for structures with metallic dampers subjected to seismic loading. Met. (Basel) 10, 127. doi:10.3390/met10010127
Elwood, K. J., Marder, K., Pampanin, S., Cuevas, A., Kral, M., Smith, P., et al. (2016). “Draft framework for assessing residual capacity of earthquake-damaged concrete buildings,” in Proceedings of the New Zealand Society of Earthquake Engineering Conference, Christchurch, New Zealand, April 1–3, 2016.
Fajfar, P. (2000). A nonlinear analysis method for performance-based seismic design. Earthq. Spectra. 16, 573–592. doi:10.1193/1.1586128
Fajfar, P. (1992). Equivalent ductility factors, taking into account low-cycle fatigue. Earthq. Eng. Struct. Dyn. 21 (10), 837–848. doi:10.1002/eqe.4290211001
Fajfar, P., and Vidic, T. (1994). Consistent inelastic design spectra: Hysteretic and input energy. Eng. Struct. Dynam. 23, 523–537. doi:10.1002/eqe.4290230505
Fardis, M. N. (2018). From force-to displacement-based seismic design of concrete structures and beyond. Geotech. Geol. Earthq. Eng. 46, 101–122. doi:10.1007/978-3-319-75741-4_4
FEMA (1998). Evaluation of earthquake damaged concrete and masonry wall buildings – basic procedures manual. Washington DC, US: Federal Emergency Management Agency, FEMA.
FEMA (2012). Seismic performance assessment of buildings. Washington, D.C., USA: Federal Emergency Management Agency. FEMA-P-58-1.
Gaetani d’Aragona, M., Polese, M., Elwood, K. J., Baradaran Shoraka, M., and Prota, A. (2017). Aftershock collapse fragility curves for non-ductile RC buildings: A scenario-based assessment. Earthq. Eng. Struct. Dyn. 46, 2083–2102. doi:10.1002/eqe.2894
Gentile, R., Cremen, G., Galasso, C., Jenkins, L. T., Manandhar, V., Mentese, E. Y., et al. (2022). Scoring, selecting, and developing physical impact models for multi-hazard risk assessment. Int. J. Disaster Risk Reduct. 82, 103365. doi:10.1016/j.ijdrr.2022.103365
Gentile, R., Del Vecchio, C., Pampanin, S., Raffaele, D., and Uva, G. (2019a). Refinement and validation of the simple lateral mechanism analysis (SLaMA) procedure for RC frames. J. Earthq. Eng. 25, 1227–1255. doi:10.1080/13632469.2018.1560377
Gentile, R., and Galasso, C. (2021a). Hysteretic energy-based state-dependent fragility for ground-motion sequences. Earthq. Eng. Struct. Dyn. 50, 1187–1203. doi:10.1002/eqe.3387
Gentile, R., and Galasso, C. (2021b). Simplicity versus accuracy trade-off in estimating seismic fragility of existing reinforced concrete buildings. Soil Dyn. Earthq. Eng. 144, 106678. doi:10.1016/j.soildyn.2021.106678
Gentile, R., Pampanin, S., Raffaele, D., and Uva, G. (2019b). Analytical seismic assessment of RC dual wall/frame systems using SLaMA: Proposal and validation. Eng. Struct. 188, 493–505. doi:10.1016/j.engstruct.2019.03.029
Gentile, R., Pampanin, S., Raffaele, D., and Uva, G. (2019c). Non-linear analysis of RC masonry-infilled frames using the SLaMA method: Part 1—mechanical interpretation of the infill/frame interaction and formulation of the procedure. Bull. Earthq. Eng. 17, 3283–3304. doi:10.1007/s10518-019-00580-w
Gentile, R., Pampanin, S., Raffaele, D., and Uva, G. (2019d). Non-linear analysis of RC masonry-infilled frames using the SLaMA method: Part 2—parametric analysis and validation of the procedure. Bull. Earthq. Eng. 17, 3305–3326. doi:10.1007/s10518-019-00584-6
Goda, K. (2015). Record selection for aftershock incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 44 (7), 1157–1162. doi:10.1002/eqe.2513
Goda, K., and Taylor, C. A. (2012). Effects of aftershocks on peak ductility demand due to strong ground motion records from shallow crustal earthquakes. Earthq. Eng. Struct. Dyn. 41 (15), 2311–2330. doi:10.1002/EQE.2188
Grant, D. N., Blandon, C. A., and Priestley, M. J. N. (2005). Modelling inelastic response in direct displacement-based design. Pavia, Italy: IUSS Press.
Housner, G. W. (1956). “Limit design of structures to resist earthquakes,” in Proceedings of the 1st world conference on earthquake engineering (Berkeley: California).
Iacoletti, S., Cremen, G., and Galasso, C. (2022). Integrating long and short-term time dependencies in simulation-based seismic hazard assessments. Earth Space Sci. 9. doi:10.1029/2022EA002253
Iacoletti, S., Cremen, G., and Galasso, C. (2023). Modeling damage accumulation during ground-motion sequences for portfolio seismic loss assessments. Dyn. Earthq. Eng. 168, 107821. doi:10.1016/J.SOILDYN.2023.107821
Jalayer, F., De Risi, R., and Manfredi, G. (2015). Bayesian Cloud Analysis: Efficient structural fragility assessment using linear regression. Bull. Earthq. Eng. 13, 1183–1203. doi:10.1007/s10518-014-9692-z
Jalayer, F., Ebrahimian, H., Miano, A., Manfredi, G., and Sezen, H. (2017). Analytical fragility assessment using unscaled ground motion records. Earthq. Eng. Struct. Dyn. 46, 2639–2663. doi:10.1002/eqe.2922
Jeon, J. S., Desroches, R., Lowes, L. N., and Brilakis, I. (2015). Framework of aftershock fragility assessment-case studies: Older California reinforced concrete building frames. Earthq. Eng. Struct. Dyn. 44, 2617–2636. doi:10.1002/EQE.2599
Kalateh-Ahani, M., and Amiri, S. (2021). A Park-Ang damage index-based framework for post-mainshock structural safety assessment. Structures 33, 820–829. doi:10.1016/j.istruc.2021.04.039
Kalkan, E., and Kunnath, S. K. (2008). Relevance of absolute and relative energy content in seismic evaluation of structures. Adv. Struct. Eng. 11, 17–34. doi:10.1260/136943308784069469
Kam, W. Y., Pampanin, S., Dhakal, R., Gavin, H. P., and Roeder, C. (2010). Seismic performance of reinforced con-crete buildings in the september 2010 Darfield (canterbury) earthquake. Bull. N. Z. Soc. Earthq. Eng. 43 (4), 340–350. doi:10.5459/bnzsee.43.4.340-350
Kam, W. Y., Pampanin, S., and Elwood, K. (2011). Seismic performance of reinforced concrete buildings in the 22 February Christchurch (Lyttelton) earthquake. Bull. New Zeal. Soc. Earthq. Eng. 44, 239–278. doi:10.5459/bnzsee.44.4.239-278
Kappos, A. J. (1997). Seismic damage indices for RC buildings: Evaluation of concepts and procedures. Prog. Struct. Eng. Mater. 1, 78–87. doi:10.1002/pse.2260010113
Kazantzi, A. K., and Vamvatsikos, D. (2018). The hysteretic energy as a performance measure in analytical studies. Earthq. Spectra. 34, 719–739. doi:10.1193/112816EQS207M
Kunnath, S. K., Reinhorn, A. M., and Lobo, R. (1992). IDARC version 3.0: A program for the inelastic damage analysis of reinforced concrete structures. New York: University at Buffalo.
Loporcaro, G., Cuevas, A., Pampanin, S., and Kral, M. V. (2022). Strain-ageing effects on the residual low-cycle fatigue life of low-carbon steel reinforcement. Mater. Struct. Constr. 55, 35. doi:10.1617/s11527-022-01885-0
Loporcaro, G., Pampanin, S., and Kral, M. V. (2018). Estimating plastic strain and residual strain capacity of earthquake-damaged steel reinforcing bars. J. Struct. Eng. 144, 04018027. doi:10.1061/(asce)st.1943-541x.0001982
Luco, N., Bazzurro, P., and Cornell, A. C. (2004). “Dynamic versus static computation of the residual capacity of a mainshock-damaged building to withstand an aftershock,” in Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, B.C., Canada, 1-6 August 2004.
Maeda, M., Al-Washali, H., and Matsukawa, K. (2019). “An overview of post-earthquake damage and residual capacity evaluation for reinforced concrete buildings in Japan,” in Proceedings of the 8th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete, Greece, 24-26 June 2019.
Mahin, S., and Bertero, V. V. (1981). An evaluation of inelastic seismic design spectra. J. Struct. Div. ASCE 107, 1777–1795. doi:10.1061/jsdeag.0005782
Malek, A., Andisheh, K., Scott, A., Pampanin, S., MacRae, G., and Palermo, A. (2018). Residual capacity and permeability-based damage assessment of concrete in damaged RC columns. J. Mater. Civ. Eng. 30, 1. doi:10.1061/(ASCE)MT.1943-5533.0002312
Marder, K., Elwood, K. J., Motter, C. J., and Clifton, G. C. (2020). Post-earthquake assessment of moderately damaged reinforced concrete plastic hinges. Earthq. Spectra. 36, 299–321. doi:10.1177/8755293019878192
Marder, K., Motter, C., Elwood, K. J., and Clifton, G. C. (2018). Testing of 17 identical ductile reinforced concrete beams with various loading protocols and boundary conditions. Earthq. Spectra. 34, 1025–1049. doi:10.1193/101717EQS215DP
Martins, L., and Silva, V. (2021). Development of a fragility and vulnerability model for global seismic risk analyses. Bull. Earthq. Eng. 19, 6719–6745. doi:10.1007/s10518-020-00885-1
Minas, S., and Galasso, C. (2019). Accounting for spectral shape in simplified fragility analysis of case-study reinforced concrete frames. Soil Dyn. Earthq. Eng. 119, 91–103. doi:10.1016/j.soildyn.2018.12.025
Mollaioli, F., Bruno, S., Decanini, L., and Saragoni, R. (2011). Correlations between energy and displacement demands for performance-based seismic engineering. Pure Appl. Geophys. 168, 237–259. doi:10.1007/s00024-010-0118-9
Nakano, Y., Maeda, M., Kuramoto, H., and Murakami, M. (2004). “Guideline for post-earthquake damage evaluation and rehabilitation of RC buildings in Japan,” in Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, B.C., Canada, 1-6 August 2004.
Nettis, A., Gentile, R., Raffaele, D., Uva, G., and Galasso, C. (2021). Cloud Capacity Spectrum Method: Accounting for record-to-record variability in fragility analysis using nonlinear static procedures. Soil Dyn. Earthq. Eng. 150, 106829. doi:10.1016/j.soildyn.2021.106829
Nuzzo, I., Caterino, N., and Pampanin, S. (2020). Seismic design framework based on loss-performance matrix. J. Earthq. Eng. 26, 4325–4345. doi:10.1080/13632469.2020.1828201
NZSEE (2017). The seismic assessment of existing building – technical guidelines for engineering assessments. Wellington, New Zealand: New Zealand Society of Earthquake Engineering.
O’Reilly, G. J. (2021). Limitations of Sa(T1) as an intensity measure when assessing non-ductile infilled RC frame structures. Bull. Earthq. Eng. 19, 2389–2417. doi:10.1007/s10518-021-01071-7
Orlacchio, M., Baltzopoulos, G., and Iervolino, I. (2020). “State-dependent seismic fragility via pushover analysis,” in Proceedings of the 17th World Conference on Earthquake Engineering, Sendai, Japan, 13-18 September 2020.
Otárola, K., Fayaz, J., and Galasso, C. (2022). Fragility and vulnerability analysis of deteriorating ordinary bridges using simulated ground-motion sequences. Earthq. Eng. Struct. Dyn. 51, 3215–3240. doi:10.1002/EQE.3720
Pampanin, S., Calvi, G. M., and Moratti, M. (2002a). “Seismic behaviour of RC beam-column joints designed for gravity loads,” in Proceedings of the 12th European Conference on Earthquake Engineering, London, UK, 9-13 September 2002.
Pampanin, S., Christopoulos, C., and Priestley, M. J. N. (2002b). Residual deformations in the performance-based seismic assessment of frame structures. Italy: IUSS Press.
Pampanin, S., Cuevas, A., Kral, M., Loporcaro, G., Scott, A., and Malek, A. (2015). “Residual capacity and repairing options for reinforced concrete buildings,”. Research Report Prepared for the Natural Hazard Research Platform, Contract 2012-UOC-02-NHRP.
Pampanin, S. (2021). “Simplified analytical/mechanical procedure for post-earthquake safety evaluation and loss assessment of buildings,” in Springer tracts civ. Eng. (New York: Springer).
Pampanin, S. (2017). “Towards the practical implementation of performance-based assessment and retrofit strategies for RC buildings: Challenges and solutions,” in Proceedings of the 4th conference on smart monitoring (Zurich, Switzerland: Assessment and Rehabilitation of Civil Structures).
Papadopoulos, A. N., and Bazzurro, P. (2021). Exploring probabilistic seismic risk assessment accounting for seismicity clustering and damage accumulation: Part II. Risk analysis. Earthq. Spectra. 37, 386–408. doi:10.1177/8755293020938816
Papadopoulos, A. N., Kohrangi, M., and Bazzurro, P. (2020). Mainshock-consistent ground motion record selection for aftershock sequences. Earthq. Eng. Struct. Dyn. 49, 754–771. doi:10.1002/EQE.3263
Park, Y., Ang, A. H.-S., and Wen, Y. K. (1985). Seismic damage analysis of reinforced concrete buildings. J. Struct. Eng. 111, 740–757. doi:10.1061/(asce)0733-9445(1985)111:4(740)
Park, Y., and Ang, A. H.-S. (1985). Mechanistic seismic damage model for reinforced concrete. J. Struct. Eng. 111, 722–739. doi:10.1061/(asce)0733-9445(1985)111:4(722)
Park, Y. J., Ang, A. H.-S., and Wen, Y. K. (1987). Damage-limiting aseismic design of buildings. Earthq. spectra 3 (1), 1–26. doi:10.1193/1.1585416
Pedone, L., Bianchi, S., Giovinazzi, S., and Pampanin, S. (2022). A framework and tool for knowledge-based seismic risk assessment of school buildings: SLaMA-school. Sustain 14, 9982. doi:10.3390/SU14169982
Pedone, L., Bianchi, S., and Pampanin, S. (2023). Adaptive knowledge-based seismic risk assessment of existing reinforced concrete buildings using the SLaMA method. Procedia Struct. Integr. 44, 227–234. doi:10.1016/j.prostr.2023.01.030
Pedone, L., Gentile, R., Galasso, C., and Pampanin, S. (2021). “Nonlinear static procedures for state-dependent seismic fragility analysis of reinforced concrete buildings,” in Proceedings of the 2nd Fib Italy YMG Symposium on Concrete and Concrete Structures, Rome, Italy, 18-19 November 2021.
Polese, M., Marcolini, M., Prota, A., and Zuccaro, G. (2013). “Mechanism based assessment of damaged building’s residual capacity,” in Proceedings of the 8th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Kos Island, Greece, 27-30 June 2013.
Polese, M., Di Ludovico, M., Prota, A., and Manfredi, G. (2012). Damage-dependent vulnerability curves for existing buildings. Earthq. Eng. Struct. Dyn. 42, 853–870. –6. doi:10.1002/eqe.2249
Polese, M., Marcolini, M., Zuccaro, G., and Cacace, F. (2015). Mechanism based assessment of damage-dependent fragility curves for RC building classes. Bull. Earthq. Eng. 13, 1323–1345. doi:10.1007/s10518-014-9663-4
Priestley, M. J. N., Calvi, G. M., and Kowalsky, M. J. (2007). Displacement based seismic design of structures. Pavia: Iuss: Indian Institute of Technology.
Priestley, M. J. N. (1993). Myths and fallacies in earthquake engineering. Bull. N. Z. Soc. Earthq. Eng. 26 (3), 329–341. doi:10.5459/bnzsee.26.3.329-341
Raghunandan, M., Liel, A. B., and Luco, N. (2015). Aftershock collapse vulnerability assessment of reinforced concrete frame structures. Earthq. Eng. Struct. Dyn. 44, 419–439. doi:10.1002/EQE.2478
Rossi, A., Del Vecchio, C., and Pampanin, S. (2022). Influence of earthquake damage and repair interventions on expected annual losses of reinforced concrete wall buildings. Earthq. Spectra. 38, 2026–2060. doi:10.1177/87552930211072878
Ruiz-García, J., and Aguilar, J. D. (2015). Aftershock seismic assessment taking into account postmainshock residual drifts. Earthq. Eng. Struct. Dyn. 44, 1391–1407. doi:10.1002/EQE.2523
Ruiz-García, J. (2012). Mainshock-aftershock ground motion features and their influence in building's seismic response. J. Earthq. Eng. 16 (5), 719–737. doi:10.1080/13632469.2012.663154
Saiidi, M., and Sozen, M. A. (1979). Simple and complex models for nonlinear seismic response of reinforced concrete structures. Urbana, IL: University of Illinois at Urbana-Champaign.
Sansoni, C., da Silva, L. C. M., Marques, R., Pampanin, S., and Lourenço, P. B. (2022). SLaMA-URM method for the seismic vulnerability assessment of UnReinforced Masonry structures: Formulation and validation for a substructure. J. Build. Eng. 63, 105487. doi:10.1016/J.JOBE.2022.105487
Silva, V., Akkar, S., Baker, J., Bazzurro, P., Castro, J. M., Crowley, H., et al. (2019). Current challenges and future trends in analytical fragility and vulnerability modeling. Earthq. Spectra. 35, 1927–1952. doi:10.1193/042418EQS101O
Smerzini, C., Galasso, C., Iervolino, I., and Paolucci, R. (2014). Ground motion record selection based on broadband spectral compatibility. Earthq. Spectra 30 (4), 1427–1448. doi:10.1193/052312EQS197M
Stone, W. C., and Taylor, A. W. (1993). Seismic performance of circular bridge columns designed in accordance with AASHTO/CALTRANS standards.
Uang, C. M., and Bertero, V. V. (1990). Evaluation of seismic energy in structures. Earthq. Eng. Struct. Dyn. 19, 77–90. doi:10.1002/eqe.4290190108
Vamvatsikos, D., and Cornell, C. A. (2005). Direct estimation of seismic demand and capacity of multidegree-of-freedom systems through incremental dynamic analysis of single degree of freedom approximation. J. Struct. Eng. 131, 589–599. doi:10.1061/(asce)0733-9445(2005)131:4(589)
Vamvatsikos, D., and Cornell, C. A. (2002). Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 31, 491–514. doi:10.1002/eqe.141
Williams, M. S., and Sexsmith, R. G. (1995). Seismic damage indices for concrete structures: A state-of-the-art review. Earthq. spectra 11 (2), 319–349. doi:10.1193/1.1585817
Yu, X., Zhou, Z., Du, W., and Lu, D. (2021). Development of fragility surfaces for reinforced concrete buildings under mainshock-aftershock sequences. Earthq. Eng. Struct. Dyn. 50, 3981–4000. doi:10.1002/eqe.3542
Zhang, L., Goda, K., De Luca, F., and De Risi, R. (2020). Mainshock-aftershock state-dependent fragility curves: A case of wood-frame houses in British columbia, Canada. Earthq. Eng. Struct. Dyn. 49, 884–903. doi:10.1002/EQE.3269
Keywords: ground-motion sequences, mainshock-aftershock, energy-based seismic engineering, seismic fragility, state-dependent fragilities
Citation: Pedone L, Gentile R, Galasso C and Pampanin S (2023) Energy-based procedures for seismic fragility analysis of mainshock-damaged buildings. Front. Built Environ. 9:1183699. doi: 10.3389/fbuil.2023.1183699
Received: 10 March 2023; Accepted: 14 April 2023;
Published: 02 May 2023.
Edited by:
Izuru Takewaki, Kyoto University, JapanCopyright © 2023 Pedone, Gentile, Galasso and Pampanin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Livio Pedone, bGl2aW8ucGVkb25lQHVuaXJvbWExLml0
 Livio Pedone
Livio Pedone Roberto Gentile
Roberto Gentile Carmine Galasso
Carmine Galasso Stefano Pampanin1
Stefano Pampanin1