An overview on seismic analysis of masonry building aggregates

Conservation of historical centres is a pressing need for Mediterranean countries, that are characterized by masonry aggregates representing the most typical construction type within cities. Masonry clustered buildings were usually designed without seismic design criteria. Moreover, the current seismic standard codes do not foresee a clear calculation method to predict their non-linear behaviour. For this reason, in this paper, a wide overview on the seismic response of masonry aggregates has been done considering analysis at different levels, from simplified large-scale evaluations to sophisticated non-linear analyses. In the former investigation kind, a vulnerability form appropriately conceived for clustered buildings has been applied to different historical centres with the aim to perform risk analysis considering both empirical approaches and real data deriving from occurred past earthquakes. In the second evaluation type, the macro-elements analysis method has been examined with reference to typical clustered buildings of the Italian territory. In particular, global assessments, performed using the 3Muri non-linear analysis program, have been performed with the final goal to derive fragility curves of structural units of masonry aggregates considering their plan position in the clustered building (end of row, internal, and corner).

Introduction

Masonry is the most widespread construction in the historical city centres of all Mediterranean countries. Masonry building aggregates formed as a result of the evolution and expansion of the centres of the old cities making large and complex structures. The construction process was noted in the vertical direction, with the construction of the new floors, and additionally, new buildings were constructed immediately next to the existing building leading to the condition that the buildings very often shared the same walls. In some situations, it is possible to distinguish individual units, however, these structures cannot be analysed as separate units as their behaviour within the complex aggregate scenario is completely different. In this respect, in order to evaluate the seismic behaviour of such structures, it is necessary to take into account the interaction of the adjacent buildings. The response of these complex compounds is connected to numerous factors, like the type and degree of connection between the adjacent buildings, mechanical characteristics of individual structural units, position, and type of floor systems, the connection of the floors and walls, and connection between the walls, irregularities in plan and height, etc. (Vicente, 2008). This is a very difficult task and there are more unknowns than familiar features. Most of these structures were built without any seismic provision, the current state of the built materials is unknown, lack of drawings and design projects, unknown construction chronology and implemented construction technique. This results in a low level of knowledge of these structures making the process of analysis more difficult. The level of knowledge should determine the methodology to be used for the assessment of the masonry aggregate buildings exposed to seismic activity (Maio, 2013). Most of the existing buildings forming the nuclei of the old towns have been constructed centuries ago without taking into account any seismic influence and this increases their vulnerability and possibly the seismic risk.

Even though each country has its own specific features with respect to masonry construction, type of material, and similar, common aspects in the structural domain are identified (low rise structures, moderate spans, and large wall thickness) (Giuffrè, 1995), even though this can be variable within a certain block. As a result, development of complex vertical, and/or horizontal features was inevitable, resulting in buildings of various shapes and heights (Formisano, 2017).

Most of the old existing structures in the old urban centres are constructed with timber flexible floors of low and insufficient in-plane stiffness, lacking an effective connection to the bearing wall, and lack of connection between the orthogonal walls. This all leads to the inability to provide the structure with so-called “box-behaviour” and seismic activity may lead to the out-of-plane failure of perimeter walls. The “codes of practice” (Giuffrè, 1993), (Giuffrè and Carocci, 1999) developed in Italy provided valuable information on various aspects of existing old masonry buildings. Looking at the current codes of various Mediterranean countries and even other European countries there is an evident lack of procedure and methodology for the assessment of such buildings. It is within the scientific and research community that various methodologies and methods have developed.

Modelling and vulnerability assessment of masonry compounds ‘‘Baixa Pombalina’’ Lisbon was done by (Ramos and Lourenço, 2004). The complex is made of 60 blocks, with each block having seven buildings and sharing the same gable walls, and a detailed nonlinear time history analysis has been conducted. The calculation showed how the ‘‘aggregate effect’’ affects the global and local behaviour of structures in the compound. Buildings treated as a part of a compound showed a better global behaviour once exposed to earthquake motion in comparison to once they have been treated as isolated structures that are more flexible. Locally, the pounding effect may cause local damage. This conclusion has been proved after the several earthquakes occurred in Italy (2009 L’Aquila, 2012 Emilia-Romagna), showing an improved group response of aggregate buildings once exposed to earthquake ground motion, even when structural units (SU) are made of masonry of low material quality (Formisano et al., 2010a), (Formisano et al., 2010b), (Formisano et al., 2011), (Formisano and Topping, 2012), (Indirli et al., 2013), (Formisano et al., 2015). The structural units assessed as being a part of an aggregate can withstand larger displacement demand exposed to seismic action than they would have resisted if they have been treated as an isolated structure. The effect was less emphasized in the intermediated units and more noticeable in the structural units located at the ends of the rows (heading SU). Dolce et al. (Dolce et al., 2006) compared two vulnerability assessment methodologies used in Italy and Greece that were applied to the buildings damaged during the 1990 Potenza earthquake, located in Southern Italy. The study showed similarities and differences that can be attributed to various aspects, for further information please see (Dolce et al., 2006). Senaldi et al. (Senaldi et al., 2010) investigated the influence of the aggregate’s row length and flexible wooden floors on the seismic behaviour of masonry buildings utilizing nonlinear dynamic analyses. The effect of the aggregate interaction of the typical construction in the Eixample district in Barcelona (Spain) was investigated by Pujades et al. (Pujades et al., 2012), indicating that the aggregate compounds experienced lower damage in comparison to the damage experienced if buildings were modelled individually. After the 2009 L’Aquila earthquake, da Porto et al. (Da Porto et al., 2013) conducted a pilot study on the damaged clustered buildings, by conducting a visual inspection, in situ analysis, and investigations for the determination of the masonry mechanical characteristics, surveying the seismic damage and its interpretation, a simplified global assessment, local mechanism collapse, etc. All obtained results were used for the most adequate repair measures to be proposed and implemented. Seismic assessment with the application of hybrid and indirect assessment techniques was conducted by (Maio et al., 2015) on a stone masonry building aggregate in Pio delle Camere.

The seismic vulnerability assessment for such clustered masonry buildings can be conducted by applying mechanical or hybrid (Kappos et al., 2006), (Kappos, 2016) methods. The latter is a combination of empirical data defined by the damage statistics and analytical data obtained from inelastic analysis of structures. Pioneer work and key thoughts were set by (Kappos et al., 1991) during the post-earthquake damage assessment of masonry infilled reinforced concrete (RC) frames and dual systems after the 1978 Thessaloniki earthquake and prediction of damage of the same buildings exposed to an earthquake of a 0.5 higher magnitude than the 1978 Thessaloniki earthquake. The development of the hybrid method was conducted as well by (Barbat et al., 1996). A methodology that was based on two segments, first the on the Italian vulnerability index and secondly on the damage survey results obtained after the earthquake implemented through a vulnerability function. This methodology was applied to the Example district in Barcelona (Spain). It is a feasible methodology for the assessment of the vulnerability of buildings on a global scale and has been implemented in various European and non-European countries (Ademović et al., 2020), (Ademovic et al., 2022), (Formisano et al., 2017), (Cherif et al., 2019), (Chieffo and Formisano, 2019), (Taibi et al., 2019), (Brando et al., 2017).

Lourenço and Roque (Lourenço and Roque, 2006) developed a simplified mechanical method and corresponding indexes (In-plan area ratio, Area to weight ratio, Base shear ratio) for quick preliminary screening and decision making regarding prioritization for further detailed analysis of historic masonry structures and in this specific case, 58 churches were examined in Portugal. This application is in line with the proposed large-scale evaluation method of aggregates, where an extension of the simplified seismic vulnerability assessment methodology proposed by (Benedetti and Petrini, 1984), with five new parameters considering the interaction effects among aggregates exposed to earthquakes, was done (Formisano et al., 2015). On the other hand, an alternative more refined approach can be used evaluating individual buildings either through finite element methods, “equivalent frame” methods, etc (D’Altri et al., 2020), (De Angelis et al., 2020), (Degli et al., 2019), (Ademović et al., 2019), (Bartoli et al., 2016), (Milani and Valente, 2015), (Ademović et al., 2013), (Ademović, 2011), (Rizzano and Sabatino, 2010), (Pasticier et al., 2008), (Roca et al., 2005), (Roca et al., 2005), (Sarhosis et al., 2017), (Giamundo et al., 2014). This approach did not find its massive implementation, even though it has been implemented (Formisano et al., 2015) in the vulnerability assessment of clustered buildings. Analogously, much more refined analyses in the non-linear dynamic field, although providing very detailed information on the seismic behaviour of masonry aggregate SU (Grillanda et al., 2020), are employed only at the scientific level, but are typically unexploited by designers, who prefer to use simpler applications like that explained in the following section.

Large-scale seismic vulnerability assessment

Seismic analysis of masonry building aggregates is a difficult task for researchers and designers due to the structural complexity of heterogeneous buildings developed in a chaotic way over the centuries within the historical centres of European countries.

Simple investigation methods based on quick vulnerability forms, where the major information on the buildings can be collected from an in-situ survey, represent a useful technique able to provide, within a given historical centres to be examined, a ranking of the structural units of masonry compounds most susceptible to damage under earthquakes.

To assess the seismic vulnerability of buildings grouped in aggregate conditions, the appropriate vulnerability form for aggregate structural units proposed in Table 1) (Formisano et al., 2015), that is based on Benedetti and Petrini’s vulnerability index method (Benedetti and Petrini, 1984), can be used.

TABLE 1

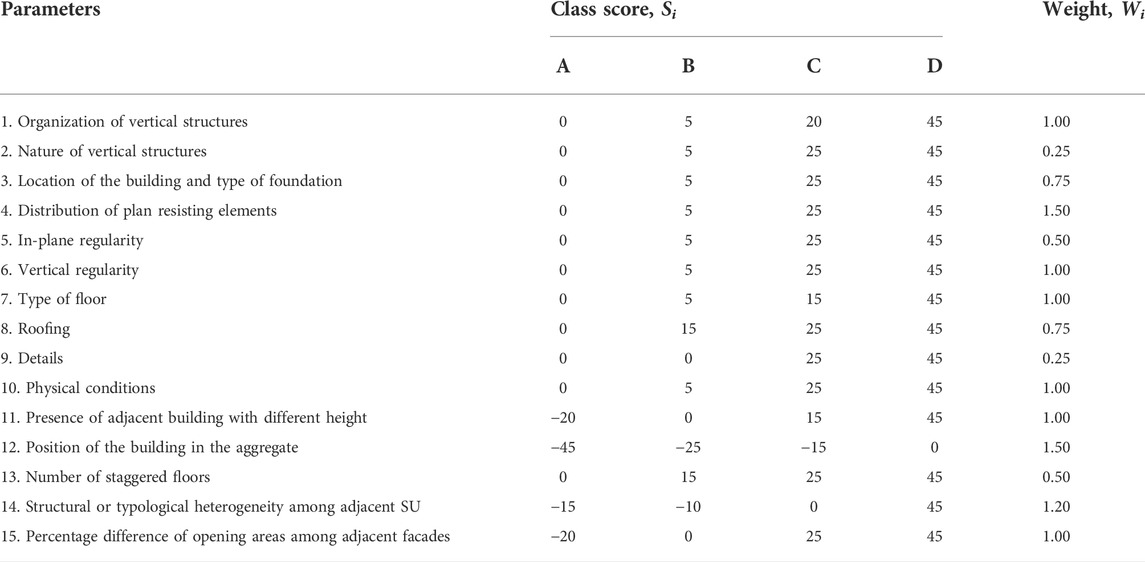
TABLE 1. Vulnerability assessment form for buildings in aggregate (Formisano et al., 2015).

The proposed vulnerability form, widely recognized internationally, has been appropriately crafted for historical aggregate buildings by adding to the original form five new parameters, that consider the effects of mutual interaction among SU under seismic action. In particular, the new parameters are added to the ten basic parameters, used in the past to survey the main structural system considered in isolated configurations.

The added parameters, extensively discussed in the literature, are [(Chieffo and Formisano, 2019), (Mosoarca et al., 2019), (Chieffo et al., 2020)]:

Parameter 11: Presence of adjacent buildings with different heights. The height interaction of a building with the adjacent ones generally negatively affects the seismic response of the structural unit.

Parameter 12: Position of the building in the aggregate. This parameter concerns the in-plane interaction among SUs. The planimetric interaction with adjacent buildings concerns the three possible positions that a building can have within an aggregate: head in a terraced block if it has three sides; corner if it has two free sides; closed if it has only one wall on the road.

Parameter 13: Number of staggered floors. This parameter considers the possible presence of staggered floors between adjacent buildings and the number of such floors, as the presence of staggered floors in the event of an earthquake can give rise to undisputed thrusts on the elements in common, that leads to an increase in stress.

Parameter 14: Structural or typological heterogeneity among adjacent SUs. This parameter accounts for the structural or typological heterogeneity among adjacent SUs. According to the formulation adopted, the building aggregates can be considered homogeneous when they present the same material and the same construction technique, that is the most favourable case.

Parameter 15: Percentage difference of opening areas among adjacent façades. This parameter considers the possibility that there is, between two adjacent buildings, a substantial difference in the external appearance of the façade, and, in particular, in the percentage of holes.

The vulnerability index, I_V, is evaluated for each SU as the weighted sum of the class selected (for each of the 15 parameters listed in Table 1 multiplied by the respective weight (Formisano et al., 2015). It is possible to notice how these parameters are distributed into four decreasing vulnerability classes (A, B, C, D), that express the influence of the single parameter on the global vulnerability of the building. A specific score, S_i, is assigned to each parameter that increases proportionally passing from Class A (the best) to Class D (the worst) and a weight, W_i, that is variable from a minimum of 0.25, for the less important parameters, up to a maximum of 1.50, for the most important factors of the form.

Thus, the vulnerability index, I_V, is evaluated by adopting the following equation:

${\mathrm{I}}_{\mathrm{V}}={\sum }_{\mathrm{i}=1}^{15}{\mathrm{S}}_{\mathrm{i}}\times {\mathrm{W}}_{\mathrm{i}}(1)$

Subsequently, ${\mathrm{I}}_{\mathrm{V}}$ can be normalized in the range [0÷1], acquiring the notation ${\mathrm{V}}_{\mathrm{I}}$, according to the following mathematical equation:

${\text{V}}_{\text{I}}=\left[\frac{{\mathrm{I}}_{\mathrm{V}}-\left({\sum }_{\mathrm{i}=1}^{15}{\mathrm{S}}_{\min }\times {\mathrm{W}}_{\mathrm{i}}\right)}{\left|{\sum }_{\mathrm{i}=1}^{15}\left[\left({\mathrm{S}}_{\max }\times {\mathrm{W}}_{\mathrm{i}}\right)-\left({\mathrm{S}}_{\min }\times {\mathrm{W}}_{\mathrm{I}}\right)\right]\right|}\right](2)$

to provide a simpler index to compare immediately the seismic vulnerability of masonry compound structural units.

Consequently, once know the V_I parameter, the typological vulnerability curves of structural units are achieved to characterize their expected damage varying the macroseismic intensity according to the well know Eq. 3 developed by Lagomarsino and Giovinazzi (Lagomarsino and Giovinazzi, 2006):

${\mathrm{\mu }}_{\mathrm{D}}=2.5\times \left[1+\tanh \left(\frac{{\mathrm{I}}_{\mathrm{EMS}-98}+6.25\times {\mathrm{V}}_{\mathrm{I}}-13.1}{\mathrm{Q}}\right)\right](3)$

From the above-mentioned equation, the vulnerability curves depend on three main factors: the normalized vulnerability index (V_I), the hazard, expressed in terms of macroseismic intensity (I_EMS-98), and a ductility factor Q, ranging from 1 to 4, and describes the ductility of typological classes of buildings (Lagomarsino and Giovinazzi, 2006). The mean typological vulnerability curves of different building typological classes can be plotted to estimate the expected level of damage under earthquakes with different intensity levels as per Eq. 3

Several applications of the above presented procedure for large-scale seismic vulnerability assessment of masonry compound structural units are found in literature papers. For the sake of example, herein the case study of Latronico, in the district of Potenza, is presented (Chieffo et al., 2022).

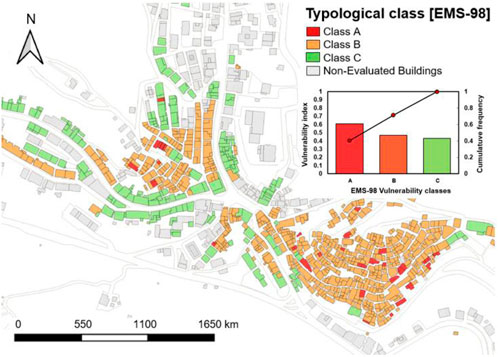
After collecting the in-situ information on the buildings of a sub-urban sector of the historical centre of Latronico, the vulnerability form was filled out for each of them. Therefore, using the QGIS open-source tool (QGIS Development Team, 2014), the distribution of the vulnerability indices of the examined structural units was plotted, as depicted in Figure 1.

FIGURE 1

FIGURE 1. Large-scale vulnerability analysis of a historical sector of the municipality of Latronico.

From the acquired vulnerability scenario, most of the buildings surveyed (85% of the cases) are associated with a vulnerability index between 0.4 and 0.6 (medium vulnerability), while only 5% of the sample have a vulnerability index enclosed in the range [0.6–0.8], that is associated to a medium-high expected vulnerability. Contrary, recent buildings (7% of the cases), erected after 1972, have a medium-low vulnerability index (0.2 < V_I<0.4).

Subsequently, according to the EMS-98 scale (Grünthal, 1998), each building has been assigned to a specific vulnerability class that essentially depends on the vertical structure typology.

Thus, as described, a “typological conversion” has been carried out between the classes surveyed using the CARTIS form (Zuccaro et al., 2015) with those provided by the EMS-98 scale ranging from A (the worst) to E (the best) (Grünthal, 1998). The results were summarized in Figure 2.

FIGURE 2

FIGURE 2. Typological vulnerability classes derived according to the EMS-98 scale.

The obtained results have shown that 5% of the examined buildings belong to Class A (MUR1, irregular masonry structures with deformable floors) and 76% of the cases belong to Class B (MUR2, irregular masonry buildings with semi-rigid horizontal structures). Finally, the remaining 19% of the buildings sample belong to Class C (squared masonry buildings with rigid horizontal structures). Furthermore, it can be observed that the distribution of the vulnerability is quite homogeneous with an average index enclosed in the range (0.4–0.6) for typological classes A, B, and C. In particular, for the presented building classes, the estimated mean typological vulnerability index is equal to 0.61, 0.47, and 0.43, respectively.

Later on, once the mean vulnerability index of the different typological classes of buildings analysed was obtained, the associated mean typological vulnerability curves were derived according to the closed-form relationship provided in (Lagomarsino and Giovinazzi, 2006). These curves are represented in Figure 3 to estimate the expected level of damage for the buildings’ stock investigated. Moreover, other four curves (V_I-σ; V_I+σ; V_I+2σ; V_I-2σ) were plotted to identify the upper and lower bounds of the statistical range of the expected damage (Chieffo and Formisano, 2019).

FIGURE 3

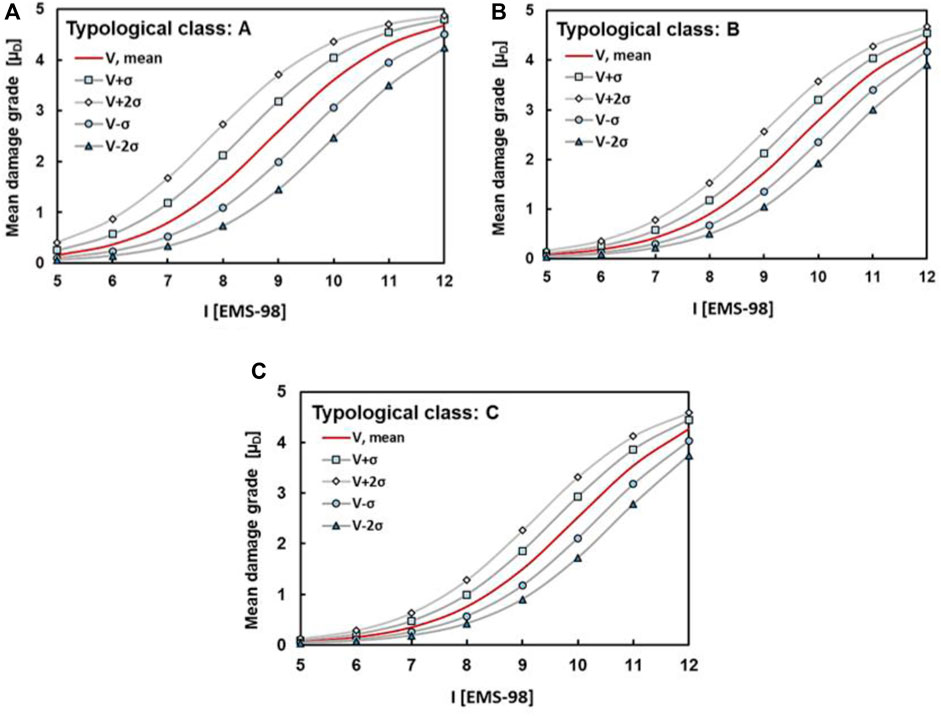
FIGURE 3. Mean typological vulnerability curves for the examined buildings sample. (A) Typology class A; (B) Typology class B; (C) Typology class C.

Mechanical approach by macro-elements analyses

There are numerous approaches to investigate numerically the seismic behaviour of masonry aggregates. One of the most common and used methods is the macro-elements analysis, where masonry walls of buildings are discretised into different parts, named macro-elements, and are represented by deformable components (piers and spandrels) and rigid ones (nodal panel zones). After the walls of the buildings are schematised into macro-elements, they are transformed into an equivalent frame to perform static non-linear analyses according to the actual seismic code aiming at finding the seismic safety factors of structural units, as well as at developing their vulnerability curves, in the two major analysis directions.

In this framework, the first Author performed a lot of applications of this kind of analysis to different historical aggregates within municipality centres of Italy. In the following, an overview of some of these case studies are presented and described.

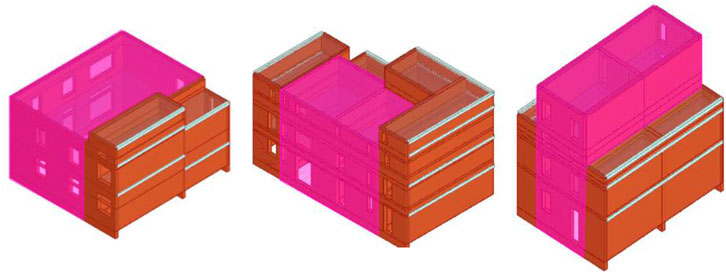
In the historical centre of Boscoreale (district of Naples), according to the information resumed by filling the CARTIS form, developed in the DPC-ReLUIS research project (Zuccaro et al., 2015), the macro-elements model (Penna et al., 2014), by utilizing the 3Muri analysis program (S.T.A. DATA, 2022), of a masonry building compound was implemented. The structural units of the masonry compound are made of rough stones with a mean thickness of about 60 cm and develop on one, two, and three stories. They were built at the same time and share the same boundary walls. The buildings have mixed reinforced concrete (RC)—hollow tiles floors and roofs, that are well connected to the walls by RC ring beams. Floors are positioned at the same height, so that staggered floors do not exist. Due to the absence of direct in-situ tests on materials, their mechanical properties were assumed according to the provisions of the actual Italian technical code NTC 2018 (Ministerial Decree of Public Works (NTC18), 2018) considering a limited knowledge level (LC1). The first-floor plan layout and the 3Muri model of the masonry aggregate are depicted in Figure 4.

FIGURE 4

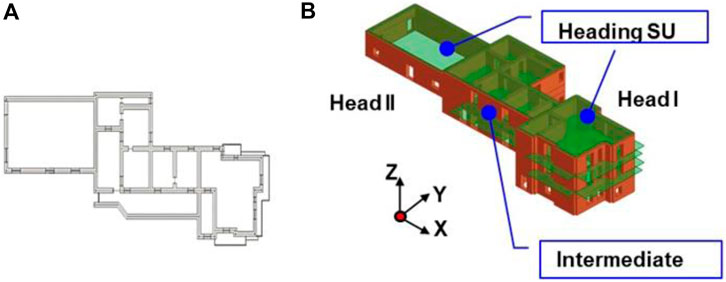
FIGURE 4. (A) First-floor plan layout; (B) 3Muri model of a masonry aggregate in Boscoreale (Naples, Italy).

Performing the seismic analyses on the whole building aggregate in the two analysis directions (x and y), the pushover curves of each of the three structural units (Head I, Intermediate, and Head II) were derived by considering as base shear the sum of shears of masonry piers belonging to each structural units, so considering the influence of adjacent walls, and as top displacement the average values of displacement values of the roof nodes of that SU. In particular, for walls in common between two structural units, the shear is divided in two equal parts between them.

The worst pushover curves in the two main analysis directions derived from performed analysis on the three SUs are depicted in Figure 5.

FIGURE 5

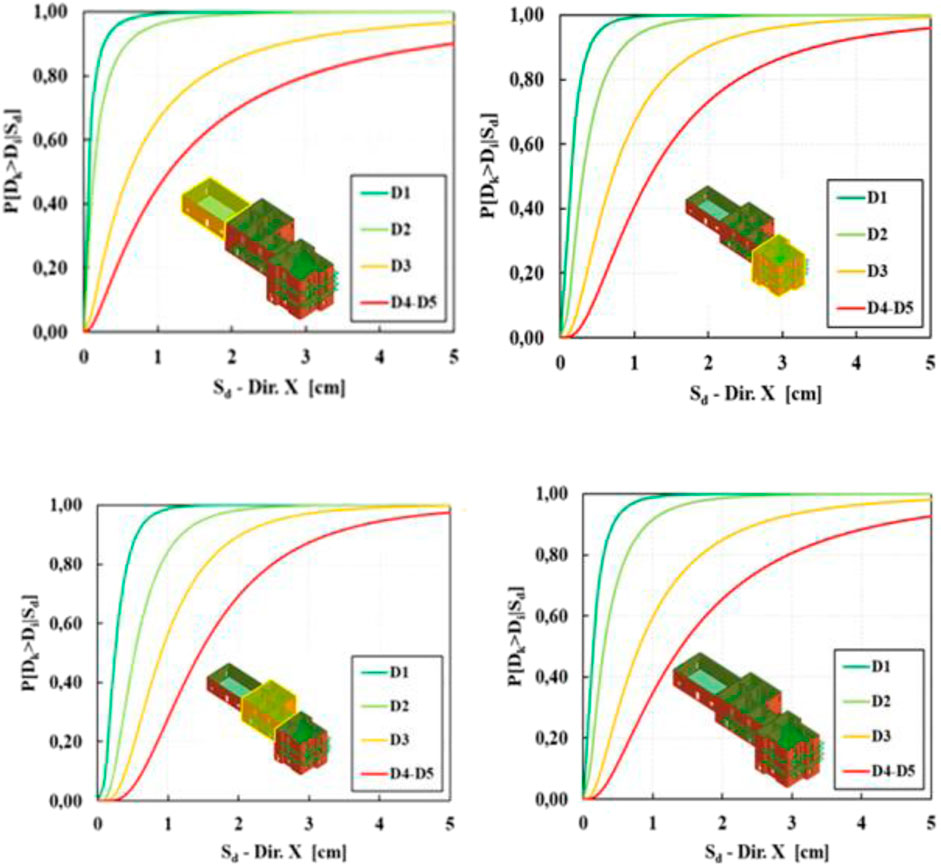
FIGURE 5. Pushover analysis curves in: (A) direction X; (B) direction Y for the SU of the masonry aggregate in Boscoreale.

The analysis results showed that the best seismic behaviour is attained from the intermediate SU, since it profits from the presence of the two adjacent buildings both in terms of base shear and ultimate displacement. Contrary, due to the in-plane and in-elevation irregularities of the whole building aggregate, torsion rotation occurred under an earthquake, so to induce much more damage to two head SUs. For this reason, in the weakest analysis direction (Y), the Head II SU, developing on one specific floor and being the more deformable SU, underwent major displacements, whereas the Head I SU showed very few plastic collapses.

In addition, fragility curves of all three SUs and the whole aggregate were achieved in both analysis directions (Figure 6 and 7). From these analyses, it was shown that in the longitudinal direction (X), there was no large difference in behaviour among SUs, as well as between SUs and the entire aggregate. Contrary, in the transverse direction (Y), under the same seismic displacement, the worst behaviour is that of the Head II SU, since it exhibited the highest collapse probabilities for different limit states considered. Intermediate SU suffered less damage than those of the Head II SU, but larger damage in comparison to the Head II SU, that showed a seismic behaviour like that of the whole aggregate.

FIGURE 6

FIGURE 6. Fragility curves of SU and building aggregate in direction X.

FIGURE 7

FIGURE 7. Fragility curves of SU and building aggregate in direction Y.

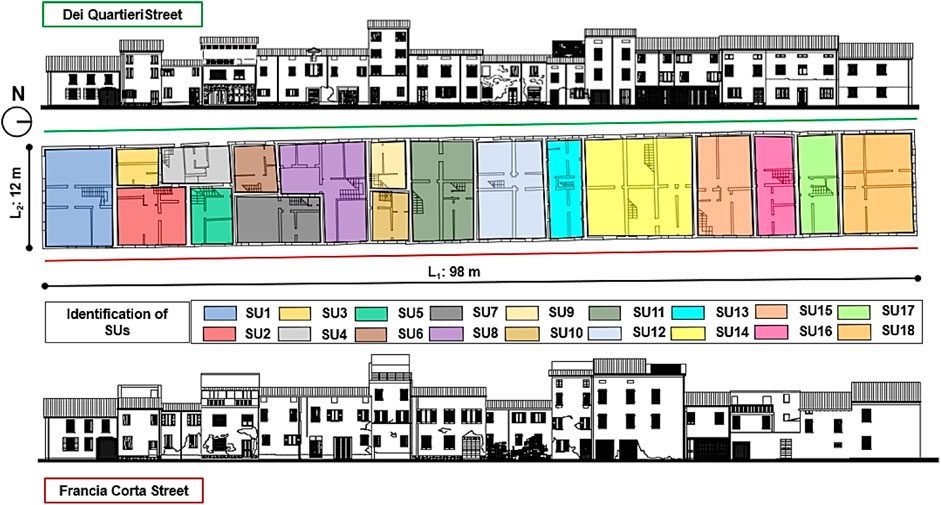
Another case study was developed in the municipality of Mirandola (district of Modena, Italy), that was hit by the 2012 Emilia-Romagna earthquake. Herein an “in-line” masonry building aggregate composed of 18 SUs was investigated (Figure 8). Buildings of the masonry compounds were built between the 1950s and 1980s, made of solid brick walls manufactured with lime mortar and have an average thickness between 25 and 50 cm. The number of floors is variable from 2 to 4 and their average height is 2.80 m. Horizontal structures and roofs are mainly made of timber beams with overlying double planking.

FIGURE 8

FIGURE 8. Identification of the aggregate case study in Mirandola (district of Modena, Italy).

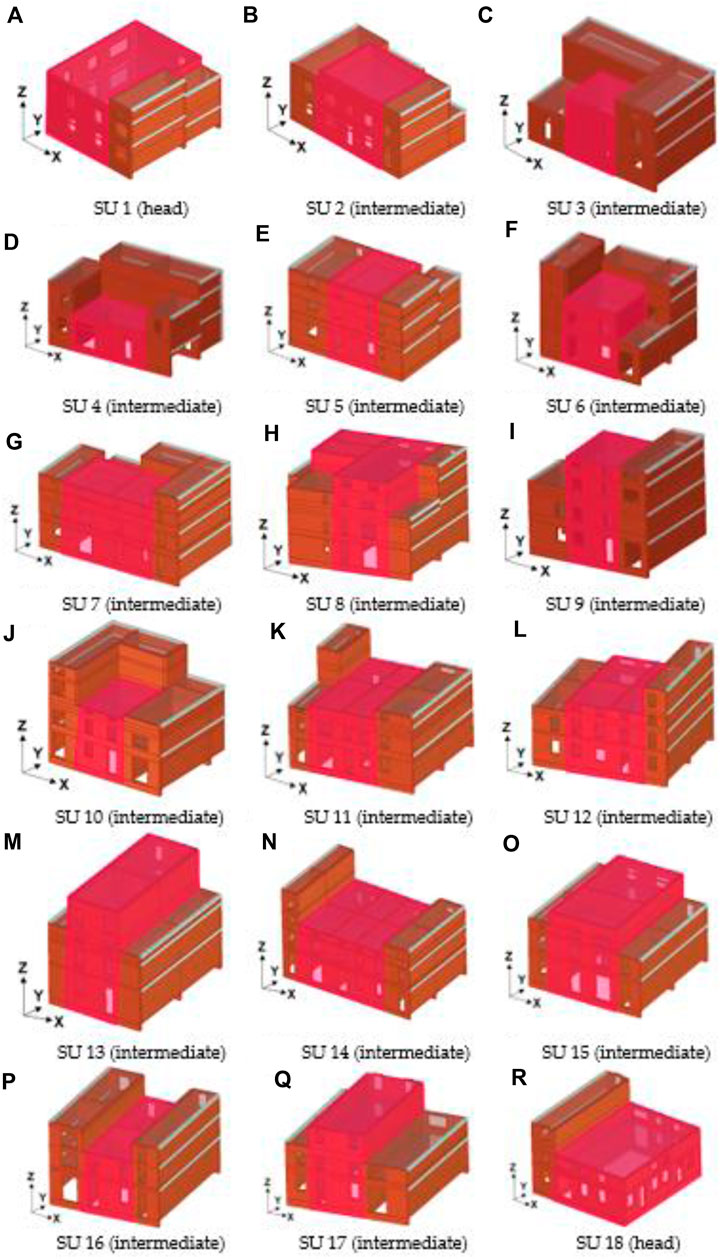
The discretisation of the masonry aggregate in SUs is depicted in Figure 9.

FIGURE 9

FIGURE 9. Division in SU of the masonry building compound in Mirandola (district of Modena, Italy).

Three SUs, namely n. 1—head, n.7—intermediate on three sides, and n.13—intermediate on two sides (Figure 10), were analysed to show their different behaviour if they are considered as isolated structures or when they were inserted in the building compound. In particular, as shown in Figure 10, the “aggregate condition”, that is attained when the building is included in the building compound, was modelled in the 3Muri software by modelling half of the SUs adjacent to that under investigation.

FIGURE 10

FIGURE 10. Three SU of the masonry building compound in Mirandola under numerical investigation.

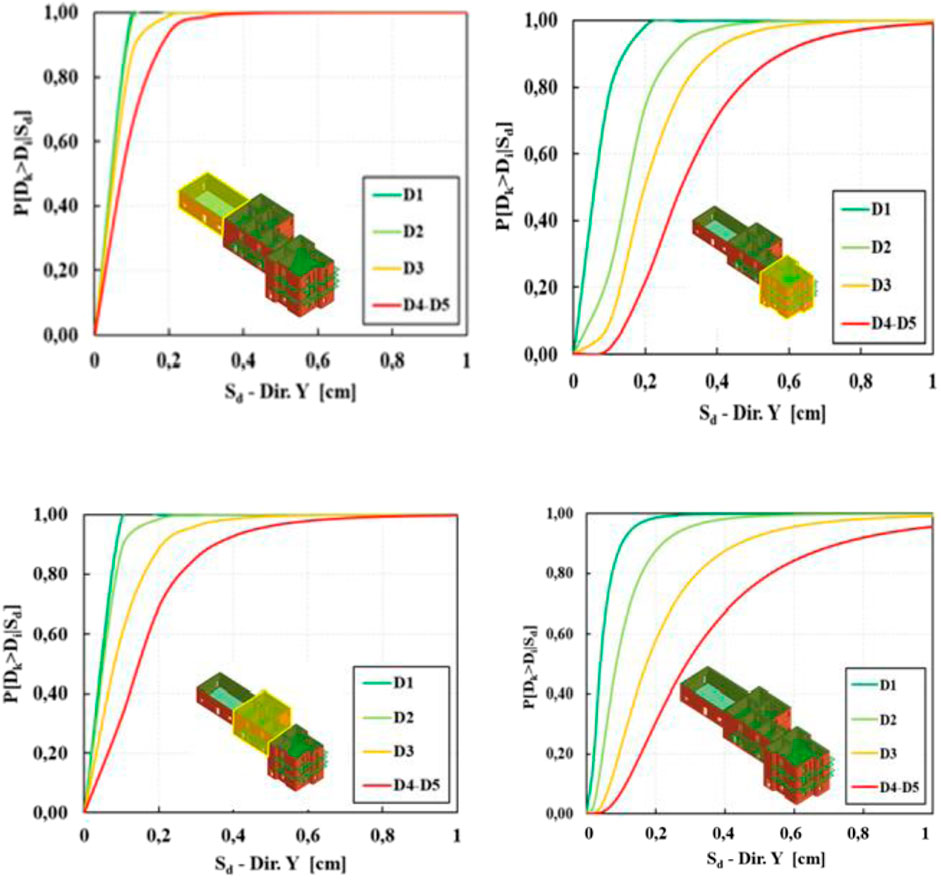
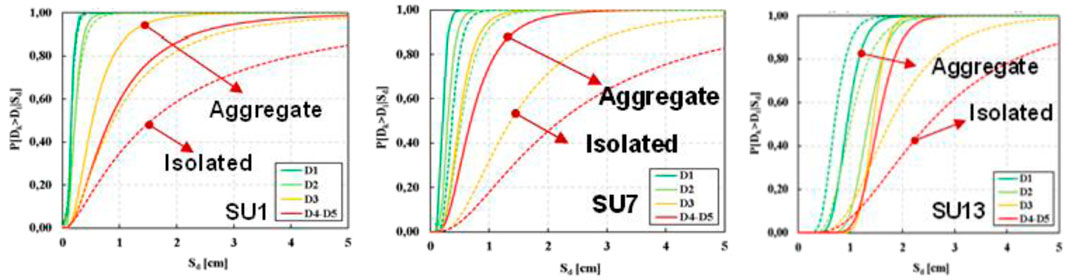
The different seismic behaviour between the isolated buildings and aggregate ones for the three examined SUs is illustrated in Figure 11, where fragility curves are plotted with dashed lines for the isolated buildings and with continuous lines for building in the aggregate condition.

FIGURE 11

FIGURE 11. Comparison of behaviour between the isolated buildings and aggregate ones.

From the achieved results it appears that the difference in behaviour between the isolated and aggregate SU is not marked with reference to serviceability limit states (D1 and D2 damage levels). Contrary, at the ultimate limit states (D3 and D4-D5 damage levels), it is shown that the isolated buildings suffer less damage than the aggregate ones. This means that the aggregate effect is detrimental for the investigated SU, as also noted by (Zucconi et al., 2017) in the post-earthquake systematic surveys. This unfavourable effect is more pronounced for the SU7, since large torsion due to the irregular shape of the aggregate limit its displacements under earthquakes.

In addition, a wide investigation was performed by modelling all of the 18 SU of the masonry building compound (Figure 12) to show the behavioural differences between isolated SU and aggregate ones in terms of the main vibration periods (Figure 13).

FIGURE 12

FIGURE 12. Modelling by 3Muri of aggregate SU of the building compound of Mirandola.

FIGURE 13

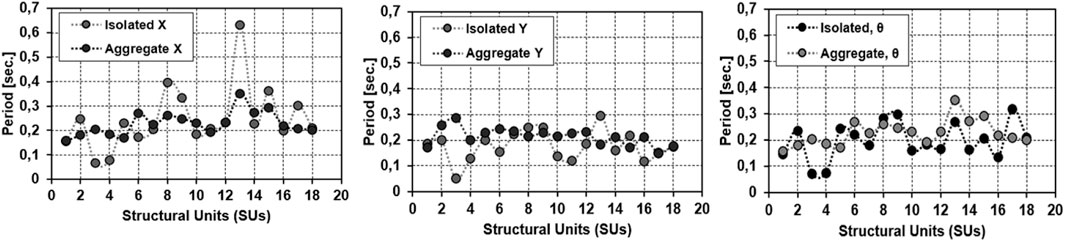
FIGURE 13. Longitudinal (X), transverse (Y), and torsion (θ) vibration modes of isolated and aggregate SU.

In Figure 13 it is noticed that, on average, for the first mode the aggregate condition provides periods on the safe side, while the opposite situation occurs for the second and the third modes. Therefore, the aggregate effect in some cases provides conservative results in terms of vibration periods, whereas in some other cases not. For this reason, a new formulation to estimate the main vibration period T_i of aggregate SU was provided according to the following Eq. 4:

${\mathrm{T}}_{\mathrm{i}}={\mathrm{C}}_{\mathrm{i}}\cdot {\mathrm{H}}^{\frac{3}{4}}=\frac{{\mathrm{M}}_{\mathrm{i}}}{{\mathrm{M}}_{\mathrm{tot}}}\cdot {\mathrm{H}}^{\frac{3}{4}}(4)$

where H is the building height and C_i is a correction factor considering the ratio between the building mass (M_i) and the whole aggregate mass (M_tot).

The estimation of the periods of different SUs in the aggregate condition was, therefore, calibrated based on the previous expression, leading to the results presented in Figure 14, that are compared to the mechanical ones obtained from 3Muri in both analyses directions (named Mec. X and Mec. Y in the figure). From the comparison of the results, it is noticed that the proposed formulation gives conservative results for most of the Examined SUs, so confirming its reliability in predicting the dynamic behaviour of aggregate SU.

FIGURE 14

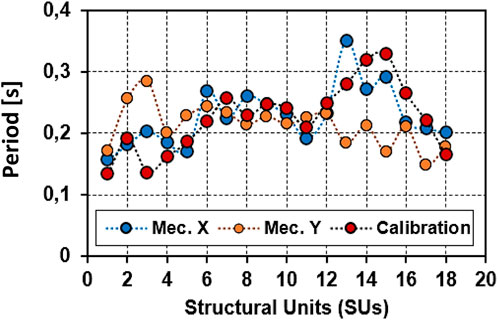
FIGURE 14. Comparison between theoretical and numerical approaches for predicting the main vibration period of aggregate SU.

Concluding remarks

In the paper, some simplified and numerical approaches to predict the seismic behaviour of structural units of masonry aggregates of historical centres were illustrated.

In the first part of the work, a large-scale assessment method based on a survey form appropriately conceived for masonry aggregates structural units was presented. An application of this quick method to a sub-urban sector of the historical centre of Latronico (district of Potenza, Italy) was done with the purpose to define a seismic vulnerability ranking among the buildings located in that zone. Coupling this approach with a well-known literature closed-form relationship to estimate the building damage under earthquakes, the seismic scenario of the investigated area of Latronico under the most probable earthquake predicted was developed, providing a medium damage level for most of SU. Also, the average vulnerability index deriving from the survey form allowed us to plot the mean typological vulnerability curves of the different building classes of Latronico to predict their possible damages under different grades of seismic events.

In the second analysis phase, numerical analyses on masonry aggregate SU by a macro-elements approach were shown. Firstly, an in-line masonry aggregate of 3 SUs within the historical centre of Boscoreale (district of Naples, Italy) was investigated by the 3Muri software, allowing to plot pushover and fragility curves. The analysis results showed that the best seismic behaviour in terms of pushover curves is attained from the intermediate SU due to the confinement effect of the two adjacent SUs. In particular, in the weakest transverse (Y) direction it was noticed that the two head SUs suffered much more damage than the intermediate one due to torsion movements given by the high seismic irregularities of the whole building compound. In the same direction, the worst behaviour in terms of fragility curves is that of the Head I SU, since it exhibited the highest collapse probabilities for different limit states considered. Secondly, another case study, represented by a masonry compound of 18 SUs arranged in a line, was inspected in the municipality of Mirandola (district of Modena, Italy), that was hit by the 2012 Emilia-Romagna earthquake. Herein, the different seismic behaviour between isolated buildings and the aggregate ones was revealed for three SU (head, constrained on two sides, and constrained on three sides) in terms of fragility curves. From the achieved results a slightly different behaviour among isolated and aggregate SU at the serviceability limit states was noticed. Contrary, at the ultimate limit states it was detected that the isolated buildings suffer much more damage than the aggregate ones. Moreover, a wide investigation based on macro-elements analysis was performed for inspecting the behavioural differences between isolated SU and aggregate ones in terms of the first three vibration periods.

A new relationship to estimate the main vibration period of aggregate SU was developed based on a correction factor considering the ratio between the mass of the examined building and the whole masonry compound mass. The results deriving from this relationship applied to the case study SU showed that the proposed formulation gives conservative results for most of them, so confirming its reliability in predicting the dynamic behaviour of aggregate SU.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

AF and NA were involved in all steps of the paper preparation, from the draft, final version of the paper, revision, reading, corrections, approval, and submitted version.

Acknowledgments

The Authors would like to acknowledge Nicola Chieffo for help in performing seismic analyses herein presented and discussed. Also, the support of the Italian DPC-ReLUIS research project is gratefully acknowledged.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ademovic, N., Hadzima-Nyarko, M., and Zagora, N. (2022). Influence of site effects on the seismic vulnerability of masonry and reinforced concrete buildings in Tuzla (Bosnia and Herzegovina). Bull. Earthq. Eng. 20, 2643–2681. doi:10.1007/s10518-022-01321-2

CrossRef Full Text | Google Scholar

Ademović, N., Hadzima-Nyarko, M., and Zagora, N. (2020). Seismic vulnerability assessment of masonry buildings in Banja Luka and Sarajevo (Bosnia and Herzegovina) using the macroseismic model. Bull. Earthq. Eng. 18, 3897–3933. doi:10.1007/s10518-020-00846-8

CrossRef Full Text | Google Scholar

Ademović, N., Hrasnica, M., and Oliveira, D. V. (2013). Pushover analysis and failure pattern of a typical masonry residential building in Bosnia and Herzegovina. Eng. Struct. 50, 13–29. doi:10.1016/j.engstruct.2012.11.031

CrossRef Full Text | Google Scholar

Ademović, N., Oliveira, D. V., and Lourenço, P. B., “Seismic evaluation and strengthening of an existing masonry building in sarajevo B&H”, Buildings 9(30):30–, 2019. https://doi. org/doi:10.3390/buildings9020030

CrossRef Full Text | Google Scholar

Ademović, N. (2011). “Structural and seismic behaviour of typical masonry buildings from Bosnia and Herzegovina,” (Portugal: University of Minho). Master Thesis Advanced Masters in Structural Analysis of Monuments and Historical Constructions.

Google Scholar

Barbat, A. H., Moya, F. Y., and Canas, J. A. (1996). Damage scenarios simulation for seismic risk assessment in urban zones. Earthq. Spectra 12, 371–394. doi:10.1193/1.1585889

CrossRef Full Text | Google Scholar

Bartoli, G., Betti, M., and Vignoli, A. (2016). A numerical study on seismic risk assessment of historic masonry towers: A case study in san gimignano. Bull. Earthq. Eng. 14 (6), 1475–1518. doi:10.1007/s10518-016-9892-9

CrossRef Full Text | Google Scholar

Benedetti, D., and Petrini, V. (1984). On the seismic vulnerability of masonry buildings: An evaluation method. L'Industria Delle Costr. 149, 66–74. in Italian.

Google Scholar

Brando, G., De Matteis, G., and Spacone, E. (2017). Predictive model for the seismic vulnerability assessment of small historic centres: Application to the inner abruzzi region in Italy. Eng. Struct. 153, 81–96. doi:10.1016/j.engstruct.2017.10.013

CrossRef Full Text | Google Scholar

Cherif, S.-E., Chourak, M., Abed, M., and Douiri, A., “Potential seismic damage assessment of residential buildings in Imzouren City (Northern Morocco)”, Buildings 8 (12):179, 2019. https://doi. org/doi:10.3390/buildings.8120179

CrossRef Full Text | Google Scholar

Chieffo, N., Formisano, A., Landolfo, R., and Milani, G. “A vulnerability index based-approach for the historical centre of the city of Latronico (Potenza, Southern Italy)”, Eng. Fail. Anal., 136, art. no. 106207, 2022. doi:10.1016/j.engfailanal.2022.106207

CrossRef Full Text | Google Scholar

Chieffo, N., and Formisano, A., “The influence of geo-hazard effects on the physical vulnerability assessment of the built heritage: An application in a district of Naples”, Buildings 9(1):26, 2019. https://doi. org/doi:10.3390/buildings.9010026

CrossRef Full Text | Google Scholar

Chieffo, N., Onescu, I., Formisano, A., Mosoarca, M., and Palade, M. (2020). Integrated empirical-mechanical seismic vulnerability analysis method for masonry buildings in timișoara: Validation based on the 2009 Italian earthquake. Open Civ. Eng. J. 14, 314–333. doi:10.2174/1874149502014010314

CrossRef Full Text | Google Scholar

Da Porto, F., Munari, M., Prota, A., and Modena, C. (2013). Analysis and repair of clustered buildings: Case study of a block in the historic city centre of L’Aquila (Central Italy). Constr. Build. Mater. 38, 1221–1237. doi:10.1016/j.conbuildmat.2012.09.108

CrossRef Full Text | Google Scholar

D’Altri, A. M., Sarhosis, V., Milani, G., Rots, J., Cattari, S., Lagomarsino, S., et al. (2020). Modeling strategies for the computational analysis of unreinforced masonry structures: Review and classification. Arch. Comput. Methods Eng. 27, 1153–1185. doi:10.1007/s11831-019-09351-x

CrossRef Full Text | Google Scholar

De Angelis, A., Maddaloni, G., and Pecce, M. R. (2020). Seismic vulnerability assessment of a monumental masonry building. Infrastructures 5, 93. doi:10.3390/infrastructures5110093

CrossRef Full Text | Google Scholar

Degli, A. S., D’Altri, A. M., Ottonelli, D., Castellazzi, G., Cattari, S., de Miranda, S., et al. (2019). Seismic assessment of interacting structural units in complex historic masonry constructions by nonlinear static analyses. Comput. Struct. 213, 51–71. doi:10.1016/j.compstruc.2018.12.001

CrossRef Full Text | Google Scholar

Dolce, M., Kappos, A., Masi, A., Penelis, G., and Vona, M. (2006). Vulnerability assessment and earthquake damage scenarios of the building stock of Potenza (Southern Italy) using Italian and Greek methodologies. Eng. Struct. 28, 357–371. doi:10.1016/j.engstruct.2005.08.009

CrossRef Full Text | Google Scholar

Formisano, A., Chieffo, N., and Mosoarca, M. (2017). Seismic vulnerability and damage speedy estimation of an urban sector within the municipality of San Potito Sannitico (Caserta, Italy). Open Civ. Eng. J. 11, 1106–1121. doi:10.2174/1874149501711011106

CrossRef Full Text | Google Scholar

Formisano, A., Di Feo, P., Grippa, M. R., and Florio, G. (2010). “L’Aquila earthquake: A survey in the historical centre of castelvecchio subequo,” in Proc. of the COST Action C26 Final Conference “Urban Habitat Constructions under Catastrophic Events, London, Naples, September 16–18. Editors F. M. Mazzolani, and Chair (CRC Press, Taylor & Francis Group), 371–376.

Google Scholar

Formisano, A., Florio, G., Landolfo, R., and Mazzolani, F. M. (2011). “Numerical calibration of a simplified procedure for the seismic behaviour assessment of masonry building aggregates”, Proc. of the Thirteenth International Conference on Civil, Structural and Environmental Engineering Computing, September 6–9, 2011, eds. B. H. V. Topping, and Y. Tsompanakis (Civil-Comp Press, Stirlingshire, UK), 172. doi:10.4203/ccp.96.172

CrossRef Full Text | Google Scholar

Formisano, A., Florio, G., Landolfo, R., and Mazzolani, F. M. (2015). Numerical calibration of an easy method for seismic behaviour assessment on large scale of masonry building aggregates. Adv. Eng. Softw. 80, 116–138. doi:10.1016/j.advengsoft.2014.09.013

CrossRef Full Text | Google Scholar

Formisano, A., Mazzolani, F. M., Florio, G., and Landolfo, R. (2010). “A quick methodology for seismic vulnerability assessment of historical masonry aggregates,” in Proc. of the COST Action C26 Final Conference “Urban Habitat Constructions under Catastrophic Events, London, Naples, September 16–18. Editors F. M. Mazzolani, and Chair (CRC Press, Taylor & Francis Group), 577–582.

Google Scholar

Formisano, A. (2012). “Seismic behaviour and retrofitting of the Poggio Picenze historical centre damaged by the L’Aquila earthquake”, Proc. of the Eleventh International Conference on Computational Structures Technology, ed. B. H. V. Topping (Civil-Comp Press, Stirlingshire, UK), 199. doi:10.4203/ccp.99.199

CrossRef Full Text | Google Scholar

Formisano, A. (2017). Theoretical and numerical seismic analysis of masonry building aggregates: Case studies in san Pio delle Camere (L’aquila, Italy). J. Earthq. Eng. 21 (2), 227–245. doi:10.1080/13632469.2016.1172376

CrossRef Full Text | Google Scholar

Giamundo, V., Sarhosis, V., Lignola, G. P., Sheng, Y., and Manfredi, G. (2014). Evaluation of different computational modelling strategies for the analysis of low strength masonry structures. Eng. Struct. 73, 160–169. doi:10.1016/j.engstruct.2014.05.007

CrossRef Full Text | Google Scholar

A. Giuffrè (Editor) (1993). Safety and conservation of historical centres: The Ortigia case (Roma, Bari: Editori Laterza). in Italian.

Google Scholar

A. Giuffrè, and C. Carocci (Editors) (1999). Code of practice for the safety and the conservation of the historical centre of Palermo (Bari: Editori Laterza). in Italian.

Google Scholar

Giuffrè, A. (1995). Seismic damage in historic town centres and attenuation criteria. Ann. Geophys. 38 (5–6), 837–843. doi:10.4401/ag-4092

CrossRef Full Text | Google Scholar

Grillanda, N., Valente, M., Milani, G., Chiozzi, A., and Tralli, A. (2020). Advanced numerical strategies for seismic assessment of historical masonry aggregates. Eng. Struct. 212, 110441. doi:10.1016/j.engstruct.2020.110441

CrossRef Full Text | Google Scholar

Grünthal, G. (1998). “European macroseismic scale 1998 (EMS-98),” in Cahiers du Centre Européen de Géodynamique et de Séismologie (Luxembourg: Conseil de l’Europe), 15.

Google Scholar

Indirli, M., Kouris, L. A. S., Formisano, A., Borg, R. P., and Mazzolani, F. M. (2013). Seismic damage assessment of unreinforced masonry structures after the abruzzo 2009 earthquake: The case study of the historical centers of L'aquila and castelvecchio subequo. Int. J. Archit. Herit. 7 (5), 536–578. doi:10.1080/15583058.2011.654050

CrossRef Full Text | Google Scholar

Kappos, A. J. (2016). An overview of the development of the hybrid method for seismic vulnerability assessment of buildings. Struct. Infrastructure Eng. 12 (12), 1573–1584. doi:10.1080/15732479.2016.1151448

CrossRef Full Text | Google Scholar

Kappos, A. J., Panagopoulos, G., Panagiotopoulos, C., and Penelis, G. (2006). A hybrid method for the vulnerability assessment of R/C and URM buildings. Bull. Earthq. Eng. 4, 391–413. doi:10.1007/s10518-006-9023-0

CrossRef Full Text | Google Scholar

Kappos, A. J., Stylianidis, K. A., and Penelis, G. G. (1991). Analytical prediction of the response of structures to future earthquakes. Eur. Earthq. Eng. 5, 10–21.

Google Scholar

Lagomarsino, S., and Giovinazzi, S. (2006). Macroseismic and mechanical models for the vulnerability and damage assessment of current buildings. Bull. Earthq. Eng. 4, 415–443. doi:10.1007/s10518-006-9024-z

CrossRef Full Text | Google Scholar

Lourenço, P. B., and Roque, J. A. (2006). Simplified indexes for the seismic vulnerability of ancient masonry buildings. Constr. Build. Mater. 4, 200–208. doi:10.1016/j.conbuildmat.2005.08.027

CrossRef Full Text | Google Scholar

Maio, R. (2013). “Seismic vulnerability assessment of old stone masonry building aggregates,” (Aveiro, Portugal: Civil Engineering Department of the University of Aveiro). MSc Thesis.

Google Scholar

Maio, R., Vicente, R., Formisano, A., and Varum, H. (2015). Seismic vulnerability of building aggregates through hybrid and indirect assessment techniques. Bull. Earthq. Eng. 13, 2995–3014. doi:10.1007/s10518-015-9747-9

CrossRef Full Text | Google Scholar

Milani, G., and Valente, M. (2015). ailure analysis of seven masonry churches severely damaged during the 2012 Emilia-Romagna (Italy) earthquake: Non-linear dynamic analyses vs conventional static approaches. Engineering Failure Analysis. 54, 13–56. doi:10.1016/J.ENGFAILANAL.2015.03.016

CrossRef Full Text | Google Scholar

Ministerial Decree of Public Works (NTC18) (2018). “Upgrading of Technical codes for constructions (in Italian),” in Official Gazette of the Italian Republic published on 2018 February 20th, Rome, Italy, 1–367.

Google Scholar

Mosoarca, M., Onescu, I., Onescu, E., Azap, B., Chieffo, N., Szitar-Sirbu, M., et al. (2019). Seismic vulnerability assessment for the historical areas of the Timisoara city, Romania. Eng. Fail. Anal. 101, 86–112. doi:10.1016/j.engfailanal.2019.03.013

CrossRef Full Text | Google Scholar

Pasticier, L., Amadio, C., and Fragiacomo, M. (2008). Non-linear seismic analysis and vulnerability evaluation of a masonry building by means of the SAP2000 V. 10 code. Earthq. Eng. Struct. Dyn. 37, 467–485. doi:10.1002/eqe.770

CrossRef Full Text | Google Scholar

Penna, A., Lagomarsino, S., and Galasco, A. (2014). A nonlinear macroelement model for the seismic analysis of masonry buildings. Earthq. Eng. Struct. Dyn. 43 (2), 159–179. doi:10.1002/eqe.2335

CrossRef Full Text | Google Scholar

Pujades, L. G., Barbat, A. H., González-Drigo, R., Avila, J., and Lagomarsino, S. (2012). Seismic performance of a block of buildings representative of the typical construction in the Eixample district in Barcelona (Spain). Bull. Earthq. Eng. 10, 331–349. doi:10.1007/s10518-010-9207-5

CrossRef Full Text | Google Scholar

QGIS Development Team (2014), QGIS geographic information system. Open Source Geospatial Foundation Project, Available at: http://qgis.osgeo.org.Qgisorg (accessed, 07 03 2022).

Google Scholar

Ramos, L. F., and Lourenço, P. B. (2004). Modeling and vulnerability of historical city centers in seismic areas: A case study in Lisbon. Eng. Struct. 26 (9), 1295–1310. doi:10.1016/j.engstruct.2004.04.008

CrossRef Full Text | Google Scholar

Rizzano, G., and Sabatino, R. (2010). “Non-linear static analysis of masonry structures by means of equivalent frames simplified approach”, Proc. of the 8th International Masonry Conference, Dresden, Germany, 4–7 July 2010.

Google Scholar

Roca, P., Molins, C., and Marì, A. R. (2005). Strength capacity of masonry wall structures by the equivalent frame method. J. Struct. Eng. 131, 1601–1610. doi:10.1061/(asce)0733-9445(2005)131:10(1601)

CrossRef Full Text | Google Scholar

Sarhosis, V., Milani, G., Formisano, A., and Fabbrocino, F. (2017). Evaluation of different approaches for the estimation of the seismic vulnerability of masonry towers. Bull. Earthq. Eng. 16 (1), 1511–1545. doi:10.1007/s10518-017-0258-8

CrossRef Full Text | Google Scholar

Senaldi, I., Magenes, G., and Penna, A. (2010). Numerical investigations on the seismic response of masonry building aggregates. Adv. Mat. Res. 133 (134), 715–720. doi:10.4028/www.scientific.net/AMR.133-134.715

CrossRef Full Text | Google Scholar

S.T.A. DATA. 3Muri-Seismic calculation of masonry structures, S.T.A. DATA srl,Turin, Italy, User manual. Available at: https://www.3muri.com/documenti/brochure/en/3Muri10.9.0_ENG.pdf (accessed on 02/05/2022).

Google Scholar

Taibi, H., AitYoucef, M., and Khellafi, M. (2019). Seismic vulnerability assessment using the macroseismic methodproposed in the framework of Risk-UE project based on the recommendations of the Algerian seismic code RPA99/Version 2003. Asian J. Civ. Eng. 21, 59–66. doi:10.1007/s42107-019-00190-6

CrossRef Full Text | Google Scholar

Vicente, R. (2008). “Estratégias e metodologias para intervenções de reabilitação urbana Avaliação da vulnerabilidade e do risco sísmico do edificado da Baixa de Coimbra,” (Aveiro, Portugal: Civil Engineering Department of the University of Aveiro). PhD Thesis.

Google Scholar

Zuccaro, G., Dolce, M., De Gregorio, D., Speranza, E., and Moroni, C. (2015). “The CARTIS form for the typological-structural characterization of urban compartments consisting of ordinary buildings. Exposure assessment in seismic risk analysis” (in Italian),” in Proc. of the 34th National Conference GNGTS, 17-19 November 2015, Trieste, Italy.

Google Scholar

Zucconi, M., Sorrentino, L., and Ferlito, R. (2017). Principal component analysis for a seismic usability model of unreinforced masonry buildings. Soil Dyn. Earthq. Eng. 96, 64–75. doi:10.1016/j.soildyn.2017.02.014

CrossRef Full Text | Google Scholar