Closed-form critical response of elastic-plastic shear building with viscous damper under pseudo-double impulse for simulating resonant response under near-fault fling-step motion

A set of approximate closed-form solutions of the maximum interstory drifts under the critical pseudo-double impulse (PDI) is derived for non-proportionally damped multi-story shear building models with bilinear hysteresis. The use of PDI and the closed-form solutions efficiently and accurately enable the capture of the critical responses of elastic-plastic multi-degree-of-freedom (MDOF) systems under the one-cycle sine wave, which substitutes for the main part of near-fault fling-step motions. The formulation of the closed-form maximum interstory drifts is based on the energy balance law. In the formulation, a quadratic function approximation of the damping force-interstory drift relation is introduced together with an updated mode-controlled energy-based approach (UMEA). While UMEA was proposed in the previous paper to derive the approximate maximum interstory drifts of undamped elastic-plastic MDOF systems under the critical PDI, it is extended so that it can be applied to non-proportionally damped MDOF systems. It is demonstrated that the proposed method can estimate the maximum interstory drifts of elastic-plastic non-proportionally damped MDOF systems under the critical PDI and the corresponding one-cycle sine wave with high accuracy. The estimation by the proposed method can be conducted much more efficiently and stably than the time-history response analysis (THRA). It is also shown that the hysteretic energy dissipation is not large enough to reduce the maximum interstory drifts. Finally, it is demonstrated that the proposed method can accurately estimate the maximum interstory drifts of elastic-plastic moment-resisting frames with viscous dampers under the resonant one-cycle sine wave.

1 Introduction

Recently observed pulse-like near-fault ground motions greatly exceed the level of code-specified ground motions. Such ground motions may concentrate the plastic deformation to specific stories and cause devastating damage to building structures. However, earthquake events are uncertain and difficult to be precisely predicted. Therefore, such kind of uncertainty and the plastic deformation characteristics should be fully considered in the structural design of buildings to improve the buildings’ resilience. Many researches on the elastic-plastic response characteristics of buildings and the effectiveness of the structural control systems under near-fault ground motions have been accumulated so far (Bertero et al. (1978), Hall et al. (1995), Malhotra (1999), Jangid and Kelly (2001), Mavroeidis and Papageorgiou (2003), Bray and Rodriguez-Marek (2004), Mavroeidis et al. (2004), Akkar et al. (2005), Baker (2007), He and Agrawal (2008), Yang et al. (2010), Khaloo et al. (2015), Vafaei and Eskandari (2015), Fang et al. (2018), Hamidi et al. (2020), Akehashi and Takewaki (2020), (2022a)). However, few researchers focused on both the uncertainty of the input ground motion and the plastic deformation characteristics.

The critical excitation method is one of the most rational approaches to certainly treat the uncertainty of the input ground motion [Drenick (1970); Shinozuka (1970); Iyengar and Manohar (1987); Abbas and Manohar (2002); Au (2006); Takewaki (2013)]. The method is aimed at finding the excitation which maximizes the structural response of models under possible inputs. Generally, an iteration of numerical analyses is required to find the critical excitation for elastic-plastic models. For example, Caughey (1960a), Caughey (1960b) used the equivalent linearization technique to approximately derive the nonlinear stationary responses, and Iwan (1961), (1965a, b) formulated transcendental equations for stationary responses of elastic-plastic models under harmonic excitation. These methods require iterative procedures to find the critical (resonant) input frequency for a specified input level. Especially in the case of elastic-plastic MDOF systems, such procedures become more complicated. Moreover, these methods cannot accurately estimate the maximum responses under near-fault ground motions because the duration of such ground motions is short and the responses are not stationary.

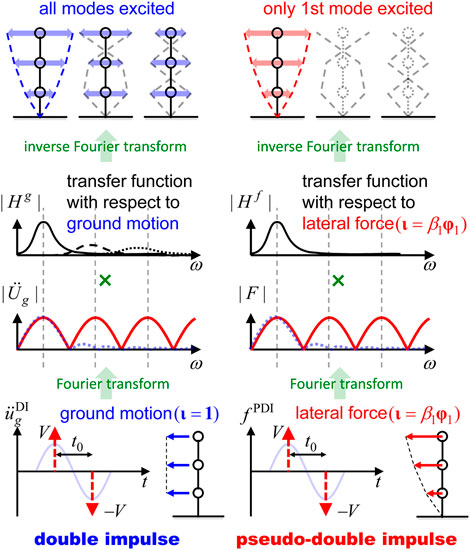
To overcome these difficulties, Akehashi and Takewaki (2021) introduced a pseudo-double impulse (PDI) to capture the critical responses of elastic-plastic MDOF systems under fling-step ground motions. PDI is a set of impulsive lateral forces, and it substitutes for the main part of fling-step ground motions. An ordinary double impulse (DI), which was proposed by Kojima and Takewaki (2015), cannot accurately simulate the maximum responses of MDOF systems because DI is treated as a ground acceleration and largely excites the higher-mode responses. On the other hand, PDI hardly excites the higher-mode responses because the undamped fundamental participation vector is adopted as the influence coefficient vector. This reflects the critical response characteristics under the actual fling-step ground motions. It has been demonstrated that the maximum interstory drifts and the maximum floor accelerations under the critical PDI correspond well to those under the critical one-cycle sine wave, which is another substitute for the fling-step ground motions [Sasani and Bertero (2000); Makris and Black (2004); Kalkan and Kunnath (2006); Hayden et al. (2014)]. Moreover, Akehashi and Takewaki (2022b) developed an innovative displacement control analysis called an ‘updated mode-controlled energy-based approach (UMEA)’ to derive approximate closed-form critical maximum interstory drifts of elastic-plastic undamped MDOF systems. UMEA effectively captures the transitional phases of the interstory drift responses and the plastic deformation concentration under the critical PDI. However, the method by Akehashi and Takewaki (2022b) cannot treat damped elastic-plastic MDOF systems. The closed-form maximum interstory drifts of damped elastic-plastic MDOF systems under the critical PDI should be derived because the simple response evaluation will be helpful for the preliminary seismic design of structural members and passive viscous dampers.

In this paper, a set of approximate closed-form solutions of the maximum interstory drifts under the critical PDI is derived for non-proportionally damped multi-story shear building models with bilinear hysteresis. In Section 2, the relation among a one-cycle sine wave, DI and PDI is explained. In Section 3, the displacement responses of elastic MDOF systems under a single impulse are investigated when the undamped fundamental participation vector is applied to the influence coefficient vector. In Section 4, a set of approximate closed-form solutions of the maximum interstory drifts under the critical PDI is derived for a non-proportionally damped MDOF system with bilinear hysteresis. This formulation is based on an extended UMEA, a quadratic function approximation of the damping force-interstory drift relation and the energy balance law. In Section 5, the time-history response analysis (THRA) is conducted to check the accuracy of the proposed approximate closed-form expression of the maximum interstory drifts for elastic-plastic non-proportionally damped MDOF systems under the critical PDI and the corresponding one-cycle sine wave. The damping force-interstory drift relations, the hysteretic energy and the dissipated energy by viscous damping are also investigated. Finally, the applicability of the proposed approximate closed-form expression to elastic-plastic moment-resisting frames with viscous damper is investigated.

2 Pseudo-double impulse

In this section, the relation among a one-cycle sine wave, a double impulse (DI) and a pseudo-double impulse (PDI) is explained briefly.

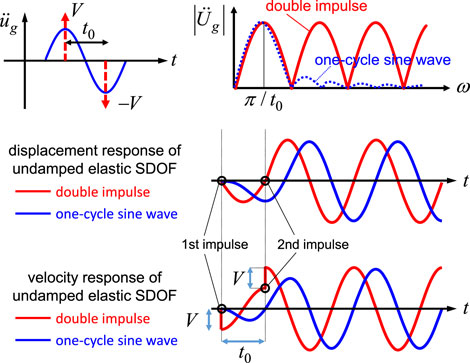
The main part of the near-fault fling-step ground motion is often expressed by the one-cycle sine wave [Sasani and Bertero (2000); Makris and Black (2004); Kalkan and Kunnath (2006); Hayden et al. (2014)]. On the other hand, Kojima and Takewaki (2015) introduced DI to more simply model the main part of the near-fault fling-step ground motion. As shown in Figure 1, the Fourier amplitude of DI and that of the one-cycle sine wave correspond well in the range of $0\le \omega \le 2\pi /t_0$, where $t_0$ is the time interval between two impulses. This leads to the good correspondence of the maximum responses of the elastic-plastic SDOF systems under the critical DI and the critical one-cycle sine wave (Kojima and Takewaki 2015; Akehashi and Takewaki 2018).

FIGURE 1

FIGURE 1. Input and response of double impulse (DI) and one-cycle sine wave.

The most important aspect of DI is that the critical maximum deformation and the critical time interval of an elastic-plastic SDOF system can be easily obtained without any repetition. This is because only the free vibration occurs after each impulse input and the energy-based approach is easily applied. Moreover, PDI has been introduced by Akehashi and Takewaki (2021), (2022b) so that this aspect can be applied to elastic-plastic MDOF systems. PDI is treated as a set of impulsive lateral forces, and the undamped fundamental participation vector is adopted as the influence coefficient vector (see Figure 2).

FIGURE 2

FIGURE 2. Double impulse (DI) and pseudo-double impulse (PDI).

Consider a N-story shear mass system. Let $m_i,c_i,k_i$ denote the mass, the damping coefficient and the story stiffness in the ith story, and $\mathbf{M},\mathbf{C},\mathbf{K},\mathbf{u},\mathbf{\iota },{\mathbf{\phi }}_n={\left({\phi }_{n,1},\mathrm{...},{\phi }_{n,N}\right)}^T,$ ${\beta }_n{\mathbf{\phi }}_n=\left\{\left({\mathbf{\phi }}_n^T\mathbf{M1}\right)/\left({\mathbf{\phi }}_n^T\mathbf{M}{\mathbf{\phi }}_n\right)\right\}{\mathbf{\phi }}_n$ denote the mass matrix, the damping matrix, the stiffness matrix, the displacement vector, the influence coefficient vector, the nth undamped eigenmode vector and the nth participation vector, respectively. The equations of motion under DI ($\mathbf{\iota }=\mathbf{1}$: one at every component) are expressed by

$\mathbf{M}\stackrel{\cdot \cdot }{\mathbf{u}}+\mathbf{C}\stackrel{\cdot }{\mathbf{u}}+\mathbf{Ku}=-\mathbf{M1}\left(V\delta \left(t\right)-V\delta \left(t-t_0\right)\right),(1)$

where $\delta \left(t\right),V$ denote the Dirac delta function and the velocity amplitude of DI. On the other hand, the equations of motion under PDI $\left(\mathbf{\iota }={\beta }_1{\mathbf{\phi }}_1\right)$ are expressed as follows.

$\mathbf{M}\stackrel{\cdot \cdot }{\mathbf{u}}+\mathbf{C}\stackrel{\cdot }{\mathbf{u}}+\mathbf{Ku}=-\mathbf{M}\left({\beta }_1{\mathbf{\phi }}_1\right)\left(V\delta \left(t\right)-V\delta \left(t-t_0\right)\right).(2)$

PDI excites only the fundamental-mode responses of elastic proportionally-damped MDOF systems because $\mathbf{\iota }={\beta }_1{\mathbf{\phi }}_1$ is adopted. The critical maximum responses under the critical PDI correspond well to those under the critical one-cycle sine wave. In addition, the critical condition of the impulse timing, which maximizes the total input energy, has also been derived (Akehashi and Takewaki (2021)).

3 Displacement response of elastic non-proportionally damped MDOF system under single impulse with $\mathbf{\iota }={\beta }_1{\mathbf{\phi }}_1$

In this section, the displacement responses of elastic MDOF systems under a single impulse (SI) with $\mathbf{\iota }={\beta }_1{\mathbf{\phi }}_1$ are investigated.

Consider an elastic proportionally damped MDOF system. The displacement response $\mathbf{u}\left(t\right)$ of the system under SI with $\mathbf{\iota }={\beta }_1{\mathbf{\phi }}_1$ (PSI) can be expressed by

$\mathbf{u}\left(t\right)={\mathbf{u}}_1\left(t\right)=\frac{-V{e}^{-h_1{\omega }_{1}t}}{{\omega }_{D1}}\left({\beta }_1{\mathbf{\phi }}_1\right)\sin \left({\omega }_{D1}t\right),(3)$

where $h_n,{\omega }_n$ denote the nth damping ratio and the nth natural circular frequency, and ${\omega }_{Dn}={\omega }_n\sqrt{1-h_n^2}$. The time $\tilde{t}$ when the interstory drift responses become the maximum can be expressed as

$\tilde{t}=\left(\pi /2-{\varphi }_1\right)/{\omega }_{D1},(\mathrm{4a})$

${\varphi }_1=\arctan \left\{h_1/\sqrt{1-h_1^2}\right\}.(\mathrm{4b})$

Consider next an elastic non-proportionally damped MDOF system. The displacement response $\mathbf{u}\left(t\right)$ of the system under PSI can be expressed by

$\mathbf{u}\left(t\right)={\displaystyle {\sum }_{i=1}^N{\mathbf{u}}_i\left(t\right)}={\displaystyle {\sum }_{i=1}^{N}V{e}^{-h_i^{\ast }{\omega }_i^{\ast }t}\left\{{\mathbf{\beta }}_i\cos \left({\omega }_{Di}^{\ast }t\right)-{\mathbf{\gamma }}_i\sin \left({\omega }_{Di}^{\ast }t\right)\right\}},(5)$

where ${\mathbf{\psi }}_n,{\lambda }_n=-h_n^{\ast }{\omega }_n^{\ast }+i{\omega }_{Dn}^{\ast }=-h_n^{\ast }{\omega }_n^{\ast }+i{\omega }_n^{\ast }\sqrt{1-{\left(h_n^{\ast }\right)}^2},{\omega }_n^{\ast },h_n^{\ast }$ denote the nth complex eigenvector, the nth eigenvalue, the nth pseudo-undamped natural circular frequency, the nth damping ratio, respectively, and

${\mathbf{\beta }}_n+i{\mathbf{\gamma }}_n=\frac{-2{\mathbf{\psi }}_n^T\mathbf{M}\left({\beta }_1{\mathbf{\phi }}_1\right)}{2{\lambda }_n{\mathbf{\psi }}_n^T\mathbf{M}{\mathbf{\psi }}_n+{\mathbf{\psi }}_n^T\mathbf{C}{\mathbf{\psi }}_n}{\mathbf{\psi }}_n.(6)$

It is noted that, depending on the non-proportionality of the damping distribution, the higher-mode responses are slightly excited under PSI. When the damping distribution has weak non-proportionality, the component $-V{e}^{-h_1^{\ast }{\omega }_1^{\ast }t}\left({\mathbf{\gamma }}_1\right)sin\left({\omega }_{D1}^{\ast }t\right)$ is dominant in $\mathbf{u}\left(t\right)$. Then, the maximum interstory drifts ${\mathbf{d}}_{\max }^{\text{PSI}}$ under PSI can be approximated by

${\mathbf{d}}_{\max }^{\text{PSI}}=\mathbf{T}\left\{{\displaystyle {\sum }_{i=1}^N{\mathbf{u}}_i\left({\tilde{t}}^{\ast }\right)}\right\},(\mathrm{7a})$

${\tilde{t}}^{\ast }=\left(\pi /2-{\varphi }_1^{\ast }\right)/{\omega }_{D1}^{\ast },(\mathrm{7b})$

${\varphi }_1^{\ast }=\arctan \left\{h_1^{\ast }/\sqrt{1-{\left(h_1^{\ast }\right)}^2}\right\},(\mathrm{7c})$

where $\mathbf{T}$ is the transformation matrix, and $\mathbf{T}$ is expressed as

$\mathbf{T}=\left(\begin{array}{cccc}1& & & \mathbf{0}\\ -1& \ddots & & \\ & \ddots & \ddots & \\ \mathbf{0}& & -1& 1\end{array}\right).(8)$

It is also noted that Equation 7 gives the exact value in the cases of elastic proportionally damped MDOF systems since ${\mathbf{u}}_2\left(t\right)=\mathrm{...}={\mathbf{u}}_N\left(t\right)=\mathbf{0}$ and ${\mathbf{\beta }}_1=\mathbf{0}$.

The accuracy of Equation 7 is investigated through numerical examples. Consider two 24-story shear building models with different damping distributions. Both models have a trapezoidal distribution of story stiffnesses $\left(k_1/k_{24}=2.5\right)$, and all the floor masses have the same value, i.e. $m_1=\mathrm{...}=m_{24}=400\times {10}^3\text{kg}$. The undamped fundamental natural period is 2.4 s, and the common story height is 4 m. The two models have non-proportional damping. The damping distribution of Model 1 is $c_1=\mathrm{...}=c_{24}=\left(60/24\right)\times {10}^7\text{Ns}/\text{m}$, and that of Model 2 is $c_1=\mathrm{...}=c_{12}=\left(120/24\right)\times {10}^7\text{Ns}/\text{m}\text{,}$$c_{13}=\mathrm{...}=c_{24}=0$. The damping distribution of Model 2 is designed so that it has stronger non-proportionality than Model 1. In other words, the higher-mode responses of Model 2 under PSI are excited more than those of Model 1. The 1-4th damping ratios of Model 1 are 0.0511, 0.169, 0.281, 0.390, and those of Model 2 are 0.0667, 0.0773, 0.111, 0.371.

Figure 3 illustrates the maximum interstory drifts under PSI with $V=0.5\text{m}/\text{s}$ evaluated by the time-history response analysis (THRA) and those evaluated by Equation 7. It is noted that only the 1-4th modes are considered in the evaluation by Equation 7. Figure 4, Figure 5 show the interstory drift response time-history in the 8th, 16th and 24th stories under PSI. The fundamental mode responses are also shown in Figure 4, Figure 5. In Model 1, the maximum interstory drifts evaluated by THRA and those evaluated by Equation 7 correspond well. As shown in Figure 4, the higher-mode responses are hardly excited. On the other hand, in Model 2, Equation 7 underestimates the maximum interstory drifts in the upper stories. This is because the higher-mode responses contribute to the maximum interstory drifts, as shown in Figure 5. However, Equation 7 estimates the maximum interstory drifts in the middle and lower stories with high accuracy. Moreover, Equation 7 effectively expresses the deformation concentration in the 13th story, where the value of the damping coefficient drastically switches.

FIGURE 3

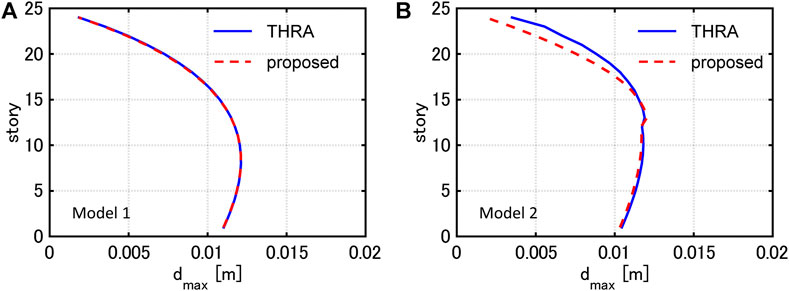
FIGURE 3. Maximum interstory drifts under PSI with $V=0.5\text{m/s}$ by time-history response analysis and proposed method, (A) Model 1, (B) Model 2.

FIGURE 4

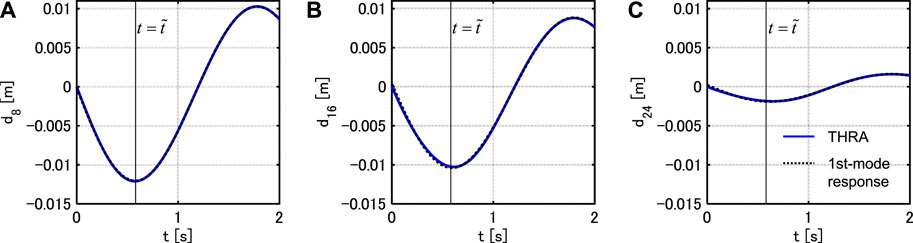
FIGURE 4. Interstory drift response time-history under PSI (Model 1), (A) 8-th story, (B) 16-th story, (C) 24-th story.

FIGURE 5

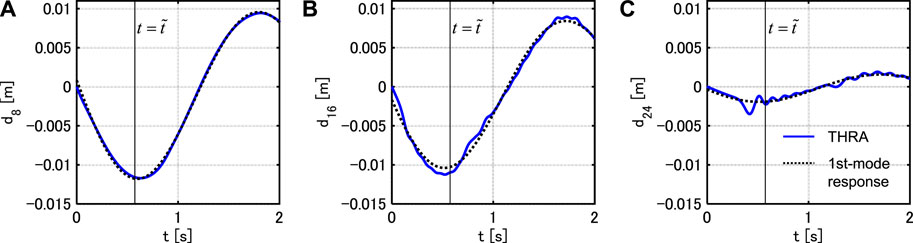
FIGURE 5. Interstory drift response time-history under PSI (Model 2), (A) 8-th story, (B) 16-th story, (C) 24-th story.

4 Derivation of approximate closed-form maximum interstory drifts under critical PDI

In this section, a set of approximate closed-form solutions of the maximum interstory drifts under the critical PDI is derived for non-proportionally damped MDOF systems with bilinear hysteresis. In Section 4.1, the updated mode-controlled energy-based approach (UMEA), which was introduced by Akehashi and Takewaki (2022b), is extended based on the formulation in Section 3 so that it can be applied to non-proportionally damped MDOF systems. In Section 4.2, a quadratic function approximation of the damping force-interstory drift relation is proposed. This leads to a closed-form expression of the dissipated energy by the viscous damping. In Section 4.3, the approximate closed-form solutions of the maximum interstory drifts are derived based on the extended UMEA, the quadratic function approximation and the energy balance law.

4.1 UMEA for damped elastic-plastic MDOF system

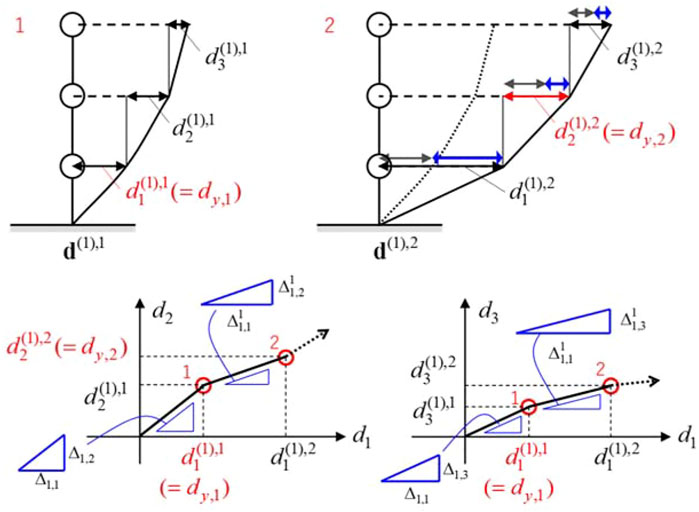
UMEA, which is a kind of displacement-controlled analyses, has been developed by Akehashi and Takewaki (2022b). UMEA leads to a set of approximate closed-form solutions of the maximum interstory drifts of elastic-plastic undamped MDOF systems under the critical PDI. UMEA provides the maximum displacement responses of the MDOF systems by considering the interstory drift increment, which is proportional to the undamped fundamental mode evaluated by the tangent story stiffnesses. It is noted that UMEA reflects the modal coupling effect due to the elastic-plastic responses under the critical PDI and the validity of UMEA was demonstrated in the previous paper [Akehashi and Takewaki (2022b)].

Although UMEA can be applied to undamped systems, it cannot be applied to damped systems. It is pointed out that viscous damping with strong non-proportionality excites the higher-mode responses, and it may influence the distribution of the maximum interstory drifts. To overcome this difficulty, UMEA is extended so that it can be applied to non-proportionally damped systems based on the formulation in Section 3. In UMEA for non-proportionally damped systems, the interstory drift increment ${\mathbf{\Delta }}_1={\left({\mathrm{\Delta }}_{\mathrm{1,1}},\mathrm{...},{\mathrm{\Delta }}_{1,N}\right)}^T$, which is proportional to ${\mathbf{d}}_{\max }^{\text{PSI}}$ in Equation 7, is given. When one of the stories yields, the corresponding story stiffness is replaced by the post-yield stiffness. Then ${\mathbf{d}}_{\max }^{\text{PSI}}$ and the interstory drift increment are updated. The updated interstory drift increment is denoted by ${\mathbf{\Delta }}_1^n={\left({\mathrm{\Delta }}_{\mathrm{1,1}}^n,\mathrm{...},{\mathrm{\Delta }}_{1,N}^n\right)}^T$ in the case of yielding of the nth story.

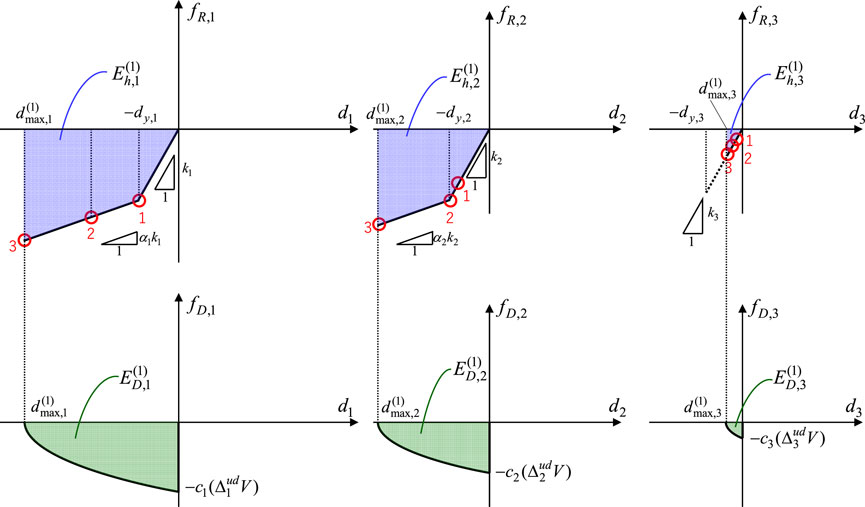
Consider the case where UMEA is applied to a 3DOF shear mass system with bilinear hysteresis (see Figure 6). $d_{y,i},{\alpha }_i,d_i$ in Figure 6 denote the yield deformation, the post-yield stiffness ratio and the interstory drift in the ith story, and $d_i^{\left(1\right),j}$ is the interstory drift in the ith story at the moment when the story j attains $d_{y,j}$. In the beginning of UMEA, the interstory drift increment ${\mathbf{\Delta }}_1$ is given. Then the first story yields first (point 1 in Figure 6). The interstory drift increment is updated from ${\mathbf{\Delta }}_1$ to ${\mathbf{\Delta }}_1^1$, which is evaluated by ${\alpha }_1{k}_1,k_2,k_3$. Next, the second story yields (point 2), and the interstory drift increment is updated from ${\mathbf{\Delta }}_1^1$ to ${\mathbf{\Delta }}_1^{\mathrm{1,2}}$, which is evaluated by ${\alpha }_1{k}_1,{\alpha }_2{k}_2,k_3$. The analysis is continued until the total hysteretic energy attains the target value (initial kinetic energy).

FIGURE 6

FIGURE 6. Overview of UMEA.

It is noted that, in the case of an undamped system, ${\mathbf{d}}_{\max }^{\text{PSI}}$ corresponds to the undamped fundamental mode evaluated by the tangent story stiffnesses. Therefore, in the case of $\mathbf{C}=\mathbf{0}$, the above-stated procedure corresponds to UMEA for undamped systems presented by Akehashi and Takewaki (2022b).

4.2 Approximation of damping force-interstory drift relation

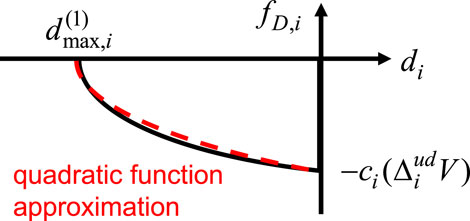
Akehashi and Takewaki (2018) introduced a quadratic function approximation of the damping force-deformation relation to derive an approximate closed-form maximum deformation of an elastic-plastic SDOF system under the critical DI. This approach is extended to the damping force-interstory drift relation in each story of an elastic-plastic MDOF system.

Let $f_{D,i},d_{\max ,i}^{\left(1\right)}$ denote the damping force and the maximum interstory drift in the ith story after the first impulse input. The interstory velocity just after the first impulse input is $-{\mathrm{\Delta }}_i^{ud}V$, where ${\left({\mathrm{\Delta }}_1^{ud},\mathrm{...},{\mathrm{\Delta }}_N^{ud}\right)}^T=\mathbf{T}\left({\beta }_1{\mathbf{\phi }}_1\right)$. The damping force-interstory drift relation in the ith story is approximated by a quadratic function, which passes the points $\left(d_i,f_{D,i}\right)=\left(0,-c_i{\mathrm{\Delta }}_i^{ud}V\right),\left(d_{\max ,i}^{\left(1\right)},0\right)$ (see Figure 7). The point $\left(d_{\max ,i}^{\left(1\right)},0\right)$ is the vertex. $f_{D,i}$ can be expressed by

$f_{D,i}=-c_i{\mathrm{\Delta }}_i^{ud}V\sqrt{1-\left(d_i/d_{\max ,i}^{\left(1\right)}\right)}.(9)$

FIGURE 7

FIGURE 7. Quadratic function approximation of damping force-interstory drift relation.

By integrating Equation 9 from $d_i=0$ to $d_i=d_{\max ,i}^{\left(1\right)}$, the dissipated energy by $f_{D,i}$ can be obtained as

${\displaystyle {\int }_0^{d_{\max ,i}^{\left(1\right)}}{f}_{D,i}d{d}_i}=\left(2/3\right)c_i\left({\mathrm{\Delta }}_i^{ud}V\right)d_{\max ,i}^{\left(1\right)}.(10)$

This formulation helps to derive ${\mathbf{d}}_{\max }^{\left(1\right)}={\left(d_{\max ,1}^{\left(1\right)},\mathrm{...},d_{\max ,N}^{\left(1\right)}\right)}^T$ in a closed form, and it can be easily extended to the case for deriving the maximum interstory drifts ${\mathbf{d}}_{\max }^{\left(2\right)}={\left(d_{\max ,1}^{\left(2\right)},\mathrm{...},d_{\max ,N}^{\left(2\right)}\right)}^T$ after the second impulse.

4.3 Approximate closed-form maximum interstory drifts

A set of approximate closed-form solutions of the maximum interstory drifts ${\mathbf{d}}_{\max }^{\left(1\right)},{\mathbf{d}}_{\max }^{\left(2\right)}$ is derived. By using the extended UMEA, a quadratic function approximation and the energy balance law, the problems of deriving ${\mathbf{d}}_{\max }^{\left(1\right)},{\mathbf{d}}_{\max }^{\left(2\right)}$ are expressed as simple problems of solving quadratic equations.

4.3.1 Derivation of ${\mathbf{d}}_{\max }^{\left(1\right)}$

UMEA is conducted in the negative direction for deriving ${\mathbf{d}}_{\max }^{\left(1\right)}$. Let us define $s_1^{\left(1\right)}$ as the story number which yields first, and $s_i^{\left(1\right)}$ denotes the story number which yields after the story $s_{i-1}^{\left(1\right)}$ $\left(i=2,\mathrm{...},N\right)$. For example, Figure 8 illustrates an example of the restoring force-interstory drift relations and the damping force-interstory drift relations of a 3DOF system for the derivation of ${\mathbf{d}}_{\max }^{\left(1\right)}$. Assume $s_1^{\left(1\right)}=1,s_2^{\left(1\right)}=2,s_3^{\left(1\right)}=3$ here. In other words, the first story yields first (point 1 in Figure 8), then the second story yields (point 2). Before the third story yields, the sum of the total hysteretic energy and the total dissipated energy by the viscous damping attains the target value (initial kinetic energy) at point 3.

FIGURE 8

FIGURE 8. Evaluation of maximum interstory drifts ${\mathbf{d}}_{\max }^{\left(1\right)}$ after the first impulse.

The input energy $E_I^{\left(1\right)}$ by the first impulse is expressed by

$E_I^{\left(1\right)}=\frac{1}{2}{\left({\beta }_1{\mathbf{\phi }}_1\right)}^T\mathbf{M}\left({\beta }_1{\mathbf{\phi }}_1\right)V^2(11)$

The energy balance law between the timing just after the first impulse acts and the timing when the system attains ${\mathbf{d}}_{\max }^{\left(1\right)}$ leads to

$E_I^{\left(1\right)}=E_h^{\left(1\right)}+E_D^{\left(1\right)}(12)$

where $E_h^{\left(1\right)},E_D^{\left(1\right)}$ denote the total hysteretic energy and the total dissipated energy by the damping. The detailed formulation of $E_h^{\left(1\right)},E_D^{\left(1\right)}$ is shown in Supplementary Appendix S1.

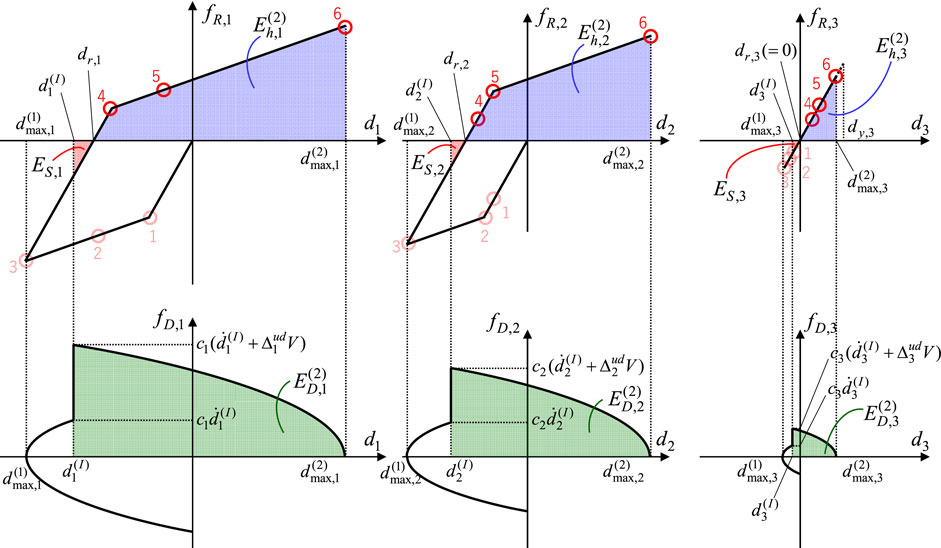
4.3.2 Derivation of ${\mathbf{d}}_{\max }^{\left(2\right)}$

Next, the distribution ${\mathbf{d}}_{\max }^{\left(2\right)}$ of the maximum interstory drifts after the second impulse is derived. In other words, the energy balance law between the timing just after the second impulse acts and the timing when the system attains ${\mathbf{d}}_{\max }^{\left(2\right)}$ is formulated.

UMEA in the positive direction is conducted just after the second impulse input. Let us define $s_1^{\left(2\right)}$ as the story number which goes into the reloading process first, and $s_i^{\left(2\right)}$ denotes the story number which goes into the reloading process after the story $s_{i-1}^{\left(2\right)}$ $\left(i=2,\mathrm{...},N\right)$. For example, Figure 9 illustrates an example of the restoring force-interstory drift relations and the damping force-interstory drift relations of the 3DOF system for the derivation of ${\mathbf{d}}_{\max }^{\left(2\right)}$, and $s_1^{\left(2\right)}=1,s_2^{\left(2\right)}=2,s_3^{\left(2\right)}=3$ here. In other words, the first story yields first (point 4 in Figure 9). Then the second story yields (point 5). Before the third story yields, the sum of the total hysteretic energy and the total dissipated energy by the viscous damping attains the target value at point 6.

FIGURE 9

FIGURE 9. Evaluation of maximum interstory drifts ${\mathbf{d}}_{\max }^{\left(2\right)}$ after the second impulse.

Let $E_K^{\left(I\right)},E_S^{\left(I\right)}$ denote the total strain energy and the total kinetic energy just after the second impulse input, and $E_h^{\left(2\right)},E_D^{\left(2\right)}$ denote the total hysteretic energy and the total dissipated energy by the damping. Based on the energy balance law between the timing just after the second impulse acts and the timing when the system attains ${\mathbf{d}}_{\max }^{\left(2\right)}$, the following equation is formulated

$E_K^{\left(I\right)}+E_S^{\left(I\right)}=E_h^{\left(2\right)}+E_D^{\left(2\right)}(13)$

The detailed formulation of $E_K^{\left(I\right)},E_S^{\left(I\right)},E_h^{\left(2\right)},E_D^{\left(2\right)}$ is shown in Supplementary Appendix S2.

5 Numerical examples

In Section 5.1, the time-history response analysis (THRA) is conducted to check the accuracy of the proposed approximate closed-form expression for elastic-plastic non-proportionally damped MDOF systems under the critical PDI. The damping force-interstory drift relations, the hysteretic energy and the dissipated energy by viscous damping are also investigated. In Section 5.2, the maximum interstory drifts under the corresponding one-cycle sine wave are compared with the proposed approximate closed-form expression. In Section 5.1, Section 5.2, Model 1 $\left(c_1=\mathrm{...}=c_{24}=\left(60/24\right)\times {10}^7\text{Ns}/\text{m}\right)$ and Model 2 $\left(c_1=\mathrm{...}=c_{12}=\left(120/24\right)\times {10}^7\text{Ns}/\text{m}\text{,}{c}_{13}=\mathrm{...}=c_{24}=0\right)$ are used again. The yield interstory drifts are $d_{y,1}=\mathrm{...}=d_{y,24}=4/150\text{m}$ and the bilinear hysteresis (kinematic hardening) in the story shear-interstory drift relation is assumed $\left({\alpha }_1=\mathrm{...}={\alpha }_{24}=0.2\right)$. In Section 5.3, the applicability of the proposed approximate closed-form expression to elastic-plastic moment-resisting frames with viscous damper is investigated.

5.1 Maximum interstory drifts under critical PDI

Figure 10 shows the distributions of the maximum interstory drifts by THRA under the critical PDI with $V=0.3,0.6,0.9,1.2,1.5m/s$ and those evaluated by the proposed method. Figure 11, Figure 12 present the damping force-interstory drift relations in the 1st, 6th and 12th stories of Models 1, 2 under the critical PDI with $V=1.2m/s$. The approximate quadratic functions designated as ‘proposed method’ are also plotted.

FIGURE 10

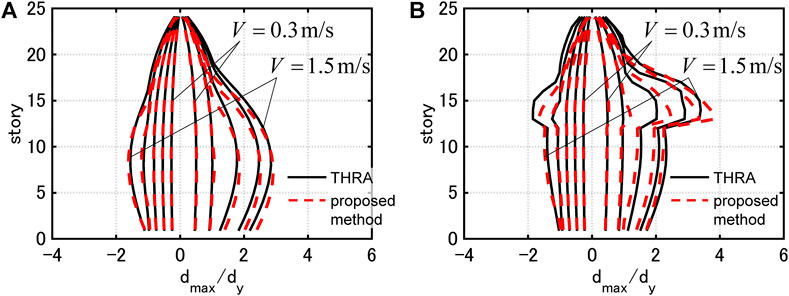
FIGURE 10. Maximum interstory drifts under critical PDI and those evaluated by proposed method,(A) Model 1 $\left(c_1=\mathrm{...}=c_{24}=\left(60/24\right)\times {10}^7\text{Ns}/\text{m}\right)$, (B) Model 2 $\left(c_1=\mathrm{...}=c_{12}=\left(120/24\right)\times {10}^7\text{Ns/m,}{c}_{13}=\mathrm{...}=c_{24}=0\right)$.

FIGURE 11

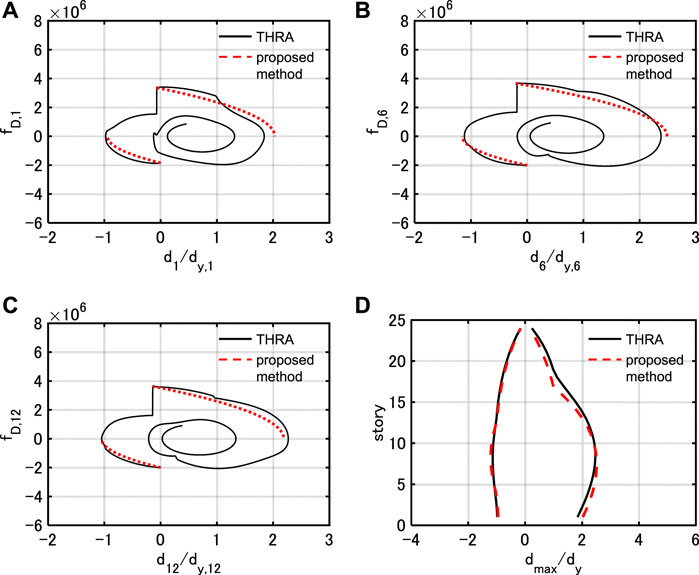
FIGURE 11. Damping force-interstory drift relation under PDI with $V=1.2\text{m/s}$ (Model 1) by time-history response analysis and proposed method, (A) 1st story, (B) 6th story, (C) 12th story, (D) maximum interstory drifts.

FIGURE 12

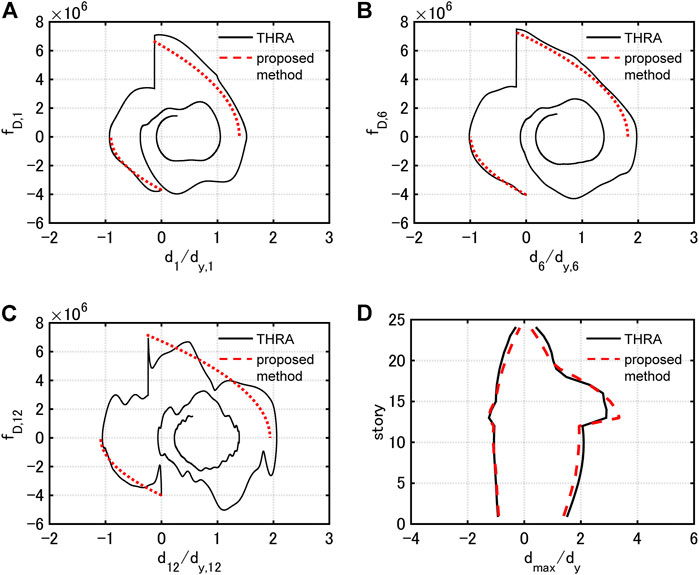
FIGURE 12. Damping force-interstory drift relation under PDI with $V=1.2\text{m/s}$ (Model 2) by time-history response analysis and proposed method, (A) 1st story, (B) 6th story, (C) 12th story, (D) maximum interstory drifts.

In the case of Model 1, the proposed method estimates the maximum interstory drifts with high accuracy for all the input levels. In addition, the approximate quadratic functions correspond well to the damping force-interstory drift relations by THRA, although the higher-mode responses slightly contribute.

In the case of Model 2, the proposed method tends to slightly overestimate the maximum interstory drifts in the 13th story. However, the proposed method estimates those in the remaining stories with high accuracy. It can be pointed out that the damping force-interstory drift relation in the 12th story by THRA does not correspond well to the corresponding quadratic function. This is because the value of the damping coefficient drastically switches at the 12, 13th stories, and the contribution of the higher-mode responses is relatively large. However, the correspondence between the estimated value of the dissipated energy (area formed by quadratic function) and the dissipated energy by THRA is fairly good.

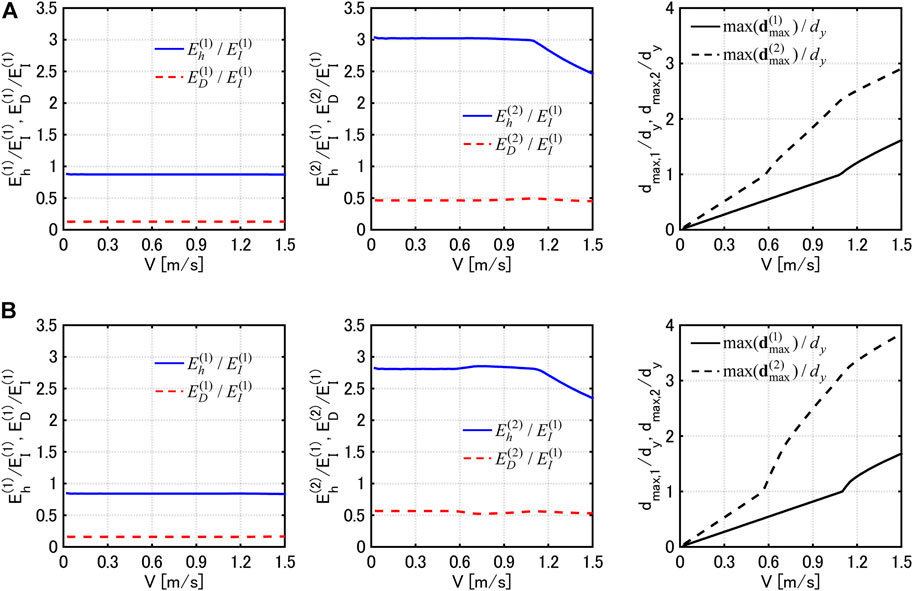
It should be noted that the proposed method estimates the maximum interstory drifts efficiently and stably. The total computational time by the proposed method is about 1/170 of that by THRA (time step increment: 0.001s, $0\le t\le 6\text{s}$). In addition, the repetition of the matrix multiplication and the convergence calculation due to the elastic-plastic responses are not required for the proposed method different from THRA.

Figure 13 shows $E_h^{\left(1\right)}/E_I^{\left(1\right)},E_D^{\left(1\right)}/E_I^{\left(1\right)},E_h^{\left(2\right)}/E_I^{\left(1\right)},E_D^{\left(2\right)}/E_I^{\left(1\right)}$ and the maximum interstory drifts for various input levels. As explained in Section 4.3, $E_h^{\left(1\right)},E_D^{\left(1\right)}$ are the total hysteretic energy and the total dissipated energy by viscous damping corresponding to ${\mathbf{d}}_{\max }^{\left(1\right)}$, and $E_h^{\left(2\right)},E_D^{\left(2\right)}$ are the total hysteretic energy and the total dissipated energy by viscous damping corresponding to ${\mathbf{d}}_{\max }^{\left(2\right)}$. Note that the input energy $E_I^{\left(1\right)}$ by the first impulse is proportional to $V^2$. It can be observed from Figure 13 that $E_h^{\left(1\right)}/E_I^{\left(1\right)},E_D^{\left(1\right)}/E_I^{\left(1\right)},E_D^{\left(2\right)}/E_I^{\left(1\right)}$ are almost constant regardless of $V$. On the other hand, due to the hysteretic energy dissipation after the first impulse, $E_h^{\left(2\right)}/E_I^{\left(1\right)}$ decreases within the range of $V\ge 1.1\text{m/s}$ for both models. However, this hysteretic energy dissipation is not large enough to reduce the maximum interstory drifts. Considering the plastic deformation concentration in specific stories, the interstory drifts may rather increase by yielding.

FIGURE 13

FIGURE 13. Comparison of $E_h^{\left(1\right)}/E_I^{\left(1\right)},E_D^{\left(1\right)}/E_I^{\left(1\right)},E_h^{\left(2\right)}/E_I^{\left(1\right)},E_D^{\left(2\right)}/E_I^{\left(1\right)}$ and maximum interstory drifts, (A) Model 1, (B) Model 2.

5.2 Maximum interstory drifts under corresponding one-cycle sine wave

Figure 14 shows the distributions of the maximum interstory drifts by THRA under the corresponding one-cycle sine wave with $V=0.3,0.6,0.9,1.2,1.5m/s$ and those evaluated by the proposed method.

FIGURE 14

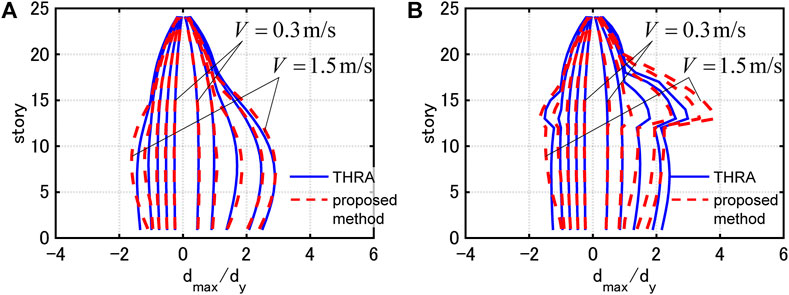
FIGURE 14. Maximum interstory drifts under corresponding one-cycle sine wave and those evaluated by proposed method, (A) Model 1, (B) Model 2.

In the case of Model 1, the maximum interstory drifts evaluated by the proposed method corresponds well to those evaluated by THRA for all the input levels. In the case of Model 2, the proposed method tends to overestimate the maximum interstory drifts in the 13–18th stories for larger input levels. This is because the non-proportionality of the damping distribution is strong and the correspondence between the critical PDI and the one-cycle sine wave gets worse. However, within the range where the plastic deformation ductility is less than 2, the maximum interstory drifts evaluated by the proposed method corresponds well to those evaluated by THRA.

5.3 Practical application of proposed method to elastic-plastic moment-resisting frame with viscous damper

In this section, the applicability of the proposed method to elastic-plastic moment resisting frames with viscous dampers is investigated. The transformation of moment frames into equivalent shear mass systems enables the application of the proposed method.

A 10-story 3-span planar moment-resisting frame is used. The details of the moment frame and the equivalent shear mass system with bilinear hysteresis are shown in the previous papers [Akehashi and Takewaki (2022b), Akehashi and Takewaki (2022c)]. The added damping coefficient $c_i$ of the equivalent shear mass system by viscous dampers in the ith story can be obtained by

$c_i={\displaystyle {\sum }_{j=1}^{N_B}{c}_{i,j}{\cos }^2{\theta }_{i,j}},(14)$

where $c_{i,j},{\theta }_{i,j}$ denote the damping coefficient of the viscous dampers at the jth bay in the ith story and the angle of the corresponding damper, and $N_B$ denotes the number of the bays.

Figure 15 shows the distribution of the added damping coefficients by the viscous dampers and the maximum interstory drifts of the moment frame and the equivalent shear mass system under the one-cycle sine wave, which corresponds to the critical PDI with $V=0.9[m/s]$. The dampers are allocated at the center bay in the 1-7th stories, and $\tan \theta =4/\left(7/2\right)=4/3.5$. It can be observed that the proposed method estimates the maximum interstory drifts of the frame with high accuracy.

FIGURE 15

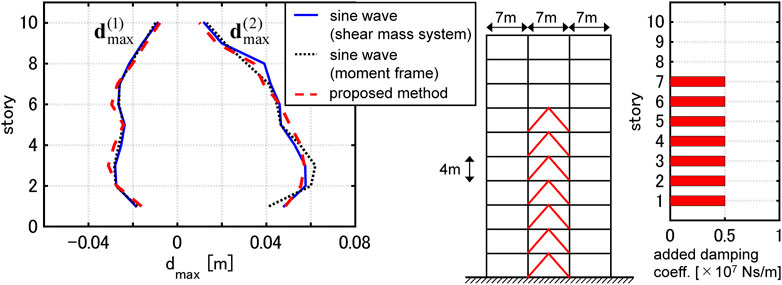
FIGURE 15. Maximum interstory drifts of moment-resisting frame and equivalent shear mass system under one-cycle sine wave and distribution of added damping coefficients.

6 Conclusion

A set of approximate closed-form solutions of the maximum interstory drifts under the critical pseudo-double impulse (PDI) was derived for non-proportionally damped multi-story shear building models with bilinear hysteresis. The main conclusions can be summarized as follows.

1) A set of approximate closed-form solutions of the maximum interstory drifts under the critical PDI was derived based on the energy balance law. While the damping was difficult to be treated in the previous paper, it was made possible to consider by extending an updated mode-controlled energy-based approach (UMEA) and introducing a quadratic function approximation of the damping force-interstory drift relation. It was demonstrated through numerical examples that the proposed method estimates the distributions of the maximum interstory drifts evaluated by the time-history response analysis (THRA) under the critical PDI. It was also demonstrated that, within the range where the plastic deformation ductility is less than 2, the maximum interstory drifts evaluated by the proposed method correspond well to those evaluated by THRA under the corresponding one-cycle sine wave.

2) The proposed method can be conducted efficiently and stably. The proposed method does not require the repetition of the matrix multiplication and the convergence calculation due to the elastic-plastic responses which are required in THRA.

3) The hysteretic energy dissipation is not large enough to reduce the maximum interstory drifts. Considering the plastic deformation concentration in specific stories, the interstory drifts may rather increase by yielding.

4) The proposed method developed for shear mass systems can estimate the maximum interstory drifts of elastic-plastic moment-resisting frames with viscous dampers under the resonant one-cycle sine wave with high accuracy.

The proposed method focuses on both the uncertainty of the input ground motion and the plastic deformation characteristics under the near-fault fling-step motions. Moreover, the proposed method can efficiently and stably estimate the critical maximum interstory drifts. Although the one-cycle sine wave substitutes well for the main part of the near-fault fling-step motions, it requires much computational load to find the critical resonant input period. By using the critical PDI, structural members and passive viscous dampers can be efficiently designed, and such design will be a resilient design because the uncertainty of the input ground motion is considered.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

HA formulated the problem, conducted the computation, and wrote the paper. IT supervised the research and wrote the paper.

Acknowledgments

Part of the present work is supported by the Grant-in-Aid for Scientific Research (KAKENHI) of Japan Society for the Promotion of Science (Nos. 18H01584 and JP20J20811). This support is greatly appreciated.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2022.964867/full#supplementary-material

Supplementary Data Sheet | Closed-form expressions on the maximum interstory drifts after the first impulse and the maximum interstory drifts after the second impulse.

References

Abbas, A. M., and Manohar, C. S. (2002). Investigations into critical earthquake load models within deterministic and probabilistic frameworks. Earthq. Eng. Struct. Dyn. 31 (4), 813–832. doi:10.1002/eqe.124

CrossRef Full Text | Google Scholar

Akehashi, H., Kojima, K., and Takewaki, I. (2018). Critical response of single-degree-of-freedom damped bilinear hysteretic system under double impulse as substitute for near-fault ground motion. Front. Built Environ. 4, 5. doi:10.3389/fbuil.2018.00005

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2020). Comparative investigation on optimal viscous damper placement for elastic-plastic MDOF structures: Transfer function amplitude or double impulse. Soil Dyn. Earthq. Eng. 130, 105987. doi:10.1016/j.soildyn.2019.105987

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2021). Pseudo-double impulse for simulating critical response of elastic-plastic MDOF model under near-fault earthquake ground motion. Soil Dyn. Earthq. Eng. 150, 106887. doi:10.1016/j.soildyn.2021.106887

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2022a). Bounding of earthquake response via critical double impulse for efficient optimal design of viscous dampers for elastic-plastic moment frames. Jpn. Archit. Rev. 5 (2), 131–149. doi:10.1002/2475-8876.12262

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2022b). Closed-form critical response of undamped bilinear hysteretic MDOF system under pseudo-double impulse for estimating resonant response under one-cycle sine wave. Soil Dyn. Earthq. Eng. 157, 107254. doi:10.1016/j.soildyn.2022.107254

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2022c). Inverse optimal damper placement via shear model for elastic–plastic moment-resisting frames under large-amplitude ground motions. Eng. Struct. 250, 113457. doi:10.1016/j.engstruct.2021.113457

CrossRef Full Text | Google Scholar

Akkar, S., Yazgan, U., and Gülkan, P. (2005). Drift estimates in frame buildings subjected to near-fault ground motions. J. Struct. Eng. 131 (7), 1014–1024. doi:10.1061/(asce)0733-9445(2005)131:7(1014)

CrossRef Full Text | Google Scholar

Au, S. K. (2006). Critical excitation of SDOF elasto-plastic systems. J. Sound. Vib. 296 (4-5), 714–733. doi:10.1016/j.jsv.2006.01.034

CrossRef Full Text | Google Scholar

Baker, J. W. (2007). Quantitative classification of near-fault ground motions using wavelet analysis. Bull. Seismol. Soc. Am. 97 (5), 1486–1501. doi:10.1785/0120060255

CrossRef Full Text | Google Scholar

Bertero, V. V., Mahin, S. A., and Herrera, R. A. (1978). Aseismic design implications of near-fault San Fernando earthquake records. Earthq. Eng. Struct. Dyn. 6 (1), 31–42. doi:10.1002/eqe.4290060105

CrossRef Full Text | Google Scholar

Bray, J. D., and Rodriguez-Marek, A. (2004). Characterization of forward-directivity ground motions in the near-fault region. Soil Dyn. Earthq. Eng. 24 (11), 815–828. doi:10.1016/j.soildyn.2004.05.001

CrossRef Full Text | Google Scholar

Caughey, T. K. (1960a). Random excitation of a system with bilinear hysteresis. J. Appl. Mech. 27 (4), 649–652. doi:10.1115/1.3644077

CrossRef Full Text | Google Scholar

Caughey, T. K. (1960b). Sinusoidal excitation of a system with bilinear hysteresis. J. Appl. Mech. 27 (4), 640–643. doi:10.1115/1.3644075

CrossRef Full Text | Google Scholar

Drenick, R. F. (1970). Model-free design of aseismic structures. J. Engrg. Mech. Div. 96 (4), 483–493. doi:10.1061/jmcea3.0001260

CrossRef Full Text | Google Scholar

Fang, C., Zhong, Q., Wang, W., Hu, S., and Qiu, C. (2018). Peak and residual responses of steel moment-resisting and braced frames under pulse-like near-fault earthquakes. Eng. Struct. 177, 579–597. doi:10.1016/j.engstruct.2018.10.013

CrossRef Full Text | Google Scholar

Hall, J. F., Heaton, T. H., Halling, M. W., and Wald, D. J. (1995). Near-source ground motion and its effects on flexible buildings. Earthq. Spectra 11, 569–605. doi:10.1193/1.1585828

CrossRef Full Text | Google Scholar

Hamidi, H., Karbassi, A., and Lestuzzi, P. (2020). Seismic response of RC buildings subjected to fling-step in the near-fault region. Struct. Concr. 21 (5), 1919–1937. doi:10.1002/suco.201900028

CrossRef Full Text | Google Scholar

Hayden, C. P., Bray, J. D., and Abrahamson, N. A. (2014). Selection of near-fault pulse motions. J. Geotech. Geoenviron. Eng. 140 (7), 04014030. doi:10.1061/(asce)gt.1943-5606.0001129

CrossRef Full Text | Google Scholar

He, W. L., and Agrawal, A. K. (2008). Analytical model of ground motion pulses for the design and assessment of seismic protective systems. J. Struct. Eng. (N. Y. N. Y). 134 (7), 1177–1188. doi:10.1061/(asce)0733-9445(2008)134:7(1177)

CrossRef Full Text | Google Scholar

Iwan, W. D. (1961). The dynamic response of bilinear hysteretic systems. Pasadena: Doctoral dissertation, California Institute of Technology.

Google Scholar

Iwan, W. D. (1965a). The dynamic response of the one-degree-of-freedom bilinear hysteretic system. New Zealand: Proc of the Third World Conf. on Earthquake Eng.

Google Scholar

Iwan, W. D. (1965b). The steady-state response of a two-degree-of-freedom bilinear hysteretic system. J. Appl. Mech. 32 (1), 151–156. doi:10.1115/1.3625711

CrossRef Full Text | Google Scholar

Iyengar, R. N., and Manohar, C. S. (1987). Nonstationary random critical seismic excitations. J. Eng. Mech. 113 (4), 529–541. doi:10.1061/(asce)0733-9399(1987)113:4(529)

CrossRef Full Text | Google Scholar

Jangid, R. S., and Kelly, J. M. (2001). Base isolation for near-fault motions. Earthq. Eng. Struct. Dyn. 30 (5), 691–707. doi:10.1002/eqe.31

CrossRef Full Text | Google Scholar

Kalkan, E., and Kunnath, S. K. (2006). Effects of fling step and forward directivity on seismic response of buildings. Earthq. Spectra 22 (2), 367–390. doi:10.1193/1.2192560

CrossRef Full Text | Google Scholar

Khaloo, A. R., Khosravi, H., and Jamnani, H. H. (2015). Nonlinear interstory drift contours for idealized forward directivity pulses using “modified fish-bone” models. Adv. Struct. Eng. 18 (5), 603–627. doi:10.1260/1369-4332.18.5.603

CrossRef Full Text | Google Scholar

Kojima, K., and Takewaki, I. (2015). Critical earthquake response of elastic-plastic structures under near-fault ground motions (Part 1: Fling-step input). Front. Built Environ. 1, 12. doi:10.3389/fbuil.2015.00012

CrossRef Full Text | Google Scholar

Makris, N., and Black, C. J. (2004). Dimensional analysis of rigid-plastic and elastoplastic structures under pulse-type excitations. J. Eng. Mech. 130 (9), 1006–1018. doi:10.1061/(asce)0733-9399(2004)130:9(1006)

CrossRef Full Text | Google Scholar

Malhotra, P. K. (1999). Response of buildings to near-field pulse-like ground motions. Earthq. Eng. Struct. Dyn. 28 (11), 1309–1326. doi:10.1002/(sici)1096-9845(199911)28:11<1309::aid-eqe868>3.0.co;2-u

CrossRef Full Text | Google Scholar

Mavroeidis, G. P., Dong, G., and Papageorgiou, A. S. (2004). Near-fault ground motions, and the response of elastic and inelastic single-degree-of-freedom (SDOF) systems. Earthq. Eng. Struct. Dyn. 33 (9), 1023–1049. doi:10.1002/eqe.391

CrossRef Full Text | Google Scholar

Mavroeidis, G. P., and Papageorgiou, A. S. (2003). A mathematical representation of near-fault ground motions. Bull. Seismol. Soc. Am. 93 (3), 1099–1131. doi:10.1785/0120020100

CrossRef Full Text | Google Scholar

Sasani, M., and Bertero, V. V. (2000). “Importance of severe pulse-type ground motions in performance-based engineering: Historical and critical,” in Proc. Of the 12th world conf. On earthq. Eng. (Upper Hutt, New Zealand: New Zealand Society for Earthq. Eng.).

Google Scholar

Shinozuka, M. (1970). Maximum structural response to seismic excitations. J. Engrg. Mech. Div. 96 (5), 729–738. doi:10.1061/jmcea3.0001284

CrossRef Full Text | Google Scholar

Takewaki, I. (2013). Critical excitation methods in earthquake engineering. Oxford: Butterworth-Heinemann.

Google Scholar

Vafaei, D., and Eskandari, R. (2015). Seismic response of mega buckling‐restrained braces subjected to fling-step and forward-directivity near-fault ground motions. Struct. Des. Tall Spec. Build. 24 (9), 672–686. doi:10.1002/tal.1205

CrossRef Full Text | Google Scholar

Yang, D., Pan, J., and Li, G. (2010). Interstory drift ratio of building structures subjected to near-fault ground motions based on generalized drift spectral analysis. Soil Dyn. Earthq. Eng. 30 (11), 1182–1197. doi:10.1016/j.soildyn.2010.04.026

CrossRef Full Text | Google Scholar